Предел степенной функции примеры решения: Как решать пределы со степенями, примеры

Предел показательно степенной функции, примеры нахождения

В процессе нахождения предела показательно-степенной функции типа limx→x0(f(x))g(x) часто работаем с такими степенными неопределенностями, как 1∞, 00, ∞0.

Для их раскрытия необходимо задействовать логарифмирование a=eln(a),  свойство логарифма a·ln(b)=ln(ba) и применение его предела заданной непрерывной функции, причем ее знак разрешено менять местами.

Для этого производятся преобразования вида:

limx→x0(f(x))g(x)=elnlimx→x0f(x))g(x)=elimx→x0(ln(f(x))g(x)=elimx→x0(g(x)ln(f(x)))==elimx→x0ln(f(x))1g(x)

Отсюда видно, что задание приводится к нахождению предела заданной функции вида elimx→x0ln(f(x))1g(x)=∞∞ или 00.

Данный случай рассматривает методы:

• непосредственного вычисления;
• использования правила Лопиталя;
• с заменой эквивалентных бесконечно малых функций;
• применение первого замечательного предела.

Для того, чтобы неопределенность была раскрыта, необходимо применять второй замечательный предел, при наличии 1∞.

Рассмотрим теорию на элементарных примерах заданий.

Пример 1

Найти предел заданной функции limx→0(x3+2x+1)32×3+x.

Решение

Для решения необходимо произвести подстановку. Получаем :

limx→0(x3+2x+1)32(x3+x)=(03+2·0+1)32(03+0)=1∞

Получение единицы в степени бесконечность называют неопределенностью, значит, необходимо решить другим методом.

Следует произвести преобразования данного предела. Получаем:

limx→0(x3+2x+1)32(x3+x)=elnlimx→0(x3+2x+1)32(x3+x)==elimx→0ln(x3+2x+1)32(x3+x)=elimx→03ln(x3+2x+1)2(x3+x)

Видим, что преобразование сводится к пределу  вида limx→03ln(x3+2x+1)2(x3+x).

Получаем

limx→03ln(x3+2x+12(x3+x)=00=32limx→0ln(x3+2x+1)x3+x==32limx→0x3+2xx3+x=32limx→0x2+2×2+1=32·02+202+1=3

Данные преобразования были выполнены при помощи применения замены логарифма на эквивалентную бесконечно малую функцию.

Тогда исходный предел принимает вид limx→0(x2+2x+1)32(x3+x)=e3.

Вычисление данного предела возможно с применением второго замечательного предела. Тогда получаем:

limx→0(x2+2x+1)32(x3+x)=limx→0(1+(x3+2x)1×3+2x(x3+2x)32(x3+x)==limx→0(1+(x3+2x))1×3+2×3(x3+2x)2(x3+x)=limx→01+(x3+2x))1×3+2×3(x2+2)2(x2+1)==limx→0(1+(x3+2x)1×3+2×3=e3

Ответ: e3.

Пример 2

Найти  и вычислить предел lim x→π2 (tgx)2 cos x

Решение

Если произведем подстановку, в результате получим ответ в виде бесконечности в степени ноль, а это является знаком, что необходимо применить другой метод для преобразования. Получаем:

lim x→π2 (tg x)2 cos x=∞0=elnlim x→π2(tg x)2cos x==e2lim x→π2(tg x)2cos x=elim x→π2(2cos x·ln·(tg x))==e2lim x→π2ln(tg x)1cos x

Отсюда видно, что решение сводится к переделу lim x→π2ln(tg x)1cos x=∞∞.

Для дальнейшего преобразования применим правило Лопиталя, так как получили неопределенность в виде частного бесконечностей.  Видим, что

lim x→π2ln(tg x)1cos x=∞∞=lim x→π2=ln(tg x)’1cos(x)’==lim x→π21tg (x)·1cos2 (x)sin (x)cos2(x)=lim x→π2cos (x)sin2(x)=cosπ2sin2π2=012=0

Отсюда следует, что пределом показательно-степенной функции является результат, полученный при вычислении. Имеем вы предел вида limx→π2(tg x)2cos x=e2·0=e0=1.

Ответ: 1.

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Предел степенной функции — Демидович

Теорема

Если p — вещественное число, то на всей области определения (x≥0) функции xp выполняется равнество:

x→a∈Rlim​xp=ap

Для бесконечного случая:

x→∞lim​xp=∞

Докажем полезную формулу, которую используем далее:

∣an−bn∣≥∣a−b∣n(a,b>0)

Сначала докажем, что если a>b>0, то

an−bn≥(a−b)n

Доказывать будем по методу математической индукции.

База индукции: n=1

a−b=a−b

Индукционный переход:

Пусть неравенство выполняется для какого-то натурального k:

ak−bk≥(a−b)k

Домножим обе части на положительную скобку (a−b):

ak+1−akb−abk+bk+1≥(a−b)k+1

Осталось только доказать, что

ak+1−bk+1>ak+1−akb−abk+bk+1

akb+abk>2bk+1

Так как a>b, то ak>bk и akb>bk+1. Поэтому неравенство выше можно усилить:

akb+abk>bk+1+abk>2bk+1

abk>bk+1

a>b

Итак, мы доказали, что

ak+1−bk+1>ak+1−akb−abk+bk+1≥(a−b)k+1ak+1−bk+1>(a−b)k+1

Индукционный переход доказан. Значит для любого натурального n при a>b>0 выполняется неравенство:

an−bn≥(a−b)n

■

---

Теперь докажем вариант этого неравенства с модулем. При этом, достаточно только потребовать a,b>0:

∣an−bn∣≥∣a−b∣n

По свойствам модуля (П-ссылка) внутри мы можем поменять местами слагаемые и сделать так, чтобы из большего вычиталось меньшее:

∣an−bn∣=∣bn−an∣∣a−b∣=∣b−a∣

Для определенности положим a>b. Но тогда an−bn>0 и a−b>0, а значит модули можно просто убрать и мы получим уже доказанное выше неравенство:

an−bn≥(a−b)n(a>b>0)

■

Теперь докажем, что функция nx​  (n∈N) имеет следующие пределы:

x→a∈Rlim​nx​=na​x→∞lim​nx​=∞

Начнем с левого предела. По определению, для любого данного ε>0 нужно найти такое δ>0, чтобы для любого x из δ-окрестности a значения функции попадали в ε-окрестность точки na​:

0<∣x−a∣<δ⇒∣nx​−na​∣<ε

Обе части последнего неравенства возведем в степень n:

∣nx​−na​∣n<εn

Усилим это неравенство с помощью уже доказанного в начале решения неравенства:

∣nx​−na​∣n≤∣x−a∣∣nx​n−na​n∣​​<εn

∣x−a∣<εn

Значит, за δ мы можем брать число εn.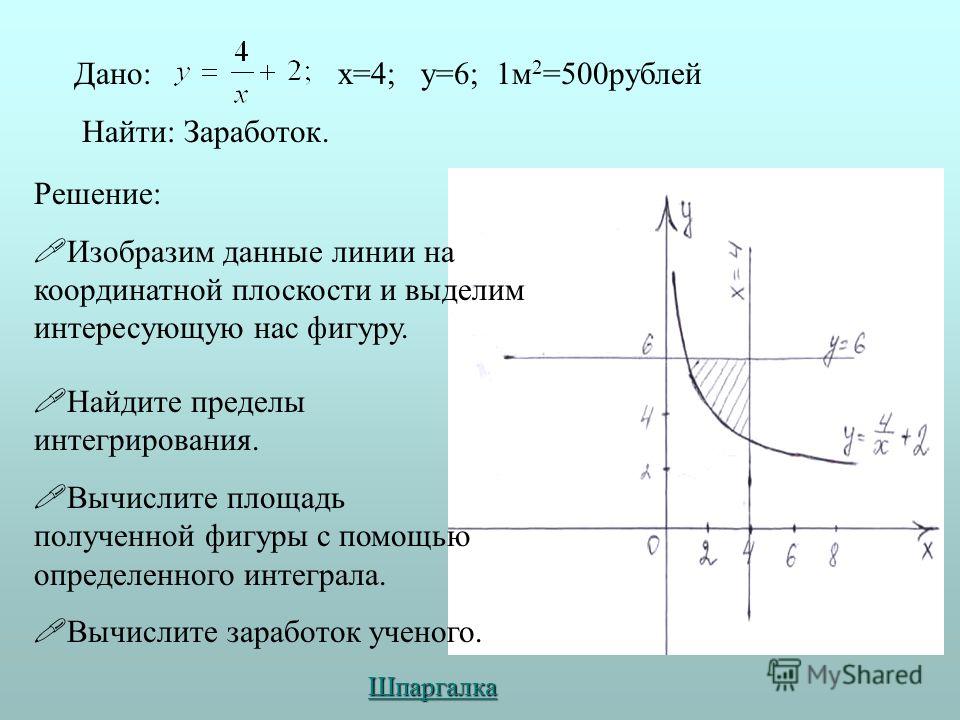 Тогда для любого такого x, что

0<∣x−a∣<δ=εn

возвращаясь обратно по цепочке преобразований, будет выполняться

∣nx​−na​∣<ε

Это по определению означает, что

x→a∈Rlim​nx​=na​

■

Доказательство при x→∞ еще проще. Пусть нам дана граница E>0. Нам нужно найти D>0, чтобы выполнялось следствие:

∣x∣>D⇒∣nx​∣>E

Обе части последнего неравенства возводим в степень n:

∣nx​∣n=∣nx​n∣=∣x∣>En

Значит, за D можно взять En.

Итак, для любого E мы берем D=En и тогда выполняются условия из определения предела. Это означает, что

x→∞lim​nx​=∞

■

---

Теперь проведем доказательство для рационального p.

Если p — рациональное число, его можно представить в виде:

p=nm​(m∈Z, n∈N)

Функцию xp можно представить следующим образом:

xp=xnm​=nxm​

Итак, нам нужно доказать, что

x→a∈Rlim​nxm​=nam​

Под знаком корня имеем степеную функцию с целым показателем. Это элементарный предел (П-ссылка), поэтому:

x→alim​xm=am

Более того, xm не равна am ни в одной пролотой окрестности точки a.

Все это позволяет нам воспользоваться теоремой о пределе сложной функции (П-ссылка):

x→alim​nxm​=y→b=amlim​ny​

Пользуясь уже доказанными пределами для корней степени n выше, получаем, что

x→alim​nxm​=y→b=amlim​ny​=nb​=nam​=ap

Для бесконечности действия аналогичные:

x→∞lim​nxm​=y→∞lim​ny​=∞

■

Исчисление I. Пределы в бесконечности, часть II

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Мобильное уведомление

Похоже, вы находитесь на устройстве с «узкой» шириной экрана ( т.е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 2.8: Пределы на бесконечности, часть II

В предыдущем разделе мы рассмотрели пределы на бесконечность многочленов и/или рациональные выражения, включающие многочлены. В этом разделе мы хотим взглянуть на некоторые другие типы функций, которые часто проявляются в пределах бесконечности. Функции, которые мы будем здесь рассматривать, — это экспоненты, натуральные логарифмы и арктангенсы. 9{-x}} = \infty\]

Суть этого примера заключалась в том, чтобы показать, что если показатель экспоненты стремится к бесконечности в пределе, то экспоненциальная функция также стремится к бесконечности в пределе. Точно так же, если экспонента стремится к минус бесконечности в пределе, тогда экспонента в пределе стремится к нулю.

Заметим также, что в последнем разделе значение предела не зависело от того, ушли ли мы в плюс или минус бесконечность. В приведенном выше примере мы уже видели, что изменение знака бесконечности может изменить ответ, поэтому не замыкайтесь на каких-либо предположениях, которые вы могли сделать из работы в предыдущем разделе! 9{ — 15x}}} \справа)\)

Показать все решения Скрыть все решения

Итак, единственная разница между этими двумя пределами заключается в том, что в первом мы берем предел, когда мы идем к плюс бесконечности, а во втором мы идем к минус бесконечности. К этому моменту мы смогли «повторно использовать» работу из первого ограничения, по крайней мере, в части второго ограничения. С экспонентами, которые часто не будут иметь место, мы собираемся рассматривать каждую из них как отдельные проблемы. 9{ — 15x}}} \right) = \infty — \infty + \infty + 0 — 0\]

Последние два термина не проблема (однако они будут в следующей части, понимаете?). Однако первые три представляют собой проблему, поскольку они представляют нам еще одну неопределенную форму.

При работе с многочленами мы выносим на множитель член с наибольшим показателем в нем. Давайте сделаем то же самое здесь. Однако теперь нам приходится иметь дело как с положительными, так и с отрицательными показателями, а также с тем, что мы подразумеваем под «самым большим» показателем. Имея дело с ними здесь, мы смотрим на термины, вызывающие проблемы, и спрашиваем: «Каков наибольший показатель степени в этих терминах?». Итак, поскольку проблемы вызывают только первые три члена ( 9{ — 25x}}} \справа)} \справа]\]

Обратите внимание, что при этом факторинге все оставшиеся экспоненты теперь имеют отрицательные показатели, и мы знаем, что для этого предела (, т. е. , уходящего в положительную бесконечность) все они будут равны нулю в пределе, и поэтому больше не будут вызывать проблем.

Теперь мы можем взять предел двух факторов. Первое — это явно бесконечность, а второе — конечное число (в данном случае — единица), поэтому раздел «Факты из бесконечных пределов» дает нам следующий предел: 9{ — 15x}}} \right)\) Показать решение

Давайте начнем так же, как и в первой части. Возьмем предел каждой из частей. На этот раз обратите внимание, что, поскольку наш предел стремится к отрицательной бесконечности, первые три экспоненты на самом деле стремятся к нулю (потому что их показатели степени стремятся к минус бесконечности в пределе). Последние две экспоненты в пределе уйдут в бесконечность (потому что их показатели в пределе уйдут в плюс бесконечность).

Получение пределов дает, 9{ — 15x}}} \right) = 0 — 0 + 0 + \infty — \infty \]

Таким образом, последние два члена являются здесь проблемой, поскольку они снова оставляют нас с неопределенной формой. { — 15x}}\). 9{ — 15x}}} \справа) = — \infty \]

Таким образом, при работе с суммами и/или разностями показательных функций мы ищем экспоненту с «самым большим» показателем и помним здесь, что «самый большой» означает показатель, наиболее удаленный от нуля. Также помните, что если мы смотрим на предел плюс бесконечность, только экспоненты с положительными показателями будут вызывать проблемы, поэтому это единственные условия, на которые мы обращаем внимание при определении наибольшего показателя. Точно так же, если мы смотрим на предел минус бесконечность, то только экспоненты с отрицательными показателями будут вызывать проблемы, и поэтому только они рассматриваются при определении наибольшего показателя.

Наконец, как вы могли догадаться из предыдущего примера, при работе с суммой и/или разностью экспонент все, что нам нужно сделать, это посмотреть на наибольшую экспоненту, чтобы определить поведение всего выражения. Опять же, помня, что если предел равен плюс бесконечности, мы рассматриваем экспоненты только с положительными показателями, а если мы смотрим на предел минус бесконечность, мы рассматриваем только экспоненты с отрицательными показателями.

Давайте теперь рассмотрим некоторые рациональные функции, включающие экспоненты. 9{ — x}}}}\) Показать решение

Основная концепция, связанная с решением этой задачи, такая же, как и с рациональными выражениями в предыдущем разделе. Мы смотрим на знаменатель и определяем экспоненциальную функцию с «наибольшей» степенью, которую мы затем выносим как из числителя, так и из знаменателя. Мы будем использовать те же рассуждения, что и в предыдущем примере, чтобы определить «наибольшую» экспоненту. В случае, когда мы рассматриваем предел плюс бесконечность, мы рассматриваем экспоненты только с положительными показателями. 9{ — x}}}}\) Показать решение

В этом случае мы собираемся минус бесконечность в пределе, поэтому мы будем смотреть на экспоненты в знаменателе с отрицательными показателями при определении «наибольшего» показателя. Однако в этой задаче есть только один, поэтому мы будем использовать его.

Опять же, не забывайте смотреть только на знаменатель. НЕ используйте экспоненту из числителя, даже если она «больше», чем экспонента в знаменателе. Мы всегда смотрим только на знаменатель, когда определяем, какой член вынести за скобки, независимо от того, что происходит в числителе. 9+ }} \ln x = — \infty \hspace{0,5 дюйма}\hspace{0,25 дюйма}\mathop {\lim }\limits_{x \to \infty} \ln x = \infty \]

Обратите внимание, что нам пришлось сделать правый предел для первого, так как мы не можем подставить отрицательные \(x\) в логарифм. Это означает, что нормального предела не будет, поскольку мы должны смотреть на \(x\) с обеих сторон рассматриваемой точки, а \(x\) слева от нуля отрицательны.

Из предыдущего примера видно, что если аргумент журнала (то, что мы берем из журнала) стремится к нулю справа ( т. е. всегда положительна), тогда журнал достигает отрицательной бесконечности в пределе, а если аргумент достигает бесконечности, то журнал также достигает бесконечности в пределе.

Заметьте также, что мы не можем смотреть на предел логарифма, когда \(x\) приближается к минус бесконечности, поскольку мы не можем подставлять отрицательные числа в логарифм.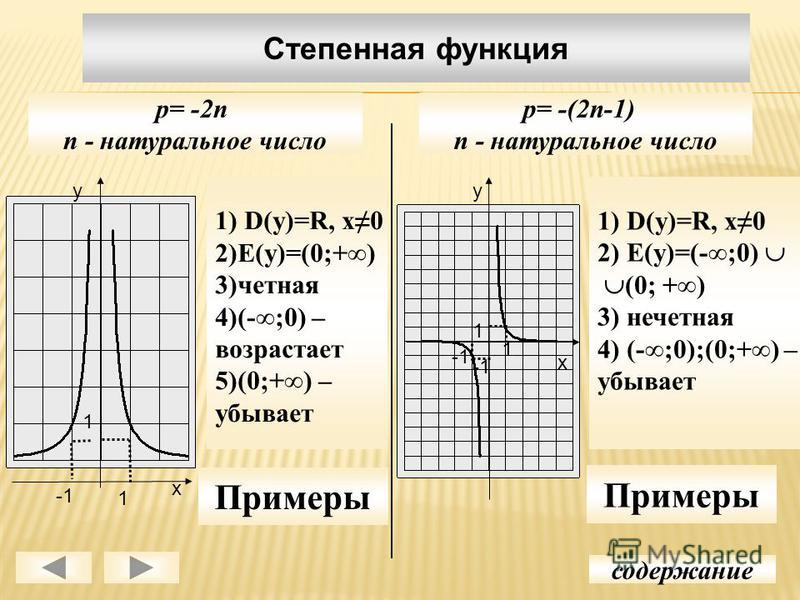 { — 1}}x\) Показать решение 9{ — 1}} \ влево ( {\ гидроразрыва {1} {x}} \ справа) = — \ гидроразрыва {\ пи {2} \]

Чтобы увидеть точное и математическое определение этого вида предела, см. раздел «Определение предела» в конце этой главы.

Предел экспоненциальной функции

В этой статье мы обсудим, как решать экспоненциальные функции, которые включают пределы. Но прежде чем обсуждать это, сначала давайте посмотрим, что такое экспоненциальная функция.

Что такое показательная функция?

Показательная функция — это функция, в которой независимая переменная, т. е. x, является показателем степени или степенью основания. Она имеет вид:

Здесь:

• а — положительное действительное число, не равное единице
• Область определения экспоненциальной функции — все действительные числа
• Диапазон экспоненциальной функции все положительные действительные числа
• Точка пересечения с y равна (0, 1), а горизонтальная асимптота y равна нулю

 

Лучшие репетиторы по математике

Поехали

Стандартные результаты пределов

Существует 5 стандартных результатов пределов, которые обсуждаются ниже. Эти стандартные результаты можно использовать в качестве формул при оценке пределов экспоненциальных функций.

Стандарт 1

   

Стандарт 2

   

Стандарт 3

     

Стандарт 4

1 0 3

11

   

В следующем разделе мы решим пару примеров, в которых будем оценивать пределы экспоненциальных функций

 

Пример 1

Оцените следующую экспоненциальную функцию:

   

3 учитывая, что предел функции должен оцениваться, когда x приближается к 0. Таким образом, когда мы ставим 0 непосредственно в приведенном выше выражении, мы получаем неопределенный вид . Следовательно, здесь мы будем использовать правило Лопиталя, которое гласит, что всякий раз, когда мы получаем неопределенную форму, мы можем взять производную числителя и знаменателя отдельно, а затем применить предел.

Итак, сначала продифференцируем числитель . Производная от первого члена равна . Аналогично, производная второго члена равна .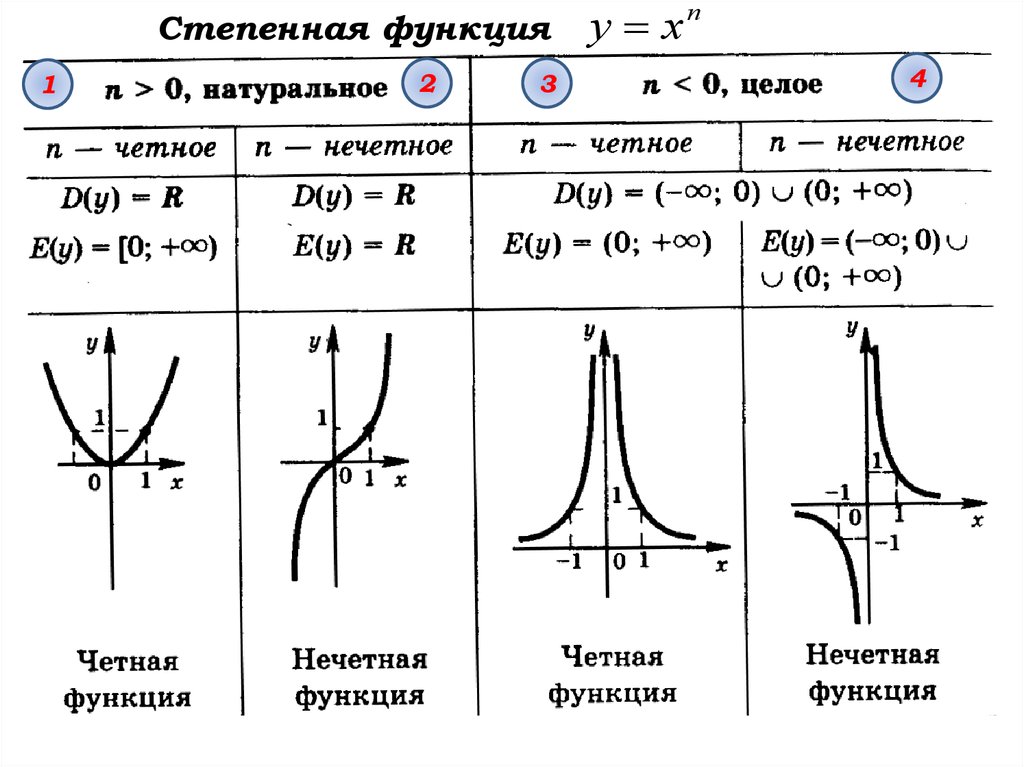

Теперь продифференцируем знаменатель. Производная x равна 1. Подставьте эти производные в приведенную выше функцию следующим образом:

   

Теперь примените ограничение к приведенному выше выражению, как показано ниже:

   

5 0

90 Пример 2 Оцените следующее выражение: 9{4x}. Производная от первого члена равна . Аналогично, производная второго члена равна .

Теперь продифференцируем знаменатель. Производная от первого члена равна . Аналогично, производная второго члена равна .

Подставьте эти производные в приведенное выше выражение следующим образом:

   

Теперь примените ограничение к приведенному выше выражению, как показано ниже:0004 Оцените предел следующей экспоненциальной функции:

   

Решение

Дано, что предел функции должен оцениваться, когда x приближается к 0. Итак, когда мы подставляем 0 непосредственно в приведенное выше выражение, мы получаем неопределенная форма. Следовательно, здесь мы будем использовать правило Лопиталя, которое гласит, что всякий раз, когда мы получаем неопределенную форму, мы можем взять производную числителя и знаменателя отдельно, а затем применить предел.

Сначала найдем производную от числителя, которая равна . Он равен . Производная знаменателя равна 2. Мы подставим эти значения в исходную функцию, как показано ниже:

Теперь мы возьмем предел выражения:

Пример 4

Оценить предел следующей экспоненциальной функции:

Решение

. Проще оценить выше потому что после подстановки мы не получим неопределенную форму или . Таким образом, в этом примере нет необходимости применять правило Лопиталя.

   

Пример 5

Оцените следующее выражение:

   

Решение

В этом примере, если мы подставим x = 2 непосредственно в вышеприведенное выражение, мы не получим неопределенную форму, поэтому правило Лопиталя неприменимо.