Графики тригонометрических функций и их преобразования
Похожие презентации:
Графики тригонометрических функций и их свойства
Графики тригонометрических функций
Графики тригонометрических функций и их свойства
Формулы приведения
Тригонометрические функции, их свойства и графики
Тригонометрия. Тригонометрические функции двойного аргумента
Графики тригонометрических функций и их свойства
Тригонометрические функции, их свойства и графики
Тригонометрические функции, их свойства и графики
Тригонометрические функции
Графики тригонометрических функций и
их свойства
Функция у = sin x, ее свойства
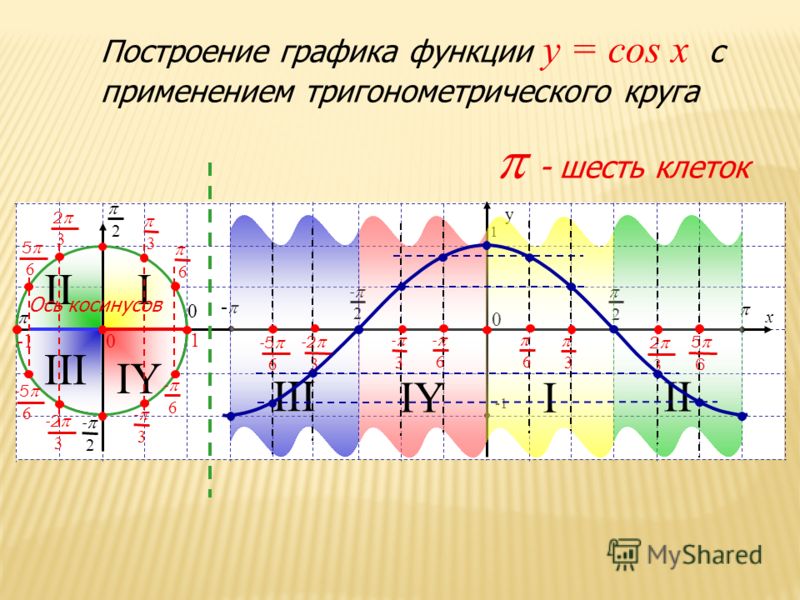
Функция у = cos x
Преобразование графиков тригонометрических функций путем
параллельного переноса
Преобразование графиков тригонометрических функций путем
сжатия и расширения
Преобразование графиков тригонометрических функций путем
зеркального отражения относительно оси абсцисс
Построение графика функции гармонических колебаний
Построение графика y=sin x с помощью числового круга
1
Функция y=sin x и ее свойства
y
y=sin x
1
-2π
-3π/2
-π
-π/2
0
π/2
π
3π/2
2π
x
-1
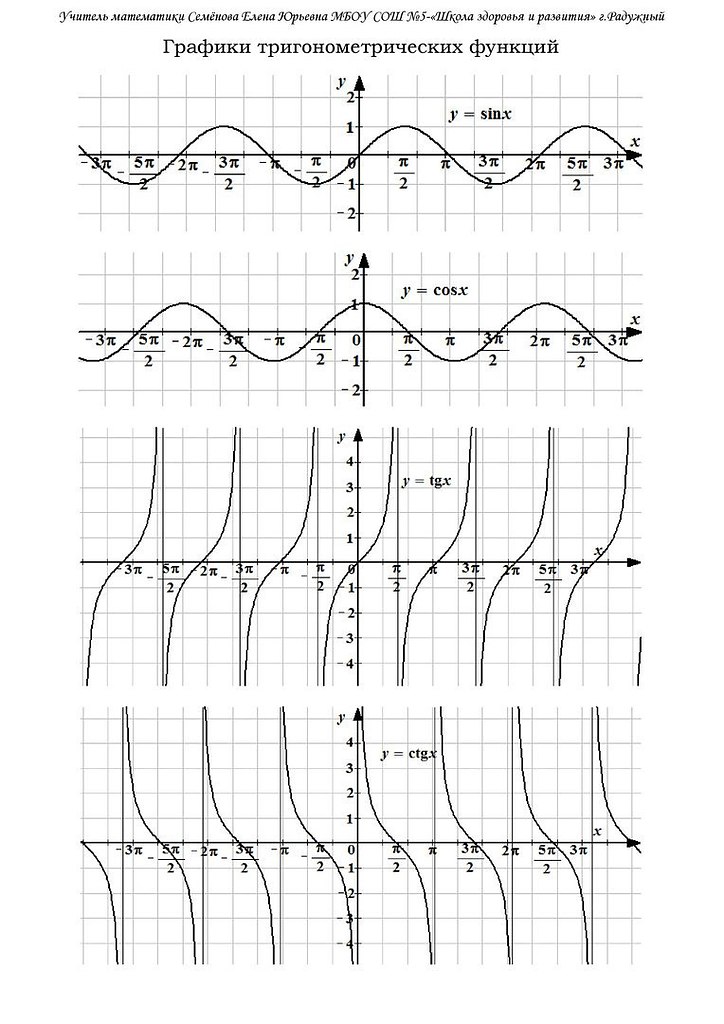
Графиком функции y=sin x является синусоида
Свойства функции:
1.
 D(y) =R
D(y) =R2. Периодическая (Т=2p)
3. Нечетная (sin(-x)=-sin x)
4. Нули функции:
у=0, sin x=0 при х = pn, n Z
2
y
1
-2π
-3π/2
-π
-π/2
0
y=sin x
π/2
π
3π/2
2π
x
-1
5. Промежутки знакопостоянства:
У>0 при х (0+2pn; p+2pn), n Z
У<0 при x (-p+2pn; 0+2pn), n Z
y
y=sin x
1
-2π
-3π/2
-π
-π/2
0
π/2
π
3π/2
2π
x
-1
6. Промежутки монотонности:
функция возрастает на промежутках
вида: [-p/2+2pn; p/2+2pn], n Z
функция убывает на промежутках
вида: [p/2+2pn; 3p/2+2pn], n Z
3
y
xмах
-2π
-3π/2
1
-π
-π/2
0
y=sin x
xмах
π/2
π
3π/2
2π
x
-1
xmin
xmin
7. Точки экстремума:
Хмах= p/2 +2pn, n Z
Хмin= -p/2 +2pn, n Z
4
Функция y=cos x
y
y=cos x
1
-3π/2
-π
-π/2
0
π/2
π
3π/2
x
-1
Графиком функции у = cos x является косинусоида
sin(x+p/2)=cos x
5
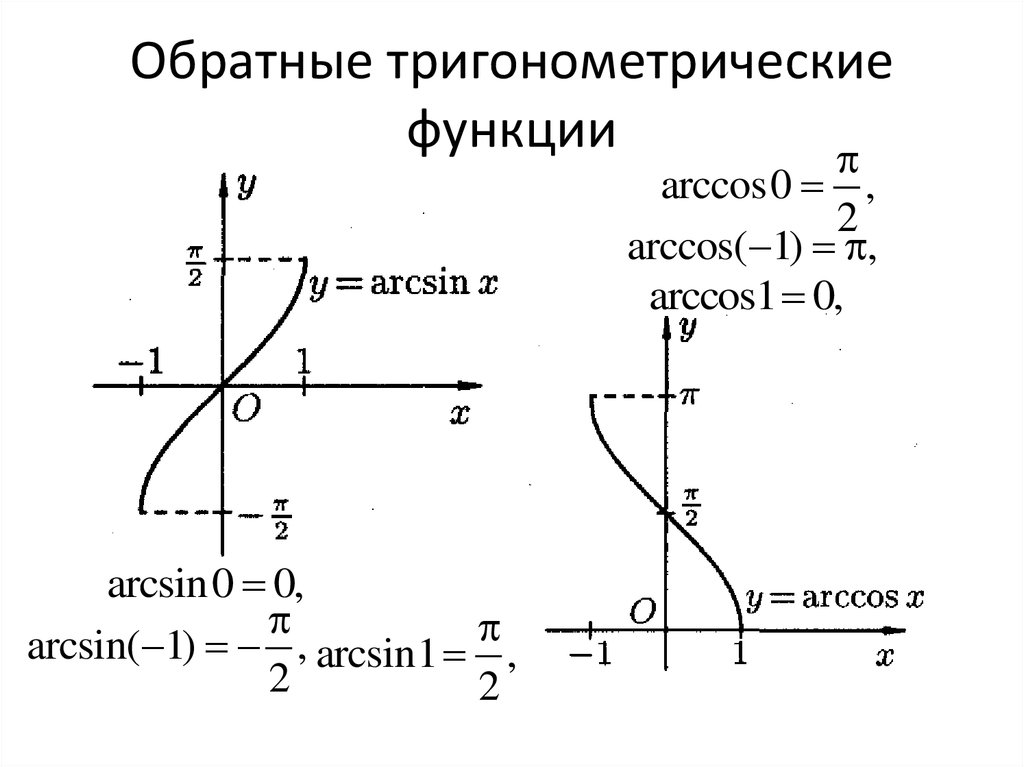
Свойства функции y=cos x
1.
2.
3.
4.
D(y) =R
Периодическая Т=2p
Четная
cos(-x)=cos x
Нули функции:
у=0, cos x=0 при х = 1/2pn, n Z
5. Промежутки знакопостоянства:
У>0 при х (-p/2+2pn; p/2+2pn), n Z
У<0 при x (p/2+2pn; 3p/2+2pn), n Z
6. Промежутки монотонности:
функция возрастает на промежутках вида:
[p+2pn; 2p+2pn], n Z
функция убывает на промежутках вида:
[0+2pn; p+2pn], n Z
7. Точки экстремума:
Хмin = p +2pn, n Z
6
Преобразование графиков
тригонометрических функций путем
параллельного переноса
График функции у = f (x+в) получается из графика функции
у = f(x) параллельным переносом на (-в) единиц вдоль оси абсцисс
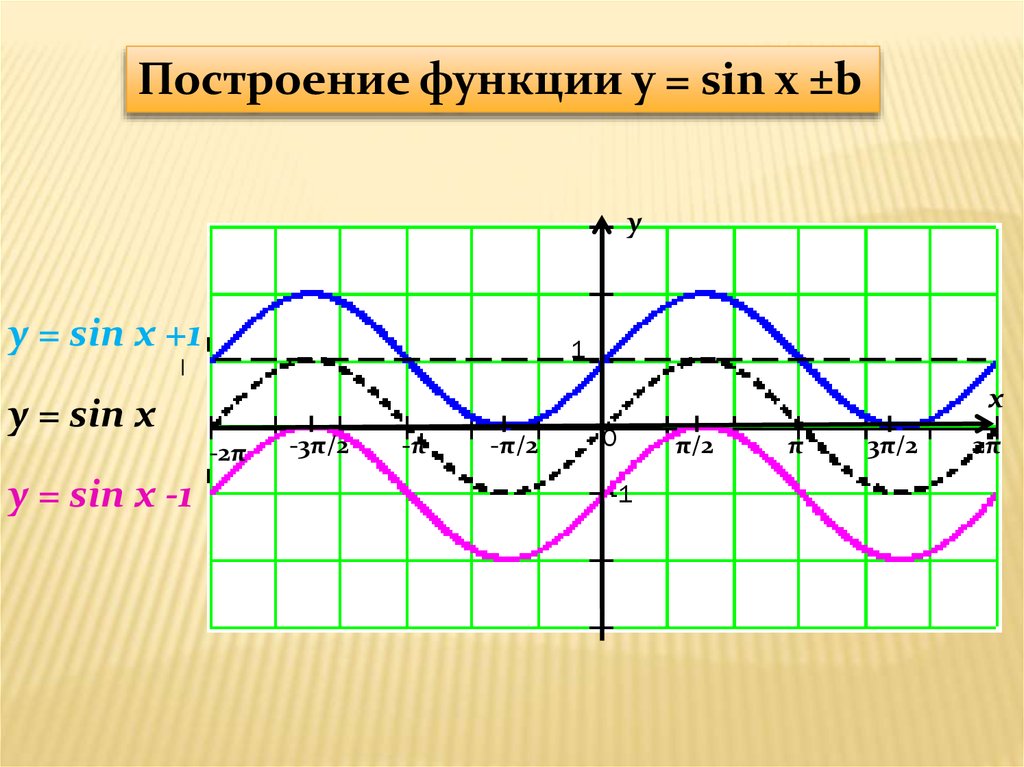
График функции у = f (x)+а получается из графика функции у = f(x)
параллельным переносом на (а) единиц вдоль оси ординат
7
Построение графика функции y=sin(x+π/4) путем перемещения
графика y=sin(x) влево по оси абсцисс на расстояние π/4
y
x
y=siny=sin
(x+ π/4)
1
-2π
-3π/2
-π
π/2
-π/2
-π/4
0
π
3π/2
2π
x
-1
8
Построение графика функции y=sinx+π путем параллельного
переноса графика y=sin(x) на расстояние π единиц вдоль оси ординат
y
4
y=sin x+π
3,14
3
2
y=sin x
1
-2π
-3π/2
-π
-π/2
0
π/2
π
3π/2
2π
x
-1
9
Преобразование графиков
тригонометрических функций путем
сжатия и растяжения
График функции у =k f (x) получается из графика функции у = f(x)
путем его растяжения в k раз (при k>1) вдоль оси ординат
График функции у = k f (x) получается из графика функции у = f(x)
путем его сжатия в k раз (при 0<k<1) вдоль оси ординат
10
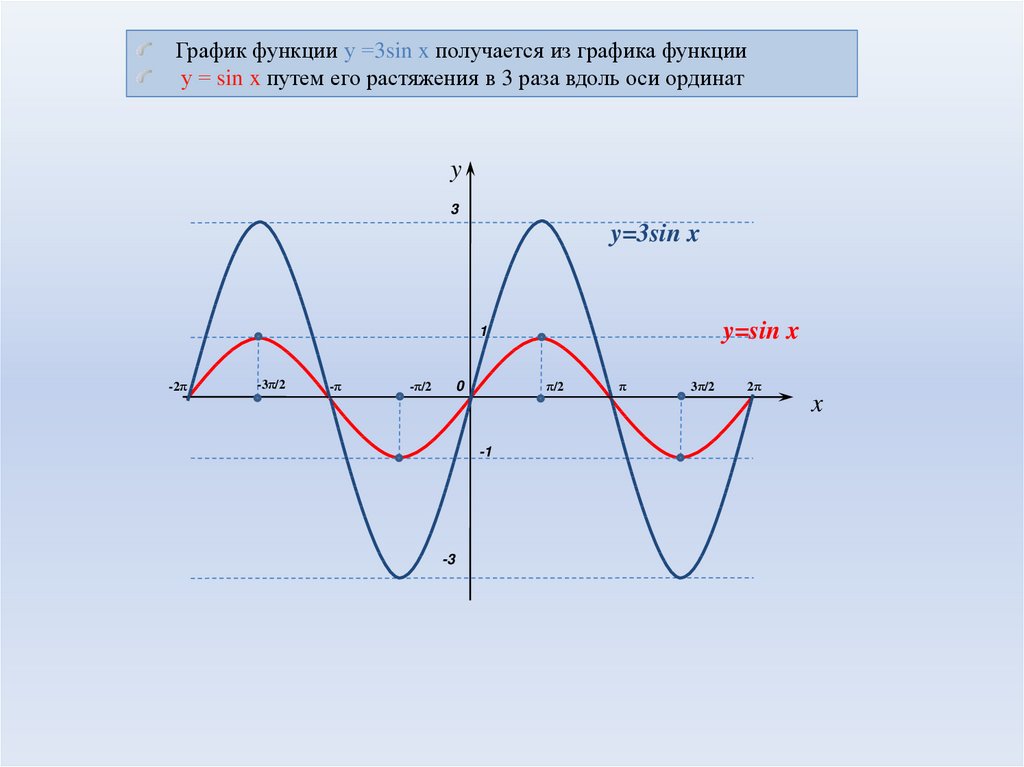
График функции у =3sin x получается из графика функции
у = sin x путем его растяжения в 3 раза вдоль оси ординат
y
3
y=3sin x
y=sin x
1
-2π
-3π/2
-π
π/2
0
-π/2
π
3π/2
2π
x
-1
-3
11
График функции у =0.
 5 sin x получается из графика функции
5 sin x получается из графика функцииу = sin x путем его сжатия в 2 раза вдоль оси ординат
y
y=sin x
y=0.5 sin x
1
0.5
-2π
-3π/2
-π
π/2
-π/2
0
π
3π/2
2π
x
-0.5
-1
12
Преобразование графиков
тригонометрических функций путем
График функции у = f (kx) получается из графика функции
у = f(x) путем его сжатия в k раз (при k>1) вдоль оси абсцисс
График функции у = f (kx) получается из графика функции
у = f(x) путем его растяжения в k раз (при 0<k<1) вдоль оси абсцисс
13
График функции у = cos (0.5x) получается из графика функции у = cos x
путем его растяжения в 2 раза (0<k<1) вдоль оси абсцисс
y
T=2π
y=cos x
1
y=cos 0.5 x
-2π
-3π/2
-π
-π/2
0
π/2
π
3π/2
2π
x
-1
T=4π
Видно, что период (T) функции увеличился в 2 раза, т.к. T = 2 π/ω,
где ω – коэффициент при переменной x (частота колебаний)
14
График функции у = cos 2x получается из графика функции
путем его сжатия в 2 раза (k>1) вдоль оси абсцисс
у = cos x
y
T = 2 πT = 2 π
-2π
-3π/2
-π
-π/2
0
π/2
y=cos x
y=cos 2 x
1
π
3π/2
2π
x
-1
Видно, что период (T) функции уменьшился в 2 раза, т.
 к. T = 2 π/ω,
к. T = 2 π/ω,где ω – коэффициент при переменной x (частота колебаний)
15
Преобразование графиков
тригонометрических функций путем
зеркального отражения относительно
оси абсцисс
Графики функций у = -f (kx) и у=-k f(x) получаются из графиков
функций у = f(kx) и y= k f(x) соответственно путем их зеркального
отображения относительно оси абсцисс
синус – функция нечетная, поэтому sin(-kx) = — sin (kx)
косинус –функция четная, значит cos(-kx) = cos(kx)
16
Графики функций y = -3sin x получается из графика функции y = 3sin x
путем ее зеркального отображения относительно оси абсцисс
y
3
y=-3sin x
1
-2π
-3π/2
-π
-π/2
π/2
0
π
3π/2
2π
x
-1
y=3sin x
-3
17
Графики функций y = -2cos x получается из графика функции
y
y=2cos x
1
-2π
-3π/2
-π
-π/2
0
π/2
π
3π/2
x
2π
-1
y=-2cos x
18
Построение графика функции гармонических колебаний
y=A sin(ωx+φ0)
Для примера строим график функции y=3 sin (2x+π/3).
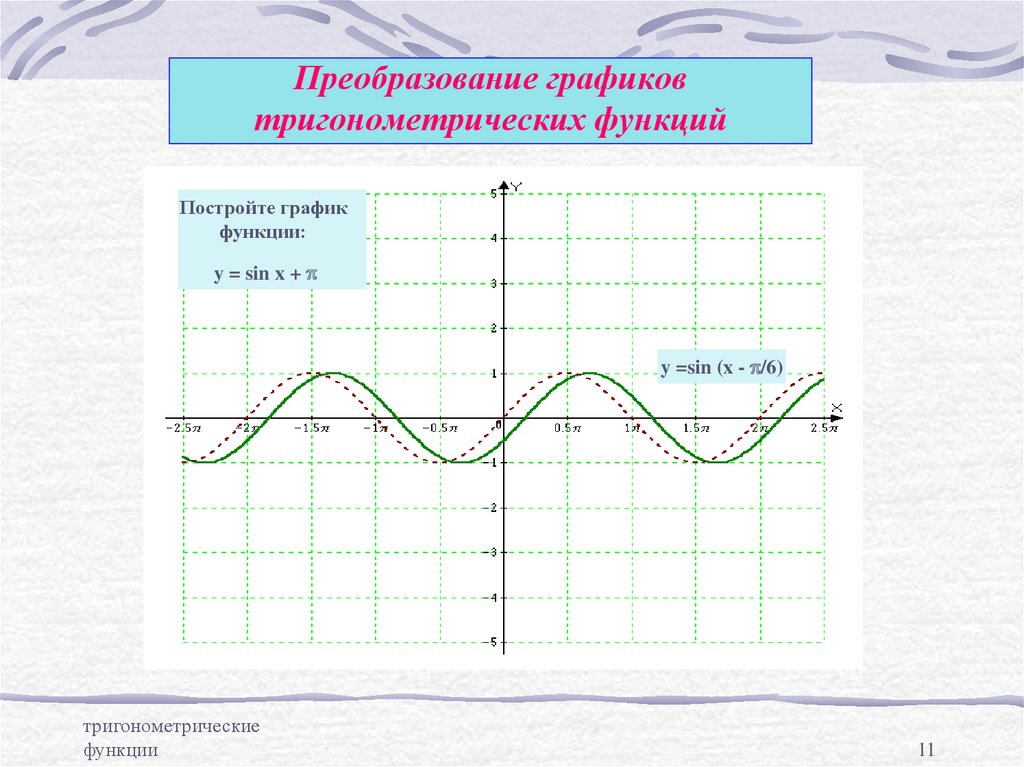
Здесь амплитуда колебаний А равняется 3 единицам,
круговая частота колебаний ω равна 2,
а начальная фаза колебаний φ0 равна π/3, т.е.:
A=3, ω=2 и φ0= π/3. Период колебаний T=2π/ω.
19
Последовательность построения графика функции y=3 sin (2x+π/3)
y
3
2
y=3 sin (2x+ π/3)
x
y=siny=sin
(x+ π/3)
y=sin (2x+ π/3)
1
-2π
-3π/2
-π
π/2
-π/2
-π/3
0
π
3π/2
2π
x
-1
-2
-3
Строим исходный график функции y= sin x
Используя параллельный перенос сдвигаем график функции y= sin x
влево по оси абсцисс на расстояние π/3
Сжимаем график функции y= sin (x+π/3) в 2 раза по оси абсцисс
Растягиваем график функции y= sin (2x+π/3) в 3 раза по оси ординат
20
Построение графика y=sin x с помощью числового круга
y
2π/3
π/2
π/3
3π/4
π/4
π/6
5π/6
II
π
I
0
2π
IV
III
7π/6
0
7π/6
π/6
π/4
π/3
π/2
2π/3
3π/4
5π/6
5π/4
4π/3
3π/2
5π/3
7π/4
11π/6
2π
π
x
11π/6
7π/4
5π/4
5π/3
4π/3
3π/2
21
English Русский Правила
Тригонометрические функции, их графики
Урок 22.
 Подготовка к ЕГЭ по математике
Подготовка к ЕГЭ по математикеВ данном видеоуроке мы напомним, какие функции называют тригонометрическими. Повторим свойства каждой функции и их графики.
Конспект урока «Тригонометрические функции, их графики»
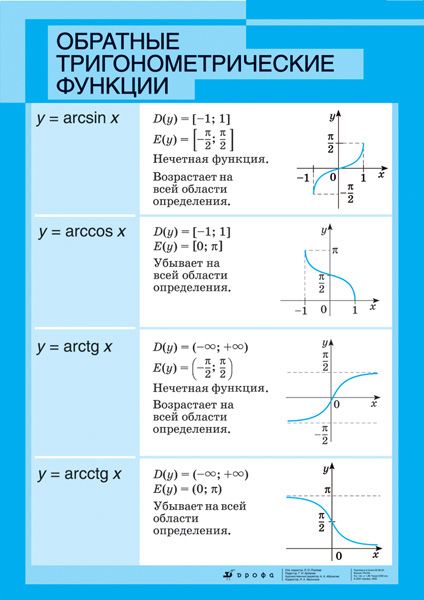
Напомним, что функции , , и называются
Итак, рассмотрим функцию .
Областью определения этой функции является множество всех действительных чисел, областью значений – промежуток .
Функция является нечётной, график симметричен относительно начала координат.
Функция периодическая с периодом , то есть .
Точки пересечения графика с осями координат:
с осью абсцисс из , то есть точка пересечения имеет координаты ;
с осью ординат из , то есть точка пересечения имеет координаты .
для ;
для
.
Функция возрастает на промежутке ;
убывает на промежутке .
Функция достигает наибольшего значения при ;
наименьшего значения при .
Рассмотрим функцию .
Областью определения этой функции является множество всех действительных чисел, областью значений – промежуток .
Функция является чётной, график симметричен относительно оси ординат.
Функция периодическая с периодом , то есть .
Точки пересечения графика с осями координат:
с осью абсцисс из , то есть точка пересечения имеет координаты ;
с осью ординат из , то есть точка пересечения имеет координаты .
для ;
для .
Функция возрастает на промежутке ;
убывает на промежутке .
Функция достигает наибольшего значения при ;
наименьшего
значения при
.
Рассмотрим функцию .
Областью определения этой функции является множество всех действительных чисел, кроме точек вида , ;
Функция является нечётной, график симметричен относительно начала координат.
Функция периодическая с периодом , то есть .
Точки пересечения графика с осями координат:
с осью абсцисс из , то есть точка пересечения имеет координаты ;
с осью ординат из , то есть точка пересечения имеет координаты .
для ;
для .
Функция возрастает на каждом промежутке области определения.
Функция не имеет наибольшего и наименьшего значений.
Рассмотрим функцию .
Областью
определения этой функции является множество всех
действительных чисел, кроме точек вида ,
;
областью значений – множество всех действительных чисел.
Функция является нечётной, график симметричен относительно начала координат. Функция периодическая с периодом , то есть .
Точки пересечения графика с осями координат:
с осью абсцисс из из , то есть точка пересечения имеет координаты ;
с осью ординат график функции точек пересечения не имеет, так как при функция не определена.
для ;
для .
Функция убывает на каждом промежутке области определения.
Функция не имеет наибольшего и наименьшего значений.
Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.
Задание первое. Найдите наибольшее значение функции, заданной формулой .
Решение.
Задание второе. Найдите наименьшее значение функции .
Решение.
Задание
третье. Вычислите период функции в
градусах.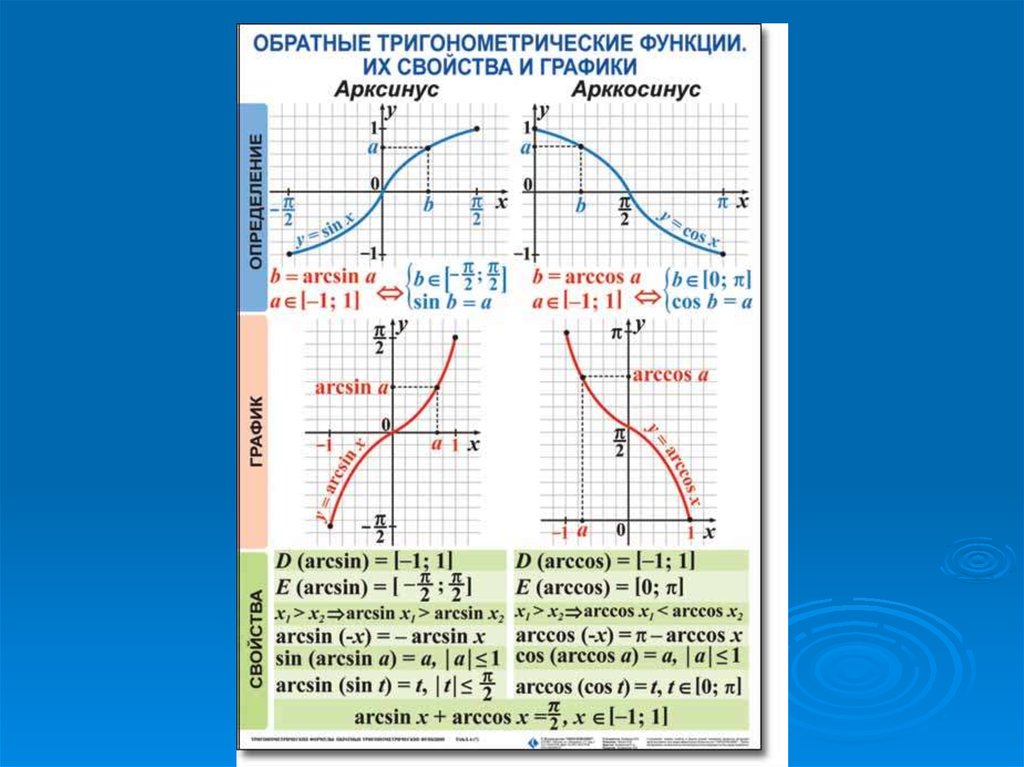
Решение.
Задание четвёртое. Установите чётность или нечётность функций:
а) , б) .
Решение.
Предыдущий урок 21 Элементарное исследование функций
Следующий урок 23 Показательная функция, её график. Логарифмическая функция, её график
Получите полный комплект видеоуроков, тестов и презентаций Подготовка к ЕГЭ по математике
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
Математические и тригонометрические функции (справочник)
Чтобы получить подробную информацию о функции, щелкните ее имя в первом столбце.
Примечание. Маркеры версии указывают версию Excel, в которой была введена функция. Эти функции недоступны в более ранних версиях. Например, маркер версии 2013 указывает, что эта функция доступна в Excel 2013 и всех более поздних версиях.
Функция | Описание |
Функция АБС | Возвращает абсолютное значение числа |
Функция ACOS | Возвращает арккосинус числа |
Функция АКОШ | Возвращает аркгиперболический косинус числа |
функция ACOT | Возвращает арккотангенс числа |
Функция ACOTH | Возвращает гиперболический арккотангенс числа |
АГРЕГАТ функция | Возвращает агрегат в списке или базе данных |
АРАБСКАЯ функция | Преобразует римское число в арабское как число . |
ASIN-функция | Возвращает арксинус числа 9.0003 |
функция АСИНХ | Возвращает аркгиперболический синус числа |
Функция АТАН | Возвращает арктангенс числа |
Функция АТАН2 | Возвращает арктангенс из координат x и y |
функция АТАНХ | Возвращает аркгиперболический тангенс числа |
БАЗОВАЯ функция | Преобразует число в текстовое представление с заданным основанием (основанием) |
ПОТОЛОК функция | Округляет число до ближайшего целого числа или до ближайшего кратного значения |
ПОТОЛОК. | Округляет число до ближайшего целого числа или до ближайшего кратного значения |
ПОТОЛОК.ТОЧНАЯ функция | Округляет число до ближайшего целого числа или до ближайшего кратного значения. Независимо от знака числа, оно округляется в большую сторону. |
КОМБИНИРОВАННАЯ функция | Возвращает количество комбинаций для заданного количества объектов |
КОМБИНА функция | Возвращает количество комбинаций с повторениями для заданного количества элементов |
Функция COS | Возвращает косинус числа |
Функция КОШ | Возвращает гиперболический косинус числа |
СОТ-функция | Возвращает котангенс угла |
Функция COTH | Возвращает гиперболический котангенс числа |
CSC-функция | Возвращает косеканс угла |
Функция CSCH | Возвращает гиперболический косеканс угла |
ДЕСЯТИЧНАЯ функция | Преобразует текстовое представление числа с заданной системой счисления в десятичное число |
ГРАДУСЫ функция | Преобразует радианы в градусы |
ДАЖЕ функция | Округляет число до ближайшего четного целого числа |
EXP-функция | Возвращает e в степени данного числа |
функция ФАКТ | Возвращает факториал числа |
Функция FACTDOUBLE | Возвращает двойной факториал числа |
Функция ЭТАЖ | Округляет число вниз до нуля |
ЭТАЖ. | Округляет число в меньшую сторону до ближайшего целого числа или до ближайшего кратного значения |
ПОЛ.ТОЧНАЯ функция | Округляет число в меньшую сторону до ближайшего целого числа или до ближайшего кратного значения. Независимо от знака числа, число округляется в меньшую сторону. |
НОД функция | Возвращает наибольший общий делитель |
Функция INT | Округляет число в меньшую сторону до ближайшего целого числа |
Функция ISO. | Возвращает число, округленное до ближайшего целого числа или до ближайшего кратного значимости 9.0003 |
LCM-функция | Возвращает наименьшее общее кратное |
LN функция | Возвращает натуральный логарифм числа |
Функция журнала | Возвращает логарифм числа по указанному основанию |
функция ЛОГ10 | Возвращает логарифм числа по основанию 10. |
функция МОПРЕМ. | Возвращает определитель матрицы массива |
МИНВЕРС функция | Возвращает матрицу, обратную массиву |
МУЛЬТИФУНКЦИЯ | Возвращает матричное произведение двух массивов |
МОД функция | Возвращает остаток от деления |
Функция ОКРУГЛ | Возвращает число, округленное до нужного кратного |
МУЛЬТИНОМНАЯ функция | Возвращает многочлен набора чисел |
Функция МУНИТ | Возвращает единичную матрицу или указанное измерение |
НЕЧЕТНАЯ функция | Округляет число до ближайшего нечетного целого числа |
ПИ-функция | Возвращает значение числа пи |
Функция МОЩНОСТИ | Возвращает результат возведения числа в степень 9. |
ПРОДУКТ функция | Умножает свои аргументы |
ЧАСТНОЕфункция | Возвращает целую часть деления |
РАДИАНЫ функция | Преобразует градусы в радианы |
СЛУЧАЙ функция | Возвращает случайное число от 0 до 1 |
Функция СЛУЧАЙ | Возвращает массив случайных чисел от 0 до 1. |
СЛУЧМЕЖДУ функция | Возвращает случайное число между указанными вами числами |
РИМСКАЯ функция | Преобразует арабские цифры в римские как текст |
ОКРУГЛ функция | Округляет число до указанного количества цифр |
Функция ОКРУГЛВНИЗ | Округляет число вниз до нуля |
Функция ОКРУГЛВВЕРХ | Округление числа от нуля до нуля |
функция СЕК | Возвращает секанс угла |
функция SECH | Возвращает гиперболический секанс угла |
Функция РЯДСУММ | Возвращает сумму степенного ряда по формуле |
ЗНАК функция | Возвращает знак числа |
SIN-функция | Возвращает синус заданного угла |
функция SINH | Возвращает гиперболический синус числа |
Функция КОРЕНЬ | Возвращает положительный квадратный корень |
Функция SQRTPI | Возвращает квадратный корень из (число * пи) |
ПРОМЕЖУТОЧНЫЙ ИТОГ функция | Возвращает промежуточный итог в списке или базе данных |
Функция СУММ | Добавляет свои аргументы |
Функция СУММЕСЛИ | Добавляет ячейки, указанные по заданным критериям |
Функция СУММЕСЛИМН | Добавляет ячейки в диапазон, отвечающие нескольким критериям |
Функция СУММПРОИЗВ | Возвращает сумму произведений соответствующих компонентов массива |
Функция СУММСК | Возвращает сумму квадратов аргументов |
Функция СУММ2М22 | Возвращает сумму разности квадратов соответствующих значений в двух массивах |
Функция СУММ2PY2 | Возвращает сумму суммы квадратов соответствующих значений в двух массивах |
Функция СУММММГ2 | Возвращает сумму квадратов разностей соответствующих значений в двух массивах |
Функция ТАН | Возвращает тангенс числа |
Функция СГАН | Возвращает гиперболический тангенс числа |
функция ОБРЕЗ | Усекает число до целого числа |
Важно: Результаты расчетов формул и некоторых функций рабочего листа Excel могут немного отличаться на ПК с Windows с архитектурой x86 или x86-64 и ПК с Windows RT с архитектурой ARM.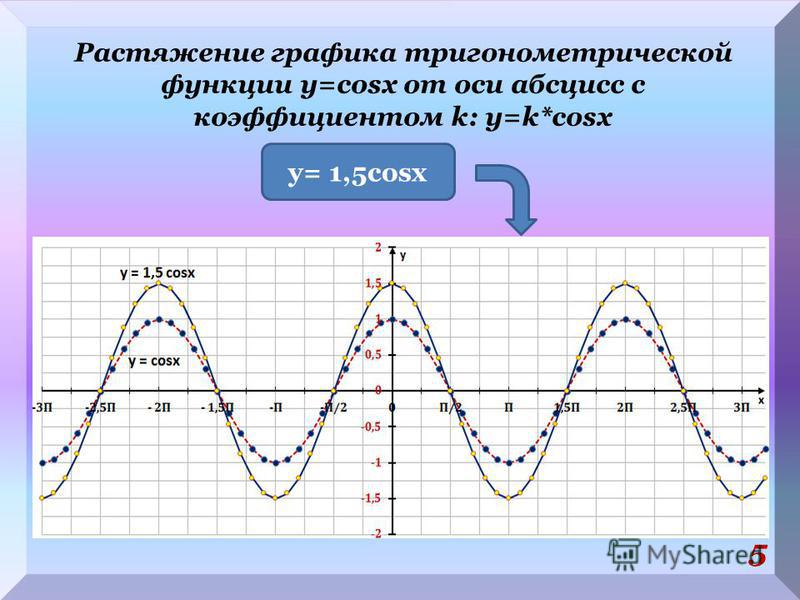 Узнайте больше о различиях.
Узнайте больше о различиях.
Что такое тригонометрические функции в Python?
Фатима Нуман
Устали от LeetCode? 😩
Изучите 24 паттерна, чтобы решить любой вопрос на собеседовании по программированию, не заблудившись в лабиринте практических задач в стиле LeetCode. Практикуйте свои навыки в практической среде кодирования, не требующей настройки. 💪
Обзор
Тригонометрия — это раздел математики, который устанавливает отношения между различными углами и их направлениями.
Тригонометрические функции
Мы используем тригонометрические функции для вычисления определенных углов, которые помогают нам понять геометрию, связанную с нашей повседневной жизнью.
Наиболее часто используемые функции включают:
- SineSineSine
- CosineCosineCosine
- TangentTangentTangent
Тригонометрические функции в Python
Тригонометрические функции в Python
и деление), экспоненциальные, логарифмические и тригонометрические функции.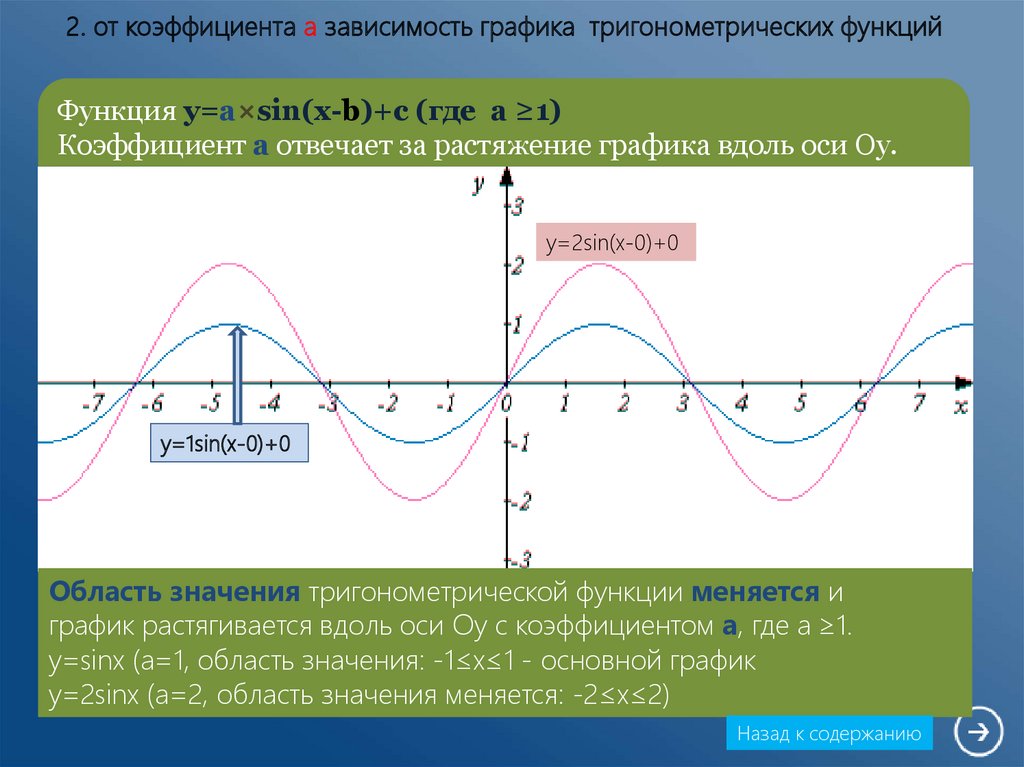 Эта библиотека известна как
Эта библиотека известна как math .
Для использования math , мы можем просто импортировать его в начале нашего кода, используя:
import math
Синтаксис для добавления математической библиотеки в Python
Мы готовы использовать любые тригонометрические функции в нашем коде.
Синтаксис
Следующий синтаксис используется для вызова любой функции math :
math.имя_функции(значение)
Давайте найдем значение синуса числа nnn, чтобы понять, как работают эти функции.
Затем мы будем использовать его следующим образом:
Код
import math
n = 1 # присвоение значения n в радианах
result = math.sin(n) # вычисление результата
print('Значение sin of', n, 'is: ', result)
Как использовать функцию синуса в математическом модуле
Объяснение
- Строка 4: Мы назвали функцию
math.для входной переменной sin (n)
sin (n) n. - Строка 5: Распечатать вывод, хранящийся в переменной
result.
Примечание : Ввод любой из тригонометрических функций, используемых в Python, в радианах.
Итак, если мы хотим преобразовать угол из градусов в радианы, мы можем использовать
math.radians(x), гдеx— это ввод в градусах.
Синтаксис для различных тригонометрических функций
В таблице ниже представлен синтаксис для math Наиболее часто используемые тригонометрические функции модуля.
| Название функции | Назначение | Синтаксис |
|---|---|---|
| Синус | Возвращает значение синуса числа | мат.грех (ввод) |
| Косинус | Возвращает значение косинуса числа | math. |
| Касательная | Возвращает значение тангенса числа | мат.тангенс(ввод) |
| Арксинус | Возвращает обратное значение синуса | math.asin(ввод) |
| Арккосинус | Возвращает значение, обратное косинусу | math.acos(ввод) |
| Арктангенс | Возвращает значение, обратное тангенсу | мат.атан(ввод) |
Код
Вы можете запустить эти функции в приведенном ниже коде:
import math
n = 0.67 #input selected
print("math.sin(n) = " , math.sin(n))
print ("math.cos(n) = ", math.cos(n))
print("math.tan(n) = ", math.tan(n))
print("math.asin(n) = ", math.asin(n))
print("math.acos(n) = ", math.acos(n))
print("math.atan(n) = ", math.atan(n) ))
Как пользоваться всеми тригонометрическими функциями, упомянутыми в приведенной выше таблице
Объяснение
- Строка 4–9: Мы вызвали тригонометрических функций для переменной
nи вычислили требуемые значения при выводе на печать.
Note: The range of inputs in
asin(),acos()andatan()functions is -1 to 1.
Hyperbolic trigonometric functions
To usehyperbolichyperbolichyperbolictrigonometric functions, we придется импортировать cmath модуль:
import cmath
Синтаксис
Синтаксис для вызова гиперболичиперболичиперболических тригонометрических функций такой же, как и для математических функций модуля.
cmath.имя_функции(значение)
Синтаксис некоторых часто используемых гиперболическихперболическихперболических функций представлен в таблице ниже:
| Имя функции | Синтаксис |
|---|---|
| Гиберболический синус | cmath.sinh(ввод) |
| Гиберболический косинус | cmath.cosh(ввод) |
| Гиберболический тангенс | cmath. |
| Гиберболический арксинус | cmath.asinh(ввод) |
| Гиберболический арккосинус | cmath.acosh(ввод) |
| Гиберболический арктангенс | cmath.atanh(ввод) |
Входными данными для упомянутых выше функций могут быть целые или комплексные числа, в зависимости от выбранной функции. Давайте теперь запустим эти функции со сложными входными данными.
Мы будем использовать функцию complex() для преобразования наших действительных и мнимых чисел в комплексные числа.
Код
import cmath
x = 2 # указанный ввод
y = 1
z = комплекс (x, y) # введение комплексного числа
print("cmath.sinh(z) = ", cmath.sinh(z))
print("cmath.cosh(z) = ", cmath.cosh(z))
print("cmath.tanh (z) = ", cmath.tanh(z))
print("cmath.asinh(z) = ", cmath.asinh(z))
print("cmath.
acosh(z) = ", cmath. acosh(z))
print("cmath.atanh(z) = " , cmath.atanh(z))
Как использовать библиотеку cmath для гиперболических функций, упомянутых в таблице выше
Объяснение
In предоставленный код, мы вызвали гиперболических тригонометрических функций, как указано в таблице.
- Строки 3–4: Мы присвоили значение
xв качестве реальной части иyв качестве мнимой части . - Строка 5: Мы создали комплексное число
z, вызвав функциюcomplex()для переменныхxиy. - Строки 6–11: Мы вызвали гиперболических функций для комплексного числа
z, и мы вычислили требуемые значения.
Примечание. Мы также можем использовать модуль
numpyдля вызова тригонометрических функций.
Вот пример, который показывает, как мы можем использовать модуль numpy для тригонометрических функций.
Code
import numpy as np
n = 1 # присвоение значения n в радианах
result = np.tan(n) # вычисление результата
print('Значение тангенса', n, 'равно:', результат)
Как использовать модуль numpy, чтобы найти значение тангенса числа
Объяснение
- Строка 4: Мы вызвали функция
numpy.tan(n)для входной переменнойn. - Строка 5: Распечатать результат, хранящийся в переменной
result.
Примечание: Мы также можем передать
math.piилиnumpy.piв качестве входных данных в тригонометрических функциях.
Давайте посмотрим на этот пример:
Код
import math
import numpy as np
n = math.

 МАТЕМАТИКА функция
МАТЕМАТИКА функция 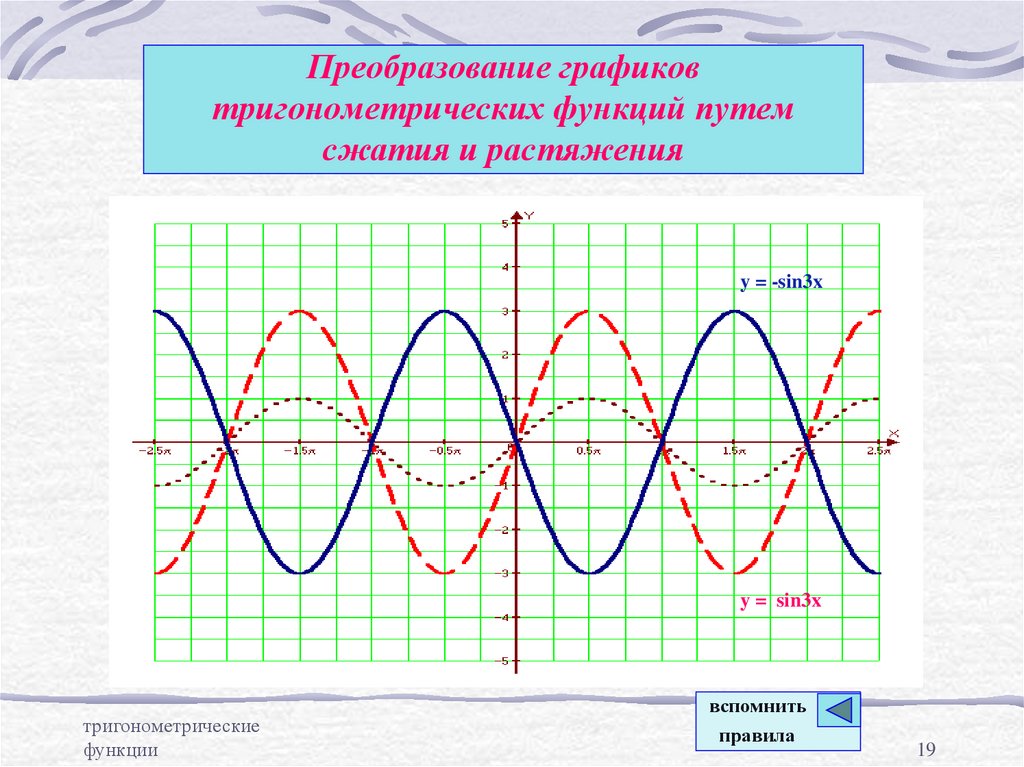 МАТЕМАТИЧЕСКАЯ функция
МАТЕМАТИЧЕСКАЯ функция 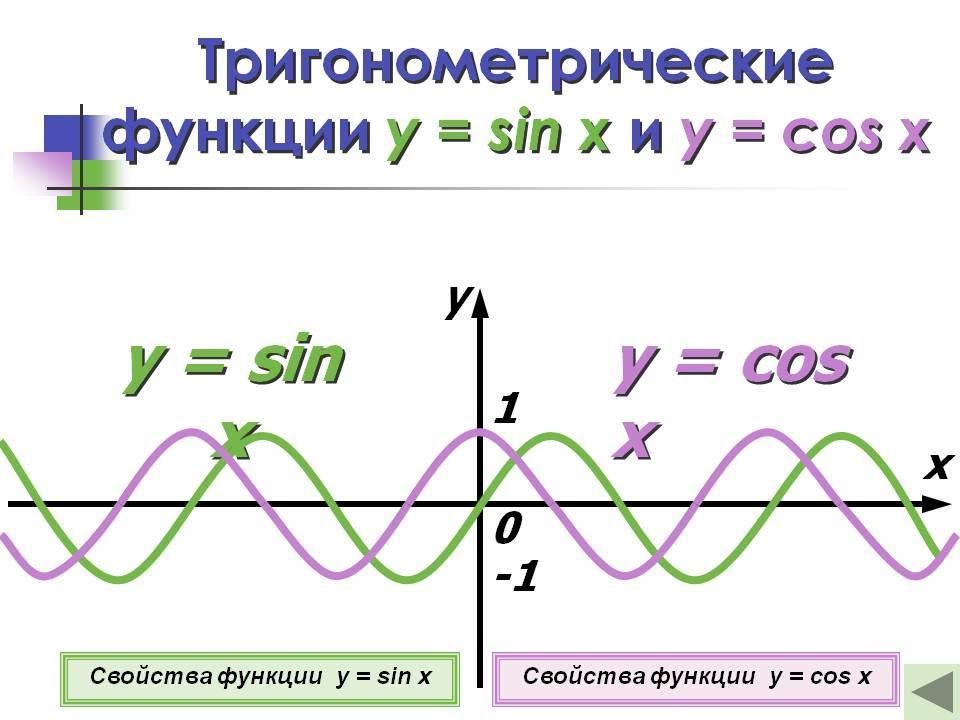 ПОТОЛОК
ПОТОЛОК 
 0003
0003 Однако вы можете указать количество строк и столбцов для заполнения, минимальные и максимальные значения, а также указать, следует ли возвращать целые числа или десятичные значения.
Однако вы можете указать количество строк и столбцов для заполнения, минимальные и максимальные значения, а также указать, следует ли возвращать целые числа или десятичные значения.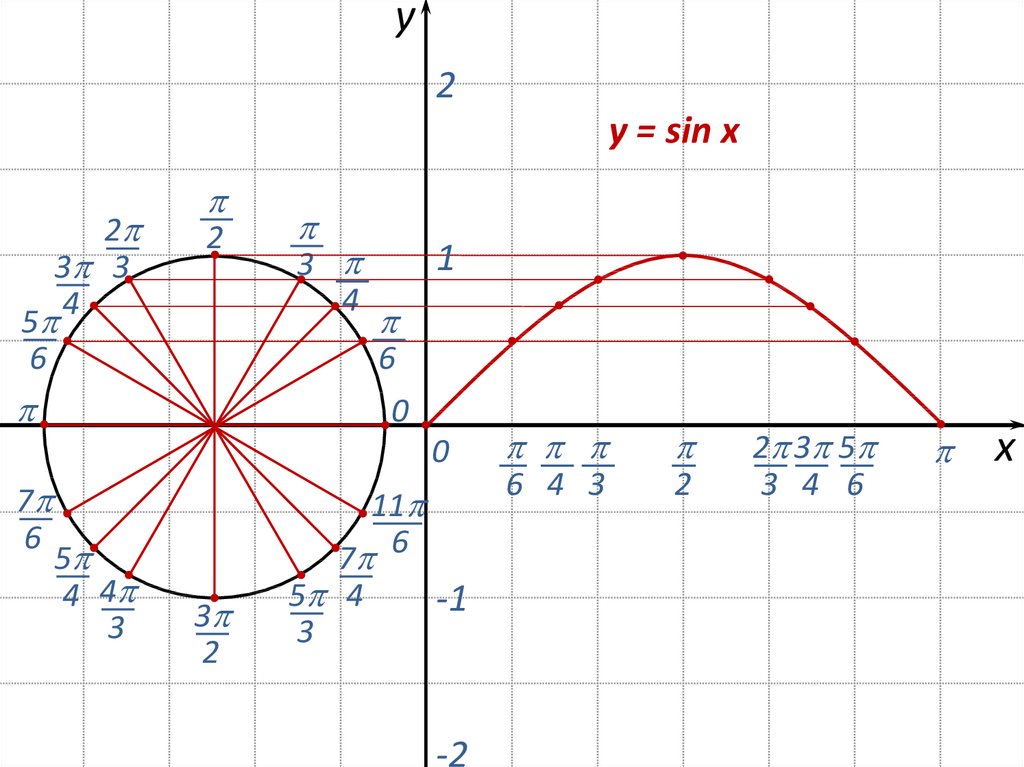 sin (n)
sin (n) 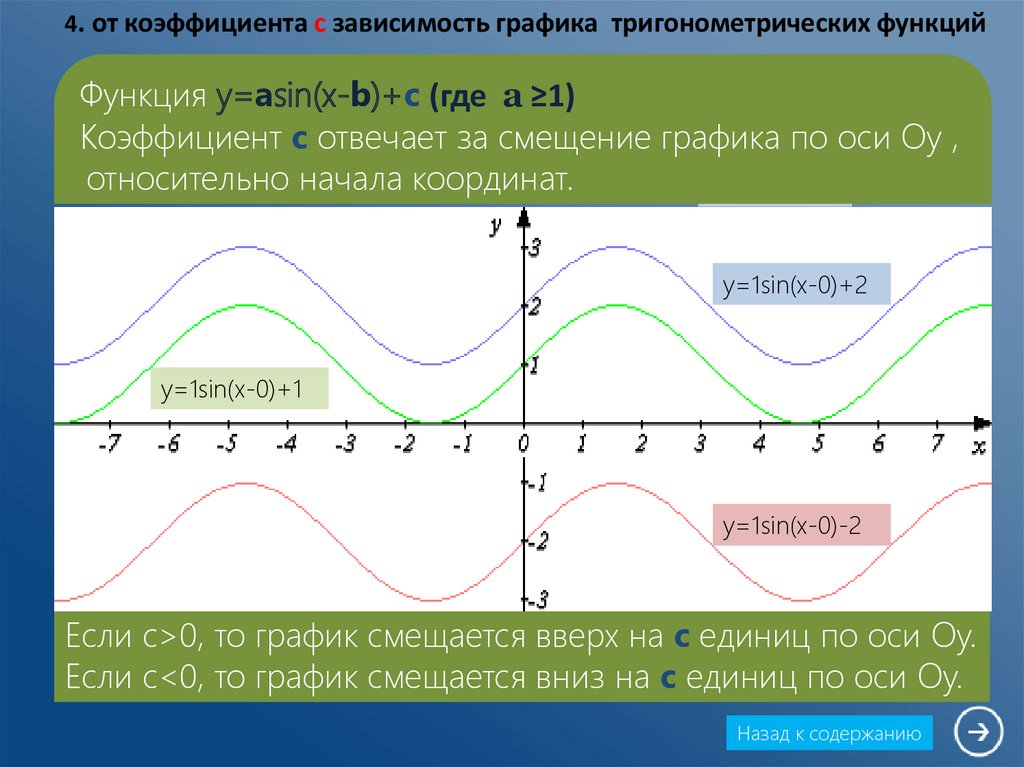 cos(вход)
cos(вход) 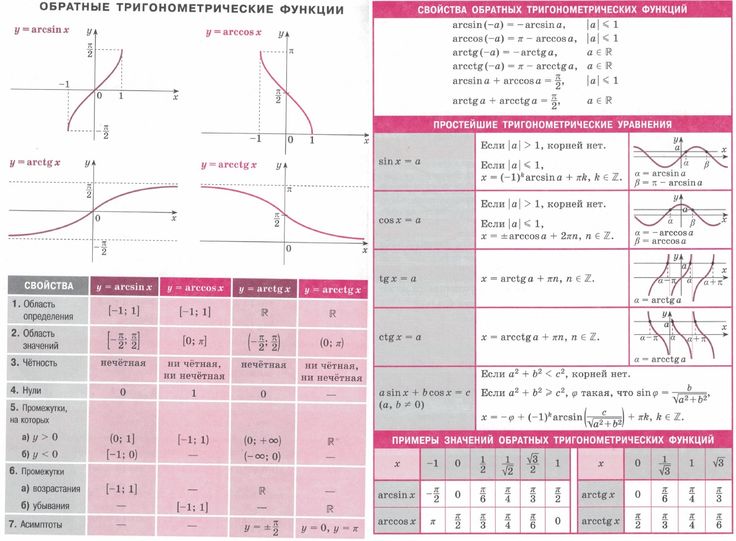
 tanh(ввод)
tanh(ввод) 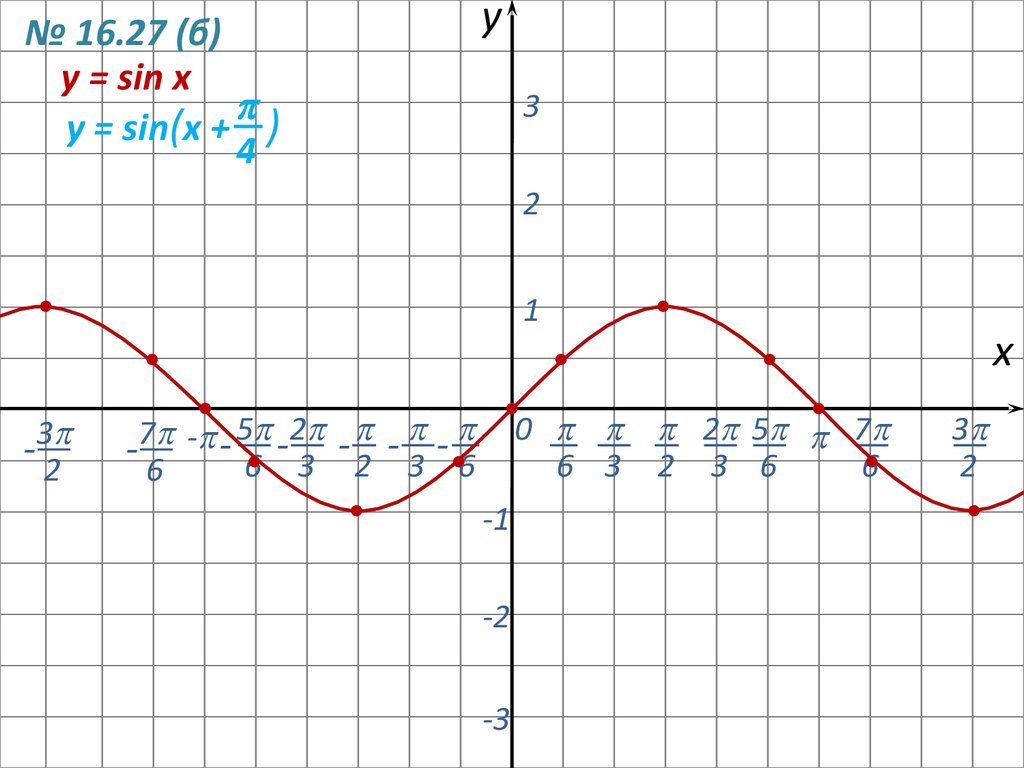 acosh(z) = ", cmath. acosh(z))
acosh(z) = ", cmath. acosh(z))