Предел x ln x : Анализ-I
Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
| Aaron |
| ||
15/07/14 |
| ||
| |||
| Xaositect |
| |||
06/10/08 |
| |||
| ||||
| Aaron |
| ||
15/07/14 |
| ||
| |||
| Shtorm |
| ||
14/02/10 |
| ||
| |||
| Aaron |
| ||
15/07/14 |
| ||
| |||
| ||||
11/11/07 |
| |||
| ||||
| Shtorm |
| ||
14/02/10 |
| ||
| |||
| Otta |
| |||
09/05/13 |
| |||
| ||||
| Aaron |
| ||
15/07/14 |
| ||
| |||
| Shtorm |
| ||
14/02/10 |
| ||
| |||
| ИСН |
| |||
18/05/06 |
| |||
| ||||
| Евгений Машеров |
| |||
11/03/08 |
| |||
| ||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 12 ] |
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
исчисление — Предел $x\ln{x}$
$\begingroup$
Я пытаюсь решить $$\lim \limits_{x \to 0}x\ln{x}$$, что согласно WolframAlpha (и Википедии) равно $0$.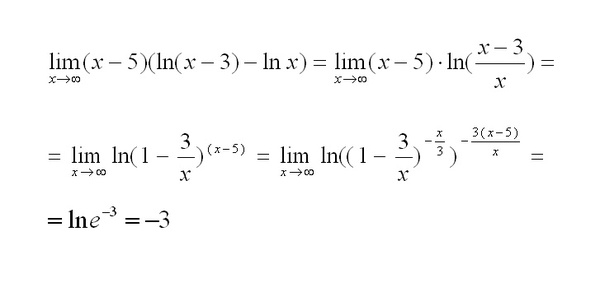 2}{\frac{1}{\frac{1}{y}}}}{1} \\
& = \lim \limits_{y \to \infty}\frac{-1}{y} \\
& = 0
\end{выравнивание}$$
2}{\frac{1}{\frac{1}{y}}}}{1} \\
& = \lim \limits_{y \to \infty}\frac{-1}{y} \\
& = 0
\end{выравнивание}$$
, но мой вопрос в том, что когда я пытаюсь решить это с помощью правила Лопиталя без замены , я получаю:
$$\begin{align} & \lim \limits_{x \to 0}x\ln{x} \\ & = \lim \limits_{x \to 0}\frac{x}{x}+\ln{x} \\ & = \lim \limits_{x \to 0}1+\ln{x} \\ & = -\infty \end{align}$$
Так что же здесь пошло не так? Это потому, что я сделал $\frac{x}{x}=1$? Если да, то как бы я поступил с этой точки?
Или это один из тех случаев, когда оговорка в правиле Лопиталя о том, что:
$$\lim \limits_{x \to c}\frac{f'(x)}{g'(x)}$$
должен существовать нарушен? Считается ли равенство $-\infty$ несуществующим?
- исчисление
- пределы
$\endgroup$
12
$\begingroup$
Короче говоря, если предел $f$ и $g$ равен и нулю, или и $\pm\infty$, и существует предел $f’/g’$, то предел $f/g $ равно этому. 9+} х\ln х = 0$.
9+} х\ln х = 0$.
$\endgroup$
5
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
исчисление — $\lim_{x \to \infty} (x — \ln x)$
спросил
Изменено 4 года, 1 месяц назад
Просмотрено 1к раз
$\begingroup$
При применении правила Лопиталя к
$$\lim_{x \to \infty} (x — \ln x)$$ 92 — х\лн х}{х}\право)\\ &= \lim_{x \to \infty} \left(\frac{2x — 1 — \ln x}{1} \right) \\ &= \infty \end{align}
Любые советы о том, почему мой подход может быть неправильным?
Спасибо
- исчисление
- пределы
- проверка-проверка
$\endgroup$
3
$\begingroup$
Если формализм Лопиталя $\lim_{x\to c}{f(x)\over g(x)}=\lim_{x\to c}{f'(x)\over g'(x )}$, когда ${f(x)\over g(x)}\to{\infty\over\infty}$ обобщается на $\lim_{x\to c}(f(x)-g(x)) =\lim_{x\to c}(f'(x)-g'(x))$, когда $f(x)-g(x)\to\infty-\infty$, только потому, что ${\infty\ over\infty}$ и $\infty-\infty$ оба являются неопределенными, у нас будет очевидная ерунда вроде 9х}{х}).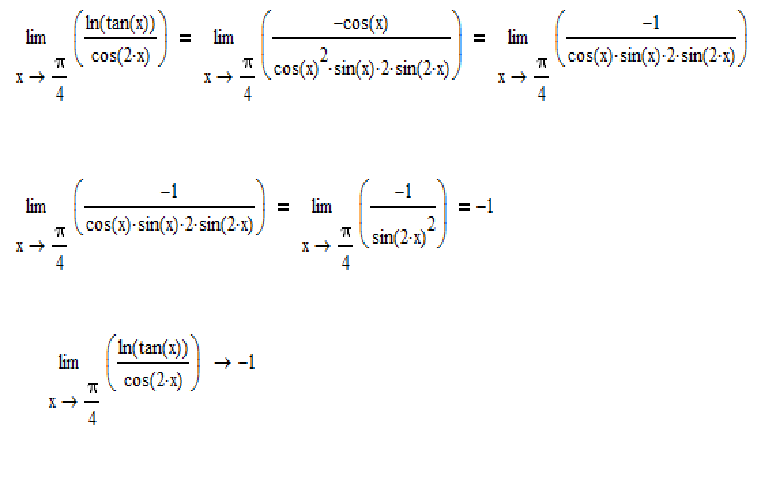

 11.2014, 19:40
11.2014, 19:40  11.2014, 19:56
11.2014, 19:56  11.2014, 20:04
11.2014, 20:04  11.2014, 20:05
11.2014, 20:05 
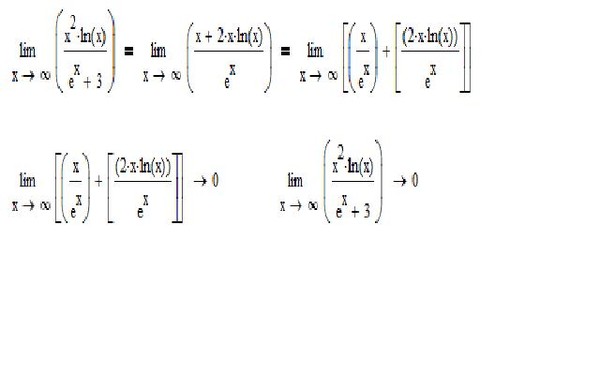 11.2014, 20:09
11.2014, 20:09 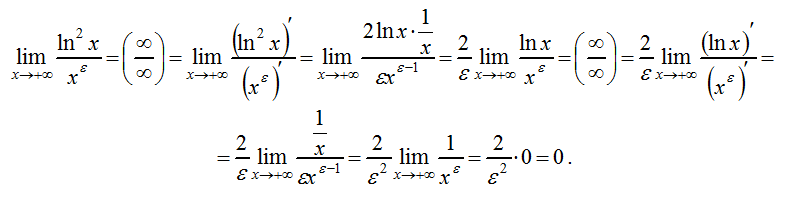 11.2014, 20:11
11.2014, 20:11 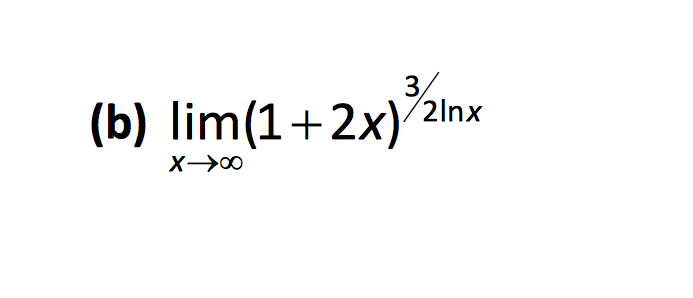 11.2014, 20:14
11.2014, 20:14  11.2014, 20:23
11.2014, 20:23 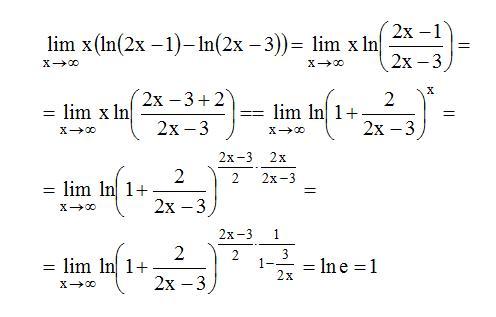 11.2014, 20:37
11.2014, 20:37  11.2014, 08:05
11.2014, 08:05