Применение эквивалентных функций при решении пределов
Метод решения
Применение эквивалентных функций позволяет упростить вычисление пределов. Если нам нужно вычислить предел дроби, то мы можем заменить множители в числителе и знаменателе эквивалентными функциями и вычислять предел от более простого выражения. Подчеркнем, что речь идет именно о множителях в дробях и произведениях. Замена эквивалентными функциями в других выражениях, например в суммах, может привести к неправильному результату. Однако, ошибки не будет, если выразить любую функцию в виде суммы эквивалентной ей функции и о малого (см. пример ⇓).
Все связанные с этим определения и теоремы приводятся на странице «О большое и о малое. Сравнение функций». Напомним некоторые из них.
Применяемые определения и теоремы
Определение эквивалентных функций
Функции f и g называются эквивалентными (асимптотически равными) при :
при ,
если на некоторой проколотой окрестности точки ,
при , причем
.
Если при , то ;
если , то .
При этом функцию называют главной частью при . См. теорему о связи эквивалентных функций с о малым
Теорема о замене функций эквивалентными в пределе частного
Если, при , и и существует предел
, то существует и предел
.
Доказательство
Отметим часто применяемое следствие этой теоремы. Пусть мы имеем частное, составленное из конечного произведения функций: . Тогда, при вычислении предела, эти функции можно заменить на эквивалентные:
,
где . Знак равенства означает, что если существует один из этих пределов, то существует и равный ему второй. Если не существует один из пределов, то не существует и второй. Разумеется, можно менять не все функции а только одну или некоторые из них.
Таблица эквивалентных функций
Далее приводится таблица функций, эквивалентных при . Здесь t может быть как переменной, так и бесконечно малой функцией при : ; .
| Эквивалентность при | Равенство при |
Предостережение
Как указывалось в самом начале, производить замену функций эквивалентными можно только в множителях дробей и произведений, предел которых мы хотим найти. В других выражениях, например в суммах, делать такую замену нельзя.
В качестве примера рассмотрим следующий предел:
.
При . Но если заменить в числителе на x, то получим ошибку:
.
Ошибки не будет, если выразить синус через эквивалентную функцию и о малое, :
.
Поскольку и , то мы снова получили неопределенность 0/0. Это указывает на то, что для вычисления этого предела применение эквивалентной функции не достаточно. Нужно применить другой метод.
Можно решить этот пример разложением в ряд Маклорена:
.
Также можно применить правило Лопиталя:
.
Примеры
Все примеры Далее мы приводим подробные решения следующих пределов, упрощая вычисления с помощью эквивалентных функций.
⇓, ⇓, ⇓, ⇓.
Пример 1
Все примеры ⇑ Найти предел:
.
Решение
Из таблицы эквивалентных функций ⇑ имеем:
. Поскольку исходная функция является дробью и каждая из этих функций входит в нее в виде множителя в числителе или знаменателе, то заменим их на эквивалентные.
.
Ответ
Пример 2
Все примеры ⇑ Найти предел:
.
Решение
Из таблицы эквивалентных функций ⇑ находим:
.
Преобразуем квадрат логарифма:
.
Поскольку исходная функция является дробью и каждая из этих функций входит в нее в виде множителя в числителе или знаменателе, то заменим их на эквивалентные.
.
Ответ
Пример 3
Все примеры ⇑ Вычислить предел.
.
Решение
Здесь мы имеем неопределенность вида один в степени бесконечность. Приводим ее к неопределенности вида 0/0. Для этого воспользуемся тем, что экспонента и натуральный логарифм являются взаимно обратными функциями.
.
Теперь в показателе экспоненты у нас неопределенность вида 0/0.
Вычисляем предел:
.
Поскольку у нас дробь, то заменим некоторые множители в числителе и знаменателе эквивалентными функциями, пользуясь приведенной выше таблицей ⇑.
;
;
.
Поскольку экспонента непрерывна для всех значений аргумента, то по теореме о пределе непрерывной функции от функции имеем:
.
Ответ
Пример 4
Все примеры ⇑ Вычислить предел.
.
Решение
При . Выясним, к чему стремится . Поскольку здесь дробь, то заменим логарифм эквивалентной функцией: . Тогда
. Таким образом, мы имеем неопределенность вида ∞–∞.
Преобразуем ее к неопределенности вида 0/0. Для этого приводим дроби к общему знаменателю.
.
Здесь мы также воспользовались формулой . После преобразований, наш предел принимает следующий вид:
.
В знаменателе мы сразу можем заменить натуральный логарифм эквивалентной функцией, как это сделали выше:
.
В числителе имеется произведение двух множителей, каждый из которых тоже можно заменить эквивалентной функцией и, таким образом, упростить вычисления. В качестве эквивалентных, попробуем найти степенные функции:
.
Тогда . Считаем, что . Раскрываем неопределенность по правилу Лопиталя.
.
Если положить , то . Тогда
.
Тот же результат можно получить, применяя разложение в ряд Тейлора при :
.
Отсюда .
Найдем эквивалентную функцию для второго множителя, используя разложение в ряд Тейлора при :
.
Отсюда .
Теперь заменим множители эквивалентными функциями:
.
Заметим, что делать замену функций на эквивалентные можно, только если функция, от которой ищется предел, является дробью или произведением. Тогда часть множителей в числителе или знаменателе можно заменить эквивалентными функциями. Так, если бы мы с самого начала заменили \ln (1+x) на x, то получили бы ошибку.
Ответ
Использованная литература:
Л.Д. Кудрявцев, А.Д. Кутасов, В.И. Чехлов, М.И. Шабунин. Сборник задач по математическому анализу. Том 1. Москва, 2003.
Автор: Олег Одинцов. Опубликовано:
Таблица эквивалентных — ПриМат
Таблица эквивалентных
Отношения бесконечно малых можно упрощать, отбрасывая бесконечно малые слагаемые большего порядка и заменяя множители в числителе и знаменателе на эквивалентные им бесконечно малые. Чтобы этот способ вычисления пределов (точнее, раскрытия неопределённостей вида [latex][\frac{0}{0}][/latex]) можно было применять к большему числу примеров, мы должны иметь достаточно большой запас известных пар эквивалентных величин. Создадим такой запас для базы[latex]x\rightarrow 0[/latex] в виде таблицы «стандартных» эквивалентных бесконечно малых.
Поскольку в этой таблице мы всегда будем рассматривать базу [latex]x\rightarrow 0[/latex], для простоты записи будем писать знак [latex]\sim[/latex] вместо [latex]_{x\rightarrow 0}^{\sim}\textrm{}[/latex].
| [latex]sinx \sim x [/latex] | [latex]e^{x}-1\sim x [/latex] |
| [latex]tgx\sim x[/latex] | [latex]a^{x}-1\sim xlna[/latex] |
| [latex]arcsinx\sim x[/latex] | [latex]ln(1+x)\sim x[/latex] |
| [latex]arctgx\sim x[/latex] | [latex](1+x)^{\alpha }-1\sim \alpha x[/latex] |
| [latex]shx\sim x[/latex] | [latex]1-cosx\sim \frac{x^{2}}{2}[/latex] |
Докажем некоторые утверждения:
1) [latex]lim_{x\rightarrow 0}\frac{arcsinx}{x}=[/latex][latex]lim_{x\rightarrow 0}\frac{1}{\frac{x}{arcsinx}}=[/latex][latex]lim_{y\rightarrow 0}\frac{1}{\frac{siny}{y}} =1[/latex]
2) [latex]lim_{x\rightarrow 0}\frac{tgx}{x}=[/latex][latex]lim_{x\rightarrow 0}\frac{sinx}{\frac{x}{cosx}}[/latex][latex]=\frac{lim_{x\rightarrow 0}\frac{sinx}{x}}{lim_{x\rightarrow 0}cosx}=[/latex][latex]\frac{1}{1}=1[/latex]
3) [latex]lim_{x\rightarrow 0}\frac{1-cosx}{x^{2}/2}=[/latex][latex]lim_{x\rightarrow 0}\frac{2sin^{2}\frac{x}{2}}{x^{2}/2}=[/latex][latex]lim_{x\rightarrow 0}\frac{2sin^{2}\frac{x}{2}}{2(\frac{x}{2})^{2}}=[/latex][latex]lim_{x\rightarrow 0}\frac{sin\frac{x}{2}}{\frac{x}{2}}\cdot \frac{sin\frac{x}{2}}{\frac{x}{2}}=[/latex][latex]lim_{x\rightarrow 0}\frac{sin\frac{x}{2}}{\frac{x}{2}}\cdot lim_{x\rightarrow 0}\frac{sin\frac{x}{2}}{\frac{x}{2}}=[/latex][latex]1\cdot 1=1[/latex]
4) [latex]lim_{x\rightarrow 0}\frac{log_{a}(1+x)}{\frac{x}{lna}}=[/latex][latex]lim_{x\rightarrow 0}ln\; a\cdot \frac{1}{x}log_{a}(1+x)=[/latex][latex]lim_{x\rightarrow 0}ln\; a\cdot log_{a}(1+x)^{\frac{1}{x}}=[/latex][latex]lim_{x\rightarrow 0}ln\; a\cdot \frac{ln(1+x)^{\frac{1}{x}}}{lna}=[/latex][latex]lim_{x\rightarrow 0}ln(1+x)^{\frac{1}{x}}=[/latex][latex]ln\; lim_{x\rightarrow 0}(1+x)^{\frac{1}{x}}=[/latex][latex]ln\; e=1[/latex]
Источники:
- Лысенко З.М. Конспект лекций по курсу математического анализа. (Тема «Сравнение функций»).
Лимит времени: 0
Информация
Тест по теме «Эквивалентные функции»
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
Ваше время:
Время вышло
Вы набрали 0 из 0 баллов (0)
| Место | Имя | Записано | Баллы | Результат |
|---|---|---|---|---|
| Таблица загружается | ||||
| Нет данных | ||||
- С ответом
- С отметкой о просмотре
Поделиться ссылкой:
Похожее
Эквивалентные функции ℹ️ определение, формулы, основные свойства, доказательство теоремы о замене функций, примеры нахождения пределов, таблица
В данной статье речь пойдет об основных понятиях эквивалентных функций, с помощью которых можно найти значение пределов.
Понятие эквивалентности поменяется не только в высшей математике, но и в логике, психологии, при переводах с иностранных языков. Оно означает «равнозначность», «равносильность», «равенство».
Определение эквивалентных функций
Эквивалентные функции — это функции, имеющие одинаковое значение. Они могут представлять собой бесконечность малых и больших величин.
Функция может иметь такое понятие лишь при наличии предела. Следует понимать, что одна и та же функция принимает значение малой или большой до бесконечности лишь в единственной точке.
Теорема о замене функций эквивалентными в пределе частного
Если при x1, стремящимся к x2, f(x)~f1(x) и g(x)~g1(x) существует предел:
то существует и предел:
Доказательство
Допустим, что следствие этой теоремы часто применяемое. Если мы имеем частное, являющееся результатом произведения функций:
в этом случае, при нахождении предела, можно сделать замену этих функций на эквивалентные:
при этом:
f(x) ~ f1(x), p(x) ~ p1(x), … , r(x) ~ r1(x), g(x) ~ g1(x), q(x) ~ q1(x), … , s(x) ~ s1(x).
Выражения равны друг другу, это значит, что при существовании одного из таких пределов, применимо существование выражения, равного первому. Соответственно, если не существует такой предел, то не может существовать и второй.
Следует отметить, что можно делать замену как одной величины функции, так и нескольких одновременно.
Таблица эквивалентных функций
Ниже приведена таблица равнозначных функций и формул при t → 0. В данном случае величина t может представлять собой как переменную, так и до бесконечности малую функцию t = t(x) при x → x
|
Эквивалентность при t → 0 |
Равенство при t → 0 |
|
sin t ~ t |
sin t = t + 0(t) |
|
arsin t ~ t |
arsin t = t + 0(t) |
|
tg t ~ t |
tg t = t + 0(t) |
|
artg t ~ t |
artg t = t + 0(t) |
|
1-cos t ~ |
1-cos t = + 0(t2) |
|
et – 1 ~ t |
et — 1 = t + 0(t) |
|
at – 1 ~ t ln a |
at – 1 = t ln a + 0(t) |
|
ln (1 + t) ~ t |
ln (1 + t) = t + 0(t) |
|
loga (1 + t) ~ |
loga (1 + t) = + 0(t) |
|
(1 + t)b — 1 ~ bt |
(1 + t)b — 1 = bt + 0(t) |
|
sh t ~ t |
sh t = t + 0(t) |
|
arsh t ~ t |
arsh t = t + 0(t) |
|
th t ~ t |
th t = t + 0(t) |
|
arsh t ~ t |
arsh t= t + 0(t) |
|
ch t – 1 ~ t2/2 |
ch t – 1 ~ t2/2 + 0(t2 ) |
Свойства замены функций равносильными доступны для дробных выражений с перемножаемыми величинами и произведений, где необходимо найти предел.
В этом случае величины в числителе или знаменателе допускается заменить равнозначными функциями. Если математическое выражение представляет собой сумму чисел, замену сделать нельзя.
Примеры решения пределов с помощью эквивалентных функций
Для сравнения рассмотрим несколько примеров.
Пример 1
Вычислить
Начнём решение, учитывая, что tg2x ~ 2x, sin3x ~ 3x при x → 0, тогда
Пример 2
Найти
Пусть arcsin x = t, тогда x = sin t и t → 0 при x → 0. Исходя из этого:
Значит, arcsin x ~ x при x → 0.
Пример 3
Вычислить
Решение: если sin (15x) ~ 15x, tg (10x) ~ 10x, тогда
Для решения пределов можно использовать онлайн калькуляторы, размещенные на ресурсах в свободном доступе.
Применение теорем об эквивалентных бесконечно малых при вычислении пределов и таблицы эквивалентностей
Замена переменных при вычислении пределов, использование непрерывности функции при вычислении пределов.
а) Правило замены переменной для непрерывной функции.
По определению непрерывности функции в точке ,
Если дана сложная функция , функция имеет предел в точке и функция непрерывна в точке , то
.
То есть при вычислении предела непрерывной функции можно перейти к пределу под знаком функции. Например, в силу непрерывности основных элементарных функций справедливы равенства:
если – непрерывные функции и т. д.
Пример 5. Вычислить
б) Правило замены переменной для пределов функций в общем виде.
Пусть существуют пределы и и при . Тогда при существует предел сложной функции и .
Это правило полезно при вычислении предела в том случае, когда вычислить трудно. Полагают и находят предел при условии, что этот предел вычисляется проще первоначального.
Пример 6. Вычислить .
Решение. Сделаем замену переменной , тогда
.
Предел называется первым замечательным пределом (раскрывает неопределенность ).
Если функция такова, что , то .Этот предел имеет важное значение при раскрытии неопределенности .
Пример 7. Вычислить
а) ; б) .
Решение. а) Имеем неопределенность .
б) .
Так как стремится не к 0, а к , то сделаем замену переменной . При при , а .
Имеем
Второй замечательный предел имеет вид
или
, где е=2,71826…– иррациональное и трансцендентное число. Если , то . Если , то .
С помощью второго замечательного предела раскрывается неопределенность , то есть ищутся пределы показательно- степенных функций , где .
Предположим, что в окрестности точки , за исключением, быть может, самой точки . Применяя формулу второго замечательного предела и возможность перехода к пределу отдельно в основании и показателе степени, получаем:
Пример 8. Вычислить .
Решение.
в окрестности за исключением точки .
Применяя вышеуказанные преобразования, получим
В процессе вычисления предела получили
Вычисляем
Следовательно, и .
Ответ:
Пример 9.Вычислить
Решение. Имеем
При вычислении этого предела аналогично используем второй замечательный предел
Применение теорем об эквивалентных бесконечно малых при вычислении пределов и таблицы эквивалентностей.
Пусть и . Если , то и называются эквивалентными бесконечно малыми в точке . Это обозначается как при .
Теорема 1. Если , при , то при .
Теорема 2. Если , при , то
Теорема 3. Алгебраическая сумма конечного числа бесконечно малых эквивалентна бесконечно малой низшего порядка. Иначе: пусть – бесконечно малая низшего порядка по сравнению с , , тогда .
Теорема 4. Если , при , причем существует и отличен от –1, то при .
Таблица эквивалентностей.
Пусть – бесконечно малая при , то есть . Тогда
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11. .
Все приведенные выше формулы справедливы при . Рассмотрим примеры на вычисление пределов с помощью теорем об эквивалентных бесконечно малых и таблицы эквивалентностей.
Пример 10. Вычислить
а) б) в)
Решение.
При вычислении этого предела применили теоремы 2 и 5 и табличные эквивалентности 1) и 7).
б) Имеем неопределенность .
Применим эквивалентность , так как . Но нельзя считать, что , поскольку при . Поэтому сделаем замену переменной при . Тогда имеем:
Использовали формулы приведения , табличные эквивалентности 1) и 11) и теорему 1: , так как .
в) В данном случае также имеем неопределенность .
Сделаем замену при .
Получаем
Применили эквивалентности 1) и 6).
Ответ: а) б) в)
Пример 11. Вычислить .
Решение. Так как при , то
Ответ:
51. Эквивалентные бесконечно малые функции. Таблица эквивалентных бесконечно малых функций.
Функции 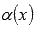 и
и 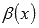 называют бесконечно
малыми при
называют бесконечно
малыми при 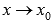 ,
если
,
если 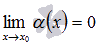 и
и 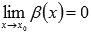
Функции 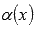 и
и 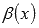 называют эквивалентными
бесконечно малыми при
называют эквивалентными
бесконечно малыми при 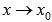 ,
если
,
если 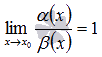
Очень удобно пользоваться заменой эквивалентных бесконечно малых при нахождении пределов. Замена производится на основе таблицы.
Таблица эквивалентных бесконечно малых.
Пусть 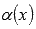 —
бесконечно малая при
—
бесконечно малая при 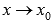 .
.

Эквивалентность
всех величин таблицы можно доказать,
основываясь на равенстве 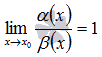 .
.
52. Теорема о применении эквивалентных бесконечно малых к вычислению пределов.
При
вычислении пределов часто применяется
следующая Теорема.
Предел отношения двух бесконечно малых
(неопределенность  )
равен пределу отношения двух других
бесконечно малых, эквивалентных данным,
т.е.
)
равен пределу отношения двух других
бесконечно малых, эквивалентных данным,
т.е.
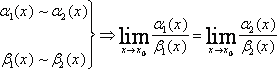
Отметим
также: если  ,
то
,
то .
.
3.2. Основные формулы эквивалентности бесконечно малых.
Известна формула первого замечательного предела:
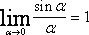
Используя это равенство, получим
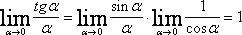
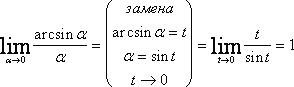
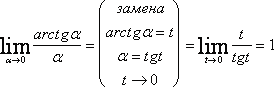
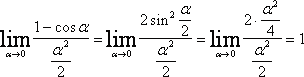
Отсюда получаем первую группу формул эквивалентности бесконечно малых.
При 
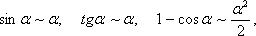
 . (1)
. (1)
Вторая группа формул связана с логарифмической функцией.
Имеем: 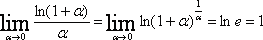
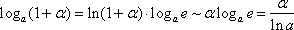
Если
при 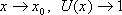 ,
то
,
то
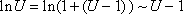
Получаем вторую группу формул:
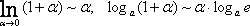
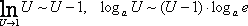 (2)
(2)
Третья группа формул связана с показательной функцией. Имеем:
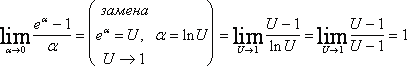 Отсюда
Отсюда 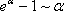
Тогда 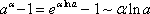
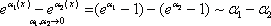
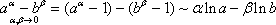
Итак, третья группа формул эквивалентности бесконечно малых
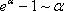 ,
, 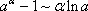
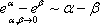 ,
, 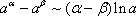 (3)
(3)
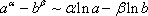
Четвертая группа формул связана со степенной функцией.
Имеем: 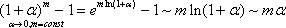
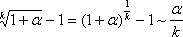
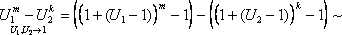
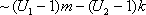
Итак, четвертая группа формул эквивалентности бесконечно малых
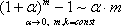 ,
, 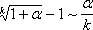
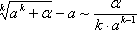
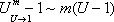 ,
, 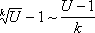
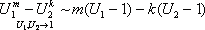 (4)
(4)
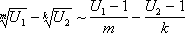
53. Односторонние пределы функции в точке. Односторонняя непрерывность функции в точке.
Определение. Предела слева (справа)
Число А(В) по определению называется пределом функции f(x) в точке х0 слева (справа), если
>0 >0 : x из x0-<x<x0 (x0<x<x0+)
f(x)-A< (f(x)-B<),
при
этом пишут: 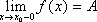
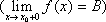
Пример.
Справедлив критерий 2 существования предела функции в точке.
Теорема.
Для того, чтобы у функции f(x) существовал предел при хх0 необходимо и достаточно, чтобы существовал левосторонний предел в т. х0, существовал правосторонний предел в т. х0 и они были бы равны между собой.
Определение. Непрерывности функции слева (справа).
Функция f(x) определенная в левосторонней окрестности т. х0 (или в правосторонней окрестности т.х0) и в самой точке х0 называется непрерывной в т. х0 слева (справа), если
>0 >0 : x из x0-<xx0 (x0x<x0+)
f(x)-f(x0-0)< (f(x)-f(x0+0)<)
При этом значения f(x0-0) (f(x0+0)) называют значениями функции в точке х0 слева (справа).
Пример 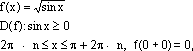 .
.
f(-0)=0.
Теорема. Критерий непрерывности функции в точке.
Для того чтобы функция f(x) была непрерывной в т. х0 необходимо и достаточно, чтобы она была непрерывна слева в т. х0, справа в т. х0 и при этом выполнялось соотношение :
f(x0-0)=f(x0+0)=f(x0)
54. Точки разрыва функции и их классификация.
Определение. Разрывной функции в т. x0.
Функция f(x) не являющаяся непрерывной в т. x0 называется разрывной в т. x0.
При этом точки разрыва функции подразделяются на точки разрыва I рода и II рода.
Определение. Точка разрыва I рода.
Если
у функции f(x) 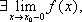
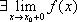 и
они конечны, то говорят, что точка x0—
точка разрыва первого рода.
и
они конечны, то говорят, что точка x0—
точка разрыва первого рода.
При
этом, если 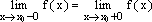 ,
то говорят, что точкаx0—
точка устранимого
разрыва.
,
то говорят, что точкаx0—
точка устранимого
разрыва.
Если
же 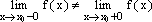 ,
то говорят, что точкаx0—
точка разрыва с конечным
скачком.
,
то говорят, что точкаx0—
точка разрыва с конечным
скачком.
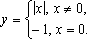 -разрывная
функция.
-разрывная
функция. 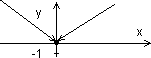
Если
положить 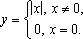 — то
произойдет устранение разрыва и функция
станет непрерывной.
— то
произойдет устранение разрыва и функция
станет непрерывной.
У
функции 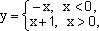 так
как
так
как
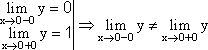 —
имеется конечный скачок.
—
имеется конечный скачок.

Определение. Точка разрыва II рода.
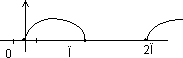
Если у функции f(x) хотя бы один из односторонних пределов не существует или равен , то говорят, что т. х0— точка разрыва II рода.
Пример 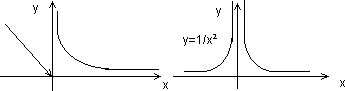
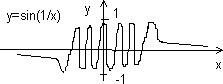
Если устремить х к 0 разными способами, то получим различные значения пределов:
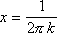 , kN, x0
, а ;
, kN, x0
, а ;
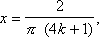 kN, x0
, а
kN, x0
, а 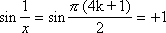 ,
,
значит функция f(x) не имеет предела â т. х0=0, то есть т. х0 точка разрыва II рода.
8. Сравнение бесконечно малых функций. Эквивалентные бесконечно малые функции. Таблица эквивалентности
Эквивалентные бесконечно малые функции.
Если 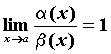 ,
то бесконечно малые функции
,
то бесконечно малые функции 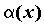 и
и 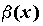 называются эквивалентными,
обозначают
называются эквивалентными,
обозначают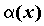 ~
~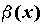 . Как
известно, сумма, разность и произведение
двух б.м.ф. есть функция бесконечно
малая. Отношение же двух б.м.ф. может
вести себя различным образом: быть
конечным числом, быть бесконечно большой
функцией, бесконечно малой или вообще
не стремиться ни к какому пределу.
. Как
известно, сумма, разность и произведение
двух б.м.ф. есть функция бесконечно
малая. Отношение же двух б.м.ф. может
вести себя различным образом: быть
конечным числом, быть бесконечно большой
функцией, бесконечно малой или вообще
не стремиться ни к какому пределу.
Две б.м.ф. сравниваются между собой с помощью их отношения.
Пусть α=α(х) и ß=ß(х) есть б.м.ф. при х→хо, т. е.
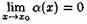 и
и 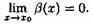
1.
Если 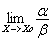 =А
0 (АєR), то α и ß называются бесконечно
малыми одного порядка.
=А
0 (АєR), то α и ß называются бесконечно
малыми одного порядка.
2.
Если, 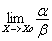 =0,
то α називатся бесконечно малой более
высокого порядка , чем ß.
=0,
то α називатся бесконечно малой более
высокого порядка , чем ß.
3.
Если 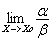 =∞,
то α называется бесконечно малой более
низкого порядка, чем ß.
=∞,
то α называется бесконечно малой более
низкого порядка, чем ß.
4.
Если 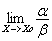 не
существует, то α и ß называются несравнимыми
бесконечно малыми.
не
существует, то α и ß называются несравнимыми
бесконечно малыми.
Отметим, что таковы же правила сравнения б.м.ф. при х →±∞, х →х0±0.
Таблица
эквивалентных бесконечно малых. Пусть 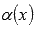 —
бесконечно малая при
—
бесконечно малая при 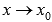 .
.

9. Понятие непрерывной функции в точке. Свойства непрерывных в точке функций
ε-δ определение
Пусть 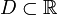 и
и 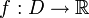 .
.
Функция f непрерывна
в точке 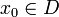 ,
если для любого ε
> 0 существует
δ > 0
такое, что
,
если для любого ε
> 0 существует
δ > 0
такое, что
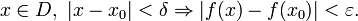
Функция f непрерывна на множестве E, если она непрерывна в каждой точке данного множества.
В этом случае
говорят, что функция f класса C0 и пишут: 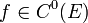 или,
подробнее,
или,
подробнее, 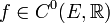 .
.
Из определения следует, что функция непрерывна в каждой изолированной точке своей области определения.
Определение непрерывности фактически повторяет определение предела функции в данной точке. Другими словами, функция f непрерывна в точке x0, предельной для множества E, если f имеет предел в точке x0, и этот предел совпадает со значением функции f(x0).
Функция непрерывна в точке, если её колебание в данной точке равно нулю.
Свойства Локальные
Глобальные
Функция, непрерывная на отрезке (или любом другом компактном множестве), равномерно непрерывна на нём.
Функция, непрерывная на отрезке (или любом другом компактном множестве), ограничена и достигает на нём свои максимальное и минимальное значения.
Областью значений функции
 ,
непрерывной на отрезке
,
непрерывной на отрезке  ,
является отрезок
,
является отрезок  где
минимум и максимум берутся по отрезку
где
минимум и максимум берутся по отрезку  .
.Если функция
 непрерывна
на отрезке
непрерывна
на отрезке  и
и  то
существует точка
то
существует точка  в
которой
в
которой  .
.Если функция
 непрерывна
на отрезке
непрерывна
на отрезке  и
число
и
число  удовлетворяет
неравенству
удовлетворяет
неравенству  или
неравенству
или
неравенству  то
существует точка
то
существует точка  в
которой
в
которой  .
.Непрерывное отображение отрезка в вещественную прямую инъективно в том и только в том случае, когда данная функция на отрезке строго монотонна.
Монотонная функция на отрезке
 непрерывна
в том и только в том случае, когда область
ее значений является отрезком с концами
непрерывна
в том и только в том случае, когда область
ее значений является отрезком с концами  и
и  .
.Если функции
 и
и  непрерывны
на отрезке
непрерывны
на отрезке  ,
причем
,
причем  и
и  то
существует точка
то
существует точка  в
которой
в
которой  Отсюда,
в частности, следует, что любое непрерывное
отображение отрезка в себя имеет хотя
бы одну неподвижную
точку.
Отсюда,
в частности, следует, что любое непрерывное
отображение отрезка в себя имеет хотя
бы одну неподвижную
точку.
«Вычисление пределов функций, используя таблицу эквивалентности бесконечно малых, первый и второй замечательные предел»
Самостоятельная работа по математике
для студентов 2 курса групп СПО
Раздел 1. Математический анализ
Тема 1.1. Вычисление пределов функций, используя таблицу эквивалентности бесконечно малых, первый и второй замечательные предел.
Цель: проверить умение студентов самостоятельно работать с литературой и применять полученные знания.
Теоретическая часть
Две бесконечно малые величины 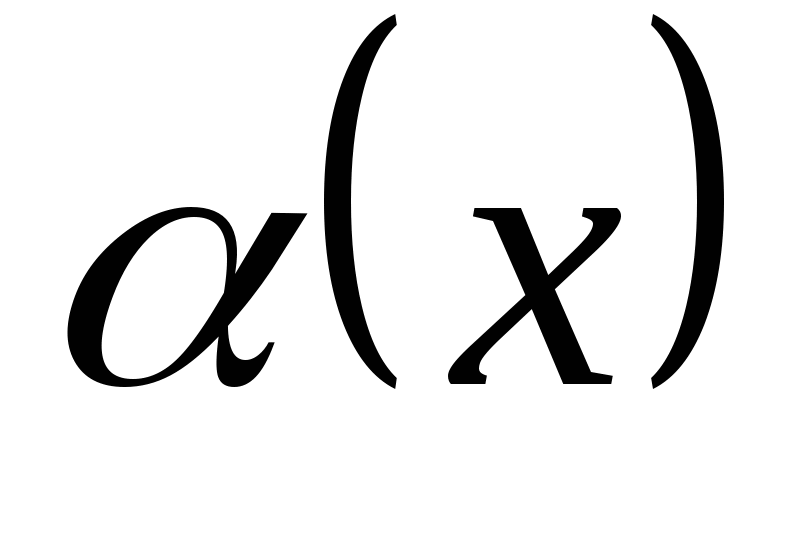 и
и 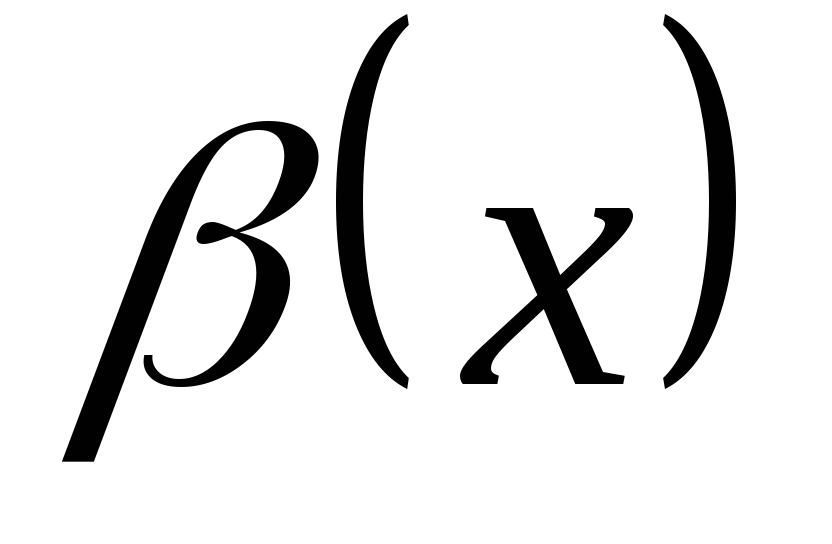 называются эквивалентными (равносильными) при
называются эквивалентными (равносильными) при  , если
, если 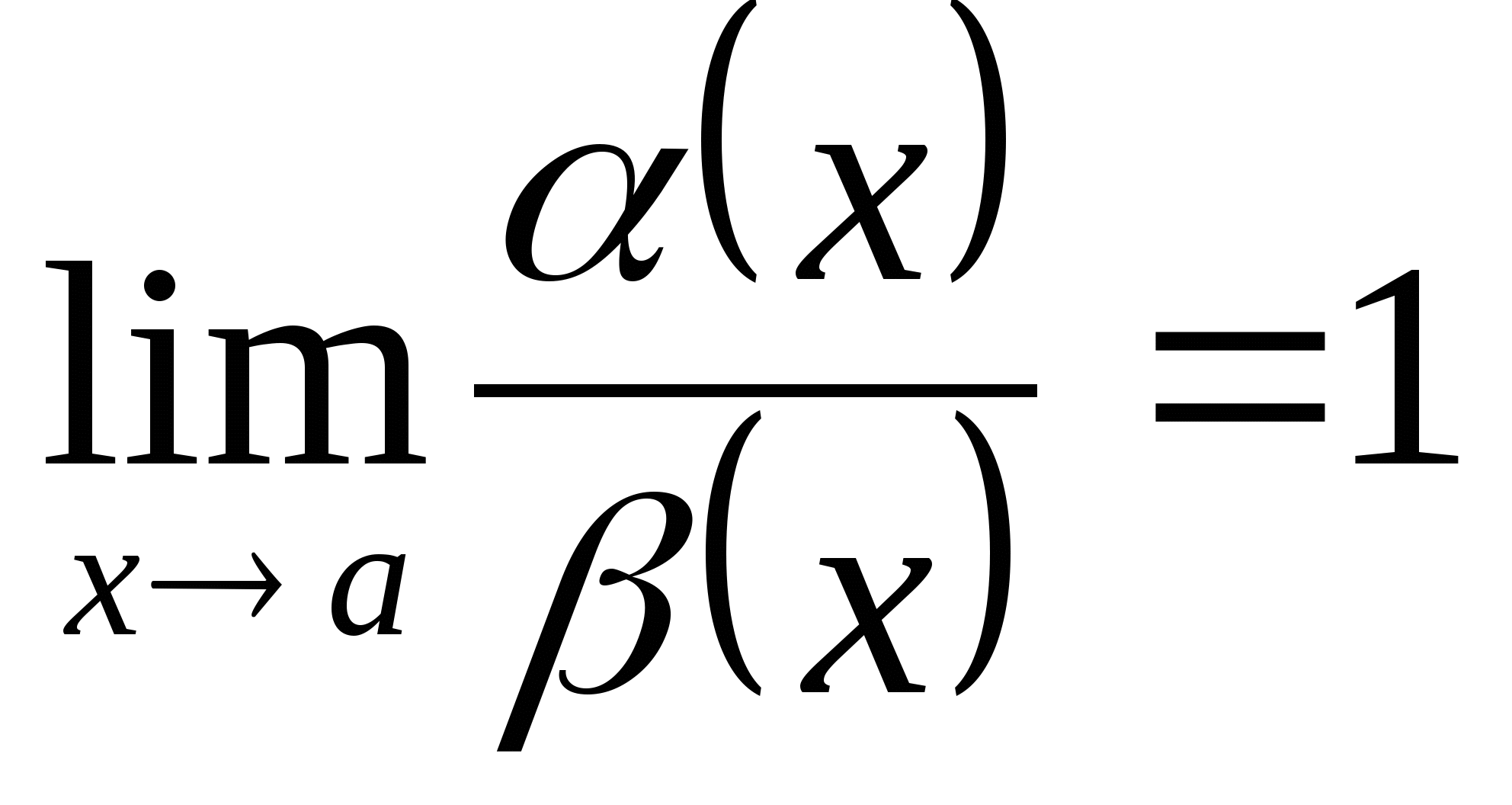 .
.
В этом случае пишут, что 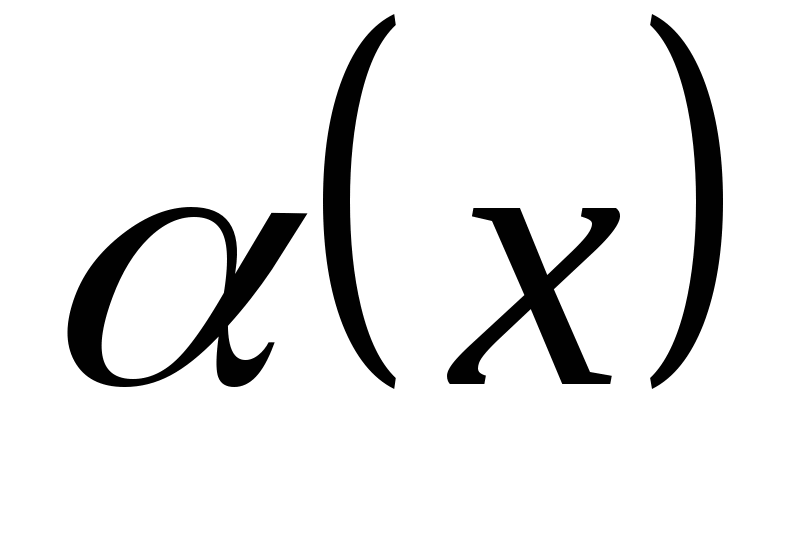 ~
~ 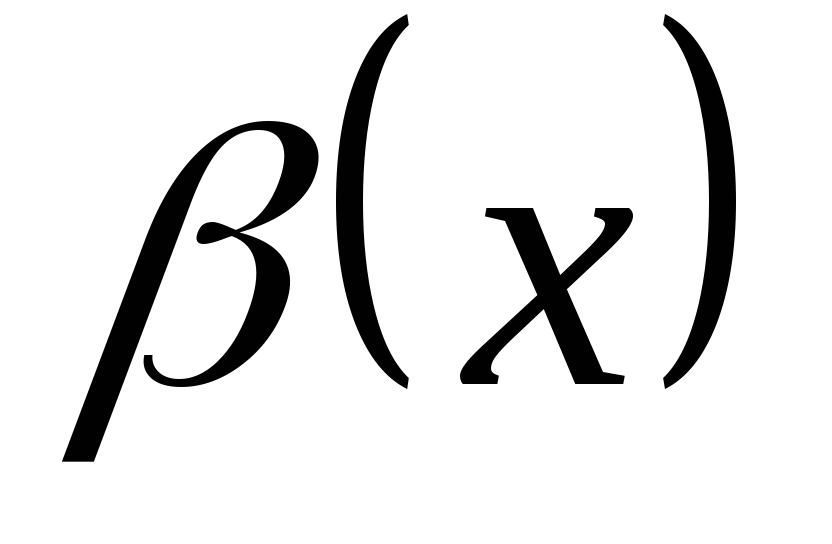 .
.
Если 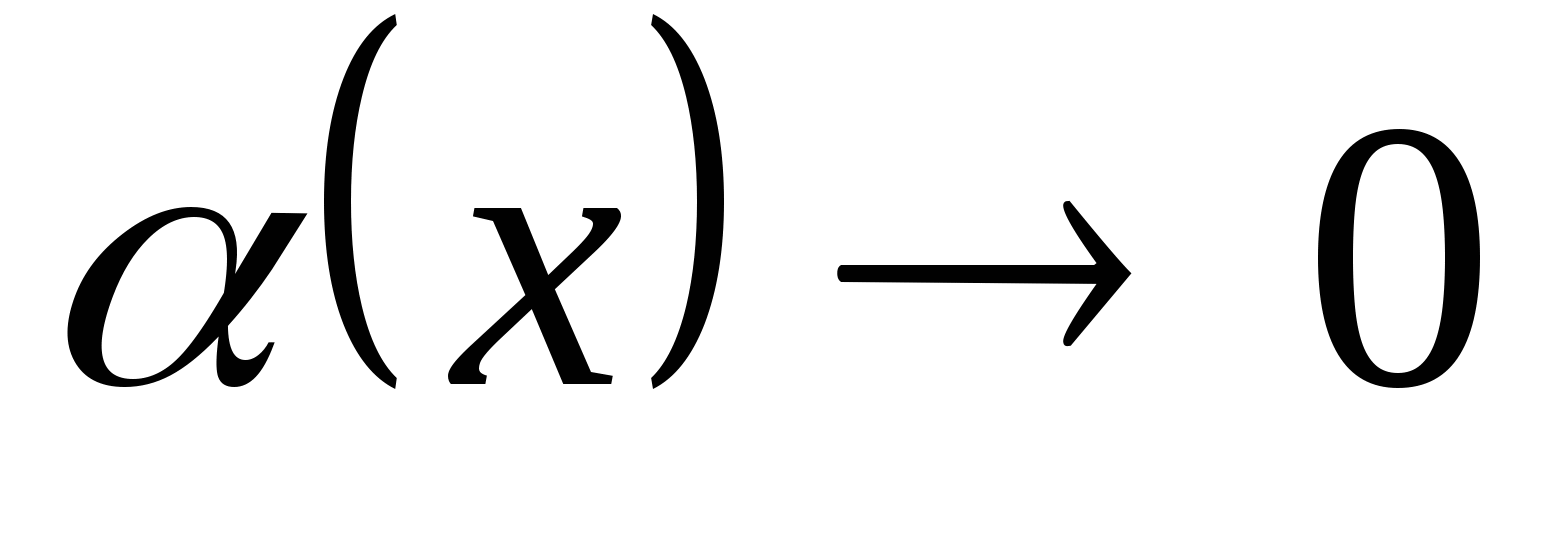 при
при  , то
, то
Теорема: Пусть при  бесконечно малая величина
бесконечно малая величина 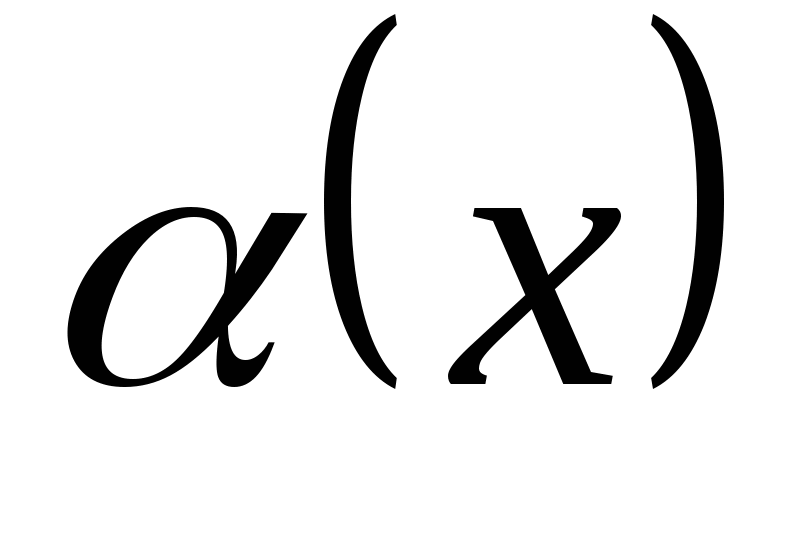 эквивалентна бесконечно малой величине
эквивалентна бесконечно малой величине 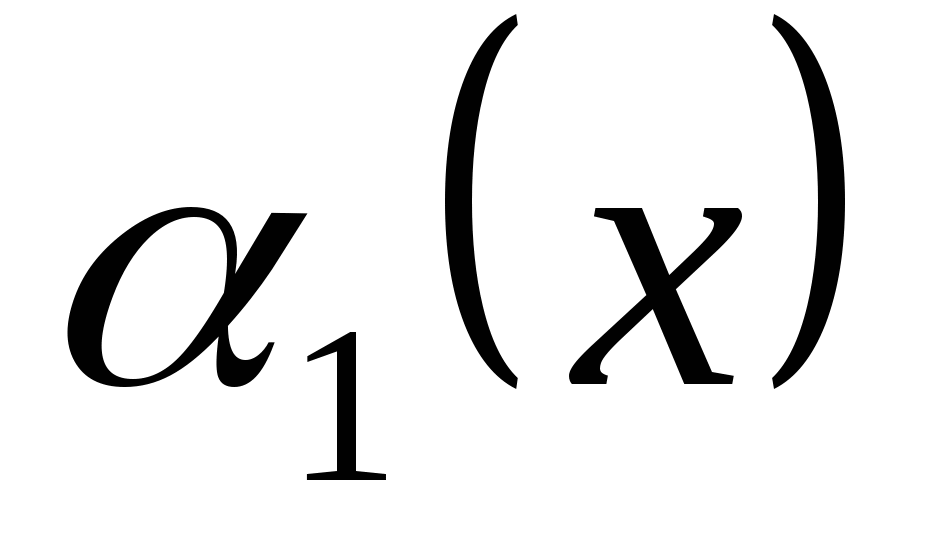 , а бесконечно малая величина
, а бесконечно малая величина 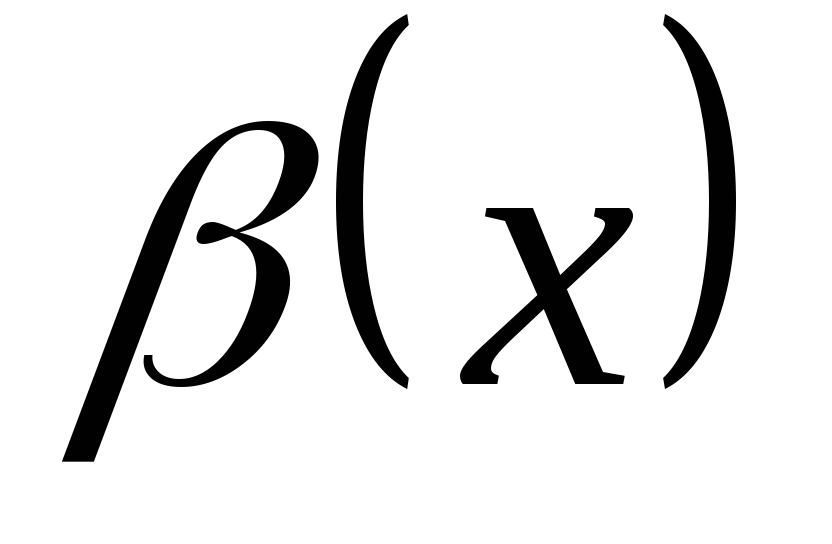 эквивалентна бесконечно малой величине
эквивалентна бесконечно малой величине 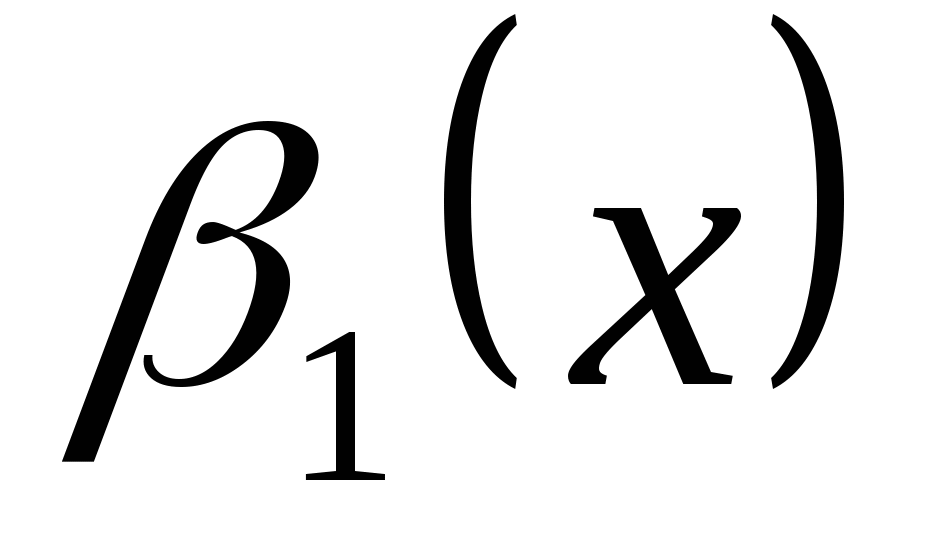 . Тогда
. Тогда 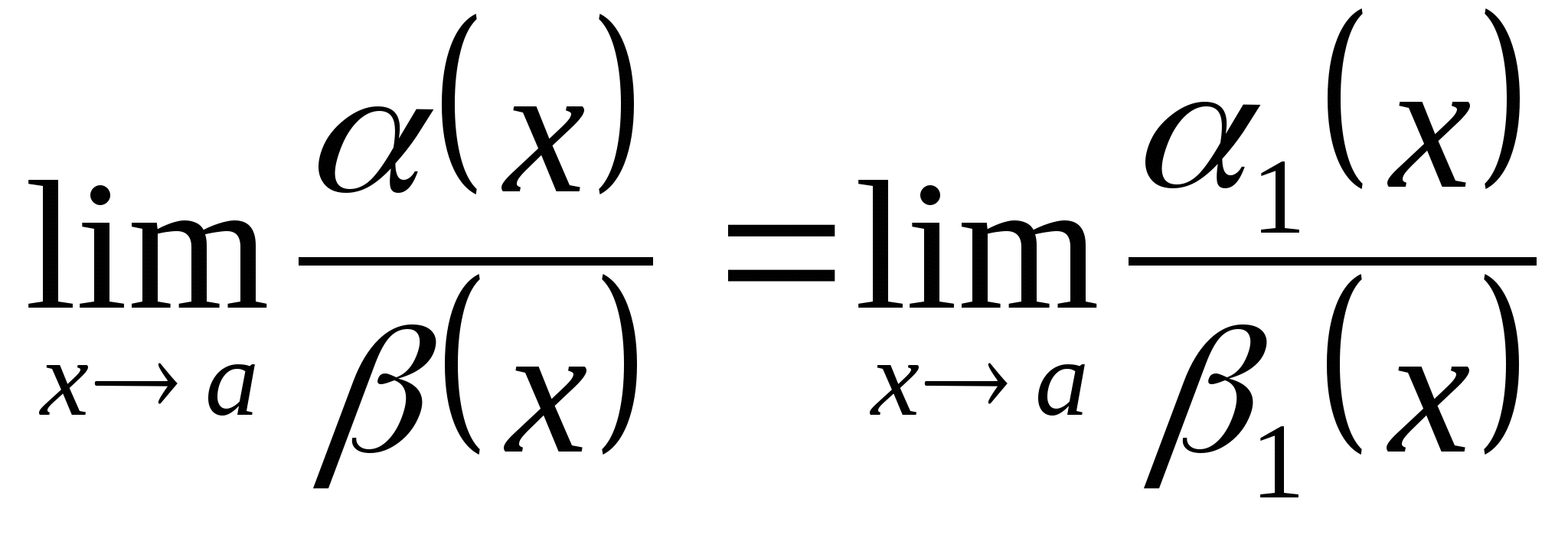 (если они существуют).
(если они существуют).
Таким образом, при вычислении пределов бесконечно малые величины при  функции можно заменять эквивалентными им.
функции можно заменять эквивалентными им.
Теорема (первый замечательный предел): Рассмотрим функцию 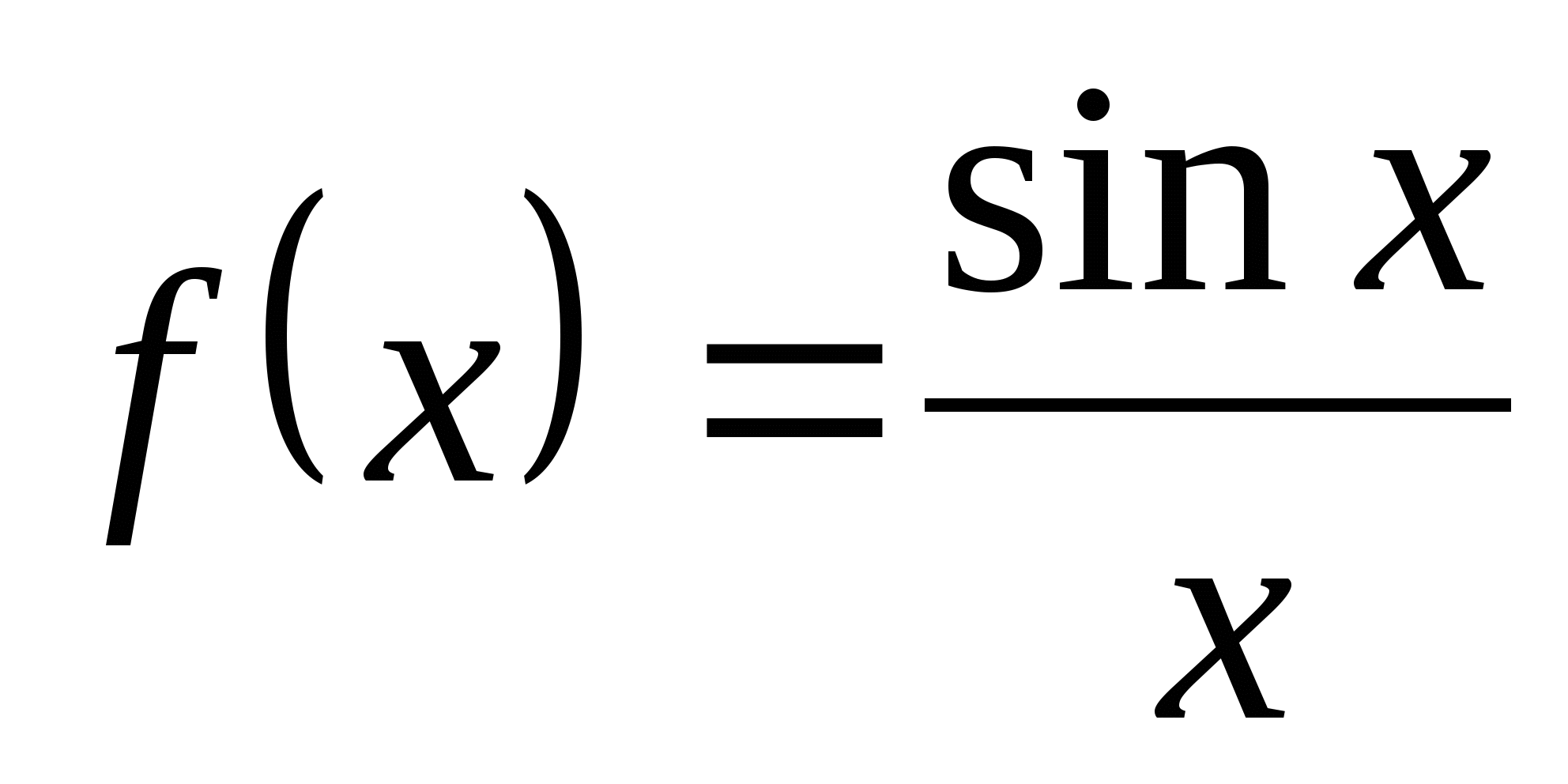 . Эта функция в точке
. Эта функция в точке 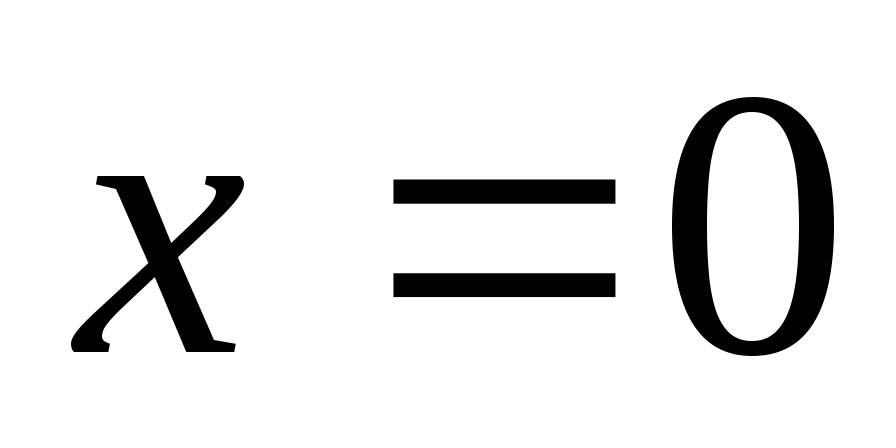 не определена, тем не менее ее предел при
не определена, тем не менее ее предел при  существует, причем
существует, причем 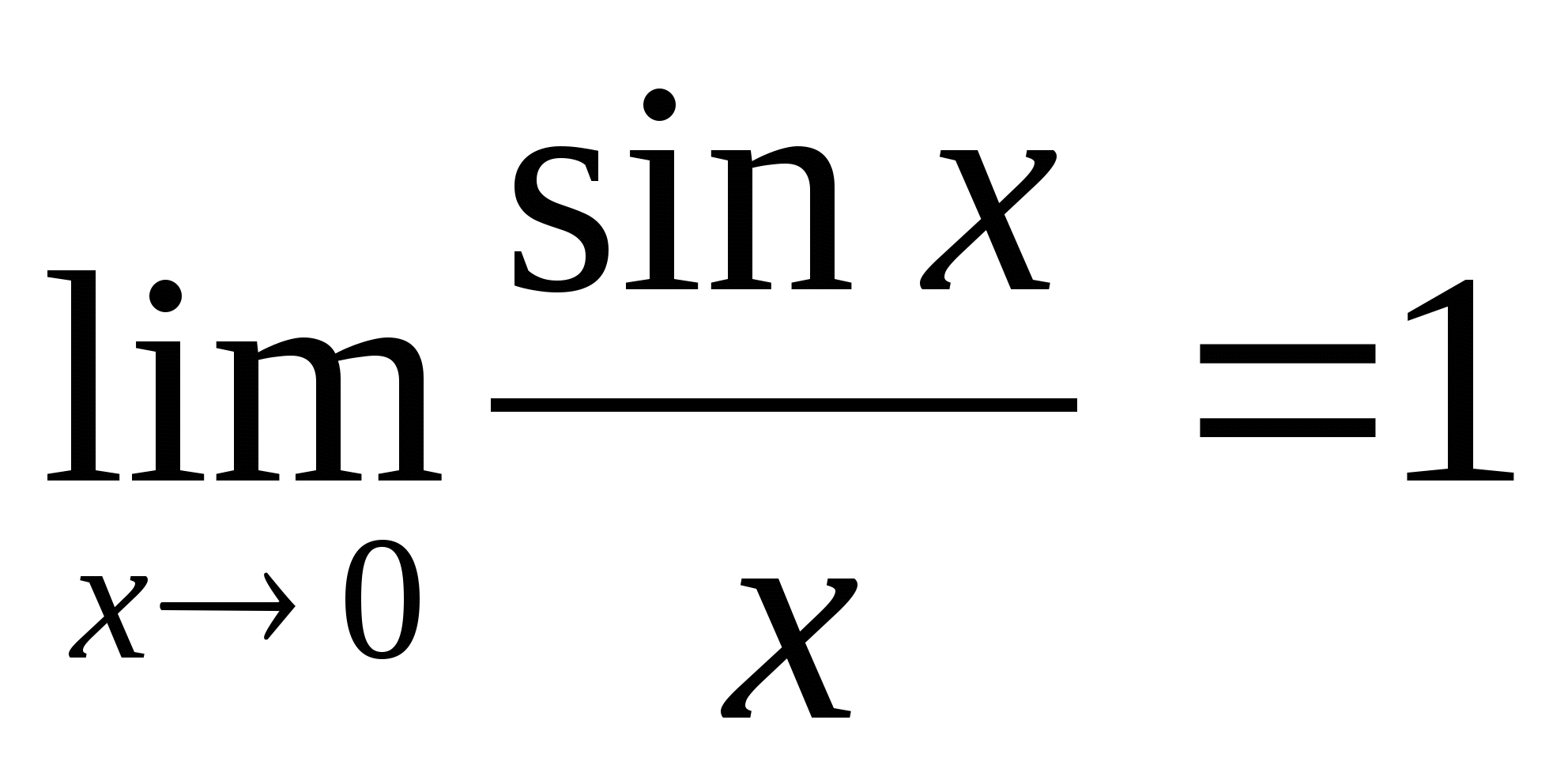 .
.
Следствия из теоремы:
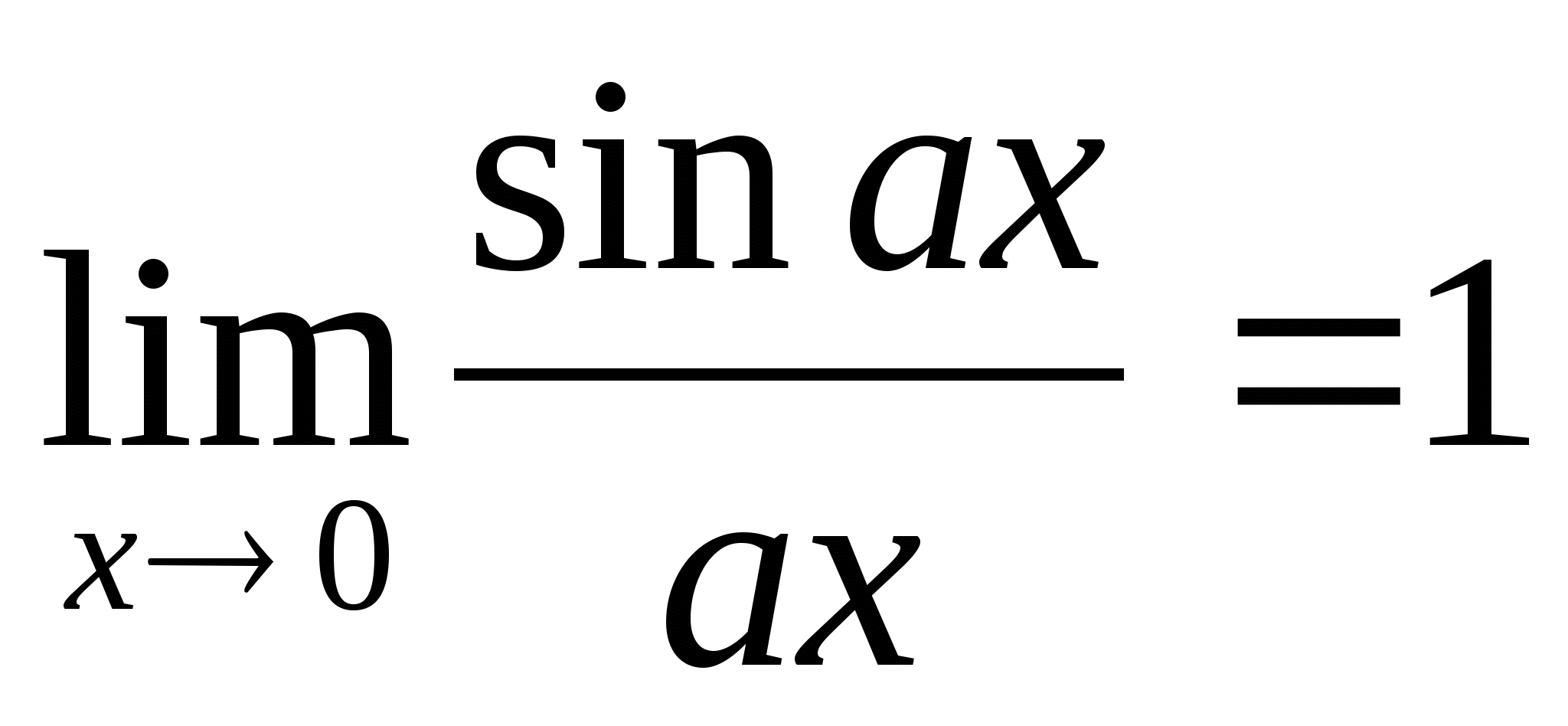 ;
; 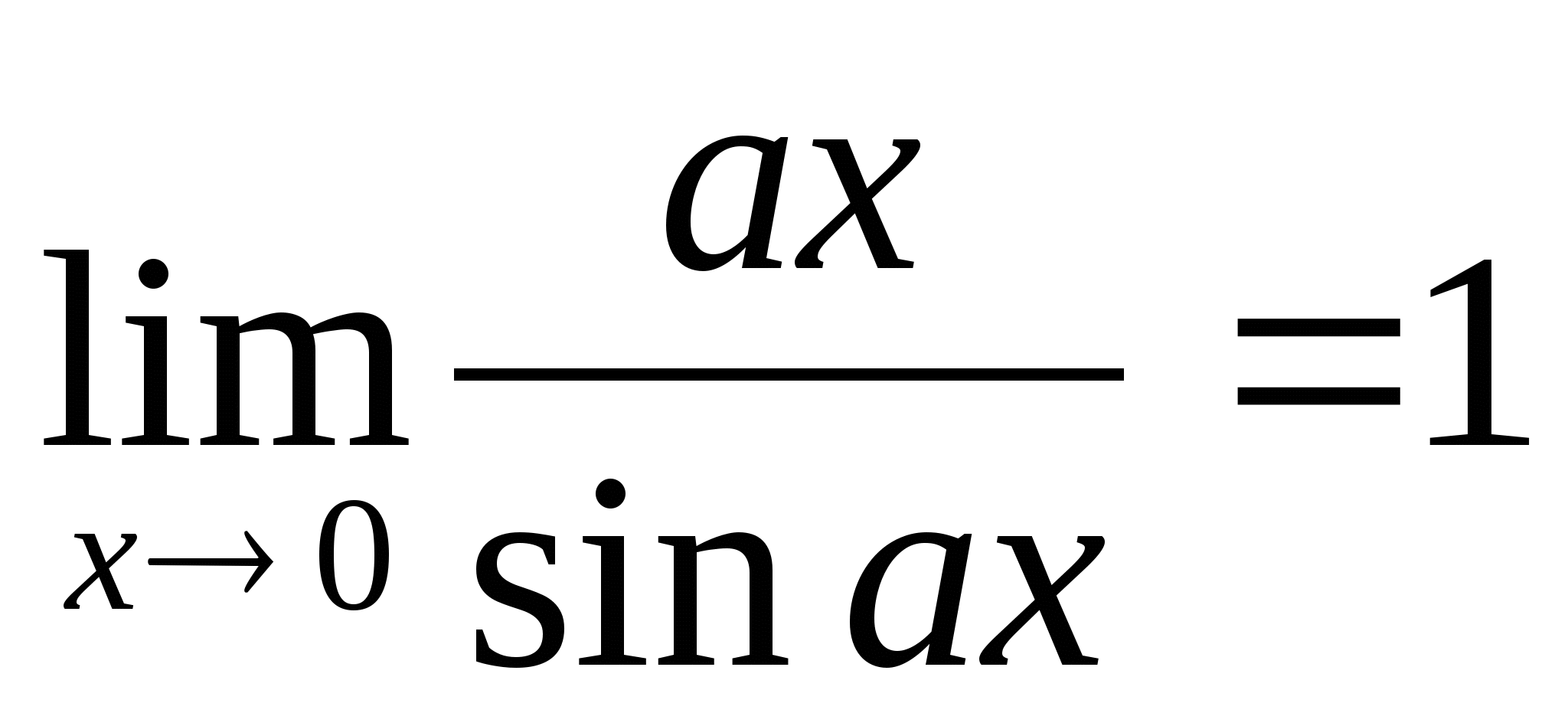 ;
; 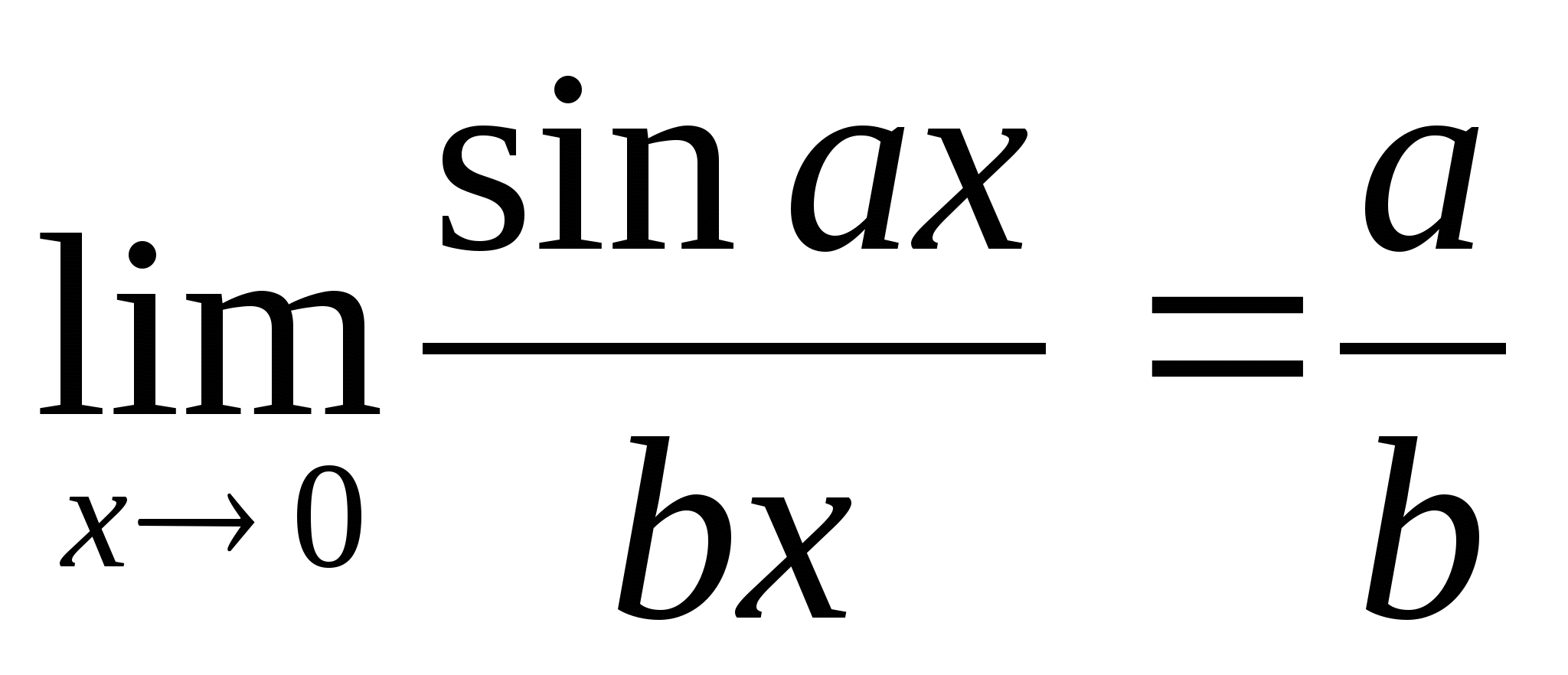 ;
; 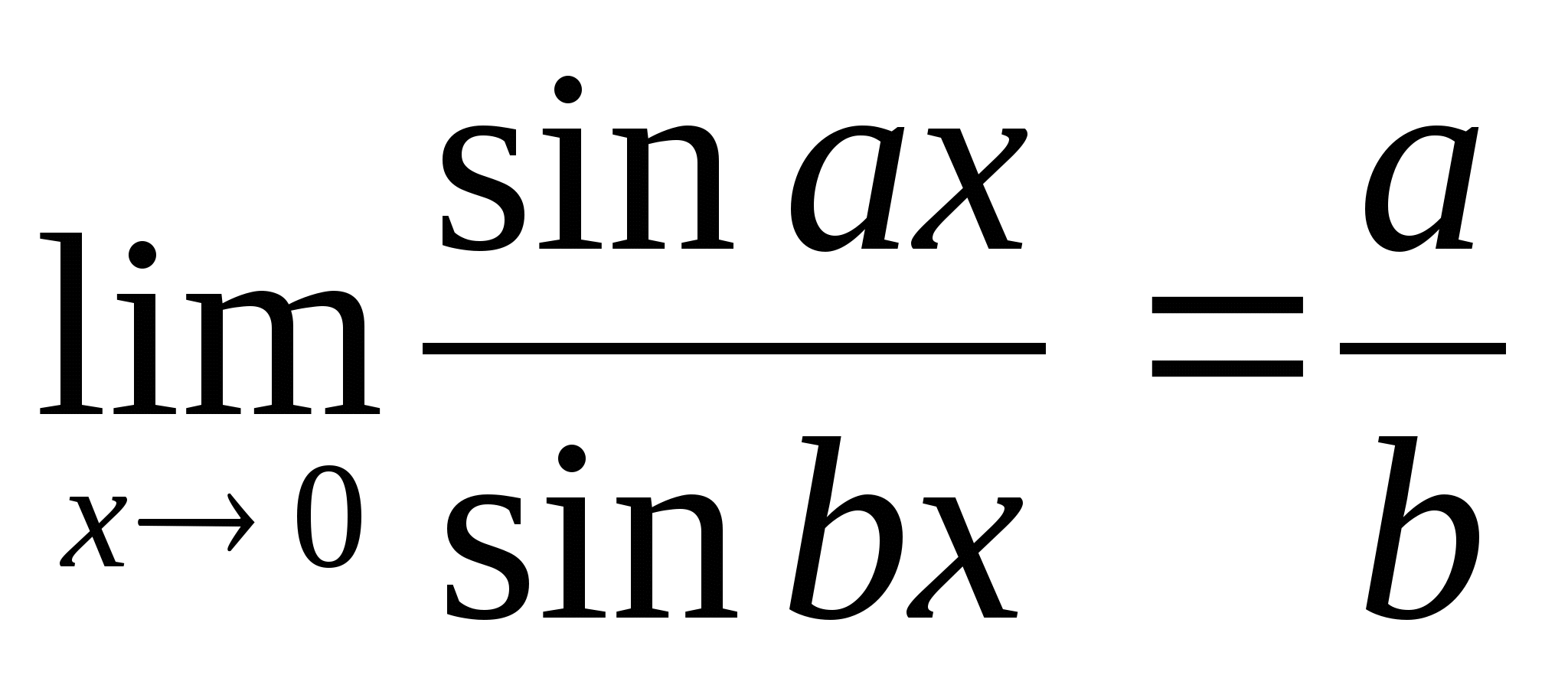 ;
;
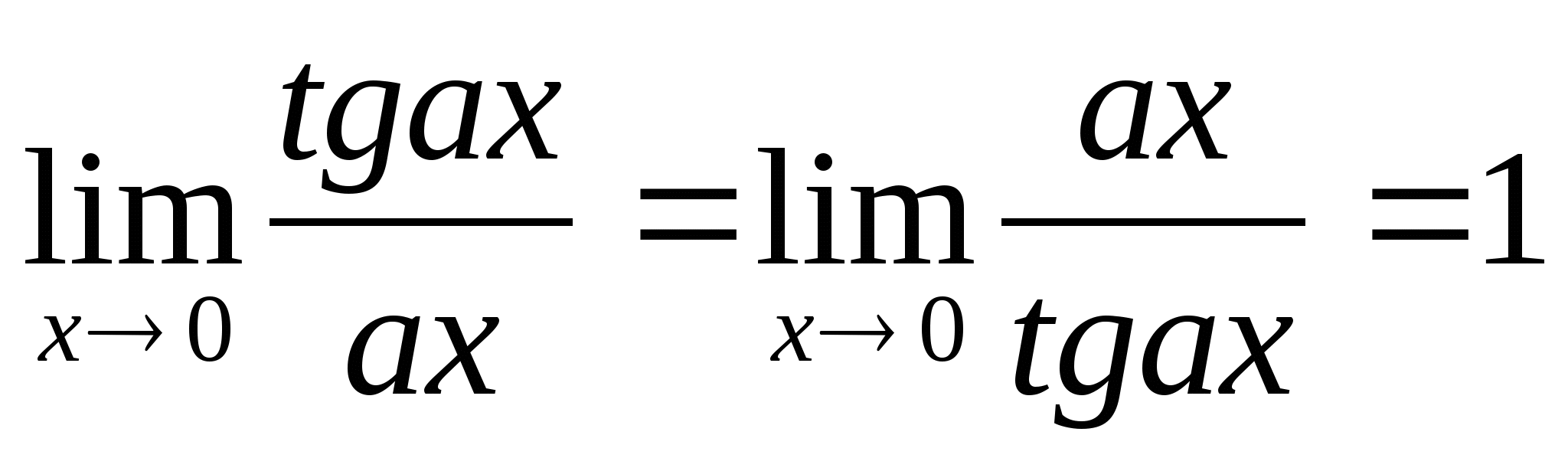 ;
; 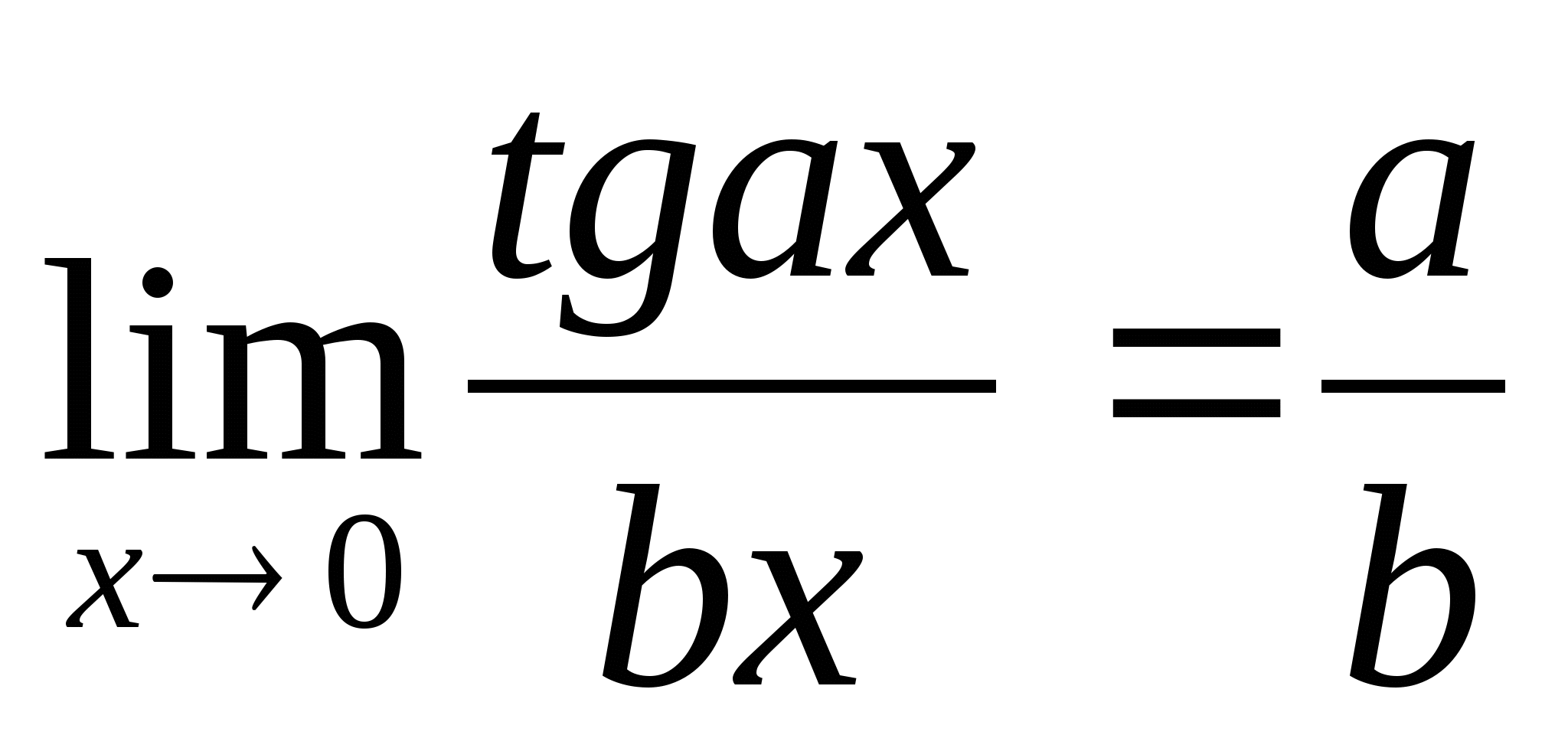 ;
; 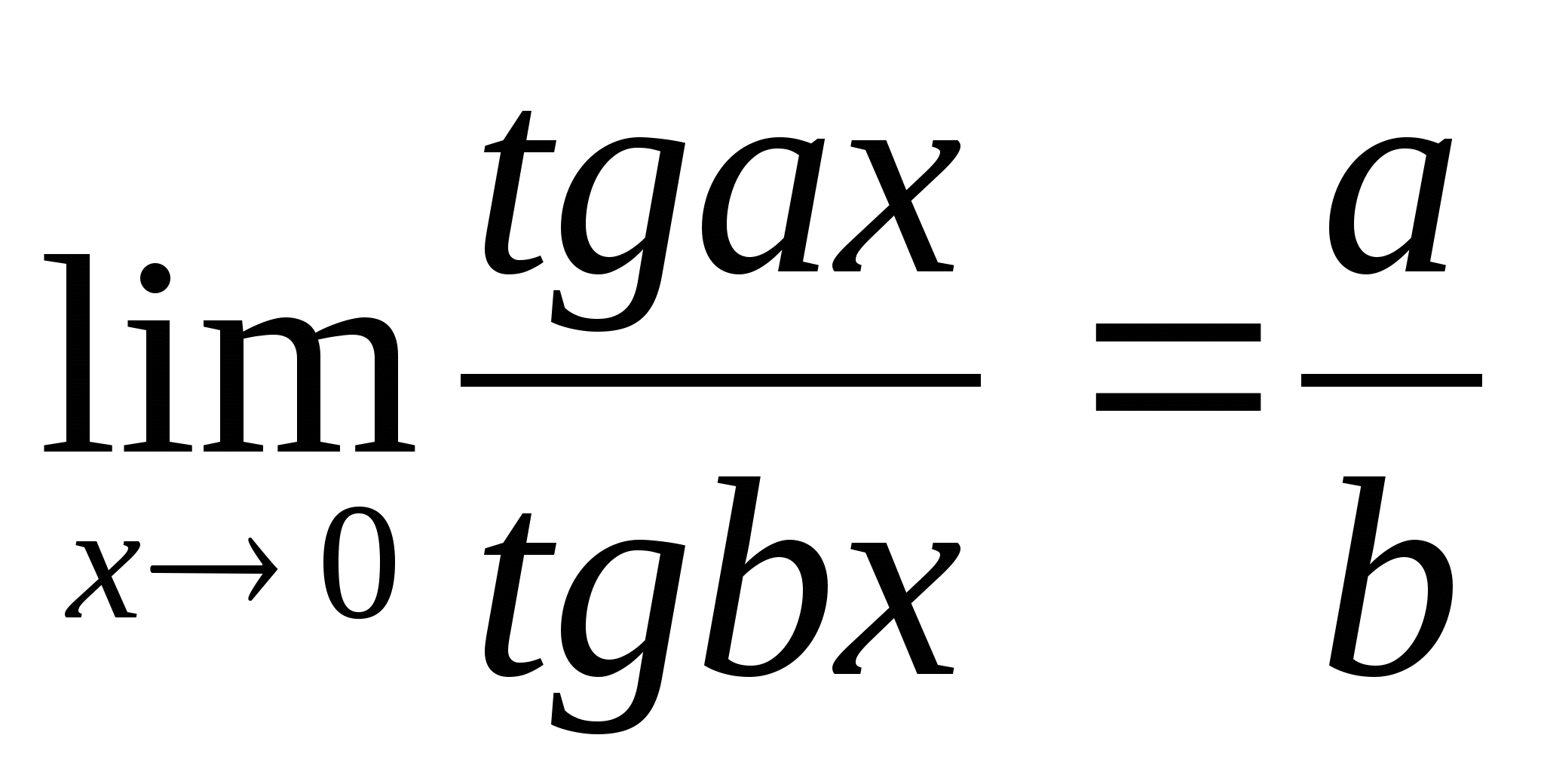 ;
;
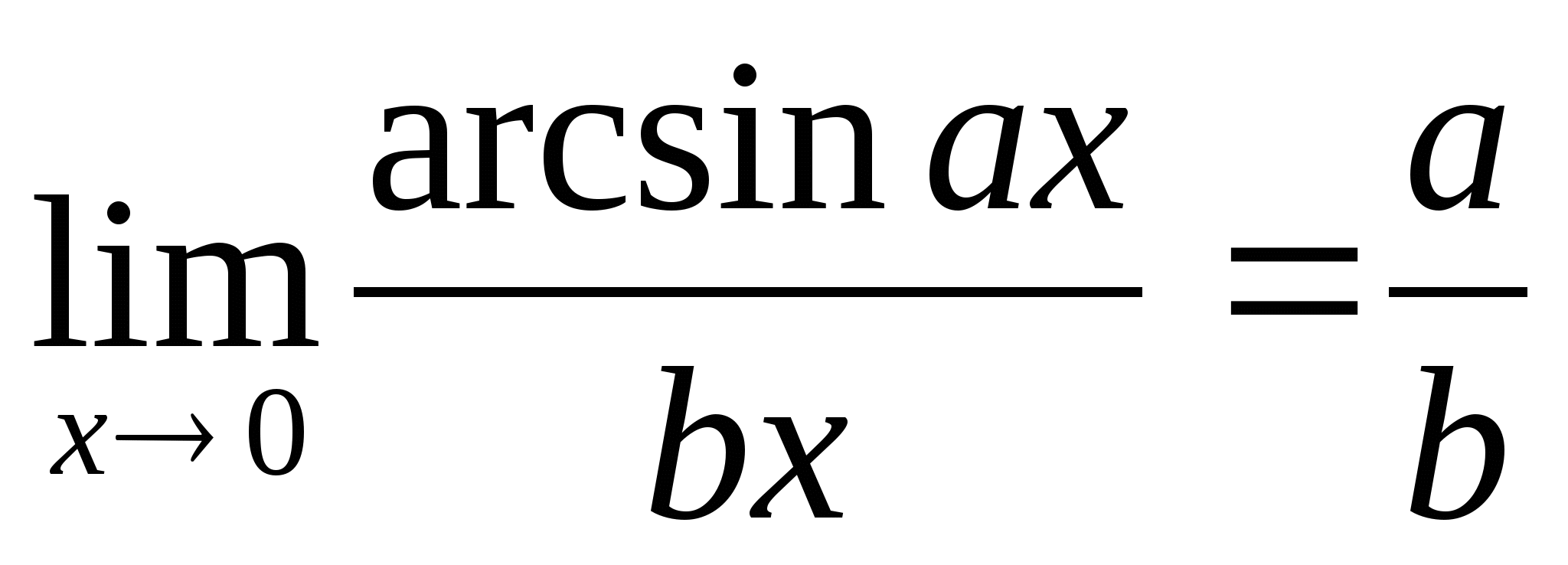 ;
; 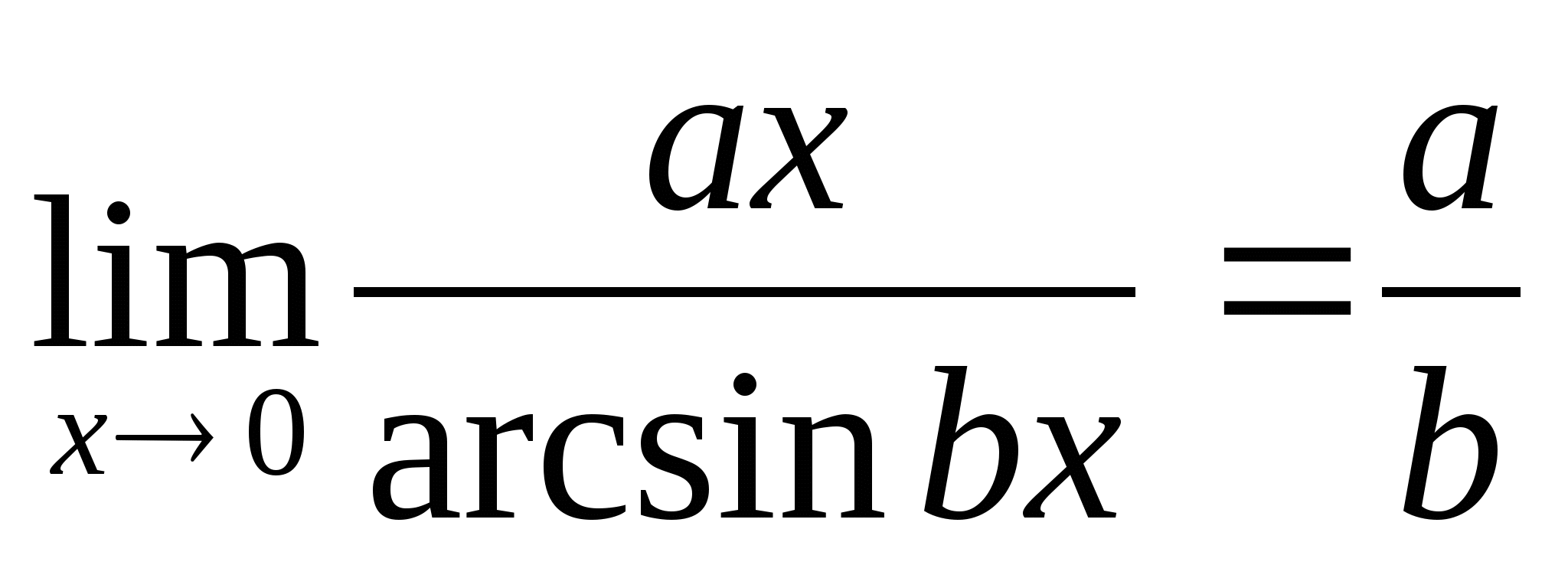 .
.
Теорема (второй замечательный предел): Выражение 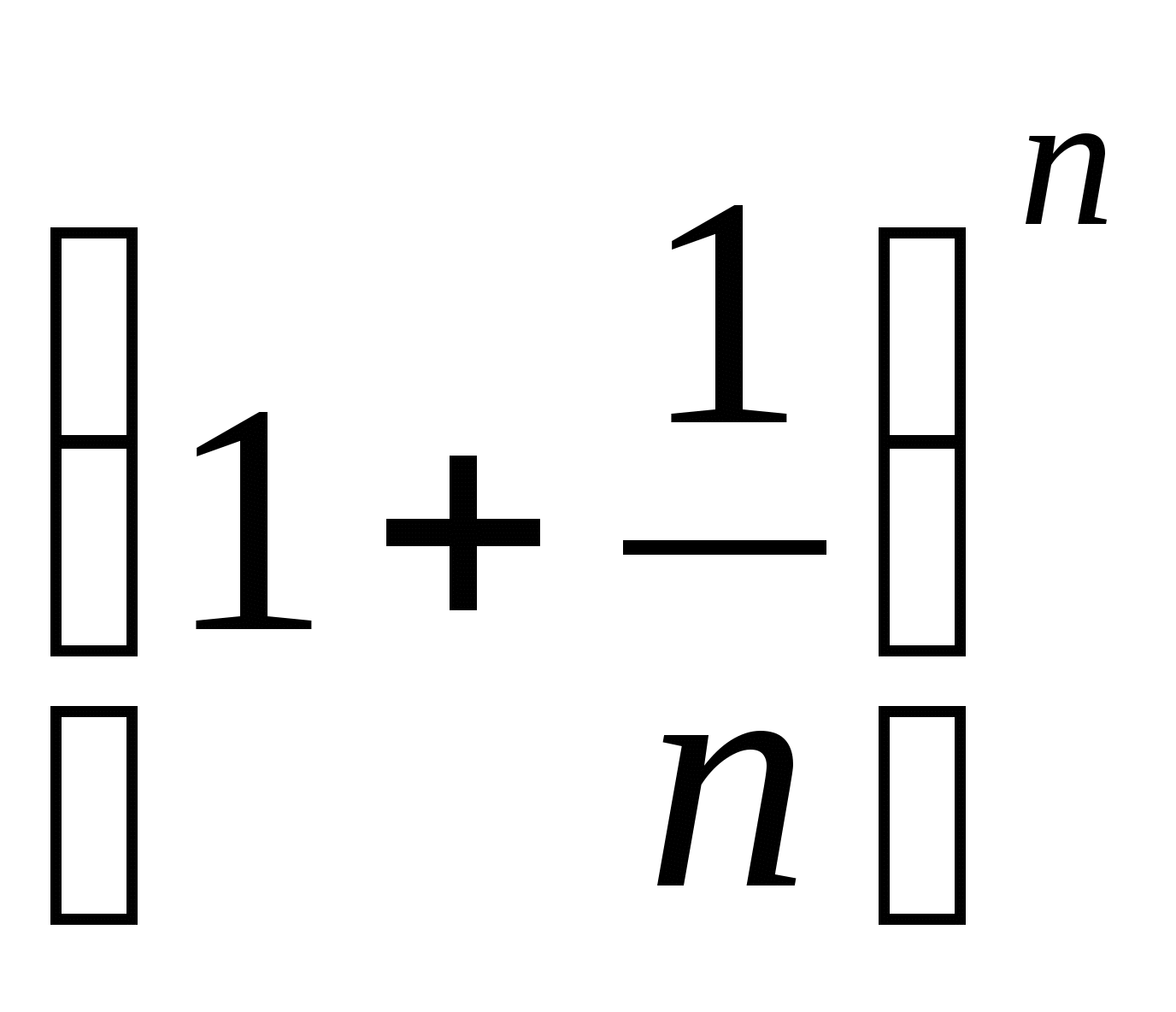 , где
, где  — натуральное число, стремится к вполне определенному пределу, когда число
— натуральное число, стремится к вполне определенному пределу, когда число  . Этот предел большее 2 и меньше 3. То есть можно утверждать
. Этот предел большее 2 и меньше 3. То есть можно утверждать 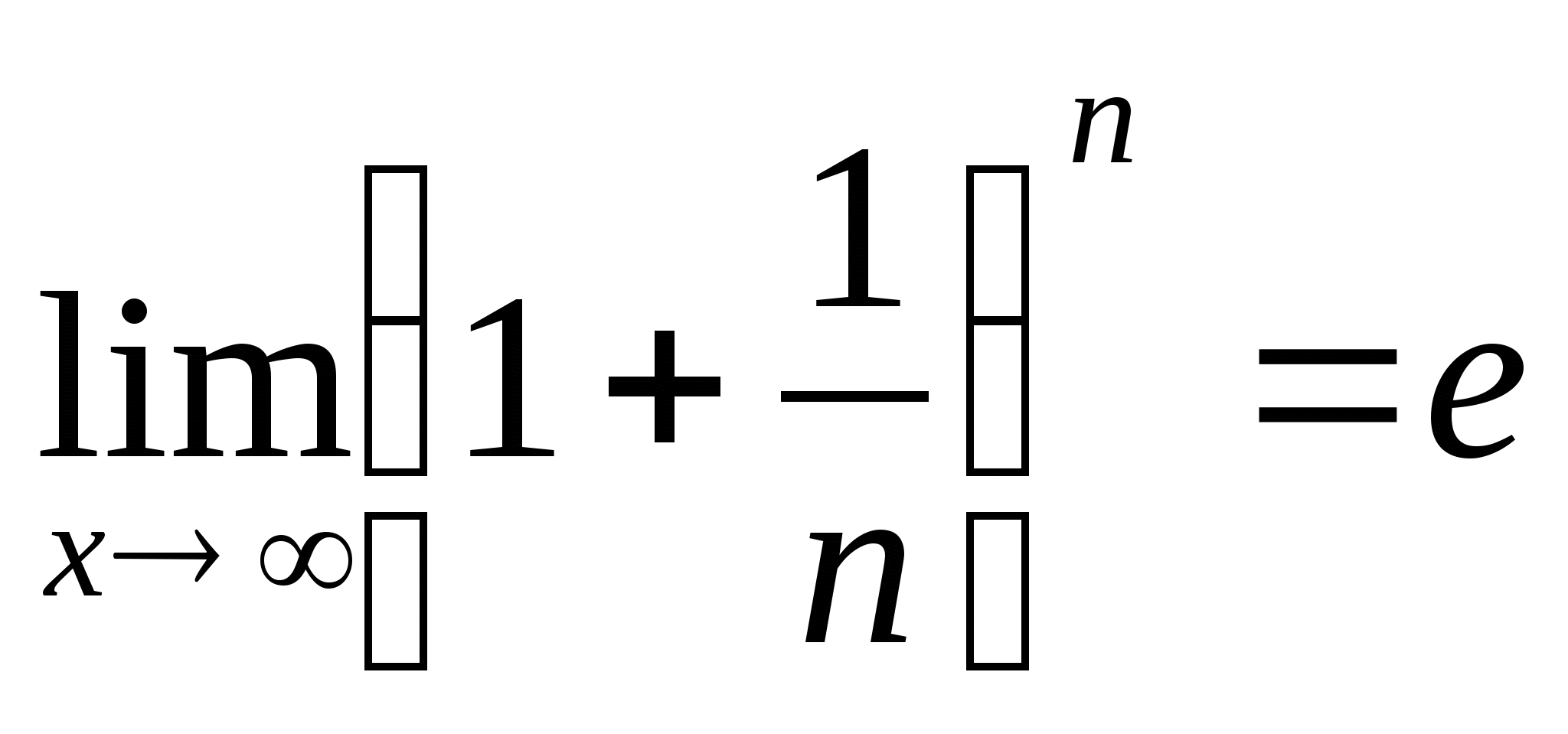 .
.
Следствия из теоремы:
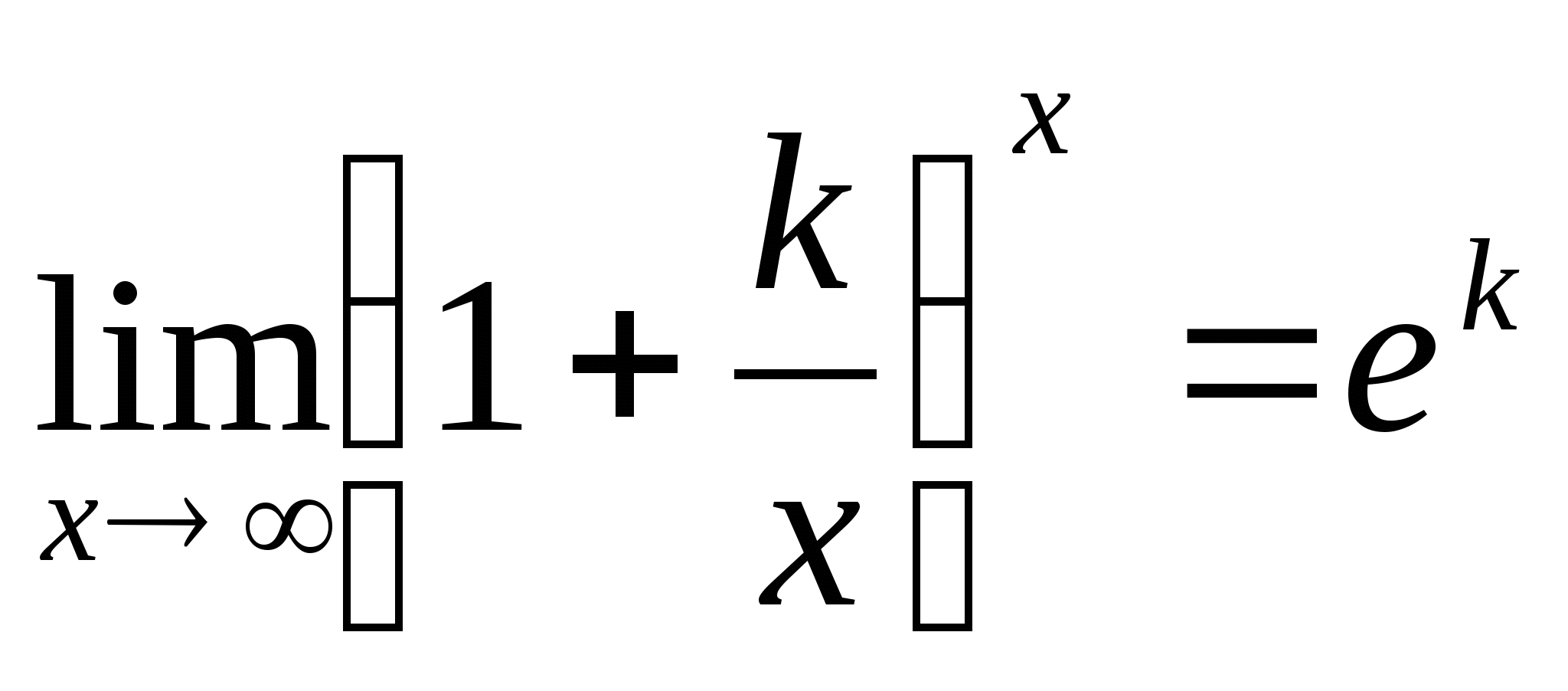 ;
; 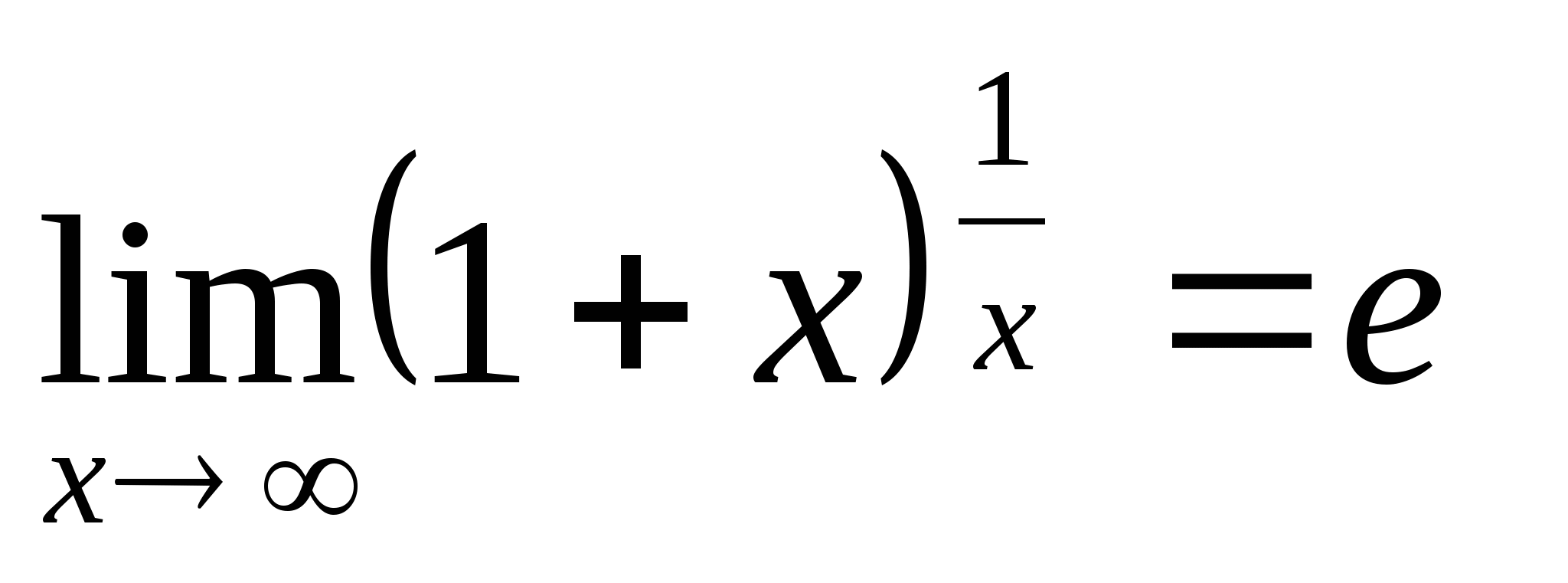 .
.
Примеры:
1. 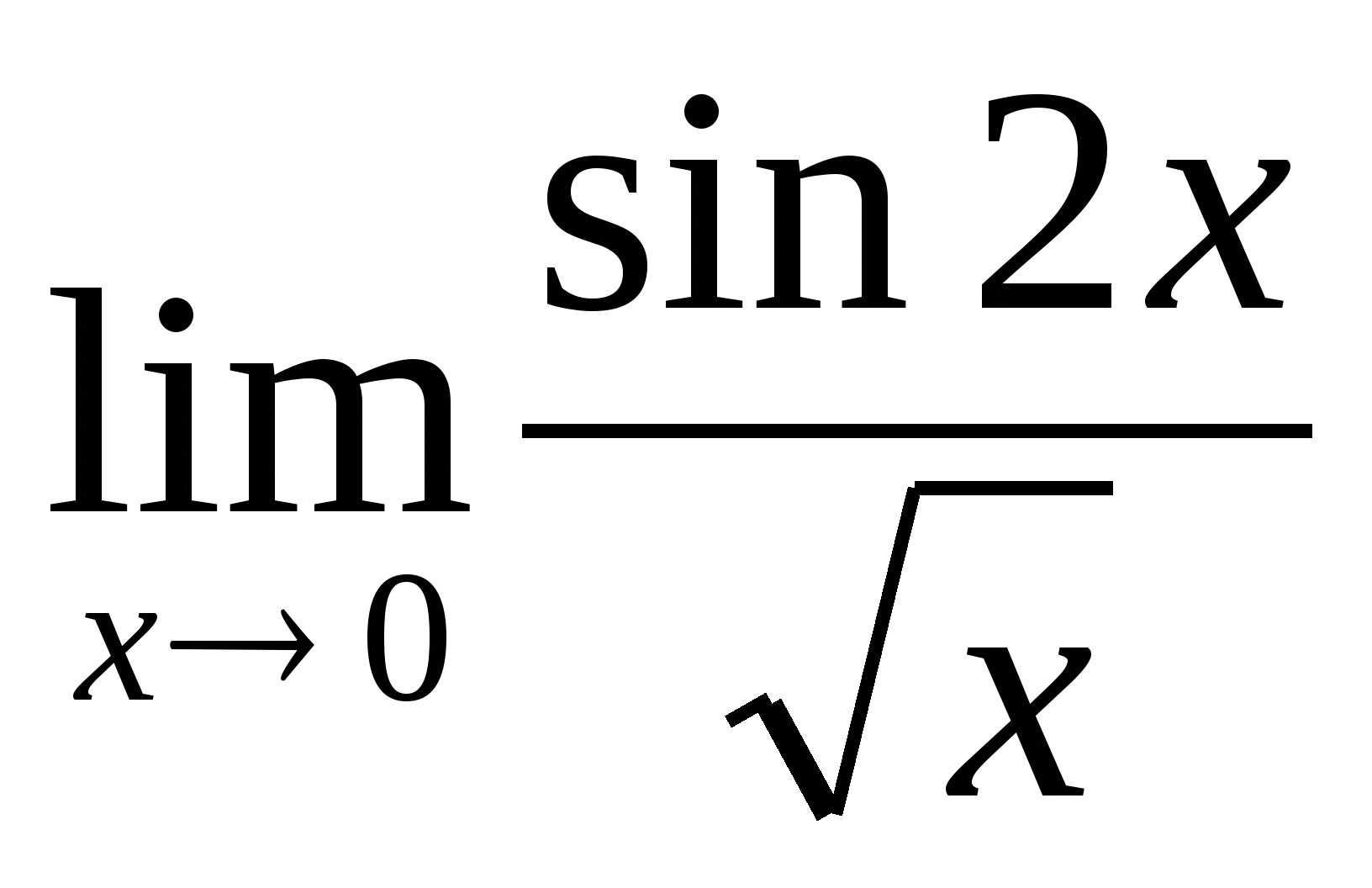
Решение: 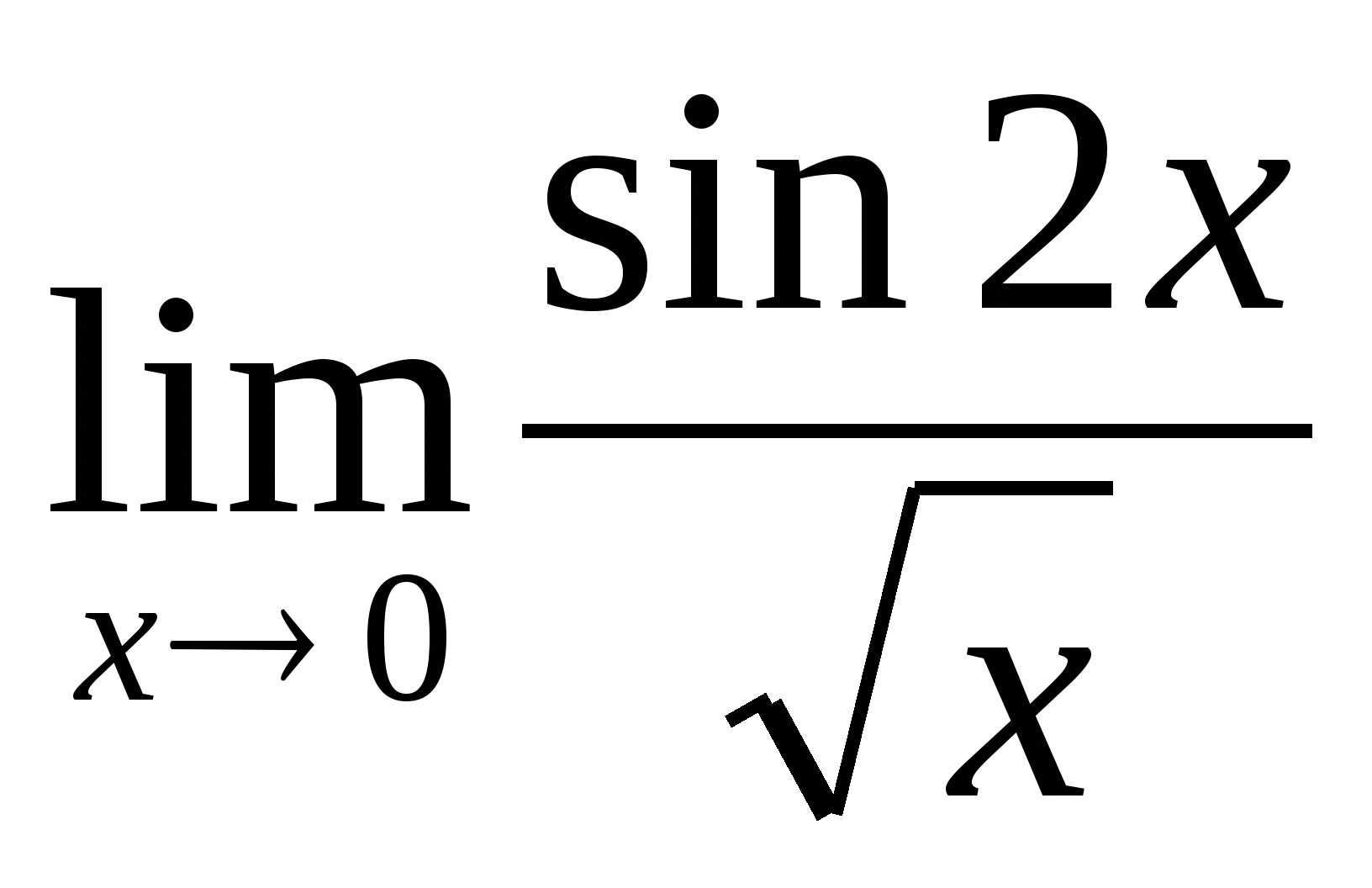 =
=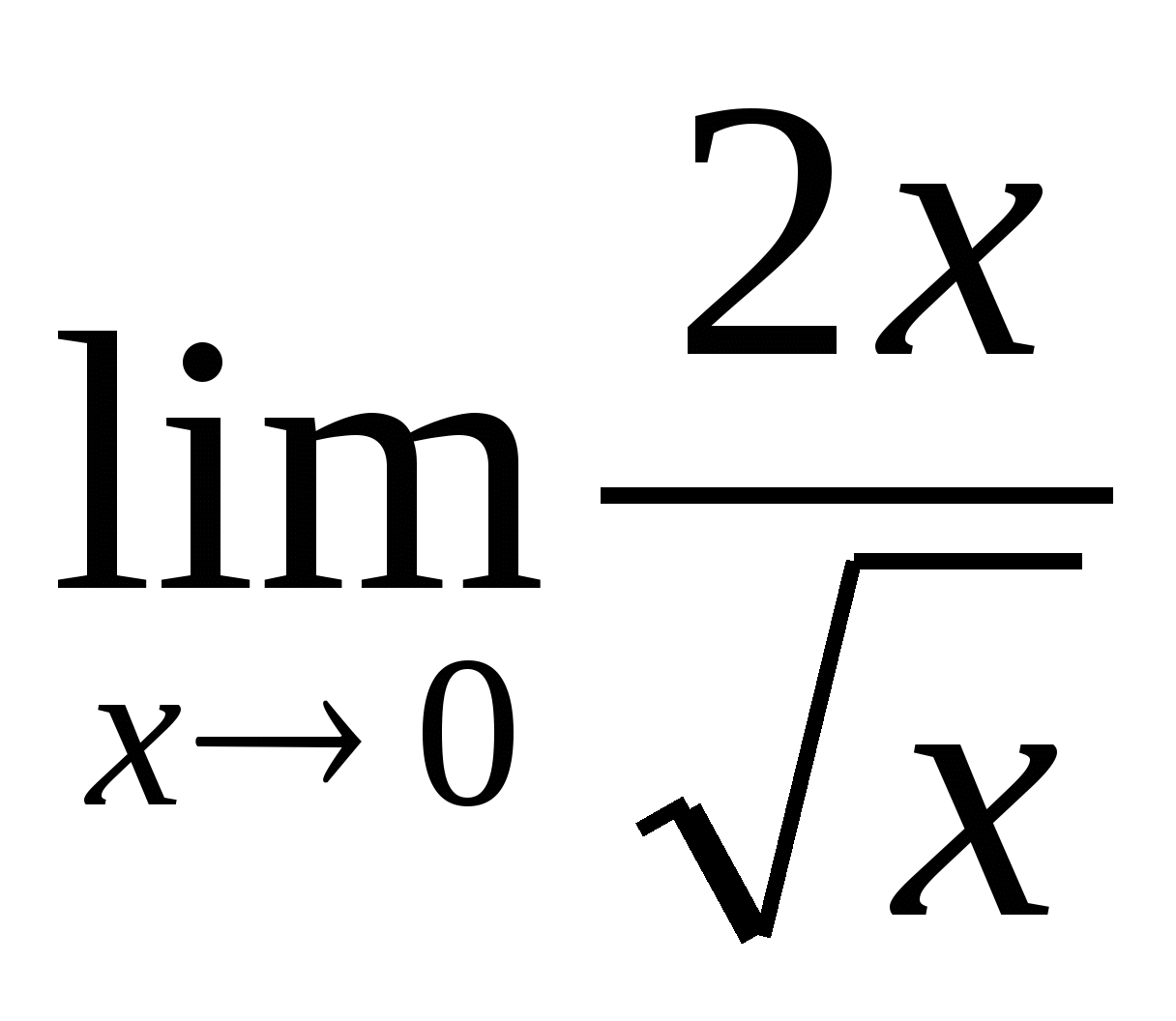 =
= 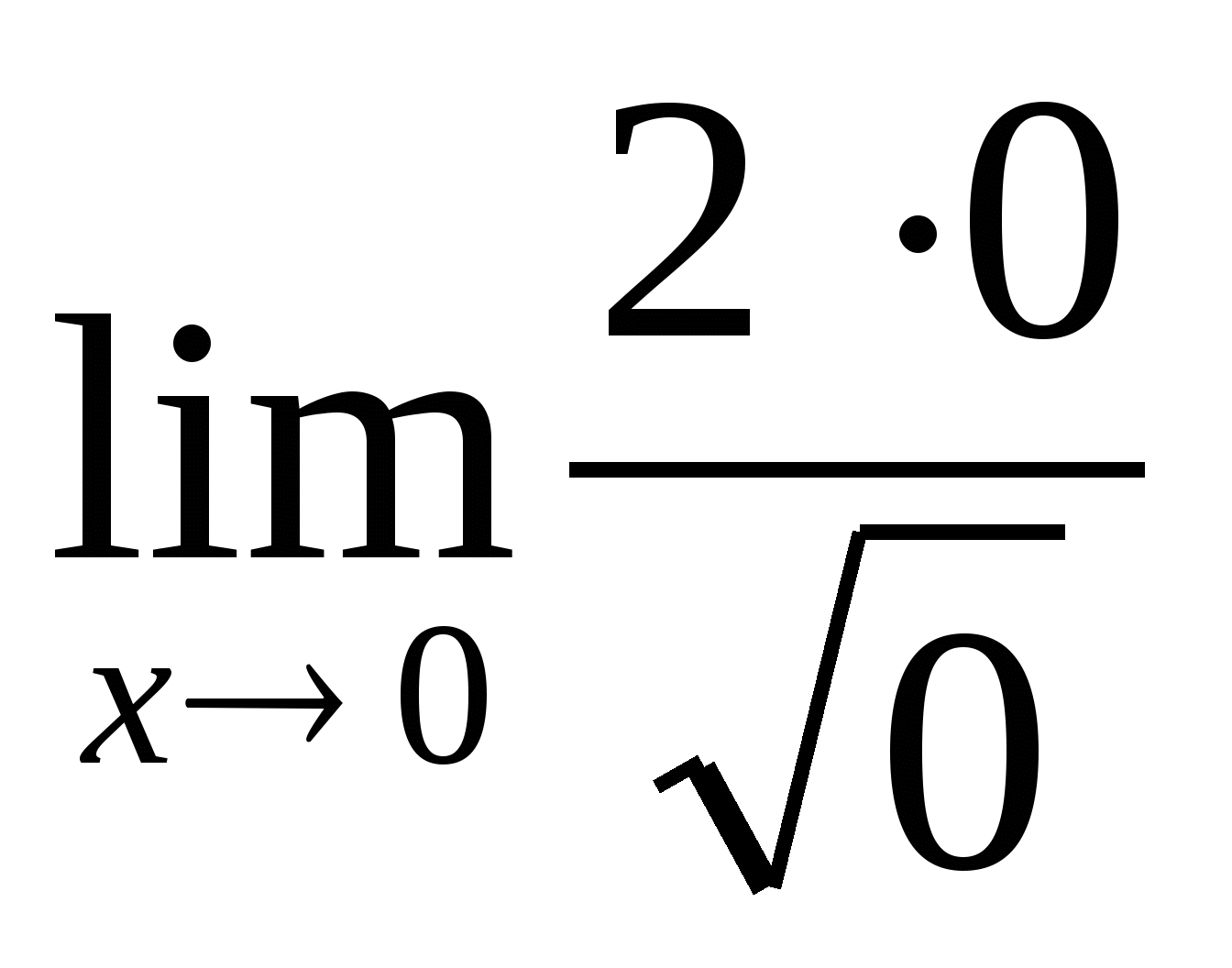 =
= 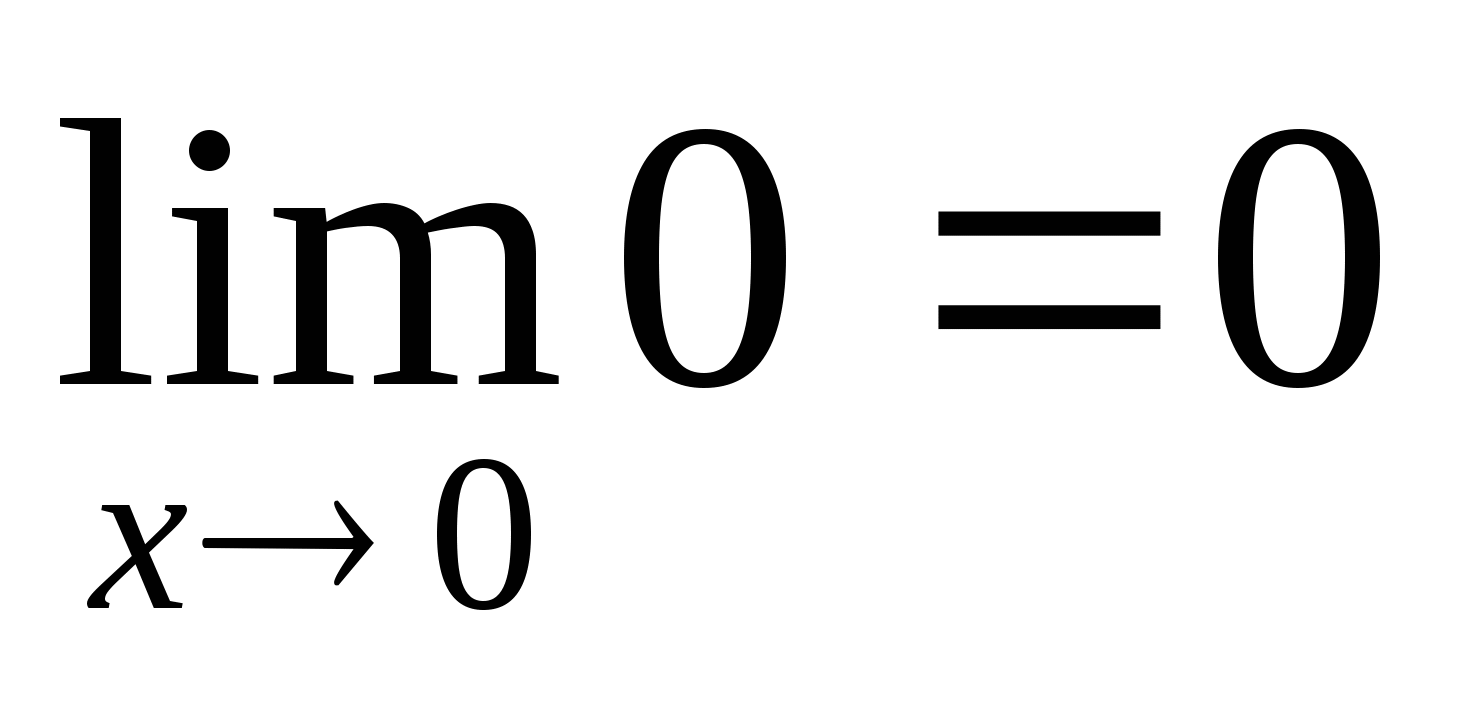
(воспользовались эквивалентностью 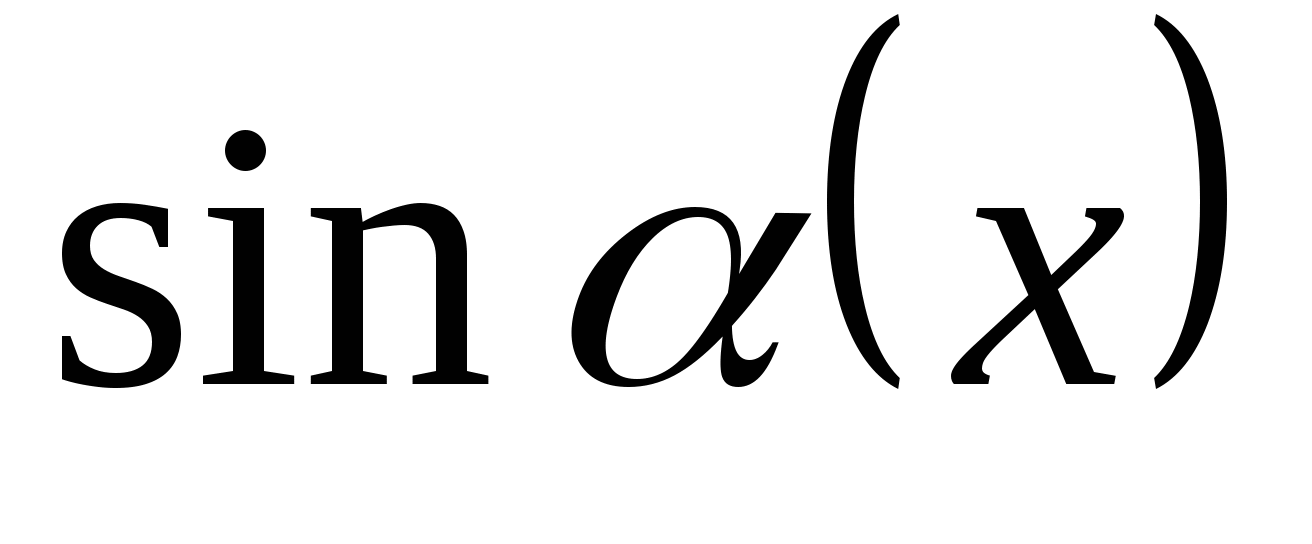 ~
~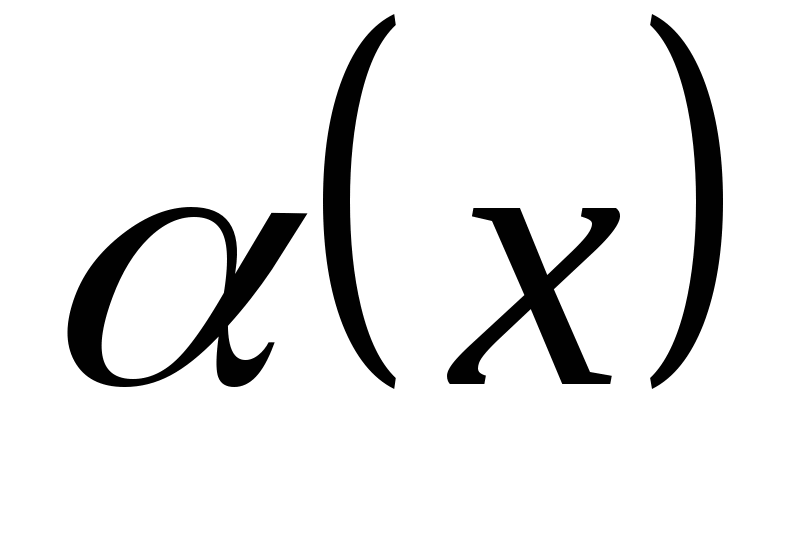 ). Ответ: 0.
). Ответ: 0.
2. 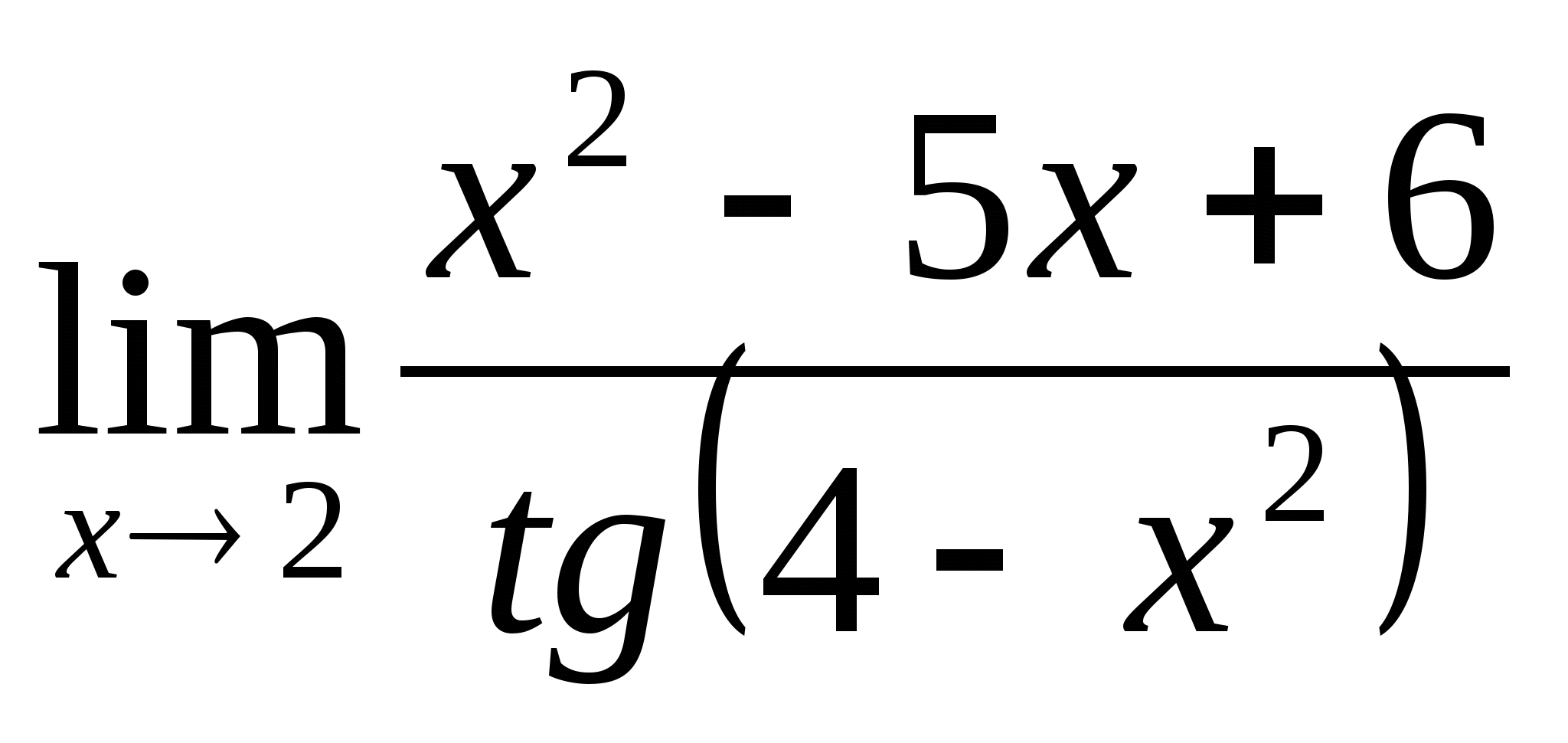
Решение: 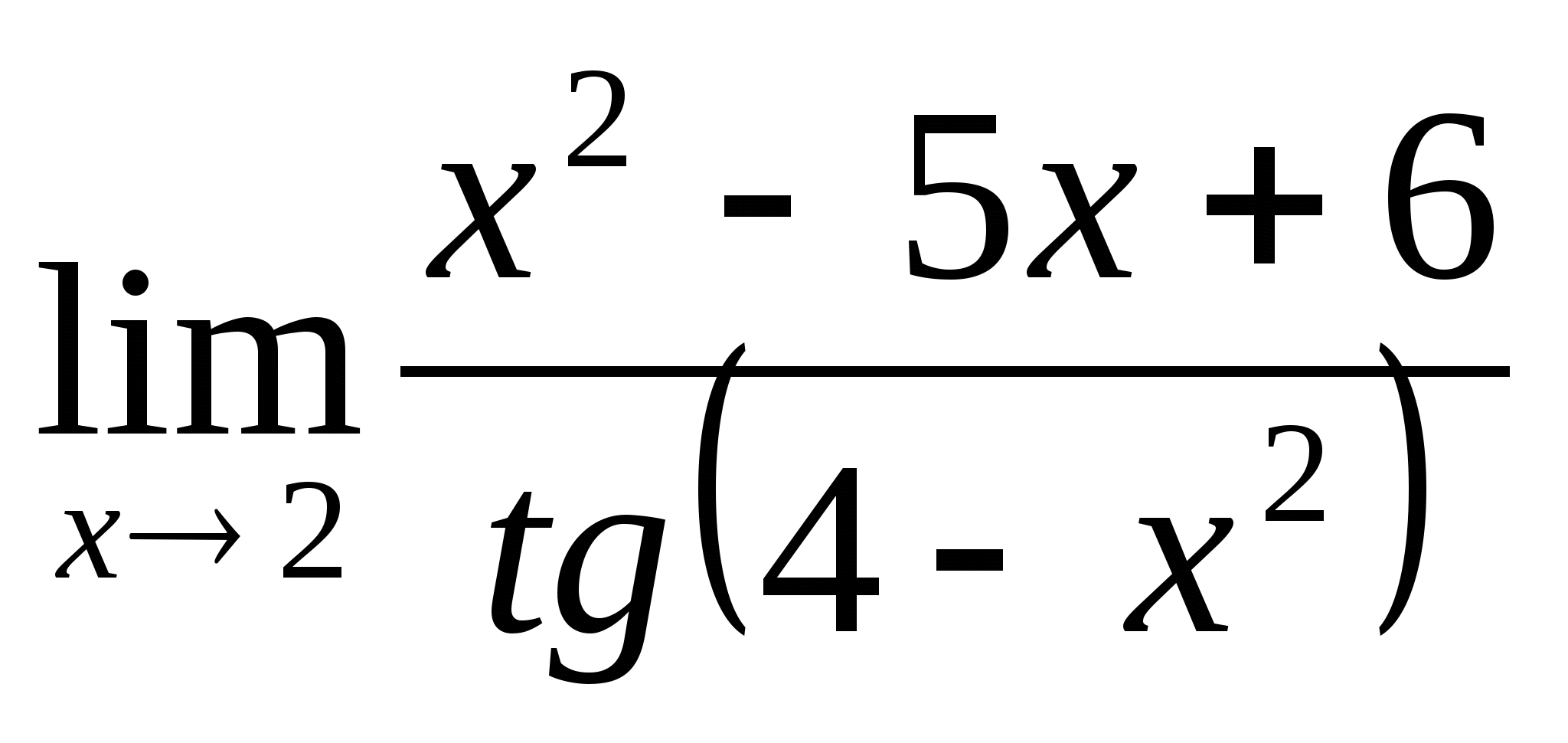 =
=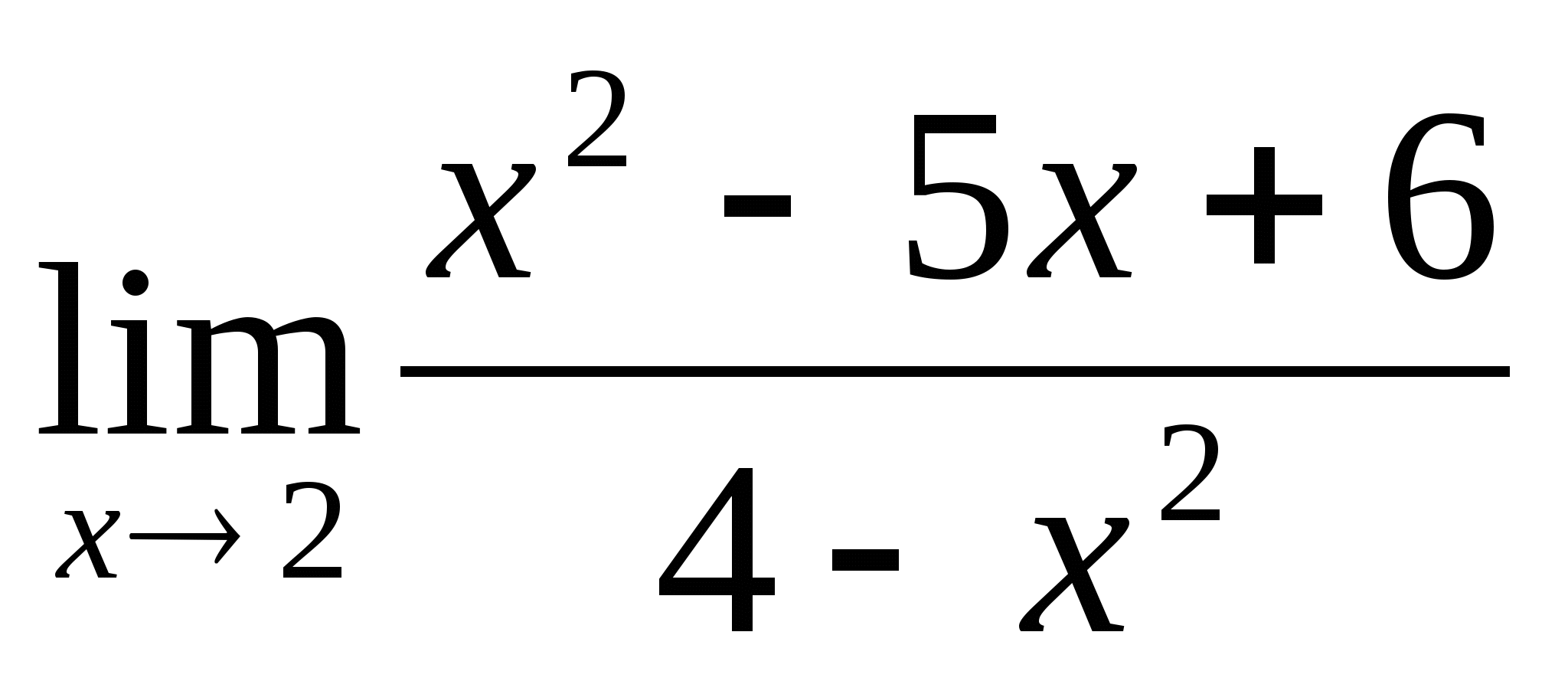 =
=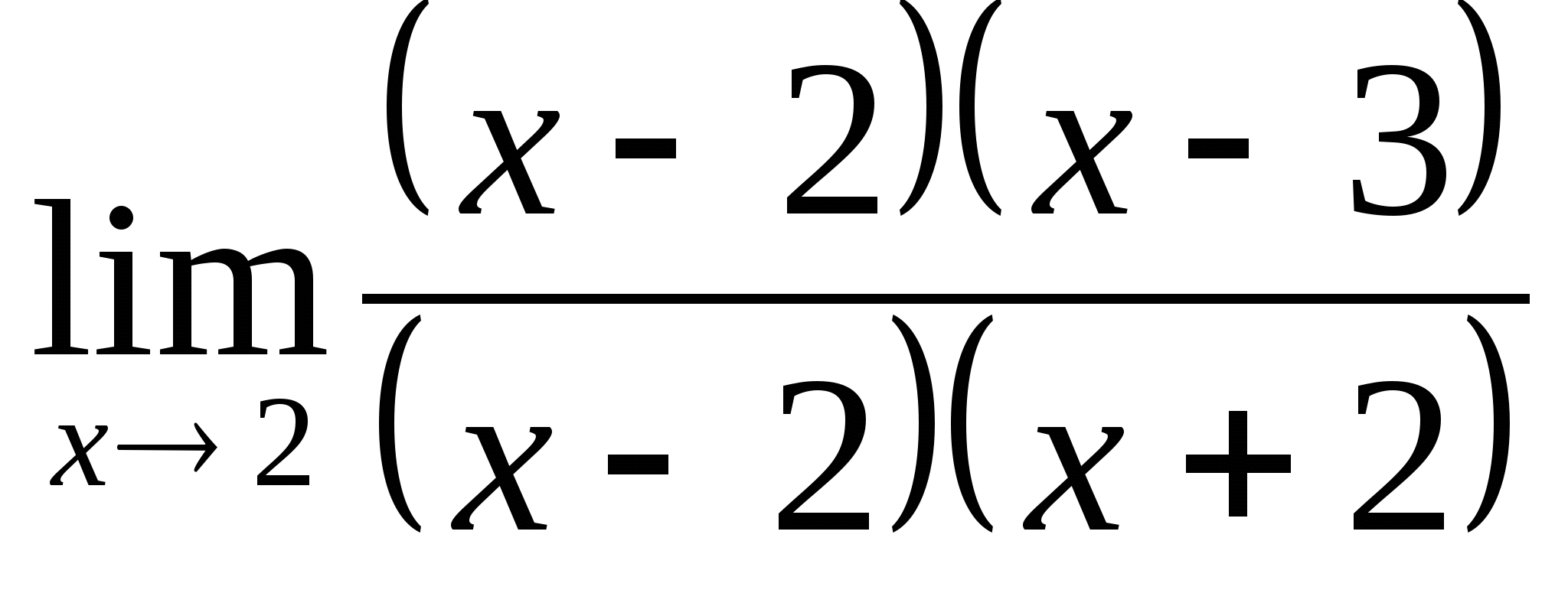 =
=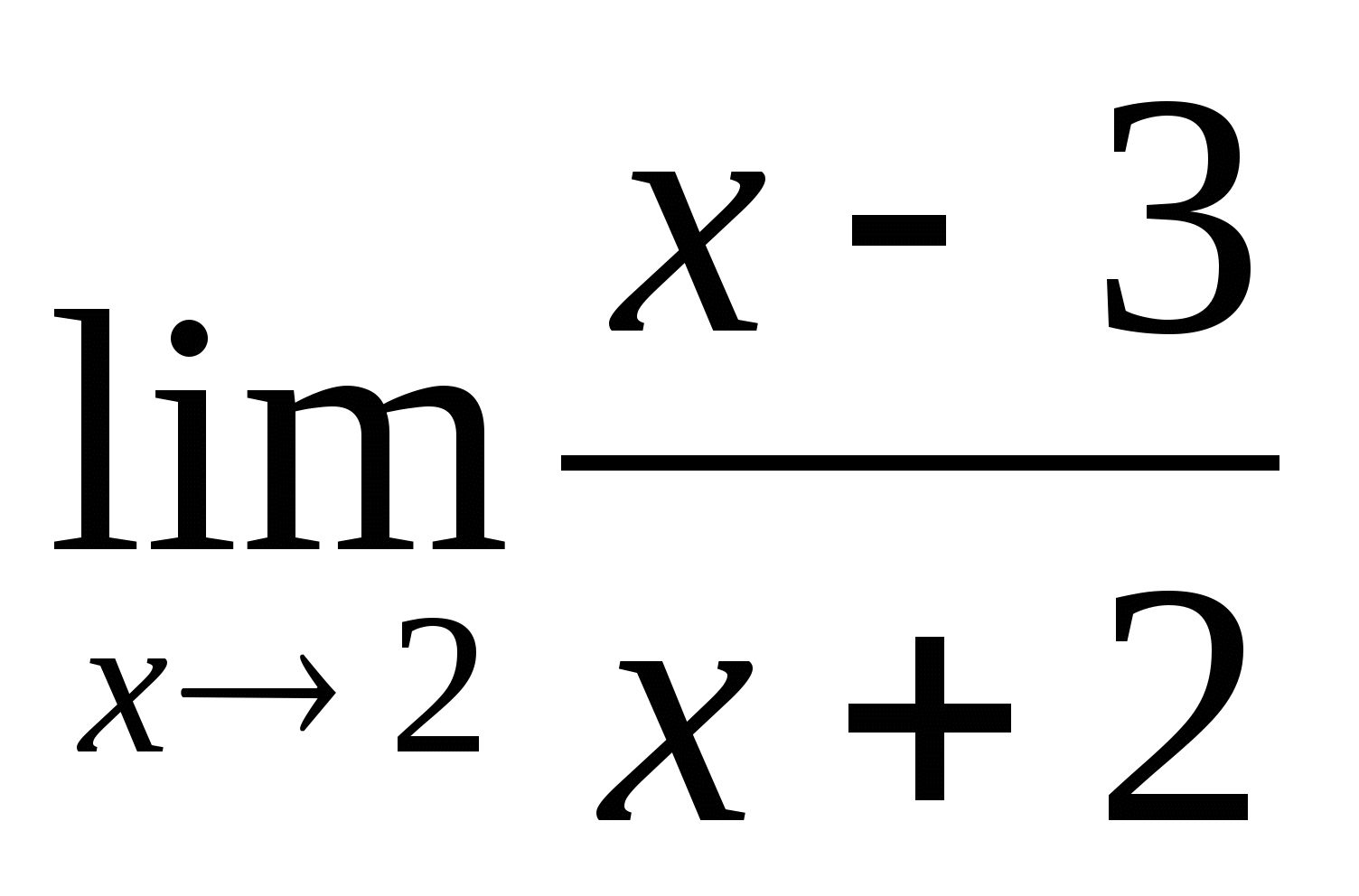 =
=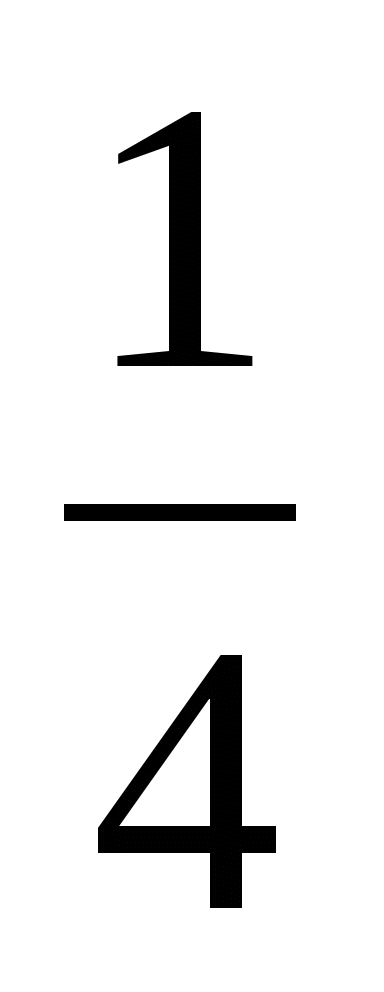
(воспользовались эквивалентностью 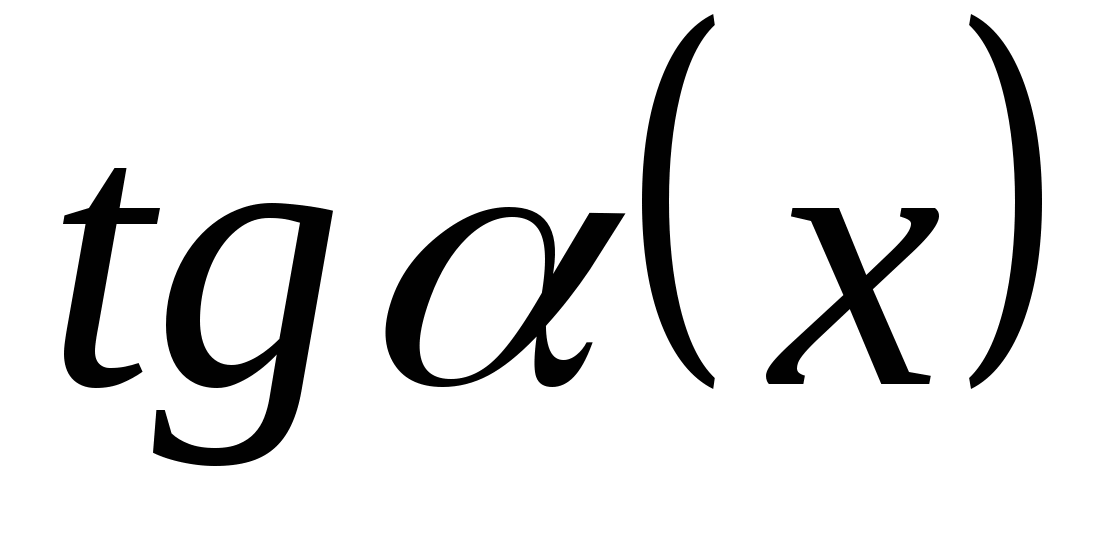 ~
~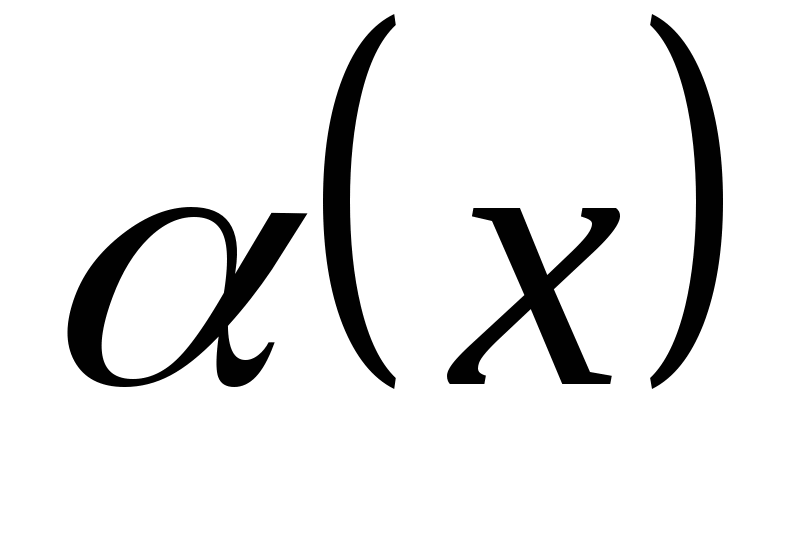 ). Ответ:
). Ответ: 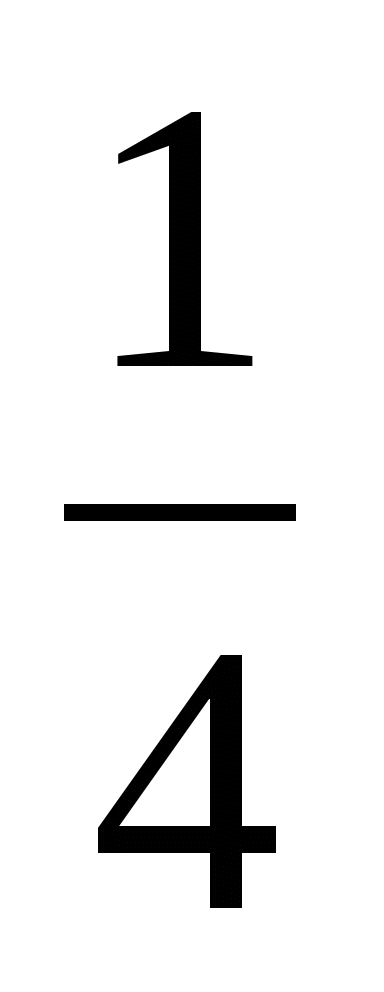 .
.
3. 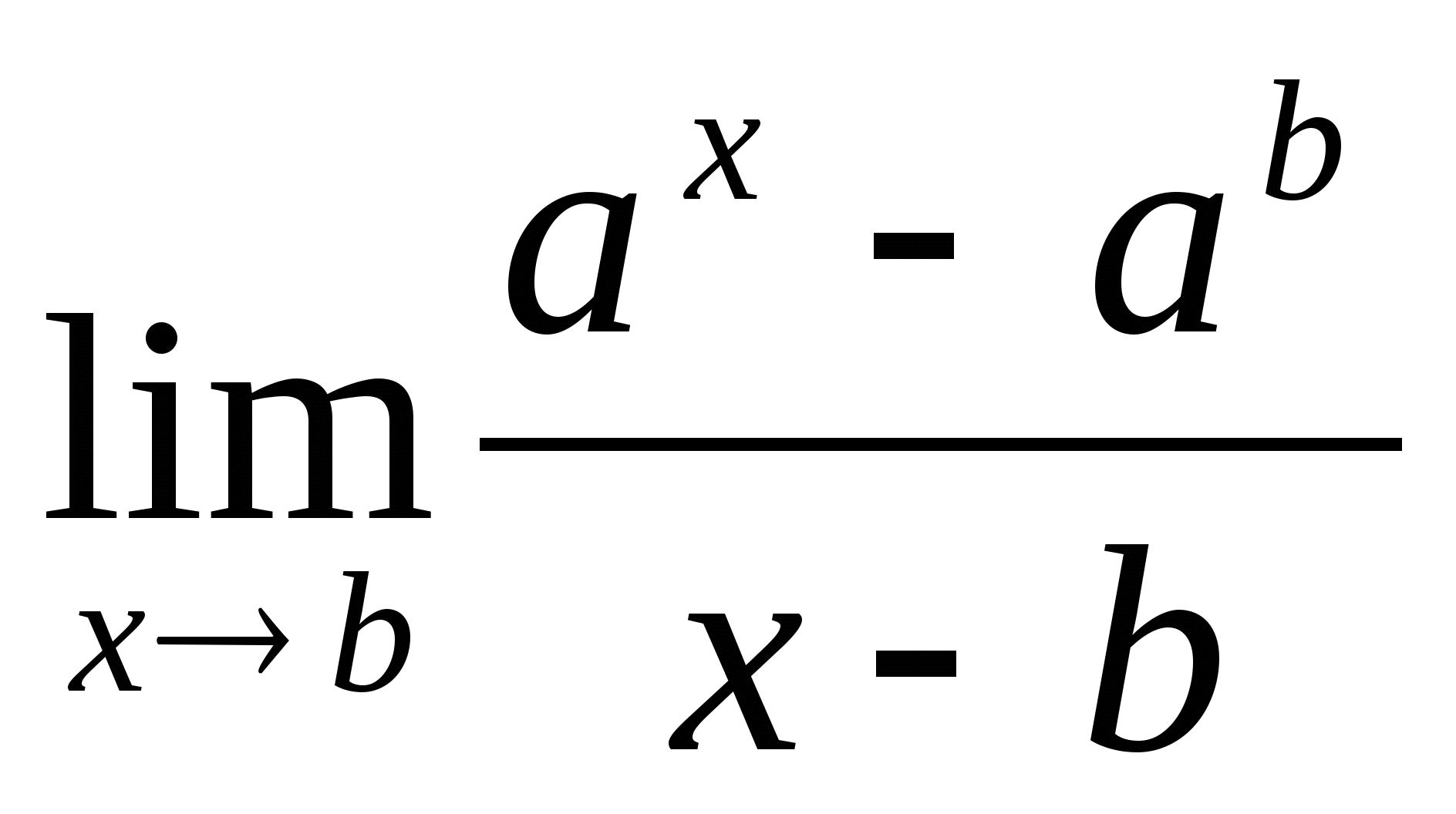
Решение: 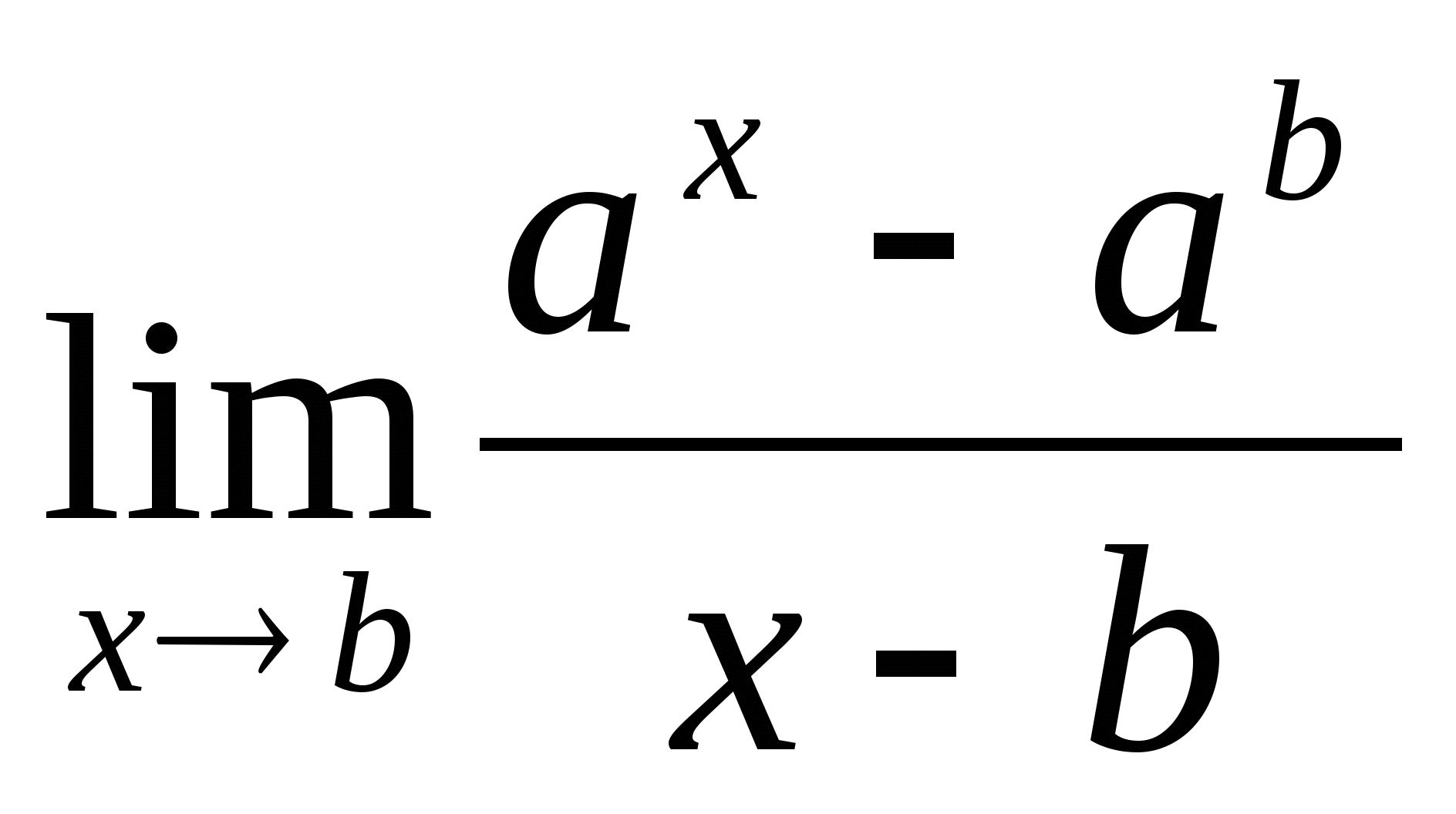 = (введем замену:
= (введем замену: 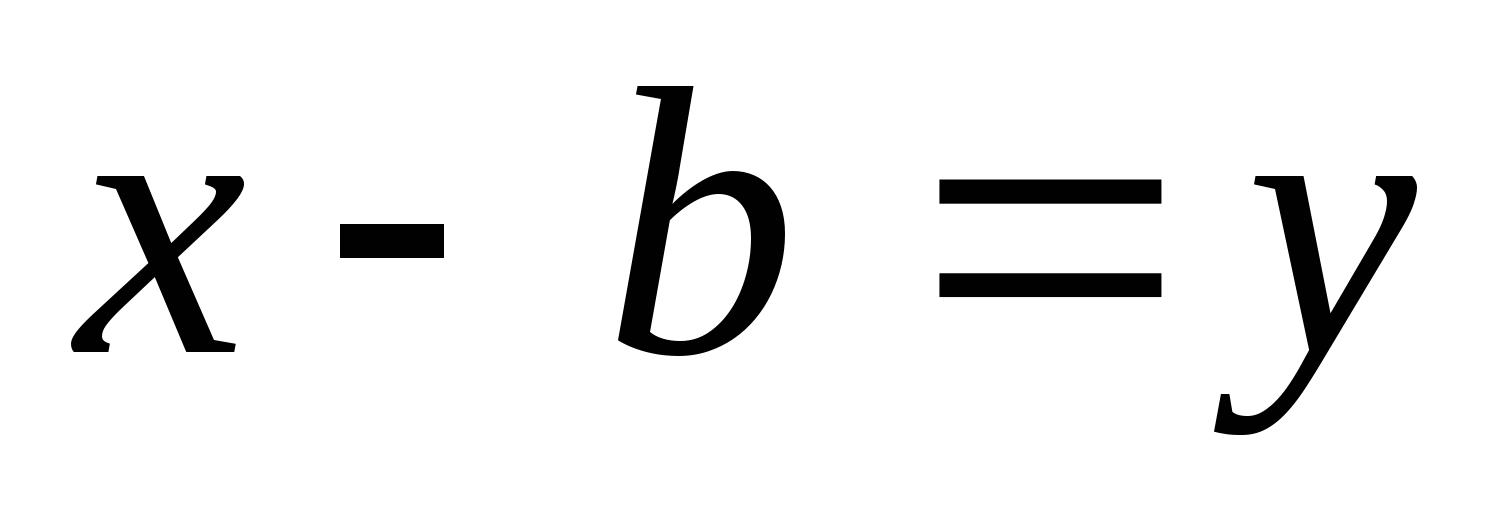

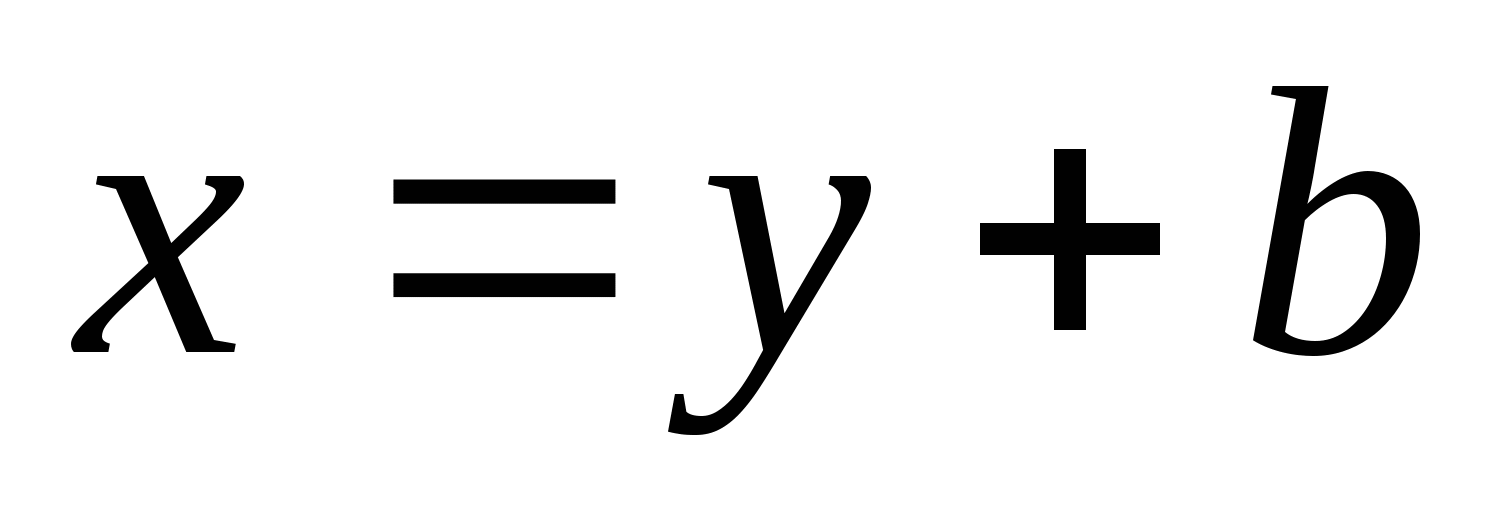 ; при
; при 

 )
)
= 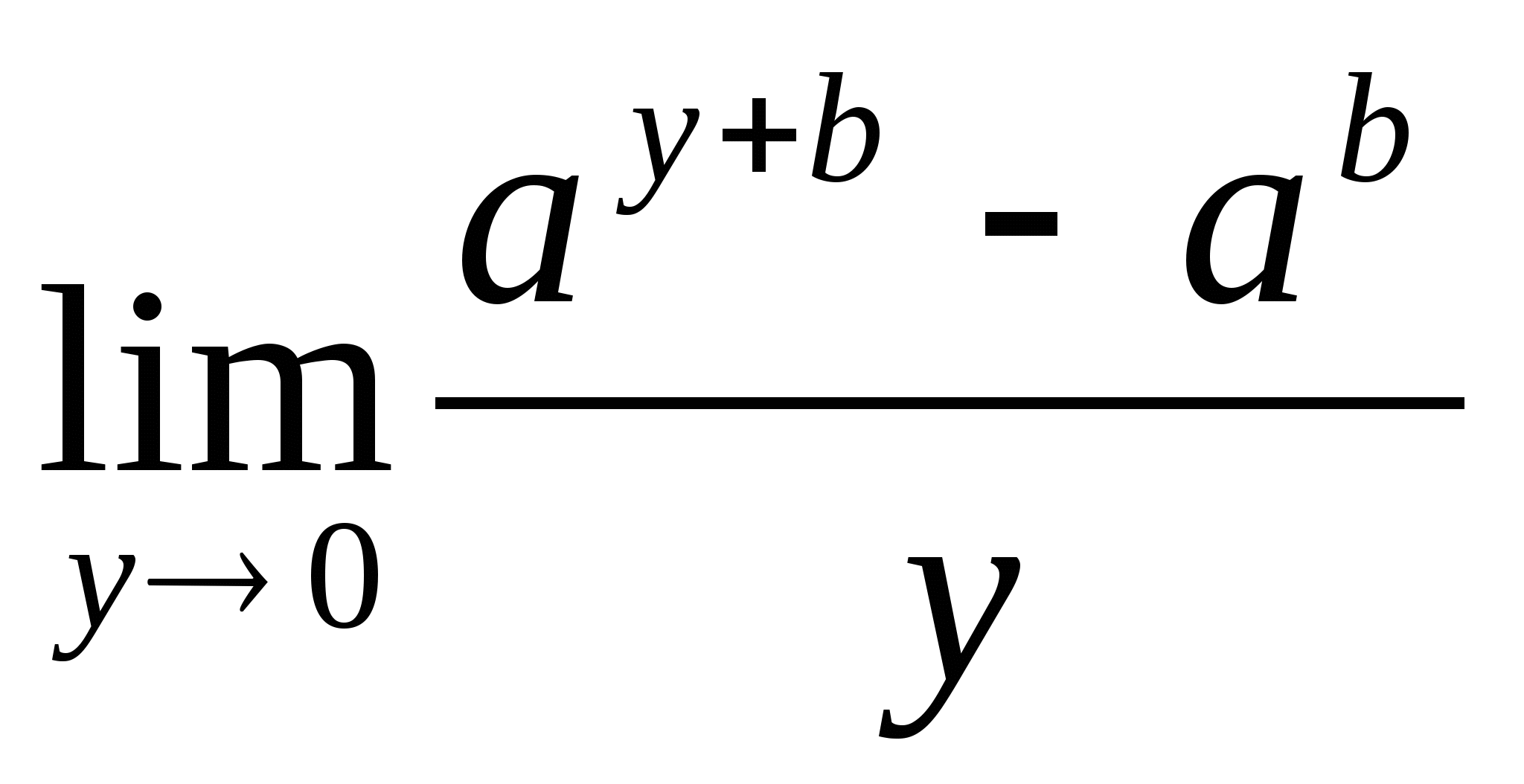 =
=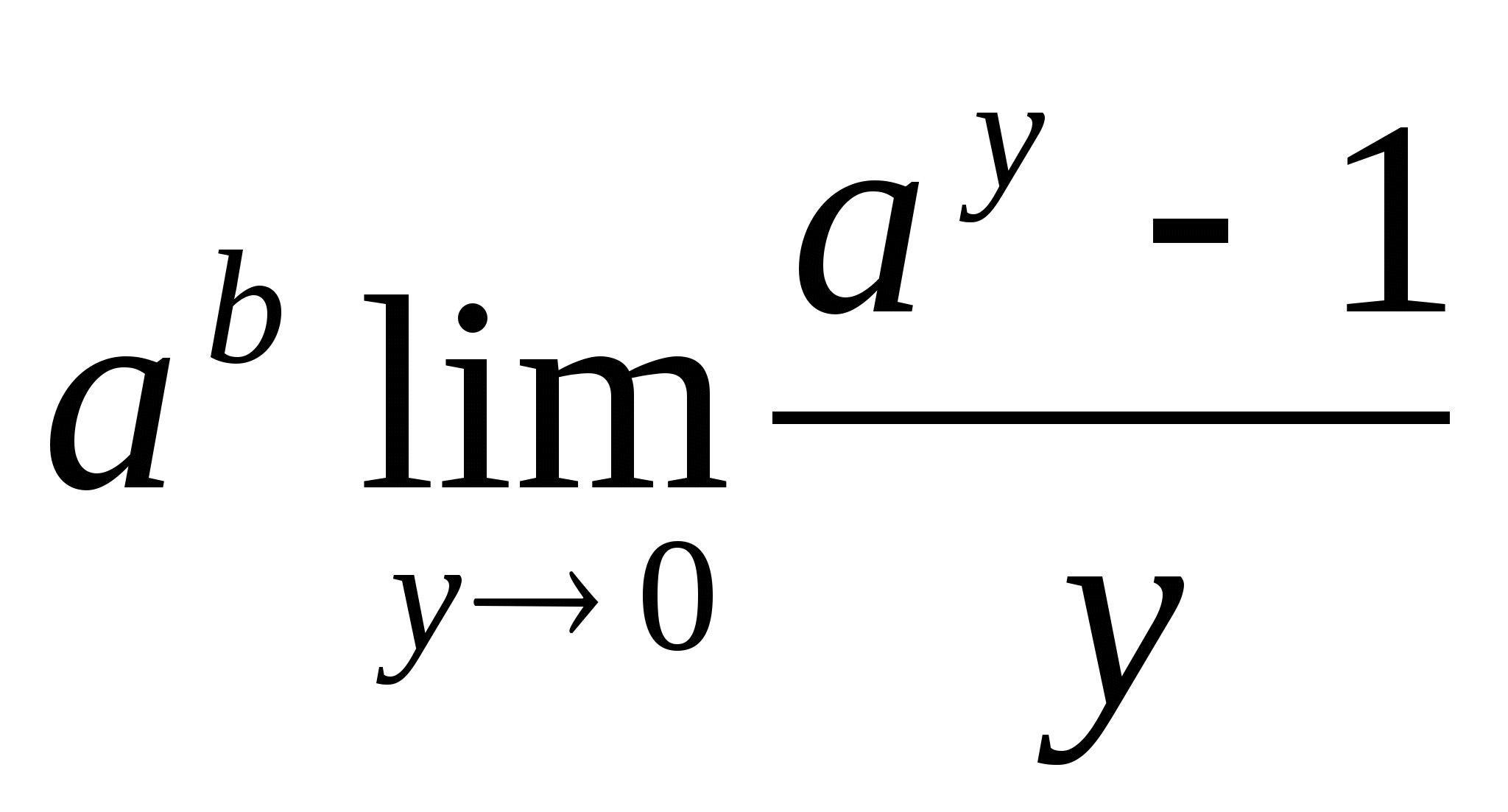 =
=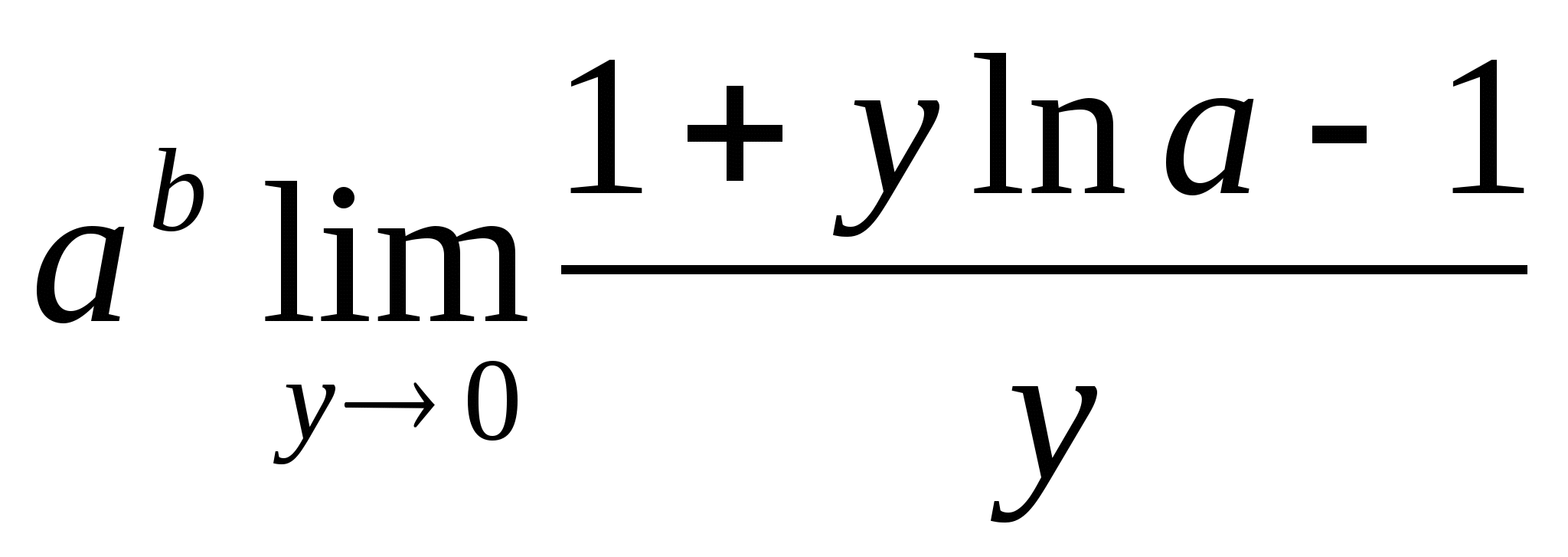 =
=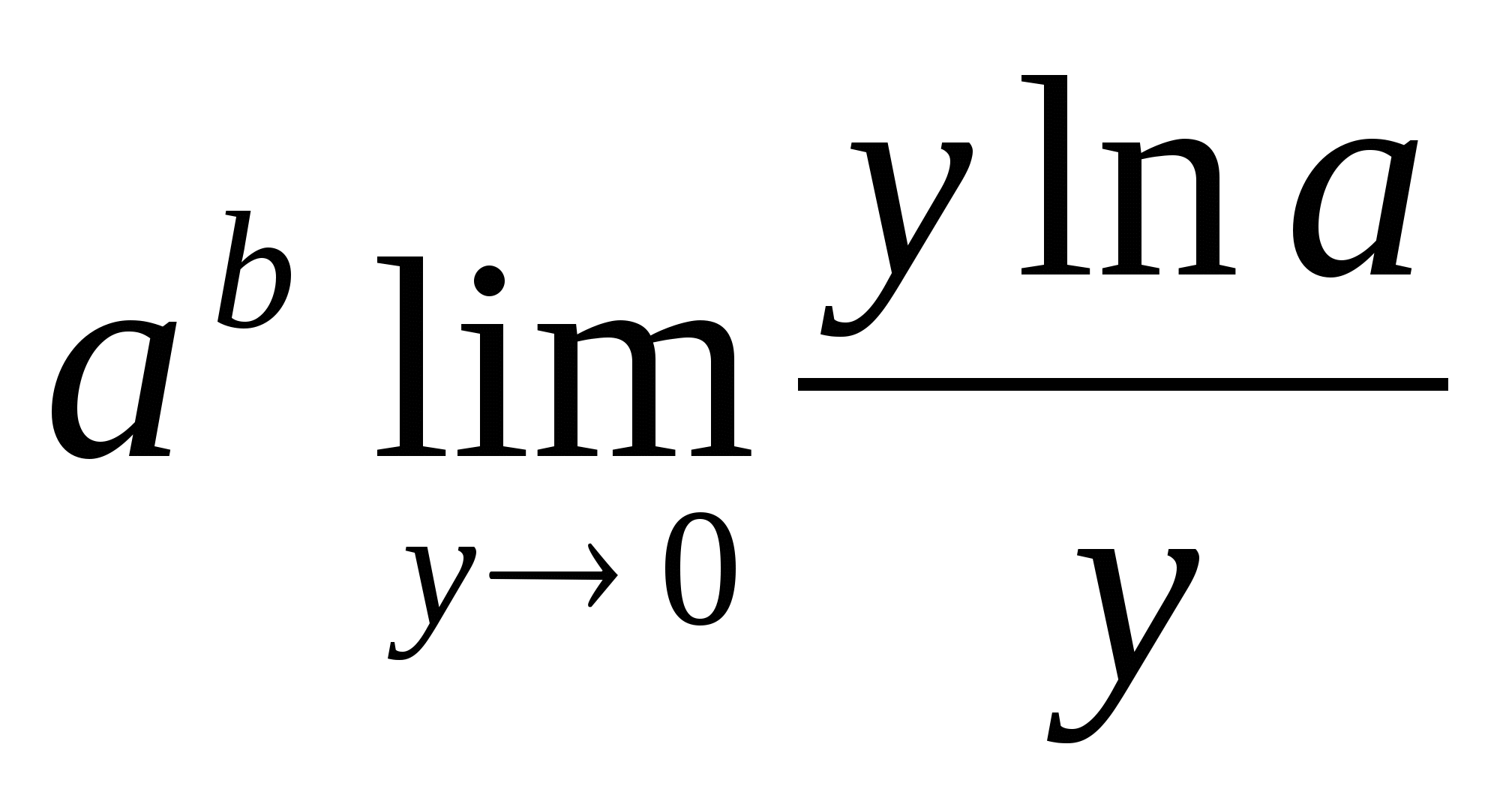 =
=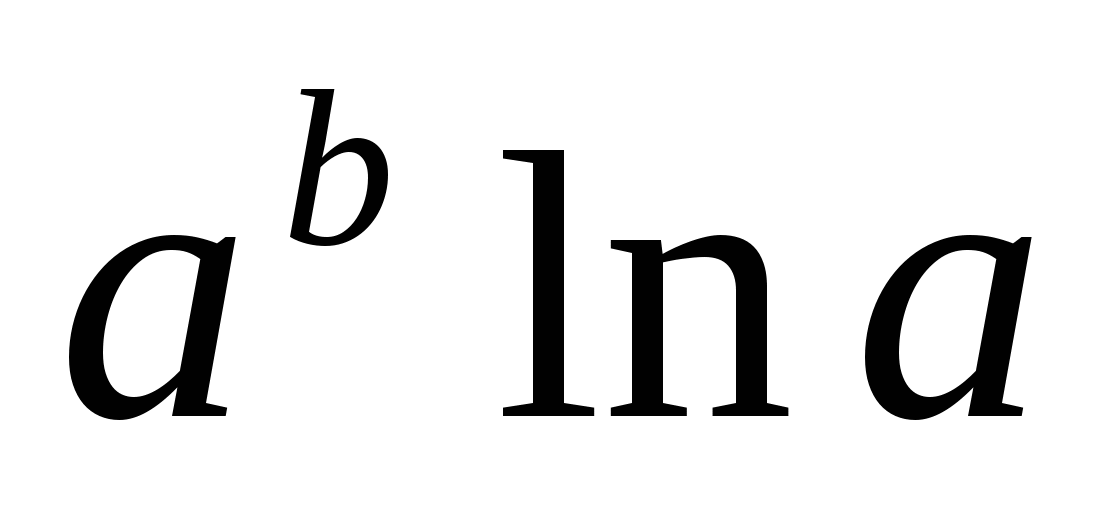
(воспользовались эквивалентностью 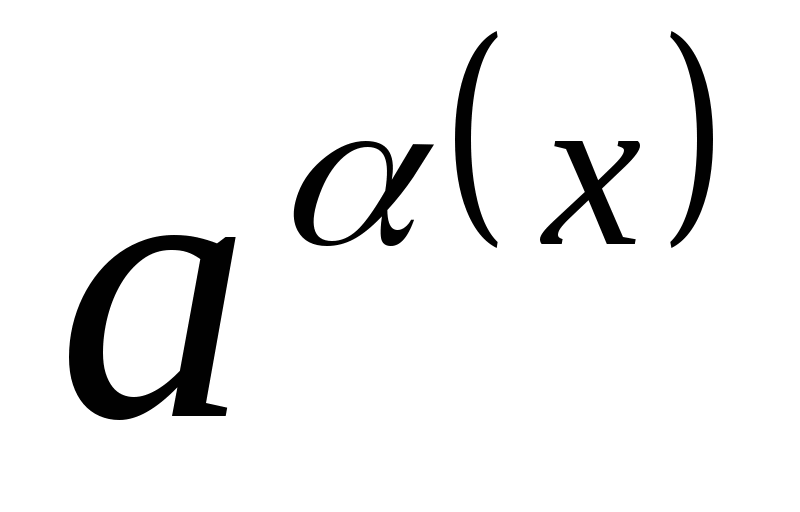 ~
~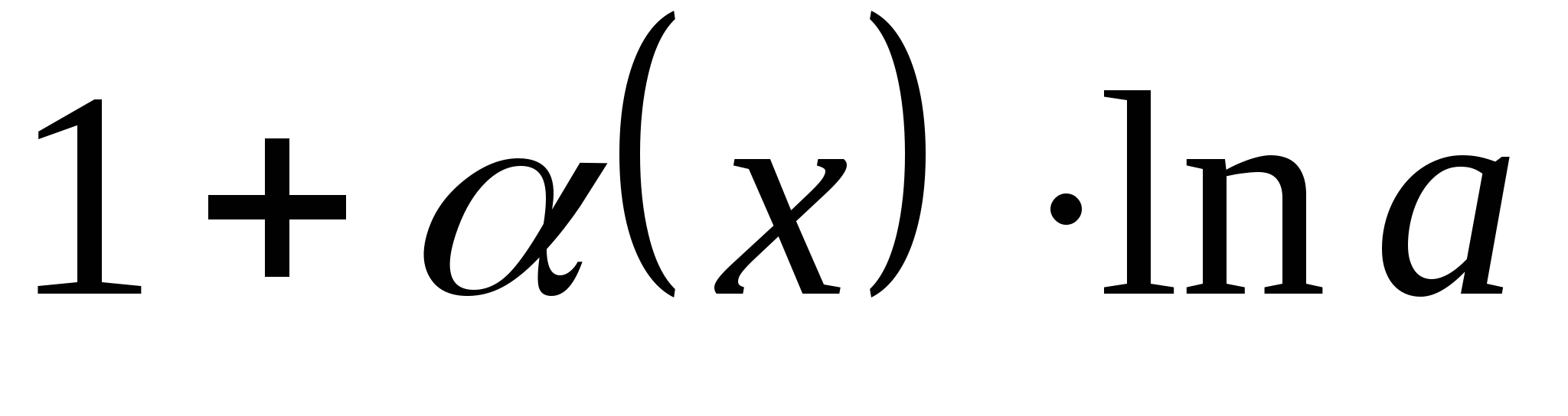 ). Ответ:
). Ответ: 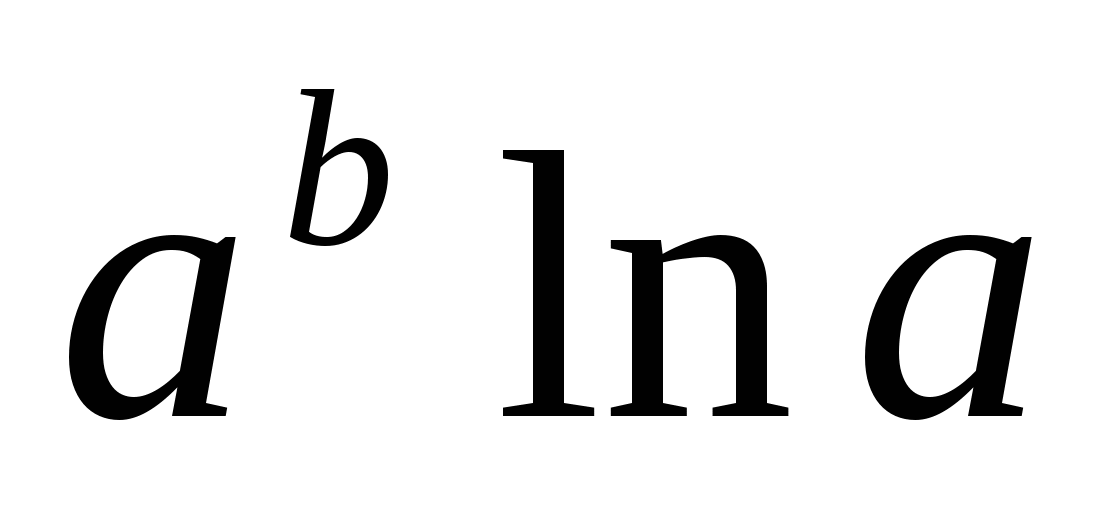 .
.
4. 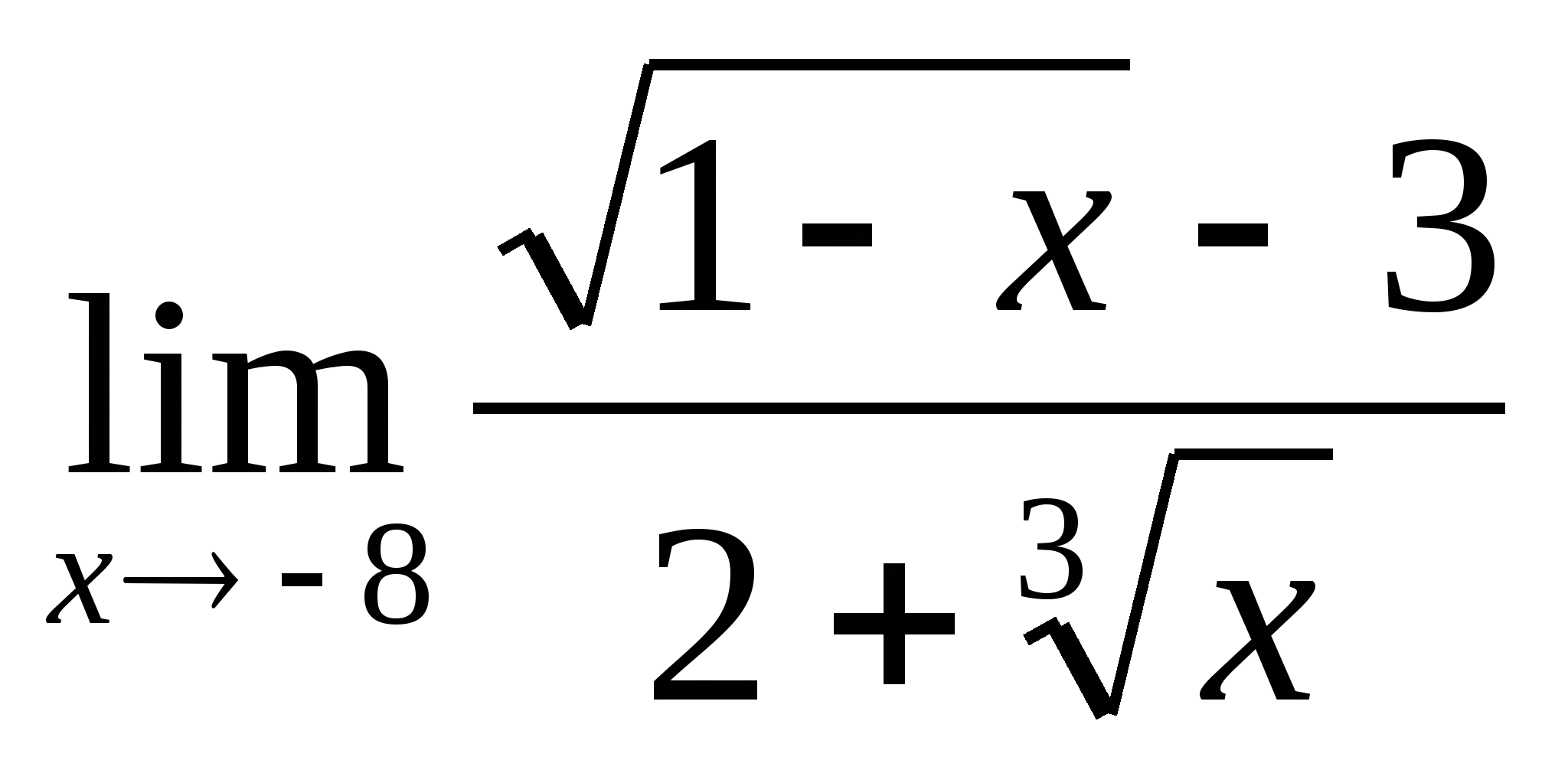
Решение: 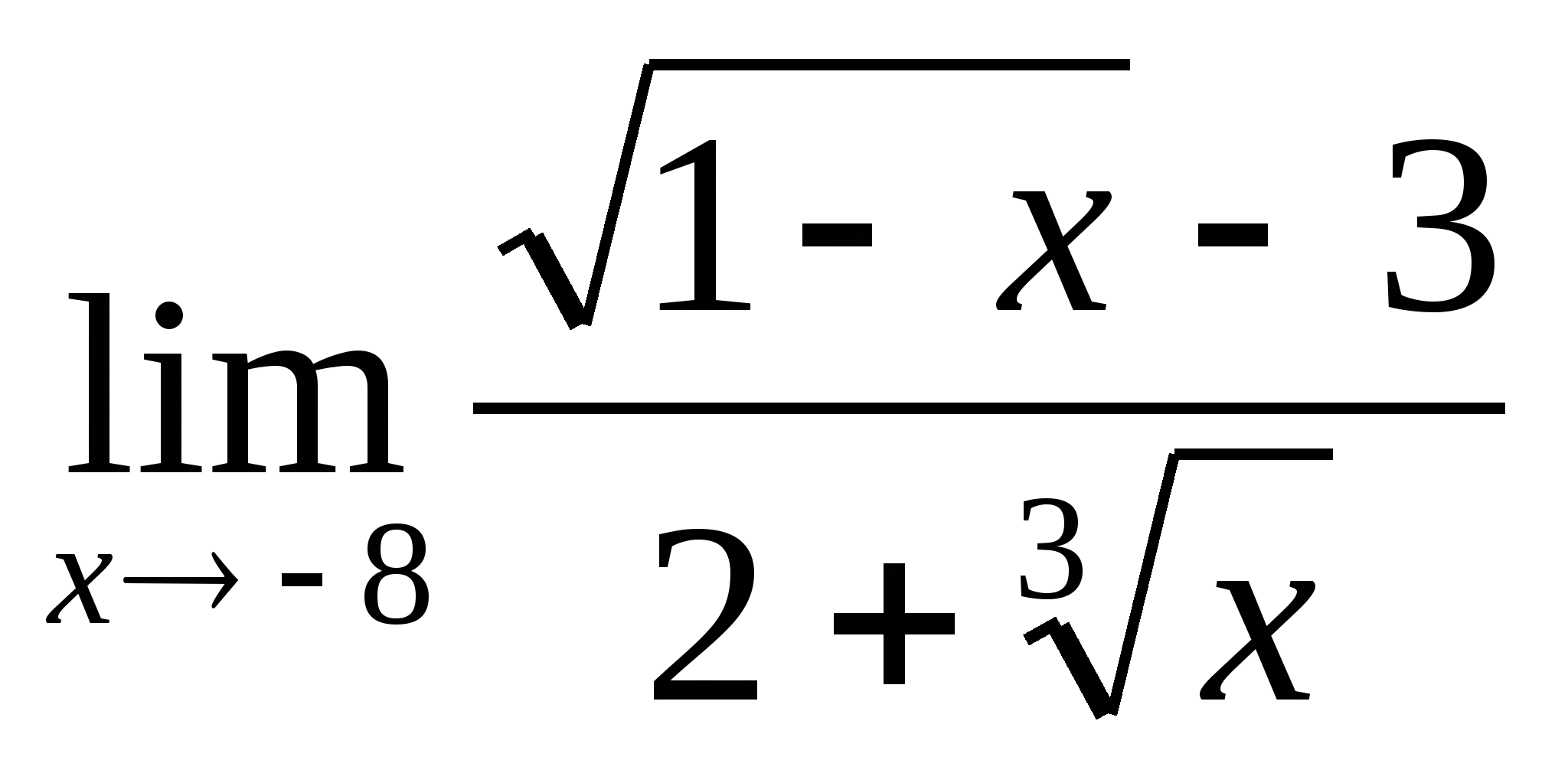 = (введем замену:
= (введем замену: 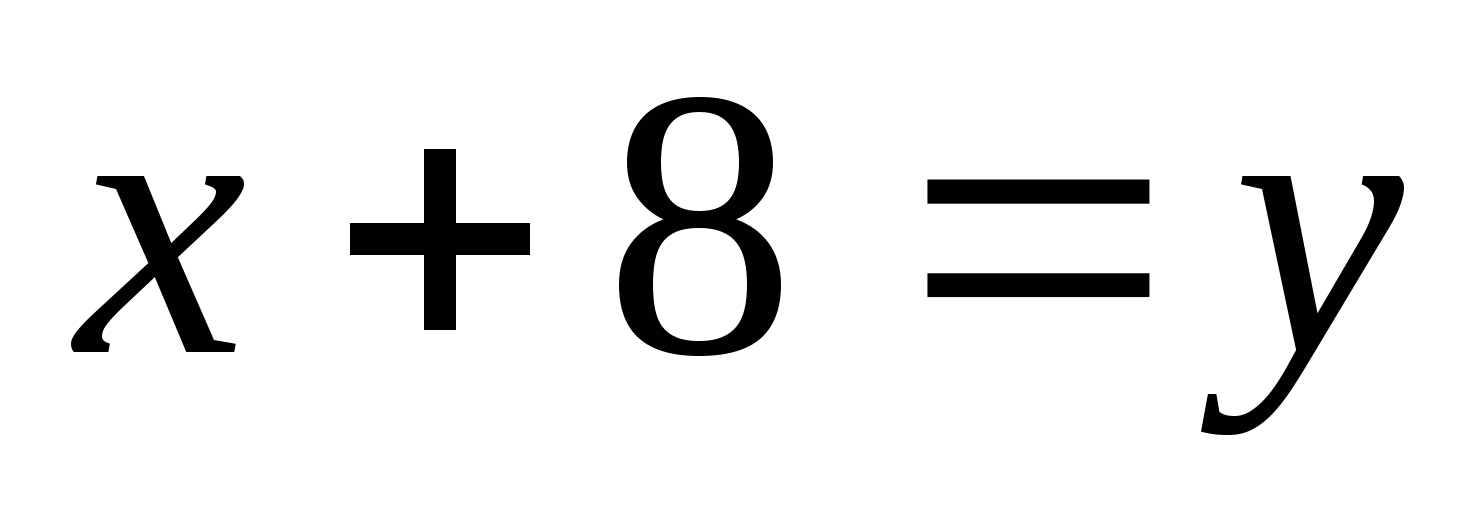

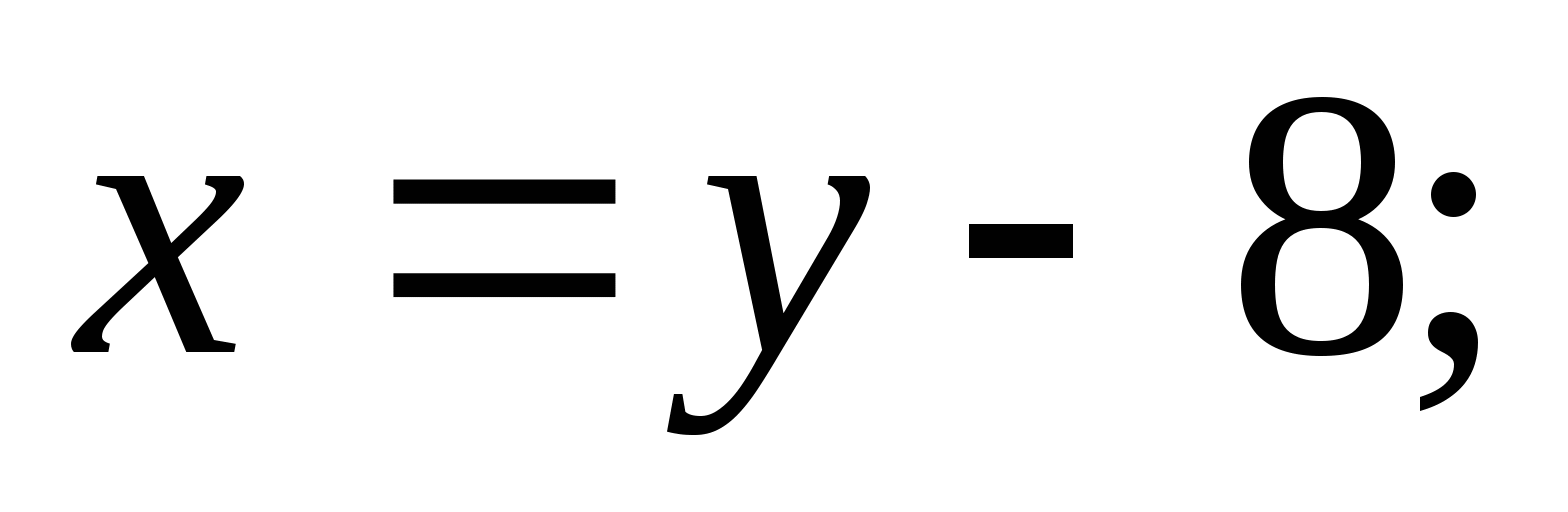 при
при 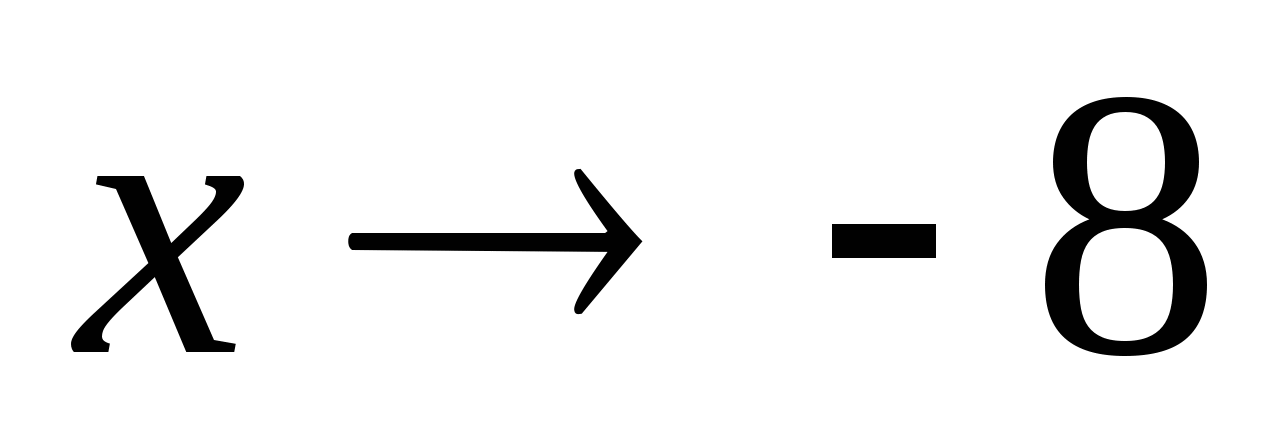

 )
)
=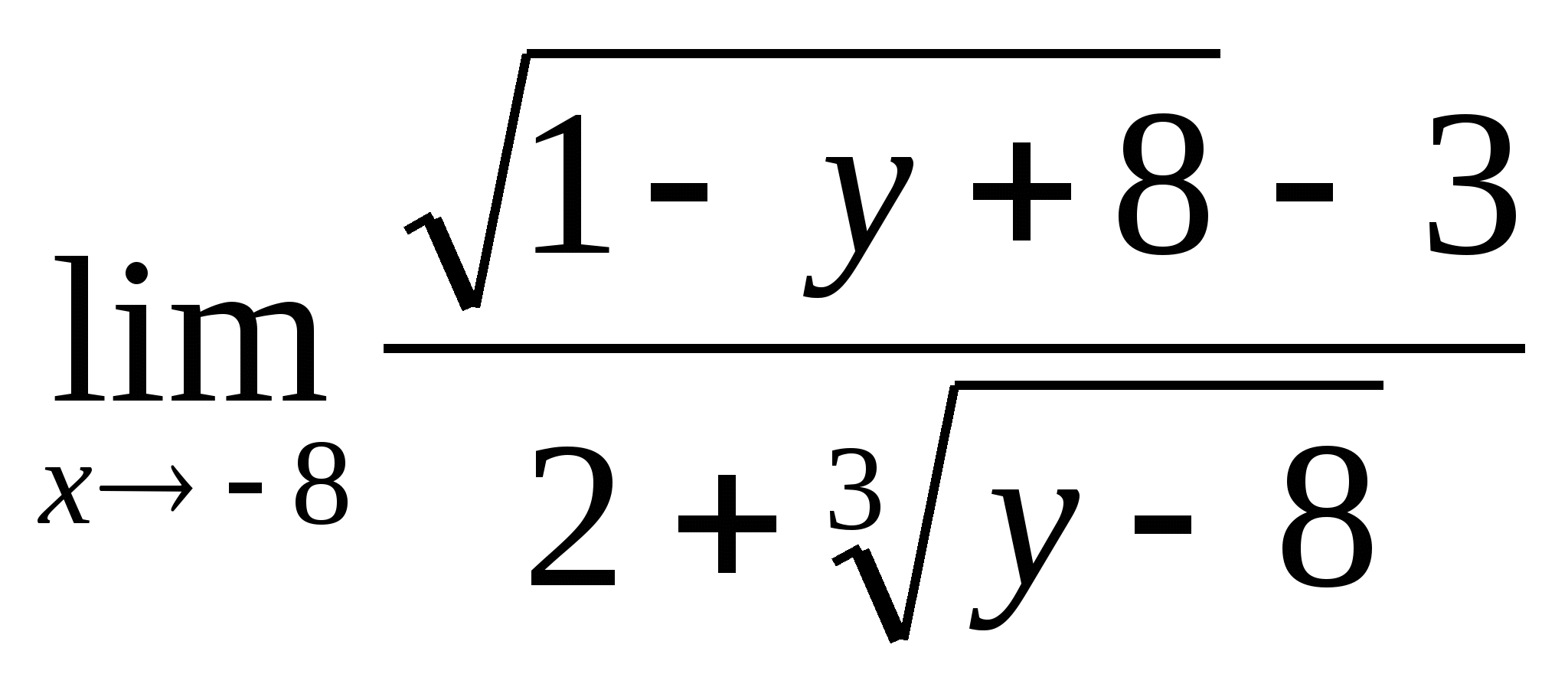 =
=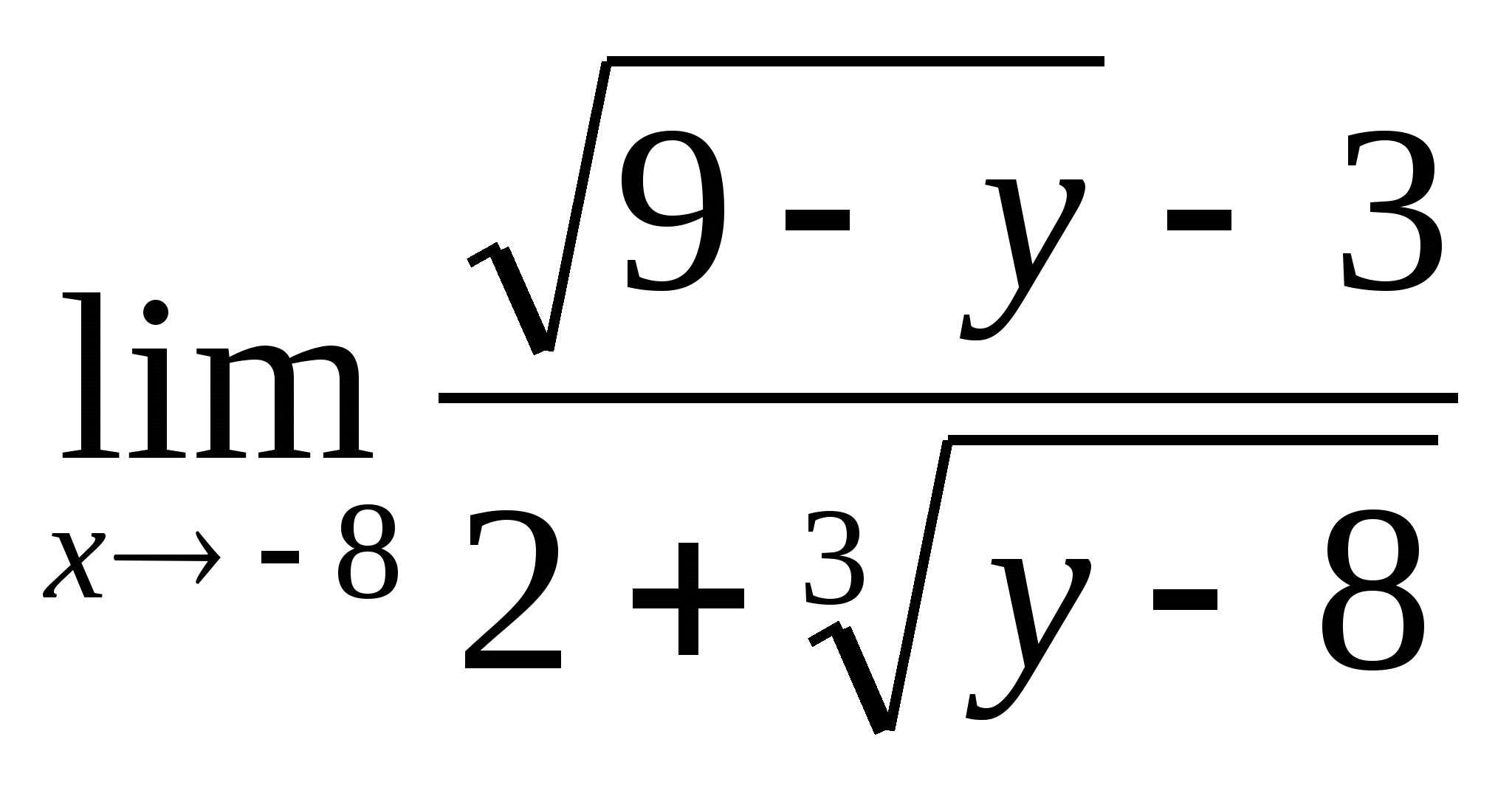 =
=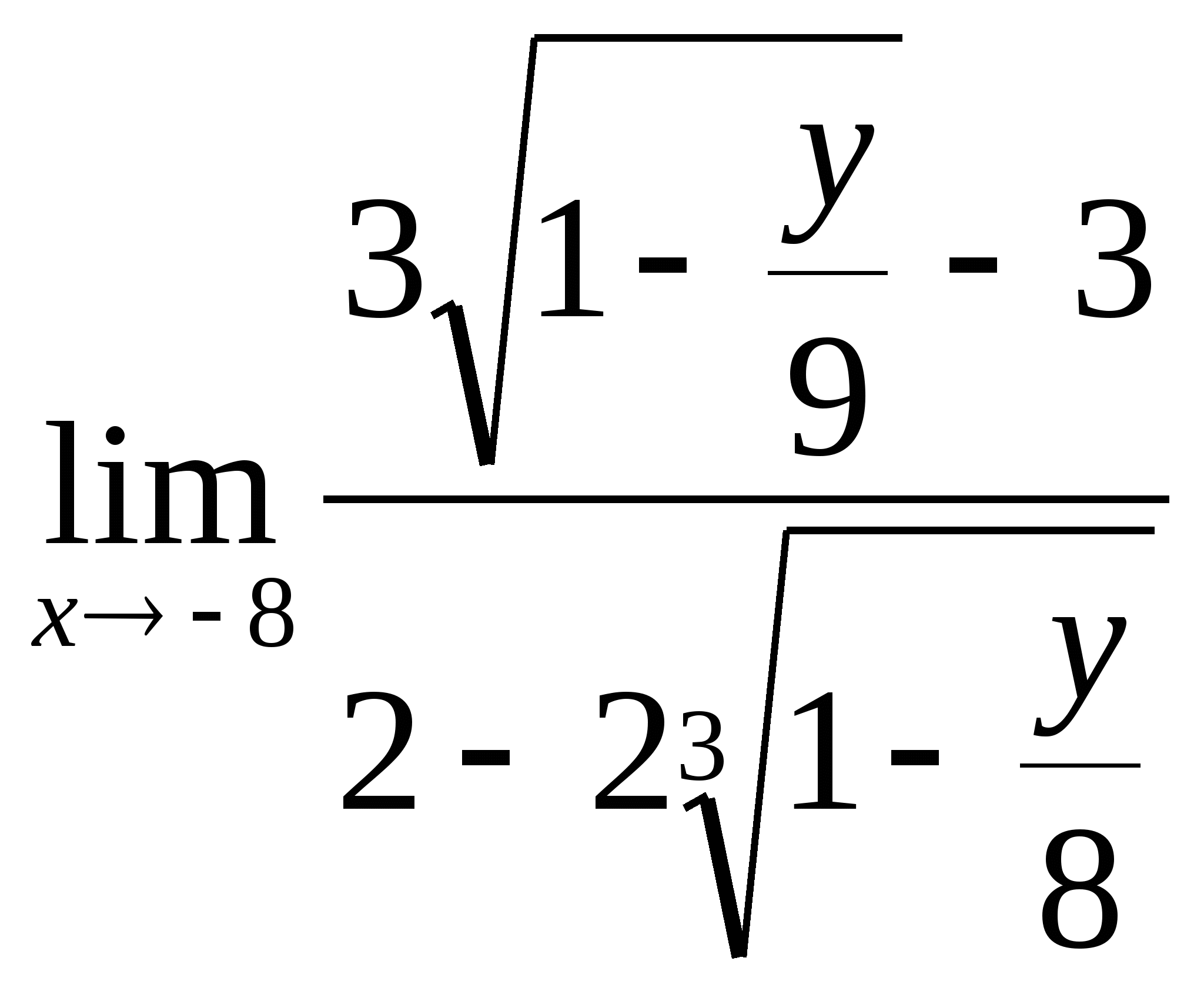 =
=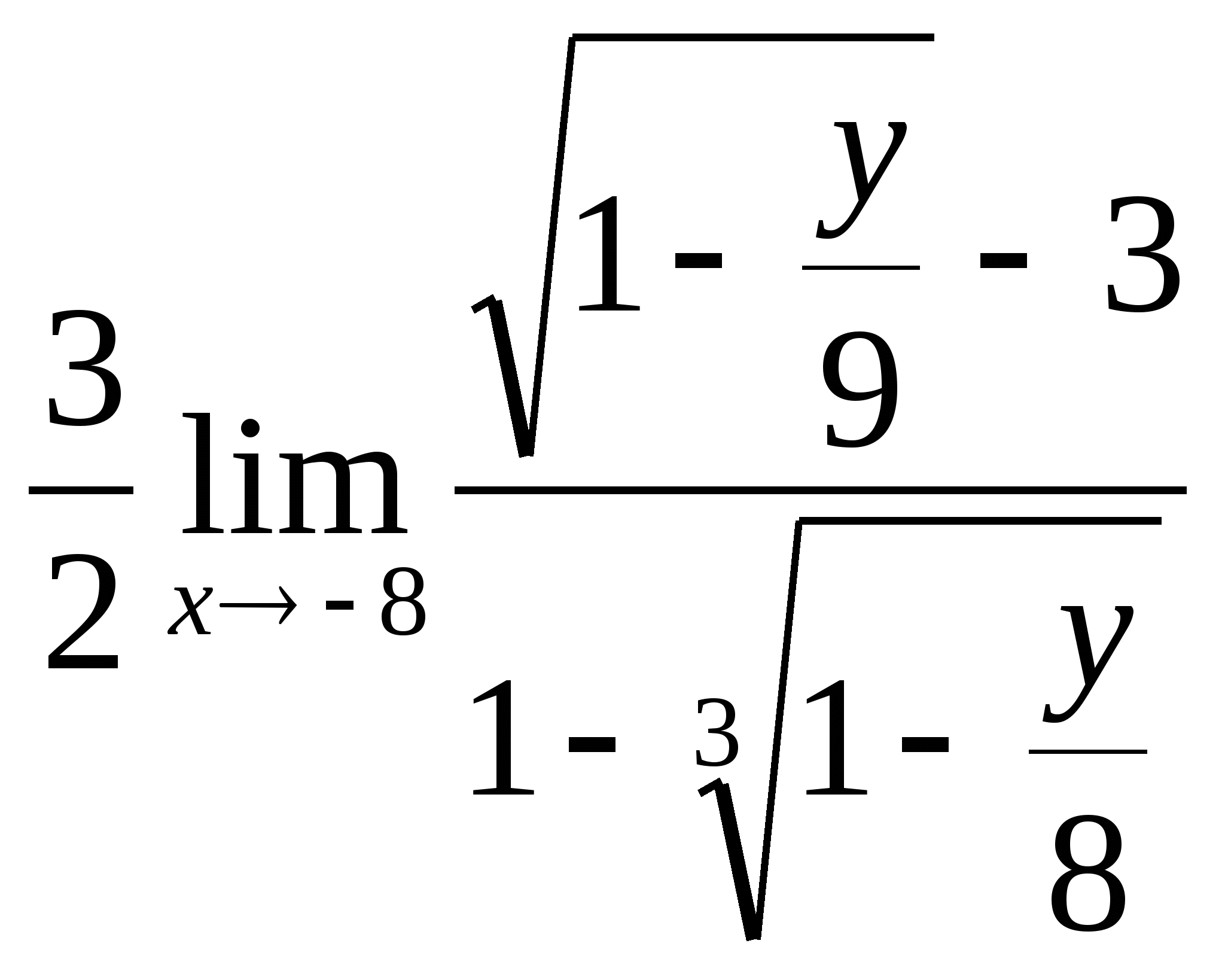 =
=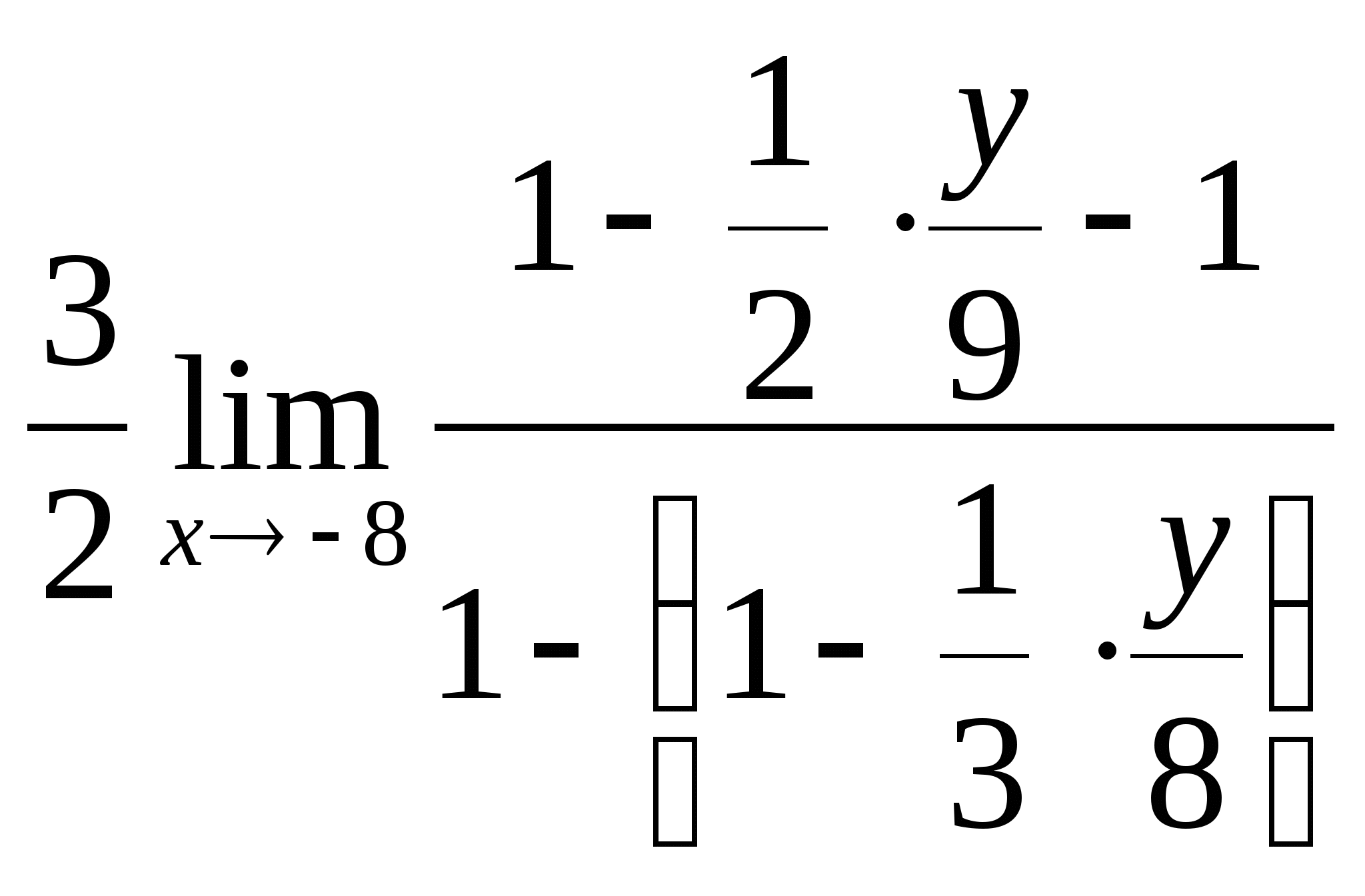 =
=
=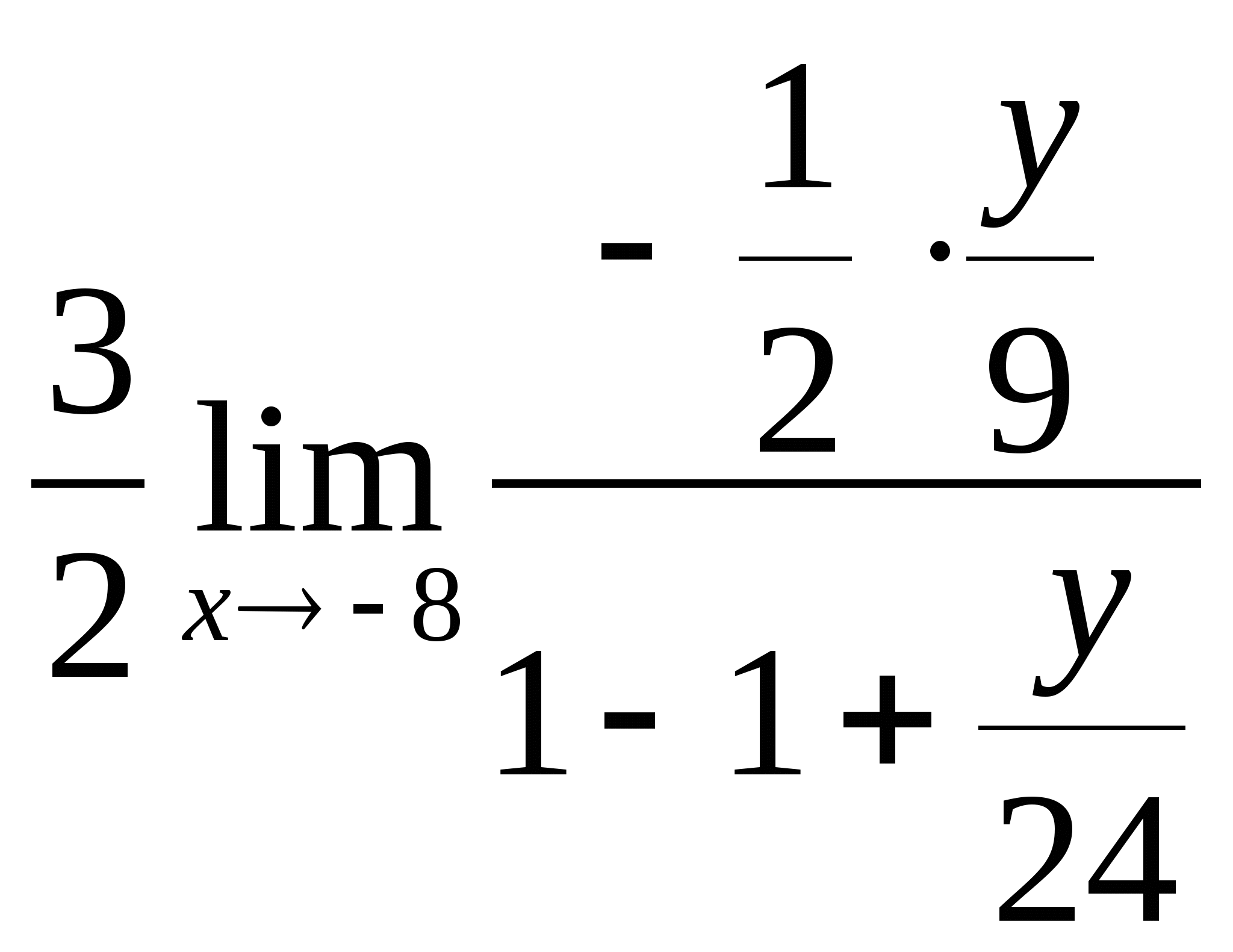 =
=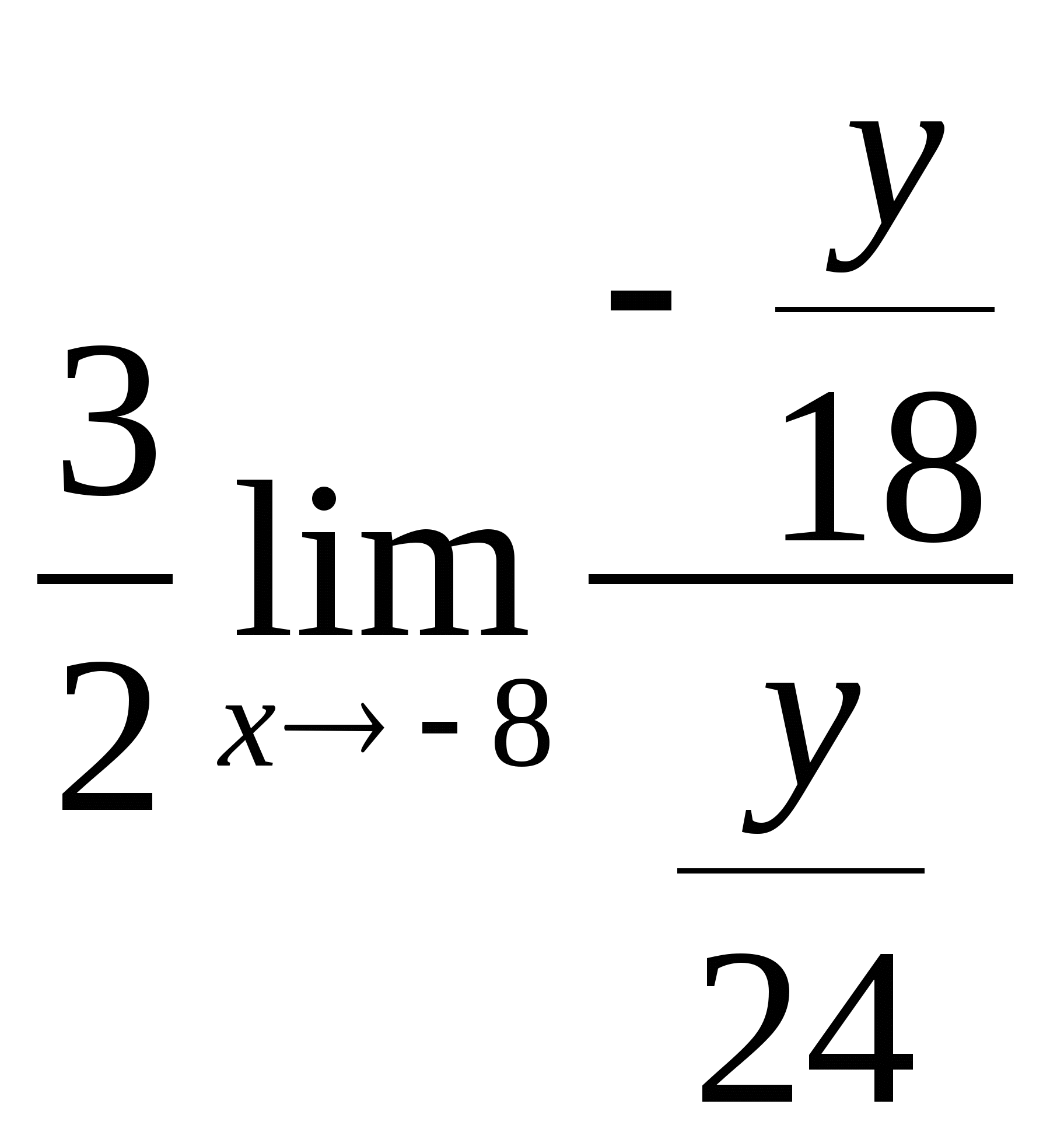 =
=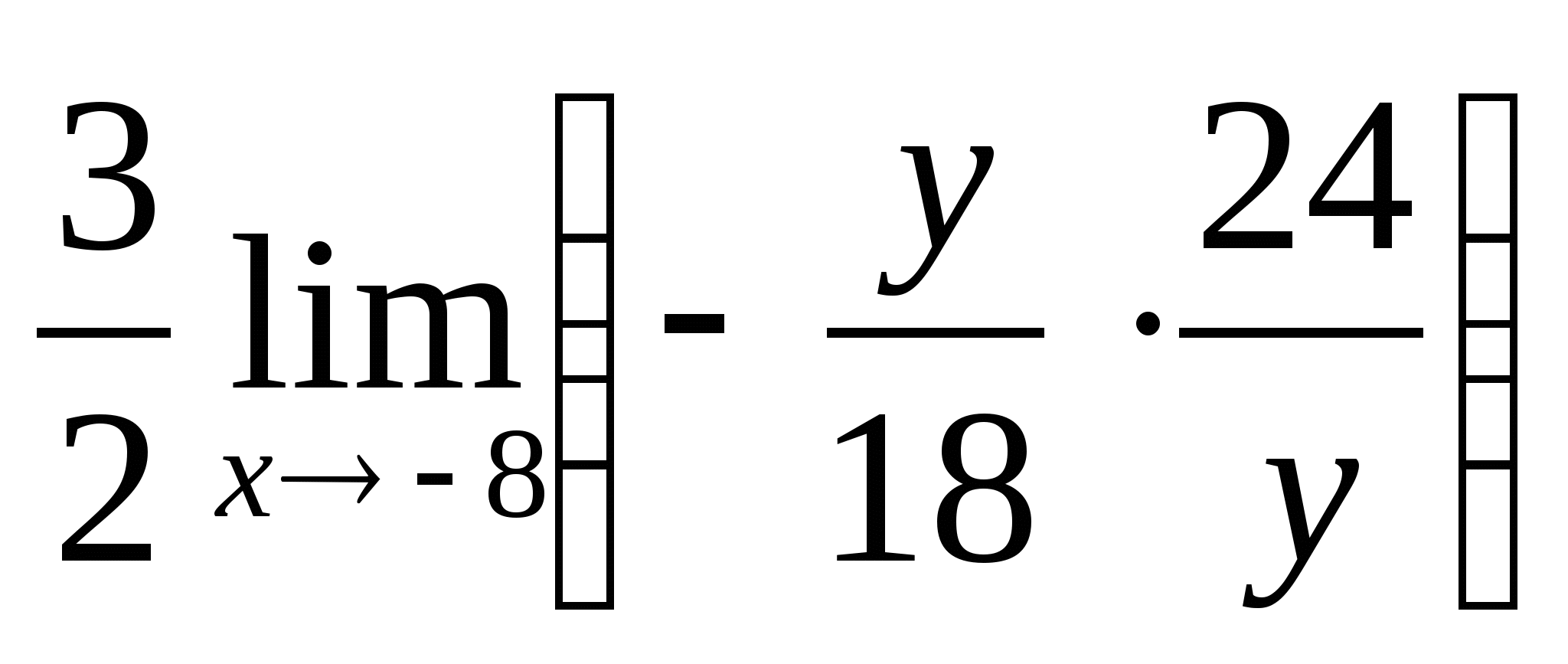 =
=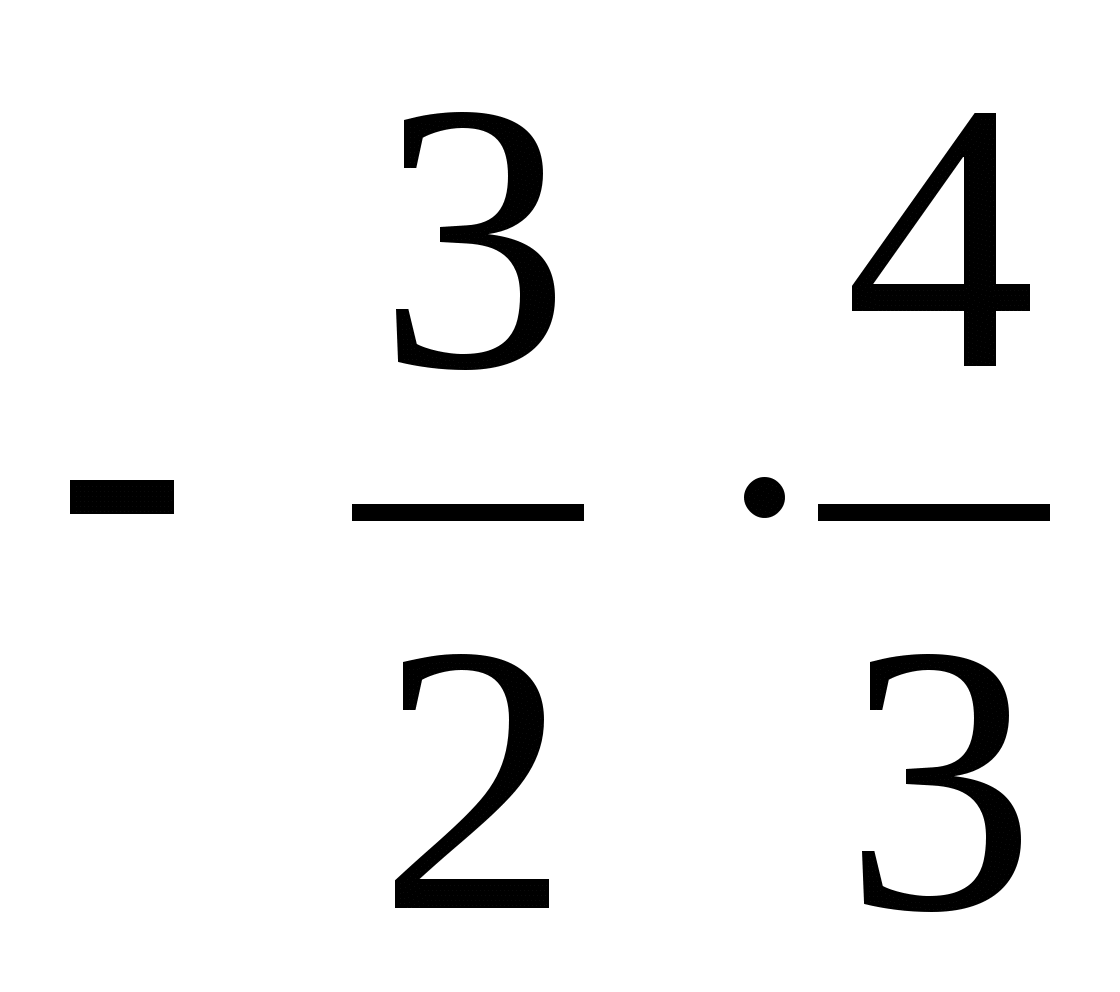 =
=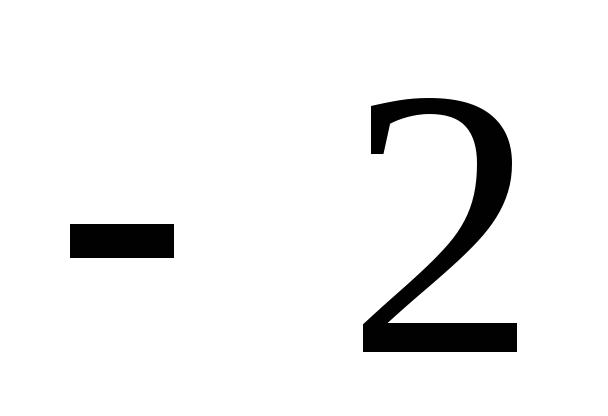 ;
;
(воспользовались эквивалентностью 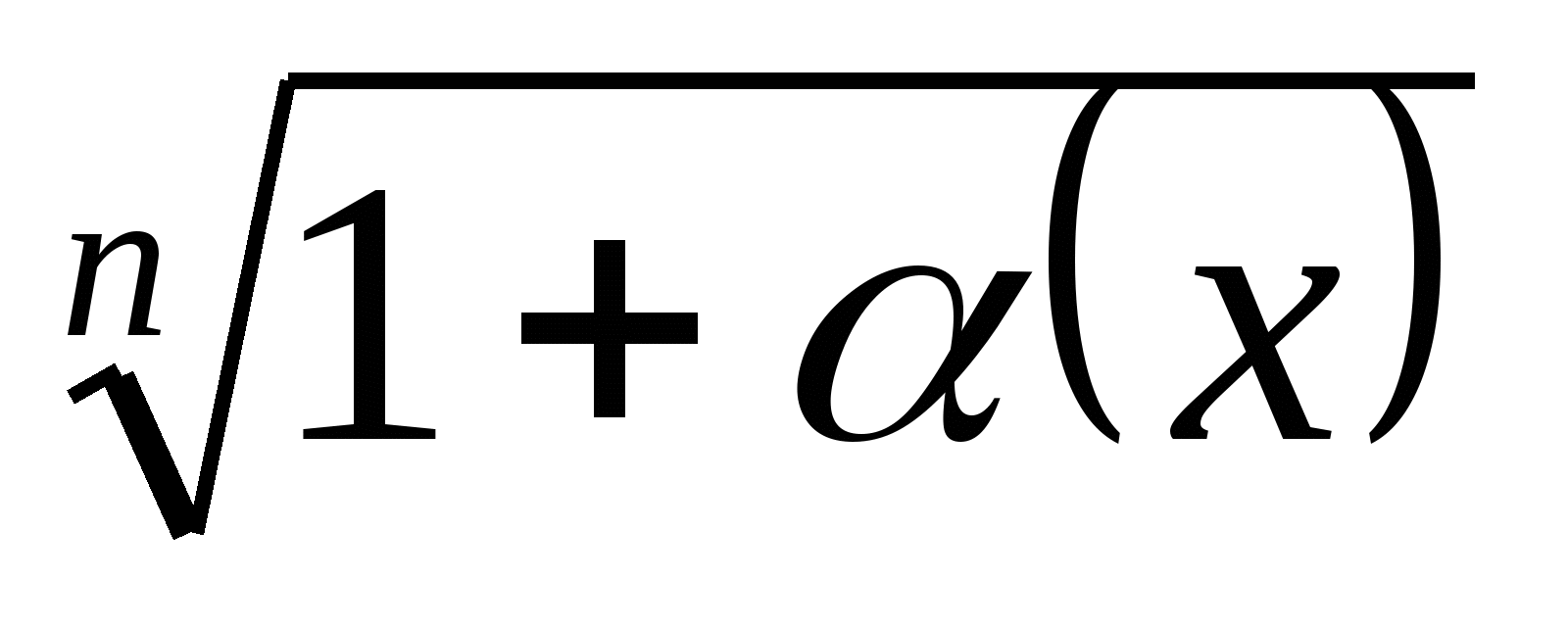 ~
~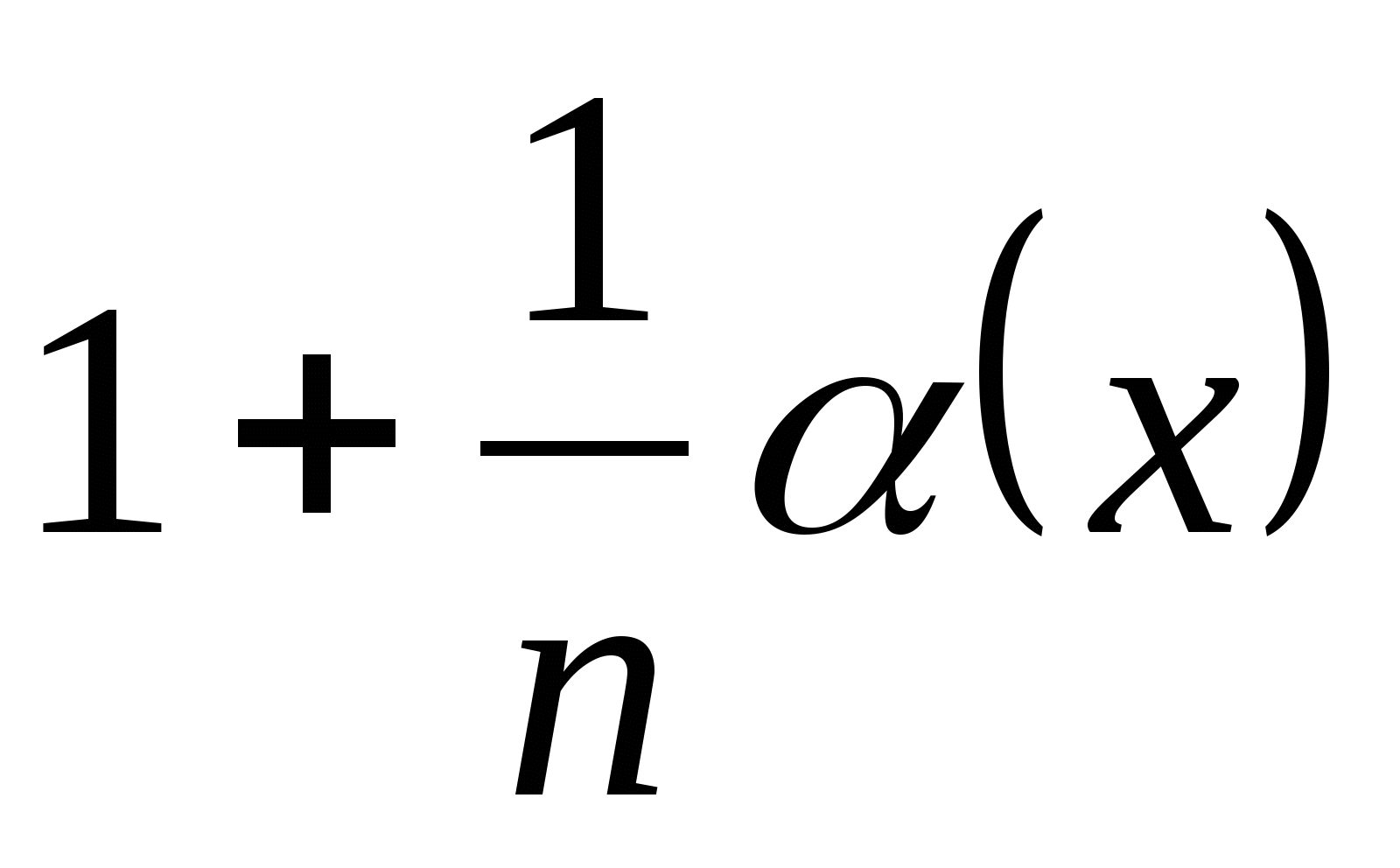 ;
; 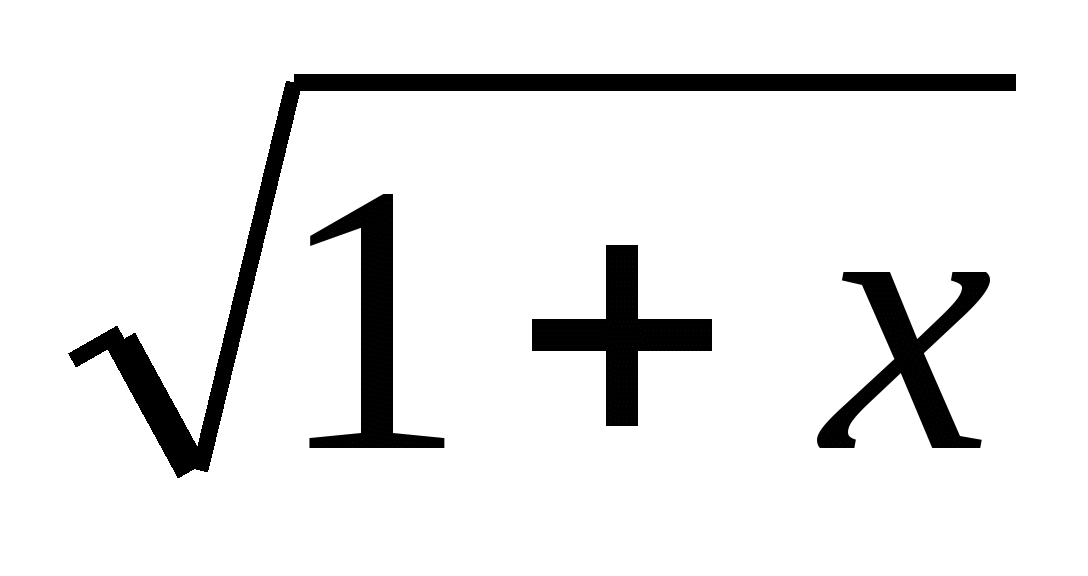 ~
~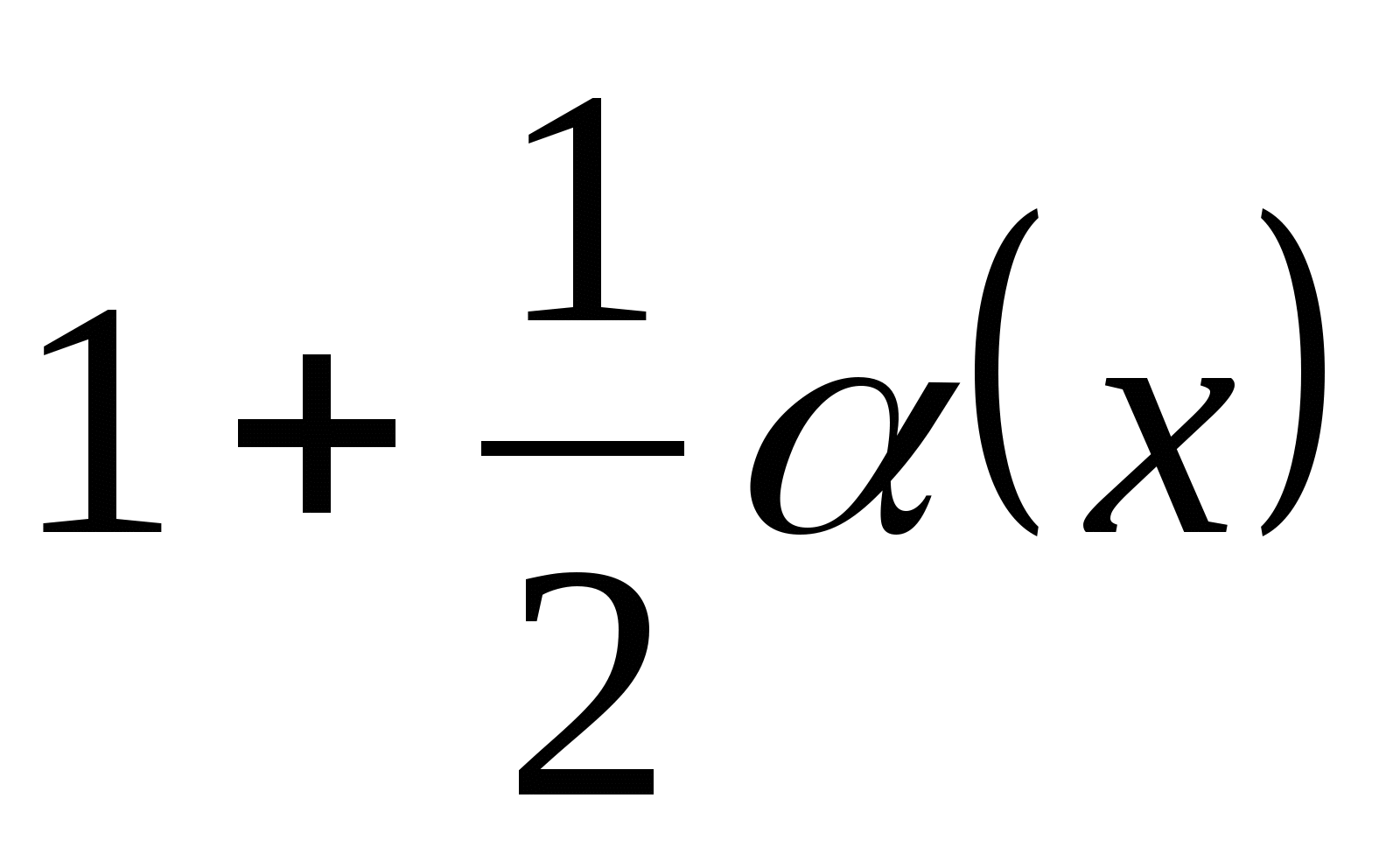 ;). Ответ:
;). Ответ: 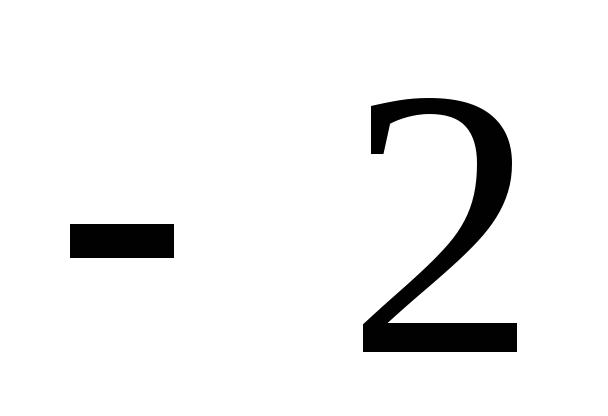 .
.
5. 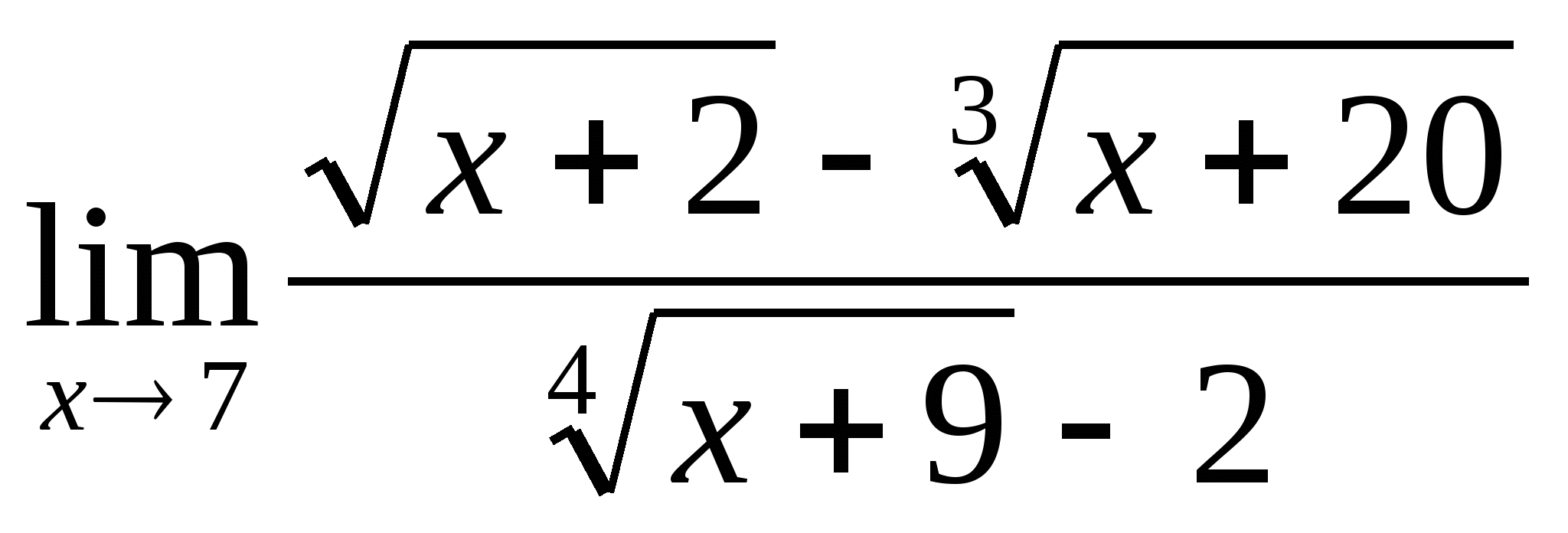
Решение: 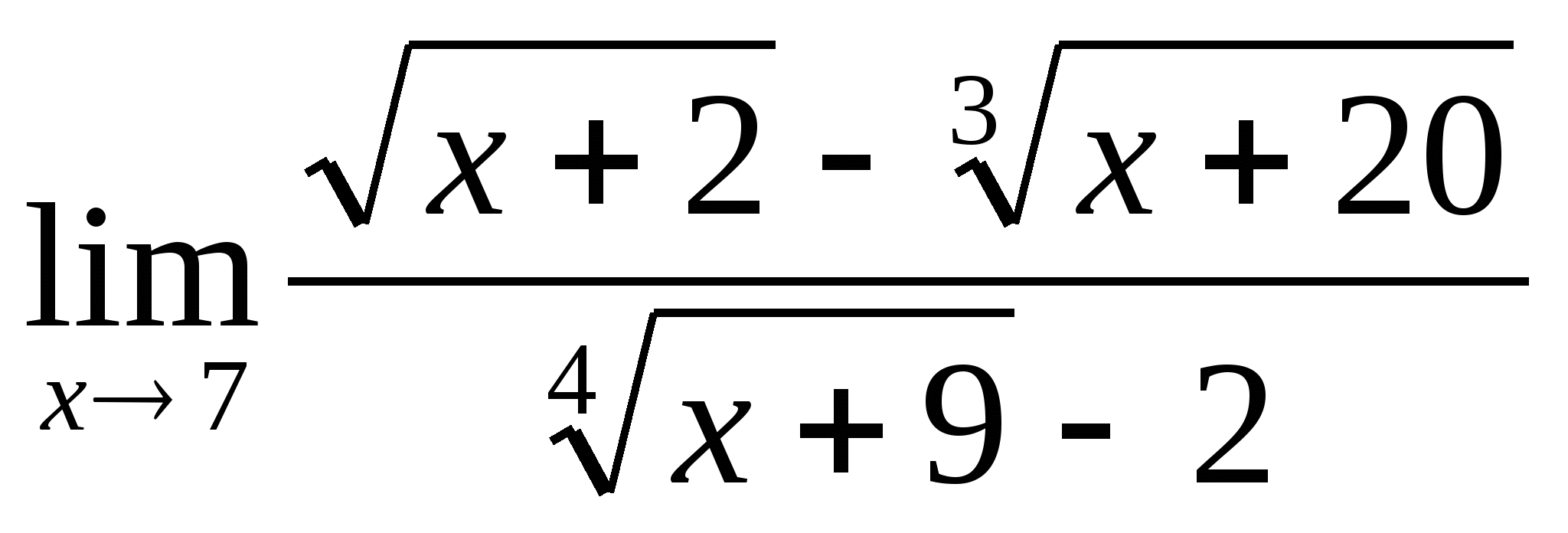 = (введем
= (введем 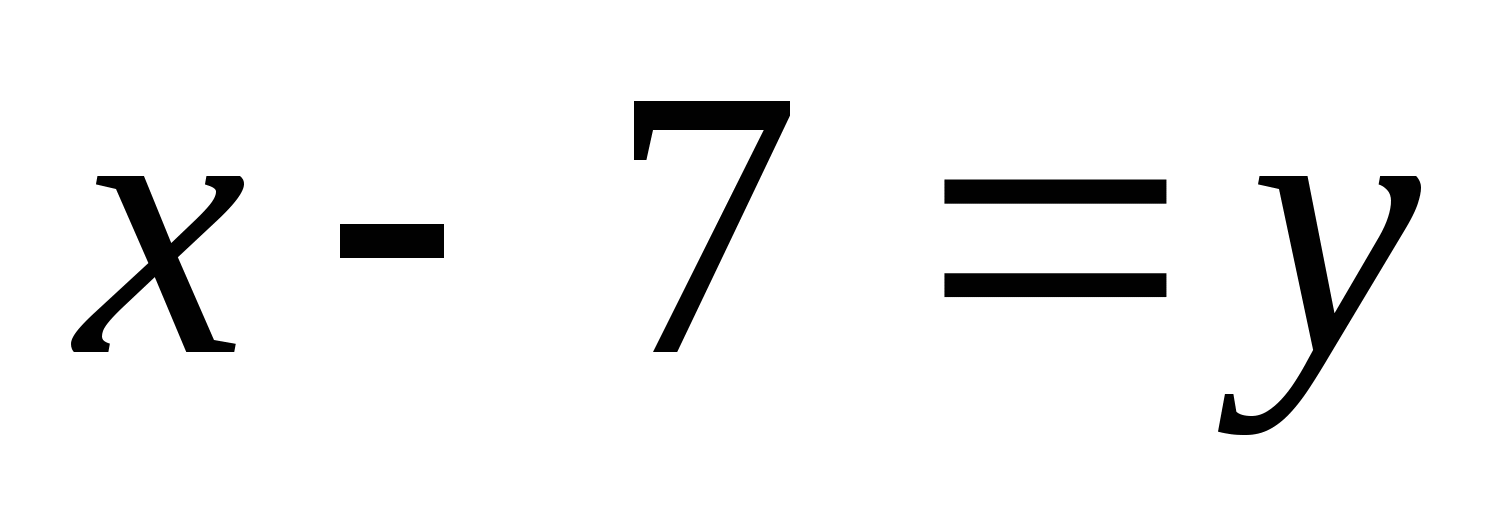

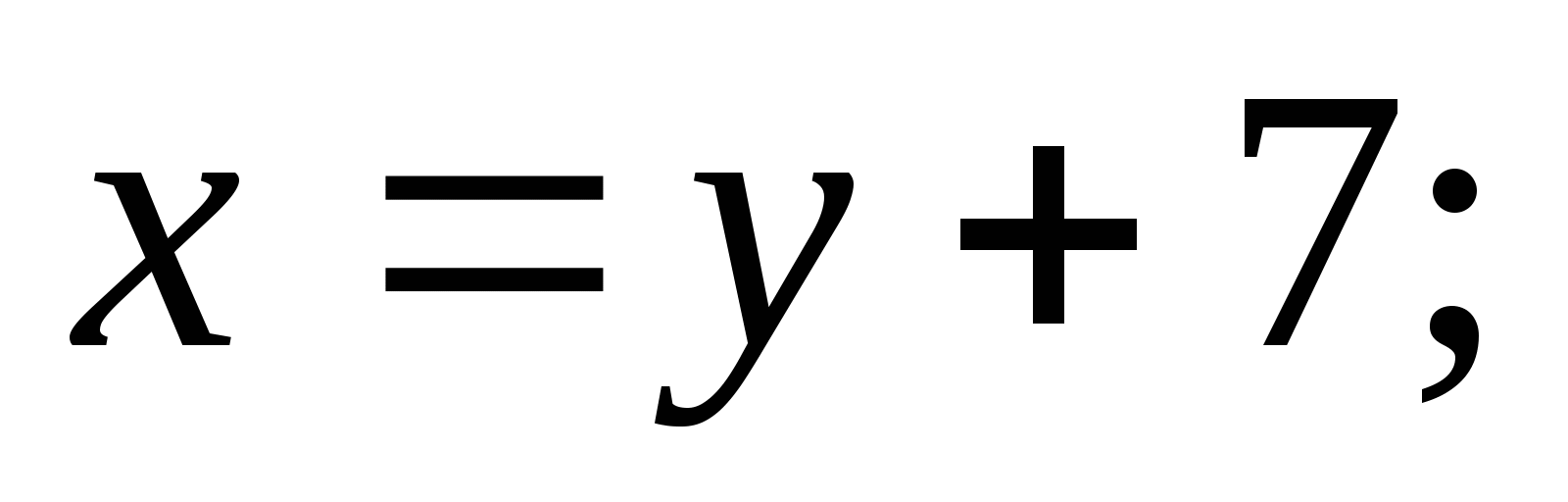 при
при 

 )
)
=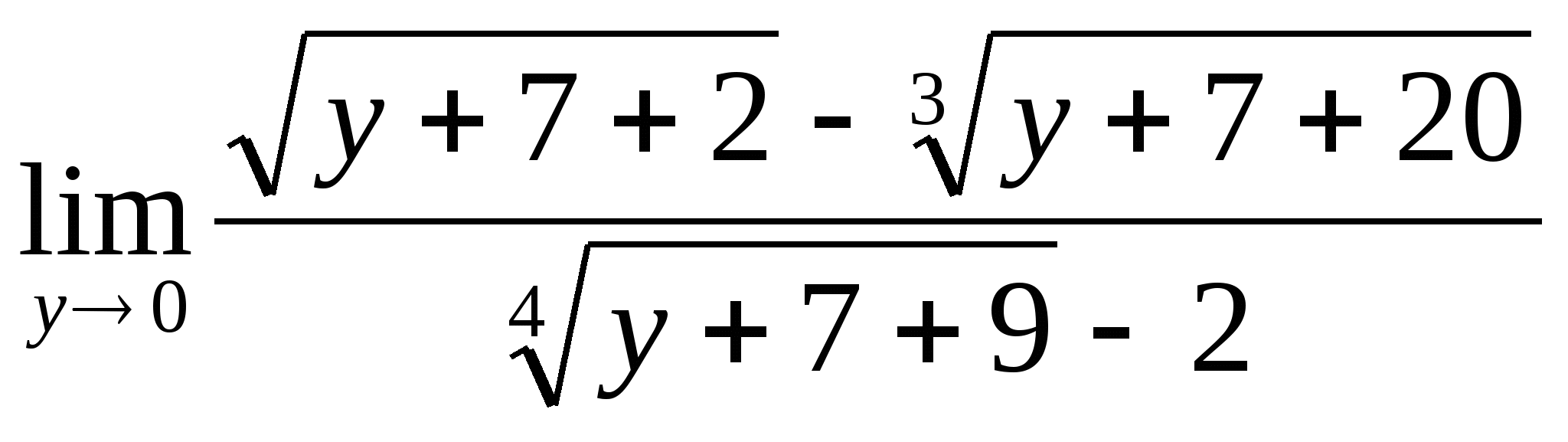 =
=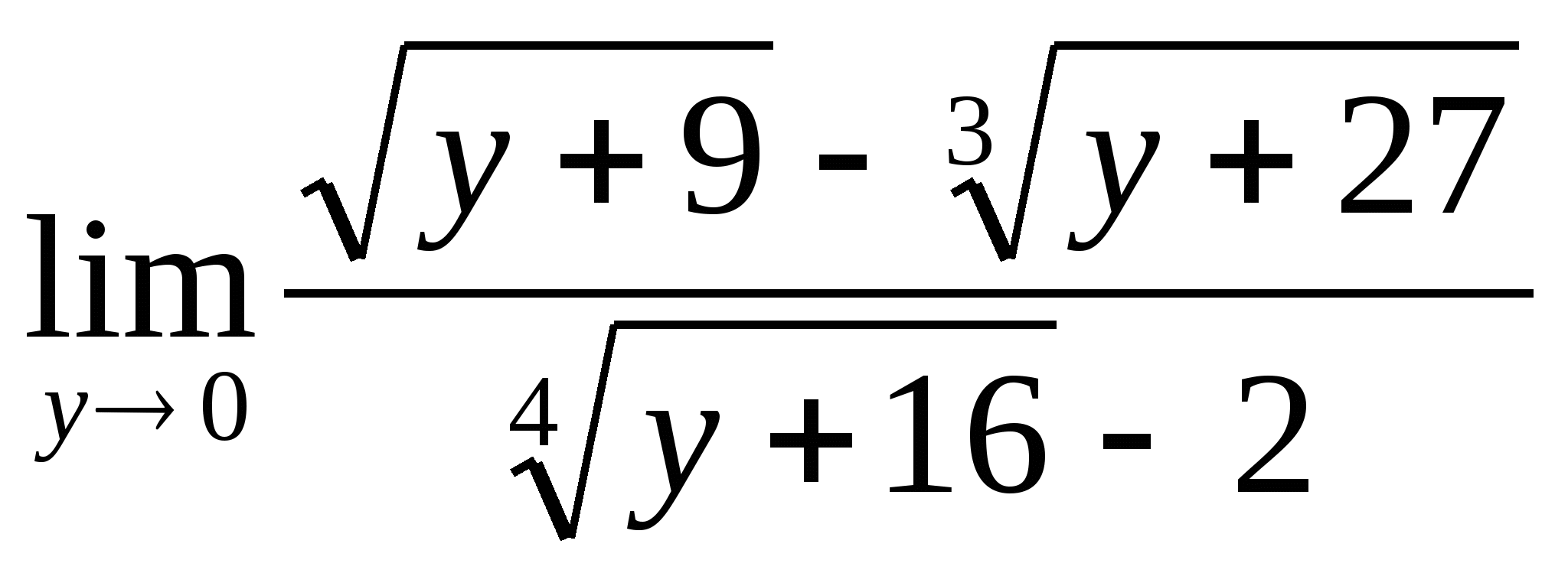 =
=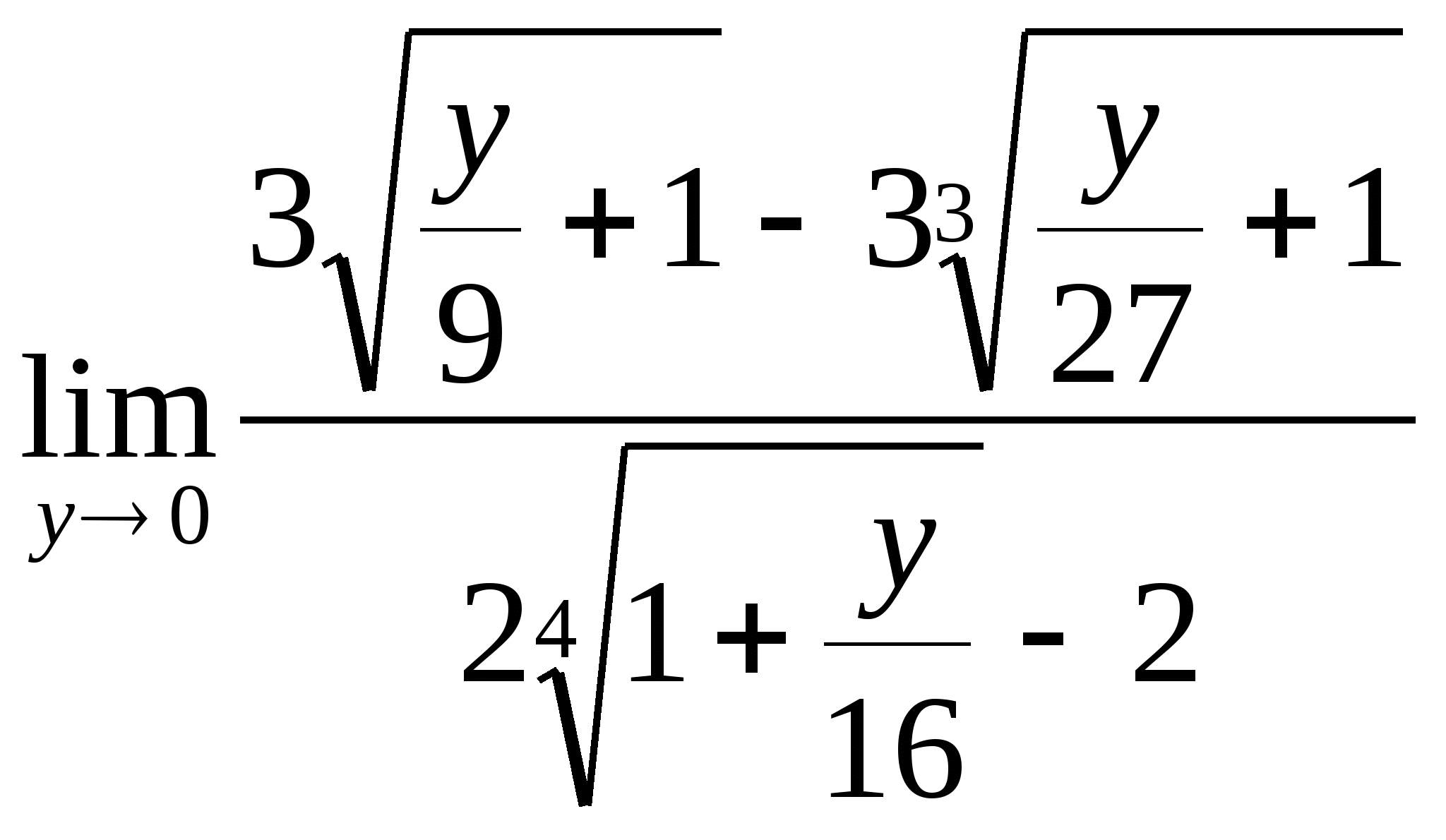 =
=
=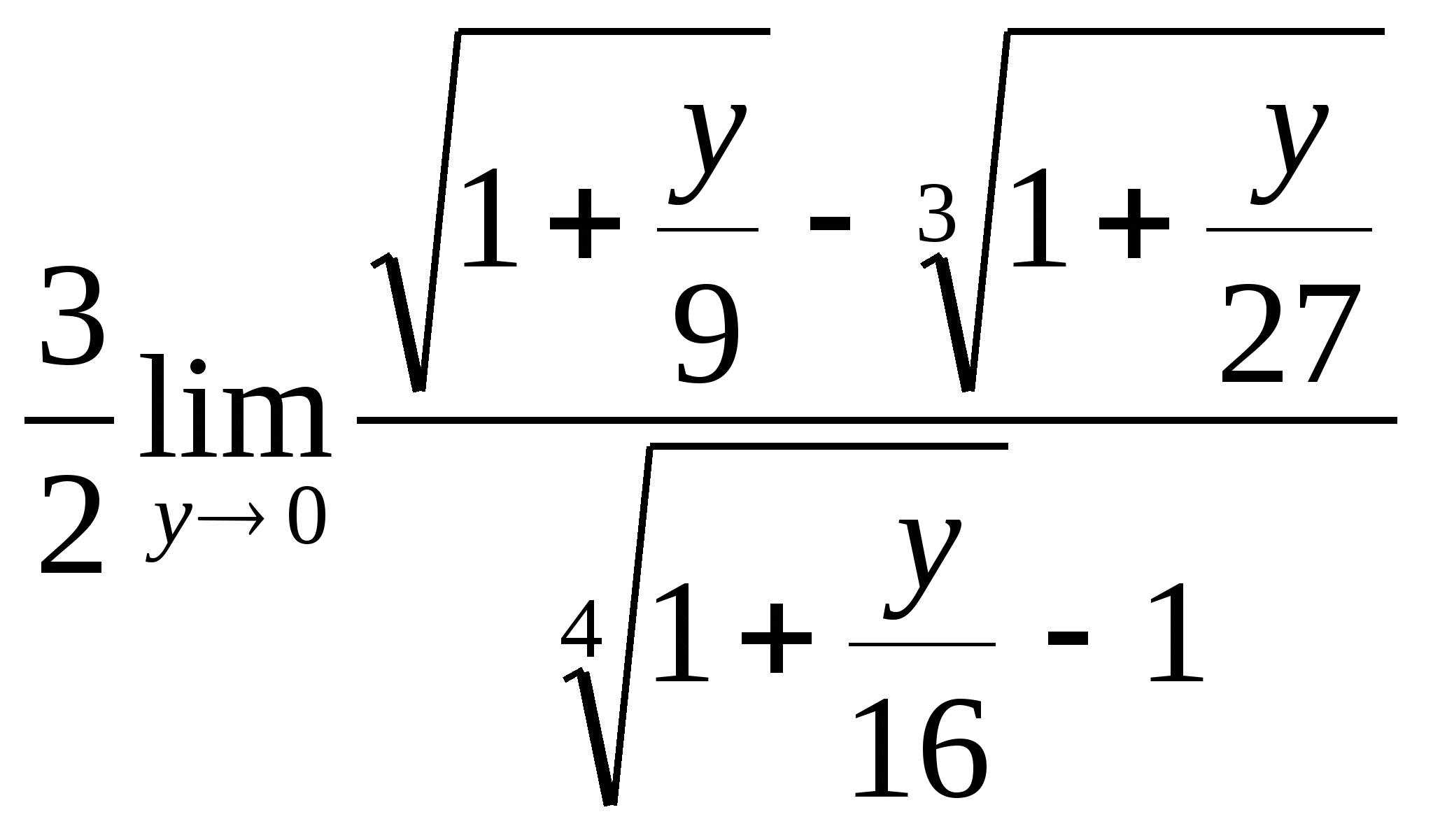 =
=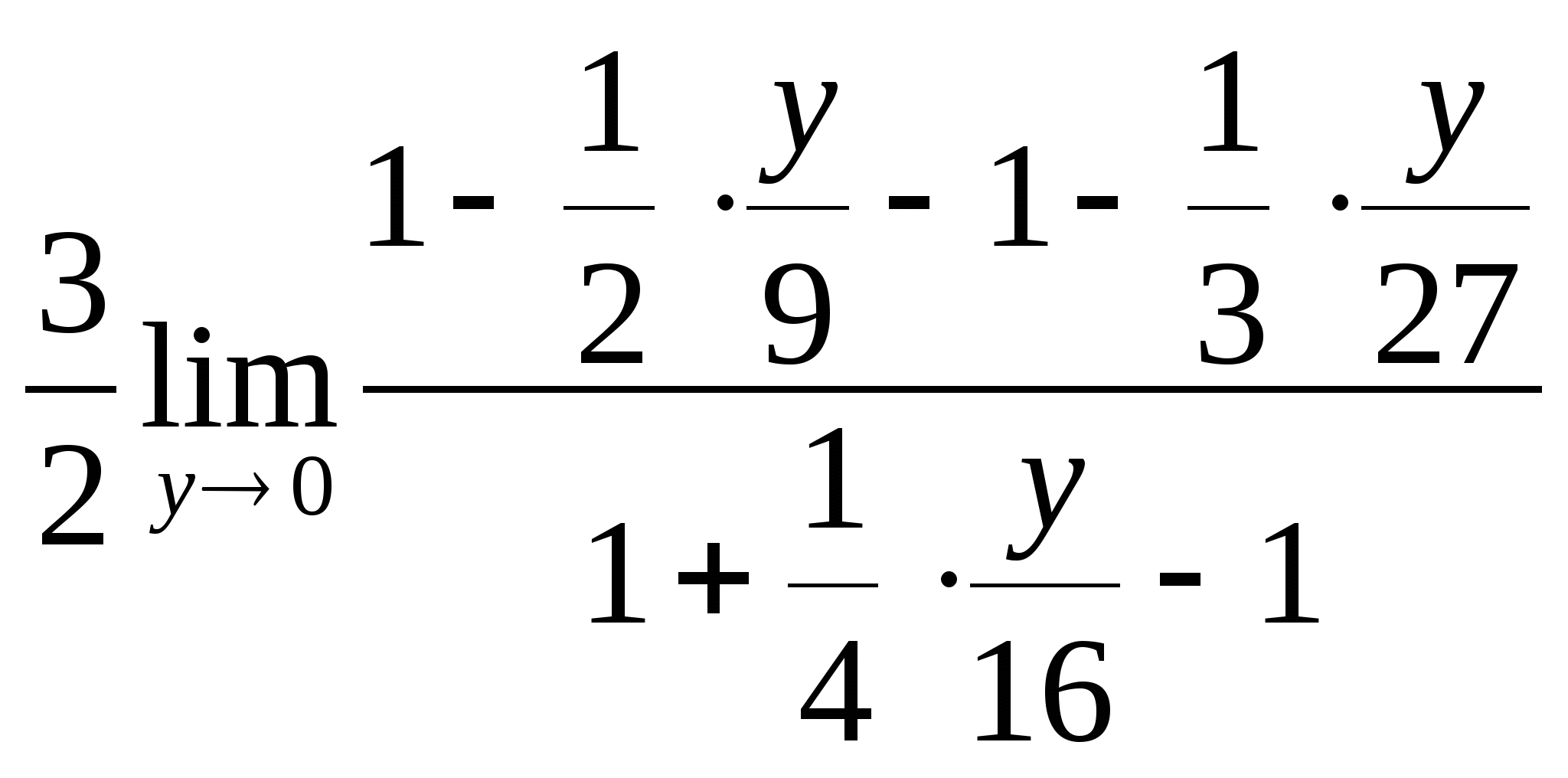 =
=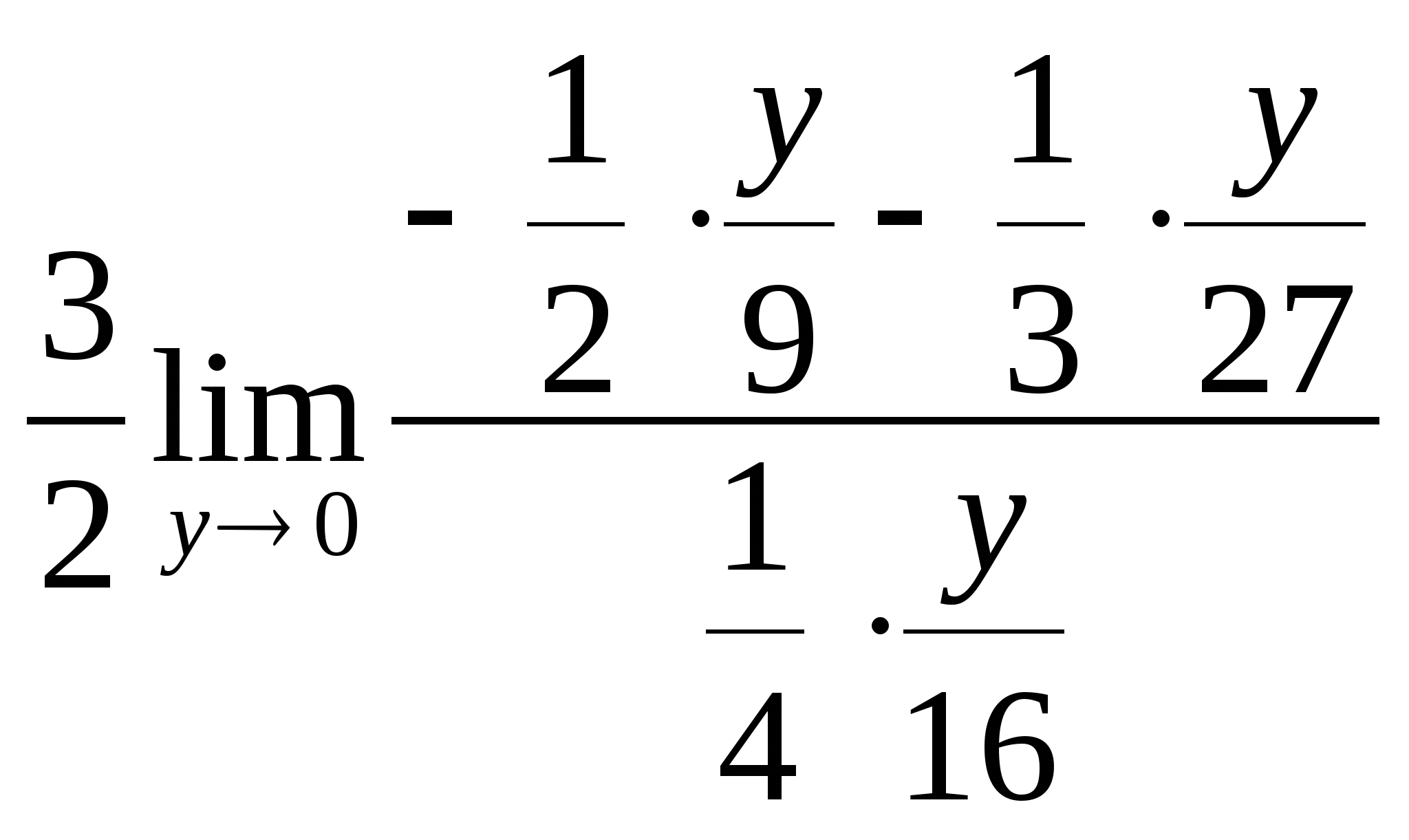 =
=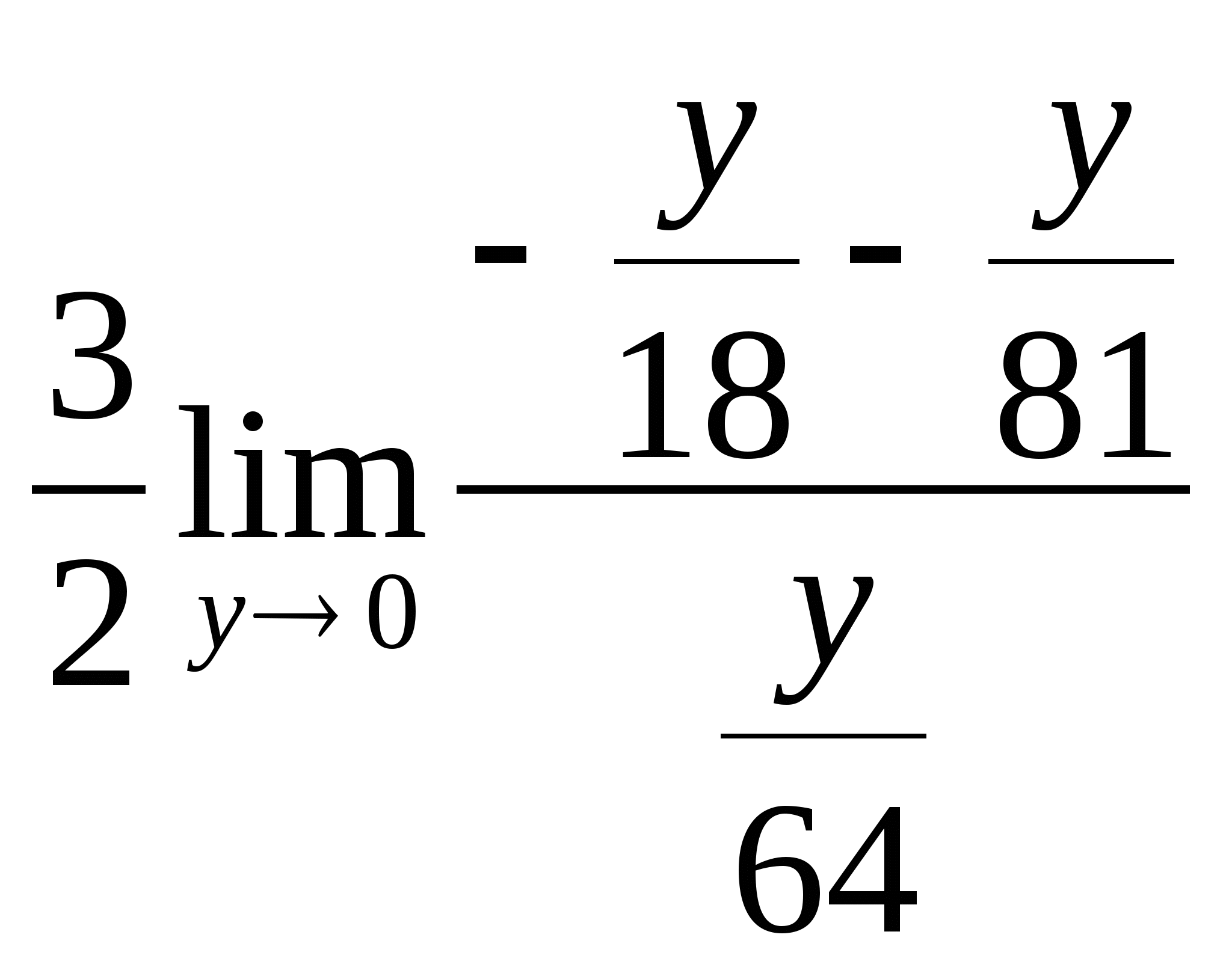 =
=
=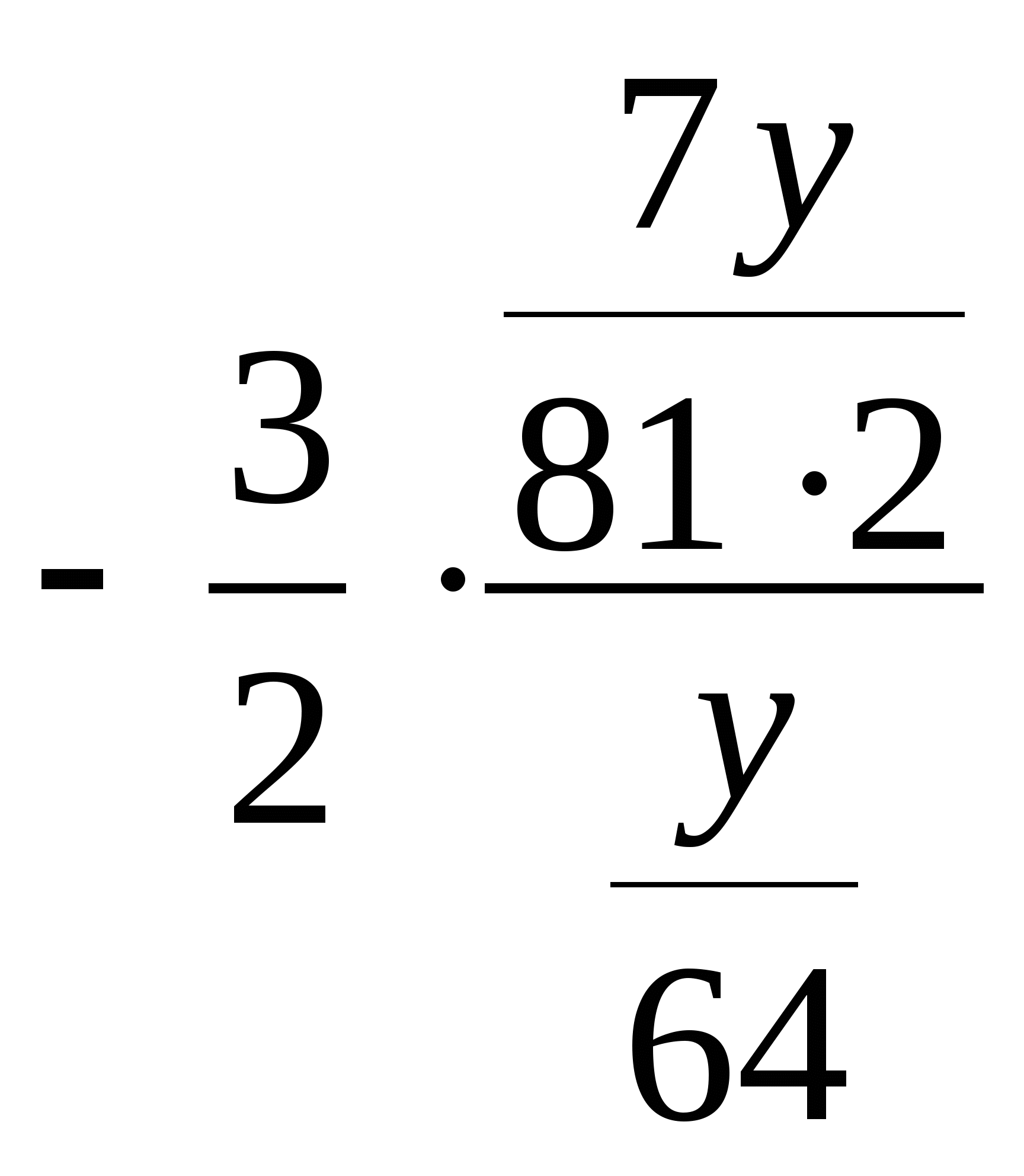 =
=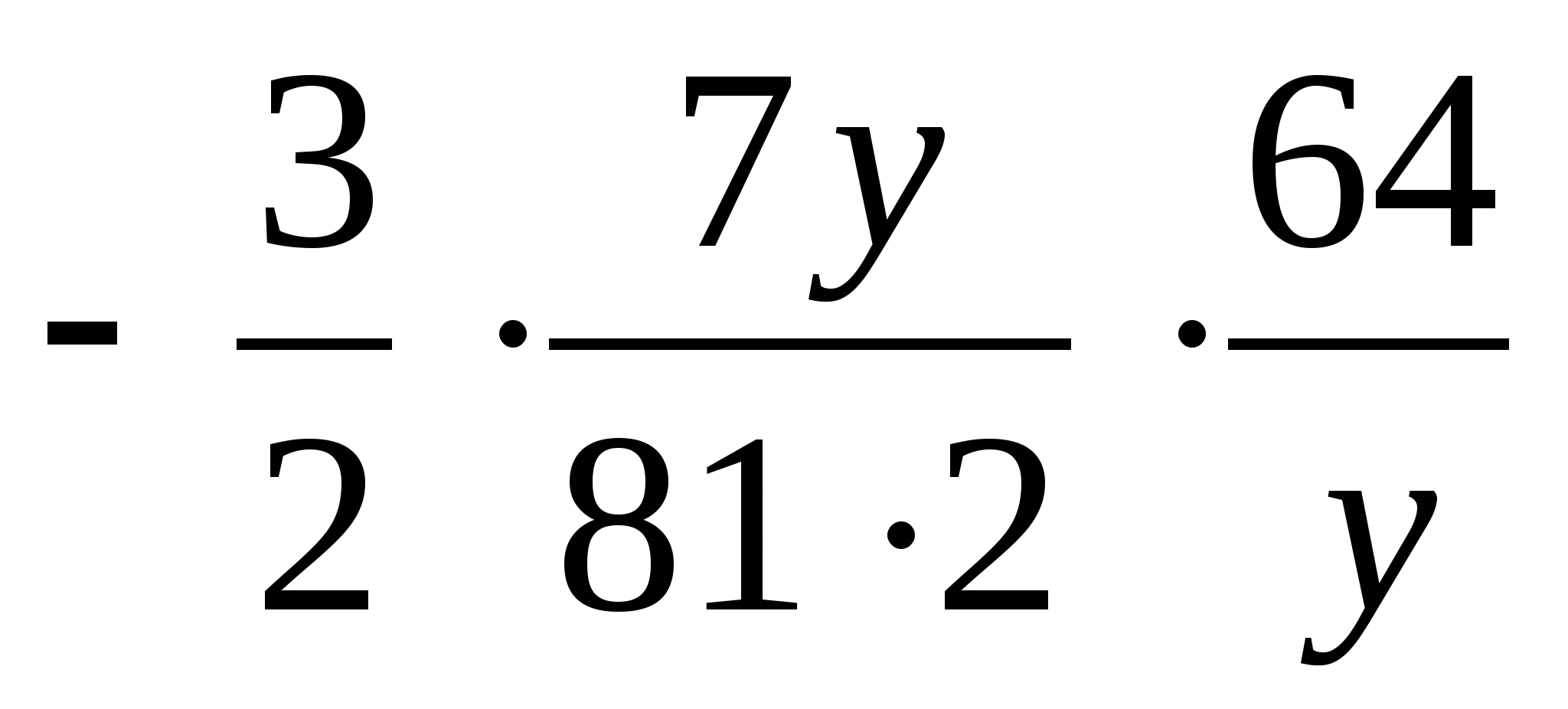 =
=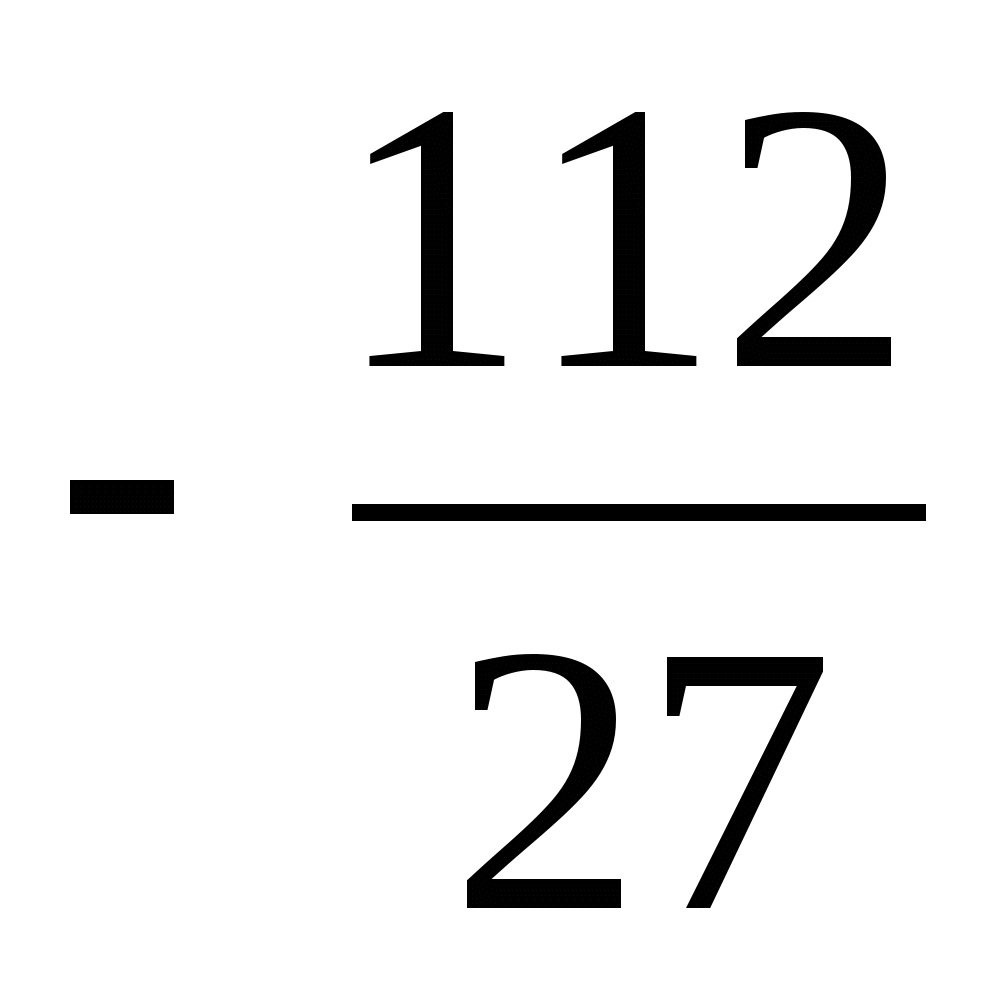 ;
;
(воспользовались эквивалентностью 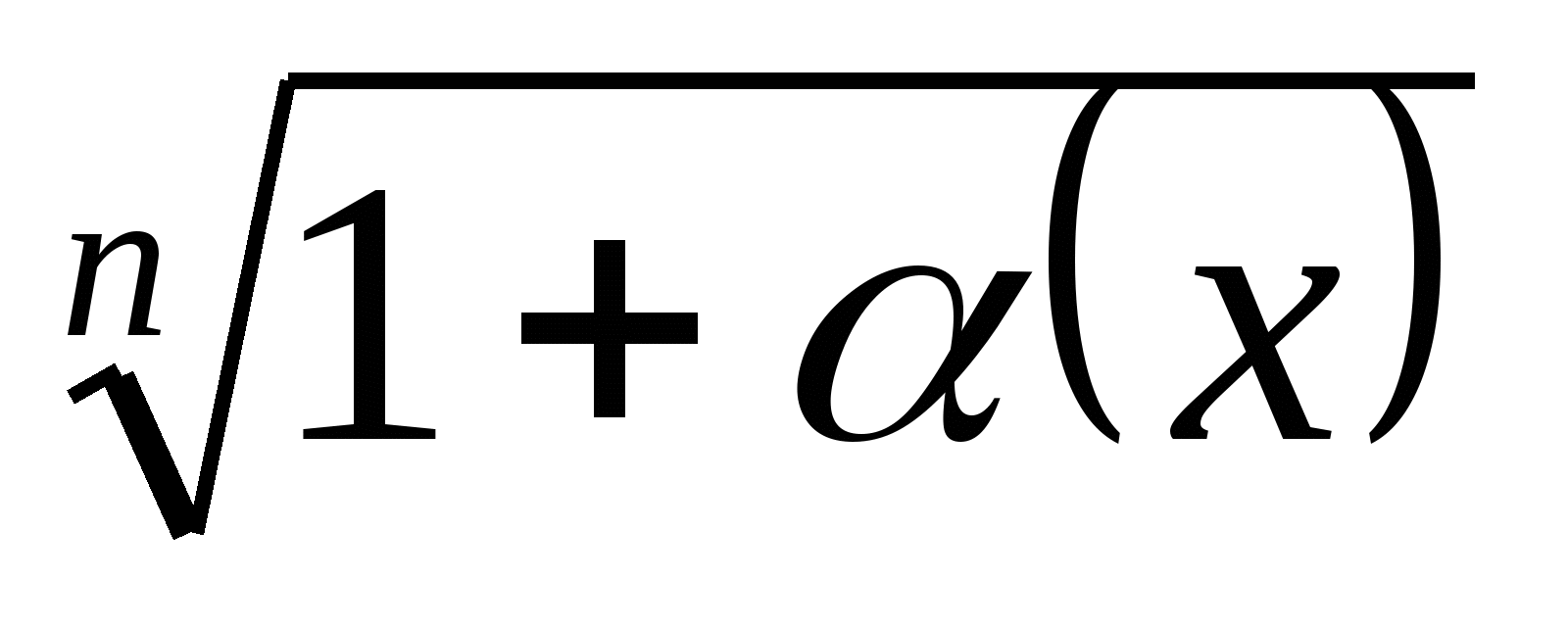 ~
~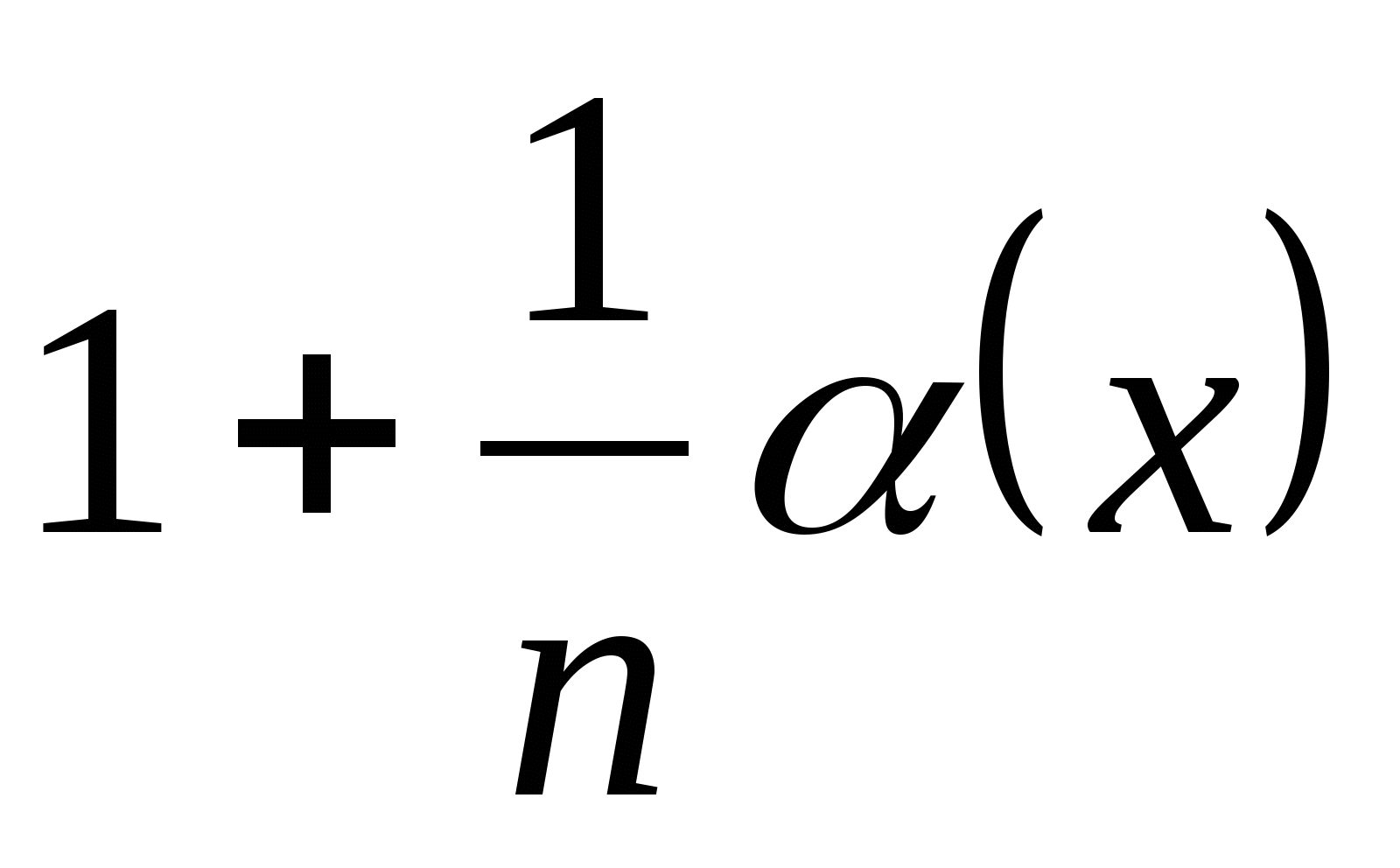 ;
; 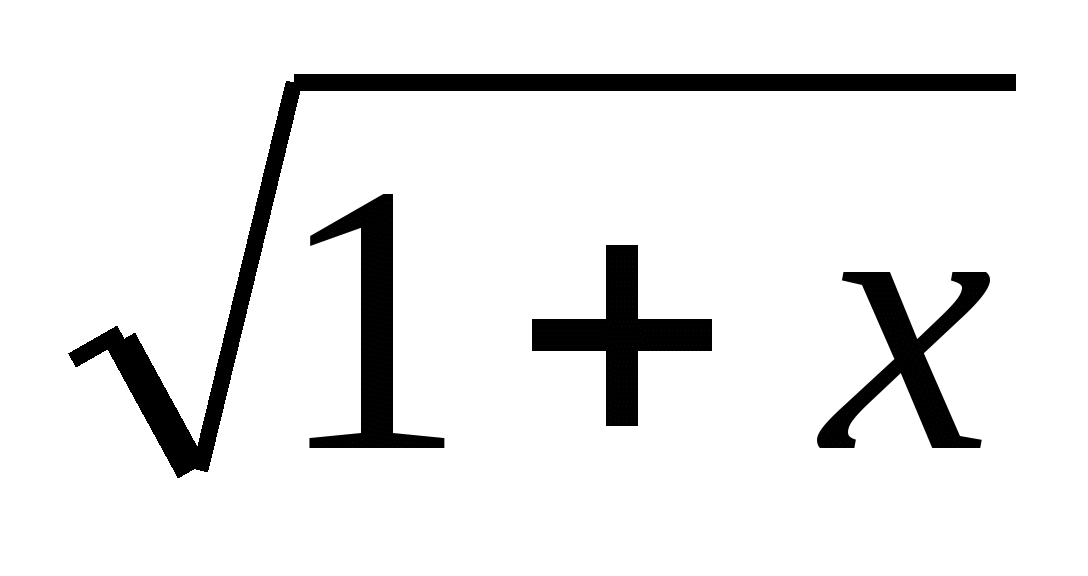 ~
~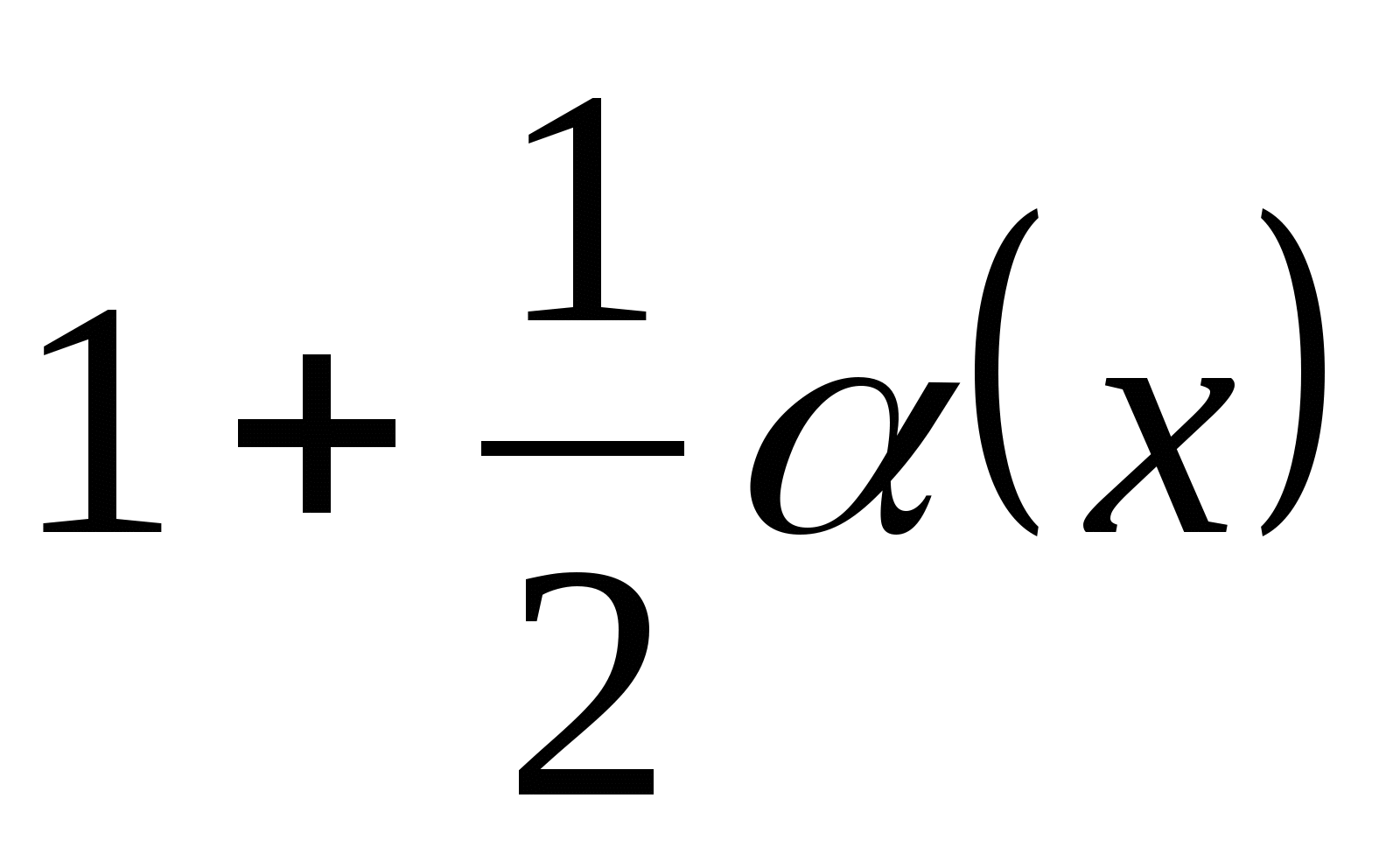 ;).
;).
Ответ: 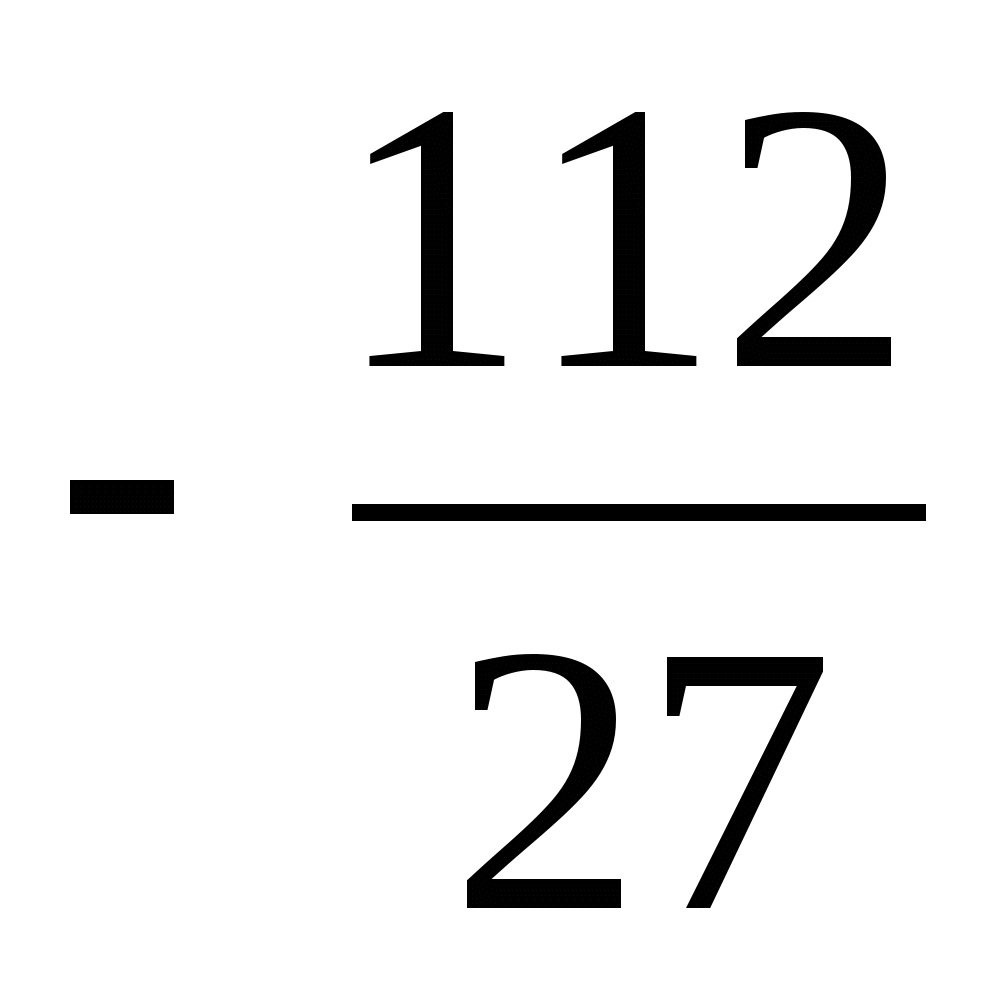 .
.
6. 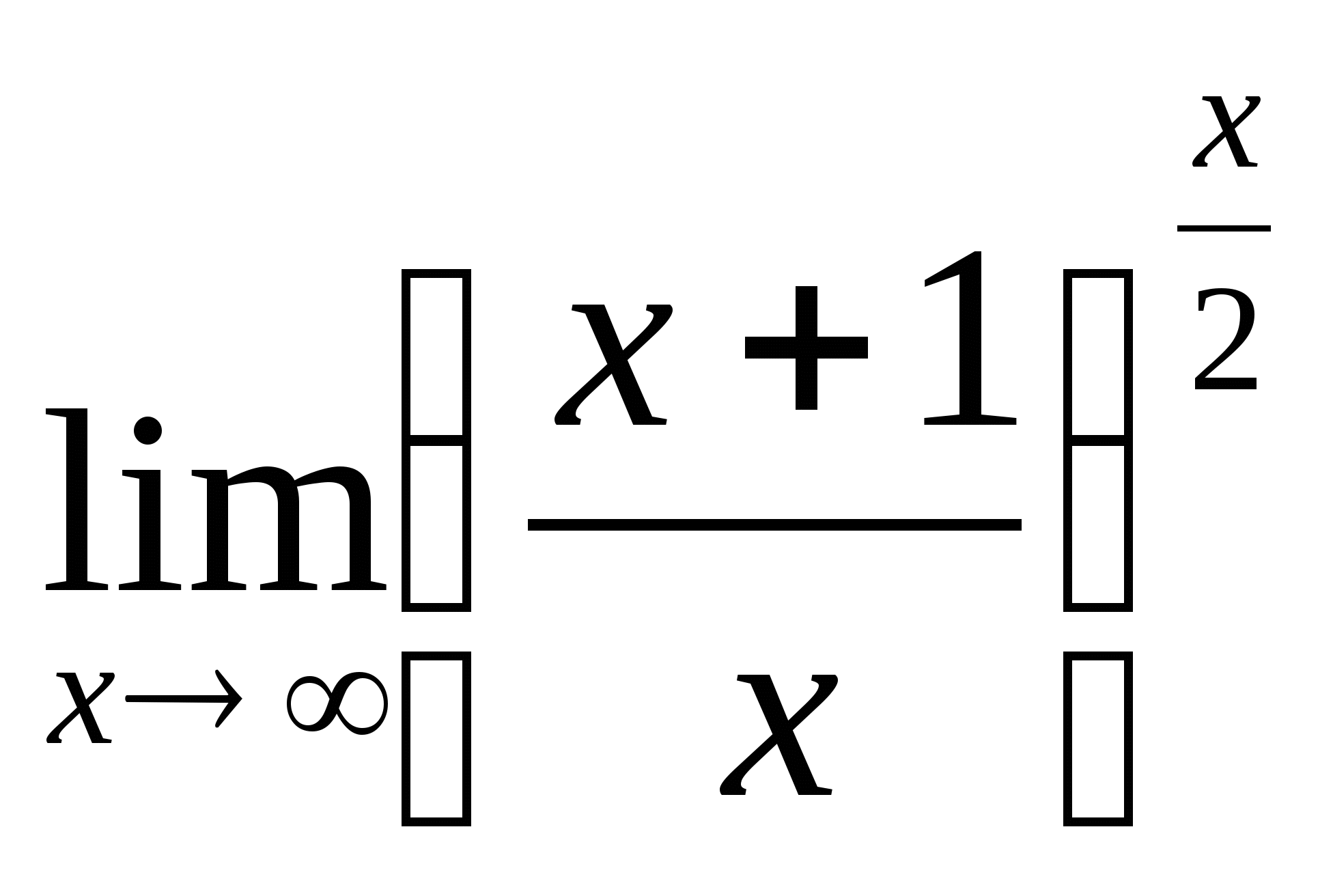
Решение: 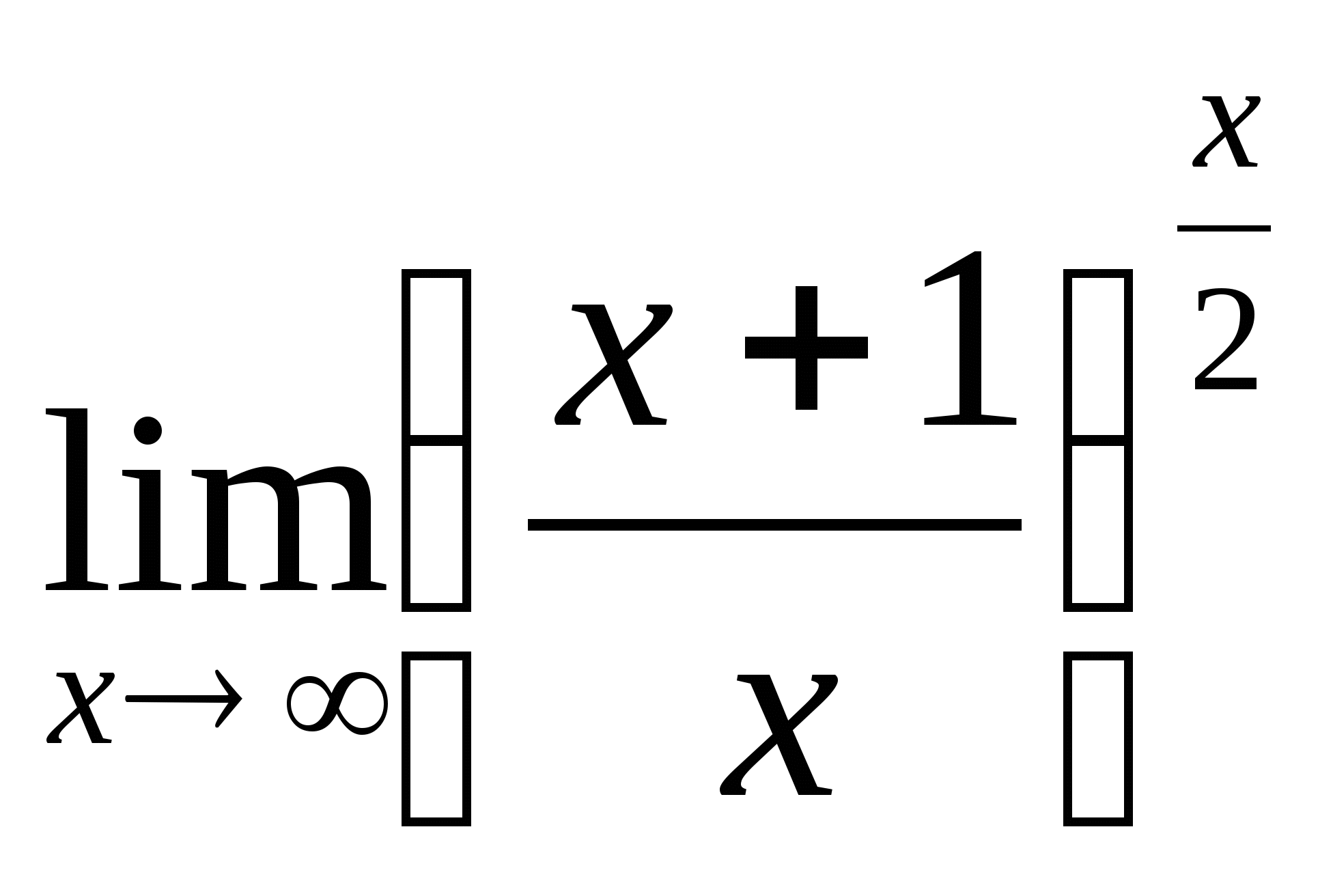 = (воспользуемся вторым замечательным пределом,
= (воспользуемся вторым замечательным пределом,
выполним необходимые преобразования — в скобках выполним деление)
=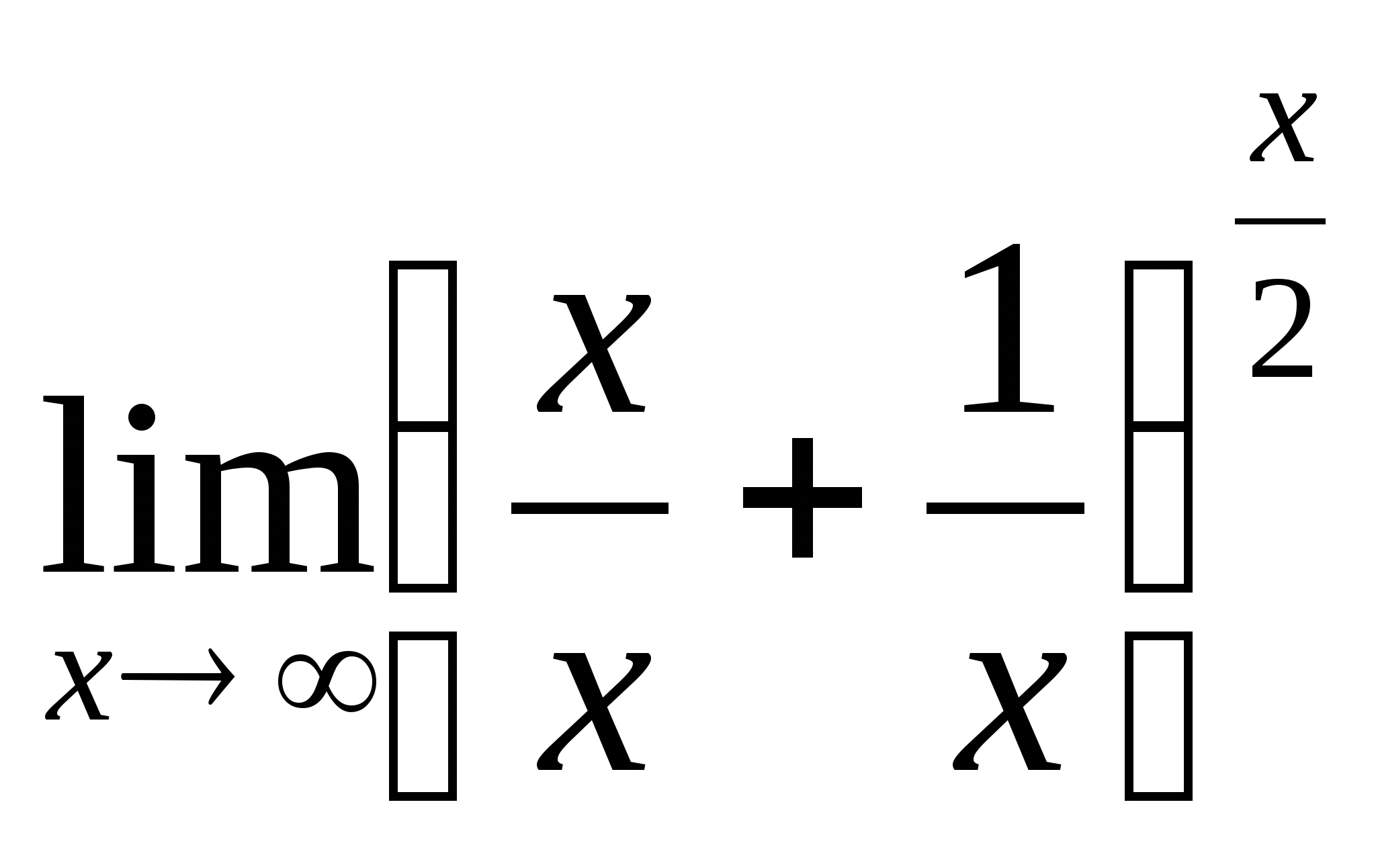 =
=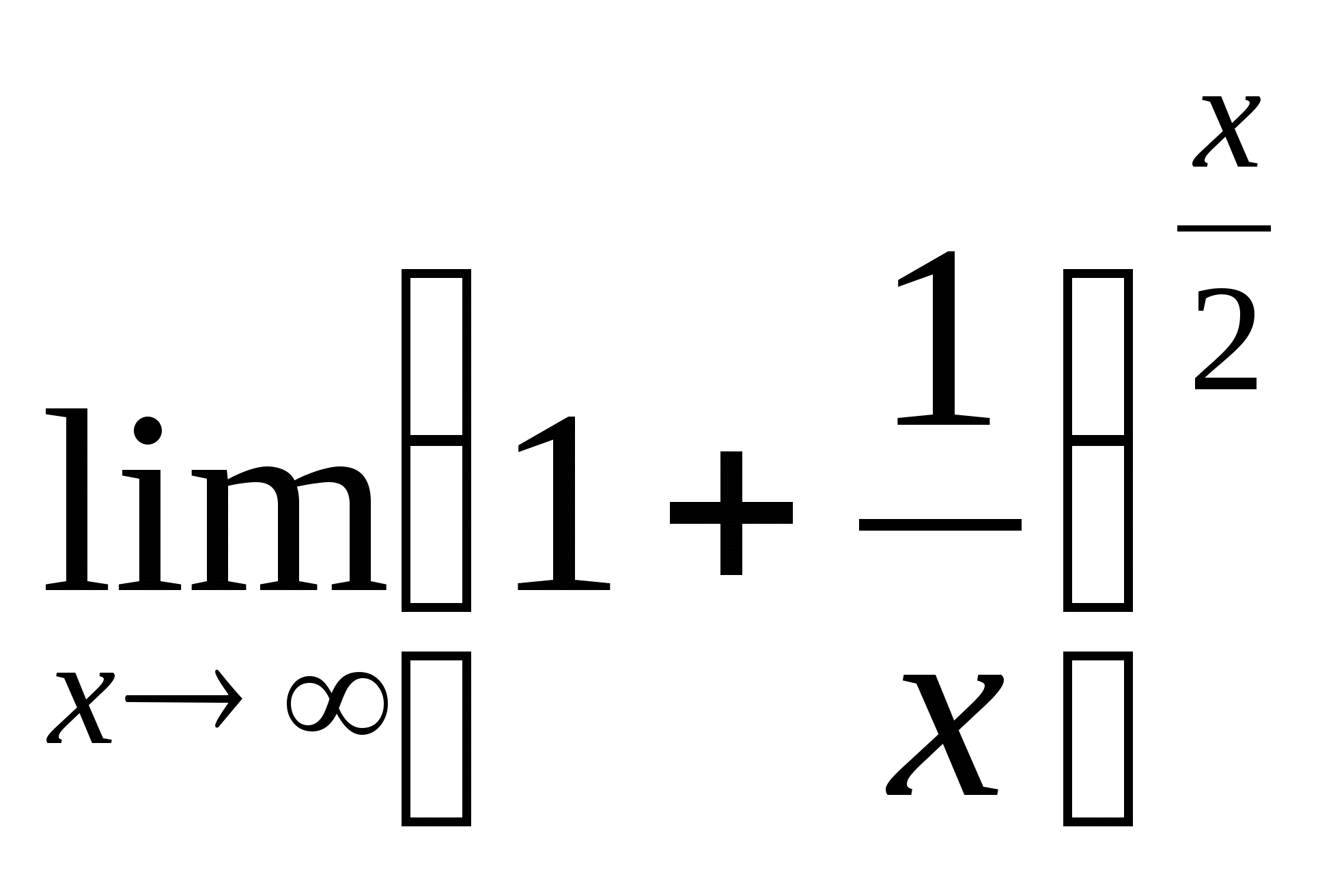 =
=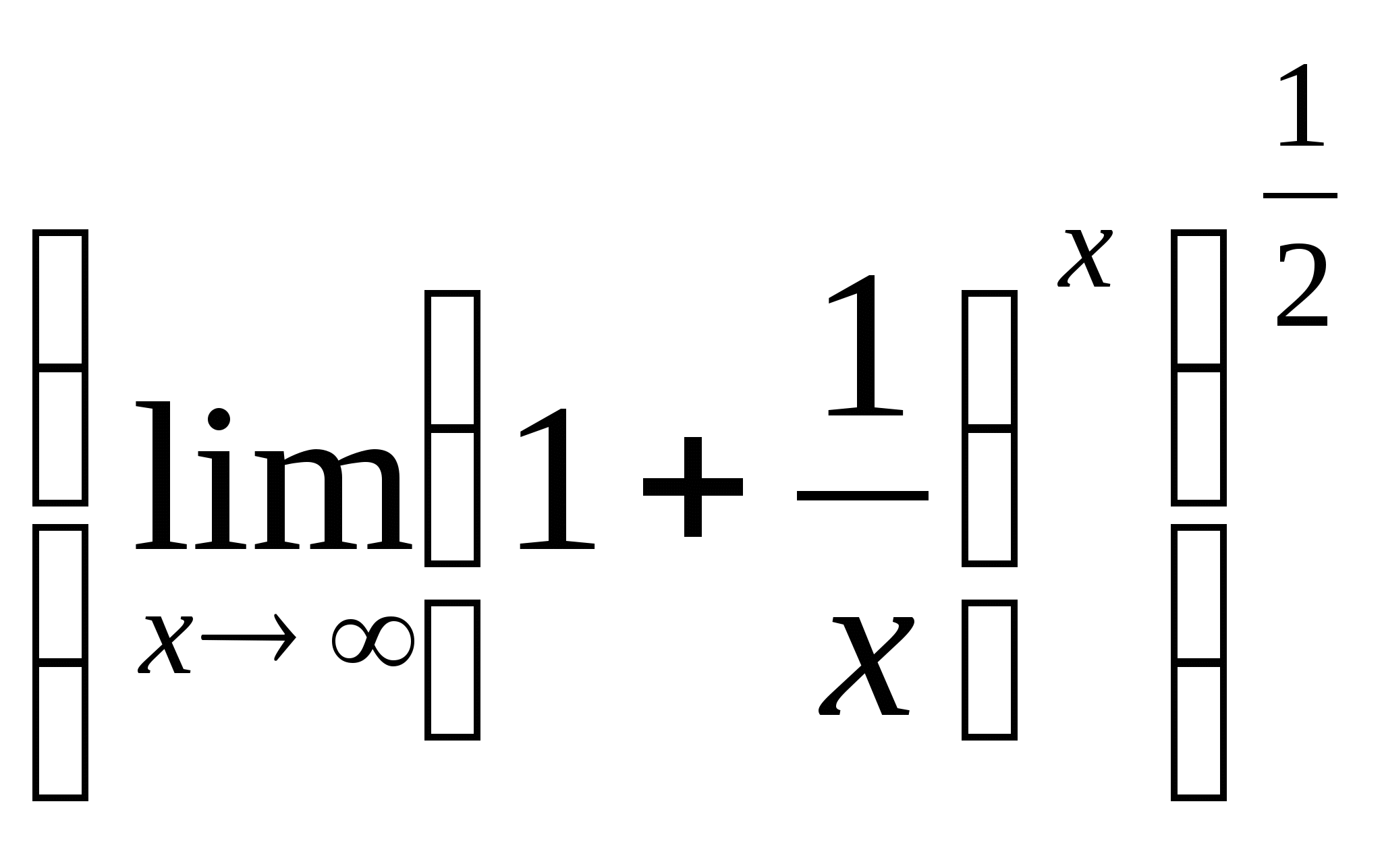 =
=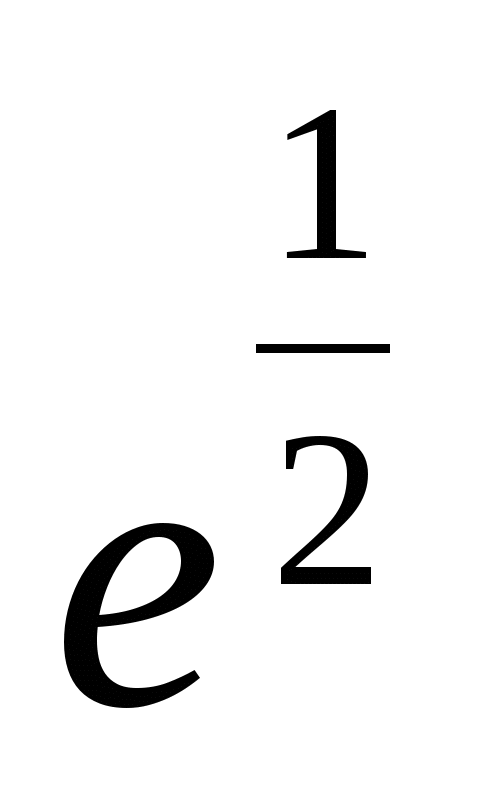
Ответ: 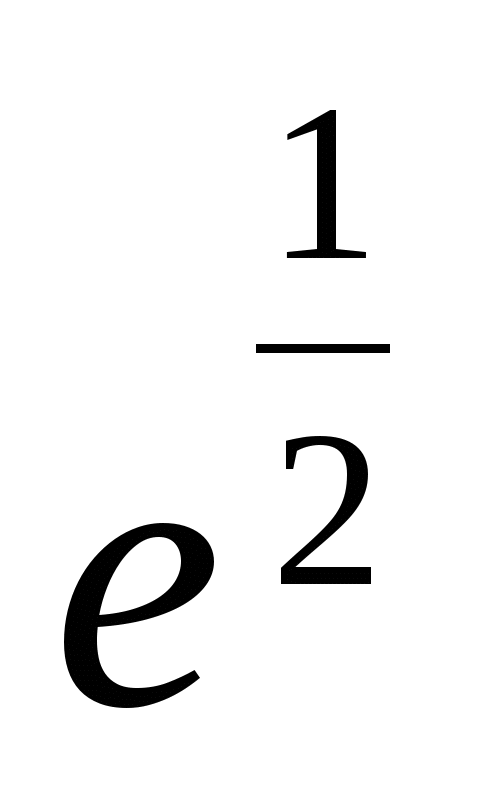 .
.
7. 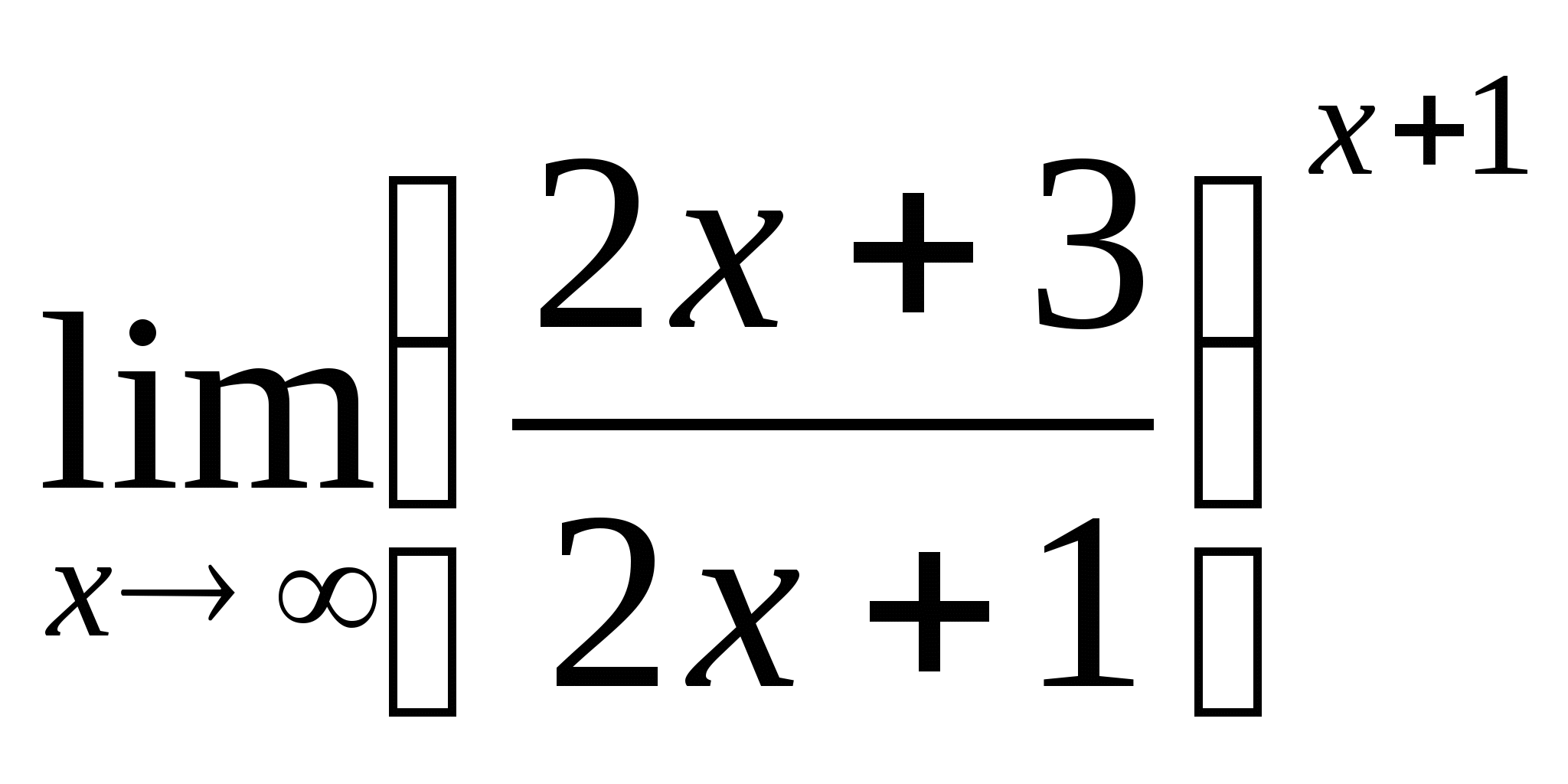
Решение: 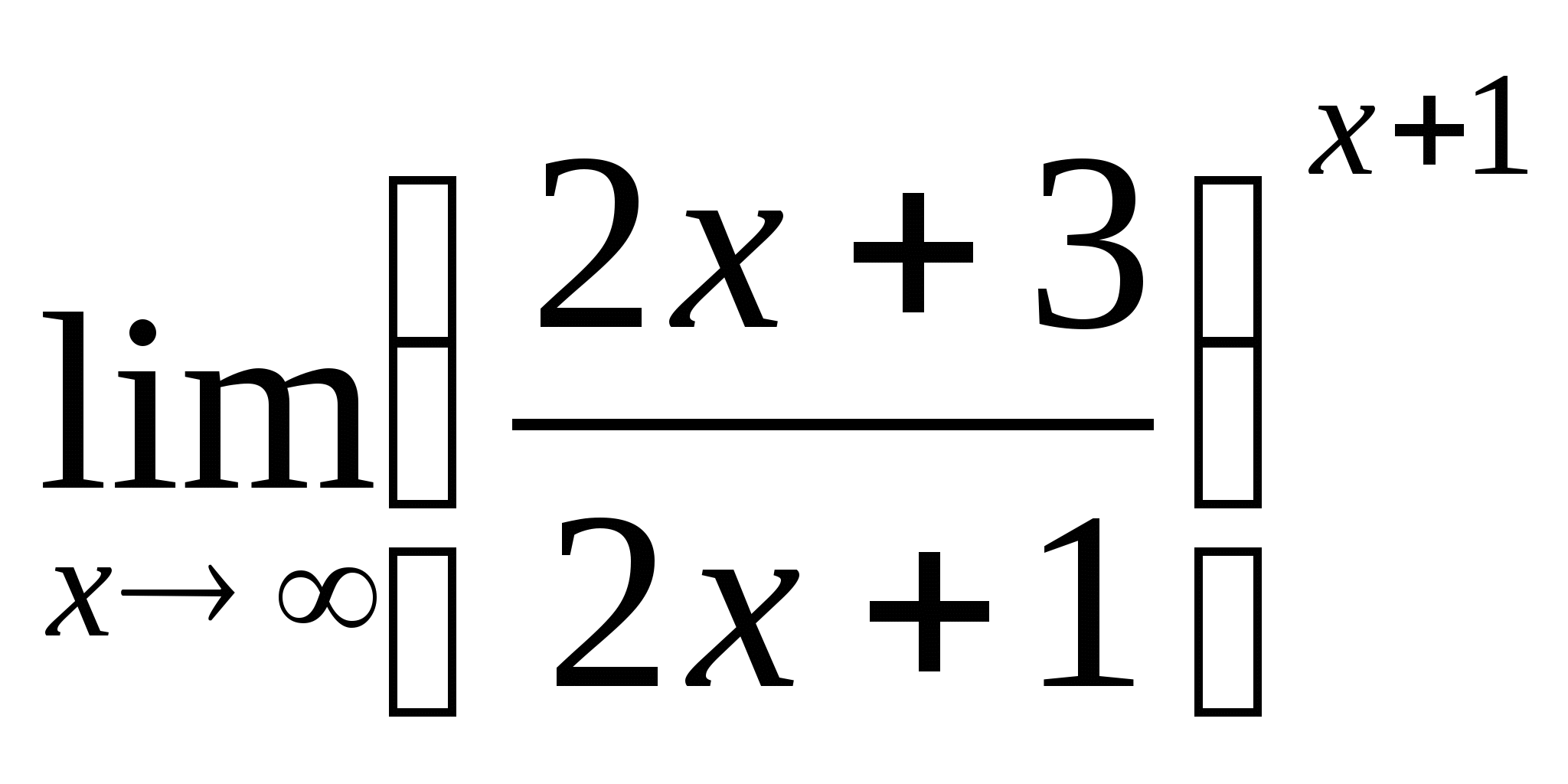 = (воспользуемся вторым замечательным пределом,
= (воспользуемся вторым замечательным пределом,
выполним необходимые преобразования – распишем предел частного, как частное пределов и решим получившиеся пределы отдельно друг от друга)
=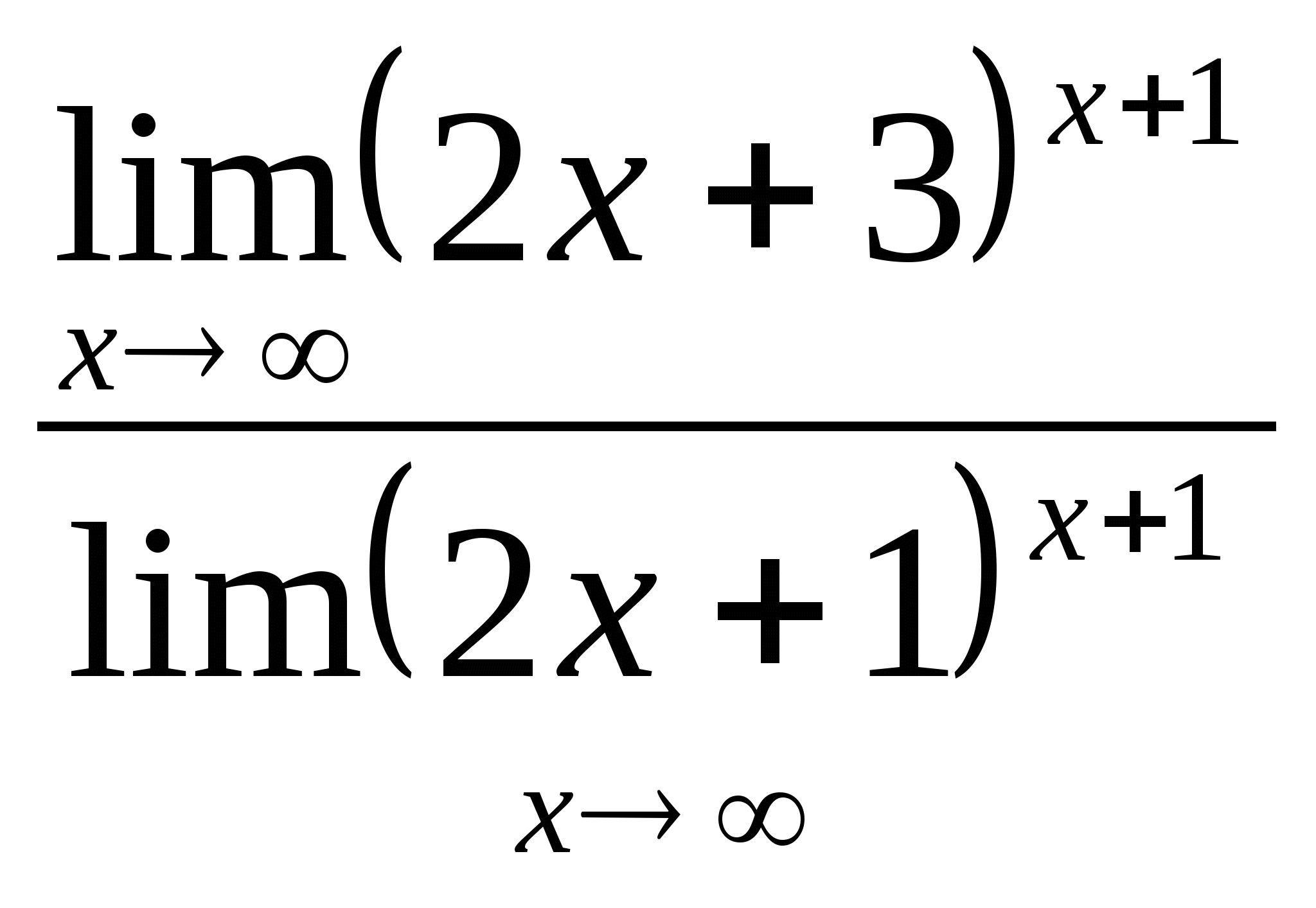 = (найдем отдельно предел числителя и предел знаменателя)
= (найдем отдельно предел числителя и предел знаменателя)
числитель: 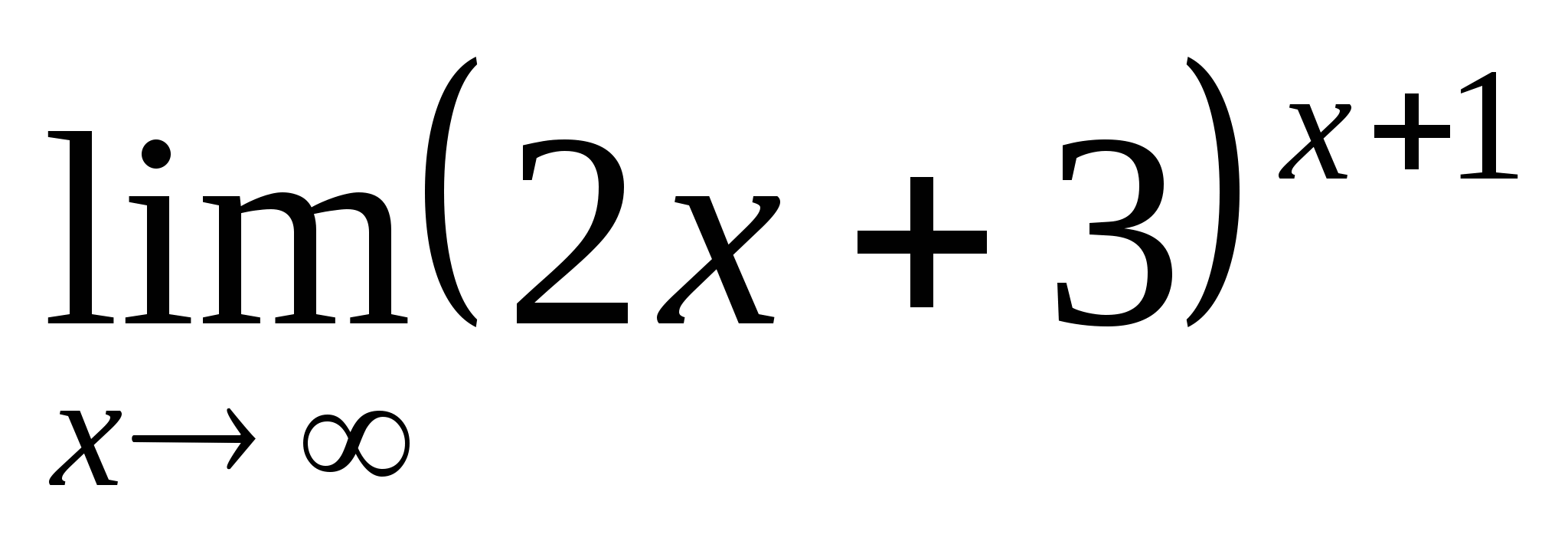 = (выделим в скобках единицу, необходимую для второго
= (выделим в скобках единицу, необходимую для второго
замечательного предела: разделим каждое слагаемое на 3),
=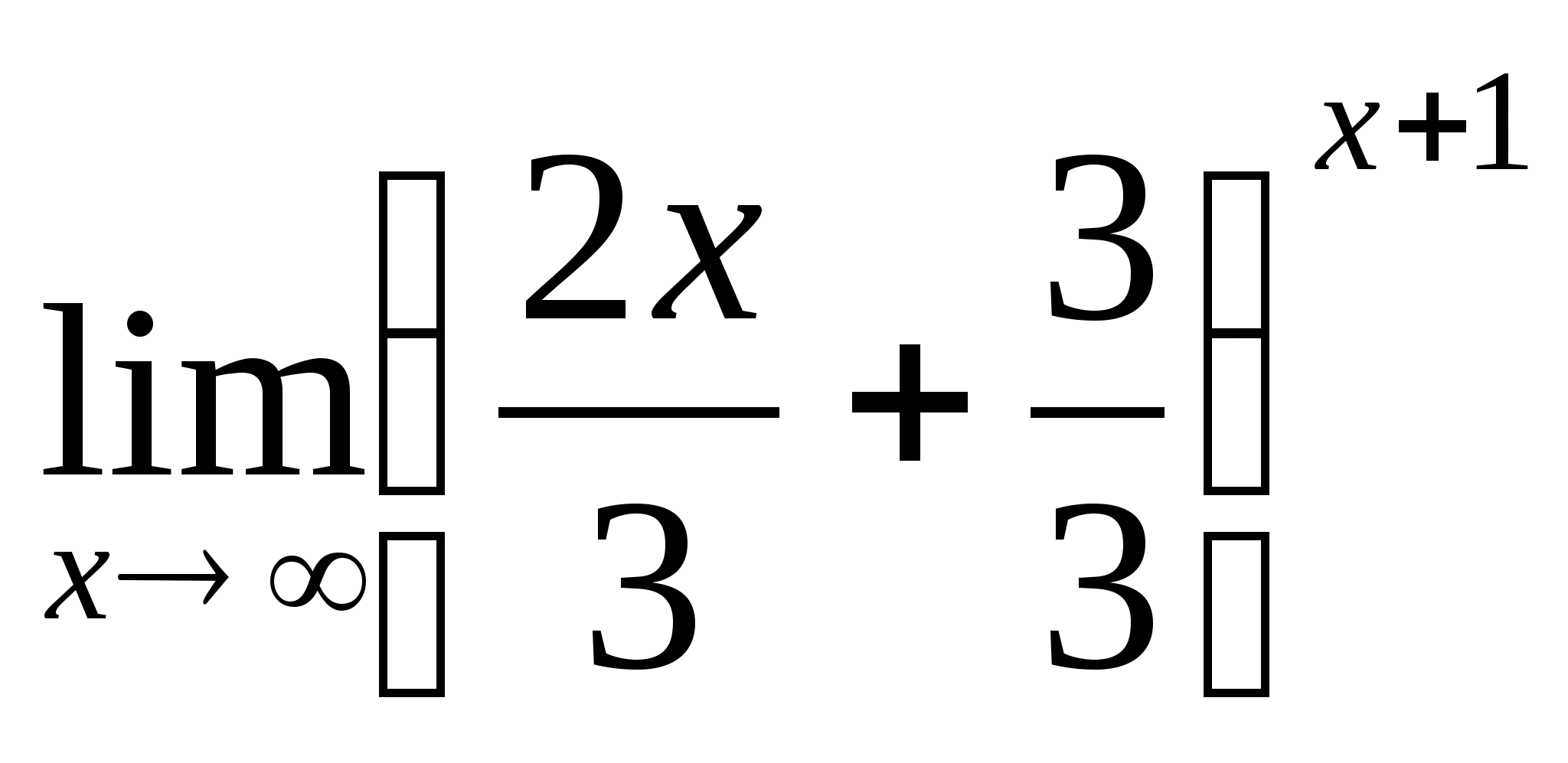 =
=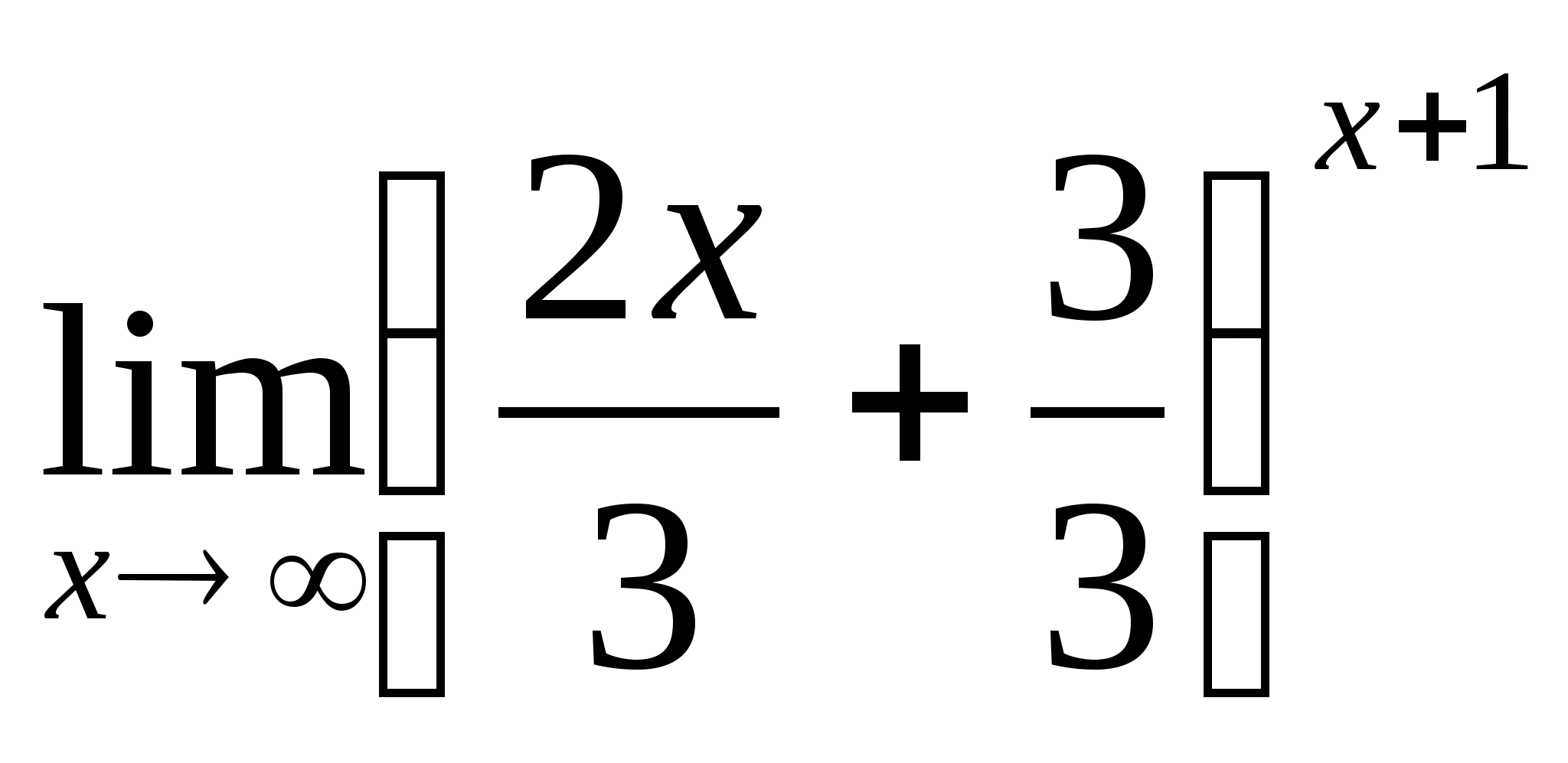 =
=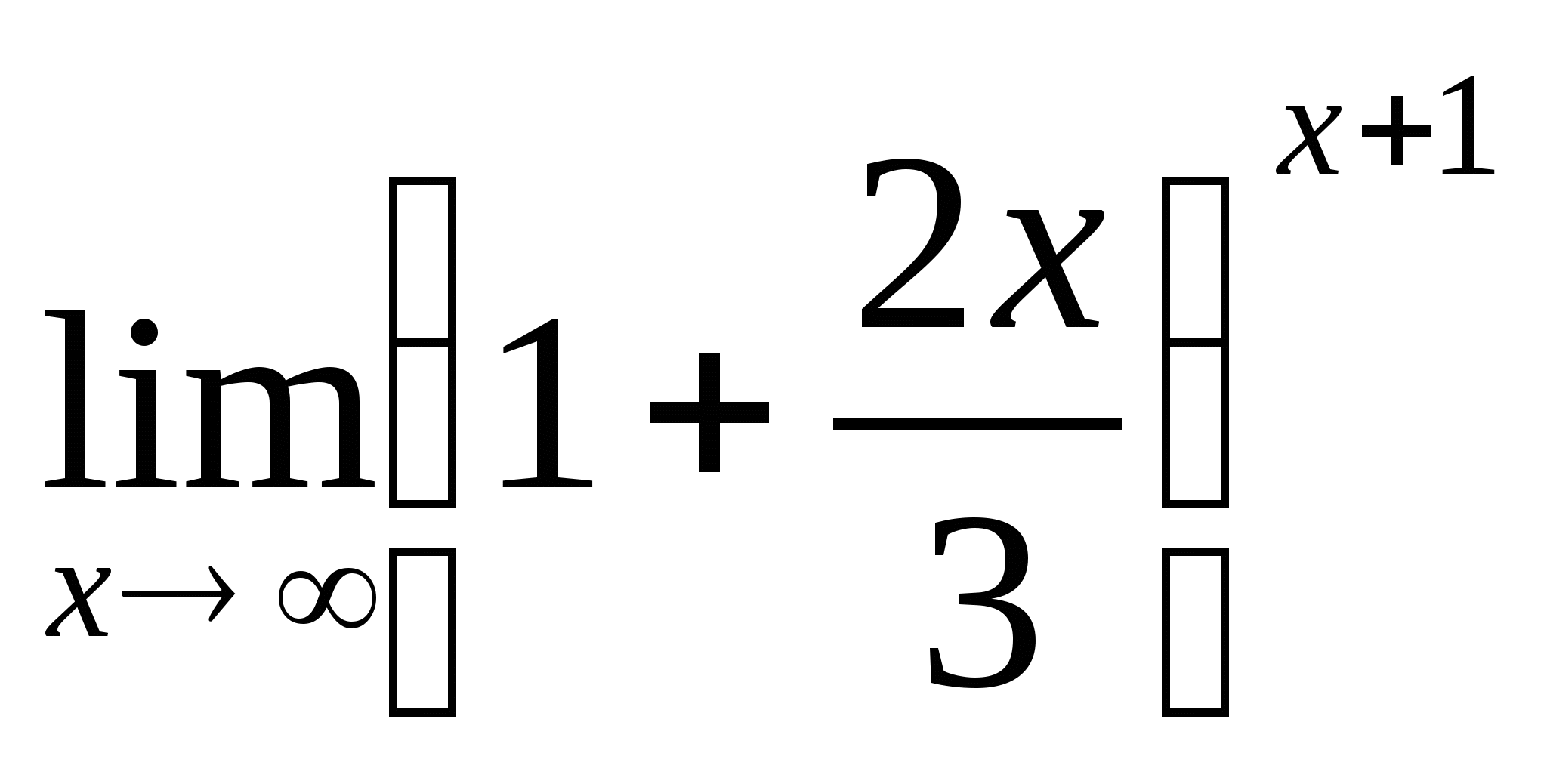 =
=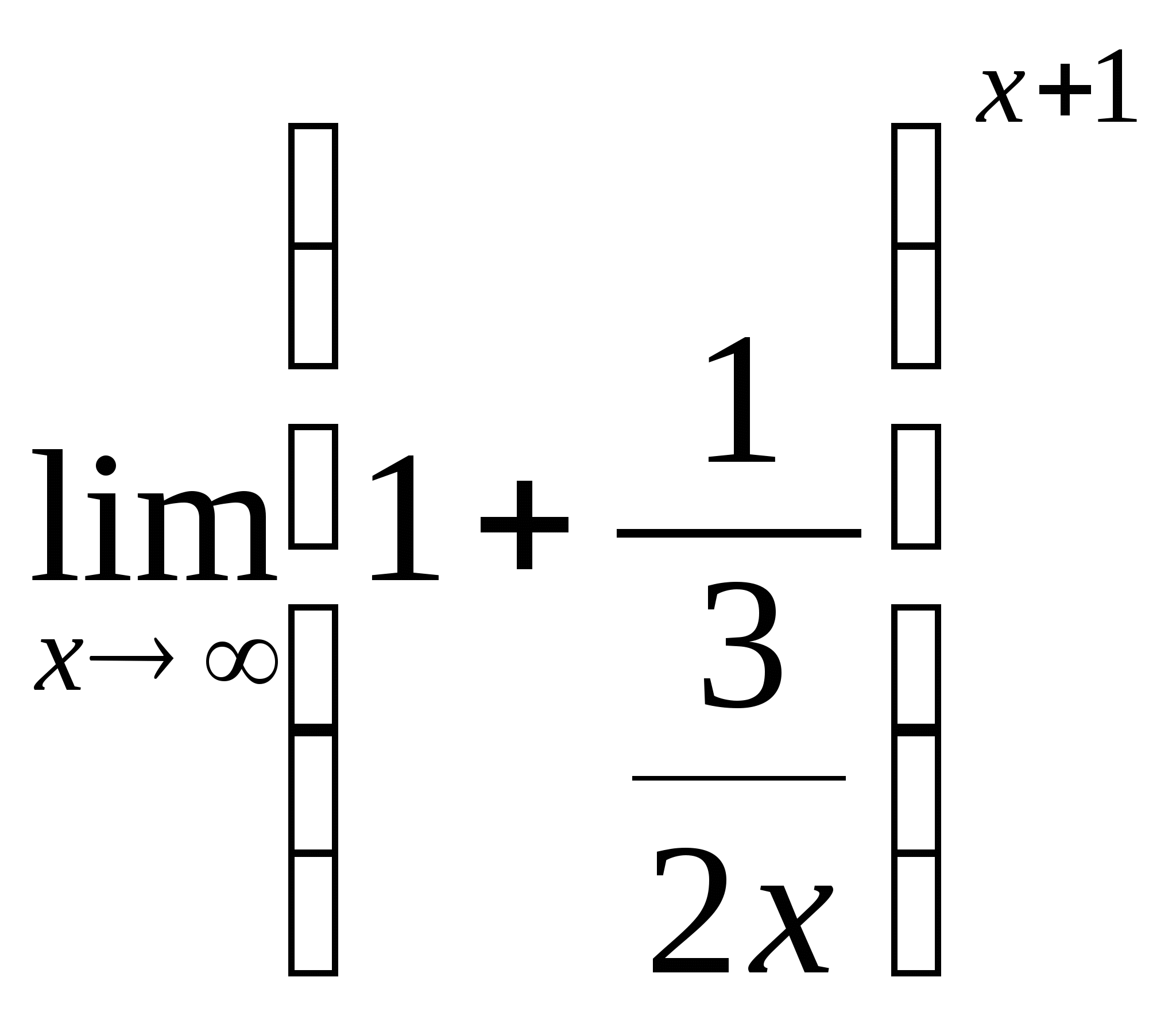 = (второе слагаемое представим в виде обратной дроби и введем
= (второе слагаемое представим в виде обратной дроби и введем 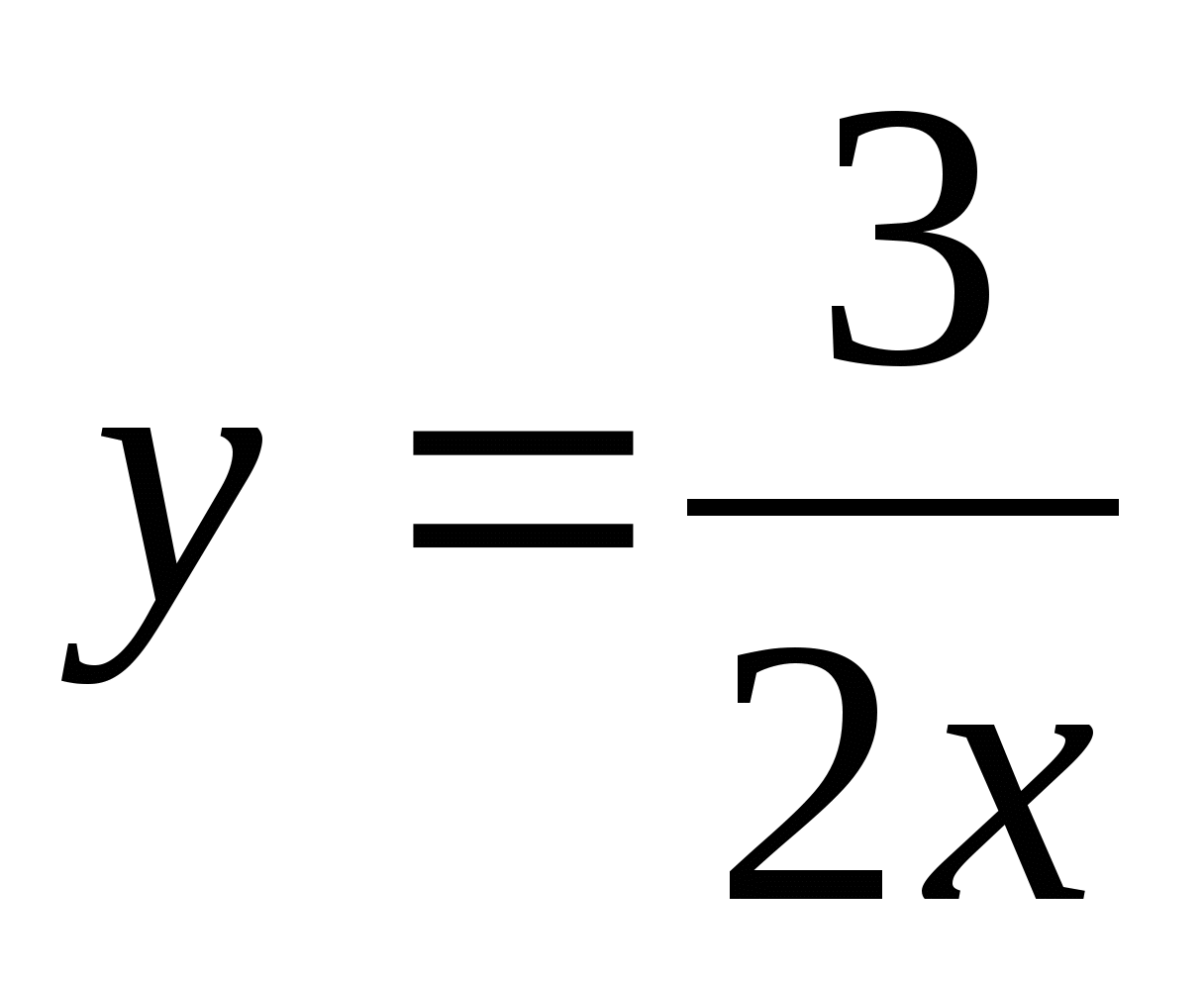

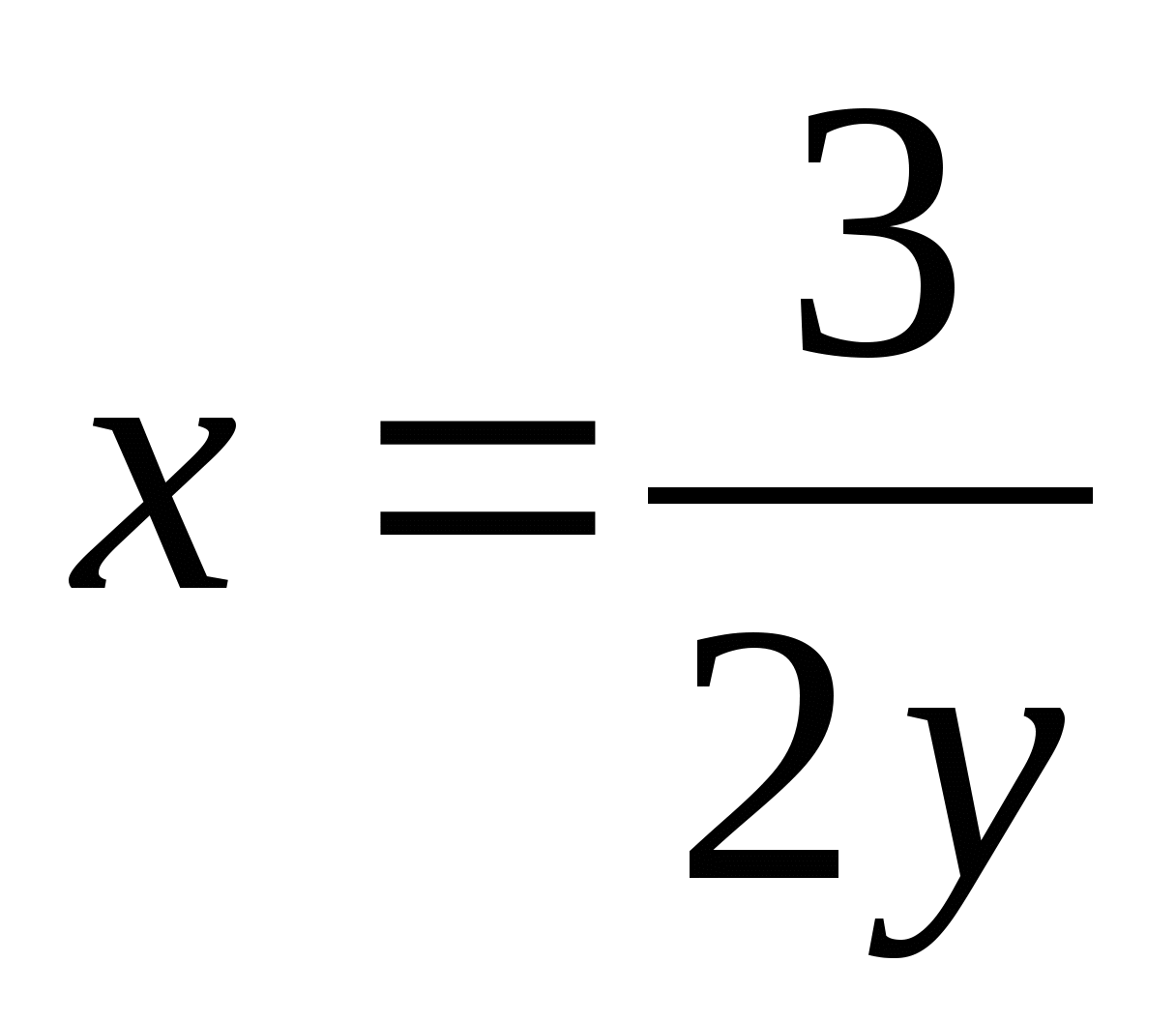 ), тогда
), тогда
=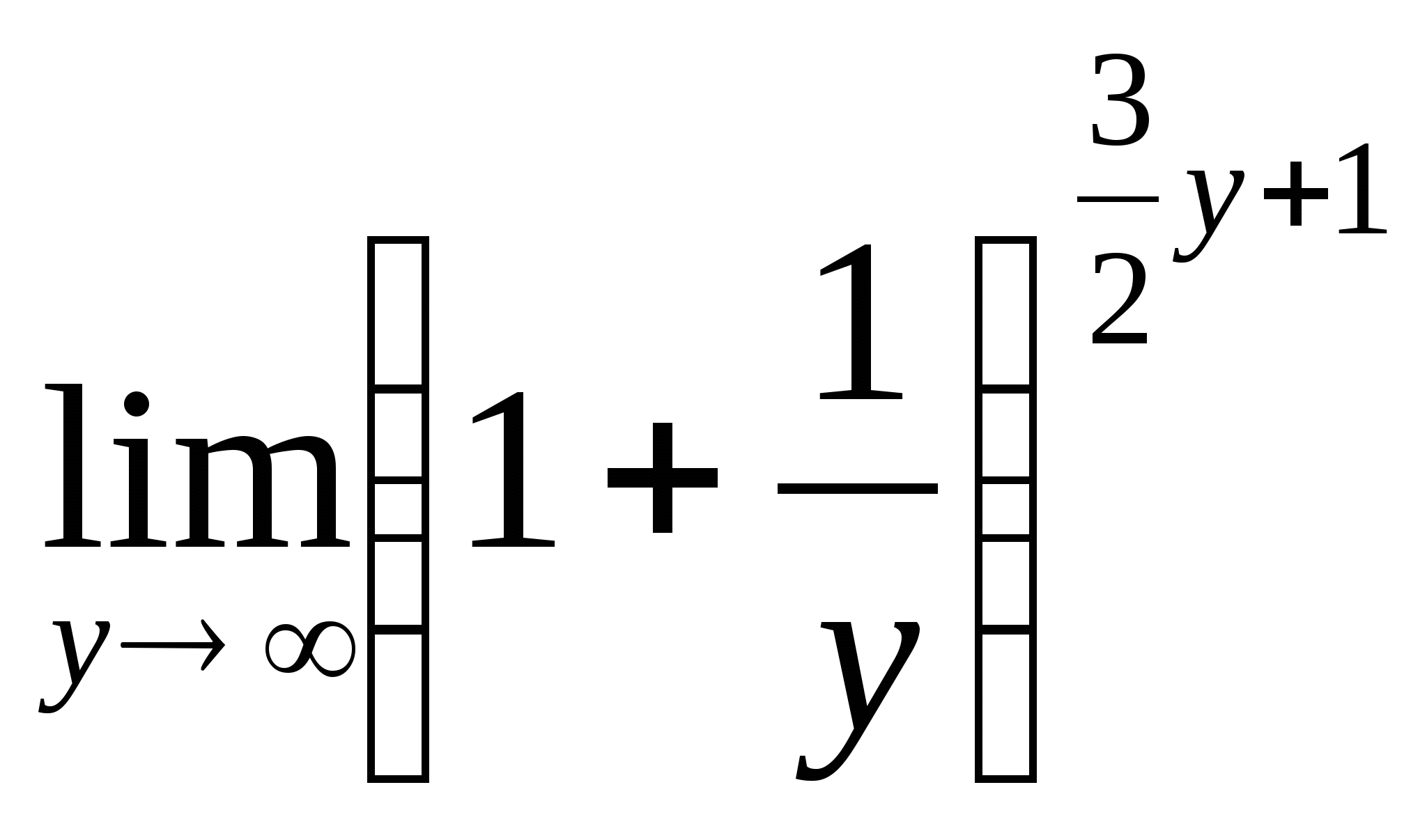 =
=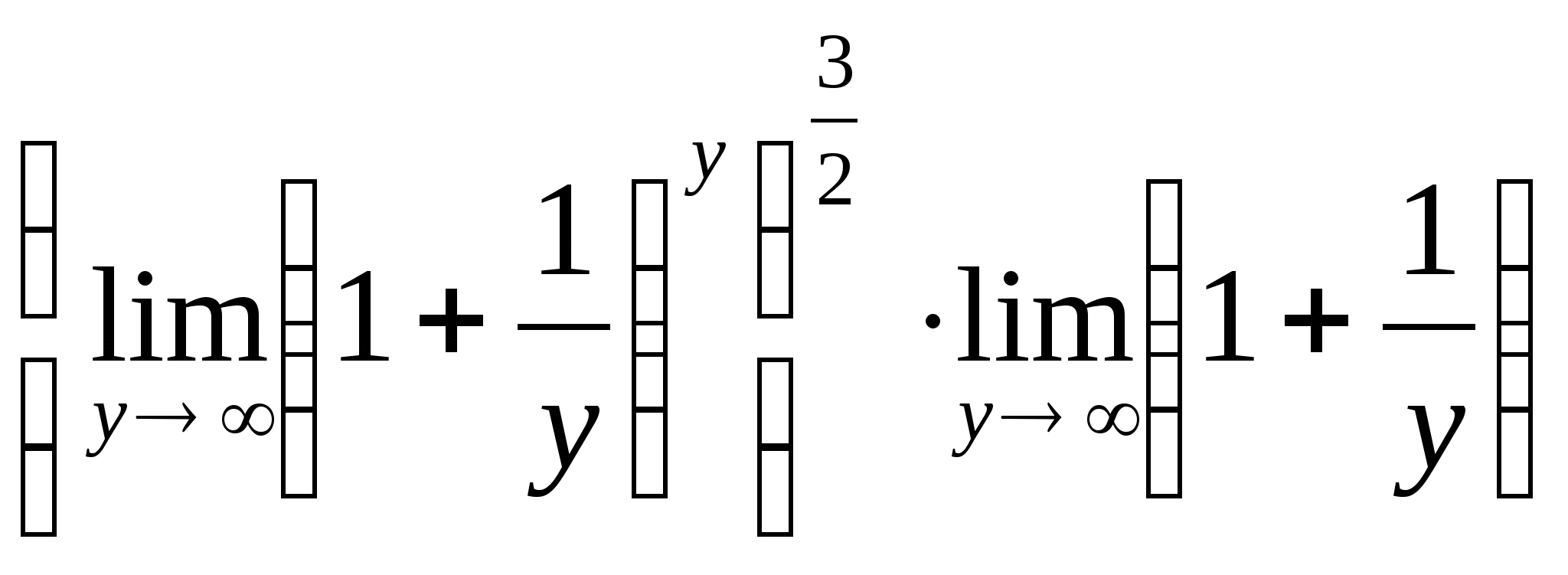 =
=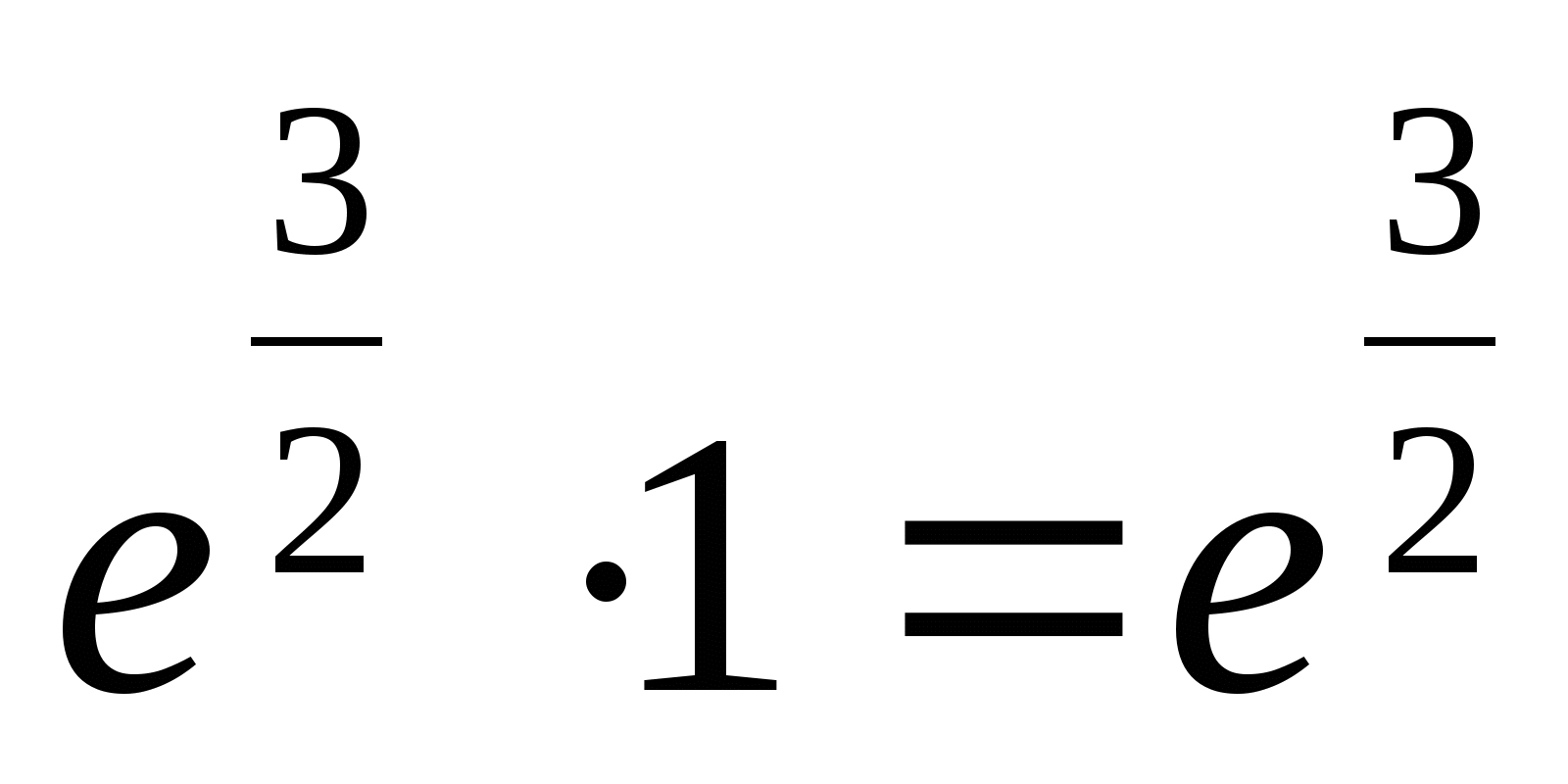 ;
;
знаменатель: 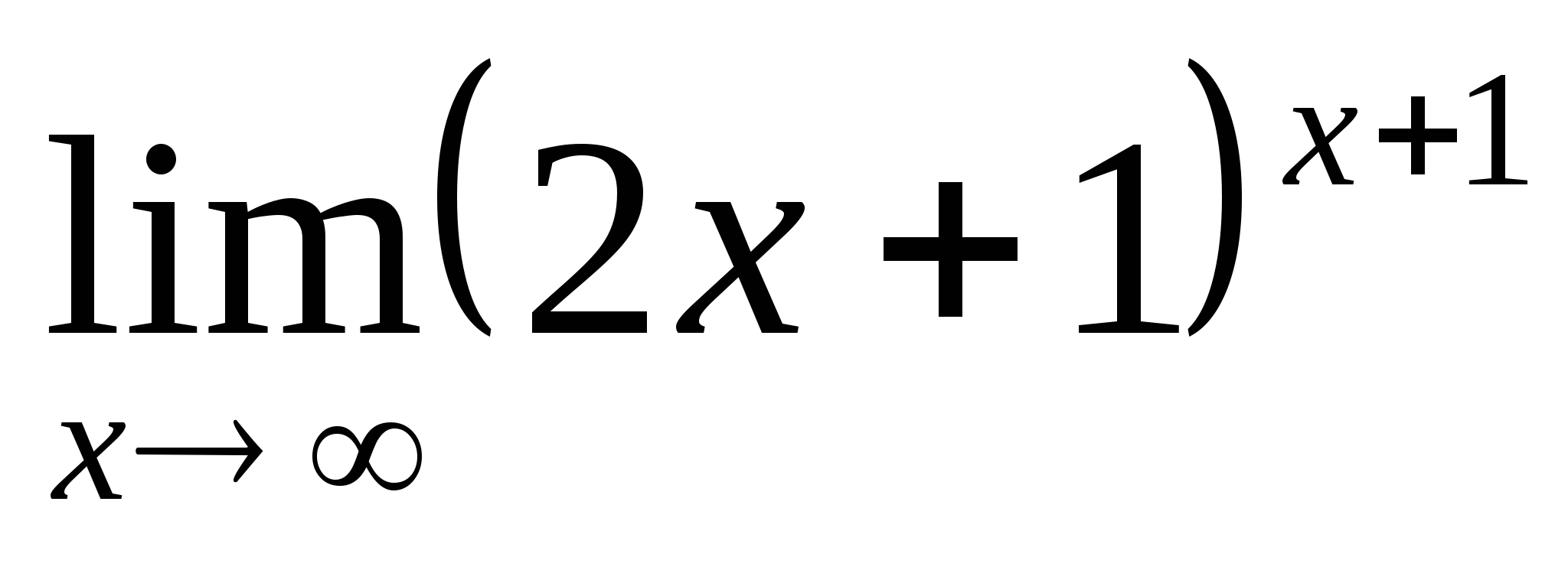 =
=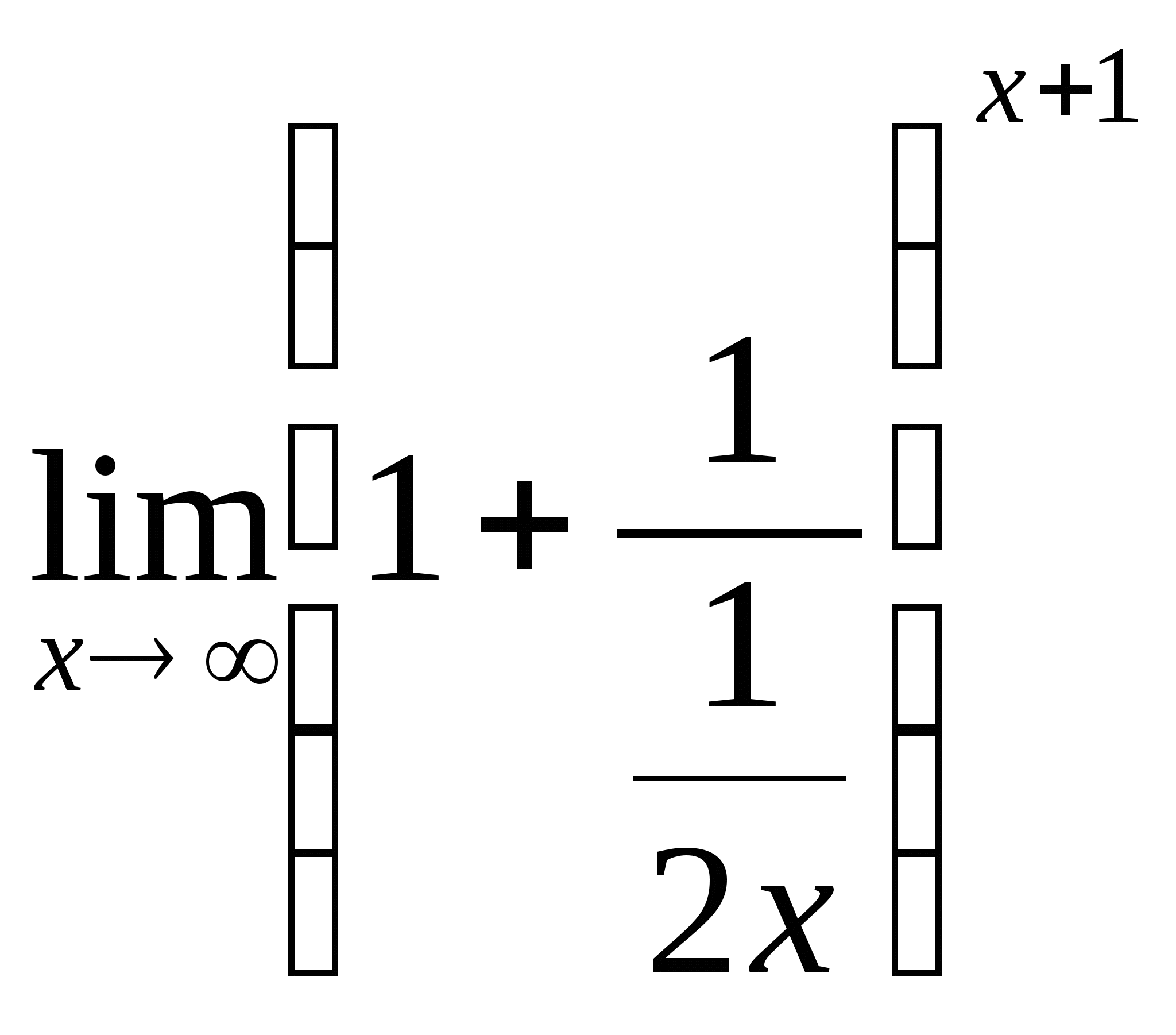 = (рассуждения аналогичные, как и в решении предела числителя только здесь введем
= (рассуждения аналогичные, как и в решении предела числителя только здесь введем 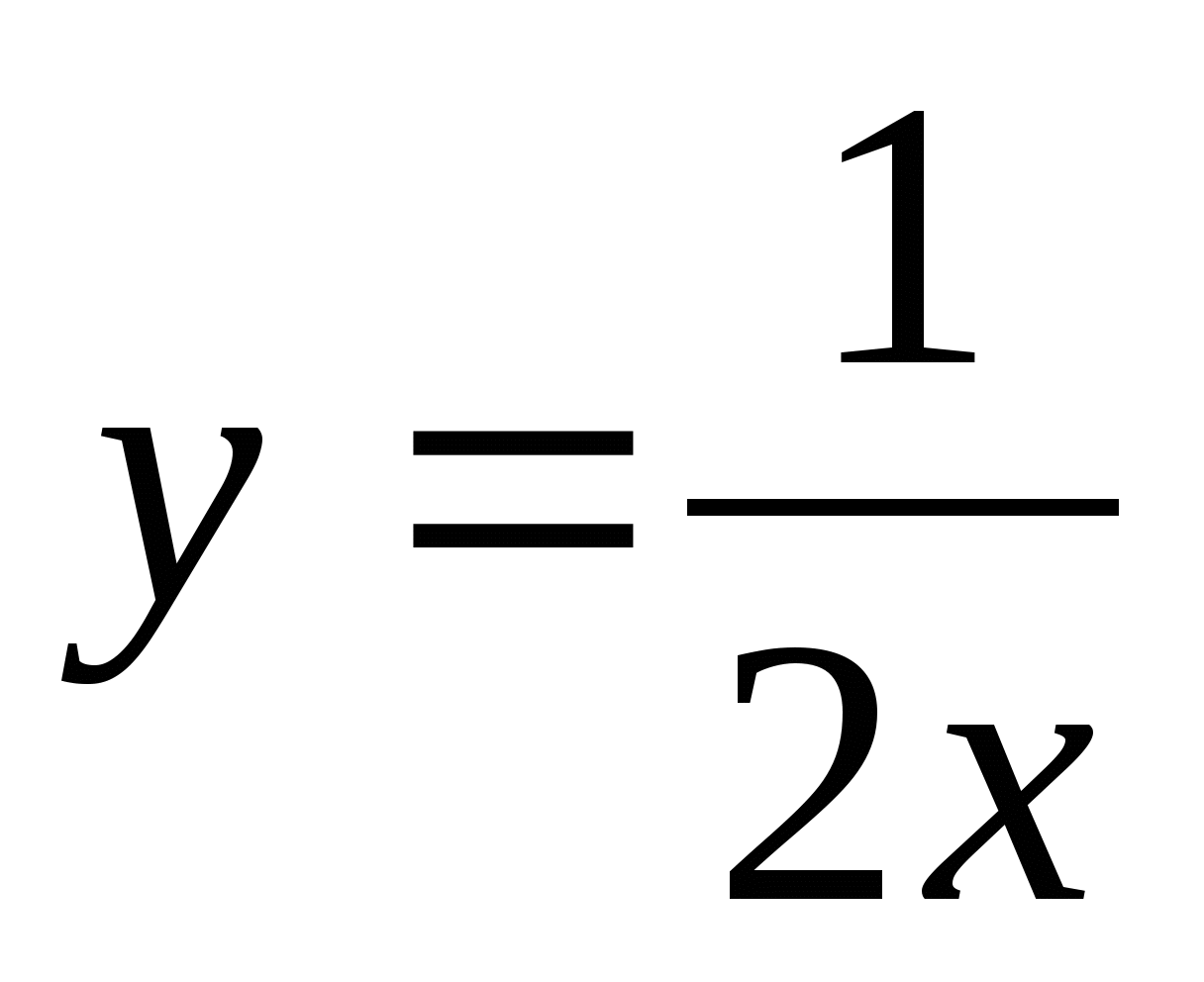

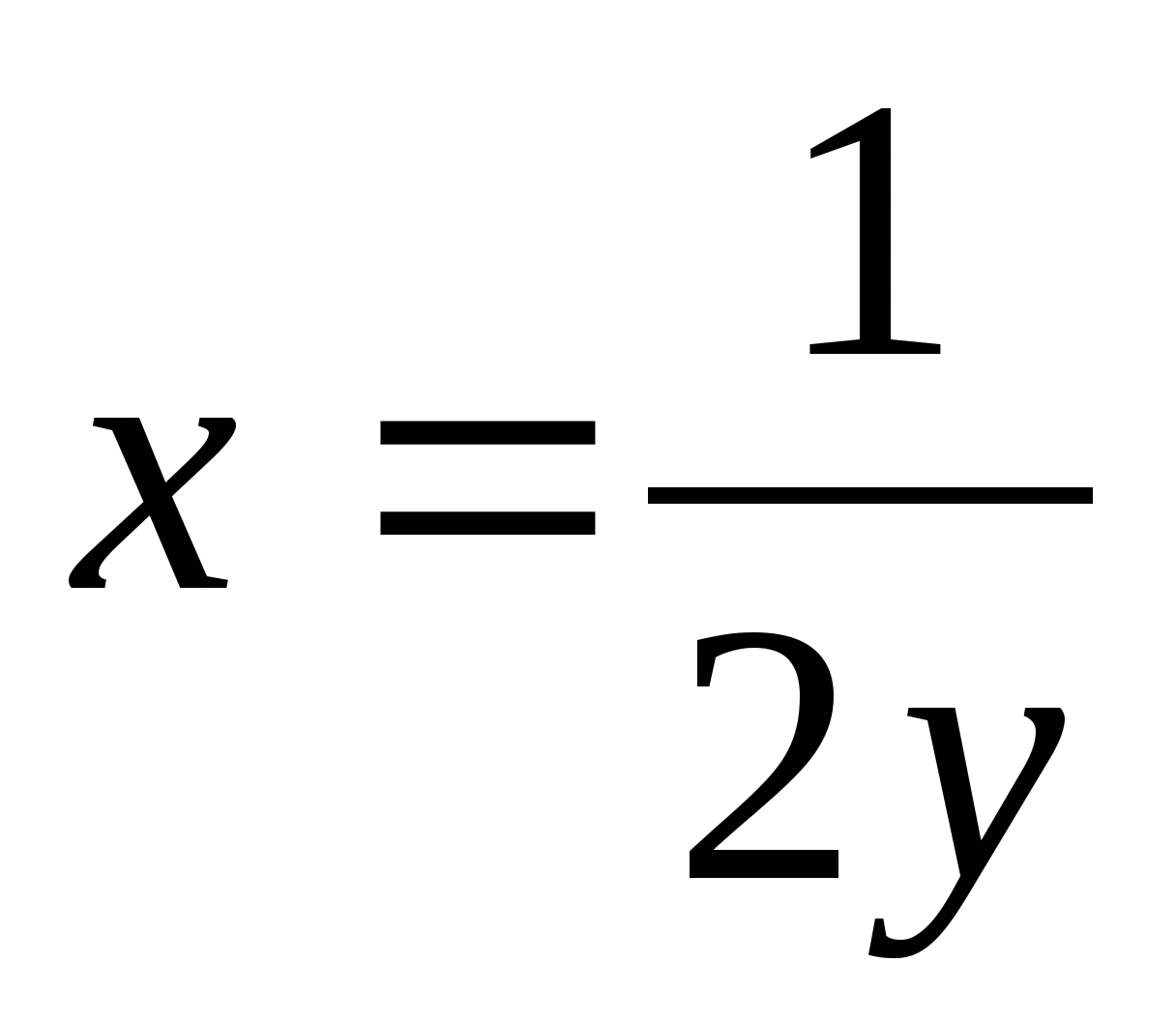 ), тогда =
), тогда =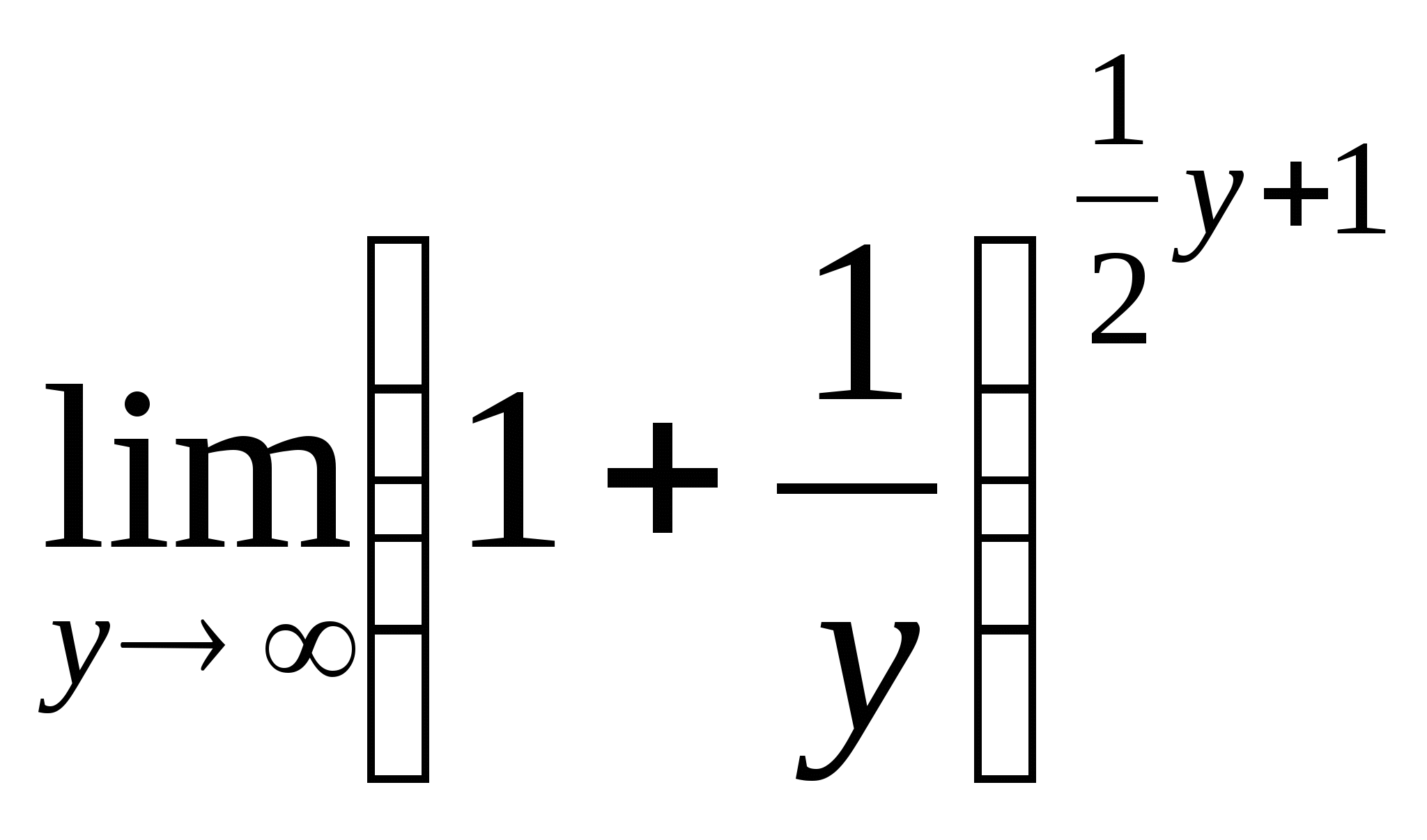 =
=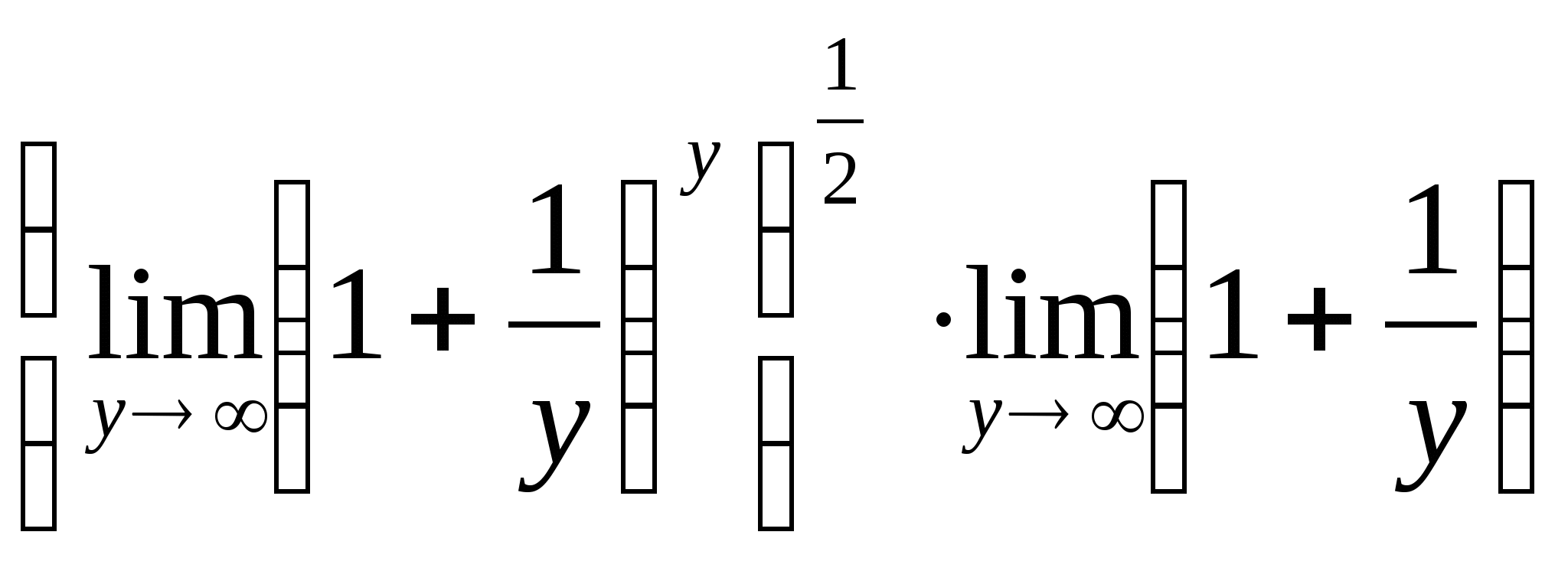 =
=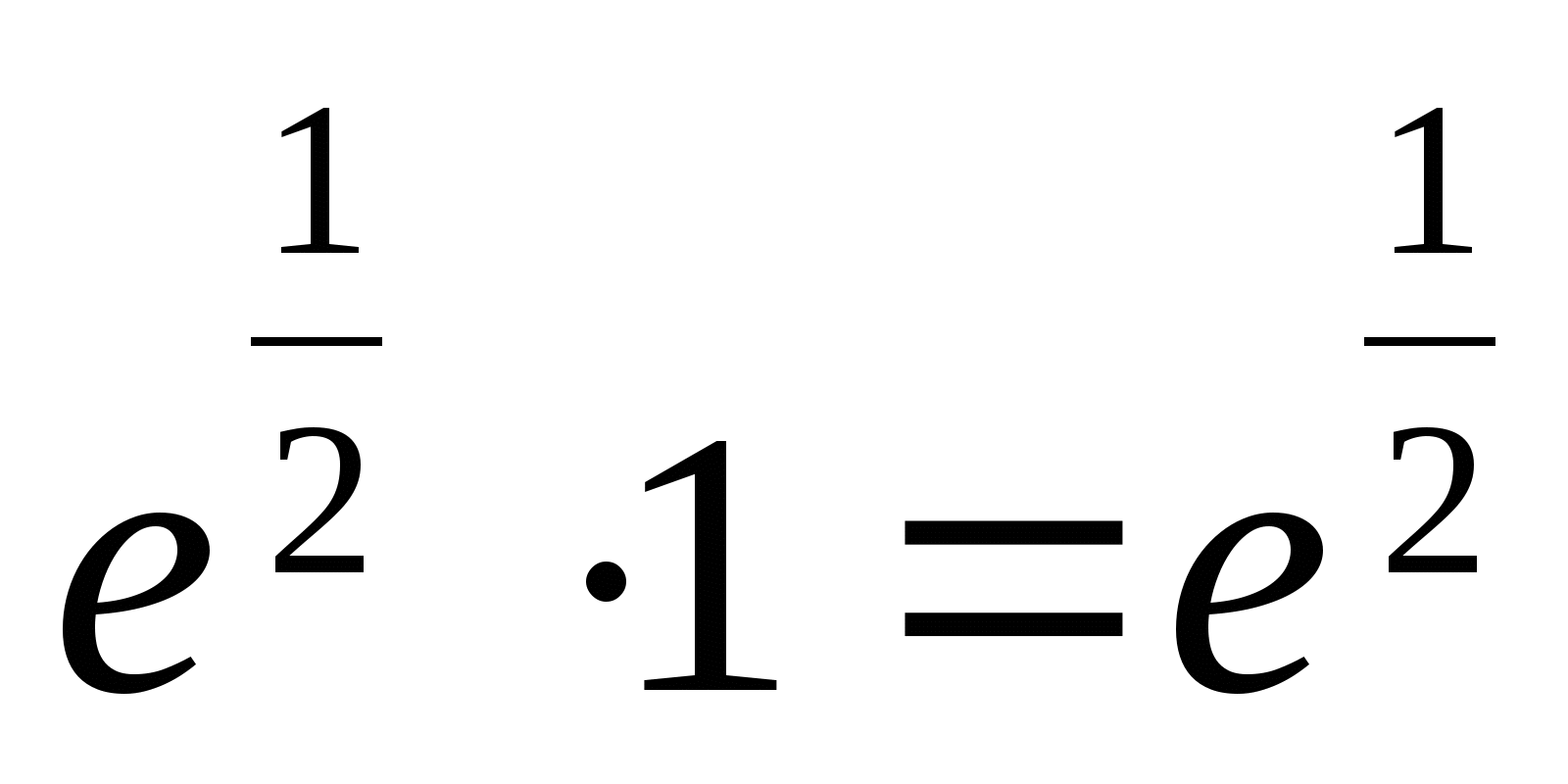 , таким образом, возвращаясь к общему решению, имеем:
, таким образом, возвращаясь к общему решению, имеем: 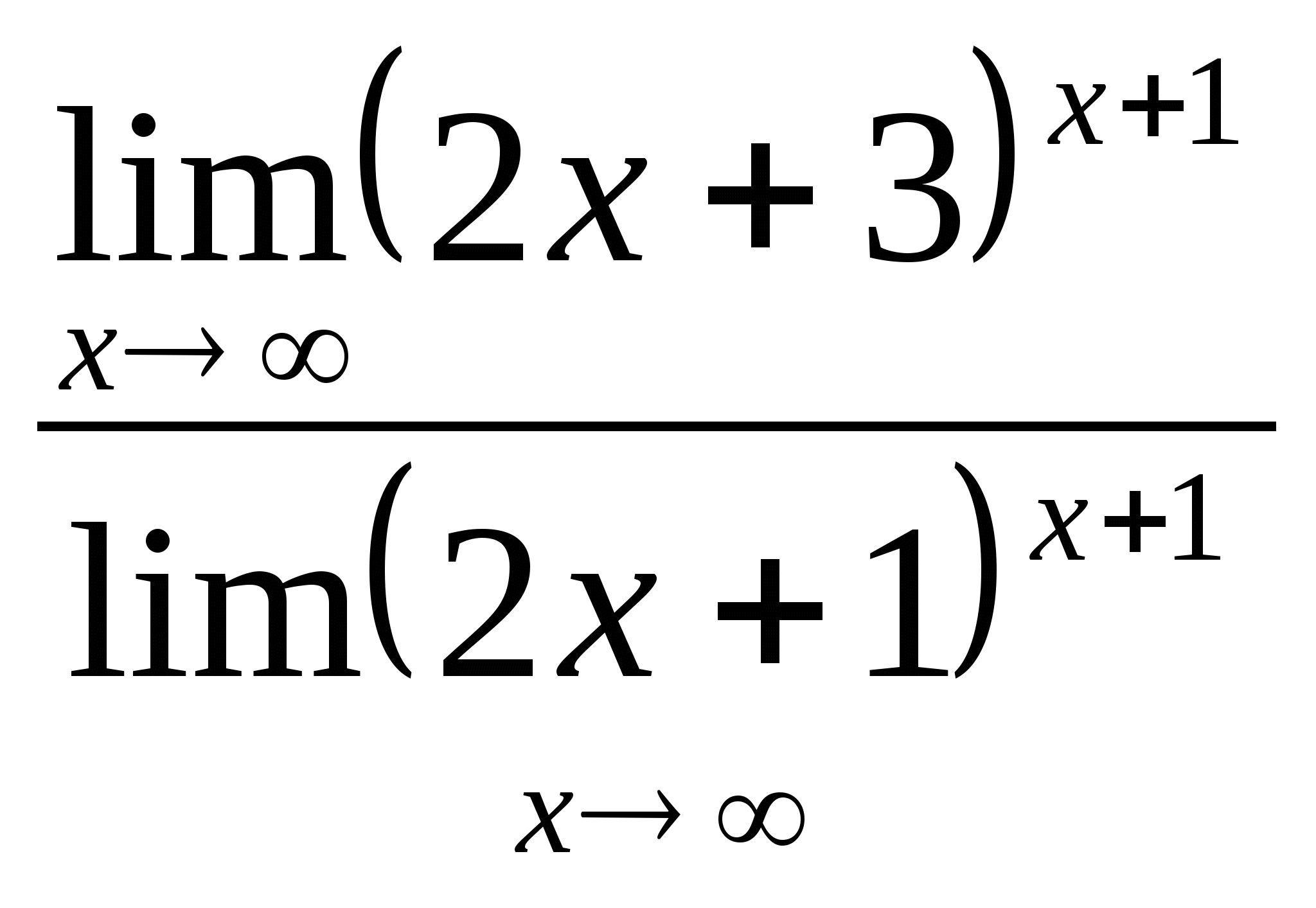 =
=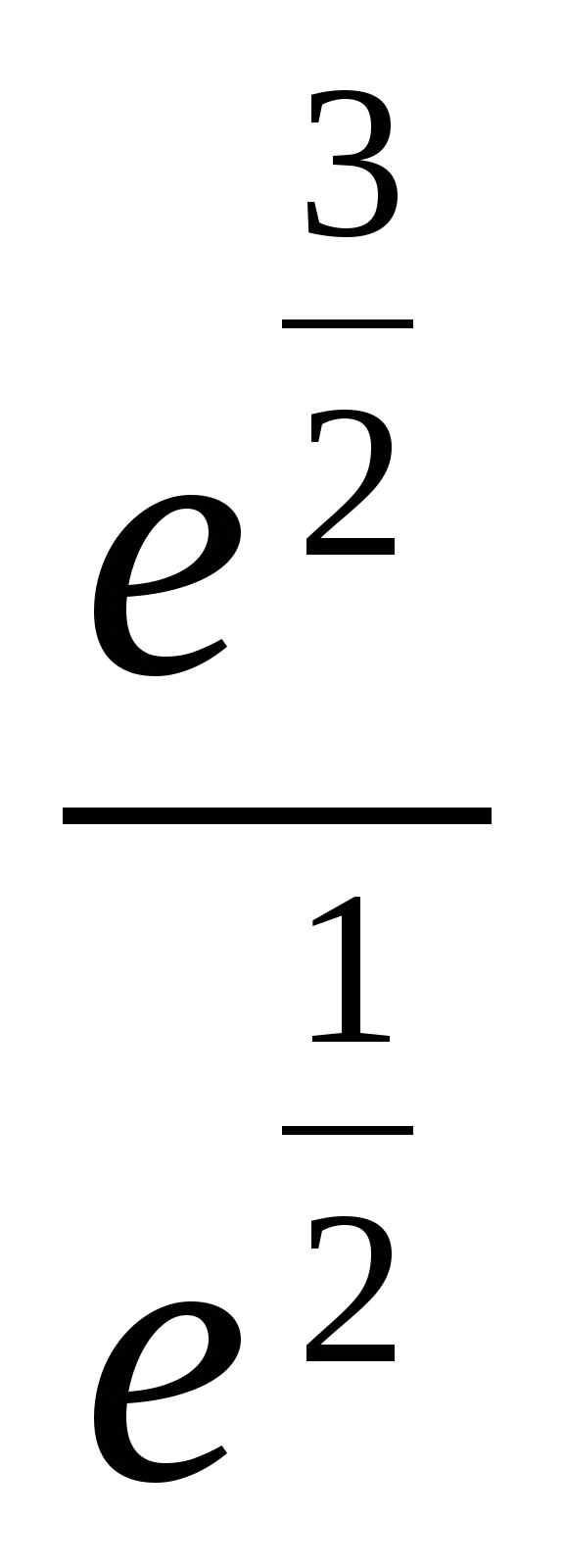 =
= .
.
Ответ:  .
.
Задания для самостоятельной работы:
Вычислите пределы функций, используя таблицу эквивалентных бесконечно малых, первый и второй замечательные пределы:
1. 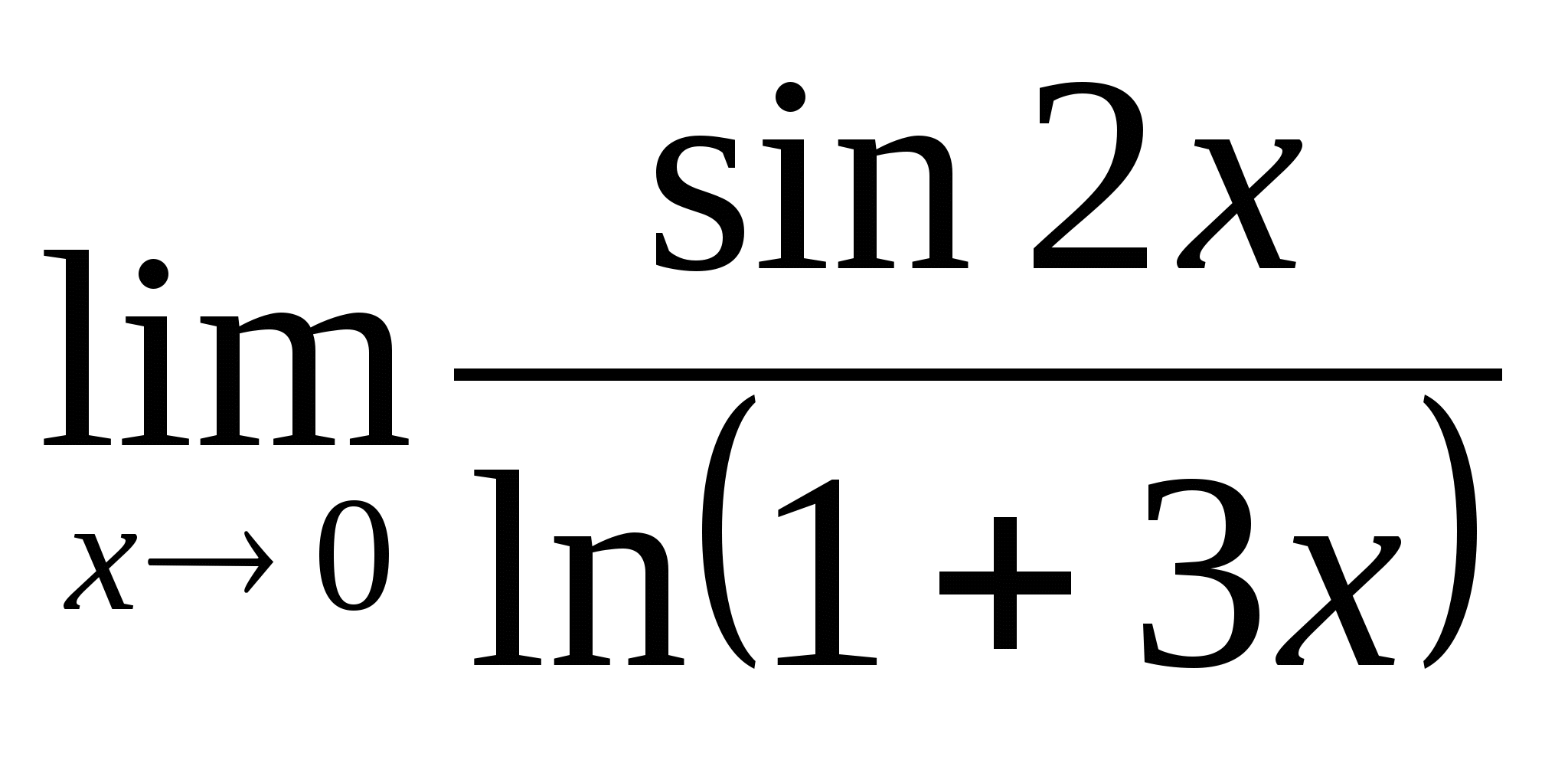 ; 2.
; 2. 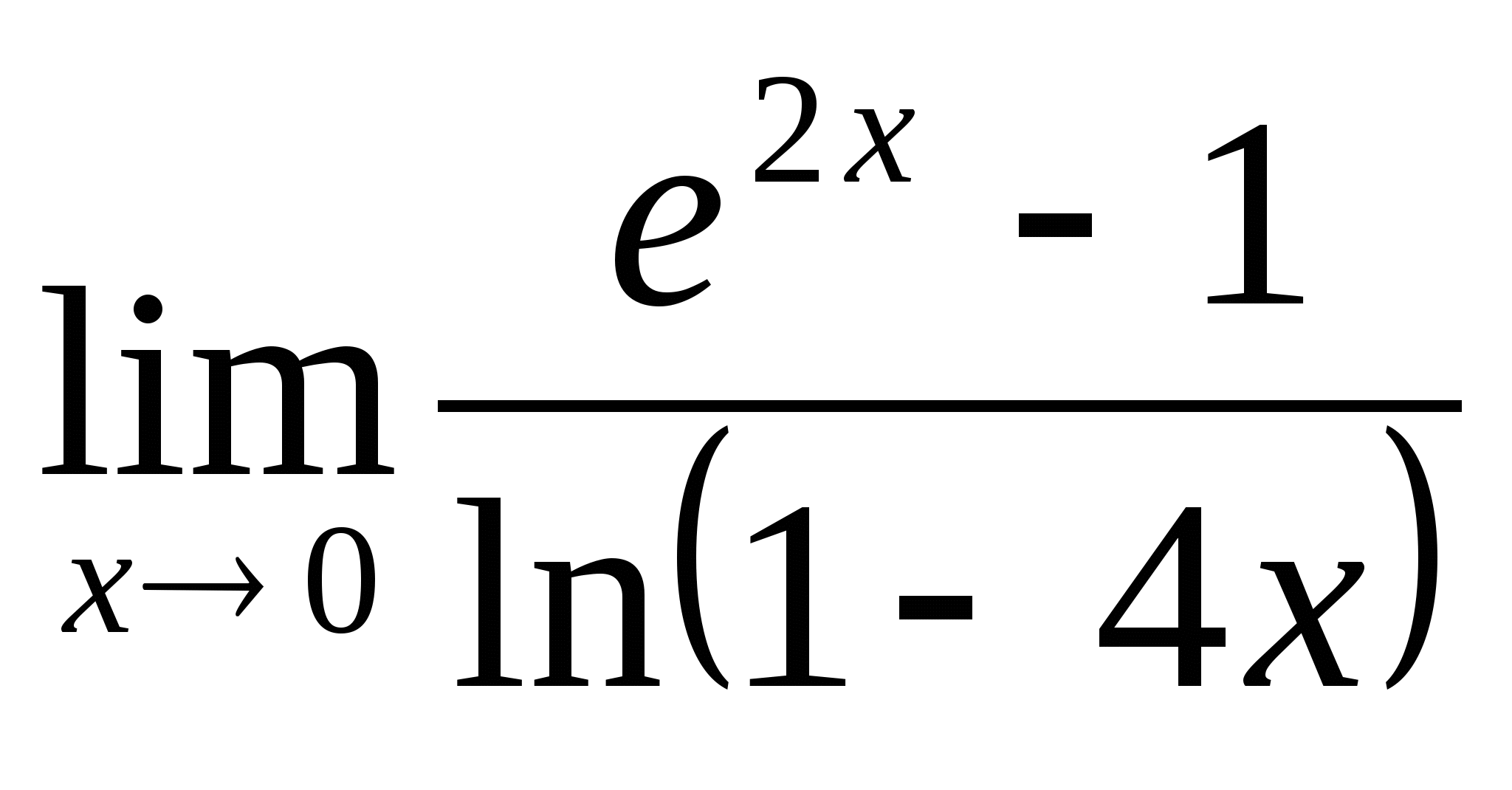 ; 3.
; 3. 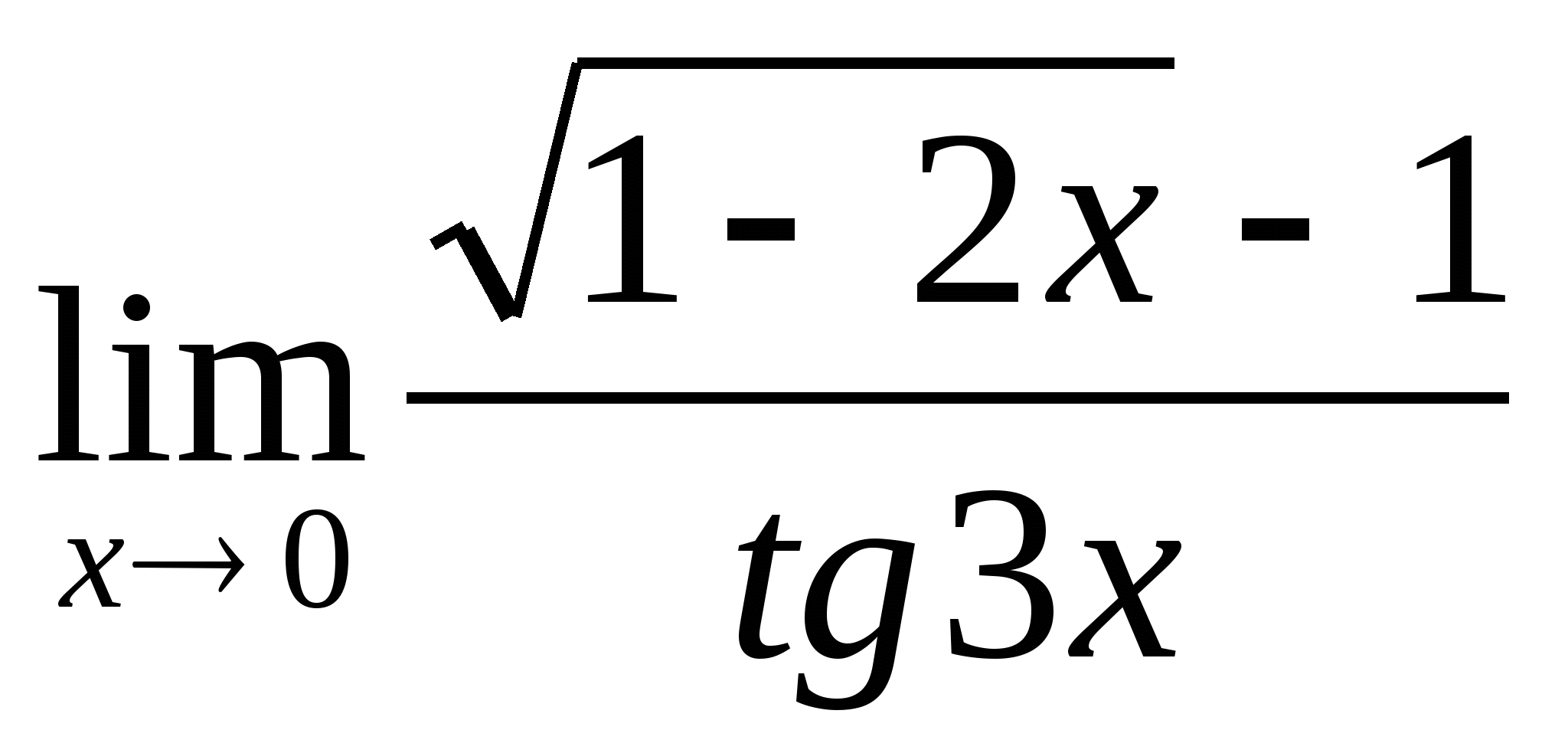 ;
;
4. 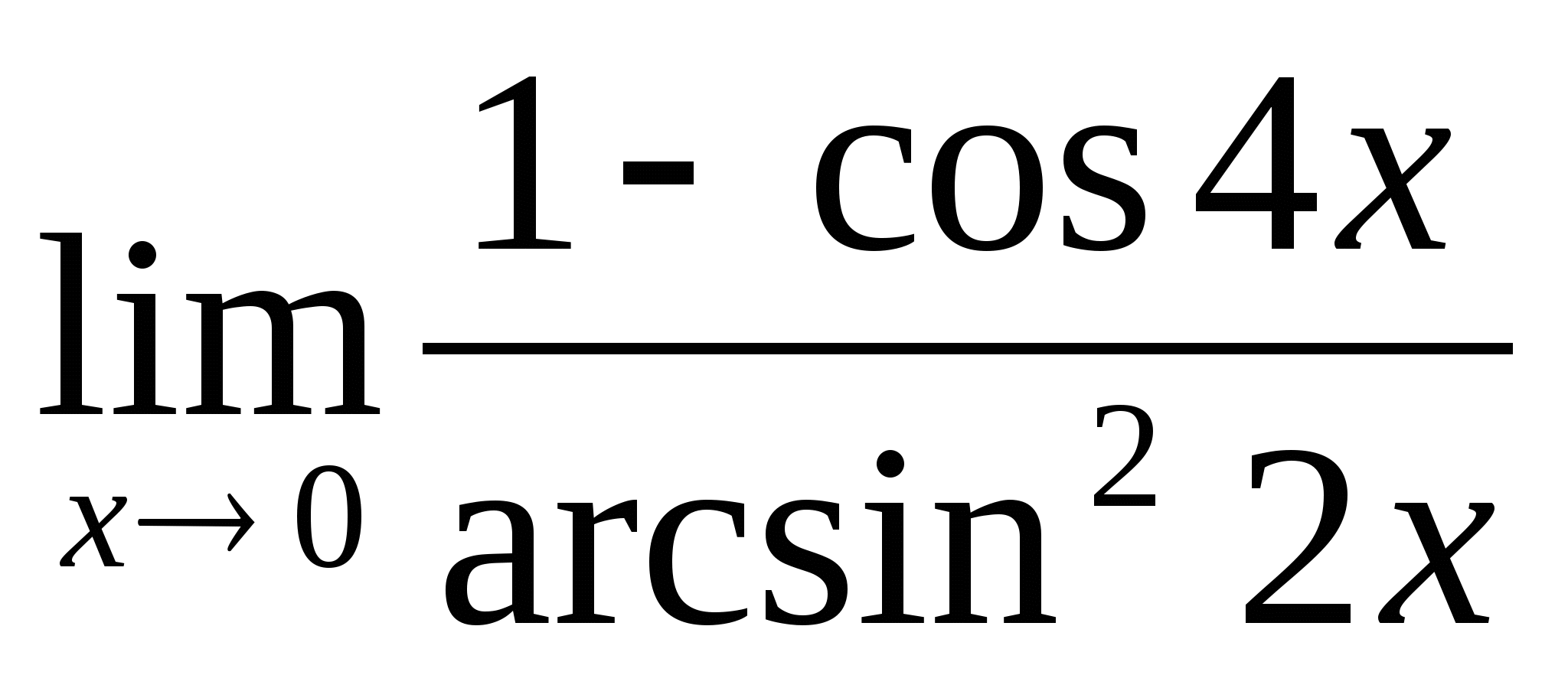 ; 5.
; 5. 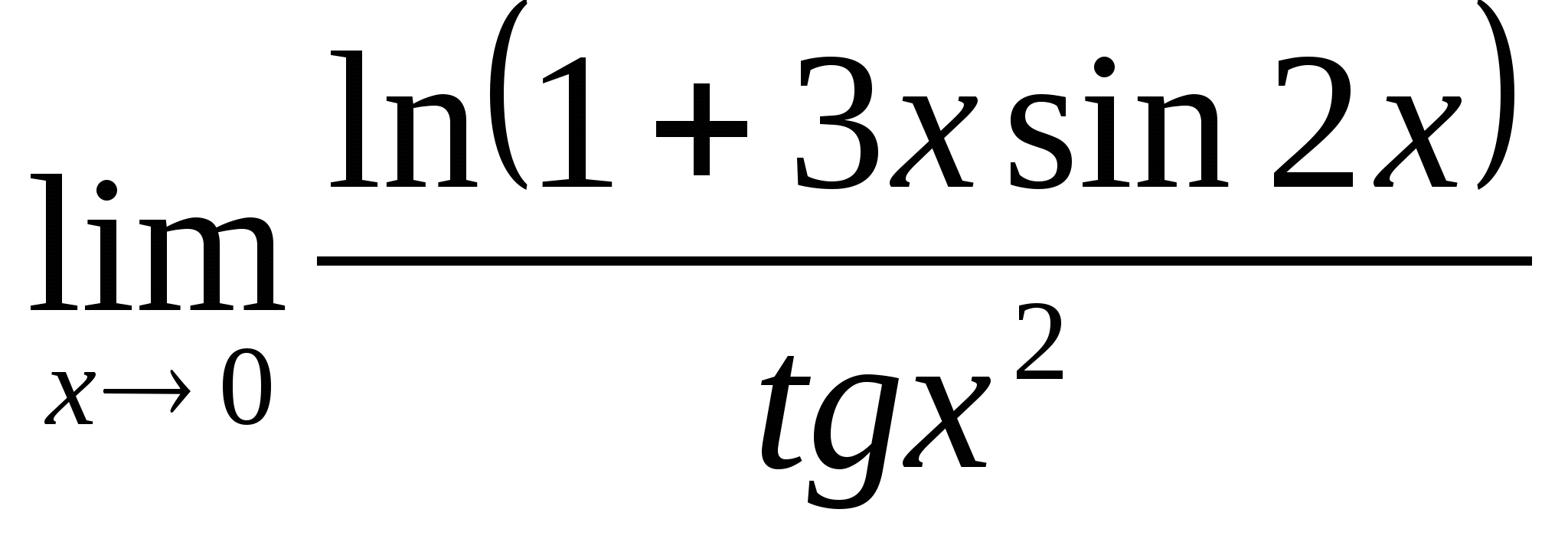 ; 6.
; 6. 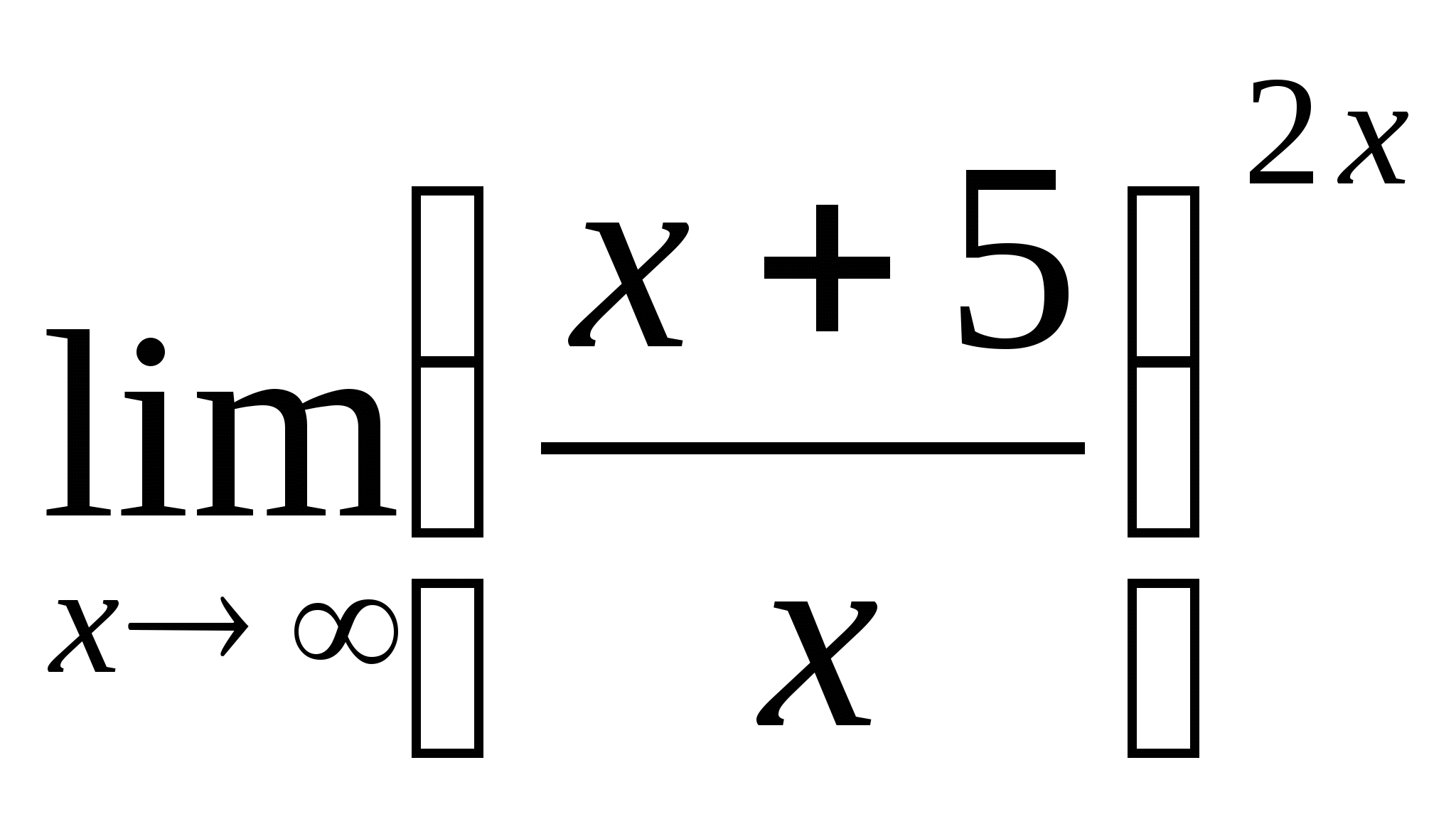 ;
;
7. 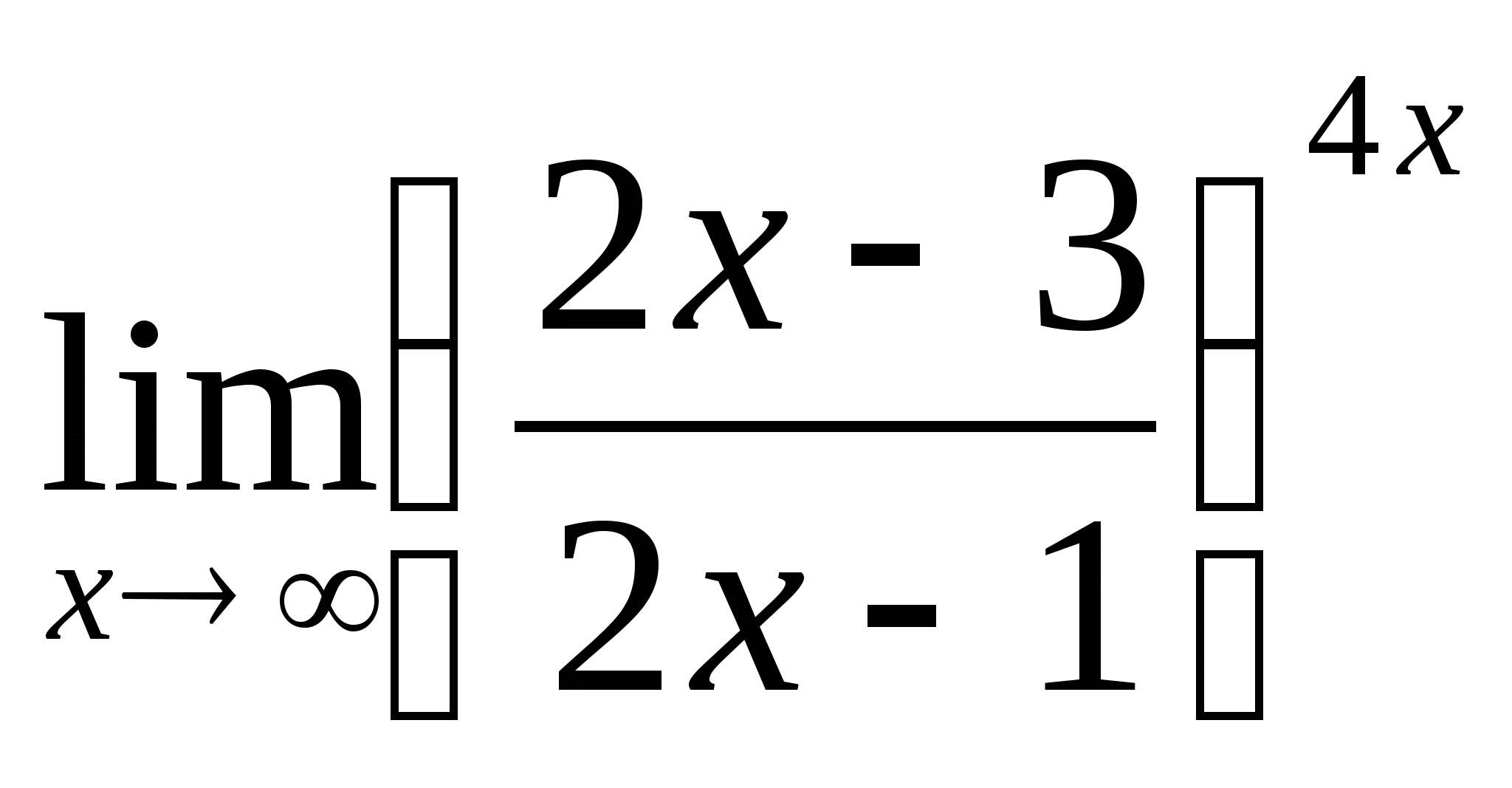 ; 8.
; 8. 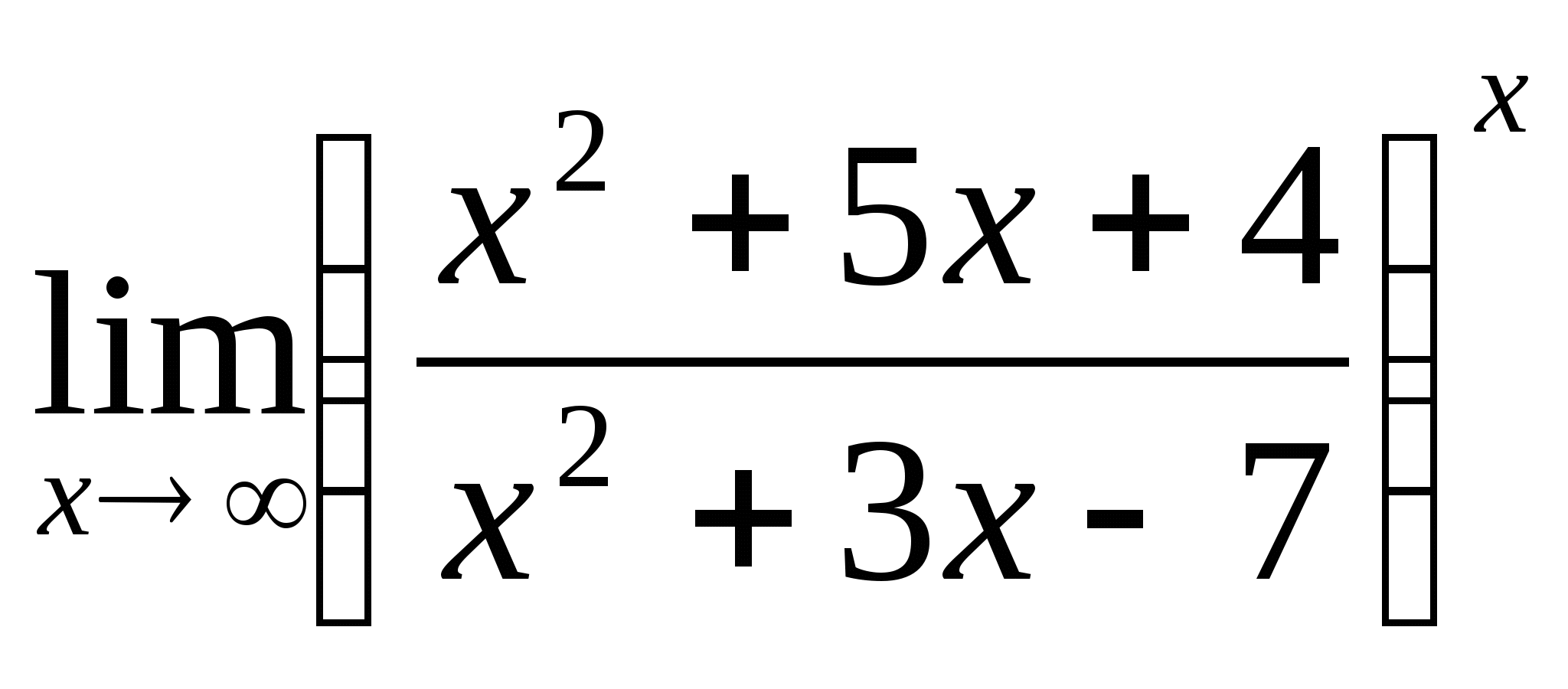 ; 9.
; 9. 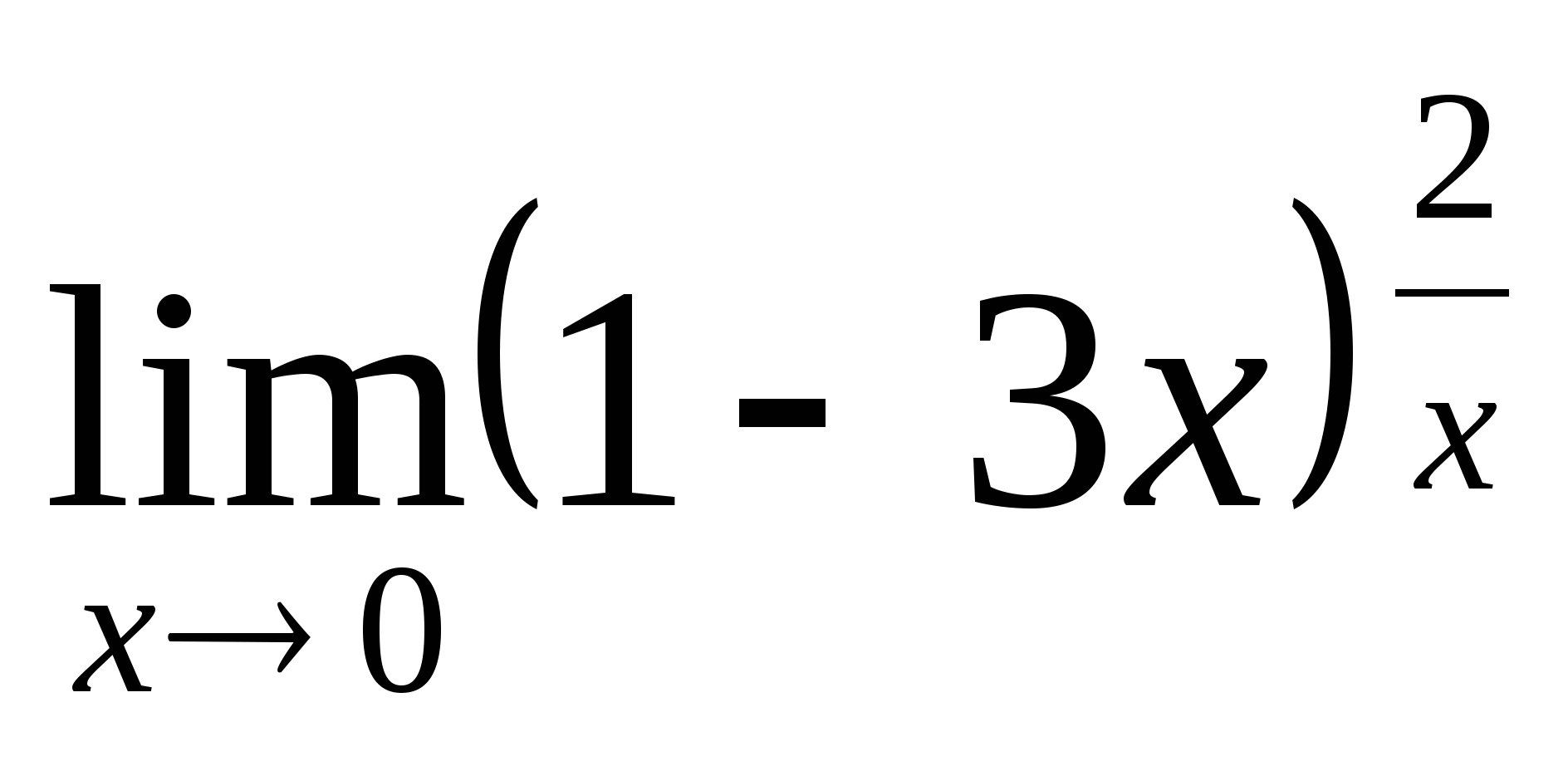 ;
;
10. 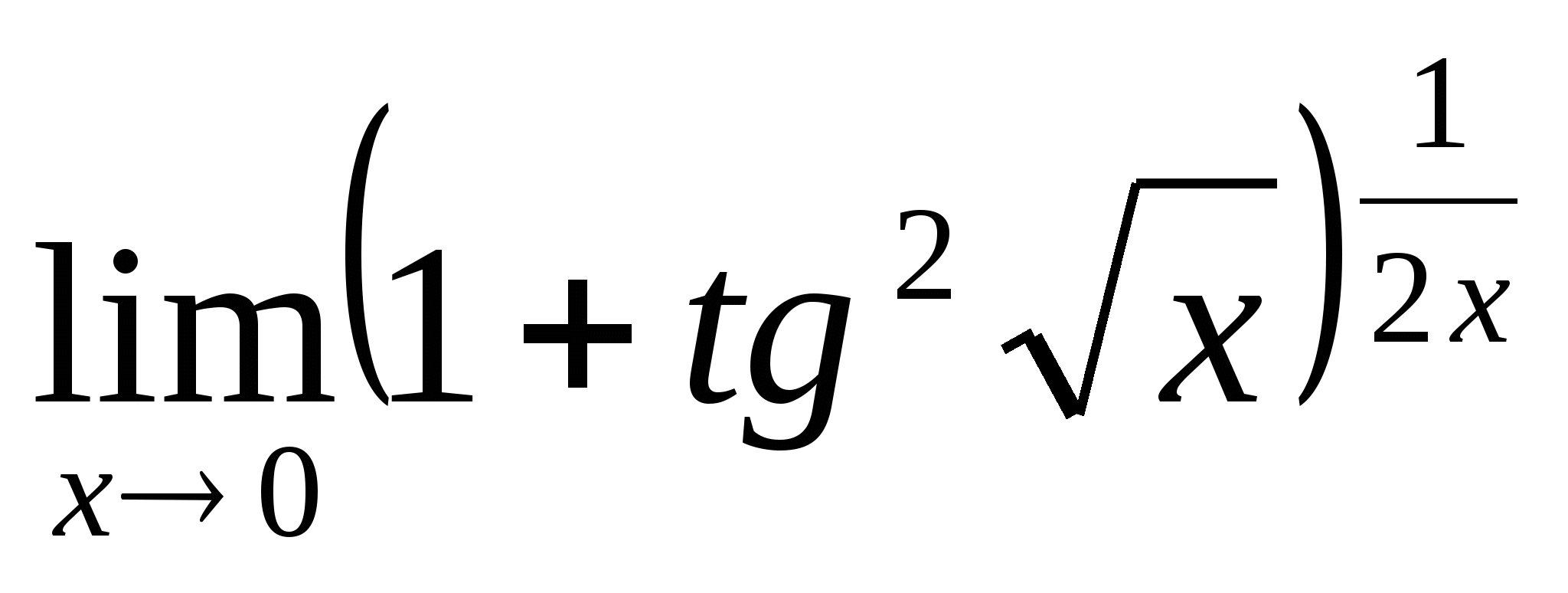 ; 11.
; 11. 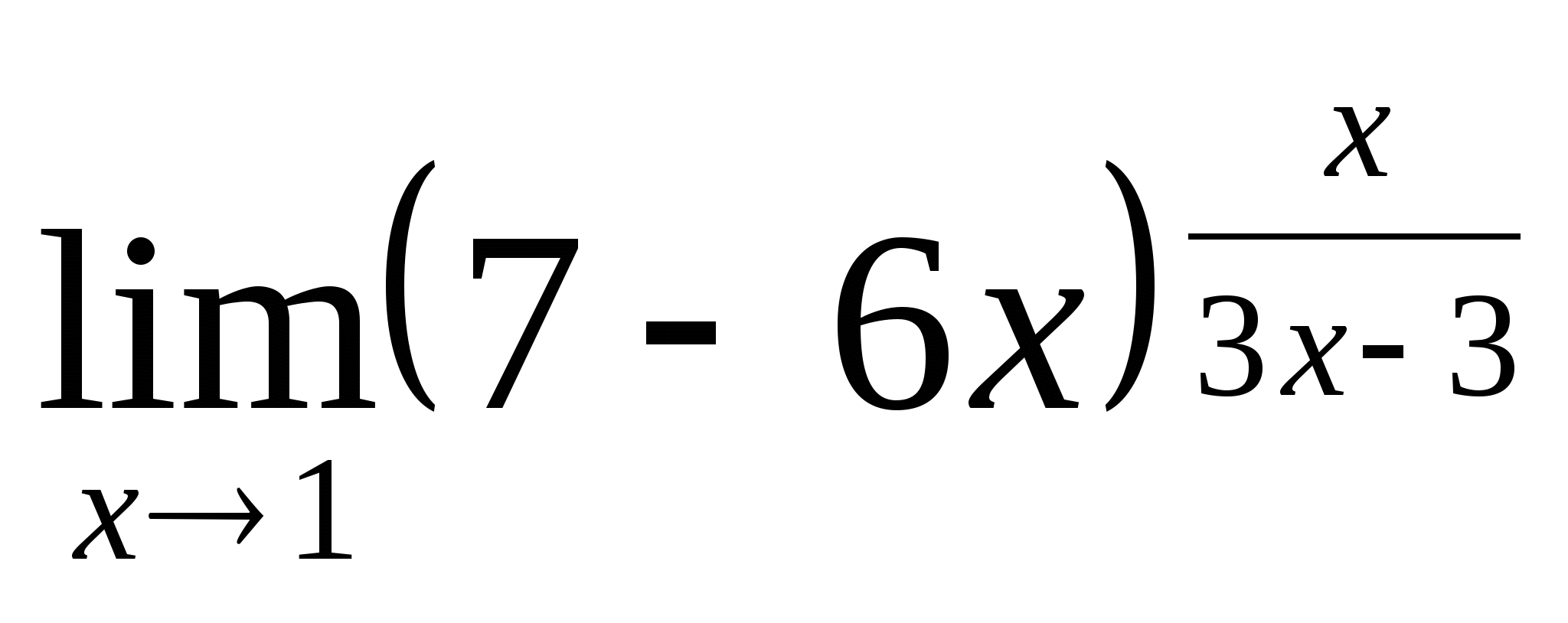 ; 12.
; 12. 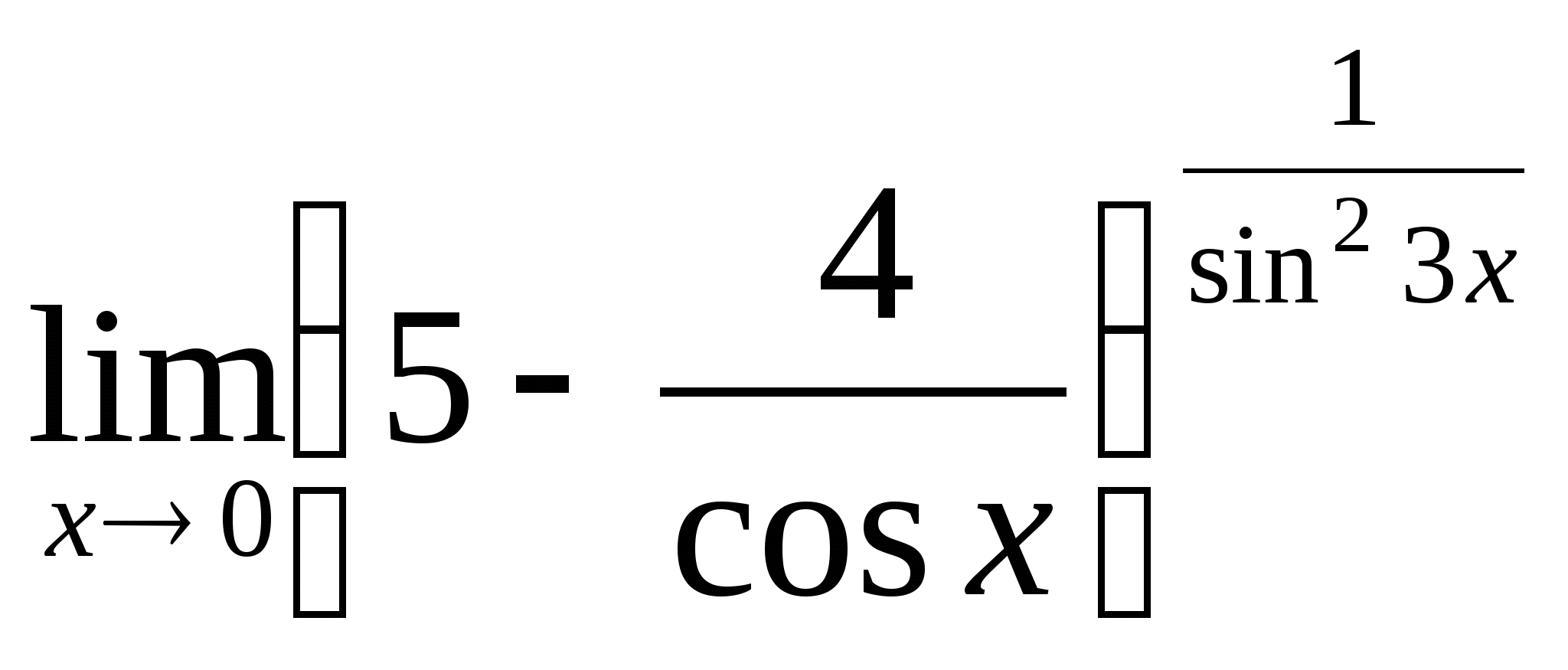 ;
;
13. 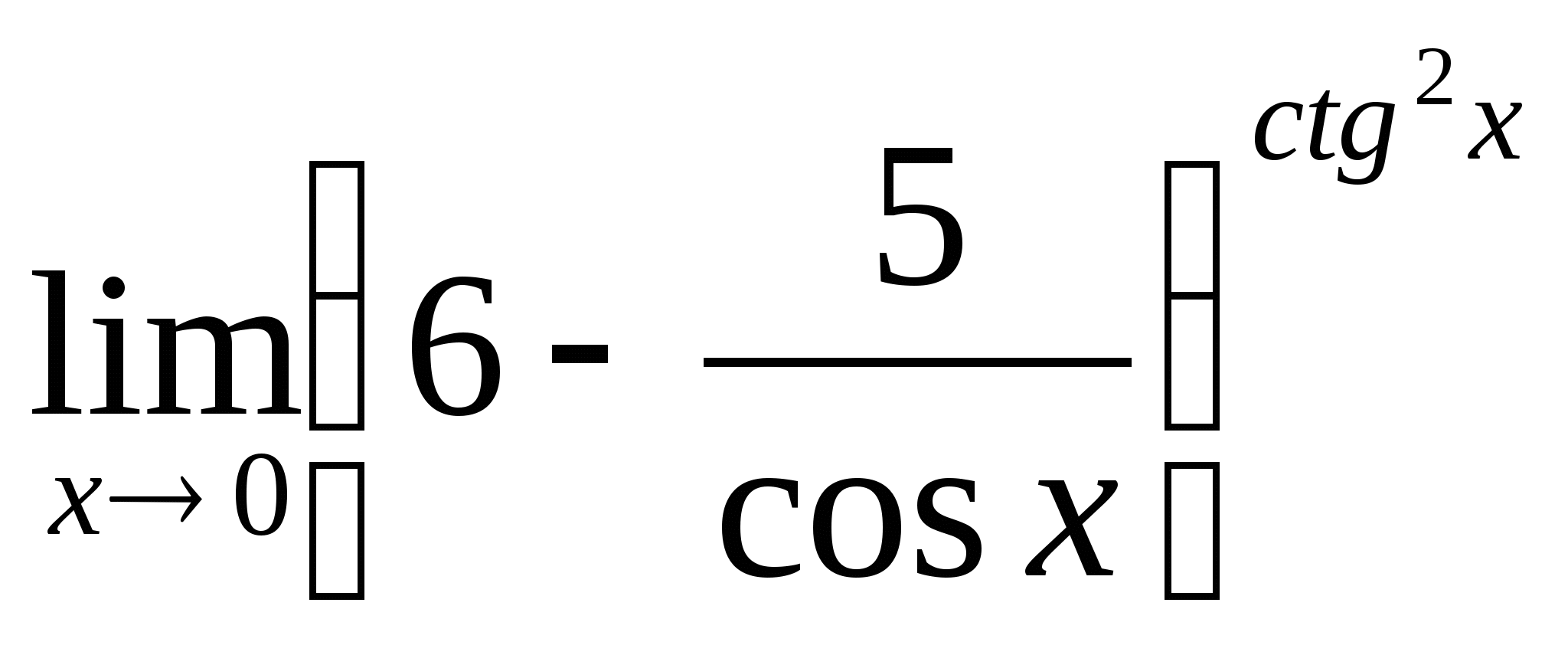 ; 14.
; 14. 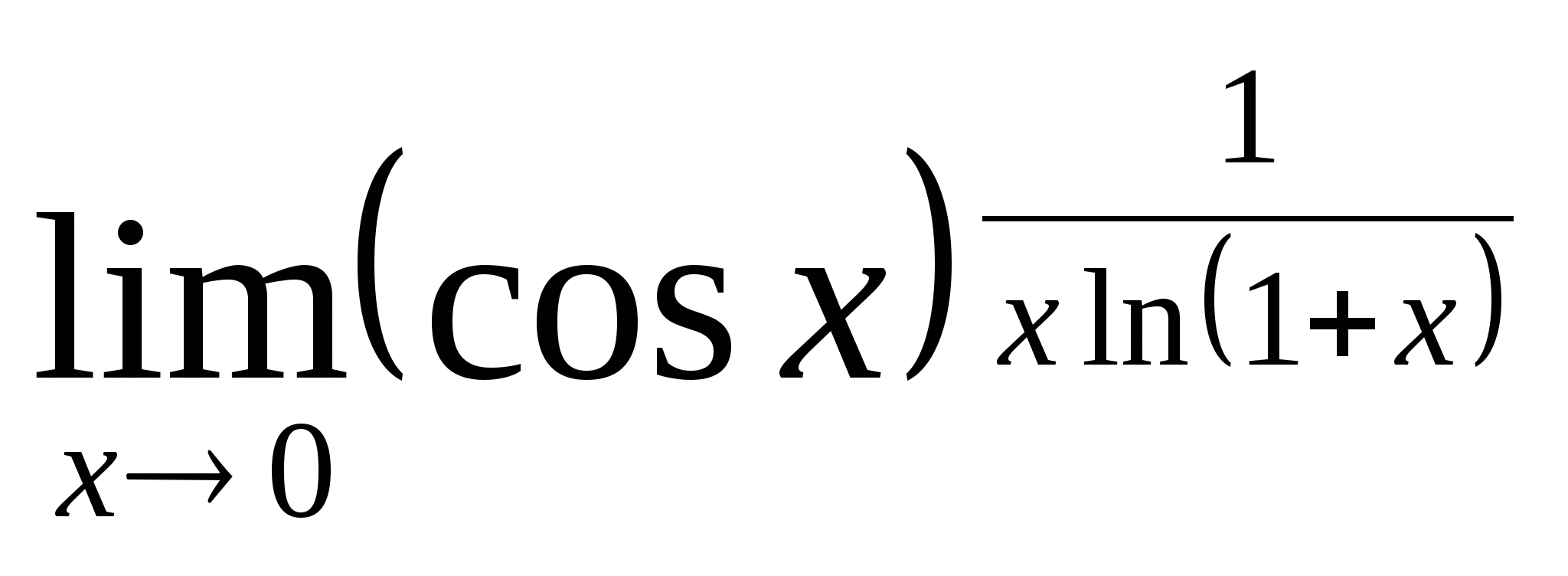 ; 15.
; 15. 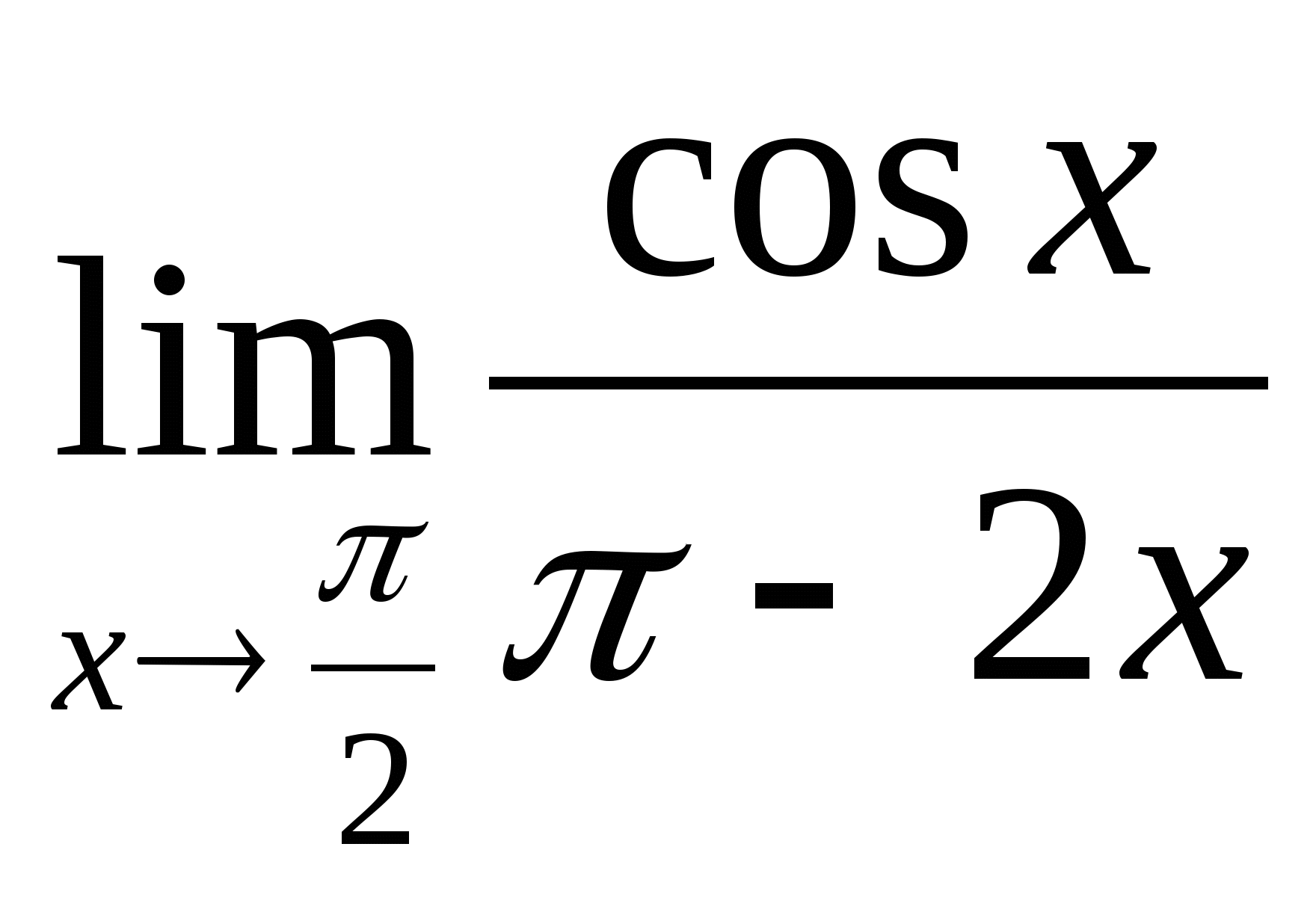 ;
;
16. 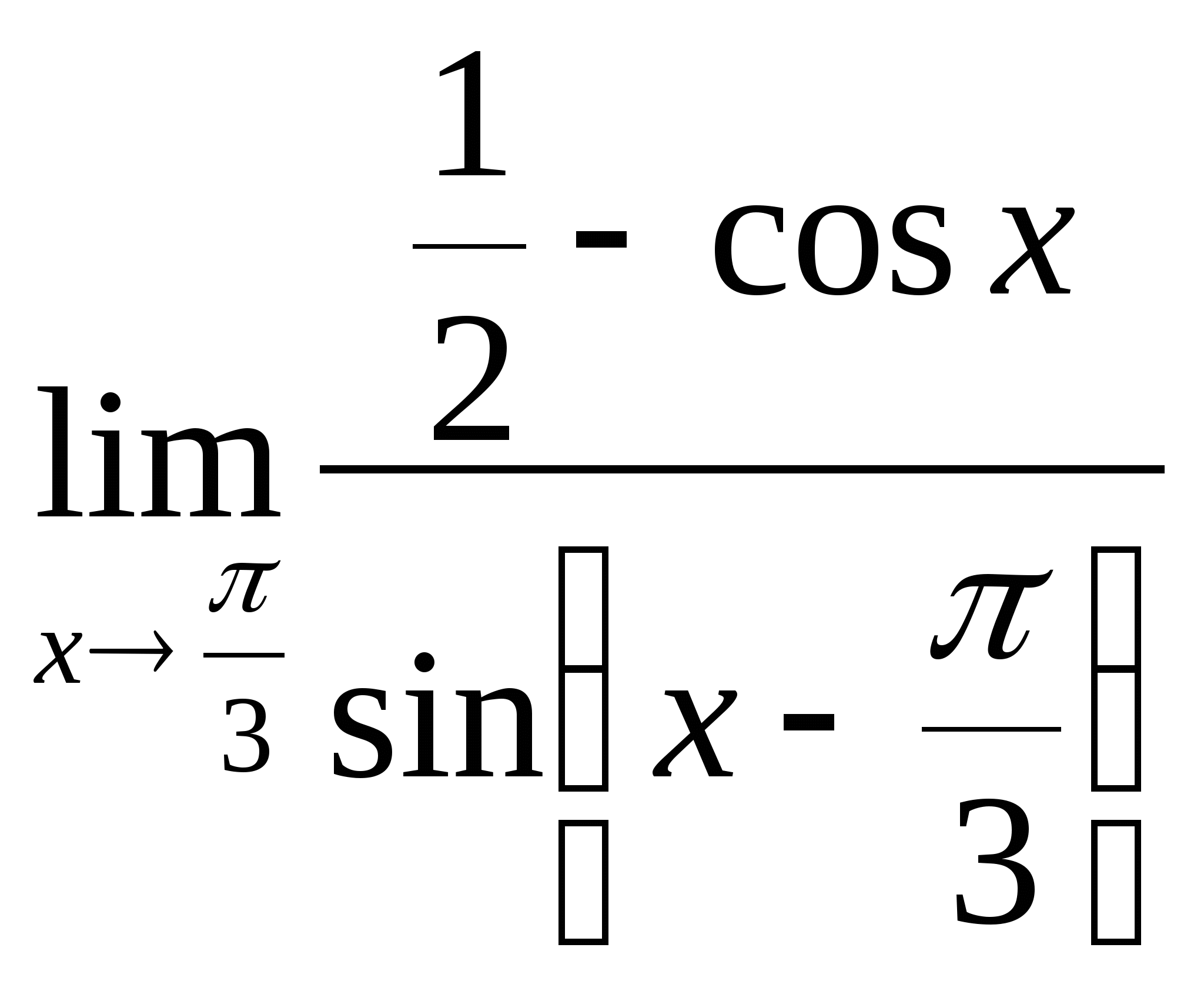 ; 17.
; 17. 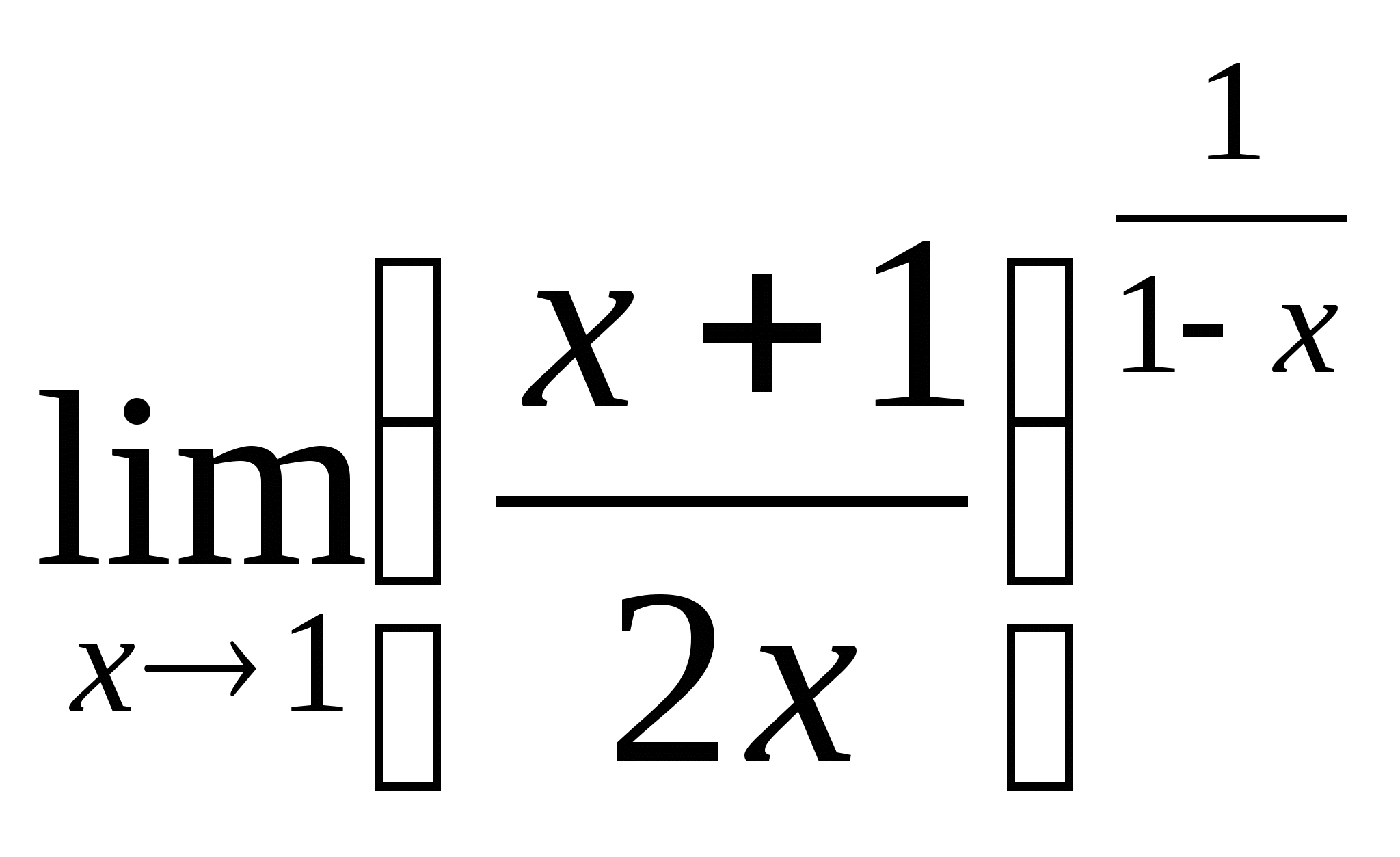 ; 18.
; 18. 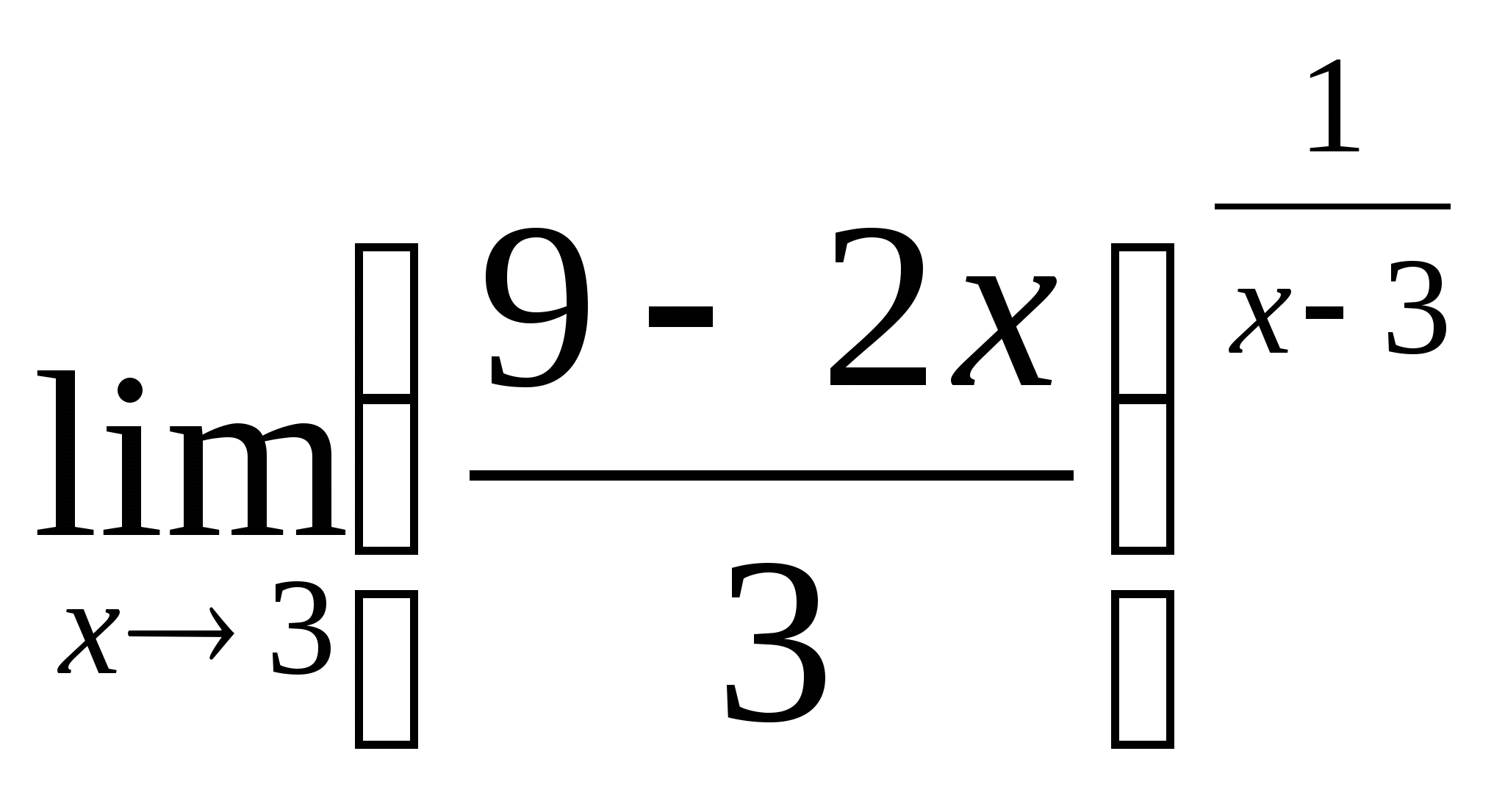 ;
;
19. 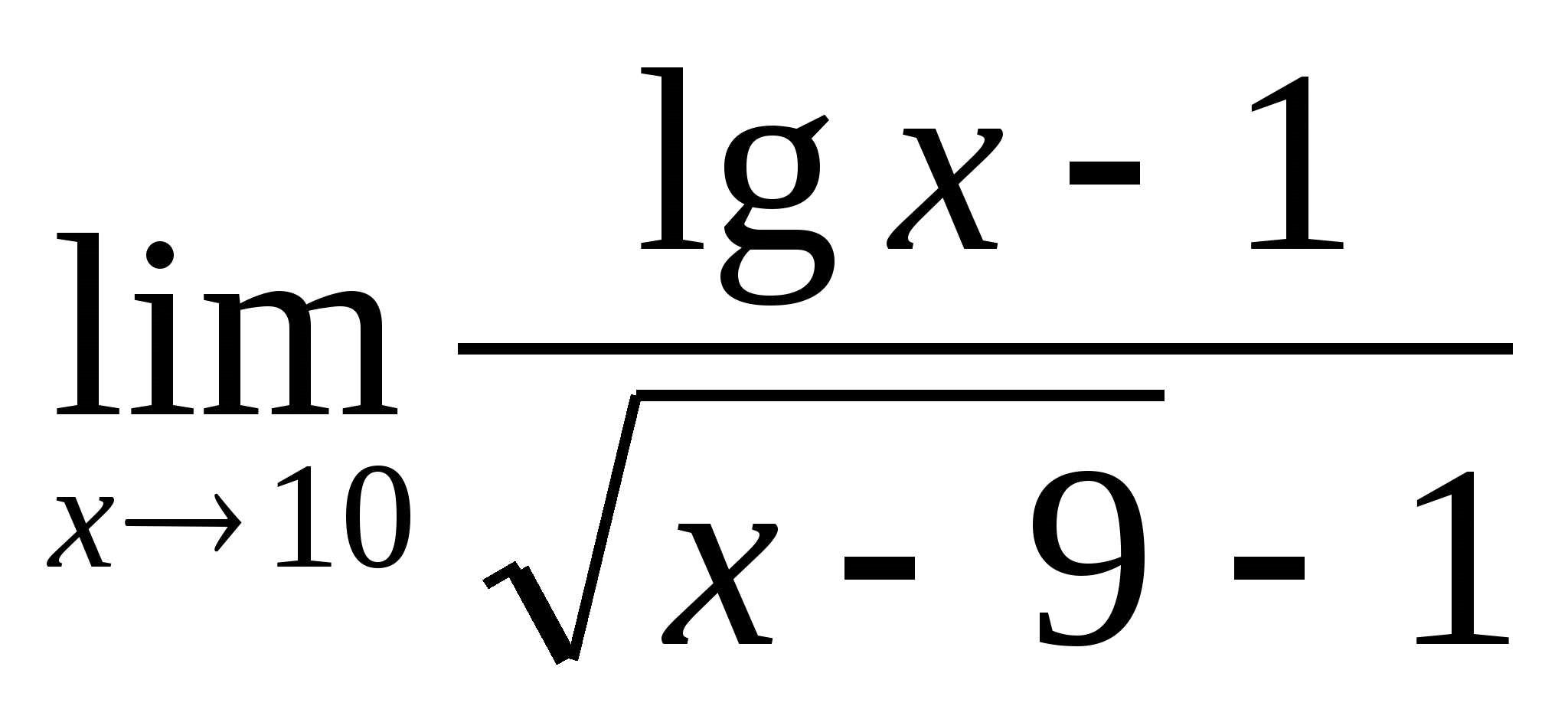 ; 20.
; 20. 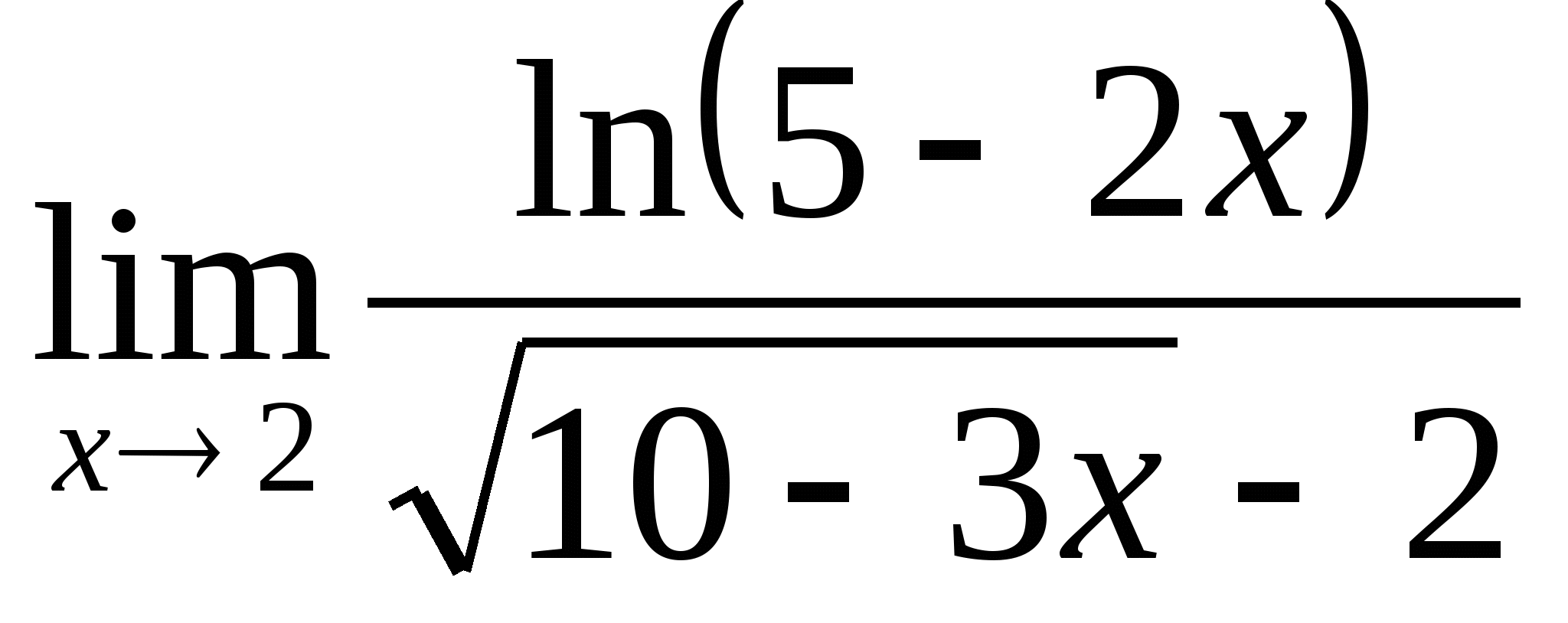 .
.
Критерий оценки:
Оценка «отлично» ставится при выполнении любых 12-15 примеров, «хорошо» — при выполнении 10 любых примеров, при решении 6-9 примеров выставляется оценки «удовлетворительно», при решении менее 6 примеров оценка студенту не выставляется.
Используемая литература:
В.М.Говорова, Н.В.Мирошина, «Математика» сборник задач с решениями для поступающих в вузы, Москва, «Издательство Астрель», 2010 год;
Ответы:
1.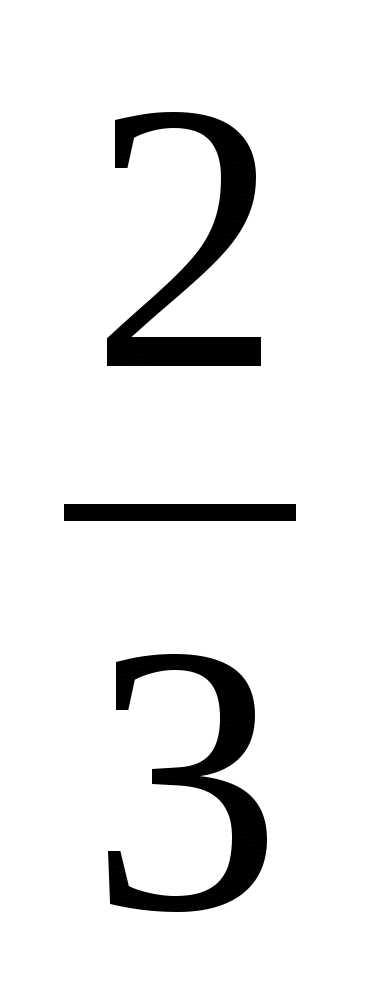 ;
;
8.
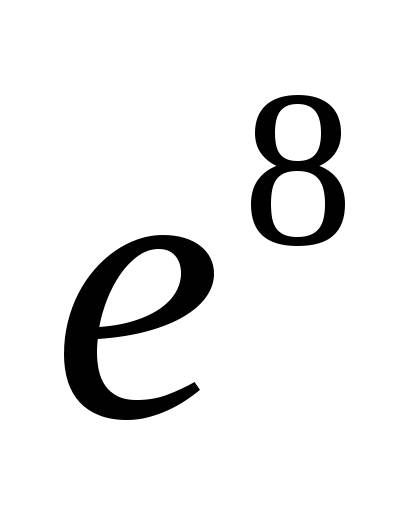 ;
;
15.
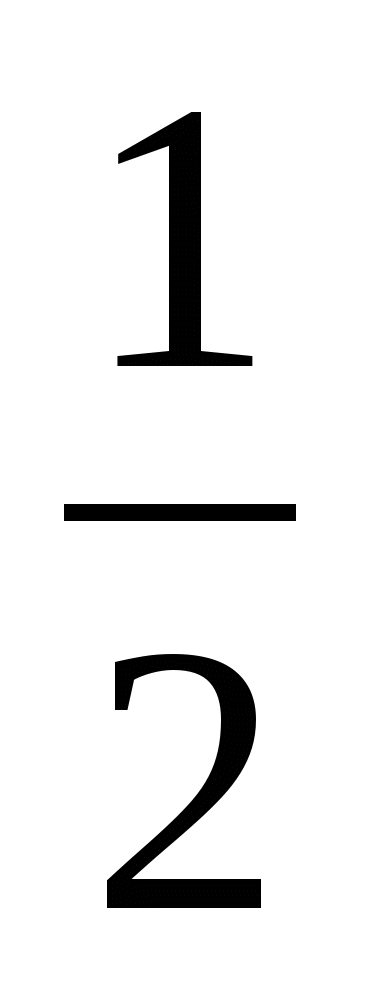 ;
;
2.
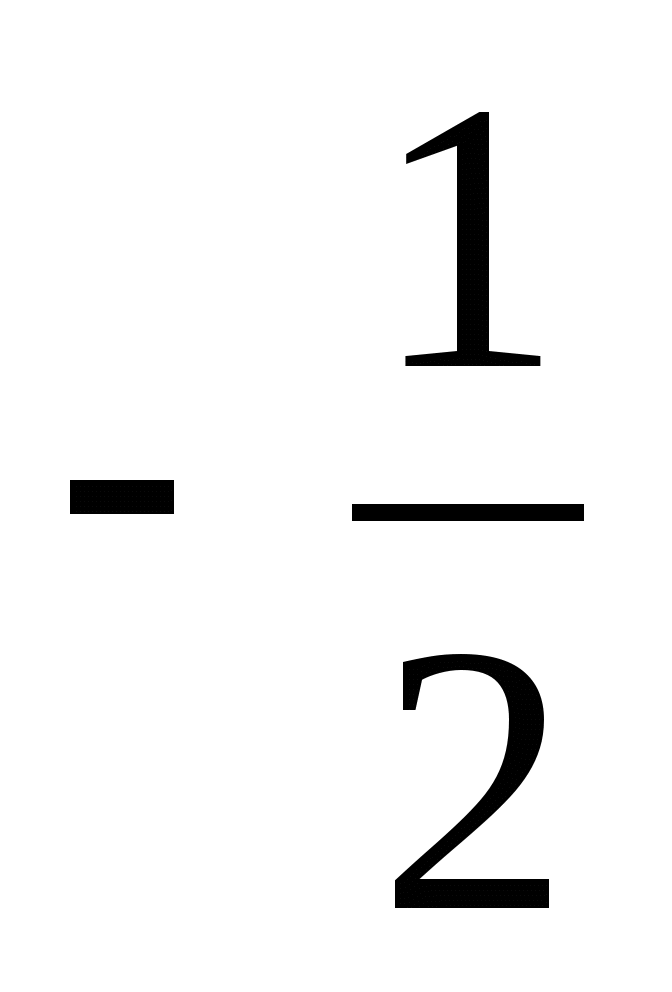 ;
;
9.
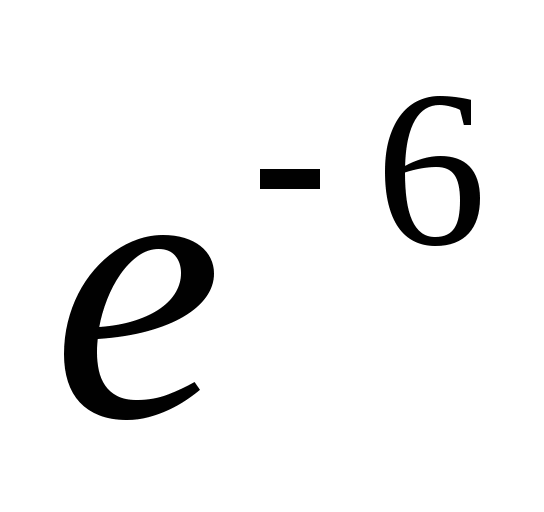 ;
;
16.
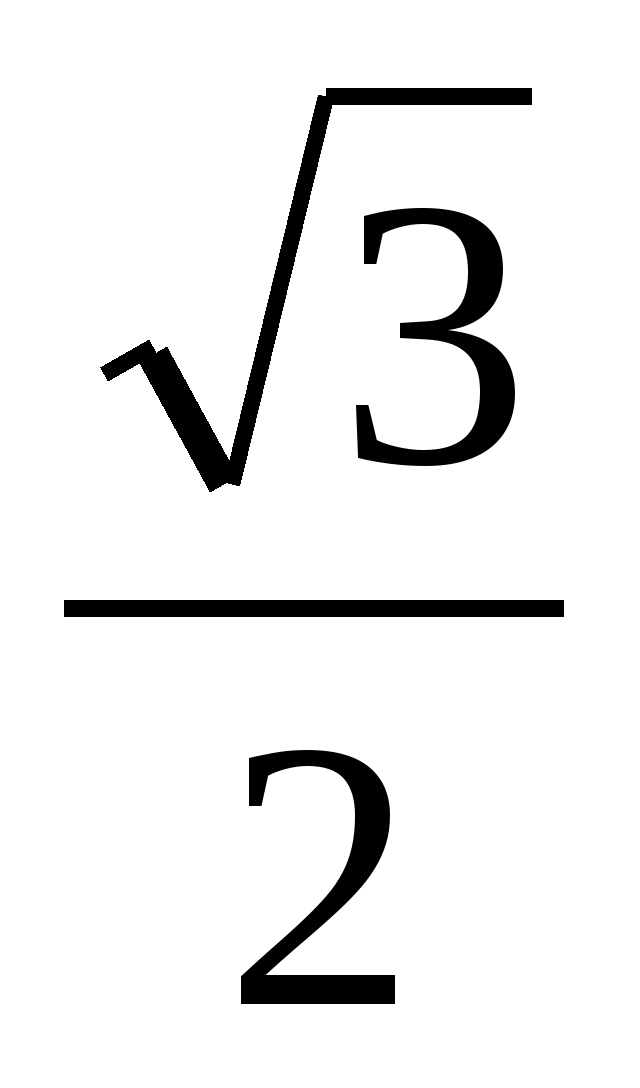 ;
;
3.
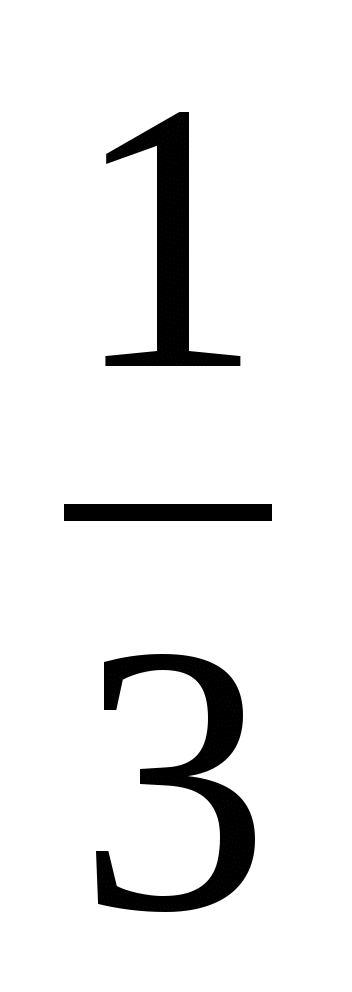 ;
;
10.
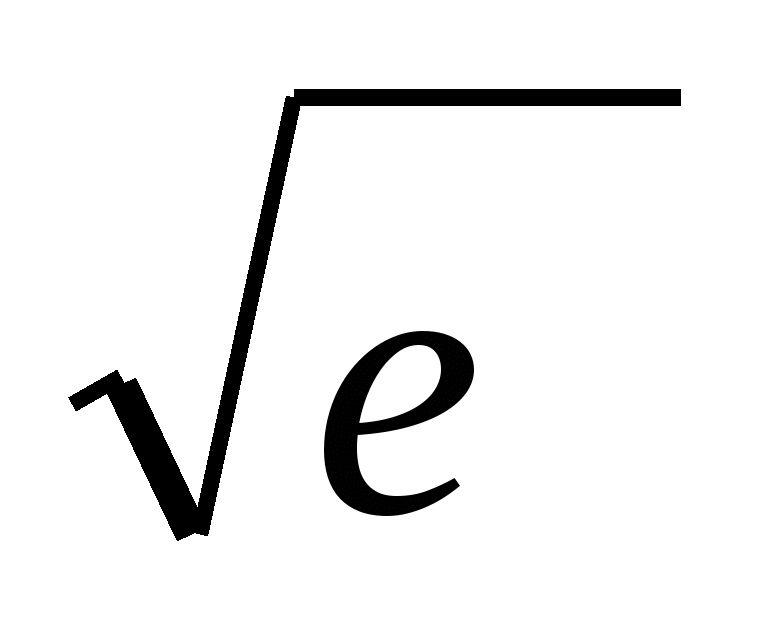 ;
;
17.
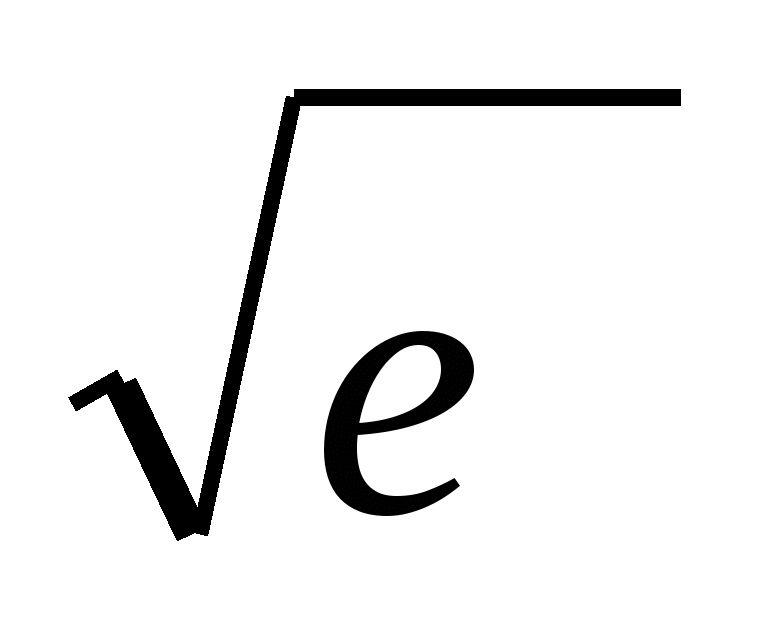 ;
;
4.
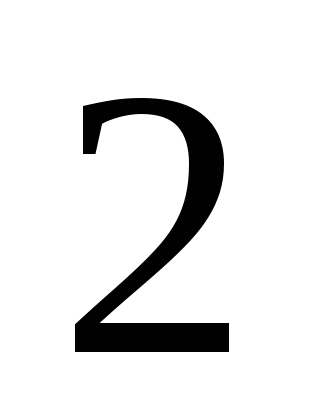 ;
;
11.
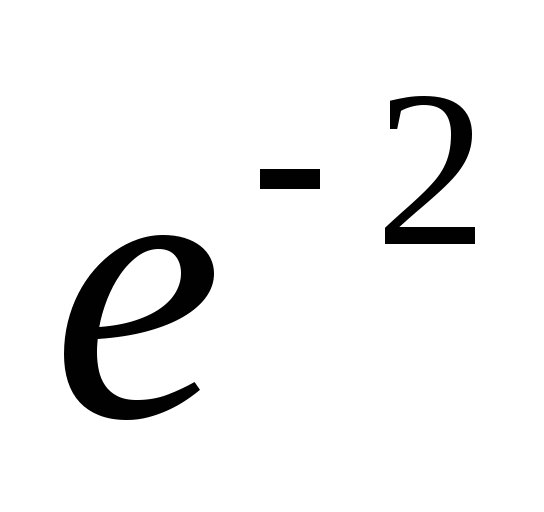 ;
;
18.
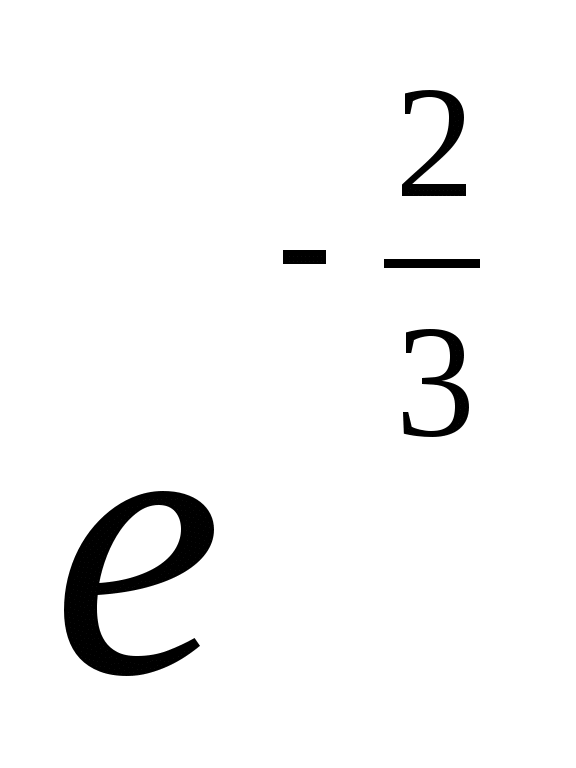 ;
;
5.
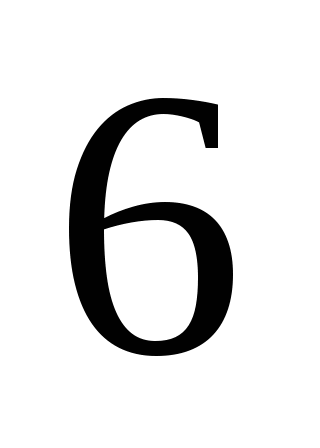 ;
;
12.
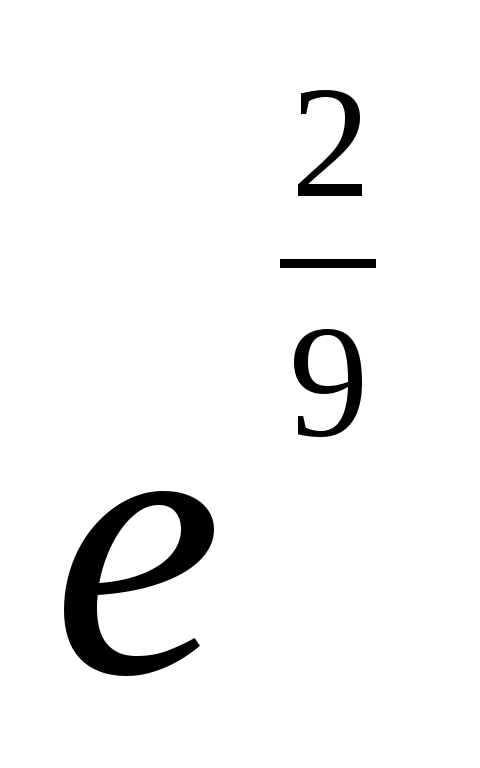 ;
;
19.
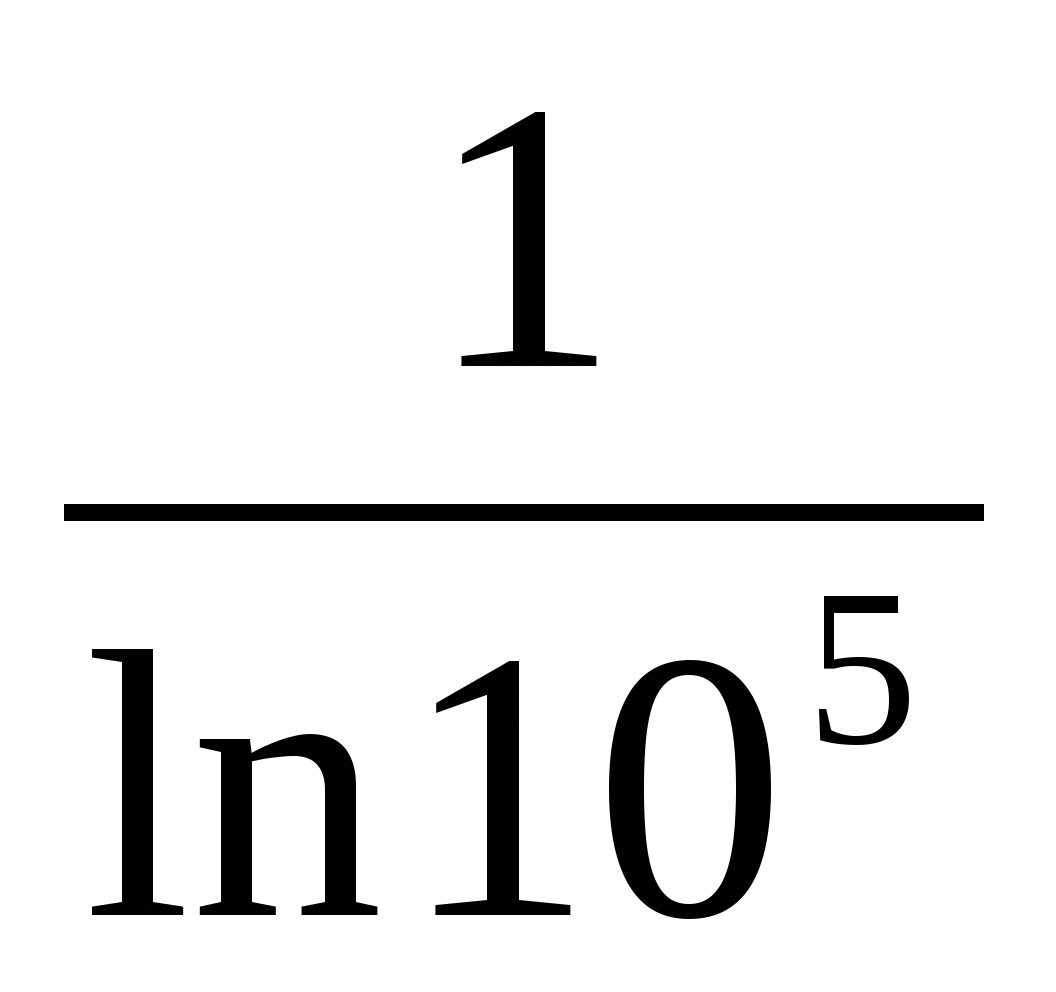 ;
;
6.
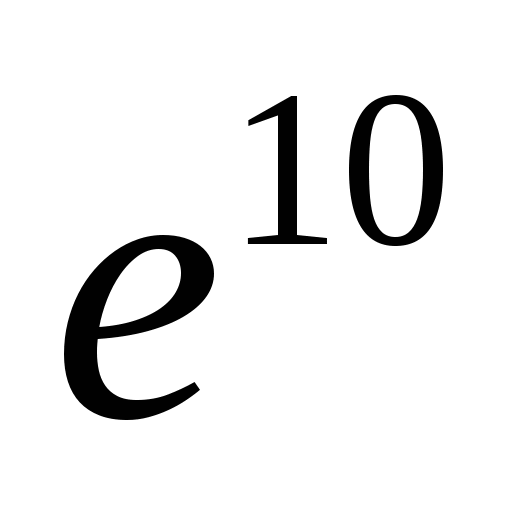 ;
;
13.
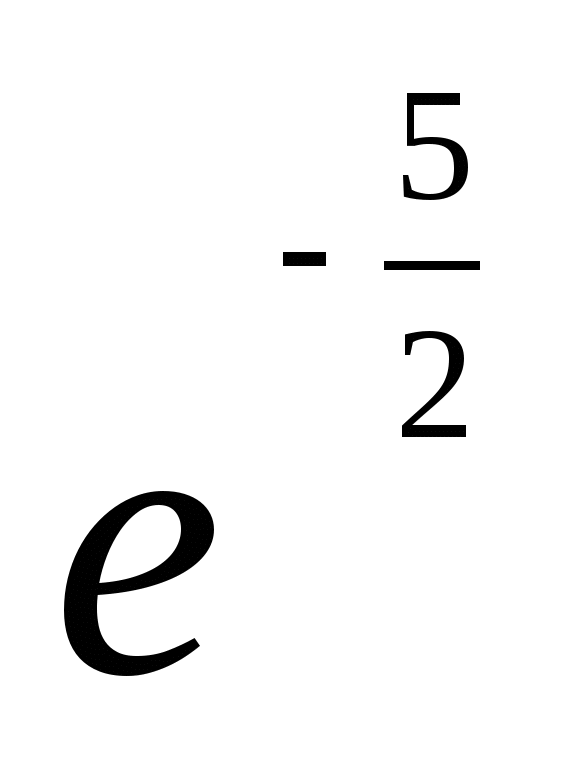 ;
;
20.
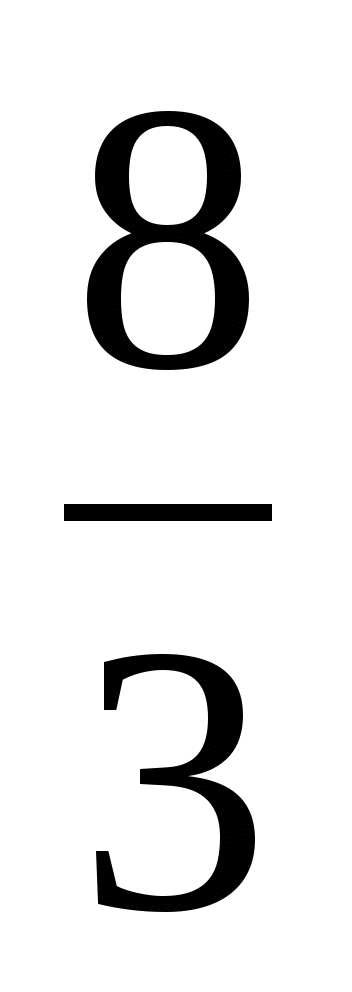 .
.
7.
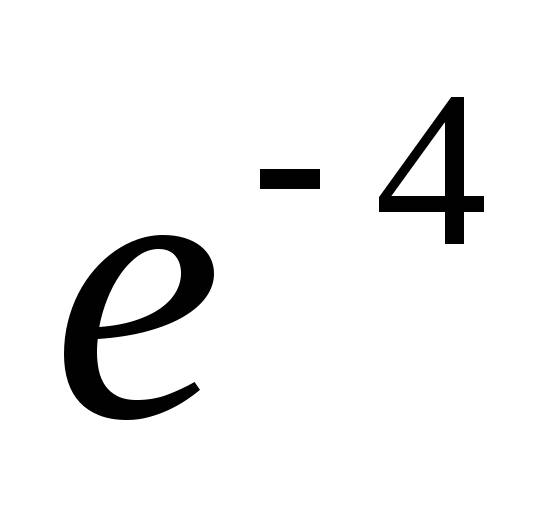 ;
;
14.
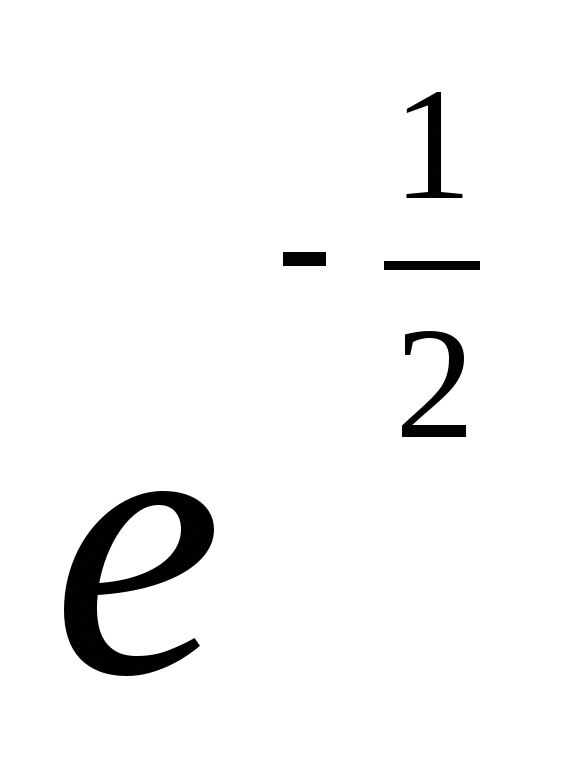
Как оценить пределы с помощью таблиц
Ошибка: Нажмите «Не робот» и повторите попытку.
Лучшее, что мы можем сделать при работе с таблицами, — это оценить предельное значение.
Примеры
Пример 1: Использование таблиц для оценки пределов
Используйте приведенные ниже таблицы, чтобы оценить значение $$ \ displaystyle \ lim_ {x \ to 5} f (x) $$.
$$ \ begin {array} {l | c} {x} & {f (x)} \\ \ hline 4.5 и 8.32571 \ hline 4.75 и 8.95692 \ hline 4.9 и 8.99084 \ hline 4,99 и 8,99987 \ hline 4.999 и 8.99992 \ hline 4.9999 и 8.99999 \\\ hline \ end {массив} $$
$$ \ begin {array} {l | c} {x} & {f (x)} \\ \ hline 5.5 и 9.64529 \ hline 5.25 и 9.26566 \ hline 5.1 и 9.04215 \ hline 5.01 и 9.00113 \ hline 5.001 и 9.00011 \ hline 5.0001 и 9.00001 \ hline \ end {массив} $$
Шаг 1Посмотрите, что происходит, когда $$ x $$ приближается слева.
По мере приближения значений $$ x $$ к 5…
$$
\ begin {array} {l | c}
{x} & {f (x)} \\
\ hline
4.5 и 8.32571 \ hline
4.75 и 8.95692 \ hline
4.9 и 8.99084 \ hline
4,99 и 8,99987 \ hline
4.999 и 8.99992 \ hline
4.9999 и 8.99999 \\\ hline
\ end {массив}
$$
… $$ f (x) $$ похоже приближается к 9.
Посмотрите, что происходит, когда $$ x $$ приближается справа.
По мере приближения значений $$ x $$ — к 5 …
$$
\ begin {array} {l | c}
{x} & {f (x)} \\
\ hline
5.5 и 9.64529 \ hline
5.25 и 9.26566 \ hline
5.1 и 9.04215 \ hline
5.01 и 9.00113 \ hline
5.001 и 9.00011 \ hline
5.0001 и 9.00001 \ hline
\ end {массив}
$$
… $$ f (x) $$ похоже приближается к 9.
Если функция приближается к одному и тому же значению в обоих направлениях, то это оценка предельного значения.
Ответ: $$ \ displaystyle \ lim_ {x \ to 5} f (x) \ приблизительно 9 $$.
Пример 2: Использование таблиц для оценки пределов
Используя приведенные ниже таблицы, оцените $$ \ displaystyle \ lim_ {x \ to-8} f (x) $$.
$$ \ begin {array} {l | c} {x} & {f (x)} \\ \ hline -8,5 и 13,1365 \ hline -8,1 и -2,4336 \ hline -8,01 и -2,91313 \ hline -8,001 и -2,99131 \ hline -8,0001 и -2,99913 \ hline -8.00001 и -2.99991 \ hline \ end {массив} $$
$$ \ begin {array} {l | c} {x} & {f (x)} \\ \ hline -7,5 и -6 \ hline -7,9 и -5,5 \ hline -7,99 и -5,15 \ hline -7.999 и -5.015 \ hline -7.9999 и -5.0015 \ hline -7.99999 и -5.00015 \ hline \ end {массив} $$
Шаг 1Посмотрите, что происходит, когда $$ x $$ приближается слева.
Поскольку значения $$ x $$ — приближаются к -8 …
$$
\ begin {array} {l | c}
{x} & {f (x)} \\
\ hline
-8,5 и 13,1365 \ hline
-8,1 и -2,4336 \ hline
-8,01 и -2,91313 \ hline
-8,001 и -2,99131 \ hline
-8,0001 и -2,99913 \ hline
-8.00001 и -2.99991 \ hline
\ end {массив}
$$
… $$ f (x) $$ похоже приближается к -3.
Посмотрите, что происходит, когда $$ x $$ приближается справа.
Поскольку значения $$ x $$ — приближаются к -8 …
$$
\ begin {array} {l | c}
{x} & {f (x)} \\
\ hline
-7.5 & -4 \ hline
-7,9 и -3,5 \ hline
-7,99 и -3,15 \ hline
-7.999 и -3.015 \ hline
-7.9999 и -3.0015 \ hline
-7.99999 и -3.00015 \ hline
\ end {массив}
$$
… $$ f (x) $$ похоже приближается к -3.
Если функция приближается к разным значениям, то предел не существует.
Ответ: $$ \ displaystyle \ lim_ {x \ to-8} f (x) $$ не существует.
Практические задачи
Проблема 1
Оцените $$ \ lim \ limits_ {x \ to12} f (x) $$, используя приведенные ниже таблицы.
$$ \ begin {array} {l | c} {x} & {f (x)} \\ \ hline 11,5 и 7 \ hline 11.9 и 7.5 \ hline 11,99 и 7,9 \ hline 11.999 и 7.99 \ hline 11.9999 и 7.999 \ hline 11.99999 и 7.9999 \ hline \ end {массив} $$
$$ \ begin {array} {l | c} {х} & f (x) \\ \ hline 12,5 и 8,5 \ hline 12.1 и 8.1 \ hline 12.01 и 8.01 \ hline 12.001 и 8.001 \ hline 12.0001 и 8.0001 \ hline 12.00001 и 8.00001 \ hline \ end {массив} $$
Покажи ответ Шаг 1Посмотрите, что происходит, когда $$ x $$ приближается слева.
Шаг 1 Ответ Поскольку значения $$ x $$ приближаются к 12 слева …
$$
\ begin {array} {l | c}
{x} & {f (x)} \\
\ hline
11,5 и 7 \ hline
11.9 и 7.5 \ hline
11,99 и 7,9 \ hline
11.999 и 7.99 \ hline
11.9999 и 7.999 \ hline
11.99999 и 7.9999 \ hline
\ end {массив}
$$
… $$ f (x) $$ похоже приближается к 8.
Посмотрите, что происходит, когда $$ x $$ приближается справа.
Шаг 2 Ответ Поскольку значения $$ x $$ — приближаются к 12 справа
$$
\ begin {array} {l | c}
{x} & {f (x))} \\
\ hline
12.5 и 8,5 \ hline
12.1 и 8.1 \ hline
12.01 и 8.01 \ hline
12.001 и 8.001 \ hline
12.0001 и 8.0001 \ hline
12.00001 и 8.00001 \ hline
\ end {массив}
$$
… f (x) похоже приближается к 8.
Если функция приближается к одному и тому же значению в обоих направлениях, то это оценка предельного значения.
.Анализ граничных значений и разделение эквивалентности с примерами

- Home
Testing
- Back
- Agile Testing
- BugZilla
- Cucumber
- 9000 J5 9000 Testing
- 9000 J5
- Назад
- JUnit
- LoadRunner
- Ручное тестирование
- Мобильное тестирование
- Mantis
- Почтальон
- QTP
- Назад
- 00050005000500050005 000 RPM
SoapUI
- Управление тестированием
- TestLink
SAP
- 900 03
- Назад
- ABAP
- APO
- Начинающий
- Basis
- BODS
- BI
- BPC
- CO
- Назад
- CRM
- Назад
- PI / PO
- PP
- SD
- SAPUI5
- Security
- Менеджер решений
- Successfactors
- SAP Tutorial
- Назад
- Apache
- AngularJS
- ASP.Net
- C
- C #
- C ++
- CodeIgniter
- СУБД
- JavaScript
- Назад
- Java
- JSP
- Kotlin
- Linux
- Linux
- Kotlin
- Linux js
- Perl
- Назад
- PHP
- PL / SQL
- PostgreSQL
- Python
- ReactJS
- Ruby & Rails
- Scala
- SQL 0000004 SQL
- UML
- VB.Net
- VBScript
- Веб-службы
- WPF
Обязательно учите!
- Назад
- Бухгалтерский учет
- Алгоритмы
- Android
- Блокчейн
- Business Analyst
- Веб-сайт сборки
- CCNA
- Облачные вычисления
- COBOL 9000 Compiler
- 0005
- Ethical Hacking
- Учебные пособия по Excel
- Программирование на Go
- IoT
- ITIL
- Jenkins
- MIS
- Сетевые подключения
- Операционная система
- Назад Управление проектами Обзоры
- 9000 Встроенный COBOL 9000 Дизайн 9000
- Salesforce
- SEO
- Разработка программного обеспечения
- VBA
- 0005
Big Data
- Назад
- AWS
- BigData
- Cassandra
- Cognos
- Хранилище данных 0005
Страница поддержки не найдена | Поддержка SAS

- Решения
- По отраслям
- Сельское хозяйство
- Банковское дело
- Связь
- Образование
- Здравоохранение
- Страхование
- Науки о жизни
- Производство
- Государственный сектор
- Малый бизнес M&E
- Все отрасли
- По отраслям
- По технологиям и темам
- Расширенная аналитика
- AI & Machine Learning
- Cloud
- COVID-19
- Data Management
- Decisioning
- Fraud & Security Intelligence
- Internet of Things
- Marketing Analytics
- Открытая интеграция
- Операционная аналитика
- Управление рисками
- Все технологии и темы
- По продуктам
- SAS Viya
- SAS Customer Intelligence 360
- SAS Detection & Investigation 9 0004 SAS Model Manager
- SAS Visual Analytics
- SAS Visual Data Mining & Machine Learning
- SAS Visual Forecasting
- Все продукты
- Пробные версии бесплатного ПО
- По ролям
- Разработчики
Пользователи Соискатели Соискатели - Партнеры
- Малый и средний бизнес
- Студенты и преподаватели
- Лидеры идей
- Пробные версии бесплатного ПО
- COVID-19 Среда обнаружения данных
- Обработка потока событий SAS в облаке SAS
Машинное обучение SAS
- Запросить демоверсию
- Запросить цену на программное обеспечение
- Связаться с торговым представителем SAS
- Аналитики Точки зрения
- Компания 000
- Каст omer Истории успеха
- Мыслительное лидерство
- Инновационный дизайн НИОКР
- Новости и основные моменты
- Экосистема партнеров
- Службы поддержки мирового класса
- Обучение
- Корпоративное обучение
Электронное обучение
- Programming 1
- Programming 2
- SAS Enterprise Guide 1
- SAS Programming for RUsers
009 Viya Enablement
009 Viya Enablement Форматы обучения- Электронное обучение
- Live Web
- Классы
- Видеоуроки
- Все форматы обучения
Вебинары Certification- Data Base Programmer
- Статистический бизнес-аналитик
- Predictive Modeler
- Вся сертификация
Подготовка к экзаменам Менеджер по сертификации Книги- Для начинающих
- Сертификация
- Скидки
- Все книги
Все предстоящие Документация- По продуктам
- Base SAS
- SAS Enterprise Guide
- SAS Enterprise Miner
- SAS / STAT
- SAS Studio
- Продукт SAS Visual Analytics
- Изменения в программном обеспечении
4 Все продукты
4 Изменения в программном обеспечении
Программирование- SAS 9.4 & SAS Viya
- SAS 9.3 и более ранние версии
Администрирование- SAS
- SAS 9.4 и более ранние версии
Установка и настройка- Центр установки
- Системные требования
- Стороннее программное обеспечение
- Техническая документация
- Вся документация
Поддержка- Главная страница поддержки
- База знаний
- Замечания по установке
- Замечания по проблемам
- Замечания по использованию
- Поиск по всем заметкам
- DATA Step Samples
- s Search
Все образцы
- Product Security
- Вся база знаний
Поддержка продуктов- Base SAS
- SAS Customer Intelligence 360
- SAS Enterprise Guide
- SAS Enterprise Miner
- SASPy
- SAS 9 / ST
- SAS Visua l Аналитика
- Все продукты
- Основные направления
- Безопасность продукта
Поддержка по ролям- Администраторы
- Разработчики
- Программисты
- Студенты
- Новички в SAS
Службы поддержки Управляйте своими треками Техническое обслуживание Содействие с лицензированием Услуги поддержки Политики поддержки Консультации Все услуги Загрузки- SAS Download Manager
- SAS Universal Viewer
Стандартные планы развертывания Стандартные планы развертывания Стандартные планы развертывания Горячие исправления- SAS Viya
- SAS 9.4
- Объявления об оперативных исправлениях
- Инструмент исправлений
- Все исправления
SAS Starter Kit Войти Сообщество- Новые пользователи SAS
- Программирование SAS
- Управление данными и развертывание
- Машинное обучение
- Визуализация данных
- Статистические процедуры
- Разработчики
- Все сообщества
- SAS Analytics Explorers
- Группы пользователей
Академики- Академические программы
9000- 000 Преподаватели
9000- Педагоги Академические скидки
Партнеры- О нашей партнерской программе
- Найти партнера
- Войти в PartnerNet
- Торговая площадка партнеров
Мероприятия- Глобальный форум SAS
- Вебинары
- Все мероприятия
- Все мероприятия
- 0034
- О компании
- Наша компания
- Обзор
- Видение и миссия
- Наши ценности
- За что мы выступаем
- Лидерство компании
- Информация о компании
- Освещение в СМИ
- Годовой отчет
000- Информационные бюллетени компании
- Точки зрения аналитика
- Бюро спикеров
- Trust Center
- Карьера
- Обзор
- Наша культура
- Наши рассказчики
- Стажировки
- Программы раннего карьерного роста
000
000000000 Офисная информация Свяжитесь с нами сас.com- sas.com
- support.sas.com
- blogs.sas.com
- community.sas.com
- developer.sas.com
Поиск
Сайты по всему миру
- Албания
- Аргентина
- Австралия
- Австрия
- Бельгия
- Босния и Герц.
- Бразилия
- Канада (английский)
- Канада (Français)
- Чили
- Китай
- Колумбия
- Хорватия
- Чешская Республика
- Дания
- Финляндия
.Предел эквивалентности для теста неполноценности
st: предел эквивалентности для теста неполноценности 
[Предыдущая дата] [Следующая дата] [Предыдущая тема] [Следующая цепочка] [Указатель даты] [Указатель темы]
Дорогие все,
Если меня интересует вычисление предела эквивалентности в 20% относительно разницы двух пропорций. Это просто (-0,2, 0,2) или мне нужно вычислить это на основе наблюдаемых данных и размера выборки (если да, то как)?
Заранее спасибо,
Рикардо
Рикардо Овалдиа, MS
Статистик
Оклахома-Сити, ОК
--- Пт, 14.08.09, Ricardo Ovaldia написал:
> От: Рикардо Овалдиа
> Тема: Re: st: Re: проверка эквивалентности
> Кому: [email protected]
> Дата: пятница, 14 августа 2009 г., 11:34
> Джозеф Ковени
> написал:
>
> >> Вы можете использовать либо -cs-, что является официальным, либо
> -rdci-, [...]
> >> Вы бы построили доверительный интервал и
> проверьте, есть ли
> >> как нижняя, так и верхняя доверительные границы попадают в
> указанные пределы >> для принятия альтернативы
> гипотеза терапевтической эквивалентности.>
> Спасибо.
> Как предложил Джозеф, я использовал -rdci- и получил:
> Agresti-Caffo 95% ДИ: -0,299 0,067
>
> Если меня интересует предел эквивалентности в 20%, могу ли я
> сравнить вышеуказанный 95% доверительный интервал с (-0,2, 0,2)? Или как мне вычислить
> правильные пределы эквивалентности?
>
> Спасибо,
> Рикардо
>
>
> Рикардо Овалдиа, MS
> Статистик
> Оклахома-Сити, ОК
>
>
> --- Вт, 13.08.09, Рикардо Овалдиа
> написал:
>
>> От: Рикардо Овалдиа
>> Тема: Re: st: Re: проверка эквивалентности
>> Кому: [email protected]
>> Дата: четверг, 13 августа 2009 г., 12:05
>> Ранее я спросил:
>>
>>> Есть ли способ выполнить тест на эквивалентность для
> а
>> Таблица 2x2.
>>> Лечение (0,1) vs. результат (0,1)?
>>
>> Я нашел оборудование Ричарда Гольдштейна. Является ли это
> программа
>> работать правильно?
>> Если да, то что означают test1 и test2?
>> если нет, есть ли альтернативы (другие бесплатные
> ПО)?
>>
>> Спасибо,
>> Рикардо.>>
>> Рикардо Овалдиа, MS
>> Статистик
>> Оклахома-Сити, ОК
>>
>>
>> --- В среду, 8/12/09, Рикардо Овалдиа
>> написал:
>>
>>> От: Рикардо Овалдиа
>>> Тема: st: Re: проверка эквивалентности
>>> Кому: [email protected]
>>> Дата: среда, 12 августа 2009 г., 18:01
>>> Есть ли способ выполнить
>>> Тест эквивалентности для таблицы 2x2.>>> Лечение (0,1) vs. результат (0,1)?
>>>
>>> Спасибо,
>>> Рикардо
>>>
>>> Рикардо Овалдиа, MS
>>> Статистик
>>> Оклахома-Сити, ОК
>>>
>>>
>>>
>>>
>>>
>>> *
>>> * Для поиска и помощи попробуйте:
>>> * Http://www.stata.com/help.cgi?search
>>> * Http://www.stata.com/support/statalist/faq
>>> * Http: // www.ats.ucla.edu/stat/stata/
>>>
>>
>>
>>
>>
>> *
>> * Для поиска и помощи попробуйте:
>> * Http://www.stata.com/help.cgi?search
>> * Http://www.stata.com/support/statalist/faq
>> * Http://www.ats.ucla.edu/stat/stata/
>>
>
>
>
>
*
* Для поиска и помощи попробуйте:
* http://www.stata.com/help.cgi?search
* http://www.stata.com/support/statalist/faq
* http://www.ats.ucla.edu/stat/stata/
.
- Электронное обучение
- Live Web
- Классы
- Видеоуроки
- Все форматы обучения
- Data Base Programmer
- Статистический бизнес-аналитик
- Predictive Modeler
- Вся сертификация
- Для начинающих
- Сертификация
- Скидки
- Все книги
- По продуктам
- Base SAS
- SAS Enterprise Guide
- SAS Enterprise Miner
- SAS / STAT
- SAS Studio
- Продукт SAS Visual Analytics
- Изменения в программном обеспечении
- 4 Все продукты
- 4 Изменения в программном обеспечении
- SAS 9.4 & SAS Viya
- SAS 9.3 и более ранние версии
- SAS
- SAS 9.4 и более ранние версии
- Центр установки
- Системные требования
- Стороннее программное обеспечение
- Техническая документация
- Вся документация
- Главная страница поддержки
- База знаний
- Замечания по установке
- Замечания по проблемам
- Замечания по использованию
- Поиск по всем заметкам
- DATA Step Samples
- s Search Все образцы
- Product Security
- Вся база знаний
- Base SAS
- SAS Customer Intelligence 360
- SAS Enterprise Guide
- SAS Enterprise Miner
- SASPy
- SAS 9 / ST
- SAS Visua l Аналитика
- Все продукты
- Основные направления
- Безопасность продукта
- Администраторы
- Разработчики
- Программисты
- Студенты
- Новички в SAS
- SAS Download Manager
- SAS Universal Viewer
- SAS Viya
- SAS 9.4
- Объявления об оперативных исправлениях
- Инструмент исправлений
- Все исправления
- Новые пользователи SAS
- Программирование SAS
- Управление данными и развертывание
- Машинное обучение
- Визуализация данных
- Статистические процедуры
- Разработчики
- Все сообщества
- SAS Analytics Explorers
- Группы пользователей
- Академические программы 9000
- 000 Преподаватели 9000
- Педагоги Академические скидки
- О нашей партнерской программе
- Найти партнера
- Войти в PartnerNet
- Торговая площадка партнеров
- Глобальный форум SAS
- Вебинары
- Все мероприятия
- Все мероприятия
- 0034
- О компании
- Наша компания
- Обзор
- Видение и миссия
- Наши ценности
- За что мы выступаем
- Лидерство компании
- Информация о компании
- Освещение в СМИ
- Годовой отчет
000 - Информационные бюллетени компании
- Точки зрения аналитика
- Бюро спикеров
- Наша компания
- Trust Center
- Карьера
- Обзор
- Наша культура
- Наши рассказчики
- Стажировки
- Программы раннего карьерного роста
000


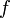 ,
непрерывной на отрезке
,
непрерывной на отрезке 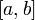 ,
является отрезок
,
является отрезок 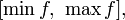 где
минимум и максимум берутся по отрезку
где
минимум и максимум берутся по отрезку 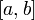 .
.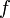 непрерывна
на отрезке
непрерывна
на отрезке 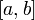 и
и 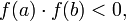 то
существует точка
то
существует точка 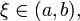 в
которой
в
которой  .
.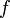 непрерывна
на отрезке
непрерывна
на отрезке 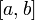 и
число
и
число 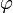 удовлетворяет
неравенству
удовлетворяет
неравенству 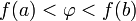 или
неравенству
или
неравенству 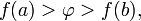 то
существует точка
то
существует точка 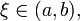 в
которой
в
которой 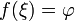 .
.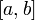 непрерывна
в том и только в том случае, когда область
ее значений является отрезком с концами
непрерывна
в том и только в том случае, когда область
ее значений является отрезком с концами 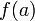 и
и 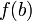 .
.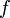 и
и 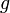 непрерывны
на отрезке
непрерывны
на отрезке 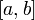 ,
причем
,
причем 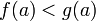 и
и 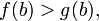 то
существует точка
то
существует точка 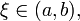 в
которой
в
которой 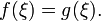 Отсюда,
в частности, следует, что любое непрерывное
отображение отрезка в себя имеет хотя
бы одну неподвижную
точку.
Отсюда,
в частности, следует, что любое непрерывное
отображение отрезка в себя имеет хотя
бы одну неподвижную
точку.