Предел функции. Односторонний предел
Задачи на нахождение предела очень часто можно встретить в таких науках как механика, физика, высшая математика, прикладная математика и т.д. Суть таких задач заключается в отыскании значения функции при движении аргумента до некоторого значения при котором функция может быть и неопределена. Поведение функции в определенной точке и называется ее пределом. Он может принимать как постоянное значение так и быть равным бесконечности ().
ОПРЕДЕЛЕНИЕ ПРЕДЕЛА ФУНКЦИИ
Пусть имеем функцию которая определена в некоторой окрестности точки . Число называется пределом функции при , если для любого малого наперед заданного положительного числа можно найти такое положительное число что для всех удовлетворяющих неравенство
выполняется неравенство
В упрощенной форме определения записывают так
При функция является бесконечно большой, если для любого числа можно найти такое число что для всех , удовлетворяющих неравенство оправдывается неравенство
В краткой форме это определение примет вид
Функция является бесконечно малой при , если выполняется
ОДНОСТОРОННИЕ ГРАНИЦЫ
Запись можно понимать как приближение к точке слева, когда и дело, когда .
аким образом, приближение точек до может быть двусторонним. На основе этого введены определения правой и левой границы.
Число есть пределом функции слева (левой границей), если для любого числа существует такое, что при выполняется неравенство
Число является пределом функции справа (правой границей) если для сколь угодно малого значения найдется такое что для всех из промежутка выполняется неравенство
Левая и правая границы называются односторонними границами.
Функция имеет предел в точке тогда и только тогда, когда существуют одновременно границы справа и слева и они равны между собой
Рассмотрим примеры из сборника задач Дубовика В.П., Юрика И.И. «Высшая математика» на нахождение границ.
————————————
Пример 1. Найти пределы.
1) (4. 331)
2) (4. 333)
3) (4. 337)
4) (4. 342)
5) (4. 348)
6) (4. 357)
Решение.
1) Первые примеры не являются сложными и их решения сводится к подстановки значения аргумента в функцию
2) Как и в предыдущем примере проводим подстановку
3) Выполняем подстановку переменной в предел
4) В такого типа примерах нужно знаменатель разложить по правилу разности квадратов, после этого выполнить подстановку
5) В таких примерах нужно числитель и знаменатель сократить на множитель, который вносит наибольший вклад
6) В подобных примерах ищут наибольший показатель переменной в числителе и знаменателе, а потом проводят анализ. При следовании корни ведут себя следующим образом
С оценки показателей видим что числитель быстрее растет чем знаменатель
следовательно функция бесконечно большая и ее предел бесконечный
На этом вводной урок нахождения пределов функций завершен. Другие примеры вычисления пределов и методику их нахождения Вы найдете в следующих материалах.
————————————
Посмотреть материалы:
- Числовая последовательность и ее предел
- Правила вычисления пределов последовательности
- Вычисление пределов по правилу Лопиталя
- Замечательные пределы на примерах
- Эквивалентные бесконечно малые функции при вычислении пределов
Курс математического анализа
Курс математического анализа
ОглавлениеПРЕДИСЛОВИЕГлава 1. ВВЕДЕНИЕ § 1.2. Множество. Интервал, отрезок § 1.3. Функция § 1.4. Понятие непрерывности функции § 1.5. Производная § 1.6. Первообразная. Неопределенный интеграл § 1.7. Понятие определенного интеграла. Площадь криволинейной фигуры Глава 2. ДЕЙСТВИТЕЛЬНОЕ ЧИСЛО § 2.1. Рациональные и иррациональные числа § 2.2. Определение неравенства § 2.3. Основная лемма. Определение арифметических действий § 2.4. Основные свойства действительных чисел § 2.5. Изоморфизм различных представлений действительных чисел.  Физические величины§ 2.6. Неравенства для абсолютных величин § 2.7. Точные верхняя и нижняя грани множества § 2.8. Символика математической логики Глава 3. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ § 3.1. Понятие предела последовательности § 3.2. Арифметические действия с пределами § 3.3. Бесконечно малая и бесконечно большая величины § 3.4. Существование предела у монотонной ограниченной последовательности § 3.5. Число е § 3.6. Леммы о вложенных отрезках, существовании точных граней множества и сечения во множестве действительных чисел § 3.7. Теорема Больцано-Вейерштрасса. Верхний и нижний пределы § 3.8. Критерий Коши существования предела § 3.9. Счетное множество. Счетность множества рациональных чисел. Несчетность множества действительных чисел Глава 4. ПРЕДЕЛ ФУНКЦИИ § 4.1. Понятие предела функции § 4.2. Непрерывность функции в точке § 4.3. Пределы функции справа и слева. Монотонная функция § 4.4. Функции, непрерывные на отрезке § 4.  § 4.8. Еще о числе е § 4.9. lim sin oo/oo § 4.10. Порядок переменной, эквивалентность (асимптотика) Глава 5. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ДЛЯ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ § 5.1. Производная § 5.2. Дифференциал функции § 5.3. Производная функции от функции § 5.4. Производная обратной функции § 5.6. Производные и дифференциалы высшего порядка § 5.7. Возрастание и убывание функции на интервале и в точке. Локальный экстремум § 5.8. Теоремы о среднем значении. Критерии возрастания и убывания функции на интервале. Достаточные критерии локальных экстремумов § 5.9. Формула Тейлора § 5.10. Формулы Тейлора для важнейших элементарных функций § 5.11. Ряд Тейлора § 5.12. Выпуклость кривой в точке. Точка перегиба § 5.13. Выпуклость кривой на отрезке § 5.14. Раскрытие неопределенностей § 5.15. Асимптота § 5.16. Схема построения графика функции § 5.17. Кусочно непрерывные и кусочно гладкие функции Глава 6. n-МЕРНОЕ ПРОСТРАНСТВО.  ГЕОМЕТРИЯ КРИВОЙ§ 6.1. n-мерное пространство. Линейное множество § 6.2. Евклидово n-мерное пространство. Пространство со скалярным произведением § 6.3. Линейное нормированное пространство § 6.4. Вектор-функция в n-мерном евклидовом пространстве § 6.5. Непрерывная кривая. Гладкая кривая § 6.6. Геометрический смысл производной вектор-функции § 6.7. Длина дуги кривой § 6.8. Касательная § 6.9. Основной триэдр кривой § 6.10. Соприкасающаяся плоскость § 6.11. Кривизна и радиус кривизны кривой § 6.12. Эволюта § 6.13. Формулы Френе. Свойства эволюты Глава 7. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ § 7.1. Открытое множество § 7.2. Предел функции § 7.3. Непрерывная функция § 7.4. Частные производные и производная по направлению § 7.5. Дифференцируемая функция. Касательная плоскость § 7.7. Независимость от порядка дифференцирования § 7.  8. Дифференциал функции. Дифференциал высшего порядка§ 7.9. Теорема Больцано-Вейерштрасса § 7.10. Замкнутые и открытые множества § 7.11. Функции на множестве. Свойства непрерывных функций на замкнутом ограниченном множестве § 7.12. Лемма о вложенных прямоугольниках и лемма Бореля § 7.13. Формула Тейлора § 7.14. локальный (абсолютный) экстремум функции § 7.15. Теоремы существования неявной функции § 7.16. Теорема существования решения системы уравнений § 7.17. Отображения § 7.18. Гладкая поверхность § 7.19. Дифференциалы неявных функций. Линеаризация § 7.20. Локальный относительный экстремум § 7.21. Замена переменных в частных производных § 7.22. Система зависимых функций Глава 8. НЕОПРЕДЕЛЕННЫЕ ИНТЕГРАЛЫ. АЛГЕБРА МНОГОЧЛЕНОВ § 8.1. Введение. Методы замены переменной и интегрирования по частям § 8.2. Комплексные числа § 8.3. Комплексные функции § 8.4. Многочлены § 8.5. Разложение рациональной функции на простейшие дроби § 8.  6. Интегрирование рациональных дробей§ 8.7. Интегрирование алгебраических иррациональностей § 8.8. Подстановки Эйлера § 8.9. Биномиальные дифференциалы. Теорема Чебышева § 8.10. Интегрирование тригонометрических выражений § 8.11. Тригонометрические подстановки § 8.12. Несколько важных интегралов, не выражаемых в элементарных функциях Глава 9. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ РИМАНА § 9.2. Ограниченность интегрируемой функции § 9.3. Суммы Дарбу § 9.4. Основная теорема § 9.5. Теоремы о существовании интеграла от непрерывной и монотонной функции на [a, b] § 9.7. Неравенства и теорема о среднем § 9.8. Интеграл как функция верхнего предела. Теорема Ньютона-Лейбница § 9.9. Вторая теорема о среднем § 9.10. Видоизменение функции § 9.11. Несобственные интегралы § 9.12. Несобственные интегралы от неотрицательных функций § 9.13. Интегрирование по частям § 9.14. Несобственный интеграл и ряд § 9.  15. Несобственные интегралы с особенностями в нескольких точках§ 9.16. Формула Тейлора с остатком в интегральной форме § 9.17. Формулы Валлиса и Стирлинга Глава 10. НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ИНТЕГРАЛОВ. ПРИБЛИЖЕННЫЕ МЕТОДЫ § 10.1. Площадь в полярных координатах § 10.2. Объем тела вращения § 10.3. Длина дуги гладкой кривой § 10.4. Площадь поверхности тела вращения § 10.5. Интерполяционный многочлен Лагранжа § 10.6. Квадратурные формулы прямоугольников § 10.7. Формула Симпсона Глава 11. РЯДЫ § 11.1. Понятие ряда § 11.2. Действия с рядами § 11.3. Ряды с неотрицательными членами § 11.4. Ряд Лейбница § 11.5. Абсолютно сходящиеся ряды § 11.6. Условно и безусловно сходящиеся ряды с действительными членами § 11.7. Последовательности и ряды функций. Равномерная сходимость § 11.8. Интегрирование и дифференцирование равномерно сходящихся рядов на отрезке § 11.9. Кратные ряды. Перемножение абсолютно сходящихся рядов § 11.  z, cos z, sinz комплексной переменнойГлава 12. КРАТНЫЕ ИНТЕГРАЛЫ § 12.2. Мера Жордана § 12.3. Важные примеры квадрируемых по Жордану множеств § 12.4. Еще один критерий измеримости множества. Полярные координаты § 12.5. Другие случаи измеримости § 12.6. Понятие кратного интеграла § 12.7. Верхняя и нижняя интегральные суммы. Основная теорема § 12.9. Свойства кратных интегралов § 12.10. Сведение кратного интеграла к интегрированию по отдельным переменным § 12.11. Непрерывность интеграла по параметру § 12.12. Геометрическая интерпретация знака определителя § 12.13. Замена переменных в кратном интеграле. Простейший случай § 12.14. Замена переменных в кратном интеграле § 12.15. Доказательство леммы 1 § 12.14 § 12.16. Полярные координаты в плоскости § 12.17. Полярные и цилиндрические координаты в пространстве § 12.18. Гладкая поверхность § 12.  19. Площадь поверхностиГлава 13. ТЕОРИЯ ПОЛЯ. ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ ПО ПАРАМЕТРУ. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ § 13.1. Криволинейный интеграл первого рода § 13.2. Криволинейный интеграл второго рода § 13.3. Поле потенциала § 13.4. Ориентация плоской области § 13.5. Формула Грина. Выражение площади через криволинейный интеграл § 13.6. Интеграл по поверхности первого рода § 13.7. Ориентация поверхностей § 13.8. Интеграл по ориентированной плоской области § 13.9. Поток вектора через ориентированную поверхность § 13.10. Дивергенция. Теорема Гаусса-Остроградского § 13.11. Ротор вектора. Формула Стокса § 13.12. Дифференцирование интеграла по параметру § 13.13. Несобственный интеграл § 13.14. Равномерная сходимость несобственного интеграла § 13.15. Равномерно сходящийся интеграл для неограниченной области Глава 14. ЛИНЕЙНЫЕ НОРМИРОВАННЫЕ ПРОСТРАНСТВА. ОРТОГОНАЛЬНЫЕ СИСТЕМЫ § 14.2. Пространство L'(L) § 14.3. Пространство L2 (L2) § 14.  4. Пространство …§ 14.5. Полнота системы элементов в банаховом пространстве § 14.6. Ортогональная система в пространстве со скалярным произведением § 14.8. Полнота системы функций в … Глава 15. РЯДЫ ФУРЬЕ. ПРИБЛИЖЕНИЕ ФУНКЦИЙ ПОЛИНОМАМИ § 15.2. Сумма Дирихле § 15.3. Формулы для остатка ряда Фурье § 15.4. Теоремы об осцилляции § 15.5. Критерий сходимости рядов Фурье. Полнота тригонометрической системы функций § 15.6. Комплексная форма записи ряда Фурье § 15.7. Дифференцирование и интегрирование рядов Фурье § 15.8. Оценка остатка ряда Фурье § 15.9. Алгебраические многочлены. Многочлены Чебышева § 15.10. Теорема Вейерштрасса § 15.11. Многочлены Лежандра Глава 16. ИНТЕГРАЛ ФУРЬЕ. ОБОБЩЕННЫЕ ФУНКЦИИ § 16.1. Понятие интеграла Фурье § 16.2. Сходимость простого интеграла Фурье к порождающей его функции § 16.3. Преобразование Фурье. Повторный интеграл Фурье. Косинус- и синус-преобразования Фурье § 16.  4. Производная преобразования Фурье§ 16.5. Обобщенные функции в смысле D § 16.6. Пространство S § 16.7. Пространство S обобщенных функций |
Левый и правый пределы
Левый и правый пределыВ некоторых случаях вы позволяете x приближаться к числу a слева или справа. правильно, а не «обе стороны сразу», как обычно.
1. означает: вычислить предел по мере того, как x приближается к c от вправо — то есть через числа больше c.
2. означает: вычислить предел по мере того, как x приближается к c от до — то есть через числа меньше с.
Эти ситуации могут возникнуть, если определено только слева или справа от c. Например, функция определена только для (поскольку квадратный корень из отрицательного числа не действительное число).
Также можно рассмотреть левый и правый пределы, когда определено по обе стороны от c.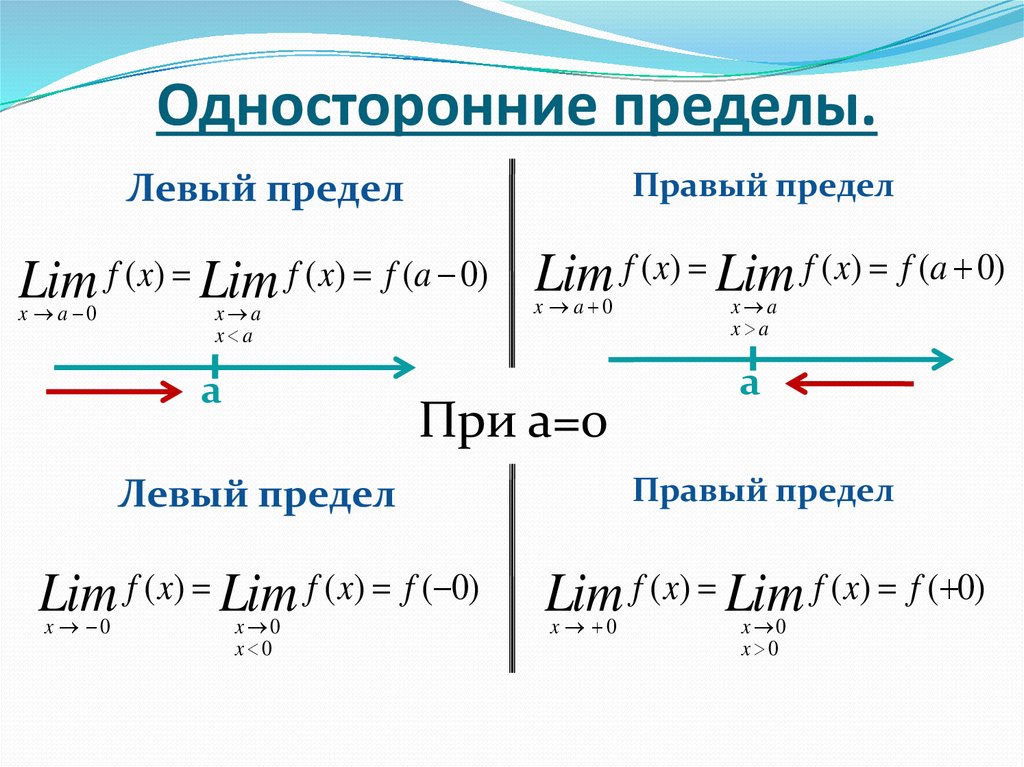
В этом случае
важный вопрос: равны ли левый и правый пределы?
Пример. На рисунках показаны графики некоторых функции. В каждом случае укажите, соответствуют ли левый и правый пределы в c определены. Если оба определены, скажите, равны ли они.
В (а) правый предел определен, потому что график приближается определенной высоте справа (высота точки). левый предел не определен, потому что график не приближается к определенная высота: имеется вертикальная асимптота. (Можно также сказать левый предел равен , как мы обсудим ниже.)
Аналогично, в (b) правый предел не определен, а определен левый предел. (Можно также сказать, что правый предел есть , как мы обсудим ниже.)
Наконец, в (c) определены как правый, так и левый пределы, но они не равны. (Это означает, что обычный («двусторонний») предел не определен.
Я не буду излагать много теорем о левых и правых пределах,
потому что в целом результаты, справедливые для обычных
(«двусторонние») пределы сохраняются для односторонни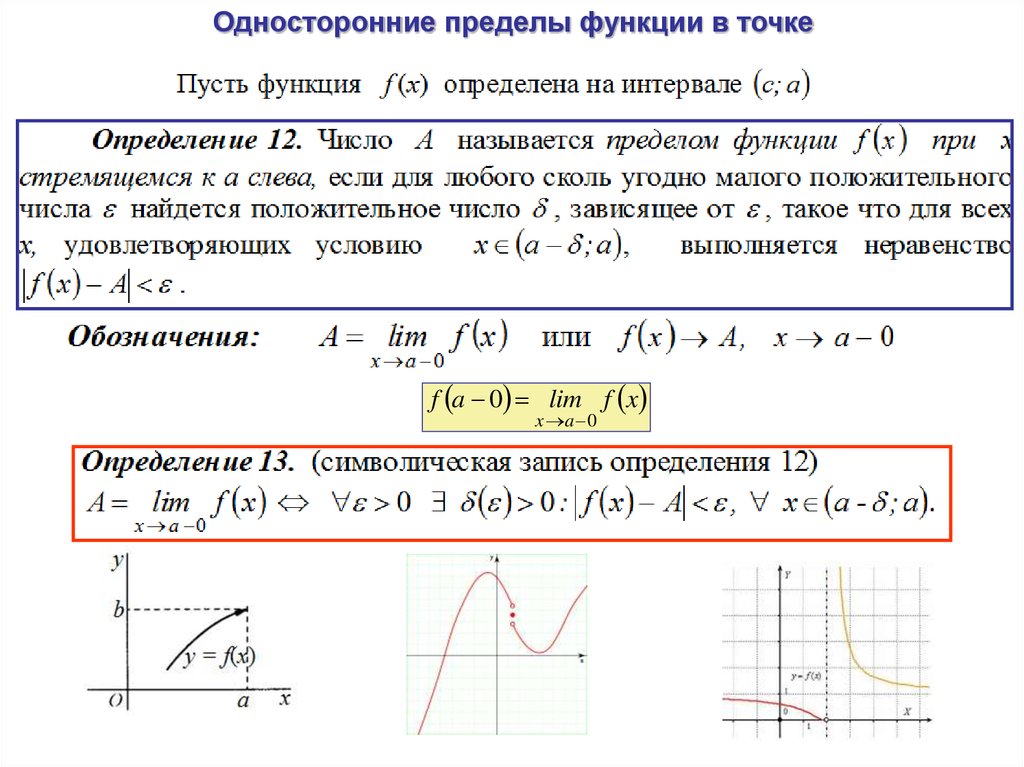х пределов.
Например
(опуская обычные технические предположения), вот правило для сумм
для правых пределов:
Вы можете видеть, что это то же самое, что правило для сумм для обычных пределы, с той лишь разницей, что теперь я пишу » » вместо » «.
Один важный момент, который мы уже отметили, — это отношение между левым и правым пределами и обычным («двусторонние») ограничения. Чтобы дать немного больше деталей, я сначала дайте формальные определения для левого и правого пределов.
Определение. (а) ( Правый пределы ) Предположим, определен на интервал для . Сказать это означает: для каждого числа существует число такое, что
(b) ( Левые пределы ) Предположим, определено на интервале для . Сказать это означает: для каждого число, существует число такое, что
Обратите внимание, что в каждом случае на самом деле может быть
определяется по обеим сторонам c.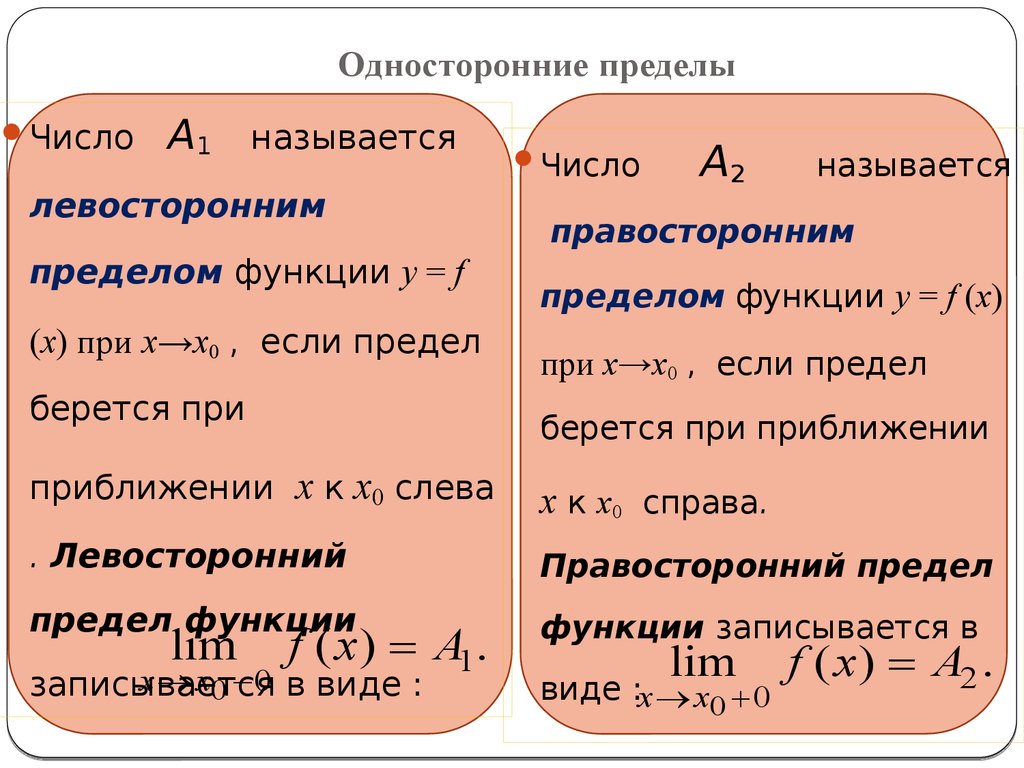
Мы говорим, что для правой руки
предел существования, его нужно только определить справа от
в; чтобы существовал левый предел, достаточно, чтобы он был равен .
определено слева от c. (Как обычно, может быть определено или не определено в c.)
Вот результат, который мы неофициально использовали до того, как это относится левый и правый пределы до обычных («двухсторонних») пределы. Доказательство — это доказательство, подобное те, которые я привел в разделах об определении лимитов и предельных теоремы; если вы учитесь на обычном курсе математического анализа для первого семестра, вы можете пропустить доказательство, если хотите.
Теорема. Предположим, определено на открытом интервале, содержащем c.
Затем определяется тогда и только тогда, когда и определены и равны.
В этом случае равно общему значению и .
Доказательство. Доказательство этой теоремы сводится к следующий факт об абсолютных значениях:
Причина в том, что
означает, что x находится внутри c, но не
равно с.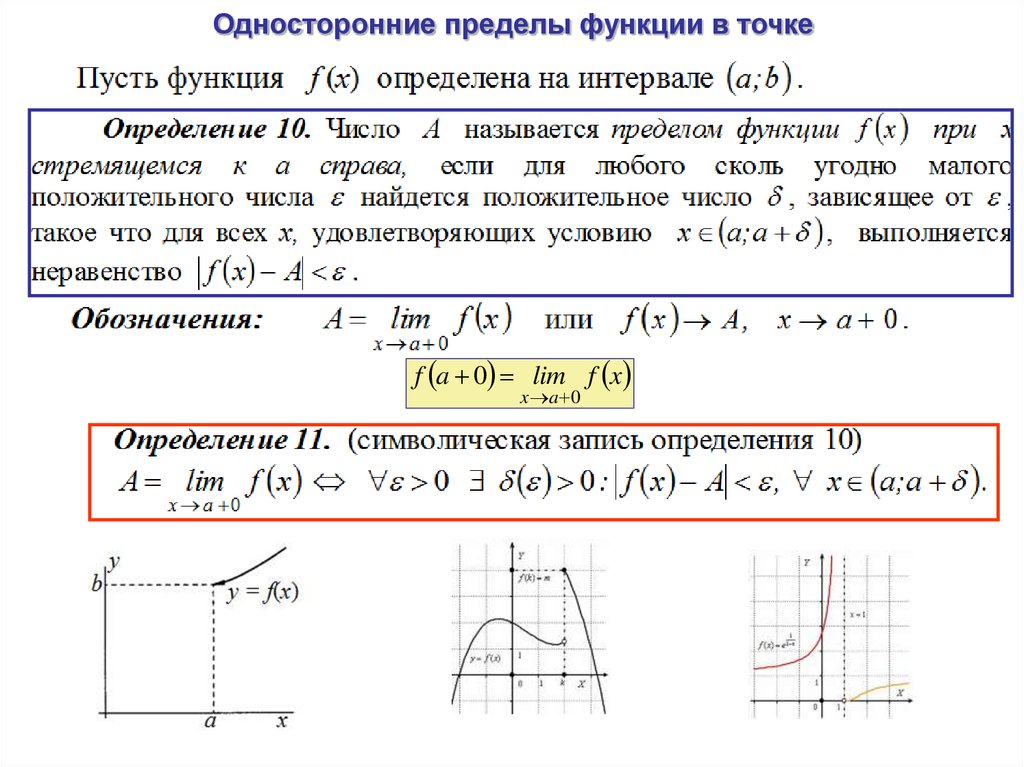
С другой стороны, означает, что x меньше с и находится в пределах с, и означает, что х больше с и в пределах с. Таким образом, если одно из этих двух утверждений верно, то верно и предыдущее утверждение, а если предыдущее утверждение истинно, то одно из них должно быть истинным.
Таким образом, предположим. я покажу это
Позволять . Так как существует число такой, что если , то .
Во-первых, если , то . Следовательно, .
Во-вторых, если , то . Следовательно, .
Далее я докажу обратное. Предположим, что
я покажу это
Позволять . Так как , есть число такое, что если , то .
Аналогично, поскольку существует такое число, что если затем .
Теперь пусть . Помните, что это означает, что это меньшее из и , так что это в как минимум такой же маленький, как любой.
Предполагать . Это означает, что либо
В первом случае у меня
Следовательно, .
Во втором случае у меня
Следовательно, .
Это доказывает, что .
На словах этот результат говорит о том, что обычный («двусторонний») предел определен тогда и только тогда, когда левый и правый пределы определены и равны, и в этом случае их общим значением является значение обычного лимита.
Пример. Вычислить
Является определенный?
Посмотрите на первый предел более внимательно. x приближается к 0 из правильно . Числа рядом с 0, но справа от него маленькие положительные числа: 0,01, например. Маленькие положительные числа дают положительные: , например. Если положительно, то , значит
(Обратите внимание, что вы не позволяете x равняться 0, поэтому , и отмена допустима.)
Поэтому,
Вот картинка:
Так как левый и правый пределы не совпадают,
неопределенный.
Пример. Предположим
Вычислить , и .
Для вычисления я использую часть определения для f, которая применяется к:
Точно так же для вычисления я использую ту часть определения f, которая относится к :
Поскольку левый и правый пределы равны, двусторонний предел определяется и .
Тот факт, что не входит в проблема.
Пример. Функция определяется
Для какого значения k определено?
Чтобы быть определенными, левый и правый пределы в 2 должны быть определены и равны. Вычислите их:
Установите левый и правый пределы равными и найдите k:
Пример. Рассмотрим функцию, график которой изображен ниже:
Вычислить .
Затем
Поскольку левые и правые пределы не совпадают,
Пример.
Рассмотрим функцию, график которой изображен ниже:
Вычислить
Зависят ли эти пределы от значения ?
Затем
Поэтому,
Значение не влияет на существование Лимит. На самом деле, предположим, я изменил функцию следующим образом:
Сейчас не определено, но
Левый и правый пределы могут привести к бесконечные пределы , поэтому я кратко обсужу идеи, прежде чем дать Некоторые примеры. Как обычно с теорией в этом курсе, точные определения приведены здесь для полноты и для тех, кто заинтересованы. Для большинства людей достаточно иметь хороший хватка как это выглядит графически когда предел бесконечен, и как бесконечные пределы могут возникнуть в предельных вычислениях.
Определение. (a) означает: Для каждого число , есть такое число , что если , то .
Иногда я буду писать » » вместо
» » для акцента, чтобы помочь отличить его
от » » в следующей части
определение.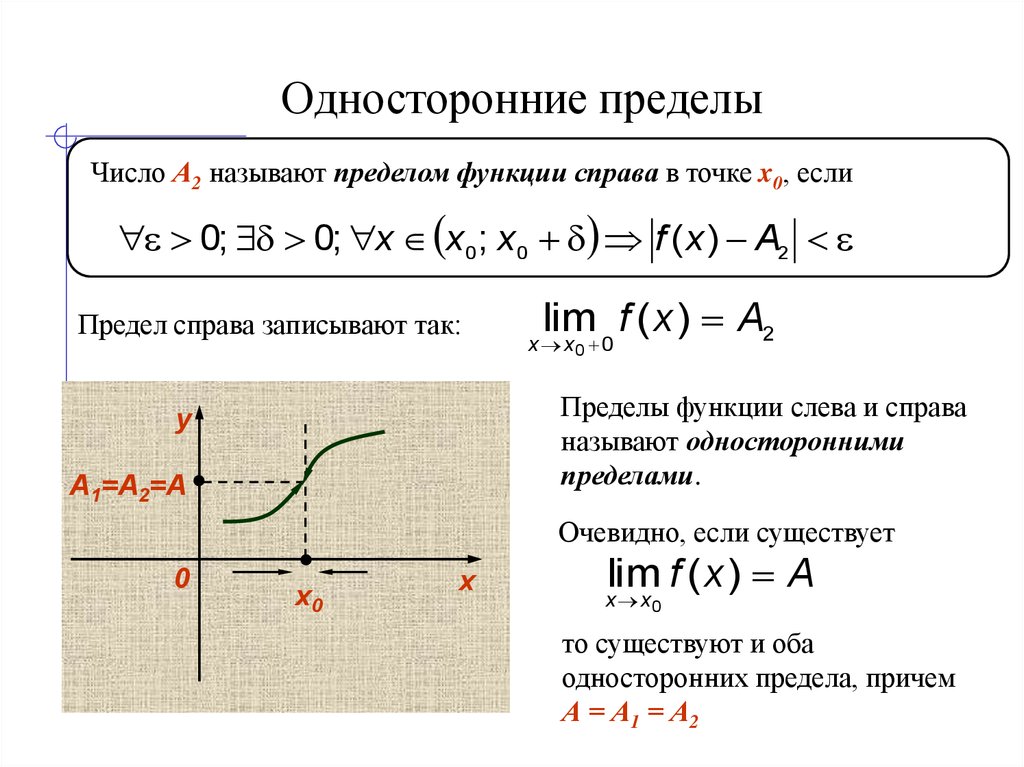
Определения правого и левого пределов:
(i) (Правые пределы) означает: Для каждого числа существует число такое, что если , то .
(ii) (Левые пределы) означает: Для каждого числа существует число такое, что если , то .
(б) означает: для каждого числа существует число , такое что если , то .
Определения правого и левого пределов:
(i) (Правые пределы) означает: Для каждого числа существует число такое, что если , то .
(ii) (Левые пределы) означает: Для каждого числа существует число такое, что если , то .
Таким образом, чтобы сказать приближается, когда x приближается к c (слева, справа или от обе стороны) означает, что по мере увеличения и положительный, без какой-либо верхней границы, когда x приближается к c.
Точно так же, чтобы сказать приближается, когда x приближается к c (слева, справа или от
обе стороны) означает, что по мере увеличения и
отрицательно, без какой-либо верхней границы, когда x приближается к c.
Во всех этих случаях не будет ошибкой сказать, что предел undefined, в том смысле, что это не номер . Но если ты можно сказать это или , это лучше, так как вы даете больше информации о происходящем.
Пример. Каждое изображение ниже показывает график функция . В каждом случае найти:
В),
Поскольку левый и правый пределы не совпадают, не определено.
В (б),
Пример. Вычислить .
Подключение дает. Лимит не определено . Но я могу сказать больше.
Попробуйте подставить число близкое к 1: Когда ,
Похоже, что получается больших и отрицательных . Фактически,
Чтобы понять, почему это так, вспомним, что x приближается к 1 от
правильно . Это означает, что он будет небольшим и
положительный. С другой стороны, .
Так как верх отрицателен, а низ положителен, результат должен
быть отрицательный .
Что касается размера, то у меня
Так как результат должен быть большой и отрицательный , это разумно, что это .
Другой способ увидеть это — нарисовать график рядом с . По мере продвижения к 1 справа график становится вниз к .
Ранее я отметил следующий факт: предположим,
Тогда двусторонний предел равен не определено . Как пример выше показывает, что с односторонними пределами дело обстоит иначе.
Если в этой ситуации имеет то же самое знак для всех значений x, достаточно близких к c и превышающих c, тогда правый предел будет или или . Конкретный знак зависит от знаков верха и низа дроби.
Точно так же, если имеет один и тот же знак для всех
x достаточно близко к c и меньше c, то левый предел
будет или или .
Опять же,
конкретный знак зависит от знаков верха и низа
доля.
Условие «одинакового знака» будет выполнено, например, если f и g полиномы — то есть, если является рациональной функцией. Это будет также удовлетворяться такими функциями, как
Пример. Вычислить .
Подключение дает. Так как это рациональная функция, то правый предел либо или ; Я должен определите, какой из двух. посмотрю верх и низ в отдельности.
Как , .
Что касается дна, так как x приближается к -3 от справа , Я считаю, что x больше, чем -3. Таким образом, , поэтому — положительно.
Поскольку приближается к отрицательному числу и приближается к положительному числу, частное равно отрицательный. Поэтому,
Я также могу увидеть это, если возьму число близкое к -3, но вправо of -3 — , например — и подключите его:
у меня большая отрицательное число , что говорит о том, что предел
должно быть .
Я мог также увидеть это, построив график функции, как в предыдущем пример.
В случае одностороннего ограничения и формы вы можете спросить: «Какой из этих методов лучший для определения значение?» Я чувствую, что для первого курса математического анализа все три являются приемлемыми .
Однако при подстановке чисел и построении графиков поддерживают для заключения, они на самом деле не дают доказательство . Графики могут быть обманчивы. И когда вы подключаете номер, откуда вы знаете, что номер, который вы выбрали, «типичный»? Первый способ — рассуждения о знаках с использованием неравенства — гораздо ближе к строгому доказательству результата.
Контактная информация
Домашняя страница Брюса Икенаги
Copyright 2018 Брюс Икенага
Исчисление I — Односторонние пределы
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т.
е. вы наверное на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 2.3: Односторонние пределы
В последних двух примерах в предыдущем разделе мы видели два несуществующих предела. Однако причина отсутствия каждого из пределов была разной для каждого из примеров.
Мы видели, что
\[\ mathop {\lim}\limits_{t \to 0} \,\,\cos \left({\frac{\pi}}{t}} \right)\]
не существовало, потому что функция не достигла единственного значения при приближении \(t\) к \(t = 0\). Чем ближе к \(t = 0\) мы двигались, тем сильнее колебалась функция, и для существования предела функция должна установиться на одном значении.
Однако мы видели, что
\[\ mathop {\ lim } \ limit_ {t \ to 0} H \ left ( t \ right) \ hspace {0,25 дюйма} {\ mbox {где}} \ hspace {0,25 дюйма} H \ left ( t \ справа) = \left\{ \begin{array}{ll}0 & {\mbox{if}}t < 0\\ 1 & {\mbox{if}}t \ge 0\end{массив} \right. \]
не существовало не потому, что функция не остановилась на одном числе, когда мы приблизились к \(t = 0\), а потому, что она остановилась на двух разных числах в зависимости от того, с какой стороны \(t = 0). \) мы были на.
В этом случае функция работала очень хорошо, в отличие от первой функции. Единственная проблема заключалась в том, что по мере приближения к \(t = 0\) функция приближалась к разным числам с каждой стороны. Мы хотели бы найти способ провести различие между этими двумя примерами. 9- }\) (обратите внимание на «-»), что означает, что мы будем рассматривать только \(x < a\).
Также обратите внимание, что, как и в случае с «нормальным» пределом (, т.
е. пределов из предыдущего раздела), нам все еще нужно, чтобы функция устанавливалась на одно число, чтобы предел существовал. Единственная разница на этот раз состоит в том, что функции нужно установить только одно число либо справа от \(x = a\), либо слева от \(x = a\) в зависимости от одностороннего предела мы имеем дело с. 9- }} H\left( t \right)\hspace{0.5in}{\rm{where}}\hspace{0.25in}H\left( t \right) = \left\{ \begin{array}{ll } 0 & {\ mbox {if}} t < 0 \\ 1 & {\ mbox {if}} t \ ge 0 \ end {array} \ right. \]
Показать решение
Чтобы напомнить нам, как выглядит эта функция, вот график.
Итак, мы можем видеть, что если мы останемся справа от \(t = 0\) ( т. е. \(t > 0\)) тогда функция движется к значению 1 по мере того, как мы приближаемся и ближе к \(t = 0\), но оставаясь правее. Поэтому мы можем сказать, что правый предел равен 9- }} \,\,\cos \left( {\frac{\pi }{t}} \right)\]
Показать решение
Из графика этой функции, показанного ниже,
мы можем видеть, что оба односторонних ограничения имеют ту же проблему, что и нормальный предел в предыдущем разделе.
Функция не ограничивается одним числом по обе стороны от \(t = 0\). Следовательно, ни левого, ни правого предела в этом случае не будет.
Таким образом, односторонние пределы не обязательно должны существовать, так же как не гарантируется существование нормальных пределов. 9- }} г\влево( х \вправо) = 4\]
Обратите внимание, что односторонние ограничения не заботятся о том, что происходит в точке, не больше, чем обычные ограничения. Их по-прежнему интересует только то, что происходит вокруг точки. Единственная реальная разница между односторонними пределами и нормальными пределами — это диапазон \(х\), на который мы обращаем внимание при определении значения предела.
Теперь давайте взглянем на первый и последний примеры в этом разделе, чтобы получить очень хороший факт о взаимосвязи между односторонними пределами и нормальными пределами. В последнем примере существовали односторонние пределы, а также нормальный предел, и все три имели значение 4. В первом примере оба односторонних предела существовали, но не имели одинакового значения, а нормальный предел имел значение 4.
не существует. 9- }} f\влево( х \вправо)\]
то нормального лимита не будет.
В этом должен быть смысл. Если бы нормальный предел существовал, то в силу этого должны были бы существовать и два односторонних предела, которые имели бы одно и то же значение в силу вышеуказанного факта. Итак, если два односторонних предела имеют разные значения (или даже не существуют), то нормальный предел просто не может существовать.
Давайте рассмотрим еще один пример, чтобы убедиться, что у нас есть все идеи о лимитах, которые мы рассмотрели в последних двух разделах. 9+ }} f\left( x \right) = 2\) Функция приближается к значению 2 по мере того, как \(x\) приближается к -4 справа.
d\(\mathop {\lim }\limits_{x \to — 4} f\left( x \right) = 2\) Мы можем сделать это одним из двух способов. Либо мы можем использовать этот факт здесь и заметить, что два односторонних предела одинаковы, и поэтому нормальный предел должен существовать и иметь то же значение, что и односторонние пределы, или просто получить ответ из графика.
Также помните, что предел может существовать в точке, даже если функция в этой точке не существует. 9+ }} f\left( x \right) = — 2\) Функция приближается к значению -2 по мере того, как \(x\) приближается к 1 справа. Помните, что предел НЕ заботится о том, что функция на самом деле делает в точке, он заботится только о том, что функция делает вокруг точки. В этом случае, всегда оставаясь справа от \(x = 1\), функция приближается к значению -2, поэтому предел равен -2. Ограничение не равно 4, так как это значение функции в точке, и снова предел не заботится об этом! 9+ }} f\left( x \right) = 5\) Функция приближается к значению 5 по мере того, как \(x\) приближается к 6 справа.
l\(\mathop {\lim }\limits_{x \to 6} f\left( x \right) = 5\) Опять же, мы можем использовать либо график, либо факт, чтобы получить это. Кроме того, еще раз помните, что пределу все равно, что происходит в точке, и поэтому предел может иметь другое значение, чем функция в точке. Имея дело с лимитами, мы всегда должны помнить, что лимиты просто не заботятся о том, что делает функция в данный момент.