Преобразование рациональных выражений: виды преобразований, примеры
Статья рассказывает о преобразовании рациональных выражений. Рассмотрим виды рациональных выражений, их преобразования, группировки, вынесения за скобки общего множителя. Научимся представлять дробные рациональные выражения в виде рациональных дробей.
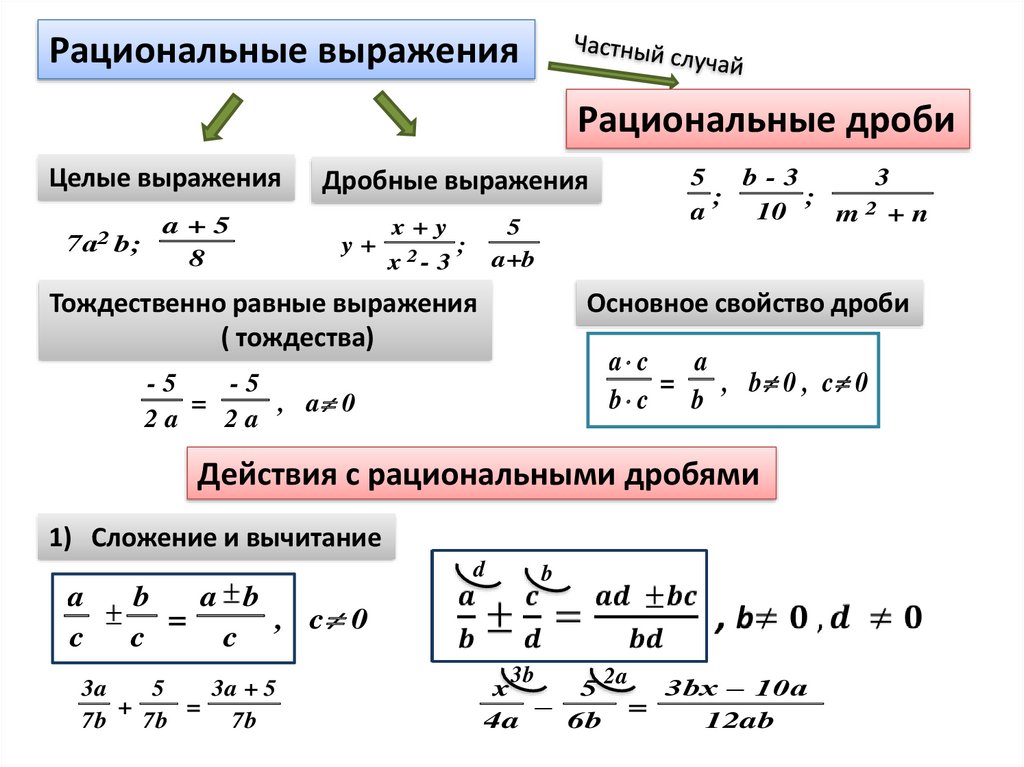
Определение и примеры рациональных выражений
Определение 1Выражения, которые составлены из чисел, переменных, скобок, степеней с действиями сложения, вычитания, умножения, деления с наличием черты дроби, называют рациональными выражениями.
Для примера имеем, что 5, 23·x-5, -3·a·b3-1c2+4a2+b21+a:(1-b), (x+1)·(y-2)x5-5·x·y·2-111·x3.
То есть это такие выражения, которые не имеют деления на выражения с переменными. Изучение рациональных выражений начинается с 8 класса, где их называют дробными рациональными выражениями. Особое внимание уделяют дробям в числителе, которые преобразовывают с помощью правил преобразования.
Это позволяет переходить к преобразованию рациональных дробей произвольного вида.
Такое выражение может быть рассмотрено как выражение с наличием рациональных дробей и целых выражений со знаками действий.
Основные виды преобразований рациональных выражений
Рациональные выражения используются для того, чтобы выполнять тождественные преобразования, группировки, приведение подобных, выполнение других действий с числами. Цель таких выражений – это упрощение.
Преобразовать рациональное выражение 3·xx·y-1-2·xx·y-1.
Решение
Видно, что такое рациональное выражение – это разность 3·xx·y-1 и 2·xx·y-1. Замечаем, что знаменатель у них идентичный. Это значит, что приведение подобных слагаемых примет вид
3·xx·y-1-2·xx·y-1=xx·y-1·3-2=xx·y-1
Ответ: 3·xx·y-1-2·xx·y-1=xx·y-1.
Пример 2Выполнить преобразование 2·x·y4·(-4)·x2:(3·x-x).
Решение
Первоначально выполняем действия в скобках 3·x−x=2·x. Данное выражение представляем в виде 2·x·y4·(-4)·x2:(3·x-x)=2·x·y4·(-4)·x2:2·x. Мы приходим к выражению, которое содержит действия с одной ступенью, то есть имеет сложение и вычитание.
Избавляемя от скобок при помощи применения свойства деления. Тогда получаем, что 2·x·y4·(-4)·x2:2·x=2·x·y4·(-4)·x2:2:x.
Группируем числовые множители с переменной x, после этого можно выполнять действия со степенями. Получаем, что
2·x·y4·(-4)·x2:2:x=(2·(-4):2)·(x·x2:x)·y4=-4·x2·y4
Ответ: 2·x·y4·(-4)·x2:(3·x-x)=-4·x2·y4.
Пример 3Преобразовать выражение вида x·(x+3)-(3·x+1)12·x·4+2.
Решение
Для начала преобразовываем числитель и знаменатель. Тогда получаем выражение вида (x·(x+3)-(3·x+1)):12·x·4+2, причем действия в скобках делают в первую очередь. В числителе выполняются действия и группируются множители. После чего получаем выражение вида x·(x+3)-(3·x+1)12·x·4+2=x2+3·x-3·x-112·4·x+2=x2-12·x+2.
Преобразуем в числителе формулу разности квадратов, тогда получаем, что
x2-12·x+2=(x-1)·(x+1)2·(x+1)=x-12
Ответ: x·(x+3)-(3·x+1)12·x·4+2=x-12.
Представление в виде рациональной дроби
Алгебраическая дробь чаще всего подвергается упрощению при решении.
Представить в виде рациональной дроби a+5a·(a-3)-a2-25a+3·1a2+5·a.
Решение
Данное выражение можно представить в виде a2-25a+3·1a2+5·a. Умножение выполняется в первую очередь по правилам.
Следует начать с умножения, тогда получим, что
a2-25a+3·1a2+5·a=a-5·(a+5)a+3·1a·(a+5)=a-5·(a+5)·1(a+3)·a·(a+5)=a-5(a+3)·a
Производим представление полученного результата с исходное. Получим, что
a+5a·(a-3)-a2-25a+3·1a2+5·a=a+5a·a-3-a-5a+3·a
Теперь выполняем вычитание:
a+5a·a-3-a-5a+3·a=a+5·a+3a·(a-3)·(a+3)-(a-5)·(a-3)(a+3)·a·(a-3)==a+5·a+3-(a-5)·(a-3)a·(a-3)·(a+3)=a2+3·a+5·a+15-(a2-3·a-5·a+15)a·(a-3)·(a+3)==16·aa·(a-3)·(a+3)=16a-3·(a+3)=16a2-9
После чего очевидно, что исходное выражение примет вид 16a2-9.
Ответ: a+5a·(a-3)-a2-25a+3·1a2+5·a=16a2-9.
Представить xx+1+12·x-11+x в виде рациональной дроби.
Решение
Заданное выражение записывается как дробь, в числителе которой имеется xx+1+1, а в знаменателе 2·x-11+x. Необходимо произвести преобразования xx+1+1. Для этого нужно выполнить сложение дроби и числа. Получаем, что xx+1+1=xx+1+11=xx+1+1·(x+1)1·(x+1)=xx+1+x+1x+1=x+x+1x+1=2·x+1x+1
Следует, что xx+1+12·x-11+x=2·x+1x+12·x-11+x
Получившаяся дробь может быть записана как 2·x+1x+1:2·x-11+x.
После деления придем к рациональной дроби вида
2·x+1x+1:2·x-11+x=2·x+1x+1·1+x2·x-1=2·x+1·(1+x)(x+1)·(2·x-1)=2·x+12·x-1
Можно решить это иначе.
Вместо деления на 2·x-11+x производим умножение на обратную ей 1+x2·x-1. Применим распределительное свойство и получаем, что
xx+1+12·x-11+x=xx+1+1:2·x-11+x=xx+1+1·1+x2·x-1==xx+1·1+x2·x-1+1·1+x2·x-1=x·1+x(x+1)·2·x-1+1+x2·x-1==x2·x-1+1+x2·x-1=x+1+x2·x-1=2·x+12·x-1
Ответ: xx+1+12·x-11+x=2·x+12·x-1.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Автор: Ирина Мальцевская
Преподаватель математики и информатики.
Преобразование рациональных выражений, урок в 8 классе,
Дата публикации: .
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Скачать:Преобразование рациональных выражений (PPTX)
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 8 класса
Пособие к учебнику Муравина Г.К.
Пособие к учебнику Макарычева Ю.Н.
Понятие о рациональном выражении
Понятие «рациональное выражение» схоже с понятием «рациональная дробь». Выражение также представляется в виде дроби. Только в числители у нас – не числа, а различного рода выражения. Чаще всего этого многочлены. Алгебраическая дробь – дробное выражение, состоящее из чисел и переменных.
При решении многих задач в младших классах после выполнения арифметических операций мы получали конкретные числовые значения, чаще всего дроби. Теперь после выполнения операций мы будем получать алгебраические дроби. Ребята, помните: чтобы получить правильный ответ, необходимо максимально упростить выражение, с которым вы работаете. Надо получить самую маленькую степень, какую возможно; одинаковые выражения в числители и знаменатели стоит сократить; с выражениями, которые можно свернуть, надо так и поступить. То есть после выполнения ряда действий мы должны получить максимально простую алгебраическую дробь.
Порядок действий с рациональными выражениями
Порядок действий при выполнении операций с рациональными выражениями такой же, как и при арифметических операциях. Сначала выполняются действия в скобках, потом – умножение и деление, возведение в степень и наконец – сложение и вычитание.
2}$.Преобразование выражений. Подробная теория (2020)
На данном уроке будут рассмотрены основные сведения о рациональных выражениях и их преобразованиях, а также примеры преобразования рациональных выражений. Данная тема как бы обобщает изученные нами до этого темы. Преобразования рациональных выражений подразумевают сложение, вычитание, умножение, деление, возведение в степень алгебраических дробей, сокращение, разложение на множители и т. п. В рамках урока мы рассмотрим, что такое рациональное выражение, а также разберём примеры на их преобразование.
Тема: Алгебраические дроби. Арифметические операции над алгебраическими дробями
Урок: Основные сведения о рациональных выражениях и их преобразованиях
Определение
Рациональное выражение — это выражение, состоящее из чисел, переменных, арифметических операций и операции возведения в степень.
Рассмотрим пример рационального выражения:
Частные случаи рациональных выражений:
1.
степень: ;
2. одночлен: ;
3. дробь: .
Преобразование рационального выражения — это упрощение рационального выражения. Порядок действий при преобразовании рациональных выражений: сначала идут действия в скобках, затем операции умножения (деления), а затем уже операции сложения (вычитания).
Рассмотрим несколько примеров на преобразование рациональных выражений.
Пример 1
Решение:
Решим данный пример по действиям. Первым выполняется действие в скобках.
Ответ:
Пример 2
Решение:
Ответ:
Пример 3
Решение:
Ответ: .
Примечание: возможно, у вас при виде данного примера возникла идея: сократить дробь перед тем, как приводить к общему знаменателю. Действительно, она является абсолютно правильной: сначала желательно максимально упростить выражение, а затем уже его преобразовывать.
Попробуем решить этот же пример вторым способом.
Как видим, ответ получился абсолютно аналогичным, а вот решение оказалось несколько более простым.
На данном уроке мы рассмотрели рациональные выражения и их преобразования , а также несколько конкретных примеров данных преобразований.
Список литературы
1. Башмаков М.И. Алгебра 8 класс. — М.: Просвещение, 2004.
2. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. — 5-е изд. — М.: Просвещение, 2010.
Статья рассказывает о преобразовании рациональных выражений. Рассмотрим виды рациональных выражений, их преобразования, группировки, вынесения за скобки общего множителя. Научимся представлять дробные рациональные выражения в виде рациональных дробей.
Определение и примеры рациональных выражений
Определение 1
Выражения, которые составлены из чисел, переменных, скобок, степеней с действиями сложения, вычитания, умножения, деления с наличием черты дроби, называют рациональными выражениями.
Для примера имеем, что 5 , 2 3 · x — 5 , — 3 · a · b 3 — 1 c 2 + 4 a 2 + b 2 1 + a: (1 — b) , (x + 1) · (y — 2) x 5 — 5 · x · y · 2 — 1 11 · x 3 .
То есть это такие выражения, которые не имеют деления на выражения с переменными. Изучение рациональных выражений начинается с 8 класса, где их называют дробными рациональными выражениями.Особое внимание уделяют дробям в числителе, которые преобразовывают с помощью правил преобразования.
Это позволяет переходить к преобразованию рациональных дробей произвольного вида. Такое выражение может быть рассмотрено как выражение с наличием рациональных дробей и целых выражений со знаками действий.
Основные виды преобразований рациональных выражений
Рациональные выражения используются для того, чтобы выполнять тождественные преобразования, группировки, приведение подобных, выполнение других действий с числами. Цель таких выражений – это упрощение.
Пример 1
Преобразовать рациональное выражение 3 · x x · y — 1 — 2 · x x · y — 1 .
Решение
Видно, что такое рациональное выражение – это разность 3 · x x · y — 1 и 2 · x x · y — 1 . Замечаем, что знаменатель у них идентичный. Это значит, что приведение подобных слагаемых примет вид
3 · x x · y — 1 — 2 · x x · y — 1 = x x · y — 1 · 3 — 2 = x x · y — 1
Ответ: 3 · x x · y — 1 — 2 · x x · y — 1 = x x · y — 1 .
Пример 2
Выполнить преобразование 2 · x · y 4 · (- 4) · x 2: (3 · x — x) .
Решение
Первоначально выполняем действия в скобках 3 · x − x = 2 · x . Данное выражение представляем в виде 2 · x · y 4 · (- 4) · x 2: (3 · x — x) = 2 · x · y 4 · (- 4) · x 2: 2 · x . Мы приходим к выражению, которое содержит действия с одной ступенью, то есть имеет сложение и вычитание.
Избавляемя от скобок при помощи применения свойства деления. Тогда получаем, что 2 · x · y 4 · (- 4) · x 2: 2 · x = 2 · x · y 4 · (- 4) · x 2: 2: x .
Группируем числовые множители с переменной x , после этого можно выполнять действия со степенями.
Получаем, что
2 · x · y 4 · (- 4) · x 2: 2: x = (2 · (- 4) : 2) · (x · x 2: x) · y 4 = — 4 · x 2 · y 4
Ответ: 2 · x · y 4 · (- 4) · x 2: (3 · x — x) = — 4 · x 2 · y 4 .
Пример 3
Преобразовать выражение вида x · (x + 3) — (3 · x + 1) 1 2 · x · 4 + 2 .
Решение
Для начала преобразовываем числитель и знаменатель. Тогда получаем выражение вида (x · (x + 3) — (3 · x + 1)) : 1 2 · x · 4 + 2 , причем действия в скобках делают в первую очередь. В числителе выполняются действия и группируются множители. После чего получаем выражение вида x · (x + 3) — (3 · x + 1) 1 2 · x · 4 + 2 = x 2 + 3 · x — 3 · x — 1 1 2 · 4 · x + 2 = x 2 — 1 2 · x + 2 .
Преобразуем в числителе формулу разности квадратов, тогда получаем, что
x 2 — 1 2 · x + 2 = (x — 1) · (x + 1) 2 · (x + 1) = x — 1 2
Ответ : x · (x + 3) — (3 · x + 1) 1 2 · x · 4 + 2 = x — 1 2 .
Представление в виде рациональной дроби
Алгебраическая дробь чаще всего подвергается упрощению при решении.
Каждое рациональное приводится к этому разными способами. Необходимо выполнить все необходимые действия с многочленами для того, чтобы рациональное выражение в итоге смогло дать рациональную дробь.
Пример 4
Представить в виде рациональной дроби a + 5 a · (a — 3) — a 2 — 25 a + 3 · 1 a 2 + 5 · a .
Решение
Данное выражение можно представить в виде a 2 — 25 a + 3 · 1 a 2 + 5 · a . Умножение выполняется в первую очередь по правилам.
Следует начать с умножения, тогда получим, что
a 2 — 25 a + 3 · 1 a 2 + 5 · a = a — 5 · (a + 5) a + 3 · 1 a · (a + 5) = a — 5 · (a + 5) · 1 (a + 3) · a · (a + 5) = a — 5 (a + 3) · a
Производим представление полученного результата с исходное. Получим, что
a + 5 a · (a — 3) — a 2 — 25 a + 3 · 1 a 2 + 5 · a = a + 5 a · a — 3 — a — 5 a + 3 · a
Теперь выполняем вычитание:
a + 5 a · a — 3 — a — 5 a + 3 · a = a + 5 · a + 3 a · (a — 3) · (a + 3) — (a — 5) · (a — 3) (a + 3) · a · (a — 3) = = a + 5 · a + 3 — (a — 5) · (a — 3) a · (a — 3) · (a + 3) = a 2 + 3 · a + 5 · a + 15 — (a 2 — 3 · a — 5 · a + 15) a · (a — 3) · (a + 3) = = 16 · a a · (a — 3) · (a + 3) = 16 a — 3 · (a + 3) = 16 a 2 — 9
После чего очевидно, что исходное выражение примет вид 16 a 2 — 9 .
Ответ: a + 5 a · (a — 3) — a 2 — 25 a + 3 · 1 a 2 + 5 · a = 16 a 2 — 9 .
Пример 5
Представить x x + 1 + 1 2 · x — 1 1 + x в виде рациональной дроби.
Решение
Заданное выражение записывается как дробь, в числителе которой имеется x x + 1 + 1 , а в знаменателе 2 · x — 1 1 + x . Необходимо произвести преобразования x x + 1 + 1 . Для этого нужно выполнить сложение дроби и числа. Получаем, что x x + 1 + 1 = x x + 1 + 1 1 = x x + 1 + 1 · (x + 1) 1 · (x + 1) = x x + 1 + x + 1 x + 1 = x + x + 1 x + 1 = 2 · x + 1 x + 1
Следует, что x x + 1 + 1 2 · x — 1 1 + x = 2 · x + 1 x + 1 2 · x — 1 1 + x
Получившаяся дробь может быть записана как 2 · x + 1 x + 1: 2 · x — 1 1 + x .
После деления придем к рациональной дроби вида
2 · x + 1 x + 1: 2 · x — 1 1 + x = 2 · x + 1 x + 1 · 1 + x 2 · x — 1 = 2 · x + 1 · (1 + x) (x + 1) · (2 · x — 1) = 2 · x + 1 2 · x — 1
Можно решить это иначе.
Вместо деления на 2 · x — 1 1 + x производим умножение на обратную ей 1 + x 2 · x — 1 .
Применим распределительное свойство и получаем, что
x x + 1 + 1 2 · x — 1 1 + x = x x + 1 + 1: 2 · x — 1 1 + x = x x + 1 + 1 · 1 + x 2 · x — 1 = = x x + 1 · 1 + x 2 · x — 1 + 1 · 1 + x 2 · x — 1 = x · 1 + x (x + 1) · 2 · x — 1 + 1 + x 2 · x — 1 = = x 2 · x — 1 + 1 + x 2 · x — 1 = x + 1 + x 2 · x — 1 = 2 · x + 1 2 · x — 1
Ответ: x x + 1 + 1 2 · x — 1 1 + x = 2 · x + 1 2 · x — 1 .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Эта статья посвящена преобразованию рациональных выражений , преимущественно дробно рациональных, – одному из ключевых вопросов курса алгебры для 8 классов. Сначала мы напомним, выражения какого вида называют рациональными. Дальше остановимся на проведении стандартных преобразований с рациональными выражениями, таких как группировка слагаемых, вынесение за скобки общих множителей, приведение подобных слагаемых и т.п. Наконец, научимся представлять дробные рациональные выражения в виде рациональных дробей.
Навигация по странице.
Определение и примеры рациональных выражений
Рациональные выражения являются одним из видов выражений , изучаемых на уроках алгебры в школе. Дадим определение.
Определение.
Выражения, составленные из чисел, переменных, скобок, степеней с целыми показателями, соединенных с помощью знаков арифметических действий +, −, · и:, где деление может быть обозначено чертой дроби, называются рациональными выражениями .
Приведем несколько примеров рациональных выражений: .
Рациональные выражения начинают целенаправленно изучаться в 7 классе. Причем в 7 классе познаются основы работы с так называемыми целыми рациональными выражениями , то есть, с рациональными выражениями, которые не содержат деления на выражения с переменными. Для этого последовательно изучаются одночлены и многочлены , а также принципы выполнения действий с ними. Эти все знания в итоге позволяют выполнять преобразование целых выражений .
В 8 классе переходят к изучению рациональных выражений, содержащих деление на выражение с переменными, которые называют дробными рациональными выражениями .
При этом особое внимание уделяется так называемым рациональным дробям (их также называют алгебраическими дробями ), то есть дробям, в числителе и знаменателе которых находятся многочлены. Это в итоге дает возможность выполнять преобразование рациональных дробей .
Полученные навыки позволяют перейти к преобразованию рациональных выражений произвольного вида. Это объясняется тем, что любое рациональное выражение можно рассматривать как выражение, составленное из рациональных дробей и целых выражений, соединенных знаками арифметических действий. А работать с целыми выражениями и алгебраическими дробями мы уже умеем.
Основные виды преобразований рациональных выражений
С рациональными выражениями можно проводить любые из основных тождественных преобразований , будь то группировка слагаемых или множителей, приведение подобных слагаемых, выполнение действий с числами и т.п. Обычно целью выполнения этих преобразований является упрощение рационального выражения .
Пример.
.
Решение.
Понятно, что данное рациональное выражение представляет собой разность двух выражений и , причем данные выражения являются подобными, так как имеют одинаковую буквенную часть. Таким образом, мы можем выполнить приведение подобных слагаемых :
Ответ:
.
Понятно, что при проведении преобразований с рациональными выражениями, как, впрочем, и с любыми другими выражениями, нужно оставаться в рамках принятого порядка выполнения действий .
Пример.
Выполните преобразование рационального выражения .
Решение.
Мы знаем, что сначала выполняются действия в скобках. Поэтому в первую очередь преобразуем выражение в скобках: 3·x−x=2·x .
Теперь можно подставить полученный результат в исходное рациональное выражение: . Так мы пришли к выражению, содержащему действия одной ступени – сложение и умножение.
Избавимся от скобок в конце выражения, применив свойство деления на произведение: .
Наконец, мы можем сгруппировать числовые множители и множители с переменной x, после чего выполнить соответствующие действия с числами и применить : .
На этом преобразование рационального выражения завершено, и в результате мы получили одночлен.
Ответ:
Пример.
Преобразуйте рациональное выражение .
Решение.
Сначала преобразуем числитель и знаменатель. Такой порядок преобразования дробей объясняется тем, что черта дроби по своей сути есть другое обозначение деления, и исходное рациональное выражение по сути есть частное вида , а действия в скобках выполняются в первую очередь.
Итак, в числителе выполняем действия с многочленами, сначала умножение, затем – вычитание, а в знаменателе сгруппируем числовые множители, и вычислим их произведение: .
Еще представим числитель и знаменатель полученной дроби в виде произведения: вдруг возможно сокращение алгебраической дроби . Для этого в числителе воспользуемся формулой разности квадратов , а в знаменателе вынесем двойку за скобки, имеем .
Ответ:
.
Итак, начальное знакомство с преобразованием рациональных выражений можно считать состоявшимся.
Переходим, так сказать, к самому сладкому.
Представление в виде рациональной дроби
Наиболее часто конечной целью преобразования выражений является упрощение их вида. В этом свете самым простым видом, к которому можно преобразовать дробно рациональное выражение, является рациональная (алгебраическая) дробь, и в частном случае многочлен, одночлен или число.
А любое ли рациональное выражение возможно представить в виде рациональной дроби? Ответ утвердительный. Поясним, почему это так.
Как мы уже сказали, всякое рациональное выражение можно рассматривать как многочлены и рациональные дроби, соединенные знаками плюс, минус, умножить и разделить. Все соответствующие действия с многочленами дают многочлен или рациональную дробь. В свою очередь любой многочлен можно преобразовать в алгебраическую дробь, записав его со знаменателем 1
. А сложение, вычитание, умножение и деление рациональных дробей в результате дают новую рациональную дробь. Следовательно, выполнив все действия с многочленами и рациональными дробями в рациональном выражении, мы получим рациональную дробь.
Пример.
Представьте в виде рациональной дроби выражение .
Решение.
Исходное рациональное выражение представляет собой разность дроби и произведения дробей вида . Согласно порядку выполнения действий мы сначала должны выполнить умножение, а уже потом – сложение.
Начинаем с умножения алгебраических дробей :
Подставляем полученный результат в исходное рациональное выражение: .
Мы пришли к вычитанию алгебраических дробей с разными знаменателями:
Итак, выполнив действия с рациональными дробями, составляющими исходное рациональное выражение, мы его представили в виде рациональной дроби .
Ответ:
.
Для закрепления материала разберем решение еще одного примера.
Пример.
Представьте рациональное выражение в виде рациональной дроби.
Из курса алгебры школьной программы переходим к конкретике. В этой статье мы подробно изучим особый вид рациональных выражений – рациональные дроби , а также разберем, какие характерные тождественные преобразования рациональных дробей имеют место.
Сразу отметим, что рациональные дроби в том смысле, в котором мы их определим ниже, в некоторых учебниках алгебры называют алгебраическими дробями. То есть, в этой статье мы под рациональными и алгебраическими дробями будем понимать одно и то же.
По обыкновению начнем с определения и примеров. Дальше поговорим про приведение рациональной дроби к новому знаменателю и о перемене знаков у членов дроби. После этого разберем, как выполняется сокращение дробей. Наконец, остановимся на представлении рациональной дроби в виде суммы нескольких дробей. Всю информацию будем снабжать примерами с подробными описаниями решений.
Навигация по странице.
Определение и примеры рациональных дробей
Рациональные дроби изучаются на уроках алгебры в 8 классе. Мы будем использовать определение рациональной дроби, которое дается в учебнике алгебры для 8 классов Ю. Н. Макарычева и др.
В данном определении не уточняется, должны ли многочлены в числителе и знаменателе рациональной дроби быть многочленами стандартного вида или нет.
Поэтому, будем считать, что в записях рациональных дробей могут содержаться как многочлены стандартного вида, так и не стандартного.
Приведем несколько примеров рациональных дробей . Так , x/8 и — рациональные дроби. А дроби и не подходят под озвученное определение рациональной дроби, так как в первой из них в числителе стоит не многочлен, а во второй и в числителе и в знаменателе находятся выражения, не являющиеся многочленами.
Преобразование числителя и знаменателя рациональной дроби
Числитель и знаменатель любой дроби представляют собой самодостаточные математические выражения, в случае рациональных дробей – это многочлены, в частном случае – одночлены и числа. Поэтому, с числителем и знаменателем рациональной дроби, как и с любым выражением, можно проводить тождественные преобразования. Иными словами, выражение в числителе рациональной дроби можно заменять тождественно равным ему выражением, как и знаменатель.
В числителе и знаменателе рациональной дроби можно выполнять тождественные преобразования .
Например, в числителе можно провести группировку и приведение подобных слагаемых, а в знаменателе – произведение нескольких чисел заменить его значением. А так как числитель и знаменатель рациональной дроби есть многочлены, то с ними можно выполнять и характерные для многочленов преобразования, например, приведение к стандартному виду или представление в виде произведения.
Для наглядности рассмотрим решения нескольких примеров.
Пример.
Преобразуйте рациональную дробь так, чтобы в числителе оказался многочлен стандартного вида, а в знаменателе – произведение многочленов.
Решение.
Приведение рациональных дробей к новому знаменателю в основном применяется при сложении и вычитании рациональных дробей .
Изменение знаков перед дробью, а также в ее числителе и знаменателе
Основное свойство дроби можно использовать для смены знаков у членов дроби. Действительно, умножение числителя и знаменателя рациональной дроби на -1
равносильно смене их знаков, а в результате получится дробь, тождественно равная данной.
К такому преобразованию приходится достаточно часто обращаться при работе с рациональными дробями.
Таким образом, если одновременно изменить знаки у числителя и знаменателя дроби, то получится дробь, равная исходной. Этому утверждению отвечает равенство .
Приведем пример. Рациональную дробь можно заменить тождественно равной ей дробью с измененными знаками числителя и знаменателя вида .
С дробями можно провести еще одно тождественное преобразование, при котором меняется знак либо в числителе, либо в знаменателе. Озвучим соответствующее правило. Если заменить знак дроби вместе со знаком числителя или знаменателя, то получится дробь, тождественно равная исходной. Записанному утверждению соответствуют равенства и .
Доказать эти равенства не составляет труда. В основе доказательства лежат свойства умножения чисел. Докажем первое из них: . С помощью аналогичных преобразований доказывается и равенство .
Например, дробь можно заменить выражением или .
В заключение этого пункта приведем еще два полезных равенства и .
То есть, если изменить знак только у числителя или только у знаменателя, то дробь изменит свой знак. Например, и .
Рассмотренные преобразования, позволяющие изменять знак у членов дроби, часто применяются при преобразовании дробно рациональных выражений.
Сокращение рациональных дробей
В основе следующего преобразования рациональных дробей, имеющего название сокращение рациональных дробей, лежит все тоже основное свойство дроби. Этому преобразованию соответствует равенство , где a , b и c – некоторые многочлены, причем b и c — ненулевые.
Из приведенного равенства становится понятно, что сокращение рациональной дроби подразумевает избавление от общего множителя в ее числителе и знаменателе.
Пример.
Сократите рациональную дробь .
Решение.
Сразу виден общий множитель 2
, выполним сокращение на него (при записи общие множители, на которые сокращают, удобно зачеркивать). Имеем . Так как x 2 =x·x
и y 7 =y 3 ·y 4
(при необходимости смотрите ), то понятно, что x
является общим множителем числителя и знаменателя полученной дроби, как и y 3
.
Проведем сокращение на эти множители: . На этом сокращение завершено.
Выше мы выполняли сокращение рациональной дроби последовательно. А можно было выполнить сокращение в один шаг, сразу сократив дробь на 2·x·y 3 . В этом случае решение выглядело бы так: .
Ответ:
.
При сокращении рациональных дробей основная проблема заключается в том, что общий множитель числителя и знаменателя далеко не всегда виден. Более того, он не всегда существует. Для того, чтобы найти общий множитель или убедиться в его отсутствии нужно числитель и знаменатель рациональной дроби разложить на множители. Если общего множителя нет, то исходная рациональная дробь не нуждается в сокращении, в противном случае – проводится сокращение.
В процессе сокращения рациональных дробей могут возникать различные нюансы. Основные тонкости на примерах и в деталях разобраны в статье сокращение алгебраических дробей .
Завершая разговор о сокращении рациональных дробей, отметим, что это преобразование является тождественным, а основная сложность в его проведении заключается в разложении на множители многочленов в числителе и знаменателе.
Представление рациональной дроби в виде суммы дробей
Достаточно специфическим, но в некоторых случаях очень полезным, оказывается преобразование рациональной дроби, заключающееся в ее представлении в виде суммы нескольких дробей, либо сумме целого выражения и дроби.
Рациональную дробь, в числителе которой находится многочлен, представляющий собой сумму нескольких одночленов, всегда можно записать как сумму дробей с одинаковыми знаменателями, в числителях которых находятся соответствующие одночлены. Например, . Такое представление объясняется правилом сложения и вычитания алгебраических дробей с одинаковыми знаменателями .
Вообще, любую рациональную дробь можно представить в виде суммы дробей множеством различных способов. Например, дробь a/b
можно представить как сумму двух дробей – произвольной дроби c/d
и дроби, равной разности дробей a/b
и c/d
. Это утверждение справедливо, так как имеет место равенство . К примеру, рациональную дробь можно представить в виде суммы дробей различными способами:
Представим исходную дробь в виде суммы целого выражения и дроби. Выполнив деление числителя на знаменатель столбиком, мы получим равенство . Значение выражение n 3 +4
при любом целом n
является целым числом. А значение дроби является целым числом тогда и только тогда, когда ее знаменатель равен 1
, −1
, 3
или −3
. Этим значениям отвечают значения n=3
, n=1
, n=5
и n=−1
соответственно.
Ответ:
−1 , 1 , 3 , 5 .
Список литературы.
- Алгебра: учеб. для 8 кл. общеобразоват. учреждений / [Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова]; под ред. С. А. Теляковского. — 16-е изд. — М. : Просвещение, 2008. — 271 с. : ил. — ISBN 978-5-09-019243-9.
- Мордкович А. Г. Алгебра. 7 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович. — 13-е изд., испр. — М.: Мнемозина, 2009. — 160 с.: ил. ISBN 978-5-346-01198-9.
- Мордкович А. Г. Алгебра. 8 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович. — 11-е изд., стер.
— М.: Мнемозина, 2009. — 215 с.: ил. ISBN 978-5-346-01155-2. - Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
— М.: Мнемозина, 2009. — 215 с.: ил. ISBN 978-5-346-01155-2.Преобразование рациональных выражений
Рациональные выражения и дроби — краеугольный пункт всего курса алгебры. Те, кто научатся работать с такими выражениями, упрощать их и раскладывать на множители, по сути смогут решить любую задачу, поскольку преобразование выражений — неотъемлемая часть любого серьёзного уравнения, неравенства и даже текстовой задачи.
В этом видеоуроке мы посмотрим, как грамотно применять формулы сокращённого умножения для упрощения рациональных выражений и дробей. Научимся видеть эти формулы там, где, на первый взгляд, ничего нет. Заодно повторим такой нехитрый приём, как разложение квадратного трёхчлена на множители через дискриминант.
{2}} \right)$ — разность кубов.Еще хотел бы отметить, что наша школьная система образования устроена таким образом, что именно с изучением этой темы, т.е. рациональных выражений, а также корней, модулей у всех учеников возникает одна и та же проблема, которую я сейчас объясню.
Дело в том, что в самом начале изучения формул сокращенного умножения и, соответственно, действий по сокращению дробей (это где-то 8 класс) учителя говорят что-то следующее: «Если вам что-то непонятно, то вы не переживайте, мы к этой теме еще вернемся неоднократно, в старших классах так точно. Мы это еще разберем». Ну а затем на рубеже 9-10 класса те же самые учителя объясняют тем же самым ученикам, которые так и не знают, как решать рациональные дроби, примерно следующее: «А где вы были предыдущие два года? Это же изучалось на алгебре в 8 классе! Чего тут может быть непонятного? Это же так очевидно!».
Однако обычным ученикам от таких объяснений нисколько не легче: у них как была каша в голове, так и осталась, поэтому прямо сейчас мы разберем два простых примера, на основании которых и посмотрим, каким образом в настоящих задачах выделять эти выражения, которые приведут нас к формулам сокращенного умножения и как потом применять это для преобразования сложных рациональных выражений.
{2}}\]
\[\sqrt{D}=7y\]
\[{{x}_{1}}=\frac{-5y+7y}{2}=y\]
\[{{x}_{2}}=\frac{-5y-7y}{2}=\frac{-12y}{2}=-6y\]
Запишем разложение нашей квадратной конструкции:
\[\left( x-y \right)\left( x+6y \right)\]
Итого если мы вернемся к исходному выражению и перепишем его с учетом изменений, то получим следующее:
\[\frac{8}{\left( x-y \right)\left( x+6y \right)}\]
Что нам дает такая запись? Ничего, потому что его не сократить, оно ни на что не умножается и не делится. Однако как только эта дробь окажется составной частью более сложного выражения, подобное разложение окажется кстати. Поэтому как только вы видите квадратный трехчлен (неважно, отягощен он дополнительными параметрами или нет), всегда старайтесь разложить его на множители.
Нюансы решения
Запомните основные правила преобразования рациональных выражений:
- Все знаменатели и числители необходимо раскладывать на множители либо через формулы сокращенного умножения, либо через дискриминант. {2}} \right)}{\left( 2x-1 \right)\left( 2x+1 \right)}=\]
\[=\frac{3\cdot \left( -1 \right)}{2\cdot \left( x-2 \right)\cdot \left( -1 \right)}=\frac{3}{2\left( x-2 \right)}\]
Ответ: $\frac{3}{2\left( x-2 \right)}$.
Нюансы решения
Итак, чему мы только что научились:
- Далеко не каждый квадратный трехчлен раскладывается на множители, в частности, это относится к неполному квадрату суммы или разности, которые очень часто встречаются как части кубов суммы или разности.
- Константы, т.е. обычные числа, не имеющие при себе переменных, также могут выступать активными элементами в процессе разложения. Во-первых, их можно выносить за скобки, во-вторых, сами константы могут быть представимы в виде степеней.
- Очень часто после разложения всех элементов на множители возникают противоположные конструкции. Сокращать эти дроби нужно крайне аккуратно, потому что при из зачеркивании либо сверху, либо снизу возникает дополнительный множитель $-1$ — это как раз и есть следствие того, что они противоположны. {2}}}=\]
\[=\frac{\left( 3a-4b \right)\left( b+2 \right)}{\left( b-2 \right)}\]
Ответ: $\frac{\left( 3a-4b \right)\left( b+2 \right)}{\left( b-2 \right)}$.
Нюансы решения
Как мы еще раз убедились, неполные квадраты суммы либо неполные квадраты разности, которые часто встречаются в реальных рациональных выражениях, однако не стоит их пугаться, потому что после преобразования каждого элемента они практически всегда сокращаются. Кроме того, ни в коем случае не стоит бояться больших конструкций в итогом ответе — вполне возможно, что это не ваша ошибка (особенно, если все разложено на множители), а это автор задумал такой ответ.
В заключение хотелось бы разобрать еще один сложных пример, который уже не относится напрямую к рациональным дробям, однако он содержит все то, что ждет вас на настоящих контрольных и экзаменах, а именно: разложение на множители, приведение к общему знаменателю, сокращение подобных слагаемых. Вот именно этим мы сейчас и займемся.
Решение сложной задачи на упрощение и преобразование рациональных выражений
\[\left( \frac{x}{{{x}^{2}}+2x+4}+\frac{{{x}^{2}}+8}{{{x}^{3}}-8}-\frac{1}{x-2} \right)\cdot \left( \frac{{{x}^{2}}}{{{x}^{2}}-4}-\frac{2}{2-x} \right)\]
Сначала рассмотрим и раскроем первую скобку: в ней мы видим три отдельных дроби с разными знаменателями поэтому первое, что нам необходимо сделать — это привести все три дроби к общему знаменателю, а для этого каждый из них следует разложить на множители:
\[{{x}^{2}}+2x+4={{x}^{2}}+2\cdot x+{{2}^{2}}\]
\[{{x}^{2}}-8={{x}^{3}}-{{2}^{2}}=\left( x-2 \right)\left( {{x}^{2}}+2x+{{2}^{2}} \right)\]
Перепишем всю нашу конструкцию следующим образом:
\[\frac{x}{{{x}^{2}}+2x+{{2}^{2}}}+\frac{{{x}^{2}}+8}{\left( x-2 \right)\left( {{x}^{2}}+2x+{{2}^{2}} \right)}-\frac{1}{x-2}=\]
\[=\frac{x\left( x-2 \right)+{{x}^{3}}+8-\left( {{x}^{2}}+2x+{{2}^{2}} \right)}{\left( x-2 \right)\left( {{x}^{2}}+2x+{{2}^{2}} \right)}=\]
\[=\frac{{{x}^{2}}-2x+{{x}^{2}}+8-{{x}^{2}}-2x-4}{\left( x-2 \right)\left( {{x}^{2}}+2x+{{2}^{2}} \right)}=\frac{{{x}^{2}}-4x-4}{\left( x-2 \right)\left( {{x}^{2}}+2x+{{2}^{2}} \right)}=\]
\[=\frac{{{\left( x-2 \right)}^{2}}}{\left( x-2 \right)\left( {{x}^{2}}+2x+{{2}^{2}} \right)}=\frac{x-2}{{{x}^{2}}+2x+4}\]
Это результат вычислений из первой скобки.
{2}}+2x+4}{\left( x-2 \right)\left( x+2 \right)}=\frac{1}{x+2}\]Ответ: $\frac{1}{x+2}$.
Нюансы решения
Как видите, ответ получился вполне вменяемый. Однако обратите внимание: очень часто при таких масштабных вычислениях, когда единственная переменная оказывается лишь в знаменателе, ученики забывают, что это знаменатель и он должен стоял внизу дроби и пишут это выражение в числитель — это грубейшая ошибка.
Кроме того, хотел бы обратить ваше отдельное внимание на то, как оформляются такие задачи. В любых сложных вычислениях все шаги выполняются по действиям: сначала отдельно считаем первую скобку, потом отдельно вторую и лишь в конце мы объединяем все части и считаем результат. Таким образом мы страхуем себя от глупых ошибок, аккуратно записываем все выкладки и при этом нисколько не тратим лишнего времени, как это может показаться на первый взгляд.
До новых встреч!
Смотрите также:
- Как выполнять сокращение рациональных дробей без ошибок? Простой алгоритм на примере пяти различных задач.
- Дробно-рациональные выражения
- Тест к уроку «Десятичные дроби» (2 вариант)
- Периодические десятичные дроби
- Быстрое возведение чисел в квадрат без калькулятора
- ЕГЭ 2022, задание 6. Касательная и уравнение с параметром
Преобразование рациональных выражений в математике с примерами решения и образцами выполнения
Оглавление:
Преобразование рационального выражения – это упрощение рационального выражения. Порядок действий при преобразовании рациональных выражений: сначала идут действия в скобках, затем операции умножения (деления), а затем уже операции сложения (вычитания).
Тождественные преобразования целых выражений
Степень с натуральным показателемЕсли а— действительное число, а n — натуральное число, отличное от единицы, то произведение n сомножителей, каждый из которых равен а, называется n-й степенью числа а и обозначается если то полагают Число а называется основанием степени, число n — показателем степени.
Например,
Свойства степени с натуральным показателем
Например,
Например,
Например,
Например,
Например,
Докажем эти свойства.
из свойства вытекает, что значит,
Операции над одночленамиОдночленом называется такое выражение, которое содержит числа, переменные, степени чисел и переменных и их произведения.
Например, одночленами являются выражения Приведем также примеры выражении, не являющихся одночленами:
Основные законы алгебры и свойства степени с натуральным показателем позволяют нам привести одночлен к стандартному виду, т. е. к такому виду, когда одночлен имеет единственный числовой множитель, стоящий на первом месте (коэффициент), а каждое произведение одинаковых переменных в нем представлено степенью. Приведем для примера к стандартному виду данные выше одночлены. Рассмотрим первый одночлен. Воспользовавшись переместительным и сочетательным законами умножения, получим Так как то в итоге получаем Аналогично,
Пусть даны два одночлена.
Если поставить между ними знак умножения, то получится одночлен, называемый произведением исходных одночленов. При возведении одночлена в натуральную степень также получается одночлен. Результат обычно приводят к стандартному виду.Примеры:
Выполнить умножение одночленов и
Решение. Имеем:
2.Возвести одночлен в четвертую степень.
Решение:
Одночлены, приведенные к стандартному виду, называются подобными, если они отличаются только коэффициентами либо совсем не отличаются.
Подобные одночлены можно складывать и вычитать, в результате чего снова получается одночлен, подобный исходным. Сложение и вычитание подобных одночленов, называется приведением подобных членов.
Пример:
Выполнить сложение одночленов
Решение:
Воспользовавшись распределительным законом, получим:
Понятие тождественного преобразования выраженияСравним значения выражений при различных значениях х.
При получим и Числа 0 и 3 называются соответственными значениями выраженийНайдем соответственные значения выражений и при и при Результат запишем в виде таблицы
Как видно из таблицы, соответственные значения могут иногда совпадать.
Два выражения, зависящие от одних и тех же переменных, называются тождественно равными, если все их соответственные значения равны. Так, тождественно равными будут выражения
Равенство, в котором левая и правая части—тождественно равные выражения, называется тождеством. Тождествами будут, во-первых, все равенства, выражающие основные законы алгебры:
Тождествами являются и равенства
Верные числовые равенства также называются тождествами.
Замена одного выражения другим, тождественно равным ему, называется тождественным преобразованием выражения. Мы уже имели некоторые примеры тождественных преобразований. Так, приведение одночлена к стандартному виду есть тождественное преобразование, выполняемое на основании определения степени или свойств степени с натуральным показателем и перемес-тительного и сочетательного законов умножения.
Многочлены. Приведение многочлена к стандартному виду Тождественными преобразованиями являются также умножение одночленов и их возведение в натуральную степень, приведение подобных членов. Другие примеры тождественных преобразований выражений будут рассмотрены ниже.Многочленом называется сумма одночленов. Если все члены многочлена записать в стандартном виде и выполнить приведение подобных членов, то получится многочлен стандартного вида. Например, выражение является многочленом. Для приведения его к стандартному виду нужно сначала привести к стандартному виду члены многочлена: а затем привести подобные члены; тогда получим
Одночлены, многочлены, а также их сумма, разность, произведение и степень составляют множество целых алгебраических выражений.
Основная задача тождественных преобразований целых выражений состоит в приведении их к стандартному виду многочлена (или одночлена). Такое преобразование всегда выполнимо.
Примеры:
Упростить (привести к стандартному виду) многочлены:
Решение:
Если перед скобками стоит знак «плюс», то скобки можно опустить, сохранив знаки всех слагаемых, заключенных в скобки.
Воспользовавшись этим правилом раскрытия скобок, получими далее
Решение:
Если перед скобками стоит знак «минус», то скобки можно опустить, изменив знаки всех слагаемых, заключенных в скобки. Воспользовавшись этим правилом раскрытия скобок, получим
Решение:
Воспользовавшись распределительным законом
получим
Таким образом, произведение одночлена на многочлен равно сумме произведений этого одночлена на каждый член многочлена.
Решение:
Обозначим выражение буквой x тогда выражение примет вид Раскрыв скобки, получим тождество
или (так как
Снова раскрывая скобки, получим окончательно:
Таким образом, произведение двух многочленов равно сумме произведений каждого члена одного многочлена на каждый член другого.
Разложение многочлена на множителиПредставление многочлена в виде произведения ряда многочленов, среди которых могут быть и одночлены, называется разложением многочлена на множители.
Рассмотрим некоторые наиболее употребительные методы разложения многочленов на множители.Вынесение общего множителя за скобки. Рассмотрим пример. В многочлене члены имеют общий множитель Чтобы разложить этот многочлен на множители, представим каждый член многочлена в виде произведения двух множителей, один из которых а затем применим распределительный закон:
В рассмотренном примере мы вынесли за скобки но можно было бы выполнить разложение на множители, вынося за скобки и т. д. Например, если вынести за скобки получим:
Обычно, если все коэффициенты многочлена целые числа, выносят за скобки множитель с коэффициентом, равным наибольшему общему делителю модуля всех коэффициентов многочлена. Одинаковые переменные, входящие во все члены, выносят с наименьшим показателем, который они имеют в данном многочлене.
Примеры:
Метод группировки. Пусть дан многочлен
Представим его в виде суммы двух многочленов:
Вынося в первом двучлене за скобки а во втором получим
В результате проделанной группировки нам удалось представить многочлен в виде суммы двух слагаемых, имеющих общий множитель Вынося этот общий множитель за скобки, получаем
Примеры:
Применение тождеств сокращенного умножения.
В некоторых случаях приведение многочлена к стандартному виду, а также разложение на множители производится с помощью тождеств сокращенного умножения.А. Преобразуем выражение в многочлен стандартного вида. Имеем
Таким образом, мы получили следующее тождество:
т. е. произведение суммы и разности двух выражений равно разности квадратов этих выражений.
Примеры:
Упростить, т. е. преобразовать выражение в многочлен стандартного вида:
Поменяем в тождестве (1) левую и правую части местами:
В таком виде это тождество удобно применять для разложения на множители разности квадратов двух выражений.
Примеры:
Разложить на множители:
Б. Преобразуем теперь в многочлен стандартного вида выражение Имеем
Таким образом, получено тождество
т. е. квадрат двучлена равен сумме трех выражений: квадрата первого члена, удвоенного произведения первого члена на второй и квадрата второго члена.
Поменяв в тождестве (2) b на -b получимПримеры:
Упростить выражения:
Решение:
Конечно, это выражение можно преобразовать к стандартному виду многочлена, представив его в виде и раскрыв скобки по правилу умножения многочленов. Однако использование тождества (2) позволяет выполнить преобразования быстрее:
Решение:
Можно было бы возвести в квадрат каждое слагаемое, а затем результаты перемножить. Однако рациональнее сделать так:
2.Доказать тождества:
Решение:
Выполним преобразования левой части тождества:
Так как в результате мы получили правую часть тождества, то тождество доказано;
Решение:
Поменяем в тождестве (2) правую и левую части местами:
В таком виде тождество удобно применять для разложения на множители.
Примеры:
Разложить на множители:
Заметим, что заданное выражение можно разложить на множители и другим способом:
Замечание:
Мы показали, что В таком случае говорят, что многочлен делится на (тогда в частном получается или на (в частном получается
В.
Рассмотрим теперь выражение и преобразуем его в многочлен стандартного вида:Таким образом,
т. е. куб двучлена равен сумме четырех выражений: куба первого члена, утроенного произведения квадрата первого члена на второй, утроенного произведения первого члена на квадрат второго и куба второго члена.
Поменяв в равенстве (3) b на -b, получим
Примеры:
Преобразовать выражения в многочлен стандартного вида:
Г. Преобразуем теперь в многочлен стандартного вида выражение Имеем
Таким образом, получено тождество
Поменяв в тождестве (4) левую и правую части, получим формулу для разложения на множители суммы кубов:
Поменяв в тождестве (4а) b на -b, получим
Примеры:
Упростить выражение
Решение:
Разложить на множители
Решение:
Тождественные преобразования дробных выражений
Числовые выражения, а также выражения с переменными, в которых используются операции сложения, вычитания, умножения, деления и возведения в натуральную степень, называются рациональными.
Если рациональное выражение не содержит операции деления на выражение с переменными, то оно называется целым. Если же при составлении рационального выражения используется операция деления на выражение с переменными, то это рациональное выражение называется дробным.Примеры дробных выражений:
Выражение не является дробным, хотя в записи выражения и используется черта дроби. Это—целое выражение, которое можно привести к стандартному виду многочлена
Во множестве рациональных выражений выделим еще одно подмножество выражений—подмножество дробей. Дробь — это выражение вида где буквами обозначены числовые выражения или выражения с переменными; а—числитель дроби, b — знаменатель. Согласно этому определению, из рассмотренных выше примеров дробями будут следующие:
Дробное выражение не является дробью.
Обращаем внимание читателя на следующее обстоятельство: не всякая дробь является дробным выражением. Так, рассмотренное выше выражение является дробью, но не является дробным выражением (нет деления на выражение с переменными).
Одна из основных задач тождественных преобразований дробных выражений состоит в том, чтобы данное выражение представить в виде дроби, числитель и знаменатель которой—целые выражения. Чтобы выделить такие дроби из множества всех дробей, условимся называть их алгебраическими. Такое преобразование, как мы увидим, всегда выполнимо.
Областью определения выражения с одной переменной называется множество значений переменной, при которых это выражение имеет смысл. Так, область определения выражения (обозначим ее Y) состоит из всех чисел, за исключением —2 и 2. Это можно записать так:
Это множество можно изобразить графически в виде числовой прямой с двумя проколотыми точками (рис. 20).
Если дано выражение с двумя переменными х и у, то областью его определения будет множество числовых пар вида при которых выражение имеет смысл. Так, выражение определено на множестве всех пар за исключением пар вида Это—множество точек координатной плоскости за исключением точек, лежащих на осях
Целые выражения с переменными определены при любых значениях переменных.
Основное свойство дроби Если дана алгебраическая дробь, причем знаменатель содержит переменные, то чтобы найти область определения дроби, нужно найти значения переменных, при которых знаменатель обращается в ноль, и исключить такие значения.Как известно, числитель и знаменатель обыкновенной дроби можно умножить или разделить на одно и то же отличное от нуля число. Например,
Естественным обобщением этого факта является основное свойство дроби, выражаемое тождеством
Основное свойство дроби имеет разнообразные применения. Так, если числитель и знаменатель дроби являются многочленами с дробными коэффициентами, то для упрощения записи целесообразно умножить числитель и знаменатель дроби на наименьшее общее кратное знаменателей всех коэффициентов. Это умножение является законным в силу основного свойства дроби.
Пример:
Упростить дробь
Решение:
Наименьшим общим кратным знаменателей всех коэффициентов будет в данном случае число 12.
Умножив и числитель, и знаменатель дроби на 12, получимОсновное свойство дроби используется для перемены знаков у членов дроби. Пусть дана дробь Умножив и числитель, и знаменатель дроби на (- 1), получим
Таким образом, значение дроби не изменится, если одновременно изменить знаки у числителя и знаменателя. Если же изменить знак только у числителя или только у знаменателя, то и дробь изменит свой знак:
Если в последних тождествах изменить знаки левой и правой частей, то получим
т. е. если надо изменить знак только числителя или только знаменателя дроби,то нужно изменить знак и перед самой дробью. Например,
Сокращение алгебраической дробиСократить дробь—это значит разделить числитель и знаменатель дроби на общий множитель. Возможность такого сокращения обусловлена основным свойством дроби.
Для того чтобы сократить алгебраическую дробь, нужно числитель и знаменатель разложить на множители. Если окажется, что числитель и знаменатель имеют общие множители, то их можно сократить.
Если общих множителей нет, то упрощение дроби посредством сокращения невозможно. Сокращение дроби есть тождественное преобразование.Примеры:
Сократить дробь
Решение:
Замечаем, что числитель и знаменатель дроби имеют общий множитель Значит надо сократить на этот общий множитель. Запись имеет такой вид:
Заметим, что области определения дробей различны. Дробь определена при а дробь определена при любых значениях х.
Значит, в результате сокращения получилась дробь, область определения которой (обозначим ее шире, чем область определения исходной дроби (обозначим ее Это можно записать так:
2.Сократить дробь
Для разложения числителя на множители применим способ группировки, представив предварительно одночлен в виде суммы тогда
Для разложения знаменателя на множители используем формулу разности квадратов:
Теперь имеем:
Приведение алгебраических дробей к общему знаменателюОбщим знаменателем нескольких алгебраических дробей называется многочлен, который делится на знаменатель каждой дроби.
Например, общим знаменателем дробей служит многочлен так как он делится и на Следует, однако, заметить, что это не единственное решение поставленной задачи: общим знаменателем данных дробей будет и многочлен и многочлен и многочлен и т. д. Обычно берут такой общий знаменатель, что любой другой общий знаменатель делится на выбранный без остатка. Такой знаменатель называется наименьшим общим знаменателем (НОЗ). В рассмотренном выше примере НОЗ равенПривести дроби к наименьшему общему знаменателю— это значит преобразовать каждую из дробей к такому виду, чтобы знаменателем служил НОЗ. Возможность такого преобразования вытекает из основного свойства дроби, позволяющего умножать числитель и знаменатель дроби на один и тот же многочлен. Так, для рассмотренных выше дробей имеем
Нам удалось привести дроби к НОЗ. Это достигнуто путем умножения числителя и знаменателя первой дроби на а числителя и знаменателя второй дроби на Многочлены называются дополнительными множителями соответственно для первой и для второй дроби.
Нетрудно понять, что дополнительный множитель для данной дроби равен частному от деления НОЗ на знаменатель данной дроби.Заметим, что области определения дробей и Различны. Дробь определена при а дробь определена при значениях х, отличных от -2 и 2.
Значит, в результате умножения числителя и знаменателя дроби на дополнительный множитель получилась дробь, область определения которой уже, чем область определения исходной дроби. Это можно записать так:
Пример:
Привести к НОЗ дроби
Решение:
В данном случае НОЗ равен Чтобы переписать данные дроби со знаменателем надо найти дополнительные множители. Для первой дроби дополнительным множителем будет Что касается второй дроби, то ее знаменатель совпадает с НОЗ. В таком случае говорят, что дополнительный множитель равен 1. Итак,
Вторую дробь оставим без изменения.
Дроби приведены к наименьшему общему знаменателю.
В общем случае, чтобы привести дроби к НОЗ, нужно все знаменатели разложить на множители, из первого знаменателя взять все множители, а из остальных добавить те, которых нет в первом.
Покажем на примерах, как это делается.Пример:
Привести к НОЗ дроби
Решение:
Разложим каждый из знаменателей на множители:
Составим НОЗ. Для зтого возьмем первый знаменатель Из второго знаменателя возьмем множитель 3, ибо его нет в первом знаменателе, а из третьего знаменателя возьмем множитель В итоге НОЗ равен
Теперь найдем дополнительные множители. Разделив НОЗ на знаменатель первой дроби, получим дополнительный множитель для первой дроби: Разделив НОЗ на знаменатель второй дроби, получим дополнительный множитель для второй дроби: Разделив НОЗ на знаменатель третьей дроби, получим дополнительный множитель для третьей дроби: 3. Теперь имеем:
Рекомендуем придерживаться следующей схемы отыскания НОЗ и дополнительных множителей (приводим ее на базе рассмотренного примера).
Пример:
Привести к наименьшему общему знаменателю дроби
Решение:
Прежде всего разложим знаменатели на множители:
Применим схему отыскания НОЗ и дополнительных множителей.
Если мы теперь числитель и знаменатель первой из данных дробей умножим на первый дополнительный множитель, а числитель и знаменатель второй дроби —на второй дополнительный множитель, то получим дроби с общим знаменателем:
Умножение и деление алгебраических дробейОбыкновенные дроби перемножаются следующим образом:
Обобщением этого равенства является тождество
где — целые алгебраические выражения. Итак, произведение двух (и вообще любого числа) алгебраических дробей тождественно равно дроби, числитель которой равен произведению числителей, а знаменатель— произведению знаменателей перемножаемых дробей.
Деление обыкновенных дробей выполняется следующим образом:
Обобщением этого равенства является тождество
Значит, частное от деления двух алгебраических дробей тождественно равно дроби, числитель которой равен произведению числителя первой дроби на знаменатель второй дроби, а знаменатель — произведению знаменателя первой дроби на числитель второй.
Примеры:
Преобразовать в дробь произведение
Решение:
Применяем правило умножения, затем выполняем необходимые сокращения:
Преобразовать в дробь частное
Решение:
Используем правило деления и выполняем сокращения:
Замечания:
Учитывая возможность сокращения алгебраической дроби, получаемой в результате умножения или деления алгебраических дробей, обычно стремятся до выполнения этих операций разложить на множители числители и знаменатели исходных дробей.
2.Сформулированные правила умножения и деления распространяются и на случай умножения или деления на многочлен, достаточно записать этот многочлен в виде дроби со знаменателем 1.
Возведение алгебраической дроби в натуральную степеньРассмотрим выражение Имеем
поэтому
Значит, степень дроби тождественно равна дроби, у которой числитель есть степень числителя, а знаменатель —степень знаменателя.
Пример:
Преобразовать в дробь степень
Решение:
Сложение и вычитание алгебраических дробейДля обыкновенных дробей справедливо равенство
Обобщением этого равенства является тождество
Оно означает, что сумма двух (и вообще любого числа) алгебраических дробей с одинаковым знаменателем тождественно равна алгебраической дроби с тем же знаменателем и с числителем, равным сумме числителей складываемых дробей.
Аналогично обстоит дело в случае вычитания дробей с одинаковым знаменателем. В самом деле,
Пример:
Преобразовать сумму в дробь.
Решение:
Для сложения и вычитания алгебраических дробей с разными знаменателями нужно прежде всего привести дроби к наименьшему общему знаменателю, а затем выполнить операции над полученными дробями с одинаковым знаменателем.
Примеры:
Упростить, т. е. преобразовать в дробь, выражение
Перепишем теперь заданную алгебраическую сумму дробей с указанием дополнительных множителей, при помощи которых дроби приводятся к общему знаменателю:
Обычно, соответствующие умножения на дополнительные множители опускают и сразу выписывают дробь, знаменателем которой является НОЗ, а числитель представляет собой сумму произведений числителей исходных дробей на соответствующие дополнительные множители, т.
е.и далее,
Упростить выражение
Решение:
Примеры на все действия с алгебраическими дробями1.Упростить выражение
Решение:
При выполнении операций над алгебраическими дробями придерживаются того же порядка, который принят для упрощения числовых выражений, а именно: умножение, деление и возведение в степень предшествуют сложению и вычитанию; при наличии скобок прежде всего выполняют действия в скобках. В данном примере порядок действий таков:
2.Упростить выражение
Решение:
Первым по счету действием является здесь умножение. Мы уже говорили, что умножению (и делению) обычно предшествует разложение числителей и знаменателей на множители. Имеем:
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Рациональное выражение примеры.
Преобразование рациональных и иррациональных выраженийНа данном уроке будут рассмотрены основные сведения о рациональных выражениях и их преобразованиях, а также примеры преобразования рациональных выражений. Данная тема как бы обобщает изученные нами до этого темы. Преобразования рациональных выражений подразумевают сложение, вычитание, умножение, деление, возведение в степень алгебраических дробей, сокращение, разложение на множители и т. п. В рамках урока мы рассмотрим, что такое рациональное выражение, а также разберём примеры на их преобразование.
Тема: Алгебраические дроби. Арифметические операции над алгебраическими дробями
Урок: Основные сведения о рациональных выражениях и их преобразованиях
Определение
Рациональное выражение — это выражение, состоящее из чисел, переменных, арифметических операций и операции возведения в степень.
Рассмотрим пример рационального выражения:
Частные случаи рациональных выражений:
1.
степень: ;2. одночлен: ;
3. дробь: .
Преобразование рационального выражения — это упрощение рационального выражения. Порядок действий при преобразовании рациональных выражений: сначала идут действия в скобках, затем операции умножения (деления), а затем уже операции сложения (вычитания).
Рассмотрим несколько примеров на преобразование рациональных выражений.
Пример 1
Решение:
Решим данный пример по действиям. Первым выполняется действие в скобках.
Ответ:
Пример 2
Решение:
Ответ:
Пример 3
Решение:
Ответ: .
Примечание: возможно, у вас при виде данного примера возникла идея: сократить дробь перед тем, как приводить к общему знаменателю. Действительно, она является абсолютно правильной: сначала желательно максимально упростить выражение, а затем уже его преобразовывать.
Попробуем решить этот же пример вторым способом.Как видим, ответ получился абсолютно аналогичным, а вот решение оказалось несколько более простым.
На данном уроке мы рассмотрели рациональные выражения и их преобразования , а также несколько конкретных примеров данных преобразований.
Список литературы
1. Башмаков М.И. Алгебра 8 класс. — М.: Просвещение, 2004.
2. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. — 5-е изд. — М.: Просвещение, 2010.
Урок и презентация на тему: «Преобразование рациональных выражений. Примеры решения задач»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 8 класса
Пособие к учебнику Муравина Г.К. Пособие к учебнику Макарычева Ю.Н.Понятие о рациональном выражении
Понятие «рациональное выражение» схоже с понятием «рациональная дробь».
Выражение также представляется в виде дроби. Только в числители у нас — не числа, а различного рода выражения. Чаще всего этого многочлены. Алгебраическая дробь — дробное выражение, состоящее из чисел и переменных.При решении многих задач в младших классах после выполнения арифметических операций мы получали конкретные числовые значения, чаще всего дроби. Теперь после выполнения операций мы будем получать алгебраические дроби. Ребята, помните: чтобы получить правильный ответ, необходимо максимально упростить выражение, с которым вы работаете. Надо получить самую маленькую степень, какую возможно; одинаковые выражения в числители и знаменатели стоит сократить; с выражениями, которые можно свернуть, надо так и поступить. То есть после выполнения ряда действий мы должны получить максимально простую алгебраическую дробь.
Порядок действий с рациональными выражениями
Порядок действий при выполнении операций с рациональными выражениями такой же, как и при арифметических операциях.
2}$.На данном уроке будут рассмотрены основные сведения о рациональных выражениях и их преобразованиях, а также примеры преобразования рациональных выражений. Данная тема как бы обобщает изученные нами до этого темы. Преобразования рациональных выражений подразумевают сложение, вычитание, умножение, деление, возведение в степень алгебраических дробей, сокращение, разложение на множители и т. п. В рамках урока мы рассмотрим, что такое рациональное выражение, а также разберём примеры на их преобразование.
Тема: Алгебраические дроби. Арифметические операции над алгебраическими дробями
Урок: Основные сведения о рациональных выражениях и их преобразованиях
Определение
Рациональное выражение — это выражение, состоящее из чисел, переменных, арифметических операций и операции возведения в степень.
Рассмотрим пример рационального выражения:
Частные случаи рациональных выражений:
1. степень: ;
2.
одночлен: ;3. дробь: .
Преобразование рационального выражения — это упрощение рационального выражения. Порядок действий при преобразовании рациональных выражений: сначала идут действия в скобках, затем операции умножения (деления), а затем уже операции сложения (вычитания).
Рассмотрим несколько примеров на преобразование рациональных выражений.
Пример 1
Решение:
Решим данный пример по действиям. Первым выполняется действие в скобках.
Ответ:
Пример 2
Решение:
Ответ:
Пример 3
Решение:
Ответ: .
Примечание: возможно, у вас при виде данного примера возникла идея: сократить дробь перед тем, как приводить к общему знаменателю. Действительно, она является абсолютно правильной: сначала желательно максимально упростить выражение, а затем уже его преобразовывать.
Попробуем решить этот же пример вторым способом.Как видим, ответ получился абсолютно аналогичным, а вот решение оказалось несколько более простым.
На данном уроке мы рассмотрели рациональные выражения и их преобразования , а также несколько конкретных примеров данных преобразований.
Список литературы
1. Башмаков М.И. Алгебра 8 класс. — М.: Просвещение, 2004.
2. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. — 5-е изд. — М.: Просвещение, 2010.
Рациональные выражения и дроби — краеугольный пункт всего курса алгебры. Те, кто научатся работать с такими выражениями, упрощать их и раскладывать на множители, по сути смогут решить любую задачу, поскольку преобразование выражений — неотъемлемая часть любого серьёзного уравнения, неравенства и даже текстовой задачи.
В этом видеоуроке мы посмотрим, как грамотно применять формулы сокращённого умножения для упрощения рациональных выражений и дробей. Научимся видеть эти формулы там, где, на первый взгляд, ничего нет.
{2}} \right)$ — разность кубов. - Как выполнять сокращение рациональных дробей без ошибок? Простой алгоритм на примере пяти различных задач.
- Все знаменатели и числители необходимо раскладывать на множители либо через формулы сокращенного умножения, либо через дискриминант.
- Работать нужно по такому алгоритму: когда мы смотрим и пытаемся выделить формулу сокращенного умножения, то, прежде всего, пытаемся все перевести в максимально возможную степень. {2}} \right)}{\left(2x-1 \right)\left(2x+1 \right)}=\]
\[=\frac{3\cdot \left(-1 \right)}{2\cdot \left(x-2 \right)\cdot \left(-1 \right)}=\frac{3}{2\left(x-2 \right)}\]
Ответ: $\frac{3}{2\left(x-2 \right)}$.
Нюансы решения
Итак, чему мы только что научились:
- Далеко не каждый квадратный трехчлен раскладывается на множители, в частности, это относится к неполному квадрату суммы или разности, которые очень часто встречаются как части кубов суммы или разности.
- Константы, т.е. обычные числа, не имеющие при себе переменных, также могут выступать активными элементами в процессе разложения. Во-первых, их можно выносить за скобки, во-вторых, сами константы могут быть представимы в виде степеней.
- Очень часто после разложения всех элементов на множители возникают противоположные конструкции. Сокращать эти дроби нужно крайне аккуратно, потому что при из зачеркивании либо сверху, либо снизу возникает дополнительный множитель $-1$ — это как раз и есть следствие того, что они противоположны. {2}}}=\]
\[=\frac{\left(3a-4b \right)\left(b+2 \right)}{\left(b-2 \right)}\]
Ответ: $\frac{\left(3a-4b \right)\left(b+2 \right)}{\left(b-2 \right)}$.
Нюансы решения
Как мы еще раз убедились, неполные квадраты суммы либо неполные квадраты разности, которые часто встречаются в реальных рациональных выражениях, однако не стоит их пугаться, потому что после преобразования каждого элемента они практически всегда сокращаются. Кроме того, ни в коем случае не стоит бояться больших конструкций в итогом ответе — вполне возможно, что это не ваша ошибка (особенно, если все разложено на множители), а это автор задумал такой ответ.
В заключение хотелось бы разобрать еще один сложных пример, который уже не относится напрямую к рациональным дробям, однако он содержит все то, что ждет вас на настоящих контрольных и экзаменах, а именно: разложение на множители, приведение к общему знаменателю, сокращение подобных слагаемых. Вот именно этим мы сейчас и займемся.
Решение сложной задачи на упрощение и преобразование рациональных выражений
\[\left(\frac{x}{{{x}^{2}}+2x+4}+\frac{{{x}^{2}}+8}{{{x}^{3}}-8}-\frac{1}{x-2} \right)\cdot \left(\frac{{{x}^{2}}}{{{x}^{2}}-4}-\frac{2}{2-x} \right)\]
Сначала рассмотрим и раскроем первую скобку: в ней мы видим три отдельных дроби с разными знаменателями поэтому первое, что нам необходимо сделать — это привести все три дроби к общему знаменателю, а для этого каждый из них следует разложить на множители:
\[{{x}^{2}}+2x+4={{x}^{2}}+2\cdot x+{{2}^{2}}\]
\[{{x}^{2}}-8={{x}^{3}}-{{2}^{2}}=\left(x-2 \right)\left({{x}^{2}}+2x+{{2}^{2}} \right)\]
Перепишем всю нашу конструкцию следующим образом:
\[\frac{x}{{{x}^{2}}+2x+{{2}^{2}}}+\frac{{{x}^{2}}+8}{\left(x-2 \right)\left({{x}^{2}}+2x+{{2}^{2}} \right)}-\frac{1}{x-2}=\]
\[=\frac{x\left(x-2 \right)+{{x}^{3}}+8-\left({{x}^{2}}+2x+{{2}^{2}} \right)}{\left(x-2 \right)\left({{x}^{2}}+2x+{{2}^{2}} \right)}=\]
\[=\frac{{{x}^{2}}-2x+{{x}^{2}}+8-{{x}^{2}}-2x-4}{\left(x-2 \right)\left({{x}^{2}}+2x+{{2}^{2}} \right)}=\frac{{{x}^{2}}-4x-4}{\left(x-2 \right)\left({{x}^{2}}+2x+{{2}^{2}} \right)}=\]
\[=\frac{{{\left(x-2 \right)}^{2}}}{\left(x-2 \right)\left({{x}^{2}}+2x+{{2}^{2}} \right)}=\frac{x-2}{{{x}^{2}}+2x+4}\]
Это результат вычислений из первой скобки.
{2}}+2x+4}{\left(x-2 \right)\left(x+2 \right)}=\frac{1}{x+2}\]Ответ: $\frac{1}{x+2}$.
Нюансы решения
Как видите, ответ получился вполне вменяемый. Однако обратите внимание: очень часто при таких масштабных вычислениях, когда единственная переменная оказывается лишь в знаменателе, ученики забывают, что это знаменатель и он должен стоял внизу дроби и пишут это выражение в числитель — это грубейшая ошибка.
Кроме того, хотел бы обратить ваше отдельное внимание на то, как оформляются такие задачи. В любых сложных вычислениях все шаги выполняются по действиям: сначала отдельно считаем первую скобку, потом отдельно вторую и лишь в конце мы объединяем все части и считаем результат. Таким образом мы страхуем себя от глупых ошибок, аккуратно записываем все выкладки и при этом нисколько не тратим лишнего времени, как это может показаться на первый взгляд.
Rational Expressions
Выражение, являющееся отношением двух многочленов:
Это похоже на дробь, но с многочленами.
Другие примеры:
x 3 + 2x − 1 6x 2 2x + 9 x 4 − x 2 Также
1 2 − x 2 Верхний полином «1», что нормально. 2x 2 + 3 Да, это так! Как еще можно было бы написать:
2x 2 + 3 1Но не
2 − √(x) 4 − x вершина не является полиномом (не допускается квадратный корень переменной) 1/x не допускается в полиноме В общем случае
Рациональная функция представляет собой отношение двух многочленов P(x) и Q(x), как это Q(x) не может быть нулем (и везде, где Q(x)=0 не определено)
Нахождение корней рациональных выражений
«Корень» (или «ноль») — это когда выражение равно нулю :
Чтобы найти корни Рационального Выражения , нам нужно только найти корни верхнего многочлена , пока Рациональное Выражение находится в «самых низких терминах».
Так что же означает «самые низкие условия»?
Самые низкие условия
Хорошо, 9Дробь 0115 находится в наименьшем выражении, когда верхний и нижний множители не имеют общих делителей.
Пример: дроби
2 6 это , а не в самом низком выражении,
, так как 2 и 6 имеют общий делитель «2»Но:
1 3 — это в наименьшем выражении,
, так как 1 и 3 не имеют общих делителейАналогично, Рациональное выражение находится в наименьших терминах, когда верх и низ не имеют общих делителей.
Пример: Rational Expressions
x 3 +3x 2 2x равно , а не в наименьшем выражении,
как x 3 +3x 2 и 2x имеют общий делитель «x»Но
x 2 +3x 2 равно в наименьшем выражении,
как x 2 +3x и 2 не имеют общих делителейИтак, чтобы найти корни рационального выражения :
- Привести рациональное выражение к наименьшим терминам,
- Затем найдите корни верхнего многочлена
Как найти корни? Прочтите «Решение полиномов», чтобы узнать, как это сделать.
Правильные и неправильные
Дроби могут быть правильными и неправильными: (В «Неправильном» нет ничего плохого, это просто другой тип) И аналогично:
Рациональное выражение также может быть правильным или неправильным !
Но что делает многочлен больше или меньше?
Степень !
Для многочлена с одной переменной Степень является наибольшим показателем этой переменной.
Примеры степени:
4x Степень равна 1 (переменная без показателя степени
на самом деле имеет показатель степени 1)4x 3 − x + 3 Степень 3 (наибольшая степень x) Итак, вот как узнать, является ли рациональное выражение правильным или неправильным :
Правильное: степень вершины меньше степени основания.
Правильный: 1 х + 1 градусов (сверху) < градусов (снизу) Другой пример: x x 3 − 1
Неправильно: степень вершины больше или равна степени основания.
Неправильный: х 2 − 1 х + 1 градусов (вверху) ≥ градусов (внизу) Другой пример: 4x 3 — 3 5x 3 + 1
, если полиномиальные, мы можем упростить его с помощью полиномиальных районов
Asymptotes
6
669
6
(линия , к которой кривая приближается по направлению к бесконечности):
Пример: (x
2 -3x)/(2x-2)График (x 2 -3x)/(2x-2) имеет:
- Вертикальная асимптота в точке x=1
- Наклонная асимптота: y=x/2-1
Рациональное выражение может иметь:
- любое количество вертикальных асимптот,
- только ноль или одна горизонтальная асимптота,
- только ноль или одна косая (наклонная) асимптота
Нахождение горизонтальных и наклонных асимптот
Найти их довольно легко.
..… но это зависит от степени полинома верхнего и нижнего .
Тот, у кого больше степень, будет расти быстрее.
Точно так же, как «Правильный» и «Неправильный», но на самом деле есть четыре возможных случая, показанных ниже.
(я показываю тестовое значение x=1000 для каждого случая, просто чтобы показать, что происходит)Давайте рассмотрим каждый из этих примеров по очереди:
Степень верха
Меньше Чем низНижний многочлен будет доминировать, а горизонтальная асимптота находится в нуле.
Пример: f(x) = (3x+1)/(4x
2 +1)Когда x равно 1000:
f(1000) = 3001/4000001 = 0,0000735 0,0000735
И по мере того, как x увеличивается, f(x) приближается к 0
Степень вершины равна
Равна НизНи одна из них не доминирует … асимптота задается старшими членами каждого многочлена.
Пример: f(x) = (3x+1)/(4x+1)
Когда x равно 1000:
f(1000) = 3001/4001 = 0,750…
И как x увеличивается, f(x) приближается к 3/4
Почему 3/4? Поскольку «3» и «4» являются «старшими коэффициентами» каждого многочлена
Члены расположены в порядке от наибольшего к наименьшему показателю(Технически 7 является константой, но здесь легче думать обо всех них как коэффициенты.)
Метод прост:
Разделить старший коэффициент верхнего полинома на старший коэффициент нижнего полинома.
Вот еще пример:
Пример: f(x) = (8x
3 + 2x 2 — 5x + 1)/(2x 3 + 15x + 2)Степени равны (оба имеют степень 3)
Просто посмотрите на старшие коэффициенты каждого многочлена:
- Вершина равна 8 (из 8x 3 )
- Низ 2 (от 2x 3 )
Таким образом, существует горизонтальная асимптота на уровне 8/2 = 4
Степень вершины равна
1 больше, чемнайти уравнение прямой.
Чтобы вычислить это, используйте полиномиальное длинное деление: разделите верх на низ, чтобы найти частное (остаток игнорируйте).
Пример: f(x) = (3x
2 +1)/(4x+1)Степень вершины равна 2, а степень основания равна 1, поэтому не будет наклонной асимптоты
Нужно разделить 3x 2 +1 на 4x+1 с использованием полиномиального длинного деления:
Ответ: (3/4)x-(3/16) (без учета остатка):
Асимптота «уравнения прямой»: (3 /4)x-(3/16)
Верхний угол равен
Более чем на 1 больше, чем нижнийЕсли верхний многочлен более чем на 1 градус выше нижнего многочлена, то нет горизонтальной или наклонной асимптоты .
Пример: f(x) = (3x
3 +1)/(4x+1)Степень вершины равна 3, а степень основания равна 1.
Вершина больше 1 градусов выше основания, поэтому нет горизонтальной или наклонной асимптоты .
Нахождение вертикальных асимптот
Существует другой тип асимптоты, который возникает из-за нижний полином только .
Но во-первых: убедитесь, что рациональное выражение в наименьших терминах!
Всякий раз, когда нижний полином равен нулю (любой из его корней), мы получаем вертикальную асимптоту.
Прочтите Решение многочленов, чтобы научиться находить корни
Из нашего примера выше:
Пример: (x
2 -3x)/(2x-2)Нижний полином равен 2x-2 , что составляет:
2(х-1)
А множитель (x-1) означает, что существует вертикальная асимптота в точке x=1 (поскольку 1-1=0)
Полный пример
Пример: Эскиз (x−1)/(x
2 −9)Прежде всего, мы можем разложить на множители нижний многочлен (это разность двух квадратов):
х-1 (х+3)(х-3)
Теперь мы можем видеть:
Корни верхнего многочлена: +1 (здесь пересекает ось x )
Корни нижнего многочлена: −3 и +3 (это Вертикальные асимптоты )
Это пересекает ось Y , когда x=0, поэтому установим x равным 0:
Пересекает ось Y в точке: 0-1 (0+3)(0-3) = -1 -9 = 1 9
Мы также знаем, что градус вершины меньше, чем градус низа, поэтому существует Горизонтальная асимптота в точке 0
Итак, мы можем набросать всю эту информацию:
А теперь мы можем нарисовать на кривой:
(сравните это с графиком (x-1)/(x 2 -9))
—>
- Войти
- Биографии репетитора
- Подготовка к тесту
СРЕДНЯЯ ШКОЛА
- ACT Репетиторство
- SAT Репетиторство
- Репетиторство PSAT
- ASPIRE Репетиторство
- ШСАТ Репетиторство
- Репетиторство STAAR
ВЫСШАЯ ШКОЛА
- Репетиторство MCAT
- Репетиторство GRE
- Репетиторство по LSAT
- Репетиторство по GMAT
К-8
- Репетиторство AIMS
- Репетиторство по HSPT
- Репетиторство ISEE
- Репетиторство по ИСАТ
- Репетиторство по SSAT
- Репетиторство STAAR
Поиск 50+ тестов
- Академическое обучение
репетиторство по математике
- Алгебра
- Исчисление
- Элементарная математика
- Геометрия
- Предварительное исчисление
- Статистика
- Тригонометрия
Репетиторство по естественным наукам
- Анатомия
- Биология
- Химия
- Физика
- Физиология
иностранные языки
- Французский
- немецкий
- Латинский
- Китайский мандарин
- Испанский
начальное обучение
- Чтение
- Акустика
- Элементарная математика
прочее
- Бухгалтерский учет
- Информатика
- Экономика
- Английский
- Финансы
- История
- Письмо
- Лето
Поиск по 350+ темам
- О
- Обзор видео
- Процесс выбора наставника
- Онлайн-репетиторство
- Мобильное обучение
- Мгновенное обучение
- Как мы работаем
- Наша гарантия
- Влияние репетиторства
- Обзоры и отзывы
- Освещение в СМИ
- О преподавателях университета
Звоните прямо сейчас, чтобы записаться на обучение:
(888) 888-0446
Все математические ресурсы SAT
16 диагностических тестов 660 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущая 1 2 Следующая →
SAT Math Help » Алгебра » Выражения » Rational Expressions
Упростите выражение.
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы сложить рациональные выражения, сначала найдите наименьший общий знаменатель. Поскольку знаменатель первой дроби равен 2(x+2), ясно, что это общий знаменатель. Следовательно, умножьте числитель и знаменатель второй дроби на 2.
Это самый упрощенный вариант рационального выражения.
Сообщить об ошибке
Упростите следующее:
Возможные ответы:
Правильный ответ: 609103
6 Объяснение:Чтобы упростить следующее, необходимо найти общий знаменатель. В этом случае первый член должен быть умножен на (x+2) как в числителе, так и в знаменателе, а также на второй член с (x-3).
Сообщить об ошибке
Если √( ab ) = 8, и a 2 = b , чему равно a ?
Возможные ответы:
16
10
2
64
4
Правильный ответ:
4
Объяснение:
Если мы подставим a 2 вместо b в подкоренном выражении, мы получим √( a 3 ) = 8. Это можно переписать как 9.0013 a 3/2 = 8. Таким образом, log a 8 = 3/2. Подстановка вариантов ответа дает 4 как правильный ответ.
Отчет о ошибке
Возможные ответы:
–9/5
37/15
–37/15
9/5
–11/5
917.
–11/5
Объяснение:
Сообщить об ошибке
Если Джилл войдет, сколько времени Джилл будет идти?
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы решить эту проблему, нам нужно задать пропорцию.
Cross Multiply
Значит, Джилл придется идти пешком
Сообщить об ошибке
Если , то какое из следующих утверждений также должно быть верным?
Возможные ответы:
Правильный ответ:
Объяснение:
Сообщить об ошибке
Что из следующего эквивалентно ? Предположим, что знаменатели всегда отличны от нуля.
Возможные ответы:
Правильный ответ:
Объяснение:
Нам нужно упростить выражение. Мы можем думать об этом как о большой дроби с числителем и знаменателем .
Чтобы упростить числитель, нам нужно объединить две дроби.
При сложении или вычитании дробей мы должны иметь общий знаменатель. имеет знаменатель , и имеет знаменатель . Наименьший общий знаменатель, который имеют эти две дроби, равен . Таким образом, мы будем писать эквивалентные дроби со знаменателем .Чтобы преобразовать дробь в знаменатель с , нам нужно будет умножить верх и низ на .
Точно так же мы умножим верхнюю и нижнюю часть на .
Теперь мы можем переписать следующим образом:
=
Вернемся к исходной дроби. Теперь мы перепишем числитель:
=
. Когда мы делим дробь на другую величину, это то же самое, что умножать дробь на обратную величину этой величины. Другими словами, .
=
Наконец, мы будем использовать свойство экспонент, которое утверждает, что, вообще говоря, .
Ответ .
Сообщить об ошибке. ) 2
4/(х + 2) 2
(4х 2 + 8х)/(х 4 + 8х)
х/(90/0 0 2 х) 40/0 – 2) 2
Правильный ответ:
4/(х – 2) 2
Объяснение:
Первый фактор.
Числители не будут множиться, но первый знаменатель размножается на (x – 2)(x + 2), а второй знаменатель размножается на x(x – 2). Умножение дробей не требует общих знаменателей, поэтому теперь ищите общие множители для деления. Есть множитель x и множитель (x + 2), которые делятся, оставляя 4 в числителе и два множителя (x – 2) в знаменателе.Отчет о ошибке
Что такое 6/8 x 20/3
Возможные ответы:
5
120/11
18/160
3/20
9/40
Правильно ответ. : 5
Объяснение:
6/8 X 20/3 первый шаг — уменьшить 6/8 -> 3/4 (разделить верх и низ на 2)
3/4 X 20/3 (перекрестное сокращение троек и 20 уменьшается до 5, а 4 уменьшается до 1)
1/1 X 5/1 = 5
Сообщить об ошибке
Оцените и упростите следующий продукт:
Возможные ответы:
Правильный ответ:
Объяснение:
Процедура умножения двух рациональных выражений такая же, как и умножения любых двух дробей: найдите произведение числителей и произведение знаменателей по отдельности, а затем максимально упростите полученное частное, как показано:
Report an Error
← Previous 1 2 Next →
Copyright Notice
View SAT Mathematics Tutors
Ryan
Certified TutorUniversity of Missouri-Columbia, Bachelor of Science , Образование.
Вашингтонский университет в Сент-Луисе, доктор юридических наук, юридический…Посмотреть SAT Репетиторы по математике
Ирина
Сертифицированный репетиторНью-Йоркский университет, бакалавриат, биохимия.
View SAT Репетиторы по математике
Лаура
Сертифицированный репетиторМичиганский университет в Дирборне, бакалавр микробиологии.
Все математические ресурсы SAT
16 диагностических тестов 660 практических тестов Вопрос дня Карточки Учитесь по концепции
Рациональное выражение — упрощение, сложение, умножение, деление
Рациональное выражение — это выражение, в котором и числитель, и знаменатель являются полиномами. Упрощение рациональных выражений осуществляется путем приведения числителя и знаменателя к их наименьшей форме. Рациональное выражение также известно как алгебраическая дробь.
Давайте узнаем больше о рациональных выражениях и операциях над рациональными выражениями.
Также мы увидим, как упростить рациональные выражения.1. Что такое рациональные выражения? 2. Упрощение рационального выражения 3. Операции над рациональными выражениями 4. Добавление или вычитание рациональных выражений 5. Умножение рациональных выражений 6. Деление рациональных выражений 7. Часто задаваемые вопросы по Rational Expressions Что такое рациональные выражения?
Рациональные выражения являются дробями с переменными. В рациональном выражении и числитель, и знаменатель являются полиномами. т. е. имеет вид p(x)/q(x), где q(x) ≠ 0, а p(x) и q(x) — многочлены. Поскольку рациональные выражения — не что иное, как дроби, мы оперируем ими точно так же, как оперируем дробями.
Вот несколько примеров рациональных выражений: (x + 1) / (x 2 — 5), (x 3 + 3x 2 — 5) / (4x — 2) и т. д. Обратите внимание, что если один из числителя и знаменателя НЕ является многочленом, то дробь НЕ называется рациональным выражением.
Ограничения Rational Expression
Деление числа на 0 невозможно. Проверьте, что такое 1/0, используя свой калькулятор, он выдаст ошибку. Таким образом, рациональное выражение (поскольку это дробь) НЕ определено для значения (значений) переменной, у которой знаменатель равен 0. Например, в выражении x / (x + 2) знаменатель принимает вид ноль при x = -2 и, следовательно, известно как ограничение рационального выражения x / (x + 2). Другими словами, мы говорим, что x / (x + 2) принимает все значения для x, но x ≠ -2. Таким образом, чтобы найти ограничение (я) рационального выражения, просто установите знаменатель равным 0 и найдите переменную.
Упрощение рационального выражения
Упрощение рациональных выражений означает приведение значения рационального выражения к его наименьшим терминам или упрощенной форме.
Упрощение рационального выражения такое же, как мы упрощаем дроби. В дробях, когда числитель и знаменатель рационального числа не имеют общего делителя, кроме 1, мы считаем, что это его упрощенная форма. То же самое работает и для упрощения рациональных выражений, но единственное отличие заключается в наличии многочленов в дроби. Давайте посмотрим, какие шаги необходимо предпринять для упрощения рациональных выражений.- Шаг 1: Разложите на множители числитель и знаменатель, убрав общие множители.
- Шаг 2: Отменить общие факторы.
- Шаг 3: Запишите оставшиеся члены в числителе и знаменателе.
- Шаг 4: Укажите ограниченные значения, если таковые имеются. Обратите внимание, что ограничения — это любые значения, делающие знаменатель равным 0, включая любые исключенные члены при упрощении.
Вот еще один пример.
Пример: Упростите рациональное выражение (3y 2 + 6y) / (6y 2 + 9y).
Решение:
Чтобы упростить данное выражение, мы просто факторизуем числитель и знаменатель и сокращаем общие члены.
(3 года 2 + 6 лет) / (6 лет 2 + 9 лет) = [3 года (у + 2) ] / [3 года (2 года + 3)]
= (у + 2) / (2у + 3) )
Чтобы найти ограничения, установите исходный знаменатель ≠ 0 и решите. Обратите внимание, что мы не должны использовать знаменатель простейшей формы при вычислении ограничений.
3y (2y + 3) ≠ 0
y ≠ 0 и y ≠ -3/2
Таким образом, простейшая форма (y + 2) / (2y + 3), где y ≠ 0, -3/ 2.
Операции над рациональными выражениями
Процесс выполнения операций над рациональным выражением такой же, как и над дробями. т. е. мы можем складывать/вычитать/умножать/делить алгебраические дроби так же, как и числовые дроби. Но при написании ограничений следует позаботиться о знаменателе каждого рационального выражения, участвующего в операции. Давайте посмотрим, как выполнять каждую из следующих операций над рациональными выражениями:
- Дополнение
- Вычитание
- Умножение
- Подразделение
Сложение и вычитание рациональных выражений
Чтобы складывать/вычитать рациональные выражения, сначала перепишите дроби с общим знаменателем.
Если знаменатели двух рациональных выражений уже одинаковы, то мы можем напрямую складывать/вычитать их числители. В общем, чтобы сложить/вычесть два рациональных выражения:- Найдите LCD (LCM) их знаменателей.
- Умножьте и разделите каждое рациональное выражение на некоторое выражение/число так, чтобы все знаменатели были такими же, как у LCD, полученного на предыдущем шаге.
- Теперь мы можем складывать/вычитать все числители, так как теперь знаменатели одинаковы.
Пример: Сложите рациональные выражения (3 / x) + (1 / (x 2 + x)).
Решение:
Данные рациональные выражения можно записать как (3 / x) + [1 / (x(x + 1) ]
Здесь LCD (общий знаменатель) равен x (x + 1). Чтобы сделать знаменатели одинаковыми, мы умножаем и делим первую дробь на (x + 1). Тогда мы получаем
(3 / х) · (х + 1) / (х + 1) + [1 / (х (х + 1) ]
= (3 (х + 1)) / (х (х +1)) + 1/(x(x+1))
Теперь мы можем сложить числители, так как знаменатели одинаковы.
= (3x + 3 + 1) / (x(x+1))
= (3x + 4) / (x(x+1)) (ИЛИ) (3x + 4) / (x 2 + x)
Здесь ограничения x ≠ 0, -1,
Умножение рациональных выражений
Чтобы умножить два рациональных выражения, мы раздельно умножаем их числители и знаменатели. Но перед этим полезнее выполнить следующие шаги:
- Упростите каждое из выражений, если оно не в самой простой форме.
- Разложите на множители числитель и знаменатель каждого выражения.
- Отменить общие члены (при отмене одно слагаемое должно быть в числителе, а другое в знаменателе).
- Упростите остальные термины.
Пример: Умножить рациональные выражения (x 2 — 3x — 10) / (x 2 + x — 2) × (x 2 + 2x — 3) / (x 2 + x — 6).
Решение:
Факторизация каждого полинома,
[(x — 5) (x + 2)] / [(x + 2) (x — 1)] × [(x + 3) (x — 1 )] / [(x + 3) (x — 2)]
Теперь сократите члены, присутствующие как в числителе, так и в знаменателе.
= [(x — 5) ̶(̶x̶ ̶+̶ ̶2̶)̶] / [ ̶(̶x̶ ̶+̶ ̶2̶)̶ ̶(̶x̶ ̶-̶ ̶1̶)̶] × [ ̶(̶x̶ ̶+̶ ̶3̶)̶ ̶(̶x̶ ̶-̶ ̶1̶)̶] / [ ̶(̶x̶ ̶+̶ ̶3̶)̶ (x — 2)]
= (x — 5) / (x — 2)
Ограничения: x ≠ -2, 1, -3, 2.
Разделение рациональных выражений
Напомним, чтобы разделить одну дробь на другую, мы умножаем первую дробь на обратную величину второй дроби. Мы следуем той же процедуре и для деления рациональных выражений. Чтобы разделить рациональное выражение на другое:
- Факторизируйте каждый многочлен в каждом рациональном выражении.
- Чтобы разделить на дробь, умножьте ее на обратную (мультипликативный обратный).
- Отменить общие факторы и упростить.
- При записи ограниченных значений позаботьтесь о знаменателях исходных дробей, а также о знаменателе обратной дроби, которую мы рассмотрели по пути.
Пример: Разделите рациональные выражения [(x 2 — 9) / (х 2 + 6х + 9)] ÷ [(х 2 — 8х + 16) / (х 2 — 7х + 12)].
Решение:
Сначала мы разложим на множители каждый многочлен.
= [(х — 3)(х + 3) / (х + 3) (х + 3)] ÷ [(х — 4) (х — 4) / (х — 3) (х — 4)]
Теперь мы изменим знак «÷» на знак «×», перевернув вторую дробь. Обратите внимание, что мы должны оставить первую дробь как есть.
= [(х — 3)(х + 3) / (х + 3) (х + 3)] × [(х — 3) (х — 4) / (х — 4) (х — 4)]
Теперь деление преобразуется в умножение. Следовательно, сократите возможные члены, как мы это делаем при умножении.
= [(x — 3) ̶(̶x̶ ̶+̶ ̶3̶)̶ / ̶(̶x̶ ̶+̶ ̶3̶)̶ (x + 3)] × [(x — 3) ̶(̶x̶ ̶-̶ ̶4̶)̶ / ̶(̶x̶ ̶-̶ ̶4̶)̶ (x — 4)]
= (x — 3) 2 / [(x + 3) (x — 4)]
Ограничения: x ≠ -3, 3, 4.
Важные замечания по рациональным выражениям:
- Рациональное выражение должно включать все значения x, кроме значений, при которых знаменатель равен нулю.
- Чтобы упростить рациональные выражения, их следует разложить на множители и исключить общие множители.
- Любая арифметическая операция над рациональным выражением выполняется точно так же, как операции применяются над дробями.
- При выполнении любой операции над рациональными выражениями при написании ограничений следует учитывать знаменатели всех исходных выражений, а также выражения, встречающиеся в пути (особенно при делении).
☛ Связанные темы:
- Калькулятор рациональных выражений
- Калькулятор упрощения рациональных выражений
- Калькулятор сложения и вычитания рациональных выражений
- Калькулятор умножения и деления рациональных выражений
Часто задаваемые вопросы по Rational Expressions
Что такое рациональное выражение в алгебре?
Рациональное выражение — это дробь, в которой числитель и знаменатель являются полиномами. Каждое рациональное выражение имеет по крайней мере одно ограничение. Ограничение — это значение переменной, при котором знаменатель рационального выражения равен нулю.
Например, x / (x — 1) не определено, когда x = 1, и является ограничением для данного выражения.Что такое примеры рациональных выражений?
В рациональном выражении числитель и знаменатель должны быть полиномами. Например, 2x / (x + 3), (x 3 — 5) / (x + 2) и т. д. являются рациональными выражениями.
Как упростить рациональное выражение?
Чтобы упростить рациональное выражение, просто разложите числитель и знаменатель на множители, а затем сократите общие множители. При снятии ограничений также необходимо учитывать факторы, которые отменяются.
Что такое процесс добавления рациональных выражений?
Процесс сложения дробей выполняется и для сложения рациональных выражений, потому что рациональные выражения не что иное, как дроби. Итак, чтобы сложить рациональные выражения, просто найдите общие знаменатели и добавьте числители.
Как свести рациональные выражения к наименьшим терминам?
Рациональные выражения сокращаются до наименьших членов путем удаления общего множителя из числителя и знаменателя.
В чем разница между умножением и делением рациональных выражений?
- Для умножения рациональных выражений вынесите на множители все участвующие выражения и сократите множители, которые находятся как в числителе, так и в знаменателе, и упростите остальные множители.
- Для деления рационального выражения (делимого) на другое рациональное выражение (делитель) сохраните делимое как есть, переверните выражение делителя для преобразования символа деления в символ умножения, а затем выполните умножение.
При умножении учитываются только знаменатели исходных выражений для записи ограничений, тогда как при делении наряду со знаменателями исходных выражений следует также учитывать числитель второй дроби, поскольку при переворачивании второй дроби числитель становится знаменателем.
Что НЕ является рациональным выражением?
Дробь называется рациональным выражением, если ее числитель и знаменатель являются полиномами. Если хотя бы одно из них не многочлен, то дробь НЕ является рациональным выражением.
Например, √x / (x + 1) НЕ является рациональным выражением, поскольку квадратный корень из x НЕ является полиномом.Как упростить рациональные выражения с помощью экспонент?
Чтобы упростить рациональные выражения с показателями, мы должны следовать правилам показателей и степеней, а затем исключить общий множитель из числителя и знаменателя.
Как найти ограничения рациональных выражений?
Чтобы найти ограничение рационального выражения, просто приравняйте каждый множитель его знаменателя к нулю и решите уравнение. Это связано с тем, что дробь не определена, если ее знаменатель равен 0,9.0003
рациональные формы Пошаговые математические задачи решают
Глава 4
Рациональные формы4.1 Введение
. и Q являются полиномами от одной или нескольких переменных, а Q отличен от нуля. Многочлен P будем называть числителем рациональной формы, а Q — знаменателем.
В главе 1 мы указывали, что если a,b и c — любые три действительных числа, причем b!=0 и c!=0, то, поскольку c/c = 1 , 92-xy+x-y)=((x-y)(x-y))/(y(y-x)-(y-x))
=((x-y)(x-y))/((y-x)(y-1))
=
= (x-y)/((-1) (y-1))
= (x-y)/(1-y)
4.
2 Умножение рациональных форм , если A, b, c, c , и d — действительные числа с b!=0 и d!=0, тогда
a/b*c/d=(ac)/(bd)
Применим это правило к рациональным формам. Произведением двух рациональных форм является рациональная форма, числитель которой является произведением числителей, а знаменатель — произведением знаменателей. Затем мы упрощаем полученную рациональную форму, сводя ее к низшим элементам, как в предыдущем разделе. 92-3s+2)
=
=((s-2)(s+1))/((s-3)(s-1))
Давайте посмотрим, как наш математический решатель умножает эту и подобные задачи . Нажмите кнопку «Решить подобное», чтобы увидеть больше примеров.
Решить аналогичную задачуВведите свою задачу
4.3 Деление рациональных форм(a)/(b)÷c/d=a/b*d/c
Применим это правило к рациональным формам и поступим, как в 4.2. 92)
=[((x+5y)(x+2y))/((x-3y)(x-2y))*((x+3y)(x-2y))/((x-5y) )(x+5y))((x-5y)(x+2y))/((x+3y)(x+2y))
=
=(x+2y)/(x-3y)
4.
4 Сложение и вычитание рациональных форм Вспоминаем из главы 1, что при сложении дробей первым шагом является нахождение их НПК, то есть НОК их знаменателей. Мы рассмотрим метод нахождения L.C.M. набора целых чисел.
Пример 1 . Найдите L.C.M. из 6, 18 и 27. 92+s-2=(s+2)(s-1)
Поскольку s-1=(-1)(1-s), мы используем только один из этих факторов в L.C.M. Таким образом, один L.C.M. равно
2*3(1-s)(s+2)
, а другой L.C.M. равно
2*3(s-1)(s+2)
Всегда есть два L.C.M., один из которых (-1) больше другого.
Складывая рациональные формы, мы сначала находим общий знаменатель, а затем выражаем каждую рациональную форму как эквивалентную рациональную форму с этим общим знаменателем. Сумма — это рациональная форма, знаменатель которой является общим знаменателем, а числитель — суммой числителей. При таком определении сложение рациональных форм производится так же, как сложение дробей. Поэтому, как отмечалось выше, работа упрощается, если мы используем Н.
К.Д., то есть Н.К.М., знаменателей. Вычитание рациональных форм производится так же, как вычитание дробей. 92+7s+3)/(2*3(s+2)(s-1))=((2s+1)(s+3))/(6(s+2)(s-1) )
4.5 Сложные дроби
Сложной дробью называется любая дробь, числитель или знаменатель (или оба) которой состоят из одной или нескольких рациональных форм. Мы упрощаем, сначала упрощая числитель, затем знаменатель и, наконец, разделив полученные рациональные формы. Это показано на следующих примерах.
Пример 1. Упростить (1/3–3/2)/(1/4–1/6).
92Пример 3. Упростить 1/(1-1/(1+1/x))
Числитель уже упрощен. Чтобы упростить знаменатель, мы должны сначала упростить 1/(1+1/x)
1/(1+1/x)
=1/(x/x+1/x)
=1/(( x+1)/x)
=1*x/(x+1)
=x/(x+1)
Таким образом, знаменатель равен
1-1/(1+1/x)
=1-x/(x+1)
=(x+1)/(x+1)-x/(x+1)
=(x+1-x)/(x+1)
=1/(x+1)
Разделив, получим 92
1.
6 Рациональные выражения — Колледж Алгебра 2eЦели обучения
В этом разделе вы:
- Упростите рациональные выражения.
- Умножение рациональных выражений.
- Разделить рациональные выражения.
- Сложение и вычитание рациональных выражений.
- Упростите сложные рациональные выражения.
Кондитерская имеет фиксированные затраты в размере 280$280 в неделю и переменные затраты в размере 9$9 за коробку выпечки. Затраты магазина в неделю в пересчете на х, х, количество изготовленных коробок, составляют 280+9.х.280+9х. Мы можем разделить затраты в неделю на количество изготовленных коробок, чтобы определить стоимость коробки выпечки.
280+9xx280+9xx
Обратите внимание, что результатом является полиномиальное выражение, деленное на второе полиномиальное выражение. В этом разделе мы рассмотрим частные полиномиальные выражения.
Упрощение рациональных выражений
Частное двух полиномиальных выражений называется рациональным выражением.
Мы можем применять свойства дробей к рациональным выражениям, например, упрощая выражения, исключая общие множители из числителя и знаменателя. Для этого нам сначала нужно разложить как числитель, так и знаменатель. Начнем с показанного рационального выражения.х2+8х+16х2+11х+28х2+8х+16х2+11х+28
Мы можем разложить числитель и знаменатель, чтобы переписать выражение.
(х+4)2(х+4)(х+7)(х+4)2(х+4)(х+7)
Тогда мы можем упростить это выражение, убрав общий множитель (x+4).(x+4).
х+4х+7х+4х+7
Как
Дано рациональное выражение, упростите его.
- Разложите числитель и знаменатель на множители.
- Отменить любые общие факторы.
Пример 1
Упрощение рациональных выражений
Упрощение x2−9×2+4x+3.×2−9×2+4x+3.
Решение
(x+3)(x−3)(x+3)(x+1)Разложить на множители числитель и знаменатель.
x−3x+1Отменить общий множитель(x+3).(x+3)(x−3 )(x+3)(x+1)Разложить на множители числитель и знаменатель.x−3x+1Отменить общий множитель (x+3).Анализ
Мы можем отменить общий множитель, потому что любое выражение, деленное само на себя, равно 1.
вопросы и ответы
Можно ли отменить термин x2x2 в примере 1?
Нет. Коэффициент — это выражение, которое умножается на другое выражение. Член x2x2 не является фактором числителя или знаменателя.
Попытайся #1
Упростить x-6×2-36.x-6×2-36.
Умножение рациональных выражений
Умножение рациональных выражений работает так же, как и умножение любых других дробей. Мы умножаем числители, чтобы найти числитель произведения, а затем умножаем знаменатели, чтобы найти знаменатель произведения.
Перед умножением полезно разложить числители и знаменатели на множители так же, как мы это делали при упрощении рациональных выражений. Нам часто удается упростить произведение рациональных выражений.Как
Даны два рациональных выражения, умножьте их.
- Разложите числитель и знаменатель на множители.
- Умножьте числители.
- Умножьте знаменатели.
- Упростить.
Пример 2
Умножение рациональных выражений
Умножение рациональных выражений и представление произведения в простейшей форме:
x2+4x−53x+18⋅2x−1x+5×2+4x−53x+18⋅2x−1x+5
Решение
(x+5)(x−1)3(x+6)⋅(2x−1)(x+5)Разложить на множители числитель и знаменатель.(x+5)(x−1)(2x−1)3 (x+6)(x+5)Умножить числители и знаменатели.(x+5)(x−1)(2x−1)3(x+6)(x+5)Отменить общие множители для упрощения.
(x− 1)(2x−1)3(x+6) (x+5)(x−1)3(x+6)⋅(2x−1)(x+5) Разложите числитель и знаменатель на множители (x+5). )(x−1)(2x−1)3(x+6)(x+5)Умножение числителей и знаменателей.(x+5)(x−1)(2x−1)3(x+6)(x +5)Отменить общие множители для упрощения.(x−1)(2x−1)3(x+6)Попытайся #2
Умножьте рациональные выражения и покажите произведение в простейшей форме:
х2+11х+30х2+5х+6х2+7х+12х2+8х+16х2+11х+30х2+5х+6х2+7х+12х2+8х+16
Деление рациональных выражений
Деление рациональных выражений работает так же, как и деление других дробей. Чтобы разделить рациональное выражение на другое рациональное выражение, умножьте первое выражение на обратную величину второго. Используя этот подход, мы перепишем 1x÷x231x÷x23 как произведение 1x⋅3×2,1x⋅3×2. Как только выражение деления было переписано как выражение умножения, мы можем умножать, как делали это раньше.
1x⋅3×2=3x31x⋅3×2=3×3
Как
Даны два рациональных выражения, разделите их.
- Перепишите как первое рациональное выражение, умноженное на обратную величину второго.
- Разложите числители и знаменатели на множители.
- Умножьте числители.
- Умножьте знаменатели.
- Упростить.
Пример 3
Деление рациональных выражений
Деление рациональных выражений и выражение частного в простейшей форме:
2×2+x−6×2−1÷x2−4×2+2x+12×2+x−6×2−1÷x2−4×2+2x+1
Решение
2×2+x−6×2−1⋅x2+2x+1×2−4 Переписать как умножение.(2x−3)(x+2)(x+1)(x−1)⋅(x+1)2(x+2) )(x−2)Коэффициент.(2x−3)(x+2)(x+1)2(x+1)(x−1)(x+2)(x−2)Умножить.(2x−3 )(x+1)(x−1)(x−2)Отменить общие множители для упрощения.2×2+x−6×2−1⋅x2+2x+1×2−4Переписать как умножение.(2x−3)(x+2) (x+1)(x−1)⋅(x+1)2(x+2)(x−2)Коэффициент.(2x−3)(x+2)(x+1)2(x+1) (x−1)(x+2)(x−2)Умножить.(2x−3)(x+1)(x−1)(x−2)Отменить общие множители для упрощения.
Попытайся #3
Разделить рациональные выражения и выразить частное в простейшей форме:
9×2−163×2+17x−28÷3×2−2x−8×2+5x−149×2−163×2+17x−28÷3×2−2x−8×2+5x−14
Сложение и вычитание рациональных выражений
Сложение и вычитание рациональных выражений работает так же, как сложение и вычитание числовых дробей.
Чтобы сложить дроби, нам нужно найти общий знаменатель. Рассмотрим пример сложения дробей.524+140=25120+3120=28120=730524+140=25120+3120=28120=730
Мы должны переписать дроби, чтобы они имели общий знаменатель, прежде чем мы сможем складывать. Мы должны делать то же самое при сложении или вычитании рациональных выражений.
Самый простой в использовании общий знаменатель — это наименьший общий знаменатель, или LCD. LCD — это наименьшее кратное, общее для знаменателей. Чтобы найти LCD двух рациональных выражений, мы факторизуем выражения и перемножаем все различные множители. Например, если факторизованные знаменатели были (x+3)(x+4)(x+3)(x+4) и (x+4)(x+5),(x+4)(x+5) , тогда ЖК-экран будет (x+3)(x+4)(x+5).(x+3)(x+4)(x+5).
Как только мы найдем ЖК, нам нужно умножить каждое выражение на форму 1, что изменит знаменатель на ЖК. Нам нужно будет умножить выражение со знаменателем (x+3)(x+4)(x+3)(x+4) на x+5x+5x+5x+5, а выражение со знаменателем (x +4)(x+5)(x+4)(x+5) на x+3x+3.
x+3x+3.Как
Даны два рациональных выражения, сложите или вычтите их.
- Разложите числитель и знаменатель на множители.
- Найдите на ЖК-дисплее выражения.
- Умножьте выражения на форму 1, которая меняет знаменатели на LCD.
- Добавьте или вычтите числители.
- Упростить.
Пример 4
Добавление рациональных выражений
Добавление рациональных выражений:
5x+6y5x+6y
Решение
Сначала нам нужно найти ЖК-дисплей. В этом случае ЖК-дисплей будет xy.xy. Затем мы умножаем каждое выражение на соответствующую форму 1, чтобы получить xyxy в качестве знаменателя для каждой дроби.
5x⋅yy+6y⋅xx5yxy+6xxy5x⋅yy+6y⋅xx5yxy+6xxy
Теперь, когда выражения имеют одинаковый знаменатель, мы просто складываем числители, чтобы найти сумму.
6x+5yxy6x+5yxy
Анализ
Умножение на yyyy или xxxx не изменяет значение исходного выражения, поскольку любое число, деленное само на себя, равно 1, а умножение выражения на 1 дает исходное выражение.
Пример 5
Вычитание рациональных выражений
Вычитание рациональных выражений:
6×2+4x+4-2×2-46×2+4x+4-2×2-4
Решение
6(x+2)2−2(x+2)(x−2)Коэффициент.6(x+2)2⋅x−2x−2−2(x+2)(x−2)⋅x+ 2x+2Умножьте каждую дробь, чтобы получить LCD в качестве знаменателя.6(x−2)(x+2)2(x−2)−2(x+2)(x+2)2(x−2)Multiply.6x− 12−(2x+4)(x+2)2(x−2)Применить распределительное свойство.4x−16(x+2)2(x−2)Вычесть.4(x−4)(x+2)2 (x−2)Упрощение.6(x+2)2−2(x+2)(x−2)Коэффициент.6(x+2)2⋅x−2x−2−2(x+2)(x −2)⋅x+2x+2Умножьте каждую дробь, чтобы получить LCD в качестве знаменателя.6(x−2)(x+2)2(x−2)−2(x+2)(x+2)2(x− 2) Умножить.6x−12−(2x+4)(x+2)2(x−2)Применить распределительное свойство.
4x−16(x+2)2(x−2)Вычесть.4(x−4) (x+2)2(x−2)Упростить.вопросы и ответы
Должны ли мы использовать ЖК-дисплей для сложения или вычитания рациональных выражений?
Нет. Подойдет любой общий знаменатель, но проще всего использовать ЖК-дисплей.
Попытайся #4
Вычтите рациональные выражения: 3x+5-1x-3,3x+5-1x-3.
Упрощение сложных рациональных выражений
Комплексное рациональное выражение — это рациональное выражение, которое содержит дополнительные рациональные выражения в числителе, знаменателе или в обоих. Мы можем упростить сложные рациональные выражения, переписав числитель и знаменатель как отдельные рациональные выражения и разделив их. Сложное рациональное выражение a1b+ca1b+c можно упростить, переписав числитель как дробь a1a1 и объединив выражения в знаменателе как 1+bcb.
1+bcb. Затем мы можем переписать выражение как задачу на умножение, используя обратную величину знаменателя. Получаем a1⋅b1+bc,a1⋅b1+bc, что равно ab1+bc.ab1+bc.Как
Дано сложное рациональное выражение, упростите его.
- Объедините выражения в числителе в одно рациональное выражение путем сложения или вычитания.
- Объедините выражения в знаменателе в одно рациональное выражение путем сложения или вычитания.
- Перепишите как числитель разделить на знаменатель.
- Переписать как умножение.
- Умножить.
- Упростить.
Пример 6
Упрощение сложных рациональных выражений
Упрощение: y+1xxyy+1xxy .
Решение
Начните с объединения выражений в числителе в одно выражение.
y⋅xx+1x Умножить на xx, чтобы получить LCD в качестве знаменателя.
xyx+1xxy+1x Добавить числители.y⋅xx+1x Умножить на xx, чтобы получить LCD в качестве знаменателя.xyx+1xxy+1x Добавить числители.Теперь числитель — это единственное рациональное выражение, а знаменатель — это единственное рациональное выражение.
xy+1xxyxy+1xxy
Мы можем переписать это как деление, а затем умножение.
xy+1x÷xyxy+1x⋅yxПереписать как умножение.y(xy+1)x2Умножить.xy+1x÷xyxy+1x⋅yxПереписать как умножение.y(xy+1)x2Умножить.
Попытайся #5
Упрощение: xy-yxyxy-yxy
вопросы и ответы
Всегда ли можно упростить сложное рациональное выражение?
Да. Мы всегда можем переписать сложное рациональное выражение как упрощенное рациональное выражение.
1.6 Секционные упражнения
Вербальный
1.
Как можно использовать факторинг для упрощения рациональных выражений?
2.
Как с помощью ЖК-дисплея объединить два рациональных выражения?
3.
Скажите, верно или нет следующее утверждение, и объясните, почему: Вам нужно найти ЖК только при сложении или вычитании рациональных выражений.
Алгебраический
Для следующих упражнений упростите рациональные выражения.
4.
x2-16×2-5x+4×2-16×2-5x+4
5.
у2+10у+25у2+11у+30у2+10у+25у2+11у+30
6.
6а2-24а+246а2-246а2-24а+246а2-24
7.
9b2+18b+93b+39b2+18b+93b+3
8.
м-12м2-144м-12м2-144
9.
2×2+7x-44×2+2x-22×2+7x-44×2+2x-2
10.
6×2+5x-43×2+19x+206×2+5x-43×2+19x+20
11.
а2+9а+18а2+3а-18а2+9а+18а2+3а-18
12.
3c2+25c-183c2-23c+143c2+25c-183c2-23c+14
13.
12n2-29n-828n2-5n-312n2-29n-828n2-5n-3
В следующих упражнениях умножьте рациональные выражения и выразите произведение в простейшей форме.
14.
x2-x-62×2+x-6⋅2×2+7x-15×2-9×2-x-62×2+x-6⋅2×2+7x-15×2-9
15.
c2+2c−24c2+12c+36⋅c2−10c+24c2−8c+16c2+2c−24c2+12c+36⋅c2−10c+24c2−8c+16
16.
2d2+9d−35d2+10d+21⋅3d2+2d−213d2+14d−492d2+9d−35d2+10d+21⋅3d2+2d−213d2+14d−49
17.
10h3-9h-92h3-19h+24⋅h3-16h+645h3-37h-2410h3-9h-92h3-19h+24⋅h3-16h+645h3-37h-24
18.
6b2+13b+64b2-9⋅6b2+31b-3018b2-3b-106b2+13b+64b2-9⋅6b2+31b-3018b2-3b-10
19.
2d2+15d+254d2−25⋅2d2−15d+2525d2−12d2+15d+254d2−25⋅2d2−15d+2525d2−1
20.
6×2-5x-5015×2-44x-20⋅20×2-7x-62×2+9x+106×2-5x-5015×2-44x-20⋅20×2-7x-62×2+9х+10
21.
t2-1t2+4t+3⋅t2+2t-15t2-4t+3t2-1t2+4t+3⋅t2+2t-15t2-4t+3
22.
2n2−n−156n2+13n−5⋅12n2−13n+34n2−15n+92n2−n−156n2+13n−5⋅12n2−13n+34n2−15n+9
23.
36×2−256×2+65x+50⋅3×2+32x+2018×2+27x+1036×2−256×2+65x+50⋅3×2+32x+2018×2+27x+10
Для следующих упражнений разделите рациональные выражения.
24.
3y2-7y-62y2-3y-9÷y2+y-22y2+y-33y2-7y-62y2-3y-9÷y2+y-22y2+y-3
25.
6п2+п-128п2+18п+9÷6п2-11п+42п2+11п-66п2+п-128п2+18п+9÷6п2-11п+42п2+11п-6
26.
q2-9q2+6q+9÷q2-2q-3q2+2q-3q2-9q2+6q+9÷q2-2q-3q2+2q-3
27.
18d2+77d−1827d2−15d+2÷3d2+29d−449d2−15d+418d2+77d−1827d2−15d+2÷3d2+29d−449d2−15d+4
28.
16×2+18x-5532×2-36x-11÷2×2+17x+304×2+25x+616×2+18x-5532×2-36x-11÷2×2+17x+304×2+25x+6
29.
144b2-2572b2-6b-10÷18b2-21b+536b2-18b-10144b2-2572b2-6b-10÷18b2-21b+536b2-18b-10
30.
16а2-24а+94а2+17а-15÷16а2-94а2+11а+616а2-24а+94а2+17а-15÷16а2-94а2+11а+6
31.
22y2+59y+1012y2+28y−5÷11y2+46y+824y2−10y+122y2+59y+1012y2+28y−5÷11y2+46y+824y2−10y+1
32.
9×2+3x-203×2-7x+4÷6×2+4x-10×2-2x+19×2+3x-203×2-7x+4÷6×2+4x-10×2-2x+1
В следующих упражнениях сложите и вычтите рациональные выражения, а затем упростите.
33.
4x+10y4x+10y
34.
122q-63p122q-63p
35.
4а+1+5а-34а+1+5а-3
36.
с+23-с-44с+23-с-44
37.
у+3у-2+у-3у+1у+3у-2+у-3у+1
38.
х-1х+1-2х+32х+1х-1х+1-2х+32х+1
39.
3zz+1+2z+5z−23zz+1+2z+5z−2
40.
4pp+1−p+14p4pp+1−p+14p
41.
хх+1+уу+1хх+1+уу+1
Для следующих упражнений упростите рациональное выражение.
42.
6y-4xy6y-4xy
43.
2а+7бб2а+7бб
44.
x4-p8px4-p8p
45.
3а+b62b3a3а+b62b3а
46.
3x+1+2x-1x-1x+13x+1+2x-1x-1x+1
47.
аб-баа+бабаб-баа+баб
48.
2×3+4x7x22x3+4x7x2
49.
2cc+2+c-1c+12c+1c+12cc+2+c-1c+12c+1c+1
50.
xy-yxxy+yxxy-yxxy+yx
Реальные приложения
51.
Бренда укладывает плитку на пол в ванной. Площадь пола 15×2−8x−715×2−8x−7 футов 2 . Площадь одной плитки равна x2−2x+1ft2.x2−2x+1ft2. Чтобы найти необходимое количество плиток, упростите рациональное выражение: 15×2−8x−7×2−2x+1,15×2−8x−7×2−2x+1.
52.
Площадь двора Лицзюаня составляет 25×2−62525×2−625 футов 2 . Участок дерна имеет площадь x2−10x+25×2−10x+25 футов 2 . Разделите две области и упростите, чтобы найти, сколько кусков дерна нужно Лицзюань, чтобы покрыть ее двор.
53.
Элрой хочет замульчировать свой сад. Его сад x2+18x+81×2+18x+81 ft 2 .
Один мешок мульчи покрывает x2−81×2−81 ft 2 . Разделите выражения и упростите, чтобы найти, сколько мешков мульчи нужно Элрою для мульчирования своего сада.Удлинители
Для следующих упражнений выполните данные операции и упростите.
54.
x2+x-6×2-2x-3⋅2×2-3x-9×2-x-2÷10×2+27x+18×2+2x+1×2+x-6×2-2x-3⋅2×2-3x-9×2-x-2÷ 10×2+27x+18×2+2x+1
55.
3y2-10y+33y2+5y-2⋅2y2-3y-202y2-y-15y-43y2-10y+33y2+5y-2⋅2y2-3y-202y2-y-15y-4
56.
4а+12а-3+2а-32а+34а2+9а4а+12а-3+2а-32а+34а2+9а
57.
x2+7x+12×2+x−6÷3×2+19x+288×2−4x−24÷2×2+x−33×2+4x−7×2+7x+12×2+x−6÷3×2+19x+288×2−4x−24÷ 2×2+x-33×2+4x-7
Сложение и вычитание рациональных выражений
Указатель уроков
Распечатать эту страницу (версия для печати) | Найти местных репетиторовДобавление и вычитание рациональных выражений:
Введение (стр. 1 из 3) Сложение и вычитание самые сложные вещи, которые вы будете делать с рациональными выражениями, потому что, как и в случае с обычными дробями, вам придется преобразовать их в общие знаменатели. Все, что вы ненавидели в добавлении дробей, вы будете ненавидеть еще больше с рациональными выражениями. Но держись за меня; ты можно дозвониться это!
Освежим взглядом на примере с правильными дробями:
- Упростите следующее:
Чтобы найти общий знаменатель, Сначала мне нужно найти наименьшее общее кратное (НОК) из трех знаменателей. (Для таких стариков, как я, всякий раз, когда вы видите «LCM», думайте «LCD» или «наименьший общий знаменатель». В этом контексте они почти одно и то же.) Есть по крайней мере несколько способов сделать это.
Вы можете использовать метод «список»,
где вы перечисляете кратные трех знаменателей, пока не найдете
число, которое есть во всех трех списках, например:5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55,…
25: 25, 50, 75, 100, 125, 150, 175, 200,…
10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100,…
Первый кратный встречаются во всех трех списках — 50, так что это будет общий знаменатель.
Другой метод, который вы могли бы используем для нахождения общего знаменателя фактор метод. Оно работает путем нахождения простого факторизация каждого знаменателя, а затем использование диаграммы для нахождения необходимых множителей для общего знаменателя.
Выглядит так:В любом случае общий знаменатель будет 50. Чтобы привести каждую дробь к общему знаменателю, нужно умножить каждую знаменатель на то, что ему нужно, чтобы превратить его в «50». Например, в 2 / 5 , знаменатель нужно умножить на 10, начиная с 10×5 = 50. Хранить вещи справедливо, вы также умножаете вершину на 10. Это потому что 10/10 = 1, и умножение вещи на 1 на самом деле не меняют их. Таким образом, вы получаете:
Преобразование другого дроби, вы получаете:
Тогда ответ:
Процесс работает аналогично для рационалов.
- Упростите следующее: Авторские права © Элизабет Стапель 2003-2011 Все права защищены
Чтобы найти общий знаменатель, Мне нужно найти наименьшее общее кратное x , x 2 , и 2 х .
В предыдущей задаче я использовал метод «листинга», чтобы найти
общий знаменатель. Но в данном случае у меня есть числа и переменные,
так что просто умножить на числа не получится. Чтобы найти общее
знаменатель выше, все, что мне нужно было сделать, это умножить каждый знаменатель на 1,
затем 2,
затем 3,
затем 4,…
и так далее, пока не найду совпадение. Но что я должен умножать переменные
по? Таким образом, «перечисление» не будет работать для рационального использования. мне придется использовать
фактор
метод вместо этого.
Вот что я получаю:Мой общий знаменатель будет 2 x 2 . Чтобы привести «2/ x » к общему знаменателю, мне нужно будет умножить на 2 x /2 x , так как в знаменателе уже есть одна копия x , но нужно 2 и еще x :
Аналогично, для 3/ х 2 , умножу на 2/2; а для 1/2 x я буду умножить на х / х .
Это дает мне:Тогда ответ:
Это выражение не может быть еще более упрощенным. x не может отменить, и 2 не может отменить в 6. Почему бы и нет? Потому что вы можете отменить только факторы, а не термины. Вы не можете достичь внутри «5 x + фактор 6 дюймов и отрывать части от него, чтобы сократить со знаменателем. Не пытайтесь!
Топ | 1 | 2 | 3 | Вернуться к оглавлению Далее >>
Цитировать эту статью как:
Стапель, Элизабет. «Сложение и вычитание рациональных выражений».
Еще хотел бы отметить, что наша школьная система образования устроена таким образом, что именно с изучением этой темы, т.е. рациональных выражений, а также корней, модулей у всех учеников возникает одна и та же проблема, которую я сейчас объясню.
Дело в том, что в самом начале изучения формул сокращенного умножения и, соответственно, действий по сокращению дробей (это где-то 8 класс) учителя говорят что-то следующее: «Если вам что-то непонятно, то вы не переживайте, мы к этой теме еще вернемся неоднократно, в старших классах так точно. Мы это еще разберем». Ну а затем на рубеже 9-10 класса те же самые учителя объясняют тем же самым ученикам, которые так и не знают, как решать рациональные дроби, примерно следующее: «А где вы были предыдущие два года? Это же изучалось на алгебре в 8 классе! Чего тут может быть непонятного? Это же так очевидно!».
Однако обычным ученикам от таких объяснений нисколько не легче: у них как была каша в голове, так и осталась, поэтому прямо сейчас мы разберем два простых примера, на основании которых и посмотрим, каким образом в настоящих задачах выделять эти выражения, которые приведут нас к формулам сокращенного умножения и как потом применять это для преобразования сложных рациональных выражений.
{2}}\]\[{{x}_{1}}=\frac{-5y+7y}{2}=y\]
\[{{x}_{2}}=\frac{-5y-7y}{2}=\frac{-12y}{2}=-6y\]
Запишем разложение нашей квадратной конструкции:
\[\left(x-y \right)\left(x+6y \right)\]
Итого если мы вернемся к исходному выражению и перепишем его с учетом изменений, то получим следующее:
\[\frac{8}{\left(x-y \right)\left(x+6y \right)}\]
Что нам дает такая запись? Ничего, потому что его не сократить, оно ни на что не умножается и не делится. Однако как только эта дробь окажется составной частью более сложного выражения, подобное разложение окажется кстати. Поэтому как только вы видите квадратный трехчлен (неважно, отягощен он дополнительными параметрами или нет), всегда старайтесь разложить его на множители.
Нюансы решения
Запомните основные правила преобразования рациональных выражений:
{2}} \right)}{\left( 2x-1 \right)\left( 2x+1 \right)}=\]
{2}}}=\]
{2}}+2x+4}{\left( x-2 \right)\left( x+2 \right)}=\frac{1}{x+2}\]
Если поставить между ними знак умножения, то получится одночлен, называемый произведением исходных одночленов. При возведении одночлена в натуральную степень также получается одночлен. Результат обычно приводят к стандартному виду.
При получим и Числа 0 и 3 называются соответственными значениями выражений
Тождественными преобразованиями являются также умножение одночленов и их возведение в натуральную степень, приведение подобных членов. Другие примеры тождественных преобразований выражений будут рассмотрены ниже.
Воспользовавшись этим правилом раскрытия скобок, получим
Рассмотрим некоторые наиболее употребительные методы разложения многочленов на множители.
В некоторых случаях приведение многочлена к стандартному виду, а также разложение на множители производится с помощью тождеств сокращенного умножения.
Поменяв в тождестве (2) b на -b получим
Рассмотрим теперь выражение и преобразуем его в многочлен стандартного вида:
Если рациональное выражение не содержит операции деления на выражение с переменными, то оно называется целым. Если же при составлении рационального выражения используется операция деления на выражение с переменными, то это рациональное выражение называется дробным.
Если дана алгебраическая дробь, причем знаменатель содержит переменные, то чтобы найти область определения дроби, нужно найти значения переменных, при которых знаменатель обращается в ноль, и исключить такие значения.
Умножив и числитель, и знаменатель дроби на 12, получим
Если общих множителей нет, то упрощение дроби посредством сокращения невозможно. Сокращение дроби есть тождественное преобразование.
Например, общим знаменателем дробей служит многочлен так как он делится и на Следует, однако, заметить, что это не единственное решение поставленной задачи: общим знаменателем данных дробей будет и многочлен и многочлен и многочлен и т. д. Обычно берут такой общий знаменатель, что любой другой общий знаменатель делится на выбранный без остатка. Такой знаменатель называется наименьшим общим знаменателем (НОЗ). В рассмотренном выше примере НОЗ равен
Нетрудно понять, что дополнительный множитель для данной дроби равен частному от деления НОЗ на знаменатель данной дроби.
Покажем на примерах, как это делается.
е.
Преобразование рациональных и иррациональных выражений
степень: ;
Попробуем решить этот же пример вторым способом.
Выражение также представляется в виде дроби. Только в числители у нас — не числа, а различного рода выражения. Чаще всего этого многочлены. Алгебраическая дробь — дробное выражение, состоящее из чисел и переменных.
2}$.
одночлен: ;
Попробуем решить этот же пример вторым способом.
{2}} \right)$ — разность кубов.
{2}}\]
{2}} \right)}{\left(2x-1 \right)\left(2x+1 \right)}=\]
{2}}}=\]
{2}}+2x+4}{\left(x-2 \right)\left(x+2 \right)}=\frac{1}{x+2}\]
..
