Как рассчитать 4 комбинации чисел? – Обзоры Вики
Формула для комбинаций: nCr = n! / р! * (n — r) !, где n представляет количество элементов, а r представляет количество элементов, выбираемых за раз.
Отсюда, как вы рассчитываете перестановки и комбинации? Какова формула перестановок и комбинаций? Формула для перестановок: nPr = n! / (nr)! Формула для комбинаций: nCr = n!/[r! (номер)!]
Как считать перестановки? Чтобы рассчитать количество перестановок, возьмите количество возможностей для каждого события, а затем умножьте это число на себя X раз, где X равно количеству событий в последовательности. Например, в четырехзначном PIN-коде каждая цифра может находиться в диапазоне от 0 до 9, что дает нам 10 возможных вариантов для каждой цифры.
Дополнительно В чем разница между перестановками и комбинациями? Перестановка — это количество различных расстановок, которые можно составить, выбрав r вещей из доступных n вещей. Комбинация — это количество различных групп по r объектов в каждой, которые можно составить из имеющихся n объектов.
Сколькими способами можно расположить 123? Это в общей сложности 7 комбинации.
Как вы решаете примеры перестановок?
Как вы делаете перестановки в Word?
- Microsoft Word > Лента > Вставка > Уравнение > Сценарий > Подстрочный индекс.
- Затем выберите нижнюю часть и снова нажмите Subscript.
- Вы получите трехуровневый индекс, как символ перестановки или комбинации.
- Затем вставьте свои числа или переменные.
Также допускают ли перестановки повторение? Перестановки: порядок имеет значение, повторения не допускаются.
Почему мы размножаемся перестановками?
Принцип умножения позволяет мы подсчитываем количество способов выполнить последовательность задач, умножая количество способов выполнить каждую задачу. Перестановка — это определенный порядок некоторых объектов.
Имеет ли значение порядок в перестановках? Если порядок не имеет значения, то у нас есть комбинация, если порядок имеет значение, у нас есть перестановка. Можно сказать, что перестановка — это упорядоченная комбинация. Количество перестановок n объектов, взятых по r за раз, определяется по следующей формуле: П (п, г) = п!
Сколько четырехзначных чисел можно образовать из цифр 1234?
Следовательно, в этом случае имеется 4 3 = 12 возможных двузначных чисел. Для третьей цифры есть только 2 варианта, а для последней цифры — один вариант. Таким образом, если вам не разрешено повторять цифру, количество возможных четырехзначных чисел, которые вы можете составить из 4, равно 1,2,3,4 4 3 2 = 24.
Сколько всего 4-значных комбинаций с 10 числами?
10 вариантов для первого циферблата, и для каждого из этих 10 вариантов для второго циферблата, и для каждого из этих 10 вариантов для третьего, и для каждого из этих 10 вариантов для четвертого. Итак, 10 х 10 х 10 х 10 = 10,000 комбинации, все возможные числа от 0000 до 9999.
Итак, 10 х 10 х 10 х 10 = 10,000 комбинации, все возможные числа от 0000 до 9999.
Каковы перестановки 123? Например, записанные в виде кортежей, есть шесть перестановки множества {1, 2, 3}, а именно (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2) и (3, 2, 1). Это все возможные порядки этого трехэлементного множества.
Какие есть примеры перестановок? Перестановки — это различные способы организации набора элементов. Например: различные способы группировки алфавитов А, В и С, взятые все одновременно, ABC, ACB, BCA, CBA, CAB, BAC. Обратите внимание, что ABC и CBA не совпадают, так как порядок расположения отличается.
Как написать перестановку?
При написании перестановок мы используем обозначение nPr, где n обозначает количество элементов для выбора, P обозначает перестановку, а r обозначает количество элементов, которые вы выбираете. Чтобы вычислить перестановку по этой формуле, вы должны использовать nPr = n! / (п — г)!.
com/embed/f-UE8EfF9k8″ frameborder=»0″ allowfullscreen=»allowfullscreen» data-original-w=»720″ data-original-h=»520″>Как вы делаете перестановки и комбинации на графическом калькуляторе?
Как вы иллюстрируете перестановку объекта?
Перестановка — это расположение объектов в определенном порядке. Члены или элементы множеств расположены здесь в последовательном или линейном порядке. Например, перестановка набора A={1,6} равна 2, например {1,6}, {6,1}. Как видите, других способов расположить элементы множества A нет.
Как быстро писать уравнения в Word?
com/embed/ge6a3wnAoUQ» frameborder=»0″ allowfullscreen=»allowfullscreen» data-original-w=»720″ data-original-h=»520″>Как в Word вставить символ пересечения? Перейти к Системные настройки > Клавиатура > вкладка Клавиатура и установите флажок Показать средства просмотра клавиатуры и символов в строке меню. Это поместит небольшой значок, обычно рядом с датой/временем, в строке меню. Множество символов. Поместите точку вставки в документ Word, затем дважды щелкните нужный символ.
4.Элементы комбинаторики — методическое пособие
Элементы комбинаторики Комбинаторика – это наука о расположении элементов в определенном порядке и о подсчете числа способов такого расположения.
Пример 1:
Пример 2: Рассмотрим задачу о формировании команды космического корабля. Известно, что возникнет вопрос психологической совместимости. Предположим, надо составить команду из 3-х человек: командира, инженера и врача.
элементного множества. Число сочетаний без повторений из элементов по равно :
различными способами.
Решение: Число способов выбора — это C74. = 7*6*5/3! = 7*6*5/6 = 7*5 = 35.
Задача 3: В футбольной команде пятого класса 7 человек.
Пример 1: Сколько различных 4-буквенных слов можно составить из символов 0,0,a,b? Решение: Другими словами, требуется найти число перестановок с повторениями на 4 элементах выборки, в которой два элемента одинаковы: Пример 2: Сколько различных перестановок можно составить из букв слова АБАКАН? Решение: Требуется найти число перестановок на множестве из 6 элементов, среди которых три элемента одинаковы: Пример 3: Сколько перестановок можно получить из букв слова КОЛОКОЛА?
увеличивается в 30 раз, т. |
основные правила и формулы Сколько комбинаций из 10 цифр
КОМБИНАТОРИКА
Комбинаторика — раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и, соответственно, получения законов распределения случайных величин. Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для правильного понимания статистических закономерностей, проявляющихся в природе и технике.
Правила сложения и умножения в комбинаторике
Правило суммы.
Пример 1.
В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного?
Решение
Дежурным можно назначить либо мальчика, либо девочку, т.е. дежурным может быть любой из 16 мальчиков, либо любая из 10 девочек.
По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами.
Правило произведения. Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n 1 способами, второе действие n 2 способами, третье — n 3 способами и так до k-го действия, которое можно выполнить n k способами, то все k действий вместе могут быть выполнены:
способами.
Пример 2.
В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?
Решение
Первым дежурным можно назначить либо мальчика, либо девочку. Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами.
Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами.
После того, как мы выбрали первого дежурного, второго мы можем выбрать из оставшихся 25 человек, т.е. 25-ю способами.
По теореме умножения двое дежурных могут быть выбраны 26*25=650 способами.
Сочетания без повторений. Сочетания с повторениями
Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать m из n различных предметов ?
Пример 3.
Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?
Решение
Нам из 10 книг нужно выбрать 4, причем порядок выбора не имеет значения. Таким образом, нужно найти число сочетаний из 10 элементов по 4:
.
Рассмотрим задачу о числе сочетаний с повторениями: имеется по r одинаковых предметов каждого из n различных типов; сколькими способами можно выбрать m () из этих (n*r) предметов?
.
Пример 4.
В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?
Решение
Т.к. среди 7 пирожных могут быть пирожные одного сорта, то число способов, которыми можно купить 7 пирожных, определяется числом сочетаний с повторениями из 7 по 4.
.
Размещения без повторений. Размещения с повторениями
Классической задачей комбинаторики является задача о числе размещений без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n различных предметов?
Пример 5.
В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии?
Решение.
В данной задаче мы не просто выбираем фотографии, а размещаем их на определенных страницах газеты, причем каждая страница газеты должна содержать не более одной фотографии. Таким образом, задача сводится к классической задаче об определении числа размещений без повторений из 12 элементов по 4 элемента:
Таким образом, 4 фотографии на 12 страницах можно расположить 11880 способами.
Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом: сколькими способами можно вы б рать и разместить по m различным местам m из n предметов, с реди которых есть одинаковые?
Пример 6.
У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера- составить каталог. Сколько различных пятизначных номеров может составить мальчик?
Сколько различных пятизначных номеров может составить мальчик?
Перестановки без повторений . Перестановки с повторениями
Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно выразить вопросом: сколькими способами можно разместить n различных предметов на n различных местах?
Пример 7.
Сколько можно составить четырехбуквенных «слов» из букв слова«брак»?
Решение
Генеральной совокупностью являются 4 буквы слова «брак» (б, р, а, к). Число «слов» определяется перестановками этих 4 букв, т. е.
Для случая, когда среди выбираемых n элементов есть одинаковые (выборка с возвращением), задачу о числе перестановок с повторениями можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов (k
Пример 8.
Сколько разных буквосочетаний можно сделать из букв слова «Миссисипи»?
Решение
Здесь 1 буква «м», 4 буквы «и», 3 буквы «c» и 1 буква «п», всего 9 букв. Следовательно, число перестановок с повторениями равно
ОПОРНЫЙ КОНСПЕКТ ПО РАЗДЕЛУ «КОМБИНАТОРИКА»
Комбинаторика — это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов. Основы комбинаторики очень важны для оценки вероятностей случайных событий, т.к. именно они позволяют подсчитать принципиально возможное количество различных вариантов развития событий.
Основная формула комбинаторики
Пусть имеется k групп элементов, причем i-я группа состоит из n i элементов. Выберем по одному элементу из каждой группы. Тогда общее число N способов, которыми можно произвести такой выбор, определяется соотношением N=n 1 *n 2 *n 3 *…*n k .
Пример 1. Поясним это правило на простом
примере. Пусть имеется две группы элементов, причем первая группа состоит из
n 1 элементов, а вторая — из n 2 элементов. Сколько
различных пар элементов можно составить из этих двух групп, таким образом,
чтобы в паре было по одному элементу от каждой группы? Допустим, мы взяли
первый элемент из первой группы и, не меняя его, перебрали все возможные
пары, меняя только элементы из второй группы. Таких пар для этого элемента
можно составить n 2 . Затем мы берем второй элемент из первой группы
и также составляем для него все возможные пары. Таких пар тоже будет n 2 .
Так как в первой группе всего n 1 элемент, всего возможных
вариантов будет n 1 *n 2 .
Пусть имеется две группы элементов, причем первая группа состоит из
n 1 элементов, а вторая — из n 2 элементов. Сколько
различных пар элементов можно составить из этих двух групп, таким образом,
чтобы в паре было по одному элементу от каждой группы? Допустим, мы взяли
первый элемент из первой группы и, не меняя его, перебрали все возможные
пары, меняя только элементы из второй группы. Таких пар для этого элемента
можно составить n 2 . Затем мы берем второй элемент из первой группы
и также составляем для него все возможные пары. Таких пар тоже будет n 2 .
Так как в первой группе всего n 1 элемент, всего возможных
вариантов будет n 1 *n 2 .
Пример 2. Сколько
трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если
цифры могут повторяться?
Решение: n 1 =6
(т.к. в качестве первой цифры можно взять любую цифру из 1, 2, 3, 4, 5, 6), n 2 =7
(т.к. в качестве второй цифры можно взять любую цифру из 0, 1, 2, 3, 4, 5,
6), n 3 =4 (т.к. в качестве третьей цифры можно взять любую цифру из 0, 2, 4,
6).
Итак, N=n 1 *n 2 *n 3 =6*7*4=168.
В том случае, когда все группы состоят из одинакового числа элементов, т.е. n 1 =n 2 =…n k =n можно считать, что каждый выбор производится из одной и той же группы, причем элемент после выбора снова возвращается в группу. Тогда число всех способов выбора равно n k . Такой способ выбора в комбинаторики носит название выборки с возвращением.
Пример 3. Сколько всех четырехзначных чисел
можно составить из цифр 1, 5, 6, 7, 8?
Решение. Для каждого разряда
четырехзначного числа имеется пять возможностей, значит N=5*5*5*5=5 4 =625.
Рассмотрим множество, состоящие из n элементов. Это множество в комбинаторике называется генеральной совокупностью .
Число размещений из n элементов по m
Определение 1. Размещением из n элементов по m в комбинаторике называется
любой упорядоченный набор из m различных
элементов, выбранных из генеральной совокупности в n элементов.
Пример 4. Различными размещениями из трех элементов {1, 2, 3} по два будут наборы (1, 2), (2, 1), (1, 3), (3, 1), (2, 3),(3, 2). Размещения могут отличаться друг от друга как элементами, так и их порядком.
Число размещений в комбинаторике обозначается A n m и вычисляется по формуле:
Замечание: n!=1*2*3*…*n (читается: «эн факториал»), кроме того полагают, что 0!=1.
Пример 5 . Сколько существует двузначных
чисел, в которых цифра десятков и цифра единиц различные
и нечетные?
Решение: т.к. нечетных цифр
пять, а именно 1, 3, 5, 7, 9, то эта задача сводится к выбору и размещению на
две разные позиции двух из пяти различных цифр, т.е. указанных чисел будет:
Определение 2. Сочетанием из n элементов по m в комбинаторике называется любой неупорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.
Пример 6 . Для множества {1, 2,
3}сочетаниями являются {1, 2}, {1, 3}, {2, 3}.
Для множества {1, 2,
3}сочетаниями являются {1, 2}, {1, 3}, {2, 3}.
Число сочетаний из n элементов по m
Число сочетаний обозначается C n m и вычисляется по формуле:
Пример 7. Сколькими способами читатель может выбрать две книжки из шести имеющихся?
Решение: Число способов равно числу сочетаний из шести книжек по две, т.е. равно:
Перестановки из n элементов
Определение 3. Перестановкой из n элементов называется любой упорядоченный набор этих элементов.
Пример 7a. Всевозможными перестановками множества, состоящего из трех элементов {1, 2, 3} являются: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), (3, 2, 1), (3, 1, 2).
Число различных перестановок из n элементов обозначается P n и вычисляется по формуле P n =n!.
Пример 8. Сколькими способами семь книг разных авторов можно расставить на полке в один ряд?
Решение: эта задача о числе
перестановок семи разных книг. Имеется P 7 =7!=1*2*3*4*5*6*7=5040
способов осуществить расстановку книг.
Имеется P 7 =7!=1*2*3*4*5*6*7=5040
способов осуществить расстановку книг.
Обсуждение. Мы видим, что число возможных комбинаций можно посчитать по разным правилам (перестановки, сочетания, размещения) причем результат получится различный, т.к. принцип подсчета и сами формулы отличаются. Внимательно посмотрев на определения, можно заметить, что результат зависит от нескольких факторов одновременно.
Во-первых, от того, из какого количества элементов мы можем комбинировать их наборы (насколько велика генеральная совокупность элементов).
Во-вторых, результат зависит от того, какой величины наборы элементов нам нужны.
И последнее, важно знать, является ли для нас существенным порядок элементов в наборе. Поясним последний фактор на следующем примере.
Пример 9. На родительском собрании
присутствует 20 человек. Сколько существует различных вариантов состава
родительского комитета, если в него должны войти 5 человек?
Решение: В этом примере нас
не интересует порядок фамилий в списке комитета. Если в результате в его
составе окажутся одни и те же люди, то по смыслу для нас это один и тот же
вариант. Поэтому мы можем воспользоваться формулой для подсчета числа сочетаний из 20 элементов по 5.
Если в результате в его
составе окажутся одни и те же люди, то по смыслу для нас это один и тот же
вариант. Поэтому мы можем воспользоваться формулой для подсчета числа сочетаний из 20 элементов по 5.
Иначе будут обстоять дела, если каждый член комитета изначально отвечает за определенное направление работы. Тогда при одном и том же списочном составе комитета, внутри него возможно 5! вариантов перестановок , которые имеют значение. Количество разных (и по составу, и по сфере ответственности) вариантов определяется в этом случае числом размещений из 20 элементов по 5.
Задачи для самопроверки
1. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5,
6, если цифры могут повторяться?
Т.к. число четное на третьем месте может стоять 0, 2, 4, 6, т.е. четыре цифры. На втором месте может стоять любая из семи цифр. На первом месте может стоять любая из семи цифр кроме нуля, т.е. 6 возможностей. Результат =4*7*6=168.
2. Сколько существует пятизначных чисел, которые одинаково читаются слева
направо и справа налево?
Сколько существует пятизначных чисел, которые одинаково читаются слева
направо и справа налево?
На первом месте может стоять любая цифра кроме 0, т.е. 9 возможностей. На втором месте может стоять любая цифра, т.е. 10 возможностей. На третьем месте тоже может стоять любая цифра из, т.е. 10 возможностей. Четвертая и пятая цифры определены заранее, они совпадают с первой и второй, следовательно, число таких чисел 9*10*10=900.
3. В классе десять предметов и пять уроков в день. Сколькими способами можно
составить расписание на один день?
4. Сколькими способами можно выбрать 4 делегата на конференцию, если в группе 20 человек?
n = C 20 4 = (20!)/(4!*(20-4)!)=(16!*17*18*19*20)/((1*2*3*4)*(16!))=(17*18*19*20)/(1*2*3*4)=4845.
5. Сколькими способами можно разложить восемь различных писем по восьми
различным конвертам, если в каждый конверт кладется только одно письмо?
В первый конверт можно положить 1 из восьми писем, во второй одно из семи оставшихся, в третий одно из шесть т. д. n = 8! = 1*2*3*4*5*6*7*8 = 40320.
д. n = 8! = 1*2*3*4*5*6*7*8 = 40320.
6. Из трех математиков и десяти экономистов надо составить комиссию,
состоящую из двух математиков и шести экономистов. Сколькими способами это
можно сделать?
Друзья! Раз уж есть у меня этот мертвый блокнот, использую-ка я его для того, чтобы задать вам задачку, над которой вчера билось три физика, два экономиста, один политеховский и один гуманитарий. Мы сломали себе весь мозг и у нас постоянно получаются разные результаты. Может быть, среди вас есть программисты и математические гении, к тому же, задачка вообще школьная и очень легкая, у нас просто не выводится формула. Потому что мы бросили занятия точными науками и вместо этого зачем-то пишем книги и рисуем картины. Простите.
Итак, предыстория.
Мне выдали новую банковскую карточку и я, как водится, играючи угадала ее пин-код. Но не подряд. В смысле, допустим, пин-код был 8794, а я назвала 9748. То есть, я триумфально угадала все цифры , которое содержались в данном четырехзначном числе. Ну да, не само число , а просто его составляющие у гадала. Но цифры-то все верные! ПРИМЕЧАНИЕ — я действовала наугад, то есть, мне не надо было расставить уже известные числа в нужном порядке, я просто действовала в духе: вот тут есть неизвестные мне четыре цифры, и я считаю, что среди них могут быть 9, 7, 4 и 8, а порядок их не важен. Мы тут же задались вопросом, сколько у меня вообще было вариантов (наверное, чтобы понять, насколько это круто, что я вот взяла и угадала). То есть, из скольких комбинаций четырех цифр мне нужно было выбирать? И тут, натурально, начался ад. У нас весь вечер взрывалась голова, и у всех, в итоге, вышли абсолютно разные варианты ответа! Я даже начала выписывать все эти комбинации в блокнот подряд по мере возрастания, но на четырех сотнях поняла, что их больше четырех сотен (во всяком случае, это опровергло ответ физика Трэша, который уверял меня, что комбинаций четыре сотни, но все равно это не совсем однозначно) — и сдалась.
Ну да, не само число , а просто его составляющие у гадала. Но цифры-то все верные! ПРИМЕЧАНИЕ — я действовала наугад, то есть, мне не надо было расставить уже известные числа в нужном порядке, я просто действовала в духе: вот тут есть неизвестные мне четыре цифры, и я считаю, что среди них могут быть 9, 7, 4 и 8, а порядок их не важен. Мы тут же задались вопросом, сколько у меня вообще было вариантов (наверное, чтобы понять, насколько это круто, что я вот взяла и угадала). То есть, из скольких комбинаций четырех цифр мне нужно было выбирать? И тут, натурально, начался ад. У нас весь вечер взрывалась голова, и у всех, в итоге, вышли абсолютно разные варианты ответа! Я даже начала выписывать все эти комбинации в блокнот подряд по мере возрастания, но на четырех сотнях поняла, что их больше четырех сотен (во всяком случае, это опровергло ответ физика Трэша, который уверял меня, что комбинаций четыре сотни, но все равно это не совсем однозначно) — и сдалась.
Собственно, суть вопроса. Какова вероятность угадывания (в любом порядке) четырех чисел, содержащихся в четырехзначном числе?
Какова вероятность угадывания (в любом порядке) четырех чисел, содержащихся в четырехзначном числе?
Или нет, переформулируем (я гуманитарий, простите, хотя к математике всегда питала огромную слабость), чтобы было яснее и четче. Сколько не повторяющихся комбинаций цифр содержится в ряду порядковых числительных от 0 до 9999? (пожалуйста, не путайте это с вопросом «сколько комбинаций не повторяющихся цифр»!! ! цифры могут повторяться! в смысле, 2233 и 3322 — это в данном случае одна и та же комбинация!!).
Или еще конкретнее. Мне нужно четыре раза угадать одну цифру из десяти. Но не подряд.
Ну или еще как-нибудь. В общем, нужно узнать, сколько у меня было вариантов числовой комбинации, из которой складывался пин-код карточки. Помогите, люди добрые! Только, пожалуйста, помогая, не начинайте сразу писать, что вариантов этих 9999 (вчера такое всем приходило в голову поначалу), потому что это же глупости — ведь в том ракурсе, который нас волнует, число 1234, число 3421, число 4312 и так далее являются одним и тем же! Ну и да, цифры же могут повторяться, ведь бывает пин-код 1111 или там, например, 0007. Можно представить вместо пин-кода номер машины. Допустим, какова вероятность угадать все однозначные цифры, из которых складывается номер машины? Или, чтобы вообще убрать теорию вероятности — из скольких числовых комбинаций мне нужно было выбрать одну?
Можно представить вместо пин-кода номер машины. Допустим, какова вероятность угадать все однозначные цифры, из которых складывается номер машины? Или, чтобы вообще убрать теорию вероятности — из скольких числовых комбинаций мне нужно было выбрать одну?
Пожалуйста, подкрепите свои ответы и рассуждения какими-нибудь точными формулами, потому что мы вчера и так чуть не свихнулись. Заранее всем большое спасибо!
P.S. Один умный человек, программист, художник и изобретатель, только что очень верно подсказал правильное решение проблемы, подарив мне несколько минут прекрасного настроения: «решение задачи такое: у неё обсессивно-комп ульсивное расстройство, лечение такое: замуж и окучивать помидоры. меня бы больше на её месте волновал не вопрос «какова вероятность», а вопрос «схуя ли я обращаю внимание на все эти цифры»? В общем-то, даже нечего добавить:)
Калькулятор ниже предназначен для генерации всех сочетаний из n по m элементов.
Число таких сочетаний, как можно рассчитать с помощью калькулятора Элементы комбинаторики. Перестановки, размещения, сочетания.
Перестановки, размещения, сочетания.
Описание алгоритма генерации под калькулятором.
Алгоритм
Комбинации генерируются в лексикографическом порядке. Алгоритм работает с порядковыми индексами элементов множества.
Рассмотрим алгоритм на примере.
Для простоты изложения рассмотрим множество из пяти элементов, индексы в котором начинаются с 1, а именно, 1 2 3 4 5.
Требуется сгенерировать все комбинации размера m = 3.
Сначала инициализуется первая комбинация заданного размера m — индексы в порядке возрастания
1 2 3
Далее проверяется последний элемент, т. е. i = 3. Если его значение меньше n — m + i, то он инкрементируется на 1.
1 2 4
Снова проверяется последний элемент, и опять он инкрементируется.
1 2 5
Теперь значение элемента равно максимально возможному: n — m + i = 5 — 3 + 3 = 5, проверяется предыдущий элемент с i = 2.
Если его значение меньше n — m + i, то он инкрементируется на 1, а для всех следующих за ним элементов значение приравнивается к значению предыдущего элемента плюс 1.
1 (2+1)3 (3+1)4 = 1 3 4
Далее снова идет проверка для i = 3.
1 3 5
Затем — проверка для i = 2.
1 4 5
Потом наступает очередь i = 1.
(1+1)2 (2+1)3 (3+1)4 = 2 3 4
И далее,
2 3 5
2 4 5
3 4 5 — последнее сочетание, так как все его элементы равны n — m + i.
Несмотря на важную роль PIN-кодов в мировой инфраструктуре, до сих пор не проводилось академических исследований о том, как, собственно, люди выбирают PIN-коды.
Исследователи из университета Кембриджа Sören Preibusch и Ross Anderson исправили ситуацию, опубликовав первый в мире количественный анализ сложности угадывания 4-циферного банковского PIN-кода.
Используя данные об утечках паролей из небанковских источников и онлайн анкетирование, учёные выяснили, что к выбору PIN-кодов пользователи относятся гораздо серьёзнее, чем к выбору паролей для веб-сайтов: большинство кодов содержат практически случайный набор цифр. Тем не менее, среди исходных данных присутствуют и простые комбинации, и дни рождения, — то есть, при некотором везении злоумышленник может просто угадать заветный код.
Отправной точкой исследования был набор 4-циферных последовательностей в паролях из базы RockYou (1.7 млн), и базы из 200 тысяч PIN-кодов от программы блокировки экрана iPhone (базу предоставил разработчик приложения Daniel Amitay). В графиках, построенных по этим данным, проступают интересные закономерности — даты, года, повторяющиеся цифры, и даже PIN-коды, заканчивающиеся на 69. На основе этих наблюдений учёные построили линейную регрессионную модель, которая оценивает популярность каждого PIN-кода в зависимости от 25 факторов, — например, является ли код датой в формате ДДММ, является ли он возрастающей последовательностью, и так далее. Этим общим условиям соответствуют 79% и 93% PIN-кодов в каждом из наборов.
Итак, пользователи выбирают 4-циферные коды на основе всего нескольких простых факторов. Если бы так выбирались и банковские PIN-коды, 8-9% из них можно было бы угадать всего за три попытки! Но, конечно, к банковским кодам люди относятся гораздо внимательнее. Ввиду отсутствия сколько-нибудь большого набора настоящих банковских данных, исследователи опросили более 1300 человек, чтобы оценить, насколько реальные PIN-коды отличаются от уже рассмотренных. Учитывая специфику исследования, у респондентов спрашивали не о самих кодах, а только о их соответствии какому-либо из вышеназванных факторов (возрастание, формат ДДММ, и т.д.).
Учитывая специфику исследования, у респондентов спрашивали не о самих кодах, а только о их соответствии какому-либо из вышеназванных факторов (возрастание, формат ДДММ, и т.д.).
Оказалось, что люди действительно гораздо тщательнее выбирают банковские PIN-коды. Примерно четверть опрошенных используют случайный PIN, сгенерированный банком. Более трети выбирают свой PIN-код, используя старый номер телефона, номер студенческого билета, или другой набор цифр, который выглядит случайным. Согласно полученным результатам, 64% владельцев карт используют псевдослучайный PIN-код, — это гораздо больше, чем 23-27% в предыдущих экспериментах с не-банковскими кодами. Ещё 5% используют цифровой паттерн (например, 4545), а 9% предпочитают паттерн на клавиатуре (например, 2684). В целом, злоумышленник с шестью попытками (три с банкоматом и три с платёжным терминалом) имеет меньше 2% шансов угадать PIN-код чужой карты.
| Фактор | Пример | RockYou | iPhone | Опрос |
|---|---|---|---|---|
| Даты | ||||
| ДДММ | 2311 | 5. 26 26 | 1.38 | 3.07 |
| ДМГГ | 3876 | 9.26 | 6.46 | 5.54 |
| ММДД | 1123 | 10.00 | 9.35 | 3.66 |
| ММГГ | 0683 | 0.67 | 0.20 | 0.94 |
| ГГГГ | 1984 | 33.39 | 7.12 | 4.95 |
| Итого | 58.57 | 24.51 | 22.76 | |
| Клавиатурный паттерн | ||||
| смежные | 6351 | 1.52 | 4.99 | — |
| квадрат | 1425 | 0.01 | 0.58 | — |
| углы | 9713 | 0.19 | 1.06 | — |
| крест | 8246 | 0.17 | 0.88 | — |
| диагональная линия | 1590 | 0.10 | 1.36 | — |
| горизонтальная линия | 5987 | 0. 34 34 | 1.42 | — |
| слово | 5683 | 0.70 | 8.39 | — |
| вертикальная линия | 8520 | 0.06 | 4.28 | — |
| Итого | 3.09 | 22.97 | 8.96 | |
| Цифровой паттерн | ||||
| заканчивается на 69 | 6869 | 0.35 | 0.57 | — |
| только цифры 0-3 | 2000 | 3.49 | 2.72 | — |
| только цифры 0-6 | 5155 | 4.66 | 5.96 | — |
| повторяющиеся пары | 2525 | 2.31 | 4.11 | — |
| одинаковые цифры | 6666 | 0.40 | 6.67 | — |
| убывающая последовательность | 3210 | 0.13 | 0.29 | — |
| возрастающая последовательность | 4567 | 3. 83 83 | 4.52 | — |
| Итого | 15.16 | 24.85 | 4.60 | |
| Случайный набор цифр | 23.17 | 27.67 | 63.68 | |
Всё бы хорошо, но, к сожалению, существенная часть опрошенных (23%) выбирает PIN-код в виде даты, — и почти треть из них использует дату своего рождения. Это существенно меняет дело, ведь почти все (99%) респонденты ответили, что хранят в бумажнике с банковскими картами различные удостоверения личности, на которых эта дата напечатана. Если злоумышленник знает день рождения владельца карты, то при грамотном подходе вероятность угадывания PIN-кода взлетает до 9%.
100 самых популярных PIN-кодов
0000, 0101-0103, 0110, 0111, 0123, 0202, 0303, 0404, 0505, 0606, 0707, 0808, 0909, 1010, 1101-1103, 1110-1112, 1123, 1201-1203, 1210-1212, 1234, 1956-2015, 2222, 2229, 2580, 3333, 4444, 5252, 5683, 6666, 7465, 7667.
P. S. На практике, разумеется, злоумышленнику гораздо проще подсмотреть ваш PIN-код, чем угадывать его. Но и от подглядывания можно защититься — даже, казалось бы, в безвыходном положении:
S. На практике, разумеется, злоумышленнику гораздо проще подсмотреть ваш PIN-код, чем угадывать его. Но и от подглядывания можно защититься — даже, казалось бы, в безвыходном положении:
Все N элементов, и ни один не повторяется, то это задача о количестве перестановок. Решение можно найти простым . На первом месте в ряду может стоять любой из N элементов, следовательно, получается N вариантов. На втором месте — любой, кроме того, который уже был использован для первого места. Следовательно, для каждого из N уже найденных вариантов есть (N — 1) вариантов второго места, и общее количество комбинаций становится N*(N — 1).
Это же можно повторить для остальных элементов ряда. Для самого последнего места остается только один вариант — последний оставшийся элемент. Для предпоследнего — два варианта, и так далее.
Следовательно, для ряда из N неповторяющихся элементов возможных перестановок равно произведению всех целых от 1 до N. Это произведение называется факториалом числа N и обозначается N! (читается «эн факториал»).
В предыдущем случае количество возможных элементов и количество мест ряда совпадали, и их число было равно N. Но возможна ситуация, когда в ряду меньше мест, чем имеется возможных элементов. Иными словами, количество элементов в выборке равно некоторому числу M, причем M Во-первых, может потребоваться сосчитать общее количество возможных способов, которыми можно выстроить в ряд M элементов из N. Такие способы называются размещениями.
Во-вторых, исследователя может интересовать число способов, которыми можно выбрать M элементов из N. При этом порядок расположения элементов уже не важен, но любые два варианта должны различаться между собой хотя бы одним элементом. Такие способы называются сочетаниями.
Чтобы найти количество размещений по M элементов из N, можно прибегнуть к такому же способу рассуждений, как и в случае с перестановками. На первом месте здесь по-прежнему может стоять N элементов, на втором (N — 1), и так далее. Но для последнего места количество возможных вариантов равняется не единице, а (N — M + 1), поскольку, когда размещение будет закончено, останется еще (N — M) неиспользованных элементов.
Таким образом, число размещений по M элементов из N равняется произведению всех целых чисел от (N — M + 1) до N, или, что то же самое, частному N!/(N — M)!.
Очевидно, что количество сочетаний по M элементов из N будет меньше количества размещений. Для каждого возможного сочетания есть M! возможных размещений, зависящих от порядка элементов этого сочетания. Следовательно, чтобы найти это количество, нужно разделить число размещений по M элементов из N на N!. Иными словами, количество сочетаний по M элементов из N равно N!/(M!*(N — M)!).
Количество комбинаций из 2 цифр. Формулы комбинаторики
Комбинаторика — это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов. Основы комбинаторики очень важны для оценки вероятностей случайных событий, т.к. именно они позволяют подсчитать принципиальновозможное количество различных вариантов развития событий.
Основная формула комбинаторики
Пусть имеется k групп элементов, причем i-я группа состоит из n i элементов. Выберем по одному элементу из каждой группы. Тогда общее число N способов,
которыми можно произвести такой выбор, определяется соотношением N=n 1 *n 2 *n 3 *…*n k .
Выберем по одному элементу из каждой группы. Тогда общее число N способов,
которыми можно произвести такой выбор, определяется соотношением N=n 1 *n 2 *n 3 *…*n k .
Пример 1. Поясним это правило на простом примере. Пусть имеется две группы элементов, причем первая группа состоит из n 1 элементов, а вторая — из n 2 элементов. Сколько различных пар элементов можно составить из этих двух групп, таким образом, чтобы в паре было по одному элементу от каждой группы? Допустим, мы взяли первый элемент из первой группы и, не меняя его, перебрали все возможные пары, меняя только элементы из второй группы. Таких пар для этого элемента можно составить n 2 . Затем мы берем второй элемент из первой группы и также составляем для него все возможные пары. Таких пар тоже будет n 2 . Так как в первой группе всего n 1 элемент, всего возможных вариантов будет n 1 *n 2 .
Пример 2. Сколько
трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если
цифры могут повторяться?
Решение: n 1 =6
(т. к. в качестве первой цифры можно взять любую цифру из 1, 2, 3, 4, 5, 6), n 2 =7
(т.к. в качестве второй цифры можно взять любую цифру из 0, 1, 2, 3, 4, 5,
6), n 3 =4 (т.к. в качестве третьей цифры можно взять любую цифру из 0, 2, 4,
6).
к. в качестве первой цифры можно взять любую цифру из 1, 2, 3, 4, 5, 6), n 2 =7
(т.к. в качестве второй цифры можно взять любую цифру из 0, 1, 2, 3, 4, 5,
6), n 3 =4 (т.к. в качестве третьей цифры можно взять любую цифру из 0, 2, 4,
6).
Итак, N=n 1 *n 2 *n 3 =6*7*4=168.
В том случае, когда все группы состоят из одинакового числа элементов, т.е. n 1 =n 2 =…n k =n можно считать, что каждый выбор производится из одной и той же группы, причем элемент после выбора снова возвращается в группу. Тогда число всех способов выбора равно n k . Такой способ выбора в комбинаторики носит название выборки с возвращением.
Пример 3. Сколько всех четырехзначных чисел
можно составить из цифр 1, 5, 6, 7, 8?
Решение. Для каждого разряда
четырехзначного числа имеется пять возможностей, значит N=5*5*5*5=5 4 =625.
Рассмотрим множество, состоящие из n элементов. Это множество в комбинаторике называется генеральной совокупностью .
Число размещений из n элементов по m
Определение 1. Размещением из n элементов по m в комбинаторике называется
любой упорядоченный набор из m различных
элементов, выбранных из генеральной совокупности в n элементов.
Размещением из n элементов по m в комбинаторике называется
любой упорядоченный набор из m различных
элементов, выбранных из генеральной совокупности в n элементов.
Пример 4. Различными размещениями из трех элементов {1, 2, 3} по два будут наборы (1, 2), (2, 1), (1, 3), (3, 1), (2, 3),(3, 2). Размещения могут отличаться друг от друга как элементами, так и их порядком.
Число размещений в комбинаторике обозначается A n m и вычисляется по формуле:
Замечание: n!=1*2*3*…*n (читается: «эн факториал»), кроме того полагают, что 0!=1.
Пример 5 . Сколько существует двузначных
чисел, в которых цифра десятков и цифра единиц различные
и нечетные?
Решение: т.к. нечетных цифр
пять, а именно 1, 3, 5, 7, 9, то эта задача сводится к выбору и размещению на
две разные позиции двух из пяти различных цифр, т.е. указанных чисел будет:
Определение 2. Сочетанием из n элементов по m в комбинаторике называется любой неупорядоченный набор из m различных элементов, выбранных из
генеральной совокупности в n элементов.
Пример 6 . Для множества {1, 2, 3}сочетаниями являются {1, 2}, {1, 3}, {2, 3}.
Число сочетаний из n элементов по m
Число сочетаний обозначается C n m и вычисляется по формуле:
Пример 7. Сколькими способами читатель может выбрать две книжки из шести имеющихся?
Решение: Число способов равно числу сочетаний из шести книжек по две, т.е. равно:
Перестановки из n элементов
Определение 3. Перестановкой из n элементов называется любой упорядоченный набор этих элементов.
Пример 7a. Всевозможными перестановками множества, состоящего из трех элементов {1, 2, 3} являются: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), (3, 2, 1), (3, 1, 2).
Число различных перестановок из n элементов обозначается P n и вычисляется по формуле P n =n!.
Пример 8. Сколькими способами семь книг разных авторов можно расставить на полке в один ряд?
Решение: эта задача о числе
перестановок семи разных книг. Имеется P 7 =7!=1*2*3*4*5*6*7=5040
способов осуществить расстановку книг.
Имеется P 7 =7!=1*2*3*4*5*6*7=5040
способов осуществить расстановку книг.
Обсуждение. Мы видим, что число возможных комбинаций можно посчитать по разным правилам (перестановки, сочетания, размещения) причем результат получится различный, т.к. принцип подсчета и сами формулы отличаются. Внимательно посмотрев на определения, можно заметить, что результат зависит от нескольких факторов одновременно.
Во-первых, от того, из какого количества элементов мы можем комбинировать их наборы (насколько велика генеральная совокупность элементов).
Во-вторых, результат зависит от того, какой величины наборы элементов нам нужны.
И последнее, важно знать, является ли для нас существенным порядок элементов в наборе. Поясним последний фактор на следующем примере.
Пример 9. На родительском собрании
присутствует 20 человек. Сколько существует различных вариантов состава
родительского комитета, если в него должны войти 5 человек?
Решение: В этом примере нас
не интересует порядок фамилий в списке комитета. Если в результате в его
составе окажутся одни и те же люди, то по смыслу для нас это один и тот же
вариант. Поэтому мы можем воспользоваться формулой для подсчета числа сочетаний из 20 элементов по 5.
Если в результате в его
составе окажутся одни и те же люди, то по смыслу для нас это один и тот же
вариант. Поэтому мы можем воспользоваться формулой для подсчета числа сочетаний из 20 элементов по 5.
Иначе будут обстоять дела, если каждый член комитета изначально отвечает за определенное направление работы. Тогда при одном и том же списочном составе комитета, внутри него возможно 5! вариантов перестановок , которые имеют значение. Количество разных (и по составу, и по сфере ответственности) вариантов определяется в этом случае числом размещений из 20 элементов по 5.
Задачи для самопроверки
1. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5,
6, если цифры могут повторяться?
2. Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево?
3. В классе десять предметов и пять уроков в день. Сколькими способами можно составить расписание на один день?
4. Сколькими способами можно выбрать 4 делегата на конференцию, если в группе 20 человек?
5. Сколькими способами можно разложить восемь различных писем по восьми
различным конвертам, если в каждый конверт кладется только одно письмо?
Сколькими способами можно разложить восемь различных писем по восьми
различным конвертам, если в каждый конверт кладется только одно письмо?
6. Из трех математиков и десяти экономистов надо составить комиссию, состоящую из двух математиков и шести экономистов. Сколькими способами это можно сделать?
Число сочетаний
Сочетанием из n по k называется набор k элементов, выбранных из данных n элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений .
Явные формулы
Число сочетаний из n по k равно биномиальному коэффициенту
При фиксированном значении n производящей функцией чисел сочетаний с повторениями из n по k является:
Двумерной производящей функцией чисел сочетаний с повторениями является:
Ссылки
- Р. Стенли Перечислительная комбинаторика.
 — М.: Мир, 1990.
— М.: Мир, 1990. - Вычисление числа сочетаний онлайн
Wikimedia Foundation . 2010 .
Смотреть что такое «Число сочетаний» в других словарях:
70 семьдесят 67 · 68 · 69 · 70 · 71 · 72 · 73 40 · 50 · 60 · 70 · 80 · 90 · 100 Факторизация: 2×5×7 Римская запись: LXX Двоичное: 100 0110 … Википедия
Световое число, условное число, однозначно выражающее внеш. условия при фотосъёмке (обычно яркость объекта съёмки и светочувствительность применяемого фотоматериала). Любому значению Э. ч. можно подобрать неск. сочетаний диафрагменное число… … Большой энциклопедический политехнический словарь
Форма числа, выделяющая два предмета как по отношению к единичному предмету, так и по отношению к множеству предметов. В современном русском языке эта форма не существует, но остатки ее влияния сохранились. Так, сочетания два стола (ср. мн. ч.… … Словарь лингвистических терминов
Комбинаторная математика, комбинаторика, раздел математики, посвященный решению задач выбора и расположения элементов нек рого, обычно конечного, множества в соответствии с заданными правилами. Каждое такое правило определяет способ построения… … Математическая энциклопедия
Каждое такое правило определяет способ построения… … Математическая энциклопедия
В комбинаторике сочетанием из по называется набор элементов, выбранных из данного множества, содержащего различных элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания… … Википедия
Занимается изучением событий, наступление которых достоверно неизвестно. Она позволяет судить о разумности ожидания наступления одних событий по сравнению с другими, хотя приписывание численных значений вероятностям событий часто бывает излишним… … Энциклопедия Кольера
1) то же, что математический Комбинаторный анализ. 2) Раздел элементарной математики, связанный с изучением количества комбинаций, подчинённых тем или иным условиям, которые можно составить из заданного конечного множества объектов… … Большая советская энциклопедия
— (греч. paradoxos неожиданный, странный) в широком смысле: утверждение, резко расходящееся с общепринятым, устоявшимся мнением, отрицание того, что представляется «безусловно правильным»; в более узком смысле два противоположных утверждения, для… … Философская энциклопедия
— (или принцип включений исключений) комбинаторная формула, позволяющая определить мощность объединения конечного числа конечных множеств, которые в общем случае могут пересекаться друг с другом … Википедия
Математическая теория, занимающаяся определением числа различных способов распределения данных предметов в известном порядке; имеет особенно важное значение в теории уравнений и в теории вероятностей. Простейшие задачи этого рода заключаются в… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Простейшие задачи этого рода заключаются в… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Книги
- Число судьбы. Гороскоп совместимости. Желания. Страсти. Фантазии (количество томов: 3) , Майер Максим. Число судьбы. Как составить индивидуальный нумерологический прогноз. Нумерология — одна из самых древних эзотерических систем. Невозможно точно установить времяее возникновения. Однако в…
В комбинаторике изучают вопросы о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов).
Рождение комбинаторики как раздела связано с трудами Б. Паскаля и П. Ферма по теории азартных игр. Большой вклад в развитие комбинаторных методов внесли Г.В. Лейбниц, Я. Бернулли и Л. Эйлер.
Французский философ, писатель, математик и физик Блез Паскаль (1623–1662) рано проявил свои выдающиеся математические способности. Круг математических интересов Паскаля был весьма разнообразен. Паскаль доказал одну
из основных теорем проективной геометрии (теорема Паскаля), сконструировал суммирующую машину (арифмометр Паскаля), дал способ вычисления биномиальных коэффициентов (треугольник Паскаля), впервые точно определил и применил для доказательства метод математической индукции, сделал существенный шаг в развитии анализа бесконечно малых, сыграл важную роль в зарождении теории вероятности. В гидростатике Паскаль установил ее основной закон (закон Паскаля). “Письма к провинциалу” Паскаля явились шедевром французской классической прозы.
В гидростатике Паскаль установил ее основной закон (закон Паскаля). “Письма к провинциалу” Паскаля явились шедевром французской классической прозы.
Готфрид Вильгельм Лейбниц (1646–1716) — немецкий философ, математик, физик и изобретатель, юрист, историк, языковед. В математике наряду с И. Ньютоном разработал дифференциальное и интегральное исчисление. Важный вклад внес в комбинаторику. С его именем, в частности, связаны теоретико-числовые задачи.
Готфрид Вильгельм Лейбниц имел мало внушительную внешность и поэтому производил впечатление довольно невзрачного человека. Однажды в Париже он зашел в книжную лавку в надежде приобрести книгу своего знакомого философа. На вопрос посетителя об этой книге книготорговец, осмотрев его с головы до ног, насмешливо бросил: “Зачем она вам? Неужели вы способны читать такие книги?” Не успел ученый ответить, как в лавку вошел сам автор книги со словами: “Великому Лейбницу привет и уважение!” Продавец никак не мог взять втолк, что перед ним действительно знаменитый Лейбниц, книги которого пользовались большим спросом среди ученых.
В дальнейшем важную роль будет играть следующая
Лемма. Пусть в множестве элементов, а в множестве — элементов. Тогда число всех различных пар , где будет равно .
Доказательство. Действительно, с одним элементом из множества мы можем составить таких различных пар, а всего в множестве элементов.
Размещения, перестановки, сочетания
Пусть у нас есть множество из трех элементов . Какими способами мы можем выбрать из этих элементов два? .
Определение. Размещениями множества из различных элементов по элементов называются комбинации, которые составлены из данных элементов по > элементов и отличаются либо самими элементами, либо порядком элементов.
Число всех размещений множества из элементов по элементов обозначается через (от начальной буквы французского слова “arrangement”, что означает размещение), где и .
Теорема. Число размещений множества из элементов по элементов равно
Доказательство. Пусть у нас есть элементы . Пусть — возможные размещения. Будем строить эти размещения последовательно. Сначала определим — первый элемент размещения. Из данной совокупности элементов его можно выбрать различными способами. После выбора первого элемента для второго элемента остается способов выбора и т.д. Так как каждый такой выбор дает новое размещение, то все эти выборы можно свободно комбинировать между собой. Поэтому имеем:
Пусть — возможные размещения. Будем строить эти размещения последовательно. Сначала определим — первый элемент размещения. Из данной совокупности элементов его можно выбрать различными способами. После выбора первого элемента для второго элемента остается способов выбора и т.д. Так как каждый такой выбор дает новое размещение, то все эти выборы можно свободно комбинировать между собой. Поэтому имеем:
Пример. Сколькими способами можно составить флаг, состоящий из трех горизонтальных полос различных цветов, если имеется материал пяти цветов?
Решение. Искомое число трехполосных флагов:
Определение. Перестановкой множества из элементов называется расположение элементов в определенном порядке.
Так, все различные перестановки множества из трех элементов — это
Число всех перестановок из элементов обозначается (от начальной буквы французского слова “permutation”, что значит “перестановка”, “перемещение”). Следовательно, число всех различных перестановок вычисляется по формуле
Пример. k
k
Действительно, каждому -элементному подмножеству данного -элементного множества соответствует одно и только одно -элементное подмножество того же множества.
Действительно, мы можем выбирать подмножества из элементов следующим образом: фиксируем один элемент; число -элементных подмножеств, содержащих этот элемент, равно ; число -элементных подмножеств, не содержащих этот элемент, равно .
Треугольник Паскаля
В этом треугольнике крайние числа в каждой строке равны 1, а каждое не крайнее число равно сумме двух чисел предыдущей строки, стоящих над ним. Таким образом, этот треугольник позволяет вычислять числа .
Теорема.
Доказательство. Рассмотрим множество из элементов и решим двумя способами следующую задачу: сколько можно составить последовательностей из элементов данного
множества, в каждой из которых никакой элемент не встречается дважды?
1 способ. Выбираем первый член последовательности, затем второй, третий и т. д. член
д. член
2 способ. Выберем сначала элементов из данного множества, а затем расположим их в некотором порядке
Домножим числитель и знаменатель этой дроби на :
Пример. Сколькими способами можно в игре “Спортлото” выбрать 5 номеров из 36?
Искомое число способов
Задачи.
1. Номера машин состоят из 3 букв русского алфавита (33 буквы) и 4 цифр. Сколько существует различных номеров автомашин?
2. На рояле 88 клавиш. Сколькими способами можно извлечь последовательно 6 звуков?
3. Сколько есть шестизначных чисел, делящихся на 5?
4. Сколькими способами можно разложить 7 разных монет в три кармана?
5. Сколько можно составить пятизначных чисел, в десятичной записи которых хотя бы один раз встречается цифра 5?
6. Сколькими способами можно усадить 20 человек за круглым столом, считая способы одинаковыми, если их можно получить один из другого движением по кругу?
7. Сколько есть пятизначных чисел, делящихся на 5, в записи которых нет одинаковых цифр?
8. На клетчатой бумаге со стороной клетки 1 см нарисована окружность радиуса 100 см, не проходящая через вершины клеток и не касающаяся сторон клеток. Сколько клеток может пересекать эта окружность?
На клетчатой бумаге со стороной клетки 1 см нарисована окружность радиуса 100 см, не проходящая через вершины клеток и не касающаяся сторон клеток. Сколько клеток может пересекать эта окружность?
9. Сколькими способами можно расставить в ряд числа так, чтобы числа стояли рядом и притом шли в порядке возрастания?
10. Сколько пятизначных чисел можно составить из цифр , если каждую цифру можно использовать только один раз?
11. Из слова РОТ перестановкой букв можно получить еще такие слова: ТОР, ОРТ, ОТР, ТРО, РТО. Их называют анаграммами. Сколько анаграмм можно составить из слова ЛОГАРИФМ?
12. Назовем разбиением натурального числа представление его в виде суммы натуральных чисел. Вот, например, все разбиения числа :
Разбиения считаются разными, если они отличаются либо числами, либо порядком слагаемых.
Сколько существует различных разбиений числа на слагаемых?
13. Сколько существует трехзначных чисел с невозрастающим порядком цифр?
14.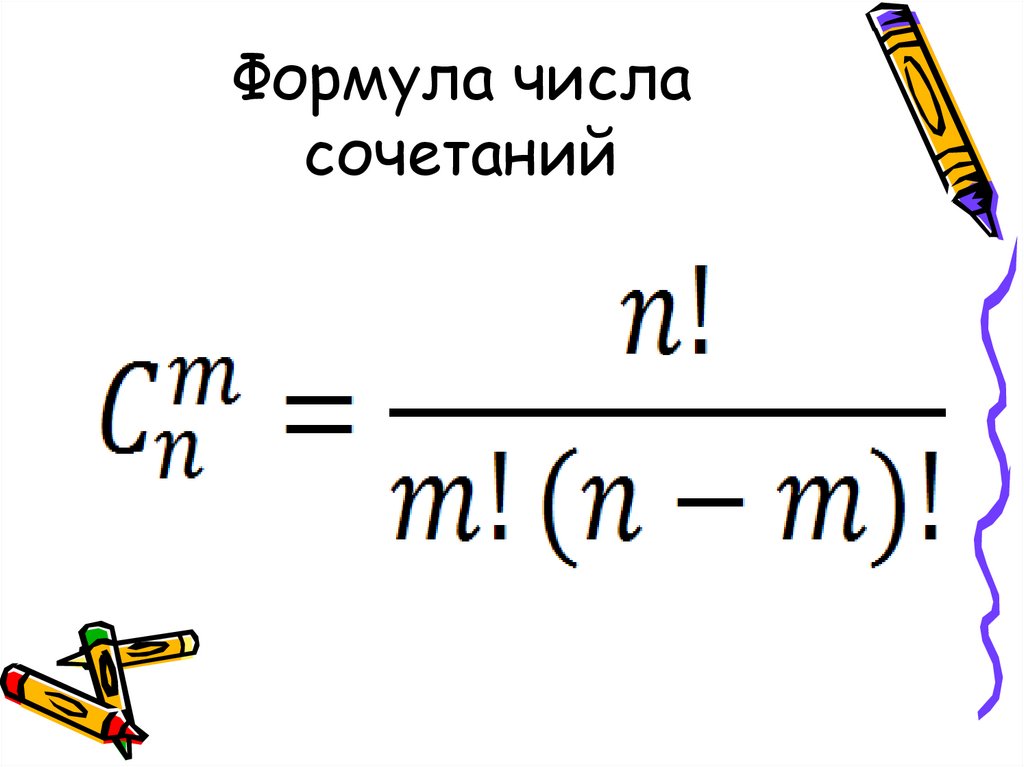 Сколько существует четырехзначных чисел с невозрастающим порядком цифр?
Сколько существует четырехзначных чисел с невозрастающим порядком цифр?
15. Сколькими способами можно рассадить в ряд 17 человек, чтобы и оказались рядом?
16. девочек и мальчиков рассаживаются произвольным образом в ряду из мест. Сколькими способами можно их рассадить так, чтобы никакие две девочки не сидели рядом?
17. девочек и мальчиков рассаживаются произвольным образом в ряду из мест. Сколькими способами можно их рассадить так, чтобы все девочки сидели рядом?
КОМБИНАТОРИКА
Комбинаторика — раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и, соответственно, получения законов распределения случайных величин. Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для правильного понимания статистических закономерностей, проявляющихся в природе и технике.
Правила сложения и умножения в комбинаторике
Правило суммы. Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В — n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m способами.
Пример 1.
В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного?
Решение
Дежурным можно назначить либо мальчика, либо девочку, т.е. дежурным может быть любой из 16 мальчиков, либо любая из 10 девочек.
По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами.
Правило произведения. Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n 1 способами, второе действие n 2 способами, третье — n 3 способами и так до k-го действия, которое можно выполнить n k способами, то все k действий вместе могут быть выполнены:
способами.
Пример 2.
В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?
Решение
Первым дежурным можно назначить либо мальчика, либо девочку. Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами.
После того, как мы выбрали первого дежурного, второго мы можем выбрать из оставшихся 25 человек, т.е. 25-ю способами.
По теореме умножения двое дежурных могут быть выбраны 26*25=650 способами.
Сочетания без повторений. Сочетания с повторениями
Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать m из n различных предметов ?
Пример 3.
Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?
Решение
Нам из 10 книг нужно выбрать 4, причем порядок выбора не имеет значения. Таким образом, нужно найти число сочетаний из 10 элементов по 4:
Таким образом, нужно найти число сочетаний из 10 элементов по 4:
.
Рассмотрим задачу о числе сочетаний с повторениями: имеется по r одинаковых предметов каждого из n различных типов; сколькими способами можно выбрать m () из этих (n*r) предметов?
.
Пример 4.
В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?
Решение
Т.к. среди 7 пирожных могут быть пирожные одного сорта, то число способов, которыми можно купить 7 пирожных, определяется числом сочетаний с повторениями из 7 по 4.
.
Размещения без повторений. Размещения с повторениями
Классической задачей комбинаторики является задача о числе размещений без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n различных предметов?
Пример 5.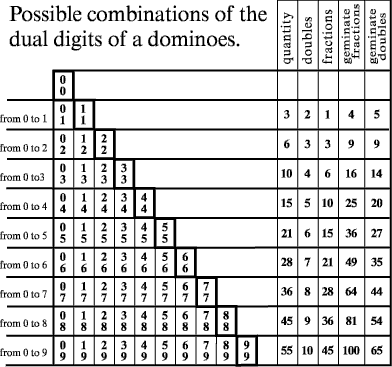
В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии?
Решение.
В данной задаче мы не просто выбираем фотографии, а размещаем их на определенных страницах газеты, причем каждая страница газеты должна содержать не более одной фотографии. Таким образом, задача сводится к классической задаче об определении числа размещений без повторений из 12 элементов по 4 элемента:
Таким образом, 4 фотографии на 12 страницах можно расположить 11880 способами.
Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом: сколькими способами можно вы б рать и разместить по m различным местам m из n предметов, с реди которых есть одинаковые?
Пример 6.
У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера- составить каталог. Сколько различных пятизначных номеров может составить мальчик?
Перестановки без повторений . Перестановки с повторениями
Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно выразить вопросом: сколькими способами можно разместить n различных предметов на n различных местах?
Пример 7.
Сколько можно составить четырехбуквенных «слов» из букв слова«брак»?
Решение
Генеральной совокупностью являются 4 буквы слова «брак» (б, р, а, к). Число «слов» определяется перестановками этих 4 букв, т. е.
Для случая, когда среди выбираемых n элементов есть одинаковые (выборка с возвращением), задачу о числе перестановок с повторениями можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов (k
Пример 8.
Сколько разных буквосочетаний можно сделать из букв слова «Миссисипи»?
Решение
Здесь 1 буква «м», 4 буквы «и», 3 буквы «c» и 1 буква «п», всего 9 букв. Следовательно, число перестановок с повторениями равно
ОПОРНЫЙ КОНСПЕКТ ПО РАЗДЕЛУ «КОМБИНАТОРИКА»
Сколько комбинаций из 10 цифр. Формулы комбинаторики. Размещения и теория вероятностей
Комбинаторика — это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов. Основы комбинаторики очень важны для оценки вероятностей случайных событий, т.к. именно они позволяют подсчитать принципиально возможное количество различных вариантов развития событий.
Основная формула комбинаторики
Пусть имеется k групп элементов, причем i-я группа состоит из n i элементов.
Выберем по одному элементу из каждой группы. Тогда общее число N способов,
которыми можно произвести такой выбор, определяется соотношением N=n 1 *n 2 *n 3 *. ..*n k .
..*n k .
Пример 1. Поясним это правило на простом примере. Пусть имеется две группы элементов, причем первая группа состоит из n 1 элементов, а вторая — из n 2 элементов. Сколько различных пар элементов можно составить из этих двух групп, таким образом, чтобы в паре было по одному элементу от каждой группы? Допустим, мы взяли первый элемент из первой группы и, не меняя его, перебрали все возможные пары, меняя только элементы из второй группы. Таких пар для этого элемента можно составить n 2 . Затем мы берем второй элемент из первой группы и также составляем для него все возможные пары. Таких пар тоже будет n 2 . Так как в первой группе всего n 1 элемент, всего возможных вариантов будет n 1 *n 2 .
Пример 2. Сколько
трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если
цифры могут повторяться?
Решение: n 1 =6
(т.к. в качестве первой цифры можно взять любую цифру из 1, 2, 3, 4, 5, 6), n 2 =7
(т.к. в качестве второй цифры можно взять любую цифру из 0, 1, 2, 3, 4, 5,
6), n 3 =4 (т. к. в качестве третьей цифры можно взять любую цифру из 0, 2, 4,
6).
к. в качестве третьей цифры можно взять любую цифру из 0, 2, 4,
6).
Итак, N=n 1 *n 2 *n 3 =6*7*4=168.
В том случае, когда все группы состоят из одинакового числа элементов, т.е. n 1 =n 2 =…n k =n можно считать, что каждый выбор производится из одной и той же группы, причем элемент после выбора снова возвращается в группу. Тогда число всех способов выбора равно n k . Такой способ выбора в комбинаторики носит название выборки с возвращением.
Пример 3. Сколько всех четырехзначных чисел
можно составить из цифр 1, 5, 6, 7, 8?
Решение. Для каждого разряда
четырехзначного числа имеется пять возможностей, значит N=5*5*5*5=5 4 =625.
Рассмотрим множество, состоящие из n элементов. Это множество в комбинаторике называется генеральной совокупностью .
Число размещений из n элементов по m
Определение 1. Размещением из n элементов по m в комбинаторике называется
любой упорядоченный набор из m различных
элементов, выбранных из генеральной совокупности в n элементов.
Пример 4. Различными размещениями из трех элементов {1, 2, 3} по два будут наборы (1, 2), (2, 1), (1, 3), (3, 1), (2, 3),(3, 2). Размещения могут отличаться друг от друга как элементами, так и их порядком.
Число размещений в комбинаторике обозначается A n m и вычисляется по формуле:
Замечание: n!=1*2*3*…*n (читается: «эн факториал»), кроме того полагают, что 0!=1.
Пример 5 . Сколько существует двузначных
чисел, в которых цифра десятков и цифра единиц различные
и нечетные?
Решение: т.к. нечетных цифр
пять, а именно 1, 3, 5, 7, 9, то эта задача сводится к выбору и размещению на
две разные позиции двух из пяти различных цифр, т.е. указанных чисел будет:
Определение 2. Сочетанием из n элементов по m в комбинаторике называется любой неупорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.
Пример 6 . Для множества {1, 2,
3}сочетаниями являются {1, 2}, {1, 3}, {2, 3}.
Для множества {1, 2,
3}сочетаниями являются {1, 2}, {1, 3}, {2, 3}.
Число сочетаний из n элементов по m
Число сочетаний обозначается C n m и вычисляется по формуле:
Пример 7. Сколькими способами читатель может выбрать две книжки из шести имеющихся?
Решение: Число способов равно числу сочетаний из шести книжек по две, т.е. равно:
Перестановки из n элементов
Определение 3. Перестановкой из n элементов называется любой упорядоченный набор этих элементов.
Пример 7a. Всевозможными перестановками множества, состоящего из трех элементов {1, 2, 3} являются: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), (3, 2, 1), (3, 1, 2).
Число различных перестановок из n элементов обозначается P n и вычисляется по формуле P n =n!.
Пример 8. Сколькими способами семь книг разных авторов можно расставить на полке в один ряд?
Решение: эта задача о числе
перестановок семи разных книг. Имеется P 7 =7!=1*2*3*4*5*6*7=5040
способов осуществить расстановку книг.
Имеется P 7 =7!=1*2*3*4*5*6*7=5040
способов осуществить расстановку книг.
Обсуждение. Мы видим, что число возможных комбинаций можно посчитать по разным правилам (перестановки, сочетания, размещения) причем результат получится различный, т.к. принцип подсчета и сами формулы отличаются. Внимательно посмотрев на определения, можно заметить, что результат зависит от нескольких факторов одновременно.
Во-первых, от того, из какого количества элементов мы можем комбинировать их наборы (насколько велика генеральная совокупность элементов).
Во-вторых, результат зависит от того, какой величины наборы элементов нам нужны.
И последнее, важно знать, является ли для нас существенным порядок элементов в наборе. Поясним последний фактор на следующем примере.
Пример 9. На родительском собрании
присутствует 20 человек. Сколько существует различных вариантов состава
родительского комитета, если в него должны войти 5 человек?
Решение: В этом примере нас
не интересует порядок фамилий в списке комитета. Если в результате в его
составе окажутся одни и те же люди, то по смыслу для нас это один и тот же
вариант. Поэтому мы можем воспользоваться формулой для подсчета числа сочетаний из 20 элементов по 5.
Если в результате в его
составе окажутся одни и те же люди, то по смыслу для нас это один и тот же
вариант. Поэтому мы можем воспользоваться формулой для подсчета числа сочетаний из 20 элементов по 5.
Иначе будут обстоять дела, если каждый член комитета изначально отвечает за определенное направление работы. Тогда при одном и том же списочном составе комитета, внутри него возможно 5! вариантов перестановок , которые имеют значение. Количество разных (и по составу, и по сфере ответственности) вариантов определяется в этом случае числом размещений из 20 элементов по 5.
Задачи для самопроверки
1. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5,
6, если цифры могут повторяться?
Т.к. число четное на третьем месте может стоять 0, 2, 4, 6, т.е. четыре цифры. На втором месте может стоять любая из семи цифр. На первом месте может стоять любая из семи цифр кроме нуля, т.е. 6 возможностей. Результат =4*7*6=168.
2. Сколько существует пятизначных чисел, которые одинаково читаются слева
направо и справа налево?
Сколько существует пятизначных чисел, которые одинаково читаются слева
направо и справа налево?
На первом месте может стоять любая цифра кроме 0, т.е. 9 возможностей. На втором месте может стоять любая цифра, т.е. 10 возможностей. На третьем месте тоже может стоять любая цифра из, т.е. 10 возможностей. Четвертая и пятая цифры определены заранее, они совпадают с первой и второй, следовательно, число таких чисел 9*10*10=900.
3. В классе десять предметов и пять уроков в день. Сколькими способами можно
составить расписание на один день?
4. Сколькими способами можно выбрать 4 делегата на конференцию, если в группе 20 человек?
n = C 20 4 = (20!)/(4!*(20-4)!)=(16!*17*18*19*20)/((1*2*3*4)*(16!))=(17*18*19*20)/(1*2*3*4)=4845.
5. Сколькими способами можно разложить восемь различных писем по восьми
различным конвертам, если в каждый конверт кладется только одно письмо?
В первый конверт можно положить 1 из восьми писем, во второй одно из семи оставшихся, в третий одно из шесть т. д. n = 8! = 1*2*3*4*5*6*7*8 = 40320.
д. n = 8! = 1*2*3*4*5*6*7*8 = 40320.
6. Из трех математиков и десяти экономистов надо составить комиссию,
состоящую из двух математиков и шести экономистов. Сколькими способами это
можно сделать?
Все N элементов, и ни один не повторяется, то это задача о количестве перестановок. Решение можно найти простым . На первом месте в ряду может стоять любой из N элементов, следовательно, получается N вариантов. На втором месте — любой, кроме того, который уже был использован для первого места. Следовательно, для каждого из N уже найденных вариантов есть (N — 1) вариантов второго места, и общее количество комбинаций становится N*(N — 1).
Это же можно повторить для остальных элементов ряда. Для самого последнего места остается только один вариант — последний оставшийся элемент. Для предпоследнего — два варианта, и так далее.
Следовательно, для ряда из N неповторяющихся элементов возможных перестановок равно произведению всех целых от 1 до N. Это произведение называется факториалом числа N и обозначается N! (читается «эн факториал»).
В предыдущем случае количество возможных элементов и количество мест ряда совпадали, и их число было равно N. Но возможна ситуация, когда в ряду меньше мест, чем имеется возможных элементов. Иными словами, количество элементов в выборке равно некоторому числу M, причем M Во-первых, может потребоваться сосчитать общее количество возможных способов, которыми можно выстроить в ряд M элементов из N. Такие способы называются размещениями.
Во-вторых, исследователя может интересовать число способов, которыми можно выбрать M элементов из N. При этом порядок расположения элементов уже не важен, но любые два варианта должны различаться между собой хотя бы одним элементом. Такие способы называются сочетаниями.
Чтобы найти количество размещений по M элементов из N, можно прибегнуть к такому же способу рассуждений, как и в случае с перестановками. На первом месте здесь по-прежнему может стоять N элементов, на втором (N — 1), и так далее. Но для последнего места количество возможных вариантов равняется не единице, а (N — M + 1), поскольку, когда размещение будет закончено, останется еще (N — M) неиспользованных элементов.
Таким образом, число размещений по M элементов из N равняется произведению всех целых чисел от (N — M + 1) до N, или, что то же самое, частному N!/(N — M)!.
Очевидно, что количество сочетаний по M элементов из N будет меньше количества размещений. Для каждого возможного сочетания есть M! возможных размещений, зависящих от порядка элементов этого сочетания. Следовательно, чтобы найти это количество, нужно разделить число размещений по M элементов из N на N!. Иными словами, количество сочетаний по M элементов из N равно N!/(M!*(N — M)!).
Друзья! Раз уж есть у меня этот мертвый блокнот, использую-ка я его для того, чтобы задать вам задачку, над которой вчера билось три физика, два экономиста, один политеховский и один гуманитарий. Мы сломали себе весь мозг и у нас постоянно получаются разные результаты. Может быть, среди вас есть программисты и математические гении, к тому же, задачка вообще школьная и очень легкая, у нас просто не выводится формула. Потому что мы бросили занятия точными науками и вместо этого зачем-то пишем книги и рисуем картины. Простите.
Простите.
Итак, предыстория.
Мне выдали новую банковскую карточку и я, как водится, играючи угадала ее пин-код. Но не подряд. В смысле, допустим, пин-код был 8794, а я назвала 9748. То есть, я триумфально угадала все цифры , которое содержались в данном четырехзначном числе. Ну да, не само число , а просто его составляющие у гадала. Но цифры-то все верные! ПРИМЕЧАНИЕ — я действовала наугад, то есть, мне не надо было расставить уже известные числа в нужном порядке, я просто действовала в духе: вот тут есть неизвестные мне четыре цифры, и я считаю, что среди них могут быть 9, 7, 4 и 8, а порядок их не важен. Мы тут же задались вопросом, сколько у меня вообще было вариантов (наверное, чтобы понять, насколько это круто, что я вот взяла и угадала). То есть, из скольких комбинаций четырех цифр мне нужно было выбирать? И тут, натурально, начался ад. У нас весь вечер взрывалась голова, и у всех, в итоге, вышли абсолютно разные варианты ответа! Я даже начала выписывать все эти комбинации в блокнот подряд по мере возрастания, но на четырех сотнях поняла, что их больше четырех сотен (во всяком случае, это опровергло ответ физика Трэша, который уверял меня, что комбинаций четыре сотни, но все равно это не совсем однозначно) — и сдалась.
Собственно, суть вопроса. Какова вероятность угадывания (в любом порядке) четырех чисел, содержащихся в четырехзначном числе?
Или нет, переформулируем (я гуманитарий, простите, хотя к математике всегда питала огромную слабость), чтобы было яснее и четче. Сколько не повторяющихся комбинаций цифр содержится в ряду порядковых числительных от 0 до 9999? (пожалуйста, не путайте это с вопросом «сколько комбинаций не повторяющихся цифр»!! ! цифры могут повторяться! в смысле, 2233 и 3322 — это в данном случае одна и та же комбинация!!).
Или еще конкретнее. Мне нужно четыре раза угадать одну цифру из десяти. Но не подряд.
Ну или еще как-нибудь. В общем, нужно узнать, сколько у меня было вариантов числовой комбинации, из которой складывался пин-код карточки. Помогите, люди добрые! Только, пожалуйста, помогая, не начинайте сразу писать, что вариантов этих 9999 (вчера такое всем приходило в голову поначалу), потому что это же глупости — ведь в том ракурсе, который нас волнует, число 1234, число 3421, число 4312 и так далее являются одним и тем же! Ну и да, цифры же могут повторяться, ведь бывает пин-код 1111 или там, например, 0007. Можно представить вместо пин-кода номер машины. Допустим, какова вероятность угадать все однозначные цифры, из которых складывается номер машины? Или, чтобы вообще убрать теорию вероятности — из скольких числовых комбинаций мне нужно было выбрать одну?
Можно представить вместо пин-кода номер машины. Допустим, какова вероятность угадать все однозначные цифры, из которых складывается номер машины? Или, чтобы вообще убрать теорию вероятности — из скольких числовых комбинаций мне нужно было выбрать одну?
Пожалуйста, подкрепите свои ответы и рассуждения какими-нибудь точными формулами, потому что мы вчера и так чуть не свихнулись. Заранее всем большое спасибо!
P.S. Один умный человек, программист, художник и изобретатель, только что очень верно подсказал правильное решение проблемы, подарив мне несколько минут прекрасного настроения: «решение задачи такое: у неё обсессивно-комп ульсивное расстройство, лечение такое: замуж и окучивать помидоры. меня бы больше на её месте волновал не вопрос «какова вероятность», а вопрос «схуя ли я обращаю внимание на все эти цифры»? В общем-то, даже нечего добавить:)
Калькулятор ниже предназначен для генерации всех сочетаний из n по m элементов.
Число таких сочетаний, как можно рассчитать с помощью калькулятора Элементы комбинаторики. Перестановки, размещения, сочетания.
Перестановки, размещения, сочетания.
Описание алгоритма генерации под калькулятором.
Алгоритм
Комбинации генерируются в лексикографическом порядке. Алгоритм работает с порядковыми индексами элементов множества.
Рассмотрим алгоритм на примере.
Для простоты изложения рассмотрим множество из пяти элементов, индексы в котором начинаются с 1, а именно, 1 2 3 4 5.
Требуется сгенерировать все комбинации размера m = 3.
Сначала инициализуется первая комбинация заданного размера m — индексы в порядке возрастания
1 2 3
Далее проверяется последний элемент, т. е. i = 3. Если его значение меньше n — m + i, то он инкрементируется на 1.
1 2 4
Снова проверяется последний элемент, и опять он инкрементируется.
1 2 5
Теперь значение элемента равно максимально возможному: n — m + i = 5 — 3 + 3 = 5, проверяется предыдущий элемент с i = 2.
Если его значение меньше n — m + i, то он инкрементируется на 1, а для всех следующих за ним элементов значение приравнивается к значению предыдущего элемента плюс 1.
1 (2+1)3 (3+1)4 = 1 3 4
Далее снова идет проверка для i = 3.
1 3 5
Затем — проверка для i = 2.
1 4 5
Потом наступает очередь i = 1.
(1+1)2 (2+1)3 (3+1)4 = 2 3 4
И далее,
2 3 5
2 4 5
3 4 5 — последнее сочетание, так как все его элементы равны n — m + i.
Несмотря на важную роль PIN-кодов в мировой инфраструктуре, до сих пор не проводилось академических исследований о том, как, собственно, люди выбирают PIN-коды.
Исследователи из университета Кембриджа Sören Preibusch и Ross Anderson исправили ситуацию, опубликовав первый в мире количественный анализ сложности угадывания 4-циферного банковского PIN-кода.
Используя данные об утечках паролей из небанковских источников и онлайн анкетирование, учёные выяснили, что к выбору PIN-кодов пользователи относятся гораздо серьёзнее, чем к выбору паролей для веб-сайтов: большинство кодов содержат практически случайный набор цифр. Тем не менее, среди исходных данных присутствуют и простые комбинации, и дни рождения, — то есть, при некотором везении злоумышленник может просто угадать заветный код.
Отправной точкой исследования был набор 4-циферных последовательностей в паролях из базы RockYou (1.7 млн), и базы из 200 тысяч PIN-кодов от программы блокировки экрана iPhone (базу предоставил разработчик приложения Daniel Amitay). В графиках, построенных по этим данным, проступают интересные закономерности — даты, года, повторяющиеся цифры, и даже PIN-коды, заканчивающиеся на 69. На основе этих наблюдений учёные построили линейную регрессионную модель, которая оценивает популярность каждого PIN-кода в зависимости от 25 факторов, — например, является ли код датой в формате ДДММ, является ли он возрастающей последовательностью, и так далее. Этим общим условиям соответствуют 79% и 93% PIN-кодов в каждом из наборов.
Итак, пользователи выбирают 4-циферные коды на основе всего нескольких простых факторов. Если бы так выбирались и банковские PIN-коды, 8-9% из них можно было бы угадать всего за три попытки! Но, конечно, к банковским кодам люди относятся гораздо внимательнее. Ввиду отсутствия сколько-нибудь большого набора настоящих банковских данных, исследователи опросили более 1300 человек, чтобы оценить, насколько реальные PIN-коды отличаются от уже рассмотренных. Учитывая специфику исследования, у респондентов спрашивали не о самих кодах, а только о их соответствии какому-либо из вышеназванных факторов (возрастание, формат ДДММ, и т.д.).
Учитывая специфику исследования, у респондентов спрашивали не о самих кодах, а только о их соответствии какому-либо из вышеназванных факторов (возрастание, формат ДДММ, и т.д.).
Оказалось, что люди действительно гораздо тщательнее выбирают банковские PIN-коды. Примерно четверть опрошенных используют случайный PIN, сгенерированный банком. Более трети выбирают свой PIN-код, используя старый номер телефона, номер студенческого билета, или другой набор цифр, который выглядит случайным. Согласно полученным результатам, 64% владельцев карт используют псевдослучайный PIN-код, — это гораздо больше, чем 23-27% в предыдущих экспериментах с не-банковскими кодами. Ещё 5% используют цифровой паттерн (например, 4545), а 9% предпочитают паттерн на клавиатуре (например, 2684). В целом, злоумышленник с шестью попытками (три с банкоматом и три с платёжным терминалом) имеет меньше 2% шансов угадать PIN-код чужой карты.
| Фактор | Пример | RockYou | iPhone | Опрос |
|---|---|---|---|---|
| Даты | ||||
| ДДММ | 2311 | 5. 26 26 | 1.38 | 3.07 |
| ДМГГ | 3876 | 9.26 | 6.46 | 5.54 |
| ММДД | 1123 | 10.00 | 9.35 | 3.66 |
| ММГГ | 0683 | 0.67 | 0.20 | 0.94 |
| ГГГГ | 1984 | 33.39 | 7.12 | 4.95 |
| Итого | 58.57 | 24.51 | 22.76 | |
| Клавиатурный паттерн | ||||
| смежные | 6351 | 1.52 | 4.99 | — |
| квадрат | 1425 | 0.01 | 0.58 | — |
| углы | 9713 | 0.19 | 1.06 | — |
| крест | 8246 | 0.17 | 0.88 | — |
| диагональная линия | 1590 | 0.10 | 1.36 | — |
| горизонтальная линия | 5987 | 0. 34 34 | 1.42 | — |
| слово | 5683 | 0.70 | 8.39 | — |
| вертикальная линия | 8520 | 0.06 | 4.28 | — |
| Итого | 3.09 | 22.97 | 8.96 | |
| Цифровой паттерн | ||||
| заканчивается на 69 | 6869 | 0.35 | 0.57 | — |
| только цифры 0-3 | 2000 | 3.49 | 2.72 | — |
| только цифры 0-6 | 5155 | 4.66 | 5.96 | — |
| повторяющиеся пары | 2525 | 2.31 | 4.11 | — |
| одинаковые цифры | 6666 | 0.40 | 6.67 | — |
| убывающая последовательность | 3210 | 0.13 | 0.29 | — |
| возрастающая последовательность | 4567 | 3. 83 83 | 4.52 | — |
| Итого | 15.16 | 24.85 | 4.60 | |
| Случайный набор цифр | 23.17 | 27.67 | 63.68 | |
Всё бы хорошо, но, к сожалению, существенная часть опрошенных (23%) выбирает PIN-код в виде даты, — и почти треть из них использует дату своего рождения. Это существенно меняет дело, ведь почти все (99%) респонденты ответили, что хранят в бумажнике с банковскими картами различные удостоверения личности, на которых эта дата напечатана. Если злоумышленник знает день рождения владельца карты, то при грамотном подходе вероятность угадывания PIN-кода взлетает до 9%.
100 самых популярных PIN-кодов
0000, 0101-0103, 0110, 0111, 0123, 0202, 0303, 0404, 0505, 0606, 0707, 0808, 0909, 1010, 1101-1103, 1110-1112, 1123, 1201-1203, 1210-1212, 1234, 1956-2015, 2222, 2229, 2580, 3333, 4444, 5252, 5683, 6666, 7465, 7667.
P. S. На практике, разумеется, злоумышленнику гораздо проще подсмотреть ваш PIN-код, чем угадывать его. Но и от подглядывания можно защититься — даже, казалось бы, в безвыходном положении:
S. На практике, разумеется, злоумышленнику гораздо проще подсмотреть ваш PIN-код, чем угадывать его. Но и от подглядывания можно защититься — даже, казалось бы, в безвыходном положении:
КОМБИНАТОРИКА
Комбинаторика — раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и, соответственно, получения законов распределения случайных величин. Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для правильного понимания статистических закономерностей, проявляющихся в природе и технике.
Правила сложения и умножения в комбинаторике
Правило суммы. Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В — n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m способами.
Пример 1.
В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного?
Решение
Дежурным можно назначить либо мальчика, либо девочку, т.е. дежурным может быть любой из 16 мальчиков, либо любая из 10 девочек.
По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами.
Правило произведения. Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n 1 способами, второе действие n 2 способами, третье — n 3 способами и так до k-го действия, которое можно выполнить n k способами, то все k действий вместе могут быть выполнены:
способами.
Пример 2.
В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?
Решение
Первым дежурным можно назначить либо мальчика, либо девочку. Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами.
После того, как мы выбрали первого дежурного, второго мы можем выбрать из оставшихся 25 человек, т.е. 25-ю способами.
По теореме умножения двое дежурных могут быть выбраны 26*25=650 способами.
Сочетания без повторений. Сочетания с повторениями
Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать m из n различных предметов ?
Пример 3.
Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?
Решение
Нам из 10 книг нужно выбрать 4, причем порядок выбора не имеет значения. Таким образом, нужно найти число сочетаний из 10 элементов по 4:
.
Рассмотрим задачу о числе сочетаний с повторениями: имеется по r одинаковых предметов каждого из n различных типов; сколькими способами можно выбрать m () из этих (n*r) предметов?
.
Пример 4.
В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?
Решение
Т.к. среди 7 пирожных могут быть пирожные одного сорта, то число способов, которыми можно купить 7 пирожных, определяется числом сочетаний с повторениями из 7 по 4.
.
Размещения без повторений. Размещения с повторениями
Классической задачей комбинаторики является задача о числе размещений без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n различных предметов?
Пример 5.
В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии?
Решение.
В данной задаче мы не просто выбираем фотографии, а размещаем их на определенных страницах газеты, причем каждая страница газеты должна содержать не более одной фотографии. Таким образом, задача сводится к классической задаче об определении числа размещений без повторений из 12 элементов по 4 элемента:
Таким образом, 4 фотографии на 12 страницах можно расположить 11880 способами.
Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом: сколькими способами можно вы б рать и разместить по m различным местам m из n предметов, с реди которых есть одинаковые?
Пример 6.
У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера- составить каталог. Сколько различных пятизначных номеров может составить мальчик?
Сколько различных пятизначных номеров может составить мальчик?
Перестановки без повторений . Перестановки с повторениями
Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно выразить вопросом: сколькими способами можно разместить n различных предметов на n различных местах?
Пример 7.
Сколько можно составить четырехбуквенных «слов» из букв слова«брак»?
Решение
Генеральной совокупностью являются 4 буквы слова «брак» (б, р, а, к). Число «слов» определяется перестановками этих 4 букв, т. е.
Для случая, когда среди выбираемых n элементов есть одинаковые (выборка с возвращением), задачу о числе перестановок с повторениями можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов (k
Пример 8.
Сколько разных буквосочетаний можно сделать из букв слова «Миссисипи»?
Решение
Здесь 1 буква «м», 4 буквы «и», 3 буквы «c» и 1 буква «п», всего 9 букв. Следовательно, число перестановок с повторениями равно
ОПОРНЫЙ КОНСПЕКТ ПО РАЗДЕЛУ «КОМБИНАТОРИКА»
Сколько комбинаций в покере ― определение комбинаторики и способы подсчета рук
Вопрос «Какие карты у оппонента?» интересен новичкам и профессиональным игрокам за столом. От ответа зависят характер и содержание раздачи, шансы на победу. Количество комбинаций известно (их десять). Но нужно знать и варианты их составления, чтобы сделать оценку диапазона оппонента. В статье — о способах расчета возможных рук соперника, применении знаний о комбинациях в покере.
Содержание
- Что такое комбинаторика в покере
- Для чего нужны знания комбинаторики
- Комбинаторика на префлопе
- Количество комбинаций в покере
- Комбинаторика на постфлопе
- Эффект изъятия карт или блокеры
- Использование комбинаторики в различных ситуациях
Что такое комбинаторика в покере
Игроки во время раздачи считают ауты — карты, позволяющие составить сильную руку. Они имеют большое значение, поскольку оказывают влияние на принятие решений. Комбинаторика — математический метод расчета количества комбинаций с конкретными вариантами рук в определенных ситуациях. Благодаря анализу с применением формул открывается важная информация:
Они имеют большое значение, поскольку оказывают влияние на принятие решений. Комбинаторика — математический метод расчета количества комбинаций с конкретными вариантами рук в определенных ситуациях. Благодаря анализу с применением формул открывается важная информация:
- Количество вариантов сочетания 7–7.
- Способы сдачи A–K или других сильных рук.
- Количество стрит-дро, которые могут быть при флопе A–10–7.
Новички не используют математику из-за мнения, что расчеты сложны. Но это доступные знания и сила покериста. Достаточно перемножить цифры, и стратегия станет более выигрышной.
Получи бесплатный курс по покеру. Каждому ученику чарты стартовых рук и крутой софт в подарок.
- Ты сформируешь крепкую покерную базу
- Научишься работать с софтом
- Узнаешь стратегии на каждый этап игры
На занятиях тренер составит тебе индивидуальный план развития.
Выбирай себе курс и оставляй заявку!
Для чего нужны знания комбинаторики
Инструмент позволяет:
- Дать оценку раздачи и своего участия в ней.

- Предположить количественный диапазон возможных стартовых рук оппонента.
- Повысить качество блефа.
- Находить оптимальные, выигрышные решения.
Профессиональные покеристы применяют методы подсчета в каждой раздаче. Цифры и математика превращаются в шансы, сложные ситуации — в простые. Вычисление вероятного количества вариаций рук соперника повышает умение анализировать. Это важное условие развития уровня игры.
Например, покерист на префлопе делает рейз с 10–10. Очень тайтовый соперник отвечает ходом в олл-ин. В такой ситуации игроки идут ва-банк с сильной карманной парой (J–J, Q–Q, K–K), бигсликом (A–K) или префлоп-натсом (A–A). По подсчетам возможны 24 карманных комбо (6 х 4) + 16 одно- и разномастных вариантов A–K. Итого: 16 / 40 = с вероятностью в 40% покерист играет против A–K, в 60% (24 / 40) соперник покажет оверпару. Комбинаторика открыла простую истину: коинфлип не выгоден по шансам.
Расчеты в уме частично заменяет покерный софт.
Но в большинстве румов он запрещен, а в живой игре программу открывать нельзя.
Комбинаторика на префлопе
На первом этапе торговли анализ вероятных карманок противника даст ценную информацию. Общий смысл на примере Техасского Холдема: на руках у оппонента могут быть пары, разно- или одномастные варианты. Метод подсчета дает сделать количественную оценку:
| Модель или вероятность | Количество |
| Возможные руки в непарных вариантах с одинаковым номиналом | 16 |
| Парные сочетания | По 6 (одного достоинства) |
| Все варианты комбинаций на префлопе | 1326 (общее число) |
| Способы комбинирования разномастных рук | 12 |
Для непарных рук
Вероятность получения игроком одномастных рук разного номинала меньше, чем аналогичных разномастных сочетаний. Существует 16 вариантов из любых 2 случайных непарных карт. Из них 4 — комбинации одной масти и 12 — разной. Всего непарные руки составляют 94% от общего количества (1248 вариантов).
Из них 4 — комбинации одной масти и 12 — разной. Всего непарные руки составляют 94% от общего количества (1248 вариантов).
Для парных рук
В Техасском Холдеме из 1326 вариаций стартовых рук только 6% будут одинаковыми по номиналу. В абсолютном выражении — 78 комбо. Расчет за столом простой: каждая пара может быть в 6 разных вариациях. При анализе ситуации цифра умножается на количество возможных рук в диапазоне.
Количество комбинаций в покере
Традиционно игроки за столом собирают сочетания из 7 карт. Количество комбинаций в покере — 10:
- Старшая карта
- Пара
- Две пары
- Сет (тройка, трипс)
- Стрит
- Флеш
- Фулл-хаус
- Каре
- Стрит-флеш
- Роял-флеш
Классические покерные комбинации
В контексте комбинаторики в покере сочетания изучаются как основы для составления рук. В Техасском Холдеме возможны 133,784,560 различных семикарточных (карманки + борд) вариаций. Сила готового сочетания прямо зависит от вероятности его сбора.
Например, подсчет шансов получения каре по системе комбинаторного анализа. Всего вариаций сочетания 13 (4 двойки, тройки, четверки и т. д.). Из колоды в 52 карты вычитаются 4 (они составляют каре). Получается 48. Цифра нужна для расчета по 3 оставшимся в готовой комбинации картам. В общем они могут составить 17,296 сочетаний. 17,296 х 13 = 224,848 способов получения каре. Вероятность сбора комбинации = 224,848 / 133,784,560 х 100 = 0,168%.
Комбинаторика на постфлопе
Для определения количественной вероятности рук в диапазоне оппонента после появления борда используются две модели. Один расчет — для парных сочетаний, другой — для непарных. Применяемая формула:
O (искомое число) = K1 x K2 или K x (K — 1) / 2
Для непарных рук
У игрока A–Q. На борде A–J–5. Расчет возможного числа комбо вида A–K у соперников:
- K1 — доступные карты, равные по номиналу первой карманной карте (тузы).
- K2 — свободные варианты с рангом второй искомой переменной (короли).

K1 = 4 (всего тузов в колоде) — 2 (у игрока и на борде) = 2. K2 = 4 (в руке и на доске королей нет). K1 * K2 = 2 x 4 = 8 потенциальных вариантов сбора A–K противником.
Для парных рук
Анализ на основе данных из прошлого примера. Формула для парных карманок меняется:
- K — все свободные карты номинала первой искомой (туза).
- K — 1 — полученное число K минус 1 единица.
K = 4 (по количеству тузов в колоде) — 2 (у игрока и на борде) = 2. K1 = 2 — 1 = 1. K * (K-1) / 2 = 2 x 1 / 2 = 1 возможный вариант сбора A–K. Больше одного оппонента с такой рукой за столом быть не может.
Вычисление способов сбора комбинации критически важно для анализа ситуации. Логически и математически тайтовый оппонент с узким диапазоном играет с A–A, A–K, K–K с вероятностью в 33%. Но модель комбинаторики подсказывает: из-за разницы в количественных шансах сбора парных сочетаний цифры совсем другие! A–K — 57%, A–A и K–K — по 21,5%.
Наглядный пример работы комбинаторного метода
Эффект изъятия карт или блокеры
В расчетах и формулах есть центральная переменная. Свободные карты влияют на итоговое число. Если у игрока или на борде есть условный туз, его не будет в диапазоне рук оппонента. Количество возможных комбинаций снижается. Такой туз называют блокером и исключают при расчете.
Пример. У игрока K–K. Доска 10–9–2. Возможных вариантов сетов 9 (по 3 пары десяток, девяток и двоек). Меняем K–K на A–10. Десятка блокирует карманные пары. Теперь число составления сетов не 9, а 7 (1 + 3 + 3).
Использование комбинаторики в различных ситуациях
Математика не выигрывает раздачи. Шансы не означают гарантию победы. Методы комбинаторики профессионалы сочетают с ридсами, собственной тактикой и стратегией. Наблюдение за соперником помогает определить его стиль и понять диапазон. Расчеты позволяют сузить процент возможных вариантов и конвертировать все в инструмент для успешной игры. Комбинации в покере собираются по воле случая, но зависят от законов математики.
Комбинации в покере собираются по воле случая, но зависят от законов математики.
Например, покерист с рукой 7–7, на борде A–Q–7–8–2. Банк — $12. После ставки в $10 оппонент отвечает пушем в $60. По шансам банка колл возможен, если покерист в 38% случаев впереди соперника. Комбинаторика позволяет рассмотреть все возможные руки противника и вероятности их составления. Итоги:
- Всего возможных вариантов комбо — 42.
- Сочетаний, которые проиграют сету семерок — 33.
- Победных в сравнении с 7–7–7 вариантов — 9.
79% (по эквити) на 21% в пользу игрока. Колл оправдан.
Часто задаваемые вопросы
Как представить диапазон соперника?
Пользоваться статистикой с помощью ридсов и анализа во время игры.
Модель вычисления комбинаций обязательна для плюсовой карьеры?
Большинство профессионалов используют все инструменты математики. Одну раздачу или турнир можно выиграть на везении, серию — нет.
В чем преимущество методики, помимо определения процентов?
Покерист начинает играть не по своим, а по чужим рукам. Такого противника очень трудно прочитать.
Как научиться мгновенно просчитывать сложные сценарии за столом?
Всегда изучать свои руки в программах. Со временем типовые ситуации будут запоминаться автоматически, расчет станет легче.
С ростом лимитов комбинаторика приобретает ценность или теряет ее?
На столах формата NL5 много рекреационных игроков. Они не думают, предугадать их ходы и диапазоны сложнее.
1.2 Комбинации и перестановки
Сначала обратимся к , считая . Хотя это звучит просто, возможно, слишком
просто учиться, это не так. Когда мы говорим о счете, это стенография
для определения размера множества или, чаще, размеров многих
наборы, все с чем-то общим, но разные размеры в зависимости от
один или несколько параметров. Например: сколько исходов возможно
когда бросают кубик? Две кости? $n$ кости? Как сказано, это
двусмысленно: что мы подразумеваем под «результатом»? Предположим, мы бросаем две кости,
скажем, красный кубик и зеленый кубик. Является ли «красный два, зеленый три» другим
результат, чем «красное три, зеленое два»? Если да, мы подсчитываем
количество возможных «физических» исходов, а именно 36. Если нет, то есть
21. Нас даже могут интересовать просто возможные итоги, т.е.
в этом случае есть 11 исходов.
Является ли «красный два, зеленый три» другим
результат, чем «красное три, зеленое два»? Если да, мы подсчитываем
количество возможных «физических» исходов, а именно 36. Если нет, то есть
21. Нас даже могут интересовать просто возможные итоги, т.е.
в этом случае есть 11 исходов.
Даже довольно простая первая интерпретация опирается на некоторую степень
знание счета; мы сначала выясним два простых факта. В
с точки зрения размеров множества, предположим, что мы знаем, что множество $A$ имеет размер $m$ и множество
$B$ имеет размер $n$. Каков размер $A$ и $B$ вместе, то есть
размер $A\cup B$? Если мы знаем, что $A$ и $B$ не имеют элементов в
общий, то размер $A\cup B$ равен $m+n$; если у них есть элементы в
общее, нам нужно больше информации. Простая, но типичная проблема этого
тип: если мы бросим два кубика, сколько существует способов получить либо 7, либо
11? Так как есть 6 способов получить 7 и два способа получить 11,
ответ: $6+2=8$. Хотя этот принцип прост, его легко
забыть требование непересекаемости двух множеств и, следовательно, использовать
это когда обстоятельства иные. Этот принцип часто
называется 9п м_i$. Этот
может быть доказано простым рассуждением по индукции.
Этот принцип часто
называется 9п м_i$. Этот
может быть доказано простым рассуждением по индукции.
Почему мы знаем, не перечисляя их всех, что существует 36 исходов?
когда бросают две игральные кости? Мы можем рассматривать результаты как два отдельных
результаты, то есть результат броска кубика номер один и
результат броска кубика номер два. По каждому из 6 исходов
первый кубик второй кубик может иметь любой из 6 исходов, поэтому сумма равна
$6+6+6+6+6+6=36$ или, более компактно, $6\cdot6=36$. Обратите внимание, что мы
здесь действительно используется принцип сложения: set $A_1$ — это все пары
$(1,x)$, набор $A_2$ — это все пары $(2,x)$ и т. д. это несколько
более тонким, чем кажется на первый взгляд. В этом простом примере
результаты кубика номер два не имеют ничего общего с результатами кубика
номер один. Вот немного более сложный пример: сколько способов
можно ли бросить два кубика так, чтобы два кубика не совпали? То есть,
исключаем 1-1, 2-2 и так далее. Здесь для каждого возможного значения на кубике
число один, есть пять возможных значений кубика номер два, но
это разные пять значений для каждого значения на номере кубика
один. Тем не менее, поскольку все одинаковы, результат равен 5+5+5+5+5+5=30$,
или $6\cdot 5=30$. В общем случае, если имеется $m$ возможностей для
одно событие и $n$ для второго события, количество возможных исходов
для обоих событий вместе равно $m\cdot n$. Это часто называют
9п м_i$. Это тоже
можно доказать по индукции.
Тем не менее, поскольку все одинаковы, результат равен 5+5+5+5+5+5=30$,
или $6\cdot 5=30$. В общем случае, если имеется $m$ возможностей для
одно событие и $n$ для второго события, количество возможных исходов
для обоих событий вместе равно $m\cdot n$. Это часто называют
9п м_i$. Это тоже
можно доказать по индукции.
Пример 1.2.1 Сколько исходов возможно при броске трех игральных костей, если не может быть двух одинаковых? Первые две кости вместе имеют $6\cdot 5=30$ возможных исходов, сверху. Для каждого из этих 30 исходов, есть четыре возможных исхода для третьего кубика, поэтому общее количество исходов $30\cdot 4=6\cdot 5\cdot 4=120$. (Обратите внимание, что мы считаем кости различимыми, то есть броском 6, 4, 1 отличается от 4, 6, 1, потому что первое и второе кости различны в двух бросках, даже несмотря на то, что числа как набор подобные.) $\квадрат$
Пример 1.2.2. Предположим, что блоки с номерами от 1 до $n$ находятся в бочке; мы
вытащите из них $k$, расположив их в линию, как мы. Как много
исходы возможны? То есть, сколько различных расположений $k$
блоки могли бы мы видеть?
Как много
исходы возможны? То есть, сколько различных расположений $k$
блоки могли бы мы видеть?
По сути, это то же самое, что и в предыдущем примере: имеется $k$ «пятен». заполняться блоками. Любой из блоков $n$ может появиться первым в линия; то любой из оставшихся $n-1$ может появиться следующим, и, таким образом, на. Таким образом, число исходов равно $n(n-1)(n-2)\cdots(n-k+1)$, согласно принцип умножения. в В предыдущем примере первое «пятно» было номером один, второе точка была номером два, третья точка была номером три, и $6\cdot5\cdot4=6(6-1)(6-2)$; обратите внимание, что $6-2=6-3+1$. $\квадрат$
Это довольно общая проблема:
Определение 1.2.3 Количество перестановок $n$ вещи, взятые $k$ за раз, $$P(n,k)=n(n-1)(n-2)\cdots(n-k+1)={n!\over (n-k)!}.$$ $\квадрат$
Перестановка некоторых объектов представляет собой конкретное линейное упорядочение
объекты; Фактически $P(n,k)$ одновременно учитывает две вещи:
количество способов выбрать и упорядочить $k$ из $n$ объектов. Полезный
частный случай $k=n$, в котором мы просто считаем число
способов упорядочить все $n$ объектов. Это
$n(n-1)\cdots(n-n+1)=n!$. Обратите внимание, что вторая форма $P(n,k)$ из
определение дает
$${n!\over (n-n)!}={n!\over 0!}.$$
Это правильно, только если $0!=1$, поэтому мы принимаем стандартное соглашение
что это правда, то есть мы определяет $0!$ как $1$.
Полезный
частный случай $k=n$, в котором мы просто считаем число
способов упорядочить все $n$ объектов. Это
$n(n-1)\cdots(n-n+1)=n!$. Обратите внимание, что вторая форма $P(n,k)$ из
определение дает
$${n!\over (n-n)!}={n!\over 0!}.$$
Это правильно, только если $0!=1$, поэтому мы принимаем стандартное соглашение
что это правда, то есть мы определяет $0!$ как $1$.
Предположим, мы хотим подсчитать только количество способов выбрать $k$ предметов. из $n$, то есть порядок нам не важен. В Пример 1.2.1, мы подсчитали количество броски трех игральных костей с разными числами. Кости были различимы или в определенном порядке: первый кубик, второй и третий. Теперь мы хотим просто посчитать, сколько комбинаций чисел есть, причем 6, 4, 1 теперь считаются той же комбинацией, что и 4, 6, 1.
Пример 1.2.4
Предположим, нам нужно перечислить все 120 возможностей в
пример 1.2.1. Список будет содержать
множество исходов, которые мы теперь хотим считать одним исходом;
6, 4, 1 и 4, 6, 1 будут в списке, но не должны учитываться
отдельно. Сколько раз один результат появится в списке?
Это задача на перестановку: есть $3!$ порядков, в которых 1, 4, 6
может появиться, и все 6 из них будут в списке. На самом деле каждый
исход появится в списке 6 раз, так как каждый исход может
появляются в заказах $3!$. Следовательно, список слишком велик в 6 раз;
правильный счет для новой задачи: $120/6=20$.
$\квадрат$
Сколько раз один результат появится в списке?
Это задача на перестановку: есть $3!$ порядков, в которых 1, 4, 6
может появиться, и все 6 из них будут в списке. На самом деле каждый
исход появится в списке 6 раз, так как каждый исход может
появляются в заказах $3!$. Следовательно, список слишком велик в 6 раз;
правильный счет для новой задачи: $120/6=20$.
$\квадрат$
Следуя тем же рассуждениям вообще, если у нас есть $n$ объектов, количество способов выбрать $k$ из них $P(n,k)/k!$, так как каждый набор из $k$ объектов будет посчитал $k!$ раз по $P(n,k)$.
Определение 1.2.5 Количество подмножеств размера $k$ множества размера $n$ (также называется $n$-множеством) $$C(n,k)={P(n,k)\более k!}={n!\over k!(n-k)!}={n\выбрать k}.$$ Обозначение $C(n,k)$ используется редко; вместо этого мы используем $n\выбрать k$, произносится как «$n$ выбирает $k$». $\квадрат$
Пример 1.2.6
Рассмотрим $n=0,1,2,3$. Несложно перечислить
подмножества малого $n$-множества; типичное $n$-множество
$\{a_1,a_2,\ldots,a_n\}$. $0$-множество, а именно пустое множество, имеет
одно подмножество, пустой набор; $1$-множество имеет два подмножества, пустое множество
и $\{a_1\}$; $2$-подмножество имеет четыре подмножества, $\emptyset$, $\{a_1\}$,
$\{a_2\}$, $\{a_1,a_2\}$; а $3$-подмножество имеет восемь:
$\emptyset$, $\{a_1\}$, $\{a_2\}$, $\{a_3\}$, $\{a_1,a_2\}$,
$\{a_1,a_3\}$, $\{a_2,a_3\}$, $\{a_1,a_2,a_3\}$.
Затем из этих списков легко вычислить $n\выбрать k$:
$$\displaylines{\cr
\матрица{
&\rlap{\lower 3pt\hbox{$\Rule{65pt}{0pt}{0.5pt}$}}\cr
&0\кр
п&1\кр
&2\кр
&3\кр
}\влево\верт
\матрица{
0&\нижний 3.5pt\hbox{}\rlap{\smash{\поднять 1.5em \hbox{$k$}}}1&2&3\cr
1\кр
1&1\кр
1&2&1\кр
1&3&3&1\кр
}\право.\cr}$$
$\квадрат$
$0$-множество, а именно пустое множество, имеет
одно подмножество, пустой набор; $1$-множество имеет два подмножества, пустое множество
и $\{a_1\}$; $2$-подмножество имеет четыре подмножества, $\emptyset$, $\{a_1\}$,
$\{a_2\}$, $\{a_1,a_2\}$; а $3$-подмножество имеет восемь:
$\emptyset$, $\{a_1\}$, $\{a_2\}$, $\{a_3\}$, $\{a_1,a_2\}$,
$\{a_1,a_3\}$, $\{a_2,a_3\}$, $\{a_1,a_2,a_3\}$.
Затем из этих списков легко вычислить $n\выбрать k$:
$$\displaylines{\cr
\матрица{
&\rlap{\lower 3pt\hbox{$\Rule{65pt}{0pt}{0.5pt}$}}\cr
&0\кр
п&1\кр
&2\кр
&3\кр
}\влево\верт
\матрица{
0&\нижний 3.5pt\hbox{}\rlap{\smash{\поднять 1.5em \hbox{$k$}}}1&2&3\cr
1\кр
1&1\кр
1&2&1\кр
1&3&3&1\кр
}\право.\cr}$$
$\квадрат$
Вы, наверное, узнаете эти цифры: это начало Треугольник Паскаля . Каждая запись в
Треугольник Паскаля получается путем добавления двух элементов из предыдущего
ряд: тот, что прямо сверху, и тот, что выше и левее. Этот
предполагает, что ${n\выбрать k}={n-1\выбрать k-1}+{n-1\выбрать k}$, и
действительно это правда. Чтобы сделать это аккуратно, мы принимаем
соглашение о том, что ${n\choose k}=0$, когда $kn$.
Чтобы сделать это аккуратно, мы принимаем
соглашение о том, что ${n\choose k}=0$, когда $kn$.
Теорема 1.2.7 $\ds{n\выберите k}={n-1\выберите k-1}+{n-1\выберите k}$.
Доказательство. Типичным $n$-множеством является $A=\{a_1,\ldots,a_n\}$. Мы рассматриваем два типа подмножества: содержащие $a_n$ и не содержащие. Если $k$-подмножество $A$ не содержит $a_n$, то оно является $k$-подмножеством $\{a_1,…,a_{n-1}\}$, и таких $n-1\выберите k$. Если это содержит $a_n$, то он состоит из $a_n$ и $k-1$ элементов $\{a_1,…,a_{n-1}\}$; так как их $n-1\выберите k-1$, таких подмножеств $n-1\выберите k-1$. Таким образом, общее количество $k$-подмножеств $A$ равно ${n-1\выбрать k-1}+{n-1\выбрать k}$.
Обратите внимание, что когда $k=0$, ${n-1\выберите k-1}={n-1\выберите -1}=0$, и когда $k=n$, ${n-1\выбрать k}={n-1\выбрать n}=0$, так что ${n\выбрать 0}={n-1\выбрать 0}$ и ${n\выбрать n}={n-1\выбрать п-1}$. Эти значения являются граничными в треугольнике Паскаля. $\qed$
Многие проблемы со счетом основаны на рассуждениях, которые у нас есть. видимый. Вот несколько вариаций на тему.
видимый. Вот несколько вариаций на тему.
Пример 1.2.8 Шесть человек должны сидеть за круглым столом; сколько сидячих мест аранжировки есть?
Не совсем ясно, что именно мы имеем в виду, чтобы считать здесь. если есть «специальное место», например, может иметь значение, кто окажется на этом сиденье. Если это не имеет значения, нас интересует только относительное положение каждого человека. Тогда может или не может быть важно, является ли определенное лицо находится слева или справа от другого. Так что этот вопрос можно интерпретируется (по крайней мере) тремя способами. Давайте ответим на них все.
Во-первых, если имеют значение фактические стулья, на которых сидят люди, то это
точно так же, как выстраивание шести человек в ряд: 6 вариантов места
номер один, 5 для второго места и так далее, всего 6 долларов! Если
стулья не имеют значения, тогда $6!$ считают одно и то же расположение слишком большим
раз, по одному разу для каждого человека, который может быть на первом месте. Итак, общее количество в
в этом случае $6!/6=5!$. Другой подход к этому: поскольку фактическое
места не имеют значения, просто посадите одного из шести человек на стул. Тогда мы
нужно расставить оставшихся 5 человек в ряд, что можно сделать в
$5!$ способов. Наконец, предположим, что нас волнует только то, кто рядом с кем,
игнорируя право и лево. Тогда предыдущий ответ считает каждый
расположение дважды, один раз для порядка против часовой стрелки и один раз для
по часовой стрелке. Итого $5!/2=P(5,3)$.
$\квадрат$
Итак, общее количество в
в этом случае $6!/6=5!$. Другой подход к этому: поскольку фактическое
места не имеют значения, просто посадите одного из шести человек на стул. Тогда мы
нужно расставить оставшихся 5 человек в ряд, что можно сделать в
$5!$ способов. Наконец, предположим, что нас волнует только то, кто рядом с кем,
игнорируя право и лево. Тогда предыдущий ответ считает каждый
расположение дважды, один раз для порядка против часовой стрелки и один раз для
по часовой стрелке. Итого $5!/2=P(5,3)$.
$\квадрат$
Мы дважды видели общий принцип в действии: если мы можем пересчитать желаемый набор таким образом, чтобы каждый элемент считался одинаковым количество раз, мы можем получить желаемое количество, просто разделив на общий фактор пересчета. Это по-прежнему будет полезной идеей. А вариация на эту тему состоит в том, чтобы пересчитать , а затем вычесть из сумма перерасчета.
Пример 1.2.9. Сколькими способами можно выстроить шесть человек так, чтобы конкретная пара людей не является соседней?
Обозначим людей $A$ и $B$. Общее количество заказов составляет $6!$, но здесь учитываются заказы с
$A$ и $B$ рядом друг с другом. Сколько из них есть? Думать о
эти два человека как единое целое; сколько существует способов выстроить
Блок $AB$ с остальными четырьмя людьми? У нас есть 5 предметов, поэтому ответ
$5!$. Каждый из этих порядков соответствует двум различным порядкам в
которые $A$ и $B$ являются смежными, в зависимости от того, является ли $A$ или $B$
первый. Таким образом, количество $6!$ слишком велико на $2\cdot5!$ и количество, которое мы
seek равен $6!-2\cdot 5!=4\cdot5!$.
$\квадрат$
9{e_n}$ есть, где
$p_i$ — различные простые числа?
Общее количество заказов составляет $6!$, но здесь учитываются заказы с
$A$ и $B$ рядом друг с другом. Сколько из них есть? Думать о
эти два человека как единое целое; сколько существует способов выстроить
Блок $AB$ с остальными четырьмя людьми? У нас есть 5 предметов, поэтому ответ
$5!$. Каждый из этих порядков соответствует двум различным порядкам в
которые $A$ и $B$ являются смежными, в зависимости от того, является ли $A$ или $B$
первый. Таким образом, количество $6!$ слишком велико на $2\cdot5!$ и количество, которое мы
seek равен $6!-2\cdot 5!=4\cdot5!$.
$\квадрат$
9{e_n}$ есть, где
$p_i$ — различные простые числа?
Пример 1.2.2 Покерная рука состоит из пяти карт из стандартных 52 карт. колода с четырьмя мастями и тринадцатью достоинствами в каждой масти; получатель чего-то карты в руке значения не имеют. Из скольких рук состоит 2 карты одного достоинства и 3 карты другого достоинства (фулл-хаус)? Сколько состоит из 5 карт одной масти (флеш)?
Пример 1. 2.3 Шестеро мужчин и шесть женщин должны сидеть за столом,
мужчины и женщины чередуются. Стулья не имеют значения, важно только, кто следующий
кому, а правое и левое разные. Сколько сидячих мест
аранжировки возможны?
2.3 Шестеро мужчин и шесть женщин должны сидеть за столом,
мужчины и женщины чередуются. Стулья не имеют значения, важно только, кто следующий
кому, а правое и левое разные. Сколько сидячих мест
аранжировки возможны?
Пример 1.2.4 Восемь человек должны сидеть за столом; стулья неважно, только кто рядом с кем, а справа и слева другой. Два человека, X и Y, не могут сидеть рядом друг с другом. Сколько посадочных мест возможно?
Пример 1.2.5 В шахматах ладья атакует любую фигуру в той же строке или столбце. как ладья, если между ними нет другой фигуры. Сколькими способами можно ли разместить на шахматной доске восемь неразличимых ладей так, чтобы двое не нападают друг на друга? Как насчет восьми неразличимых ладей на доска $10\times 10$?
Пример 1.2.6 Предположим, мы хотим поставить 8 неатакующих ладей на поле. шахматная доска. Сколькими способами мы можем это сделать, если 16 наиболее Квадраты «северо-запад» должны быть пустыми? А если только 4 самых Квадраты «северо-запад» должны быть пустыми?
Пример 1. 2.7 «Правильная» последовательность скобок — это последовательность, в которой скобки
могут быть правильно сопоставлены, например $()(())$. Нетрудно заметить, что это
возможно именно тогда, когда число левых и правых скобок равно
то же самое, и каждый начальный сегмент последовательности имеет по крайней мере как
многие левые скобки как правые. Например, $())\ldots$ не может
возможно, будет расширена до юридической последовательности. Покажите, что количество
допустимые последовательности длины $2n$ равны $C_n={2n\выбрать n}-{2n\выбрать n+1}$.
Числа $C_n$ называются Каталонский
номера .
2.7 «Правильная» последовательность скобок — это последовательность, в которой скобки
могут быть правильно сопоставлены, например $()(())$. Нетрудно заметить, что это
возможно именно тогда, когда число левых и правых скобок равно
то же самое, и каждый начальный сегмент последовательности имеет по крайней мере как
многие левые скобки как правые. Например, $())\ldots$ не может
возможно, будет расширена до юридической последовательности. Покажите, что количество
допустимые последовательности длины $2n$ равны $C_n={2n\выбрать n}-{2n\выбрать n+1}$.
Числа $C_n$ называются Каталонский
номера .
Комбинации и перестановки
\(\def\d{\displaystyle}
\def\курс{Математика 228}
\ новая команда {\ f} [1] {\ mathfrak # 1}
\ новая команда {\ s} [1] {\ mathscr # 1}
\def\N{\mathbb N}
\def\B{\mathbf{B}}
\def\circleA{(-.5,0) круг (1)}
\ деф \ Z {\ mathbb Z}
\def\circleAlabel{(-1.5,.6) узел[выше]{$A$}}
\def\Q{\mathbb Q}
\def\circleB{(.5,0) круг (1)}
\def\R{\mathbb R}
\def\circleBlabel{(1. {-1}}
\def\nrml{\triangleleft}
\ деф \ ст {:}
\ деф \ ~ {\ широкая тильда}
\def\rem{\mathcal R}
\def\sigalg{$\sigma$-алгебра }
\def\Гал{\mbox{Гал}}
\def\iff{\leftrightarrow}
\def\If{\Leftrightarrow}
\ деф \ земля {\ клин}
\def\И{\bigwedge}
\защита\вход{\вход}
\def\AAnd{\d\bigwedge\mkern-18mu\bigwedge}
\def\Ви{\bigvee}
\def\VVee{\d\Vee\mkern-18mu\Vee}
\ деф \ имп {\ стрелка вправо}
\def\Imp{\Rightarrow}
\def\Fi{\Leftarrow}
\def\var{\mbox{var}}
\def\Th{\mbox{Th}}
\защита\вход{\вход}
\def\sat{\mbox{Sat}}
\def\con{\mbox{Con}}
\def\iffmodels{\bmodels\models}
\def\dbland{\bigwedge \!\!\bigwedge}
\def\дом{\mbox{дом}}
\def\rng{\mbox{диапазон}}
\def\isom{\cong}
\DeclareMathOperator{\wgt}{wgt}
\newcommand{\vtx}[2]{узел[заливка,круг,внутренний интервал=0pt, минимальный размер=4pt,метка=#1:#2]{}}
\ новая команда {\ va} [1] {\ vtx {выше} {# 1}}
\ новая команда {\ vb} [1] {\ vtx {ниже} {# 1}}
\ новая команда {\ vr} [1] {\ vtx {право} {# 1}}
\ новая команда {\ vl} [1] {\ vtx {слева} {# 1}}
\renewcommand{\v}{\vtx{выше}{}}
\def\circleA{(-.
{-1}}
\def\nrml{\triangleleft}
\ деф \ ст {:}
\ деф \ ~ {\ широкая тильда}
\def\rem{\mathcal R}
\def\sigalg{$\sigma$-алгебра }
\def\Гал{\mbox{Гал}}
\def\iff{\leftrightarrow}
\def\If{\Leftrightarrow}
\ деф \ земля {\ клин}
\def\И{\bigwedge}
\защита\вход{\вход}
\def\AAnd{\d\bigwedge\mkern-18mu\bigwedge}
\def\Ви{\bigvee}
\def\VVee{\d\Vee\mkern-18mu\Vee}
\ деф \ имп {\ стрелка вправо}
\def\Imp{\Rightarrow}
\def\Fi{\Leftarrow}
\def\var{\mbox{var}}
\def\Th{\mbox{Th}}
\защита\вход{\вход}
\def\sat{\mbox{Sat}}
\def\con{\mbox{Con}}
\def\iffmodels{\bmodels\models}
\def\dbland{\bigwedge \!\!\bigwedge}
\def\дом{\mbox{дом}}
\def\rng{\mbox{диапазон}}
\def\isom{\cong}
\DeclareMathOperator{\wgt}{wgt}
\newcommand{\vtx}[2]{узел[заливка,круг,внутренний интервал=0pt, минимальный размер=4pt,метка=#1:#2]{}}
\ новая команда {\ va} [1] {\ vtx {выше} {# 1}}
\ новая команда {\ vb} [1] {\ vtx {ниже} {# 1}}
\ новая команда {\ vr} [1] {\ vtx {право} {# 1}}
\ новая команда {\ vl} [1] {\ vtx {слева} {# 1}}
\renewcommand{\v}{\vtx{выше}{}}
\def\circleA{(-. 5,0) круг (1)}
\def\circleAlabel{(-1.5,.6) узел[выше]{$A$}}
\def\circleB{(.5,0) круг (1)}
\def\circleBlabel{(1.5,.6) узел[выше]{$B$}}
\def\circleC{(0,-1) круг (1)}
\def\circleClabel{(.5,-2) узел[справа]{$C$}}
\def\twosetbox{(-2,-1.4) прямоугольник (2,1.4)}
\def\threesetbox{(-2.5,-2.4) прямоугольник (2.5,1.4)}
\def\ansfilename{практика-ответы}
\def\shadowprops{{fill=black!50,shadow xshift=0.5ex,shadow yshift=0.5ex,path fading={круг с размытым краем 10 процентов}}}
\ новая команда {\ hexbox} [3] {
\def\x{-cos{30}*\r*#1+cos{30}*#2*\r*2}
\def\y{-\r*#1-sin{30}*\r*#1}
\рисовать (\х,\у) +(90:\r) — +(30:\r) — +(-30:\r) — +(-90:\r) — +(-150:\r) — +(150: \r) — цикл;
\draw (\x,\y) узел{#3};
}
\renewcommand{\bar}{\overline}
\newcommand{\card}[1]{\left| #1 \справа|}
\newcommand{\twoline}[2]{\begin{pmatrix}#1 \\ #2 \end{pmatrix}}
\новая команда{\lt}{<}
\новая команда{\gt}{>}
\newcommand{\amp}{&}
\)
5,0) круг (1)}
\def\circleAlabel{(-1.5,.6) узел[выше]{$A$}}
\def\circleB{(.5,0) круг (1)}
\def\circleBlabel{(1.5,.6) узел[выше]{$B$}}
\def\circleC{(0,-1) круг (1)}
\def\circleClabel{(.5,-2) узел[справа]{$C$}}
\def\twosetbox{(-2,-1.4) прямоугольник (2,1.4)}
\def\threesetbox{(-2.5,-2.4) прямоугольник (2.5,1.4)}
\def\ansfilename{практика-ответы}
\def\shadowprops{{fill=black!50,shadow xshift=0.5ex,shadow yshift=0.5ex,path fading={круг с размытым краем 10 процентов}}}
\ новая команда {\ hexbox} [3] {
\def\x{-cos{30}*\r*#1+cos{30}*#2*\r*2}
\def\y{-\r*#1-sin{30}*\r*#1}
\рисовать (\х,\у) +(90:\r) — +(30:\r) — +(-30:\r) — +(-90:\r) — +(-150:\r) — +(150: \r) — цикл;
\draw (\x,\y) узел{#3};
}
\renewcommand{\bar}{\overline}
\newcommand{\card}[1]{\left| #1 \справа|}
\newcommand{\twoline}[2]{\begin{pmatrix}#1 \\ #2 \end{pmatrix}}
\новая команда{\lt}{<}
\новая команда{\gt}{>}
\newcommand{\amp}{&}
\)
Расследуй!8
У вас есть набор фишек пяти разных цветов: красного, синего, зеленого, фиолетового и желтого.
Сколько различных стопок по две фишки можно составить, если нижняя фишка должна быть красной или синей? Объясните свой ответ, используя как аддитивный, так и мультипликативный принцип.
Сколько различных стопок по три фишки можно составить, если нижняя фишка должна быть красной или синей, а верхняя фишка должна быть зеленой, фиолетовой или желтой? Как эта проблема связана с предыдущей?
Сколько существует различных стопок по три фишки, в которых ни один цвет не повторяется? Как насчет стеков из четырех фишек?
Предположим, вы хотите взять три фишки разного цвета и положить их в карман. Сколько различных вариантов у вас есть? Что, если вы хотите четыре фишки разного цвета? Как эти проблемы связаны с предыдущими?
Перестановка — это (возможная) перестановка объектов. Например, есть 6 перестановок букв a, b, c :
\begin{уравнение*} abc, ~~ acb, ~~ bac, ~~ bca, ~~ каб, ~~ cba. \end{уравнение*}
\end{уравнение*}Мы знаем, что у нас есть все перечисленные выше — есть 3 варианта, какую букву поставить первой, затем 2 варианта, какая буква будет следующей, что оставляет только 1 вариант для последней буквы. Мультипликативный принцип говорит, что мы умножаем \(3\cdot 2 \cdot 1\text{.}\)
Пример 1.3.1
Сколько существует перестановок букв a, b, c, d, e, f ?
Решение
Мы НЕ хотим пытаться перечислить все это. Однако, если бы мы это сделали, нам нужно было бы выбрать букву для записи в первую очередь. Есть 6 вариантов этой буквы. Для каждого выбора первой буквы есть 5 вариантов второй буквы (мы не можем повторить первую букву, мы переставляем буквы и имеем только по одной каждой), и для каждой из них есть 4 варианта третьей, 3 варианты для четвертого, 2 варианта для пятого и, наконец, только 1 вариант для последней буквы. Итак, есть \(6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 = 720\) перестановки 6 букв.
Здесь будет полезна небольшая запись: \(n!\text{,}\) читать как «\(n\) факториал», это произведение всех положительных целых чисел, меньших или равных \(n\) (для из соображений удобства мы также определяем 0! как 1). Таким образом, количество перестановок 6 букв, как видно из предыдущего примера, равно \(6! = 6\cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1\text{.}\) Это обобщает:
Перестановки \(n\) элементов
Существуют \(n! = n\cdot (n-1)\cdot (n-2)\cdot \cdots \cdot 2\cdot 1\) перестановки \(n\) (различных) элементов.
Example1.3.2 Подсчет биективных функций
Сколько функций \(f:\{1,2,\ldots,8\} \to \{1,2,\ldots, 8\}\) являются биективными ?
Решение
Вспомните, что означает биективность функции: каждый элемент в домене кодов должен быть образом ровно одного элемента домена. Используя двухстрочную запись, мы могли бы записать одну из этих биекций как
. \begin{уравнение*}
f = \twoline{1 \amp 2 \amp 3 \amp 4 \amp 5 \amp 6 \amp 7 \amp 8} {3 \amp 1 \amp 5 \amp 8 \amp 7 \amp 6 \amp 2 \amp 4}
\end{уравнение*}
\begin{уравнение*}
f = \twoline{1 \amp 2 \amp 3 \amp 4 \amp 5 \amp 6 \amp 7 \amp 8} {3 \amp 1 \amp 5 \amp 8 \amp 7 \amp 6 \amp 2 \amp 4}
\end{уравнение*}
На самом деле мы просто переставляем элементы кодового домена, поэтому мы создаем перестановку из 8 элементов. На самом деле «перестановка» — это еще один термин, используемый для описания биективных функций из конечного множества в себя.
Если вы в это верите, то вы видите, что ответ должен быть \(8! = 8 \cdot 7 \cdot\cdots\cdot 1 = 40320\text{.}\) Это можно увидеть и непосредственно: для каждого элемента домена, мы должны выбрать отдельный элемент кодового домена для сопоставления. Есть 8 вариантов, куда отправить 1, затем 7 вариантов, куда отправить 2, и так далее. Умножаем по принципу мультипликативности.
Иногда мы не хотим переставлять все буквы/цифры/элементы, которые нам даны.
Пример 1.3.3
Сколько 4-буквенных «слов» можно составить из букв от a до f без повторяющихся букв?
Решение
Это похоже на задачу перестановки 4 букв, только теперь у нас больше вариантов для каждой буквы. Для первой буквы есть 6 вариантов. Для каждого из них есть 5 вариантов второй буквы. Затем есть 4 варианта для третьей буквы и 3 варианта для последней буквы. Общее количество слов равно \(6\cdot 5\cdot 4 \cdot 3 = 360\text{.}\). Это не \(6!\), потому что мы никогда не умножали на 2 и 1. Мы могли бы начать с \ (6!\), а затем сократите 2 и 1 и, таким образом, напишите \(\frac{6!}{2!}\text{.}\)
Для первой буквы есть 6 вариантов. Для каждого из них есть 5 вариантов второй буквы. Затем есть 4 варианта для третьей буквы и 3 варианта для последней буквы. Общее количество слов равно \(6\cdot 5\cdot 4 \cdot 3 = 360\text{.}\). Это не \(6!\), потому что мы никогда не умножали на 2 и 1. Мы могли бы начать с \ (6!\), а затем сократите 2 и 1 и, таким образом, напишите \(\frac{6!}{2!}\text{.}\)
В общем, мы можем спросить, сколько существует перестановок \(k\) объектов, выбирающих эти объекты из большего набора \(n\) объектов. (В приведенном выше примере \(k = 4\text{,}\) и \(n = 6\text{.}\)) Мы пишем это число \(P(n,k)\) и иногда называем его \(k\)-перестановка \(n\) элементов . Из приведенного выше примера мы видим, что для вычисления \(P(n,k)\) мы должны применить принцип умножения к \(k\) числам, начиная с \(n\) и считая в обратном порядке. Например
\begin{уравнение*} P(10, 4) = 10\cdot 9\кдот 8 \кдот 7. \end{уравнение*} Еще раз обратите внимание, что \(P(10,4)\) начинается с вида \(10!\text{,}\), но мы останавливаемся после 7. Мы можем формально объяснить эту «остановку», отделив часть факториал нам не нужен:
Мы можем формально объяснить эту «остановку», отделив часть факториал нам не нужен:
Осторожно: факториал в знаменателе равен не \(4!\), а \((10-4)!\text{.}\)
\(k\)-перестановки \(n\) элементов
\(P(n,k)\) — количество \(k\)-перестановок \(n\) элементов , количество способов расположить \(k\) объектов, выбранных из \( п\) различных объектов.
\begin{уравнение*} P(n,k) = \frac{n!}{(n-k)!}. \end{уравнение*}Обратите внимание, что когда \(n = k\text{,}\) мы имеем \(P(n,n) = \frac{n!}{(n-n)!} = n!\) (поскольку мы определили \( 0!\) на 1). Это имеет смысл — мы уже знаем, что \(n!\) дает количество перестановок всех \(n\) объектов.
Example1.3.4 Подсчет инъективных функций
Сколько функций \(f:\{1,2,3\} \to \{1,2,3,4,5,6,7,8\}\) являются инъективными ?
Решение
Обратите внимание, что здесь не имеет смысла запрашивать количество биекций , поскольку их нет (поскольку кодовый домен больше, чем домен, нет никаких сюръекций). Но чтобы функция была инъективной, мы просто не можем использовать элемент кодового домена более одного раза.
Но чтобы функция была инъективной, мы просто не можем использовать элемент кодового домена более одного раза.
Нам нужно выбрать элемент из кодового домена, который будет изображением 1. Есть 8 вариантов. Затем нам нужно выбрать один из оставшихся 7 элементов, чтобы он был образом 2. Наконец, один из оставшихся 6 элементов должен быть образом 3. Таким образом, общее количество функций равно \(8\cdot 7 \cdot 6 = Р(8,3)\текст{.}\)
В целом это демонстрирует, что число инъекций \(f:A \to B\text{,}\), где \(\card{A} = k\) и \(\card{B} = n \text{,}\) равно \(P(n,k)\text{.}\)
Вот еще один способ найти количество \(k\)-перестановок \(n\) элементов: сначала выберите, какие \(k\) элементов будут в перестановке, затем посчитайте, сколько существует способов их расположить. После того, как вы выбрали \(k\) объектов, мы знаем, что есть \(k!\) способов упорядочить (переставить) их. Но как выбрать \(k\) объектов из \(n\text{?}\) У вас есть \(n\) объектов, и вам нужно выберите \(k\) из них. Вы можете сделать это \({n \выбрать k}\) способами. Тогда для каждого выбора из этих \(k\) элементов мы можем переставить из них \(k!\) способов. Используя принцип умножения, мы получаем другую формулу для \(P(n,k)\text{:}\)
Вы можете сделать это \({n \выбрать k}\) способами. Тогда для каждого выбора из этих \(k\) элементов мы можем переставить из них \(k!\) способов. Используя принцип умножения, мы получаем другую формулу для \(P(n,k)\text{:}\)
Теперь, поскольку у нас уже есть замкнутая формула для \(P(n,k)\), мы можем подставить ее в:
\begin{уравнение*} \frac{n!}{(n-k)!} = {n \выберите k} \cdot k!. \end{уравнение*}Если мы разделим обе части на \(k!\), мы получим замкнутую формулу для \({n \choose k}\text{.}\)
Замкнутая формула для \({n \выбрать k}\)
\begin{уравнение*} {n \выберите k} = \frac{n!}{(n-k)!k!} \end{уравнение*} Мы говорим, что \(P(n,k)\) считает перестановки , а \({n \выбрать k}\) считает комбинации . Формулы для каждого из них очень похожи, просто в знаменателе \({n \choose k}\text{.}\) есть лишний \(k!\) что \({n \choose k}\) не различает различные порядки, в которых могут появляться \(k\) объекты. Мы просто выбираем (или выбираем) \(k\) объекты, а не упорядочиваем их. Возможно, «комбинация» — обманчивый ярлык. Мы не имеем в виду кодовый замок (где порядок определенно имеет значение). Возможно, лучшая метафора — это сочетание вкусов — вам просто нужно решить, какие вкусы сочетать, а не в каком порядке их комбинировать.
Мы просто выбираем (или выбираем) \(k\) объекты, а не упорядочиваем их. Возможно, «комбинация» — обманчивый ярлык. Мы не имеем в виду кодовый замок (где порядок определенно имеет значение). Возможно, лучшая метафора — это сочетание вкусов — вам просто нужно решить, какие вкусы сочетать, а не в каком порядке их комбинировать.
Чтобы еще больше проиллюстрировать связь между комбинациями и перестановками, мы закончим пример.
Пример 1.3.5
Вы решили устроить званый обед. Несмотря на то, что вы невероятно популярны и у вас 14 разных друзей, у вас достаточно стульев, чтобы пригласить только 6 из них.
Сколько у вас есть вариантов, кого из 6 друзей пригласить?
Что делать, если вам нужно решить не только, кого из друзей пригласить, но и где их рассадить за длинным столом? Сколько вариантов у вас есть тогда?
Решение
Вы должны просто выбрать 6 друзей из 14.
 Это можно сделать \({14 \выбрать 6}\) способами. Мы можем найти это число либо с помощью треугольника Паскаля, либо по закрытой формуле: \(\frac{14!}{8!\cdot 6!} = 3003\text{.}\)
Это можно сделать \({14 \выбрать 6}\) способами. Мы можем найти это число либо с помощью треугольника Паскаля, либо по закрытой формуле: \(\frac{14!}{8!\cdot 6!} = 3003\text{.}\)Здесь вы должны подсчитать все способы, которыми вы можете переставить 6 друзей, выбранных из группы из 14. Таким образом, ответ равен \(P(14, 6)\text{,}\), который можно рассчитать как \(\frac{14 !}{8!} = 2192190\текст{.}\)
Заметьте, что мы можем думать об этой задаче на счет как о счетных функциях: сколько инъективных функций имеется в вашем наборе из 6 стульев и в вашем наборе из 14 друзей (эти функции инъективны, потому что ни один стул не может двигаться). двум твоим друзьям).
Как связаны эти числа? Обратите внимание, что \(P(14,6)\) в раз больше на , чем \({14 \choose 6}\text{.}\) Это имеет смысл. \({14 \выбрать 6}\) выбирает 6 друзей, но \(P(14,6)\) упорядочивает 6 друзей, а также выбирает их. На самом деле, мы можем точно сказать, насколько больше \(P(14,6)\). В обеих задачах на подсчет мы выбираем 6 из 14 друзей. Для первого мы останавливаемся там, на 3003 способах. Но во второй задаче на подсчет каждый из этих 3003 вариантов выбора из 6 друзей можно упорядочить ровно \(6!\) способами. Итак, теперь у нас есть \(3003\cdot 6!\) вариантов, и это ровно \(2192190\text{.}\)
В обеих задачах на подсчет мы выбираем 6 из 14 друзей. Для первого мы останавливаемся там, на 3003 способах. Но во второй задаче на подсчет каждый из этих 3003 вариантов выбора из 6 друзей можно упорядочить ровно \(6!\) способами. Итак, теперь у нас есть \(3003\cdot 6!\) вариантов, и это ровно \(2192190\text{.}\)
Можно также посмотреть на первую задачу иначе. Мы хотим выбрать 6 из 14 друзей, но нас не волнует порядок, в котором они выбираются. Чтобы выбрать 6 из 14 друзей, мы можем попробовать это:
\begin{уравнение*} 14 \cdot 13 \cdot 12 \cdot 11 \cdot 10 \cdot 9. \end{уравнение*}
Это разумное предположение, так как у нас есть 14 вариантов для первого гостя, затем 13 для второго и так далее. Но догадка неверна (на самом деле это произведение равно \(2192190 = Р(14,6)\)). Он различает разные порядки, в которых мы могли бы пригласить гостей. Чтобы исправить это, мы могли бы разделить на количество различных расстановок 6 гостей (чтобы все они считались одним исходом). Существует ровно \(6!\) способов разместить 6 гостей, поэтому правильный ответ на первый вопрос
Существует ровно \(6!\) способов разместить 6 гостей, поэтому правильный ответ на первый вопрос
\begin{уравнение*} \frac{14 \cdot 13 \cdot 12 \cdot 11\cdot 10 \cdot 9}{6!}. \end{уравнение*}
Обратите внимание, что это можно записать как 9.0005
\begin{уравнение*} \frac{14!}{8!\cdot 6!}. \end{уравнение*}
, что у нас было изначально.
ПодразделУпражнения
¶1
Пиццерия предлагает 10 начинок.
Сколько пицц с тремя начинками они могли включить в свое меню? Предположим, что двойная начинка не допускается.
Сколько всего пицц возможно с от нуля до десяти начинок (но не с двойной начинкой)?
- 9{10} = 1024\) пицц. Скажите «да» или «нет» каждой начинке.
- \(P(10,5) = 30240\) способов. Назначьте каждому из 5 мест в левой колонке уникальную начинку для пиццы.
2
Кодовый замок состоит из циферблата с 40 цифрами. Чтобы открыть замок, вы поворачиваете циферблат вправо, пока не дойдете до первой цифры, затем влево, пока не дойдете до второй цифры, затем снова вправо до третьей цифры. Числа должны быть разными. Сколько различных комбинаций возможно? 93\)).
Чтобы открыть замок, вы поворачиваете циферблат вправо, пока не дойдете до первой цифры, затем влево, пока не дойдете до второй цифры, затем снова вправо до третьей цифры. Числа должны быть разными. Сколько различных комбинаций возможно? 93\)).
3
Используя цифры от 2 до 8, найдите количество различных пятизначных чисел, таких что:
Цифры могут использоваться более одного раза.
Цифры не могут повторяться, но могут идти в любом порядке.
Цифры не могут повторяться и должны быть записаны в возрастающем порядке.
Какой из приведенных выше вопросов на подсчет является комбинацией, а какой перестановкой? Объясните, почему это имеет смысл.
4
Сколько существует треугольников с вершинами из точек, показанных ниже? Обратите внимание, что мы не допускаем вырожденных треугольников, у которых все три вершины лежат на одной линии, но допускаем непрямоугольные треугольники. Объясните, почему ваш ответ правильный.
Объясните, почему ваш ответ правильный.
Подсказка
Вам нужно ровно две точки на оси \(x\) или \(y\), но не пересчитывайте прямоугольные треугольники.
5
Сколько четырехугольников можно нарисовать, используя точки внизу в качестве вершин (углов)?
Решение
\({7\выберите 2}{7\выберите 2} = 441\) четырехугольников. Мы должны выбрать две из семи точек в верхнем ряду и две из семи точек в нижнем ряду. Однако не имеет значения, какую из двух точек (в каждой строке) мы выбираем первой, потому что после выбора этих четырех точек остается ровно один четырехугольник, который они определяют.
6
Сколько четырехугольников возможно в предыдущей задаче:
Квадраты?
Прямоугольники?
Параллелограммы?
Трапеции? 2 Здесь, как и в исчислении, трапеция определяется как четырехугольник с по крайней мере одной парой параллельных сторон.
 В частности, параллелограммы — это трапеции.
В частности, параллелограммы — это трапеции.Трапеции, не являющиеся параллелограммами?
Раствор
5 кв. Вам нужно пропустить ровно по одной точке сверху и снизу, чтобы длины сторон стали равными. Как только вы выбираете точку сверху, определяются остальные три точки.
- \({7 \выберите 2}\) прямоугольников. Как только вы выберете две точки сверху, будут определены две нижние.
Это сложно, так как вам нужно беспокоиться о нехватке места. Один из способов подсчета: разбить дела по расположению левого верхнего угла. Вы получаете \({7 \выберите 2} + ({7 \выберите 2}-1) + ({7 \выберите 2} — 3) + ({7 \выберите 2} — 6) + ({7 \выберите 2 } — 10) + ({7 \выберите 2} — 15) = 91\) параллелограммов.
Все
\({7\выбрать 2}{7\выбрать 2} — \left[ {7 \выбрать 2} + ({7 \выбрать 2}-1) + ({7 \выбрать 2} — 3) + ( {7 \выберите 2} — 6) + ({7 \выберите 2} — 10) + ({7 \выберите 2} — 15) \right]\text{.
 }\) Все, кроме параллелограммов.
}\) Все, кроме параллелограммов.
7
Анаграмма слова — это просто перестановка его букв. Сколько существует различных анаграмм слова «не защищено авторским правом»? (Это самое длинное общеупотребительное английское слово без повторяющихся букв.)
8
Сколько существует анаграмм слова «оценки», начинающихся на букву «а»?
Решение
После первой буквы (а) мы должны переставить оставшиеся 7 букв. Есть только две буквы (s и e), так что на самом деле это всего лишь вопрос о битовой строке (представьте, что s — это 1, а e — 0). Таким образом, есть \({7 \выберите 2} = 21\) анаграмм, начинающихся с «а».
9
Сколько существует анаграмм слова «анаграмма»?
10
На деловом выезде ваша компания из 20 бизнесменов и деловых женщин играет в гольф.
Вам нужно разбиться на четверки (группы по 4 человека): первая четверка, вторая четверка и так далее.
 Сколько способов вы можете сделать это?
Сколько способов вы можете сделать это?После всей вашей тяжелой работы вы понимаете, что на самом деле вы хотите, чтобы каждая четверка включала одного из пяти членов Совета. Сколько способов вы можете сделать это?
Решение
- \({20 \выбрать 4}{16 \выбрать 4}{12 \выбрать 4}{8 \выбрать 4}{4 \выбрать 4}\) способов. Выберите 4 из 20 человек для первой четверки, затем 4 из оставшихся 16 для второй четверки и так далее (используйте принцип умножения для объединения).
- \(5!{15 \выбрать 3}{12 \выбрать 3}{9 \выбрать 3}{6 \выбрать 3}{3 \выбрать 3}\) способов. Сначала определите время игры 5 членов правления, затем выберите 3 из 15 не членов правления для игры в гольф с первым членом правления, затем 3 из оставшихся 12 для игры в гольф со вторым и так далее.
11
Сколько различных рассадок возможно для короля Артура и его 9 рыцарей вокруг их круглого стола?
Решение
\(9!\) (за столом сидят 10 человек, но не важно, где сидит король Артур, только кто сидит слева от него, два места слева от него и так далее). 9{10}\) функций. Существует 17 вариантов изображения каждого элемента в домене.
9{10}\) функций. Существует 17 вариантов изображения каждого элемента в домене.
13
Рассмотрим функции \(f: \{1,2,3,4\} \to \{1,2,3,4,5,6\}\text{.}\)
Сколько всего функций?
Сколько функций инъективны?
Сколько инъективных функций увеличивают ? Возрастание означает, что если \(a \lt b\), то \(f(a) \lt f(b)\text{,}\) или, другими словами, выходы становятся больше по мере увеличения входов.
14
Мы видели, что формула для \(P(n,k)\) равна \(\dfrac{n!}{(n-k)!}\text{.}\) Ваша задача здесь состоит в том, чтобы объяснить почему это это правильная формула.
Предположим, у вас есть 12 фишек разного цвета. Сколько разных стопок по 5 фишек можно составить? Объясните свой ответ и почему он аналогичен формуле для \(P(12,5)\text{.
 }\)
}\)Снова используя сценарий с 12 фишками, сколько будет считаться \(12!\)? Что значит \(7!\)? Объяснять.
Объясните, почему имеет смысл делить \(12!\) на \(7!\) при вычислении \(P(12,5)\) (в терминах чипов).
Ваше объяснение подходит для чисел, отличных от 12 и 5? Объясните формулу \(P(n,k) = \frac{n!}{(n-k)!}\), используя переменные \(n\) и \(k\text{.}\)
Задачи на перестановки и комбинации
Перестановки и комбинации используются для решения задач.
| Пример 1. Сколько трехзначных чисел можно составить, используя цифры 1, 2 и 3 без повторений? Метод (1), перечисляющий все возможные числа с использованием древовидной диаграммы.  Мы можем составить 6 чисел, используя 3 цифры и не повторяя цифры. метод (2) подсчета: ПОСМОТРИТЕ НА ДРЕВЕСНУЮ СХЕМУ ВЫШЕ. У нас есть 3 варианта для первой цифры, 2 варианта для второй цифры и 1 вариант для третьей цифры. Используя принцип счета, мы можем сказать: Общее количество трехзначных чисел определяется как Произведение 3 2 1 = 3 имеет специальное обозначение! и читается 3 факториала. Вообще н! читается как факториал и определяется как Мы также определяем 0! = 1.  Пример 2. Сколько разных слов можно составить из букв A, B, E и L? Решение: у нас есть 4 варианта для первой буквы, 3 варианта для второй буквы, 2 варианта для третьей буквы и 1 вариант для четвертой буквы. Следовательно, количество слов равно Пример 3. Сколько двузначных чисел можно составить, используя цифры 1, 2, 3 и 4, не повторяя цифры? На этот раз мы хотим использовать 2 цифры одновременно, чтобы получить 2-значные числа. Для первой цифры у нас есть 4 варианта, а для второй цифры у нас есть 3 варианта (4 — 1 уже используется). Используя принцип подсчета, количество двузначных чисел, которые мы можем составить, используя 4 цифры, определяется выражением Вышеупомянутая проблема связана с расположение 2 цифры из 4 в определенном порядке.  Это также называется перестановкой. Это также называется перестановкой. Самая важная идея в перестановках состоит в том, что порядок важен . Когда вы используете цифры 3 и 4 для составления числа, числа 34 и 43 различны, поэтому важен порядок цифр 3 и 4. Обычно перестановка r (2 цифры в приведенном выше примере) элементов из набора n (4 цифры в приведенном выше примере) элементов записывается как n P r , а формула имеет вид Пример 4: Расчет 4 П 2 6 П 5 4 П 4 Решение: 4 P 2 = 4! / (4 — 2)! = 24/2 = 12 6 Р 5 = 6! / (6 — 5)! = 654321 / 1! = 720 4 P 4 = 4! / (4 — 4)! = 4! / 0! = 4! = 4321 = 24 (Теперь мы понимаем необходимость определения 0! = 1) Пример 5.  Сколько слов из 3 букв можно составить из букв в слове ЛЮБОВЬ? Сколько слов из 3 букв можно составить из букв в слове ЛЮБОВЬ? Решение: В слове «любовь» 4 буквы, и составление слов из 3 букв аналогично расположению этих 3 букв, и порядок важен, поскольку LOV и VOL — разные слова из-за порядка одинаковых букв L, O и V. Следовательно это проблема перестановки. Количество слов определяется 4 P 3 = 4! / (4 — 3)! = 24 КомбинацииПример 6: Сколько прямых можно провести, используя 3 не лежащие на одной прямой (не лежащие на одной прямой) точки A, B и C на плоскости? Решение: Количество комбинаций равно количеству перестановок, деленному на r! to устраняет те, которые учитывались более одного раза, потому что порядок не важен.  Пример 7: Расчет 3 С 2 5 С 5 Решение: 3 С 2 = 3! / [ (3 — 2)!2! ] = 6 / [1 2] = 3 (задача точек и прямых решена выше в примере 6) 5 С 5 = 5! / [(5 — 5)!5! ] = 5! / [0!5!] = 5! / [1 5!] = 1 (есть только один способ выбрать (без порядка) 5 элементов из 5 элементов и выбрать их все один раз!) Пример 8: Нам нужно сформировать команду из 5 человек в классе из 12 учеников.  Сколько различных команд можно сформировать? Сколько различных команд можно сформировать? Решение: Нет ничего, что указывало бы на то, что порядок, в котором выбираются члены команды, важен, и поэтому это проблема комбинирования. Следовательно, количество команд равно 12 С 5 = 12! / [(12 — 5)!5! ] = 792 Задачи
решения вышеуказанных проблем
Еще Ссылки и ссылки элементарная статистика и вероятности. |
сообщите об этом объявлении
Перестановка и комбинация: различия и примеры
В математике и статистике перестановки и комбинации — это два разных способа взять набор элементов или опций и создать подмножества. Например, если у вас десять человек, сколько подмножеств из трех можно составить? Хотя перестановка и комбинация кажутся синонимами в повседневном языке, математически они имеют разные определения.
- Перестановки : Порядок результатов имеет значение.
- Комбинации : Порядок не имеет значения.
Давайте разберемся в разнице между перестановкой и комбинацией более подробно. И тогда вы узнаете, как рассчитать общее количество каждого.
В некоторых сценариях порядок результатов имеет значение. Например, если у вас есть замок, где вам нужно ввести четыре цифры, порядок имеет значение. Если правильные числа 8 3 6 2, вы не можете ввести те же числа в любом другом порядке (например, 6 8 2 3) и ожидать, что замок откроется! Следовательно, это перестановка.
На самом деле мы должны называть этот тип блокировки блокировкой перестановки!И наоборот, порядок опций не имеет значения для комбинаций. Представьте, что вы готовите пиццу с пепперони (P), ветчиной (H) и грибами (M). Неважно, готовите ли вы пиццу PHM, HMP или MPH. Это все та же пицца! В данном случае порядок не имеет значения, так что это комбинация.
В некоторых случаях определение того, является ли что-либо перестановкой или комбинацией, зависит от условий, определяемых решаемой вами задачей. Например, выбор пяти человек в группу, где у всех одинаковая роль, является комбинацией, поскольку порядок их выбора не имеет значения.
Однако, если вы выбираете пять человек и их роль зависит от того, когда вы их выбираете, это перестановка, потому что порядок имеет значение. Например, первый человек может быть ведущим, второй — вести заметки и так далее.
Например, первый человек может быть ведущим, второй — вести заметки и так далее.
Примеры перестановок и комбинаций
| Перестановки | Комбинация |
| Последовательность цифр для замка. | номеров для выигрыша в лотерею. |
| Подбор людей в команду по должности. | Выбор детей в качестве членов класса. |
| Выбор первого, второго и третьего мест. | Выбор трех финалистов. |
Формулы подсчета перестановок и комбинаций
Часто, когда вы работаете с перестановками и комбинациями, вам нужно подсчитать количество возможных вариантов. Теперь, когда вы понимаете разницу между концепциями, давайте посмотрим, как вы считаете количество перестановок и комбинаций. Когда у вас есть как минимум две перестановки, у вас будет больше возможностей, чем соответствующее количество комбинаций.
Почему так? Пример с пиццей показывает, что PHM, HMP и MHP представляют собой одну и ту же комбинацию. Однако, если мы используем эти три буквы в качестве пароля, это три разные перестановки.
Однако, если мы используем эти три буквы в качестве пароля, это три разные перестановки.
Пример перестановки
Порядок перестановок имеет значение. Предположим, нам нужно знать количество возможностей для четырехзначного замка. Есть 10 возможных значений, и мы выбираем 4. Статистики формулируют этот сценарий как «10 выбирают 4» и обозначают его как 10 P 4 , где P означает, что мы работаем с перестановками. Сколько существует перестановок для этого сценария?
Это зависит от того, разрешаем ли мы повторяющиеся значения или нет. Может ли последовательность блокировки использовать 1 1 2 3? Или вы можете использовать каждую цифру только один раз?
Если последовательность может повторять значения, то каждая из четырех цифр имеет десять вариантов (0–9). Следовательно, четырехзначный замок имеет 10 * 10 * 10 * 10 = 10 4 = 10 000 перестановок. Однако, если значения не могут повторяться, то существует 10 * 9* 8 * 7 = 5040. Уменьшающиеся значения во втором расчете представляют меньше вариантов, доступных для каждой последующей цифры, когда вы не можете повторно использовать предыдущие значения.
Пример комбинации
Теперь предположим, что у нас есть 10 начинок для пиццы, и мы выбираем 4 из них. Мы обозначаем это как 10 C 4 .
Эта схема с 10 вариантами и выбором 4 аналогична примеру с перестановкой, за исключением того, что теперь мы работаем в условиях, когда порядок не имеет значения, что помогает проиллюстрировать разницу между перестановкой и комбинацией. Сколько существует комбинаций?
Для расчета количества комбинаций с повторениями используйте следующее уравнение:
Где:
- n = количество вариантов.
- р = размер каждой комбинации.
Восклицательный знак (!) обозначает факториал. В общем, н! равно произведению всех чисел до n. Например, 3! = 3 * 2 * 1 = 6. Исключение 0! = 1, что упрощает уравнения.
В нашем примере n = 10 и r = 4, потому что доступно 10 начинок, и мы выберем 4. Давайте введем эти значения в уравнение, позволяющее повторить:
Существует 715 комбинаций, в которых можно повторять ингредиенты. Это означает, что мы можем получить двойную, тройную или даже четверную порцию пепперони!
Это означает, что мы можем получить двойную, тройную или даже четверную порцию пепперони!
Если нельзя повторять значения, формула следующая:
Ввод значений в уравнение без повторения:
Существует 210 комбинаций, когда нельзя повторять ингредиенты. Мы можем получить ингредиент только один раз — никаких двойных пепперони!
Как и ожидалось, число возможностей для 10 C 4 намного ниже, чем для примера 10 P 4 .
Использование перестановок и комбинаций для решения вероятностных задач
Этот обзор лишь поверхностно описывает использование перестановок и комбинаций. Для получения более подробной информации о каждом из них, а также рабочих примеров для решения вероятностных задач, пожалуйста, прочитайте мои отдельные статьи о:
- Использование перестановок для решения вероятностных задач
- Использование комбинаций для решения вероятностных задач
Сколько комбинаций с 3 числами
Ибрагим
#1
Сколько комбинаций с 3 числами? Есть 3 x 2 x 1 = 6 способов расположить три цифры. В наборе из 720 вариантов каждая комбинация из трех цифр представлена шесть раз. Итак, давайте просто разделим на 6. 720/6 = 120.
Сколько существует 12-значных комбинаций?
Таким образом, возможны 479 001 600 комбинаций, если повторение запрещено. Если разрешен повторный набор, возможны 1212 комбинаций.
Как узнать количество возможных комбинаций?
Комбинации — это способ расчета общего результата события, когда порядок исхода не имеет значения. Для расчета комбинаций используем формулу nCr = n! / р! * (н р) ! , где n — общее количество элементов, а r — количество элементов, выбранных за один раз, поэтому сколько существует комбинаций чисел?
Правильный ответ: для букв есть 26 вариантов для каждой из 3-х дорожек, а для цифр есть 10 вариантов для каждой из 3-х дорожек. Таким образом, общее количество комбинаций равно: 26 х 26 х 26 х 10 х 10 х 10 = 17 576 000 ≈ 18 миллионов.
Таким образом, общее количество комбинаций равно: 26 х 26 х 26 х 10 х 10 х 10 = 17 576 000 ≈ 18 миллионов.
Сколько существует четырехзначных 12-значных комбинаций?
Для каждого выбора первых двух цифр у вас есть 10 вариантов выбора третьей цифры. Таким образом, у вас есть 10x10x10 = 1000 вариантов для первых трех цифр. Ведь у вас есть десять вариантов четвертой цифры, значит, есть 10х10х10х10 = 10 000 возможных комбинаций из 4 цифр из 09.
Каковы все возможные комбинации числа 1234?
Если вы ставите на 1234 клетки, вы выигрываете, если выпадет одна из следующих комбинаций: 1234, 1243, 1324, 1342, 1423, 1432, 2134, 2143, 2314, 2341, 2413, 2431, 3124, 3142, 3214, 3241, 3412, 3421, 4123, 4132, 4213, 4231, 4312 или 4321.
Сколько возможных комбинаций для четырехзначного кода?
Существует 10 000 возможных комбинаций.
Сколько комбинаций в 4 числах без повторений?
Таким образом, имеется 4 x 3 x 2 x 1 = 24 возможности размещения 4 объектов. Итак, я делю 5040/24 = 210. Таким образом, есть 210 различных комбинаций четырех цифр, выбранных из 09, причем цифры не повторяются.
Итак, я делю 5040/24 = 210. Таким образом, есть 210 различных комбинаций четырех цифр, выбранных из 09, причем цифры не повторяются.
Как вы решаете перестановки и комбинации?
Если порядок не важен, у нас есть комбинация. Если порядок важен, у нас есть перестановка. Можно сказать, что перестановка — это упорядоченная комбинация.
Количество перестановок n объектов одновременно определяется по следующей формуле: P(n,r) = n!
Сколько 5-значных комбинаций использует 0 9?
Количество возможных комбинаций для 5-значного числа (каждая может содержать 09) равно 99999. Количество 5-значных комбинаций равно 105 = 100 000. Так что на один больше, чем 99 999.
Сколько комбинаций можно составить из 7 номеров?
127 комбинаций.
Часто задаваемые вопросы (FAQ)
1. Как найти количество перестановок?
Для расчета перестановок мы используем уравнение nPr, где n — общее количество вариантов, а r — набор выбранных элементов. Используйте уравнение nPr = n, чтобы решить это уравнение! / (Нет) !.
Используйте уравнение nPr = n, чтобы решить это уравнение! / (Нет) !.
2. Сколькими способами можно расположить 4 числа?
Опять же, если повторение не разрешено, мы можем заполнить первую позицию одной из этих 5 цифр, теперь мы можем заполнить вторую позицию только 4 цифрами, третью — 3 цифрами, четвертую — 2 оставшимися цифрами, поэтому поместите пять с последним оставшимся числом. Затем мы можем отсортировать эти числа в соответствии с 5 * 4 * 3 * 2 * 1-way (т.е. 120-way).
3. Что такое перестановка 12?
Перестановка 12 = 47 00
Эти 47
00 строк из 12 цифр, например 1,2,3,4,5,6,7,8,9,10,11,12 и 2,4,6,8,10, 12, 11.9, 7.5,3.1 Математики вместо комбинаций называют перестановки 12 чисел.
4. Сколько четырехзначных комбинаций дает 1 6?
6 х 5 х 4 х 3 = 360 возможных комбинаций. Дано четырехзначное целое число. каждое число может варьироваться от 1 до 6. Нет двух одинаковых чисел.
каждое число может варьироваться от 1 до 6. Нет двух одинаковых чисел.
5. Как вы подсчитываете количество попаданий?
Общее количество возможных исходов равно 6,3 ∙ 2 = 6. Этот принцип называется основным принципом подсчета, и действует оно следующим образом. Если событие х (в данном случае курица, говядина и овощи) может произойти х способами, а событие у (в данном случае картофель фри или картофельное пюре) может произойти разными способами.
6. Каковы все комбинации для 4-значного замка?
В 4-значном замке 9999 различных комбинаций. И теперь у нас есть в общей сложности 1000 + 9000 = 10 000 комбинаций.
7. Сколько существует четырехцветных комбинаций?
Если у меня есть 4 цвета, то есть 5 возможных комбинаций, а если у меня есть 5 цветов, то есть 10 возможных комбинаций.
8. Как выбрать 4-значный кодовый замок?
Как открыть четырехзначный кодовый замок Найдите комбинацию цифр. Перейти к первому выпуску. Поместите четвертое колесо на замок второй цифры цифровой комбинации.
Используйте третье колесо, чтобы найти третье число в комбинации. Найдите четвертую цифру комбинации на нижнем колесе замка и отцентрируйте ее.
9. Сколько 3-значных комбинаций с 5 цифрами?
10 возможных комбинаций.
10. Сколько комбинаций 3 с 4 номерами?
Опять же, есть 4 варианта, поэтому количество возможных трехзначных чисел равно 4 4 4. 4 варианта встречаются для последней цифры, поэтому количество возможных четырехзначных чисел равно 4 4 4 = 256.
Заключение
Есть 3 x 2 x 1 = 6 способов расположить три цифры. В наборе из 720 вариантов каждая комбинация из трех цифр представлена шесть раз. Так что давайте просто разделим на 6. 720/6 = 120,
479 001 600 возможных комбинаций, если повторение запрещено. Если разрешен повторный набор, возможны 1212 комбинаций.
Байронхилл
#2
Сколько комбинаций с 3 числамиСколько комбинаций с 3 числамиЕсли ключ связи имеет 3 цифры, слот меняется с 0 на 9 w. Много разных команд? ۔
Допустим 09это десять и три. Следовательно, общее количество разрешений (как есть) составляет от 1000 000 до 999
.1000
Если считается 0, если на дисплее отображается 0, то да.
10 3 или, если всего девять номеров 9 3 (= 729)
Tehseen24
#3
Сколько комбинаций с 3 числами? Смешение трех чисел — это 3 x 2 x 1 = 6 различных способов обращения с тремя цифрами. В расположении 720 вариантов каждое сочетание трех цифр отображается несколько раз. Таким образом, мы должны по существу изолировать на 6. 720/6 = 120. Можно составить все выполнимые комбинации из 3 цифр, считая от 000 до 999, но это создает несколько комбинаций цифр, которые имеют копии связанной цифры ( например, 099).
Таким образом, мы должны по существу изолировать на 6. 720/6 = 120. Можно составить все выполнимые комбинации из 3 цифр, считая от 000 до 999, но это создает несколько комбинаций цифр, которые имеют копии связанной цифры ( например, 099).
3-значные комбинации замков:
Несмотря на то, что 3-значные замки имеют 1000 различных кодов, существуют способы их открытия без распознавания комбинации. К счастью, способ взломать их практически не требует выполнения множества различных комбинаций чисел. Это скорее результат доминирования тонких изменений в ощущении замка, когда вы просматриваете измененные числа.
Чтобы попробовать это самостоятельно, возьмите замок, состав которого вы тоже знаете, и изучите сопутствующие авансы:
- Один из основных способов взлома замков такого типа — возможность приложить достаточное усилие, чтобы подняться вверх. дужка (лепестковая часть замка).
- Вам нужно будет отодвинуть дужку от корпуса замка так же, как если бы вы открывали замок.

- Наименее трудный способ сделать это — закрепить замок на массивном предмете, чтобы можно было надавить на корпус замка.
- Начните с самой сокращенной строки чисел и просматривайте всех, сохраняя при этом большее напряжение на ручке замка.
- В тот момент, когда вы назовете правильный номер, вы должны услышать легкий щелчок. Если попрактиковаться, вы также заметите, что внутреннее колесо «приходит в норму», благодаря чему циферблат будет очень ■■■■■■ вращаться.
- После перемещения по основному правому номеру посмотрите на следующий циферблат и обновите цикл.
- Вы измените аналогичную технику с третьим циферблатом, но будет несколько проще сказать, когда вы продолжите на правильном номере, потому что замок должен открыться.
Резюме:
Трехзначный микс имеет шесть различных способов наблюдения. Вставка из 720 вариантов, каждые три цифры показывались несколько раз. Трехзначная защелка имеет 1000 уникальных возможностей кода.
Кроме того, есть несколько способов открыть его, не распознавая его.
Как узнать кодовый замок?
Несмотря на смешанные замки, например, стандартный 40-значный Master Lock, его довольно сложно взломать без триумфального микса. Это возможно при самой экстремальной практике. Стратегия открытия миксового замка без микса, как правило, связана с приложением правильной меры восходящего напряжения к скобе.
Как узнать количество потенциальных миксов?
Смешивание — это способ получения общего результата события, когда запрос результата не имеет никакого значения. Для определения смесей мы используем рецепт NCR = n! /р! * (н р)! Где n — это полное количество компонентов 2, а r — это количество компонентов, выбранных за один раз, так какое количество смесей существует?
Верно, ответ: для букв есть 26 возможностей для каждой из 3-х дорожек, а для цифр 10 возможностей для каждой из 3-х дорожек. Таким образом, абсолютное число смесей равно: 26 х 26 х 26 х 10 х 10 х 10 = 17 576 000 ≈ 18 миллионов.
Резюме:
Стандартный 40-значный мастер-замок, который трудно взломать без триумфального микса. Смешивания — это способ получения общего результата события, когда запрос результата не имеет никакого значения.
Комбинации из трех цифр:
| Возможный способ расположения | 3 х 2 х 1 = 6 |
|---|---|
| Самая маленькая комбинация | 000 |
| Самая большая комбинация | 999 |
Часто задаваемые вопросы:
Некоторые вопросы, связанные с 3 комбинациями цифр, следующие:
1: Каким числом способов можно контролировать 8 номеров?
Введите свои вещи (или их названия), по одной на каждую строку в контейнере внизу, затем в этот момент нажмите «Показать!» чтобы понять, сколько способов за ними можно наблюдать, и что это за администрация. Примечание. 8 элементов содержат 40 320 уникальных миксов.
2: Как бы вы создали все этапы?
В случае, если n нечетно, нажмите на первый компонент и продолжайте, а если n четно, нажмите на i-й компонент (я счетчик, начинающийся с 0) и последний компонент и перефразируйте уточненный выше расчет, пока я не буду больше скромнее, чем н. В каждом цикле вычисление будет производить все изменения, связанные с текущим последним компонентом.
3: Может ли Excel выполнять изменения?
Работа Excel PERMUT предлагает количество изменений (сочетаний, где запрос является значительным) для заданного количества статей. Работа PERMIT не допускает увольнений. Чтобы разрешить повторяющиеся изменения, используйте работу PERMUTATIONA.
4: Какие числовые числа можно составить из 3 цифр?
Таким образом, всего имеется 9 × 10 × 10 = 900 трехзначных чисел. Таким образом, всего получается 900 трехзначных чисел.
5: Какое количество миксов имеет блокировка микса?
Возможные числа от 0 до 39, что позволяет принимать 40 уникальных потенциальных решений при каждом повороте циферблата. Для каждой смеси требуется ровно три числа (например, три оборота циферблата). Например: 35-40-5.
Для каждой смеси требуется ровно три числа (например, три оборота циферблата). Например: 35-40-5.
6: Какие трехзначные числа можно составить без перефразирования?
Различные трехзначные числа, которые можно обрамить, используя цифры 0, 2, 5 без перефразирования какой-либо цифры в числе, это 205, 250, 502 и 520. Соответственно, четыре трехзначных числа можно обрамить, используя цифры 0, 2, 5.
7: Какие комбинации чисел существуют для 3-значного замка?
2 Вскрытие замка: Согласно корреляции, этот замок с тремя дисками (три колеса, каждое с цифрами от 0 до 9) имеет 10 × 10 × 10 = 1000 возможных комбинаций.
8: какое трехзначное число существует без перефразирования цифры?
По этим линиям есть 9 различных способов заполнить десятку. Более того, существует 8 различных способов ввода цифры единицы измерения. Необходимое количество чисел = (9×9×8)=648.
9: Какова вероятность трехзначного числа?
Вероятность кадрирования трехзначного числа одинаковыми цифрами при составлении трехзначных чисел из цифр 0, 2, 4, 6, 8 равна. Отныне вероятность того, что трехзначные числа с одинаковыми цифрами = 4/100 = 1/25.
Отныне вероятность того, что трехзначные числа с одинаковыми цифрами = 4/100 = 1/25.
10: Что такое 3-значный цифровой код блокировки?
Подсказка 1: (6, 8, 2) одно число правильное и универсальное. Подсказка 2: (6, 1, 4) одно число правильное, но неправильное. Подсказка 3: (2, 0, 6) Два числа правильные, но расположены неправильно. Подсказка 4: (7, 3, 8) Все не так.30
Заключение:
Трехзначные комбинации имеют шесть способов управления. Вставка из 720 потенциальных клиентов, каждые три цифры отображаются шесть раз. Трехзначный замок имеет 1000 различных возможностей кода. Также представлены некоторые методы для его открытия без идентификации. Стандартный 40-значный Master Lock, который трудно взломать без триумфального микса. Смешивания — это способ получения общего результата события, когда запрос результата не имеет никакого значения.
Похожие статьи:
Сколько комбинаций с 3 числами? Есть 3 х 2 х 1 = 6 способов расположить три цифры.В наборе из 720 вариантов каждая комбинация из трех цифр представлена шесть раз. Итак, давайте просто разделим на 6. 720/6 = 120. Сколько существует 12-значных комбинаций? Таким образом, возможны 479 001 600 комбинаций, если повторение запрещено. Если разрешен повторный набор, возможны 1212 комбинаций. Как узнать количество возможных комбинаций? Комбинации — это способ рассчитать общий результат…
Сколько стоит бриллиант в 9 карат? Бриллиант весом 9 карат стоит примерно 19 000 долларов за карат, при условии, что цвет и чистота оцениваются как K/SI2. В действительности вы можете рассчитывать заплатить от 20 000 до 40 000 долларов за карат за бриллиант приличной огранки. Что такое бриллиант? [Алмаз] Алмаз, богатый углеродом минерал. Это самое трудное известное природное вещество, а также самый известный камень. Благодаря высокой прочности алмазы используются в большом количестве важных коммерческих процессов…
Кристин Вудс
#4
Сколько комбинаций с 3 цифрамиЕсли 3-значные позиции в ключе связи 0-9, много ли различных команд? 3
Допустим, 09 — это десять и три. Следовательно, общее количество конфигураций (как есть) составляет от 1000 000 до 999.
Сколько комбинаций с 3 номерамимед1301
#5
Сколько комбинаций с 3 числами? Существует 3 x 2 x 1 = 6 методов для организации трех цифр. В расположении 720 возможных результатов каждая комбинация из трех цифр используется несколько раз. Таким образом, мы должны просто изолировать посредством 6,720/6 = 120, перестановок и комбинаций красочные способы, которыми объекты из набора могут быть названы, как правило, без облегчения, для формирования подмножеств. Этот выбор подмножеств называется перестановкой, когда порядок выбора является фактором, и комбинацией, когда порядок не является фактором.
Этот выбор подмножеств называется перестановкой, когда порядок выбора является фактором, и комбинацией, когда порядок не является фактором.
• Если заказ не считается, это Комбинация.
• Когда порядок учитывается, это перестановка.
КомбинацииЕсть также два вида комбинаций, имейте в виду, что заказ сейчас касается , а не :
- Дублирование разрешено : например, мячи в вашем инвентаре (5,5,5,10,10)
- Без дублирования : например, цифры (2,14,15,27,30,33)
Их сложнее всего прояснить, поэтому мы вернемся к этому позже.
2. неповторяющиеся комбинацииИменно так работают рисунки. Цифры представлены по одной, и если у нас есть счастливые цифры (не проблема, какая последовательность), мы добьемся успеха!
Простейший способ описать это:
- предположим, что последовательность имеет значение (т.
 е. перестановки),
е. перестановки), - , затем измените его, чтобы последовательность не имела значения.
Возвращаясь к нашей иллюстрации с шарами для пула, предположим, что мы просто хотим знать, какие 3 шара для пула выбраны, а не в каком порядке.
Ранее мы знали, что 3 из 16 дали нам варианты.
Но многие из них одинаковы для нас сейчас, потому что мы не следим за тем, какой порядок. Например, предположим, что выбраны шары 1, 2 и 3. Вот возможные варианты:
| Порядок не имеет значения | Порядок имеет значение |
|---|---|
| 1 2 3 | 1 2 3 |
| 1 3 2 | |
| 2 1 3 | |
| 2 3 1 | |
| 3 1 2 | |
| 3 2 1 |
Итак, у трансформаций в 6 раз больше перспектив.
На самом деле, есть простой способ выяснить, как можно расположить по порядку множество способов «1 2 3», и мы уже говорили об этом ранее. Ответ
Ответ
3! = 3 × 2 × 1 = 6
Пример(Другая иллюстрация 4 эффекта можно разместить 4! = 4 × 3 × 2 × 1 = 24 различных способа, попробуйте сами!)
. Таким образом, мы адаптируем нашу формулу перестановок, чтобы сократить ее на количество возможных порядков объектов (поскольку нас больше не интересует их порядок)
n! (п — г)! х 1р! = п! р! (п — г)!
Эта формула настолько важна, что часто просто пишется с такими большими перерывами
н! г!(п-г)! = (nr)
где «n» количество вещей на выбор,
и мы выбираем r из них,
без повторения,
порядок не имеет значения.
Постоянно называется «n выбрать r» (по аналогии с «16 выбрать 3»)
И также понимается как биномиальный коэффициент.
СводкаМеморандумЕсли ордер не считается, это Комбинация. Когда порядок имеет значение, это перестановка. понять, как работают эти формулы, — это только полдела.
решить, как продемонстрировать реальную ситуацию, может быть относительно сложно.
Все эти памятки означают «n выбирают r»
C (n, r) = n C r = n C r = (nr) = n! р! (п — г)!
Только запомните формулу
n! р! (п — г)!
Пример шаров для пула (без заказа)
Итак, наша иллюстрация шара для пула (теперь без заказа)
.16! 3! (16 − 3)!
= 16! 3! × 13!
= ×
= 560
Обратите внимание на формулу 16! 3! × 13! дает равное возвращение как 16! 13! × 3!
Итак, взяв 3 шара из 16 или 13 шаров из 16, имеем равный состав комбинаций:
16!3!(16−3)! = 16!13!(16−13)! = 16!3! × 13! = 560
На самом деле формула красивая и пропорциональная:
n! г!(п-г)! = (nr) = (n n−r)
Также следует помнить, что 16!/13! уменьшается до 16×15×14, мы можем избежать большого количества вычислений, сделав это следующим образом:
16×15×143×2×1
= 33606
= 560
Треугольник Паскаля Мы также можем использовать Треугольник Паскаля, чтобы понять нормы. Спускаемся к строке «n» (самая верхняя строка — 0), а дальше вместе с позициями и значением наш ответ. прямо сейчас выдержка, отображающая строку 16
Спускаемся к строке «n» (самая верхняя строка — 0), а дальше вместе с позициями и значением наш ответ. прямо сейчас выдержка, отображающая строку 16
1 15 105 455 1365 …
1 16 120 560 1820 4368 …
Этап — это числовая процедура, которая определяет количество потенциальных планов игры в наборе, когда запрос на варианты действий имеет значение. Обычные числовые проблемы включают в себя выбор всего нескольких вещей из множества вещей в конкретном запросе.
Изменения как можно чаще ошибочно принимают за другой численный метод, называемый блендами. Тем не менее, в блендах запрос выбранных вещей не влияет на выбор. В конце концов, планы мышц живота и изменения рассматриваются как различные варианты действий, в то время как в смесях эти планы действий эквивалентны.
В арифметике изменение множества есть, говоря откровенно, образ действий его индивидуумов в последовательность прямых запросов, или, опять же, если множество сейчас запрошено, обновление его компонентов. «Сцена» также относится к демонстрации или взаимодействию при изменении прямого запроса аранжированного набора.
«Сцена» также относится к демонстрации или взаимодействию при изменении прямого запроса аранжированного набора.
Сцены варьируются от смесей, которые представляют собой определения отдельных лиц из множества, не задумывающихся об аранжировке. Например, в виде кортежей имеется шесть изменений множества {1, 2, 3}, в частности (1, 2, 3), (1, 3, 2), (2, 1, 3), (2 , 3, 1), (3, 1, 2) и (3, 2, 1). Это по большей части потенциальные порядки этого трехкомпонентного набора. Перестроенные слова слов, буквы которых различаются, являются дополнительными этапами: буквы теперь запрашиваются в первом слове, а переставленное слово представляет собой перестановку букв. Исследование изменений ограниченных множеств является важной темой в области комбинаторики и сбора гипотез.
Стадии используются почти во всех областях арифметики и во многих различных областях науки. В разработке программного обеспечения они используются для проверки аранжировки вычислений; в квантовом материаловедении для описания состояний частиц; и в науке для изображения последовательности РНК.
Количество изменений «n» безошибочно определяемых элементов равно n факториалу, обычно составленному как n! что подразумевает результат всех определенных целых чисел, не точно или эквивалентных n.
На самом деле замена множества S характеризуется биекцией из S в себя. То есть это пропускная способность от одного S к другому, для которого каждый компонент встречается ровно один раз в качестве оценки изображения. Это отождествляется с пересмотром компонентов S, где каждый компонент s заменяется сравнением f(s). Например, упомянутое выше изменение (3, 1, 2) изображается пропускной способностью.
Ассортимент всех ступеней набора образует сбор, называемый симметричным набором набора. Собирательная деятельность — это структура (выполнение двух заданных изменений в последовательности), которая приводит к еще одной корректировке. Поскольку свойства изменений не опираются на представление о компонентах набора, неудивительно, что этапы набора рассматриваются для концентрации на этапах.
В рудиментарной комбинаторике k-этапы, или неполные изменения, представляют собой упорядоченные действия k отдельных компонентов, выбранных из набора. В момент, когда k эквивалентно размеру набора, это изменения набора.
СводкаЧасто задаваемые вопросыУф, это было слишком много, так что, возможно, вы могли бы прочитать это еще раз, чтобы быть уверенным. Но понять, как работают эти формулы, — это только полдела. решить, как продемонстрировать реальную ситуацию, может быть относительно сложно. Но, по крайней мере, вы больше не подвергаетесь 4 интерпретациям «Приказ не имеет значения/не считается» и «Репризы разрешены/не допускаются»
Люди задают многочисленные вопросы о комбинациях с 3 числами. Некоторые из них предлагаются ниже с ответом
. 1. Как вы рассчитываете перестановки?
Чтобы определить количество изменений, возьмите количество возможностей для каждого случая и затем увеличьте это число без чьей-либо помощи на X случаев, где X эквивалентно количеству случаев в группе.
2. Что означает перестановка в математике?
Этап — это числовая оценка количества способов, которыми может быть установлен конкретный набор, когда имеет значение запрос плана игры.
3. Какие возможны комбинации для 3-значного кода?
Если предположить, что вам нужны обычно мыслимые трехзначные числа без какой-либо избыточности цифр, то у вас есть 10 вариантов для основной цифры, у вас есть 9 вариантов для второй цифры, и у вас есть 8 вариантов для третьей цифры, что дает вам 10x9x8 = 720 всего.
4. Сколько комбинаций цифр существует между 000 и 999?
Самое маленькое трехзначное число, которое у меня есть, — это ноль, состоящее из 000, а самое большое — 999, и каждое целое число находится где-то в диапазоне от 000 до 999. Следовательно, у меня есть 1000 чисел или 1000 возможных сочетаний.
ЗаключениеПерестановка и комбинация — это различные способы, которыми объекты из набора могут быть выбраны, по большей части без замены, для формирования подмножеств.
Это определение подмножеств известно как стадия, когда запрос на выбор является компонентом, и смесью, когда запрос не является переменной. Размышляя о пропорции количества разыскиваемых подмножеств к количеству всех потенциальных подмножеств для некоторых выстрелов в темноте в семнадцатом веке, французские математики Блез Паскаль и Пьер де Ферма дали толчок усовершенствованию комбинаторики и гипотезы правдоподобия.
Связанные статьи
Разница между перестановкой и комбинацией Может ли кто-нибудь сказать мне разницу между макетом и комбинацией? Заранее спасибо, я прочитал несколько статей в Интернете, но мне удалось найти некоторую информацию, которая может помочь мне понять. Поэтому, пожалуйста, объясните это легко. Преемственность и изменение Когда мы говорим о порядке и сочетании в повседневном языке, мы часто используем два термина вместе. Однако оба они имеют особое значение в математике, и это различие часто вызывает проблемы.быстро, …
Принцип подсчета Каковы основные принципы счета? законопроект. Для обработки больших объемов статистических данных требуется эффективный метод подсчета ( Количество результатов события. запишите количество результатов события E как n (E). Правило добавления. Пусть E1 и E2 — взаимоисключающие события ( Правило умножения. Общее правило умножения. Какова основная теорема подсчета? Основная теорема подсчета карт — это u…
Рида
#6
Сколько комбинаций с 3 номерамиРазрешение
S1 = первое место
S2 = второе место
S3 = третье место
Связь = S1 S2 S3
5 Используйте комбинацию, где бы вы ни находились.
Может вращаться по часовой или против часовой стрелки.
Для S1 предусмотрено 20 циклов (09, по часовой и по часовой стрелке)
20 кубиков для S2
20 кубиков для S3
Общее количество штук
20 * 20 * 20 = 8000
У меня 1000 вот где я решал… смысл, так что первый цилиндр имеет 10 цифр, поэтому второй и третий в порядке. Следовательно, первый цилиндр содержит 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 или десять дисков. Другой цилиндр также имеет десять дисков. Следовательно, каждый из десяти дисков первого цилиндра может быть совместим с одним из десяти дисков второго цилиндра. 0 в первом цилиндре можно найти на каждом десятом диске во втором цилиндре. То же самое происходит и с остальной частью первого цилиндра. Итак, если вы говорите 10 и у вас есть 10 возможных комбинаций на d, то у вас есть 10 дисков x 10 комбинаций каждая = 100 комбинаций, поэтому у вас есть 100 возможных комбинаций для первых 2 барабанов. Третий цилиндр также имеет 10 дисков. Каждый из этих 10 дисков может быть назначен каждому из первых и вторых контактов 100 цилиндров. 10 это, скажем, на третьем цилиндре х 100 комментариев, можно сказать через = 1000 комментариев: Di i pe я должен хорошо объяснить …
Каждый из этих 10 дисков может быть назначен каждому из первых и вторых контактов 100 цилиндров. 10 это, скажем, на третьем цилиндре х 100 комментариев, можно сказать через = 1000 комментариев: Di i pe я должен хорошо объяснить …
10 * 10 * 10 = 1000
Предположим, что числа повторяются.
10x10x10 = 1000
Примечание: включая 000
Сколько комбинаций с 3 цифрамиVegita
#7
Сколько комбинаций с 3 числами9×9 = 81×9 = 729
Сколько комбинаций с 3 числамиМехназ_Мехмуд
#8
Сколько существует комбинаций из 3 чисел?
3 x 2 x 1 даст вам 6 различных способов расположения трех цифр. Если вам нужны все возможные трехзначные числа без повторения цифр, то у вас есть 10 вариантов для первой цифры, 9 вариантов для второй цифры и 8 вариантов для третьей цифры, что дает вам 10x9x8 = 720. Шесть уникальных комбинаций три цифры включены в 720 возможных комбинаций. Чтобы вычислить эту комбинацию, разделите 2 на 6. Таким образом генерируется 120 возможных комбинаций.
Если вам нужны все возможные трехзначные числа без повторения цифр, то у вас есть 10 вариантов для первой цифры, 9 вариантов для второй цифры и 8 вариантов для третьей цифры, что дает вам 10x9x8 = 720. Шесть уникальных комбинаций три цифры включены в 720 возможных комбинаций. Чтобы вычислить эту комбинацию, разделите 2 на 6. Таким образом генерируется 120 возможных комбинаций.
Как рассчитать возможные возможные комбинации?
Порядок исходов события не имеет значения при расчете результатов комбинации. Для расчета комбинаций нам понадобится формула nCr = n. Для расчета комбинаций нам понадобится формула nCr = n. где n обозначает общее количество элементов, а r обозначает количество элементов, выбираемых за раз.
Как рассчитать повторяющиеся комбинации?
Если мы выбираем r-комбинацию из n элементов с повторением, то имеется
C(n+r-1,r)=C(n+r-1,n-1) способов
Повторение в сочетании разрешено?
Всякий раз, когда есть регулярная комбинация, порядок НЕ важен, повторений может не быть. Допускаются комбинации с повторениями, порядок которых не имеет значения.
Допускаются комбинации с повторениями, порядок которых не имеет значения.
В 1234 ячейках есть 24 возможных комбинации для каждой комбинации, так что для каждой «одной» комбинации из ячеек вы, скорее всего, выиграете примерно одну из 417 раз.
Сколько в диапазоне 000 999 комбинаций состоит из трех разных цифр?
Значение ключа трехзначного замка находится в диапазоне от «000» до «999». Есть 1000 возможных комбинаций, которые нужно попробовать, чтобы открыть замок.
Сколько комбинаций в 12-значном числе?
Количество возможных комбинаций с 12-значным числом: 4 095 .
Что означает сочетание без повторения? Комбинация без повторения означает способ выбора объектов из списка . Объекты могут быть выбраны только один раз для каждого правила выбора, независимо от того, в каком порядке они выбраны.
Когда следует использовать перестановку или комбинацию?
Перестановка используется, когда порядок имеет значение, а комбинация используется, когда порядок не имеет значения. Следовательно, перестановку можно определить как упорядоченную комбинацию. Количество перестановок n объектов одновременно определяется следующим уравнением:
Р (п, г) = п!
Откуда мы знаем, сколько комбинаций возможно?
Перестановка показывает количество способов организации определенного набора переменных (в данном случае чисел).
Сколько 5-значных комбинаций?
Количество возможных комбинаций для 5-значного числа (каждая может содержать 09) равно 99999. Количество 5-значных комбинаций равно 105 = 100 000. Так что на один больше, чем 99 999.
Что ты имеешь в виду 9Комбинация 0810 по алгебре? Комбинация — это математический метод, который определяет количество возможных комбинаций в группе элементов, где порядок выбора не имеет значения . Комбинации можно спутать с перестановками.
Комбинации можно спутать с перестановками.
Комбинация – это выбор всех или части набора элементов, независимо от порядка, в котором элементы обозначаются . Например, предположим, что у нас есть набор из трех букв: A, B и C, мы можем спросить, сколькими способами мы можем выбрать 2 буквы из этого набора. Каждый вероятный выбор будет примером комбинации. Сколько существует комбинаций из 3 чисел?
3 x 2 x 1 даст вам 6 различных способов расположения трех цифр. Если вам нужны все возможные трехзначные числа без повторения цифр, то у вас есть 10 вариантов выбора для первой цифры, 9 вариантов для второй цифры и 8 вариантов для третьей цифры, что дает вам 10×9.x8 = 720. Шесть уникальных комбинаций из трех цифр включены в 720 возможных комбинаций. Чтобы вычислить эту комбинацию, разделите 2 на 6. Таким образом генерируется 120 возможных комбинаций.
Как рассчитать возможные возможные комбинации?
Порядок исходов события не имеет значения при расчете результатов комбинации. Для расчета комбинаций нам понадобится формула nCr = n. Для расчета комбинаций нам понадобится формула nCr = n. где n обозначает общее количество элементов, а r обозначает количество элементов, выбираемых за раз.
Как рассчитать повторяющиеся комбинации?
Если мы выбираем r-комбинацию из n элементов с повторением, то имеется
C(n+r-1,r)=C(n+r-1,n-1) способов
Повторение в сочетании разрешено?
Всякий раз, когда есть регулярная комбинация, порядок НЕ важен, повторений может не быть. Допускаются комбинации с повторениями, порядок которых не имеет значения.
Сколько существует комбинаций числа 1234? В 1234 ячейках есть 24 возможные комбинации для каждой комбинации, поэтому для каждой «одной» комбинации ящиков вы, вероятно, выиграете примерно одну из 417 раз.
Сколько комбинаций в диапазоне 000 999 состоит из трех разных цифр?
Значение ключа трехзначного замка находится в диапазоне от «000» до «999». Есть 1000 возможных комбинаций, которые нужно попробовать, чтобы открыть замок.
Сколько комбинаций в 12-значном числе?
Количество возможных комбинаций с 12-значным номером: 4 095 .
Что означает сочетание без повторения?Комбинация без повторения означает способ выбора объектов из списка . Объекты могут быть выбраны только один раз в соответствии с правилом выбора, независимо от того, в каком порядке они выбраны.
Когда следует использовать перестановку или комбинацию?
Перестановка используется, когда порядок имеет значение, а комбинация используется, когда порядок не имеет значения. Следовательно, перестановку можно определить как упорядоченную комбинацию. Количество перестановок n объектов одновременно определяется этим уравнением:
Р (п, г) = п!
Откуда мы знаем, сколько комбинаций возможно?
Если мы хотим узнать, сколько возможных комбинаций, мы можем использовать математическую модель, называемую перестановкой. Перестановка показывает количество способов организации определенного набора переменных (в данном случае чисел).
Перестановка показывает количество способов организации определенного набора переменных (в данном случае чисел).
Сколько 5-значных комбинаций?
Количество возможных комбинаций для 5-значного числа (каждая может содержать 09) равно 99999. Количество 5-значных комбинаций равно 105 = 100 000. Так что на один больше, чем 99999.
Что значит комбинация в алгебре?Комбинация — это математический метод, который определяет количество возможных комбинаций в группе элементов, где порядок выбора не имеет значения . Комбинации можно спутать с перестановками.
Что вы имеете в виду под комбинацией в реальной жизни? Комбинация – это выбор всех или части набора элементов, независимо от порядка, в котором элементы обозначаются . Например, предположим, что у нас есть набор из трех букв: A, B и C, мы можем спросить, сколькими способами мы можем выбрать 2 буквы из этого набора. Каждый вероятный выбор будет примером комбинации.
Каждый вероятный выбор будет примером комбинации.
Сколько комбинаций с 4 цифрами
10 000 возможных комбинаций Существует 10 000 возможных комбинаций, в которых цифры от 0 до 9 могут образовывать четырехзначный код. 21 сентября 2012 г.
Содержание
возможные комбинации 1234?
Сколькими способами можно написать 1234? 4 * 3 * 2 * 1 = 24 перестановки.
Сколько времени нужно, чтобы взломать 4-значный PIN-код?
111 часов
Таким образом, каждый ввод ПИН-кода занимает примерно 40 секунд, а это означает, что подбор четырехзначного ПИН-кода займет до ~111 часов.
Сколько существует комбинаций из 4 цифр, использующих 1 6?
360 возможных комбинаций
6 x 5 x 4 x 3 = 360 возможных комбинаций. Дано 4-значное целое число. каждая цифра может быть от 1 до 6.
Сколько комбинаций из 3 номеров можно составить из 5 номеров?
10 возможных комбинаций
Итак, 5 выберите 3 = 10 возможных комбинаций. Однако есть более короткий путь, чтобы найти 5, выбрав 3. Формула комбинаций: nCr = n! / ((n – r)!
Однако есть более короткий путь, чтобы найти 5, выбрав 3. Формула комбинаций: nCr = n! / ((n – r)!
Какой самый сложный 4-значный пароль?
Все 10 000 одинаково сложны, если вы выберете один наугад. 1111 математически угадать не легче, чем 3861. Поскольку люди склонны предпочитают шаблоны, хотя, вероятно, лучше выбрать последовательность, которая не является широко используемым шаблоном.0531
Какие есть хорошие 4-значные пароли?
Исследователи компании Data Genetics, занимающейся анализом данных, обнаружили, что три самые популярные комбинации — «1234», «1111» и «0000» — составляют около 20 процентов всех четырехзначных паролей.
Каковы распространенные 4-значные пароли?
почти 11% из 3,4 миллионов паролей 1234!!! Следующим по популярности 4-значным PIN-кодом является 1111, и более 6% паролей являются такими. На третьем месте 0000 с почти 2%. Таблица 20 самых популярных паролей показана справа.
Сколько существует перестановок 4 чисел?
Если вы имели в виду «перестановки», то вы, вероятно, задаетесь вопросом: «Сколькими различными способами я могу расположить четыре числа в порядке?» Ответ на этот вопрос (вы правильно поняли) — 24.
Сколько существует положительных четырехзначных чисел?
Первые 999 номеров состоят только из трех или менее цифр; 9999 — это последнее четырехзначное число. Следовательно, 9000 – это число, состоящее из четырех или менее цифр, за вычетом трех или менее цифр.
Сколько существует комбинаций из 4 чисел без повторения?
15
Количество возможных комбинаций из 4 цифр без повторения равно 15.
Какие 10000 комбинаций из 4 цифр?
Итак, из 10 000 возможных комбинаций четырехзначных кодов, какая самая популярная? Как вы уже догадались: 1234. Тревожные ~11% из 3,4 миллиона паролей составляют 1234. На 20 самых популярных паролей приходится почти 27% от общего числа.
Как считать комбинации?
Формула для комбинаций обычно n! / (r! (n — r)!), где n — общее количество возможностей начать, а r — количество сделанных выборов. В нашем примере у нас есть 52 карты; следовательно, n = 52. Мы хотим выбрать 13 карт, поэтому r = 13.
Сколько существует комбинаций чисел 1 2 3 4?
Объяснение: Если мы смотрим на количество чисел, которые мы можем составить, используя числа 1, 2, 3 и 4, мы можем вычислить это следующим образом: для каждой цифры (тысячи, сотни, десятки, единицы) мы есть 4 варианта чисел. Итак, мы можем создать 4×4×4×4=44=256 чисел.
Сколько комбинаций может быть в 5 числах?
Количество комбинаций из 5 цифр: 10 5=100 000. Итак, на единицу больше, чем 99 999. Вы можете обобщить это: количество комбинаций из N цифр равно 10 N. Теперь это предполагает, что вы считаете 00000 или 00534 «пятизначными числами».
Сколько комбинаций из 3 чисел можно составить из 6 чисел?
Видите ли, существует 3 x 2 x 1 = 6 возможных способов расположения трех цифр. Следовательно, в этом наборе из 720 вариантов каждая уникальная комбинация из трех цифр представлена 6 раз. Итак, мы просто делим на 6. 720 / 6 = 120.
Как сделать 4 выбрать 3?
4 ВЫБЕРИТЕ 3 = 4 возможных комбинации. 4 — это общее количество всех возможных комбинаций для выбора 3 элементов за раз из 4 различных элементов без учета порядка элементов в статистических и вероятностных исследованиях или экспериментах.
4 — это общее количество всех возможных комбинаций для выбора 3 элементов за раз из 4 различных элементов без учета порядка элементов в статистических и вероятностных исследованиях или экспериментах.
Какой четырехзначный код самый безопасный?
8068
Самый безопасный 4-значный PIN-код — «8068» — по крайней мере, так было, пока исследователи из Data Genetics не сообщили всем на этой неделе. Исследователи изучили набор из 3,4 миллиона четырехзначных личных идентификационных номеров и обнаружили, что «8068» встречается только 25 раз.
Какие хорошие 6-значные пароли?
Как и ожидалось, 123456 возглавляет список, за ним следуют 111111 и 123123. …
Каковы шансы угадать пятизначный код?
Всего существует 100 000 комбинаций паролей. Следовательно, вероятность того, что хакер угадает, составляет 1 из 100 000.
Какой самый распространенный четырехзначный лотерейный номер?
Самыми популярными номерами, выбранными игроками для игр New York’s Numbers и Win 4, являются 111 и 0000, говорят организаторы лотереи.

 При
бесповторной выборке все равно, каким образом осуществляется выбор: берутся все
При
бесповторной выборке все равно, каким образом осуществляется выбор: берутся все 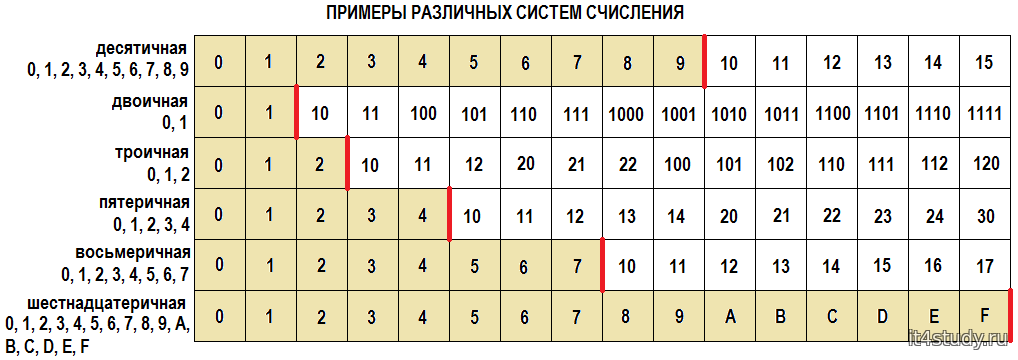

 Сколько разных
Сколько разных Давайте его посчитаем: C74=C73
по св-ву
1. C73
Давайте его посчитаем: C74=C73
по св-ву
1. C73  Члены команды выбирают капитана и вратаря.
Сколькими способами это можно сделать?
Члены команды выбирают капитана и вратаря.
Сколькими способами это можно сделать?
 е. достигает 27.000 комбинаций. Окончательно,
т.к. каждой буквенной комбинации можно поставить в соответствие числовую
комбинацию, то полное количество автомобильных номеров равно 270.000.000.
е. достигает 27.000 комбинаций. Окончательно,
т.к. каждой буквенной комбинации можно поставить в соответствие числовую
комбинацию, то полное количество автомобильных номеров равно 270.000.000. — М.: Мир, 1990.
— М.: Мир, 1990.