Все 10000 комбинаций из 4 цифр. Сложно ли угадать PIN-код
Несмотря на важную роль PIN-кодов в мировой инфраструктуре, до сих пор не проводилось академических исследований о том, как, собственно, люди выбирают PIN-коды.
Исследователи из университета Кембриджа Sören Preibusch и Ross Anderson исправили ситуацию, опубликовав первый в мире количественный анализ сложности угадывания 4-циферного банковского PIN-кода.
Используя данные об утечках паролей из небанковских источников и онлайн анкетирование, учёные выяснили, что к выбору PIN-кодов пользователи относятся гораздо серьёзнее, чем к выбору паролей для веб-сайтов: большинство кодов содержат практически случайный набор цифр. Тем не менее, среди исходных данных присутствуют и простые комбинации, и дни рождения, — то есть, при некотором везении злоумышленник может просто угадать заветный код.
Отправной точкой исследования был набор 4-циферных последовательностей в паролях из базы RockYou (1.7 млн), и базы из 200 тысяч PIN-кодов от программы блокировки экрана iPhone (базу предоставил разработчик приложения Daniel Amitay).
Итак, пользователи выбирают 4-циферные коды на основе всего нескольких простых факторов. Если бы так выбирались и банковские PIN-коды, 8-9% из них можно было бы угадать всего за три попытки! Но, конечно, к банковским кодам люди относятся гораздо внимательнее. Ввиду отсутствия сколько-нибудь большого набора настоящих банковских данных, исследователи опросили более 1300 человек, чтобы оценить, насколько реальные PIN-коды отличаются от уже рассмотренных. Учитывая специфику исследования, у респондентов спрашивали не о самих кодах, а только о их соответствии какому-либо из вышеназванных факторов (возрастание, формат ДДММ, и т.
Оказалось, что люди действительно гораздо тщательнее выбирают банковские PIN-коды. Примерно четверть опрошенных используют случайный PIN, сгенерированный банком. Более трети выбирают свой PIN-код, используя старый номер телефона, номер студенческого билета, или другой набор цифр, который выглядит случайным. Согласно полученным результатам, 64% владельцев карт используют псевдослучайный PIN-код, — это гораздо больше, чем 23-27% в предыдущих экспериментах с не-банковскими кодами. Ещё 5% используют цифровой паттерн (например, 4545), а 9% предпочитают паттерн на клавиатуре (например, 2684). В целом, злоумышленник с шестью попытками (три с банкоматом и три с платёжным терминалом) имеет меньше 2% шансов угадать PIN-код чужой карты.
| Фактор | Пример | RockYou | iPhone | Опрос |
|---|---|---|---|---|
| Даты | ||||
| ДДММ | 2311 | 5.26 | 1.38 | 3. 07 07 |
| ДМГГ | 3876 | 9.26 | 6.46 | 5.54 |
| ММДД | 1123 | 10.00 | 9.35 | 3.66 |
| ММГГ | 0683 | 0.67 | 0.20 | 0.94 |
| ГГГГ | 1984 | 33.39 | 7.12 | 4.95 |
| Итого | 58.57 | 24.51 | 22.76 | |
| Клавиатурный паттерн | ||||
| смежные | 6351 | 1.52 | 4.99 | — |
| квадрат | 1425 | 0.01 | 0.58 | — |
| углы | 9713 | 0.19 | 1.06 | — |
| крест | 8246 | 0.17 | 0.88 | — |
| диагональная линия | 1590 | 0.10 | 1.36 | — |
| горизонтальная линия | 5987 | 0.34 | 1.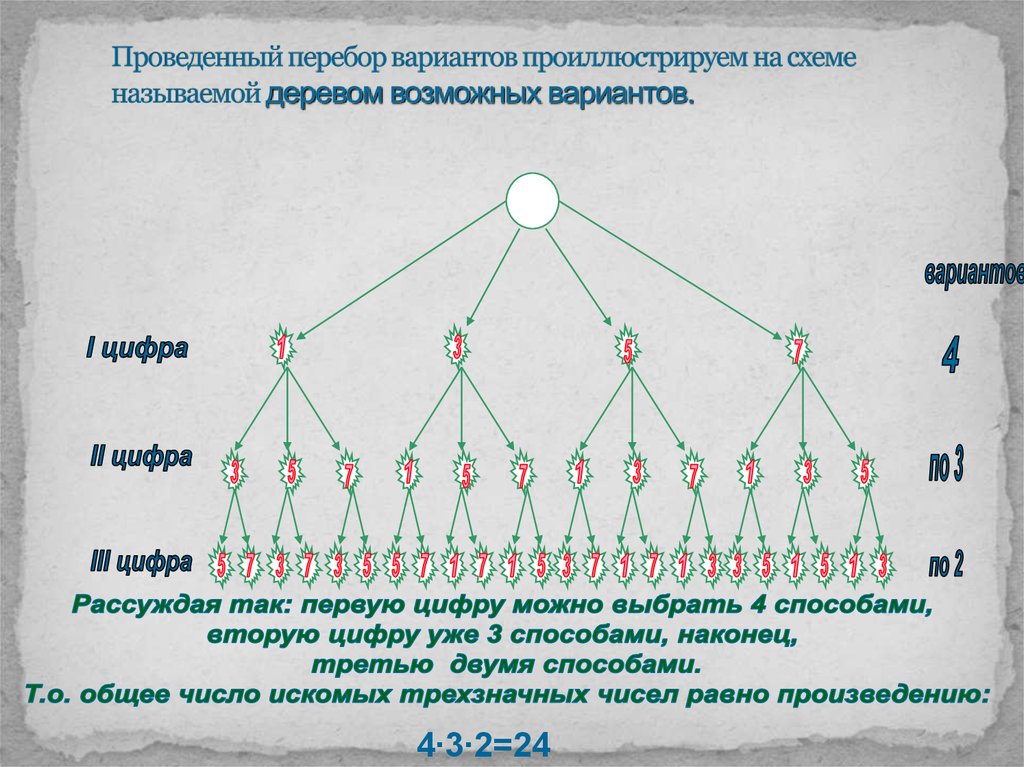 42 42 | — |
| слово | 5683 | 0.70 | 8.39 | — |
| вертикальная линия | 8520 | 0.06 | 4.28 | — |
| Итого | 3.09 | 22.97 | 8.96 | |
| Цифровой паттерн | ||||
| заканчивается на 69 | 6869 | 0.35 | 0.57 | — |
| только цифры 0-3 | 2000 | 3.49 | 2.72 | — |
| только цифры 0-6 | 5155 | 4.66 | 5.96 | — |
| повторяющиеся пары | 2525 | 2.31 | 4.11 | — |
| одинаковые цифры | 6666 | 0.40 | 6.67 | — |
| убывающая последовательность | 3210 | 0.13 | 0.29 | — |
| возрастающая последовательность | 4567 | 3.83 | 4. 52 52 | — |
| Итого | 15.16 | 24.85 | 4.60 | |
| Случайный набор цифр | 23.17 | 27.67 | 63.68 | |
Всё бы хорошо, но, к сожалению, существенная часть опрошенных (23%) выбирает PIN-код в виде даты, — и почти треть из них использует дату своего рождения. Это существенно меняет дело, ведь почти все (99%) респонденты ответили, что хранят в бумажнике с банковскими картами различные удостоверения личности, на которых эта дата напечатана. Если злоумышленник знает день рождения владельца карты, то при грамотном подходе вероятность угадывания PIN-кода взлетает до 9%.
100 самых популярных PIN-кодов
0000, 0101-0103, 0110, 0111, 0123, 0202, 0303, 0404, 0505, 0606, 0707, 0808, 0909, 1010, 1101-1103, 1110-1112, 1123, 1201-1203, 1210-1212, 1234, 1956-2015, 2222, 2229, 2580, 3333, 4444, 5252, 5683, 6666, 7465, 7667.
P.S. На практике, разумеется, злоумышленнику гораздо проще подсмотреть ваш PIN-код, чем угадывать его. Но и от подглядывания можно защититься — даже, казалось бы, в безвыходном положении:
Калькулятор ниже предназначен для генерации всех сочетаний из n по m элементов.
Описание алгоритма генерации под калькулятором.
Алгоритм
Комбинации генерируются в лексикографическом порядке. Алгоритм работает с порядковыми индексами элементов множества.
Рассмотрим алгоритм на примере.
Для простоты изложения рассмотрим множество из пяти элементов, индексы в котором начинаются с 1, а именно, 1 2 3 4 5.
Требуется сгенерировать все комбинации размера m = 3.
Сначала инициализуется первая комбинация заданного размера m — индексы в порядке возрастания
1 2 3
Далее проверяется последний элемент, т. е. i = 3. Если его значение меньше n — m + i, то он инкрементируется на 1.
е. i = 3. Если его значение меньше n — m + i, то он инкрементируется на 1.
1 2 4
Снова проверяется последний элемент, и опять он инкрементируется.
Теперь значение элемента равно максимально возможному: n — m + i = 5 — 3 + 3 = 5, проверяется предыдущий элемент с i = 2.
Если его значение меньше n — m + i, то он инкрементируется на 1, а для всех следующих за ним элементов значение приравнивается к значению предыдущего элемента плюс 1.
1 (2+1)3 (3+1)4 = 1 3 4
Далее снова идет проверка для i = 3.
1 3 5
Затем — проверка для i = 2.
1 4 5
Потом наступает очередь i = 1.
(1+1)2 (2+1)3 (3+1)4 = 2 3 4
И далее,
2 3 5
2 4 5
3 4 5 — последнее сочетание, так как все его элементы равны n — m + i.
Друзья! Раз уж есть у меня этот мертвый блокнот, использую-ка я его для того, чтобы задать вам задачку, над которой вчера билось три физика, два экономиста, один политеховский и один гуманитарий.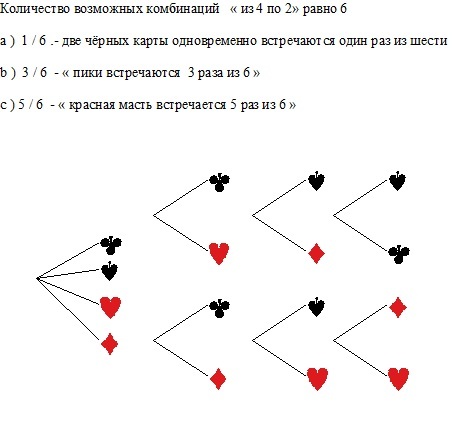
Итак, предыстория.
Мне выдали новую банковскую карточку и я, как водится, играючи угадала ее пин-код. Но не подряд. В смысле, допустим, пин-код был 8794, а я назвала 9748. То есть, я триумфально угадала все цифры , которое содержались в данном четырехзначном числе. Ну да, не само число , а просто его составляющие у гадала. Но цифры-то все верные! ПРИМЕЧАНИЕ — я действовала наугад, то есть, мне не надо было расставить уже известные числа в нужном порядке, я просто действовала в духе: вот тут есть неизвестные мне четыре цифры, и я считаю, что среди них могут быть 9, 7, 4 и 8, а порядок их не важен.
Мы тут же задались вопросом, сколько у меня вообще было вариантов (наверное, чтобы понять, насколько это круто, что я вот взяла и угадала). То есть, из скольких комбинаций четырех цифр мне нужно было выбирать? И тут, натурально, начался ад. У нас весь вечер взрывалась голова, и у всех, в итоге, вышли абсолютно разные варианты ответа! Я даже начала выписывать все эти комбинации в блокнот подряд по мере возрастания, но на четырех сотнях поняла, что их больше четырех сотен (во всяком случае, это опровергло ответ физика Трэша, который уверял меня, что комбинаций четыре сотни, но все равно это не совсем однозначно) — и сдалась.
То есть, из скольких комбинаций четырех цифр мне нужно было выбирать? И тут, натурально, начался ад. У нас весь вечер взрывалась голова, и у всех, в итоге, вышли абсолютно разные варианты ответа! Я даже начала выписывать все эти комбинации в блокнот подряд по мере возрастания, но на четырех сотнях поняла, что их больше четырех сотен (во всяком случае, это опровергло ответ физика Трэша, который уверял меня, что комбинаций четыре сотни, но все равно это не совсем однозначно) — и сдалась.Собственно, суть вопроса. Какова вероятность угадывания (в любом порядке) четырех чисел, содержащихся в четырехзначном числе?
Или нет, переформулируем (я гуманитарий, простите, хотя к математике всегда питала огромную слабость), чтобы было яснее и четче. Сколько

Или еще конкретнее. Мне нужно четыре раза угадать одну цифру из десяти. Но не подряд.
Ну или еще как-нибудь. В общем, нужно узнать, сколько у меня было вариантов числовой комбинации, из которой складывался пин-код карточки. Помогите, люди добрые! Только, пожалуйста, помогая, не начинайте сразу писать, что вариантов этих 9999 (вчера такое всем приходило в голову поначалу), потому что это же глупости — ведь в том ракурсе, который нас волнует, число 1234, число 3421, число 4312 и так далее являются одним и тем же! Ну и да, цифры же могут повторяться, ведь бывает пин-код 1111 или там, например, 0007. Можно представить вместо пин-кода номер машины. Допустим, какова вероятность угадать все однозначные цифры, из которых складывается номер машины? Или, чтобы вообще убрать теорию вероятности — из скольких числовых комбинаций мне нужно было выбрать одну?
Пожалуйста, подкрепите свои ответы и рассуждения какими-нибудь точными формулами, потому что мы вчера и так чуть не свихнулись. Заранее всем большое спасибо!
Заранее всем большое спасибо!
P.S. Один умный человек, программист, художник и изобретатель, только что очень верно подсказал правильное решение проблемы, подарив мне несколько минут прекрасного настроения: «решение задачи такое: у неё обсессивно-комп ульсивное расстройство, лечение такое: замуж и окучивать помидоры. меня бы больше на её месте волновал не вопрос «какова вероятность», а вопрос «схуя ли я обращаю внимание на все эти цифры»? В общем-то, даже нечего добавить:)
Размещения, сочетания и перестановки из трёх элементов
Что изучает комбинаторика
Представьте себе, что вы забыли пароль входа в аккаунт. Помните только, что это было трёхзначное число из цифр 1,2,3 и эти цифры не повторялись. Есть ли у вас шансы с помощью перебора зайти в аккаунт, если даётся всего три попытки? Такие задачи в современной жизни возникают довольно часто, и их решения изучаются в особом разделе математики — комбинаторике.
Комбинаторика – раздел математики, изучающий различные комбинации, которые можно составить из дискретных объектов, входящих в некоторое множество.
«Дискретные объекты» — это какие-то предметы, растения, животные, люди, здания, числа; всё, что можно «отделить» («дискретный» означает «отдельный») . Множество подобных объектов – это какая-то конечная группа, выбранная по какому-нибудь признаку.
Например:
Множество
Дискретные объекты – элементы множества
Фрукты
Яблоко, груша, слива, вишня, клубника
Деревья
Дуб, ель, сосна, береза
Домашние питомцы
Собака, кот, попугай
Цифры
0,1,2,3,4,5,6,7,8,9
Виды комбинаций
Составлять из дискретных объектов комбинации можно по-разному, их можно размещать, переставлять, сочетать; а также, брать каждый объект только один раз или помногу.
Комбинации из трёх элементов без повторений
Рассмотрим комбинации из трёх цифр 1,2,3 без повторений.
Перестановки
Нужно переставлять три цифры так, чтобы их порядок был разным:
123, 231, 312, 132, 321, 213
Таких комбинаций 6. 3 = 6$
3 = 6$
Комбинации из трёх элементов с повторениями
Рассмотрим комбинации из трёх цифр 1,2,3 с повторениями.
Перестановки
Нужно переставлять три цифры так, чтобы их порядок был разным:
111
112
113
211
212
213
311
312
313
121
122
123
221
222
223
321
322
323
131
132
133
231
232
233
331
332
333
Всего – 27 комбинаций.
Записывают $ \overline{P_3} = 27$
Сочетания
Нужно выбирать от 1 до 3 цифр одновременно (порядок неважен), и смотреть, сколькими способами это можно сделать:
По 1 цифре: можно выбрать 1, или 2, или 3 – всего 3 комбинации
По 2 цифры: можно выбрать
13
23
33
Всего 6 комбинаций
По 3 цифры можно выбрать
111
112
113
122
123
222
133
232
233
333
Всего 10 комбинаций
Записывают: $ \overline{C_3^1} = 3, \overline{C_3^2} = 6, \overline{C_3^3} = 10$
Размещения
Нужно выбирать от 1 до 3 цифр одновременно (порядок неважен), и смотреть, сколькими способами это можно сделать:
По 1 цифре: можно выбрать 1, или 2, или 3 – всего 3 комбинации
По 2 цифры: можно выбрать
11
21
31
12
22
32
13
23
33
Всего 9 комбинаций
По 3 цифры: получаем все перестановки – 27 комбинаций
Записывают: $ \overline{A_3^1} = 3, \overline{A_3^2} = 9, \overline{A_3^3} = 27$
Примеры
Пример 1. 2 = 6$$
2 = 6$$
Ответ: 6 способов
Пример 4. Сколько всего трёхзначных чисел, в записи которых встречаются только цифры 1 и 2?
Поскольку числа трёхзначные, а цифр только две, цифры буду повторяться. Все возможные двузначные числа из 1 и 2:
Все возможные трёхзначные числа:
111
112
211
212
121
122
221
222
Всего – 8 комбинаций.
Ответ: 8 чисел
Пример 5. Сколько всего трехзначных чисел можно записать с помощью цифр 0,1,2 без повторений?
Речь идёт о перестановках без повторений.
012, 120, 201, 021, 210, 102
Из которых нужно исключить 012 и 021, т.к. это – не трёхзначные числа.
120, 201, 210, 102
Получаем 4 комбинации.
Ответ: 4 числа
Пример 6. Сколько всего трехзначных чисел можно записать с помощью цифр 0,1,2 с повторениями?
Все возможные комбинации по 2 из трёх цифр:
00
01
02
10
11
12
20
21
22
Впереди не может быть 0. Получаем возможные трёхзначные числа:
Получаем возможные трёхзначные числа:
100
101
102
200
201
202
110
111
112
210
211
212
120
121
122
220
221
222
18 комбинаций.
Ответ: 4 числа
Сколько вариантов пароля из 4 цифр
Вот 20 самых популярных кодов блокировки. А у вас на смартфоне не один из них?
Все 10000 комбинаций из 4 цифр. Сложно ли угадать PIN-код
Несмотря на важную роль PIN-кодов в мировой инфраструктуре, до сих пор не проводилось академических исследований о том, как, собственно, люди выбирают PIN-коды.
Исследователи из университета Кембриджа Sören Preibusch и Ross Anderson исправили ситуацию, опубликовав первый в мире количественный анализ сложности угадывания 4-циферного банковского PIN-кода.
Используя данные об утечках паролей из небанковских источников и онлайн анкетирование, учёные выяснили, что к выбору PIN-кодов пользователи относятся гораздо серьёзнее, чем к выбору паролей для веб-сайтов: большинство кодов содержат практически случайный набор цифр. Тем не менее, среди исходных данных присутствуют и простые комбинации, и дни рождения, — то есть, при некотором везении злоумышленник может просто угадать заветный код.
Тем не менее, среди исходных данных присутствуют и простые комбинации, и дни рождения, — то есть, при некотором везении злоумышленник может просто угадать заветный код.
Отправной точкой исследования был набор 4-циферных последовательностей в паролях из базы RockYou (1.7 млн), и базы из 200 тысяч PIN-кодов от программы блокировки экрана iPhone (базу предоставил разработчик приложения Daniel Amitay). В графиках, построенных по этим данным, проступают интересные закономерности — даты, года, повторяющиеся цифры, и даже PIN-коды, заканчивающиеся на 69. На основе этих наблюдений учёные построили линейную регрессионную модель, которая оценивает популярность каждого PIN-кода в зависимости от 25 факторов, — например, является ли код датой в формате ДДММ, является ли он возрастающей последовательностью, и так далее. Этим общим условиям соответствуют 79% и 93% PIN-кодов в каждом из наборов.
Итак, пользователи выбирают 4-циферные коды на основе всего нескольких простых факторов. Если бы так выбирались и банковские PIN-коды, 8-9% из них можно было бы угадать всего за три попытки! Но, конечно, к банковским кодам люди относятся гораздо внимательнее. Ввиду отсутствия сколько-нибудь большого набора настоящих банковских данных, исследователи опросили более 1300 человек, чтобы оценить, насколько реальные PIN-коды отличаются от уже рассмотренных. Учитывая специфику исследования, у респондентов спрашивали не о самих кодах, а только о их соответствии какому-либо из вышеназванных факторов (возрастание, формат ДДММ, и т.д.).
Если бы так выбирались и банковские PIN-коды, 8-9% из них можно было бы угадать всего за три попытки! Но, конечно, к банковским кодам люди относятся гораздо внимательнее. Ввиду отсутствия сколько-нибудь большого набора настоящих банковских данных, исследователи опросили более 1300 человек, чтобы оценить, насколько реальные PIN-коды отличаются от уже рассмотренных. Учитывая специфику исследования, у респондентов спрашивали не о самих кодах, а только о их соответствии какому-либо из вышеназванных факторов (возрастание, формат ДДММ, и т.д.).
Оказалось, что люди действительно гораздо тщательнее выбирают банковские PIN-коды. Примерно четверть опрошенных используют случайный PIN, сгенерированный банком. Более трети выбирают свой PIN-код, используя старый номер телефона, номер студенческого билета, или другой набор цифр, который выглядит случайным. Согласно полученным результатам, 64% владельцев карт используют псевдослучайный PIN-код, — это гораздо больше, чем 23-27% в предыдущих экспериментах с не-банковскими кодами. Ещё 5% используют цифровой паттерн (например, 4545), а 9% предпочитают паттерн на клавиатуре (например, 2684). В целом, злоумышленник с шестью попытками (три с банкоматом и три с платёжным терминалом) имеет меньше 2% шансов угадать PIN-код чужой карты.
Ещё 5% используют цифровой паттерн (например, 4545), а 9% предпочитают паттерн на клавиатуре (например, 2684). В целом, злоумышленник с шестью попытками (три с банкоматом и три с платёжным терминалом) имеет меньше 2% шансов угадать PIN-код чужой карты.
| Фактор | Пример | RockYou | iPhone | Опрос |
|---|---|---|---|---|
| Даты | ||||
| ДДММ | 2311 | 5.26 | 1.38 | 3.07 |
| ДМГГ | 3876 | 9.26 | 6.46 | 5.54 |
| ММДД | 1123 | 10.00 | 9.35 | 3.66 |
| ММГГ | 0683 | 0.67 | 0.20 | 0.94 |
| ГГГГ | 1984 | 33.39 | 7.12 | 4.95 |
| Итого | 58.57 | 24.51 | 22.76 | |
| Клавиатурный паттерн | ||||
| смежные | 6351 | 1.52 | 4. 99 99 | — |
| квадрат | 1425 | 0.01 | 0.58 | — |
| углы | 9713 | 0.19 | 1.06 | — |
| крест | 8246 | 0.17 | 0.88 | — |
| диагональная линия | 1590 | 0.10 | 1.36 | — |
| горизонтальная линия | 5987 | 0.34 | 1.42 | — |
| слово | 5683 | 0.70 | 8.39 | — |
| вертикальная линия | 8520 | 0.06 | 4.28 | — |
| Итого | 3.09 | 22.97 | 8.96 | |
| Цифровой паттерн | ||||
| заканчивается на 69 | 6869 | 0.35 | 0.57 | — |
| только цифры 0-3 | 2000 | 3.49 | 2.72 | — |
| только цифры 0-6 | 5155 | 4.66 | 5.96 | — |
| повторяющиеся пары | 2525 | 2. 31 31 | 4.11 | — |
| одинаковые цифры | 6666 | 0.40 | 6.67 | — |
| убывающая последовательность | 3210 | 0.13 | 0.29 | — |
| возрастающая последовательность | 4567 | 3.83 | 4.52 | — |
| Итого | 15.16 | 24.85 | 4.60 | |
| Случайный набор цифр | 23.17 | 27.67 | 63.68 |
Всё бы хорошо, но, к сожалению, существенная часть опрошенных (23%) выбирает PIN-код в виде даты, — и почти треть из них использует дату своего рождения. Это существенно меняет дело, ведь почти все (99%) респонденты ответили, что хранят в бумажнике с банковскими картами различные удостоверения личности, на которых эта дата напечатана. Если злоумышленник знает день рождения владельца карты, то при грамотном подходе вероятность угадывания PIN-кода взлетает до 9%.
100 самых популярных PIN-кодов
P. S. На практике, разумеется, злоумышленнику гораздо проще подсмотреть ваш PIN-код, чем угадывать его. Но и от подглядывания можно защититься — даже, казалось бы, в безвыходном положении:
S. На практике, разумеется, злоумышленнику гораздо проще подсмотреть ваш PIN-код, чем угадывать его. Но и от подглядывания можно защититься — даже, казалось бы, в безвыходном положении:
Описание алгоритма генерации под калькулятором.
Алгоритм
Комбинации генерируются в лексикографическом порядке. Алгоритм работает с порядковыми индексами элементов множества. Рассмотрим алгоритм на примере. Для простоты изложения рассмотрим множество из пяти элементов, индексы в котором начинаются с 1, а именно, 1 2 3 4 5. Требуется сгенерировать все комбинации размера m = 3. Сначала инициализуется первая комбинация заданного размера m — индексы в порядке возрастания1 2 3 Далее проверяется последний элемент, т. е. i = 3. Если его значение меньше n — m + i, то он инкрементируется на 1.1 2 4 Снова проверяется последний элемент, и опять он инкрементируется.1 2 5 Теперь значение элемента равно максимально возможному: n — m + i = 5 — 3 + 3 = 5, проверяется предыдущий элемент с i = 2. Если его значение меньше n — m + i, то он инкрементируется на 1, а для всех следующих за ним элементов значение приравнивается к значению предыдущего элемента плюс 1. 1 (2+1)3 (3+1)4 = 1 3 4 Далее снова идет проверка для i = 3.1 3 5 Затем — проверка для i = 2.1 4 5 Потом наступает очередь i = 1. (1+1)2 (2+1)3 (3+1)4 = 2 3 4 И далее,2 3 5 2 4 5 3 4 5 — последнее сочетание, так как все его элементы равны n — m + i.
Если его значение меньше n — m + i, то он инкрементируется на 1, а для всех следующих за ним элементов значение приравнивается к значению предыдущего элемента плюс 1. 1 (2+1)3 (3+1)4 = 1 3 4 Далее снова идет проверка для i = 3.1 3 5 Затем — проверка для i = 2.1 4 5 Потом наступает очередь i = 1. (1+1)2 (2+1)3 (3+1)4 = 2 3 4 И далее,2 3 5 2 4 5 3 4 5 — последнее сочетание, так как все его элементы равны n — m + i.
Друзья! Раз уж есть у меня этот мертвый блокнот, использую-ка я его для того, чтобы задать вам задачку, над которой вчера билось три физика, два экономиста, один политеховский и один гуманитарий. Мы сломали себе весь мозг и у нас постоянно получаются разные результаты. Может быть, среди вас есть программисты и математические гении, к тому же, задачка вообще школьная и очень легкая, у нас просто не выводится формула. Потому что мы бросили занятия точными науками и вместо этого зачем-то пишем книги и рисуем картины. Простите.
Мне выдали новую банковскую карточку и я, как водится, играючи угадала ее пин-код. Но не подряд. В смысле, допустим, пин-код был 8794, а я назвала 9748. То есть, я триумфально угадала все цифры , которое содержались в данном четырехзначном числе. Ну да, не само число , а просто его составляющие у гадала. Но цифры-то все верные! ПРИМЕЧАНИЕ — я действовала наугад, то есть, мне не надо было расставить уже известные числа в нужном порядке, я просто действовала в духе: вот тут есть неизвестные мне четыре цифры, и я считаю, что среди них могут быть 9, 7, 4 и 8, а порядок их не важен. Мы тут же задались вопросом, сколько у меня вообще было вариантов (наверное, чтобы понять, насколько это круто, что я вот взяла и угадала). То есть, из скольких комбинаций четырех цифр мне нужно было выбирать? И тут, натурально, начался ад. У нас весь вечер взрывалась голова, и у всех, в итоге, вышли абсолютно разные варианты ответа! Я даже начала выписывать все эти комбинации в блокнот подряд по мере возрастания, но на четырех сотнях поняла, что их больше четырех сотен (во всяком случае, это опровергло ответ физика Трэша, который уверял меня, что комбинаций четыре сотни, но все равно это не совсем однозначно) — и сдалась.
Собственно, суть вопроса. Какова вероятность угадывания (в любом порядке) четырех чисел, содержащихся в четырехзначном числе?
Или нет, переформулируем (я гуманитарий, простите, хотя к математике всегда питала огромную слабость), чтобы было яснее и четче. Сколько не повторяющихся комбинаций цифр содержится в ряду порядковых числительных от 0 до 9999? (пожалуйста, не путайте это с вопросом «сколько комбинаций не повторяющихся цифр»!! ! цифры могут повторяться! в смысле, 2233 и 3322 — это в данном случае одна и та же комбинация!!).
Или еще конкретнее. Мне нужно четыре раза угадать одну цифру из десяти. Но не подряд.
Ну или еще как-нибудь. В общем, нужно узнать, сколько у меня было вариантов числовой комбинации, из которой складывался пин-код карточки. Помогите, люди добрые! Только, пожалуйста, помогая, не начинайте сразу писать, что вариантов этих 9999 (вчера такое всем приходило в голову поначалу), потому что это же глупости — ведь в том ракурсе, который нас волнует, число 1234, число 3421, число 4312 и так далее являются одним и тем же! Ну и да, цифры же могут повторяться, ведь бывает пин-код 1111 или там, например, 0007. Можно представить вместо пин-кода номер машины. Допустим, какова вероятность угадать все однозначные цифры, из которых складывается номер машины? Или, чтобы вообще убрать теорию вероятности — из скольких числовых комбинаций мне нужно было выбрать одну?
Можно представить вместо пин-кода номер машины. Допустим, какова вероятность угадать все однозначные цифры, из которых складывается номер машины? Или, чтобы вообще убрать теорию вероятности — из скольких числовых комбинаций мне нужно было выбрать одну?
Пожалуйста, подкрепите свои ответы и рассуждения какими-нибудь точными формулами, потому что мы вчера и так чуть не свихнулись. Заранее всем большое спасибо!
P.S. Один умный человек, программист, художник и изобретатель, только что очень верно подсказал правильное решение проблемы, подарив мне несколько минут прекрасного настроения: « решение задачи такое: у неё обсессивно-комп ульсивное расстройство, лечение такое: замуж и окучивать помидоры. меня бы больше на её месте волновал не вопрос «какова вероятность», а вопрос «схуя ли я обращаю внимание на все эти цифры»? В общем-то, даже нечего добавить:)
Детские считалки
За основу пароля берём любой детский стишок или считалку. Желательно, чтобы она водилась лишь в ваших краях и не была общеизвестна. А лучше собственного сочинения! Хотя подойдут любые детские рифмы, главное, чтобы строки намертво засели с юных лет в вашей голове.
А лучше собственного сочинения! Хотя подойдут любые детские рифмы, главное, чтобы строки намертво засели с юных лет в вашей голове.
Пароль будет состоять из первых букв каждого слова. Причём буква будет писаться в верхнем регистре, если она является первой в предложении. Заменяем некоторые буквы похожими по написанию цифрами (например, «ч» на «4», «о» на «0», «з» на «3»). Если не хотите излишне запутываться с заменой букв на цифры, поищите считалку, уже содержащую в себе цифры. Не забываем о знаках препинания, разделяющих слова и предложения, — они пригодятся.
Пример:
Черепаха хвост поджала
И за зайцем побежала.
Оказалась впереди,
Кто не верит — выходи!
Заменяем буквы «ч», «з» и «о» на схожие цифры. Вторая, третья и четвёртая строчки начинаются с заглавных букв, и поэтому пишутся в верхнем регистре. Включаем четыре знака препинания. Разумеется, пишем русскими буквами, но на английской раскладке клавиатуры.
17-символьный пароль готов! Может быть, он и не идеален, так как содержит повторяющиеся знаки, последовательные строчные буквы и цифры. Но назвать его простым уж точно язык не повернётся.
Но назвать его простым уж точно язык не повернётся.
Жаргон и терминология
Подразумевается использование профессионального жаргона, понятного крайне узкому числу людей. Эти слова куда более далеки от обычного человека, нежели криминальные изречения, широко освещаемые на телеэкране и улицах любого города.
Например, можно использовать выписку из больницы или заковыристое медицинское определение.
Пример:
Циклопентанпергидрофенантрен — термин, состоящий из 28 букв. Длинновато получается, посему предлагаю выкинуть гласные буквы и разбавить оставшиеся согласные верхним регистром.
Памятные даты
Разумеется, ваш день рождения или день начала семейной жизни — это не самая удачная основа для пароля. Событие должно быть исключительной важности, и о нём должны знать только вы. К примеру, это может быть день, когда вы впервые съели жвачку, сбежали с урока или сломали каблук. Так как базис пароля будут составлять цифры, не лишним видится перемешивание их с буквами.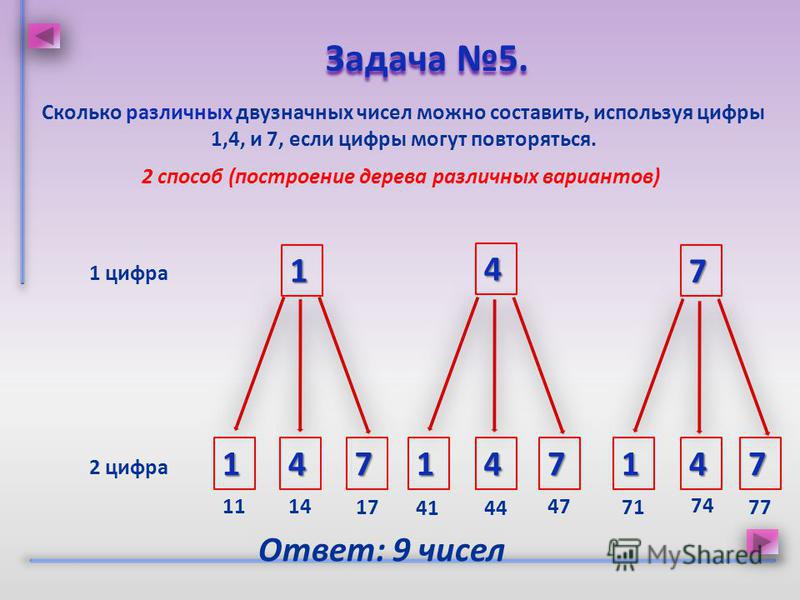
Пример:
Замените точки, разделяющие день, месяц и год, на любую букву, например маленькую английскую “ l” , которая очень похожа на довольно часто использующийся разделитель «/». Между датами проставим символ нижнего подчёркивания «_». Нули заменим на буквы «о».
Генерация паролей и способы запоминания.
Для подбора правильного пароля вполне можно использовать генерацию паролей . Такой сервис весьма доступен. Можно без особых усилий подобрать комбинацию, которую нелегко будет распознать. Здесь, правда, есть один подводный камень: сложную комбинацию сложно и запомнить. Редкие сочетания сложно ложатся в память. Рассмотрим далее, как сделать так, чтобы не забыть или не потерять пароль.
В большинстве случаев при генерации пароля используется одна и та же комбинация. Иногда пароль модернизируется и выходит что-то вроде «parol1», «parol2» и т.д. Шаг хитрый, но зато можно быть уверенным, что пароль не забудется .
При использовании генератора паролей получается бессмысленный и нелогичный набор символов.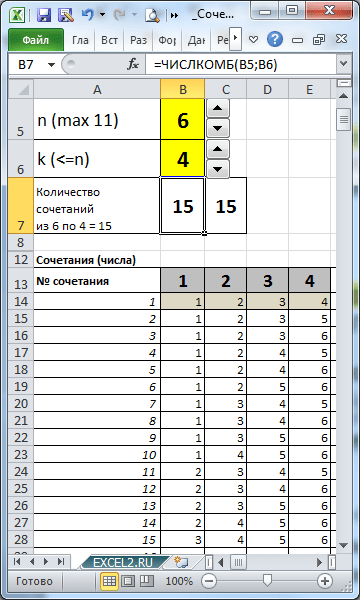 Его нужно где-то хранить. Интересно, что у многих есть привычка записывать его на бумажке и клеить на монитор. Например, в офисе, где множество сотрудников, клиентов и случайных людей. С таким же успехом на рабочем столе можно создать файл с названием «мои пароли». Эффект будет тот же.
Его нужно где-то хранить. Интересно, что у многих есть привычка записывать его на бумажке и клеить на монитор. Например, в офисе, где множество сотрудников, клиентов и случайных людей. С таким же успехом на рабочем столе можно создать файл с названием «мои пароли». Эффект будет тот же.
Итак, вот общие советы по хранению и запоминанию паролей:
1. Для каждого ресурса лучше создавать новый уникальный пароль.
2. Не нужно хранить комбинации паролей на рабочем столе компьютера — хакеры вполне могут проникнуть и в ПК.
3. Пароль не нужно держать у всех на виду.
4. Если пароль записан на листочке бумаги, нужно создавать его копию.
5. Не нужно вводить пароли в «странных» или подозрительных сайтах или программах. Администрации порталов никогда не требуют сообщать им пароль — он используется только для входа.
6. Если для хранения паролей используется специальная программа, нужно создавать ее копию.
Как посчитать количество комбинаций из 4 цифр – Сколько комбинаций у 4-х значного кодового замка?
Все 10000 комбинаций из 4 цифр.
 Сложно ли угадать PIN-код
Сложно ли угадать PIN-кодНесмотря на важную роль PIN-кодов в мировой инфраструктуре, до сих пор не проводилось академических исследований о том, как, собственно, люди выбирают PIN-коды.
Исследователи из университета Кембриджа Sören Preibusch и Ross Anderson исправили ситуацию, опубликовав первый в мире количественный анализ сложности угадывания 4-циферного банковского PIN-кода.
Используя данные об утечках паролей из небанковских источников и онлайн анкетирование, учёные выяснили, что к выбору PIN-кодов пользователи относятся гораздо серьёзнее, чем к выбору паролей для веб-сайтов: большинство кодов содержат практически случайный набор цифр. Тем не менее, среди исходных данных присутствуют и простые комбинации, и дни рождения, — то есть, при некотором везении злоумышленник может просто угадать заветный код.
Отправной точкой исследования был набор 4-циферных последовательностей в паролях из базы RockYou (1.7 млн), и базы из 200 тысяч PIN-кодов от программы блокировки экрана iPhone (базу предоставил разработчик приложения Daniel Amitay). В графиках, построенных по этим данным, проступают интересные закономерности — даты, года, повторяющиеся цифры, и даже PIN-коды, заканчивающиеся на 69. На основе этих наблюдений учёные построили линейную регрессионную модель, которая оценивает популярность каждого PIN-кода в зависимости от 25 факторов, — например, является ли код датой в формате ДДММ, является ли он возрастающей последовательностью, и так далее. Этим общим условиям соответствуют 79% и 93% PIN-кодов в каждом из наборов.
В графиках, построенных по этим данным, проступают интересные закономерности — даты, года, повторяющиеся цифры, и даже PIN-коды, заканчивающиеся на 69. На основе этих наблюдений учёные построили линейную регрессионную модель, которая оценивает популярность каждого PIN-кода в зависимости от 25 факторов, — например, является ли код датой в формате ДДММ, является ли он возрастающей последовательностью, и так далее. Этим общим условиям соответствуют 79% и 93% PIN-кодов в каждом из наборов.
Итак, пользователи выбирают 4-циферные коды на основе всего нескольких простых факторов. Если бы так выбирались и банковские PIN-коды, 8-9% из них можно было бы угадать всего за три попытки! Но, конечно, к банковским кодам люди относятся гораздо внимательнее. Ввиду отсутствия сколько-нибудь большого набора настоящих банковских данных, исследователи опросили более 1300 человек, чтобы оценить, насколько реальные PIN-коды отличаются от уже рассмотренных. Учитывая специфику исследования, у респондентов спрашивали не о самих кодах, а только о их соответствии какому-либо из вышеназванных факторов (возрастание, формат ДДММ, и т. д.).
д.).
Оказалось, что люди действительно гораздо тщательнее выбирают банковские PIN-коды. Примерно четверть опрошенных используют случайный PIN, сгенерированный банком. Более трети выбирают свой PIN-код, используя старый номер телефона, номер студенческого билета, или другой набор цифр, который выглядит случайным. Согласно полученным результатам, 64% владельцев карт используют псевдослучайный PIN-код, — это гораздо больше, чем 23-27% в предыдущих экспериментах с не-банковскими кодами. Ещё 5% используют цифровой паттерн (например, 4545), а 9% предпочитают паттерн на клавиатуре (например, 2684). В целом, злоумышленник с шестью попытками (три с банкоматом и три с платёжным терминалом) имеет меньше 2% шансов угадать PIN-код чужой карты.
0000, 0101-0103, 0110, 0111, 0123, 0202, 0303, 0404, 0505, 0606, 0707, 0808, 0909, 1010, 1101-1103, 1110-1112, 1123, 1201-1203, 1210-1212, 1234, 1956-2015, 2222, 2229, 2580, 3333, 4444, 5252, 5683, 6666, 7465, 7667.
P.S. На практике, разумеется, злоумышленнику гораздо проще подсмотреть ваш PIN-код, чем угадывать его. Но и от подглядывания можно защититься — даже, казалось бы, в безвыходном положении:
Но и от подглядывания можно защититься — даже, казалось бы, в безвыходном положении:
Калькулятор ниже предназначен для генерации всех сочетаний из n по m элементов.
Число таких сочетаний, как можно рассчитать с помощью калькулятора Элементы комбинаторики. Перестановки, размещения, сочетания .
Описание алгоритма генерации под калькулятором.
Алгоритм
Комбинации генерируются в лексикографическом порядке. Алгоритм работает с порядковыми индексами элементов множества.
Рассмотрим алгоритм на примере.
Для простоты изложения рассмотрим множество из пяти элементов, индексы в котором начинаются с 1, а именно, 1 2 3 4 5.
Друзья! Раз уж есть у меня этот мертвый блокнот, использую-ка я его для того, чтобы задать вам задачку, над которой вчера билось три физика, два экономиста, один политеховский и один гуманитарий. Мы сломали себе весь мозг и у нас постоянно получаются разные результаты. Может быть, среди вас есть программисты и математические гении, к тому же, задачка вообще школьная и очень легкая, у нас просто не выводится формула. Потому что мы бросили занятия точными науками и вместо этого зачем-то пишем книги и рисуем картины. Простите.
Потому что мы бросили занятия точными науками и вместо этого зачем-то пишем книги и рисуем картины. Простите.
Мне выдали новую банковскую карточку и я, как водится, играючи угадала ее пин-код. Но не подряд. В смысле, допустим, пин-код был 8794, а я назвала 9748. То есть, я триумфально угадала все цифры , которое содержались в данном четырехзначном числе. Ну да, не само число , а просто его составляющие у гадала. Но цифры-то все верные! ПРИМЕЧАНИЕ — я действовала наугад, то есть, мне не надо было расставить уже известные числа в нужном п
количество комбинаций из 4 цифр
сколько комбинаций можно составить из 4 цифр
В разделе Естественные науки на вопрос Сколько можно составить четырехзначных комбинаций из четырех разных чисел? заданный автором сбросить лучший ответ это Задача не совсем определенная. Если требуется использовать только 4 цифры, то решается так: На первом месте (разряд тысяч) может стоять любая из 4 заданных цифр (если одна из цифр 0, то нужно уточнить, что подразумевается под определением «четырехзначных комбинаций». Если имеется в виду «чисел», то только 3 цифры, так как комбинации с ведущим нулем не являются числами, если же именно «комбинаций» и комбинации не рассматриваются как числа, то даже если одна из цифр заданного набора — 0, то все равно, на первом месте может стоять любая из 4 цифр) , на втором месте (разряд сотен) — любая из оставшихся 3 цифр, на третьем месте (разряд десятков) — любая из оставшихся 2 цифр, на четвертом месте — единственная оставшаяся цифра. Общее количество комбинаций 4*3*2*1=4!=24 (n! — называется n-факториал, и равно произведению 1*2*3*…*n). Если в набор заданных цифр входит 0, а сами комбинации рассматриваются как числа, то общее количество чисел 3*3*2*1=(n-1)*(n-1)!=18.
Если имеется в виду «чисел», то только 3 цифры, так как комбинации с ведущим нулем не являются числами, если же именно «комбинаций» и комбинации не рассматриваются как числа, то даже если одна из цифр заданного набора — 0, то все равно, на первом месте может стоять любая из 4 цифр) , на втором месте (разряд сотен) — любая из оставшихся 3 цифр, на третьем месте (разряд десятков) — любая из оставшихся 2 цифр, на четвертом месте — единственная оставшаяся цифра. Общее количество комбинаций 4*3*2*1=4!=24 (n! — называется n-факториал, и равно произведению 1*2*3*…*n). Если в набор заданных цифр входит 0, а сами комбинации рассматриваются как числа, то общее количество чисел 3*3*2*1=(n-1)*(n-1)!=18.
Ответ от 22 ответа[гуру]
Привет! Вот подборка тем с ответами на Ваш вопрос: Сколько можно составить четырехзначных комбинаций из четырех разных чисел?
Ответ от Игрок[новичек]
малыш всего комбинаций 24
Ответ от Европейский[активный]
С пинкодом проще в банк обратиться (или в сотовую компанию) с паспортом ))
Ответ от худосочие[новичек]
байты в Float по ModBUS крутим? )) (я — да — так сюда и попал)
Ответ от Workings[гуру]
4 х 3 х 2 х 1
Это равно 24
Ответ от Марина Мингалимова[новичек]
Здравствуйте уважаемые математики! ПОМОГИТЕ ПОЖАЛУЙСТА. Я забыла пин код там точно есть 1, 7, 0, одна из цифр повторяется дважды. Какие варианты есть. Два раза уже вводила код не верно. Осталась одна попытка. ввела 1170 не помогло, второй раз не помню. Помогите!
Я забыла пин код там точно есть 1, 7, 0, одна из цифр повторяется дважды. Какие варианты есть. Два раза уже вводила код не верно. Осталась одна попытка. ввела 1170 не помогло, второй раз не помню. Помогите!
Ответ от 2 ответа[гуру]
Привет! Вот еще темы с нужными ответами:
Размещение на Википедии
Посмотрите статью на википедии про Размещение
Ответить на вопрос:
Сколько комбинаций в пароле из 4 цифр?Ноль тоже учитывать.
0123,0223,0222, до фигища для пароля не используют только цифры)) ) попробуй на майле смени на 4 цифры во первых не надежно во вторых надо буквы добавлять английские
Десять тысяч (если учитывать «0000»)
Надо составить все возможные комбинации из чисел 1, 2, 3. Как подсчитать количество таких возможных комбинаций?
Смотри литературу по комбинаторике. Расчет такой: Пусть «_» будет местом под первую цифру, а «__» — вторую, «___» — третью. Тогда _ может изменяться на все три цифры; __ может изменяться на две цифры, чтобы не повторяться с первой; ___ может быть только одной из цифр. 3 = 27
3 = 27
ты пропустил 223 а вообще формула «количество_цифр»в степени»количество_цифр»(например, 2в степени2,3в степени 3 и т. д.)
А причем тут Программное обеспечение?
Нет не правильно, унего не та формула … Всего 216 Это перемножение всех комбинации для однотипынх чисел из трех таблиц
как решается 1,2,3 123, 321
Количество комбинаций из трех чисел
Вопрос — сколько существует трехзначных чисел с различными цифрами? Ответ: произвольный набор способов вычисляется по правилам произведения: k1*k2…*kN 10*10*10=1000 комбинаций
10*10*10 = 1000 результатов
999 комбинаций, по количеству трехзначных чисел, вроде так
Не 999 а правильно 1000 потому что еще есть комбинация 000
как узнать 3 цифры на обратной стороне банковской карточки
Сколько комбинаций возможно из 7 разных цифр?
оооо… с математикой у меня не очень , но точно скажу МНОГО!!
Берём вначале 1 место (им. в виду цифр) . Там могут стоять 9 цифр. На втором 10. На третьем — 10. На четвертом 10 и т. д. Для решения умножаем. 10 в 6 степени это 10 000 000 и умножаете на 9. Итого ответ: 90 000 000
На третьем — 10. На четвертом 10 и т. д. Для решения умножаем. 10 в 6 степени это 10 000 000 и умножаете на 9. Итого ответ: 90 000 000
7! вроде бы так(!-это знак в алгебре)
Как посчитать максимальное количество комбинаций из трех цифр?
Так умнож их друг в друга.
165 цветов с одним материалом дадут 165 вариантов. Со 160 материалами 165*160 вариантов. А эти варианты с 13 оттенками каждый дадут (165*160)*13 вариантов
Как найти 4-значную комбинацию?
Для каждого выбора первых двух цифр у вас есть 10 вариантов выбора третьей цифры. Таким образом, у вас есть 10x10x10 = 1000 вариантов для первых трех цифр. Наконец, у вас есть 10 вариантов для четвертой цифры, и, следовательно, есть 10x10x10x10 = 10 000 возможных 4-значных комбинации от 0 до 9.
Кроме того, сколько возможных комбинаций существует для 4-значного кода?
Существуют 10,000 возможных комбинаций что цифры 0-9 могут быть преобразованы в четырехзначный код.
Аналогично, сколько 4-значных чисел можно образовать из 10-ти цифр?
Но целые числа 999, начинающиеся с 1 и заканчивающиеся 999, имеют менее 4 цифр, поэтому желаемое число — 9999-999 или 9000 способы. 2. Есть 9 способов выбрать первую цифру (от 1 до 9), есть 10 способов выбрать 2-ю, 3-ю и 4-ю цифры, так что 9 10 10 10 = 9000 способов.
2. Есть 9 способов выбрать первую цифру (от 1 до 9), есть 10 способов выбрать 2-ю, 3-ю и 4-ю цифры, так что 9 10 10 10 = 9000 способов.
Здесь сколько комбинаций из 5 чисел?
Количество 5-значных комбинаций 10 5 =100,000. Итак, один больше 99,999 10. Вы можете обобщить это: количество комбинаций из N цифр равно XNUMX N.
Какой самый сложный 4-значный пароль? Все 10.000 одинаково сложно, если вы выберете один случайным образом. 1111 математически угадать не легче, чем 3861. Поскольку люди имеют тенденцию отдавать предпочтение шаблонам, выбор последовательности, которая не является широко используемым шаблоном, вероятно, лучше.
Какой самый распространенный четырехзначный код?… Почти 11% из 3.4 миллиона паролей являются
1234 .
Следующим по популярности 4-значным PIN-кодом является 1111, из которого состоит более 6% паролей.
| PIN-код | Частота | |
|---|---|---|
| #1 | 1234 | 10. 713% 713% |
| #2 | 1111 | 6.016% |
| #3 | 0000 | 1.881% |
| #4 | 1212 | 1.197% |
Исследователи из компании Data Genetics, занимающейся анализом данных, обнаружили, что три самых популярных комбинации:«1234», «1111» и «0000»— приходится около 20 процентов всех четырехзначных паролей.
Сколько четырехзначных чисел можно составить с помощью цифр 4, 0, 1, 2, 3, 4 и 5 повторений не допускаются?Итак, ответ: есть 720 4-значные целые числа, которые могут быть образованы цифрами 0–6 без повторов.
Сколько 4-значных чисел можно составить из 4-х цифр?Наконец, есть 4 варианта выбора последней цифры, поэтому количество возможных 4-значных чисел равно 4 4 4 = 256.
Сколько четырехзначных чисел можно составить из чисел 4 1 3 4 без повторения чисел?Общее количество чисел, которые могут быть образованы числами 1,2,3,4,5 (без повторяющихся цифрi) = 5 * 4 * 3 * 2 *! = 5! знак равно 120.
Если повторение разрешено, то количество перестановок 10 цифр равно 10,000,000,000.
Сколько комбинаций из 3 чисел можно составить из 5 чисел?Итак, 5 выбираем 3 = 10 возможных комбинаций.
Сколько всего комбинаций из 50 чисел?Команду любых 5 номеров можно выбрать из 50 номеров в (50C5) комбинации. Теперь мы должны выбрать 10 номеров из первоначального набора из 50 номеров, чтобы охватить все предыдущие «пятизначные комбинации».
Какой 4-значный код используется меньше всего?Наименее популярный четырехзначный PIN-код в мире: 8068.
Какой самый безопасный ПИН-код?«Статистически, 8068 — самый безопасный PIN-код », — говорит Тайлер Моффитт, старший аналитик по исследованию угроз в Webroot. «Другие хорошие числа — 7637, 6835 и 9629. Но это главным образом потому, что они не следуют никакому шаблону, не являются датой, или повторением чисел, или столбцом клавиатуры (2580)».
6174 известен как Постоянная Капрекара в честь индийского математика Д. Р. Капрекара. Это число отличается следующим правилом:… Расположите цифры по убыванию, а затем по возрастанию, чтобы получить два четырехзначных числа, добавляя при необходимости ведущие нули.
Какова вероятность угадать мой 4-значный PIN-код за 5 попыток?Исследования показывают, что воры могут угадать один из пяти PIN-кодов, попробовав всего три комбинации. Насколько легко вору будет угадать ваш четырехзначный PIN-код? Если бы ему пришлось угадывать случайным образом, его шансы получить правильное число были бы один в 10,000— или, если у него будет три попытки, одна из 3,333.
Какое число самое редкое?Количество 6174 действительно загадочное число. На первый взгляд это может показаться не таким очевидным. Но, как мы скоро увидим, любой, кто умеет вычитать, может раскрыть тайну, которая делает 6174 таким особенным.
Это одни из самых известных кодов в истории.
- Сдвиг Цезаря. Названный в честь Юлия Цезаря, который использовал его для кодирования своих военных сообщений, сдвиг Цезаря настолько прост, насколько это возможно. …
- Диск Альберти. …
- Площадь Виженера. …
- Надпись Шугборо. …
- Рукопись Войнича. …
- Иероглифы. …
- Машина Enigma. …
- Криптос.
«Статистически, 8068 — самый безопасный PIN-код», — говорит Тайлер Моффитт, старший аналитик по исследованию угроз в Webroot. «Другие хорошие числа — 7637, 6835 и 9629. Но это главным образом потому, что они не следуют никакому шаблону, не являются датой, или повторением чисел, или столбцом клавиатуры (2580)».
Какое число запомнить труднее всего?6174 известна как постоянная Капрекара в честь индийского математика Д. Р. Капрекара. Это число примечательно следующим правилом: возьмите любое четырехзначное число, используя как минимум две разные цифры (допускаются начальные нули).
Р. Капрекара. Это число примечательно следующим правилом: возьмите любое четырехзначное число, используя как минимум две разные цифры (допускаются начальные нули).
6*6*5*4*3 = 2160 — это сумма нет. цифры что может быть сформирован из 0,1,2,3,4,5,6 без повторения.
Сколько четырехзначных четных чисел можно составить из цифр 6 1 3 5 7 9 повторение цифр не допускается?Первоначальный ответ: Сколько 4-значных четных чисел можно образовать из цифр 1, 3, 5, 6, 8 и 9, если повторение цифр не допускается? ответ 120 четырехзначный целые числа.
Сколько четных 4-значных чисел можно составить с помощью 0 6?Итак, ответ: есть 720 4-значные целые числа, которые могут быть образованы цифрами 0–6 без повторов.
Как посчитать количество возможных вариантов
Содержание
- 1 Определение числа сочетаний
- 2 Найти сочетания из n по k
- 3 Видеоролик о сочетаниях
- 4 Полезные ссылки
- 5 Решебник по ТВ
- 6 Основная формула комбинаторики
- 7 Число размещений из n элементов по m
- 8 Число сочетаний из n элементов по m
- 9 Перестановки из n элементов
- 9.
 0.1 Элементы комбинаторики. Перестановки, размещения, сочетания
0.1 Элементы комбинаторики. Перестановки, размещения, сочетания
- 9.
Определение числа сочетаний
Пусть имеется $n$ различных объектов. Чтобы найти число сочетаний из $n$ объектов по $k$, будем выбирать комбинации из $m$ объектов все возможными способами, при этом будем обращать внимание на разный состав комбинаций, но не порядок (он тут не важен, в отличие от размещений).
Например, есть три объекта <1,2,3>, составляем сочетания по 2 объекта в каждом. Тогда выборки <1,2>и <2,1>- это одно и то же сочетание (так как комбинации отличаются лишь порядком). А всего различных сочетаний из 3 объектов по 2 будет три: <1,2>, <1,3>, <2,3>.
На картинке наглядно проиллюстрировано получение всех возможных сочетаний из 4 различных объектов по 2 (их будет 6, см. калькулятор сочетаний ниже, который даст формулу расчета).
Общая формула, которая позволяет найти число сочетаний из $n$ объектов по $k$ имеет вид:
Найти сочетания из n по k
Чтобы вычислить число сочетаний $C_n^k$ онлайн, используйте калькулятор ниже.
Видеоролик о сочетаниях
Не все понятно? Посмотрите наш видеообзор для формулы сочетаний: как использовать Excel для нахождения числа сочетаний, как решать типовые задачи и использовать онлайн-калькулятор.
Расчетный файл из видео можно бесплатно скачать
Полезные ссылки
Решебник по ТВ
Решебник с задачами по комбинаторике и теории вероятностей:
Комбинаторика — это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов. Основы комбинаторики очень важны для оценки вероятностей случайных событий, т.к. именно они позволяют подсчитать принципиальновозможное количество различных вариантов развития событий.
Основная формула комбинаторики
Пусть имеется k групп элементов, причем i-я группа состоит из ni элементов. Выберем по одному элементу из каждой группы. Тогда общее число N способов, которыми можно произвести такой выбор, определяется соотношением N=n1*n2*n3*. *nk.
Тогда общее число N способов, которыми можно произвести такой выбор, определяется соотношением N=n1*n2*n3*. *nk.
Пример 1. Поясним это правило на простом примере. Пусть имеется две группы элементов, причем первая группа состоит из n1 элементов, а вторая — из n2 элементов. Сколько различных пар элементов можно составить из этих двух групп, таким образом, чтобы в паре было по одному элементу от каждой группы? Допустим, мы взяли первый элемент из первой группы и, не меняя его, перебрали все возможные пары, меняя только элементы из второй группы. Таких пар для этого элемента можно составить n2. Затем мы берем второй элемент из первой группы и также составляем для него все возможные пары. Таких пар тоже будет n2. Так как в первой группе всего n1 элемент, всего возможных вариантов будет n1*n2.
Пример 2. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если цифры могут повторяться?
Решение: n1=6 (т. к. в качестве первой цифры можно взять любую цифру из 1, 2, 3, 4, 5, 6), n2=7 (т.к. в качестве второй цифры можно взять любую цифру из 0, 1, 2, 3, 4, 5, 6), n3=4 (т.к. в качестве третьей цифры можно взять любую цифру из 0, 2, 4, 6).
к. в качестве первой цифры можно взять любую цифру из 1, 2, 3, 4, 5, 6), n2=7 (т.к. в качестве второй цифры можно взять любую цифру из 0, 1, 2, 3, 4, 5, 6), n3=4 (т.к. в качестве третьей цифры можно взять любую цифру из 0, 2, 4, 6).
Итак, N=n1*n2*n3=6*7*4=168.
В том случае, когда все группы состоят из одинакового числа элементов, т.е. n1=n2=. nk=n можно считать, что каждый выбор производится из одной и той же группы, причем элемент после выбора снова возвращается в группу. Тогда число всех способов выбора равно n k . Такой способ выбора в комбинаторики носит название выборки с возвращением.
Пример 3. Сколько всех четырехзначных чисел можно составить из цифр 1, 5, 6, 7, 8?
Решение. Для каждого разряда четырехзначного числа имеется пять возможностей, значит N=5*5*5*5=5 4 =625.
Рассмотрим множество, состоящие из n элементов. Это множество в комбинаторике называется генеральной совокупностью.
Число размещений из n элементов по m
Определение 1. Размещением из n элементов по m в комбинаторике называется любой упорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.
Пример 4. Различными размещениями из трех элементов <1, 2, 3>по два будут наборы (1, 2), (2, 1), (1, 3), (3, 1), (2, 3),(3, 2). Размещения могут отличаться друг от друга как элементами, так и их порядком.
Число размещений в комбинаторике обозначается An m и вычисляется по формуле:
Замечание: n!=1*2*3*. *n (читается: «эн факториал»), кроме того полагают, что 0!=1.
Пример 5. Сколько существует двузначных чисел, в которых цифра десятков и цифра единиц различные и нечетные?
Решение: т.к. нечетных цифр пять, а именно 1, 3, 5, 7, 9, то эта задача сводится к выбору и размещению на две разные позиции двух из пяти различных цифр, т. е. указанных чисел будет:
е. указанных чисел будет:
Определение 2. Сочетанием из n элементов по m в комбинаторике называется любой неупорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.
Пример 6. Для множества <1, 2, 3>сочетаниями являются <1, 2>, <1, 3>, <2, 3>.
Число сочетаний из n элементов по m
Число сочетаний обозначается Cn m и вычисляется по формуле:
Пример 7. Сколькими способами читатель может выбрать две книжки из шести имеющихся?
Решение: Число способов равно числу сочетаний из шести книжек по две, т.е. равно:
Перестановки из n элементов
Определение 3. Перестановкой из n элементов называется любой упорядоченный набор этих элементов.
Пример 7a. Всевозможными перестановками множества, состоящего из трех элементов <1, 2, 3>являются: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), (3, 2, 1), (3, 1, 2).
Число различных перестановок из n элементов обозначается Pn и вычисляется по формуле Pn=n!.
Пример 8. Сколькими способами семь книг разных авторов можно расставить на полке в один ряд?
Решение:эта задача о числе перестановок семи разных книг. Имеется P7=7!=1*2*3*4*5*6*7=5040 способов осуществить расстановку книг.
Обсуждение. Мы видим, что число возможных комбинаций можно посчитать по разным правилам (перестановки, сочетания, размещения) причем результат получится различный, т.к. принцип подсчета и сами формулы отличаются. Внимательно посмотрев на определения, можно заметить, что результат зависит от нескольких факторов одновременно.
Во-первых, от того, из какого количества элементов мы можем комбинировать их наборы (насколько велика генеральная совокупность элементов).
Во-вторых, результат зависит от того, какой величины наборы элементов нам нужны.
И последнее, важно знать, является ли для нас существенным порядок элементов в наборе. Поясним последний фактор на следующем примере.
Поясним последний фактор на следующем примере.
Пример 9. На родительском собрании присутствует 20 человек. Сколько существует различных вариантов состава родительского комитета, если в него должны войти 5 человек?
Решение: В этом примере нас не интересует порядок фамилий в списке комитета. Если в результате в его составе окажутся одни и те же люди, то по смыслу для нас это один и тот же вариант. Поэтому мы можем воспользоваться формулой для подсчета числа сочетаний из 20 элементов по 5.
Иначе будут обстоять дела, если каждый член комитета изначально отвечает за определенное направление работы. Тогда при одном и том же списочном составе комитета, внутри него возможно 5! вариантов перестановок, которые имеют значение. Количество разных (и по составу, и по сфере ответственности) вариантов определяется в этом случае числом размещений из 20 элементов по 5.
Задачи для самопроверки
1. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если цифры могут повторяться?
Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если цифры могут повторяться?
2. Сколько существует пятизначных чисел, которые одинаково читаются слева направо и справа налево?
3. В классе десять предметов и пять уроков в день. Сколькими способами можно составить расписание на один день?
4. Сколькими способами можно выбрать 4 делегата на конференцию, если в группе 20 человек?
5. Сколькими способами можно разложить восемь различных писем по восьми различным конвертам, если в каждый конверт кладется только одно письмо?
6. Из трех математиков и десяти экономистов надо составить комиссию, состоящую из двух математиков и шести экономистов. Сколькими способами это можно сделать?
Подсчет числа перестановок, размещений и сочетаний.
Ниже калькулятор, подсчитывающий число перестановок, размещений и сочетаний. Под ним, как водится, ликбез, если кто подзабыл.
Элементы комбинаторики. Перестановки, размещения, сочетания
Итак, есть множество из n элементов.
Вариант упорядочивания данного множества называется перестановкой (permutation).
Например, есть множество, состоящее из 3 элементов — А, В, и С. Пример перестановки — СВА. Число всех перестановок из n элементов:
Пример: Для случая А, В, С число всех перестановок 3! = 6. Перестановки: АВС, АСВ, ВАС, ВСА, САВ, СВА
Если из множества n элементов выбирают m в определенном порядке, это называется размещением (arrangement).
Пример размещения из 3 по 2: АВ или ВА — это два разных размещения. Число всех размещений из n по m
Пример: Для случая А, В, С число всех размещений из 3 по 2 равно 3!/1! = 6. Размещения: АВ, ВА, АС, СА, ВС, СВ
Также бывают размещения с повторениями, как ясно из названия, элементы на определенных позициях могут повторяться.
Число всех размещений из n по m с повторениями:
Пример: Для случая А, В, С число всех размещений из 3 по 2 с повторениями равно 3*3 = 9. Размещения: AA, АВ, АС, ВА, BB, ВС, СА, СВ, CC
Если из множества n элементов выбирают m, и порядок не имеет значения, это называется сочетанием (combination).
Пример сочетания из 3 по 2: АВ. Число всех сочетаний из n по m
Пример: Для случая А, В, С число всех сочетаний из 3 по 2 равно 3!/(2!*1!) = 3. Сочетания: АВ, АС, СВ
Приведем до кучи формулу соотношения между перестановками, размещениями и сочетаниями:
Комбинации (комбинаторика) — выбор подмножества несмотря на порядок
Мы иногда делаем выбор из множества без учета порядка . Такой выбор называется комбинацией. Если вы играете в карты, например, вы знаете, что в большинстве ситуаций порядок, в котором вы держите карты, не имеет значения.Пример 1 Найдите все комбинации 3-х букв, взятых из набора в 5 букв {A, B, C, D, E}.
РешениеЭти комбинации следующие:
{A, B, C}, {A, B, D},
{A, B, E}, {A, C, D},
{A, C, E}, {A, D, E},
{B, C, D}, {B, C, E},
{B, D, E}, {C, D, E}.
Существует 10 комбинаций из трех букв, выбранных из пяти букв.
Когда мы находим все комбинации из набора с 5 объектами, если мы берем 3 объекта за один раз, мы находим все 3-элементные подмножества. В таком случае порядок объектов не рассматривается. Тогда,
В таком случае порядок объектов не рассматривается. Тогда,
{A, C, B} называется одним и тем же набором как и {A, B, C}.
Подмножество
Множество A есть подмножеством B, и означает что A это подмножество и/или совпадает с B если каждый элемент A является элементом B.
Элементы подмножество не упорядочены. Когда рассматриваются комбинации, не рассматривается порядок!
Комбинация
Комбинация, содержащая k объектов является подмножеством, состоящим из k объектов.
Мы хотим записать формулу для вычисления число сочетаний из n объектов, если взято к объектов одновременно.
Обозначения комбинации
Число сочетаний из n объектов, если взято к объектов одновременно, обозначается nCk.
Мы называем nCkчисло сочетаний. Мы хотим записать общую формулу для nCk для любого k ≤ n. Во-первых, это верно, что nCn = 1, потому что множество с n элементами имеет только одно подмножестов с n элементами, есть само множество. Во-вторых, nC1 = n, потому что множество с n элементами имеет только n подмножеств с 1 элементом в каждом. Наконец, nC0 = 1, потому что множество с n элементами имеет только одно подмножество с 0 элементами, то есть пустое множество ∅. Чтобы рассмотреть другие сочетания, давайте вернемся к примеру 1 и сравним число комбинаций с числом перестановок.
Во-вторых, nC1 = n, потому что множество с n элементами имеет только n подмножеств с 1 элементом в каждом. Наконец, nC0 = 1, потому что множество с n элементами имеет только одно подмножество с 0 элементами, то есть пустое множество ∅. Чтобы рассмотреть другие сочетания, давайте вернемся к примеру 1 и сравним число комбинаций с числом перестановок.
Обратите внимание, что каждая комбинация из 3-х элементов имеет 6, или 3!, перестановок.
3! • 5C3 = 60 = 5P3 = 5 • 4 • 3,
so
.
В общем, число сочетаний из k элементов, выбранных из n объектов , nCk раз перестановок этих элементов k!, должно быть равно числу перестановок n элементов по k элементов:
k!.nCk = nPk
nCk = nPk/k!
nCk = (1/k!).nPk
nCk =
Комбинации k объектов из n объектов
Общее число комбинаций к элементов из n объектов обозначается nCk, определяется
(1) nCk = ,
или
(2) nCk =
Другой тип обозначения для nCk это биноминальный коэффициент . Причина для такой терминологии будет понятна ниже.
Причина для такой терминологии будет понятна ниже.
Биноминальный коэффициент
Пример 2 Вычислите , используя формулы (1) и (2).
Решение
a) Согласно (1),
.
b) Согласно (2),
Имейте в виду, что не означает n/k.
Пример 3 Вычислите и .
Решение Мы используем формулу (1) для первого выражения и формулу (2) для второго. Тогда
,
используя (1), и
,
испоьлзуя формулу (2).
Обратите внимание, что
,
и используя результат примера 2 дает нам
.
Отсюда вытекает, что число 5-ти элементного подмножества из множества 7 элементов то же самое, что и число 2-элементного подмножества множества из 7 элементов. Когда 5 элементов выбираются из набора, они не включают в себя 2 элемента. Чтобы увидеть это, рассмотрим множество {A, B, C, D, E, F, G}:
В целом, мы имеем следующее. Этот результат дает альтернативный способ вычисления комбинации.
Подмножества размера k и размера
и nCk = nCn-k
Число подмножеств размера к множества с n объектами такое же, как и число подмножеств размера n — к. Число сочетаний k объектов из множества n объектов, такое же как и число сочетаний из n объектов, взятых одновременно.
Число сочетаний k объектов из множества n объектов, такое же как и число сочетаний из n объектов, взятых одновременно.
Теперь мы будем решать задачи с комбинациями.
Пример 4 Мичиганская лотерея. Проводящаяся в штате Мичиган два раза в неделю лотерея WINFALL имеет джек-пот, который, по крайней мере, равен 2 млн. долларов США. За один доллар игрок может зачеркнуть любые 6 чисел от 1 до 49. Если эти числа совпадают с теми, которые выпадают при проведении лотереи, игрок выигрывает. (Источник: Мичиганская лоттерея)
a) Сколько возможных комбинаций из 6-ти чисел в этой лотерее?
б) Предположим, что 10 минут у Вас идет на то, чтобы купить лотерейный билет и зачеркнуть 6 чисел. Сколько лотерейных билетов вы можете купить за 4 дня?
c) Сколько людей вы должны были бы нанять на 4 дня, чтобы купить билеты со всеми возможными комбинациями и быть уверенным, что вы выиграете?
Решение
a) Здесь нет порядка чисел. Вы зачеркиваете любые 6 чисел от 1 до 49. Тогда, число возможных комбинаций равно
Тогда, число возможных комбинаций равно
b) Во первых, мы посчитаем число минут в 4 -х днях:
4days • (24 ч/1 день).(60 мин/1 ч) = 5760 мин.
Тогда, вы могли бы купить 576 билетов за 4 дня.
c) Вам необходимо было бы нанять 13,983,816/576, или около 24278 человек чтобы купить билеты со всеми возможными комбинациями для гарантированного выигрыша. (С условием, что билеты можно покупать 24 часа в сутки.)
Пример 5 Сколько комитетов может быть сформировано из группы 5-ти губернаторов и 7-ми сенаторов, если каждый комитет состоит из 3-х губернаторов и 4-х сенаторов?
Решение Три губернатора могут быть избраны 5C3 путями и 4 сенатора могут быть избраны 7C4 путями. Если мы используем фундаментальный метод подсчета, то получим, что число возможных комитетов равно
Комбинаторика в информатике — Умскул Учебник
На этой странице вы узнаете- Как и для чего информатика использует целый раздел математики?
- Как работают безопасные пароли?
- Зачем считать, если можно не считать?
Что общего у автомобильного номера, карточной игры и расписания школьных занятий? Наука, их изучающая, — комбинаторика.
Комбинаторика — это раздел математики, который занимается решением задач, связанных с выбором и расположением элементов какого-либо множества по заданным параметрам.
| Как и для чего информатика использует целый раздел математики? Мы прибегаем к помощи комбинаторики, когда речь идет о данных как о наборе последовательностей, которые состоят из определенных элементов, расположенных в определенном порядке. |
Что может служить примерами таких данных?
- автомобильные номера — набор букв и цифр в определенном порядке;
- карточные игры — наборы карт, которые могут находиться у вас на руках;
- расписание занятий — варианты порядка проведения уроков.
Собственно, комбинаторика может помочь нам:
- узнать общее количество возможных автомобильных номеров;
- оценить шанс нахождения бубновой десятки на руках у вашего соперника;
- посмотреть на другие возможные варианты расписания, которое можно было бы составить и поудобнее.

Самое простое, с чем нам может помочь комбинаторика — это подсчет комбинаций элементов, от которого мы сможем отталкиваться дальше. Для удобства различают два основных вида расположения элементов в последовательностях:
- Размещения — элементы набора могут использоваться в последовательности определенной длины любое количество раз (в том числе ни разу).
Пример: кодовый замок. Никто не запретит нам использовать любую цифру любое количество раз или не использовать совсем.
- Перестановки — возможные последовательности образуются изменением порядка следования элементов друг за другом. Каждый элемент набора используется ровно 1 раз.
Пример: распределение 5 человек на дежурства в течение 5 дней. Было бы справедливо, если бы один человек дежурил только один раз, но вот в какой из дней — уже есть выбор.
Подсчет количества комбинацийКоличество комбинаций зависит от вариантов расстановки элементов. Чем больше символов может стоять на каждой позиции, тем больше будет комбинаций. Полное их количество рассчитывается как произведение количества возможных символов на каждой позиции.
Чем больше символов может стоять на каждой позиции, тем больше будет комбинаций. Полное их количество рассчитывается как произведение количества возможных символов на каждой позиции.
В размещениях каждый элемент может быть на любой позиции и может встретиться любое количество раз. То есть на каждой из k позиций может быть любой из n символов, тогда всего размещений может быть N=nk.
В перестановках последовательности отличаются только порядком следования элементов. Значит, каждый из элементов будет использоваться ровно 1 раз.
- На первой позиции может стоять любой из n символов;
- На второй — любой из оставшихся n − 1 символов;
- На третьей — любой из еще не использовавшихся, то есть n − 2;
- В конце концов — на самой последней позиции может использоваться только 1 оставшийся символ.
Поэтому количество комбинаций перестановок рассчитывается как факториал количества символов: произведение всех чисел от 1 до количества.
В остальных случаях — составляем выражение согласно требованиям:
- Считаем, какое количество символов может находиться на каждой позиции.
- Перемножаем полученные значения.
Например, мы выбираем пароль по следующим условиям:
- длина пароля — 6 символов;
- используются только символы “P”, “A”, “S”, “W”, “O”, “R”, “D”, “1”, “2”, “3”;
- “Р” должен быть на первом месте и больше не встречаться в пароле;
- “3” должен быть на последнем месте и больше не встречаться в пароле.
Определим, какие символы на каких позициях могут находиться:
Теперь можем составить выражение, чтобы найти количество всех возможных вариантов пароля. Перемножим количество возможных символов на каждой позиции:
N = 1 * 8 * 8 * 8 * 8 * 1 = 4096.
| Как работают безопасные пароли? При регистрации на сайтах нас просят придумать пароль. Некоторые сайты дают задачку со звездочкой: Доля разумности в этих требованиях присутствует. Использование сложного пароля создает множество возможных комбинаций знаков. Такой пароль не взломать простым перебором. Одна фирма по кибербезопасности посчитала, что пароль длиной 11 символов, состоящий только из цифр, взламывается меньше чем за секунду. При использовании цифр, букв в разных регистрах и спецсимволов, на взлом уйдет 34 года. Если символов будет не 11, а 12, то взлом сложного пароля займет около 3000 лет. |
| Зачем считать, если можно не считать? Для более сложных расчетов нам может понадобиться написать программу, которая будет производить определенные действия с перестановками или размещениями. |
Для облегчения работы с ними в Python существует модуль itertools, который содержит инструменты для их создания:
- permutations(набор символов) — создает перестановки переданного набора
from itertools import permutations
for i in permutations(“abc”):
print(i)
Вывод:
('a', 'b', 'c')
('a', 'c', 'b')
('b', 'a', 'c')
('b', 'c', 'a')
('c', 'a', 'b')
('c', 'b', 'a')
- product(набор символов, repeat = длина последовательности) — создает размещения заданной длины из заданного набора символов
from itertools import product
for i in product("abcd", repeat = 2):
print(i)
Вывод:
('a', 'a')
('a', 'b')
('a', 'c')
('a', 'd')
('b', 'a')
('b', 'b')
('b', 'c')
('b', 'd')
('c', 'a')
('c', 'b')
('c', 'c')
('c', 'd')
('d', 'a')
('d', 'b')
('d', 'c')
('d', 'd')
Все комбинации будут возвращены в виде списка символов.
Пример.
Допустим, мы будем составлять пароли длиной 6 символов из того же набора символов “P”, “A”, “S”, “W”, “O”, “R”, “D”, “1”, “2”, “3”, но с дополненными условиями:
- символ “Р” может использоваться в пароле любое количество раз, но обязательно должен быть на первом месте;
- символ “3” должен быть использован в пароле ровно 3 раза;
- в пароле не должно быть сочетания “123”.
Пошагово наш код должен состоять из следующих элементов:
- Для создания всех вариаций пароля будем использовать product модуля itertools, все пароли будем перебирать циклом for. Также предварительно создадим переменную-счетчик подходящих паролей.
- Нам нужно проверить все условия задачи. Элемент комбинации с индексом 0 равен “Р”, “3” встречается в ней ровно 3 раза, а также в списке символов комбинации не должно быть набора (“1”, “2”, “3”).
- При нахождении подходящего пароля будем увеличивать наш счетчик на 1, в конце программы выведем его значение на экран.

from itertools import product
cnt = 0
for i in product("PASWORD123", repeat = 6):
if i[0] == "P" and i.count("3") == 3 and ("1", "2", "3") not in i:
cnt += 1
print(cnt)
Вывод: 810Фактчек
- Размещения — наборы последовательностей определенной длины, состоящие из определенных символов, которые могут встречаться в последовательности сколько угодно раз. Количество размещений N зависит от длины последовательности k и количества символов n как N=nk.
- Перестановки — наборы последовательностей, отличающиеся только порядком следования символов друг за другом. Количество перестановок N зависит от количества символов в них n как N = n!.
- В общем виде количество комбинаций высчитывается как произведение количества возможных символов на каждой позиции.
- Для записи перестановок в Python используется permutations из модуля itertools, для записи размещений — product из того же модуля.

Задание 1.
Сколько будет размещений длинной 5, состоящих из набора “123”?
- 243
- 125
- 120
- 6
Задание 2.
Что такое перестановки?
- Комбинации, состоящие из символов определенного набора, разной длины.
- Комбинации, состоящие из символов определенного набора, одной длины.
- Комбинации, состоящие из символов определенного набора и отличающиеся только порядком следования символов друг за другом.
- Комбинации, состоящие из символов определенного набора и отличающиеся только длиной.
Задание 3.
Сколько может быть паролей длиной 4, состоящих из набора символов “ПАРОЛЬ”, в которых любой символ может использоваться сколько угодно раз, кроме “Ь” (используется только один раз и только на последнем месте)?
- 15
- 20
- 125
- 625
Задание 4.
Какая из записей на языке Python создаст размещения набора “ПАРОЛЬ” длинной 4?
- itertools(“ПАРОЛЬ”, repeat = 4)
- product(4, repeat = “ПАРОЛЬ”)
- permutations(“ПАРОЛЬ”, repeat = 4)
- product(“ПАРОЛЬ”, repeat = 4)
Ответы: 1. 4, что равно 10 000.
4, что равно 10 000.
Формула биномиального коэффициента — это общий способ расчета количества комбинаций. Здесь количество комбинаций k элементов из множества с n элементами равно n!/(k!*(n-k)!), в которых восклицательный знак указывает на факториал. Нужно углубиться? Мы вас прикрыли.
Формула количества комбинаций
Количество комбинаций, которые можно составить из четырех чисел, можно найти с помощью простого уравнения. Думайте о каждом числе как о человеке, а о каждом месте в комбинации — как о месте. На каждом месте может быть только один человек, и только 10 человек могут сидеть на одном месте. (Существует 10 чисел, потому что однозначные числа идут от 0 до 9..)
Фото любезно предоставлено: Оскар Вонг/Getty Images В любой заданной комбинации любое из 10 чисел может занять любое из четырех мест. Для первого места есть 10 вариантов в любой комбинации. При этом для второго места есть 10 вариантов в любой заданной комбинации. То же самое относится и к третьему и четвертому сиденьям. Чтобы найти общее количество вариантов для всех комбинаций, умножьте количество вариантов для первого места на количество вариантов для второго места, количество вариантов для третьего места и количество вариантов для четвертого места.
Чтобы найти общее количество вариантов для всех комбинаций, умножьте количество вариантов для первого места на количество вариантов для второго места, количество вариантов для третьего места и количество вариантов для четвертого места.
Другими словами, вам нужно умножить 10 х 10 х 10 х 10. В итоге вы обнаружите, что существует 10 000 возможных комбинаций четырех чисел.
Если вы скажете, что существует 10 000 возможных комбинаций с четырьмя числами, вы будете и правы, и неправы. То есть ответ 10 000 означает, что любой из 10 номеров может занимать любое из четырех мест. Следуя этой теории, одна из 10 000 комбинаций может быть 1111, 0000, 2222 или 3333. Давайте добавим гаечный ключ в уравнение.
Фото любезно предоставлено: Tetra Images/Getty ImagesВ реальном мире четырехзначные комбинации часто не имеют повторяющихся чисел. На самом деле, многие компании не позволяют людям устанавливать четырехзначные пароли, которые повторяют одно и то же число снова и снова. Итак, сколько существует возможных комбинаций четырехзначных чисел, в которых числа не повторяются?
Забудьте на мгновение о сиденьях и вернитесь к удобной математической формуле, называемой формулой биномиального коэффициента. Формула выглядит следующим образом:
Формула выглядит следующим образом:
- n!/(k! x (n-k)!)
Если вы не знали, каждый восклицательный знак представляет факториал. Хотя и название, и формула выглядят сложными, на практике все намного проще. Оказывается, концепция людей на местах будет полезна и для этого. «K» означает количество людей, которые могут сидеть на любом из мест, а «n» означает количество мест, на которых может сидеть любой из этих людей.
В случае попытки вычислить количество комбинации из четырех чисел, k=10 и n=4. Уравнение выглядит так:
- 4!/(10! x (4-10)!)
Не вдаваясь в факториалы, получаем:
- 10 x 9 x 8 x 7 = 5040
Вы заметили тенденцию? здесь? На первое место может сесть любой из 10 номеров. Теперь на второе место осталось всего девять номеров. Если выпадет еще один человек, останется только восемь человек, которые могут сесть на третье место, и, наконец, останется только семь номеров, которые могли бы сесть на четвертое место.
Видишь? Биномиальный коэффициент намного проще, чем кажется. С биномиальным коэффициентом любое число, выбранное для одного места, исключается из числа претендентов на другие места. Грубо говоря, это вдвое уменьшает общее количество комбинаций.
Что это говорит о пароле вашего смартфона
Давайте будем честными. Если вы действительно не увлекаетесь числами, вы, вероятно, искали не только для того, чтобы узнать количество возможных комбинаций из четырех цифр. На самом деле вы, вероятно, нашли свой путь в этот уголок Интернета, потому что пытаетесь установить четырехзначный пароль. И очень похвально, что вы думаете о своем коде доступа.
Фото любезно предоставлено: Attia-Fotograffie/Getty Images Четырехзначные пароли могут показаться довольно простыми, поскольку это одни из самых коротких паролей, которые вы, вероятно, будете использовать. Тем не менее, они также имеют тенденцию быть одними из самых важных. Вы можете использовать комбинации из четырех цифр, чтобы открыть телефон или быстрее войти в определенные приложения, но где еще вы используете комбинации из четырех цифр? Большинство банков просят клиентов выбрать четырехзначный PIN-код для авторизации транзакций и использования банкоматов.
Хакеры пользуются тем фактом, что комбинации из четырех цифр используются в качестве паролей для вещей, о защите которых вы, вероятно, заботитесь гораздо меньше, чем PIN-код вашей банковской карты. Люди далеко не так изобретательны, как должны были бы, когда дело доходит до паролей. Если кто-то сможет взломать код на вашем экране блокировки, вполне вероятно, что он также сможет авторизовать транзакцию по вашей дебетовой карте — в конце концов, очень высока вероятность того, что эти числа будут одинаковыми.
Банки тоже не решают проблему. Часто у людей есть 10 000 вариантов PIN-кода, потому что многие банки допускают повторение цифр. Если ваш банк немного лучше разбирается в безопасности, у вас будет только 5040 комбинаций на выбор. Многие люди используют комбинации из четырех цифр, которые либо повторяются, либо расположены в последовательном порядке. Например, очень часто выбирают 1234, а другие люди снова и снова комбинируют одно и то же число, например 1111 или 2222.
Не позволяйте вашим знаниям о биномиальном коэффициенте пропасть даром. Есть буквально тысячи комбинаций из четырех чисел, из которых вы можете выбирать. Не просто выберите год своего рождения или дату своего рождения. Ради всего хорошего, пожалуйста, не выбирайте 1234. Если вы хотите, чтобы чей-то любопытный взгляд не касался вашего смартфона, вам придется постараться намного больше. Выбирайте пароли с умом и сохраняйте свою личность (и информацию) в безопасности.
БОЛЬШЕ ОТ REFERENCE.COM
Создать перестановки [UDF]
Автор: Оскар Кронквист Последнее обновление статьи: 19 февраля 2019 г. Я заполняю номер, который я хочу, чтобы он автоматически переставлял числа и подробно перечислял, например, если я наберу 1234, и список будет:
1234, 1243, 1423, 4123, 1324, 1342, 1432, 4132, 3124, 3142, 3412, 4312, 2134, 2143, 2413, 4213, 2314, 2341, 2431, 4231, 3214, 3241, 3421, 4321.
Ответ:
Этот udf создает перестановки из текстовой строки. Вы также можете выбрать количество букв в каждой перестановке.
Вы также можете выбрать количество букв в каждой перестановке.
Формула массива в ячейке A3:A26:
=ListPermut(«1234»,4)
Как создать эту формулу массива
- Выберите диапазон ячеек A3:A26
- Введите приведенную выше формулу массива в строке формул
- Нажмите и удерживайте Ctrl + Shift
- Нажмите Enter один раз
- Отпустить все клавиши
Код VBA
Функция ListPermut (str As String, num As Integer)
«Перестановки без повторения
Dim c, r, p As Long
Dim rng() As Long, temp As Long, i As Long
Dim temp1 As Long, y() As Long, d As Long
Dim tmpOut(), tmpArr() как вариант
Dim j как целое число
Dim a Boolean
ReDim tmpArr (0)
ReDim tmpOut(0)
Для j = 1 To Len(str)
tmpArr (UBound (tmpArr)) = Mid (str, j, 1)
ReDim сохранить tmpArr (UBound (tmpArr) + 1)
Следующий j
ReDim Preserve tmpArr (UBound (tmpArr) - 1)
p = WorksheetFunction.Permut (Len (str), Len (str))
ReDim rng(1 To p, 1 To Len(str))
Для c = 1 To Len(str)
гнг(1, с) = с
Следующий с
Для r = 2 To p
Для c = 1 To num
tmpOut(UBound(tmpOut)) = tmpOut(UBound(tmpOut)) & tmpArr(rng(r - 1, c) - 1)
Следующий с
Если UBound(tmpOut) <> 0 Тогда
Если tmpOut(UBound(tmpOut)) = tmpOut(UBound(tmpOut) - 1) Тогда
tmpOut(UBound(tmpOut)) = ""
Еще
ReDim Preserve tmpOut(UBound(tmpOut) + 1)
Конец, если
Еще
ReDim Preserve tmpOut(UBound(tmpOut) + 1)
Конец, если
Для c = Len(str) To 1 Step -1
Если rng(r - 1, c - 1) < rng(r - 1, c) Тогда temp = c - 1 Выход For End If Next c For c = Len(str) To 1 Шаг -1 rng(r, c) = rng(r - 1, c) Далее c For c = Len(str) To 1 Шаг -1 Если rng(r - 1, c) > rng(r - 1, temp) Тогда
temp1 = rng(r - 1, темп)
rng(r, темп) = rng(r - 1, c)
rng(r, c) = temp1
ReDim y(Len(str) - temp)
я = 0
Для d = temp + 1 To Len(str)
y(i) = rng(r, d)
я = я + 1
Следующий д
я = 0
Для d = Len(str) To temp + 1 Step -1
rng(r, d) = y(i)
я = я + 1
Следующий д
Выход для
Конец, если
Следующий с
Если г = р Тогда
Для c = 1 To num
tmpOut(UBound(tmpOut)) = tmpOut(UBound(tmpOut)) & tmpArr(rng(r, c) - 1)
Следующий с
Если tmpOut(UBound(tmpOut)) = tmpOut(UBound(tmpOut) - 1) Тогда
ReDim Preserve tmpOut(UBound(tmpOut) - 1)
Конец, если
Конец, если
Следующий г
ListPermut = Application. Transpose(tmpOut)
Конечная функция
Transpose(tmpOut)
Конечная функция
Куда скопировать код vba?
Нажмите Alt+F11
Получить файл Excel
Chris_ListPermut_norep.xls
Категория перестановок
Вернуть все комбинации
Сегодня у меня есть две функции, которые я хотел бы продемонстрировать, они вычисляют все возможные комбинации из диапазона ячеек. Что […]
Найдите числа, наиболее близкие к сумме
Excelxor — отличный сайт для вдохновения, меня очень впечатлил этот пост Какие числа дают в сумме […]
Список перестановок без повторения [UDF]
В этом сообщении блога описывается, как создавать перестановки, повторение НЕ разрешено. Перестановки — это элементы, расположенные в заданном порядке, что означает […]
Чередование уникальных групп без повторения
В этой статье демонстрируется формула Что находится на этой странице Формула вопроса Формула массива Объяснение формулы массива Получить файл Excel […]
Перестановки с повторением и без повторения
О разнице между перестановками и комбинациями я говорил в прошлом посте, сегодня хочу поговорить о двух видах […]
Список перестановок с повторением [UDF]
В этом сообщении блога демонстрируется пользовательская функция (UDF), которая создает перестановки. Повторение разрешено. Пользовательская функция позволяет указать […]
Повторение разрешено. Пользовательская функция позволяет указать […]
Список всех перестановок с условием
Недавно я получил вопрос о перестановках, по сути, как найти каждую перестановку между 0 и 9 […]
Список перестановок с повторением и сколько выбрать из
В этой статье демонстрируется макрос, который позволяет создать список перестановок, повторения разрешены, на основе числа […]
Функции в этой статье
ListPermut
Более 1300 формул Excel
Категории Excel
Домашняя страница
Последние обновленные статьи.
Функции Excel
Более 300 функций Excel с подробной информацией, включая синтаксис, аргументы, возвращаемые значения и примеры для большинства функций, используемых в формулах Excel.
Формулы Excel
Более 1300 формул, организованных в подкатегории.
Таблицы Excel
Таблицы Excel упрощают работу с данными, добавляя или удаляя данные, фильтруя, суммируя, сортируя, улучшая читаемость с помощью форматирования ячеек, ссылок на ячейки, формул и многого другого.
Расширенный фильтр
Позволяет фильтровать данные на основе выбранного значения, заданного текста или других критериев. Он также позволяет фильтровать существующие данные или перемещать отфильтрованные значения в новое место.
Проверка данных
Позволяет контролировать, что пользователь может вводить в ячейку. Это позволяет вам указать условия и показать собственное сообщение, если введенные данные недействительны.
Раскрывающийся список
Позволяет пользователю работать более эффективно, отображая список, из которого пользователь может выбрать значение. Это позволяет вам контролировать то, что отображается в списке, и это быстрее, чем ввод в ячейку.
Именованные диапазоны
Позволяет назвать одну или несколько ячеек, это упрощает поиск ячеек с помощью поля Имя, чтение и понимание формул, содержащих имена вместо ссылок на ячейки.
Excel Solver
Excel Solver — это бесплатная надстройка, которая использует целевые ячейки, ограничения, основанные на формулах на листе, для выполнения анализа «что, если» и других проблем принятия решений, таких как перестановки и комбинации.
Диаграммы
Функция Excel, позволяющая визуализировать данные в виде графика.
Условное форматирование
Форматирование ячеек или значений ячеек на основе условия или критериев. Существует несколько встроенных инструментов условного форматирования, которые можно использовать, или использовать пользовательскую формулу условного форматирования.
Сводные таблицы
Позволяет быстро суммировать большие объемы данных в очень удобной для пользователя форме. Эта мощная функция Excel позволяет эффективно анализировать, упорядочивать и классифицировать важные данные.
VBA
VBA означает Visual Basic для приложений и представляет собой язык программирования, разработанный Microsoft. Он позволяет автоматизировать трудоемкие задачи и создавать пользовательские функции.
Макросы
Программа или подпрограмма, встроенная в VBA, которую может создать любой. Используйте средство записи макросов, чтобы быстро создавать собственные макросы VBA.
UDF
UDF расшифровывается как User Defined Functions и представляет собой настраиваемые функции, которые может создать каждый.
Архив
Список всех опубликованных статей.
Что такое перестановка 4 чисел? – Reviews Wiki
Если вы имели в виду «перестановки», то вы, вероятно, задаетесь вопросом «сколько различных способов я могу расположить четыре числа?» Ответ на этот вопрос (вы правильно поняли) 24 .
Сколько существует комбинаций из 4 предметов? т.е. есть 4 объекта, поэтому общее количество возможных комбинаций, в которых они могут быть расположены, равно 4! = 4 х 3 х 2 х 1 = 24 .
Сколько раз можно переставить 1234? Первоначальный ответ: Сколько различных комбинаций можно составить из чисел 1234? Итак, есть {1,2,3,4} этих 4 чисел. Таким образом, всего 64 пути .
Дополнительно Как рассчитать количество возможных комбинаций? Формула для комбинаций обычно n! / (r! ( n — r)!), где n — общее количество возможностей начать, а r — количество сделанных выборов. В нашем примере у нас есть 52 карты; следовательно, n = 52. Мы хотим выбрать 13 карт, значит, r = 13,9.0003
В нашем примере у нас есть 52 карты; следовательно, n = 52. Мы хотим выбрать 13 карт, значит, r = 13,9.0003
Сколькими способами можно расположить 123? Всего 7 комбинаций .
Как рассчитать перестановки?
Формула перестановки: P(n,r) = n! / (н-р)! Обобщенное выражение формулы: «Сколькими способами можно расположить r из множества n, если порядок имеет значение?» Перестановку также можно рассчитать вручную, выписав все возможные перестановки.
Сколько четырехзначных чисел можно составить из цифр 1234? Следовательно, в этом случае имеется 4 3 = 12 возможных двузначных чисел. Для третьей цифры есть только 2 варианта, а для последней цифры — один вариант. Таким образом, если вам не разрешено повторять цифру, количество возможных четырехзначных чисел, которые вы можете составить из 1,2,3,4, равно 4 3 2 1 = 9.0221 24 .
Сколько комбинаций из 4 цифр состоит из 10 номеров? 10 вариантов для первого циферблата, и для каждого из этих 10 вариантов для второго циферблата, и для каждого из этих 10 вариантов для третьего, и для каждого из этих 10 вариантов для четвертого. Итак, 10 x 10 x 10 x 10 = 90 221 10 000 комбинаций 90 222 , все возможные числа от 0000 до 9999.
Итак, 10 x 10 x 10 x 10 = 90 221 10 000 комбинаций 90 222 , все возможные числа от 0000 до 9999.
Как рассчитать аранжировку?
Помните, что комбинации — это способ подсчета общих исходов события, где порядок исходов не имеет значения. Для расчета комбинаций будем использовать формула nCr = n! / р! * (н-р)! , где n представляет количество элементов, а r представляет количество элементов, выбираемых за раз.
Также Как рассчитать перестановку вручную? Чтобы вычислить количество перестановок, возьмите количество возможностей для каждого события, а затем умножьте это число само на себя Х раз, где Х равно количеству событий в последовательности . Например, в четырехзначном PIN-коде каждая цифра может находиться в диапазоне от 0 до 9, что дает нам 10 вариантов для каждой цифры.
Как рассчитать перестановки и комбинации?
Какова формула перестановок и комбинаций? Формула для перестановок: nPr = n!/(n-r)! Формула для комбинаций: nCr = n!/[r! (n-r)!]
com/embed/tnF9f3zCCKI» frameborder=»0″ allowfullscreen=»allowfullscreen» data-original-w=»720″ data-original-h=»520″>Сколько 4-значных чисел можно составить, не превосходя 4321?
Следовательно, ответ 23 .
Сколько четырехзначных чисел можно составить?
Заполнить сотый разряд можно 4 способами, так как цифры не могут повторяться. Есть 3 возможных способа заполнить первое место четырехзначного числа. ∴ 60 четырехзначных чисел можно составить из цифр 2, 3, 5, 6, 7 и 9. Давайте обсудим концепции, связанные с перестановками и комбинациями и круговой перестановкой.
Сколько четырехзначных чисел можно составить, используя 7502? Ответ: 18 .
Сколько времени потребуется, чтобы угадать 4-значный PIN-код? потребуется до 112 часов , чтобы подобрать 4-значный PIN-код, потому что каждый ввод PIN-кода занимает 40 секунд.
Сколько перестановок в 10 числах?
Если разрешено повторение, то количество перестановок 10 цифр равно 10 000 000 000 . Если повторение не разрешено, то количество перестановок 10 цифр равно 3 628 800.
Если повторение не разрешено, то количество перестановок 10 цифр равно 3 628 800.
Сколько существует перестановок 4-х цифр без повторения выбора из десяти цифр от 0 до 9 включительно? Первоначальный ответ: Сколько 4-значных комбинаций возможно с использованием 0-9 без повторения каких-либо цифр? 5,040 .
Как вы делаете перестановки и комбинации?
Как вы решаете задачи на перестановки? Чтобы вычислить количество перестановок, 90 221 возьмите количество возможностей для каждого события, а затем умножьте это число на X, умноженное на 90 222, где X равно количеству событий в последовательности. Например, в четырехзначном PIN-коде каждая цифра может находиться в диапазоне от 0 до 9, что дает нам 10 вариантов для каждой цифры.
Как вы делаете перестановки на TI 84?
com/embed/TuowYf5LULw» frameborder=»0″ allowfullscreen=»allowfullscreen» data-original-w=»720″ data-original-h=»520″>Как делать перестановки без калькулятора?
Как рассчитать перестановки и комбинации в Excel?
Как вы делаете перестановки в Word?
- Microsoft Word > Лента > Вставка > Уравнение > Сценарий > Подстрочный индекс.

- Затем выберите нижнюю часть и снова нажмите Subscript.
- Вы получите трехуровневый индекс, как символ перестановки или комбинации.
- Затем введите свои числа или переменные.
Какие примеры перестановок можно привести? Перестановки — это различные способы организации набора элементов. Например: Различные способы, которыми алфавиты A, B и C могут быть сгруппированы вместе, взятые все одновременно, таковы: ABC, ACB, BCA, CBA, CAB, BAC . Обратите внимание, что ABC и CBA не совпадают, так как порядок расположения отличается.
|
Комбинаторный калькулятор, калькулятор комбинаций, вариаций, перестановок
Узнайте, сколькими способами можно выбрать k предметов из n предметов набора. С/без повторения, с/без порядка.
Расчет:
Ck(n)=(kn)=k!(n−k)!n! n=10 k=4 C4(10)=(410)=4!(10 −4)!10!=4⋅3⋅2⋅110⋅9⋅8⋅7=210
Количество комбинаций: 210
Вариантов
Разновидностью k-го класса из n элементов является упорядоченная группа k-элементов, образованная из множества n элементов. Элементы не повторяются и зависят от порядка элементов группы (поэтому расположены).
Элементы не повторяются и зависят от порядка элементов группы (поэтому расположены).
Количество вариаций можно легко подсчитать, используя комбинаторное правило произведения. Например, если у нас есть набор n = 5 чисел 1,2,3,4,5 и мы должны сделать вариации третьего класса, их V 3 (5) = 5 * 4 * 3 = 60. Vk(n)=n(n−1)(n−2)…(n−k+1)=(n−k)!n! н! мы называем факториалом числа n, которое является произведением первых n натуральных чисел. Обозначение с факториалом только более понятное, эквивалентное. Для вычислений вполне достаточно использовать процедуру, вытекающую из комбинаторного правила произведения.
Перестановки
Перестановка является синонимом вариации n-го класса n-элементов. Таким образом, это любая упорядоченная группа из n элементов, состоящая из n элементов. Элементы не повторяются и зависят от порядка элементов в группе.
P(n)=n(n−1)(n−2). ..1=n!
Типичный пример: у нас есть 4 книги, и сколькими способами мы можем расположить их рядом на полке?
..1=n!
Типичный пример: у нас есть 4 книги, и сколькими способами мы можем расположить их рядом на полке?
Вариации с повторением
Разновидностью k-го класса из n элементов является упорядоченная группа k-элементов, состоящая из множества n элементов, причем элементы могут повторяться и зависят от их порядка. Типичным примером является образование чисел из чисел 2,3,4,5 и нахождение их количества. Рассчитываем их количество по комбинаторному правилу произведения: Vk′(n)=n⋅n⋅n⋅n…n=nk
Перестановки с повторением
Повторяющаяся перестановка представляет собой упорядоченную группу k-элементов из n-элементов, при этом некоторые элементы повторяются в группе. Повторение некоторых (или всех в группе) уменьшает количество таких повторяющихся перестановок.
Pk1k2k3…km′(n)=k1!k2!k3!…km!n!
Типичный пример — узнать, сколько семизначных чисел образовано из чисел 2,2,2, 6,6,6,6.
Комбинации
Комбинация k-го класса из n элементов представляет собой неупорядоченную группу k-элементов, образованную из множества n элементов. Элементы не повторяются, и порядок элементов группы не имеет значения. В математике неупорядоченные группы называются множествами и подмножествами. Их количество является комбинационным числом и рассчитывается следующим образом: Ck(n)=(kn)=k!(n−k)!n! Типичный пример комбинаций: у нас 15 учеников, и мы должны выбрать троих. Сколько их будет?
Комбинации с повтором
Здесь мы выбираем k групп элементов из n элементов, независимо от порядка, и элементы могут повторяться. k логически больше n (иначе мы получили бы обычные комбинации).
Их счет:
Ck′(n)=(kn+k−1)=k!(n−1)!(n+k−1)!
Пояснение к формуле — количество комбинаций с повторением равно количеству расположений n − 1 разделителей на n-1 + k местах. Типичный пример: мы идем в магазин, чтобы купить 6 шоколадок. Предлагают всего 3 вида. Сколько вариантов у нас есть?
к = 6, п = 3.
Типичный пример: мы идем в магазин, чтобы купить 6 шоколадок. Предлагают всего 3 вида. Сколько вариантов у нас есть?
к = 6, п = 3.
Основы комбинаторики в текстовых задачах
- Раздача 5016
У вас есть тест с восемью вопросами, где вы можете выбрать один из 3 ответов на каждый вопрос, и всегда один ответ правильный. Вероятность того, что мы ответим правильно на 5 или 6 вопросов при случайном заполнении (то есть мы все угадаем ответы), равна ……. Th - Вероятность 3080
В словацком языке существует восемь стилей выпускных тем. Министр образования рисует 4 из них. Какова вероятность того, что он выберет хотя бы одну из пары? - Экзамен
В классе 25 учеников. Сколькими способами можно выбрать 5 студентов для экзамена? - Трёхзначное число 2
Найдите количество всех трёхзначных натуральных чисел, которые можно составить из цифр 1,2,3,4, и которые при соблюдении одного и того же времени имеют следующие условия: на одной позиции стоит одна из чисел 1,3,4, на месте сотен 4 или 2.
- Семь
Семь друзей соглашаются отправить всем праздничную открытку. Сколько открыток было отправлено? - Парковка 72644
Сколькими способами десять автомобилей могут припарковаться рядом на стоянке? - Пик
В гору ведут 2 дорожки и один подъемник. а) Сколько существует вариантов туда и обратно? б) Сколько существует вариантов добраться туда и обратно по разным путям? c) Сколько существует вариантов туда и обратно, чтобы мы прошли хотя бы один подъемник? - Джекпот
Сколько раз я должен разыграть этот джекпот, чтобы выиграть? Джекпот из семи игр с (1 X 2), то есть победа дома или на выезде. - Процент 67364
Составьте все четырехзначные числа, в которых цифры 0, 2, 5 и 9 не повторяются. А) Сколько таких чисел? Вы решаете, используя древовидную диаграмму. Б) Какой процент из них четные? - Студенты 34
Студенты были опрошены в рамках статистического проекта, чтобы определить, имеют ли молодые люди больше шансов иметь татуировки. Результаты перечислены в двусторонней таблице ниже: возраст; Минимум одна татуировка; Нет татуировки; Всего по ряду Возраст 18–29; 165 ; 342; 507 Возраст 30–9 лет0024
Результаты перечислены в двусторонней таблице ниже: возраст; Минимум одна татуировка; Нет татуировки; Всего по ряду Возраст 18–29; 165 ; 342; 507 Возраст 30–9 лет0024 - Вероятность — билеты
Какова вероятность, что если у вас есть 25 билетов из 5000, вы не выиграете первый (один) приз? - Все кратные
Набор A представляет собой набор всех кратных 2, а набор B представляет собой набор всех кратных 3. Если P (A)=0,6 и P (B)=0,3. Найдите P (АУБ). - Хоккеисты
После того, как мы покатались, пятеро хоккеистов садятся. Какова вероятность того, что два лучших бомбардира этого экипажа сядут рядом? - Равносторонний 75284
Даны 6 отрезков длиной 3 см, 4 см, 5 см, 7 см, 8 см и 9 см. Сколько равносторонних треугольников можно составить из них? Перечислите все варианты. - Комби-треугольник
На каждой стороне квадрата отмечены 10 различных точек вне вершин квадрата. Сколько треугольников можно построить из этого набора точек, где каждая вершина треугольника лежит на другой стороне квадрата? - Книжный магазин
Книжный магазин Mabini (MBS) снижает цены на книги по математике в целях продвижения. В магазине есть 6 книг по алгебре, 6 книг по геометрии и 5 книг по статистике, которые нужно расставить на полке. Книги одного типа должны располагаться рядом друг с другом. Сколько ж
В магазине есть 6 книг по алгебре, 6 книг по геометрии и 5 книг по статистике, которые нужно расставить на полке. Книги одного типа должны располагаться рядом друг с другом. Сколько ж
more math problems »
- decimals
- fractions
- triangle ΔABC
- percentage %
- permille ‰
- prime factors
- complex numbers
- LCM
- GCD
- LCD
- combinatorics
- equations
- статистика
- … все математические калькуляторы
Анализ PIN-кода
Мой хороший друг, Ян, недавно прислал мне интернет-анекдот. Заголовок был примерно такой: «Утекли ПИН-коды всех кредитных карт в мире» В теле сообщения просто указано 0000 0001 0002 0003 0004 … |
Сообщения Яна заставили меня посмеяться. Затем, позже в тот же день, я прочитал этот мультфильм XKCD. Слияние этих двух юмористических тем стало основой для этой статьи.
Слияние этих двух юмористических тем стало основой для этой статьи.
| ||
Мне нравится работа Рэндалла. Мой фаворит, на сегодняшний день, это. У меня есть подписанная копия на стене моего офиса. Как и многие его творения, этот мультфильм отлично подходит для раздвоения читателей; люди читают его, а затем либо улыбаются и посмеиваются, либо тупо смотрят на него, а затем «А? Я не понимаю!» комментарий. Затем вы объясняете это и получаете ответ «Дааааааа… нет, я все еще не понимаю!» Эзотерический юмор в действии. Вы тоже можете быть крутым и купить его подписанные работы. |
|
Какой ПИН-код встречается реже всего?
Существует 10 000 возможных комбинаций цифр от 0 до 9 для формирования 4-значного пин-кода. Какой из этих десяти тысяч кодов используется реже всего? Какой из этих пин-кодов наименее предсказуем? Какой из этих пин-кодов самый предсказуемый? Если бы вам дали задание попытаться взломать случайную кредитную карту, многократно вводя PIN-коды, в каком порядке вы должны попытаться угадать, чтобы максимизировать свои шансы выбрать правильный номер в кратчайшие сроки? |
Если бы вам пришлось высказать предположение о том, какой четырехзначный PIN-код используется реже всего, что бы вы предположили?
Это косвенно относится к мультфильму XKCD. В мультфильме Рэндалла план преступника имел неприятные последствия, потому что выбранный им номерной знак был настолько уникальным, что очень запомнился. Какой номерной знак наименее запоминающийся? Спросите у любого знакомого шпиона (хихикая), как лучше всего слиться с толпой. Их ответ будет не выделяться, казаться «нормальным» и ничем не выделяться.
В мультфильме Рэндалла план преступника имел неприятные последствия, потому что выбранный им номерной знак был настолько уникальным, что очень запомнился. Какой номерной знак наименее запоминающийся? Спросите у любого знакомого шпиона (хихикая), как лучше всего слиться с толпой. Их ответ будет не выделяться, казаться «нормальным» и ничем не выделяться.
Известно, что люди плохо генерируют случайные пароли. Я надеюсь, что эта статья напугает вас и заставит быть немного осторожнее при выборе следующего PIN-кода. Хотите знать, каким может быть наименее часто используемый PIN-код? Как насчет самого популярного? Читать дальше… |
Эта статья , а не предназначена для использования в качестве библии хакера или в качестве утилиты, ресурса или инструмента, помогающего потенциальным ворам совершать гнусные действия. Я буду раскрывать только те данные, которые достаточны для обоснования моей точки зрения, и постараюсь не приводить конкретных данных, кроме очевидных примеров. Я не хочу быть пособником для скрипт-кидди. Пожалуйста, не пишите мне по электронной почте с просьбой предоставить базу данных, которую я использовал; если вы это сделаете, вы будете тратить свое время, так как я не собираюсь отвечать. Я не собираюсь продавать, дарить или разглашать исходные данные — не спрашивайте!
Я не хочу быть пособником для скрипт-кидди. Пожалуйста, не пишите мне по электронной почте с просьбой предоставить базу данных, которую я использовал; если вы это сделаете, вы будете тратить свое время, так как я не собираюсь отвечать. Я не собираюсь продавать, дарить или разглашать исходные данные — не спрашивайте!
Источник
Очевидно, у меня нет доступа к базе данных PIN-кодов кредитных карт. Вместо этого я собираюсь использовать прокси. Я собираюсь использовать данные, собранные из опубликованных/выставленных/обнаруженных таблиц паролей и нарушений безопасности.
Soap Box — раскрытие базы данных паролей
За прошедшие годы было множество нарушений безопасности таблицы паролей: некоторые очень громкие, некоторые низкопрофильные, но все они досадные (и многие чрезвычайно дорогие; как в виде прямых штрафов, так и косвенной потери бизнеса из-за подрыва доверия и репутации). Обмануть меня один раз, ну нет, даже это неприемлемо, но обмануть меня дважды… Я пойду еще дальше: Любой разработчик , который хранит таблицу паролей своей базы данных в открытом виде, должен быть настолько подавлен этим отсутствием безопасности, что они не должны спать по ночам, пока они не исправят это. Если вы работаете в компании и знаете, что ваша база данных клиентов «защищен» такой легкой охраной, а затем бегите, не идите, в офис вашего генерального директора / президента, стучите в дверь и настаивайте, чтобы он (она) дал поручение решить этот вопрос с крайним предубеждением. Не уходите, пока не получите утвердительный ответ. Барсук, барсук, потом снова барсук. Сделайте себя пресловутой занозой в их боку. |
Я не пытаюсь продавать здесь свои услуги в качестве консультанта (хотя, если вам интересно, мои ставки очень разумны по сравнению со стоимостью юридической защиты, потенциальными санкциями FTC, коллективными исками, негативной реакцией акционеров, штрафами, потерями репутации и бизнеса…) В отрасли есть множество экспертов по безопасности, которые могут вам помочь (если вам нужна помощь в их фильтрации и у вас нет рефералов, лучше всего начать с кого-то, у кого есть квалификация CISSP).
Итог Безопасность усиливается за счет уровней, и простое применение шифрования к таблице вашей базы данных может помочь защитить данные вашего клиента, если эта таблица будет раскрыта. Он не защищает от всех возможных атак, но не делает ничего, кроме хороших вещей. Какая возможная причина хранить вещи в открытом тексте?
Назад к данным
Путем объединения открытых баз данных паролей, с которыми я столкнулся, и фильтрации результатов только для тех строк, которые содержат ровно четыре цифры [0-9] вывод представляет собой базу данных всех четырехзначных комбинаций символов, которые люди использовали в качестве паролей своих учетных записей. |
Учитывая, что у пользователей есть свободный выбор пароля, если пользователи выбирают четырехзначный пароль для своей учетной записи в Интернете, несложно использовать его в качестве прокси для четырехзначных PIN-кодов.
Мне удалось найти почти 3,4 миллиона четырехзначных паролей. Каждое из 10 000 комбинаций цифр от 0000 до 9999 были представлены в наборе данных.
Каждое из 10 000 комбинаций цифр от 0000 до 9999 были представлены в наборе данных.
Самый популярный пароль — 1234… |
… IT | … IT . Совершенно ошеломляет отсутствием воображения … |
… почти 11% из 3,4 миллионов паролей 1234 !!! |
Следующим по популярности 4-значным PIN-кодом является 1111 , который используется более чем в 6% паролей. На третьем месте 0000 с почти 2%. Таблица 20 первых найденных паролей показана справа. Ошеломляющие 26,83% всех паролей можно угадать, попробовав эти 20 комбинаций! (Статистически, с 10 000 возможных комбинаций, если бы пароли были равномерно распределены случайным образом, мы ожидали бы, что эти двадцать паролей будут составлять всего 0,2% от общего числа, а не 26,83% встречающихся) Если присмотреться к нескольким верхним записям, все обычные подозреваемые присутствуют: 1111, 2222, 3333… 9999, а также 1212 и (хихикает) 6969. Неудивительно, что такие шаблоны, как 1122 и 1313 , встречаются в самом верху списка, а также 4321 или 1010 . 2001 появляется под номером 19. 1984 следует за ним на 26-й позиции, и поклонникам Джеймса Бонда может быть интересно узнать, что 0007 находится между ними на 23-й позиции (другой вариант 0070 следует ненамного дальше, на 28-й позиции). |
|
Первый «загадочный» пароль, с которым я столкнулся, был 2580 в позиции № 22. Каково значение этих цифр? Почему так много людей должны выбрать этот код, чтобы он появился так высоко в списке?
Потом я понял, что 2580 – это прямо посередине телефонной клавиатуры! | ||
(Интересно, что это очень убедительное доказательство, подтверждающее гипотезу о том, что 4-значный список паролей является отличным прокси для базы данных PIN-кодов. | ||
(Еще одна интересная мелочь заключается в том, что люди, кажется, предпочитают четные числа нечетным, а такие коды, как 2468 , встречаются выше, чем эквивалент нечетного числа, такой как 1357 ).
Как отмечалось выше, в таблицах частот преобладают наиболее популярные пароли. Самый популярный PIN-код 1234 популярнее, чем самых низких 4200 кодов вместе взятых!
Верно, вы можете взломать более 10% всех кодов с одной попытки! Расширяя это, вы можете получить 20%, используя всего пять номеров!
Ниже приведен кумулятивный график частоты:
По статистике, треть всех кодов можно угадать, попробовав всего 61 комбинацию!
Порог совокупной вероятности в 50% достигается всего за 426 кодов (гораздо меньше 5000, которые можно было бы предсказать при случайном равномерном распределении). Параноик еще?
Параноик еще?
Итак, мы исследовали наиболее часто используемые PIN-коды и обнаружили, что они обычно предсказуемы и легко запоминаются, давайте на секунду обратимся к концу стопки. Какие ПИН-коды наименее «интересны» (наименее используемые)? В моем наборе данных ответ – 8068, всего 25 вхождений на 3,4 миллиона (это соответствует 0,000744 %, что намного меньше, чем можно было бы предсказать при случайном распределении, и на пять порядков отстает от самого популярного варианта). Справа приведены двадцать наименее популярных 4-значных паролей.
|
|
Многие часто встречающиеся PIN-коды можно интерпретировать как годы, например . 1967 1956 1937 … Похоже, что многие люди используют год рождения (или, возможно, годовщину) в качестве своего PIN-кода. Это, безусловно, поможет им запомнить свой код, но значительно повысит его предсказуемость.
Просто посмотрите на статистику: Каждому 19?? комбинацию можно найти в верхней пятой части набора данных!
Ниже приведен график этого в графическом формате. На этой диаграмме каждая желтая линия представляет собой PIN-код, начинающийся с 19??
На этой диаграмме каждая желтая линия представляет собой PIN-код, начинающийся с 19??
Если бы все пароли были распределены равномерно, не должно быть существенной разницы между частотой появления , например , 1972 и любого другого PIN-кода, оканчивающегося на семьдесят два ??72 . Однако, как мы увидим, это совсем не так.
1972 встречается в порядковом номере #76 (с частотой 0,099363%). Вот гистограмма для всех случаев ??72 вероятностей.
Вы можете ясно видеть всплеск в 1972 году (с меньшими пиками в 7272 и 1472 )
Если вы вычислите отношение пика 1972 к среднему значению всех других ??72 PIN, вы получите отношение 22: 1
PINS, начинающиеся с 19?? происходят гораздо чаще. Конечно, это не только 1972 год. Вот график отношения 19на не-19 для всех сотен комбинаций. По оси x отложены все комбинации двух последних цифр XX, и для каждой из них рассчитано отношение 19XX к среднему значению всех остальных вхождений ??XX. Вот диаграмма:
Это довольно хорошее приближение для демографической диаграммы! (обозначается красной пунктирной линией тренда), что, вероятно, позволит объективно оценить возраст (годы рождения) людей, использующих различные веб-сайты. (Конечно, хакеры инвертируют эту стратегию и используют возраст цели, чтобы попытаться предоставить информацию для угадывания PIN-кода пользователя. Глядя на этот график, это может дать им до 9 баллов.0063 40x преимущество!)
(Конечно, хакеры инвертируют эту стратегию и используют возраст цели, чтобы попытаться предоставить информацию для угадывания PIN-кода пользователя. Глядя на этот график, это может дать им до 9 баллов.0063 40x преимущество!)
Почти все коэффициенты выше 1.0. Заметными исключениями являются ??34 и ??00 (что легко объяснить, учитывая огромную популярность 1234 и 0000 карликовых 1934 и 1900 соответственно). Точно так же 33 44 55 66 … ниже, чем ожидалось, поскольку четверные коды, такие как 3333, маскируют даже повышение 1933.
На графике также есть всплески, соответствующие популярным PINS 1919, 1984 и 1999
Мне нравятся красивые способы графической визуализации данных. Картинки действительно рисуют тысячи слов. Еще один интересный способ визуализации данных ПИН-кода — это сетка распределения. На этой тепловой карте по оси X отложены две левые цифры от [00] до [99], а по оси Y — две правые цифры от [00] до [99]. Цвет используется для представления частоты. Возникновения с более высокой частотой — от желтого до белого, а проявления с более низкой частотой — от красного, от темно-красного до черного. Примечание для компьютерщиков Масштабирование является логарифмическим. |
На этот сюжет можно смотреть целый день!
Яркая линия на ведущей диагонали показывает повторяющиеся двустишия, которые люди любят использовать для своих PIN-кодов 0000 0101 0202 … 5454 5555 5656 … 9898 9999 .
Каждая одиннадцатая точка на ведущей диагонали ярче, что соответствует четверным числам напр. 4444 5555 . Вот версия в большем масштабе:
Интересное
Из этой карты можно узнать много интересного. Вот только парочка:
Во-первых, это интересные гармоники затенения (здесь их легче увидеть на графике в оттенках серого). Вы можете разобрать «сетку» на графике. Более светлые области, соответствующие парам чисел, которые находятся близко друг к другу. По какой-то причине люди не любят выбирать пары чисел, между которыми есть большие числовые промежутки. Такие комбинации, как 45 и 67 , встречаются гораздо чаще, чем такие комбинации, как 29.и 37 | ||
Здесь мы видим строку, соответствующую 19XX . Интенсивность точек относится к графику, который мы построили ранее Существует большое количество кодов, начинающихся с 19, особенно ближе к старшему концу. | ||
Имеется сильное смещение в сторону нижнего левого квадранта. Люди любят начинать свой PIN-код с 0, а тем более с цифры 1. На диаграмме справа показана относительная частота первой цифры четырехзначного пин-кода. Как видите, преобладает цифра 1 (и не только из-за феномена 19XX ). | ||
Маленькие яркие точки усеивают график в местах, соответствующих числовым рядам (как по возрастанию, так и по убыванию), таким как 2345, 4321 и 5678. Я выделил только пару на графике слева. Также видны переходы с шагом в два например. 2468 | ||
Очень распространены повторяющиеся пары пар чисел, например XYXY Сотни наборов повторяющихся пар двустиший составляют ошеломляющие 17,8% всех наблюдаемых PIN-кодов. |
Целью этой публикации было исследование закономерностей и частотности четырехзначных PIN-кодов. Однако в базе данных, которую я собрал, также есть полностью цифровой пароль разной длины. На них тоже стоит взглянуть.
На них тоже стоит взглянуть.
Я нашел около 7 миллионов паролей, состоящих исключительно из цифр. Примерно половина из них были четырехзначными кодами, которые мы только что рассмотрели.
Шестизначные коды являются следующей по популярности длиной, за ней следуют восьмизначные коды.
Я надеюсь, надеюсь, что люди, которые имеют пароли из девяти цифр, имеют , а не , используя свои номера социального страхования!
Ниже приведены 20 самых популярных паролей различной длины, а также их доля в пространстве имен одинакового размера.
| # | 5 | 6 | 7 | 8 | 9 | 10 | PSWD | % | PSWD | % | PSWD | % | PSWD | % | PSWD | % | PSWD | % |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| #1 | 12345 | 22. 802% 802% | 123456 | 11.684% | 1234567 | 3.440% | 12345678 | 11.825% | 123456789 | 35.259% | 1234567890 | 20.431% |
| #2 | 11111 | 4.484% | 123123 | 1.370% | 7777777 | 1.721% | 11111111 | 1.326% | 987654321 | 3.661% | 0123456789 | 2.323% |
| #3 | 55555 | 1.769% | 111111 | 1.296% | 1111111 | 0. 637% 637% | 88888888 | 0.959% | 123123123 | 1.587% | 0987654321 | 2.271% |
| #4 | 00000 | 1.258% | 121212 | 0.623% | 8675309 | 0.465% | 87654321 | 0.815% | 789456123 | 1.183% | 1111111111 | 2.087% |
| #5 | 54321 | 1.196% | 123321 | 0.591% | 1234321 | 0.220% | 00000000 | 0.675% | 999999999 | 0. 825% 825% | 1029384756 | 1.293% |
| #6 | 13579 | 1.112% | 666666 | 0.577% | 0000000 | 0.188% | 12341234 | 0.569% | 147258369 | 0.591% | 9876543210 | 0.971% |
| #7 | 77777 | 0.618% | 000000 | 0.521% | 4830033 | 0.158% | 69696969 | 0.348% | 741852963 | 0.455% | 0000000000 | 0.942% |
| #8 | 22222 | 0. 454% 454% | 654321 | 0.506% | 7654321 | 0.154% | 12121212 | 0.320% | 111111111 | 0.425% | 1357924680 | 0.479% |
| #9 | 12321 | 0.412% | 696969 | 0.454% | 5201314 | 0.128% | 11223344 | 0.293% | 123454321 | 0.413 % | 1122334455 | 0.441% |
| #10 | 99999 | 0.397% | 112233 | 0.417% | 0123456 | 0. 124% 124% | 12344321 | 0.275% | 123654789 | 0.378% | 1234512345 | 0.402% |
| #11 | 33333 | 0.338% | 159753 | 0.283% | 2848048 | 0.124% | 77777777 | 0.262% | 147852369 | 0.356% | 1234554321 | 0.380% |
| #12 | 00700 | 0.261% | 292513 | 0.250% | 7005425 | 0.120% | 99999999 | 0.223% | 111222333 | 0. 304% 304% | 5555555555 | 0.259% |
| #13 | 0.244% | 131313 | 0.235% | 1080413 | 0.111% | 22222222 | 0.219% | 963852741 | 0.255% | 1212121212 | 0.244% | |
| #14 | 88888 | 0.217% | 123654 | 0.228% | 7895123 | 0.107% | 55555555 | 0.205% | 321654987 | 0.253% | 9999999999 | 0.231% |
| #15 | 38317 | 0. 216% 216% | 222222 | 0.212% | 1869510 | 0.102% | 33333333 | 0.176% | 420420420 | 0.241% | 2222222222 | 0.219% |
| #16 | 09876 | 0.185% | 789456 | 0.209% | 3223326 | 0.100% | 44444444 | 0.165% | 007007007 | 0.227% | 7777777777 | 0.206% |
| #17 | 44444 | 0.179% | 999999 | 0.194% | 1212123 | 0. 096% 096% | 66666666 | 0.160% | 135792468 | 0.164% | 3141592654 | 0.195% |
| #18 | 98765 | 0.169% | 101010 | 0.190% | 1478963 | 0.088% | 11112222 | 0.140% | 397029049 | 0.158% | 3333333333 | 0.186% |
| #19 | 01234 | 0.160% | 777777 | 0.188% | 2222222 | 0.085% | 13131313 | 0.131% | 012345678 | 0. 154% 154% | 7894561230 | 0.165% |
| #20 | 42069 | 0.154% | 007007 | 0.186% | 5555555 | 0.082% | 10041004 | 0.127 % | 123698745 | 0,152% | 1234567891 | 0,161% |
Некоторые интересные наблюдения (и небольшие догадки для пятизначных паролей)0063 еще меньше фантазии
в выборе своих кодов (22,8% выбрали 12345). Происходят все обычные подозрения, но новым дополнением является ребяческое добавление в позиции № 20 конкатенации 420 и 69.Для шестизначного пароля снова появляется 696969. Также следует отметить 159753 (знак «X» над цифровой клавиатурой). Джеймс Бонд возвращается с номером 007007.
Для семизначного числа резервный номер 1234567 имеет гораздо более низкую частоту (хотя по-прежнему самый высокий). Я предполагаю, что это связано с тем, что многие люди могут использовать свой номер телефона (без кода города) в качестве семизначного пароля. Телефонные номера довольно отчетливы и уже запомнены, поэтому, когда требуется семизначный код, они легко приходят на ум. Более высокая частота использования телефонных номеров снижает необходимость использовать воображение (или его отсутствие) и выбирать что-то еще.
Я предполагаю, что это связано с тем, что многие люди могут использовать свой номер телефона (без кода города) в качестве семизначного пароля. Телефонные номера довольно отчетливы и уже запомнены, поэтому, когда требуется семизначный код, они легко приходят на ум. Более высокая частота использования телефонных номеров снижает необходимость использовать воображение (или его отсутствие) и выбирать что-то еще.
Дженни здесь? Четвертый по популярности семизначный пароль — 8675309 (это популярная песня 80-х).
Восьмизначные пароли, как и ожидалось. Много шаблонов и много повторений.
Обычные девятизначные пароли также следуют шаблонам и повторениям. 789456123 отображается как простой «Вдоль верхней, средней и нижней части клавиатуры» 147258369 связан в вертикальном направлении (и другие варианты отображаются высоко вверх). Снова получаем момент 420 с 420420420, а также взбалтываемые, не перемешиваемые, а повторяющиеся возвраты 007007007.
Интересно, что для десяти цифр появляется 1029384756 (чередование возрастающих/убывающих цифр), а также нечетных/четных 1357924680.
Ура математике! В позиции #17 десятизначного списка паролей мы получаем 3141592654 (первые несколько цифр Pi )
Если вы разработчик , тестировщик или руководитель надеюсь, вы достаточно параноики, чтобы немедленно проверить, не хранят ли ваши системы конфиденциальную информацию, такую как пароли, в незашифрованном виде. Единственная причина, по которой я смог провести этот анализ, заключается в том, что Если вы являетесь потребителем и узнаете какие-либо из чисел, которые я использовал в этой статье, в качестве ваших паролей/пин-кодов, я надеюсь, что вы проявите здравый смысл и немедленно измените их на что-то менее предсказуемое. В качестве альтернативы вы можете быть ленивым и ничего не менять (в этом случае, по крайней мере, единственный человек, которому вы вредите своей апатией, — это вы сами). |
После публикации этой статьи я обратил внимание на то, что, конечно же, в дополнение к юбилейным годам многие люди инкапсулируют даты в формате MMDD (например, дни рождения…) для своих PIN-кодов.
Это ясно объясняет нижний левый угол, где, если вы посмотрите на тепловую карту, есть огромное изменение контраста на высоте около 30-31 (количество дней в месяце), простирающееся до 12 по оси X. . (Спасибо zero79 за первое указание на это).
Многие люди также задавались вопросом о значении 1004 в четырехсимвольной таблице PIN-кодов. Это исходит от говорящих на корейском языке. При произнесении «1004» это чхонса (чхон = 1000, са = 4).
«Чхонса» также является корейским словом для Ангела .
Кажется уместным закончить еще одним мультфильмом XKCD. Надежность пароля
Полный список всех статей можно найти здесь. Нажмите здесь, чтобы получать уведомления о новых статьях по электронной почте.

 0.1 Элементы комбинаторики. Перестановки, размещения, сочетания
0.1 Элементы комбинаторики. Перестановки, размещения, сочетания