8 класс. Алгебра. Алгебраические дроби. — Преобразование рациональных выражений.
Комментарии преподавателяУрок: Преобразование рациональных выражений
Вспомним сначала определение рационального выражения.
Определение. Рациональное выражение – алгебраическое выражение, не содержащее корней и включающее только действия сложения, вычитания, умножения и деления (возведения в степень).
Под понятием «преобразовать рациональное выражение» мы имеем в виду, прежде всего, его упрощение. А это осуществляется в известном нам порядке действий: сначала действия в скобках, затем произведение чисел (возведение в степень), деление чисел, а затем действия сложения/вычитания.
Основной целью сегодняшнего урока будет приобретение опыта при решении более сложных задач на упрощение рациональных выражений.
Пример 1. Упростить рациональное выражение .
Решение. Сначала может показаться, что указанные дроби можно сократить, т. к. выражения в числителях дробей очень похожи на формулы полных квадратов соответствующих им знаменателей. В данном случае важно не спешить, а отдельно проверить, так ли это.
Проверим числитель первой дроби: . Теперь числитель второй: .
Как видно, наши ожидания не оправдались, и выражения в числителях не являются полными квадратами, т. к. у них отсутствует удвоение произведения. Такие выражения, если вспомнить курс 7 класса, называют неполными квадратами. Следует быть очень внимательными в таких случаях, т. к. перепутывание формулы полного квадрата с неполным – очень частая ошибка, а подобные примеры проверяют внимательность учащегося.
Поскольку сокращение невозможно, то выполним сложение дробей. У знаменателей нет общих множителей, поэтому они просто перемножаются для получения наименьшего общего знаменателя, а дополнительным множителем для каждой из дробей является знаменатель другой дроби.
У знаменателей нет общих множителей, поэтому они просто перемножаются для получения наименьшего общего знаменателя, а дополнительным множителем для каждой из дробей является знаменатель другой дроби.
Конечно же, далее можно раскрыть скобки и привести затем подобные слагаемые, однако, в данном случае можно обойтись меньшими затратами сил и заметить, что в числителе первое слагаемое является формулой суммы кубов, а второе – разности кубов. Для удобства вспомним эти формулы в общем виде:
и .
В нашем же случае выражения в числителе сворачиваются следующим образом:
, второе выражение аналогично. Имеем:
.
Ответ. .
Пример 2. Упростить рациональное выражение .
Решение. Данный пример похож на предыдущий, но здесь сразу видно, что в числителях дробей находятся неполные квадраты, поэтому сокращение на начальном этапе решения невозможно. Аналогично предыдущему примеру складываем дроби:
Аналогично предыдущему примеру складываем дроби:
, здесь мы аналогично способу, указанному выше, заметили и свернули выражения по формулам суммы и разности кубов.
Ответ. .
Пример 3. Упростить рациональное выражение .
Решение. Можно заметить, что знаменатель второй дроби раскладывается на множители по формуле суммы кубов. Как мы уже знаем, разложение знаменателей на множители является полезным для дальнейшего поиска наименьшего общего знаменателя дробей.
.
Укажем наименьший общий знаменатель дробей, он равен: , т. к. делится на знаменатель третьей дроби, а первое выражение вообще является целым, и для него подойдет любой знаменатель. Указав очевидные дополнительные множители, запишем:
.
Ответ.
Рассмотрим более сложный пример с «многоэтажными» дробями.
Пример 4. Доказать тождество при всех допустимых значениях переменной.
Доказать тождество при всех допустимых значениях переменной.
Доказательство. Для доказательства указанного тождества постараемся упростить его левую часть (сложную) до того простого вида, который от нас требуется. Для этого выполним все действия с дробями в числителе и знаменателе, а затем разделим дроби и упростим результат.
. Доказано при всех допустимых значениях переменной.
Доказано.
Источник конспекта: http://interneturok.ru/ru/school/algebra/8-klass/algebraicheskie-drobi-arifmeticheskie-operacii-nad-algebraicheskimi-drobyami/preobrazovanie-ratsionalnyh-vyrazheniy?konspekt&chapter_id=13
Источник видео: http://www.youtube.com/watch?v=Mtxotj-mhiQ
Презентация «Преобразование рациональных выражений» — алгебра 8 класс
Слайды и текст этой презентации
| Слайд №1 | |
| Алгебраические дроби 6.  Преобразование рациональных выражений Преобразование рациональных выражений(уроки 17 — 18). 26.06.2011 8 классалгебра 1 Кравченко Г. М. | |
| Слайд №2 | |
| Изучить правила преобразования рациональных выражений; Научиться упрощать выражения; Научиться доказывать тождества. Цели: 26.06.2011 2 Кравченко Г. М. | |
| Слайд №3 | |
| 26.06.2011 Кравченко Г. М. 3 Рациональные числа — все целые числа и все дроби, как положительные так и отрицательные. Целое выражение — выражение представленное в виде многочлена . Дробное выражение – это алгебраическая дробь. Рациональное выражение – алгебраическое выражение составленное из чисел и переменных | |
| Слайд №4 | |
| 26.06.2011 Кравченко Г. М. 4 Для преобразования рациональных выражений принят тот же порядок действий, что и для преобразования числовых выражений.  Это значит, что сначала выполняют действия в скобках, затем действия второй ступени (умножение, деление, возведение в степень), а затем действия первой ступени (сложение, вычитание). Рассмотрим наиболее сложные задания: | |
| Слайд №5 | |
| 26.06.2011 Кравченко Г. М. 5 Рассмотрим пример 1. Упростить выражение. 1 1 1 1 | |
| Слайд №6 | |
| 26.06.2011 Кравченко Г. М. 6 Решение Рассмотрим пример 2. Упростить выражение: Для упрощения выражения выбираем способ преобразования по действиям. | |
| Слайд №7 | |
| 26.06.2011 Кравченко Г. М. 7 1 1 1 1 | |
| Слайд №8 | |
| 26.06.2011 Кравченко Г. М. 8 Рассмотрим пример 3. Упростить выражение: | |
| Слайд №9 | |
26. 06.2011 06.20119 Кравченко Г. М. | |
| Слайд №10 | |
| 26.06.2011 Кравченко Г. М. 10 1 1 1 1 1 1 | |
| Слайд №11 | |
| 26.06.2011 Кравченко Г. М. 11 Доказать тождество – это значит установить, что при всех допустимых значениях переменной его левая и правая части тождественно равные выражения. Преобразовывают левую часть и получают в итоге правую часть; 2)Преобразовывают правую часть и получают в итоге левую часть; 3)По отдельности преобразовывают правую, а затем левую часть и в итоге получают равные выражения; 4) Составляют разность левой и правой части и в итоге получают нуль. Какой способ выбрать – зависит от конкретного вида тождества, которое предлагают доказать. | |
| Слайд №12 | |
| 26.06.2011 Кравченко Г. М. 12 Рассмотрим пример 4.  Доказать тождество. Для доказательства тождества выбираем первый способ: преобразуем левую часть. Решение 1 | |
| Слайд №13 | |
| 26.06.2011 Кравченко Г. М. 13 1 1 1 1 И так, 8 = 8. Тождество справедливо лишь для допустимых значений переменной у. | |
| Слайд №14 | |
| Ответить на вопросы: 26.06.2011 14 Кравченко Г. М. Какие числа называются рациональными? Какое выражение называется дробным? Какое выражение называется рациональным? Что значит доказать тождество? Какие способы доказательства тождества можно назвать? | |
- Автор: Виктория
- Распечатать
Оцените статью:
(5 голосов, среднее: 5 из 5)
Поделитесь с друзьями!
Большой сборник презентаций в помощь школьнику.

закрыть
Скопируйте этот код и вставьте его на своем сайте:
<div><strong><a href=»https://volna.org/algebra/prieobrazovaniie_ratsionalnykh_vyrazhienii.html» title=»Презентация «Преобразование рациональных выражений» — алгебра 8 класс» target=»_blank» >Презентация «Преобразование рациональных выражений» — алгебра 8 класс</a></strong><iframe src=»https://volna.org/iframe/1073/» frameborder=»0″ marginwidth=»0″ marginheight=»0″ scrolling=»no» allowfullscreen></iframe></div>
Как объединить и упростить алгебраические дроби — Помощь с IGCSE GCSE Maths
Home Уравнения и неравенства Линейные уравнения Конструирование уравнений Одновременные уравнения. Прямая вариация Обратная вариация Графики в практических ситуациях Графики преобразования Разница между расстоянием и скоростью во времени Графики расстояние-время Графики скорости-времени Ускорение и замедление Площадь под графиком скорости-времени Графики функций Параболы Графическое решение квадратичных функций Графическое решение уравнений Графики неравенств Функции Вычисление функций Обратные функции Составные функции Геометрия Измерение Координатная геометрия Тригонометрия Векторы/матрицы/преобразования Вероятность Статистика | Как объединить и упростить алгебраические дроби Эта часть шаг за шагом объяснит вам, как складывать и упрощать алгебраические дроби. Как упростить алгебраические дроби Вероятно, в экзаменационной работе IGCSE GCSE по математике вас попросят упростить алгебраическую дробь. Хорошо бы спросить себя, что имеется в виду под упрощением дробей? Посмотрите здесь, если вы не уверены. Изучите следующий пример вопроса, чтобы узнать, как упростить алгебраические дроби. Как избавиться от Высшего общего фактора (ВКФ), если на первый взгляд кажется, что между всеми терминами нет общего фактора? Видео расскажут вам, как именно подходить к этим типам вопросов, и вы сможете уверенно отвечать на эти типы вопросов на экзамене по математике IGCSE GCSE. Отличная работа! вы усвоили несколько очень важных уроков математики и теперь понимаете, как складывать и упрощать алгебраические дроби. Вы получите аналогичный вопрос на своем экзамене по математике, так что вы хорошо изучили эту часть во время повторения математики! Не останавливайтесь, а изучайте законы индексов по ссылкам. Я объясню, что такое законы индексов, и предоставлю вам множество примеров вопросов. Увидимся там!! Учи математику!! |
Что такое недопустимая алгебраическая дробь.
 Как решать алгебраические дроби? Теория и практика. Умножение и деление алгебраических дробей
Как решать алгебраические дроби? Теория и практика. Умножение и деление алгебраических дробейТема: Повторение алгебры за 8 класс
Урок: Алгебраические дроби
Во-первых, давайте вспомним, что такое алгебраические дроби. Алгебраическая дробь – это выражение вида , где – многочлены, — числитель, — знаменатель.
Так как являются многочленами, то необходимо иметь в виду стандартные операции, которые возможны с многочленами, а именно: приведение к стандартному виду, факторизация и приведение числителя и знаменателя.
Пример #1
Уменьшить дробь
Воспользуемся формулами сокращенного умножения квадрата суммы и разности квадратов.
Комментарии: сначала мы разложили дробь по формулам сокращенного умножения, а затем воспользовались одним из основных свойств дроби: и числитель, и знаменатель алгебраической дроби можно умножать или делить на один и тот же многочлен, в том числе число, не равное 0 Таким образом, получается, что мы разделили и числитель, и знаменатель на многочлен, поэтому обязательно нужно учесть, что этот многочлен не равен 0, т. е.
е.
Пример #2
Из условия пока не ясно, какая связь между этими двумя функциями. Для этого нам нужно упростить первую из них, разложив ее на множители.
однако необходимо не забывать об условии сокращения дроби, т. е. о том, что
После всех сокращений мы получаем то
с той лишь разницей, что .
Построим две функции.
Мы видим явную разницу между этими двумя графиками: по сути они одинаковые, но на первом графике нужно выставить точку с координатой (1;0), так как именно этот не входит в ОДЗ первая функция.
В общем, мы рассмотрели, что такое дробь, решили пару примеров о том, как важно следить за областью определения (диапазоном допустимых значений), то есть за значениями, которые может принимать.
Теперь перейдем к вопросу о том, какие действия можно производить с алгебраическими дробями, помимо тех, что уже были упомянуты выше.
Естественно, алгебраические дроби, как и арифметические дроби, можно складывать, вычитать, умножать, делить, возводить в степень, получая при этом рациональные алгебраические выражения (такие выражения, которые составлены из чисел, переменных с помощью арифметических операций и возведения в натуральную степень ).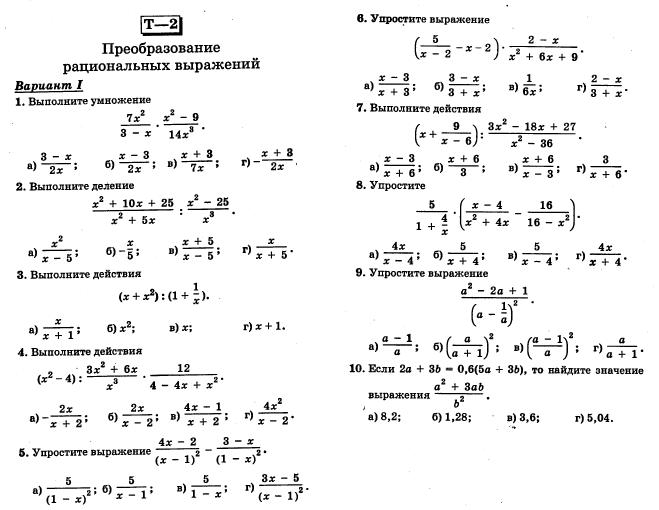 После некоторых упрощений такие выражения сводятся к дробям, для которых исходными выражениями также являются алгебраические дроби.
После некоторых упрощений такие выражения сводятся к дробям, для которых исходными выражениями также являются алгебраические дроби.
Список действий/условий, с которыми вы можете столкнуться при решении задач на алгебраические дроби:
Упрощение рациональных выражений
Доказать идентификаторы
Решение рационального уравнения
Упрощение/Рассчитайте фракцию
Пример № 3
Решение. Самое простое рациональное уравнение
1777Решение. Самое простое рациональное уравнение
1777Решение. 0 тогда и только тогда, когда числитель равен 0, а знаменатель не равен 0. В нашем случае знаменатель равен . Следовательно, решение дроби сводится к линейному уравнению
Пример #4
решить уравнение
Прежде всего попробуем сократить дробь
При условии, что .
Поскольку мы уже упростили дробь в левой части исходного уравнения, мы можем подставить новое значение и решить уравнение.
Теперь попробуем извлечь полный квадрат из полученного квадратного уравнения
Воспользуемся формулой сокращенного умножения разности квадратов
Произведение равно 0 тогда и только тогда, когда хотя бы один из множителей равен 0. Кроме того, не забываем, что в начале у нас было условие существования нашего выражения в виде . Запишем систему уравнений.
=> => Мы видим, что это противоречит нашему условию, поэтому у нас остается только один ответ.
Итак, давайте посмотрим на особенности, которые имеет решенный нами выше пример:
1. Числитель с разностью кубов и знаменателем желательно уменьшить сразу, так как это возможно в данном случае и значительно упрощает дальнейшую решение уравнения, однако надо помнить, что знаменатель дроби не может равняться 0 и записывать это условие.
2. Приведя дробь к квадратному уравнению, мы вспомнили об одном из методов решения квадратных уравнений — методе выбора полного квадрата.
В этом уроке мы вспомнили, что такое алгебраическая дробь, какие действия нужно производить с числителем и знаменателем при решении таких дробей, какие вообще действия можно производить с дробями такого рода и решили несколько простых задач.
Библиография
- Башмаков М.И. Алгебра 8 класс. — М.: Просвещение, 2004.
- Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и другие. Алгебра 8. 5-е издание. — М.: Просвещение, 2010. .
- Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. — М.: Просвещение, 2006.
- Вся элементарная математика ().
- Школьный помощник ().
- Интернет-портал Testmath.com.ua ().
Домашнее задание
Когда учащийся переходит в среднюю школу, математика делится на 2 предмета: алгебра и геометрия. Понятий становится все больше, задачи усложняются. Некоторые люди с трудом понимают дроби. Пропустил первый урок по этой теме, и вуаля. дроби? Вопрос, который будет мучить всю школьную жизнь.
Пропустил первый урок по этой теме, и вуаля. дроби? Вопрос, который будет мучить всю школьную жизнь.
Понятие алгебраической дроби
Начнем с определения. Под алгебраическая дробь Выражения P/Q понимаются, где P — числитель, а Q — знаменатель. Под буквенной записью может скрываться число, числовое выражение, числовое-алфавитное выражение.
Прежде чем задаться вопросом, как решать алгебраические дроби, сначала нужно понять, что такое выражение является частью целого.
Как правило, целое равно 1. Число в знаменателе показывает, на сколько частей была разделена единица. Числитель нужен для того, чтобы узнать, сколько элементов взято. Дробная черта соответствует знаку деления. Допускается запись дробного выражения в виде математической операции «Деление». В данном случае числитель — делимое, знаменатель — делитель.
Основное правило обыкновенных дробей
Когда учащиеся проходят эту тему в школе, им даются примеры для закрепления. Чтобы правильно их решать и находить разные выходы из сложных ситуаций, нужно применять основное свойство дробей.
Чтобы правильно их решать и находить разные выходы из сложных ситуаций, нужно применять основное свойство дробей.
Звучит так: Если умножить и числитель, и знаменатель на одно и то же число или выражение (отличное от нуля), то значение обыкновенной дроби не изменится. Частным случаем этого правила является деление обеих частей выражения на одно и то же число или многочлен. Такие преобразования называются тождественными равенствами.
Ниже мы рассмотрим, как решать сложение и вычитание алгебраических дробей, выполнять умножение, деление и сокращение дробей.
Математические действия с дробями
Рассмотрим, как решить основное свойство алгебраической дроби, как применить его на практике. Если вам нужно умножить две дроби, сложить их, разделить одну на другую или вычесть, вы всегда должны следовать правилам.
Итак, для операции сложения и вычитания следует найти дополнительный множитель, чтобы привести выражения к общему знаменателю. Если изначально дроби даны с одинаковыми выражениями Q, то нужно этот пункт опустить.
Этот термин часто используется как сокращение дроби . Это означает следующее: если числитель и знаменатель разделить на выражение, отличное от единицы (одинаковое для обеих частей), то получится новая дробь. Делимое и делитель меньше, чем раньше, но из-за основного правила дробей они остаются равными исходному примеру.
Целью этой операции является получение нового неприводимого выражения. Эту задачу можно решить, сократив числитель и знаменатель на наибольший общий делитель. Алгоритм работы состоит из двух пунктов:
- Нахождение НОД обеих частей дроби.
- Деление числителя и знаменателя на найденное выражение и получение несократимой дроби, равной предыдущей.

В таблице ниже показаны формулы. Для удобства его можно распечатать и носить с собой в блокноте. Однако, чтобы в дальнейшем при решении контрольной или экзамена не возникало затруднений в вопросе, как решать алгебраические дроби, эти формулы необходимо выучить наизусть.
Некоторые примеры с решениями
С теоретической точки зрения рассматривается вопрос о том, как решать алгебраические дроби. Приведенные в статье примеры помогут лучше понять материал.
1. Преобразовать дроби и привести их к общему знаменателю.
2. Преобразовать дроби и привести их к общему знаменателю.
После изучения теоретической части и рассмотрения практических вопросов вопросов больше возникнуть не должно.
В этой статье мы рассмотрим основные операции с алгебраическими дробями :
- сокращение дроби
- умножение дробей
- деление дробей
Начнем с сокращений алгебраических дробей .
Казалось бы, алгоритм очевиден.
К сократить алгебраические дроби , нужно
1. Разложить на множители числитель и знаменатель дроби.
2. Уменьшить одинаковые множители.
Однако школьники часто допускают ошибку, «сокращая» не факторы, а термины. Например, есть любители, которые «сокращают» на дроби и получают в результате, что, конечно же, не соответствует действительности.
Рассмотрим примеры:
1. Уменьшить дробь:
1. Разлагаем числитель по формуле квадрата суммы, а знаменатель по формуле разности квадратов
2. Разделить числитель и знаменатель на
2. Уменьшить дробь:
1. Разложить числитель на множители. Поскольку числитель содержит четыре слагаемых, применяем группировку.
2. Разложить знаменатель на множители. То же самое относится и к группировке.
3. Запишем полученную дробь и сократим те же множители:
Умножение алгебраических дробей.
При умножении алгебраических дробей числитель умножается на числитель, а знаменатель умножается на знаменатель.
Важно! Не нужно торопиться выполнять умножение в числителе и знаменателе дроби. После того, как мы записали произведение числителей дробей в числитель, а произведение знаменателей в знаменатель, нам нужно разложить каждый множитель и уменьшить дробь.
Рассмотрим примеры:
3. Упростим выражение:
1. Запишем произведение дробей: в числителе произведение числителей, а в знаменателе произведение знаменателей:
2. Разлагаем каждую скобку на множители:
Теперь нужно уменьшить те же множители. Обратите внимание, что выражения и отличаются только знаком: и в результате деления первого выражения на второе мы получаем -1.
Итак,
Деление алгебраических дробей выполняем по следующему правилу:
То есть Чтобы разделить на дробь, нужно умножить на «перевернутую».
Мы видим, что деление дробей сводится к умножению, и умножение в конечном итоге сводится к сокращению дробей.
Рассмотрим пример:
4. Упростите выражение:
WikiHow — это вики, что означает, что многие наши статьи написаны несколькими авторами. При создании этой статьи над ее редактированием и улучшением работали 9 человек, в том числе анонимно.
На первый взгляд алгебраические дроби кажутся очень сложными, и неподготовленному школьнику может показаться, что с ними ничего нельзя сделать. Нагромождение переменных, чисел и даже сил внушает страх. Однако одни и те же правила используются для сокращения дробей (например, 15/25) и алгебраических дробей.
Шаги
Сокращение дробей
Научитесь работать с простыми дробями. Операции с обыкновенными и алгебраическими дробями аналогичны. Например, возьмем дробь 15/35. Чтобы упростить эту дробь, найдите общий делитель . Оба числа делятся на пять, поэтому мы можем извлечь 5 в числителе и знаменателе:
15→
5*335 → 5*7
Теперь можно уменьшить общие делители , то есть вычеркнуть 5 в числителе и знаменателе. В результате получаем упрощенную дробь 3/7 . В алгебраических выражениях общие множители выделяют так же, как и в обычных. В предыдущем примере мы смогли легко извлечь 5 из 15 — тот же принцип применим и к более сложным выражениям, таким как 15x — 5. Найдем общий множитель. В данном случае это будет 5, так как оба слагаемых (15х и -5) делятся на 5. Как и прежде, выделим общий множитель и перенесем его влево .
В результате получаем упрощенную дробь 3/7 . В алгебраических выражениях общие множители выделяют так же, как и в обычных. В предыдущем примере мы смогли легко извлечь 5 из 15 — тот же принцип применим и к более сложным выражениям, таким как 15x — 5. Найдем общий множитель. В данном случае это будет 5, так как оба слагаемых (15х и -5) делятся на 5. Как и прежде, выделим общий множитель и перенесем его влево .
15х — 5 = 5 * (3х — 1)
Чтобы проверить, все ли верно, достаточно выражение в скобках умножить на 5 — в результате будут те же числа, что были вначале. Сложные термины можно различать так же, как и простые. Для алгебраических дробей применяются те же принципы, что и для обыкновенных дробей. Это самый простой способ сократить дробь. Рассмотрим следующую дробь:
(x+2)(x-3)(x+2)(x+10)
Обратите внимание, что и в числителе (вверху), и в знаменателе (внизу) есть член (x+2), поэтому можно уменьшить так же, как общий множитель 5 в 15/35:
(x+2) (x-3)→
(x-3)(x+2) (x+10 ) → (x+10)
В результате получаем упрощенное выражение: (x-3)/(x+10)
Сокращение алгебраических дробей
Найдите общий множитель в числителе, то есть в верхней части дроби. При уменьшении алгебраической дроби первым шагом является упрощение обеих ее частей. Начните с числителя и постарайтесь учесть как можно больше факторов. Рассмотрим в этом разделе следующую дробь:
При уменьшении алгебраической дроби первым шагом является упрощение обеих ее частей. Начните с числителя и постарайтесь учесть как можно больше факторов. Рассмотрим в этом разделе следующую дробь:
15x+6
Начнем с числителя: 9x — 3. Для 9x и -3 общим множителем является число 3. Вынесем 3 за скобки, как мы это делаем с обычными числами: 3*(3х-1). В результате этого преобразования получится следующая дробь:
3(3x-1)15x+6
Найдите общий множитель в числителе. Продолжим выполнение приведенного выше примера и выпишем знаменатель: 15x+6. Как и раньше, находим, на какое число делятся обе части. И в этом случае общий множитель равен 3, поэтому мы можем написать: 3 * (5x +2). Перепишем дробь в следующем виде:
3(3x-1)3(5x+2)
Сократить одинаковые члены. На этом этапе вы можете упростить дробь. Сократите одинаковые члены в числителе и знаменателе. В нашем примере это число равно 3.
В нашем примере это число равно 3.
→
(3x-1)3 (5x+2) → (5x+2)
Определите, что дробь имеет простейшую форма. Дробь полностью упрощается, когда в числителе и знаменателе не осталось общих множителей. Обратите внимание, что вы не можете сокращать те термины, которые находятся внутри скобок — в приведенном выше примере нет способа извлечь x из 3x и 5x, поскольку (3x -1) и (5x + 2) являются полными членами. Таким образом, дробь не поддается дальнейшему упрощению, и окончательный ответ таков:
(3x-1)(5x+2)
Потренируйтесь самостоятельно сокращать дроби. Лучший способ освоить метод — решать задачи самостоятельно. Правильные ответы даны под примерами.
4(x+2)(x-13)(4x+8)
Ответ: (x=13)
2x 2-x5x
9×072 (2×077-11 Ответ: )/5Special Moves
Переместите знак «минус» из дроби. Предположим, нам дана следующая дробь:
Предположим, нам дана следующая дробь:
5(4x)
Обратите внимание, что (x-4) и (4-x) «почти» идентичны, но их нельзя сразу отменить, потому что они «перевернуты». Однако (х — 4) можно записать как -1 * (4 — х), так же как (4 + 2х) можно записать как 2 * (2 + х). Это называется «перестановка знака».
-1*3(4-x)5(4x)
Теперь можно сократить те же члены (4-x):
-1 * 3 (4-x)5 (4x)
Итак, вот окончательный ответ: -3/5 . Научитесь распознавать разницу квадратов. Разность квадратов — это когда квадрат одного числа вычитается из квадрата другого числа, как в выражении (а 2 — b 2). Разность совершенных квадратов всегда можно разложить на две части — сумму и разность соответствующих квадратных корней. Тогда выражение примет следующий вид:
A 2 — b 2 = (a+b)(a-b)
Этот трюк очень полезен при поиске общих терминов в алгебраических дробях.
- Проверьте, правильно ли вы разложили то или иное выражение. Для этого перемножьте множители — в результате должно получиться такое же выражение.
- Чтобы полностью упростить дробь, всегда выбирайте самые большие множители.
Типы выражений из алгебры могут принимать вид рациональных дробей, которые характерны для тождественных преобразований этих дробей. Чаще всего можно встретить другое название алгебраических дробей. Таким образом, понятия рациональных и алгебраических дробей эквивалентны.
Привести рациональную дробь к новому знаменателю, поменять знаки, уменьшить. Остановимся на преобразовании дробей в виде суммы с несколькими показателями. В заключение приведем несколько примеров, в которых подробно рассмотрим решения.
Определение и примеры рациональных дробей
Определение 1
рациональная дробь – это дробь, в числителе и знаменателе которой стоят многочлены с натуральными, целыми и рациональными коэффициентами.
Полиномы могут быть заданы в нестандартной форме, что указывает на необходимость дополнительных преобразований.
Рассмотрим примеры рациональных дробей.
Пример 1
2 a 2 b — b, x + 2, 3 x + 2 2 3 x 2 y z x 2 + y 2 + z 2, x 8, 1 4 x 2 — 3 x + 1 2 x + 3 считаются рациональными дробями.
А 5 (х + у) у 2 — х 4 у и а Ь — Ь а 3 + 1 а + 1 а 2 таковыми не являются, так как не имеют выражений с полиномами.
Преобразования числителя и знаменателя рациональной дроби
Числитель и знаменатель считаются самодостаточными числовыми выражениями. Из этого следует, что с ними можно производить различные преобразования, т. е. в числителе или знаменателе допускается замена его идентичным выражением, равным ему.
Для проведения тождественных преобразований необходимо сгруппировать и привести одинаковые члены, а знаменатель заменить аналогичным ему более простым выражением. Числители и знаменатели содержат полиномы, а это значит, что с ними можно производить преобразования, аналогичные полиномам. Также это могут быть приведения к стандартной форме или представление в виде продукта.
Также это могут быть приведения к стандартной форме или представление в виде продукта.
Пример 2
Преобразовать 3 a — a b — 2 b 5 6 b + 2 3 7 a b a 3 b 2 — 5 a 2 b + 3 a b — 15 так, чтобы числитель принял стандартный вид многочлена, а знаменатель является их продуктом.
Раствор
Сначала нужно привести к стандартному виду. Применяя свойство степени, получаем выражение вида
3 a — a b — 2 b 5 6 b + 2 3 7 a b = 3 a — a b — 5 3 b 2 + 2 3 7 a b = = 3 a + — а б + 2 3 7 а б — 5 3 б 2 = 3 а + 1 3 7 а б — 5 3 б 2
Вам необходимо выполнить преобразование знаменателя. Представим его в виде произведения, то есть разложим на многочлены. Для этого сгруппируем первое и третье слагаемое, а второе с четвертым. Выносим общий множитель за скобки и получаем выражение вида
а 3 b 2 — 5 а 2 b + 3 а b — 15 = (а 3 b 2 + 3 а b) + (- 5 а 2 b — 15 ) = = a b (a 2 b + 3) — 5 (a 2 b + 3)
Видно, что полученное выражение имеет общий множитель, который необходимо вынести за скобки, чтобы получить
a b (a 2 b + 3) — 5 (a 2 b + 3) = a 2 b + 3 (ab — 5)
Теперь мы подошли к произведению многочленов.
После преобразований получаем, что данная дробь принимает вид 3 a + 1 3 7 a b — 5 3 b 2 a 2 b + 3 (ab — 5) .
Ответ: 3 a — a b — 2 b 5 6 b + 2 3 7 a b a 3 b 2 — 5 a 2 b + 3 a b — 15 = 3 a + 1 3 7 a b — 5 3 b 2 a 2 b + 3 (а б — 5) .
Данные преобразования необходимы для использования в преобразованиях.
Приведение к новому знаменателю
При изучении обыкновенных дробей мы знакомимся с основным свойством дроби, которое гласит, что при умножении числителя и знаменателя на любое натуральное число получается дробь, равная предыдущей. Это свойство относится и к рациональным дробям: при умножении на ненулевые многочлены в числителе и знаменателе мы получаем дробь, равную предыдущей.
Для любых многочленов a , b и c , где b и c отличны от нуля, верно равенство вида a b = a c b c, тогда они тождественны. Например, x y + 1 2 x — 5 = (x y + 1) (x 2 + 3 b 2) (2 x — 5) (x 2 + 3 b 2) справедливо для всей ОДЗ переменных x и y.
Из этого следует, что при решении необходимо использовать приведение рациональной дроби к новому знаменателю. То есть его умножение как числителя, так и знаменателя на ненулевой многочлен. В результате получаем дробь, равную заданной.
То есть его умножение как числителя, так и знаменателя на ненулевой многочлен. В результате получаем дробь, равную заданной.
Если рассмотреть такой пример рациональной дроби вида x — y 2 · x, то при приведении к новому знаменателю мы получим новый, но равный предыдущему. Нужно умножить числитель и знаменатель на выражение x 2 + y, тогда мы имеем, что выражение x — y x 2 + y 2 x (x 2 + y) с помощью преобразования примет вид рациональной дроби x 3 + х у — х 2 у — у 2 2 х 3 + 2 х у . Такие сокращения используются для сложения или вычитания дробей. Вы можете углубить свои знания в разделе приведения алгебраических дробей к новому знаменателю.
Изменение знаков перед дробью, в ее числителе и знаменателе
Основное свойство дроби используется для того, чтобы можно было менять знаки членов дроби. Эти преобразования типичны для рациональных дробей.
Определение 2
При одновременной замене знаков числителя и знаменателя получим дробь, равную заданной. Давайте напишем это утверждение так: a — b = a b .
Рассмотрим пример.
Пример 3
Дробь вида — x — 2 x — y заменяется на x + 2 y — x, равное ей.
Определение 3
При работе с дробями можно менять знак только в числителе или только в знаменателе. Меняя знак дроби, мы получаем тождественно равную дробь. Давайте напишем это утверждение так:
a b = — — a b и a b = — a — b .
Доказательство
Первое свойство используется для доказательства. Получаем, что — — a b = — ((- a) : b) = (- 1) (((- 1) a) : b) = (- 1) (- 1) a: b = a : b = a b .
С помощью преобразований доказывается равенство вида a b = — a — b.
Пример 4
Например, x x — 1 замените — — x x — 1 или — x 1 — x .
Имеются два полезных равенства вида -a b = -a b и a -b = -a b . Отсюда мы замечаем, что при изменении знака в числителе или только в знаменателе будет меняться и знак дроби. Получаем — 3 x 3 y + z = — 3 x 3 y + z и x + 3 — x + 5 = — x + 3 x — 5 .
Чаще всего такие преобразования подходят для дробно-рациональных выражений и их преобразований.
Сокращение рациональных дробей
Основой преобразования является свойство дроби. То есть применяется a c b c = a b, где мы имеем, что a , b и c — некоторые полиномы, где b и c равны нулю.
Пример 5
Сократите дробь 2 x 2 y 3 2 x y 7 .
Раствор
Обратите внимание, что 2 является общим множителем, поэтому вам нужно сократить выражение на него. Получаем, что 2 x 2 y 3 2 x y 7 = 2 x 2 y 3 2 x y 7 = x 2 y 3 x y 7 . понятно что х 2 = х х и у 7 = у 3 у 4 , тогда х — общий множитель. После сокращения получаем, что x 2 y 3 x y 7 = (x x) y 3 x (y 3 y 4) = x y 4 . Приведение выполняется последовательно, что позволяет получить точные ответы 2 x 2 y 3 2 x y 7 = (2 x y 3) x (2 x y 3) y 4 = x y 4 .
Ответ: 2 x 2 y 3 2 x y 7 = x y 4 .
При сокращении не всегда виден общий знаменатель. Это маленькая проблема. Не всегда есть возможность увидеть это сразу. Возможно, вам придется разложить числитель и знаменатель на множители.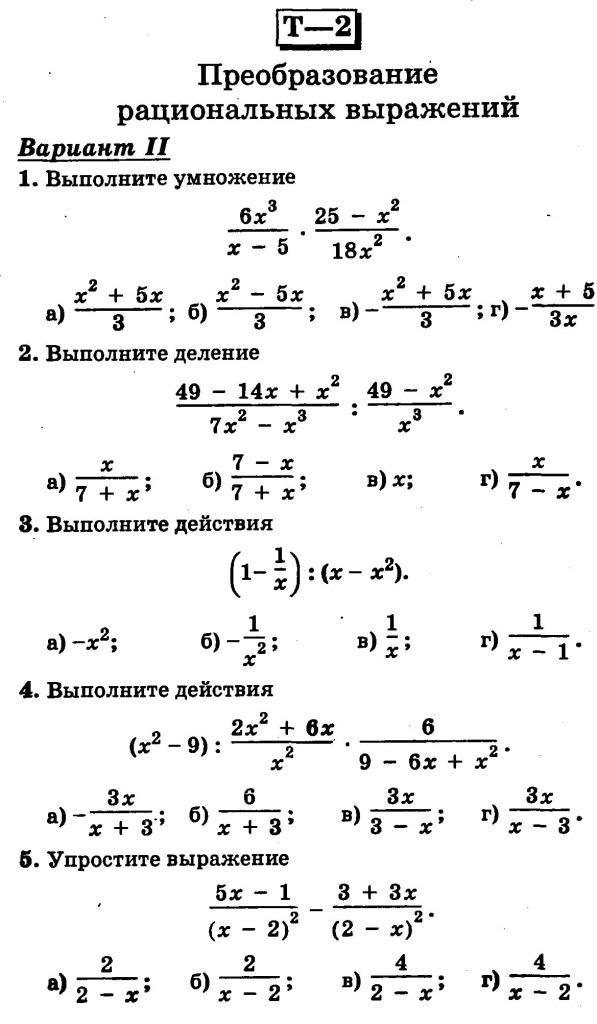 Это облегчит решение. Нюансы подробно обсуждаются в теме приведения алгебраических дробей.
Это облегчит решение. Нюансы подробно обсуждаются в теме приведения алгебраических дробей.
При сокращении важно обратить внимание на то, что чаще всего приходится разлагать и числитель, и знаменатель на множители.
Представление рациональной дроби в виде суммы дробей
Если дробей несколько, то преобразование производится особым образом. Такую рациональную дробь необходимо представить в виде выражения, в котором есть одночлены.
Пример 6
Например, 3 a 2 + a b — 5 a + b = 3 a 2 a + b + a b a + b — 5 a + b.
Это основано на правиле сложения и вычитания дробей с одинаковыми знаменателями.
Любая рациональная дробь представляется в виде суммы дробей по-разному. Мы запишем это как утверждение a b = c d + a b — c d . Если х у — х х + 1 представить в виде суммы дробей, то получим выражения вида
х у — х х + 1 = 1 х + х 2 у — х 2 — х — 1 х 2 + х, х у — х х + 1 = х х — 1 + х 2 у — х у — 2 х 2 х 2 — 1 и так далее.
В особую группу выделены представления рациональных дробей с одной переменной.

 0009 нулевой индекс
0009 нулевой индекс 

