Свойства степени с натуральным показателем
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Разгадайте ребусы
СтепеньПовторение
Обобщение
Урок повторения и
обобщения по теме
«Свойства степени
с натуральным
показателем»
3. Цели:
1. Повторить и обобщить наши знания поданной теме.
2. Ликвидировать имеющиеся пробелы.
3. Подготовиться к изучению следующей темы.

4. «Пусть кто-нибудь попробует вычеркнуть из математики степени, и он увидит, что без них далеко не уедешь.» М.В.Ломоносов
5. Повторим!
Сформулируйте определениестепени числа с натуральным
показателем.
Степенью числа a с натуральным
показателем n, большим 1, называется
произведение n множителей, каждый из
которых равен а:
аⁿ = а·а·а·…·а
n
Степенью числа а с показателем 1
называется само число а:
а¹ = а
Определение степени
5
Основание
7
Показатель
Умножение степеней с одинаковыми
основаниями
a a a
m
n
m n
При умножении степеней с
одинаковыми основаниями основание
оставляют прежним, а показатели
складывают.
Деление степеней с одинаковыми
основаниями
a a a
m
n
При делении степеней с
одинаковыми основаниями
основание оставляют прежним, а
из показателя делимого
вычитают показатель делителя.
m n
Возведение в степень степени
a
m
n
a
mn
При возведении степени в степень
основание оставляют прежним, а
показатели перемножают.

Возведение в степень дроби
a
b
n
an
bn
При возведении в степень дроби возводят в эту
степень числитель и знаменатель дроби.
Возведение в степень произведения
ab
n
a b
n
n
При возведении в степень произведения возводят в эту
степень каждый множитель и результаты
перемножают.
Задание 1.Найдите с помощью стрелок верные высказывания.
Слева указаны начала определений, справа — окончания определений.
Соедините линиями верные высказывания.
а) При умножении степеней с
одинаковыми основаниями …
1)основанием степени
б) При делении степеней с
одинаковыми основаниями ….
2) Показатель степени
в) Число а называют
3) произведение n множителей,
каждый из которых равен а.
г) При возведении степени в степень
…
4)… основание остается прежним , а
показатели складываются.
д)Степенью числа а с натуральным
показателем n, большим 1,
называется
е) Число n называют
5)… основание остается прежним, а
показатели перемножаются.

ж) Выражение а n называют
7)…основание остается прежним , а
показатели вычитаются.
6) Степенью
Ответы: а – 4, б – 7, в – 1, г – 5, д – 3, е – 2, ж – 6.
7 баллов – молодец!
6 баллов – очень хорошо!
5 баллов – хорошо!
4 балла – не очень хорошо!
3 балла – плохо!
0-2 балла – очень плохо!
Задание 2 (устно). Записать в виде степени
4
3
у у уу
=
9
у
2
3
4
((х ) ) =
24
х
=
= 64
6
8
4
8
2
8
Задание 3. Записать в виде степени с основанием с.
Вариант 1.
Вариант 2.
1. С5 • С3
1. С7 : С5
2. С8 : С6
2. (С4)3 • С
3. (С4)3
3. С4 • С5 • С0
4. С5 • С3 : С6
4. С16 : С8
5. С14 • С8
5. (С3)5
Р
Ш
М
Ю
К
Н
А
Т
Е
Д
С8
С5
С1 С40 С13 С12 С9 С15 С2 С22
Особо следует отметить переработанную им математическую
символику, близкую к современной. Коэффициенты он
обозначал a, b, c…, а неизвестные — x, y, z.

Натуральный показатель степени принял современный вид.
Задание 4. Определите, какие ответы правильные, а какие
ложные.
• истинному ответу поставьте в соответствие 1, ложному – 0.
• получив упорядоченный набор из единиц и нулей, вы узнаете
имя еще одного известного математика.
а) x2 x3 = x5
б) s3 s5 s8 = s16
в) x7 : x4 = x28
г) (c+d)8 :(c+d) 7 = c+d
д) (x5 )6 = x 30
• Ада Августа Лавлейс
• Софи Жермен
• Исаак Ньютон
• Готфрид Вильгельм Лейбниц
11001
10101
11101
11011
Задание 4. Определите, какие ответы правильные, а какие
ложные.
• истинному ответу поставьте в соответствие 1, ложному – 0.
• получив упорядоченный набор из единиц и нулей, вы узнаете
имя еще одного известного математика.
а) x2 x3 = x5
б) s3 s5 s8 = s16
в) x7 : x4 = x28
г) (c+d)8 :(c+d) 7 = c+d
д) (x5 )6 = x 30
• Ада Августа Лавлейс
• Софи Жермен
• Исаак Ньютон
• Готфрид Вильгельм Лейбниц
11001
10101
11101
11011
В период работы над арифметической машиной Лейбниц занимался
двоичной системой счисления.
 В рукописи на латинском языке, подписанной
В рукописи на латинском языке, подписанной15 марта 1679 года, Лейбниц разъяснил, как выполнить вычисления в
двоичной системе счисления, в частности умножение, а позже разработал в
общих чертах проект вычислительной машины, работающей в двоичной
системе счисления.
Подробнее о трудах Лейбница, а также о том, кто из ученых стал развивать
его идеи, можно прочитать здесь:
https://ru.wikipedia.org/wiki/Лейбниц_Готфрид_Вильгельм
https://ru.wikipedia.org/wiki/Двоичная_система_счисления
Задание 5. Решение задач.
1. т · т4 · (т2)2 · т0
2. (23)7 : (25)3
3. (р2)4 : р5
4. (34)2 · (32)3 : 311
23. «Пусть кто-нибудь попробует вычеркнуть из математики степени, и он увидит, что без них далеко не уедешь.» М.В.Ломоносов
Спасибо за работу на уроке!English Русский Правила
Урок в 7 классе по теме: «Умножение и деление степеней» Учитель: Носова Татьяна Николаевна г.Николаевск-на-Амуре, Хабаровского к
Вы можете ознакомиться и скачать
Урок в 7 классе по теме: «Умножение и деление степеней» Учитель: Носова Татьяна Николаевна г. Николаевск-на-Амуре, Хабаровского к.
Презентация содержит 20 слайдов.
Презентации для любого
класса можно скачать бесплатно. Если материал и наш сайт презентаций Вам
понравились
–
поделитесь им с друзьями с помощью социальных кнопок и добавьте в закладки в
своем
браузере.
Николаевск-на-Амуре, Хабаровского к.
Презентация содержит 20 слайдов.
Презентации для любого
класса можно скачать бесплатно. Если материал и наш сайт презентаций Вам
понравились
–
поделитесь им с друзьями с помощью социальных кнопок и добавьте в закладки в
своем
браузере.
Слайды и текст этой презентации
Слайд 1
Описание слайда:
Урок в 7 классе по теме: «Умножение и деление степеней» Учитель: Носова Татьяна Николаевна г.Николаевск-на-Амуре, Хабаровского края
Слайд 2
Описание слайда:
Основные шаги современного урока
Организация демонстрации овладение учащимися имеющимися знаниями (шаг 1)
Организация самооценивания обучаемого степенью владения актуальным опытом (шаг 2)
Учебно – практическая задача (шаг 3)
Установление связи, формулирование свойства. Сообщение учащимися пределов познания(шаг 4)
Организация изучения нового материала (шаг 5)
Обобщение изученного, проведение диагностической работы (шаг 6)
Сообщение учащимися пределов познания(шаг 4)
Организация изучения нового материала (шаг 5)
Обобщение изученного, проведение диагностической работы (шаг 6)
Слайд 3
Описание слайда:
Умножение и деление степеней Педагогическая цель: Ученик научится различать свойства умножения и деления степеней с натуральным показателем; применять свойства в случае с одинаковыми основаниями. Ученик получит возможность уметь выполнять преобразования степеней с разными основаниями и уметь выполнять преобразования в комбинированных заданиях.
Слайд 4
Описание слайда:
ЗАДАЧИ: Организовать работу учащихся посредством повторения ранее изученного материала Обеспечить уровень воспроизведения посредством выполнения упражнений различного типа Организовать проверку по самооценке учащихся посредством тестирования
Слайд 5
Описание слайда:
Шаг 1
а) Актуализация знаний:
1) Верно ли, что: 2 •2• 2 = 23 ;
5 •5•5•5 =45; (-3)3=9, 71=7, 250=25, x •x •x •x •x=4x
Обосновать.
Слайд 6
Описание слайда:
Шаг 2
Тест для самопроверки: (индивидуальная работа в двух вариантах.)
А1) Представьте произведение 7•7•7•7•x•x•x в виде степени:
(7х4) ; 2) 74 х ; 3) 74х³; 4)7х
А2) Представить в виде произведения степень (-3)3 х2
1)-3• х• х; 2) -3• 3•3 •х•х ; 3)(-3)(-3)(-3)х•х 4) -3•х
A3) Вычислите: -2• 32 + 4• 53
464; 2) 482; 3) 518; 4) -1018
Количество заданий в тесте я подбираю в соответствии с подготовкой уровня класса.
Слайд 7
Описание слайда:
Шаг 3 и Шаг 4
Задача: 1)вычислите: 2 2 •2 3 = ? 33 •32 •3 =?
2)Упростите: а 2 а 20 = ? b 30 •b 10 •b 15 = ?
В ходе решения задачи 1) и 2) учащиеся предлагают решение, а я, как учитель, организую класс на нахождение способа для упрощения степеней при умножении с одинаковыми основаниями.
Учитель: придумать способ для упрощения степеней при умножении с одинаковыми основаниями.
На кластере появляется запись:
показатели степеней
При умножении При делении
+ -
С одинаковыми основаниями
Формулируется тема урока.
Слайд 8
Описание слайда:
Шаг 3 Шаг 4 показатели степеней При умножении При делении С одинаковыми основаниями
Слайд 9
Описание слайда:
Шаг 3,4
Формулируется тема урока. Умножение степеней.
Учитель: придумайте правило деления степеней с одинаковыми основаниями.
Рассуждения: каким действием проверяется деление?
а5 : а 3 = ? , что а2• а3 = а5
Возвращаюсь к схеме – кластер и дополняем запись — … при делении вычитаем и дописываем тему урока. … и деление степеней. 4)Сообщение учащимся пределов познания (как минимум и как максимум).
Учитель: задачей минимума на сегодняшний урок является научиться применять свойства умножения и деления степеней с одинаковыми основаниями, а максимума: применять умножение и деление совместно.
На доске записываем: аm• аn = аm+n ; аm : аn = аm-n
4)Сообщение учащимся пределов познания (как минимум и как максимум).
Учитель: задачей минимума на сегодняшний урок является научиться применять свойства умножения и деления степеней с одинаковыми основаниями, а максимума: применять умножение и деление совместно.
На доске записываем: аm• аn = аm+n ; аm : аn = аm-n
Слайд 10
Описание слайда:
Шаг3,4 показатели степеней При умножении При делении С одинаковыми основаниями
Слайд 11
Описание слайда:
Шаг 5
а) По учебнику:
№403 (а, в, д) задания с разными формулировками
№404 (а, д, е) самостоятельная работа, затем организую взаимопроверку, даю ключи. б) При каком значении m справедливо равенство? а16 • аm = а32 ; хh • х14 = х28; х8 •(*) = х14
Задание: придумать аналогичные примеры для деления.
в) № 417(а), №418 (а)
Ловушки для учеников: х 3 • х n= х3n ; 3 4 •3 2 = 96;
а 16: а 8 = а2.
6) Обобщение изученного, проведение диагностической работы ( что побуждает учеников, а не учителя изучать данную тему ) (шаг 6)
б) При каком значении m справедливо равенство? а16 • аm = а32 ; хh • х14 = х28; х8 •(*) = х14
Задание: придумать аналогичные примеры для деления.
в) № 417(а), №418 (а)
Ловушки для учеников: х 3 • х n= х3n ; 3 4 •3 2 = 96;
а 16: а 8 = а2.
6) Обобщение изученного, проведение диагностической работы ( что побуждает учеников, а не учителя изучать данную тему ) (шаг 6)
Слайд 12
Описание слайда:
Шаг 6
6) Обобщение изученного, проведение диагностической работы ( что побуждает учеников, а не учителя изучать данную тему ) (шаг 6)
Диагностическая работа.
Тест ( ключи поместить на обратной стороне теста).
Варианты заданий:
представьте в виде степени частное х15: х3;
представьте в виде степени произведение (-4)2(-4)5(-4)7; при каком m справедливо равенство а16• аm = а32; найдите значение выражения h0 : h3 при h =0,2; вычислите значение выражения (52 •50 ) : 52.
Слайд 13
Описание слайда:
Итог урока. Рефлексия. Делю класс на две группы.
Итог урока. Рефлексия. Делю класс на две группы.
Найдите аргументы I группа : в пользу знания свойств степени, а II группа – аргументы, которые будут говорить о том, что можно обойтись без свойств . Все ответы выслушиваем, делаем выводы. На последующих уроках можно предложить статистические данные и назвать рубрику «В голове не укладывается!»
Средний человек съедает 32• 10 2 кг огурцов в течение жизни.
Оса способна совершить беспосадочный перелёт на 3,2• 10 2 км.
Когда стекло трескается, трещина распространяется со скоростью около 5 •10 3 км/ч.
Лягушка съедает за свою жизнь более 3 тонн комаров. Используя степень, запишите в кг.
Наиболее плодовитой считается океанская рыба – луна ( Моlа mola), которая откладывает за один нерест до 300000000 икринок диаметром около 1,3 мм.
Слайд 14
Описание слайда:
7) Домашнее задание. Историческая справка. Какие числа называют числами Ферма. 7) Домашнее задание. Историческая справка. Какие числа называют числами Ферма. П.19. №403, №408, №417 Используемая литература: 1) Учебник «Алгебра -7» , авторы Ю.Н.Макарычев, Н.Г.Миндюк и др. 2)Дидактический материал для 7 класса, Л.В.Кузнецова, Л.И. Звавич, С.Б.Суворова. 3)Энциклопедия по математике. 4) Журнал «Квант» 5) СМИ
Слайд 15
Описание слайда:
Слайд 16
Описание слайда:
Задачи учителя на стадии «осмысления»: создать условия для анализа и систематизации учащимся информации; помочь соотнести старые знания с новыми; обеспечить учащемуся возможность задуматься о природе изучаемого объекта, научиться формулировать вопросы по мере соотнесения старой и новой информации Из технологии критического мышления
Слайд 17
Описание слайда:
Кластеры: последовательность действий
Посередине чистого листа (классной доски) необходимо написать ключевое слово или тезис, который является «сердцем» текста. Вокруг «накидать» слова или предложения, выражающие идеи, факты, образы, подходящие для данной темы.
По мере записи, появившиеся слова соединяются прямыми линиями с ключевым понятием. У каждого из «спутников» в свою очередь тоже появляются «спутники», устанавливаются новые логические связи.
Вокруг «накидать» слова или предложения, выражающие идеи, факты, образы, подходящие для данной темы.
По мере записи, появившиеся слова соединяются прямыми линиями с ключевым понятием. У каждого из «спутников» в свою очередь тоже появляются «спутники», устанавливаются новые логические связи.
Слайд 18
Описание слайда:
Правила в работе над кластерами: Не бояться записывать все, что приходит на ум. Дать волю воображению и интуиции. Продолжать работу, пока не кончится время или идеи не иссякнут. Постараться построить как можно больше связей. Не следовать по заранее определенному плану.
Слайд 19
Описание слайда:
Приём «Вопросительные слова» используется тогда, когда учащиеся уже имеют некоторые сведения по теме и ориентируются в ряде базовых понятий, связанных с изучаемым материалом; «Вопросительные слова» помогают им создать так называемое «поле интереса»; учащиеся учатся задавать вопросы
Слайд 20
Описание слайда:
Мысли по аналогии: вопросы для оценки степени понимания «На что это похоже?» «С чем (кем) это можно сравнить?» «Встречали ли Вы нечто подобное раньше?» «Где мы уже с этим сталкивались?»
шагов в обучении делению в длину с основанием, отличным от 10
••• Hemera Technologies/AbleStock. com/Getty Images
com/Getty Images
Обновлено 25 апреля 2017 г. может показаться сложным, потому что вы всегда работали с основанием десять. Выполнение длинного деления включает в себя оценку, умножение и вычитание, но этот процесс упрощается всеми обычными математическими фактами, которые вы запомнили с начальной школы. Поскольку эти математические факты часто неприменимы к другим системам счисления, кроме десяти, вам нужно найти способы компенсировать недостаток.
При нахождении кратных и вычитании из делимого всегда помните, что вы не работаете с основанием десять, поэтому обычные факты умножения могут не применяться.
 Вы можете проверить свой ответ, переведя делитель, делимое и ответ в десятичную систему счисления. Калькулятор, вероятно, не даст правильного ответа в системе счисления, которую вы используете, если только он не способен выполнять вычисления в системе счисления, отличной от десяти. При работе с основанием большим, чем десять, помните, что другие символы (например, алфавит) должны будут служить цифрами для 11, 12 и т. д.
Вы можете проверить свой ответ, переведя делитель, делимое и ответ в десятичную систему счисления. Калькулятор, вероятно, не даст правильного ответа в системе счисления, которую вы используете, если только он не способен выполнять вычисления в системе счисления, отличной от десяти. При работе с основанием большим, чем десять, помните, что другие символы (например, алфавит) должны будут служить цифрами для 11, 12 и т. д.
Перечислите однозначные числа, кратные делителю в новом основании. В качестве примера приведем задачу на деление по основанию семь. Если бы вы делили 1431 (по основанию 7) на 23 (по основанию 7), вы бы сначала перечислили 23 х 1 = 23, 23 х 2 = 46, 23 х 3 = 102, 23 х 4 = 125, 23 х 5 = 151 и 23 х 6 = 204. Поскольку вы работаете с основанием семь, вам не нужно умножать делитель более чем на 6. Это устраняет недостаток незнания фактов умножения в этом основании. Если бы вы работали с другой базой, вы бы указали другие множители
Выберите наибольшее кратное, которое не больше первых цифр делимого. В данном примере подходящим кратным будет 125, поскольку 151 и 204 больше 143. Напишите «4» над делимым, поскольку 23 (по основанию 7) умножить на 4 равно 125 (по основанию 7).
В данном примере подходящим кратным будет 125, поскольку 151 и 204 больше 143. Напишите «4» над делимым, поскольку 23 (по основанию 7) умножить на 4 равно 125 (по основанию 7).
Вычтите соответствующее кратное из первых цифр делимого. В примере 143 (по основанию 7) минус 125 (по основанию 7) равно 15 (по основанию 7).
Уменьшите все конечные цифры. В этом примере уменьшите «1», чтобы получить временный остаток 151 (основание 7).
Повторяйте шаги до тех пор, пока остаток не станет меньше делителя. Из списка кратных 23 x 5 = 151, поэтому напишите «5» над делимым справа от 4 и вычтите 151 из 151, что оставит вас с нулем.
Запишите любой остаток больше нуля справа от ответа, поставив перед ним заглавную «R». В примере конечный остаток равен нулю, поэтому нет необходимости указывать какой-либо остаток. Окончательный ответ на 1431 (основание 7), деленное на 23 (основание 7), равно 45 (основание 7).
Связанные статьи
Ссылки
- MATH Central: Дивизион в разных базах
- Purple Math ‘: Количество базы
- Бакс Общественный колледж: подразделение Powerpoint
Советы
- 444. делимое, всегда помните, что вы не работаете с основанием десять, поэтому обычные факты умножения могут не применяться.
- Вы можете проверить свой ответ, переведя делитель, делимое и ответ в десятичную систему счисления.
- Калькулятор, вероятно, не даст правильного ответа в системе счисления, которую вы используете, если только он не способен выполнять вычисления в системе счисления, отличной от десяти.

- При работе с основанием большим, чем десять, помните, что другие символы (например, алфавит) должны будут использоваться для обозначения цифр 11, 12 и т. д. . Он имеет степень бакалавра Южного Бирмингемского колледжа и степень магистра специального образования Университета Элона. Талмадж является переводчиком-добровольцем в Государственном историческом музее Беннет-плейс.
Авторы фотографий
Hemera Technologies/AbleStock.com/Getty Images
5.5: Деление многочленов — Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 18358 9{2}+\frac{5}{2}x+1\)
Деление на многочлен
Тот же метод, описанный для деления на одночлен , не работает для многочленов с двумя или более членами в знаменателе.
 В этом разделе мы рассмотрим процесс, называемый полиномиальным делением в длину, который основан на алгоритме деления действительных чисел. Для ясности будем считать, что все выражения в знаменателе отличны от нуля.
В этом разделе мы рассмотрим процесс, называемый полиномиальным делением в длину, который основан на алгоритме деления действительных чисел. Для ясности будем считать, что все выражения в знаменателе отличны от нуля.Пример \(\PageIndex{5}\) 9{2}−8x−4\) — делимое.
Шаг 1 : Чтобы определить первый член частного, разделите старший член делимого на старший член делителя.
Рисунок \(\PageIndex{1}\)Шаг 2 : Умножьте первый член частного на делитель, не забывая о распределении, и выровняйте такие же члены с делимым.
Рисунок \(\PageIndex{2}\)Шаг 3 : Вычтите полученное количество из делимого. Постарайтесь вычесть оба члена.
Рисунок \(\PageIndex{3}\)Шаг 4 : Сократите оставшиеся термины и повторите процесс с шага 1.
Рисунок \(\PageIndex{4}\)Обратите внимание, что начальный термин удален и что результат имеет степень, на единицу меньшую, чем делимое. Полный процесс показан ниже:
Рисунок \(\PageIndex{5}\)Полиномиальное длинное деление заканчивается, когда степень остатка меньше степени делителя.
 Здесь остаток равен \(0\). Следовательно, бином делит многочлен равномерно, и ответом является частное, показанное над линией деления. 9{2}+5x+2\)
Здесь остаток равен \(0\). Следовательно, бином делит многочлен равномерно, и ответом является частное, показанное над линией деления. 9{2}+5x+2\)Далее мы продемонстрируем случай, когда остаток не равен нулю.
Рисунок \(\PageIndex{6}\)Как и в случае с действительными числами, окончательный ответ добавляет к частному дробь, в которой остаток является числителем, а делитель — знаменателем. В общем, при делении мы имеем
\[\frac{dividend}{divisor}=\color{Cerulean}{quotient}\color{black}{+\frac{\color{OliveGreen}{remainder}}{divisor} }\]
Если обе части умножить на делитель, то получится 9{2})÷(2x)=3x\). Умножьте \(3x\) на делитель \(2x−1\) и выровняйте результат с одинаковыми членами делимого.
Рисунок \(\PageIndex{8}\)Вычтите результат из делимого и уменьшите постоянный член \(+3\).
Рисунок \(\PageIndex{9}\)Вычитание удаляет главный член и \(-5x-(-3x)=-5x+3x=-2x\). Частное \(−2x\) и \(2x\) равно \(−1\). Умножьте \(2x−1\) на \(−1\) и выровняйте результат.
Рисунок \(\PageIndex{10}\)
Вычтем еще раз и заметим, что у нас остался остаток. 9{2}−x+1−\frac{7}{5}x−3\)
Разделение полиномиальных функций
Мы можем использовать обозначение функции для обозначения деления следующим образом:
Разделение функций: \((f/g)(x)=\frac{f(x)}{g(x)}\) Таблица \(\PageIndex{1}\) Частное двух полиномиальных функций не обязательно имеет область определения всех действительных чисел. Значения для \(x\), которые составляют функцию в знаменателе \(0\), ограничены доменом. Это будет обсуждаться более подробно позднее. Пока предположим, что все функции в знаменателе отличны от нуля. 9{2}+2x-3-\frac{4}{3x-1}\)
Замените \(−1\) на переменную \(x\).
Ответ :
\((f/g)(-1)=-5\)
Ключевые выводы
- При делении на одночлен разделите все члены в числителе на одночлен, а затем упростите каждое слагаемое.


 Вы можете проверить свой ответ, переведя делитель, делимое и ответ в десятичную систему счисления. Калькулятор, вероятно, не даст правильного ответа в системе счисления, которую вы используете, если только он не способен выполнять вычисления в системе счисления, отличной от десяти. При работе с основанием большим, чем десять, помните, что другие символы (например, алфавит) должны будут служить цифрами для 11, 12 и т. д.
Вы можете проверить свой ответ, переведя делитель, делимое и ответ в десятичную систему счисления. Калькулятор, вероятно, не даст правильного ответа в системе счисления, которую вы используете, если только он не способен выполнять вычисления в системе счисления, отличной от десяти. При работе с основанием большим, чем десять, помните, что другие символы (например, алфавит) должны будут служить цифрами для 11, 12 и т. д.
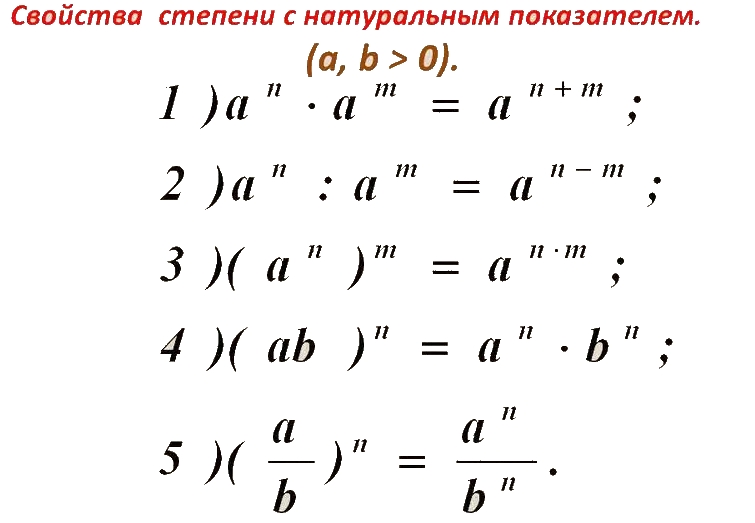 В этом разделе мы рассмотрим процесс, называемый полиномиальным делением в длину, который основан на алгоритме деления действительных чисел. Для ясности будем считать, что все выражения в знаменателе отличны от нуля.
В этом разделе мы рассмотрим процесс, называемый полиномиальным делением в длину, который основан на алгоритме деления действительных чисел. Для ясности будем считать, что все выражения в знаменателе отличны от нуля. Здесь остаток равен \(0\). Следовательно, бином делит многочлен равномерно, и ответом является частное, показанное над линией деления. 9{2}+5x+2\)
Здесь остаток равен \(0\). Следовательно, бином делит многочлен равномерно, и ответом является частное, показанное над линией деления. 9{2}+5x+2\)
