При каком значении векторы перпендикулярны: При каком значении n векторы a(n;-2;1) и b (n,n;1) перпендикулярны ?

Содержание

Условие ортогональности векторов — онлайн калькулятор

Справочник
Онлайн-калькуляторы
Тесты с ответами

Ортогональные (перпендикулярные) векторы образуют между собой прямой угол. 2 вектора ортогональны, если их скалярное произведение равно 0. Теперь помощь в автоматических расчетах и доказательстве вы можете получить онлайн.

Вычислять, ортогональны ли векторы, понадобится школьникам и студентам при решении плоских и пространственных задач. Для получения точного ответа воспользуйтесь нашим сервисом. Решение доступно без регистрации и оплаты.

Задайте размерность векторов. Число меняется кнопками «+», «-».

Вариант 1.

Выберите представление векторов координатами.

Выберите представление векторов координатами.
Выберите представление векторов координатами

Вариант 2.

Выберите представление векторов точками
Выберите представление векторов точками
Выберите представление векторов точками

Находим скалярное произведение векторов и сравниваем его с 0. Получаем ответ.

Материалы, которые помогут вам лучше разобраться в теме:

Векторы на плоскости и в пространстве — основные определения
Координаты вектора в декартовой системе координат (ДСК)
Нахождение длины вектора, примеры и решения
Нахождение координат вектора через координаты точек

Ответ:

Решение

Ответ:

list» :key=»`error-${eIdx}`» v-html=»e»/>

Похожие калькуляторы:

Длина вектора. Модуль вектора
Векторное произведение векторов
Умножение вектора на число

Угол между векторами
Смешанное произведение векторов
Сложение и вычитание двух векторов

Скалярное произведение векторов
Определение вектора по двум точкам
Разложение вектора по базису
Проверить являются ли вектора базисом

Компланарность векторов
Коллинеарность векторов
Проекция вектора на вектор

Площадь треугольника, построенного на векторах
Площадь параллелограмма, построенного на векторах

Проверка ортогональности векторов калькулятором

К основным условиям ортогональности векторов добавляется правило. При умножении любого из двух векторов на произвольное вещественное число их ортогональность не нарушается. Каждый из признаков можно проверить самостоятельно. Для этого потребуется:

найти скалярное произведение векторов;
сравнить результат с 0.

Если ответ нужен срочно или надо свериться с вычислениями, чтобы найти ошибку, отправьте задание на расчет. Благодаря неограниченному количеству доступных проверок подготовка к занятиям станет более качественной. Закрепленный на практике материал быстрее усваивается. Учащийся сможет в дальнейшем применять изученный алгоритм в подобных задачах.

Формула в калькуляторе определяет, при каком значении векторы ортогональны. Расчет происходит по заданным вами условиям – через координаты или точки. Вы получаете готовое решение с последовательными вычислениями и ответом.

В разделе с векторами вы найдете другие калькуляторы, которые позволят так же быстро справиться с доказательством их свойств. Действуйте по инструкции и получайте правильные ответы.

Если тема не усваивается, обратитесь к нам и получите недорогой урок от опытного преподавателя.

Понравился калькулятор? Поделись с друзьями!

Разделы калькуляторов

Решение матриц
Точка, прямая, плоскость
Конвертеры
Объем фигур
Калькуляторы площади фигур
Решение уравнений
Операции над векторами
Периметр фигур

Поможем с любой работой

Дипломные работы
Курсовые работы
Рефераты
Контрольные работы
Решение задач
Отчеты по практике

Все наши услуги

Узнай бесплатно стоимость работы

Не получается написать работу самому?

Доверь это кандидату наук!

Как найти вектор перпендикулярный вектору

ФОРМУЛА

Чтобы вектор $\ \overline{a}$ был перпендикулярен вектору $\ \overline{b}$ , необходимо, чтобы его скалярное произведение было равно нулю, т. е.

$\ (\overline{a}, \overline{b})=0 $

Если векторы задаются на плоскости своими координатами $\ \overline{a}=\left(a_{x} ; a_{y}\right) $ и $\ \overline{b}=\left(b_{x} ; b_{y}\right) $, то условие их перпендикулярности принимает вид:

$\ (\overline{a}, \overline{b})=a_{x} \cdot b_{x}+a_{y} \cdot b_{y}=0 $

Если векторы заданы в пространстве и имеют координаты $\ \overline{a}=\left(a_{x} ; a_{y} ; a_{z}\right) $ и $\ \overline{b}=\left(b_{x} ; b_{y} ; b_{z}\right) $, то перпендикулярное условие записывается в виде:

$\ (\overline{a}, \overline{b})=a_{x} \cdot b_{x}+a_{y} \cdot b_{y}+a_{z} \cdot b_{z}=0 $

ПРИМЕРЫ РАСПОЛОЖЕНИЯ ПЕРПЕНДИКУЛЯРНОГО ВЕКТОРА

ПРИМЕР

Задание: Даны два вектора $\ \overline{a}=(2 ;-1) $ и $\ \overline{b}=(-3 ; m) $ . При каком значении $\ m $ эти векторы будут перпендикулярны?

Решение: Чтобы векторы $\ \overline{a} $ и $\ \overline{b} $ были перпендикулярны, необходимо, чтобы их скалярное произведение было равно нулю, то есть условие выполняется:

$\ (\overline{a}, \overline{b})=a_{x} \cdot b_{x}+a_{y} \cdot b_{y}=0 $

Подставляем координаты указанных векторов в это выражение и из полученного равенства находим $\ m $:

$\ 2 \cdot(-3)+(-1) \cdot m=0 $

$\ -6-m=0 $

$\ m=-6 $

Ответ: Векторы $\ \overline{a} $ и $\ \overline{b} $ будут перпендикулярны $\ m=-6 $

ПРИМЕР

Задание: Два вектора $\ \overline{a}=(3 ;-2 ; m) $ и $\ \overline{b}=(-1 ; m ; 1) $ даны.

При каком значении $\ m $ эти векторы будут перпендикулярны?

Решение: $\ \overline{a}$ и $\ \overline{b}$ будут перпендикулярны, когда их скалярное произведение равно нулю. А поскольку векторы заданы в пространстве, условие должно быть выполнено:

$\ (\overline{a}, \overline{b})=a_{x} \cdot b_{x}+a_{y} \cdot b_{y}+a_{z} \cdot b_{z}=0 $

Подставив в него указанные координаты векторов, мы получим:

$\ 3 \cdot(-1)+(-2) \cdot m+m \cdot 1=0 $

$\ 3-2 \cdot m+m=0 $

Из полученного уравнения находим $\ m=-6 $:

$\ 3-m=0 \Rightarrow m=-3 $

Ответ: Векторы $\ \overline{a}$ и $\ \overline{b}$ будут перпендикулярны $\ m=-3 $

Физика

166

Реклама и PR

Педагогика

Психология

Социология

Астрономия

Биология

Культурология

Экология

Право и юриспруденция

Политология

Экономика

Финансы

История

Философия

Информатика

Право

Информационные технологии

Экономическая теория

Менеджент

719

Математика

338

Химия

Микро- и макроэкономика

Медицина

Государственное и муниципальное управление

География

542

Информационная безопасность

Аудит

Безопасность жизнедеятельности

Архитектура и строительство

Банковское дело

Рынок ценных бумаг

Менеджмент организации

Маркетинг

238

Кредит

Инвестиции

Журналистика

Конфликтология

Этика

Формулы дифференцирования Как найти вектор коллинеарный вектору Как найти смешанное произведение векторов Как найти векторное произведение векторов Как найти скалярное произведение векторов

Узнать цену работы

Узнай цену

своей работы

Имя

Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругое

Принимаю Политику конфиденциальности

Подпишись на рассылку, чтобы не пропустить информацию об акциях

Как доказать что векторы перпендикулярны

Содержание

Необходимое и достаточное условие перпендикулярности двух векторов
Условие перпендикулярности на координатной плоскости
Нахождение вектора, перпендикулярного данному
Нахождение координат вектора, перпендикулярного двум заданным векторам

Ключевые слова:
перпендикулярность, прямая линия, параллельность, вектор, коллинеарные вектора, координаты

Условие перпендикулярности векторов

Условие коллинеарности векторов

См. также:
Углы на плоскости, Координаты вектора

Напомним определение перпендикулярных векторов на плоскости и в трехмерном пространстве.

Два ненулевых вектора называются перпендикулярными, если угол между ними равен девяноста градусам ( радиан).

Для перпендикулярности двух ненулевых векторов и необходимо и достаточно, чтобы их скалярное произведение равнялось нулю, то есть, чтобы выполнялось равенство .

Пусть векторы и перпендикулярны. Докажем выполнение равенства .

По определению скалярное произведение векторов равно произведению их длин на косинус угла между ними. Так как векторы и перпендикулярны, то угол между ними равен девяноста градусам, следовательно, , что и требовалось доказать.

Переходим ко второй части доказательства.

Теперь считаем, что . Докажем, что векторы и перпендикулярны.

Так как векторы и ненулевые, то из равенства следует, что . Таким образом, косинус угла между векторами и равен нулю, следовательно, угол равен , что указывает на перпендикулярность векторов и .

Итак, необходимое и достаточное условие перпендикулярности двух векторов полностью доказано.

Как же выглядит условие перпендикулярности двух векторов в координатной форме?

В разделе скалярное произведение в координатах мы показали, что для двух векторов с заданными координатами и на плоскости справедливо равенство , а для двух векторов и в пространстве . Таким образом, необходимое и достаточное условие перпендикулярности двух векторов в координатах имеет вид на плоскости, а в трехмерном пространстве .

Рассмотрим применение полученных условий на практике, для этого разберем решение нескольких примеров.

Перпендикулярны ли векторы .

Вычислим их скалярное произведение по координатам . Следовательно, условие перпендикулярности двух векторов на плоскости выполнено, то есть, они перпендикулярны.

да, векторы перпендикулярны.

Перпендикулярны ли векторы и , где — координатные векторы прямоугольной системы координат в трехмерном пространстве.

Векторы и имеют соответственно координаты и (при необходимости смотрите статью координаты вектора в прямоугольной системе координат). Проверим выполнение необходимого и достаточного условия перпендикулярности двух векторов:

Так как , то векторы и не перпендикулярны.

нет, не перпендикулярны.

Найдите значение , при котором векторы и перпендикулярны.

Воспользуемся условием перпендикулярности двух векторов в пространстве в координатной форме

векторы перпендикулярны при .

В некоторых случаях возможно ответить на вопрос о перпендикулярности двух векторов без использования необходимого и достаточного условия перпендикулярности. Например, когда известны длины всех сторон треугольника, построенного на двух векторах, то можно найти угол между векторами и посмотреть, равен ли он девяноста градусам.

Стороны АВ, АС и ВС треугольника АВС равны соответственно 8, 6 и 10 см. Убедитесь, что векторы и перпендикулярны.

Если векторы и перпендикулярны, то треугольник АВС – прямоугольный и его гипотенузой является сторона ВС. Тогда по теореме Пифагора должно выполняться равенство . Проверим его справедливость: .

Следовательно, АВ и АС – катеты прямоугольного треугольника АВС, поэтому, векторы и перпендикулярны.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8828 — | 7538 — или читать все.

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Данная статья раскрывает смысл перпендикулярности двух векторов на плоскости в трехмерном пространстве и нахождение координат вектора, перпендикулярному одному или целой паре векторов.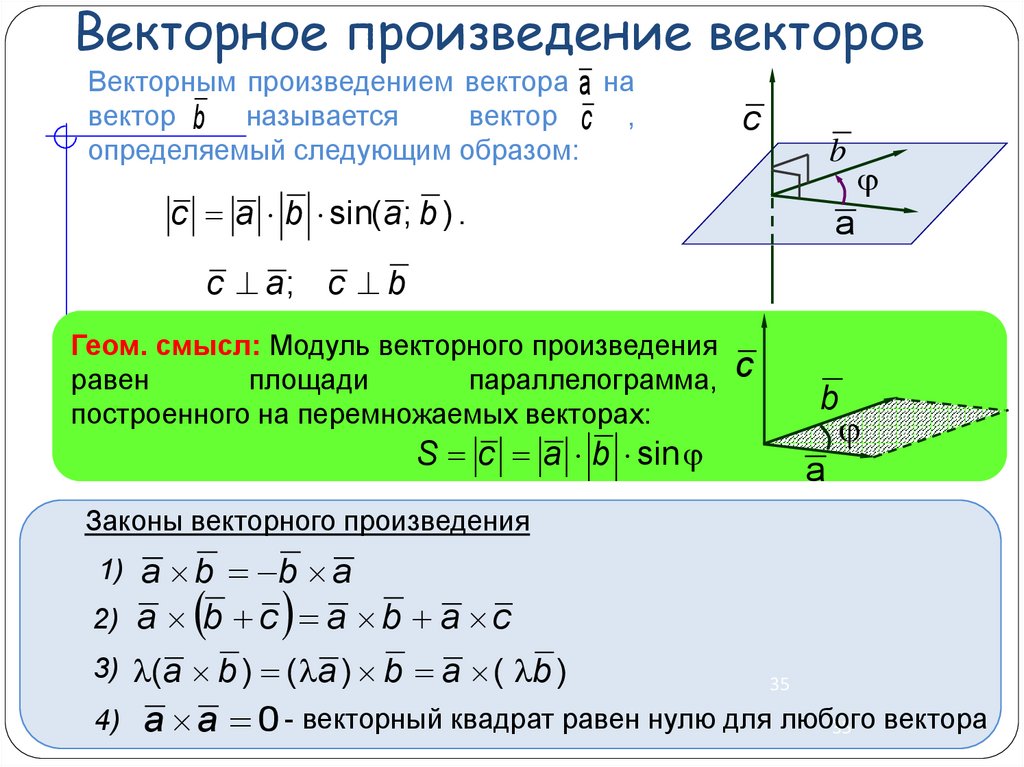 Тема применима для задач, связанных с уравнениями прямых и плоскостей.

Мы рассмотрим необходимое и достаточное условие перпендикулярности двух векторов, решим по методу нахождения вектора, перпендикулярному заданному, затронем ситуации по отысканию вектора, который перпендикулярен двум векторам.

Необходимое и достаточное условие перпендикулярности двух векторов

Применим правило о перпендикулярных векторах на плоскости и в трехмерном пространстве.

При условии значения угла между двумя ненулевыми векторами равным 90 ° ( π 2 радиан) называют перпендикулярными.

Что это значит, и в каких ситуациях необходимо знать про их перпендикулярность?

Установление перпендикулярности возможно через чертеж. При отложении вектора на плоскости от заданных точек можно геометрически измерить угол между ними. Перпендикулярность векторов если и будет установлена, то не совсем точно. Чаще всего данные задачи не позволяют делать это при помощи транспортира, поэтому данный метод применим только в случае, когда ничего больше о векторах неизвестно.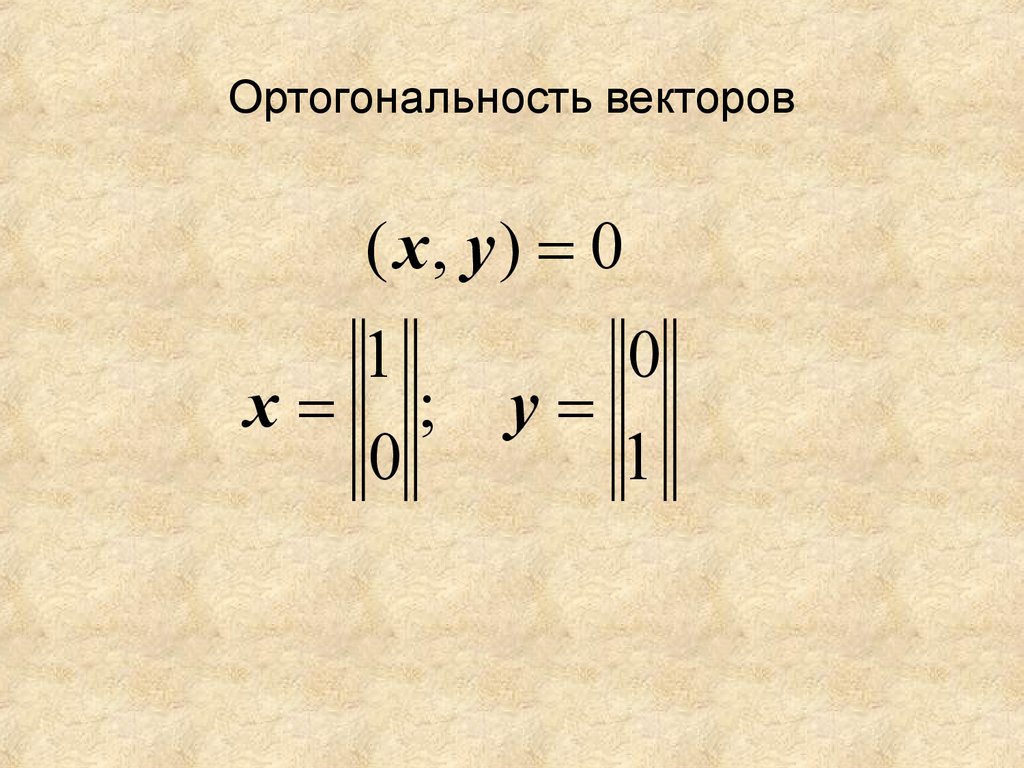 векторов a → и b → равен 90 ° . По определению это и есть необходимое и достаточное свойство.

Условие перпендикулярности на координатной плоскости

Раздел скалярного произведения в координатах демонстрирует неравенство ( a → , b → ) = a x · b x + a y · b y , справедливое для векторов с координатами a → = ( a x , a y ) и b → = ( b x , b y ) , на плоскости и ( a → , b → ) = a x · b x + a y · b y для векторов a → = ( a x , a y , a z ) и b → = ( b x , b y , b z ) в пространстве. Необходимым и достаточным условием перпендикулярности двух векторов в координатной плоскости имеет вид a x · b x + a y · b y = 0 , для трехмерного пространства a x · b x + a y · b y + a z · b z = 0 .

Применим на практике и рассмотрим на примерах.

Проверить свойство перпендикулярности двух векторов a → = ( 2 , — 3 ) , b → = ( — 6 , — 4 ) .

Для решения данной задачи необходимо найти скалярное произведение. Если по условию оно будет равным нулю, значит, они перпендикулярны.

( a → , b → ) = a x · b x + a y · b y = 2 · ( — 6 ) + ( — 3 ) · ( — 4 ) = 0 . Условие выполнено, значит, заданные векторы перпендикулярны на плоскости.

Ответ: да, заданные векторы a → и b → перпендикулярны.

Даны координатные векторы i → , j → , k → . Проверить, могут ли векторы i → — j → и i → + 2 · j → + 2 · k → быть перпендикулярными.

Для того, чтобы вспомнить, как определяются координаты вектора, нужно прочитать статью про координаты вектора в прямоугольной системе координат. Таким образом получаем, что у заданных векторов i → — j → и i → + 2 · j → + 2 · k → имеются соответствующие координаты ( 1 , — 1 , 0 ) и ( 1 , 2 , 2 ) . Подставляем числовые значения и получаем: i → + 2 · j → + 2 · k → , i → — j → = 1 · 1 + ( — 1 ) · 2 + 0 · 2 = — 1 .

Выражение не равно нулю, ( i → + 2 · j → + 2 · k → , i → — j → ) ≠ 0 , а это означает, что векторы i → — j → и i → + 2 · j → + 2 · k → не перпендикулярны, так как условие не выполнилось.

Ответ: нет, векторы i → — j → и i → + 2 · j → + 2 · k → не перпендикулярны.

Даны векторы a → = ( 1 , 0 , — 2 ) и b → = ( λ , 5 , 1 ) . Найти значение λ , при котором данные векторы перпендикулярны.

Используем условие перпендикулярности двух векторов в пространстве в квадратной форме, тогда получим

a x · b x + a y · b y + a z · b z = 0 ⇔ 1 · λ + 0 · 5 + ( — 2 ) · 1 = 0 ⇔ λ = 2

Ответ: векторы перпендикулярны при значении λ = 2 .

Имеются случаи, когда вопрос о перпендикулярности невозможен даже при необходимом и достаточном условии. При известных данных о трех сторонах треугольника на двух векторах, возможно, найти угол между векторами и проверить его.

Дан треугольник А В С со сторонами А В = 8 , А С = 6 , В С = 10 см. проверить на перпендикулярность векторы A B → и A C → .

При перпендикулярности векторов A B → и A C → треугольник A B C считается прямоугольным. Тогда применим теорему Пифагора, где В С – гипотенуза треугольника. Равенство B C 2 = A B 2 + A C 2 должно выполниться. Отсюда следует, что 10 2 = 8 2 + 6 2 ⇔ 100 = 100 . Значит, А В и А С являются катетами треугольника А В С , следовательно, A B → и A C → перпендикулярны.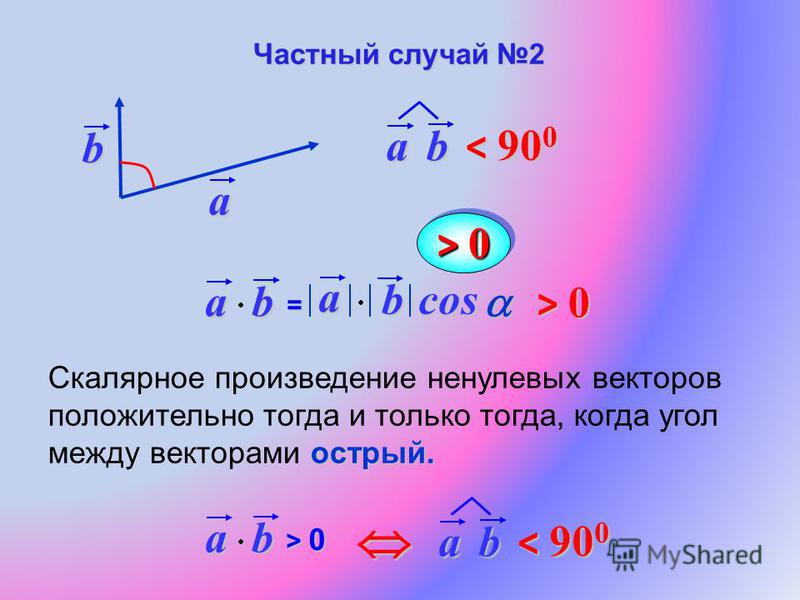

Нахождение вектора, перпендикулярного данному

Важно научиться находить координаты вектора, перпендикулярного заданному. Это возможно как на плоскости, так и в пространстве при условии перпендикулярности векторов.

Нахождение вектора, перпендикулярного данному в плоскости.

Ненулевой вектор a → может иметь бесконечное количество перпендикулярных векторов на плоскости. Изобразим это на координатной прямой.

Задан ненулевой вектор a → , лежащий на прямой а. Тогда заданный b → , расположенный на любой прямой, перпендикулярной прямой а, становится перпендикулярным и a → . Если вектору i → перпендикулярен вектор j → или любой из векторов λ · j → при λ равной любому действительному числу кроме нуля, то нахождение координат вектора b → , перпендикулярному a → = ( a x , a y ) , сводится к бесконечному множеству решений. Но необходимо найти координаты вектора, перпендикулярного a → = ( a x , a y ) . Для этого необходимо записать условие перпендикулярности векторов в такой форме a x · b x + a y · b y = 0 .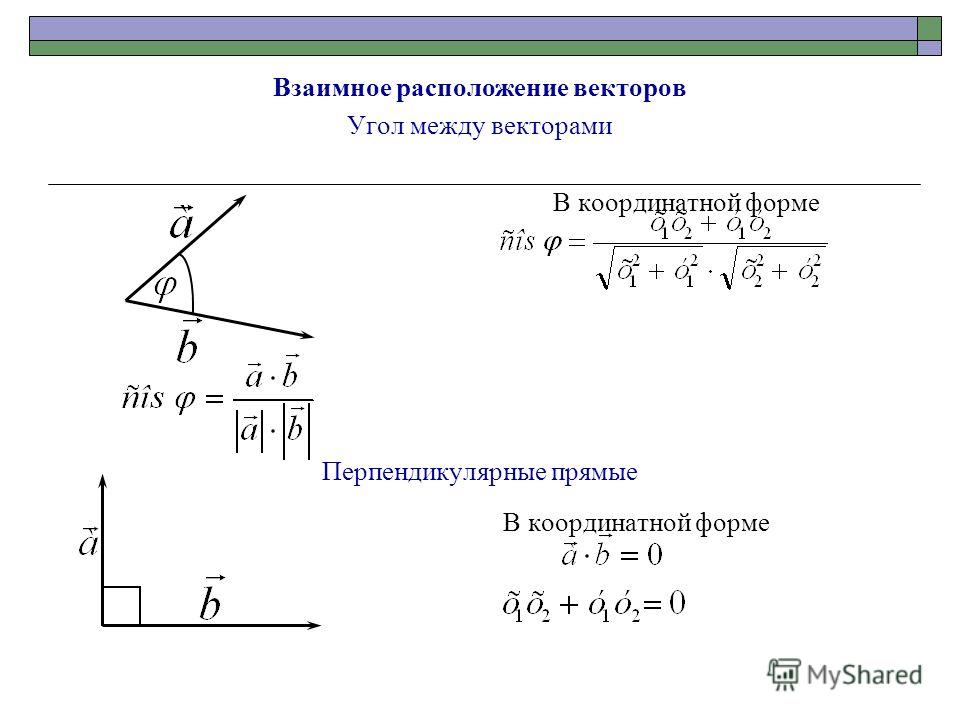 Имеем b x и b y , являющиеся искомыми координатами перпендикулярного вектора. Когда a x ≠ 0 , значение b y является ненулевым, а b x вычислим из неравенства a x · b x + a y · b y = 0 ⇔ b x = — a y · b y a x . При a x = 0 и a y ≠ 0 присваиваем b x любое значение кроме нуля, а b y находим из выражения b y = — a x · b x a y .

Дан вектор с координатами a → = ( — 2 , 2 ) . Найти перпендикулярный данному вектор.

Обозначим искомый вектор как b → ( b x , b y ) . Найти его координаты можно из условия перпендикулярности векторов a → и b → . Тогда получим: ( a → , b → ) = a x · b x + a y · b y = — 2 · b x + 2 · b y = 0 . Присвоим b y = 1 и подставим: — 2 · b x + 2 · b y = 0 ⇔ — 2 · b x + 2 = 0 . Отсюда из формулы получим b x = — 2 — 2 = 1 2 . Значит, вектор b → = ( 1 2 , 1 ) является вектором, перпендикулярным a → .

Если ставится вопрос о трехмерном пространстве, задача решается по такому же принципу. При заданном векторе a → = ( a x , a y , a z ) существует бесконечное множество перпендикулярных векторов. Зафиксирует это на координатной трехмерной плоскости. Дана a → , лежащая на прямой a . Перпендикулярную прямой a плоскость обозначаем α . В этом случае любой ненулевой вектор b → из плоскости α перпендикулярен a → .

Необходимо найти координаты b → , перпендикулярного ненулевому вектору a → = ( a x , a y , a z ) .

Пусть задан b → с координатами b x , b y и b z . Чтобы найти их, необходимо применить определение условия перпендикулярности двух векторов. Равенство a x · b x + a y · b y + a z · b z = 0 должно выполняться. Из условия a → — ненулевой, значит, одна из координат имеет значение не равное нулю. Предположим, что a x ≠ 0 , ( a y ≠ 0 или a z ≠ 0 ). Следовательно, имеем право разделить на эту координату все неравенство a x · b x + a y · b y + a z · b z = 0 , получим выражение b x + a y · b y + a z · b z a x = 0 ⇔ b x = — a y · b y + a z · b z a x . Присваиваем координатам b y и b x любое значение, вычисляем значение b x , исходя из формулы, b x = — a y · b y + a z · b z a x . Искомый перпендикулярный вектор будет иметь значение a → = ( a x , a y , a z ) .

Рассмотрим доказательство на примере.

Дан вектор с координатами a → = ( 1 , 2 , 3 ) . Найти вектор, перпендикулярный данному.

Обозначим искомый вектор за b → = ( b x , b y , b z ) . Исходя из условия о перпендикулярности векторов, скалярное произведение должно быть равным нулю.

a ⇀ , b ⇀ = 0 ⇔ a x · b x + a y · b y + a z · b z = 0 ⇔ 1 · b x + 2 · b y + 3 · b z = 0 ⇔ b x = — ( 2 · b y + 3 · b z )

Если значение b y = 1 , b z = 1 , тогда b x = — 2 · b y — 3 · b z = — ( 2 · 1 + 3 · 1 ) = — 5 . Отсюда следует, что координаты вектора b → ( — 5 , 1 , 1 ) . Вектор b → является одним из перпендикулярных векторов заданному.

Ответ: b → = ( — 5 , 1 , 1 ) .

Нахождение координат вектора, перпендикулярного двум заданным векторам

Нужно найти координаты вектора в трехмерном пространстве. Он перпендикулярен не коллинеаренным векторам a → ( a x , a y , a z ) и b → = ( b x , b y , b z ) . При условии коллинеарности векторов a → и b → в задаче достаточно будет найти вектор, перпендикулярный a → или b → .

При решении применяется понятие векторного произведения векторов.

Векторным произведением векторов a → и b → называют вектор, одновременно перпендикулярный и a → и b → . Для решения данной задачи применяется векторное произведение a → × b → . Для трехмерного пространства имеет вид a → × b → = a → j → k → a x a y a z b x b y b z

Разберем подробнее векторное произведение на примере задачи.

Заданы векторы b → = ( 0 , 2 , 3 ) и a → = ( 2 , 1 , 0 ) . Найти координаты любого перпендикулярного вектора данным одновременно.

Для решения необходимо найти векторное произведение векторов. (Необходимо обратиться к пункту вычисления определителя матрицы для нахождения вектора). Получим :

a → × b → = i → j → k → 2 1 0 0 2 3 = i → · 1 · 3 + j → · 0 · 0 + k → · 2 · 2 — k → · 1 · 0 — j → · 2 · 3 — i → · 0 · 2 = 3 · i → + ( — 6 ) · j → + 4 · k →

Ответ: ( 3 , — 6 , 4 ) — координаты вектора, одновременно перпендикулярного заданным a → и b → .

Объяснение урока: Параллельные и перпендикулярные векторы в пространстве

В этом объяснении мы научимся распознавать параллельные и перпендикулярные векторы в пространстве.

Вектор в пространстве определяется двумя величинами: величиной и направлением. Особые отношения формируются между двумя или более векторами когда они указывают в одном направлении или в противоположных направлениях. В этом случае говорят, что векторы параллельны. Это может быть представлен математически.

Определение: параллельные векторы в пространстве

Векторы ⃑𝐴 и ⃑𝐵 параллельны тогда и только тогда, когда они скалярны. кратны друг другу: ⃑𝐴=𝑘⃑𝐵, где 𝑘 — ненулевое действительное число.

Другой способ думать об этом состоит в том, что если два вектора параллельны, то отношения каждого из их соответствующих компоненты одинаковые. Итак, если у нас есть два вектора ⃑𝐴=𝑎,𝑎,𝑎 и ⃑𝐵=𝑏,𝑏,𝑏, то 𝑎𝑏=𝑎𝑏=𝑎𝑏.

Второе особое отношение, которое может возникнуть между двумя векторами, — это когда направления двух векторов образуют 9угол 0∘. Когда это происходит, мы говорим, что два вектора перпендикулярны друг другу. Чтобы определить, когда два вектора перпендикулярны, мы можем использовать скалярное произведение.

Определение: скалярное произведение

Скалярные произведения двух векторов, ⃑𝐴 и ⃑𝐵, можно определить как ⃑𝐴⋅⃑𝐵=‖‖⃑𝐴‖‖‖‖⃑𝐵‖‖𝜃, потому что где 𝜃 — угол, образованный между ⃑𝐴 и ⃑𝐵.

В случае, когда векторы ⃑𝐴 и ⃑𝐵 перпендикулярны, 𝜃=90∘. Следовательно, cos𝜃=0, а значит, ⃑𝐴⋅⃑𝐵=0.

Примечание:

Когда два вектора параллельны, угол между ними равен 0∘ или 180∘.

Другой способ определения скалярного произведения двух векторов ⃑𝐴=𝑎,𝑎,𝑎 и ⃑𝐵=𝑏,𝑏,𝑏 находится по формуле ⃑𝐴⋅⃑𝐵=𝑎𝑏+𝑎𝑏+𝑎𝑏.

Конечно, если векторы перпендикулярны, то эта сумма произведений соответствующих компонент будет равна нулю: 𝑎𝑏+𝑎𝑏+𝑎𝑏=0.

Определение: перпендикулярные векторы в пространстве

Векторы ⃑𝐴 и ⃑𝐵 перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю: ⃑𝐴⋅⃑𝐵=0.

Давайте теперь рассмотрим несколько примеров с параллельными и перпендикулярными векторами.

Пример 1. Использование свойств параллельных и перпендикулярных векторов для решения задачи

Верно или неверно: если составляющая вектора в направлении другого вектора равна нулю, то они параллельны.

Ответ

Чтобы наглядно представить, что здесь происходит, начнем с рассмотрения двух векторов, ⃑𝐴 и ⃑𝐵. Это могут быть любые два произвольных вектора. Предположим, что эти векторы начинаются в одной и той же точке. Вот как они могут выглядеть.

Теперь добавим компонент ⃑𝐴 в направлении ⃑𝐵.

Используя эту диаграмму вместе с некоторой правой тригонометрией, мы можем видеть, что величина компонента ⃑𝐴 в направлении ⃑𝐵 можно рассчитать, используя ‖‖⃑𝐴‖‖𝜃cos.

В вопросе указано, что эта величина должна быть равна нулю. С ‖‖⃑𝐴‖‖≠0, cos𝜃 должен быть равен нулю. Решение это для 𝜃 дает нам 𝜃=90. ∘

Это говорит нам о том, что когда компонент ⃑𝐴 в направлении ⃑𝐵 равен 0, угол между векторами должен быть прямым. Следовательно, ⃑𝐴 и ⃑𝐵 перпендикулярны друг другу.

Наше решение вопроса — «Ложь»: если составляющая вектора в направлении другого вектора равна нулю, то они не параллельны.

Еще один способ решить эту задачу — изобразить два параллельных вектора, как показано на рисунке.

Поскольку векторы ⃑𝐴 и ⃑𝐵 параллельны, угол между двумя векторами 𝜃=0∘. Следовательно, составляющая ⃑𝐴 в направлении ⃑𝐵 есть ‖‖⃑𝐴‖‖(0)cos∘. С cos(0)=1∘, эта компонента есть просто вектор ⃑𝐴. ⃑𝐴 отличен от нуля; следовательно, ответ на вопрос должен быть «Неверно».

В следующем примере мы найдем недостающие параметры, чтобы два заданных вектора были параллельны.

Пример 2. Поиск пропущенного значения с помощью пары параллельных векторов

Найдите значения 𝑚 и 𝑛 так, чтобы вектор 2⃑𝑖+7⃑𝑗+𝑚⃑𝑘 параллелен вектору 6⃑𝑖+𝑛⃑𝑗−21⃑𝑘.

Ответ

Чтобы решить эту задачу, мы можем использовать тот факт, что когда два вектора параллельны друг другу, они скалярно кратны друг другу. Следовательно, 2⃑𝑖+7⃑𝑗+𝑚⃑𝑘=𝑐6⃑𝑖+𝑛⃑𝑗+21⃑𝑘, где 𝑐 — это просто константа, которую можно найти.

Приравнивая коэффициенты каждой из компонент вектора, мы получаем три уравнения: 2=6𝑐,7=𝑐𝑛,𝑚=−21𝑐.

Мы можем решить первое из этих уравнений, чтобы найти 𝑐. При этом получаем 𝑐=13.

Теперь нам просто нужно подставить это значение в два других уравнения и найти недостающие значения. Чтобы найти 𝑛, мы имеем 7=𝑛3𝑛=21.

Чтобы найти 𝑚, у нас есть 𝑚=−213𝑚=−7.

Теперь мы пришли к нашему решению, которое состоит в том, что значения 𝑚 и 𝑛, которые делают векторы параллельными, равны 𝑚=−7 и 𝑛=21.

Мы можем проверить наше решение, убедившись, что отношения соответствующих компонентов двух векторов равны.

Для двух параллельных векторов должно быть верно, что 26=7𝑛=𝑚−21.

Если мы подставим полученные значения, то получим 26=721=-7-21, которые все упрощаются до 13. Это подтверждает правильность нашего решения.

В следующем примере мы рассмотрим, как мы можем идентифицировать перпендикулярные векторы.

Пример 3. Определение вектора, не перпендикулярного заданной прямой

Какой из следующих векторов не перпендикулярен прямой, вектор направления которой ⃑𝑟 равен (2,−3,5)?

(10,10,2)
(-10,-5,1)
(2,-2,-2)
(1,-2,3)
(2,3,1) )

Ответ

Чтобы два вектора были перпендикулярны друг другу, должно быть верно, что их скалярное произведение равно нулю. Чтобы найти решение, нам просто нужно найти, какой из векторов не дает нуля при расставлении точек (2,−3,5).

Начнем с вектора в A. Мы находим, что скалярное произведение дает нам (10,10,2)⋅(2,−3,5)=10×2+10×(−3)+2×5=20−30+10=0.

Следовательно, (10,10,2) перпендикулярно (2,−3,5).

Далее мы можем проверить вектор в B. Получаем (−10,−5,1)⋅(2,−3,5)=(−10)×2+(−5)×(−3)+1×5=−20+15+5=0.

Так как это ноль, ответ также не B.

Расставляя точки над вектором в C с помощью (2,−3,5), мы получаем (2,−2,−2)⋅(2,−3,5)=2×2+(−2)×(−3)+(−2)×5=4+6−10=0.

Таким образом, решение тоже не может быть C.

Далее нам нужно проверить вектор D: (1,−2,3)⋅(2,−3,5)=1×2+(−2)×(−3)+3×5=2+6+15=23.

Поскольку это скалярное произведение не равно нулю, (1,−2,3) и (2,−3,5) не перпендикулярны. Итак, наше решение вопроса состоит в том, что вектор, не перпендикулярный прямой, равен D, (1,−2,3).

Мы можем быстро проверить вектор E, просто чтобы убедиться, что этот вектор перпендикулярен прямой: (2,3,1)⋅(2,−3,5)=2×2+3×(−3)+1×5=4−9+5=0.

Поскольку этот результат равен нулю, это помогает подтвердить наше решение: D.

В следующем примере мы будем определять, являются ли два вектора параллельными, перпендикулярными или ни тем, ни другим.

Пример 4. Определение того, являются ли два вектора параллельными, перпендикулярными или нет

Даны два вектора ⃑𝐵=(64⃑𝑖−56⃑𝑗+8⃑𝑘), определите, являются ли эти два вектора параллельны, перпендикулярны или иным образом.

Ответ

Начнем с того, что вспомним условия, при которых эти векторы параллельны или перпендикулярны. Векторы параллельны, если ⃑𝐴=𝑘⃑𝐵, где 𝑘 — ненулевая действительная константа. Векторы перпендикулярно, если ⃑𝐴⋅⃑𝐵=0. Если ни одно из этих условий не выполняется, то векторы не параллельны и не перпендикулярны друг другу.

Начнем с проверки, параллельны ли они. Если они параллельны, то верно, что (8⃑𝑖−7⃑𝑗+⃑𝑘)=𝑘(64⃑𝑖−56⃑𝑗+8⃑𝑘).

Мы можем проверить, так ли это, попытавшись найти значение 𝑘. Мы можем составить три уравнения, приравнивая компоненты этих векторов. Мы получаем 8 = 64 𝑘, −7 = −56 𝑘, 1 = 8 𝑘.

Решив любое из этих уравнений, мы получим одно и то же значение 𝑘=18. Это говорит нам о том, что наши векторы на самом деле параллельны.

Мы уже нашли решение, но для иллюстрации метода завершим доказательство того, что они не перпендикулярны. Находим скалярное произведение ⃑𝐴 и ⃑𝐵 быть (8⃑𝑖−7⃑𝑗+⃑𝑘)⋅(64⃑𝑖−56⃑𝑗+8⃑𝑘)=8×64+(−7)×(−56)+1×8=512+392+8=912.

Так как это не равно нулю, векторы не перпендикулярны, что не противоречит нашему решению, что векторы параллельны.

Теперь мы знаем, как определить, параллельны два вектора или перпендикулярны. Мы можем использовать это, чтобы выяснить, параллельны или перпендикулярны две прямые линии. В следующем примере мы увидим, как мы можем найти недостающую константу в уравнении прямой линии по другой линии, перпендикулярной ей.

Пример 5. Решение задачи с парой перпендикулярных прямых

Если прямая 𝑥+8−10=𝑦+8𝑚=𝑧+10−8 перпендикулярна 𝑥+5−4=𝑦+810 и 𝑧=8, найдите 𝑚.

Ответ

Итак, нам дали уравнения двух прямых в трехмерном пространстве и сказали, что они перпендикулярны друг другу. Мы можем использовать эту информацию, чтобы найти недостающую константу.

Во-первых, нам нужно найти вектор направления каждой линии. Мы знаем, что строка вида 𝑥−𝑥𝑎=𝑦−𝑦𝑏=𝑧−𝑧𝑐 проходит через точку (𝑥,𝑦,𝑧) и имеет вектор направления (𝑎,𝑏,𝑐).

Используя это, мы можем видеть, что линия 𝑥+8−10=𝑦+8𝑚=𝑧+10−8 имеет вектор направления (−10,𝑚,−8).

Другая строка не совсем такого вида, потому что у нас 𝑧=8. Однако это всего лишь означает, что 𝑧-координата этой прямой постоянна, так как наша прямая существует в плоскости 𝑧=8. Итак, в векторе направления 𝑧-компонента будет быть нулем. Следовательно, вектор направления линии 𝑥+5−14=𝑦+810 при 𝑧=8 равен (−4,10,0).

Теперь, когда у нас есть векторы направления двух прямых, нам нужно взять скалярное произведение этих векторов и установите его равным нулю, так как две линии перпендикулярны друг другу. Это дает нам (−10,𝑚,−8)⋅(−4,10,0)=0.

Все, что нам нужно сделать, это решить это, чтобы найти 𝑚. Мы получаем (-10)×(-4)+𝑚×10+(-8)×0=040+10𝑚=010𝑚=-40𝑚=-4.

Вот мы и пришли к решению: чтобы эти две прямые были перпендикулярны, 𝑚=−4.

Теперь мы видели множество примеров того, как мы можем находить и использовать параллельные и перпендикулярные векторы. Напомним некоторые ключевые моменты эксплейнера.

Ключевые точки

Когда два вектора параллельны, угол между ними равен 0∘ или 180∘. Когда два вектора перпендикулярны, угол между ними равен 90∘.
Два вектора, ⃑𝐴=𝑎,𝑎,𝑎 и ⃑𝐵=𝑏,𝑏,𝑏 параллельны, если ⃑𝐴=𝑘⃑𝐵. Это эквивалентно тому, что отношения соответствующих компонентов каждого из векторов равны: 𝑎𝑏=𝑎𝑏=𝑎𝑏.
Два вектора, ⃑𝐴=𝑎,𝑎,𝑎 и ⃑𝐵=𝑏,𝑏,𝑏, перпендикулярны, если их скалярное произведение равно нулю, ⃑𝐴⋅⃑𝐵=0, или если 𝑎𝑏+𝑎𝑏+𝑎𝑏=0.
Мы можем использовать приведенные выше отношения между параллельными и перпендикулярными векторами, чтобы определить, параллельны или перпендикулярны две прямые.

Как найти перпендикулярные векторы: почему, как, когда, где Физические величины, имеющие как величину, так и направление, называются векторами.

Чтобы проиллюстрировать концепцию вектора, сначала нам нужно принять во внимание векторную величину. Например, сила является вектором. Предположим, что вес тела равен 5 Н, это означает, что величина веса равна 5 Н и он действует в направлении вниз. Если говорить о двух векторах, то при выполнении условия, что их скалярное произведение равно нулю, можно сказать, что они перпендикулярны друг другу.

Например, если мы рассматриваем скалярное произведение векторов A и B, то-

A.B= AB cos x

90 градусов x= x=2 Здесь x определяется как угол между двумя векторами x. , то значение скалярного произведения A и B равно ABcos90=0 (поскольку cos90=0). И наоборот, если скалярное произведение двух векторов равно 0, то можно сказать, что они перпендикулярны друг другу.

A.B=0

ab cos x = 0

cos x = 0

cos x = cos 90

x = 90

Концепция перпендикулярных векторов может быть проиллюстрирована с некоторыми численными проблемами, написанными ниже

Пример

The

. значения двух векторов A и B равны (5i+3j-8k) и (i+j+k) соответственно. Эти два вектора перпендикулярны или нет?
A.B
=(5i+3j-8k).(i+j+k)
=5i.i+3j.j-8k.k [так как i.i=1,j.j=1 и k.k=1]
=5+3-8
=8-8
=0
Согласно полученному ранее правилу, когда скалярное произведение двух векторов равно нулю, говорят, что они перпендикулярны друг другу. Следовательно, векторы А и В перпендикулярны друг другу.
Два вектора (3i+7j+7k) и (-7i-aj+7k) перпендикулярны друг другу. Найдите значение а.
Сначала нам нужно вычислить скалярное произведение этих двух векторов.
(3i+7j+7k).(-7i-aj+7k)
=(-21-7a+49)
Поскольку мы знаем, что в случае перпендикулярных векторов скалярное произведение двух векторов должно быть 0 Таким образом-
(-21-7A+49) = 0
или, -7a+28 = 0
или, 7a = 28
или, A = 28/7
или A = 4
Подобная концепция не используется ни в какой рабочей силе. Безработная сила – это сила, действующая перпендикулярно направлению перемещения тела.
Нет рабочей силы из Википедии
W = F.S
= FSCOSX
Здесь, W = Работа выполнена
F = Force
S = смещение
x = 90 градус
W = FS Cos9 Cos9 Cos9.0
                                              =0
Здесь выполненная работа равна 0, что означает, что сила не совершает никакой работы. Следовательно, это называется отсутствием рабочей силы.
Пример
Человек идет по горизонтальной поверхности с багажом на голове. Здесь совершенная работа равна 0, так как сила тяжести и его перемещение на земле перпендикулярны друг другу.
Как найти вектор, перпендикулярный двум векторам?
Здесь применяется условие, что оба вектора, на которых перпендикулярен третий вектор, должны быть непараллельными векторами. Вычислив векторное произведение двух непараллельных векторов, мы сможем получить вектор, перпендикулярный обоим из них по отдельности. Например, A и B — два непараллельных вектора, где A= (a1i+a2j+a3k) и B= (b1i+b2j+b3k), тогда их перпендикулярный вектор будет = перекрестное произведение A и B
перекрестное произведение два вектора из wikipedia
P = (A1i+A2J+A3K)*(B1I+B2J+B3K)
или, p = (A1B2K-A1B3J-A2B1K+A2B3I+A3B1J-A3B2I)
[как i*I = 0, I*J. =k,i*k=-j,j*j=0,j*k=i,j*i=-k,k*k=0,k*i=j,k*j=-i]
Или, p = i(a2b3-a3b2)+j(a3b1-a1b3)+k(a1b2-a2b1)
Таким образом, искомый перпендикулярный вектор равен i(a2b3-a3b2)+j(a3b1-a1b3)+k(a1b2 -a2b1)
Теперь, если мы хотим перепроверить, перпендикулярен вектор или нет, нам нужно рассмотреть отдельные скалярные произведения p.A и p.B.
Теперь, p.A= {i(a2b3-a3b2)+j(a3b1-a1b3)+k(a1b2-a2b1)}.(a1i+a2j+a3k)
                       = a1a2b3-a1b2a3+b1a2a3-a1a2b3+a1a2b3
                     = 0
И    p.B= {i(a2b3-a3b2)+j(a3b1-a1b3)+k(a1b2-a2b1)}. (B1i+B2J+B3K)
= B1A2B3-B1B2A3+B1B2A3-A1B2B3+A1B2B3-B1A2B3
= 0
, поэтому из вышеуказанных расчетов можно увидеть, что перпендикулярный век . Отсюда доказано, что перекрестное произведение двух непараллельных векторов дает перпендикулярный к ним вектор.
Как найти единицу вектор перпендикуляр к два вектора?
Возьмем два вектора X и Y.
Перекрестное произведение X и Y равно X*Y
Величина X и Y равна = |X*Y|
Таким образом, требуемый единичный вектор, перпендикулярный и X, и Y, равен =( X*Y)/ |X*Y|
Единичный вектор из 9(½)
Как определить, перпендикулярны ли два вектора?
Чтобы определить, перпендикулярны два вектора друг другу или нет, мы должны сначала вычислить их скалярное произведение. По результату мы сможем сделать вывод, перпендикулярны векторы или нет. Значение 0 скалярного произведения означает, что векторы перпендикулярны друг другу, тогда как ненулевое значение означает, что векторы не перпендикулярны друг другу. (½) 9(½)
                                                      =10 N
Как найти вектор, перпендикулярный трем векторам?
Возьмем три различные точки, лежащие в одной плоскости, но не на одной прямой. Эти точки имеют три разных вектора положения, равные x, y, z соответственно. Пусть r будет вектором положения другой точки на той же плоскости, где лежат остальные три точки. Итак, векторы (r-x), (y-x) и (z-x) компланарны . Используя формулу для компланарных векторов, можно сказать, что
        (r-x). (y-x)* (z-x)=0
    Или (r-x).(x*y+y*z+z*x)=0
Следовательно, (x*y+y*z+z*x) перпендикулярно (r-x) и, следовательно, перпендикулярно плоскости трех различных точек.
Как найти перпендикулярное расстояние между двумя векторами?
Перпендикулярное расстояние — это кратчайшее расстояние между двумя векторами. Формула кратчайшего расстояния между двумя векторами:

Пример
r1=(i+j+k)+k1(i-j-k)
r2=(2i+2j+2k)+k2(2i-2j-2k)
a1=i+j+k
a2=2i+2j+2k
b1=i-j-k
b2=2i-2j-2k
a2-a1=(2i+2j+2k)-(i+j+k)
         =2i+ +2K-I-J-K
= I+J+K
B1*B2 = (I-J-K)*(2-2J-2K)
= -2K+2J+2K+2I+2J-2I
= 4J
Кратчайшее расстояние=|(b1*b2). (a1-a2)|/|b1*b2|
                           =|4j.(i+j+k)/4|
                            =|1|
                           =1 единица
Как найти параллельные и перпендикулярные векторы?
Мы можем использовать следующую формулу для нахождения параллельных векторов:
k.a=b
Здесь k — константа, а a и b — два вектора.
Пример
Существуют два вектора a и b, значения которых равны (3i+6j) и (4i+8j) соответственно. Эти два вектора параллельны друг другу или нет?
в соответствии с формулой, написанной выше K.A = B
K. (3 6) = (4 8)
3K = 4 6K = 8
или, k = 4/3 или, k = 8/6 = 4/3
Так как значения k одинаковы в обоих случаях, то векторы a и b параллельны друг другу.
Точно так же мы можем определить, являются ли любые два вектора перпендикулярными или нет, вычислив их наклоны. Если значение произведения этих наклонов равно -1, то можно сказать, что векторы являются перпендикулярными или ортогональными векторами.
Есть два вектора (3i-5j) и (5i+3j). Определите, перпендикулярны они или нет?
Пусть A = (3-5J)
и B = (5i+3J)
Следовательно -5/3)*(⅗)
                                  =-1
Итак, векторы a и b перпендикулярны.
Как найти перпендикулярные векторы в 3D?
Давайте возьмем пример, чтобы получить ответ.
p=(1 2 -2) и q=(-2 2 1). Эти два трехмерных вектора перпендикулярны или нет?
p.q= (-2+4-2)
     =0
Следовательно, p и q — два перпендикулярных трехмерных вектора.
Прежде чем приступить к концепции перпендикулярных векторов, сначала нам нужно узнать о векторах. Физические величины, имеющие как величину, так и направление, называются векторами.
Чтобы проиллюстрировать концепцию вектора, сначала нам нужно принять во внимание векторную величину. Например, сила является вектором. Предположим, что вес тела равен 5 Н, это означает, что величина веса равна 5 Н и он действует в направлении вниз. Если говорить о двух векторах, то при выполнении условия, что их скалярное произведение равно нулю, можно сказать, что они перпендикулярны друг другу. Например, если мы рассмотрим скалярное произведение векторов A и B, то-
                                               A.B= AB cos x
Здесь x определяется как угол между двумя векторами A и B. 0). И наоборот, если скалярное произведение двух векторов равно 0, то можно сказать, что они перпендикулярны друг другу.
A.B = 0
AB COS X = 0
COS X = 0
cos x = cos 90
x = 90
Концепция перпендикулярных векторов может быть проиллюстрирована с некоторыми численными проблемами, написанными ниже
Пример
Значения двух векторов A и B (5I+3J- 8k) и (i+j+k) соответственно. Эти два вектора перпендикулярны или нет?
A.B
=(5i+3j-8k).(i+j+k)
=5i.i+3j.j-8k.k [так как i.i=1,j.j=1 и k.k=1]
=5+3-8
=8-8
=0
Согласно полученному ранее правилу, когда скалярное произведение двух векторов равно нулю, говорят, что они перпендикулярны друг другу. Следовательно, векторы А и В перпендикулярны друг другу.
2) Два вектора (3i+7j+7k) и (-7i-aj+7k) перпендикулярны друг другу. Найдите значение а.
Сначала нам нужно вычислить скалярное произведение этих двух векторов.
(3i+7j+7k).(-7i-aj+7k)
=(-21-7a+49)
Как мы знаем, что в случае перпендикулярных векторов продукт точки двух векторов должен быть 0. Таким образом-
(-21-7a+49) = 0
или, -7a+28 = 0
или, 7a=28
                                Или a=28/7
                                  Или a=4
      Подобная работа не используется. Безработная сила – это сила, действующая перпендикулярно направлению перемещения тела.
W = F.S
= FSCOSX
Здесь, W = работа, выполненная
F = Сила
S = смещение
x = 90 градусов
W = FS COS90
= 0 90 градусов
W = FS COS90
= 0 90 градусов
W = FS COS90
= 0 90.0003
Здесь выполненная работа равна 0, что означает, что сила не совершает никакой работы. Следовательно, это называется отсутствием рабочей силы.
Пример
Человек идет по горизонтальной поверхности с багажом на голове. Здесь совершенная работа равна 0, так как сила тяжести и его перемещение на земле перпендикулярны друг другу.
Как найти вектор, перпендикулярный двум векторам?
Здесь применяется условие, что оба вектора, на которых перпендикулярен третий вектор, должны быть непараллельными векторами. Вычислив векторное произведение двух непараллельных векторов, мы сможем получить вектор, перпендикулярный обоим из них по отдельности.
Например, A и B — два непараллельных вектора, где A= (a1i+a2j+a3k) и B= (b1i+b2j+b3k), тогда их перпендикулярный вектор будет = перекрестное произведение A и B
                   p = (a1i+a2j+a3k)*(b1i+b2j+b3k)
            Или, p = (a1b2k-a1b3j-a2b1k+a2b3i+a3b1j-a3b2i)
          [As ij*i=0,i*i=0,i*i ,i*k=-j,j*j=0,j*k=i,j*i=-k,k*k=0,k*i=j,k*j=-i]
            Или, p= i(a2b3-a3b2)+j(a3b1-a1b3)+k(a1b2-a2b1)
Таким образом, искомый перпендикулярный вектор равен i(a2b3-a3b2)+j(a3b1-a1b3)+k(a1b2-a2b1 )
Теперь, если мы хотим проверить, является ли вектор перпендикулярным или нет, нам нужно рассмотреть отдельные скалярные произведения p. A и p.B.
Теперь p.A= {i(a2b3-a3b2)+j(a3b1-a1b3)+k(a1b2-a2b1)}.(a1i+a2j+a3k)
               = a1a2b3-a1b2a3+b1a2a3a+a1a2b3-a1a2b3
                     = 0
И    p.B= {i(a2b3-a3b2)+j(a3b1-a1b3)+k(a1b2-a2b1)}. (b1i+b2j+b3k)
                = b1a2b3-b1b2a3+b1b2a3-a1b2b3+a1b2b3-b1a2b3
                = 0
Таким образом, из приведенных выше расчетов видно, что перпендикулярный вектор p перпендикулярен обоим векторам A и B по отдельности. Отсюда доказано, что перекрестное произведение двух непараллельных векторов дает перпендикулярный к ним вектор.
Как найти единичный вектор, перпендикулярный двум векторам?
Возьмем два вектора X и Y.
Перекрестное произведение X и Y равно X*Y
Величина X и Y равна = |X*Y|
Таким образом, требуемый единичный вектор, перпендикулярный и X, и Y, равен =( X*Y)/ |X*Y| 9(½)
Как определить, перпендикулярны ли два вектора?
Чтобы определить, перпендикулярны два вектора друг другу или нет, мы должны сначала вычислить их скалярное произведение. По результату мы сможем сделать вывод, перпендикулярны векторы или нет. Значение 0 скалярного произведения означает, что векторы перпендикулярны друг другу, тогда как ненулевое значение означает, что векторы не перпендикулярны друг другу.
Пример
Вес автомобиля F=3i+3j+3k действует вниз. Его перемещение в горизонтальной плоскости равно D=-3i+3j. Что можно сказать о проделанной работе по машине?
Работа выполнена = F.D
= (3i+3J+3K). ( -3i+3J+0K)
= -9+
= 0
Здесь, в вышеупомянутой задаче. Продукт точки равен 0. Так что 0. Так что 0. Так что 0. Так что 0. Так что 0. Так что 0. Так что 0. можно сделать вывод, что F и D перпендикулярны друг другу.
Как найти равнодействующую двух перпендикулярных векторов? 9(½)
Пример
Две силы F1 и F2 действуют на тело, где значение F1 равно 8 Н, а значение F2 равно 6 Н, и они взаимно перпендикулярны. Чему будет равна результирующая сила?
F1 = 8 N
F2 = 6 N
C = 90 градусов
R = (F1^2+F2^2-2F1F2COSC)^(½) 9(½)
                                                      =10 N
Как найти вектор, перпендикулярный трем векторам?
Возьмем три различные точки, лежащие в одной плоскости, но не на одной прямой. Эти точки имеют три разных вектора положения, равные x, y, z соответственно. Пусть r будет вектором положения другой точки на той же плоскости, где лежат остальные три точки.
Итак, векторы (r-x), (y-x) и (z-x) компланарны. Используя формулу для компланарных векторов, можно сказать, что
        (r-x). (y-x)* (z-x)=0
    Или (r-x).(x*y+y*z+z*x)=0
Следовательно, (x*y+y*z+z*x) перпендикулярно (r-x) и, следовательно, перпендикулярно плоскости трех различных точек.
Как найти перпендикулярное расстояние между двумя векторами?
Перпендикулярное расстояние — это кратчайшее расстояние между двумя векторами. Формула кратчайшего расстояния между двумя векторами:

Пример
r1=(i+j+k)+k1(i-j-k)
r2=(2i+2j+2k)+k2(2i-2j-2k)
a1=i+j+k
a2=2i+2j+2k
b1=i-j-k
b2=2i-2j-2k
a2-a1=(2i+2j+2k)-(i+j+k)
         =2i+ +2K-I-J-K
= I+J+K
B1*B2 = (I-J-K)*(2-2J-2K)
= -2K+2J+2K+2I+2J-2I
= 4J
Кратчайшее расстояние=|(b1*b2). (a1-a2)|/|b1*b2|
                           =|4j.(i+j+k)/4|
                            =|1|
                           =1 единица
Как найти параллельные и перпендикулярные векторы?
Мы можем использовать следующую формулу для нахождения параллельных векторов:
k.a=b
Здесь k — константа, а a и b — два вектора.
Пример
Существуют два вектора a и b, значения которых равны (3i+6j) и (4i+8j) соответственно. Эти два вектора параллельны друг другу или нет?
в соответствии с формулой, написанной выше K.A = B
K. (3 6) = (4 8)
3K = 4 6K = 8
или, k = 4/3 или, k = 8/6 = 4/3
Так как значения k одинаковы в обоих случаях, то векторы a и b параллельны друг другу.
Точно так же мы можем определить, являются ли любые два вектора перпендикулярными или нет, вычислив их наклоны. Если значение произведения этих наклонов равно -1, то можно сказать, что векторы являются перпендикулярными или ортогональными векторами.
Пример
Есть два вектора (3i-5j) и (5i+3j). Определите, перпендикулярны они или нет?
Пусть A = (3-5J)
и B = (5i+3J)
Следовательно -5/3)*(⅗)
                                  =-1
Итак, векторы a и b перпендикулярны.
Как найти перпендикулярные векторы в 3D?
Давайте возьмем пример, чтобы получить ответ.
p=(1 2 -2) и q=(-2 2 1). Эти два трехмерных вектора перпендикулярны или нет ?
p.q= (-2+4-2)
     =0
Следовательно, p и q — два перпендикулярных трехмерных вектора.
Ортогональный вектор – объяснение и примеры
В области векторной геометрии мы рассмотрели почти все концепции векторов. Мы рассмотрели векторы нормалей, векторные уравнения, скалярные произведения векторов и многие другие. Но одно из самых важных понятий в этой области — это понимание ортогональный вектор.
Ортогональные векторы определяются как:
«2 вектора называются ортогональными, если они перпендикулярны друг другу, и после выполнения анализа скалярного произведения результат, который они дают, равен нулю».
В этой теме мы сосредоточимся на следующих областях:
Что такое ортогональный вектор?
Как найти ортогональный вектор?
Каковы свойства ортогонального вектора?
Примеры
Практические задачи

Что такое ортогональный вектор?
В математических терминах слово «ортогональный» означает направленный под углом 90°. Два вектора u,v  называются ортогональными, если они перпендикулярны, т. е. образуют прямой угол, или если их скалярное произведение равно нулю .
Таким образом, мы можем сказать ,
u⊥v или u·v=0
Следовательно, скалярное произведение используется для проверки того, направлены ли два вектора, которые наклонены рядом друг с другом, на угол 90° или нет.
Если мы углубимся в свойства ортогонального вектора, то узнаем, что нулевой вектор, который по сути является нулем, практически ортогонален каждому вектору. Мы можем подтвердить это, потому что u.0=0 для любого вектора u нулевой вектор ортогонален каждому вектору. Это связано с тем, что нулевой вектор равен нулю и, очевидно, даст нулевой или нулевой результат при умножении на любое число или любой вектор.
Два вектора u и y, в пространстве скалярного произведения V ортогональны, если их скалярное произведение равно нулю
(u,y)=0
Теперь, когда мы знаем, что скалярное произведение является основным ключом к выяснению того, являются ли два вектора ортогональными или нет, давайте рассмотрим несколько примеров для лучшего понимания.
Пример 1
Проверить, ортогональны ли векторы a = i + 2j и b = 2i – j.
Решение
Чтобы проверить, являются ли 2 вектора ортогональными или нет, мы будем вычислять скалярное произведение этих векторов:
a. b = (1 · 2) + (2 · (-1))
a.b = 2 – 2
a.b = 0
Следовательно, поскольку скалярное произведение равно 0, два вектора ортогональны.
Пример 2
Являются ли векторы a = (3, 2) и b = (7, -5} ортогональными? будет вычислять скалярное произведение этих векторов:
a.b = (3,7) + (7, (-5))
a.b = 21 – 35
a.b = -14
Поскольку скалярное произведение этих двух векторов не равно нулю, эти векторы не ортогональны.
Как найти ортогональный вектор?
Мы уже обсуждали, что один из способов нахождения ортогональных векторов — проверка их скалярного произведения. Если скалярное произведение дает нулевой ответ, очевидно, что перемножаемые векторы на самом деле были ортогональными или перпендикулярными.
Общее, которое можно использовать в этом отношении, выглядит следующим образом:
a.b = 0
Это понятие может быть также расширено в виде компонентов вектора.
Общее уравнение в этом случае становится примерно таким: они всегда должны предоставлять точечный продукт, который дает нам нулевой результат.
Но давайте рассмотрим и другие сценарии и методологии.
Перемножаемые 2 вектора могут существовать в любой плоскости. Для них нет ограничений ограничиваться только двумерными плоскостями. Итак, давайте расширим наше исследование и на трехмерные плоскости.
Ортогональный вектор в случае двумерной плоскости
Большинство задач в математике ограничены двумерными плоскостями. Такая плоскость существует только с двумя осями, а именно с осью x и осью y. В разделе об единичных векторах мы также обсудили, что эти оси также могут быть представлены в терминах единичных векторов; ось x в виде единичного вектора i и ось Y в виде единичного вектора j.
Теперь давайте рассмотрим, что есть 2 вектора с именами a и b , которые существуют в двумерной плоскости. Мы должны засвидетельствовать, ортогональны ли эти два вектора друг другу или нет, другими словами, перпендикулярны ли они друг другу.
Мы пришли к выводу, что для проверки ортогональности мы оцениваем скалярное произведение векторов, существующих на плоскости. Итак, скалярное произведение векторов a и b будет примерно таким, как показано ниже:
a.b = |a| х |б| x cosθ
Если два вектора ортогональны или перпендикулярны, то угол θ между ними будет равен 90°.
Как мы знаем,
cosθ = cos 90°
И,
cos 90° = 0
Итак, мы можем переписать уравнение скалярного произведения как:
a.b = |a| х |б| x cos 90°
a.b = 0
Мы также можем выразить это явление через компоненты вектора.
a.b = ax.bx + ay.by
И мы упоминали выше, что в терминах представления на основе единичных векторов; мы можем использовать символы i и j.
Следовательно,
a.b = ai.bi + aj.bj
a.b = 0
Следовательно, если скалярное произведение также дает ноль в случае умножения компонентов, то два вектора ортогональны.
Пример 3
Найти, являются ли векторы a = (5, 4) и b = (8, -10) ортогональны друг другу или нет.
Решение
Чтобы проверить, ортогональны ли два вектора, мы вычислим скалярное произведение этих векторов: 10)
а.б = 40 – 40
а.б = 0
Таким образом, доказано, что два вектора ортогональны по своей природе.
Пример 4
Найти, являются ли векторы a = (2, 8) и b = (12, -3) ортогональны друг другу или нет.
Решение:
Чтобы проверить, являются ли два вектора ортогональными или нет, мы вычислим скалярное произведение этих векторов:
a.b = ai.bi + aj.bj
a.b = (2.12) + (8. -3)
а.б = 24 – 24
а.б = 0
Таким образом, доказано, что два вектора ортогональны по своей природе.
Ортогональный вектор в случае трехмерной плоскости
Большинство реальных задач требуют, чтобы векторы уходили в трехмерную плоскость. Когда мы говорим о трехмерных плоскостях, нас сопровождает еще одна ось, а именно ось z.
В этом случае с учетом третьей оси ось z будет состоять из 3-х компонент, каждая из которых направлена вдоль соответствующей оси, если мы говорим, что любой вектор существует в трехмерной плоскости. В таком случае тремя компонентами вектора в трехмерной плоскости будут x-компонента, y-компонента и z-компонента.
Если мы представим эти компоненты в терминах единичных векторов, то мы уже знаем, что для осей x и y мы используем символы i и j для представления их компонентов. Но теперь, когда у нас есть третья ось и одновременно третий компонент, нам нужно дополнительное третье представление.
Итак, для этой третьей оси мы используем символ k для представления единичного вектора вдоль оси z.
Теперь предположим, что в трехмерной плоскости существуют 2 вектора. Эти векторы, очевидно, будут иметь 3 компонента, и скалярное произведение таких векторов можно найти ниже:
a. b = ax.bx + ay.by + az.bz
Или, в терминах единичных векторов i, j, и k :
a.b = ai.bi + aj.bj + ak .bk
a.b = 0
Следовательно, если этот результат дает скалярное произведение 0, мы сможем заключить, что 2 вектора в трехмерной плоскости перпендикулярны или ортогональны по своей природе.
Пример 5
Проверить, являются ли векторы a = (2, 3, 1) и b = (3, 1, -9) ортогональны или нет.
Решение
Чтобы проверить, являются ли эти 2 вектора ортогональными или нет, мы будем вычислять их скалярное произведение. Поскольку эти 2 вектора имеют 3 компонента, следовательно, они существуют в трехмерной плоскости.
Итак, мы можем написать:
а.б = а.и.б + аj.bj + ак.бк
Теперь, подставляя значения в формулу:
а.б = (2.3) + (3.1) + (1. -9)
a.b = 6 + 3 -9
a.b = 0
Поскольку скалярное произведение равно нулю, следовательно, эти 2 вектора в трехмерной плоскости ортогональны по своей природе.
Пример 6
Определите, являются ли два вектора a = i + 2j и b = 2i -j + 10k ортогональными или нет.
Решение
Чтобы проверить, являются ли эти 2 вектора ортогональными или нет, мы будем вычислять их скалярное произведение. Поскольку эти 2 вектора имеют 3 компонента, следовательно, они существуют в трехмерной плоскости.
Итак, мы можем написать:
a.b = ai.bi + aj.bj + ak.bk
Теперь, подставляя значения в формулу:
a.b = (1.2) + (2. -1) + (0.10)
a.b = 2 -2 + 0
a.b = 0
Поскольку скалярное произведение равно нулю, следовательно, эти 2 вектора в трехмерном плоскости ортогональны по своей природе.
Пример 7
Проверить, являются ли два вектора a = (2, 4, 1) и b = (2, 1, -8) ортогональными.
Решение
Чтобы проверить, являются ли эти 2 вектора ортогональными или нет, мы будем вычислять их скалярное произведение. Поскольку эти 2 вектора имеют 3 компонента, следовательно, они существуют в трехмерной плоскости.
Итак, мы можем написать:
а.б = а.и.б + аj.bj + ак.бк
Теперь, подставляя значения в формулу:
а.б = (2.2) + (4.1) + (1 .-8)
a.b = 4 + 4 – 8
a.b = 0
Поскольку скалярное произведение равно нулю, следовательно, эти 2 вектора в трехмерной плоскости ортогональны по своей природе.
Свойства ортогональных векторов
Теперь, когда мы получили всю необходимую информацию об ортогональных векторах и получили четкое представление о том, как проверить, являются ли векторы ортогональными или нет, давайте проанализируем некоторые свойства ортогональных векторов. ортогональные векторы.
Перпендикулярно в природе
Векторы, которые называются ортогональными, всегда будут перпендикулярны по своей природе и всегда будут давать скалярное произведение, равное 0, поскольку перпендикулярность означает, что между ними будет угол 90°.
Нулевой вектор ортогонален
Нулевой вектор всегда будет ортогонален каждому вектору, с которым существует нулевой вектор. Это связано с тем, что любой вектор при умножении на нулевой вектор всегда будет давать скалярное произведение, равное нулю.
Перекрестное произведение ортогональных векторов
Перекрестное произведение двух ортогональных векторов никогда не может быть равно нулю. Это связано с тем, что формула векторного произведения включает тригонометрическую функцию sin, а sin 90° всегда равен 1. Следовательно, векторное произведение ортогональных векторов никогда не будет равно 0.
Определите, ортогональны ли векторы (1, 2) и (2, -1).
Определите, ортогональны ли векторы (1, 0, 3) и (4, 7, 4).
Докажите, что векторное произведение ортогональных векторов не равно нулю.
Ответы
Да
Нет
Докажите с помощью формулы перекрестного произведения
Все диаграммы построены с использованием GeoGesbra.
Предыдущий урок | Главная страница | Следующий урок
Скалярное произведение и нормали к линиям и плоскостям
Скалярное произведение и нормали к линиям и плоскостям
Скалярное произведение и нормали к линиям и плоскостям
Уравнение прямой в форме ax + by = c можно записать в виде скалярного произведения:
(а, б) ^. (х, у) = с, или А ^. Х = с,
, где A = (a, b) и X = (x, y).
Уравнение прямой в виде ax + by + cz = d можно записать в виде точки продукт:
(а,б,в) ^. (х, у, г) = d или A ^. Х = д,
, где A = (a, b, c) и X = (x, y, z).
Нормальный вектор A
Если P и Q находятся в плоскости уравнения A ^. X = d, тогда A ^. P = d и A ^. Q = d, поэтому
А ^. (Q — P) = д — д = 0,
Это означает, что вектор A ортогонален любому вектору PQ между точками P и Q плоскости.
Но вектор PQ можно рассматривать как касательный вектор или вектор направления самолета. Это означает, что вектор A ортогонален плоскости, то есть A ортогонален каждому вектору направления плоскости.
Ненулевой вектор, ортогональный векторам направления плоскости, называется вектор нормали к плоскости . Таким образом, вектор коэффициентов A является нормальным вектор на плоскость.
Это также означает, что вектор OA ортогонален плоскости, поэтому прямая OA перпендикулярно плоскости.
Осторожно: НЕВЕРНО, что для любой точки P на плоскости A ортогональна к P (если только d = 0).
Упражнение: Покажите, что если A — вектор нормали к плоскости, а k — ненулевое постоянна, то kA также является нормальным вектором к той же плоскости.
Дебаты: Для любой плоскости является ли вектор 0 ортогональным всем направлениям вектора плоскости?
Упражнение с линиями на плоскости: Те же рассуждения применимы к линиям. На миллиметровой бумаге нарисуйте линию m с уравнением 2x + 3y = 6, а также нанесите точку А = (2,3). Убедитесь, что линии OA и m перпендикулярны. Также постройте линию 2x + 3y = 0. Как эта линия связана с m и OA? Наконец, найдите уравнение для линия ОА. Чему равен нормальный вектор этой прямой?
Пример: Поиск плоскости по известной нормали . Предположим, что А = (1, 2, 3). Найдите уравнение плоскости через P = (1, -1, 4) с нормальной вектор А.
Решение: Уравнение должно быть (1, 2, 3) ^. X = d для некоторой константы d. Но поскольку P находится на плоскости, если мы положим X = P, мы должен получить правильное значение d. Таким образом, d = (1, 2, 3) ^. (1, -1, 4) = 1 -2 + 12 = 11. Уравнение A ^. Х = 11.
Единица нормального вектора
Единичный вектор является вектором длины 1. Любой ненулевой вектор можно разделить по его длине, чтобы сформировать единичный вектор. Таким образом, для плоскости (или линии) нормаль вектор можно разделить на его длину, чтобы получить единичный вектор нормали.
Пример: Для уравнения x + 2y + 2z = 9 вектор A = (1, 2, 2) является нормальным вектором. |А| = квадратный корень из (1+4+4) = 3. Таким образом, вектор (1/3)A — единичный вектор нормали к этой плоскости. Кроме того, (-1/3)A является единичным вектором.
Единичные векторы нормалей: (1/3, 2/3, 2/3) и (-1/3, -2/3, -2/3)
Упражнение: Найдите единичный вектор нормали к плоскости с помощью уравнения -2x -4y -4z = 0. Как это связано с примером? Не могли бы вы использовать пример для найти единицу нормальной в этом случае?
Упражнение на линии на плоскости: Продолжение с линией m с уравнением 2x + 3y = 6, найдите единичные векторы нормалей для этой прямой. Кроме того, найдите нормальную единицу вектор для линии OA. Ищите отношения.
Уравнения прямых в пространстве
Мы видели, что одно уравнение вида A ^. X = h определяет линию на плоскости или плоскость в трехмерном пространстве. В каждом случае мы можем неформально мотивируйте это тем, что пространство решений имеет размерность на единицу меньше, чем размер содержащего пространства.
Эта интуитивная идея становится строгой во всех измерениях в линейной алгебре. курс.
Линия в пространстве не может быть задана одним линейным уравнением, так как для любого ненулевого вектора А, такое уравнение имеет плоскость в качестве решения.
Но линия — это пересечение двух плоскостей, так что если у нас есть две такие плоскости, с двумя уравнениями A ^. X = h и B ^. X = k, то совокупность решений обоих уравнений вместе есть прямая. Наоборот, если у нас есть два таких уравнения, у нас есть две плоскости. Две плоскости могут пересекаться в линию, или они могут быть параллельны или даже одной плоскости.
Векторы нормали A и B ортогональны векторам направления прямая, и на самом деле вся плоскость через О, которая содержит А и В, является плоскостью ортогонален прямой.
Векторы нормалей и векторное произведение
Для двух векторов A и B векторное произведение A x B ортогонально обоим векторам A и к B. Это очень полезно для построения нормалей.
Пример (Пример уравнения плоскости повторно) Дано, P = (1, 1, 1), Q = (1, 2, 0), R = (-1, 2, 1). Найдите уравнение плоскости через эти точки.
Во-первых, вектор нормали представляет собой векторное произведение двух векторов направления на плоскости (не обе в одном направлении!).
Пусть один вектор равен PQ = Q — P = (0, 1, -1), а другой — PR = R — P = (-2, 1, 0). Перекрестное произведение
(Q — P) x (R — P) = (1, 2, 2) = вектор нормали A, и уравнение имеет вид A ^. X = d для некоторого d
Используя метод из приведенного выше примера, мы можем найти d = A ^. P = 5. Таким образом, уравнение имеет вид A ^. Х = 5, что совпадает с одним из уравнений в предыдущем примере.
Упражнение. Проверить, что для этого A, A ^. Вопросы и ответы ^. R тоже = 5. Почему так?
Упражнение. Найдите нормальную единицу измерения для этого самолета. Какое уравнение, если А выбирается в качестве единицы нормального?
Двугранные углы и векторы нормали
Для двух плоскостей мера двугранного угла между двумя плоскостями определяется как мера угла, образованного пересечением двух плоскостей с другой плоскостью, ортогональной линии пересечения. (Есть два угла — пара дополнительных углов.)
Угловая мера между нормальными направлениями двух плоскостей одинакова как мера двугранных углов, поэтому двугранный угол может быть измерен взяв скалярное произведение нормальных направлений и используя косинус Теорема для скалярных произведений.
Артикул:
Mathworld: Двугранный Углы
Mathforum: Октаэдр
Артикул:
Нормальный векторы и уравнения в Texas A&M
Назад к индексу координат вектора

параллельных векторов — определение, примеры, формула т. е. для любого вектора
a сам вектор и противоположный ему вектор -a являются векторами, которые всегда параллельны a . Расширяя это дальше, любой скаляр, кратный a , параллелен а. т. е. вектор a и k a всегда являются параллельными векторами, где k — скаляр (действительное число).
Давайте узнаем больше о параллельных векторах вместе с их определением, формулой и примерами.
1. Что такое параллельные векторы?
2. Как найти параллельные векторы?
3. Скалярное произведение параллельных векторов
4. Перекрестное произведение параллельных векторов
5. Формула параллельных векторов
6. Единичный вектор, параллельный заданному вектору
7. Свойства параллельных векторов
8. Часто задаваемые вопросы о параллельных векторах
Что такое параллельные векторы?
Два вектора называются параллельными тогда и только тогда, когда угол между ними равен 0 градусов. Параллельные векторы также известны как коллинеарные векторы. т. е. два параллельных вектора всегда будут параллельны одной и той же прямой, но они могут быть либо в одном направлении, либо в совершенно противоположном направлении. На следующем изображении векторы, показанные на крайнем левом рисунке, НЕ параллельны, поскольку они имеют разные направления (т. е. ни одно и то же, ни противоположные направления).
Параллельные векторы, направленные в противоположные стороны, иногда также называют антипараллельными векторами. На изображении выше последний рисунок показывает антипараллельные векторы. Но как математически идентифицировать параллельные векторы? Посмотрим.
Как найти параллельные векторы?
Два вектора a и b называются параллельными векторами, если один из них кратен другому. т. е. a = k b , где «k» — скаляр (действительное число). Здесь «k» может быть положительным, отрицательным или 0. В этом случае
a и b имеют одинаковые направления, если k положительно.
a и b имеют противоположные направления, если k отрицательно.
Вот несколько примеров параллельных векторов:
a и 3 a параллельны и имеют те же направления, что и 3 > 0.
v и (-1/2) v параллельны и имеют те же направления, что и (-1/2) < 0,
a = <1, -3> и b = <3, -9> параллельны, поскольку b = <3, -9> = 3 <1, -3> = 3 a .
В приведенных выше примерах пример 2 относится к антипараллельным векторам.
Скалярное произведение параллельных векторов
Скалярное произведение любых двух параллельных векторов равно произведению их величин. Рассмотрим два параллельных вектора а и б . Тогда угол между ними равен θ = 0. По определению скалярного произведения
a · b = | и | | б | cos θ
= | и | | б | 0
= | и | | б | (1) (потому что cos 0 = 1)
= | и | | б |
Следовательно, скалярное произведение двух параллельных векторов равно произведению их величин.
Перекрестное произведение параллельных векторов
Перекрестное произведение любых двух параллельных векторов является нулевым вектором. Рассмотрим два параллельных вектора a и b . Тогда угол между ними равен θ = 0. По определению перекрестного произведения
a × b = | и | | б | грех θ \ (\ шляпа {n} \)
= | и | | б | грех 0 $\шляпа{п}$
= | и | | б | (0) $\шляпа{n}$ (поскольку sin 0 = 0)
= 0
Обратите внимание, что 0 здесь является вектором, а не скаляром. Таким образом, векторное произведение двух параллельных векторов является нулевым вектором (не просто нулем).
Формула параллельных векторов
Параллельные векторы можно определить с помощью скалярного множителя, скалярного произведения или перекрестного произведения. Вот формула параллельных векторов в соответствии с ее значением, объясненным в предыдущих разделах.
Единичный вектор, параллельный заданному вектору
Единичный вектор, параллельный заданному вектору a , обозначается $\hat{a}$ и задается как $\hat{a}$ = a / | и |. Здесь обратите внимание на две вещи:
и и и / | и | (что равно 1/| a | · a) являются скалярными кратными друг другу. Следовательно, a и $\hat{a}$ параллельны.
Величина / | и | есть | и | / | и | = 1. Следовательно, $\hat{a}$ — единичный вектор.
Следовательно, a / | и | является единичным вектором, параллельным a . Он получается делением вектора на его величину.
Пример: Найдите единичный вектор, параллельный вектору a = 3 i + 4 j .
Решение:
Дано, что a = 3 i + 4 j .
Его величина | и | = √(3 ² + 4 ² ) = √(25) = 5.
Таким образом, единичный вектор, параллельный a , равен
$\ hat{a}$ = / | и |
= (3 i + 4 j ) / 5
= (3/5) i + (4/5) j
Свойства параллельных векторов
Два вектора a и b параллельны друг другу тогда и только тогда, когда a = k b , где k — скаляр.
Здесь a и b находятся в направлениях, если k > 0, и в противоположных направлениях, если k < 0.
Каждый вектор a параллелен самому себе, так как a = 1 a.
Два вектора a и b называются параллельными, если их векторное произведение равно нулю. то есть а × б = 0 .
Для любых двух параллельных векторов a и b их скалярное произведение равно произведению их модулей. т. е. a · b = | и | | б |.
☛ Похожие темы:
Векторные формулы
Компоненты вектора
Типы векторов
Калькулятор результирующего вектора
Часто задаваемые вопросы о параллельных векторах
Что такое определение параллельных векторов?
Два вектора a и b называются параллельными векторами , если выполняется одно из условий:
Если один вектор является скалярным кратным другого. т. е. a = k b , где k — скаляр.
Если их векторное произведение равно 0, то есть a × b = 0 .
Если их скалярное произведение равно произведению их величин. т. е. a · b = | и | | б |.
Как найти вектор, параллельный заданному вектору?
Чтобы найти вектор, параллельный заданному вектору a , просто умножьте его на любой скаляр. Например, 3 a , -0,5 a , √2 a и т. д. параллельны вектору a .
Как определить, параллельны ли два вектора?
Чтобы определить, параллельны ли два заданных вектора, просто посмотрите, можно ли взять общий множитель из одного вектора так, чтобы он был кратен другому вектору. Другой способ — проверить, равно ли их векторное произведение 0.
В чем разница между перпендикулярными и параллельными векторами?
Вот различия между перпендикулярными и параллельными векторами.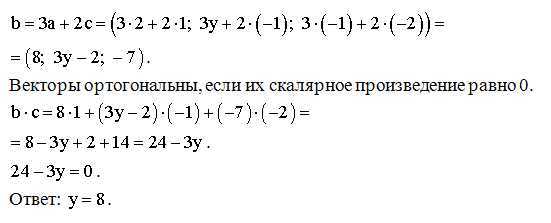
Перпендикулярные векторы Параллельные векторы
Два вектора называются перпендикулярными, если угол между ними равен 90 градусов. Два вектора называются параллельными, если угол между ними равен 0 градусов.
Скалярное произведение двух перпендикулярных векторов равно 0. Перекрестное произведение двух параллельных векторов равно 0 .
Если a и b перпендикулярны, то | а × б | = | и || б |. Если a и b параллельны, то a · b = | и || б |.
Параллелен ли вектор самому себе?
Каждый вектор a кратен самому себе. то есть a = 1 a . Таким образом, каждый вектор параллелен самому себе. Кроме того, угол между вектором и самим собой всегда равен 0 градусов. Таким же образом мы можем сказать, что вектор параллелен самому себе.
Какова формула для единичного вектора, параллельного результирующим векторам?
Мы знаем, что единичный вектор, параллельный вектору a , равен a / | и |. Таким образом, единичный вектор, параллельный равнодействующей двух векторов a и b , равен ( a+b) / | а+б |.
В чем разница между параллельными векторами и наклонными линиями?
Параллельные векторы и наклонные линии находятся в трехмерном пространстве. Параллельные прямые никогда не пересекаются и параллельны относительно координат x, y и z. Наклонные линии также находятся в трехмерном пространстве, но не параллельны и не пересекаются. Наклонные линии — это линии, присутствующие в разных плоскостях.
Что такое равные и параллельные векторы?
Равные векторы имеют одинаковую величину и одинаковое направление. Параллельные векторы могут иметь разные величины, но они имеют одинаковые/противоположные направления. Например:
a и a являются равными векторами.
a и 3 a — параллельные векторы.
Vector math — документация Godot Engine (stable) на английском языке
Введение
Этот учебник представляет собой краткое и практическое введение в линейную алгебру. это относится к разработке игр. Линейная алгебра — это изучение векторов и их использование. Векторы имеют множество применений как в 2D-, так и в 3D-разработке. и Годо широко их использует. Развитие хорошего понимания вектора математика необходима, чтобы стать сильным разработчиком игр.
Примечание
Этот учебник не является формальным учебником по линейной алгебре. Мы будет только смотреть на то, как это применяется к разработке игр. Для более широкого взгляда на математику, см. https://www.khanacademy.org/math/linear-алгебра
Системы координат (2D)
В 2D-пространстве координаты определяются с помощью горизонтальной оси ( x ) и вертикальная ось ( y ). Определенная позиция в 2D-пространстве записывается как пара значений, таких как (4, 3) .
Примечание
Если вы новичок в компьютерной графике, может показаться странным, что положительный y ось указывает вниз вместо вверх, как вы, вероятно, узнали на уроке математики. Однако это обычное в большинстве приложений компьютерной графики.
Любая позиция в 2D-плоскости может быть идентифицирована парой чисел в этом путь. Однако мы также можем думать о позиции (4, 3) как о смещении . от точки (0, 0) или начала координат . Нарисуйте стрелку, указывающую от от начала до точки:
Это вектор . Вектор представляет много полезной информации. В качестве а также говоря нам, что точка находится по адресу (4, 3) , мы также можем думать о это как угол θ и длиной (или величиной) м . В этом случае стрелка представляет собой вектор положения — он обозначает позицию в пространстве, относительную к происхождению.
Очень важный момент, который следует учитывать в отношении векторов, заключается в том, что они представляют 90 187 относительного 90 188 направления и величины. Нет понятия о положение вектора. Следующие два вектора идентичны:
Оба вектора представляют точку на 4 единицы правее и на 3 единицы ниже некоторой отправная точка. Неважно, где на плоскости ты рисуешь вектор, он всегда представляет относительное направление и величину.
Векторные операции
Вы можете использовать любой метод (координаты x и y или угол и величина) для относятся к вектору, но для удобства программисты обычно используют обозначение координат. Например, в Godot начало координат находится в верхнем левом углу. углу экрана, чтобы разместить 2D-узел с именем Node2D на 400 пикселей вправо и 300 пикселей вниз, используйте следующий код:
$Node2D.position = Vector2(400, 300)
Godot поддерживает как Vector2, так и Vector3 для использования в 2D и 3D соответственно. Одинаковый математические правила, обсуждаемые в этой статье, применимы к обоим типам.
Доступ для участников
Доступ к отдельным компонентам вектора можно получить непосредственно по имени.
# создать вектор с координатами (2, 5) переменная a = Vector2 (2, 5) # создаем вектор и назначаем x и y вручную переменная b = Vector2() б.х = 3 б.у = 1
Добавление векторов
При сложении или вычитании двух векторов добавляются соответствующие компоненты:
var c = a + b # (2, 5) + (3, 1) = (5, 6)
Мы также можем увидеть это визуально, добавив второй вектор в конце первый:
Обратите внимание, что сложение a + b дает тот же результат, что и b + a .
Скалярное умножение
Примечание
Векторы представляют как направление, так и величину. Ценность представляющий только величину, называется скаляром .
Вектор можно умножить на скаляр :
вар с = а * 2 # (2, 5) * 2 = (4, 10) var d = b / 3 # (3, 6) / 3 = (1, 2)
Примечание
Умножение вектора на скаляр не меняет его направление, только его величина. Вот как ты масштаб вектор.
Практическое применение
Давайте рассмотрим два распространенных способа сложения и вычитания векторов.
Механизм
Вектор может представлять любую величину с величиной и направлением. Типичными примерами являются: положение, скорость, ускорение и сила. В На этом изображении космический корабль на шаге 1 имеет вектор положения (1,3) и вектор скорости (2,1) . Вектор скорости показывает, насколько далеко корабль движется каждый шаг. Мы можем найти позицию для шага 2, добавив скорость до текущего положения.
Совет
Скорость измеряет изменение положения в единицу времени. новое положение находится путем прибавления скорости к предыдущему положению.
Наведение на цель
В этом сценарии у вас есть танк, который хочет направить свою башню на робот. Вычитание положения танка из положения робота дает вектор, указывающий от танка к роботу.
Подсказка
Чтобы найти вектор, указывающий от A до B используйте B-A .
Единичные векторы
Вектор с величиной из 1 называется единичным вектором . Они есть также иногда упоминается как векторов направления или нормалей . Ед. изм векторы полезны, когда вам нужно отслеживать направление.
Нормализация
Нормализация вектора означает уменьшение его длины до 1 при сохраняя свое направление. Это делается путем деления каждой из его составляющих по своей величине. Поскольку это такая распространенная операция, Vector2 и Vector3 предоставляют метод нормализации:
а = а.нормализованный()
Предупреждение
Поскольку нормализация включает деление на длину вектора, вы не можете нормализовать вектор длины 0 . Пытаться это приведет к ошибке.
Отражение
Обычно единичные векторы используются для обозначения нормалей . Обычный векторы — это единичные векторы, выровненные перпендикулярно поверхности, определяющие его направление. Они обычно используются для освещения, столкновений и других операции с поверхностями.
Например, представьте, что у нас есть движущийся мяч, который мы хотим отскочить от стена или другой объект:
Нормаль поверхности имеет значение (0, -1) , потому что это горизонтальная поверхность. Когда мяч сталкивается, мы берем его остаточное движение (количество оставшийся после удара о поверхность) и отразите его с помощью нормали. В Годо, класс Vector2 имеет метод bounce() справиться с этим. Вот пример GDScript диаграммы выше с использованием Кинематическое тело2D:
# объект "столкновение" содержит информацию о столкновении переменная коллизия = move_and_collide(скорость * дельта) если столкновение: переменная отражения = столкновение.остаток.отскок(столкновение.нормальный) скорость = скорость.отскок(столкновение.норма) move_and_collide (отражать)
Скалярный продукт
Скалярное произведение — одно из самых важных понятий в векторной математике. но часто неправильно понимают. Скалярное произведение — это операция над двумя векторами, возвращает скаляр . В отличие от вектора, который содержит как величину, так и направление, скалярное значение имеет только величину.
Формула скалярного произведения принимает две распространенные формы:
и
Однако в большинстве случаев проще всего использовать встроенный метод. Обратите внимание, что порядок двух векторов не имеет значения:
переменная c = a.dot(b) var d = b.dot(a) # Они эквивалентны.
Скалярное произведение наиболее полезно при использовании с единичными векторами, что делает первая формула уменьшите до cosθ . Это означает, что мы можем использовать точку произведение, чтобы сообщить нам что-то об угле между двумя векторами:
При использовании единичных векторов результат всегда будет между -1 (180°) и 1 (0°).
Облицовка
Мы можем использовать этот факт, чтобы определить, обращен ли объект к другому объект. На диаграмме ниже игрок P пытается избежать зомби A и B . Предположим, что поле зрения зомби равно 9.0187 180° , они видят игрока?
Зеленые стрелки fA и fB представляют собой единичных векторов , представляющих направления зомби, а синий полукруг представляет его поле Посмотреть. Для зомби A мы находим вектор направления AP , указывающий на игрок использует P - A и нормализует его, однако у Годо есть помощник метод для этого называется direction_to . Если угол между этим вектор и обращенный вектор меньше 90°, то зомби может видеть игрок.
В коде это будет выглядеть так:
переменная AP = A.direction_to(P) если AP.dot(fA) > 0: print("А видит Р!")
Перекрестное произведение
Как и скалярное произведение, перекрестное произведение представляет собой операцию над двумя векторами. Однако результатом перекрестного произведения является вектор с направлением что перпендикулярно обоим. Его величина зависит от их относительного угла. Если два вектора параллельны, результатом их перекрестного произведения будет нулевой вектор.
Перекрестное произведение вычисляется следующим образом:
переменная c = Vector3() c.x = (a.y * b.z) - (a. z * b.y) су = (а.з * б.х) - (а.х * б.з) c.z = (a.x * b.y) - (a.y * b.x)
С Godot вы можете использовать встроенный метод:
переменная c = a.cross(b)
Примечание
В векторном произведении важен порядок. а.крест(б) нет дают тот же результат, что и b.cross(a) . Результирующие векторы точка в противоположных направлениях.
Расчет нормалей
Одним из распространенных применений векторных произведений является нахождение нормали к поверхности плоскости. или поверхность в трехмерном пространстве. Если у нас есть треугольник ABC , мы можем использовать вектор вычитание, чтобы найти два ребра AB и AC . Используя перекрестное произведение, AB x AC дает вектор, перпендикулярный обеим нормалям поверхности.
Вот функция для вычисления нормали треугольника:

функция get_triangle_normal(a, b, c): # найти нормаль к поверхности по трем вершинам переменная сторона1 = б - а переменная сторона2 = с - а переменная нормальная = сторона1.
No related posts.