Формула знаменателя геометрической прогрессии — онлайн справочник для студентов
ОПРЕДЕЛЕНИЕ
Геометрическая прогрессия представляет собой последовательность чисел, каждая из которых, начиная со второй, получается из предыдущей, умножая на то же число q, которое называется знаменателем прогрессии.
Пусть \(\ B=\left\{b_{1}, b_{2}, \ldots, b_{n}, \ldots\right\} \) — геометрическая прогрессия, \(\ b_{n} \) — n-й член прогрессии, тогда знаменатель этой прогрессии может быть рассчитан по формуле:
\(\ q=\frac{b_{n+1}}{b_{n}} \)
Если разность геометрической прогрессии \(\ \mathrm{q}>1 \), то прогрессия будет возрастать, если \(\ |q|Примеры решения проблем
ПРИМЕР 1
Найти знаменатель геометрической прогрессии \(\ \left(b_{n}\right) \) , если \(\ b_{5}=-6, b_{7}=-54 \)
Express \(\ b_{7}-b_{5} \) с использованием знаменателя прогрессии q:
\(\ b_{7}=b_{6} \cdot q=\left(b_{5} \cdot q\right) \cdot q=b_{5} \cdot q^{2} \)
отсюда
\(\ q^{2}=\frac{b_{7}}{b_{5}}=\frac{-54}{-6}=9 \Rightarrow q=\pm 3 \)
ПРИМЕР 2
состоит в том, чтобы найти знаменатель прогрессии. {2}\right)}=\frac{1}{3} \Rightarrow q=3
\)
{2}\right)}=\frac{1}{3} \Rightarrow q=3
\)
Физика
166
Реклама и PR
31
Педагогика
80
Психология
72
Социология
7
Астрономия
9
Биология
30
Культурология
86
Экология
8
Право и юриспруденция
36
Политология
13
Экономика
49
9
История
16
Философия
8
Информатика
20
Право
35
Информационные технологии
6
Экономическая теория
7
Менеджент
719
Математика
338
Химия
20
Микро- и макроэкономика
1
Медицина
5
Государственное и муниципальное управление
2
География
542
Информационная безопасность
2
Аудит
11
Безопасность жизнедеятельности
3
Архитектура и строительство
1
Банковское дело
1
Рынок ценных бумаг
6
Менеджмент организации
2
Маркетинг
238
Кредит
3
Инвестиции
2
Журналистика
1
Конфликтология
15
Этика
9
Формулы дифференцирования Формула разности арифметической прогрессии Формулы прогрессий Формула суммы геометрической прогрессии Формула суммы арифметической прогрессии
Узнать цену работы
Узнай цену
своей работы
Имя
Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругоеПодпишись на рассылку, чтобы не пропустить информацию об акциях
Внеклассный урок — Геометрическая прогрессия
Геометрическая прогрессия
Геометрическая прогрессия – это такая последовательность отличных от нуля чисел, которая получается в результате умножения каждого последующего члена на одно и то же число, не равное нулю. |
Пример геометрической прогрессии: 2, 6, 18, 54, 162.
Здесь каждый член после первого в 3 раза больше предыдущего. То есть каждый последующий член является результатом умножения предыдущего члена на 3:
2 · 3 = 6
6 · 3 = 18
18 · 3 = 54
54 · 3 = 162.
Знаменатель геометрической прогрессии.
Знаменатель геометрической прогрессии – это число, равное отношению второго и любого последующего члена к предыдущему члену прогрессии. Ее обычно обозначают буквой q. |
В нашем примере при делении второго члена на первый, третьего на второй и т.д. мы получаем 3. Число 3 и является знаменателем данной геометрической прогрессии.
Свойства геометрической прогрессии:
1) Квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению двух соседних членов, стоящих перед ним и после него: bn2 = bn-1 · bn+1
2) Верно и обратное утверждение: если в последовательности чисел квадрат любого ее члена, начиная со второго, равен произведению двух соседних членов, стоящих перед ним и после него, то эта последовательность является геометрической прогрессией: |
Пример:
Вернемся к нашей геометрической прогрессии 2, 6, 18, 54, 162. Возьмем четвертый член и возведем его в квадрат:
Возьмем четвертый член и возведем его в квадрат:
542 = 2916.
Теперь перемножим члены, стоящие слева и справа от числа 54:
18 · 162 = 2916.
Как видим, квадрат третьего члена равен произведению соседних второго и четвертого членов.
Как найти определенный член геометрической прогрессии.
Чтобы найти n-й член геометрической прогрессии, следует применить формулу: bn = b1· qn – 1 |
Пример 1: Возьмем некую геометрическую прогрессию, в которой первый член равен 2, а знаменатель геометрической прогрессии равен 1,5. Надо найти 4-й член этой прогрессии.
Дано:
b1 = 2
q = 1,5
n = 4
————
b4 — ?
Решение.
Применяем формулу bn = b1 · qn – 1, вставляя в нее соответствующие значения:
b4 = 2 · 1,54 – 1 = 2 · 1,53 = 2 · 3,375 = 6,75.
Ответ: Четвертый член заданной геометрической прогрессии – число 6,75.
Пример 2: Найдем пятый член геометрической прогрессии, если первый и третий члены равны соответственно 12 и 192.
Дано:
b1 = 12
b3 = 192
————
b5 — ?
Решение.
1) Сначала нам надо найти знаменатель геометрической прогрессии, без которой решить задачу невозможно. В качестве первого шага с помощью нашей формулы выводим формулу для b3:
b3 = b1 · q3 – 1 = b1 · q2
Теперь мы можем найти знаменатель геометрической прогрессии: b3 192
q2 = —— = —— = 16
b1 12
q = √16 = 4 или –4.
2) Осталось найти значение b5.
Если q = 4, то
b5 = b1q5-1 = 12 · 44 = 12 · 256 = 3072.
При q = –4 результат будет тот же. Таким образом, задача имеет одно решение.
Ответ: Пятый член заданной геометрической прогрессии – это число 3072.
Как найти сумму первых n членов геометрической прогрессии.
При q ≠ 1 сумму любого количества первых членов геометрической прогрессии можно найти с помощью одной из следующих формул: bnq – b1 b1 (qn – 1) Если q = 1, то все члены прогрессии просто равны первому члену: Sn = nb1 |
Пример: Найдем сумму первых пяти членов геометрической прогрессии (bn), в которой первый член равен 2, а знаменатель геометрической прогрессии 3.
Дано:
b1 = 2
q = 3
n = 5
————
S5 – ?
Решение.
Применяем вторую формулу из двух приведенных выше:
b1 (q5 – 1) 2 (35 – 1) 2 · (243 – 1) 484
S5 = ————— = ————— = ———————— = ————— = 242
q – 1 3 – 1 2 2
Ответ: Сумма первых пяти членов заданной геометрической прогрессии равна 242.
Сумма бесконечной геометрической прогрессии.
Следует различать понятия «сумма бесконечной геометрической прогрессии» и «сумма n членов геометрической прогрессии». Второе понятие относится к любой геометрической прогрессии, а первое – только к такой, где знаменатель меньше 1 по модулю.
Сумма бесконечной геометрической прогрессии – это предельное число, к которому сходится последовательность прогрессии. Говоря иначе, какой бы длинной не была геометрическая прогрессия, сумма ее членов не больше какого-то определенного числа и практически равна этому числу. Оно и называется суммой геометрической прогрессии. Не любая геометрическая прогрессия имеет такую предельную сумму. Она может быть только у такой прогрессии, знаменатель которой – дробное число меньше 1. |
Пример-пояснение:
Составим геометрическую прогрессию, в которой первый член – число 2, а знаметатель равен 1/2:
2, 1, 1/2, 1/4, 1/8, 1/16, 1/32, 1/64 и т.д.
Сложим все полученные члены прогрессии:
2 + 1 + 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 = 255/64 ≈ 3,98 ≈ 4.
Можно продолжить прогрессию до 10, 100, миллиона членов, но во всех случаях сумма членов прогрессии будет практически равна 4. Число 4 и является суммой данной геометрической прогрессии.
Чтобы найти сумму бесконечной геометрической прогрессии, не надо складывать все ее члены. Для этого существует замечательная и довольно простая формула. 2
2
Знаменатель геометрической прогрессии — Энциклопедия по экономике
Причем, эти отклонения при составлении нормативных таблиц необходимо выбирать близкими к ряду геометрической прогрессии. Величина знаменателя геометрической прогрессии принимается такой, чтобы получаемые по нормативам времена или элементы режимов резания не выходили за пределы допускаемой погрешности, принятой при расчете нормативных таблиц для данных конкретных организационно-технических условий производства. [c.384]
Времена, определенные по нормативной линии для максимального и минимального в данном интервале значений фактора, отклоняются от принятого норматива в одинаковой мере, но в разные стороны, причем это отклонение определяется заранее принятой точностью норматива, выраженной в процентах (знаменателем геометрической прогрессии). Следовательно, [c.384]
Обозначив через Kt знаменатель геометрической прогрессии для значений /ь /2> /3,. .., / или
[c.387]
.., / или
[c.387]
В зависимости от точности составляемых нормативных таблиц назначается знаменатель геометрической прогрессии для зависимого переменного [c.388]
Так как принимается определенное значение знаменателей геометрической прогрессии для зависимого / и независимого переменного А, то значения как t, так и А, фактически изменяющихся при построении нормативной таблицы, будут находиться в определенных интервалах. Каждый интервал определяется практическими границами значения величины независимого переменного (А). [c.388]
II. Знаменатель геометрической прогрессии для зависимой переменной, в данном случае подачи s в мм/об, принимаем равным Ks = 1,10. [c.389]
III. По принятому значению знаменателя геометрической прогрессии для зависимой переменной К3 определяем знаменатель геометрической прогрессии для значений независимого переменного, в данном случае диаметров сверл D в мм [c.389]
I. Знаменатель геометрической прогрессии для зависимой переменной, в данном случае времени t в мин. , принимаем равным /С[c.390]
, принимаем равным /С[c.390]
II. По принятому значению знаменателя геометрической прогрессии Kt определяем для значений независимого переменного, в данном случае пришабриваемых плоскостей F в см [c.390]
Следует заметить, что этот коэффициент представляет собой сумму членов геометрической прогрессии, где первый член равен геометрической прогрессии, преобразуем полученное выражение для наращенной суммы ренты к такому виду [c.91]
Дисконтированные отдельные платежи РМТ( + г)»1, РМТ (1+1) 1У РМТ(( + г)»1)3 представляют собой геометрическую прогрессию с первым членом РМТ( + i) l и знаменателем (1 +/)» Ее сумма имеет вид [c.99]
Преобразование модели (8.15) к виду (8.32) называется обратным преобразованием Койка. [c.203]Применим теперь изложенные методологические соображения к ряду динамики глобального использованного народного дохода за период 1950—1967 гг. и исчислим — при гипотезе изменения этого ряда по показательной кривой — знаменатель (д) геометрической прогрессии всеми перечисленными способами, дабы выявить тот, который дает максимальное приближение к эмпирическим данным по критерию минимума среднего квадра-тического отклонения. Результаты получились следующие (табл. 1).
[c.130]
Результаты получились следующие (табл. 1).
[c.130]
Для параметрического ряда, построенного по законам геометрической прогрессии, степень его густоты характеризует знаменатель прогрессии ф, который и определяет густоту сетки ряда. [c.11]
Для экономии времени коэффициент дисконтирования аннуитета может быть вычислен по формуле суммы геометрической прогрессии со знаменателем I/O + г) [c.278]
В рассмотренном условном примере сменные детали имеют всего четыре срока службы — t 2/ 4t 8t. Все они, во-первых, кратны t, т. е. межремонтному периоду, а во-вторых, образуют геометрическую прогрессию со знаменателем 2. Возникает вопрос каким образом можно на практике обеспечить подобную закономерность (или другую, которая может оказаться более целесообразной, в частности арифметическую прогрессию), если детали многих агрегатов в настоящее время характеризуются значительным разнообразием сроков службы В самом деле, в нашем условном примере исключены детали со сроками службы 3t, Ы, 6/ и It. [c.58]
[c.58]
Последовательность V,]/2,V3,…Vn может быть рассмотрена как геометрическая прогрессия а0, ар а2,. .., а со знаменателем q=V и первым членом a0=V. Тогда [c.137]
Это степенной ряд, который сходится в силу того, что (1-г) есть число геометрической прогрессии со знаменателем (1-г) и равняется S = bj/(l-q) = 1 / (l-(l-r)) = 1/r > 1. Таким образом, из каждой условной единицы денег, выпущенных ЦБ, образуется 1/г денег в результате прохождения по банковской системе. [c.152]
В квадратных скобках мы получили геометрическую прогрессию с первым членом а = (1 + i )» и знаменателем g/(l + i ). Ис- [c.122]
Sn является суммой первых п членов геометрической прогрессии, первый член которой Ь = —, а знаменатель q = —. Используя [c.52]
С древнейших времен для построения рядов предпочтительных чисел использовалась геометрическая прогрессия, т. е. такая последовательность чисел, в которой отношение последующего к предыдущему члену (оно называется знаменателем прогрессии) остается постоянным. Примерами геометрической прогрессии являются последовательности [c.261]
Примерами геометрической прогрессии являются последовательности [c.261]
Относительная разность между любыми соседними членами ряда постоянна. Это свойство вытекает из самой природы геометрической прогрессии. Возьмем в качестве примера простейшую прогрессию со знаменателем, равным двум [c.261]
Из операций (5), (6) и состоит основной итерационный цикл. Теоретическими исследованиями доказана сходимость метода (аккуратные формулировки теорем см. в [10], [11], [25]) со скоростью геометрической прогрессии, знаменатель которой может быть сделан сколь угодно малым за счет достаточно большого а. Однако этот результат не очень полезен в практической работе дело в том, что увеличение а повышает эффективность внешнего итерационного цикла (5), (6), но одновременно отрицательно сказывается на эффективности внутреннего итерационного процесса, с помощью которого решается задача (5). В частности, [c.462]
Формула геометрической прогрессии со знаменателем, меньшим единицы, например, 1/(1 + г) или 1/1,10 в нашем примере выглядит так [c. 61]
61]
Применяя к правой части уравнения формулу суммы членов геометрической прогрессии с первым членом R и знаменателем (1 + j), получим [c.195]
В строчных нормативах /н. ш содержится в скрытом виде основное время. Это время изменяется внутри строки в геометрической прогрессии со знаменателем Kt = 1,26 или 1,34. С таким же шагом изменяются шкалы факторов D и L обработки. Если, например, длину обработки увеличить (сдвинуть) на три шага, то основное время внутри / . ш увеличится тоже на три шага, т. е. в 1,263 раз (в 2 раза). Это приведет к абсолютному возрастанию tH. ш, которое легко определить вычитанием. Таким способом просто установить нужную величину t0. [c.89]
Разработка типажа ведется на основе рядов предпочтительных чисел (ГОСТ 8032—56), которые строятся по закону геометрической прогрессии со знаменателем [c.49]
Правая часть равенства является геометрической прогрессией из я членов. Первый ее член равен 1, а знаменатель прогрессии составляет (1 + i)-Сумма такой прогрессии равна
[c. 60]
60]
Сумма в скобках этого выражения является геометрической прогрессией с q членами (первый член равен (1+i) ) и знаменателем (1+i)»- Используя формулу для суммы геометрической прогрессии, получим [c.227]
Рассмотрим ситуацию, в которой корпорация планирует выплачивать дивиденд D в конце текущего периода. Предположим, прогнозируется, что дивиденды увеличиваются согласно геометрической прогрессии ориентировочно с общим знаменателем 1 + k и акция приобретается для того, чтобы давать доходность i за период, где -1 цена акции на единицу дивиденда получается путем предельного перехода от обыкновенного аннуитета со сроком п периодов, в котором первый платеж равен 1 и последующие платежи увеличиваются в геометрической прогрессии с одинаковым знаменателем 1 + k. Настоящая стоимость этого аннуитета равна [c.237]
Дисконтированные отдельные платежи R(1+i)-1, R((1-И)-1)2, R((1 + i)-1)3 представляют собой геометрическую прогрессию с первым членом R(1 + i)-1 и знаменателем (1 + i) -1. Ее сумма имеет вид [c.39]
Ее сумма имеет вид [c.39]
Значения t, tz, t3,…, tn зависимой переменной (время или элементы режимов резания) должны представлять собой ряд геометрической прогрессии, знаменатель которой выбирается в зависимости от точности разрабатываемых нормативов и определяется в конечном итоге масштабом производства. [c.387]
Одним из важнейших направлений конструкторской унификации является сокращение номенклатуры изделий, имеющих одинаковое или сходное эксплуатационное назначение. Оно реализуется в первую очередь путем создания параметрических рядов (гамм) изделий. Каждый ряд представляет собой совокупность изделий, аналогичных по кинематике, рабочему процессу, но различных по габаритным, мощностным или другим основным эксплуатационным параметрам (грузоподъемность грузового автомобиля или крана, рабочий объем двигателя, производительность компрессора и т. д.). Параметрический ряд, как правило, создается в соответствии с ГОСТ 8032—84 Предпочтительные числа и ряды предпочтительных чисел . Обычно пользуются четырьмя десятичными рядами R5 RIO , R20 R40 с соответствующими знаменателями геометрической прогрессии 1,6 1,25 1,12 1,06. Расчет параметрических рядов для выбора экономически рационального разрежения ряда производится по Типовым методикам оптимизации параметрического (типоразмерного) ряда и соответствующей типовой методике для многомерных рядов. Имеются экономико-математические модели их оптимизации, основанные как на классических методах в условиях непрерывности и дифференцируемости функции затрат и функции спроса и наличии экстремума общих затрат, так и неклассических методах оптимизации, разработанных, в частности, Институтом математики Сибирского отделения АН СССР. Параметрические ряды формируют в каждой отрасли перспективный типаж изделий, что весьма ограничивает их возможную номенклатуру.
[c.107]
Обычно пользуются четырьмя десятичными рядами R5 RIO , R20 R40 с соответствующими знаменателями геометрической прогрессии 1,6 1,25 1,12 1,06. Расчет параметрических рядов для выбора экономически рационального разрежения ряда производится по Типовым методикам оптимизации параметрического (типоразмерного) ряда и соответствующей типовой методике для многомерных рядов. Имеются экономико-математические модели их оптимизации, основанные как на классических методах в условиях непрерывности и дифференцируемости функции затрат и функции спроса и наличии экстремума общих затрат, так и неклассических методах оптимизации, разработанных, в частности, Институтом математики Сибирского отделения АН СССР. Параметрические ряды формируют в каждой отрасли перспективный типаж изделий, что весьма ограничивает их возможную номенклатуру.
[c.107]
Определение экономически целесообразного ряда величин основного параметра стандартизируемого или унифицируемого элемента системы. При стандартизации и унификации применяют градацию по одному из следующих рядов чисел построенному по арифметической прогрессии, при которой разность двух соседних членов ряда постоянна (Nn— —i = onst) построенному на основе геометрической прогрессии, при которой каждый член ряда является произведением предыдущего члена и постоянной для принятого ряда величины знаменателя геометрической прогрессии x(Nn=NiXn l) по ступенчато-арифметическим рядам, в которых разность значений остается постоянной только для части ряда. Обычно эта разность принимается меньшей для малых типоразмеров изделия и большей для больших типоразмеров.
[c.134]
Обычно эта разность принимается меньшей для малых типоразмеров изделия и большей для больших типоразмеров.
[c.134]
Геометрической прозрессие-й называют такую последовательность чисел Of, a2,. .., ап,. .. (членов прогрессии), в которой каждое последующее число получается из предыдущего умножением его на. определенное число q (знаменатель геометрической прогрессии). [c.10]
В большинстве случаев оптимальный. нагрузочный ряд семейства агрегатов (мощность, момент, давление) будет выражаться геометрической прогрессией с постоянным или ступенчато изменяющимся знаменателем. Для этого необходимо, чтобы и основной параметр агрегата (диаметр, расстояние между центрами) также изменялся по геометрической прогрессии. Характер связи знаменателей нагрузочного и размерного ряда зависит от типа агрегата. Налример, в ходовых колесах и электрогидравлических толкателях связь будет квадратичной, в редукторах и тормозах — кубической. Часто на. практике с целью получения размерного ряда, состоящего из круглых величин, а главное — для наименьшей ломки давно сложившихся размеров применяется арифметическая прогрессия с постоянной или ступенчато изменяющейся разностью. Предпочтение следует отдавать рядам, построенным по геометрической прогрессии. В первую очередь следует применять Предпочтительные числа и ряды предпочтительных чисел по ГОСТу 8032-56. Отступления от этого ГОСТа должны.быть технически обоснованы.
[c.34]
Предпочтение следует отдавать рядам, построенным по геометрической прогрессии. В первую очередь следует применять Предпочтительные числа и ряды предпочтительных чисел по ГОСТу 8032-56. Отступления от этого ГОСТа должны.быть технически обоснованы.
[c.34]
Так как знаменатели лерехода для узлов, комплектующих мостовой кран, неодинаковы и. изменяются в пределах от 1,4 до 1,8, то в качестве знаменателя перехода всего крана целесообразно принять среднюю величину, равную I,i6 я совпадающую со стандартным знаменателем пятого ряда по ГОСТу 8032-56 Предпочтительные числа и ряды предпочтительных чисел . Тогда нагрузочный ряд мостовых кранов должен представлять геометрическую прогрессию со зламенате-лем 1,6. [c.38]
Еще в Древней Римской империи диаметры колес в водопроводах были выбраны в соответствии с геометрической прогрессией. В конце XVII — начале XVIII вв. в Германии для расчета темперированного музыкального строя была применена геометрическая прогрессия со знаменателем л/2 Во Франции в 1805 г. размеры типографского шрифта были установлены в соответствии с геометрической прогрессией. В конце прошлого века русский ученый академик А.В. Гадолин разработал теорию рационального построения кинематических соотношений в металлообрабатывающих станках, основанную на использовании закономерных рядов чисел, и научно
[c.261]
размеры типографского шрифта были установлены в соответствии с геометрической прогрессией. В конце прошлого века русский ученый академик А.В. Гадолин разработал теорию рационального построения кинематических соотношений в металлообрабатывающих станках, основанную на использовании закономерных рядов чисел, и научно
[c.261]
В радиоэлектронике параметрические стандарты приведены в соответствие с рекомендациями Международной электротехнической комиссии (МЭК). Этими рекомендациями установлены предпочтительные числа по рядам ЕЗ, Е6, Е12, Е24, Е48, Е96 и Е192. Наиболее широкое применение имеют первые четыре. Они построены на базе геометрических прогрессий со следующими знаменателями [c.268]
Уточним эго предложение. Имеется в виду, что сумма этого ряда стремится к 1 при неограниченном увеличении числа слагаемых. Действительно, вынесем за скобку а, тогда сумма перепишется как а [1 + (1 — а) + (I — а)2 + -h. .J. Но сумма в квадратных скобках представляет собой сумму бесконечной геометрической прогрессии со знаменателем 0 [c. 21]
21]
Геометрическая прогрессия в математике с примерами решения и образцами выполнения
Оглавление:
Определение геометрической прогрессии:
Рассмотрим последовательность, членами которой являются степени числа 2 с натуральными показателями:
Каждый член этой последовательности, начиная со второго, получается умножением предыдущего члена на 2. Эта последовательность является примером геометрической прогрессии.
Определение:
Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число.
Иначе говоря, последовательность — геометрическая прогрессия, если для любого натурального п выполняются условия
где q — некоторое число. Обозначим, например, через последовательность натуральных степеней числа 2. В этом случае для любого натурального п верно равенство здесь q = 2.
Из определения геометрической прогрессии следует, что отношение любого ее члена, начиная со второго, к предыдущему члену равно q, т. е. при любом натуральном n верно равенство
Число q называют знаменателем геометрической прогрессии.
Очевидно, что знаменатель геометрической прогрессии отличен от нуля.
Чтобы задать геометрическую прогрессию, достаточно указать ее первый член и знаменатель.
Приведем примеры.
Если то получим геометрическую прогрессию
Условиями задается геометрическая прогрессия
Если то имеем прогрессию
Если то получим геометрическую прогрессию
Зная первый член и знаменатель геометрической прогрессии, можно найти последовательно второй, третий и вообще любой ее член:
Точно так же находим, что Вообще, чтобы найти мы должны
Мы получили формулу n-го члена геометрической прогрессии.
Приведем примеры решения задач с использованием этой формулы.
Пример:
В геометрической прогрессии Найдем b7.
По формуле n-го члена геометрической прогрессии
Пример:
Найдем восьмой член геометрической прогрессии
Зная первый и третий члены геометрической прогрессии, можно найти ее знаменатель. Так как
Решив уравнение
найдем, что
Таким образом, существуют две прогрессии, удовлетворяющие условию задачи.
Если
Если
Задача имеет два решения:
Пример:
После каждого движения поршня разрежающего насоса из сосуда удаляется 20% находящегося в нем воздуха. Определим давление воздуха внутри сосуда, после шести движений поршня, если первоначально давление было 760 мм рт. ст.
Так как после каждого движения поршня из сосуда удаляется 20% имевшегося воздуха, то остается 80% воздуха. Чтобы узнать давление воздуха в сосуде после очередного движения поршня, нужно давление после предыдущего движения поршня умножить на 0,8.
Мы имеем геометрическую прогрессию, первый член которой равен 760, а знаменатель равен 0,8. Число, выражающее давление воздуха в сосуде (в мм рт. ст.) после шести движений поршня, является седьмым членом этой прогрессии. Оно равно
Число, выражающее давление воздуха в сосуде (в мм рт. ст.) после шести движений поршня, является седьмым членом этой прогрессии. Оно равно
Произведя вычисления, получим:
Формула суммы n первых членов геометрической прогрессииДревняя индийская легенда рассказывает, что изобретатель шахмат попросил в награду за свое изобретение столько пшеничных зерен, сколько их получится, если на первую клетку шахматной доски положить одно зерно, на вторую — в 2 раза больше, т. е. 2 зерна, на третью — еще в 2 раза больше, т. е. 4 зерна, и т. д. до 64-й клетки. Сколько зерен должен был получить изобретатель шахмат?
Число зерен, о которых идет речь, является суммой шестидесяти четырех членов геометрической прогрессии, первый член которой равен 1, а знаменатель равен 2. Обозначим эту сумму через S:
Умножим обе части записанного равенства на знаменатель прогрессии, получим:
Вычтем почленно из второго равенства первое и проведем упрощения:
Можно подсчитать, что масса такого числа пшеничных зерен больше триллиона тонн. Это заведомо превосходит количество пшеницы, собранной человечеством до настоящего времени.
Это заведомо превосходит количество пшеницы, собранной человечеством до настоящего времени.
Выведем теперь формулу суммы n первых членов произвольной геометрической прогрессии. Воспользуемся тем же приемом, с помощью которого была вычислена сумма S.
Пусть дана геометрическая прогрессия Обозначим сумму n первых ее членов через :
Умножим обе части этого равенства на q:
Учитывая, что
получим:
Вычтем почленно из равенства (2) равенство (1) и приведем подобные члены:
Отсюда следует, что при
Мы получили формулу суммы n первых членов геометрической прогрессии, в которой . Если q = 1, то все члены прогрессии равны первому члену и
При решении многих задач удобно пользоваться формулой суммы п первых членов геометрической прогрессии, записанной в другом виде. Подставим в формулу (I) вместо выражение Получим:
Пример:
Найдем сумму первых десяти членов геометрической прогрессии в которой
Так как известны первый член и знаменатель прогрессии, то удобно воспользоваться формулой (II). Получим:
Получим:
Пример:
Найдем сумму слагаемые которой являются последовательными членами геометрической прогрессии
Первый член прогрессии равен 1, а знаменатель равен х. Так как является членом этой прогрессии с номером n, то задача состоит в нахождении суммы п первых ее членов. Воспользуемся формулой (I):
Таким образом, если то
Умножив левую и правую части последнего равенства на х — 1, получим тождество
В частности, при n = 2 и n = 3 приходим к известным формулам
Пример:
Найдем сумму шести первых членов геометрической прогрессии если известно, что
Зная можно найти знаменатель прогрессии q. Так как
Значит,
Таким образом, существуют две прогрессии, удовлетворяющие условию задачи.
Сумма бесконечной геометрической прогрессии при
|q|< 1Пусть длина отрезка АВ равна 2 ед. (рис. 50). Отметим точку В1 — середину отрезка А В, затем точку В2 — середину правой его половины, затем точку В3 — середину получившегося справа отрезка и т. д. Длины отрезков и т. д. образуют бесконечную геометрическую прогрессию, знаменатель которой равен
д. Длины отрезков и т. д. образуют бесконечную геометрическую прогрессию, знаменатель которой равен
Найдем сумму n первых членов этой прогрессии:
При увеличении числа слагаемых n значение дроби приближается к нулю. Действительно,
Поэтому при неограниченном увеличении n разность становится сколь угодно близкой к числу 2 или, как говорят, стремится к числу 2.
Таким образом, сумма n первых членов геометрической прогрессии при неограниченном увеличении n стремится к числу 2. Число 2 называют суммой бесконечной геометрической прогрессии и пишут:
Это равенство легко истолковать геометрически: сумма длин отрезков равна длине отрезка АВ.
Рассмотрим теперь произвольную геометрическую прогрессию
у которой |q|< 1
Запишем формулу суммы п первых членов прогрессии:
Преобразуем выражение в правой части равенства:
Значит,
Можно доказать, что если то при неограниченном увеличении n множитель стремится к нулю, а значит, стремится к нулю и произведение Поэтому при неограниченном увеличении n сумма Sn стремится к числу
Число называют суммой бесконечной геометрической прогрессии у которой
Это записывают так:
Обозначив сумму прогрессии буквой S, получим формулу
Заметим, что если то сумма n первых членов геометрической прогрессии при неограниченном увеличении n не стремится ни к какому числу. Бесконечная геометрическая прогрессия имеет сумму только при
Бесконечная геометрическая прогрессия имеет сумму только при
Пример:
Найдем сумму бесконечной геометрической прогрессии
У этой прогрессии значит, условие |q| < 1 выполнено. По формуле получим:
Пример:
Дан квадрат, сторона которого равна 4 см. Середины его сторон являются вершинами второго квадрата, середины сторон второго квадрата являются вершинами третьего квадрата и т. д. (рис. 51). Найдем сумму площадей всех квадратов.
Из геометрических соображений ясно, что площадь каждого следующего квадрата равна половине площади предыдущего. Таким образом, последовательность площадей квадратов является геометрической прогрессией, первый член которой равен 16, а знаменатель равен Найдем сумму этой геометрической прогрессии:
Значит, сумма площадей всех квадратов равна 32 см2.
Из курса VIII класса нам известно, что каждое рациональное число может быть представлено в виде бесконечной десятичной периодической дроби. Чтобы выразить рациональное число — целое число, а n — натуральное, в виде бесконечной десятичной дроби, достаточно разделить числитель на знаменатель. Наоборот, каждая бесконечная десятичная периодическая дробь представляет некоторое рациональное число. Покажем на примере, как с помощью формулы суммы бесконечной геометрической прогрессии можно представить бесконечную десятичную периодическую дробь в виде отношения
Чтобы выразить рациональное число — целое число, а n — натуральное, в виде бесконечной десятичной дроби, достаточно разделить числитель на знаменатель. Наоборот, каждая бесконечная десятичная периодическая дробь представляет некоторое рациональное число. Покажем на примере, как с помощью формулы суммы бесконечной геометрической прогрессии можно представить бесконечную десятичную периодическую дробь в виде отношения
Пример:
Представим бесконечную десятичную периодическую дробь 0,(18) в виде обыкновенной дроби.
По аналогии с конечными десятичными дробями представим бесконечную десятичную дробь 0,(18) в виде суммы:
Слагаемые в правой части равенства — члены геометрической прогрессии, у которой первый член равен 0,18, а знаменатель равен 0,01, т. е. условие выполнено. Найдем сумму этой прогрессии:
Значит,
Таким же способом можно представить в виде обыкновенной дроби любую бесконечную десятичную периодическую дробь.
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Геометрическая прогрессия.
 n)}{1-q}}, где
n)}{1-q}}, гдеb1 — первый член прогрессии,
q — знаменатель прогрессии,
n — номер члена
Для нахождения суммы членов геометрической прогрессии вы можете воспользоваться нашим онлайн калькулятором. Просто введите данные и получите результат.
Знаменатель геометрической прогрессии
Знаменатель геометрической прогрессии можно вычислить с помощью текущего и следующего членов геометрической прогрессии по формуле:
q = bn+1 / bn
Члены геометрической прогрессии
Общая формула для вычисления n-ого члена геометрической прогрессии по первому члену и знаменателю:
bn = b1 ⋅ qn – 1
Следующий член геометрической прогрессии можно найти по предыдущему члену и знаменателю:
bn+1 = bn ⋅ q
Предыдущий член геометрической прогрессии можно найти по следующему члену и знаменателю:
bn-1 = bn / q
Также член геометрической прогрессии можно найти, если известны следующий и предыдущий члены:
bn = √bn-1 ⋅ bn+1, где n > 1
Для чего нужна геометрическая прогрессия и ее история возникновения.

Еще в древности итальянский математик монах Леонардо из Пизы (более известный под именем Фибоначчи) занимался решением практических нужд торговли. Перед монахом стояла задача определить, с помощью какого наименьшего количества гирь можно взвесить товар? В своих трудах Фибоначчи доказывает, что оптимальной является такая система гирь: Это одна из первых ситуаций, в которой людям пришлось столкнуться с геометрической прогрессией, о которой ты уже наверное слышал и имеешь хотя бы общее понятие. Как только полностью разберешься в теме, подумай, почему такая система является оптимальной?
В настоящее время, в жизненной практике, геометрическая прогрессия проявляется при вложении денежных средств в банк, когда сумма процентов начисляется на сумму, скопившуюся на счете за предыдущий период. Иными словами, если положить деньги на срочный вклад в сберегательный банк, то через год вклад увеличится на от исходной суммы, т.е. новая сумма будет равна вкладу, умноженному на . Ещё через год уже эта сумма увеличится на , т. е. получившаяся в тот раз сумма вновь умножится на и так далее. Подобная ситуация описана в задачах на вычисление так называемых сложных процентов – процент берется каждый раз от суммы, которая есть на счете с учетом предыдущих процентов. Об этих задачах мы поговорим чуть позднее.
е. получившаяся в тот раз сумма вновь умножится на и так далее. Подобная ситуация описана в задачах на вычисление так называемых сложных процентов – процент берется каждый раз от суммы, которая есть на счете с учетом предыдущих процентов. Об этих задачах мы поговорим чуть позднее.
Есть еще много простых случаев, где применяется геометрическая прогрессия. Например, распространение гриппа: один человек заразил человек, те в свою очередь заразили еще по человека, и таким образом вторая волна заражения – человек, а те в свою очередь, заразили еще
Общий вид геометрической прогрессии
b1, b1q, b2q, …, bn-1q
- q – знаменатель прогрессии; это и есть постоянный множитель.
- b ≠ 0, q ≠ 0
Члены прогрессии:
- b1
- b2 = b1q
- b3 = b2q = b1q2
- и т.
 д.
д.
Цифры 1,2,3… – это их порядковые номера, т.е. место, которое они занимают в последовательности.
Виды прогрессии:
- возрастающая: b1 > 0 и q1 > 0
- убывающая: 0 < q < 1
- знакочередующаяся: q < 0
- стационарная: q = 1.
Формула суммы n-первых членов геометрической прогрессии
где, q ≠ 1
Бесконечно убывающая геометрическая прогрессия — это прогрессия, у которой |q| < 1. Для неё определяется понятие суммы членов бесконечно убывающей геометрической прогрессии как число, к которому неограниченно приближается сумма первых членов рассматриваемой прогрессии при неограниченном возрастании числа .
Определение геометрической прогрессии
Определение. Последовательность, каждый член которой, начиная со второго, получается из предыдущего умножением на одно и то же число , называется геометрической прогрессией. Число
Число
, называется геометрической прогрессией. Число называется знаменателем прогрессии.
То есть геометрическая прогрессия определяется рекуррентным соотношением
Примеры геометрических прогрессий.
- Последовательность — геометрическая прогрессия со знаменателем — геометрическая прогрессия со знаменателем
- Последовательность — геометрическая прогрессия со знаменателем — геометрическая прогрессия со знаменателем
- Последовательность — геометрическая прогрессия со знаменателем — геометрическая прогрессия со знаменателем
Теорема 1. Пусть — геометрическая прогрессия со знаменателем — геометрическая прогрессия со знаменателем Тогда для всех натуральных справедлива формула
Доказательство. Воспользуемся рекуррентным определением геометрической прогрессии:
Итак, для n-го члена геометрической прогрессии справедлива формула
Теорема 2. Квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению предыдущего и последующего членов:
Квадрат любого члена геометрической прогрессии, начиная со второго, равен произведению предыдущего и последующего членов:
Доказательство. Из определения геометрической прогрессии
Следовательно,
откуда
Обратное утверждение тоже верно. Если для всех членов последовательности начиная со второго, выполняется равенство начиная со второго, выполняется равенство то эта последовательность — геометрическая прогрессия.
Пример 1. Сумма первого и третьего членов геометрической прогрессии равна 10, а сумма второго и четвёртого членов — 30. Найдём первый член и знаменатель прогрессии.
Решение. По условию
Выразим члены геометрической прогрессии через и и : Тогда система запишется в виде
Разделив второе уравнение системы на первое, получим Следовательно, Следовательно,
Бесконечно убывающая геометрическая прогрессия.
Совсем недавно мы говорили о том, что может быть как больше, так и меньше нуля, однако, есть особые значения при которых геометрическая прогрессия называется бесконечно убывающей.
| При – прогрессия называется бесконечно убывающей. |
Как ты думаешь, почему такое название?
Для начала запишем какую-нибудь геометрическую прогрессию, состоящую из членов.
Допустим, , а , тогда:
Мы видим, что каждый последующий член меньше предыдущего в раза, но будет ли какое-либо число ? Ты сразу же ответишь – «нет». Вот поэтому и бесконечно убывающая – убывает, убывает, а нулем никогда не становится.
Чтобы четко понять, как это выглядит визуально, давай попробуем нарисовать график нашей прогрессии. Итак, для нашего случая формула приобретает следующий вид:
На графиках нам привычно строить зависимость от , поэтому:
Суть выражения не изменилась: в первой записи у нас была показана зависимость значения члена геометрической прогрессии от его порядкового номера, а во второй записи – мы просто приняли значение члена геометрической прогрессии за , а порядковый номер обозначили не как , а как . Все, что осталось сделать – построить график.
Посмотрим, что у тебя получилось. Вот какой график получился у меня:
Видишь? Функция убывает, стремится к нулю, но никогда его не пересечет, поэтому она бесконечно убывающая. Отметим на графике наши точки, а заодно и то, что обозначает координата и :
Попробуй схематично изобразить график геометрической прогрессии при , если первый ее член также равен . Проанализируй, в чем разница с нашим предыдущим графиком?
Справился? Вот какой график получился у меня:
Теперь, когда ты полностью разобрался в основах темы геометрической прогрессии: знаешь, что это такое, знаешь, как найти ее член, а также знаешь, что такое бесконечно убывающая геометрическая прогрессия, перейдем к ее основному свойству.
Характеристическое свойство геометрической прогрессии
Правило
Cумма бесконечной геометрической прогрессии
Если |q| < 1 то при n → ∞
| S = | b1 |
| 1 – q |
Решение задач на геометрическую прогрессию
Рассмотрим несколько типичных задач, посвященных геометрической прогрессии.
Задача 1:
Дана геометрическая прогрессия 3, 6, 12, … . Найти 8-ой член геометрической прогрессии и сумму первых 10 членов.
Решение:
b1 = 3
q = 6 / 3 = 2
b8 = b1 ⋅ q7 = 3 ⋅ 27 = 3 ⋅ 128 = 384
S10 = b1 ⋅ (1 — q10) / (1 — q) = 3 ⋅ (1 — 210) / (1 — 2) = 3 ⋅ (1 — 1024) / (–1) = 3069
Ответ: 384 и 3069
Задача 2:
Число 486 является членом геометрической прогрессии 2, 6, 18, … . Найдите его номер.
Решение:
b1 = 2
q = 6 / 2 = 3
Применив формулу для вычисления n-ого члена геометрической прогрессии, можно получить n:
486 = 2 ⋅ 3n – 1
243 = 3n – 1
35 = 3n – 1
n — 1 = 5
n = 6
Ответ: 6
Задача 3:
Сумма n первых членов геометрической прогрессии равна –93. b1 = –3, q = 2. Найти n.
Решение:
Чтобы вычислить число членов геометрической прогрессии, можно воспользоваться формулой ее суммы:
Sn = b1 ⋅ (1 — qn) / (1 — q)
–93 = –3 ⋅ (1 — 2n) / (1 — 2)
–93 = –3 ⋅ (1 — 2n) / (–1)
–31 = 1 — 2n
2n = 32
n = 5
Ответ: 5
Сумма первых n членов геометрической прогрессии
Вычислим сумму первых n членов геометрической прогрессии знаменатель которой знаменатель которой :
(1)
Умножим это равенство на :
или
(2)
Вычтем из равенства (2) равенство (1), и приведя подобные члены, получим Отсюда, так как Отсюда, так как имеем
или
(3)
Так как то формулу (3) можно переписать в виде
(4)
Пример 2. Считается, что шахматы были изобретены в V в. н. э. в Индии. По легенде, когда создатель шахмат показал своё изобретение правителю страны, тому настолько понравилась игра, что он решил щедро отблагодарить её создателя, позволив мудрецу самостоятельно выбрать награду.
Считается, что шахматы были изобретены в V в. н. э. в Индии. По легенде, когда создатель шахмат показал своё изобретение правителю страны, тому настолько понравилась игра, что он решил щедро отблагодарить её создателя, позволив мудрецу самостоятельно выбрать награду.
Мудрец попросил короля за первую клетку шахматной доски дать ему одно зерно пшеницы, за вторую — два, за третью — четыре, и так далее, удваивая количество зёрен за каждую клетку. Правитель рассмеялся, услышав столь ничтожную на первый взгляд просьбу, и, быстро согласившись, повелел своим казначеям подсчитать и выдать нужное количество зерна. Однако спустя неделю зерно всё ещё не было подсчитано. Интересно, в чём же причина такой задержки?
Давайте подсчитаем величину награды, то есть найдём сумму геометрической прогрессии
По формуле (3) получаем
Именно столько зёрен должен был выдать король. Это примерно 1200 триллионов тонн или 1500 куб. км. пшеницы, что эквивалентно амбару размерами 10х10х15 км. Для справки, это примерно в 1800 раз больше всего урожая пшеницы 2009 года.
Для справки, это примерно в 1800 раз больше всего урожая пшеницы 2009 года.
Примерно такие расчёты и показали королю, когда тот поинтересовался, почему зерно всё ещё не выдано.
Наверное, вы спросите, чем же всё закончилось. Легенда гласит, что король «не остался в долгу» перед хитрым изобретателем, и, выдав ему пшеницу (конечно, намного меньше), предложил тому пересчитать каждое зёрнышко, чтобы не было сомнений в том, что он честно с ним расплатился.
Источники
- https://mnogoformul.ru/summa-chlenov-geometricheskoy-progres
- http://worksbase.ru/matematika/teoriya/14-geometricheskaya-progressiya.html
- https://youclever.org/book/geometricheskaya-progressiya-1
- https://MicroExcel.ru/geometricheskaya-progressiya/
- http://www.grandars.ru/student/vysshaya-matematika/g-progressiya.html
- https://umath.ru/theory/posledovatelnosti/geometricheskaya-progressiya/
- https://formula-xyz.ru/geometricheskaya-progressiya.html
- https://ru.
 0=1$ не должно быть соглашением. И я видел несколько причин, по которым это должно быть (обращение к пустому произведению, использование элементарной комбинаторики и приложение к геометрическому/степенному ряду — три, о которых я могу думать прямо сейчас). 90 = 1$ при работе с сериями, и значение оказывается 0-м членом ряда, но это просто удобство записи (иначе вам пришлось бы выделять постоянные члены для бесконечных хлопот и никакого выигрыша).
0=1$ не должно быть соглашением. И я видел несколько причин, по которым это должно быть (обращение к пустому произведению, использование элементарной комбинаторики и приложение к геометрическому/степенному ряду — три, о которых я могу думать прямо сейчас). 90 = 1$ при работе с сериями, и значение оказывается 0-м членом ряда, но это просто удобство записи (иначе вам пришлось бы выделять постоянные члены для бесконечных хлопот и никакого выигрыша).$\endgroup$
3
Твой ответ
Зарегистрируйтесь или войдите
Зарегистрироваться через Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
Геометрическая серия | Purplemath
IntroExamplesArith.
 и гео. Посл.Ариф. Серия
и гео. Посл.Ариф. СерияPurplemath
Вы можете вычислить сумму конечного числа членов геометрической прогрессии. И по причинам, которые вы изучите в математическом анализе, вы можете взять сумму бесконечной геометрической последовательности , но только в том особом случае, что обыкновенное отношение r находится между -1 и 1; то есть вы должны иметь | р | < 1.
Для геометрической последовательности с первым членом a 1 = a и знаменателем r сумма первых n членов определяется как: Ниже
MathHelp.com
Примечание. Ваша книга может иметь немного другую форму приведенной выше формулы частичной суммы. Например, « a » можно умножить на числитель, множители в дроби можно поменять местами, или суммирование может начаться с 9.0061 i = 0 и имеют степень n + 1 в числителе. Все эти формы эквивалентны, и приведенная выше формулировка может быть получена из полиномиального длинного деления.

В особом случае | р | < 1, бесконечная сумма существует и имеет следующее значение:
Первые несколько членов равны −6, 12, −24: 1 = (3)(−2) = −6
а 2 = 3(−2) 2 = (3)(4) = 12
a 3 = 3(−2) 3 = (3)(−8) = −24
Итак, это представляет собой геометрический ряд со знаменателем r = −2. (Я также могу сказать, что это должен быть геометрический ряд из-за формы, заданной для каждого члена: по мере увеличения индекса каждый член будет умножаться на дополнительный коэффициент −2.)
Первый член последовательности равен . а = -6. Подключив формулу суммирования, я получаю:
Таким образом, значение суммирования:
2 097 150
Оценка S
10 для 250, 100, 40, 16,….
Обозначение «S10» означает, что мне нужно найти сумму первых десяти членов.
 Первый член равен a = 250. Разделив пары членов, я получаю:
Первый член равен a = 250. Разделив пары членов, я получаю:100 ÷ 250 = 2/5
40 ÷ 100 = 2/5
…и так далее, так что добавляемые члены образуют геометрическую последовательность со знаменателем р = 2/5.
В отличие от формулы для n -й частичной суммы арифметического ряда, мне не нужно значение последнего члена при нахождении n -й частичной суммы геометрического ряда. Так что у меня есть все необходимое для продолжения. Когда я подставляю значения первого члена и обыкновенного отношения, формула суммирования дает мне:
Я не буду «упрощать» это, чтобы получить десятичную форму, потому что это почти наверняка будет считаться «неправильным». » отвечать. Вместо этого мой ответ:
Примечание. Если вы попытаетесь выполнить приведенные выше вычисления на своем калькуляторе, он вполне может вернуть десятичное приближение 416,62297.
 .. вместо дробного (и точного) ответа.
.. вместо дробного (и точного) ответа.Как вы можете видеть на снимке экрана выше, ввод значений в дробной форме и использование команды «преобразовать в дробь» по-прежнему приводит к десятичному приближению к ответу. Но (правда!) десятичное приближение почти наверняка будет расценено как «неправильный» ответ. Потратьте время, чтобы найти дробную форму.
Найдите
a n , если S 4 = 26/27 и r = 1/3.
Мне дали сумму первых четырех членов, S 4 , и значение обыкновенного отношения r . Поскольку существует обыкновенное отношение, я знаю, что это должен быть геометрический ряд. Подключив к формуле суммы геометрического ряда, я получаю:
Умножая с обеих сторон на 27/40, чтобы найти первый член a = a 1 , я получаю:
Затем, подставляя в формулу для члена — n
геометрическая последовательность, я получаю:
Покажите с помощью геометрического ряда, что 0,3333.
 .. равно 1/3.
.. равно 1/3.
В этом есть хитрость. Сначала мне нужно разбить повторяющуюся десятичную дробь на отдельные термины; то есть «0,3333…» становится:
0,3 + 0,03 + 0,003 + 0,0003 + …
Разделение десятичной формы таким образом явно выделяет повторяющийся образец неконечной (то есть бесконечной) десятичной дроби: Для каждого члена я десятичная точка, за которой следует неуклонно растущее количество нулей, а затем заканчивается цифрой «3». Эту расширенно-десятичную форму можно записать в дробной форме, а затем преобразовать в форму геометрического ряда:
Это доказывает, что 0,333… является (или, по крайней мере, может быть выражено как) бесконечным геометрическим рядом с a = 3/10 и r = 1/10. Поскольку | р | < 1, я могу использовать формулу для суммирования бесконечных геометрических рядов:
Для приведенного выше доказательства, используя формулу суммирования, чтобы показать, что «расширение» геометрического ряда 0,333.
 .. имеет значение одной трети равно «показ», которого требовало упражнение (поэтому очень важно выполнять свою работу аккуратно и логично). И вы можете использовать этот метод для преобразования любого повторяющегося десятичного числа в его дробную форму.
.. имеет значение одной трети равно «показ», которого требовало упражнение (поэтому очень важно выполнять свою работу аккуратно и логично). И вы можете использовать этот метод для преобразования любого повторяющегося десятичного числа в его дробную форму.Сначала я разобью его на составные части, чтобы найти закономерность:
1,363636.. = 1 + 0,36 + 0,0036 + 0,000036 + 0,000036 + …
Две повторяющиеся цифры, поэтому дроби немного отличаются. Но это по-прежнему геометрический ряд:
Это показывает, что исходная десятичная дробь может быть выражена как ведущая «1», добавленная к геометрическому ряду, имеющему a = 9/25 и r = 1/100. Поскольку значение обыкновенного отношения достаточно мало, я могу применить формулу для бесконечного геометрического ряда. Тогда сумма оценивается как:
Таким образом, эквивалентная дробь в форме неправильной дроби и в форме смешанных чисел:
Кстати, этот метод также можно использовать для доказательства того, что 0,999.
 .. = 1.
.. = 1.URL: https ://www.purplemath.com/modules/series5.htm
Страница 1Страница 2Страница 3Страница 4
Арифметико-геометрическая прогрессия | Brilliant Math & Science Wiki
Сандип Бхардвадж, Пранджал Джайн, Махиндра Джейн, а также
способствовал
Содержимое
- Определение
- Сумма AGP
- Сумма AGP до бесконечности
- Приложения
- Смотрите также
9{100}+2. \ _\площадь
\end{выровнено}−SSSS=22−1(2100−1)−100⋅2101(поскольку первые 100 терминов находятся в GP)=100⋅2101−2⋅2100+2=200⋅2100−2⋅2100 +2=198⋅2100+2.
 □
□В этой задаче решающим шагом было умножение на обыкновенное отношение и вычитание последовательностей, что позволило нам свести ее к знакомой нам ГП. Теперь выведем общую формулу суммы членов АГП с начальным членом aaa, общей разностью ddd и общим отношением rrr:
Сумма первых nnn членов AGP равна 9{99}= \, ?1+2⋅2+3⋅22+4⋅23+⋯+100⋅299=?
Теперь, когда мы нашли сумму конечного числа членов, давайте рассмотрим случай бесконечного числа членов. Мы, конечно, не можем вручную суммировать бесконечные члены, поэтому нам придется найти общий подход. Мы начинаем с обсуждения проблемы, с которой вы столкнулись, вверху этой страницы:
12+24+38+416+532+⋯= ?\большой\dfrac{\color{#3D99F6}{1}}{\color{#D61F06}{2}}+\dfrac{\color{#3D99F6}{ 2}}{\color{#D61F06}{4}}+\dfrac{\color{#3D99F6}{3}}{\color{#D61F06}{8}}+\dfrac{\color{#3D99F6}{4}}{\color{#D61F06}{16}}+\dfrac{\color{#3D99F6}{5}}{\color{#D61F06}{32}}+\cdots=\, ?21 +42+83+164+325+⋯=?
Предположим, что данная серия является SSS, тогда
S=12+24+38+416+532+⋯ .
 S=\dfrac 12 +\dfrac 24 +\dfrac 38+\dfrac{4}{16}+\dfrac{5}{32}+\cdots. S=21+42+83+164+325+⋯.
S=\dfrac 12 +\dfrac 24 +\dfrac 38+\dfrac{4}{16}+\dfrac{5}{32}+\cdots. S=21+42+83+164+325+⋯.Умножая SSS на 12\frac 1221, получаем
S2=14+28+316+432+564+⋯ . \dfrac S2=\dfrac 14 +\dfrac 28 +\dfrac{3}{16}+\dfrac{4}{32}+\dfrac{5}{64}+\cdots.2S=41+82 +163+324+645+⋯.
Теперь, вычитая S2\frac S22S из SSS, получаем
S=12+24+38+416+532+⋯S2=0+14+28+316+432+564+⋯S(1−12)=12+14+18+116+132+⋯⇒S2= 12+14+18+116+132+⋯ , \begin{массив} {rlllllllll} S&=\dfrac 12 &+\dfrac 24 &+\dfrac 38 &+\dfrac{4}{16} &+\dfrac{5}{32}+ \cdots \\ \dfrac S2&=0&+\dfrac 14 & +\dfrac 28 & +\dfrac{3}{16}&+\dfrac{4}{32}+\dfrac{5}{64}+\cdots \\ \hline S \left(1- \dfrac 12 \right)& =\dfrac 12& +\dfrac 14 & + \dfrac 18 & +\dfrac{1}{16} & +\dfrac{1}{32} +\cdots \ \ \Стрелка вправо \dfrac S2&=\dfrac 12 &+\dfrac 14 &+ \dfrac 18 &+\dfrac {1}{16} &+\dfrac {1}{32} +\cdots, \end{array}S2SS(1−21)⇒2S=21=0=21=21+42+41+41+41+83+82+ 81+81+164+163+161+161+325+⋯+324+645+⋯+321+⋯+321+⋯,92 } = 2 1−2121+(1−21)21×21=2.

Второе суммирование представляет собой геометрическую прогрессию с суммой до бесконечности 141−12=12 \frac { \frac{1}{4} } { 1 — \frac{1}{2} } = \frac{1}{ 2} 1−2141=21.
Следовательно, сумма 2−12=1,5 □ 2 — \frac{1}{2} = 1,5 \ _\квадрат 2−21=1,5 □.Решение 2:
Данную серию можно записать как
14+38+516+732+⋯ .\dfrac 14+\dfrac 38 +\dfrac{5}{16}+\dfrac{7}{32}+\cdots .41+83+165+327 +⋯.
Умножив и разделив ряд на 444, получим 92} \right) =\dfrac 14 \left( 2+4 \right)=1.5. \ _\квадрат S=41⎝⎜⎜⎜⎛1−211+(1−21)22⋅21⎠⎟⎟⎟⎞=41(2+4)=1,5. □
Решение приведенных ниже задач проверит, владеете ли вы концепциями и решением проблем:
1 5 7 9
Найдите значение ppp по данному
3+14(3+p)+142(3+2p)+143(3+3p)+⋯=8. 3+\dfrac{1}{4}(3+p)+\dfrac{1}{4^{2}}(3+2p)+\dfrac{1}{4^3}(3+3p)+ \cdots =8,3+41(3+p)+421(3+2p)+431(3+3p)+⋯=8.
 i } i=1∑∞2ii2.
92 и2. Мы будем использовать другой подход, чтобы свести это к «линейно-геометрической прогрессии», которая является AGP.
i } i=1∑∞2ii2.
92 и2. Мы будем использовать другой подход, чтобы свести это к «линейно-геометрической прогрессии», которая является AGP.Пусть сумма будет S,S,S, тогда, поскольку обыкновенное отношение равно 12 \frac{1}{2} 21, мы умножим SSS на 12. \frac{1}{2} .21. Вычитание 12S\frac{1}{2}S21S из SSS дает
S=12+44+98+1616+2532+⋯12S=+14+48+916+1632+⋯12S=12+34+58+716+932+⋯ . \begin{массив} { г lllllll} S& =\frac 12 & +\frac {4}{4} & +\frac{9}{8} &+\frac{16}{16} &+\frac{25}{32} &+\cdots \ \ \frac{1}{2} S& = & + \frac 14 & +\frac {4}{8} & +\frac{9}{16} &+\frac{16}{32} &+\cdots \\ \hline \frac{1}{2} S & =\frac 12 & +\frac {3}{4} & +\frac{5}{8} &+\frac{7}{16} &+\frac{9 }{32} &+\cdots .\\ \end{массив} S21S21S=21==21+44+41+43+89+84+85+1616+169+167+ 3225+3216+329+⋯+⋯+⋯.
Мы можем распознать здесь AGP, но пусть T=12ST=\frac{1}{2} ST=21S и продолжаем эту процедуру получения разницы:
T=12+34+58+716+932+⋯12T=+14+38+516+732+⋯12T=12+24+28+216+232+⋯ .
 \begin{массив} { г lllllll}
T & =\frac 12 & +\frac {3}{4} & +\frac{5}{8} &+\frac{7}{16} &+\frac{9}{32} &+\cdots\\
\frac{1}{2} T & = & + \frac 14 & +\frac {3}{8} & +\frac{5}{16} &+\frac{7}{32} &+\cdots \\
\hline
\frac{1}{2} T & = \frac{1}{2} & + \frac{2}{4} & + \frac{2}{8} & + \frac{2}{16} & + \frac{2}{32} & + \cdots .\\
\end{массив} T21T21T=21==21+43+41+42+85+83+82+167+165+162+ 329+327+322+⋯+⋯+⋯.
\begin{массив} { г lllllll}
T & =\frac 12 & +\frac {3}{4} & +\frac{5}{8} &+\frac{7}{16} &+\frac{9}{32} &+\cdots\\
\frac{1}{2} T & = & + \frac 14 & +\frac {3}{8} & +\frac{5}{16} &+\frac{7}{32} &+\cdots \\
\hline
\frac{1}{2} T & = \frac{1}{2} & + \frac{2}{4} & + \frac{2}{8} & + \frac{2}{16} & + \frac{2}{32} & + \cdots .\\
\end{массив} T21T21T=21==21+43+41+42+85+83+82+167+165+162+ 329+327+322+⋯+⋯+⋯.Теперь обратите внимание, что, за исключением первого члена, мы получаем GP с начальным членом 24 \frac{2}{4} 42 и знаменателем 12 \frac{1}{2} 21. Как оказалось, первый член часто не вписывался в шаблон последовательности, и нам просто повезло раньше. Таким образом, мы получаем
12T=12+241−12=12+1=32. \frac{1}{2} T = \frac{1}{2} + \frac{ \frac{2}{4} } { 1 — \frac{1}{2} } = \frac{1}{ 2} + 1 = \фракция{3}{2} . 21T=21+1−2142=21+1=23.
Следовательно, T=3, T=3 ,T=3, что подразумевает S=2T=6. □ S = 2T = 6. \ _\квадрат S=2T=6. □
Заметьте, что если мы возьмем разность членов квадратичной последовательности, мы получим линейную последовательность.
 Это справедливо и в более общем плане: если мы возьмем разность членов в последовательности степени nnn, мы получим последовательность степени n−1n−1 n−1. Это подробно рассмотрено в разделе «Метод различий». Мы будем неоднократно использовать эту идею для работы с такой «полиномиально-геометрической прогрессией». 9i } i=1∑∞3ii3.
Это справедливо и в более общем плане: если мы возьмем разность членов в последовательности степени nnn, мы получим последовательность степени n−1n−1 n−1. Это подробно рассмотрено в разделе «Метод различий». Мы будем неоднократно использовать эту идею для работы с такой «полиномиально-геометрической прогрессией». 9i } i=1∑∞3ii3.Обратите внимание, что у нас есть «кубическая геометрическая прогрессия» со знаменателем 13 \frac{1}{3} 31. Умножим на 13 \frac{1}{3} 31 и возьмем разницу:
S=13+89+2727+6481+125243+⋯13S=+19+827+2781+64243+⋯23S=13+79+1927+3781+61243+⋯ . \begin{массив} { г lllll} S & = \frac{1}{3} & + \frac{8}{9} & + \frac{ 27}{27} & + \frac{ 64}{81} & + \frac{ 125}{243 } & + \cdots \\ \frac{1}{3} S & = & + \frac{1}{9} & + \frac{8}{27} & + \frac{ 27}{81} & + \frac{ 64}{ 243 } & + \cdots \\ \hline \frac{2}{3} S & = \frac{1}{3} & + \frac{7}{9{i+1} } 32S−31=i=1∑∞3i+13i2+3i+1, что является «квадратично-геометрической прогрессией». Установите это как ТТТ.
 Затем умножение на 13 \frac{1}{3} 31 и получение разницы дает
Затем умножение на 13 \frac{1}{3} 31 и получение разницы даетТ=79+1927+3781+61243+⋯13Т=+727+1981+37243+⋯23Т=79+1227+1881+24243+⋯ . \begin{массив} { г lllll} T & = \frac{7}{9} & + \frac{ 19}{27} & + \frac{ 37}{81} & + \frac{ 61}{243} & + \cdots \\ \frac{1}{3} T & = & + \frac{7}{27} & + \frac{ 19}{81} & + \frac{ 37}{ 243} & + \cdots \\ \hline \frac{2}{3} T & = \frac{7}{9{i+2}} 32T−97=i=1∑∞3i+26(i+1), что является «линейно-геометрической прогрессией. Установите это как U U U. Затем умножьте на 13 \ frac{1}{3} 31 и вычитание разницы дает
U=1227+1881+24243+⋯13U=+1281+18342++⋯23U=1227+681+6243+⋯ . \begin{массив} { г lllll} U & = \frac{12}{27} & + \frac{18}{81} & + \frac{24}{243} & + \cdots \\ \frac{1}{3} U & = & + \frac{12}{81} & + \frac{ 18}{342} & + + \cdots \\ \hline \frac{2}{3} U & = \frac{12}{27} & + \frac{6}{81} & + \frac{6}{243} & + \cdots. \\ \end{массив} U31U32U=2712==2712+8118+8112+816+24324+34218+2436+⋯++⋯+⋯. 9{i+3} } ,32U−2712=i=1∑∞3i+36, что является геометрической прогрессией с бесконечной суммой 6811−13=19 \frac{ \frac{6}{81 } } { 1 — \frac{1}{3} } = \frac{1}{9} 1−31816=91.

Это дает нам
23U=1227+19⇒U=5623T=79+56⇒T=2
S=13+2912⇒S=338. □\begin{выровнено} \frac{2}{3} U &= \frac{12}{27} + \frac{1}{9} &&\Стрелка вправо U = \frac{5}{6} \\ \frac{2}{3} T &= \frac{7}{9} + \frac{5}{6} &&\Rightarrow T = \frac{29}{12} \\ \frac{2}{3} S &= \frac{1}{3} + \frac{29n} + \cdots S=0,1+0,02+0,003+0,0004+⋯+10nn+⋯
Учитывая, что бесконечная сумма S SS может быть выражена как ab \frac abba, где aaa и bbb взаимно простые натуральные числа, найти а+ба+ба+б.
Чтобы улучшить свои навыки решения задач по арифметическим прогрессиям, геометрическим прогрессиям и арифметико-геометрическим прогрессиям, вы можете посетить следующие вики:
- Арифметические и геометрические прогрессии: решение задач
Процитировать как: Арифметико-геометрическая прогрессия. Brilliant.org . Извлекаются из https://brilliant.org/wiki/arithmetic-geometric-progression/
Представление повторяющихся десятичных дробей в виде отношения целых чисел с использованием геометрического ряда — Криста Кинг Математика
Действия по превращению повторяющейся десятичной дроби в геометрический ряд
Мы можем использовать формулу суммы геометрической прогрессии, чтобы быстро и точно преобразовать повторяющуюся десятичную дробь в отношение целых чисел, другими словами, в дробь с целыми числами в числитель и знаменатель.

Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Мы выполним следующие шаги:
Отделите неповторяющуюся часть от повторяющейся части десятичной дроби.
В таблице сопоставьте каждую повторяющуюся часть с ее последним десятичным знаком.
Создайте сумму каждой части, разделив повторяющиеся части на их конечные десятичные разряды.
9n=\frac{a}{1-r}???.Используйте формулу для преобразования ряда в одну дробь.
Добавьте эту дробь геометрического ряда к дроби неповторяющейся части.
Представление повторяющейся десятичной дроби в виде геометрического ряда
Пройти курс
Хотите узнать больше об исчислении 2? У меня есть пошаговый курс для этого.
 🙂
🙂Учить больше
Как выразить повторяющуюся десятичную дробь как отношение целых чисел с помощью геометрического ряда
Пример
Выразить повторяющуюся десятичную дробь как отношение целых чисел.
???1.6\над чертой{73}???
Бар над ???.073??? указывает, что это часть десятичной дроби, которая повторяется. Это говорит нам о том, что десятичная дробь выглядит как
???1.673737373737373…???
Нас попросили преобразовать это десятичное значение в дробь с действительными числами в числителе и знаменателе.
Наш первый шаг — отделить неповторяющуюся часть от повторяющейся части десятичной дроби.
???1.6+.073737373737373…???
Добавляем ???0??? на десятом месте нашей повторяющейся части, потому что она занимает место ???.6??? мы вырвались в неповторяющуюся часть. Повторяющаяся последовательность начинается с первого ???7??? в сотых долях, и нам нужно сохранить его там, когда мы разделяем десятичные дроби, поэтому очень важно поставить ???0???.

Далее мы разделим каждую часть повторяющейся последовательности на отдельную строку таблицы ниже, заменив десятичные знаки перед ней на ???0???с. Как только мы построили левый столбец, мы поместим соответствующее место во второй столбец. 9n=\frac{a}{1-r}???
, чтобы превратить сумму в одну дробь. Вычтем из повторяющейся части первую дробь.
???1.6\overline{73}=1.6+\frac{73}{1,000}\left(1+\frac{1}{100}+\frac{1}{10,000}+…\right )???
С нашей серией в этой форме мы можем идентифицировать ???a??? и ???р??? по формуле суммы геометрического ряда. ???а??? всегда значение, которое мы учитывали, оно находится прямо перед круглыми скобками. ???р??? это всегда второй член в круглых скобках, значение сразу после ???1???. 9n = 1,6+ \ frac {\ frac {73} {1000}} {1- \ frac {1} {100}}???
???1,6+\frac{73}{1000}}{\frac{100}{100}-\frac{1}{100}}???
???1,6+\frac{\frac{73}{1000}}{\frac{99}{100}}???
???1.6+\frac{73}{1,000}\cdot\frac{100}{99}???
???1.
 6+\frac{73}{10}\cdot\frac{1}{99}???
6+\frac{73}{10}\cdot\frac{1}{99}??????1,6+\фрак{73}{990}???
Теперь нам просто нужно заменить неповторяющуюся часть нашей исходной десятичной дроби на дробь, а затем объединить эти две дроби.
???\влево(1+\фракция{6}{10}\право)+\фракция{73}{990}???
???\влево(\frac{10}{10}+\frac{6}{10}\right)+\frac{73}{990}???
???\frac{16}{10}+\frac{73}{990}???
???\frac{99}{99}\left(\frac{16}{10}\right)+\frac{73}{990}???
???\frac{1,584}{990}+\frac{73}{990}???
???\фракция{1,657}{990}???
Если у вас есть доступ к калькулятору, вы всегда можете перепроверить себя. В этом случае просто используйте свой калькулятор, чтобы разделить ???1657??? на ???990???. Если вы сделали это правильно, вы должны получить исходное повторяющееся десятичное число, ???1.6\overline{73}???.
Получить доступ к полному курсу Calculus 2
Начать
Изучайте математикуКриста Кинг математика, учитесь онлайн, онлайн-курс, онлайн-математика, исчисление 2, исчисление 2, исчисление 2, исчисление ii, исчисление с одной переменной, вычисление с одной переменной, последовательности, ряды, последовательности и ряды, бесконечные ряд, геометрический ряд, повторяющиеся десятичные дроби, геометрический ряд повторяющихся десятичных дробей, отношение целых чисел
0 лайков12.4: Геометрические последовательности и ряды
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 5197
- OpenStax
- ОпенСтакс
- Определить, является ли последовательность геометрической
- Найти общий член (\(n\)-й член) геометрической прогрессии
- Найти сумму первых \(n\) членов геометрической прогрессии
- Найдите сумму бесконечного геометрического ряда
- Применение геометрических последовательностей и рядов в реальном мире
Цели обучения
К концу этого раздела вы сможете:
Прежде чем начать, пройдите этот тест на готовность.
 9{x}\), найти a. \(f(1)\) б. \(f(2)\) в. \(f(3)\).
9{x}\), найти a. \(f(1)\) б. \(f(2)\) в. \(f(3)\).
Если вы пропустили эту проблему, просмотрите пример 3.49. - \(4,8,16,32,64,128, \точки\)
- \(-2,6,-12,36,-72,216, \точки\)
- \(27,9,3,1, \frac{1}{3}, \frac{1}{9}, \ldots\)
- \(7,21,63,189,567,1,701, \точки\)
- \(64,16,4,1, \frac{1}{4}, \frac{1}{16}, \dots\)
- \(2,4,12,48,240,1440, \точки\)
- Ответить
- Последовательность геометрическая со знаменателем \(r=3\).
- Последовательность геометрическая со знаменателем \(d=\frac{1}{4}\).

- Последовательность не является геометрической. Общей пропорции нет.
- \(-150,-30,-15,-5,-\frac{5}{2}, 0, \dots\)
- \(5,10,20,40,80,160, \точки\)
- \(8,4,2,1, \frac{1}{2}, \frac{1}{4}, \ldots\)
- Ответить
- Последовательность не является геометрической. Общей пропорции нет.
- Последовательность геометрическая со знаменателем \(r=2\).
- Последовательность геометрическая со знаменателем \(r=\frac{1}{2}\).
- Ответить
\(7,-21,63,-189,567\)
- Ответить
\(6,-24,96,-384,1536\)
- Ответить
\(\frac{1}{6,561}\)
- Ответить
\(\frac{1}{16 384}\)
- Ответ
\(3 145 725\)
- Ответить
\(10 460 353 200\)
- Ответить
\(96\)
- Ответ
\(\frac{256}{3}\)
- Ответить
\(\frac{4}{9}\)
- Ответить
\(\ гидроразрыва{8}{9}\)
- Ответить
$\(10 000\)
- Ответить
$\(88 868,36\)
- Ответить
$\(698 201,57\)
- Геометрические последовательности
- Геометрический ряд
- Аннуитеты будущей стоимости и геометрические ряды
- Применение геометрического ряда: налоговая скидка
- Общий термин (\(n\)-й член) геометрической последовательности: 9{n-1}+\ldots\)
- Сумма бесконечного геометрического ряда: Для бесконечного геометрического ряда, первый член которого равен \(a_{1}\) и знаменатель \(r\),
Если \(|r|<1\), сумма является - аннуитет
- Аннуитет – это инвестиция, представляющая собой последовательность равных периодических вкладов. 908:50
- обыкновенное отношение
- Отношение между последовательными элементами в геометрической последовательности, \(\frac{a_{n}}{a_{n-1}}\), равно \(r\), обычному отношению, где \(r\) больше больше или равно двум.
- геометрическая последовательность
- Геометрическая последовательность — это последовательность, в которой соотношение между последовательными членами всегда одинаково
- бесконечный геометрический ряд
- Бесконечный геометрический ряд — это бесконечная сумма бесконечной геометрической последовательности. 908:50
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- ОпенСтакс
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Программа OER или Publisher
- ОпенСтакс
-
- Показать страницу TOC
- нет
- Теги
- обыкновенное отношение
- геометрическая последовательность
- бесконечный геометрический ряд
- источник@https://openstax.
 org/details/books/intermediate-алгебра-2e
org/details/books/intermediate-алгебра-2e
Определить, является ли последовательность геометрической
Теперь мы готовы рассмотреть второй особый тип последовательности, геометрическую последовательность.
Последовательность называется геометрической последовательностью , если соотношение между последовательными элементами всегда одинаково. Отношение между последовательными элементами в геометрической последовательности равно \(r\), обыкновенному отношению , где \(n\) больше или равно двум.
Определение \(\PageIndex{1}\)
Геометрическая последовательность — это последовательность, в которой соотношение между последовательными элементами всегда одинаково.
Отношение между последовательными членами, \(\frac{a_{n}}{a_{n-1}}\), равно \(r\), обыкновенное отношение . \(n\) больше или равно двум.
Рассмотрим эти последовательности.
Рисунок 12.3.1Пример \(\PageIndex{1}\)
Определите, является ли каждая последовательность геометрической. Если да, укажите обыкновенное отношение.
Решение :
Чтобы определить, является ли последовательность геометрической, мы находим отношение показанных последовательных членов.
а. Найдите отношение последовательных членов
\(\begin{aligned} 4, \quad& \:8, \quad 16, \quad 32, \quad 64, \quad 128, \dots \\ &\frac{8} {4} \quad\frac{16}{8}\quad\frac{32}{16}\quad\frac{64}{32}\quad\frac{128}{64} \\ &\:2 \ quad\:\:\: 2 \quad\quad2\quad\quad2\quad\quad2 \end{выровнено}\)
Последовательность геометрическая. Общий паек равен \(r=2\).
б. Найдите соотношение последовательных членов
\(\begin{aligned}-\:2,\quad &\:\:\:6,\quad -12,\quad 36,\quad \:-72\quad \ :\:216,\dots \\ & \frac{6}{-2}\quad\frac{-12}{6}\quad\frac{36}{-12}\quad\frac{-72}{ 36}\quad\frac{216}{-72} \\ & -3\quad -2\quad\:\: -3\quad \:\:\:-2\quad \:\:-3 \end {выровнено}\)
Последовательность не является геометрической.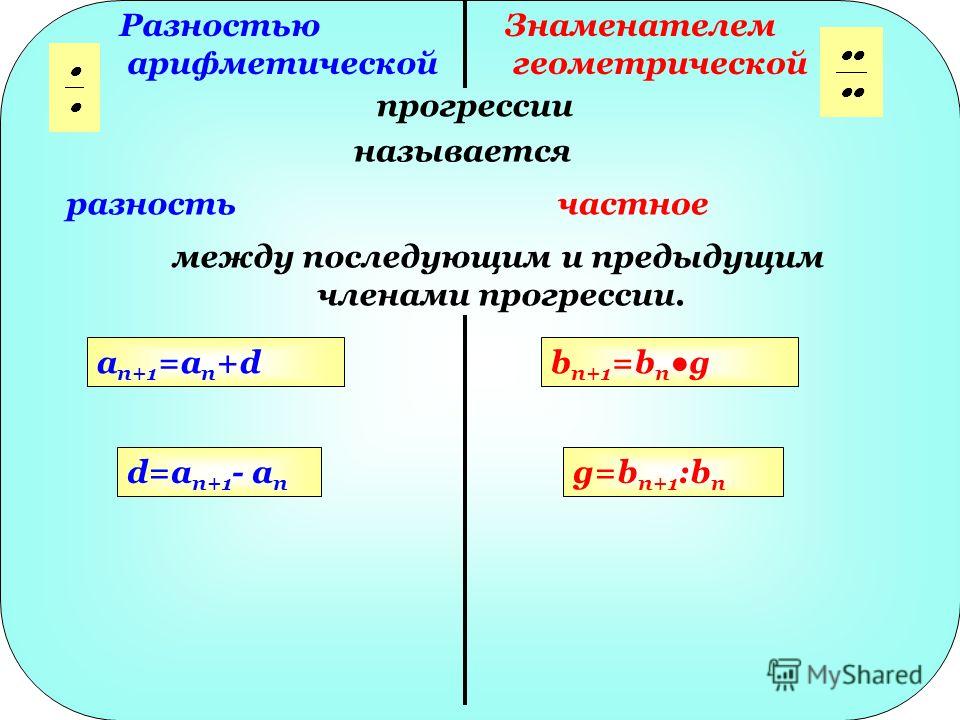 Общей пропорции нет.
Общей пропорции нет.
в. Найдите отношение последовательных членов
\(\begin{align}27,\quad &\:\:9,\quad 3,\quad 1,\quad \frac{1}{3},\quad \frac{1}{9}, \ ldots \\ & \ frac {9} {27} \ quad \ frac {3} {9} \ quad \ frac {1} {3} \ quad \ frac {\ frac {1} {3} {1} \ quad \ frac {\ frac {1} {9}} {\ frac {1} {3}} \\ &\ frac {1} {3} \ quad \; \: \ frac {1} {3} \ quad\frac{1}{3}\quad\:\frac{1}{3}\quad\:\frac{1}{3}\end{aligned}\)
Последовательность геометрическая. Обычное отношение равно \(r=\frac{1}{3}\).
Упражнение \(\PageIndex{1}\)
Определите, является ли каждая последовательность геометрической. Если да, укажите общее соотношение.
Упражнение \(\PageIndex{2}\)
Определите, является ли каждая последовательность геометрической. Если да, укажите общее соотношение.
Если мы знаем первый член \(a_{1}\) и знаменатель \(r\), мы можем перечислить конечное число членов последовательности.
Пример \(\PageIndex{2}\)
Запишите первые пять членов последовательности, где первый член равен \(3\), а знаменатель равен \(r=−2\).
Решение :
Начнем с первого члена и умножим его на обыкновенное отношение. Затем мы умножаем этот результат на обыкновенное отношение, чтобы получить следующий член, и так далее.
\(\begin{array}{cccc}{a_{1}} & {a_{2}} & {a_{3}} & {a_{4}} & {a_{5}} \\ {3 } & {3 \cdot(-2)} & {-6 \cdot(-2)} & {12 \cdot(-2)} & {-24 \cdot(-2)} \\& {-6} & {12} & {-24} & {48}\end{массив}\)
Ответ :
Последовательность \(3,-6,12,-24,48, \dots\)
Упражнение \(\PageIndex{3}\)
Запишите первые пять членов последовательности, где первый член равен \(7\), а знаменатель равен \(r=−3\).
Упражнение \(\PageIndex{4}\)
Запишите первые пять членов последовательности, где первый член равен \(6\), а знаменатель равен \(r=−4\).
Найдите общий член (\(n\)-й член) геометрической последовательности
Точно так же, как мы нашли формулу для общего члена последовательности и арифметической прогрессии, мы также можем найти формулу для общего члена геометрической прогрессии. геометрическая последовательность. 9{13}\)
геометрическая последовательность. 9{13}\)
Упрощение.
\(a_{14}=\frac{1}{128}\)
Упражнение \(\PageIndex{5}\)
Найдите тринадцатый член последовательности, где первый член равен \(81\) а обыкновенное отношение равно \(r=\frac{1}{3}\).
Упражнение \(\PageIndex{6}\)
Найдите двенадцатый член последовательности, где первый член равен \(256\), а знаменатель равен \(r=\frac{1}{4}\) .
Иногда мы не знаем обыкновенного отношения, и мы должны использовать данную информацию, чтобы найти его, прежде чем мы найдем запрошенный термин.
Пример \(\PageIndex{4}\)
Найдите двенадцатый член последовательности \(3, 6, 12, 24, 48, 96, …\) Найдите общий член последовательности.
Решение :
Чтобы найти двенадцатый член, мы используем формулу \(a_{n}=a_{1} r^{n-1}\), поэтому нам нужно сначала определить \(a_ {1}\) и обыкновенное отношение \(r\). {n-1}\) 9{n}\right)}{1-r}\)
{n-1}\) 9{n}\right)}{1-r}\)
где \(a_{1}\) — первый член, \(r\) — знаменатель, а \(r\) не равно один.
Мы применяем эту формулу в следующем примере, где даны первые несколько членов последовательности. Обратите внимание, что сумма геометрической последовательности обычно становится очень большой, когда обыкновенное отношение больше единицы.
Пример \(\PageIndex{5}\)
Найти сумму первых \(20\) членов геометрической прогрессии \(7, 14, 28, 56, 112, 224, …\)
9{20}\справа)}{1-2}\)
Упрощение.
\(S_{20}=7,340,025\)
Упражнение \(\PageIndex{9}\)
Найдите сумму первых \(20\) членов геометрической последовательности \(3, 6, 12, 24, 48, 96, …\)
Упражнение \(\PageIndex{10}\)
Найдите сумму первых \(20\) членов геометрической прогрессии \(6, 18, 54, 162, 486, 1,458, …\)
В следующем примере нам дана сумма в виде суммирования. {i}\), где \(r\) является общим соотношение. 9{n}\right)}{1-r}\), что требует \(a_{1}\) и \(r\). Мы выпишем несколько терминов, чтобы получить необходимую информацию.
{i}\), где \(r\) является общим соотношение. 9{n}\right)}{1-r}\), что требует \(a_{1}\) и \(r\). Мы выпишем несколько терминов, чтобы получить необходимую информацию.
| Выпишите первые несколько терминов. | |||
| Идентифицировать \(a_{1}\). | |||
| Найдите обыкновенное отношение. | |||
| Зная \(a_{1}=6\), \(r=3\) и \(n=15\), используйте формулу суммы. 9{15}}\end{array}\) По мере того, как \(n\) становится все больше и больше, сумма становится все больше и больше. Это верно, когда \(|r|≥1\) и мы называем ряд расходящимся. Мы не можем найти сумму бесконечного геометрического ряда, когда \(|r|≥1\). Давайте рассмотрим бесконечный геометрический ряд, знаменатель которого на долю меньше единицы, Эта формула дает нам сумму бесконечной геометрической прогрессии. Обратите внимание, что \(S\) не имеет нижнего индекса \(n\), как в \(S_{n}\), поскольку мы не добавляем конечное число терминов. Определение \(\PageIndex{5}\)Для бесконечного геометрического ряда, первый член которого равен \(a_{1}\) и знаменатель \(r\), Если \(|r|<1 \), сумма \(S=\frac{a_{1}}{1-r}\) Если \(|r|≥1\), то бесконечный геометрический ряд не имеет суммы. Говорят, что ряд расходится. Пример \(\PageIndex{7}\)Найти сумму бесконечного геометрического ряда \(54+18+6+2+\frac{2}{3}+\frac{2}{9}+ \ldots\) Решение : Чтобы найти сумму, мы сначала должны проверить, что обыкновенное отношение \(|r|<1\), а затем мы можем использовать формулу суммы \(S=\frac{ а_{1}}{1-r}\). Найдите знаменатель. \(\begin{array}{ll}{r=\frac{18}{54}} & {r=\frac{6}{18} \dots} \\ {r=\frac{1}{ 3}} & {r=\frac{1}{3} \quad|r|<1}\end{массив}\) Идентифицировать \(a_{1}\). \(a_{1}=54\) Зная \(a_{1}=54, r=\frac{1}{3}\), используйте формулу суммы. \(S=\frac{a_{1}}{1-r}\) Подставьте значения. \(S=\frac{54}{1-\frac{1}{3}}\) Упростить. \(S=81\) Ответ : \(S=80\) Упражнение \(\PageIndex{13}\)Найдите сумму бесконечного геометрического ряда \(48+ 24+12+6+3+\frac{3}{2}+\dots\) Упражнение \(\PageIndex{14}\)Найдите сумму бесконечного геометрического ряда \(64+16+4+1+\frac{1}{4}+\frac{1}{16}+ \многоточие\) Интересное использование бесконечных геометрических рядов — запись повторяющейся десятичной дроби. Пример \(\PageIndex{8}\)Запишите повторяющуюся десятичную дробь \(0,5\) в виде дроби. Решение : Перепишите \(0,5\), показав повторяющиеся пять. Используйте разрядное значение, чтобы переписать это как сумму. Это бесконечный геометрический ряд. 0,5555555555555\(\ldots\) Найдите обыкновенное отношение. \(\begin{array}{ll}{r=\frac{0,05}{0,5}} & {r=\frac{0,005}{0,05} \dots} \\ {r=0,1} & {r= 0,1 \quad|r|<1}\end{массив}\) Определить \(a_{1}\) \(a_{1}=0,5\) Зная \(a_{1}=0,5 ,r=0,1\), используйте формулу суммы. \(S=\frac{a_{1}}{1-r}\) Подставьте значения. \(S=\frac{0.5}{1-0.1}\) Упрощение. \(S=\frac{0.5}{0.9}\) Умножьте числитель и знаменатель на \(10\). \(S=\frac{5}{9}\) Нас просят найти форму дроби. \(0,5 = \frac{5}{9}\) Упражнение \(\PageIndex{15}\) Запишите повторяющуюся десятичную дробь \(0,4\) в виде дроби. Упражнение \(\PageIndex{16}\)Запишите повторяющуюся десятичную дробь \(0,8\). Применение геометрических последовательностей и рядов в реальном миреОдно из применений геометрических последовательностей связано с потребительскими расходами. Если налоговая скидка предоставляется каждому домохозяйству, эффект на экономику во много раз превышает размер индивидуальной скидки. Пример \(\PageIndex{9}\) Правительство решило предоставить каждому домохозяйству налоговую скидку в размере $\(1000\) для стимулирования экономики. Согласно государственной статистике, каждое домохозяйство потратит \(80\)% скидки на товары и услуги. Предприятия и частные лица, которые извлекли выгоду из этого \(80\)%, затем потратят \(80\)% того, что они получили, и так далее. 9{2}+\ldots\) Здесь первый член равен \(1000, a_{1}=1000\). Обычное отношение равно \(0,8, r=0,8\). Мы можем оценить эту сумму, поскольку \(0,8<1\). Воспользуемся формулой суммы бесконечного геометрического ряда. \(S=\frac{a_{1}}{1-r}\) Подставьте значения \(a_{1}=1000\) и \(r=0,8\). \(S=\frac{1,000}{1-0,8}\) Оценить. \(S=5,000\) Ответ : Суммарный эффект $\(1,000\), полученных каждым домохозяйством, будет $\(5,000\) роста экономики. Упражнение \(\PageIndex{17}\)Каково общее влияние на экономику государственной налоговой льготы в размере $\(1000\) каждому домохозяйству с целью стимулирования экономики, если каждое домохозяйство будет тратить \( 90\)% скидки на товары и услуги? Упражнение \(\PageIndex{18}\) Каково общее влияние на экономику государственной налоговой льготы в размере $\(500\) каждому домохозяйству с целью стимулирования экономики, если каждое домохозяйство будет тратить \( 85\)% скидки на товары и услуги? 9{n t}\) при начислении процентов \(n\) раз в год. | |||
| \(3\)-й депозит \(P\) на конец года \(3\) | \(П\) |
|---|
Через три года стоимость ренты равна
равно \(1+r\). Подставляем эти значения в формулу суммы. Будьте осторожны, у нас есть два разных использования \(r\). \(r\) в формуле суммы является знаменателем последовательности. В данном случае это \(1+r\), где \(r\) — процентная ставка. 9{t}-1\right)}{r} \end{aligned}\)Помните, что наша предпосылка заключалась в том, что в конце каждого года вносится один депозит.
Мы можем адаптировать эту формулу для \(n\) депозитов, сделанных в год, и проценты начисляются \(n\) раз в год.
Определение \(\PageIndex{6}\)
Для основной суммы \(P\), инвестированной в конце периода начисления процентов, с процентной ставкой \(r\), которая начисляется \(n \) раз в год, новый баланс, \(A\) , после \(t\) лет, равен 9{n t}-1\right)}{\frac{r}{n}}\), нам нужно идентифицировать \(P, r, n\) и \(t\).
Определить \(P\), сумму, инвестируемую каждый месяц.
\(P=100\)
Определить \(r\), годовую процентную ставку, в десятичной форме.
\(r=0,05\)
Укажите \(n\), сколько раз будет вноситься вклад и проценты, начисляемые каждый год.
\(n=12\)
Определить \(t\), количество лет.
\(t=18\)
Зная \(P=100, r=0,05, n=12\) и \(t=18\), используем формулу суммы. 9{12.18}-1\right)}{\frac{0.05}{12}}\)
Используйте калькулятор для расчета. Обязательно используйте скобки по мере необходимости.
\(A_{t}=34,920 .20\)
Ответ :
У ребенка будет $\(34 920,20\)
Упражнение \(\PageIndex{19}\)
Новые бабушка и дедушка решают вкладывать $\(200\) в месяц в аннуитет для своего внука. Счет будет платить \(5\)% годовых, которые ежемесячно начисляются. Сколько будет на счету ребенка к его двадцать первому дню рождения?Упражнение \(\PageIndex{20}\)
Артуро только что получил свою первую постоянную работу после окончания колледжа в возрасте \(27\). Он решил инвестировать $\(200\) в месяц в IRA (аннуитет). Проценты по аннуитету составляют \(8\)%, которые начисляются ежемесячно. Сколько будет на счету Артуро, когда он уйдет на пенсию в свой шестьдесят седьмой день рождения?
Он решил инвестировать $\(200\) в месяц в IRA (аннуитет). Проценты по аннуитету составляют \(8\)%, которые начисляются ежемесячно. Сколько будет на счету Артуро, когда он уйдет на пенсию в свой шестьдесят седьмой день рождения?
Доступ к этим онлайн-ресурсам для получения дополнительных инструкций и практики с последовательностями.
Ключевые понятия
\(S=\frac{a_{1}}{1-r}\)
Мы говорим, что ряд сходится.
Если \(|r|≥1\), то бесконечный геометрический ряд не имеет суммы. Говорят, что ряд расходится.
Глоссарий
Эта страница под названием 12. 4: Геометрические последовательности и серии распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
4: Геометрические последовательности и серии распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
Исчисление II — специальная серия
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т.е. вы наверное на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 4-5: Специальная серия
В этом разделе мы кратко рассмотрим три специальные серии. На самом деле, особенный может быть неправильным термином. Все три были названы, что делает их в некотором роде особенными, однако основная причина, по которой мы собираемся рассмотреть два из них в этом разделе, заключается в том, что это единственные типы сериалов, которые мы будем рассматривать, для которых мы сможет получить фактические значения для ряда. Третий тип является расходящимся и поэтому не имеет значения для беспокойства. 9п}\конец{выравнивание*}\]
На самом деле, особенный может быть неправильным термином. Все три были названы, что делает их в некотором роде особенными, однако основная причина, по которой мы собираемся рассмотреть два из них в этом разделе, заключается в том, что это единственные типы сериалов, которые мы будем рассматривать, для которых мы сможет получить фактические значения для ряда. Третий тип является расходящимся и поэтому не имеет значения для беспокойства. 9п}\конец{выравнивание*}\]
Теперь из теоремы 3 из раздела «Последовательности» мы знаем, что указанный выше предел будет существовать и будет конечным при условии \( — 1 < r \le 1\). Однако обратите внимание, что мы не можем допустить \(r = 1\), так как это даст деление на ноль. Следовательно, это будет существовать и будет конечным при условии \(- 1 \[\ mathop {\lim }\limits_{n \to \infty} {s_n} = \frac{a}{{1 — r}}\]
9n}} = \frac{a}{{1 — r}}\] Обратите внимание, что при использовании этой формулы нам нужно убедиться, что мы находимся в правильной форме. Пример 1 Определите, сходятся или расходятся следующие ряды. Если они сходятся, укажите значение ряда. Другими словами, если ряд начинается с \(n = 0\), то показатель степени на \(r\) должен быть \(n\). Точно так же, если ряд начинается с \(n = 1\), то показатель степени на \(r\) должен быть \(n — 1\).
Другими словами, если ряд начинается с \(n = 0\), то показатель степени на \(r\) должен быть \(n\). Точно так же, если ряд начинается с \(n = 1\), то показатель степени на \(r\) должен быть \(n — 1\). 9{n + 1}}} \) Показать решение
Этот ряд на самом деле не похож на геометрический ряд. Однако обратите внимание, что обе части члена ряда представляют собой числа, возведенные в степень. Это означает, что его можно представить в виде геометрического ряда. Нам просто нужно решить, какая форма является правильной формой. Поскольку ряд начинается с \(n = 1\), мы хотим, чтобы показатели степени чисел были равны \(n — 1\).
Придать этому правильную форму будет довольно легко. Давайте сначала немного перепишем вещи. Перед одним из \(n\) в показателе степени стоит минус, а этого не может быть в геометрической форме. Итак, давайте сначала избавимся от этого. 9п}} \]
Итак, давайте сначала избавимся от этого. 9п}} \]
Итак, мы привели его в правильную форму и видим, что \(a = 5\) и \(r = — \frac{{64}}{5}\). Также обратите внимание, что \(\left| r \right| \ge 1\) и поэтому этот ряд расходится.
Вернувшись в раздел «Серии — Основы», мы говорили об исключении терминов из серий, но на самом деле не приводили примеров того, как эту идею можно использовать на практике. Теперь мы можем сделать несколько примеров.
Пример 2 Используйте результаты предыдущего примера, чтобы определить значение следующего ряда. 9\infty {{a_n}} \). Теперь это конечное значение, поэтому этот ряд также будет сходящимся.
Другими словами, если у нас есть два ряда и они отличаются только наличием или отсутствием конечного числа конечных членов, они будут либо оба сходящимися, либо оба будут расходящимися. Различие нескольких членов так или иначе не изменит сходимости ряда. Это важная идея, и мы будем использовать ее несколько раз в следующих разделах, чтобы упростить некоторые тесты, которые мы будем рассматривать. 92} + 3i + 2}} = \frac{1}{{\left( {i + 2} \right)\left( {i + 1} \right)}} = \frac{1}{{i + 1}} — \frac{1}{{i + 2}}\]
92} + 3i + 2}} = \frac{1}{{\left( {i + 2} \right)\left( {i + 1} \right)}} = \frac{1}{{i + 1}} — \frac{1}{{i + 2}}\]
Подробности о дробях мы оставим вам. К настоящему моменту вы уже должны быть достаточно опытны в этом, так как мы потратили немало времени на вычисление частичных дробей в главе «Методы интегрирования». Если вам нужно освежить в памяти, вы должны вернуться и просмотреть этот раздел.
Итак, что это дает нам? Что ж, давайте начнем выписывать члены общей частичной суммы для этого ряда, используя форму частичной дроби. 9п {\ влево ( {\ гидроразрыва {1} {{я + 1}} — \ гидроразрыва {1} {{я + 2}}} \ справа)} \\ & = \ влево ( {\ гидроразрыва {1} { 1} — \require{cancel} \cancel{{\frac{1}{2}}}} \right) + \left( {\require{cancel} \cancel{{\frac{1}{2}}} — \require{cancel} \bcancel{{\frac{1}{3}}}} \right) + \left( {\require{cancel} \bcancel{{\frac{1}{3}}} — \ require{cancel} \cancel{{\frac{1}{4}}}} \right) + \cdots + \left( {\require{cancel} \cancel{{\frac{1}{n}}} — \require{cancel} \bcancel{{\frac{1}{{n + 1}}}}} \right) + \left( {\require{cancel} \bcancel{{\frac{1}{{n + 1}}}} — \frac{1}{{n + 2}}} \right)\\ & = 1 — \frac{1}{{n + 2}}\end{align*}\]
Обратите внимание, что все термины, кроме первого и последнего, отменены. Это происхождение названия телескопической серии .
Это происхождение названия телескопической серии .
Это также означает, что мы можем определить сходимость этого ряда, взяв предел частичных сумм.
\[\ mathop {\lim }\limits_{n \to \infty} {s_n} = \mathop {\lim }\limits_{n \to \infty} \left( {1 — \frac{1}{{n + 2}}} \справа) = 1\]
Последовательность частичных сумм сходится, поэтому ряд сходится и имеет значение 9п {\ влево ( {\ гидроразрыва {1} {{я + 1}} — \ гидроразрыва {1} {{я + 3}}} \ справа)} \\ & = \ гидроразрыва {1} {2} \ влево [ {\ влево ( {\ гидроразрыва {1} {2} — \ требуют {отменить} \ отменить {{\ гидроразрыва {1} {4}}}} \ справа) + \ влево ( {\ гидроразрыва {1} {3 } — \require{cancel} \bcancel{{\frac{1}{5}}}} \right) + \left( {\require{cancel} \cancel{{\frac{1}{4}}} — \require{cancel} \bcancel{{\frac{1}{6}}}} \right) + \cdots + \left( {\require{cancel} \cancel{{\frac{1}{n}}} — \frac{1}{{n + 2}}} \right) + \left( {\require{cancel} \cancel{{\frac{1}{{n + 1}}}} — \frac{1 }{{n + 3}}} \right)} \right]\\ & = \frac{1}{2}\left[ {\ frac {1} {2} + \ frac {1} {3} — \ frac {1} {{n + 2}} — \ frac {1} {{n + 3}}} \ right] \ end {выровнять*}\]
В этом случае вместо последовательных условий отмена срока будет отменена сроком, который находится дальше по списку. В итоге на этот раз осталось два начальных и два конечных члена. Обратите также внимание, что для того, чтобы немного помочь в работе, мы исключили \(\frac{1}{2}\) из ряда.
В итоге на этот раз осталось два начальных и два конечных члена. Обратите также внимание, что для того, чтобы немного помочь в работе, мы исключили \(\frac{1}{2}\) из ряда.
Лимит частичных сумм,
\[\ mathop {\ lim } \ limit_ {n \ to \ infty} {s_n} = \ mathop {\ lim } \ limit_ {n \ to \ infty} \ frac {1} {2} \ left ( {\ frac {5}{6} — \frac{1}{{n + 2}} — \frac{1}{{n + 3}}} \right) = \frac{5}{{12}}\] 92} + 4n + 3}}} = \frac{5}{{12}}\]
Обратите внимание, что не всегда очевидно, является ли ряд телескопическим или нет, пока вы не попытаетесь получить частичные суммы, а затем не увидите, действительно ли они телескопируются. Нет теста, который скажет нам, что у нас есть серия телескопов сразу. Также обратите внимание, что только потому, что вы можете делать частичные дроби на члене ряда, не означает, что ряд будет телескопическим рядом. Следующий ряд, например, не является телескопическим рядом, несмотря на тот факт, что мы можем дробить члены ряда. 9\ infty {\ left ( {\ frac {1} {{n + 1}} + \ frac {1} {{n + 2}}} \ right)} \]
9\ infty {\ left ( {\ frac {1} {{n + 1}} + \ frac {1} {{n + 2}}} \ right)} \]
Для того, чтобы серия была телескопической серией, мы должны получить условия для отмены, и все эти условия положительны, поэтому ни один из них не будет отменен.
Теперь нам нужно вернуться и решить проблему, которая впервые была поднята в предыдущем разделе. В этом разделе мы заявили, что сумма или разность сходящихся рядов также сходится и что наличие мультипликативной константы не влияет на сходимость ряда. Теперь, когда у нас есть еще несколько серий, давайте поработаем на небольшом примере, показывающем это. 9{n + 1}}} \\ & = 4\left( {\frac{5}{{12}}} \right) — \frac{{1296}}{5}\\ & = — \frac{{3863}}{{15}}\end{align*}\]
Мы не обсуждали сходимость этого ряда, потому что он представлял собой сумму двух сходящихся рядов, а это гарантировало сходимость исходного ряда.
Серия Harmonic
Это третья и последняя серия, которую мы рассмотрим в этом разделе. Вот гармонический ряд. 9\ infty {\ гидроразрыва {1} {п}} \]
Вот гармонический ряд. 9\ infty {\ гидроразрыва {1} {п}} \]
Вы можете немного прочитать о том, почему это называется гармоническим рядом (имеет отношение к музыке) на странице гармонического ряда в Википедии.
Гармонический ряд расходится, и нам нужно подождать до следующего раздела, чтобы показать это. Эта серия здесь, потому что у нее есть название, и поэтому мы хотели поместить ее здесь вместе с двумя другими именованными сериями, которые мы рассмотрели в этом разделе. Мы также собираемся использовать гармонический ряд, чтобы проиллюстрировать пару идей о расходящихся рядах, которые мы уже обсуждали для сходящихся рядов. Мы сделаем это на следующем примере. 9\infty {\frac{1}{n}}} \right) — \frac{{11}}{6}\]
В этом случае мы вычитаем конечное число из расходящегося ряда. Это вычитание не изменит расходимости ряда. У нас будет либо бесконечность минус конечное число, что по-прежнему будет бесконечностью, либо ряд без значения минус конечное число, которое по-прежнему не будет иметь значения.



 д.
д. 0=1$ не должно быть соглашением. И я видел несколько причин, по которым это должно быть (обращение к пустому произведению, использование элементарной комбинаторики и приложение к геометрическому/степенному ряду — три, о которых я могу думать прямо сейчас). 90 = 1$ при работе с сериями, и значение оказывается 0-м членом ряда, но это просто удобство записи (иначе вам пришлось бы выделять постоянные члены для бесконечных хлопот и никакого выигрыша).
0=1$ не должно быть соглашением. И я видел несколько причин, по которым это должно быть (обращение к пустому произведению, использование элементарной комбинаторики и приложение к геометрическому/степенному ряду — три, о которых я могу думать прямо сейчас). 90 = 1$ при работе с сериями, и значение оказывается 0-м членом ряда, но это просто удобство записи (иначе вам пришлось бы выделять постоянные члены для бесконечных хлопот и никакого выигрыша). и гео. Посл.Ариф. Серия
и гео. Посл.Ариф. Серия
 Первый член равен a = 250. Разделив пары членов, я получаю:
Первый член равен a = 250. Разделив пары членов, я получаю: .. вместо дробного (и точного) ответа.
.. вместо дробного (и точного) ответа. .. равно 1/3.
.. равно 1/3. .. имеет значение одной трети равно «показ», которого требовало упражнение (поэтому очень важно выполнять свою работу аккуратно и логично). И вы можете использовать этот метод для преобразования любого повторяющегося десятичного числа в его дробную форму.
.. имеет значение одной трети равно «показ», которого требовало упражнение (поэтому очень важно выполнять свою работу аккуратно и логично). И вы можете использовать этот метод для преобразования любого повторяющегося десятичного числа в его дробную форму. .. = 1.
.. = 1. □
□ S=\dfrac 12 +\dfrac 24 +\dfrac 38+\dfrac{4}{16}+\dfrac{5}{32}+\cdots. S=21+42+83+164+325+⋯.
S=\dfrac 12 +\dfrac 24 +\dfrac 38+\dfrac{4}{16}+\dfrac{5}{32}+\cdots. S=21+42+83+164+325+⋯.
 i } i=1∑∞2ii2.
92 и2. Мы будем использовать другой подход, чтобы свести это к «линейно-геометрической прогрессии», которая является AGP.
i } i=1∑∞2ii2.
92 и2. Мы будем использовать другой подход, чтобы свести это к «линейно-геометрической прогрессии», которая является AGP. \begin{массив} { г lllllll}
T & =\frac 12 & +\frac {3}{4} & +\frac{5}{8} &+\frac{7}{16} &+\frac{9}{32} &+\cdots\\
\frac{1}{2} T & = & + \frac 14 & +\frac {3}{8} & +\frac{5}{16} &+\frac{7}{32} &+\cdots \\
\hline
\frac{1}{2} T & = \frac{1}{2} & + \frac{2}{4} & + \frac{2}{8} & + \frac{2}{16} & + \frac{2}{32} & + \cdots .\\
\end{массив} T21T21T=21==21+43+41+42+85+83+82+167+165+162+ 329+327+322+⋯+⋯+⋯.
\begin{массив} { г lllllll}
T & =\frac 12 & +\frac {3}{4} & +\frac{5}{8} &+\frac{7}{16} &+\frac{9}{32} &+\cdots\\
\frac{1}{2} T & = & + \frac 14 & +\frac {3}{8} & +\frac{5}{16} &+\frac{7}{32} &+\cdots \\
\hline
\frac{1}{2} T & = \frac{1}{2} & + \frac{2}{4} & + \frac{2}{8} & + \frac{2}{16} & + \frac{2}{32} & + \cdots .\\
\end{массив} T21T21T=21==21+43+41+42+85+83+82+167+165+162+ 329+327+322+⋯+⋯+⋯. Это справедливо и в более общем плане: если мы возьмем разность членов в последовательности степени nnn, мы получим последовательность степени n−1n−1 n−1. Это подробно рассмотрено в разделе «Метод различий». Мы будем неоднократно использовать эту идею для работы с такой «полиномиально-геометрической прогрессией». 9i } i=1∑∞3ii3.
Это справедливо и в более общем плане: если мы возьмем разность членов в последовательности степени nnn, мы получим последовательность степени n−1n−1 n−1. Это подробно рассмотрено в разделе «Метод различий». Мы будем неоднократно использовать эту идею для работы с такой «полиномиально-геометрической прогрессией». 9i } i=1∑∞3ii3. Затем умножение на 13 \frac{1}{3} 31 и получение разницы дает
Затем умножение на 13 \frac{1}{3} 31 и получение разницы дает

 🙂
🙂
 6+\frac{73}{10}\cdot\frac{1}{99}???
6+\frac{73}{10}\cdot\frac{1}{99}???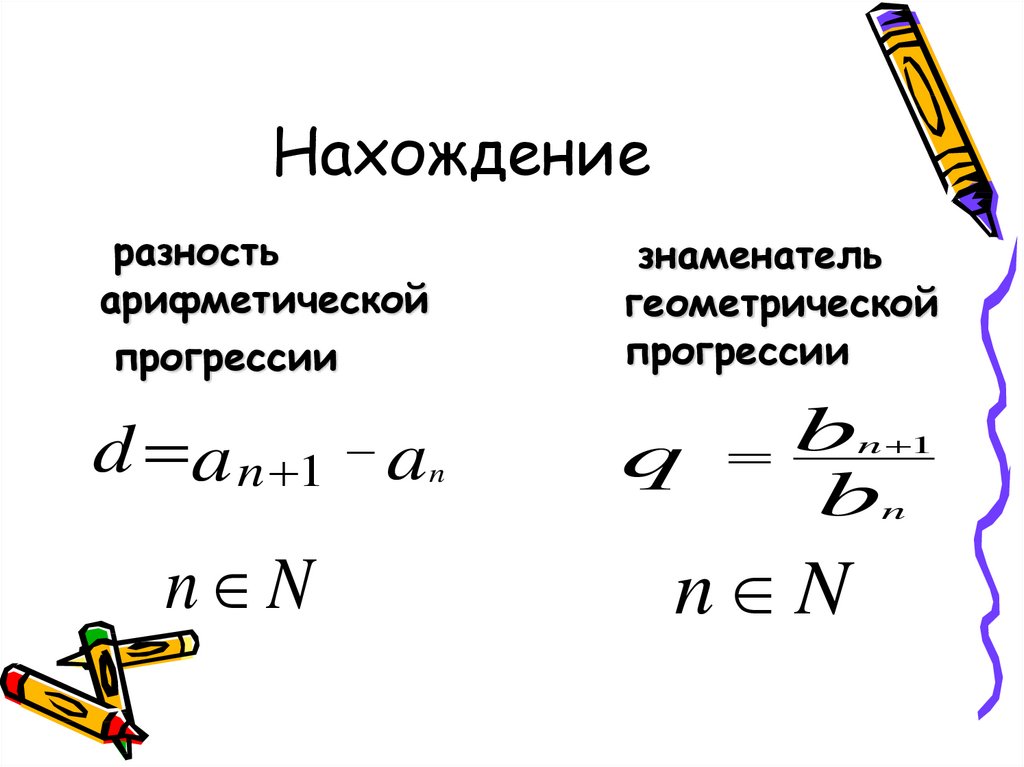 9{x}\), найти a. \(f(1)\) б. \(f(2)\) в. \(f(3)\).
9{x}\), найти a. \(f(1)\) б. \(f(2)\) в. \(f(3)\). 