Перезагрузка» (США, Австралия, 2003) – Афиша-Кино
Отрицательные отзывы о фильме
The Matrix Reloaded (2003, США, Австралия), IMDb: 7.2
О фильме В ролях Отзывы (132)Похожие
Рецензия «Афиши» на фильм
Станислав Зельвенский
1341 отзыв, 979 оценка, рейтинг 20350
Что такое «матрица», я не понимаю. Даже перезагрузка не помогает. Кажется, это что-то из высшей алгебры. Или низшей геометрии. Или термодинамики… Считается, что если посмотреть «Матрицу» №1 дважды, то все поймешь, но у меня ни разу за четыре года такого желания не возникло. «Матрица» №1, по-моему, — самый перехваленный фильм десятилетия. За дебют братьев Вачовски «Связь» я бы таких «Матриц» десяток отдал. От «Матрицы» в памяти остались красивая драка в каком-то большом зале с колоннами и зеленые падающие цифры (и то потому, что скринсейвер такой стоял). Длинный тяжеловесный боевик с претенциозными посылами: ничего нет, все — иллюзия, люди — машины… Культ среди подростков вполне понятен — подростки обожают такую копеечную квазифилософию. Но попадаются и взрослые, вполне разумные люди, у которых при упоминании «Матрицы» расширяются зрачки и учащается пульс. Вот это и вправду удивительно. Я, честное слово, видел диссертацию про «Матрицу». «Матрицу» №2 обсуждали целый год — смаковали скупые подробности, оценивали подбор актеров, угадывали возможный сюжет. Актеры, сюжет? Люди, проснитесь. Вспомните любимый фильм: все — иллюзия. Артист Лоренс Фишберн, герой второго плана из трэшевых гангстерских боевиков, — гений кунг-фу и народный вождь по имени Морфеус! Вы можете говорить об этом без смеха? Что касается сюжета, то вот он, наконец, пожалуйста: подземный город Зион атакуют полчища металлических осьминожек. Команда космического корабля «Навуходоносор» — похожий на крупного хомяка Морфеус, веселый негр Линк, женщина в латексе Тринити и полу-Иисус полу-Супермен Нео — пытается Зион спасти. Для этого они сражаются с летающими близнецами-альбиносами, самокопирующимся пижоном по имени Смит и еще одним, не помню, как зовут, — он все время коверкает французские ругательства.
Но попадаются и взрослые, вполне разумные люди, у которых при упоминании «Матрицы» расширяются зрачки и учащается пульс. Вот это и вправду удивительно. Я, честное слово, видел диссертацию про «Матрицу». «Матрицу» №2 обсуждали целый год — смаковали скупые подробности, оценивали подбор актеров, угадывали возможный сюжет. Актеры, сюжет? Люди, проснитесь. Вспомните любимый фильм: все — иллюзия. Артист Лоренс Фишберн, герой второго плана из трэшевых гангстерских боевиков, — гений кунг-фу и народный вождь по имени Морфеус! Вы можете говорить об этом без смеха? Что касается сюжета, то вот он, наконец, пожалуйста: подземный город Зион атакуют полчища металлических осьминожек. Команда космического корабля «Навуходоносор» — похожий на крупного хомяка Морфеус, веселый негр Линк, женщина в латексе Тринити и полу-Иисус полу-Супермен Нео — пытается Зион спасти. Для этого они сражаются с летающими близнецами-альбиносами, самокопирующимся пижоном по имени Смит и еще одним, не помню, как зовут, — он все время коверкает французские ругательства. В плане вымученности и напыщенности «Матрица» соперничает только с картиной «Звездные войны» — еще одним мегаломанским надувательством, претендующим на роль новой Библии.
В плане вымученности и напыщенности «Матрица» соперничает только с картиной «Звездные войны» — еще одним мегаломанским надувательством, претендующим на роль новой Библии.
Это ведь правда — «Матрицу» воспринимают как религиозное откровение. Она учит нас, что каждый элемент реальности — это компьютерная программа. Пожилая негритянка — файл. Чувство — последовательность цифр… Постойте! «Матрица» — это американский кинофильм, где люди в стильных черных очках дерутся ногами.
И вообще: Нео — мессия? Нео — герой нового поколения? Нео — то имя, которое вы попросили вытатуировать у себя на копчике? Тот самый Нео, который ходит с выражением вечной недоуменной озабоченности на лице, а в нужный момент, чтобы взлететь, превращает асфальт в батут? Перекреститесь. Главная проблема этого парня — в том, что ему необходимо поцеловать в губы Монику Беллуччи…
Раз пятьсот я прочел в разных журналах о том, что братья Вачовски изобрели какие-то революционные методы киносъемки и, натурально, перевернули современный кинематограф. Вообще-то, в арсенале режиссеров — ровно два эффектных приема. Первый: замедленные съемки. Второй: кто-то открывает дверь, а за ней оказывается совершенно не то, что по логике должно находиться. Вачовски оба приема эксплуатируют умело, с чувством и размахом. Но не маловато ли для революции? Для фильма, каждая минута которого стоит в среднем миллион американских долларов?
Вообще-то, в арсенале режиссеров — ровно два эффектных приема. Первый: замедленные съемки. Второй: кто-то открывает дверь, а за ней оказывается совершенно не то, что по логике должно находиться. Вачовски оба приема эксплуатируют умело, с чувством и размахом. Но не маловато ли для революции? Для фильма, каждая минута которого стоит в среднем миллион американских долларов?
Нет, конечно, «Матрица» сшибает — как сшибает все огромное, тяжелое и дорогое. «Матрица» проезжает многотонным грузовиком по глазным нервам, сбивает с ног низкочастотным dolby surround. Армия клонов, война миров, последний день Помпеи. На «Матрицу» невозможно не пойти — эта программа слишком грандиозна для того, чтобы ее просто игнорировать. Она и вправду перевернула кинематограф, поставила на колени, уложила на лопатки. Она взяла не умом и красотой — она взяла его силой. Шестеренки крутятся, кинопроектор работает, как пулемет, — тысяча выстрелов в минуту. Агенты Смиты самокопируются и наступают, погибают и снова самокопируются. Все — декорация, иллюзия, симулякры. «Матрицы» нет: «Матрица», как оказалось, была рекламным роликом к «Матрице» №2, а «Матрица» №2 — это рекламный ролик к «Матрице» №3 (выход в ноябре). Люди — подсобный материал, питающий своей энергией машины. Люди принесут деньги, и на них построят новые «Матрицы», еще лучше прежних. Конец света, как расскажет Нео бог-отец, происходил много раз: это уже шестая версия мира. Перезагрузиться и снова войти, потом снова перезагрузиться. Matrix reloaded, Matrix reloaded. Хватит! Escape, delete, turn off…
Все — декорация, иллюзия, симулякры. «Матрицы» нет: «Матрица», как оказалось, была рекламным роликом к «Матрице» №2, а «Матрица» №2 — это рекламный ролик к «Матрице» №3 (выход в ноябре). Люди — подсобный материал, питающий своей энергией машины. Люди принесут деньги, и на них построят новые «Матрицы», еще лучше прежних. Конец света, как расскажет Нео бог-отец, происходил много раз: это уже шестая версия мира. Перезагрузиться и снова войти, потом снова перезагрузиться. Matrix reloaded, Matrix reloaded. Хватит! Escape, delete, turn off…
Да, и вот еще: по поводу зрачков и пульса. Я из второго фильма все узнал. Это такая специальная программа, ее добавляют в программу пирожного. Откусываешь — и начинается. Программу написал тип, который по-французски ругается, — не помню, как зовут. Он, кстати, — тоже программа.
24 мая 2003
Лучшие отзывы о фильме «Матрица: Перезагрузка»
Александр Пушкарёв
39 отзывов, 1123 оценок, рейтинг 19
5
Сложно оценить этот фильм — ведь оказалось, что это лишь промежуточный этап.

Конечно, все ждали большего — это же Маааатрица.
и.. ожидания были самым коварным образом разрушены.Как самостоятельный фильм — с началом и концом «перезагрузку» рассматривать нельзя — скорее как серию из сериала, в которой если ты не знаешь предыстории делать неего.
Просто так этот фильм сейчас смотреть не станешь — только вместе со всей трилогией.
И, согласитесь, получается почти цельная картина.Много времени прошло со времён первой «матрицы», актёры снялись в других проектах, играют и правда не так активно как раньше — с ленцой — как здесь верно заметили.
Фильм затянут- самое яркое, что осталось в памяти после просмотра — сцена драки и погони на дороге и братья-близнецы.
И тем не менее фильм заставляет досмотреть себя до конца.
Он важен в идейном понимании, в нём даются объяснения мотивов и поступков героев, а также предыстория; братья Вачовски вновь делают тонкие намёки на высокоинтеллектуальные труды.Это как «Убить Билла 2» после невообразимого успеха первой части у всех слоёв населения, ожидали чего-то похожего, а получили размеренный и не насыщенный такими яркими картинками фильм.
 Но это ведь не значит, что он плохой. Это излишнее ожидание в напряжении заставило зрителей так думать.
Но это ведь не значит, что он плохой. Это излишнее ожидание в напряжении заставило зрителей так думать.Если первая «матрица» была прологом, то вторая — скорее не предыстория к третьей, а промежуточное звено — связывающее воедино первую и третью части- если рассматривать фильм с этой позиции — свою роль он выполнил превосходно.
24 марта 2009
Ася Чащинская
9 отзывов, 17 оценок, рейтинг 13
1
Предлагаю считать, что никакой второй и третьей «Матрицы» не существует.
(Иными словами, будем думать, мол, вышли некогда фильмы «Матрица: Перезагрузка» и «Матрица: Революция», но они никакого отношения к первой «Матрице» не имеют. Вышли и вышли. Ну что ж теперь поделаешь…)
21 июня 2011
Андрей Гориченский
1 отзыв, 665 оценка, рейтинг 1
3
Где-то на поверхности Реального мира машины запускают свои адские буры, стремясь добраться до последнего оплота человечества, города Зион.
 Поскольку в случае их успеха человечество, вероятно, погибнет, правительство Зиона начинает усиленно готовиться к обороне, а фанатик Морфеус ставит все карты на избранного Нео, который должен добраться до Источника и повернуть там какой-то рубильник, чтобы остановить войну. Чтобы попасть к Источнику, необходимо для начала разыскать Мастера Ключей — маленького и сухонького старичка-азиата.
Поскольку в случае их успеха человечество, вероятно, погибнет, правительство Зиона начинает усиленно готовиться к обороне, а фанатик Морфеус ставит все карты на избранного Нео, который должен добраться до Источника и повернуть там какой-то рубильник, чтобы остановить войну. Чтобы попасть к Источнику, необходимо для начала разыскать Мастера Ключей — маленького и сухонького старичка-азиата.Думаю, все согласятся, что братьям Вачовски мы можем простить положительно все. Все-таки именно они открыли нам истинную природу этого мира, да еще и попутно совершили переворот в мире спецэффектов и жанре киберпанка. Так что мы закроем глаза на получасовые заумные речи Архитектора, половину из которых все равно никто не поймет. На то, что кино-революция, символ новой философии потихоньку превращается в монументальный, красочный, сильный, но заумный все-таки боевик. Но кое-что лично я не смогу простить. Если в конце первой части Нео своим полетом сказал нам с экрана: «Предела нет», то что мешает ему во второй части взять и схлопнуть всю Матрицу в точку? Зачем возводить стены, которые только что самолично обрушил? Наверное, я что-то пропустил или прослушал, наверное, Архитектор объяснял это, но ради чего, зачем, зачем, зачем все это по второму кругу? Все равно что родился, осознал что живой, по-настоящему живой, и вдруг обнаружил, что надо на работу устраиваться, семью заводить.
 Научился летать, а тебе говорят: «Летать можно только по квартире. И вообще, у нас тут это не принято».
Научился летать, а тебе говорят: «Летать можно только по квартире. И вообще, у нас тут это не принято».29 января 2013
Ната Натанова
4 отзыва, 4 оценки, рейтинг 1
5Глюконат Матрицы
Этим полнолунным ночером опять просмотрела, можно сказать, эпохальный иллюзион — х.з. что за х.ф. «Матрица».
Что ж, кто только уже не писал на сей счет о том, что завсегда можно забацать эффектный и эффективный концептуальный микс, если немного перемежевать типичный обывательский лохотрон крошками пресловутой «правды», напоминающей наблюдаемую повседневную реальность, вкупе с использованием самого передового технологического арсенала от профи науки, большого бизнеса и киноискусства. И я прошлась…
http://www.afisha.ru/movie/172091/review/362569/?ref=blog18 февраля 2011
Подборки «Афиши»
Лучшие фильмы про боевые искусства
фильмов для тех, кто устал от обычных вестернов
Почему вашему ребенку новые «Звездные войны» понравятся не меньше старых
Осенний прогноз: до -40% на планы выходного дня в Питере
Мероприятия
Создайте уникальную страницу своего события на «Афише»
Это возможность рассказать о нем многомиллионной аудитории и увеличить посещаемость
- Абакан,
- Азов,
- Альметьевск,
- Ангарск,
- Арзамас,
- Армавир,
- Артем,
- Архангельск,
- Астрахань,
- Ачинск,
- Балаково,
- Балашиха,
- Балашов,
- Барнаул,
- Батайск,
- Белгород,
- Белорецк,
- Белореченск,
- Бердск,
- Березники,
- Бийск,
- Благовещенск,
- Братск,
- Брянск,
- Бугульма,
- Бугуруслан,
- Бузулук,
- Великий Новгород,
- Верхняя Пышма,
- Видное,
- Владивосток,
- Владикавказ,
- Владимир,
- Волгоград,
- Волгодонск,
- Волжский,
- Вологда,
- Вольск,
- Воронеж,
- Воскресенск,
- Всеволожск,
- Выборг,
- Гатчина,
- Геленджик,
- Горно-Алтайск,
- Грозный,
- Губкин,
- Гудермес,
- Дербент,
- Дзержинск,
- Димитровград,
- Дмитров,
- Долгопрудный,
- Домодедово,
- Дубна,
- Евпатория,
- Екатеринбург,
- Елец,
- Ессентуки,
- Железногорск,
- Жуковский,
- Зарайск,
- Заречный,
- Звенигород,
- Зеленогорск,
- Зеленоград,
- Златоуст,
- Иваново,
- Ивантеевка,
- Ижевск,
- Иркутск,
- Искитим,
- Истра,
- Йошкар-Ола,
- Казань,
- Калининград,
- Калуга,
- Каменск-Уральский,
- Камышин,
- Каспийск,
- Кемерово,
- Кингисепп,
- Кириши,
- Киров,
- Кисловодск,
- Клин,
- Клинцы,
- Ковров,
- Коломна,
- Колпино,
- Комсомольск-на-Амуре,
- Копейск,
- Королев,
- Коряжма,
- Кострома,
- Красногорск,
- Краснодар,
- Краснознаменск,
- Красноярск,
- Кронштадт,
- Кстово,
- Кубинка,
- Кузнецк,
- Курган,
- Курск,
- Лесной,
- Лесной Городок,
- Липецк,
- Лобня,
- Лодейное Поле,
- Ломоносов,
- Луховицы,
- Лысьва,
- Лыткарино,
- Люберцы,
- Магадан,
- Магнитогорск,
- Майкоп,
- Махачкала,
- Миасс,
- Можайск,
- Московский,
- Мурманск,
- Муром,
- Мценск,
- Мытищи,
- Набережные Челны,
- Назрань,
- Нальчик,
- Наро-Фоминск,
- Находка,
- Невинномысск,
- Нефтекамск,
- Нефтеюганск,
- Нижневартовск,
- Нижнекамск,
- Нижний Новгород,
- Нижний Тагил,
- Новоалтайск,
- Новокузнецк,
- Новокуйбышевск,
- Новомосковск,
- Новороссийск,
- Новосибирск,
- Новоуральск,
- Новочебоксарск,
- Новошахтинск,
- Новый Уренгой,
- Ногинск,
- Норильск,
- Ноябрьск,
- Нягань,
- Обнинск,
- Одинцово,
- Озерск,
- Озеры,
- Октябрьский,
- Омск,
- Орел,
- Оренбург,
- Орехово-Зуево,
- Орск,
- Павлово,
- Павловский Посад,
- Пенза,
- Первоуральск,
- Пермь,
- Петергоф,
- Петрозаводск,
- Петропавловск-Камчатский,
- Подольск,
- Прокопьевск,
- Псков,
- Пушкин,
- Пушкино,
- Пятигорск,
- Раменское,
- Ревда,
- Реутов,
- Ростов-на-Дону,
- Рубцовск,
- Руза,
- Рыбинск,
- Рязань,
- Салават,
- Салехард,
- Самара,
- Саранск,
- Саратов,
- Саров,
- Севастополь,
- Северодвинск,
- Североморск,
- Северск,
- Сергиев Посад,
- Серпухов,
- Сестрорецк,
- Симферополь,
- Смоленск,
- Сокол,
- Солнечногорск,
- Сосновый Бор,
- Сочи,
- Спасск-Дальний,
- Ставрополь,
- Старый Оскол,
- Стерлитамак,
- Ступино,
- Сургут,
- Сызрань,
- Сыктывкар,
- Таганрог,
- Тамбов,
- Тверь,
- Тихвин,
- Тольятти,
- Томск,
- Туапсе,
- Тула,
- Тюмень,
- Улан-Удэ,
- Ульяновск,
- Уссурийск,
- Усть-Илимск,
- Уфа,
- Феодосия,
- Фрязино,
- Хабаровск,
- Ханты-Мансийск,
- Химки,
- Чебоксары,
- Челябинск,
- Череповец,
- Черкесск,
- Чехов,
- Чита,
- Шахты,
- Щелково,
- Электросталь,
- Элиста,
- Энгельс,
- Южно-Сахалинск,
- Якутск,
- Ялта,
- Ярославль
- Оценки
- Все
- Сортировка
- по дате,
- по рейтингу рецензии
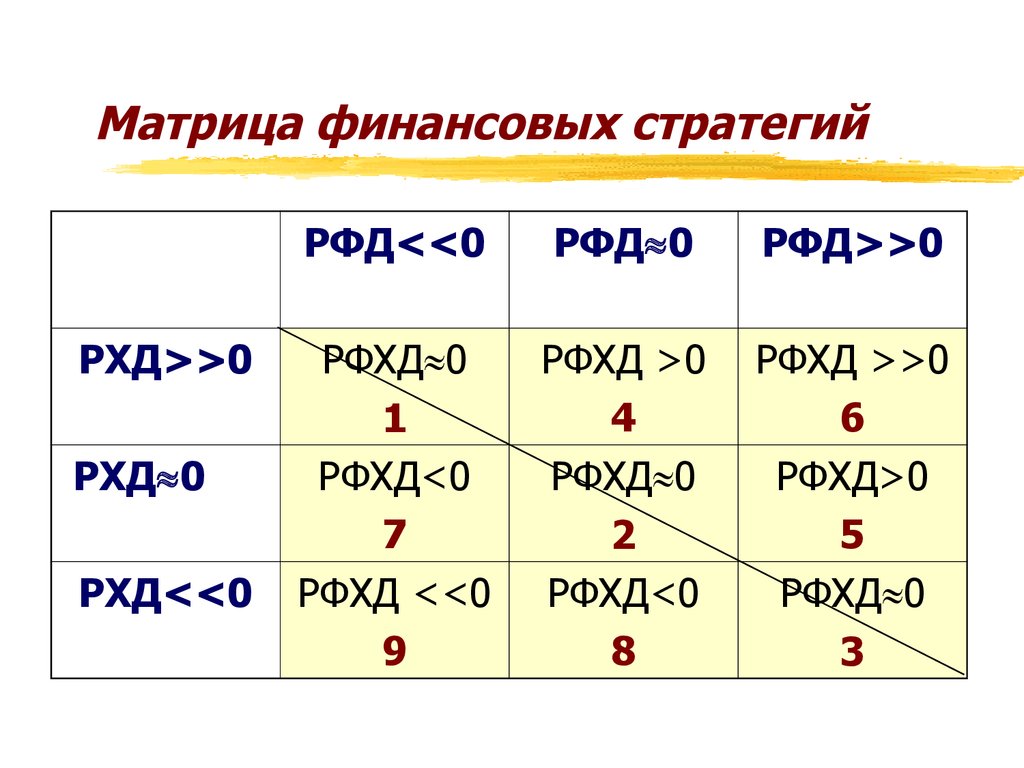
Матрица отрицательно — Энциклопедия по экономике
Из модели диверсификации следует, что эффективность функционирования стабилизируется, когда использование продукта разбросано во времени и пространстве, в особенности когда изменения в эффективности каждого отрицательно коррелируют между собой или друг от друга. В матрице рост — доля рынка рующий эффект ожидается от продукта группы корова , однако существует возможность, что каждый про-
[c.135]
В матрице рост — доля рынка рующий эффект ожидается от продукта группы корова , однако существует возможность, что каждый про-
[c.135] Чтобы квалифицированно ответить на этот вопрос, необходимо провести системный сравнительный анализ, выявить положительные и отрицательные моменты, а затем уже решать, в каком направлении вести поиски. В этой связи особую ценность представляют разработка модели федерального экономического пространства в системе товарно-денежных отношений и матрицы видов системно-экономической деятельности на федеральном, региональном и местном уровнях управления теоретическое осмысление технологии перехода к многоуровневой системе образования, оценка проводимых экспериментов и критический анализ происходящих революционных процессов в высшей школе. [c.70]
 Во-первых, они неотрицательны, т. е.
[c.136]
Во-первых, они неотрицательны, т. е.
[c.136] Выбору оптимального варианта методом итераций помогает составление положительно-отрицательной матрицы. В этом диалектическом сочетании противоположностей выражается как бы сама суть отбора оптимального решения. Набору всего положительного в избираемом варианте решения противопоставляется все отрицательное, могущее затруднить реализацию идеи и внедрение ее в практику. Теоретический анализ, доведенный до наивысшей степени объективности, позволяет выбрать действительно оптимальное решение. [c.218] В формализованном виде отрицательный ответ о продолжении процедуры преобразования матрицы в формализованном виде выглядит так [c.50]
Решение подобных задач требует определенности в формулировании их условий установления количества игроков и правил игры, выявления возможных стратегий игроков, возможных выигрышей (отрицательный выигрыш понимается как проигрыш). Важным элементом в условии задач является стратегия, т. е. совокупность правил, которые в зависимости от ситуации в игре определяют однозначный выбор данного игрока. Количество стратегий у каждого игрока может быть конечным и бесконечным, отсюда и игры подразделяются на конечные и бесконечные. При исследовании конечной игры задаются матрицы выигрышей, а бесконечной — функции выигрышей. Для решения задач применяются алгебраические методы, основанные на системе линейных уравнений и неравенств, итерационные методы, а также сведение задачи к некоторой системе дифференциальных уравнений.
[c.51]
Количество стратегий у каждого игрока может быть конечным и бесконечным, отсюда и игры подразделяются на конечные и бесконечные. При исследовании конечной игры задаются матрицы выигрышей, а бесконечной — функции выигрышей. Для решения задач применяются алгебраические методы, основанные на системе линейных уравнений и неравенств, итерационные методы, а также сведение задачи к некоторой системе дифференциальных уравнений.
[c.51]
Если матрица (10.12) имеет как положительные, так и отрицательные собственные значения, то вопрос не решается столь однозначно. Возможно, в этом случае имеет смысл предпочесть короткую модель (10.2), если след матрицы (10.12) положителен. [c.246]
В основе Бостонской матрицы, или матрицы роста/доли рынка лежит модель жизненного цикла товара, в соответствии с которой товар в своем развитии проходит четыре стадии выход на рынок (товар- проблема ), рост (товар- звезда ), зрелость (товар— дойная корова ) и спад (товар- собака>>). При этом денежные потоки и прибыль предприятия также меняются отрицательная прибыль сменяется ее ростом и затем постепенным снижением.
На этот раз в четвертой ячейке столбца ответов мы получили отрицательный результат. Это означает, что нам следует инвестировать отрицательную сумму в размере 9,81% капитала в сберегательный счет. Чтобы решить проблему отрицательного X (т.е. когда значение на пересечении строки i и крайнего правого столбца меньшее или равно нулю), мы должны удалить из первоначальной расширенной матрицы строку i + 2 и столбец i и решить задачу для новой расширенной матрицы. Если значения последних двух строк крайнего правого столбца меньше или равны нулю, нам не о чем беспокоиться, поскольку они соответствуют множителям Лагранжа и могут принимать отрицательные значения. Так как отрицательное значение переменной соответствует отрицательному весу четвертого компонента, мы удалим из первоначальной расширенной матрицы четвертый столбец и шестую строку.
Как мы уже знаем (см. главу 2), добавление рыночных систем увеличивает среднее геометрическое по портфелю в целом. Однако возникает проблема каждая следующая рыночная система вносит все меньший и меньший вклад в среднее геометрическое и все больше ухудшает его, понижая эффективность из-за одновременных, а не последовательных результатов. Поэтому не следует торговать слишком большим числом рыночных систем. Более того, реальное применение теоретически оптимальных портфелей осложняется из-за залоговых требований. Другими словами, вам лучше торговать 3 рыночными системами при полном оптимальном f, чем 300 рыночными системами при значительно пониженных уровнях, согласно уравнению (8.08). Скорее всего вы придете к выводу, что оптимальное число рыночных систем для торговли должно быть невелико. Особенно это обстоятельство важно, когда у вас много ордеров к исполнению и увеличивается вероятность ошибок.

 Альтернативное решение состоит в введении дополнительных ограничений в матрице портфеля (например, для каждой рыночной системы можно ограничить максимальные веса единицей и ввести дополнительные ограничения по залоговым средствам). Подобные дополнительные ограничения
[c.241]
Альтернативное решение состоит в введении дополнительных ограничений в матрице портфеля (например, для каждой рыночной системы можно ограничить максимальные веса единицей и ввести дополнительные ограничения по залоговым средствам). Подобные дополнительные ограничения
[c.241]Теперь, соединяя вместе анализ матрицы весов, учет положительных и отрицательных влияний и выходных значений кластеров, мы в состоянии оценить значимость вклада каждой из переменных. Б случае, если разные подходы приведут к разным выводам, следует, скорее, доверять результатам кластерного анализа в силу его многомерной природы. [c.110]
Очевидно, следует переместиться по стороне АВ как можно дальше от точки А, чтобы как можно больше уменьшить целевую функцию. Стало быть, можно взять в качестве координаты х, точки В ее максимальное возможное значение, допускаемое системой уравнений (3.5), соответствующей матрице (3.15), т.е. такое, при котором ни одна из переменных не становится отрицательной.
[c. 70]
70]
Внутренние источники — это люди, работаю-щие в организации. В ряде стран, например Японии, при появлении вакансий в аппарате управления принято вначале объявлять внутренний конкурс на замещение должности из числа своих сотрудников и только затем, в случае отрицательных результатов, приглашать к участию в конкурсе специалистов со стороны. Считается, что это улучшает моральный климат в коллективе, укрепляет веру сотрудников в свою организацию. При работе с резервом во всех крупных фирмах существуют так называемые матрицы перемещений, в которых находит отражение настоящее положение каждого руководителя, его возможные перемещения и степень готовности к занятию следующей должности (гостов занять немедленно через год, через два года, но для этого необходимо повышение квалификации в определенных областях и т. д.)1. [c.222]
Кроме того, для отображения отрицательных значений изменения объема продаж используется более сложная форма рассмотренной матрицы (рис. 2.4). [c.38]
Поясните содержание, положительные и отрицательные стороны таких методов анализа продуктового портфеля, как матрица Бостонской консультационной группы и матрица корпорации Дженерал Электрик .
О — безразличный выбор. Результаты опроса заносятся в групповую матрицу (табл. 7.2), которая позволяет наглядно представить первичную информацию и упростить математическую обработку собранных данных. Социометрическая матрица представляет собой таблицу, в которой по строкам помещены ответы каждого нз опрошенных членов группы (по дихотомическому критерию) + означает предпочтение (положительный выбор), — — отвергается (отрицательный выбор), О — фиксирует отсутствие выбора. [c.222]
Предполагается, что F x) является дважды непрерывно дифференцируемой и неоклассической, кроме того, ее матрица вторых производных отрицательно определена. [c.227]
Однако наличие второго слагаемого позволяет в ряде случаев добиться отрицательной определенности матрицы Г. Для этого диагональные элементы должны быть отрицательны и достаточно велики по модулю. Второе слагаемое в диагональных элементах имеет вид [c.348]
После того, как выбран вектор Xk, удовлетворяющий уравнению (9. 137) и обеспечивающий отрицательную определенность матрицы Г, решение задачи (9.121) позволяет найти вектор xok = а (Л/с), а по нему ok = f(xok). Условия для пересчета коэффициентов аппроксимации /оа запишутся в виде
[c.361]
137) и обеспечивающий отрицательную определенность матрицы Г, решение задачи (9.121) позволяет найти вектор xok = а (Л/с), а по нему ok = f(xok). Условия для пересчета коэффициентов аппроксимации /оа запишутся в виде
[c.361]
Если исходная задача является задачей максимизации, то все элементы матрицы стоимостей следует умножить на (-1) и сложить их с достаточно большим числом так, чтобы матрица не содержала бы отрицательных элементов. Затем задачу следует решать как задачу минимизации. [c.504]
Аналогичное утверждение можно сформулировать и доказать для отрицательно (полу)определенных матриц заменой А на —А. (Примеч. пер.) [c.36]
Прежде чем переходить к проблемам планирования па основе межотраслевых балансов, необходимо выяснить, существует ли обратная матрица, используемая в формуле (2.4), а такж е не получим ли мы отрицательные значения валовых выпусков отраслей. [c.264]
Проверим целесообразность размещения грузов в клетках, в которых находятся вершины углов. Очевидно, более целесообразно переместить по 14 т груза (наименьшее значение груза в отрицательных клетках) из клетки Ь2а в клетку Ьгат, из клетки 65яз в клетку Ь5а2, из клетки 63а2 — в клетку Ьт,а. После перемещения матрица примет вид (матрица 7). Матрицу 7 постройте самостоятельно. Целевая функция, как это следует из матрицы 7, привела к последующему сокращению грузооборота (его величину определите самостоятельно).
[c.49]
Очевидно, более целесообразно переместить по 14 т груза (наименьшее значение груза в отрицательных клетках) из клетки Ь2а в клетку Ьгат, из клетки 65яз в клетку Ь5а2, из клетки 63а2 — в клетку Ьт,а. После перемещения матрица примет вид (матрица 7). Матрицу 7 постройте самостоятельно. Целевая функция, как это следует из матрицы 7, привела к последующему сокращению грузооборота (его величину определите самостоятельно).
[c.49]
Один инструмент-матрица «Assessing Opportunities for Innovation», рассматривающая связанные риски под шестью заголовками (привлекательность рынка, деловая синергия, осуществимость идеи, требования к ресурсам, прибыль пользователя и защита идеи), привлекла наибольшее внимание. Путем последовательного перебора множества из двадцати шести положительных и отрицательных индикаторов пользователи могут выбрать идею, наиболее соответствующую их ситуации. Данная матрица может использоваться для проведения скрининга нескольких перспективных идей, однако наиболее эффективно использовать ее для выявления факторов риска, связанных с воплощением выбранной идеи. Это весьма важный момент. Несмотря на то что факт отказа от идеи -явление достаточно неприятное, фирмам следует знать заранее риски, которые их ожидают в случае обращения к той или другой идее Матрица помогает выбирать среднее между риском и потенциальным выигрышем.
[c.25]
Это весьма важный момент. Несмотря на то что факт отказа от идеи -явление достаточно неприятное, фирмам следует знать заранее риски, которые их ожидают в случае обращения к той или другой идее Матрица помогает выбирать среднее между риском и потенциальным выигрышем.
[c.25]
Далее обозначим рассматриваемую многотранспортную сеть как сеть G, матрицу соответствующей системы — как матрицу G. В системе уравнений (11 ) заменим все отрицательные коэффициенты их модулями. Получим систему уравнений, отображающую сеть Кенига. Назовем ее сетью G, а ее матрицу— матрицей G. Такое обозначение сетей и матриц не вызовет путаницы, так как из текста всегда будет ясно, что имеется в виду. Подчеркнем, что если некоторый. элемент g v матрицы G равен нулю, то соответствующий ему элемент ёцм матрицы G также равен нулю, а если элемент g матрицы G отличен от нуля,- то и соответствующий ему элемент g v матрицы G также отличен от нуля. [c.150]
Когда вы удаляете строки и столбцы, важно помнить, какие строки каким переменным соответствуют, особенно когда таких строк и столбцов несколько. Допустим, нам надо найти веса в портфеле при Е = 0,1965. Единичная матрица, которую мы сначала получим, будет содержать отрицательные значения для весов Toxi o (Xi) и сберегательного счета (ХД Поэтому вернемся к нашей первоначальной расширенной матрице [c.199]
Допустим, нам надо найти веса в портфеле при Е = 0,1965. Единичная матрица, которую мы сначала получим, будет содержать отрицательные значения для весов Toxi o (Xi) и сберегательного счета (ХД Поэтому вернемся к нашей первоначальной расширенной матрице [c.199]
Оказывается, что ответ на него в общем случае отрицательный. Имеются такие наборы образов, что какую бы матрицу синаптических связей и пороги нейронов, гарантирующие их стационарность, мы не выбрали, в сети с неизбежностью возникнут иные аттракторы. [c.100]
В столбце, обозначенном HIT/MISS, приведены отклонения от целевого значения того прогноза, который 6-3-1 сеть сделала по исходной входной матрице. Погрешность всюду была промасштабирова-на так, чтобы значения располагались от -100 до 100, при этом положительный знак соответствует превышению цели, а отрицательный — недобору. Малые по абсолютной величине числа означают точный прогноз (например, апрель 1984), а большие — значительную ошибку (август 1984). Если абсолютная величина ошибки велика, скажем, больше 40, то в этом случае определить вклад отдельной переменной затруднительно. Следующие 6 столбцов таблицы содержат отклонения выхода сети от целевого значения, соответствующие шести описанным выше входным матрицам. Здесь погрешности также промасштабированы и лежат от -100 до 100. По этим данным
[c.146]
Следующие 6 столбцов таблицы содержат отклонения выхода сети от целевого значения, соответствующие шести описанным выше входным матрицам. Здесь погрешности также промасштабированы и лежат от -100 до 100. По этим данным
[c.146]
По мнению Бостонской консультативной группы, от того, в какой ячейке матрицы расположен товар, зависит показатель движения наличности. Обратите внимание на то, что движение наличности ( ash flow) — не одно и то же, что прибыльность (profitability). Прибыли увеличивают движение наличности, но значительные инвестиции в развитие производства, оборудование и маркетинг нередко приводят к тому, что компания может одновременно иметь прибыль и отрицательный показатель движения наличности. [c.230]
Первое уравнение (4.17) показывает, как изменится выпуск при увеличении цены на продукцию фирмы. Поскольку матрица Гесса Н отрицательно определена, то и матрица Н»1 также отрицательно определена, поэтому [c.234]
Определитель этой матрицы называется гессианом. Характеристика Г.м. (ее отрицательная или положительная определенность и полуопределенность) служит условием для определения вида стационарной точки является ли она соответственно максимумом, минимумом или седловой точкой в задаче оптимизации функции.
[c.60]
Характеристика Г.м. (ее отрицательная или положительная определенность и полуопределенность) служит условием для определения вида стационарной точки является ли она соответственно максимумом, минимумом или седловой точкой в задаче оптимизации функции.
[c.60]
Кроме того, матрица Гессе вторых производных этой функции по С должна быть при С = 0 отрицательно определенной. [c.342]
Чтобы функция FQ( ) была выпукла, достаточно, чтобы матрица Т = Tij была отрицательно определенной. Первые слагаемые в (9.108) отличаются от элементов 7 j матрицы Гессе исходной задачи неотрицательным множителем, так как функция FQ монотонно возрастающая. Если вторые слагаемые в этих выражениях равны нулю, то вогнутой функции достижимости исходной задачи будет соответствовать вогнутость и FQ( ). [c.348]
Первое из них представляет собой п уравнений относительно составляющих вектора А, а второе — условие отрицательной определенности квадратичной формы, которое проверяется по критерию Сильвестра применительно к матрице Гессе функции R . [c.357]
[c.357]
Здесь и ниже через R f0 и R i обозначены частные производные R по соответствующим переменным. Условиям отрицательной определенности должна удовлетворять матрица Гессе функции R с элементами (см. (9.125)) [c.360]
Желательно, чтобы эти условия выполнялись для всех С а не только для С = 0. Из условий Гершгорина отрицательной определенности матрицы Г [c.361]
Если прибыль рассматривать как отрицательные затраты, то исходная задача максимизации может быть сведена к минимизационной задаче о назначениях. Для того чтобы матрица стоимостей не содержала отрицательных элементов, сложим каждый элемент матрицы с числом 5760 и введем два вида фиктивной продукции (4 и 5), которой соответствует нулевая прибыль. В результате будут получены следующие матрицы [c.508]
Очевидно, что матрицы В В и В В являются неотрицательно определенными /Б, а А — отрицательно (неположительно) определенная матрица тогда и только тогда, когда —А — положительно (полу) определенная матрица. Квадратная нулевая матрица является одновременно неположительно и неотрицательно определенной.
[c.27]
Квадратная нулевая матрица является одновременно неположительно и неотрицательно определенной.
[c.27]
Если матрица Гессе Н0(с) не является ни положительно, ни отрицательно определенной, но тем не менее не вырождена, то точка с не может быть точкой локального экстремума (см. теорему 2). Значит, точка с — седловая. [c.169]
[Машинное обучение] [EM Algorithm — 1] Математическое основание: положительная / отрицательная матрица + вогнутая (выпуклая) Функция + (максимальная) Функция вероятности + гессенская матрица + неравенство Дженсен.
Алгоритм Е.М.
EM (алгоритм максимизации расходов), для максимального алгоритма значения, эти математические знания используются:
(1) положительная / отрицательная матрица
(2) [строгое] вогнутая функция
(3) [строгое] выпуклая функция
(4) [максимальная] функция вероятности
(5) Гессенская матрица
(6) Дженсен Неравенство
Положительная определенная матрица, правильная матрица;
Отрицательная определенная матрица, нагрузка матрицы
Свойства положительных матриц:
(1) A — матрица положительной точки зрения, то | A | слой> 0, строка правильной матрицы постоянна
(2) обратная матрица правильной матрицы A также является правильной матрицей
(3) Если A, B является правильной матрицей, то A + B также является правильной матрицей.
(4) продукт положительного реального числа и правильная матрица является правильной матрицей
(5) Действительно симметричная матрица A является правильным, и только тогда, когда A и Unit Matrix Contract
В зависимости от определения и характера правильной матрицы существует два метода определения нормализации симметричной матрицы A:
(1) Как найти все характеристики A.
Положительная настройка: если характерное значение a положительно, то a является правильным;
Отрицательный: если характерное значение a отрицательно, a фиксируется.
(2) Рассчитать основные формулы подразделения А.
Положительный: если основные формулы a больше нуля, то a является правильным;
Отрицательный: если основная формула A, основная формула нечетной нумерации отрицательная, четное число положительное, то A фиксируется.
Если функция f (x) удовлетворяет следующие условия, f (x) — это вогнутая функция:
Если вы удалите =, если вы удалите его, только <, то f (x) — строгая вогнутая функция.
Если функция f (x) удовлетворяет следующие условия, F (X) является выпуклой функцией:
Если вы удалите =, только>, то f (x) является строгой выпуклой функцией.
Например, следующие функции являются вогнутой функцией:
Руководство второго порядка определяется, что вогнутая функция все еще строго вогнутая функция:
Если f (производное второго порядка x выше> = 0, f (x) — вогнутая функция
Если f (x) производного второго порядка устанавливается в диапазоне> 0, f (x) — строгая вогнутая функция,
Графика на левой стороне показана ниже, являются строгими вогнутыми функциями, а правая сторона является строгой выпуклой функцией:
В статистике функция вероятности является функцией по параметрам статистической модели.
Когда данный выход X, функция вероятности L (θ | x) (θ | x) (θ | x) параметра θ равна вероятности переменной x после данного параметра θ точка: l (θ | x ) = p (x = x | θ)
Это можно увидеть:Функция вероятности является функцией условной вероятности
Один пример ниже отДругие статьичасть:
Рассмотреть вопрос о монете эксперимент. Как правило, вероятность того, что монета на передней части монеты, а обратный вид соответствует.pH = 0.5Если вы можете знать возможность бросать несколько результатов через несколько раз. Например, вероятность того, чтобы быть положительным спереди составляет 0,25. Условная вероятность представлена:
Как правило, вероятность того, что монета на передней части монеты, а обратный вид соответствует.pH = 0.5Если вы можете знать возможность бросать несколько результатов через несколько раз. Например, вероятность того, чтобы быть положительным спереди составляет 0,25. Условная вероятность представлена:
вHУказывает на переднее лицо вверх.
С точки зрения статистики мы заботимся о возможности положительных фасилитаторов лица для лица, когда бросание монеты известно в результатах ряд бросков. Мы можем построить статистическую модель: предположим, что монета будет иметьpHВероятность обращена вверх, и есть1 − pHВероятность обратной поверхности обращена вверх. В это время условная вероятность может быть переписана на функцию вероятности:
То есть для функции вероятности, при наблюдении на двух бросках сталкивается,pH = 0.5 изВероятностьЭто 0,25 (это не значит, что при наблюдении двух передних лицpH = 0.5 изВероятностьЭто 0,25).
Если вы рассмотритеpH = 0.6Таким образом, стоимость функции вероятности также изменится.
Обратите внимание, что значение функции вероятности велика. Это показывает, если параметрpHЕсли значение превращается 0,6, результаты наблюдали, что вероятность непрерывного переднего лица является больше, чем гипотеза.pH = 0.5Когда вы. То есть параметрыpHПолученный в результате 0,6 более убедительно, чем в результате 0,5, более «разумных». Таким образом, важность функции вероятности не является конкретным значением, но функция не велика, когда параметры меняются. Для той же функции вероятности, если существует значение параметра, это самое «разумное» значение параметра, если есть значение параметра.。
использованная литература:
[1]https://baike.baidu.com/item/%E6%AD%A3%E5%AE%9A%E7%9F%A9%E9%98%B5/11030459?fr=aladdin
[2]http://jacoxu.com/jacobian%E7%9F%A9%E9%98%B5%E5%92%8Chessian%E7%9F%A9%E9%98%B5/
(end)
описание, особенности, принципы работы с ней OTUS
В математике существует немалое количество важных элементов и значений для проведения расчетов. Некоторые из них изучаются в школах, а какие-то – в ВУЗах. Немаловажной составляющей является матрица.
Некоторые из них изучаются в школах, а какие-то – в ВУЗах. Немаловажной составляющей является матрица.
Далее речь зайдет об этой математической единице – что она собой представляет, для чего необходима, какие действия с ней выполняются.
Что это
Матрица представляет собой прямоугольную таблицу элементов. Это – своеобразная таблица чисел.
Некий математический объект, который записывается в виде прямоугольной таблице элементов кольца или поля. Он представлен совокупностью строк и столбцов, на пересечении которых располагаются числа. Последний – его компоненты.
Размер матрицы определяется количеством строк и столбцов. Исторически существуют разнообразные «предметы» данного типа. Пример — треугольные. Сейчас каждым математиком изучаются понятия квадратной матрицы и прямоугольной.
Возможные действия
С рассматриваемыми объектами можно выполнять различные действия:
- сложение;
- вычитание;
- умножение числа на заданную матрицу;
- нахождение определителя;
- комплексное сопряжение.

Далее поможем разобраться со всеми этими алгебраическими манипуляциями с наглядными примерами. Предложенная информация пригодится не только математикам, но и программистам.
Сложение
Складывать можно только матрицы, которые содержат в своем составе одинаковое количество чисел. Результатом будет служить объект такого же размера.
Чтобы провести операцию, требуется просто сложить их соответствующие компоненты. Пример приведен ниже.
Здесь манипуляции проделывались через матрицы a и b размером два на два. Сложение происходит и относительно положительных чисел, и относительно отрицательных.
Вычитание
При решении задач по математике, связанных с рассматриваемой темой, важно помнить об элементарных действиях. Вычитание производится по тем же принципам, что и сложение. На выходе получается матрица аналогичного размера.
Умножение на число
Любую матрицу допустимо умножить на произвольное число. Для этого предстоит:
- умножить каждый элемент оной на заданное число;
- произвести запись объекта с новыми данными.

Выше представлен пример умножения числа на заданную матрицу.
Между собой
Также в математике можно перемножать между собой рассматриваемые объекты. Но умножение матриц друг с другом представляется возможным не всегда.
Такая операция допускается, если число столбцов в объекте A равно числу строк объекта B. Каждый элемент, получившийся в i-ой строке и j-м столбце – это сумма произведений соответствующих компонентов в i-й строчке первого множителя и j-м столбце второго.
Все это – примеры того, как математик умножает рассматриваемые объекты между собой. Первый случай – теоретическая запись, второй – наглядное решение.
Транспонирование
Умножение числа на заданную матрицу – это не трудно. Но есть еще транспонирование. Так называют операцию, когда строки и столбцы меняются местами.
Выше – запись транспортированного объекта.
Определитель
Как осуществлять сложение двух матриц, а также их умножение, понятно. Достаточно помнить базовые алгебраические правила. Но рассматриваемый компонент может иметь определитель. Его также называют детерминантом. Встречается в линейной алгебре.
Но рассматриваемый компонент может иметь определитель. Его также называют детерминантом. Встречается в линейной алгебре.
Определитель – численная характеристика квадратной матрицы. Она необходима для решения большого количества задач.
Для поиска определителя требуется вычислить разность произведений элементов главной и побочной диагоналей.
Определитель матрицы первого порядка (состоящей из одного компонента) – это то самое число, что в ней содержится. Если объект размером 3×3, справиться будет сложнее.
Для проведения расчетов необходимо запомнить, что:
- Значение определителя будет равно сумме произведений главной диагонали и произведений элементов, лежащих на треугольниках с гранью параллельной главной диагонали.
- От последней нужно вычесть произведение элементов побочной диагонали и произведение составляющих, лежащих на треугольниках с гранью параллельной побочной диагонали.
- На практике определители крупных матриц необходимо в исключительных случаях.

Выше представлен пример нахождения детерминанта в квадратном объекте 2×2.
Обратные «модели»
Обратная матрица тоже встречается при решении задач. Вырожденная «модель» — это квадратный объект строк и столбцов n-го порядка, когда определитель равен нулю. Невырожденная – когда не равен ему соответственно.
Матрица A-1 – обратная, если для нее актуально соотношение типа: A x A-1=A-1 x A = E.
Если A-1 не вырождена, то существует всего одна обратная матрица A-1. Она будет равна значению:
А вот несколько наглядных примеров:
Как найти
Для того, чтобы определить A-1, необходимо:
- Найти детерминант A.
- Проверить, чтобы он не был равен нулю.
- Найти миноры матрицы – Mij.
- Определить Aij= (-1)i+jMij.
- Построить матрицу алгебраических дополнений:
- Поделить каждое из слагаемых (каждый элемент матрицы) объекта на детерминант A.

Умножение числа на матрицу, как и другие операции – это не так трудно. Зная соответствующую базу, человек сможет производить вручную или через специальные калькуляторы необходимые подсчеты. А некоторые видео уроки объяснят теорию простым языком.
Как лучше разобраться в теме
Для того, чтобы лучше понимать рассматриваемую тему, можно отправиться на специализированные IT-курсы. Там помогут:
- получить практику;
- освоить разнообразные направления математики и информационных технологий;
- обзавестись новыми полезными знакомствами;
- заниматься максимально комфортно – в удобное время, через интернет.
В конце обучения выдается сертификат, подтверждающий знания в выбранном направлении. Предложения есть как для новичков, так и для продвинутых математиков/разработчиков/системных администраторов.
Хотите освоить современную IT-специальность? Огромный выбор курсов по востребованным IT-направлениям есть в Otus!
Также, возможно, вам будет интересен следующий курс:
Как читать корреляционную матрицу
В статистике нас часто интересует понимание взаимосвязи между двумя переменными.
Например, мы можем захотеть понять взаимосвязь между количеством часов, отработанных студентом, и полученными им экзаменационными баллами.
Одним из способов количественной оценки этой взаимосвязи является использование коэффициента корреляции Пирсона , который является мерой линейной связи между двумя переменными . Он имеет значение от -1 до 1, где:
- -1 указывает на совершенно отрицательную линейную корреляцию между двумя переменными
- 0 указывает на отсутствие линейной корреляции между двумя переменными
- 1 указывает на совершенно положительную линейную корреляцию между двумя переменными.
Чем дальше коэффициент корреляции от нуля, тем сильнее связь между двумя переменными.
По теме: Что считается «сильной» корреляцией?
Но в некоторых случаях мы хотим понять корреляцию между более чем одной парой переменных. В этих случаях мы можем создать матрицу корреляции , представляющую собой квадратную таблицу, которая показывает коэффициенты корреляции между несколькими переменными.
В приведенной ниже матрице корреляции показаны коэффициенты корреляции между несколькими переменными, связанными с образованием:
Каждая ячейка в таблице показывает корреляцию между двумя конкретными переменными. Например, выделенная ячейка ниже показывает, что корреляция между «часами, потраченными на учебу» и «оценкой за экзамен» составляет 0,82 , что указывает на сильную положительную корреляцию. Больше часов, потраченных на учебу, тесно связано с более высокими баллами на экзаменах.
А выделенная ячейка ниже показывает, что корреляция между «часами, потраченными на учебу» и «часами, потраченными на сон» составляет -0,22 , что указывает на слабую отрицательную корреляцию. Больше часов, потраченных на учебу, связано с меньшим количеством часов, потраченных на сон.
А выделенная ячейка ниже показывает, что корреляция между «количеством часов, проведенных во сне» и «показателем IQ» составляет 0,06 , что указывает на то, что они в основном не связаны. Существует очень небольшая связь между количеством часов, которые студент спит, и его показателем IQ.
Существует очень небольшая связь между количеством часов, которые студент спит, и его показателем IQ.
Также обратите внимание, что все коэффициенты корреляции по диагонали таблицы равны 1, потому что каждая переменная полностью коррелирует сама с собой. Эти ячейки бесполезны для интерпретации.
Вариации корреляционной матрицыОбратите внимание, что корреляционная матрица совершенно симметрична. Например, верхняя правая ячейка показывает то же значение, что и нижняя левая ячейка:
Это связано с тем, что обе ячейки измеряют корреляцию между «часами, потраченными на учебу» и «рейтингом школы».
Поскольку матрица корреляции симметрична, половина коэффициентов корреляции, показанных в матрице, являются избыточными и ненужными. Таким образом, иногда будет отображаться только половина корреляционной матрицы:
А иногда матрица корреляции раскрашивается, как тепловая карта, чтобы коэффициенты корреляции было еще легче читать:
Когда использовать корреляционную матрицуНа практике корреляционная матрица обычно используется по трем причинам:
1. Корреляционная матрица удобно обобщает набор данных.
Корреляционная матрица удобно обобщает набор данных.
Матрица корреляции — это простой способ суммировать корреляции между всеми переменными в наборе данных. Например, предположим, что у нас есть следующий набор данных, который содержит следующую информацию для 1000 учащихся:
Было бы очень сложно понять взаимосвязь между каждой переменной, просто глядя на необработанные данные. К счастью, корреляционная матрица может помочь нам быстро понять корреляции между каждой парой переменных.
2. Корреляционная матрица служит диагностикой регрессии.
Одним из ключевых допущений множественной линейной регрессии является то, что ни одна независимая переменная в модели не имеет сильной корреляции с другой переменной в модели.
Когда две независимые переменные сильно коррелированы, это приводит к проблеме, известной как мультиколлинеарность , и может затруднить интерпретацию результатов регрессии.
Один из самых простых способов обнаружить потенциальную проблему мультиколлинеарности — посмотреть на матрицу корреляции и визуально проверить, сильно ли коррелируют какие-либо переменные друг с другом.
3. Корреляционная матрица может использоваться в качестве исходных данных для других анализов.
Корреляционная матрица используется в качестве исходных данных для других сложных анализов, таких как исследовательский факторный анализ и модели структурных уравнений.
Дополнительные ресурсыВ следующих руководствах объясняется, как создать корреляционную матрицу с помощью различных статистических программ:
Как создать корреляционную матрицу в Excel
Как создать корреляционную матрицу в SPSS
Как создать корреляционную матрицу в Stata
Как создать корреляционную матрицу в Python
Как создать корреляционную матрицу в Matlab
Матрица корреляции в Excel — voxt.ru
Матрица корреляции Excel
Корреляционная матрица в Excel — это способ обобщения данных корреляции, показывающих взаимосвязь между двумя переменными, и каждая таблица в матрице корреляции показывает нам взаимосвязь между двумя переменными, чтобы создать матрицу корреляции, мы можем сделать это из вкладки анализа данных и из раздела корреляции.
Объяснение
Матрица — это набор чисел, упорядоченных по строкам и столбцам в структурированном формате. Корреляция — это поиск или измерение зависимости или отношений между переменными. Он показывает, как одна переменная зависит от другой, а влияние роста или снижения одной переменной влияет на другую. Для измерения корреляции также можно использовать более двух переменных, и это называется корреляцией нескольких переменных. Результирующие коэффициенты могут быть положительными, отрицательными или нулевыми, т. Е. -1, +1 или 0.
- Положительная корреляция — это та, где результирующий коэффициент равен +1, что означает, что обе переменные движутся в одном направлении.
- Отрицательная корреляция — это та, при которой результирующий коэффициент равен -1, что означает, что переменные имеют тенденцию двигаться в противоположных направлениях.
- Нулевая корреляция — это когда результирующий коэффициент равен 0, а переменные не зависят друг от друга.

Давайте посмотрим на несколько примеров, чтобы понять, как создать корреляционную матрицу в Excel.
Вы можете скачать этот шаблон Excel матрицы корреляции здесь — Шаблон Excel матрицы корреляции
Пример # 1
Теперь давайте посмотрим, как найти корреляционную матрицу в Excel с помощью пакета Analysis Toolpak в Excel.
Пакет Analysis Toolpak — это опция надстройки, доступная в Excel на вкладке «ДАННЫЕ» на ленте.
Если этот параметр недоступен, добавьте его из списка надстроек. Добавить,
- Щелкните «Файл» и выберите «Параметры».
- В разделе «Параметры» выберите вкладку «Надстройки», затем нажмите кнопку «Перейти» рядом с раскрывающимся списком в поле «Управление».
- Установите флажок для пакета инструментов анализа и нажмите ОК.
Набор инструментов будет добавлен на вкладку «Данные» в разделе «Анализ» как «Анализ данных».
- Теперь, чтобы создать матрицу корреляции и использовать функцию Excel корреляции, щелкните Анализ данных, выберите Корреляцию во всплывающем окне Инструменты анализа и нажмите ОК.
Появится всплывающее окно с запросом диапазона ввода.
- Выберите диапазон данных переменных в поле диапазона ввода.
- Установите флажок для меток в первой строке (если у вас есть метки переменных в первой строке)
- Выберите параметр «Диапазон вывода» и выберите / введите номер ячейки, в которой вы хотите получить таблицу результатов. Щелкните ОК.
- Это таблица результатов корреляции для переменных A и B.
Пример # 2
Давайте посмотрим на пример корреляционной матрицы в Excel для нескольких переменных.
- Введите данные для нескольких переменных.
- Теперь, чтобы использовать функцию корреляции, щелкните Анализ данных, выберите Корреляцию во всплывающем окне Инструменты анализа и нажмите ОК.

Появится всплывающее окно с запросом диапазона ввода.
- Выберите диапазон данных переменных в поле диапазона ввода.
- Установите флажок для меток в первой строке (если у вас есть метки переменных в первой строке)
- Выберите опцию Output Range и выберите / введите номер ячейки, в которой вы хотите получить таблицу результатов.
- Щелкните ОК.
- В этом примере мы использовали три переменные, чтобы найти корреляционную матрицу. Диапазон (A1: C7) — это данные для переменных, а диапазон (A9: D12) — это таблица результатов для корреляционной матрицы.
Здесь переменные показаны в строках и столбцах. Результат корреляции между переменными должен быть прочитан путем проверки переменной в строке и переменной в столбце, смежном с этой строкой.
Выводы таблицы:
- Результат для переменных A и B равен 0,97, что означает, что они положительно коррелированы.
- Результат для переменных B и C равен -0,6, что означает, что они имеют отрицательную корреляцию.

- Переменные A и C не коррелированы, поэтому результат равен -0,4.
Связь между переменными ясно видна на графике следующим образом.
То, что нужно запомнить- Данные для любого количества переменных могут быть добавлены в существующую таблицу, а диапазон следует скорректировать, чтобы выяснить корреляцию.
- Корреляция показывает причинно-следственную связь между факторами.
- Результаты, близкие к диапазону корреляций, будут определять зависимость / взаимосвязь переменных.
- Коэффициент корреляции рассчитывается с использованием математических расчетов, но он не всегда указывает на наличие связи между переменными в действительности, хотя результат показывает, что она есть.
УЗНАТЬ БОЛЬШЕ >>
Post Views: 3 089
Похожие записи
Прокрутить вверхИзучение частей объектов с помощью неотрицательной матричной факторизации
Реферат
Основано ли восприятие целого на восприятии его частей? Имеются психологические 1 и физиологические 2,3 доказательства существования представлений в мозге, основанных на частях, и некоторые вычислительные теории распознавания объектов опираются на такие представления 4,5 . Но мало что известно о том, как мозг или компьютеры могут запоминать части объектов. Здесь мы демонстрируем алгоритм неотрицательной матричной факторизации, способный запоминать части лиц и семантические особенности текста. Это отличается от других методов, таких как анализ основных компонентов и векторное квантование, которые изучают целостные, а не основанные на частях представления. Неотрицательная матричная факторизация отличается от других методов использованием ограничений неотрицательности. Эти ограничения приводят к представлению на основе частей, поскольку они допускают только аддитивные, а не вычитательные комбинации. Когда неотрицательная матричная факторизация реализуется в виде нейронной сети, представления на основе частей возникают благодаря двум свойствам: частота срабатывания нейронов никогда не бывает отрицательной, а сила синапсов не меняет знак.
Но мало что известно о том, как мозг или компьютеры могут запоминать части объектов. Здесь мы демонстрируем алгоритм неотрицательной матричной факторизации, способный запоминать части лиц и семантические особенности текста. Это отличается от других методов, таких как анализ основных компонентов и векторное квантование, которые изучают целостные, а не основанные на частях представления. Неотрицательная матричная факторизация отличается от других методов использованием ограничений неотрицательности. Эти ограничения приводят к представлению на основе частей, поскольку они допускают только аддитивные, а не вычитательные комбинации. Когда неотрицательная матричная факторизация реализуется в виде нейронной сети, представления на основе частей возникают благодаря двум свойствам: частота срабатывания нейронов никогда не бывает отрицательной, а сила синапсов не меняет знак.
Это предварительный просмотр содержимого подписки, доступ через ваше учреждение
Соответствующие статьи
Статьи открытого доступа со ссылками на эту статью.
Алгоритм улучшения речи на основе неотрицательной скрытой марковской модели и дивергенции Кульбака-Лейблера
- Ян Сян
- , Лимин Ши
- … Мадс Гросбёлл Кристенсен
Журнал EURASIP по обработке аудио, речи и музыки Открытый доступ 08 сентября 2022 г.
Возрастные различия в симметрии походки, полученные из кинематической синергии и мышечной синергии нижних конечностей в детстве
- Цилян Сюн
- , Цзиньлян Ван
- … Юань Лю
Биомедицинская инженерия онлайн Открытый доступ 04 сентября 2022 г.

Эффективное тактильное кодирование проскальзывания объекта
- Лоуренс Виллемет
- , Николя Юлу
- и Михаэль Виртлевски
Научные отчеты Открытый доступ 01 августа 2022 г.
Варианты доступа
Подписка на журнал
Получить полный доступ к журналу на 1 год
199,00 €
всего 3,90 € за выпуск
Подписаться
Расчет налогов будет завершен во время оформления заказа.
Купить статью
Получите ограниченный по времени или полный доступ к статье на ReadCube.
32,00 $
Купить
Все цены указаны без учета стоимости.
Рис. 1. Неотрицательная матричная факторизация (NMF) изучает представление лиц на основе частей, тогда как векторное квантование (VQ) и анализ основных компонентов (PCA) изучают целостные представления. Рисунок 2: Итерационный алгоритм факторизации неотрицательной матрицы. Рисунок 3: Вероятностная модель скрытых переменных, лежащая в основе неотрицательной матричной факторизации. Рисунок 4: Неотрицательная матричная факторизация (NMF) обнаруживает семантические признаки m = 30 991 статьи из энциклопедии Grolier.Ссылки
Палмер, С. E. Иерархическая структура перцептивного представления.
 Познан. Психол. 9, 441–474 (1977).
Познан. Психол. 9, 441–474 (1977).Артикул Google ученый
Ваксмут Э., Орам М. В. и Перретт, Д. И. Распознавание объектов и их составных частей: ответы отдельных единиц височной коры макаки. Церебр. Cortex 4 , 509–522 (1994).
КАС пабмед Статья Google ученый
Логотетис, Н. К. и Шейнберг Д. L. Зрительное распознавание объектов. год. Преподобный Нейроски. 19 , 577–621 (1996).
КАС пабмед Статья Google ученый
Бидерман И. Распознавание по компонентам: теория понимания человеческого образа. Психолог. 94 , 115–147 (1987).
ПабМед Статья Google ученый
Ульман С. Зрение высокого уровня: распознавание объектов и зрительное восприятие (MIT Press, Кембридж, Массачусетс, 1996).

МАТЕМАТИКА Книга Google ученый
Турк,М. и Пентланд, А. Собственные лица для распознавания. Дж. Когн. Неврологи. 3 , 71–86 (1991).
КАС пабмед Статья Google ученый
Филд,Д. J. Какова цель сенсорного кодирования? Нейронные вычисления. 6 , 559–601 (1994).
Артикул Google ученый
Фолдиак, П. и Янг, М. Разреженное кодирование в коре приматов. Справочник по теории мозга и нейронным сетям 895–898 (MIT Press, Кембридж, Массачусетс, 1995).
Google ученый
Ольсхаузен, Б. А. и Филд, Д. J. Появление свойств рецептивного поля простых клеток путем изучения разреженного кода для естественных изображений. Природа 381 , 607–609 (1996).

ОБЪЯВЛЕНИЕ КАС пабмед Статья Google ученый
Ли, Д. Д. и Сын, Х. S. Обучение без учителя с помощью выпуклого и конического кодирования. Доп. Нейронная информация. проц. Сист. 9 , 515–521 (1997).
Google ученый
Паатеро, П. Метод наименьших квадратов для надежного неотрицательного факторного анализа. Химометр. Интел. лаборатория 37 , 23–35 (1997).
КАС Статья Google ученый
Накаяма,К. и Симодзё, С. Ощущение и восприятие визуальных поверхностей. Science 257 , 1357–1363 (1992).
ОБЪЯВЛЕНИЕ КАС пабмед Статья Google ученый
Хинтон, Г. Э., Даян П., Фрей Б. Дж. и Нил, Р. М. Алгоритм «бодрствования-сна» для неконтролируемых нейронных сетей.
 Наука 268 , 1158–1161 (1995).
Наука 268 , 1158–1161 (1995).ОБЪЯВЛЕНИЕ КАС пабмед Статья Google ученый
Солтон, Г. и Макгилл, М. J. Введение в современный поиск информации (McGraw-Hill, Нью-Йорк, 1983).
МАТЕМАТИКА Google ученый
Ландауэр, Т. К. и Дюме, С. Т. Теория латентного семантического анализа познания. Псих. Ред. 104 , 211–240 (1997).
Артикул Google ученый
Юттен, К. и Эро, Дж. Слепое разделение источников, часть I: адаптивный алгоритм, основанный на нейромиметической архитектуре. Сигнал Проц. 24 , 1–10 (1991).
МАТЕМАТИКА Статья Google ученый
Белл, А. Дж. и Сейновски, Т. J. Подход к максимизации информации для слепого разделения и слепой деконволюции.
 Нейронные вычисления. 7 , 1129–1159 (1995).
Нейронные вычисления. 7 , 1129–1159 (1995).КАС пабмед Статья Google ученый
Бартлетт, М. С., Ладес, Х. М. и Сейновски, Т. Дж. Представления независимых компонентов для распознавания лиц. Проц. SPIE 3299 , 528–539 (1998).
ОБЪЯВЛЕНИЕ Статья Google ученый
Шепп, Л. А. и Варди, Ю. Реконструкция максимального правдоподобия для эмиссионной томографии. IEEE Trans. Мед. Визуализация. 2 , 113–122 (1982).
Артикул Google ученый
Ричардсон, В. H. Байесовский итерационный метод восстановления изображения. J. Опт. соц. Являюсь. 62 , 55–59 (1972).
ОБЪЯВЛЕНИЕ Статья Google ученый
Люси, Л.
 B. Итеративный метод исправления наблюдаемых распределений. Астрон. J. 74 , 745–754 (1974).
B. Итеративный метод исправления наблюдаемых распределений. Астрон. J. 74 , 745–754 (1974).ОБЪЯВЛЕНИЕ Статья Google ученый
Демпстер, А. П., Лейред, Н. М. и Рубин, Д. Б. Максимальная вероятность из неполных данных с помощью алгоритма EM. Дж. Роял Стат. соц. 39 , 1–38 (1977).
MathSciNet МАТЕМАТИКА Google ученый
Сол, Л. и Перейра, Ф. Материалы второй конференции по эмпирическим методам обработки естественного языка (редакторы Карди, К. и Вайшедель, Р.) 81–89 (Морган Кауфманн, Сан-Франциско, 1997).
Google ученый
Ссылки на скачивание
Благодарности
Мы признательны за поддержку Bell Laboratories и MIT. К. Папагеоргиу и Т. Поджо предоставили нам базу данных лиц, а Р. Спроут — корпус энциклопедии Гролье. Мы благодарим Л. Сола за то, что он убедил нас в преимуществах алгоритмов EM-типа. Нам помогли дискуссии с Б. Андерсоном, К. Кларксоном, Р. Фройндом, Л. Кауфманом, Э. Ритманом, С. Ровейсом, Н. Рубином, Дж. Тененбаумом, Н. Тишби, М. Цодыксом, Т. Тайсоном и М. Райт.
Мы благодарим Л. Сола за то, что он убедил нас в преимуществах алгоритмов EM-типа. Нам помогли дискуссии с Б. Андерсоном, К. Кларксоном, Р. Фройндом, Л. Кауфманом, Э. Ритманом, С. Ровейсом, Н. Рубином, Дж. Тененбаумом, Н. Тишби, М. Цодыксом, Т. Тайсоном и М. Райт.
Информация об авторе
Авторы и организации
Bell Laboratories, Lucent Technologies , Murray Hill, 07974, Нью-Джерси, США
Дэниел Д. Ли и Х. Себастьян Сеунг
9 Департамент мозговых наук и науки Массачусетский технологический институт, Кембридж, 02139, Массачусетс, США
Х. Себастьян Сеунг
Авторы
- Дэниел Д. Ли
Посмотреть публикации авторов
Вы также можете искать этого автора в PubMed Google Scholar
- H. Sebastian Seung
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
Права и разрешения
Перепечатка и разрешения
Об этой статье
Дополнительная литература
Оценка тенденций в рабочих местах и наборах навыков с использованием анализа данных: тематическое исследование
- Армин Алибасик
- Химаншу Упадхьяй
- Мохаммед Атиф Омар
Журнал больших данных (2022)
Прогнозирование комбинаций лекарств с использованием вложения графов гетерогенных сетей
- Фэй Сун
- Шийин Тан
- Сяоке Ма
Биоинформатика BMC (2022)
Алгоритм улучшения речи на основе неотрицательной скрытой марковской модели и дивергенции Кульбака-Лейблера
- Ян Сян
- Лиминг Ши
- Мадс Гросбёлль Кристенсен
Журнал EURASIP по обработке аудио, речи и музыки (2022)
Возрастные различия в симметрии походки, полученные из кинематической синергии и мышечной синергии нижних конечностей в детстве
- Цилян Сюн
- Цзиньлян Ван
- Юань Лю
Биомедицинская инженерия онлайн (2022)
scSemiAE: глубокая модель с полууправляемым обучением для транскриптомики одиночных клеток
- Цзяи Донг
- Инь Чжан
- Фэй Ван
Биоинформатика BMC (2022)
Комментарии
Отправляя комментарий, вы соглашаетесь соблюдать наши Условия и Правила сообщества. Если вы обнаружите что-то оскорбительное или не соответствующее нашим условиям или правилам, отметьте это как неприемлемое.
Если вы обнаружите что-то оскорбительное или не соответствующее нашим условиям или правилам, отметьте это как неприемлемое.
Как возвести квадратную матрицу в отрицательную половинную степень R?
Операция сингулярной мощности может быть выполнена на самой квадратной матрице, где указанная мощность применяется к каждому элементу матрицы. Base R имеет множество методов и процедур для вычисления мощности для любого k > 1 , где k — целочисленное значение. Однако возведение матриц в нецелую степень является сложной задачей, и число доступных решений ограничено. Внешние пакеты можно вызывать для более надежного расчета мощности на языке программирования R.
Способ 1: Использование метода sqrtm
Пакет expm в R используется для вычисления экспоненциальных степеней, логарифмических степеней и квадратных корней матриц в R. Пакет необходимо сначала установить в рабочее пространство, выполнив следующую команду :
install.packages("expm")
В пакете есть метод sqrtm(), который используется для вычисления квадратного корня из квадратных матриц в R. методаsolve() в R, который, как правило, решает уравнение a %*% x = b относительно x, где b может быть либо вектором, либо матрицей, либо действительным числом <0. Этот метод доступен в самой базе R.
решить( мат , мощность)
В случае если степень пуста, вычисляется обратная матрица мат, то есть матрица возводится в степень -1. Таким образом, подводя итог, мы вычисляем половинную мощность с помощью метода sqrtm() и инвертируем ее с помощью методаsolve() » )
мат <- matrix (1 : 9, ncol = 3)
print ( "Original Matrix" )
print (mat)
print ( "Power matrix" )
pow <- solve ( sqrtm (mat))
print (pow)
 Соответствующие ему векторы, а также значения получаются в виде массивов. Транспонирование векторов вместе с вектором значений затем используется для возврата настроенного значения функции для вычисления мощности матрицы. Однако этот метод считается непригодным для работы со случайными квадратными матрицами, так как он руководствуется многими ограничениями, некоторые из которых:
Соответствующие ему векторы, а также значения получаются в виде массивов. Транспонирование векторов вместе с вектором значений затем используется для возврата настроенного значения функции для вычисления мощности матрицы. Однако этот метод считается непригодным для работы со случайными квадратными матрицами, так как он руководствуется многими ограничениями, некоторые из которых:- Этот метод не работает для матрицы, которая не имеет разложения по собственным значениям.
- Этот метод не работает для недиагонализированной матрицы.
- Матрица должна быть предпочтительно симметричной.
Code:
R
|
Output:
[1] "Original Matrix "
[1] [2]
[1,] 0,088150 0,001017
[2,] 0,001017 0,084634
[1] «Модифицированная матрица»
[1] [2]
[1,] 3,36830 -0,02004
[2,] -0,02004 3,43755 Отрицательное значение матрицы – определение, свойства, примеры
17 мая 2022 г. 17 мая 2022 г. / Автор
Прасанна
17 мая 2022 г. / Автор
Прасанна
Негатив матрицы — это вещественная или целочисленная матрица, состоящая из всех элементов как отрицательных. Отрицательные матрицы являются подмножеством неположительных матриц. Мы можем получить отрицательную матрицу, умножив требуемую матрицу на −1. Отрицательный матричный элемент представляет собой отрицательное число, т. е. a ij <0 для всех i, j, где i — количество строк данной матрицы, а j — количество столбцов данной матрицы.
Изучите свойства, определения и примеры отрицательной матрицы. Изучите всю информацию о матрицах в статьях о матрицах 10-го класса по математике на нашем веб-сайте бесплатно. Вы можете легко выучить все матрицы, такие как нулевая матрица, матрица идентичности, добавление матрицы и т. Д. Без какой-либо путаницы.
Определение отрицательной матрицы — это матрица, в которой все элементы отрицательные. Если мы возьмем матрицу A, то отрицательная часть матрицы станет -A.
А = [а ij ], тогда -А = -[а иж ].
Свойства отрицательной матрицы
Следующие свойства применимы к отрицательной матрице. Прочтите свойства отрицательной матрицы, прежде чем решать все проблемы, связанные с отрицательной матрицей.
- В отрицательной матрице все элементы матрицы отрицательны, т.е. a_(ij)<0 для всех i, j.
- Отрицательные матрицы являются подмножеством неположительных матриц.
- Если вы добавите матрицу с ее отрицательной матрицей, то вы получите нулевую матрицу, т.е. A + (-A) = 0
Также получите
- Свойства сложения матриц
- Треугольная матрица
- Матрица столбцов
- Заказ Матрицы
- Вычитание двух матриц
- Равные матрицы
Решенные примеры для негатива матрицы
Ознакомьтесь с приведенными ниже примерами, чтобы узнать больше о негативе матрицы. Мы дали четкое объяснение, чтобы облегчить вашу подготовку.
Пример 1. Если \( A =\left[
\begin{matrix}
9&7 \cr
5&14 \cr
\end{matrix}
\right]
\), то найдите отрицательную матрицу матрицы A.
Решение: Данной матрицей является \( A =\left[
\begin{matrix}
9&7 \cr
5&14 \cr
\end{matrix}
\right]
\)
Отрицательная матрица A = -A.
Теперь, меняя знаки каждого элемента матрицы A,
получаем \( A = (-1)\left[
\begin{matrix}
9&7 \cr
5&14 \cr
\end{matrix}
\right]
\) = \( \left[
\begin{matrix}
-9&-7 \cr
-5&-14 \cr
\end{matrix}
\right]
\)
Следовательно, отрицательная матрица A = -A = \( \left[
\begin{matrix}
-9&-7 \cr
-5&-14 \cr
\end{matrix}
\right]
\)
Пример 2. Если \( M =\left[
\begin{matrix}
10&-2 \cr
-6&4 \cr
\end{matrix}
\right]
\), то найти отрицательную матрицу M.
Решение: Дана матрица \( M =\left[
\begin{matrix}
10&-2 \cr
-6&4 \cr
\end{matrix}
\right]
\)
Отрицательное матрица M = -M.
Теперь, меняя знаки каждого элемента матрицы M,
получаем \( M = (-1)\left[
\begin{matrix}
10&-2 \cr
-6&4 \cr
\end{matrix}
\right]
\) = \( \left[
\begin{matrix}
-10&2 \cr
6&-4 \cr
\end{matrix}
\right]
\)
Следовательно, отрицательная матрица M = -M = \( \left[
\begin{matrix}
-10&2 \cr
6&-4 \cr
\end{matrix}
\right]
\ )
Пример 3. Если \( I =\left[
\begin{matrix}
1&0 \cr
0&1 \cr
\end{matrix}
\right]
\), то найти отрицательную матрицу I.
Решение: Дана матрица \( I =\left[
\begin{matrix}
1&0 \cr
0&1 \cr
\end{matrix}
\right]
\)
Теперь найдем отрицательную матрицу I.
Отрицательную матрицу I = -I.
Теперь, меняя знаки каждого элемента матрицы M,
получаем \( I = (-1)\left[
\begin{matrix}
1&0 \cr
0&1 \cr
\end{matrix}
\right ]
\) = \( \left[
\begin{matrix}
-1&0 \cr
0&-1 \cr
\end{matrix}
\right]
\)
Следовательно, отрицательная матрица I = -I = \( \left[
\begin{matrix}
-1&0 \cr
0&-1 \cr
\end{matrix}
\right]
\)
Пример 4. Найти сложение матрицы A и -A равно нулю, где \( A =\left[
Найти сложение матрицы A и -A равно нулю, где \( A =\left[
\begin{matrix }
10&12 \cr
11&13 \cr
\end{matrix}
\right]
\)
Решение: Дана матрица \( A =\left[
\begin{matrix}
10&12 \cr
\end{matrix}
\right]
\)
Сначала найдите отрицательное значение матрицы A = – A
Теперь, меняя знаки каждого элемента матрицы A.
отрицание матрицы \( A =(-1)\left[
\begin{matrix}
10&12 \cr
11&13 \cr
\end{matrix}
\right]
\) = \( \left[
\begin{matrix}
-10&-12 \cr
-11&-13 \cr
\end{matrix}
\right]
\)
-A = \( \left[
\begin{matrix}
-10& -12 \cr
-11&-13 \cr
\end{matrix}
\right]
\)
Теперь добавим A и -A.
A + (- A) = \( \left[
\begin{matrix}
10&12 \cr
11&13 \cr
\end{matrix}
\right]
\) + \( \left[
\begin{matrix}
-10&-12 \cr
-11&-13 \cr
\end{matrix}
\right]
\) = \( \left[
\begin{matrix}
10 – 10&12 – 12 \cr
11 – 11&13 – 13 \cr
\end{matrix}
\right]
\) = \( \left[
\begin{matrix}
0&0 \cr
0&0 \cr
\end{matrix}
\right]
\)
Следовательно, A + (-A) = 0.
Часто задаваемые вопросы о негативе матрицы
1. Что такое отрицательная матрица?
Отрицательную матрицу можно получить, умножив данную матрицу на -1. Все элементы й отрицательной матрицы неположительны.
2. Как получить отрицательную матрицу?
Просто умножьте его на -1, чтобы получить отрицательную матрицу.
3. Какая отрицательная матрица для \( \left[
\begin{matrix}
3&-8 \cr
2&-5 \cr
\end{matrix}
\right]
\)
Отрицательная матрица данной матрицы равна \( \left[
\begin{matrix}
-3&88 \cr
-2&5 \cr
\end{matrix}
\right]
\)
4. Что мы получаем добавлением А и -А.
Мы получаем ноль, складывая A и -A. A + (-A) = 0.
Резюме
Подробно объясняется процесс нахождения негатива матрицы. Не забудьте прочитать каждую концепцию, представленную на нашем веб-сайте, чтобы сделать вашу подготовку эффективной. Вы можете очень легко и быстро выучить любую концепцию с помощью наших статей.
Вы можете очень легко и быстро выучить любую концепцию с помощью наших статей.
Оптимизация и расширение неотрицательной матричной факторизации | BMC Bioinformatics
- Методология Статья
- Открытый доступ
- Опубликовано:
- Сихуэй Линь ORCID: orcid.org/0000-0003-1679-9120 1 и
- Пол С. Бутрос 1,2,3
Биоинформатика BMC том 21 , Номер статьи: 7 (2020) Процитировать эту статью
13 тыс.
 обращений
обращений21 цитирование
1 Альтметрический
Сведения о показателях
Abstract
Background
Неотрицательная матричная факторизация (NMF) — это метод, широко используемый в различных областях, включая искусственный интеллект (ИИ), обработку сигналов и биоинформатику. Однако существующие алгоритмы и пакеты R нельзя применять к большим матрицам из-за их медленной сходимости или к матрицам с отсутствующими элементами. Кроме того, большинство исследований NMF сосредоточено только на слепой декомпозиции: декомпозиции без использования предварительных знаний. Наконец, отсутствие хорошо проверенной методологии выбора гиперпараметров ранга также вызывает озабоченность по поводу полученных результатов.
Результаты
Мы принимаем идею последовательного покоординатного спуска в NMF для увеличения скорости сходимости. Мы демонстрируем, что NMF может естественным образом обрабатывать пропущенные значения, и это свойство приводит к новому методу определения гиперпараметра ранга. Кроме того, мы демонстрируем некоторые новые приложения NMF и показываем, как использовать маскирование для внедрения предварительных знаний и желаемых свойств для достижения более значимой декомпозиции.
Выводы
С помощью анализа сложности и экспериментов мы показываем, что наша реализация сходится быстрее, чем известные методы. Мы также показываем, что использование NMF для деконволюции содержимого опухоли может привести к результатам, аналогичным существующим методам, таким как ISOpure. Предлагаемое нами вменение пропущенных значений является более точным, чем традиционные методы, такие как множественное вменение, и сравнимо с missForest, обеспечивая при этом значительно лучшую вычислительную эффективность. Наконец, мы утверждаем, что предлагаемый метод ранговой настройки, основанный на вменении пропущенных значений, теоретически превосходит существующие методы. Все алгоритмы реализованы в пакете R NNLM, который находится в свободном доступе на CRAN и Github.
Наконец, мы утверждаем, что предлагаемый метод ранговой настройки, основанный на вменении пропущенных значений, теоретически превосходит существующие методы. Все алгоритмы реализованы в пакете R NNLM, который находится в свободном доступе на CRAN и Github.
История вопроса
Неотрицательная матричная факторизация (NMF или NNMF) [1] широко используется в качестве общего метода уменьшения размерности и извлечения признаков из неотрицательных данных. Основное отличие NMF от других методов факторизации, таких как SVD, заключается в неотрицательности, которая допускает только аддитивные комбинации внутренних «частей», то есть скрытых признаков. Это продемонстрировано в [1], где NMF запоминает части лиц, и лицо естественным образом представляется как аддитивная линейная комбинация различных частей. Действительно, негативные комбинации не так интуитивны и естественны, как позитивные комбинации.
В биоинформатике NMF иногда используется для поиска «метагенов» по профилям экспрессии, которые могут быть связаны с некоторыми биологическими путями [2, 3].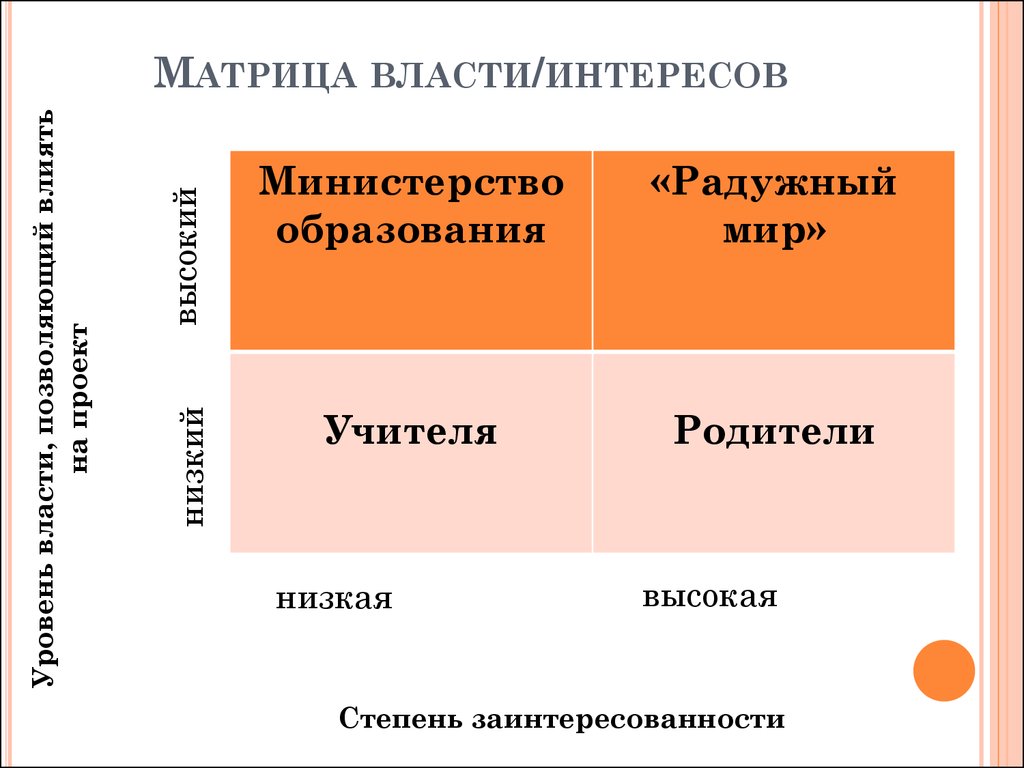 NMF использовался для извлечения мутационных сигнатур тринуклеотидов из мутаций, обнаруженных в геномных последовательностях рака, и было высказано предположение, что профиль тринуклеотидов каждого типа рака представляет собой положительную линейную комбинацию этих сигнатур [4].
NMF использовался для извлечения мутационных сигнатур тринуклеотидов из мутаций, обнаруженных в геномных последовательностях рака, и было высказано предположение, что профиль тринуклеотидов каждого типа рака представляет собой положительную линейную комбинацию этих сигнатур [4].
Существует несколько различных алгоритмов разложения NMF, в том числе мультипликативные алгоритмы, предложенные в [1], градиентный спуск и альтернативный неотрицательный метод наименьших квадратов (ANLS). ANLS привлекает внимание благодаря своей гарантии сходимости к стационарной точке и более быстрому алгоритму для неотрицательных наименьших квадратов (NNLS).
В этой статье мы сначала унифицируем различные формы регуляризации компонентов результата, которые поощряют желаемые свойства, такие как ортогональность и разреженность, и показываем, как можно модифицировать обычные мультипликативные алгоритмы [1] для адаптации к этим регуляризациям, вдохновленным [3]. Затем мы принимаем подход ANLS, но включаем решение проблемы NNLS с использованием покоординатного алгоритма, предложенного в [5], в котором каждая неизвестная переменная может быть решена последовательно и явно как простые задачи квадратичной оптимизации.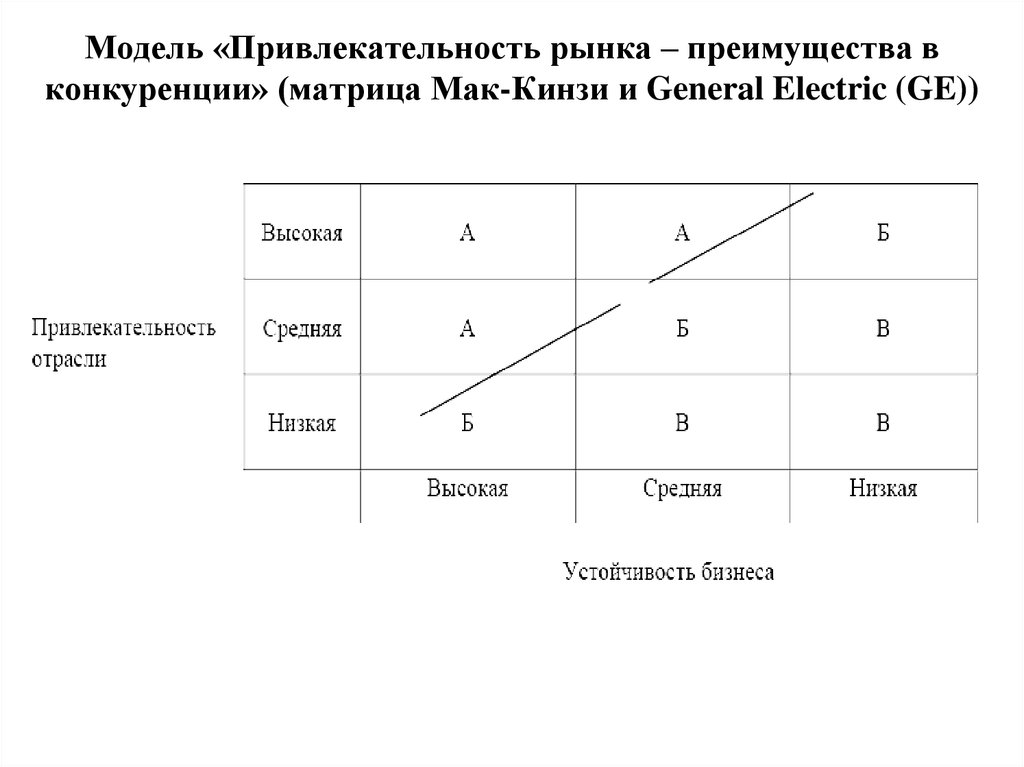 Мы демонстрируем, что этот алгоритм может сходиться намного быстрее, чем традиционные мультипликативные алгоритмы. Для NMF с потерями по расхождению Кульбака-Лейблера мы расширяем эту методологию, приближаясь к потерям с помощью квадратичной функции.
Мы демонстрируем, что этот алгоритм может сходиться намного быстрее, чем традиционные мультипликативные алгоритмы. Для NMF с потерями по расхождению Кульбака-Лейблера мы расширяем эту методологию, приближаясь к потерям с помощью квадратичной функции.
NMF — это метод уменьшения размерности, так как результирующие разложенные матрицы имеют меньшее количество элементов, чем исходная матрица. Это означает, что для выполнения декомпозиции не нужны все элементы исходной матрицы, поэтому NMF должен иметь возможность обрабатывать отсутствующие элементы в целевой матрице. Действительно, факторизация может быть выполнена путем отбрасывания элементов потерь, связанных с отсутствующими записями, если целевая функция потерь представляет собой сумму потерь за одну запись, например, среднеквадратичную ошибку (MSE) или расхождение Кульбака-Лейблера (KL). Кроме того, реконструированная матрица имеет значения элементов, отсутствующих в исходной матрице. Это раскрывает возможности NMF для вменения пропущенных значений. Вдохновленные этим наблюдением и популярной стратегией настройки обучения и проверки в моделях с учителем, мы представляем новый метод оптимизации единственного гиперпараметра 9.0031 k , т.е. ранг разложения NMF.
Вдохновленные этим наблюдением и популярной стратегией настройки обучения и проверки в моделях с учителем, мы представляем новый метод оптимизации единственного гиперпараметра 9.0031 k , т.е. ранг разложения NMF.
NMF практически не контролируется. Он выполняет слепую декомпозицию, которая ставит под сомнение смысл результата. Это может ограничить применение неконтролируемых методов в областях, где критична высокая интерпретируемость, включая большинство биомедицинских исследований. С другой стороны, декомпозиция без использования известных открытий (априорных знаний) может оказаться неэффективной, особенно при небольшом размере выборки. Чтобы преодолеть эти проблемы, мы применяем метод маскирования к разложению NMF во время алгоритмов итерации, чтобы сохранить определенные структуры или шаблоны в одной или обеих результирующих матрицах, которые могут быть разработаны в соответствии с нашими предварительными знаниями или исследовательским интересом. Этот метод можно использовать для выполнения декомпозиции, управляемой путем или подсетью, или для выделения различных типов клеток из смешанных образцов тканей.
Все эти алгоритмические инновации реализованы в популярном языке программирования R. Они служат альтернативой широко используемому пакету NMF [6], который сначала был переведен из пакета MATLAB, а затем оптимизирован с помощью C++ для некоторых алгоритмов. Ожидается, что разреженный чередующийся NNLS (ANLS) в [3] будет быстрым в теории, но его реализация в R приводит к снижению производительности на практике. Наш пакет NNLM сочетает в себе эффективный алгоритм NNLS с использованием Rcpp, который плавно интегрирует R и C++ [7] и является бесплатным и открытым исходным кодом.
Таким образом, основные результаты этой работы включают:
объединение различных типов регуляризации и получение соответствующих мультипликативных алгоритмов;
разработка более быстрого алгоритма NMF с использованием последовательного покоординатного спуска;
введение метода обработки отсутствующих записей в целевой матрице, что приводит к новому методу определения ранга k и новому применению NMF для вменения отсутствующих значений;
представляет метод маскирования для интеграции предшествующих знаний и желаемых свойств и демонстрирует, как его можно использовать для достижения деконволюции содержимого опухоли.

Результаты.
Сравнение алгоритмов. сравните SCD с мультипликативными алгоритмами Ли. Результаты представлены на рис. 1 и в таблице 1. Здесь видно, что алгоритмы SCD и Lee имеют примерно одинаковое время выполнения для каждой эпохи, т. е. обновление
W и H вводятся один раз. Однако SCD обычно сходится намного быстрее, достигая той же точности за меньшее количество эпох и за гораздо более короткое время. Очевидно, что алгоритмы со средней потерей KL медленнее, чем алгоритмы с MSE для каждой эпохи, но немного больше уменьшают ошибку в каждую эпоху. Мультипликативный алгоритм с MSE работает быстрее, когда обновление нескольких эпох ( N i >1) выполняется в каждой внешней чередующейся итерации (LEE-MSE против LEE-MSE-1). Рис. 1Сравнение различных алгоритмов по сходимости
Полноразмерное изображение
Таблица 1 Сравнение производительности различных алгоритмов на подмножестве набора данных о немелкоклеточном раке легкого, при k =15Полноразмерная таблица
Вменение отсутствующих значений
Сравнение различных методов вменения показано на рис. {3\times 50}\) выбираются независимо и равномерно из интервала (0 ,1) и (0,10) соответственно. A был построен с помощью WH плюс шум, выбранный независимо для каждой записи из стандартного нормального распределения. Все отрицательные значения в A устанавливаются равными 0 (очень маловероятно). Мы выбираем MSE как потерю и запускаем целевой алгоритм 5 раз, каждый раз удаляя случайные 30% записей.
{3\times 50}\) выбираются независимо и равномерно из интервала (0 ,1) и (0,10) соответственно. A был построен с помощью WH плюс шум, выбранный независимо для каждой записи из стандартного нормального распределения. Все отрицательные значения в A устанавливаются равными 0 (очень маловероятно). Мы выбираем MSE как потерю и запускаем целевой алгоритм 5 раз, каждый раз удаляя случайные 30% записей.
Результат показан на рис. 3. Как мы могли видеть, разные прогоны (обозначенные разными цветами) дают согласованные результаты. Среднеквадратичные ошибки (MSE) восстановления отсутствующих записей сведены к минимуму при k =3 для всех циклов.
Рис. 3Определение оптимального ранга k в NMF с помощью вменения
Изображение в натуральную величину
Деволюция содержимого опухоли
Деконволюция выражения представляет постоянный интерес в биоинформатике и клинических исследованиях [11, 12].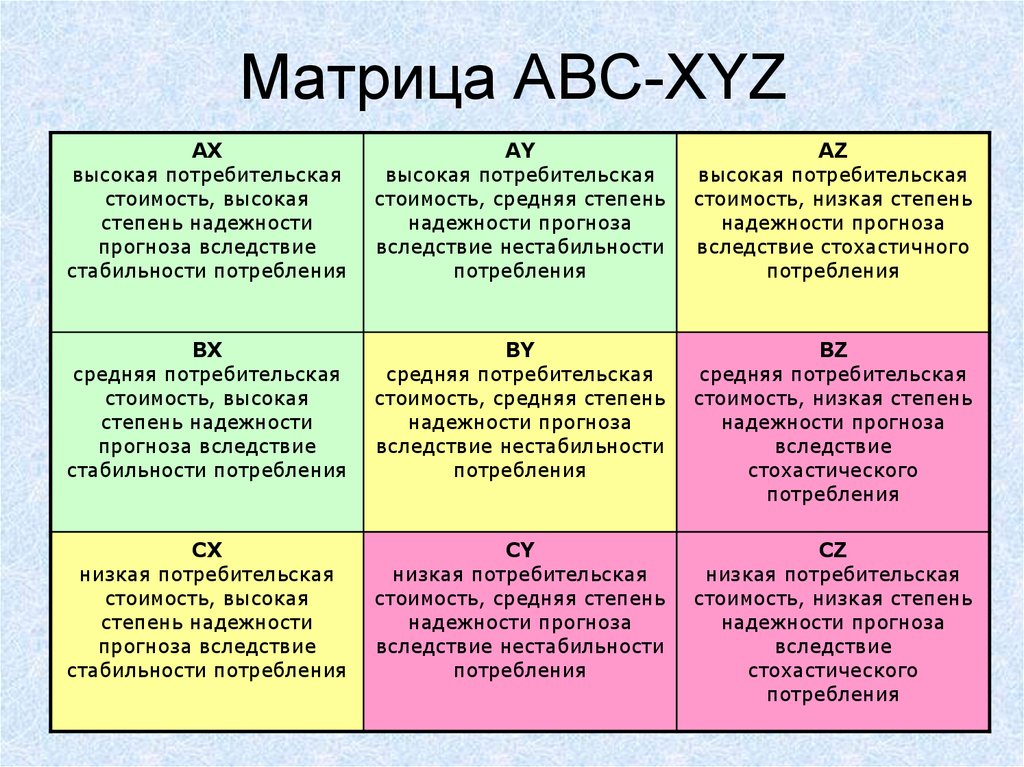 Были предложены некоторые методы, связанные с NMF [13]. Однако наши уникальные методы использования матриц масок являются более гибкими и мощными, поскольку можно почти направить декомпозицию к любой интересующей биологической процедуре, интегрируя предшествующие знания в исходную матрицу и матрицу маски. По сравнению с байесовскими методами, такими как ISOpure [14], методы на основе NMF намного быстрее.
Были предложены некоторые методы, связанные с NMF [13]. Однако наши уникальные методы использования матриц масок являются более гибкими и мощными, поскольку можно почти направить декомпозицию к любой интересующей биологической процедуре, интегрируя предшествующие знания в исходную матрицу и матрицу маски. По сравнению с байесовскими методами, такими как ISOpure [14], методы на основе NMF намного быстрее.
Мы используем часть данных по аденокарциноме легких Бера [15], которые содержат 30 опухолей и 10 нормальных образцов с 250 транскриптами, доступными в пакете Isopure R [16]. Сравнение с результатом ISOpure с использованием полного набора данных (80 опухолей и 5151 транскрипт) показано на рис. 4. Мы видим, что наш результат, основанный на небольшой части набора данных, дает сопоставимый результат.
Рис. 4Сравнение NMF с ISOpure [16] для деконволюции содержимого опухоли
Полноразмерное изображение
Обсуждение
Мы объединяем общие регуляризации NMF в общую форму, чтобы исследовать возможности смешивания различных типов регуляризаций. Выбор весов регуляризации должен зависеть от задачи. Например, независимость или ортогональность ( J 2 ) могут оказаться предпочтительными для деконволюции контента, в то время как разреженность ( J 3 ) может оказаться более важной для обнаружения метагенов или подсетей. J 1 можно использовать для уменьшения дисперсии в матрицах результатов, используемых для последующего анализа, такого как обнаружение прогностических биомаркеров. Другой способ выбрать эти гиперпараметры — использовать тот же подход, который был представлен в разделе «Выбор из 9».0031 k » раздел для настройки k , т. е. выбрать те, которые минимизируют ошибку реконструкции или вариацию. Это можно сделать вместе с выбором k .
Выбор весов регуляризации должен зависеть от задачи. Например, независимость или ортогональность ( J 2 ) могут оказаться предпочтительными для деконволюции контента, в то время как разреженность ( J 3 ) может оказаться более важной для обнаружения метагенов или подсетей. J 1 можно использовать для уменьшения дисперсии в матрицах результатов, используемых для последующего анализа, такого как обнаружение прогностических биомаркеров. Другой способ выбрать эти гиперпараметры — использовать тот же подход, который был представлен в разделе «Выбор из 9».0031 k » раздел для настройки k , т. е. выбрать те, которые минимизируют ошибку реконструкции или вариацию. Это можно сделать вместе с выбором k .
Выбор MSE или KL в качестве функции потерь зависит от характера и распределения записей. Общий принцип заключается в использовании MSE, когда распределение записей сосредоточено вокруг определенной области, т. е. величины примерно одинаковы (например, исследование моделирования в разделе «Выбор k 9раздел 0032»). Однако для очень асимметричных распределений (например, данных подсчета) или данных с выбросами потеря KL может соответствовать лучше, так как если в этом случае используется MSE, большие записи могут преобладать в потерях, в то время как маленькие записи имеют небольшое влияние, что приводит к факторизация с большой дисперсией. В последнем случае можно также выполнить декомпозицию в пространстве журнала, если все записи имеют значения больше 1, или в пространстве журнала (1+ A ) с MSE. Однако интерпретация результатов также должна быть изменена.
е. величины примерно одинаковы (например, исследование моделирования в разделе «Выбор k 9раздел 0032»). Однако для очень асимметричных распределений (например, данных подсчета) или данных с выбросами потеря KL может соответствовать лучше, так как если в этом случае используется MSE, большие записи могут преобладать в потерях, в то время как маленькие записи имеют небольшое влияние, что приводит к факторизация с большой дисперсией. В последнем случае можно также выполнить декомпозицию в пространстве журнала, если все записи имеют значения больше 1, или в пространстве журнала (1+ A ) с MSE. Однако интерпретация результатов также должна быть изменена.
Хотя NMF можно выполнить с отсутствующими элементами, когда отсутствующий процесс коррелирует с самим значением, т. е. отсутствует полностью случайно (MCAR), результирующая реконструкция может быть необъективной. Кроме того, когда имеется много пропусков, особенно когда в значительной степени отсутствует определенная строка или столбец, композиция и реконструкция могут иметь большие вариации и, следовательно, ненадежны. Тот же аргумент относится и к предлагаемому методу выбора k .
Тот же аргумент относится и к предлагаемому методу выбора k .
Техника маскирования проста, но полезна во многих случаях. Здесь мы только демонстрируем его применение для деконволюции содержимого опухоли с помощью эксперимента на небольшом наборе данных только для демонстрации его возможностей. Результат, сопоставимый с таким обычным методом, как ISOpure, побуждает нас к дальнейшей работе в этом направлении, например, к анализу метагенов и подсетей, а также к деконволюции контента.
Все методологии, описанные в этом документе, реализованы в пакете R NNLM, доступном на CRAN и Github. Весь код для экспериментов в этой статье можно найти на виньетке пакета.
Заключение
В этой работе мы обобщаем члены регуляризации в NMF и распространяем мультипликативный алгоритм на общий случай. Мы разрабатываем новый решатель, основанный на последовательном покоординатном спуске для потерь KL и MSE, и демонстрируем его эффективность с помощью анализа сложности и численных экспериментов. Наш метод и реализация также могут естественным образом обрабатывать отсутствующие записи и использоваться для вменения отсутствующих значений посредством реконструкции. Мы показываем, что метод вменения NMF более эффективен и точен, чем популярные методы. Руководствуясь вменением пропущенного значения, мы вводим простой и интуитивно понятный метод определения ранга NMF. Наконец, вводя метод маскирования, мы показываем, что NMF может применяться для деконволюции содержимого опухоли и может достигать результатов, аналогичных существующим методам, таким как ISOpure, с большей вычислительной эффективностью.
Наш метод и реализация также могут естественным образом обрабатывать отсутствующие записи и использоваться для вменения отсутствующих значений посредством реконструкции. Мы показываем, что метод вменения NMF более эффективен и точен, чем популярные методы. Руководствуясь вменением пропущенного значения, мы вводим простой и интуитивно понятный метод определения ранга NMF. Наконец, вводя метод маскирования, мы показываем, что NMF может применяться для деконволюции содержимого опухоли и может достигать результатов, аналогичных существующим методам, таким как ISOpure, с большей вычислительной эффективностью.
Методы
В этом разделе мы обобщим мультипликативные алгоритмы [1], чтобы включить регуляризации в (3), и кратко обсудим, как их можно получить. Затем мы вводим новый и более быстрый алгоритм для NMF со среднеквадратичной потерей (раздел «Чередующийся неотрицательный метод наименьших квадратов (ANLS)») и потерей расстояния KL-дивергенции (раздел «Последовательное квадратичное приближение для потери расхождения Кульбака-Лейблера») с регуляризациями. , по альтернирующей схеме. В разделе «Отсутствующие элементы» мы обращаемся к общей проблеме всех алгоритмов, заключающейся в том, что некоторые элементы целевой матрицы могут быть ненадежными или не наблюдаться. Представленный нами метод естественным образом приводит к интуитивному и логически надежному методу определения неизвестного параметра ранга k (раздел «Выбор k ») и новый подход к вменению отсутствующих значений для данных массива (раздел «Вменение отсутствующих значений»). Затем мы повторно изучаем NMF в разделе «Маскирование, деконволюция контента и проектируемая факторизация» и разрабатываем метод для интеграции предшествующих знаний в NMF и управления декомпозицией более биологически значимым способом, который может быть эффективным в приложениях.
, по альтернирующей схеме. В разделе «Отсутствующие элементы» мы обращаемся к общей проблеме всех алгоритмов, заключающейся в том, что некоторые элементы целевой матрицы могут быть ненадежными или не наблюдаться. Представленный нами метод естественным образом приводит к интуитивному и логически надежному методу определения неизвестного параметра ранга k (раздел «Выбор k ») и новый подход к вменению отсутствующих значений для данных массива (раздел «Вменение отсутствующих значений»). Затем мы повторно изучаем NMF в разделе «Маскирование, деконволюция контента и проектируемая факторизация» и разрабатываем метод для интеграции предшествующих знаний в NMF и управления декомпозицией более биологически значимым способом, который может быть эффективным в приложениях.
Обзор
NMF разлагает матрицу A на две матрицы с неотрицательными элементами меньшего ранга, 9{к\раз м}\). Без потери обобщения строки A представляют признаки (например, гены, профили пользователей и т.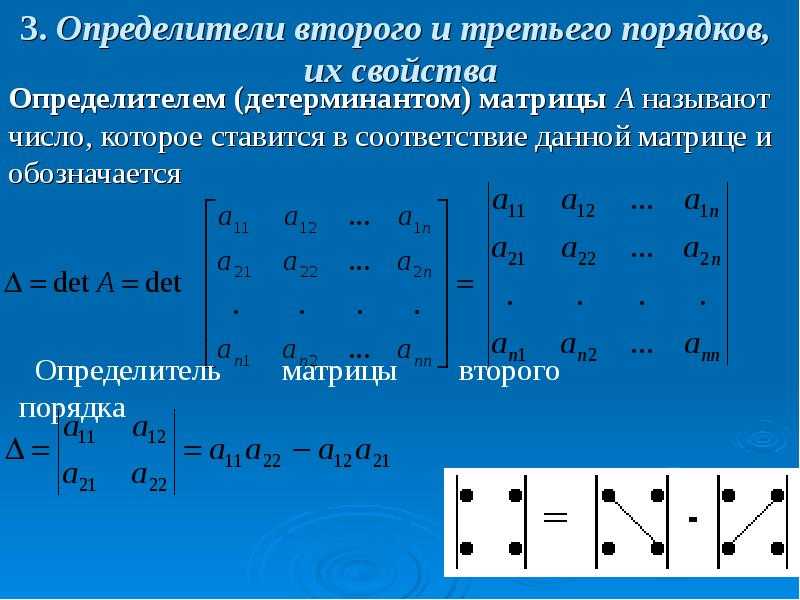 д.), а столбцы A представляют выборки. В зависимости от контекста W можно интерпретировать как сопоставление признаков. Строки W представляют профили заболеваний или метагены [2]. Столбцы H представляют собой компактные представления выборок, т. е. профили выборок.
д.), а столбцы A представляют выборки. В зависимости от контекста W можно интерпретировать как сопоставление признаков. Строки W представляют профили заболеваний или метагены [2]. Столбцы H представляют собой компактные представления выборок, т. е. профили выборок.
Математически NMF можно сформулировать как задачу оптимизации следующим образом:
$$ \min\limits_{W \ge 0, H \ge 0} L(A, WH) + J_{W}(W) + J_{H}(H). $$ 9{2}\), или расстояние расхождения KL x log( x / y )− x + y . Последнее можно интерпретировать как отклонение от модели Пуассона.
J W ( W ) и J H ( H ). разреженность, меньшая величина или лучшая ортогональность. Вводятся различные формы регуляризации [3, 11], но в основном их можно объединить в виде следующей формы: 9{T}\right) \\ J_{3}(X) &:= \sum\limits_{i,j} |x_{ij}| = \текст{тр}(ХЕ). \end{aligned} $$
(3)
I — единичная матрица, E — матрица правильной размерности, все элементы которой равны 1, X · i и X i · — это столбец и строка i th соответственно.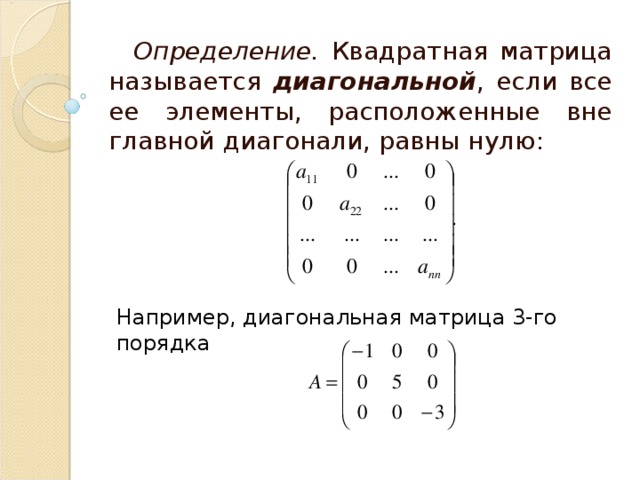
J 1 — штраф за гребень для контроля величины и гладкости. J 1 также помогает стабилизировать численные алгоритмы. J 2 ( X ) используется для минимизации корреляций между столбцами, то есть для максимизации независимости или угла между X · i , X · 7 · ] . J 3 — это LASSO-подобный штраф, который контролирует матричную разреженность. [3] ввел другой тип регуляризации для обеспечения разреженности по столбцам следующим образом: 9{Т}\справа). $$
(4)
Очевидно, \(\bar {J} = J_{1} + J_{2}\), частный случай (2).
Обычно (1) решается с помощью альтернативного алгоритма, который решает W и H поочередно и итеративно. Благодаря неотрицательному ограничению штрафы не вносят дополнительной сложности.
Добавление регуляризации к мультипликативному алгоритму Ли
Два мультипликативных алгоритма обновления предложены в [1] для квадратичных потерь и потерь KL-дивергенции. Они адаптированы [11] для случаев с регуляризацией разреженности. Здесь мы модифицируем эти алгоритмы, чтобы интегрировать все вышеперечисленные регуляризации следующим образом. 9{T}W + \beta_{1} I + \beta_{2} (E-I)\right]H + \beta_{3}E \right)_{\bar{k}j}}. $$
Они адаптированы [11] для случаев с регуляризацией разреженности. Здесь мы модифицируем эти алгоритмы, чтобы интегрировать все вышеперечисленные регуляризации следующим образом. 9{T}W + \beta_{1} I + \beta_{2} (E-I)\right]H + \beta_{3}E \right)_{\bar{k}j}}. $$
(5)
С дивергенцией Кульбака-Лейблера,
$$ h_{\bar{k}j} \leftarrow h_{\bar{k}j} \frac{\sum_{l} \left(w_{l\bar{k}}a_{lj}/\ sum_{q}w_{lq} h_{qj}\right)} { \left(\sum_{l} w_{l\bar{k}} + (\beta_{1}-\beta_{2}) h_{ \bar{k}j} + \beta_{2} \sum_{l} h_{lj} + \beta_{3} \right) }. $$
(6)
Когда β i =0, i =1,2,3, это исходные мультипликативные алгоритмы из [1]. Если β 1 =0, эти уточнения сводятся к уравнениям (10) и (23) в [11]. Доказательство при β 1 ≠0 проводится аналогично [11]. Правила обновления для W аналогичны (5) и (6).
Эти мультипликативные алгоритмы просты в реализации, но у них есть тот недостаток, что когда запись W или H инициализируется как нуль или положительное значение, оно остается нулевым или положительным на протяжении всех итераций. Поэтому все записи должны быть инициализированы положительными. Как следствие, истинная разреженность в общем случае не может быть достигнута, если не наложен жесткий порог, так как многие записи будут достаточно малы, чтобы пороговое значение было равно нулю. 9{2} + \left(\sum_{l\neq \bar{k}} v_{\bar{k}l} h_{lj} + u_{\bar{k}j}\right) h_{\bar{ k}j} \right) \\ \end{aligned} $$
Поэтому все записи должны быть инициализированы положительными. Как следствие, истинная разреженность в общем случае не может быть достигнута, если не наложен жесткий порог, так как многие записи будут достаточно малы, чтобы пороговое значение было равно нулю. 9{2} + \left(\sum_{l\neq \bar{k}} v_{\bar{k}l} h_{lj} + u_{\bar{k}j}\right) h_{\bar{ k}j} \right) \\ \end{aligned} $$
(9)
Поскольку E − I полуотрицательно определено, для обеспечения единственности и сходимости алгоритма накладываем ограничение, что β 1 > β 2 , и в этом случае \(v_{\bar {k}\bar {k}} > 0\) для всех \(\bar {k}\) .
Если все элементы H фиксированы, кроме \(h _ {\bar {k}j}\), то приведенное выше является квадратичной функцией \(h _ {\bar {k}j}\) с неотрицательное ограничение, которое может быть явно оптимизировано с помощью
9{*}_{\bar{k}j} =& \max\left(0, -\frac{\sum_{l\neq\bar{k}} v_{\bar{k}l} h_{lj} + u_{\bar{k}j}}{v_{\bar{k}\bar{k}}}\right) \\ =& \max\left(0, h_{\bar{k}j} - \ frac {\ sum_ {l} v _ {\ bar {k} l} h_ {lj} + u _ {\ bar {k} j}} {v _ {\ bar {k} \ bar {k}}} \ right) . \end{align} $$
\end{align} $$
(10)
Очевидно, что j =1,…, m можно обновлять независимо и параллельно. Затем у нас есть следующий алгоритм SCD для решения H , когда W фиксировано.
9{(t)}_{ij}\right \}\).
Из (10) видно, что каждая итерация невозрастающая и поэтому алгоритм сходится к некоторой фиксированной точке. Любой вход в фиксированную точку должен быть либо на границе с ее градиентом, указывающим за пределы допустимой области ( H ≤0), либо в стационарной точке. Формальное доказательство сходимости можно найти в [5].
Переменный алгоритм фиксирует W и находит H с помощью NNLS, а затем фиксирует H и вычисляет W по тому же алгоритму. Эта процедура повторяется до тех пор, пока изменение A − W H не станет достаточно малым. Каждое обновление является невозрастающим, поэтому альтернирующий алгоритм сходится.
Вместо инициализации H (0) =0 для каждой итерации мы используем теплый старт , т. е. инициализируем H (0) как результат предыдущей итерации.
е. инициализируем H (0) как результат предыдущей итерации.
Последовательная квадратичная аппроксимация потерь из-за расхождения Кульбака-Лейблера 9{(t)}_{lj} - \beta_{3}}{a + \beta_{1}} \right). $$
(14)
Можно вывести аналогичную формулу для обновления \(W_{i\bar {k}}\). Обратите внимание, что когда запись \(\hat A = WH\) равна 0, расхождение KL равно бесконечности. Чтобы избежать этого, мы добавляем небольшое число к знаменателям как в (13), так и в (14).
Сложность и скорость сходимости
Первый шаг SCD (уравнение 11) имеет сложность kmn из-за W T A . Второй шаг (уравнение 12) стоит 9{2} N_{i} + 2nmk\right)N_{o}\right)\), где N o - количество внешних итераций для чередования W и H . N i N o - общее количество эпох, т.е. один полный просмотр по всем записям W и H . Для мультипликативного алгоритма Ли с MSE при фиксированном W сложность решения H составляет км для W T A на числителе, K 2 N для W T W на DANMAT x N i for multiple H at the denominator for N i times, which add up to k n m + k 9{2}N_{i}N_{o}\право)\).
Для мультипликативного алгоритма Ли с MSE при фиксированном W сложность решения H составляет км для W T A на числителе, K 2 N для W T W на DANMAT x N i for multiple H at the denominator for N i times, which add up to k n m + k 9{2}N_{i}N_{o}\право)\).
Очевидно, что алгоритмы с квадратичной потерей ошибки быстрее, чем алгоритмы, основанные на KL (в k раз ) с точки зрения сложности, и могут выиграть от нескольких внутренних итераций N i W T A и A H T ), как правило, K ≪ M , N , что в целом должно быть уменьшено M , N , что в целом должно быть уменьшено M , N . 0031 N или . Напротив, алгоритмы с потерей KL не могут извлечь выгоду из внутренних итераций из-за пересчета WH на каждой внутренней итерации. Хотя SCD и алгоритм Ли схожи по сложности, можно ожидать гораздо более быстрой сходимости в SCD. Это связано с тем, что алгоритм Ли, по сути, представляет собой градиентный спуск со специальным размером шага [1], который является методом первого порядка, в то время как SCD является подходом второго порядка, подобным Ньютону-Рафсону.
0031 N или . Напротив, алгоритмы с потерей KL не могут извлечь выгоду из внутренних итераций из-за пересчета WH на каждой внутренней итерации. Хотя SCD и алгоритм Ли схожи по сложности, можно ожидать гораздо более быстрой сходимости в SCD. Это связано с тем, что алгоритм Ли, по сути, представляет собой градиентный спуск со специальным размером шага [1], который является методом первого порядка, в то время как SCD является подходом второго порядка, подобным Ньютону-Рафсону.
Отсутствующие записи
По разным причинам не всегда будут присутствовать все записи A . В некоторых случаях, даже если запись наблюдается, она может быть ненадежной. В этом случае может быть лучше рассматривать их как отсутствующие записи. Поскольку в основном предполагается, что матрица A имеет низкий ранг k , информация в A является избыточной для такого разложения. Следовательно, факторизация может быть выполнена при наличии пропущенных записей в A , используя только наблюдаемые.
На самом деле, поскольку функция потерь обычно является суммой потерь всех элементов, естественно просто отбросить потери, связанные с отсутствующими элементами. Для любого j пусть I j ={ i : a ij не отсутствует} и \(\bar {I}_{j} {ij} \text { отсутствует}\}\). При обновлении j -го столбца H следует удалить все \(\bar {I}_{j}\) строки W , т. е. U 9{T}A_{I_{j}\cdot} + \beta_{3} E, \end{aligned} $$
(15)
, где \(W_{I_{j}\cdot}\) и \ ( A_{I_{j}\cdot }\) обозначают подматрицы W и A с индексами строк в I j . В отличие от неотсутствующего случая, V зависит от j .
Аналогичную модификацию можно применить к аналогу KL (14) и мультипликативным алгоритмам Ли (5, 6), заменив W T W и W T A так же, как в (15). Обратите внимание, что повторный расчет V только увеличивает сложность метода, основанного на MSE, но не на основе KL, и в этом случае его, тем не менее, необходимо пересчитывать. Способность обрабатывать пропущенные значения имеет решающее значение в приложениях и, как оказалось, приводит к появлению нового метода вменения пропущенных значений (описанного в разделе «Вменение пропущенных значений» и нового метода выбора k (описано в разделе «Выбор k »).
Способность обрабатывать пропущенные значения имеет решающее значение в приложениях и, как оказалось, приводит к появлению нового метода вменения пропущенных значений (описанного в разделе «Вменение пропущенных значений» и нового метода выбора k (описано в разделе «Выбор k »).
Вменение отсутствующих значений
Как обсуждалось в разделе «Отсутствующие записи», информация в A в основном избыточна для целей факторизации. Следовательно, приемлемые результаты все еще могут быть достигнуты с отсутствующими элементами, присутствующими в матрице A . Реконструкции \(\шляпа {A} = WH\) по отсутствующим записям являются разумными прогнозами для отсутствующих значений.
Преимущество импутации NMF заключается в том, что он учитывает все полные записи при импутации одной отсутствующей записи, что означает, что NMF может фиксировать сложную зависимость между статьями, в то время как обычный статистический алгоритм импутации пропущенных значений, например, missForest [9] и MICE [10], обычно моделируют отсутствующие записи по функциям (столбец за столбцом или строка за строкой) и перебирают все функции несколько раз, чтобы зафиксировать сложную зависимость.
Выбор из
k Выбор гиперпараметров является типичной проблемой для всех алгоритмов обучения без учителя. Ранг k является единственным, но критическим параметром, который априори неизвестен. Брюнет и др. [2] предлагает попробовать несколько запусков каждого k и использует матрицу консенсуса для определения к . Эта идея предполагает, что назначение кластеров стабильно от запуска к запуску, если кластеризация в k классов сильна. Однако это предположение нуждается в проверке, и целью NMF не всегда является кластеризация. Кроме того, идея консенсуса состоит в том, чтобы выбрать k с меньшим разбросом в кластеризации, что не обязательно является правильным показателем для выбора k . Мы утверждаем, что разумный k должен уметь удалять шум и восстанавливать сигнал. Одна из идей, взятая из шумоподавляющего автокодировщика [17], заключается в добавлении шума к матрице A , разложите зашумленную версию на множители и сравните восстановленную матрицу с исходной A . Можно ожидать, что «правильный» k должен давать наименьшую частоту ошибок. Это может быть общим подходом для многих алгоритмов обучения без учителя. A также должно быть неотрицательным, что предполагает, что введенный шум может также внести смещение.Кроме того, выбор распределения шума является еще одним гиперпараметром, который не является очевидным для выбора.0011
Можно ожидать, что «правильный» k должен давать наименьшую частоту ошибок. Это может быть общим подходом для многих алгоритмов обучения без учителя. A также должно быть неотрицательным, что предполагает, что введенный шум может также внести смещение.Кроме того, выбор распределения шума является еще одним гиперпараметром, который не является очевидным для выбора.0011
Учитывая возможность обработки отсутствующих записей в NMF, описанную в предыдущем разделе, и мощное вменение пропущенных значений NMF, продемонстрированное в разделе «Вменение пропущенных значений», мы предлагаем новый подход, похожий на хорошо известный метод обучения. раздельный подход к валидации в обучении с учителем.
- 1.
Некоторая часть (например, 30%) записей случайно удалена (выбрана как отсутствующая) из A .
- 2.
Удаленные записи вменены NMF с набором различных к с.
- 3.
Вмененные записи сравниваются с их наблюдаемыми значениями, и выбирается k , дающая наименьшую ошибку.

Приведенный выше подход можно аргументировать предположением, что только правильный k , если он существует, имеет правильную декомпозицию, которая может восстановить недостающие записи. В отличие от разделения обучения и проверки в обучении с учителем, из-за обычно большого количества записей в A у нас обычно очень большой «размер выборки». К этому подходу также можно легко адаптировать идею перекрестной проверки. Эта идея должна применяться к любому методу обучения без учителя, который обрабатывает пропущенные значения. Обратите внимание, что здесь также можно легко включить начальную загрузку и перекрестную проверку.
Маскирование, деконволюция содержимого и проектируемая факторизация
Микрочипы являются популярными методами измерения экспрессии мРНК. Строго говоря, профиль мРНК определенного образца опухоли обычно представляет собой смесь раковых и здоровых профилей, поскольку собранные ткани «загрязнены» здоровыми клетками. Чистый профиль рака обычно больше подходит для последующего анализа [14].
Для этой цели можно использовать NMF, отформатировав его как
$$ A \ приблизительно W H + W_{0} H_{1}, $$
(16)
, где матрица W — неизвестный профиль рака, а матрица W 0 — известный профиль здоровья. Строки A представляют зонды или гены, а столбцы представляют пациентов или образцы. Здесь задача состоит в том, чтобы решить W , H и H 1 по заданным A и W 0 , что можно рассматривать как «управляемый» NMF. В этом разложении число столбцов W можно интерпретировать как количество неизвестных раковых профилей или типов клеток. Соответствующий процент опухоли образца j можно оценить как
$$ \hat r_{j} = \frac{\sum_{i} W_{i, \cdot} H_{\cdot, j}} {\sum_{i} \left(W_{i \cdot} H_ {\cdot j} + W_{0, i\cdot} H_{1, \cdot j}\right)}. $$
(17)
Более общая реализация заключается в использовании матриц масок для W и H , где замаскированные записи фиксируются на своих начальных значениях или равны 0, если они не инициализированы. Действительно, можно рассматривать это как форму жесткой регуляризации. Сразу видно, что описанная выше деконволюция является частным случаем этого метода маскирования, при котором замаскированные записи инициализируются известным профилем и фиксируются. Этот метод предназначен для интеграции знаний предметной области, таких как подсети генов, пути и т. Д., Чтобы направить NMF к более биологически значимому разложению.
Действительно, можно рассматривать это как форму жесткой регуляризации. Сразу видно, что описанная выше деконволюция является частным случаем этого метода маскирования, при котором замаскированные записи инициализируются известным профилем и фиксируются. Этот метод предназначен для интеграции знаний предметной области, таких как подсети генов, пути и т. Д., Чтобы направить NMF к более биологически значимому разложению.
Например, предположим \(\mathcal {S} = \{S_{1},..., S_{L}\}\), где каждый S l , l =1 ,..., L представляет собой набор генов в определенной подсети или пути l . One can design W as a matrix of K columns ( K ≥ L ), with w i l =0 when i ∉ S l . Факторизация NMF изучит вес или вклад w il реального гена i в подсети или пути l из данных. Можно также интерпретировать \( h_{l j}\left (\sum _{i} w_{i l}\right) \) как уровень экспрессии подсети или пути l у пациента j . Кроме того, W · j вместо j = L +1,…, K являются неизвестными подсетями или путями. Обратите внимание, что K заранее неизвестен, но может быть определен методом, представленным в разделе «Выбор k ».
Можно также интерпретировать \( h_{l j}\left (\sum _{i} w_{i l}\right) \) как уровень экспрессии подсети или пути l у пациента j . Кроме того, W · j вместо j = L +1,…, K являются неизвестными подсетями или путями. Обратите внимание, что K заранее неизвестен, но может быть определен методом, представленным в разделе «Выбор k ».
Аналогично, если S l представляет собой набор маркерных генов (тех, которые, как известно, экспрессируются только в определенном типе клеток/ткани), для ткани l , если \(w_{i l } = 0, \, i \in \bigcup \limits _{q\neq l} S_{q}\), можно найти относительное содержание каждого типа ткани в образце. Формула, аналогичная уравнению (17) можно использовать для вычисления пропорций известных ( j =1,…, L ) и неизвестные ( j = L +1,…, K ) типы клеток/тканей.
Другим возможным применением маскирования является метаанализ различных типов рака, который находит метагены, общие для всех видов рака. Например, предположим, что A 1 , A 2 являются выражениями микрочипов рака легких и рака предстательной железы. Установив определенные части матрицы коэффициентов H в 0, например,
Например, предположим, что A 1 , A 2 являются выражениями микрочипов рака легких и рака предстательной железы. Установив определенные части матрицы коэффициентов H в 0, например,
$$ \left(A_{1}\,A_{2}\right) = \left(W_{0}\,W_{1}\,W_{2}\right) \left(\begin{массив }{cc} H_{01} & H_{02} \\ H_{1} & 0\\ 0 & H_{2} \end{массив}\right), $$
(18)
мы можем ожидать что W 1 и W 2 являются специфическими профилями для рака легких и простаты, а W 0 является общим профилем.
Доступность данных и материалов
Подмножество набора данных Botling NSCLC [8], используемое в статье, доступно в пакете R NNLM. Код для всех экспериментов также можно найти в виньетке по адресу https://cran.r-project.org/web/packages/NNLM/vignettes/Fast-And-Versatile-NMF.pdf. Пакет NNLM доступен на CRAN и на https://github.com/linxihui/NNLM.
Сокращения
- ANLS:
Чередующийся неотрицательный метод наименьших квадратов
- KL расхождение:
Дивергенция Кульбака-Лейблера
- МКЛ:
Среднее отклонение KL
- MSE:
Среднеквадратическая ошибка
- NMF/NNMF:
Неотрицательная матричная факторизация
- ННЛМ:
Неотрицательная линейная модель
- NNLS:
Неотрицательный метод наименьших квадратов
- SCD:
Последовательный покоординатный спуск
Ссылки
Lee DD, Seung HS.
 Изучение частей объектов методом неотрицательной матричной факторизации. Природа. 1999 г.; 401: 899–91.
Изучение частей объектов методом неотрицательной матричной факторизации. Природа. 1999 г.; 401: 899–91.Артикул Google ученый
Брюне Ж.-П., Тамайо П., Голуб Т.Р., Месиров Ж.П. Обнаружение метагенов и молекулярных паттернов с использованием матричной факторизации. Proc Natl Acad Sci USA. 2007 г.; 101 (12): 4164–89.
Артикул Google ученый
Ким Х., Парк Х. Разреженные неотрицательные матричные факторизации с помощью чередующихся неотрицательных ограниченных наименьших квадратов для анализа данных микрочипов. Биоинформатика. 2007 г.; 23 (12): 1495–502.
КАС Статья Google ученый
Александров Л.Б., Ник-Зайнал С., Ведж Д.С., Кэмпбелл П.Дж., Стрэттон М.Р. Расшифровка сигнатур мутационных процессов, действующих при раке человека. Нат Жене.
 2013; 3: 246–59.
2013; 3: 246–59.КАС Google ученый
Franc V, Navara M, Hlavac V. Последовательный координатный алгоритм для неотрицательной задачи наименьших квадратов. Вычислить паттерны анальных изображений. 2005 г.; 3691: 407–414.
Артикул Google ученый
Gaujoux R, Seoighe C. Гибкий пакет R для неотрицательной матричной факторизации. Биоинформатика BMC. 2010 г.; 11:367.
Артикул Google ученый
Eddelbuettel D., Francois R.Rcpp: Полная интеграция R и C++. Программное обеспечение J Stat. 2011 г.; 40(8):1–18.
Артикул Google ученый
Ботлинг Дж., Эдлунд К., Лор М., Хеллвиг Б. и др. Открытие биомаркеров при немелкоклеточном раке легкого: интеграция профилирования экспрессии генов, метаанализа и проверки тканевого микрочипа.
 Клин Рак Рез. 2013; 19(1):194–204.
Клин Рак Рез. 2013; 19(1):194–204.КАС Статья Google ученый
Stekhoven DJ, Buehlmann P. MissForest - непараметрическое вменение пропущенных значений для данных смешанного типа. Биоинформатика. 2012 г.; 28:112–18.
КАС Статья Google ученый
Van Buuren S, Groothuis-Oudshoorn K. Белковые продукты BRCA1: функциональные мотивы. Программное обеспечение J Stat. 2011 г.; 45(3):1–67.
Google ученый
Zhang J, Wei L, Feng X, Ma Z, Wang Y. Факторизация неотрицательной матрицы выражения шаблона: алгоритм и приложения для слепого разделения источников. Компьютер Intel Neurosci. 2008 г.; 2008: 1–10. https://doi.org/10.1155/2008/168769.
Артикул Google ученый
Аббас А.
 Р., Вулслегель К., Сешасаи Д., Модрусан З., Кларк Х.Ф. Деконволюция данных микрочипов крови позволяет выявить паттерны клеточной активации при системной красной волчанке. ПЛОС Один. 2009 г.; 4(7):e6098. https://doi.org/10.1371/journal.pone.0006098.
Р., Вулслегель К., Сешасаи Д., Модрусан З., Кларк Х.Ф. Деконволюция данных микрочипов крови позволяет выявить паттерны клеточной активации при системной красной волчанке. ПЛОС Один. 2009 г.; 4(7):e6098. https://doi.org/10.1371/journal.pone.0006098.Артикул Google ученый
Gaujoux R, Seoighe C. Полууправляемая неотрицательная матричная факторизация для деконволюции экспрессии генов: тематическое исследование. Заразить Генет Эвол. 2011 г.; 12(5):913–21.
Артикул Google ученый
Quon G, Haider S, Deshwar AG, Cui A, Boutros PC, Morris Q. Вычислительная очистка профилей экспрессии отдельных опухолевых генов приводит к значительному улучшению прогностического прогнозирования. Геном Мед. 2013; 29:29.
Артикул Google ученый
Beer D, Kardia S, Huang C, Giordano T, Levin A, Misek D и др.
 Профили экспрессии генов предсказывают выживаемость пациентов с аденокарциномой легких. Нат Мед. 2002 г.; 8(8):816–24.
Профили экспрессии генов предсказывают выживаемость пациентов с аденокарциномой легких. Нат Мед. 2002 г.; 8(8):816–24.КАС Статья Google ученый
Ангел К.В., Куон Г., Хайдер С., Нгуен Ф., Дешвар А.Г., Моррис К.Д., Бутрос П.С. Реализация вычислительного алгоритма очистки смешанных профилей опухолей. Биоинформатика BMC. 2015 г.; 16:156.
Артикул Google ученый
Винсент П., Ларошель Х., Бенжио Ю., Манзагол П.А. Извлечение и составление надежных функций с помощью шумоподавляющих автоэнкодеров. В: Материалы 25-й международной конференции по машинному обучению — ICML ’08. ACM Press: 2008 г. https://doi.org/10.1145/139.0156.13.
Загрузить ссылки
Благодарности
Авторы благодарят всех сотрудников лаборатории Бутроса за поддержку, особенно доктора Кеннета Чу и доктора Каталину Ангел.
Финансирование
Это исследование было проведено при поддержке Института исследований рака Онтарио в отношении ПХБ за счет финансирования, предоставленного правительством Онтарио. Эта работа была поддержана раком простаты Канады и с гордостью финансируется Фондом Movember - Грант № RS2014-01. Д-р Бутрос был поддержан премией Исследовательского института Терри Фокса для новых исследователей и премией CIHR для новых исследователей. Этот проект был поддержан Genome Canada в рамках контракта на крупномасштабный прикладной проект с PCB и соавторами. Эта работа была поддержана программой Discovery Frontiers: Advancing Big Data Science in Genomics Research, которая совместно финансируется Советом по естественным наукам и инженерным исследованиям (NSERC) Канады, Канадскими институтами исследований в области здравоохранения (CIHR), Genome Canada и Канадский фонд инноваций (CFI). Эта работа финансировалась правительством Канады через Genome Canada и Институт геномики Онтарио (OGI-125). Финансирующая организация не играла никакой роли в разработке исследования и сборе, анализе или интерпретации данных, а также в написании рукописи.
Финансирующая организация не играла никакой роли в разработке исследования и сборе, анализе или интерпретации данных, а также в написании рукописи.
Информация об авторе
Авторы и организации
Информатика и биокомпьютинг, Институт онкологических исследований Онтарио, Торонто, Канада
Xihui Lin и Paul C. Boutros
Калифорнийский университет генетики, Анхелес, 9000 , СШАКомплексный онкологический центр Jonsson, Калифорнийский университет, Лос-Анджелес, США
Paul C. Boutros
Paul C. Boutros
Авторы
- Xihui Lin
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Paul C. Boutros
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
Contributions
XL и PBC разработали методы. XL проводил эксперименты. Все авторы принимали участие в написании рукописи. Оба автора прочитали и одобрили окончательный вариант рукописи.
XL проводил эксперименты. Все авторы принимали участие в написании рукописи. Оба автора прочитали и одобрили окончательный вариант рукописи.
Автор, ответственный за переписку
Сихуэй Лин.
Декларация этики
Одобрение этики и согласие на участие
Неприменимо.
Согласие на публикацию
Неприменимо.
Конкурирующие интересы
Авторы заявляют об отсутствии конкурирующих интересов.
Дополнительная информация
Примечание издателя
Springer Nature остается нейтральной в отношении юрисдикционных претензий в опубликованных картах и институциональной принадлежности.
Права и разрешения
Открытый доступ Эта статья распространяется в соответствии с условиями международной лицензии Creative Commons Attribution 4.0 (http://creativecommons.org/licenses/by/4.0/), которая разрешает неограниченное использование, распространение, и воспроизведение на любом носителе, при условии, что вы укажете автора(ов) оригинала и источник, предоставите ссылку на лицензию Creative Commons и укажете, были ли внесены изменения. Отказ от права Creative Commons на общественное достояние (http://creativecommons.org/publicdomain/zero/1.0/) применяется к данным, представленным в этой статье, если не указано иное.
Отказ от права Creative Commons на общественное достояние (http://creativecommons.org/publicdomain/zero/1.0/) применяется к данным, представленным в этой статье, если не указано иное.
Перепечатка и разрешения
Об этой статье
Положительно определенные матрицы | Реальная статистика с использованием Excel
Определение 1 : n × n симметричная матрица A является положительно определенной, если для любого n × 1 вектор-столбец X ≠ 0, X A является положительно полуопределенным, если для любого n × 1 вектор-столбец X , X T AX ≥ 0,
Observation : Note that if A = [ a ij ] and X = [ x i ], then
If we set X to be the column вектор с x K = 1 и x I = 0 для всех I ≠ K , затем x T AX = A x T , = A x , = A x = A x , = A и , = A. x , = и x . положительно определенный, тогда a kk > 0, что означает, что все элементы диагонали A положительны. Точно так же, если A положительно полуопределенно, то все элементы на его диагонали неотрицательны.
x , = и x . положительно определенный, тогда a kk > 0, что означает, что все элементы диагонали A положительны. Точно так же, если A положительно полуопределенно, то все элементы на его диагонали неотрицательны.
Собственность 1 : если B - M × N , затем A = B T B IS Symmetric
Доказательство: если B = [888888 гг. m × n матрица, затем A = B T B = [ a kj ] представляет собой n × n матрицу, где a kj = . A является симметричным, так как по свойству 1 матричных операций, A T = ( B T B ) T = B T T = 88 B T T = 88 B 6 T T = 8 B 6 T T = 8 B 6 T T = 9) T ) Т = Б Т Б = А .
Наблюдение : Если X = [ x i ] представляет собой вектор-столбец размером м × 1, тогда X T X = .
Свойство 2 : Если B является матрицей размера m × n , то A = B T B является положительно полуопределенной.
Доказательство. Как мы заметили в свойстве 1, A является симметричной n × n матрицей. Для любого n × 1 вектор-столбец X , BX является вектором-столбцом m × 1 [ c i ] where c i = , and so
Property 3 : If B is an m × n matrix of rank n where n ≤ m , then A = B T B — положительно определенная матрица.
Доказательство. Из доказательства свойства 2 мы знаем, что X T AX = для любого n × 1 вектор-столбец X . Теперь пусть X будет любым отличным от нуля числом 9.2388 n × 1 вектор-столбец. Если все равны нулю, то BX = 0. Но по свойству 3 матричного ранга если следует, что X = 0, что является противоречием. Поскольку BX ≠ 0, то хотя бы одно из c i ≠ 0, а значит, > 0, а это означает, что X T AX = > 0, а значит, A положительно определено.
Теперь пусть X будет любым отличным от нуля числом 9.2388 n × 1 вектор-столбец. Если все равны нулю, то BX = 0. Но по свойству 3 матричного ранга если следует, что X = 0, что является противоречием. Поскольку BX ≠ 0, то хотя бы одно из c i ≠ 0, а значит, > 0, а это означает, что X T AX = > 0, а значит, A положительно определено.
Свойство 4 : Следующее эквивалентно для симметричного n × n матрица A :
- A положительно полуопределенная
- Существует матрица U такая, что A = U T U
- Все собственные значения A неотрицательны
Доказательство: предположим (c) и покажем (b). Поскольку A симметрично, по теореме 1 спектрального разложения A имеет спектральное разложение A = CDC T , где D состоит из собственных значений λ 1 , …, λ n из A . По предположению все они неотрицательны, поэтому существует диагональная матрица D ½ , главная диагональ которой состоит из , …, . Since D ½ D ½ = D , we have
По предположению все они неотрицательны, поэтому существует диагональная матрица D ½ , главная диагональ которой состоит из , …, . Since D ½ D ½ = D , we have
and so the desired matrix is U = ( CD ½ ) T .
Предположим (b) и покажите (a). Пусть X – любой вектор-столбец размером 92 388 n 92 389 × 1. Затем
Предположим (а) и покажите (с). Пусть A положительно полуопределенно и пусть X будет собственным вектором, соответствующим собственному значению λ . Поскольку A является положительным семидефинитом, x T AX ≥ 0. Поскольку x является собственным вегектором, соответствующим λ , AX = λx и SO 0 ≤ 8. AX = λx и SO 0 ≤ 8888. T λX = λX T X . Поскольку X T X = || Х|| > 0, следует, что λ ≥ 0.
.
Доказательство: предположим (c) и покажем (b). С 9 2388 A является симметричным, по теореме 1 спектрального разложения, A имеет спектральное разложение A = CDC T , где D состоит из Eigenvalues λ . n из A . По условию все они положительны, поэтому существует диагональная матрица D ½ , главная диагональ которой состоит из , …, . С D ½ D ½ = D , у нас есть
, поэтому искомая матрица равна U = ( CD ½ ) T при условии, что мы можем показать, что 929 обратима. Теперь C является ортогональной матрицей, поэтому C -1 = C T . Поскольку D ½ является диагональной матрицей, det D ½ = произведение элементов на диагонали. Так как все элементы главной диагонали положительны, то det D ½ ≠ 0, поэтому D ½ обратимо. Таким образом, U инвертируется с обратным ( D ½ ) -1 C T ) T , который составляет CE , где E = диаг. элементов , …,
Поскольку D ½ является диагональной матрицей, det D ½ = произведение элементов на диагонали. Так как все элементы главной диагонали положительны, то det D ½ ≠ 0, поэтому D ½ обратимо. Таким образом, U инвертируется с обратным ( D ½ ) -1 C T ) T , который составляет CE , где E = диаг. элементов , …,
Предположим (b) и покажите (a). Пусть X будет любым вектором-столбцом n × 1. Тогда
Если || УБ || 2 = 0, тогда UX = 0. Поскольку U обратимо, X = U -1 UX = 0, что является противоречием. Таким образом, X T AX = || UX || 2 > 0.
Предположим (а) и покажем (в). Пусть A положительно определено и пусть X будет собственным вектором, соответствующим собственному значению λ . Поскольку A положительно определено, X T AX > 0. Поскольку x является собственным вектором, соответствующим λ , AX = λx и SO 0 < x T AX = x T λx = 8888888 λx T λx = 88888888 λx 6. Так как X T X = || Х|| > 0, то λ > 0.
Поскольку A положительно определено, X T AX > 0. Поскольку x является собственным вектором, соответствующим λ , AX = λx и SO 0 < x T AX = x T λx = 8888888 λx T λx = 88888888 λx 6. Так как X T X = || Х|| > 0, то λ > 0.
Свойство 6 : Определитель положительно определенной матрицы положителен. Кроме того, положительно полуопределенная матрица положительно определена тогда и только тогда, когда она обратима.
Доказательство. Первое утверждение следует из свойства 1 собственных значений и собственных векторов и свойства 5. Второе следует из первого и свойства 4 линейных независимых векторов.
Наблюдение : Если A является положительно полуопределенной матрицей, то она симметрична, и поэтому имеет смысл говорить о спектральном разложении A .
Определение 2 : Если A является положительно полуопределенной матрицей, то квадратный корень из A , обозначенный A ½ , определяется как N × N Матрикс CD ½ C T , где C C T , где C C. Define из . D ½ — диагональная матрица, главная диагональ которой состоит из , …, .
Свойство 7 : Если A является положительно полуопределенной матрицей, то A ½ является симметричной матрицей и A = A ½ A ½
Доказательство:
С. Диагональной матрицы является симметричным, мы имеем
Свойства 8 : any Cavariance Matrix. Если ковариационная матрица обратима, то она положительно определена.
Доказательство. Мы покажем доказательство выборочной ковариации n × n матрицы S для X . Доказательство для матрицы населения аналогично. Обратите внимание, что
Доказательство для матрицы населения аналогично. Обратите внимание, что
, где x = [ x IJ ] - K × N , такой, что для каждого I, { x 1 { x 2199: 1 { x IJ : 1 { x IJ : 1 { x IJ : 1 { x IJ
9: 1888888 гг. выборка для случайной величины x i . Теперь пусть Y будет любым вектором-столбцом размером n x 1. Таким образом,Теперь следующие матрицы могут быть представлены в виде скалярного произведения, которое дает один и тот же скаляр c i
Таким образом,
показывает, что любая ковариационная матрица является положительно полуопределенной. Второе утверждение следует из свойства 6.
Наблюдение . Следствием свойств 4 и 8 является то, что все собственные значения ковариационной (или корреляционной) матрицы являются неотрицательными действительными числами.
Функция реальной статистики : Ресурсный пакет реальной статистики предоставляет следующую функцию массива, где R1 — это массив k × k .
MSQRT (R1): создает массив k × k , который является квадратным корнем матрицы, представленной диапазоном R1.
Пример 1 1.
Рисунок 1 – Квадратный корень матрицы
Диапазон A9:C9 содержит собственные значения матрицы A , а диапазон A10:C12 содержит соответствующие собственные векторы (которые повторяются как матрица C ). Их можно рассчитать с помощью eVECTORS(A4:C6). D ½ — диагональная матрица, главная диагональ которой состоит из квадратных корней собственных значений.
Таким образом, квадратный корень из A дается в диапазоне I4:K6, рассчитанном по формуле массива достигается с помощью формулы массива =MSQRT(A4:C6).
Обратите внимание, что спектральное разложение A = CDC T записывается формулой массива
=MMULT(E4:G6,MMULT(DIAGONAL(A9:C9),E14:G16))
Положительно определенная матрица
Марко Табога, доктор философии
Квадратная матрица
положительно определенный, если до умножения и после умножения на одно и то же
вектор всегда дает в результате положительное число, независимо от того, как мы
выбрать вектор.
Положительно определенные симметричные матрицы обладают тем свойством, что все их собственные значения положительны.
Содержание
Реальные квадратичные формы
Ограничение внимания на симметричные матрицы
Определенность
Фокус на позитивность
. Положительный определенный матричный
Собственные значения положительно-полуопределенной матрицы
Сложный случай
Решаемые упражнения
Упражнение 1
Упражнение 2
Упражнение 3
Вещественные квадратичные формы
3 Начнем с определения квадратичных форм. На данный момент мы ограничимся внимание на действительные матрицы и действительные векторы. В конце этой лекции мы обсудить более общий сложный случай.
Определение
Позволять
быть
реальная матрица. Квадратичная форма в
это
трансформациягде
это
вектор и
является его транспонированием.
Квадратичная форма в
это
трансформациягде
это
вектор и
является его транспонированием.
Преобразование является скаляром, потому что это вектор-строка и его произведение на вектор столбца дает скаляр в результате.
Пример ОпределитьДано а вектор , квадратичная форма, определяемая матрицей is
Ограничение внимания симметричными матрицами
Когда мы изучаем квадратичные формы, мы можем ограничить наше внимание симметричными матрицы без ограничения общности.
Помните, что матрица симметричен тогда и только тогда если
Любую квадратичную форму можно записать как где в ногу мы использовали тот факт, что является скаляром, а транспонирование скаляра равно самому скаляру.
матрикс симметричный потому что
Таким образом, мы доказали, что всегда можем написать квадратичную форму
как где
симметричен.
Определенность
Квадратные матрицы можно классифицировать на основе знака квадратичных форм. что они определяют.
В дальнейшем iff означает «тогда и только тогда, когда».
Определение Позволять быть пространством всех векторы, имеющие действительные записи. А вещественная симметричная матрица говорят:
положительно определенный тогда и только тогда, когда для любого ненулевого ;
положительно полуопределенный тогда и только тогда, когда для любого ;
отрицательно определенный тогда и только тогда, когда для любого ненулевого ;
отрицательный полуопределенный тогда и только тогда, когда для любого ;
неопределенный, если и только если существуют такой, что а также .

Давайте сделаем пример.
Пример ОпределитьДано а вектор , квадратичная форма, определяемая матрицей isSince в сумма всякий раз или же (следовательно ), матрица положительно определена.
Фокус на позитиве
С этого момента мы в основном сосредоточимся на положительно определенных и полуопределенных матрицы. Результаты, полученные для этих матриц, могут быть оперативно адаптированы к отрицательно определенные и полуопределенные матрицы. Собственно говоря, если отрицательно (полу)определенно, то положительно (полу)определенно. Таким образом, результаты часто можно адаптировать, просто переключение знака.
Положительно определенная матрица полного ранга
Далее следует важный факт.
Предложение
Позволять
быть
матрица. Если
положительно определена, то
полный ранг.
Если
положительно определена, то
полный ранг.
Доказательство
Доказательство от противного. Предположим, что не является полноценным. Тогда его столбцы не линейно независимы. Как следствие, есть вектор такой что мы можно предварительно умножить обе части уравнения на а также получить с положительно определена, это возможно, только если , противоречие. Таким образом должен быть полноценным.
Собственные значения положительно определенной матрицы
Следующее предложение дает критерий определенности.
Предложение Настоящий симметричный матрица положительно определена тогда и только тогда, когда все ее собственные значения строго положительные действительные числа.
Доказательство
Докажем часть «только если», начиная
из предположения, что
положительно определена. Позволять
быть собственным значением
а также
один из связанных с ним собственных векторов. Симметрия
подразумевает, что
реален (см. лекцию о
характеристики
собственных значений и собственных векторов). Более того,
можно выбрать реальным, поскольку реальное решение
к
уравнение
гарантированно существует (потому что
имеет дефект ранга по определению собственного значения). Тогда мы
естьгде
является нормой
.
С
является собственным вектором,
.
Кроме того, в силу свойства определенности нормы
.
Таким образом, мы
естьпотому что
по гипотезе, что
положительно определена (выше мы показали, что квадратичная форма
включает действительный вектор
,
что требуется в нашем определении положительной определенности). Мы доказали
что любое собственное значение
является строго положительным, что и требовалось. Давайте теперь докажем часть «если», начиная
из предположения, что все собственные значения
являются строго положительными действительными числами.
Позволять
быть собственным значением
а также
один из связанных с ним собственных векторов. Симметрия
подразумевает, что
реален (см. лекцию о
характеристики
собственных значений и собственных векторов). Более того,
можно выбрать реальным, поскольку реальное решение
к
уравнение
гарантированно существует (потому что
имеет дефект ранга по определению собственного значения). Тогда мы
естьгде
является нормой
.
С
является собственным вектором,
.
Кроме того, в силу свойства определенности нормы
.
Таким образом, мы
естьпотому что
по гипотезе, что
положительно определена (выше мы показали, что квадратичная форма
включает действительный вектор
,
что требуется в нашем определении положительной определенности). Мы доказали
что любое собственное значение
является строго положительным, что и требовалось. Давайте теперь докажем часть «если», начиная
из предположения, что все собственные значения
являются строго положительными действительными числами. С
вещественно и симметрично, его можно диагонализовать как
следует: где
ортогонален и
представляет собой диагональную матрицу, имеющую собственные значения
на главной диагонали (как было доказано в лекции о
нормальные матрицы). Собственные значения
строго положительны, поэтому мы можем
написатьгде
диагональная матрица такая, что ее
-й
вход
удовлетворяет для
.
Следовательно,
а также,
для любого вектора
,
мы
есть
матрица
,
будучи ортогональным, обратим
(отсюда полноценный). Матрица
является диагональным (следовательно, треугольным) и его диагональные элементы строго положительны,
что подразумевает, что
обратим (следовательно, полноранговый)
свойства треугольника
матрицы. Продукт
из двух полноранговых матриц является полноранговой. Следовательно,
является полноценным.
Таким образом, потому что
.
В силу положительной определенности нормы отсюда следует, что
а также,
как
следствие, Таким образом,
положительно определена.
С
вещественно и симметрично, его можно диагонализовать как
следует: где
ортогонален и
представляет собой диагональную матрицу, имеющую собственные значения
на главной диагонали (как было доказано в лекции о
нормальные матрицы). Собственные значения
строго положительны, поэтому мы можем
написатьгде
диагональная матрица такая, что ее
-й
вход
удовлетворяет для
.
Следовательно,
а также,
для любого вектора
,
мы
есть
матрица
,
будучи ортогональным, обратим
(отсюда полноценный). Матрица
является диагональным (следовательно, треугольным) и его диагональные элементы строго положительны,
что подразумевает, что
обратим (следовательно, полноранговый)
свойства треугольника
матрицы. Продукт
из двух полноранговых матриц является полноранговой. Следовательно,
является полноценным.
Таким образом, потому что
.
В силу положительной определенности нормы отсюда следует, что
а также,
как
следствие, Таким образом,
положительно определена.
Собственные значения положительной полуопределенной матрицы
Очень похожее утверждение верно для положительно полуопределенных матриц.
В дальнейшем положительное действительное число означает действительное число, которое больше, чем или равным нулю.
Предложение Настоящий симметричный матрица положительно полуопределенным тогда и только тогда, когда все его собственные значения положительные действительные числа.
Доказательство
Мы не повторяем все детали
доказательство, и мы просто подчеркнем, где предыдущее доказательство (для положительного
определенный случай) необходимо изменить. Первое изменение находится в части «только если»,
где мы сейчас
естьпотому что
по гипотезе, что
является положительно полуопределенной. Второе изменение находится в части «если», где мы
имеют
потому что
записи
уже не гарантируются строго положительными и, как следствие,
не гарантируется полный ранг. Это следует из того
Это следует из того
Сложный кейс
Когда матрица и векторы могут быть комплексными, квадратичная форма становитсягде обозначает сопряженное транспонировать .
Позволять быть пространством всех вектора со сложными элементами. А сложная матрица говорят:
положительно определенный тогда и только тогда, когда действительна (т. е. имеет нулевую комплексную часть) и для любого ненулевого ;
положительно полуопределенный тогда и только тогда, когда действительна (т. е. имеет нулевую комплексную часть) и для любого .
Аналогично определяются отрицательно определенный и полуопределенный случаи.
Обратите внимание, что сопряженная транспозиция не затрагивает действительный скаляр. Как
следствие, если комплексная матрица положительно определена (или полуопределена),
тогда для
Любые
,
что подразумевает, что
.
Другими словами, если комплексная матрица положительно определена, то она
эрмитов.
Как
следствие, если комплексная матрица положительно определена (или полуопределена),
тогда для
Любые
,
что подразумевает, что
.
Другими словами, если комплексная матрица положительно определена, то она
эрмитов.
Также в комплексном случае положительно определенная матрица является полноранговым (приведенное выше доказательство практически не изменилось).
Более того, поскольку эрмитова, она нормальна и ее собственные значения вещественны. У нас все еще есть это является положительно полуопределенным (определенным) тогда и только тогда, когда его собственные значения положительные (соответственно строго положительные) действительные числа. Доказательства почти идентичны тем, которые мы видели для реального случая. При адаптации этих доказательств, нам просто нужно помнить, что в комплексе случай
Решенные упражнения
Ниже вы можете найти несколько упражнений с поясненными решениями.
Упражнение 1
Позволять быть комплексной матрицей и один из его собственных векторов. Вы можете написать квадратичную форму с точки зрения ?
Решение
Пусть быть собственным значением, связанным с . Затем
Упражнение 2
Можете ли вы сказать, является ли матрица является положительно определенный?
Решение
Пусть быть вектор. Обозначим его записи через а также . Затем, Затем, если а также является положительно полуопределенной. Однако оно не является положительно определенным, поскольку существует существуют ненулевые векторы, например вектортакой что .
Упражнение 3
Предположим, что представляет собой комплексную отрицательно определенную матрицу. Что вы можете сказать о знаке его собственные значения?
Решение
Если
отрицательно определена,
тогда для
Любые
.


 Но это ведь не значит, что он плохой. Это излишнее ожидание в напряжении заставило зрителей так думать.
Но это ведь не значит, что он плохой. Это излишнее ожидание в напряжении заставило зрителей так думать. Поскольку в случае их успеха человечество, вероятно, погибнет, правительство Зиона начинает усиленно готовиться к обороне, а фанатик Морфеус ставит все карты на избранного Нео, который должен добраться до Источника и повернуть там какой-то рубильник, чтобы остановить войну. Чтобы попасть к Источнику, необходимо для начала разыскать Мастера Ключей — маленького и сухонького старичка-азиата.
Поскольку в случае их успеха человечество, вероятно, погибнет, правительство Зиона начинает усиленно готовиться к обороне, а фанатик Морфеус ставит все карты на избранного Нео, который должен добраться до Источника и повернуть там какой-то рубильник, чтобы остановить войну. Чтобы попасть к Источнику, необходимо для начала разыскать Мастера Ключей — маленького и сухонького старичка-азиата. Научился летать, а тебе говорят: «Летать можно только по квартире. И вообще, у нас тут это не принято».
Научился летать, а тебе говорят: «Летать можно только по квартире. И вообще, у нас тут это не принято».





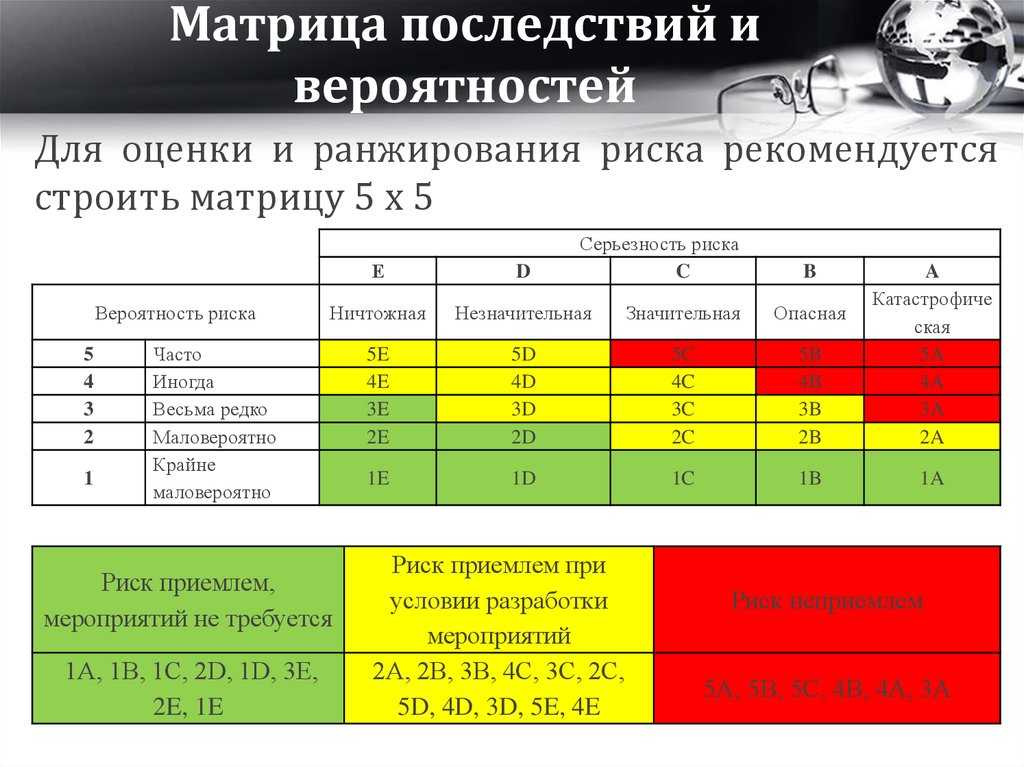

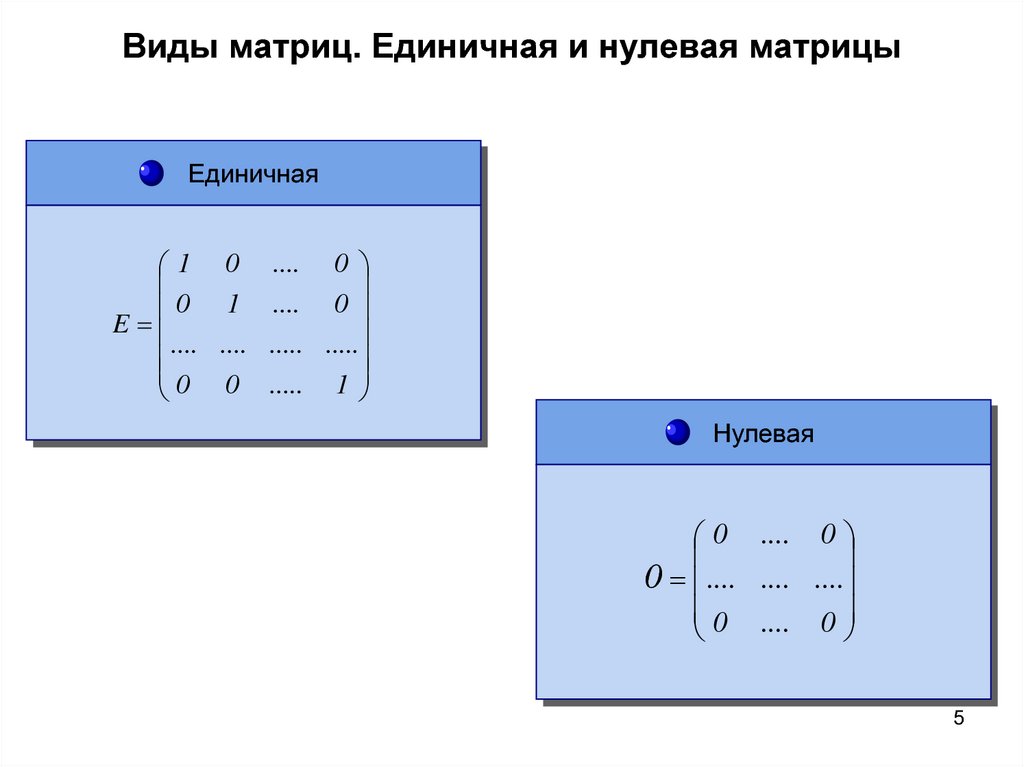
 Познан. Психол. 9, 441–474 (1977).
Познан. Психол. 9, 441–474 (1977).

 Наука 268 , 1158–1161 (1995).
Наука 268 , 1158–1161 (1995). Нейронные вычисления. 7 , 1129–1159 (1995).
Нейронные вычисления. 7 , 1129–1159 (1995). B. Итеративный метод исправления наблюдаемых распределений. Астрон. J. 74 , 745–754 (1974).
B. Итеративный метод исправления наблюдаемых распределений. Астрон. J. 74 , 745–754 (1974). packages("expm")
packages("expm")  обращений
обращений

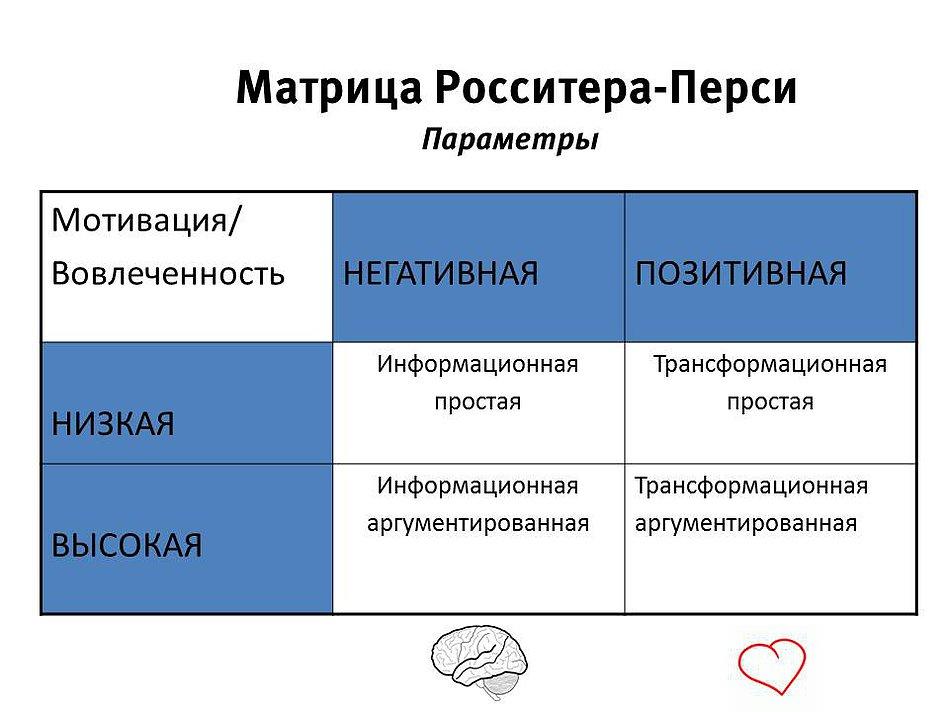 Изучение частей объектов методом неотрицательной матричной факторизации. Природа. 1999 г.; 401: 899–91.
Изучение частей объектов методом неотрицательной матричной факторизации. Природа. 1999 г.; 401: 899–91. 2013; 3: 246–59.
2013; 3: 246–59. Клин Рак Рез. 2013; 19(1):194–204.
Клин Рак Рез. 2013; 19(1):194–204.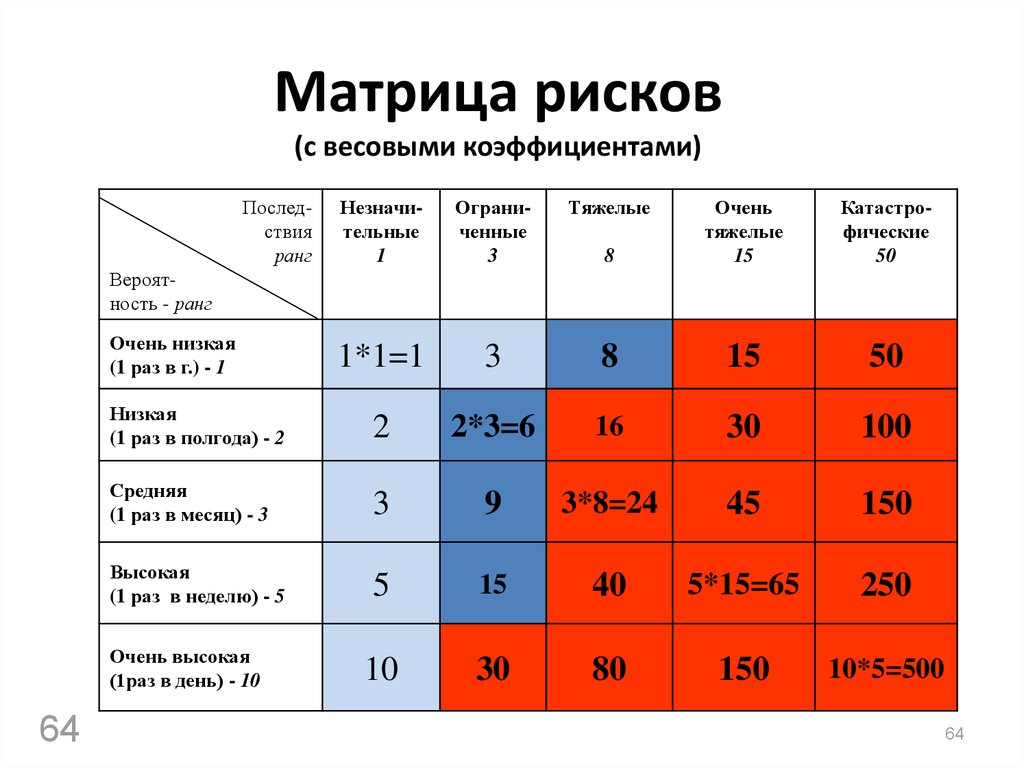 Р., Вулслегель К., Сешасаи Д., Модрусан З., Кларк Х.Ф. Деконволюция данных микрочипов крови позволяет выявить паттерны клеточной активации при системной красной волчанке. ПЛОС Один. 2009 г.; 4(7):e6098. https://doi.org/10.1371/journal.pone.0006098.
Р., Вулслегель К., Сешасаи Д., Модрусан З., Кларк Х.Ф. Деконволюция данных микрочипов крови позволяет выявить паттерны клеточной активации при системной красной волчанке. ПЛОС Один. 2009 г.; 4(7):e6098. https://doi.org/10.1371/journal.pone.0006098. Профили экспрессии генов предсказывают выживаемость пациентов с аденокарциномой легких. Нат Мед. 2002 г.; 8(8):816–24.
Профили экспрессии генов предсказывают выживаемость пациентов с аденокарциномой легких. Нат Мед. 2002 г.; 8(8):816–24.