При умножении степеней с одинаковыми показателями: Умножение степеней с одинаковыми основаниями — урок. Алгебра, 7 класс.

Содержание

Свойства степени с натуральным показателем / Алгебра / Справочник по математике 5-9 класс

Главная
Справочники
Справочник по математике 5-9 класс
Алгебра
Свойства степени с натуральным показателем

Основное свойство степени

Для любого числа и любых натуральных чисел и справедливо равенство: .

Тождество выражает основное свойство степени.

Основное свойство степени распространяется и на произведение трех и более степеней: .

Из основного свойства степеней получаем правило умножения степеней:

при умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели степеней складывают.

Примеры:

Частное степеней

Для любого числа и любых натуральных чисел и , таких, что , справедливо равенство: .

Правило деления степеней:

при делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.

Примеры:

Если правило деления применить к частному (т.е. когда ), то получится

Степень с нулевым показателем не была определена, но при всяком и любом натуральном справедливо равенство:

Получается, можно считать, что при , справедливо равенство:

Степень числа , не равного нулю, с нулевым показателем равна единице.

Примеры:

Возведение степени в степень

Для любого числа и любых натуральных чисел и справедливо равенство: .

Правило возведения степени в степень:

при возведении степени в степень показатели перемножают, а основание оставляют прежним.

Пример:

Возведение произведения в степень

Для любых чисел и и любого натурального числа справедливо равенство: .

Аналогичное свойство справедливо и для произведения трех и более множителей: .

Правило возведения произведения в степень:

при возведении произведения в степень каждый множитель возводят в эту степень и полученные результаты перемножают.

Пример:

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Введение в алгебру

Линейное уравнение с одной переменной

Решение задач с помощью уравнений

Тождественно равные выражения. Тождества

Степень с натуральным показателем

Одночлены

Многочлены

Сложение и вычитание многочленов

Умножение одночлена на многочлен

Умножение многочлена на многочлен

Разложение многочленов на множители

Формулы сокращенного умножения

Функции

Системы линейных уравнений с двумя переменными

Алгебра

Правило встречается в следующих упражнениях:

7 класс

Номер 393, Мерзляк, Полонский, Якир, Учебник

Номер 413, Мерзляк, Полонский, Якир, Учебник

Номер 417, Мерзляк, Полонский, Якир, Учебник

Номер 418, Мерзляк, Полонский, Якир, Учебник

Номер 501, Мерзляк, Полонский, Якир, Учебник

Номер 512, Мерзляк, Полонский, Якир, Учебник

Номер 677, Мерзляк, Полонский, Якир, Учебник

Номер 680, Мерзляк, Полонский, Якир, Учебник

Номер 726, Мерзляк, Полонский, Якир, Учебник

Номер 902, Мерзляк, Полонский, Якир, Учебник

формулировки, доказательства, примеры.

Что нужно запомнить

Понятие степени в математике вводится еще в 7 классе на уроке алгебры. И в дальнейшем на протяжении всего курса изучения математики это понятие активно используется в различных своих видах. Степени — достаточно трудная тема, требующая запоминания значений и умения правильно и быстро сосчитать. Для более быстрой и качественной работы со степенями математики придумали свойства степени. Они помогают сократить большие вычисления, преобразовать огромный пример в одно число в какой-либо степени. Свойств не так уж и много, и все они легко запоминаются и применяются на практике. Поэтому в статье рассмотрены основные свойства степени, а также то, где они применяются.

Свойства степени

Мы рассмотрим 12 свойств степени, в том числе и свойства степеней с одинаковыми основаниями, и к каждому свойству приведем пример. Каждое из этих свойств поможет вам быстрее решать задания со степенями, а так же спасет вас от многочисленных вычислительных ошибок.

1-е свойство.

Про это свойство многие очень часто забывают, делают ошибки, представляя число в нулевой степени как ноль.

2-е свойство.

3-е свойство.

Нужно помнить, что это свойство можно применять только при произведении чисел, при сумме оно не работает! И нельзя забывать, что это, и следующее, свойства применяются только к степеням с одинаковыми основаниями.

4-е свойство.

Если в знаменателе число возведено в отрицательную степень, то при вычитании степень знаменателя берется в скобки для правильной замены знака при дальнейших вычислениях.

Свойство работает только при делении, при вычитании не применяется!

5-е свойство.

6-е свойство.

Это свойство можно применить и в обратную сторону. Единица деленная на число в какой-то степени есть это число в минусовой степени.

7-е свойство.

Это свойство нельзя применять к сумме и разности! При возведении в степень суммы или разности используются формулы сокращенного умножения, а не свойства степени.

8-е свойство.

9-е свойство.

Это свойство работает для любой дробной степени с числителем, равным единице, формула будет та же, только степень корня будет меняться в зависимости от знаменателя степени.

Также это свойство часто используют в обратном порядке. Корень любой степени из числа можно представить, как это число в степени единица деленная на степень корня. Это свойство очень полезно в случаях, если корень из числа не извлекается.

10-е свойство.

Это свойство работает не только с квадратным корнем и второй степенью. Если степень корня и степень, в которую возводят этот корень, совпадают, то ответом будет подкоренное выражение.

11-е свойство.

Это свойство нужно уметь вовремя увидеть при решении, чтобы избавить себя от огромных вычислений.

12-е свойство.

Каждое из этих свойств не раз встретится вам в заданиях, оно может быть дано в чистом виде, а может требовать некоторых преобразований и применения других формул. Поэтому для правильного решения мало знать только свойства, нужно практиковаться и подключать остальные математические знания.

Применение степеней и их свойств

Они активно применяются в алгебре и геометрии. Степени в математике имеют отдельное, важное место. С их помощью решаются показательные уравнения и неравенства, а так же степенями часто усложняют уравнения и примеры, относящиеся к другим разделам математики. Степени помогают избежать больших и долгих расчетов, степени легче сокращать и вычислять. Но для работы с большими степенями, либо со степенями больших чисел, нужно знать не только свойства степени, а грамотно работать и с основаниями, уметь их разложить, чтобы облегчить себе задачу. Для удобства следует знать еще и значение чисел, возведенных в степень. Это сократит ваше время при решении, исключив необходимость долгих вычислений.

Особую роль понятие степени играет в логарифмах. Так как логарифм, по сути своей, и есть степень числа.

Формулы сокращенного умножения — еще один пример использования степеней. В них нельзя применять свойства степеней, они раскладываются по особым правилам, но в каждой формуле сокращенного умножения неизменно присутствуют степени.

Так же степени активно используются в физике и информатике. Все переводы в систему СИ производятся с помощью степеней, а в дальнейшем при решении задач применяются свойства степени. В информатике активно используются степени двойки, для удобства счета и упрощения восприятия чисел. Дальнейшие расчеты по переводам единиц измерения или же расчеты задач, так же, как и в физике, происходят с использованием свойств степени.

Еще степени очень полезны в астрономии, там редко можно встретить применение свойств степени, но сами степени активно используются для сокращения записи различных величин и расстояний.

Степени применяют и в обычной жизни, при расчетах площадей, объемов, расстояний.

С помощью степеней записывают очень большие и очень маленькие величины в любых сферах науки.

Показательные уравнения и неравенства

Особое место свойства степени занимают именно в показательных уравнениях и неравенствах. Эти задания очень часто встречаются, как в школьном курсе, так и на экзаменах. Все они решаются за счет применения свойств степени. Неизвестное всегда находится в самой степени, поэтому зная все свойства, решить такое уравнение или неравенство не составит труда.

В предыдущей статье мы рассказали, что из себя представляют одночлены. В этом материале разберем, как решать примеры и задачи, в которых они применяются. Здесь будут рассмотрены такие действия, как вычитание, сложение, умножение, деление одночленов и возведение их в степень с натуральным показателем. Мы покажем, как определяются такие операции, обозначим основные правила их выполнения и то, что должно получится в результате. Все теоретические положения, как обычно, будут проиллюстрированы примерами задач с описаниями решений.

Удобнее всего работать со стандартной записью одночленов, поэтому все выражения, которые будут использованы в статье, мы приводим в стандартном виде. Если изначально они заданы иначе, рекомендуется сначала привести их к общепринятой форме.

Правила сложения и вычитания одночленов

Наиболее простые действия, которые можно проводить с одночленами – это вычитание и сложение. В общем случае результатом этих действий будет являться многочлен (одночлен возможен в некоторых частных случаях).

Когда мы складываем или вычитаем одночлены, сначала записываем в общепринятой форме соответствующую сумму и разность, после чего упрощаем получившееся выражение. Если есть подобные слагаемые, их нужно привести, скобки – раскрыть. Поясним на примере.

Пример 1

Условие: выполните сложение одночленов − 3 · x и 2 , 72 · x 3 · y 5 · z .

Решение

Запишем сумму исходных выражений. Добавим скобки и поставим между ними плюс. У нас получится следующее:

(− 3 · x) + (2 , 72 · x 3 · y 5 · z)

Когда мы выполним раскрытие скобок, получится — 3 · x + 2 , 72 · x 3 · y 5 · z . Это многочлен, записанный в стандартной форме, который и будет результатом сложения данных одночленов.

Ответ: (− 3 · x) + (2 , 72 · x 3 · y 5 · z) = − 3 · x + 2 , 72 · x 3 · y 5 · z .

Если у нас задано три, четыре и больше слагаемых, мы осуществляем это действие точно так же.

Пример 2

Условие: проведите в правильном порядке указанные действия с многочленами

3 · a 2 — (- 4 · a · c) + a 2 — 7 · a 2 + 4 9 — 2 2 3 · a · c

Решение

Начнем с раскрытия скобок.

3 · a 2 + 4 · a · c + a 2 — 7 · a 2 + 4 9 — 2 2 3 · a · c

Мы видим, что полученное выражение можно упростить путем приведения подобных слагаемых:

3 · a 2 + 4 · a · c + a 2 — 7 · a 2 + 4 9 — 2 2 3 · a · c = = (3 · a 2 + a 2 — 7 · a 2) + 4 · a · c — 2 2 3 · a · c + 4 9 = = — 3 · a 2 + 1 1 3 · a · c + 4 9

У нас получился многочлен, который и будет результатом данного действия.

Ответ: 3 · a 2 — (- 4 · a · c) + a 2 — 7 · a 2 + 4 9 — 2 2 3 · a · c = — 3 · a 2 + 1 1 3 · a · c + 4 9

В принципе, мы можем выполнить сложение и вычитание двух одночленов с некоторыми ограничениями так, чтобы получить в итоге одночлен. Для этого нужно соблюсти некоторые условия, касающиеся слагаемых и вычитаемых одночленов. О том, как это делается, мы расскажем в отдельной статье.

Правила умножения одночленов

Действие умножения не налагает никаких ограничений на множители. Умножаемые одночлены не должны соответствовать никаким дополнительным условиям, чтобы в результате получится одночлен.

Чтобы выполнить умножение одночленов, нужно выполнить следующие шаги:

Правильно записать произведение.
Раскрыть скобки в полученном выражении.
Сгруппировать по возможности множители с одинаковыми переменными и числовые множители отдельно.
Выполнить необходимые действия с числами и применить к оставшимся множителям свойство умножения степеней с одинаковыми основаниями.

Посмотрим, как это делается на практике.

Пример 3

Условие: выполните умножение одночленов 2 · x 4 · y · z и — 7 16 · t 2 · x 2 · z 11 .

Решение

Начнем с составления произведения.

Раскрываем в нем скобки и получаем следующее:

2 · x 4 · y · z · — 7 16 · t 2 · x 2 · z 11

2 · — 7 16 · t 2 · x 4 · x 2 · y · z 3 · z 11

Все, что нам осталось сделать – это умножить числа в первых скобках и применить свойство степеней для вторых. В итоге получим следующее:

2 · — 7 16 · t 2 · x 4 · x 2 · y · z 3 · z 11 = — 7 8 · t 2 · x 4 + 2 · y · z 3 + 11 = = — 7 8 · t 2 · x 6 · y · z 14

Ответ: 2 · x 4 · y · z · — 7 16 · t 2 · x 2 · z 11 = — 7 8 · t 2 · x 6 · y · z 14 .

Если у нас в условии стоят три многочлена и больше, мы умножаем их по точно такому же алгоритму. Более подробно вопрос умножения одночленов мы рассмотрим в рамках отдельного материала.

Правила возведения одночлена в степень

Мы знаем, что степенью с натуральным показателем называют произведение некоторого числа одинаковых множителей. На их количество указывает число в показателе. Согласно этому определению, возведение одночлена в степень равнозначно умножению указанного числа одинаковых одночленов. Посмотрим, как это делается.

Пример 4

Условие: выполните возведение одночлена − 2 · a · b 4 в степень 3 .

Решение

Мы можем заменить возведение в степень на умножение 3 -х одночленов − 2 · a · b 4 .

Запишем и получим нужный ответ:

(− 2 · a · b 4) 3 = (− 2 · a · b 4) · (− 2 · a · b 4) · (− 2 · a · b 4) = = ((− 2) · (− 2) · (− 2)) · (a · a · a) · (b 4 · b 4 · b 4) = − 8 · a 3 · b 12

Ответ: (− 2 · a · b 4) 3 = − 8 · a 3 · b 12 .

А как быть в том случае, когда степень имеет большой показатель? Записывать большое количество множителей неудобно. Тогда для решения такой задачи нам надо применить свойства степени, а именно свойство степени произведения и свойство степени в степени.

Решим задачу, которую мы привели выше, указанным способом.

Пример 5

Условие: выполните возведение − 2 · a · b 4 в третью степень.

Решение

Зная свойство степени в степени, мы можем перейти к выражению следующего вида:

(− 2 · a · b 4) 3 = (− 2) 3 · a 3 · (b 4) 3 .

После этого мы возводим в степень — 2 и применяем свойство степени в степени:

(− 2) 3 · (a) 3 · (b 4) 3 = − 8 · a 3 · b 4 · 3 = − 8 · a 3 · b 12 .

Ответ: − 2 · a · b 4 = − 8 · a 3 · b 12 .

Возведению одночлена в степень мы также посвятили отдельную статью.

Правила деления одночленов

Последнее действие с одночленами, которое мы разберем в данном материале, – деление одночлена на одночлен. В результате мы должны получить рациональную (алгебраическую) дробь (в некоторых случаях возможно получение одночлена). Сразу уточним, что деление на нулевой одночлен не определяется, поскольку не определяется деление на 0.

Для выполнения деления нам нужно записать указанные одночлены в форме дроби и сократить ее, если есть такая возможность.

Пример 6

Условие: выполните деление одночлена − 9 · x 4 · y 3 · z 7 на − 6 · p 3 · t 5 · x 2 · y 2 .

Решение

Начнем с записи одночленов в форме дроби.

9 · x 4 · y 3 · z 7 — 6 · p 3 · t 5 · x 2 · y 2

Эту дробь можно сократить. После выполнения этого действия получим:

3 · x 2 · y · z 7 2 · p 3 · t 5

Ответ: — 9 · x 4 · y 3 · z 7 — 6 · p 3 · t 5 · x 2 · y 2 = 3 · x 2 · y · z 7 2 · p 3 · t 5 .

Условия, при которых в результате деления одночленов мы получим одночлен, приводятся в отдельной статье.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Одной из главных характеристик в алгебре, да и во всей математике является степень. Конечно, в 21 веке все расчеты можно проводить на онлайн-калькуляторе, но лучше для развития мозгов научиться делать это самому.

В данной статье рассмотрим самые важные вопросы, касающиеся этого определения. А именно, поймем что это вообще такое и каковы основные его функции, какие имеются свойства в математике.

Рассмотрим на примерах то, как выглядит расчет, каковы основные формулы. Разберем основные виды величины и то, чем они отличаются от других функций.

Поймем, как решать с помощью этой величины различные задачи. Покажем на примерах, как возводить в нулевую степень, иррациональную, отрицательную и др.

Онлайн-калькулятор возведения в степень

Что такое степень числа

Что же подразумевают под выражением «возвести число в степень»?

Степенью n числа а является произведение множителей величиной а n-раз подряд.

Математически это выглядит следующим образом:

a n = a * a * a * …a n .

Например:

2 3 = 2 в третьей степ. = 2 * 2 * 2 = 8;
4 2 = 4 в степ. два = 4 * 4 = 16;
5 4 = 5 в степ. четыре = 5 * 5 * 5 * 5 = 625;
10 5 = 10 в 5 степ. = 10 * 10 * 10 * 10 * 10 = 100000;
10 4 = 10 в 4 степ. = 10 * 10 * 10 * 10 = 10000.

Ниже будет представлена таблица квадратов и кубов от 1 до 10.

Таблица степеней от 1 до 10

Ниже будут приведены результаты возведения натуральных чисел в положительные степени – «от 1 до 100».

Ч-ло	2-ая ст-нь	3-я ст-нь
1	1	1
2	4	8
3	9	27
4	16	64
5	25	125
6	36	216
7	49	343
8	64	512
9	81	279
10	100	1000

Свойства степеней

Что же характерно для такой математической функции? Рассмотрим базовые свойства.

Учеными установлено следующие признаки, характерные для всех степеней:

a n * a m = (a) (n+m) ;
a n: a m = (a) (n-m) ;
(a b) m =(a) (b*m) .

Проверим на примерах:

2 3 * 2 2 = 8 * 4 = 32. С другой стороны 2 5 = 2 * 2 * 2 * 2 * 2 =32.

Аналогично: 2 3: 2 2 = 8 / 4 =2. Иначе 2 3-2 = 2 1 =2.

(2 3) 2 = 8 2 = 64. А если по-другому? 2 6 = 2 * 2 * 2 * 2 * 2 * 2 = 32 * 2 = 64.

Как видим, правила работают.

А как же быть со сложением и вычитанием ? Всё просто. Выполняется сначала возведение в степень, а уж потом сложение и вычитание.

Посмотрим на примерах:

3 3 + 2 4 = 27 + 16 = 43;
5 2 – 3 2 = 25 – 9 = 16. Обратите внимание: правило не будет выполняться, если сначала произвести вычитание: (5 — 3) 2 = 2 2 = 4.

А вот в этом случае надо вычислять сначала сложение, поскольку присутствуют действия в скобках: (5 + 3) 3 = 8 3 = 512.

Как производить вычисления в более сложных случаях ? Порядок тот же:

при наличии скобок – начинать нужно с них;
затем возведение в степень;
потом выполнять действия умножения, деления;
после сложение, вычитание.

Есть специфические свойства, характерные не для всех степеней:

Корень n-ой степени из числа a в степени m запишется в виде: a m / n .
При возведении дроби в степень: этой процедуре подвержены как числитель, так и ее знаменатель.
При возведении произведения разных чисел в степень, выражение будет соответствовать произведению этих чисел в заданной степени. То есть: (a * b) n = a n * b n .
При возведении числа в отрицательную степ., нужно разделить 1 на число в той же ст-ни, но со знаком «+».
Если знаменатель дроби находится в отрицательной степени, то это выражение будет равно произведению числителя на знаменатель в положительной степени.
Любое число в степени 0 = 1, а в степ. 1 = самому себе.

Эти правила важны в отдельных случаях, их рассмотрим подробней ниже.

Степень с отрицательным показателем

Что делать при минусовой степени, т. е. когда показатель отрицательный?

Исходя из свойств 4 и 5 (смотри пункт выше), получается :

A (- n) = 1 / A n , 5 (-2) = 1 / 5 2 = 1 / 25.

И наоборот:

1 / A (- n) = A n , 1 / 2 (-3) = 2 3 = 8.

А если дробь?

(A / B) (- n) = (B / A) n , (3 / 5) (-2) = (5 / 3) 2 = 25 / 9.

Степень с натуральным показателем

Под ней понимают степень с показателями, равными целым числам.

Что нужно запомнить:

A 0 = 1, 1 0 = 1; 2 0 = 1; 3.15 0 = 1; (-4) 0 = 1…и т. д.

A 1 = A, 1 1 = 1; 2 1 = 2; 3 1 = 3…и т. д.

Кроме того, если (-a) 2 n +2 , n=0, 1, 2…то результат будет со знаком «+». Если отрицательное число возводится в нечетную степень, то наоборот.

Общие свойства, да и все специфические признаки, описанные выше, также характерны для них.

Дробная степень

Этот вид можно записать схемой: A m / n . Читается как: корень n-ой степени из числа A в степени m.

С дробным показателем можно делать, что угодно: сокращать, раскладывать на части, возводить в другую степень и т. д.

Степень с иррациональным показателем

Пусть α – иррациональное число, а А ˃ 0.

Чтобы понять суть степени с таким показателем, рассмотрим разные возможные случаи:

А = 1. Результат будет равен 1. Поскольку существует аксиома – 1 во всех степенях равна единице;

А r 1 ˂ А α ˂ А r 2 , r 1 ˂ r 2 – рациональные числа;

0˂А˂1.

В этом случае наоборот: А r 2 ˂ А α ˂ А r 1 при тех же условиях, что и во втором пункте.

Например, показатель степени число π. Оно рациональное.

r 1 – в этом случае равно 3;

r 2 – будет равно 4.

Тогда, при А = 1, 1 π = 1.

А = 2, то 2 3 ˂ 2 π ˂ 2 4 , 8 ˂ 2 π ˂ 16.

А = 1/2, то (½) 4 ˂ (½) π ˂ (½) 3 , 1/16 ˂ (½) π ˂ 1/8.

Для таких степеней характерны все математические операции и специфические свойства, описанные выше.

Заключение

Подведём итоги — для чего же нужны эти величины, в чем преимущество таких функций? Конечно, в первую очередь они упрощают жизнь математиков и программистов при решении примеров, поскольку позволяют минимизировать расчеты, сократить алгоритмы, систематизировать данные и многое другое.

Где еще могут пригодиться эти знания? В любой рабочей специальности: медицине, фармакологии, стоматологии, строительстве, технике, инженерии, конструировании и т. д.

Очевидно, что числа со степенями могут слагаться, как другие величины , путем их сложения одно за другим со своими знаками .

Так, сумма a 3 и b 2 есть a 3 + b 2 .
Сумма a 3 — b n и h 5 -d 4 есть a 3 — b n + h 5 — d 4 .

Коэффициенты одинаковых степеней одинаковых переменных могут слагаться или вычитаться.

Так, сумма 2a 2 и 3a 2 равна 5a 2 .

Это так же очевидно, что если взять два квадрата а, или три квадрата а, или пять квадратов а.

Но степени различных переменных и различные степени одинаковых переменных , должны слагаться их сложением с их знаками.

Так, сумма a 2 и a 3 есть сумма a 2 + a 3 .

Это очевидно, что квадрат числа a, и куб числа a, не равно ни удвоенному квадрату a, но удвоенному кубу a.

Сумма a 3 b n и 3a 5 b 6 есть a 3 b n + 3a 5 b 6 .

Вычитание степеней проводится таким же образом, что и сложение, за исключением того, что знаки вычитаемых должны соответственно быть изменены.

Или:
2a 4 — (-6a 4) = 8a 4
3h 2 b 6 — 4h 2 b 6 = -h 2 b 6
5(a — h) 6 — 2(a — h) 6 = 3(a — h) 6

Умножение степеней

Числа со степенями могут быть умножены, как и другие величины, путем написания их одно за другим, со знаком умножения или без него между ними.

Так, результат умножения a 3 на b 2 равен a 3 b 2 или aaabb.

Или:
x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y

Результат в последнем примере может быть упорядочен путём сложения одинаковых переменных.
Выражение примет вид: a 5 b 5 y 3 .

Сравнивая несколько чисел(переменных) со степенями, мы можем увидеть, что если любые два из них умножаются, то результат — это число (переменная) со степенью, равной сумме степеней слагаемых.

Так, a 2 . a 3 = aa.aaa = aaaaa = a 5 .

Здесь 5 — это степень результата умножения, равная 2 + 3, сумме степеней слагаемых.

Так, a n .a m = a m+n .

Для a n , a берётся как множитель столько раз, сколько равна степень n;

И a m , берётся как множитель столько раз, сколько равна степень m;

Поэтому, степени с одинаковыми основами могут быть умножены путём сложения показателей степеней.

Так, a 2 .a 6 = a 2+6 = a 8 . И x 3 .x 2 .x = x 3+2+1 = x 6 .

Или:
4a n ⋅ 2a n = 8a 2n
b 2 y 3 ⋅ b 4 y = b 6 y 4
(b + h — y) n ⋅ (b + h — y) = (b + h — y) n+1

Умножьте (x 3 + x 2 y + xy 2 + y 3) ⋅ (x — y).
Ответ: x 4 — y 4 .
Умножьте (x 3 + x — 5) ⋅ (2x 3 + x + 1).

Это правило справедливо и для чисел, показатели степени которых — отрицательные .

1. Так, a -2 .a -3 = a -5 . Это можно записать в виде (1/aa).(1/aaa) = 1/aaaaa.

2. y -n .y -m = y -n-m .

3. a -n .a m = a m-n .

Если a + b умножаются на a — b, результат будет равен a 2 — b 2: то есть

Результат умножения суммы или разницы двух чисел равен сумме или разнице их квадратов. 5}$. Ответ: $\frac{2x}{1}$ или 2x.

3. Уменьшите показатели степеней a 2 /a 3 и a -3 /a -4 и приведите к общему знаменателю.
a 2 .a -4 есть a -2 первый числитель.
a 3 .a -3 есть a 0 = 1, второй числитель.
a 3 .a -4 есть a -1 , общий числитель.
После упрощения: a -2 /a -1 и 1/a -1 .

4. Уменьшите показатели степеней 2a 4 /5a 3 и 2 /a 4 и приведите к общему знаменателю.
Ответ: 2a 3 /5a 7 и 5a 5 /5a 7 или 2a 3 /5a 2 и 5/5a 2 .

5. Умножьте (a 3 + b)/b 4 на (a — b)/3.

6. Умножьте (a 5 + 1)/x 2 на (b 2 — 1)/(x + a).

7. Умножьте b 4 /a -2 на h -3 /x и a n /y -3 .

8. Разделите a 4 /y 3 на a 3 /y 2 . Ответ: a/y.

9. Разделите (h 3 — 1)/d 4 на (d n + 1)/h.

Как умножать степени? Какие степени можно перемножить, а какие — нет? Как число умножить на степень?

В алгебре найти произведение степеней можно в двух случаях:

1) если степени имеют одинаковые основания;

2) если степени имеют одинаковые показатели.

При умножении степеней с одинаковыми основаниями надо основание оставить прежним, а показатели — сложить:

При умножении степеней с одинаковыми показателями общий показатель можно вынести за скобки:

Рассмотрим, как умножать степени, на конкретных примерах.

Единицу в показателе степени не пишут, но при умножении степеней — учитывают:

При умножении количество степеней может быть любое. Следует помнить, что перед буквой знак умножения можно не писать:

В выражениях возведение в степень выполняется в первую очередь.

Если нужно число умножить на степень, сначала следует выполнить возведение в степень, а уже потом — умножение:

www.algebraclass.ru

Сложение, вычитание, умножение, и деление степеней

Сложение и вычитание степеней

Так, сумма a 3 и b 2 есть a 3 + b 2 .
Сумма a 3 — b n и h 5 -d 4 есть a 3 — b n + h 5 — d 4 .

Коэффициенты одинаковых степеней одинаковых переменных могут слагаться или вычитаться.

Так, сумма 2a 2 и 3a 2 равна 5a 2 .

Это так же очевидно, что если взять два квадрата а, или три квадрата а, или пять квадратов а.

Так, сумма a 2 и a 3 есть сумма a 2 + a 3 .

Это очевидно, что квадрат числа a, и куб числа a, не равно ни удвоенному квадрату a, но удвоенному кубу a.

Сумма a 3 b n и 3a 5 b 6 есть a 3 b n + 3a 5 b 6 .

Или:
2a 4 — (-6a 4) = 8a 4
3h 2 b 6 — 4h 2 b 6 = -h 2 b 6
5(a — h) 6 — 2(a — h) 6 = 3(a — h) 6

Умножение степеней

Так, результат умножения a 3 на b 2 равен a 3 b 2 или aaabb.

Или:
x -3 ⋅ a m = a m x -3
3a 6 y 2 ⋅ (-2x) = -6a 6 xy 2
a 2 b 3 y 2 ⋅ a 3 b 2 y = a 2 b 3 y 2 a 3 b 2 y

Так, a 2 .a 3 = aa.aaa = aaaaa = a 5 .

Здесь 5 — это степень результата умножения, равная 2 + 3, сумме степеней слагаемых.

Так, a n .a m = a m+n .

Для a n , a берётся как множитель столько раз, сколько равна степень n;

И a m , берётся как множитель столько раз, сколько равна степень m;

Поэтому, степени с одинаковыми основами могут быть умножены путём сложения показателей степеней.

Так, a 2 .a 6 = a 2+6 = a 8 . И x 3 .x 2 .x = x 3+2+1 = x 6 .

Или:
4a n ⋅ 2a n = 8a 2n
b 2 y 3 ⋅ b 4 y = b 6 y 4
(b + h — y) n ⋅ (b + h — y) = (b + h — y) n+1

Умножьте (x 3 + x 2 y + xy 2 + y 3) ⋅ (x — y).
Ответ: x 4 — y 4 .
Умножьте (x 3 + x — 5) ⋅ (2x 3 + x + 1).

Это правило справедливо и для чисел, показатели степени которых — отрицательные .

1. Так, a -2 .a -3 = a -5 . Это можно записать в виде (1/aa).(1/aaa) = 1/aaaaa.

2. y -n .y -m = y -n-m .

3. a -n .a m = a m-n .

Если a + b умножаются на a — b, результат будет равен a 2 — b 2: то есть

Результат умножения суммы или разницы двух чисел равен сумме или разнице их квадратов.

Если умножается сумма и разница двух чисел, возведённых в квадрат , результат будет равен сумме или разнице этих чисел в четвёртой степени.

Так, (a — y).(a + y) = a 2 — y 2 .
(a 2 — y 2)⋅(a 2 + y 2) = a 4 — y 4 .
(a 4 — y 4)⋅(a 4 + y 4) = a 8 — y 8 .

Деление степеней

Числа со степенями могут быть поделены, как и другие числа, путем отнимая от делимого делителя, или размещением их в форме дроби. 3$

Необходимо очень хорошо усвоить умножение и деление степеней, так как такие операции очень широко применяются в алгебре.

Примеры решения примеров с дробями, содержащими числа со степенями

1. Уменьшите показатели степеней в $\frac $ Ответ: $\frac $.

2. Уменьшите показатели степеней в $\frac $. Ответ: $\frac $ или 2x.

5. Умножьте (a 3 + b)/b 4 на (a — b)/3.

6. Умножьте (a 5 + 1)/x 2 на (b 2 — 1)/(x + a).

7. Умножьте b 4 /a -2 на h -3 /x и a n /y -3 .

8. Разделите a 4 /y 3 на a 3 /y 2 . Ответ: a/y.

Свойства степени

Напоминаем, что в данном уроке разбираются свойства степеней с натуральными показателями и нулём. Степени с рациональными показателями и их свойства будут рассмотрены в уроках для 8 классов.

Степень с натуральным показателем обладает несколькими важными свойствами, которые позволяют упрощать вычисления в примерах со степенями.

Свойство № 1

Произведение степеней
При умножении степеней с одинаковыми основаниями основание остаётся без изменений, а показатели степеней складываются.
a m · a n = a m + n , где « a » — любое число, а « m », « n » — любые натуральные числа.
Данное свойство степеней также действует на произведение трёх и более степеней.
Упростить выражение.
b · b 2 · b 3 · b 4 · b 5 = b 1 + 2 + 3 + 4 + 5 = b 15
Представить в виде степени.
6 15 · 36 = 6 15 · 6 2 = 6 15 · 6 2 = 6 17
Представить в виде степени.
(0,8) 3 · (0,8) 12 = (0,8) 3 + 12 = (0,8) 15
Обратите внимание, что в указанном свойстве речь шла только об умножении степеней с одинаковыми основаниями . Оно не относится к их сложению.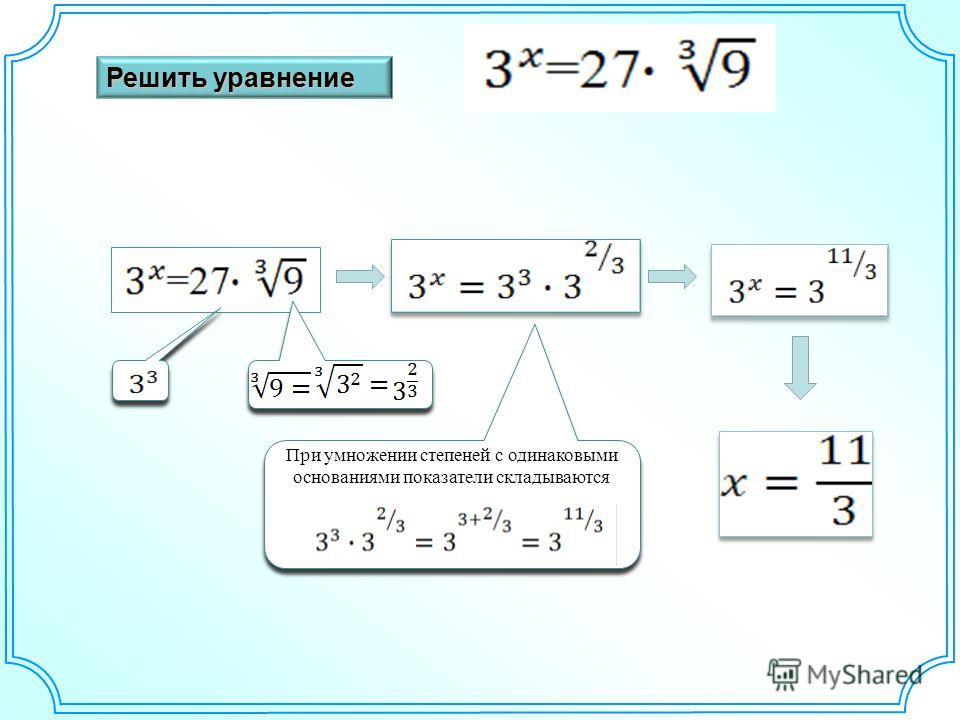
Нельзя заменять сумму (3 3 + 3 2) на 3 5 . Это понятно, если
посчитать (3 3 + 3 2) = (27 + 9) = 36 , а 3 5 = 243
Свойство № 2

Частное степеней
При делении степеней с одинаковыми основаниями основание остаётся без изменений, а из показателя степени делимого вычитают показатель степени делителя.
Записать частное в виде степени
(2b) 5: (2b) 3 = (2b) 5 − 3 = (2b) 2
Вычислить.
11 3 − 2 · 4 2 − 1 = 11 · 4 = 44
Пример. Решить уравнение. Используем свойство частного степеней.
3 8: t = 3 4
Ответ: t = 3 4 = 81
Пользуясь свойствами № 1 и № 2, можно легко упрощать выражения и производить вычисления.
Пример. Упростить выражение.
4 5m + 6 · 4 m + 2: 4 4m + 3 = 4 5m + 6 + m + 2: 4 4m + 3 = 4 6m + 8 − 4m − 3 = 4 2m + 5
Пример. Найти значение выражения, используя свойства степени.
2 11 − 5 = 2 6 = 64
Обратите внимание, что в свойстве 2 речь шла только о делении степеней с одинаковыми основаниями.
Нельзя заменять разность (4 3 −4 2) на 4 1 . Это понятно, если посчитать (4 3 −4 2) = (64 − 16) = 48 , а 4 1 = 4
Свойство № 3

Возведение степени в степень
При возведении степени в степень основание степени остаётся без изменения, а показатели степеней перемножаются.
(a n) m = a n · m , где « a » — любое число, а « m », « n » — любые натуральные числа.

Обратите внимание, что свойство № 4, как и другие свойства степеней, применяют и в обратном порядке.
(a n · b n)= (a · b) n
То есть, чтобы перемножить степени с одинаковыми показателями можно перемножить основания, а показатель степени оставить неизменным.
Пример. Вычислить.
2 4 · 5 4 = (2 · 5) 4 = 10 4 = 10 000
Пример. Вычислить.
0,5 16 · 2 16 = (0,5 · 2) 16 = 1
В более сложных примерах могут встретиться случаи, когда умножение и деление надо выполнить над степенями с разными основаниями и разными показателями. В этом случае советуем поступать следующим образом.
Например, 4 5 · 3 2 = 4 3 · 4 2 · 3 2 = 4 3 · (4 · 3) 2 = 64 · 12 2 = 64 · 144 = 9216
Пример возведения в степень десятичной дроби.
4 21 · (−0,25) 20 = 4 · 4 20 · (−0,25) 20 = 4 · (4 · (−0,25)) 20 = 4 · (−1) 20 = 4 · 1 = 4
Свойства 5

Степень частного (дроби)
Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель, и первый результат разделить на второй.
(a: b) n = a n: b n , где « a », « b » — любые рациональные числа, b ≠ 0, n — любое натуральное число.
Пример. Представить выражение в виде частного степеней.
(5: 3) 12 = 5 12: 3 12
Напоминаем, что частное можно представить в виде дроби. Поэтому на теме возведение дроби в степень мы остановимся более подробно на следующей странице.
Степени и корни
Операции со степенями и корнями. Степень с отрицательным ,
нулевым и дробным показателем. О выражениях, не имеющих смысла.
Операции со степенями.
1. При умножении степеней с одинаковым основанием их показатели складываются:
a m · a n = a m + n .
2. При делении степеней с одинаковым основанием их показатели вычитаются .
3. Степень произведения двух или нескольких сомножителей равна произведению степеней этих сомножителей.
4. Степень отношения (дроби) равна отношению степеней делимого (числителя) и делителя (знаменателя):
(a / b ) n = a n / b n .
5. При возведении степени в степень их показатели перемножаются:
Все вышеприведенные формулы читаются и выполняются в обоих направлениях слева направо и наоборот.
П р и м е р. (2 · 3 · 5 / 15) ² = 2 ² · 3 ² · 5 ² / 15 ² = 900 / 225 = 4 .
Операции с корнями. Во всех нижеприведенных формулах символ означает арифметический корень (подкоренное выражение положительно).
1. Корень из произведения нескольких сомножителей равен произведению корней из этих сомножителей:
2. Корень из отношения равен отношению корней делимого и делителя:
3. При возведении корня в степень достаточно возвести в эту степень подкоренное число:
4. Если увеличить степень корня в m раз и одновременно возвести в m -ую степень подкоренное число, то значение корня не изменится:
5. Если уменьшить степень корня в m раз и одновременно извлечь корень m -ой степени из подкоренного числа, то значение корня не изменится:

Расширение понятия степени. До сих пор мы рассматривали степени только с натуральным показателем; но действия со степенями и корнями могут приводить также к отрицательным , нулевым и дробным показателям. Все эти показатели степеней требуют дополнительного определения.
Степень с отрицательным показателем. Степень некоторого числа с отрицательным (целым) показателем определяется как единица, делённая на степень того же числа с показателем, равным абсолютной велечине отрицательного показателя:
Т еперь формула a m : a n = a m — n может быть использована не только при m , большем, чем n , но и при m , меньшем, чем n .
П р и м е р. a 4: a 7 = a 4 — 7 = a — 3 .
Если мы хотим, чтобы формула a m : a n = a m — n была справедлива при m = n , нам необходимо определение нулевой степени.
Степень с нулевым показателем. Степень любого ненулевого числа с нулевым показателем равна 1.
П р и м е р ы. 2 0 = 1, (– 5) 0 = 1, (– 3 / 5) 0 = 1.
Степень с дробным показателем. Для того, чтобы возвести действительное число а в степень m / n , нужно извлечь корень n –ой степени из m -ой степени этого числа а:
О выражениях, не имеющих смысла. Есть несколько таких выражений.
где a ≠ 0 , не существует.
В самом деле, если предположить, что x – некоторое число, то в соответствии с определением операции деления имеем: a = 0· x , т.e. a = 0, что противоречит условию: a ≠ 0
— любое число.
В самом деле, если предположить, что это выражение равно некоторому числу x , то согласно определению операции деления имеем: 0 = 0 · x . Но это равенство имеет место при любом числе x , что и требовалось доказать.
0 0 — любое число.
Р е ш е н и е. Рассмотрим три основных случая:
1) x = 0 – это значение не удовлетворяет данному уравнению
2) при x > 0 получаем: x / x = 1, т.e. 1 = 1, откуда следует,
что x – любое число; но принимая во внимание, что в
нашем случае x > 0 , ответом является x > 0 ;
Правила умножения степеней с разным основанием
СТЕПЕНЬ С РАЦИОНАЛЬНЫМ ПОКАЗАТЕЛЕМ,
СТЕПЕННАЯ ФУНКЦИЯ IV
§ 69. Умножение и деление степеней с одинаковыми основаниями
Теорема 1. Чтобы перемножить степени с одинаковыми основаниями, достаточно показатели степеней сложить, а основание оставить прежним , то есть
Доказательство. По определению степени
2 2 2 3 = 2 5 = 32; (-3) (-3) 3 = (-3) 4 = 81.
Мы рассмотрели произведение двух степеней. На самом же деле доказанное свойство верно для любого числа степеней с одинаковыми основаниями.
Теорема 2. Чтобы разделить степени с одинаковыми основаниями, когда показатель делимого больше показателя делителя, достаточно из показателя делимого вычесть показатель делителя, а основание оставить прежним, то есть при т > п
(a =/= 0)
Доказательство. Напомним, что частным от деления одного числа на другое называется число, которое при умножении на делитель дает делимое. Поэтому доказать формулу , где a =/= 0, это все равно, что доказать формулу
Если т > п , то число т — п будет натуральным; следовательно, по теореме 1
Теорема 2 доказана.
Следует обратить внимание на то, что формула
доказана нами лишь в предположении, что т > п . Поэтому из доказанного пока нельзя делать, например, таких выводов:
К тому же степени с отрицательными показателями нами еще не рассматривались и мы пока что не знаем, какой смысл можно придать выражению 3 — 2 .
Теорема 3. Чтобы возвести степень в степень, достаточно перемножить показатели, оставив основание степени прежним , то есть
Доказательство. Используя определение степени и теорему 1 этого параграфа, получаем:
что и требовалось доказать.
Например, (2 3) 2 = 2 6 = 64;
518 (Устно.) Определить х из уравнений:
1) 2 2 2 2 3 2 4 2 5 2 6 = 2 x ; 3) 4 2 4 4 4 6 4 8 4 10 = 2 x ;
2) 3 3 3 3 5 3 7 3 9 = 3 x ; 4) 1 / 5 1 / 25 1 / 125 1 / 625 = 1 / 5 x .
519. (У с т н о.) Упростить:
520. (У с т н о.) Упростить:
521. Данные выражения представить в виде степеней с одинаковыми основаниями:
1) 32 и 64; 3) 8 5 и 16 3 ; 5) 4 100 и 32 50 ;
2) -1000 и 100; 4) -27 и -243; 6) 81 75 8 200 и 3 600 4 150 .
Свойства степени Арифметика
Привет, мой друг, тебе интересно узнать все про свойства степени, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое свойства степени , настоятельно рекомендую прочитать все из категории Арифметика.
Напоминаем, что в данном уроке разбираются свойства степеней с натуральными показателями и нулем. Степени с рациональными показателями и их свойства будут рассмотрены в уроках для 8 классов.
Степень с натуральным показателем обладает несколькими важными свойствами, которые позволяют упрощать вычисления в примерах со степенями.
Свойство № 1

Произведение степеней

При умножении степеней с одинаковыми основаниями основание остается без изменений, а показатели степеней складываются.
a^m • aⁿ = a^{m + n}, где a — любое число, а m, n — любые натуральные числа.
Данное свойство степеней также действует на произведение трех и более степеней.
Примеры.
Упростить выражение.
b • b² • b³ • b⁴ • b⁵ = b ^{1 + 2 + 3 + 4 + 5} = b¹⁵

Представить в виде степени.
6¹⁵ • 36 = 6¹⁵ • 6² = 6¹⁵ • 6² = 6¹⁷

Представить в виде степени.
(0,8)³ • (0,8)¹² = (0,8)^{3 + 12} = (0,8)¹⁵

Обратите внимание, что в указанном свойстве речь шла только об умножении степеней с одинаковыми основаниями. Оно не относится к их сложению.
Нельзя заменять сумму (3³ + 3²) на 3³. Это понятно, если посчитать 3³ = 27 и 3² = 9; 27 + 9 = 36, а 3⁵ = 243
Свойство № 2

Частное степеней

При делении степеней с одинаковыми основаниями основание остается без изменений, а из показателя степени делимого вычитают показатель степени делителя.
a^m • aⁿ = a^{m — n}, где a — любое число, не равное нулю, а m, n — любые натуральные числа такие, что m > n.
Примеры.
Записать частное в виде степени
(2b)⁵ : (2b)³ = (2b)^{5 — 3} = (2b)²

Вычислить.
11³ • 4 ²
11² • 4
= 11^{3 — 2} • 4 ^{2 — 1} = 11 • 4 = 44

Пример . Об этом говорит сайт https://intellect.icu . Решить уравнение. Используем свойство частного степеней.
3⁸ : t = 3⁴
t = 3⁸ : 3⁴
t = 3^{8 — 4}
t = 3⁴
Ответ: t = 3⁴ = 81

Пользуясь свойствами № 1 и № 2, можно легко упрощать выражения и производить вычисления.
Пример. Упростить выражение.
4^{5m + 6} • 4^{m + 2} : 4^{4m + 3} = 4^{5m + 6 + m + 2} : 4^{4m + 3} = 4^{6m + 8 — 4m — 3}= 4^{2m + 5}

Пример. Найти значение выражения, используя свойства степени .
512 • 4
32
=
512 • 4
32
=
2⁹ • 2²
2⁵
=
2^{9 + 2}
2⁵
=
2¹¹
2⁵
= 2^{11 — 5} = 2 ⁶ = 64

Обратите внимание, что в свойстве 2 речь шла только о делении степеней с одинаковыми основаниями.
Нельзя заменять разность (4³ — 4²) на 4¹. Это понятно, если посчитать 4³ = 64 и 4² = 16; 64 — 16 = 48, а 4¹ = 4
Будьте внимательны!
Свойство № 3

Возведение степени в степень

При возведении степени в степень основание степени остается без изменения, а показатели степеней перемножаются.
(aⁿ)^m = a^{n • m}, где a — любое число, а m, n — любые натуральные числа.
Свойства 4

Степень произведения

При возведении степени в степень произведения в эту степень возводится каждый множитель и результаты перемножаются.
(a • b)ⁿ = aⁿ • bⁿ, где a, b — любые рациональные числа; n — любое натуральное число.

Обратите внимание, что свойство № 4, как и другие свойства степеней, применяют и в обратном порядке.
(aⁿ • bⁿ)= (a • b) ⁿ
То есть, чтобы перемножить степени с одинаковыми показателями можно перемножить основания, а показатель степени оставить неизменным.
Пример. Вычислить.
2⁴ • 5⁴ = (2 • 5)⁴ = 10⁴ = 10 000

Пример. Вычислить.
0,5¹⁶ • 2¹⁶ = (0,5 • 2)¹⁶ = 1

В более сложных примерах могут встретиться случаи, когда умножение и деление надо выполнить над степенями с разными основаниями и разными показателями. В этом случае советуем поступать следующим образом.
Например, 4⁵ • 3² = 4³ • 4² • 3² = 4³ • (4 • 3)² = 64 • 12² = 64 • 144 = 9216
Пример возведения в степень десятичной дроби.
4²¹ • (-0,25)²⁰ = 4 • 4 ²⁰ • (-0,25) ²⁰ = 4 • (4 • (-0,25))²⁰ = 4 • (- 1)²⁰ = 4 • 1 = 4
Свойства 5

Степень частного (дроби)

Чтобы возвести в степень частное, можно возвести в эту степень отдельно делимое и делитель, и первый результат разделить на второй.
(a : b)ⁿ = aⁿ : bⁿ, где a, b — любые рациональные числа, b ≠ 0, n — любое натуральное число.
Пример. Представить выражение в виде частного степеней.
(5 : 3)¹² = 5¹² : 3¹²

Напоминаем, что частное можно представить в виде дроби. Поэтому на теме возведение дроби в степень мы остановимся более подробно на следующей странице.
Как ты считаеешь, будет ли теория про свойства степени улучшена в обозримом будующем? Надеюсь, что теперь ты понял что такое свойства степени и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Арифметика
Умножение показателей с одинаковым основанием — Embibe
Автор: trisha
Последнее изменение 30 июня 2022 г.
Автор Триша
Последнее изменение 30 июня 2022 г.
Умножение экспоненты — это процесс умножения двух выражений, содержащих экспоненту. В зависимости от основания и степени при умножении показателей степени применяются определенные правила. Различные основания, отрицательные показатели и нецелые показатели иногда могут усложнять понимание учащимися. В этом уроке давайте больше узнаем об умножении показателей.
Короче говоря, умножение степеней или показателей степени с одним и тем же основанием подразумевает, что разные степени должны быть умножены друг на друга, чтобы получить ответ. Здесь для справки приведен пример:
2 ³ *2 ⁴ = 2 ³⁺⁴ =2 ⁷ = 128
Хотите знать, как это происходит? Существуют определенные правила, регулирующие экспоненциальные степени или основания. Продолжайте читать статью дальше, чтобы узнать подробности.

УЗНАТЬ БОЛЬШЕ О ПОКАЗАТЕЛЯХ И СТЕПЕНЯХ
Ниже приведены семь законов экспоненты, которые вы должны знать:
Закон 1: Умножение полномочий с общим основанием
Общая форма этого закона ? ^? × ? ^? = ? ^{? + n}
Закон 2: Деление показателей с одинаковым основанием
Общая форма этого закона ? ^? ÷ ? ^? = ? ^{? – ?}
Закон 3: Закон силы силы
Общая форма этого закона ? ^?? = ? ^{? × ?}
Закон 4: Закон умножения степеней с разными основаниями, но одинаковыми показателями.
Общая форма этого закона ? ^? × ? ^? =( ? × ? ) ^?
Закон 5: Закон разделения властей с разными основаниями, но одинаковыми показателями.
Общая форма этого закона ? ^? ÷ ? ^? = ? ^? /? ^? =( ?/? ) ^?
Закон 6: Закон отрицательных показателей.
Общая форма этого закона ? ^{– ?} =1/ a ⁿ ^{Закон 7: Правило нулевой мощности
Общая форма этого закона: a ⁰ =1.}
Правила умножения показателей степени с одинаковым основанием
Рассмотрим два числа или выражения, имеющие одинаковое основание, то есть a ⁿ и a ^m . Здесь основание «а». При перемножении членов с одинаковым основанием степени складываются, т. е. a ^m × a ⁿ = a ^{m+n}
Давайте рассмотрим несколько примеров, чтобы понять, как добавляются силы.
Пример 1: Умножить 2 ³ × 2 ²
Решение: Здесь основание такое же, то есть 2. По правилу добавим степени 2 ³ × 2 ² = 2 ⁽³⁺²⁾ = 2 ⁵ = 32.
Проверим ответ. 2 ³ × 2 ² = (2 × 2 × 2) × (2 × 2) = 2 × 2 × 2 × 2 × 2 = 2 ⁵ = 32
Пример 2: Найти произведение 10 ⁴⁵ и 10 ³⁹
Решение: В заданном вопросе основание такое же, то есть 10. По правилу сложим степени, 10 ⁴⁵ × 10 ³⁹ = 10 ^(45+39) = 10 ⁸⁴ .
Подробные правила формул приведены здесь, в таблице ниже:
Экспоненциальные формы Правила
Когда базы одинаковые. a ^-n × a ^-m = a ^-(n+m) = 1/a ^{n+m}
Когда основания разные, а отрицательные степени одинаковы . a ^-n × b ^-n = (a × b) ^-n = 1/(a × b) ⁿ
Когда основания и отрицательные степени различны. а ^-n × b ^-m = (a ^-n ) × (b ^-m )
Умножение дробных степеней с одинаковым основанием
Дробная экспонента – это выражение, имеющее дробную степень. Иллюстрацией дробного показателя степени является 23/5. С помощью следующей таблицы давайте изучим рекомендации по умножению дробных показателей.
Экспоненциальные формы Правила
Когда основания одинаковы. а ^н/м × а ^k/j = a ^n/m+k/j
Когда основания разные, но дробные степени одинаковы.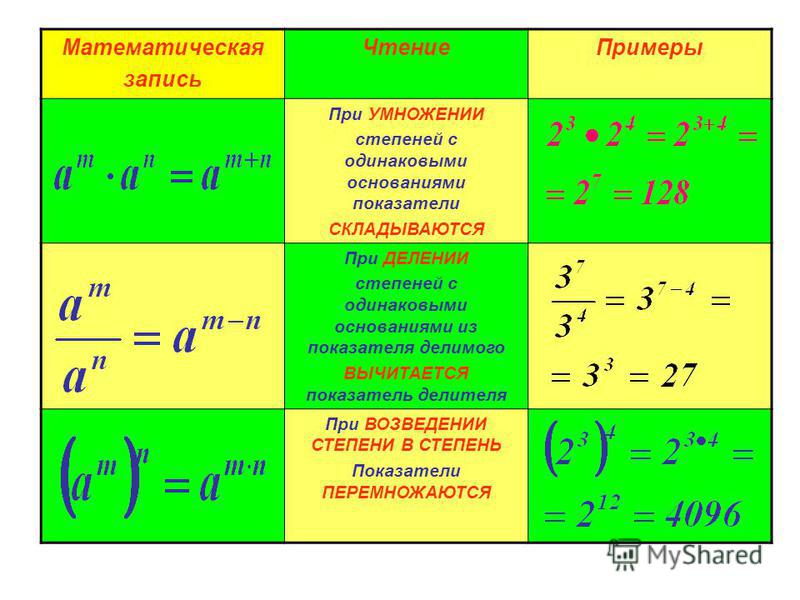 a ^н/м × b ^н/м = (a×b) ^н/м
Когда основания и дробные степени различны. a ^н/м × b ^к/дж = (a ^н/м ) × (b ^к/дж )
Задачи на экспоненты1
Оцените следующие вопросы на умножение степеней с одинаковым основанием:
4 ⁻³
(12) ^-5
(43) ^-3
(-3) ^-4
(-23) ^-5
9003 (2
(-23) ^-5
9003 (2
(-23) ^-5
(2
(-23) ^-5
(2
. 0 + 3 ^-1) × 3 ²
(2 ^-1 × 3 ^-1) ÷ 2 ^-3
та же база» поможет вам в подготовке к экзамену по математике. Следите за обновлениями на embibe.com!
Добейтесь наилучших результатов с помощью 3D-обучения, книжной практики, тестов и разрешения сомнений в Embibe
Каковы 7 законов показателей?
Показатель степени, часто называемый степенью, представляет собой число, указывающее, сколько раз можно умножить базовое число само на себя. Например, число 43 указывает вам умножить четыре на само себя три раза. Основание — это число, возводимое в степень, тогда как показатель степени или степень — это надстрочное число над ним.
Например, 5 ³ = 5 × 5 × 5 = 125; уравнение записывается как «пять в степени три». Сила двойки также известна как «квадрат», тогда как сила трех известна как «куб». Эти слова часто употребляются при вычислении площади или объема различных форм.
Законы экспоненты
Вы должны понимать семь правил экспоненты, часто называемых законами экспоненты. Каждое правило демонстрирует, как решать различные виды арифметических задач, а также как умножать, делить и складывать степени.
Продукт власти Правило
ОТВЕТСТВЕННОЕ ПРАВИТЕЛЬСТВО ДОЛЖНОСТИ
Мощность правила мощности
Мощность правила продукта
Мощность власти правила
. Правило степеней
Сохраняйте одинаковые основания при умножении двух оснований одного и того же значения, а затем складывайте показатели степени, чтобы получить результат.
5 ² × 5 ³ =?
Оставьте базовые значения одинаковыми, поскольку они оба равны пяти, а затем сложите показатели степени (2+3).
5 ² × 5 ³ = 5 ⁵
Чтобы получить ответ, умножьте пять на себя пять раз.
5 ⁵ = 5 × 5 × 5 × 5 × 5 = 3125
Правило отношения степеней
Умножение и деление диаметрально противоположны; точно так же правило частного является полной противоположностью правила произведения. Сохраняйте постоянное основание при делении двух оснований с одинаковым значением, а затем вычитайте значения степени.
4 ⁵ ÷ 4 ³ =?
Поскольку оба основания в этом уравнении равны четырем, они остаются прежними. Затем вычтите делитель из делимого, используя показатели степени.
4 ⁵ ÷ 4 ³ =4 ²
Наконец, при необходимости упростим уравнение.
4 ² = 4 × 4 = 16
Правило мощности степени
Это правило объясняет, как решать уравнения, в которых одна степень усиливается другой.
(2 ⁴ ) ⁴ =?
Умножьте показатели степени в уравнениях, подобных приведенному выше, сохраняя при этом постоянное основание.
(2 ⁴ ) ⁴ = 2 ¹⁶
Степень правила произведения
Распределить показатель степени на каждую часть основания при умножении любого основания на показатель степени.
(х × у) ³ =?
В этом уравнении обеим переменным x и y должна быть присвоена степень числа три.
(x × y) ³ = x ³ y ³
Если есть показатели степени, связанные с основанием, это правило также применяется.
(x ² × y ²) ³ = x ⁶ Y ⁶
Мощность коэффициента правила
Проще говоря, цитат является результатом для разделения двух номеров. В этом правиле вы повышаете частное силой. Показатель степени, как и сила правила произведения, должен распространяться на все значения в скобках, с которыми он связан.
(2/3) ⁴ =?
В этом случае умножьте обе переменные в скобках на четыре.
(2/3) ⁴ = 2 ⁴ /3 ⁴
Правило нулевой степени
Любое основание, возведенное в нулевую степень, равно единице.
3 ⁰ = 1
Правило отношения степеней — самый простой способ описать это понятие.
3 ³ /3 ³ =?
Вычтите степени друг из друга, используя правило отношения степеней, которое аннулирует их и оставляет только основание. Любое целое число равно единице при разделении само на себя.
3 ³ /3 ³ = 3/3 = 1
Правило отрицательного показателя степени
Когда для возведения числа используется отрицательный показатель, преобразуйте его в обратный, чтобы показатель степени был положительным. Чтобы сделать основание отрицательным, не используйте отрицательный показатель степени. Обратные числа — это числа, которые умножаются на единицу, чтобы получить значение единицы. Например, умножьте два на 12, чтобы получить один.
х ^-2 =?
Чтобы увеличить число, используйте следующую формулу:
Разделите число на дробь (поставьте на единицу)
Замените знаменатель на числитель и наоборот.
Когда отрицательное число в дроби перемещается вправо, оно становится положительным числом.
x ^-2 = 1/x ²
Таблица: законы показателей
Название формулы Formula
Product of Powers Rule x ^m × x ⁿ = x ^m+n
Quotient of Powers Rule x ^m ÷ x ⁿ = x ^m-n
Power of a Power Rule (x ^m ) ⁿ = x ^m×n
Power of Product Rule (x × y) ⁿ = x ⁿ × y ⁿ
Power of Quotient Rule (x / y) ⁿ = x ⁿ / y ⁿ
Zero Power Rule x ⁰ =1
Negative Exponent Rule x ^-n = (1 /х ^п )
Примеры вопросов
Вопрос 1: Каково упрощение 7 ³ × 7 ¹ ?
Решение:
7 ³ × 7 ¹ = 7 ³⁺¹ = 7 ⁴
ВОПРОС 2: SYSTORIFY и VITCE 10 ² /50018 ВОПРОС 2: SYTHIFY ANTSTARK 10 ² /50018 ВОПРОС 2. ² .
Решение:
Данное выражение можно записать в виде; 96
Здесь начинается новый материал
Урок 3: Умножение степеней с одинаковым основанием
Введение
Сегодня мы будем учиться косвенным методом, а это значит, что я задам много вопросов и ваши ответы получат вы к результатам. Мне нужно, чтобы все подняли руку , прежде чем ответить, чтобы это сработало. Чтобы найти некоторые ответы, вам, возможно, придется подумать или провести исследование на компьютере. Это часть жизни математика. 93 и найдите формулу умножения показателей степени с одинаковым основанием.
Затем мы применим его к примеру реальной жизни из науки, которая больше, чем жизнь. Вы узнаете, сколько песчинок у нас на этой планете.
Онлайн-упражнения будут выполнены в другой раз, хотя они находятся на этом веб-сайте в уроке 3b. Вы можете взглянуть на них, если хотите подготовиться к будущим урокам.
Заключительное действие — выполнить некоторую работу на рабочем листе . Когда у вас есть вопросы, вы можете задать их мне.
Сегодняшний урок следует методу обнаружения, где есть много вопросов, которые я задаю, и вы можете задать мне много вопросов в процессе вашего открытия.
Вы можете присылать мне комментарии на этой веб-странице.
Теперь вы можете перейти к « Launch », чтобы продолжить изучение материала, если вы не хотите видеть цели урока и основные моменты.
Основные моменты того, что вы изучаете сегодня: 95
Сегодняшний непрямой урок использует эти инструменты, чтобы помочь вам открыть правила умножения показателей степени с одинаковым основанием:
Вопрос о звездах и песчинках (5 мин)
~~Онлайн-упражнения (10 мин)~~
Рабочий лист (20 мин)
Цель: В ходе этого урока вы…
путем исследования и открытия узнаете, каковы правила умножения одних и тех же базовых показателей.
участвуют в непрямом методе урока, где нет лекции, а есть набор примеров вопросов, которые заставят вас найти ответ или запросить информацию.
Умножение степеней с одинаковым основанием имеет ярлык, при котором степени складываются друг с другом. Это удобно, например, при умножении чисел в экспоненциальном представлении.
Запуск (5 мин)
1. Конкретный пример – чистая математика
Что означает чистая математика?
Теперь мы узнаем, каково общее правило умножения показателей степени с одинаковым основанием. Мы позаботимся о том, чтобы вы поняли, как это работает и почему.
99 песчинок.
Если весь песок в мире объединить в один огромный пляж, его размеры будут 1 м * 100 м * 100 000 км.

Как узнать, больше ли звезд во Вселенной, чем песчинок в мире?
Поработайте над этим самостоятельно в течение двух минут, а затем задавайте вопросы. Чтобы получить ответ с помощью логического набора шагов, вам нужно задать следующие вопросы:
Какие соответствующие числа и единицы измерения нам нужны для решения этой задачи?
Чтобы узнать объем песка в кубических метрах, вам нужно знать
а) Сколько 100 000 км в метрах? 1км=1000м
б) Какие три суммы на картинке в экспоненциальном представлении
в) Сколько кубометров песка в мире.
No related posts.