учебное пособие — Научно-исследовательский портал Уральского федерального университета
Представленное пособие включает методы решения основных задач теории сетевого планирования и управления, а также методы отыскания вероятностных характеристик сетевого планирования для трехпараметрических и двухпараметрических моделей. Рассмотрены вопросы построения сетевого графика, отыскания критического пути, расчета резервов времени событий и работ. Издание снабжено вариантами индивидуальных заданий, охватывающие все разобранные виды задач, задачами, приложением и библиографическим списком.
| Язык оригинала | Русский |
|---|---|
| Место публикации | Москва |
| Издатель | Общество с ограниченной ответственностью «Издательство ЮРАЙТ» |
| Число страниц | 95 |
| Издание | 2-е изд. |
| ISBN (печатное издание) | 978-5-534-07646-2, 978-5-7996-1167-5 |
| Состояние | Опубликовано — 2018 |
| Имя | Сер. 68 Профессиональное образование 68 Профессиональное образование |
|---|
- APA
- Author
- BIBTEX
- Harvard
- Standard
- RIS
- Vancouver
@book{6469aa586c454624b8f91f1758041892,
title = «ПРИКЛАДНАЯ МАТЕМАТИКА. ЗАДАЧИ СЕТЕВОГО ПЛАНИРОВАНИЯ: учебное пособие»,
ЗАДАЧИ СЕТЕВОГО ПЛАНИРОВАНИЯ: учебное пособие»,
abstract = «Представленное пособие включает методы решения основных задач теории сетевого планирования и управления, а также методы отыскания вероятностных характеристик сетевого планирования для трехпараметрических и двухпараметрических моделей. Рассмотрены вопросы построения сетевого графика, отыскания критического пути, расчета резервов времени событий и работ. Издание снабжено вариантами индивидуальных заданий, охватывающие все разобранные виды задач, задачами, приложением и библиографическим списком.»,
author = «Плескунов, {Михаил Александрович}»,
editor = «Короткий, {Александр Илларионович}»,
year = «2018»,
language = «Русский»,
isbn = «978-5-534-07646-2»,
series = «Сер. 68 Профессиональное образование»,
publisher = «Общество с ограниченной ответственностью {«}Издательство ЮРАЙТ{«}»,
address = «Российская Федерация»,
edition = «2-е изд.»,
}
Плескунов, МА & Короткий, АИ (ред. ) 2018, ПРИКЛАДНАЯ МАТЕМАТИКА. ЗАДАЧИ СЕТЕВОГО ПЛАНИРОВАНИЯ: учебное пособие. Сер. 68 Профессиональное образование, 2-е изд. ред., Общество с ограниченной ответственностью «Издательство ЮРАЙТ», Москва.
) 2018, ПРИКЛАДНАЯ МАТЕМАТИКА. ЗАДАЧИ СЕТЕВОГО ПЛАНИРОВАНИЯ: учебное пособие. Сер. 68 Профессиональное образование, 2-е изд. ред., Общество с ограниченной ответственностью «Издательство ЮРАЙТ», Москва.
TY — BOOK
T1 — ПРИКЛАДНАЯ МАТЕМАТИКА. ЗАДАЧИ СЕТЕВОГО ПЛАНИРОВАНИЯ
T2 — учебное пособие
AU — Плескунов, Михаил Александрович
A2 — Короткий, Александр Илларионович
PY — 2018
Y1 — 2018
N2 — Представленное пособие включает методы решения основных задач теории сетевого планирования и управления, а также методы отыскания вероятностных характеристик сетевого планирования для трехпараметрических и двухпараметрических моделей. Рассмотрены вопросы построения сетевого графика, отыскания критического пути, расчета резервов времени событий и работ. Издание снабжено вариантами индивидуальных заданий, охватывающие все разобранные виды задач, задачами, приложением и библиографическим списком.
AB — Представленное пособие включает методы решения основных задач теории сетевого планирования и управления, а также методы отыскания вероятностных характеристик сетевого планирования для трехпараметрических и двухпараметрических моделей. Рассмотрены вопросы построения сетевого графика, отыскания критического пути, расчета резервов времени событий и работ. Издание снабжено вариантами индивидуальных заданий, охватывающие все разобранные виды задач, задачами, приложением и библиографическим списком.
Рассмотрены вопросы построения сетевого графика, отыскания критического пути, расчета резервов времени событий и работ. Издание снабжено вариантами индивидуальных заданий, охватывающие все разобранные виды задач, задачами, приложением и библиографическим списком.
UR — https://elibrary.ru/item.asp?id=37501199
UR — https://elibrary.ru/item.asp?id=41294780
M3 — Учебное издание
SN — 978-5-534-07646-2
SN — 978-5-7996-1167-5
T3 — Сер. 68 Профессиональное образование
BT — ПРИКЛАДНАЯ МАТЕМАТИКА. ЗАДАЧИ СЕТЕВОГО ПЛАНИРОВАНИЯ
PB — Общество с ограниченной ответственностью «Издательство ЮРАЙТ»
CY — Москва
ER —
Решение прикладных задач по математике
Перегляд файлу
Попередній слайд 1 / 60 Наступний слайд
Зміст слайдів
Номер слайду 1
Мастер-класс «Решение прикладных задач по математике»
Номер слайду 2
Хочется начать свое выступление словами Н.
Номер слайду 3
Каждому человеку в своей жизни приходится выполнять математические расчеты, пользоваться вычислительной техникой, находить в справочниках нужные формулы, владеть приемами геометрических измерений, читать информацию представленную в виде таблиц, диаграмм, графиков.
Номер слайду 4
Математика присутствует почти во всех отраслях нашей жизни: В промышленности. В архитектуре. В медицине. В быту. В технике
Номер слайду 5
Прикладная направленность школьного курса математики осуществляется с целью повышения качества математического образования учащихся, применения их математических знаний к решению задач в повседневной практике и в дальнейшей профессиональной деятельности.
Номер слайду 6
«Прикладная задача» — задача, поставленная вне математики и решаемая математическими средствами.
Номер слайду 7
Прикладные задачина актуальном материалеприменения общих учебных уменийжизненную ситуациюдеятельностнымистроятсятребуютмоделируютявляются
Номер слайду 8
К прикладной задаче следует предъявлять следующие требования: задачи должны соответствовать программе курса, вводится в процесс обучения как необходимый компонент, служить достижению цели обучения;вводимые в задачу понятия, термины должны быть доступными для учащихся, содержание и требование задач должны “сближаться” с реальной действительностью;способы и методы решения задач должны быть приближены к практическим приемам и методам;прикладная часть задач не должна покрывать ее математическую сущность.
Номер слайду 9
Применение прикладных задач, мы начинаем в 5 классе при изучении темы «Прямоугольный параллелепипед. Объем прямоугольного параллелепипеда.» Учащимся предлагается выполнение проекта по нахождению площади поверхности комнаты для поклейки обоев.
Номер слайду 10
Номер слайду 11
Площадь фигуры. Нужно посчитать какую площадь нужно, чтобы поклеить комнату, если:высота стен 2.70 м, ширина(AВ и CD)-4 м, длина(АС и BD)-6 м, Sокна 2.1 м2, Sдвери-2,1 м2 ABCD
Нужно посчитать какую площадь нужно, чтобы поклеить комнату, если:высота стен 2.70 м, ширина(AВ и CD)-4 м, длина(АС и BD)-6 м, Sокна 2.1 м2, Sдвери-2,1 м2 ABCD
Номер слайду 12
Сколько рулонов обоев нужно, чтобы поклеить комнату, если: площадь 24 м2, высота стен 2.70 м, ширина(AВ и CD)-4 м,длина(АС и BD)-6 м, Sокна 2.1 м2, Sдвери-2,1 м2 Sобоев(1 рулон)-10 м2 Площадь фигур. ABCD
Номер слайду 13
Решение: Пусть комната-прямоугольник, тогда: Вычислим SАВ, учитывая окно: (4*2,7)-2,1=8,7 м2. SСД=4*2,7=10,8 м2. SВД, учитывая дверь=(6*2,7)-2,1=14,1 м2. SАС=6*2,7=16,2 м2 Возьмём 1 рулон обоев, средней стоимостью 190 гривен, в котором 10 м2, тогда: Рассмотрим прямоугольник АВСД: АВ=8,7 м2 : 10 м2 = 0,87, ОКРУГЛИМ 0,9 м2 ВД=14,1 м2 : 10 м2 =1,41, ОКРУГЛИМ 1,4 м2 АС=16,2 м2 : 10 м2 = 1,62,ОКРУГЛИМ 1,6 м2 СД= 10,8 м2 : 10 м2 = 1,08, ОКРУГЛИМ 1,1 м2 В ИТОГЕ: 0,9+1,4+1,6+1,1=5 РУЛОНОВ ОБОЕВ(950 ГРИВЕН)
Номер слайду 14
Для учеников 9-10 классов задание усложняется: необходимо просчитать экономическую выгоду по оклейке комнаты рулонами обоев разной ширины. Предоставляем работы учащихся.
Предоставляем работы учащихся.
Номер слайду 15
Задание с обоями. Головчанский Владимир и Чебан Максим 10-Б
Номер слайду 16
Задание: По данным характеристикам комнаты и обоев расчитать, какими обоями будет выгодней поклеить всю спальную комнату: Узкие. Широкие
Номер слайду 17
Характеристика спальной комнаты: Комната. Ширина (AB) — 2,7м. Высота (h) — 2,6м. Длина (CB) — 4,2м. Дверь. Ширина (LK) — 0,9м. Высота (h2) — 2,1м. Окно. Ширина (MN) — 1,4 м. Высота (h3) — 1,5 м Спальня. Окно. Дверь. ADCBLKMN
Номер слайду 18
Характеристика обоев: Узкие1 рулон. Цена: 77 грн. Длина(𝑭𝒁𝟏): 10 метр. Ширина(𝒁𝑸𝟏): 0.5 метр Широкие1 рулон. Цена: 310 грн. Длина(𝑭𝒁𝟐): 15 метр. Ширина(𝒁𝑸𝟐): 1 метр ppt_xppt_x
Номер слайду 19
Площади рулонов: Площадь 1 рулона узких обоев: Площадь 1 рулона широких обоев: S(уз.об.) = FZ1*ZQ1= 10 * 0.5 = 5 м²S(шир.об.) = FZ2*ZQ2 = 15 * 1 = 15 м²
Номер слайду 20
Расчeты площадей стен, двери и окна: Для удобства условно обозначим все стороны комнаты как : DD1 A1 A-сторона a, B1 A1 AB-сторона b, CC1 B1 B-сторона c, CC1 D1 D-сторона d,Сторона a= стороне c. Найдём их площадь: S(a) = 4.2 * 2.6 = 10.9 м²S(a+c) = 2 * S(a) = 21.8 м²Сторона b = стороне d. Найдём их площадь: S(b) = 2.7 * 2.6 = 7.02 м²S(b+d) = 2 * S(b) = 14.04 м²S(окна) = 1.4 * 1.5 = 2.1 м²S(двери) = 0.9 * 2.1 = 1.89 м²ADBCA1 D1 B1 C1
Найдём их площадь: S(a) = 4.2 * 2.6 = 10.9 м²S(a+c) = 2 * S(a) = 21.8 м²Сторона b = стороне d. Найдём их площадь: S(b) = 2.7 * 2.6 = 7.02 м²S(b+d) = 2 * S(b) = 14.04 м²S(окна) = 1.4 * 1.5 = 2.1 м²S(двери) = 0.9 * 2.1 = 1.89 м²ADBCA1 D1 B1 C1
Номер слайду 21
Общая площадь комнаты: Чтобы определить общую площадь обоев, необходимых для ремонта комнаты, нужно из общей площади стен вычесть площадь окна и двери: S(общ.)S(a+c) + S(b+d) — S(окна) — S(двери)21.8 + 14.04 — 2.1 — 1.8931.85ppt_xppt_xppt_xppt_xppt_xppt_xppt_xppt_xppt_x
Номер слайду 22
Какими обоями выгоднее поклеить?Сколько понадобится рулонов, чтобы обклеить всю комнату узкими обоями?(Часть рулона купить нельзя, можно только целый. Округлять нужно в большую сторону)Сколько понадобится рулонов, чтобы обклеить всю комнату широкими обоями?Кол-во рулонов. S(общ.) / S(уз.об.)731.85 / 5 = 6,37 Стоимость:539 грн7 * 77(Коло-во) * (цена 1 рулона)Кол-во рулонов. S(общ.) / S(уз.об.)331.85 / 15 = 2.2 Стоимость:930 грн3* 310(Коло-во) * (цена 1 рулона)ppt_xppt_xppt_xppt_xppt_xppt_xppt_xppt_xppt_xppt_xppt_xppt_xppt_xppt_xppt_xppt_xppt_xppt_xppt_xppt_xppt_xppt_xppt_xppt_xppt_xppt_xppt_xppt_xppt_xppt_xppt_xppt_xppt_xppt_xppt_xppt_xppt_xppt_xppt_x
Номер слайду 23
Итог: Спальную комнату выгоднее обклеить узкими обоями. 2
2
Номер слайду 27
ABDCA1 D1 B1 C1 EGJLFKTR
Номер слайду 28
Определяем количтво рулонов обоев на кухню и их цену. Найдём периметр комнаты и высчитаем кол-во полотен и рулонов. P(кухни)=3,14*2 + 2,24*2 = 10,76м N(полотен на комнату) = P(кухни) / h(рулона) = 10.76 / 1.06 = 10.2 шт. N(рулонов) = N(полотен на комнату) / N(полотен в рулоне) = 10,2 / 2 = 5шт. (+1 рулон на запас)Заметки: Широкие обои h(рулона) – 1.06(По данным производителя)N(полотен в рулоне) = 2шт.(По данным производителя).
Номер слайду 29
Ценаx1 рулон – 680 грн. x6 рулонов – 680 * 6 = 4080 грн.
Номер слайду 30
А что если взять те же обои только с шириной 60 см.?Сколько полотен будет на комнату?Сколько рулонов понадобится?И сколько это всё будет стоить?N(полотен на комнату) = P(кухни) / h(рулона) = 10.76 / 0.6 = 18 шт. N(рулонов) = N(полотен на комнату) / N(полотен в рулоне) = 18 / 2 = 9 шт. (+1 рулон на запас)Заметки: Тонкие обоиh(рулона)= 0.6 м. P=10.76 м. N(полотен в рулоне)=2 шт. (По данным производителя) x1 рулон – 500 грн.x10 рулонов – 500 * 10 = 5000 грн.
(По данным производителя) x1 рулон – 500 грн.x10 рулонов – 500 * 10 = 5000 грн.
Номер слайду 31
Вывод. Измеряв все стены и найдя их площадь, можно сказать, что лучше использовать широкие обои, т.к. по цене выйдет дешевле и при окончании поклейки обоев, не будет сильно заметно стыков полотен обоев
Номер слайду 32
В 6 классе изучаем тему «Отношения и пропорции». Детям был предложен проект «Применение пропорций в повседневной жизни»
Номер слайду 33
Пропорции на кухне. Задание с салатом Автор: Миненко Валерия и Никитчук Валерия
Номер слайду 34
Задание: Рассчитать пропорции ингредиентов для салата “Оливье”.
Номер слайду 35
Ингредиенты ( на 1 кг салата ): Картофель отварной (очищенный) — 4 шт. = 180 г (1 шт. = 45 г) Морковь отварная (очищенная) — 2 шт. = 120 г (1 шт. = 60 г)Яйца вареные (очищенные) — 2 шт. = 100 г (1 яйцо 50 г)Огурцы соленые — 2 шт. = 100 г (1 шт. = 50 г)Ветчина — 250 г Майонез — 130 г. Горошек зеленый консервированный — 120 г. Всего: 1000 г.
Всего: 1000 г.
Номер слайду 36
Что есть из перечисленного: Картофель отварной (очищенный) — 2 шт. 90 г (1 шт. = 45 г)Морковь отварная (очищенная) — 2 шт. 120 г (1 шт. = 60 г) Яйца вареные (очищенные) — 2 шт. 100 г (1 шт. = 50 г)Огурцы соленые — 2 шт. 100 г (1 шт. = 50 г) Ветчина -200 г Майонез — 130 г Горошек зеленый консервированный — 120 г Всего: 860 г
Номер слайду 37
Расчёт: Чтобы приготовить салат с теми продуктами которые у нас, нам нужно уменьшить остальные ингредиенты соответственно. Возьмём: Картофель отварной (очищенный) — 2 шт. 90 г (1 шт. = 45 г)Морковь отварная (очищенная) — 1 шт. 60 г (1 шт. = 60 г) Яйца вареные (очищенные) — 1 шт. 50 г (1 шт. = 50 г)Огурцы соленые — 1 шт. 50 г (1 шт. = 50 г) Ветчина -150 г Майонез — 65 г Горошек зеленый консервированный — 60 г Всего 525г
Номер слайду 38
Остаток: Картофель отварной (очищенный) — 0 шт. Морковь отварная (очищенная) — 1 шт. 60 г Яйца вареные (очищенные) — 1 шт. 50 г Огурцы соленые — 1 шт. 50 г Ветчина — 50 г Майонез — 65 г Горошек зеленый консервированный — 60 г Всего: 335г
Номер слайду 39
Вывод: Т. к. у нас вместо 4 картошин есть только две, а ветчины в 1.25 раза меньше, но не смотря на то что ветчины было в 1.25 раза меньше, нам пришлось уменьшить ингредиенты в два раза. Это всё для того чтобы соблюдать пропорции приготовления.
к. у нас вместо 4 картошин есть только две, а ветчины в 1.25 раза меньше, но не смотря на то что ветчины было в 1.25 раза меньше, нам пришлось уменьшить ингредиенты в два раза. Это всё для того чтобы соблюдать пропорции приготовления.
Номер слайду 40
Салат «Цезарь»{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Ингредиент. Вес. Цена. Зеленый салат100 г2,88 грн. Помидор100 г3,79 грн. Куриное филе100 г10,49 грн. Сыр Пармезан? г? грн. Хлеб белый100 г4,25 грн. Всего550 г52,61 грн. Вычислите, сколько весит и стоит отсутствующий ингредиент:
Номер слайду 41
Решение: Известно, что общий вес всех ингредиентов равна 550г, тогда:550-400=150г (вес недостающего ингредиента). Также известна сумма всех ингредиентов(равна 52,61 грн), тогда:52,61-42,82=9,79 грн(цена за 150г искомого ингредиента).
Номер слайду 42
Пропорции в построении выкроек. Размеры элементов кукольного сарафана отличаются от соответствующих размеров сарафана девушки в одно и тоже число раз. Задача: Длина изделия на выкройке 75см. Вычислите масштаб чертежа, если на нем длина сарафана будет равна 15см. Ответ: 1:5
Вычислите масштаб чертежа, если на нем длина сарафана будет равна 15см. Ответ: 1:5
Номер слайду 43
Пропорции в медицине. При изготовлении лекарств тоже соблюдаются пропорции. Здесь необходима точность, так как при нарушении пропорций, составляющих лекарство ингредиентов, может получиться не лекарство, а яд. Задача из народных рецептов: Для приготовления настойки прополиса нужно залить измельчённый прополис водой в отношении 2:5. Сколько потребуется воды для 150 г. прополиса. Решение 2:5=150:х х=150*5:2 x = 375г. Ответ: потребуется 375г. воды
Номер слайду 44
При изучении темы «Окружность и круг. Длина окружности», выполняем практическую работу, с помощью которой находим число π
Номер слайду 45
Задача от шеф-повара. Продаются блинчики двух видов, диаметром 30см и 20см. Все блины имеют одинаковую толщину, то в каком случае покупатель съест больше: когда съест один большой блинчик или два маленьких?
Номер слайду 46
Номер слайду 47
Математические знания и навыки необходимы практически во всех профессиях, прежде всего в тех, которых связаны с естественными науками, техникой, экономикой. «Образование не дает ростков в душе, если оно не проникает до значительной глубины» Древнегреческий философ Протагор из Абдеры (481 – 411г. до н.э.)
«Образование не дает ростков в душе, если оно не проникает до значительной глубины» Древнегреческий философ Протагор из Абдеры (481 – 411г. до н.э.)
Номер слайду 48
Сравнение тарифных планов
Номер слайду 49
Содержание. Vodafone1 Lifecell2 Проблемный вопрос33 Сравнительная таблица44 Итоги7 В рамках тарифа35 За рамками тарифа6
Номер слайду 50
Vodafone. Украинский оператор мобильной связи Водафон занимает одну из лидирующих позиций на рынке. Отличная репутация, многообразие тарифных планов на любой вкус, выгодные условия общения и горячие акционные предложения – все это позволяет компании Водафон привлекать еще большее число абонентов.
Номер слайду 51
Lifecell. Lifecell – украинский оператор мобильной связи, владельцем 100% акций которого является международная компания-лидер Turkcell. На сегодняшний день оператор Lifecell является не только оператором №1 для смартфонов в Украине, но и лидером по внедрению инноваций.
Номер слайду 52
Каждый оператор пытается привлечь своими предложениями. Но действительно ли тарифы настолько выгодные?Проблемный вопрос
Но действительно ли тарифы настолько выгодные?Проблемный вопрос
Номер слайду 53
Сравнительная таблица
Номер слайду 54
В рамках тарифа: Звонки на другие сети выгоднее в Lifecell. Интернет выгоднее в Lifecell
Номер слайду 55
За рамками тарифа: Интернет выгоднее в Vodafone. Звонки на другие сети выгоднее в Lifecell
Номер слайду 56
итоги. Наше небольшое сравнение тарифов мобильных операторов показало простую вещь — даже для абонентов, которые не готовы много тратить на мобильную связь, есть интересные предложения. Но, учитывая все показатели, Lifecell ВЫГОДНЕЕ!
Номер слайду 57
Вывод: Итак, в современном обществе необходим человек, умеющий решать реальные жизненные проблемы на основе предметных знаний и умений. Наша задача- сформировать данную компетентность. Это возможно только в процессе решения проблем повседневной жизни и в этом плане огромным потенциалом обладают прикладные задачи.
Номер слайду 58
Наука в школе есть одна. Во всех профессиях нужна. Учителям, врачам и поварам. Бухгалтерам, певцам и продавцам. Всем математика важна. Царица всех наук она.
Во всех профессиях нужна. Учителям, врачам и поварам. Бухгалтерам, певцам и продавцам. Всем математика важна. Царица всех наук она.
Номер слайду 59
Мастер-класс «Решение прикладных задач по математике»Подготовили и провели учителя математики ЭМЛ Гриднева Елена Яковлевна, Калмыкова Виктория Валерьевна
Номер слайду 60
Спасибо за внимание и участие
Прикладные математические задачи — примеры математики из реального мира
Задачи по прикладной математике — примеры математики из реального мира охватывают многие области применения математики в реальной жизни, от алгебры до продвинутого исчисления и дифференциальных уравнений.
Пожалуйста, имейте в виду, что цель этой статьи и большинства прикладных математических задач не в том, чтобы научить вас математике напрямую.
Если вы используете это в качестве справочного материала, убедитесь, что вы правильно цитируете нас и даете ссылку на оригинал. Спасибо 🙂
Прикладные математические задачи Схема
Вот что мы рассмотрим в этой статье о Sphero RVR SDK.
- Почему прикладные математические примеры?
- Примеры прикладной алгебры и предварительного исчисления
- Примеры прикладной линейной алгебры
- Примеры прикладного исчисления
- Примеры прикладных дифференциальных уравнений
- Прикладные числовые примеры
- Предлагаемые учебники
- Полезные ссылки
Почему Kinvert делает примеры по прикладной математике?
Хотя у меня есть степень инженера-механика и инженера-аэрокосмиста, я не всегда хорошо разбирался в математике.
Как и большинство вещей в моей жизни, я борюсь с вещами, в которых не вижу смысла.
Конечно, я мог бы найти, что х + 5 = 10, конечно, х = 5. Кого это волнует?
Но когда я пытался решить реальную задачу, я самостоятельно изобрел метод Ньютона, численное интегрирование и т. д.
д.
Я учусь, когда знаю, ПОЧЕМУ я учусь.
Вот о чем эта статья о примерах прикладной математики. Я здесь не для того, чтобы напрямую учить вас математике, по крайней мере, в этих статьях. Все это существует, чтобы помочь вам показать причину и использование математики в реальном мире.
Если вы знаете реальное использование математической концепции, сообщите мне об этом в комментариях ниже!
Мы будем обновлять эти прикладные математические задачи и математические примеры из реального мира
Это живой список, который со временем будет обновляться. Некоторые из этих тем могут содержать так много примеров, что нам придется ссылаться на них в отдельной статье. Например, если мы перечислим каждый пример, в котором мы используем функцию, что является темой алгебры, этот список сам по себе будет содержать почти каждый реальный математический пример, который мы будем делать.
Мы разделили эти прикладные математические задачи и математические примеры из реального мира на математические дисциплины.
Примеры прикладной алгебры и предварительного исчисления
Видишь этого робота? Наши студенты справились. Без применения алгебры это было бы невозможно.
- Введение
- Реальные числа
- Они постоянно используются практически для всего
- Синтетический отдел
- Раздел используется постоянно. Если вы застряли на необитаемом острове и хотите сделать вертолет из кокосов, вам может понадобиться Synthetic Division .
- Реальные числа
- Графики
- Расстояние между двумя точками
- Строительство моста в Minecraft — https://youtu.be/P2vd-8ilNs0
- Навигация
- Средняя точка между двумя точками
- Фактическое использование в Minecraft — https://youtu.be/0hjUqseXf0w Факторинг
- Шифрование RSA (кибербезопасность)
- Фактическое использование в Minecraft — https://youtu.be/0hjUqseXf0w Факторинг
- кругов
- Компьютерная графика
- Расстояние между двумя точками
- Линейные уравнения
- Неравенства
- Через какое время инвестиции окупятся
- Словесные задачи прикладного линейного уравнения
- Калибровка джойстика — https://youtu.
 be/Vb_GaXuB15c
be/Vb_GaXuB15c - Строительство моста в Minecraft — https://youtu.be/P2vd-8ilNs0
- Неравенства
- Полиномы
- Степень многочлена
- https://youtu.be/JoV-zLmy6O8
- Квадратные уравнения
- Пример прикладной математики – двойной определенный интеграл – определение подъемной силы на крыле гоночного автомобиля
- Пример прикладной математики — определенный интеграл — торможение данными телеметрии гоночного автомобиля F1
- Полиномы высшего порядка
- Степень многочлена
- Комплексные числа
- Электротехника
- Текущий закон Кирхгофа
- Закон напряжения Кирхгофа
- Электромагнетизм
- Электротехника
- Функции
- Почти все
- Введение в некоторые виды использования — https://youtu.be/r0xLvCLoBOA
- Составные функции
- Найти кинетическую энергию как функцию времени — https://youtu.
 be/eeGOUeX2keo
be/eeGOUeX2keo - Функция изменения температуры от времени – перевести в шкалу Ренкина из градусов Цельсия
- Найти кинетическую энергию как функцию времени — https://youtu.
- Экспоненциальные функции
- Прикладные экспоненциальные функции Словесные задачи
- Экспоненциальный рост
- Проблемы с процентами
- Сравнение инвестиций с начислением сложных процентов — https://youtu.be/awNP8DlvzMA
- Проблемы с процентами
- Экспоненциальный спад
- Экономика
- Логарифмические функции
- Проценты
- Компаундирование
- децибел
- Графики
- Шкала Рихтера
- Коники
- Орбитальная механика
- Эллипс
- Орбитальная механика
- Парабола
- Орбитальная механика
- Гипербола
- Орбитальная механика
- Системы линейных уравнений – замена и исключение
- Пример прикладной математики.
 Исключение. Равновесие твердых тел
Исключение. Равновесие твердых тел - Пример прикладной математики — Исключение — Сила на носовом обтекателе F1
- Равновесие твердого тела
- Пример прикладной математики — Оценка стоимости дома Cude — https://youtu.be/VHxOWbF1VLM
- Строительство моста в Minecraft — https://youtu.be/P2vd-8ilNs0
- Оценка цены/стоимости автомобиля — https://youtu.be/mbGPkzwjY1o
- Предварительный нагрев 3D-принтера — https://youtu.be/us8YRqdNEbA
- Пример прикладной математики.
- Матрицы
- Компьютерная графика
- Детерминанты
- Определение момента или крутящего момента на гаечном ключе
- Матрица Алебра
- См. «Линейная алгебра» ниже – Примеры прикладной линейной алгебры
- Разложение на частичные дроби
- Системы нелинейных уравнений
- Последовательности
Примеры прикладной линейной алгебры
- Скалярное произведение – скалярное произведение
- Пример прикладной математики — скалярное произведение — нахождение угла между двумя векторами
- Много других применений
- Векторное произведение — кросс-произведение
- Определение момента или крутящего момента на гаечном ключе
- Магнитные поля
- Ликвидация
- Пример прикладной математики.
 Исключение. Равновесие твердых тел
Исключение. Равновесие твердых тел - Пример прикладной математики — Исключение — Сила на носовом обтекателе F1
- Пример прикладной математики.
- Основа
- Компьютерная графика
- Прогнозы
- Компьютерная графика
- Метод наименьших квадратов
- Подгонка уравнений к данным
- Машинное обучение
- Детерминанты
- Определение момента или крутящего момента на гаечном ключе
- собственных значений
- собственных векторов
- Вибрация MDOF
- Положительная разница
- Разложение по единственному значению
- Линейное преобразование
- Компьютерная графика
Примеры прикладного исчисления
- Пределы
- Дифференциация
- Скорость изменения
- Скорость и ускорение
- Неопределенные интегралы
- Определенные интегралы
- Расстояние, пройденное автомобилем F1 при торможении
- Пример прикладной математики — определенный интеграл — торможение данными телеметрии гоночного автомобиля F1
- Массовый расход через 2D-профиль постоянной площади
- Распределенная нагрузка
- Центроиды
- Площадь Момент инерции
- Работа
- Линейный импульс и импульс
Серия - Аппроксимирующие функции
- Ряд Фурье
- SDOF Периодическая вынужденная вибрация
- Спектрограммы
- Параметрические уравнения
- Частная производная
- Дифференциалы
- Двойные интегралы
- Сохранение массы
- Закон сохранения импульса
- Пример прикладной математики — двойной определенный интеграл — определение подъемной силы крыла гоночного автомобиля
- Пример прикладной математики — двойной интеграл в полярных координатах — расход на входе воздушной камеры F1
- Пример прикладной математики — двойной интеграл — расход на входе боковой платформы F1
- Тройные интегралы
- Сохранение массы
- Закон сохранения импульса
- Изменение переменных
- Векторные поля
- Завиток
- Гидродинамика – завихренность и безвихревость
- Общие
- Магнитные поля
- Гидродинамика
- Уравнения Максвелла
- Завиток
- Линейные интегралы
- Тираж
- Закон Ампера
- Закон Фарадея
- Уравнения Максвелла
- Масса проволоки
- Работа, выполненная векторным полем
- Теорема Грина
- Планиметр – область поиска
- Поверхностные интегралы
- Электрический флюс
- Электрический заряд на поверхности
- Электрические поля
- Закон Гаусса
- Емкость
- Сила давления на площадь
- Массовый расход
- Расхождение
- Бернулли
- Теорема Стокса
Примеры прикладных дифференциальных уравнений
В колледже я сначала боролся с дифференциальными уравнениями, потому что единственное, что я действительно видел, это определенные схемы и гармоническое движение.
Итак, я решил найти применение, и в итоге я смоделировал теплопередачу через тормозные роторы. Лично я лучше всего изучаю математику, когда вижу ее реальное применение. Давайте посмотрим на реальное использование дифференциальных уравнений.
Если мне чего-то не хватает, сообщите мне об этом в разделе комментариев ниже.
- Первый Орден
- Разделяемые переменные
- Подвесной мост
- Линейные уравнения
- Закон охлаждения Ньютона
- Конечная скорость
- Сопротивление воздуха
- Наклонный скольжение
- Точные уравнения
- Решения заменой
- Нелинейный
- Сопротивление воздуха
- Краткое числовое значение
- Разделяемые переменные
- Линейный второй порядок
- Простое гармоническое движение
- Высший порядок
- Линейный
- Прогиб консольной балки
- Прогиб балки с простой опорой
- Свободная вибрация
- Вращательный дисбаланс
- Изгиб колонны
- Пример прикладной математики — дифференциальное уравнение начального значения 2-го порядка — изгиб переднего крыла F1
- Начальное значение
- Прогиб консольной балки
- Пример прикладной математики — дифференциальное уравнение начального значения 2-го порядка — изгиб переднего крыла F1
- Граничное значение
- Прогиб балки с простой опорой
- Однородный
- Свободная вибрация
- Неоднородный
- Принудительная вибрация
- Вращательный дисбаланс
- Уменьшение заказа
- Однородная линейная с постоянными коэффициентами
- Неопределенные коэффициенты
- Изменение параметров
- Коши Эйлер
- Ликвидация
- Движение снаряда
- Нелинейный
- Ракетное движение
- Движение в силовом поле
- Нелинейные пружины
Серия - Линейный
- Серия Power
- Преобразование Лапласа
- Автомобиль на кочке
- Пружины и масса
- Прогиб балки
- Системы дифференциальных уравнений
- Балка, закрепленная на обоих концах
- Уравнения с частными производными
- Навье Стоукс
- Куэтт Флоу
Прикладные численные примеры
- Метод Ньютона
- Пример прикладной математики – метод Ньютона – определение отношения площадей для сопла ракеты
- Суммы Римана
- Метод стрельбы
- Прогиб балки
- Интерполяция
- Правило трапеций
- Правило Симпсона
- Серия Тейлора
- Точное приближение в CS
- Рунге Кутта
- БВП
- Эллиптический
- Параболический
- Гиперболический
Мы приветствуем ваши предложения!
Если вы знаете о реальном использовании определенной математической концепции, пожалуйста, сообщите нам об этом в комментариях ниже.
Кроме того, пожалуйста, помните, что эта работа еще не завершена. Со временем мы добавим больше примеров математики из реального мира в этот прикладной список математики.
Рекомендуемые учебники по математике
Исчисление — в колледже я в основном использовал исчисление «Ранние трансцендентальные функции» Ларсона и других — Проверить цену на Amazon — https://amzn.to/2LuiI3K
Другое рекомендуемое чтение/ диапазон>
Если вы оказались здесь, есть большая вероятность, что вам понравится:
Робототехника для домашнего обучения – обучение робототехнике дома
Учебная программа Anki Cozmo
Лучшие обучающие игрушки STEM
Полное руководство по проектам робототехники
Лучшие бесплатные образовательные веб-сайты
Wolfram|Alpha Примеры: прикладные Математика
Wolfram|Alpha Примеры: Прикладная математика О-о! Wolfram|Alpha не работает без JavaScript.
Пожалуйста, включите JavaScript. Если вы не знаете, как это сделать, вы можете найти инструкции здесь. Как только вы это сделаете, обновите эту страницу, чтобы начать использовать Wolfram|Alpha.
Примеры для
Прикладная математика — это раздел математики, посвященный использованию и применению результатов, приемов и методов математики и специальных знаний в предметной области для понимания и решения реальных проблем в науке, технике, бизнесе, обществе, машиностроение и промышленность. Обширная база вычислительных знаний и мощных математических алгоритмов Wolfram|Alpha позволяет вам применять математические методы для вычислений, анализа и исследования множества проблем, возникающих в практических приложениях. 92=1Больше примеровДинамические системы
Используйте Wolfram|Alpha для изучения динамических систем с дискретным и непрерывным временем и систем управления.
Анализ логистической карты:
логистическая карта r=3,569935Анализ модели хищник-жертва Лотки-Вольтерры:
модель хищник-жертва Дополнительные примерыТеория игр
Получите информацию и анализ рисков и выгод сотрудничества и конфликтов в различные математические игры.
Получить информацию о математической игре:
Battle of the Sexeschicken gametic-tac-toe игра «камень-ножницы-бумага» Численный анализИспользуйте численный анализ для вычисления корней уравнений, решения численных интегралов и решения обыкновенных дифференциальных уравнений.
Найти корень уравнения с помощью метода Ньютона:
с помощью метода Ньютона решить x cos x = 0Использовать численные методы для поиска корней чисел:
найти корень из 2 методом деления пополамПриблизить интеграл с помощью указанного численного метода: 93 y, y(1) = 5, от 1 до 10Больше примеровФракталы
Спросите о фракталах как над реальными, так и над сложными областями.
Постройте фракталы, заданные динамическими системами:
Набор Жюлиа -0,40+0,65iМандельброт наборБольше примеровСВЯЗАННЫЕ ПРИМЕРЫ
Оценка количества объектов требуется для упаковки или покрытия другого объекта.

 be/Vb_GaXuB15c
be/Vb_GaXuB15c  be/eeGOUeX2keo
be/eeGOUeX2keo  Исключение. Равновесие твердых тел
Исключение. Равновесие твердых тел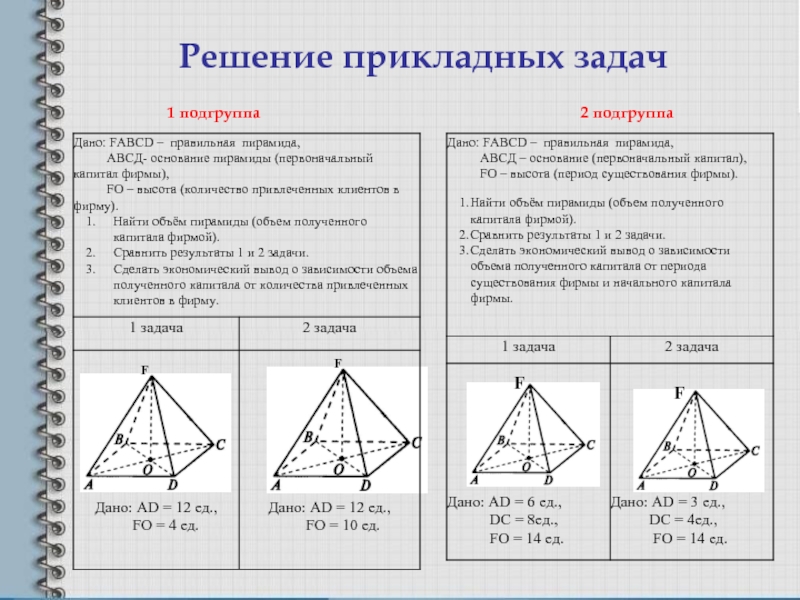 Исключение. Равновесие твердых тел
Исключение. Равновесие твердых тел