Урок по теме «Пересечение и объединение множеств». 6-й класс
Тип урока: изучение нового материала.
Цели:
- формирование знаний о пересечении и объединении множеств;
- развитие умений и нахождение числа элементов пересечения и объединения множеств, выявлять закономерность, обобщать и делать выводы, воспитание ответственного отношения к учебе.
Ход урока
1. Организационный момент.
2. Повторение изученного по теме «Множества».
Вопросы для учащихся:
- Что такое множество?
- Что такое элементы множества?
- Какое множество конечно и бесконечно?
- Какое множество называется пустым?
3. Изучение нового материала «Пересечение множеств».
Учитель. Рассмотрим следующие два множества: М – множество всех точек круга, N – множество точек прямой, пересекающей круг.
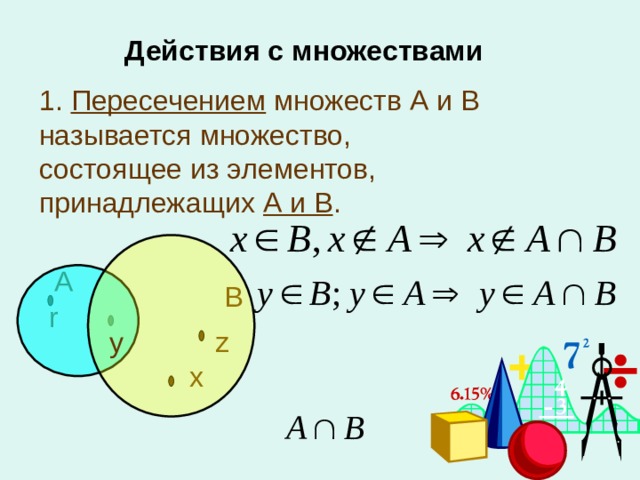
Точно так же можно определить пересечение любых двух множеств М и N. Пересечением множеств М и N называется множество, состоящее из всех элементов, принадлежащих каждому из множеств М и N. Пересечение множеств М и N обозначают М ∩ N. Читают: «пересечение М и N» или «М пересечение N». Знак ∩ называется знаком пересечения
. Обсудим несколько примеров.
Пример 1. М – множество всех учениц какой-то школы, N – множество всех учащихся данного класса этой школы. Тогда М ∩ N – это множество всех девочек из данного класса.
Пример 2. М – множество всех квартир на 1-м этаже в каком-то доме, N – множество всех квартир в данном подъезде этого дома. Тогда М ∩ N – это множество всех квартир на 1-м этаже в данном подъезде.
Пересечение множеств точек двух фигур на плоскости легче представить, если нарисовать эти фигуры. Сделаем это, например, для двух кругов. Множество всех точек первого круга обозначим М, второго – N. Для пересечения М ∩ Nмогут быть три варианта; они изображены на рисунке.
Если конечные множества записаны при помощи фигурных скобок списками своих элементов, то легко записать их пересечение.
Примеры:
Пересечение можно образовывать не только для двух множеств, но и для любого их числа.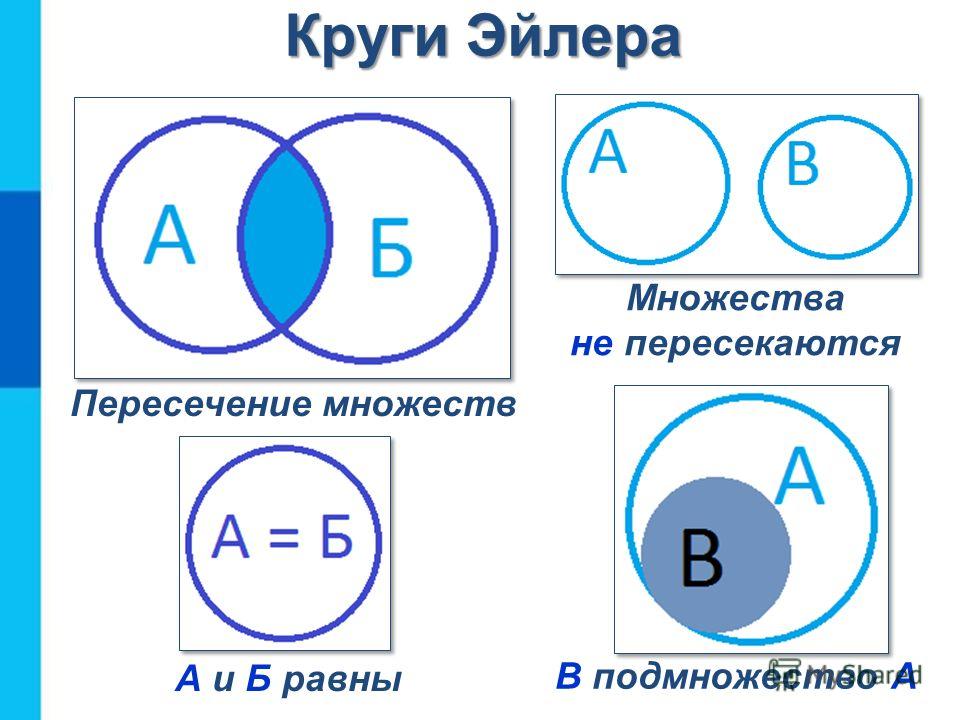
Определяется это точно так же, как и для двух множеств: пересечением данных множеств называется множество, состоящее из всех элементов, принадлежащих каждому из этих множеств. Пересечение множеств М, N и Р обозначается М ∩N ∩ Р.
Вопрос для учащихся:
Что обозначает запись Р ∩ Q ∩ R ∩ S? Какому множеству равно это пересечение, если
4. Первичное закрепление понятия пересечения множеств.
Вопросы:
- Что такое пересечение двух множеств; нескольких множеств?
- Что значит, что два множества не пересекаются? Приведите 2-3 примера непересекающихся множеств.
- Какое множество обозначается знаком ?
Практические задания:
1. Для каждой пары множеств М и Nзапишите их пересечение:
N – множество всех неправильных дробей.
2. Для каждой пары множеств М и N укажите их пересечение:
- М – множество всех нечетных чисел, N – множество всех натуральных чисел, делящихся на 4;
- М – множество всех правильных дробей, N – множество всех десятичных дробей;
- М – множество всех натуральных чисел, делящихся на 3, N – множество всех натуральных чисел, делящихся на 5.
3.
а) треугольник АВС;
б) прямоугольник KLMN.
4. Рассмотрите три множества {1, 2}, {2, 3}, и {3, 1}. Убедитесь, что их пересечение пусто, а пересечение любых двух из этих множеств не пусто.
5.
Пусть М – множество всех букв слова СЛОН, N – множество всех букв слова СТОН, Р – множество всех букв слова СТОГ, S – множество всех букв слова СЛОГ.
- Запишите всевозможные попарные пересечения этих множеств. Имеются ли среди них равные?
- Запишите всевозможные пересечения троек этих множеств. Имеются ли среди них равные?
- Запишите пересечение всех этих множеств. Равно ли оно какому-то из множеств, найденных вами в пунктах а) и б)?
5. Изучение нового материала «Объединение множеств».
Учитель. Объединением множеств М и N называется множество всех элементов, принадлежащих хотя бы одному из множеств М и N.
Объединение множеств М и N обозначают М N. Читают: «объединение М и N» или «М объединение N». Знак называется знаком объединения.
Разберем несколько примеров. Обдумайте каждый из них.
Пример 1. М – множество всех учеников данного класса, получивших на сегодняшний день пятерку по какому-нибудь предмету,
Пример 2. М – множество всех правильных дробей, N – множество всех неправильных дробей. Тогда М N – это множество всех обыкновенных дробей.
Пример 3. М – множество всех букв слова КОШКА, N – множество всех букв слова МЫШКА. Тогда М N = {А, К, М, О, Ш, Ы}.
Задание для учащихся: Приведите сами какой-нибудь пример объединения двух множеств.
Учитель. Как и пересечение, объединение можно образовать не только для двух множеств, но и для любого их числа: объединением данных множеств называется множество, состоящее…
Закончите определение.
Догадайтесь, как записать объединение трех множеств М, N и Р.
Если конечные множества записаны при помощи фигурных скобок списками своих элементов, то, как и для пересечения, легко записать их объединения.
Для любых множеств М и N можно образовать их пересечение М ∩ N и объединение М N. Это похоже на то, что происходит при действиях над числами: для любых двух чисел m и n можно образовать их произведение m n и сумму m+n. Так получаются действия, которые назвали умножением и сложением. Поэтому образование пересечения и образование объединения можно назвать действиями над множествами.
Выполняются ли те же законы для пересечения и объединения множеств? Давайте рассуждать. Начнем с переместительного закона.
Повторим, что такое пересечение двух множеств: множество 
Но сказать «каждому из множеств М и N» или «каждому из множеств N и М» — значит сказать одно и то же: ведь ясно, что неважно, в каком порядке перечислять здесь множества. Значит, множества М ∩N и N ∩М состоят из одних и тех же элементов, т.е.
М ∩ N = N ∩М.
Данное равенство и означает, что переместительный закон для пересечения верен.
Чтобы проверить сочетательный закон, надо убедиться, что для любых трех множеств М, N и Р выполняется равенство
М ∩(N ∩Р)= (М ∩N) ∩РЛегко понять, что в левой и правой частях этого равенства записаны множества, состоящие из всех элементов, принадлежащих каждому из множеств М, N и Р, т.е. состоящие из одних и тех же элементов. Это и означает, что требуемое равенство выполняется.
6. Первичное закрепление изученного понятия объединения множеств.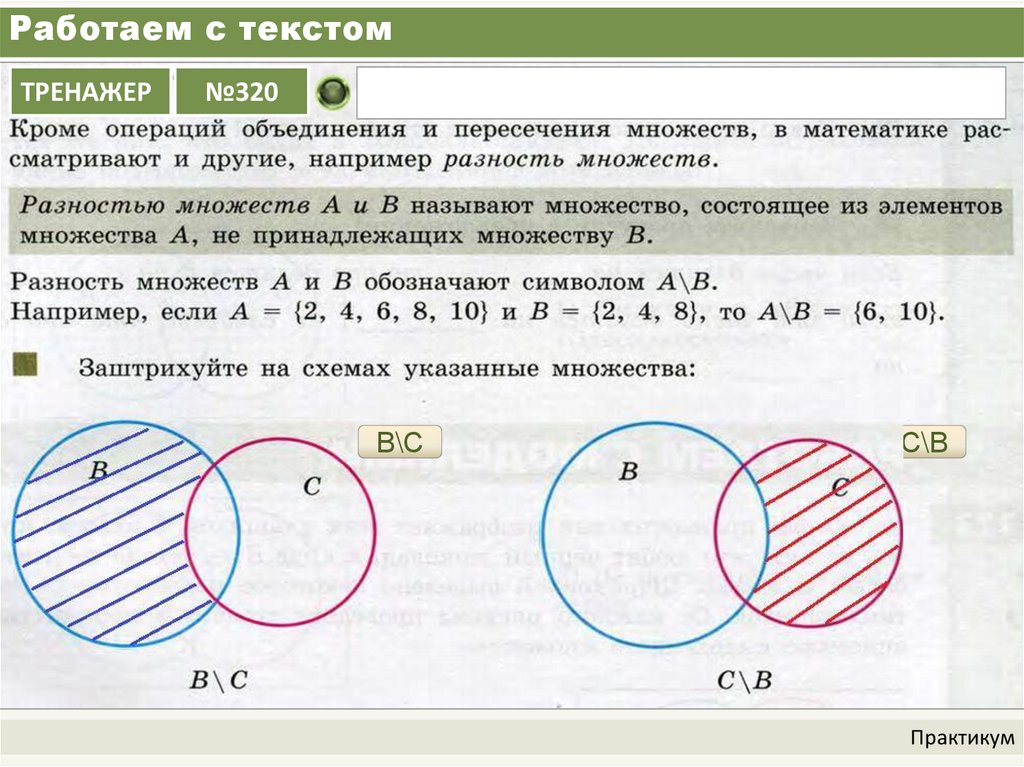
Вопросы:
- Что такое объединение двух множеств; нескольких множеств?
- О выполнении каких законов для действий пересечения и объединения множеств идет речь в объяснительном тексте этого параграфа?
- Каким множеством – конечным или бесконечным – будет объединение: а) двух конечных множеств; б) двух бесконечных множеств; в) конечного и бесконечного множеств?
Практические задания:
1. Для каждой пары множеств М и N запишите их объединение:
2. Для каждой пары множеств М и N укажите их объединение:
- М – множество всех нечетных чисел, N – множество всех четных чисел;
- М – множество всех квадратов на плоскости, N – множество всех прямоугольников на той же плоскости, четырехугольников;
- М – множество всех натуральных чисел, делящихся на 3, N – множество всех натуральных чисел, делящихся на 15.
3. Пусть М – множество всех букв слова СЛОН, N – множество всех букв слова СТОН, Р – множество всех букв слова СТОГ, S – множество всех букв слова СЛОГ.
- Запишите всевозможные попарные объединения этих множеств. Имеются ли среди них равные?
- Запишите всевозможные объединения троек этих множеств. Имеются ли среди них равные?
- Запишите объединение всех этих множеств. Равно ли оно какому-то из множеств, найденных вами в пунктах а) и б)?
7. Изучение нового – вывод правила подсчета числа элементов объединения и пересечения множеств.
Учитель. Чтобы вывести правило давайте разберем конкретный пример. Пусть М = {Вася, Валя, Вера, Игорь}, т.е. m=4;
N = {Валя, Гриша, Игорь}, т.е. n=3.
Запишем объединение этих множеств:
М N = {Вася, Валя, Вера, Гриша, Игорь}.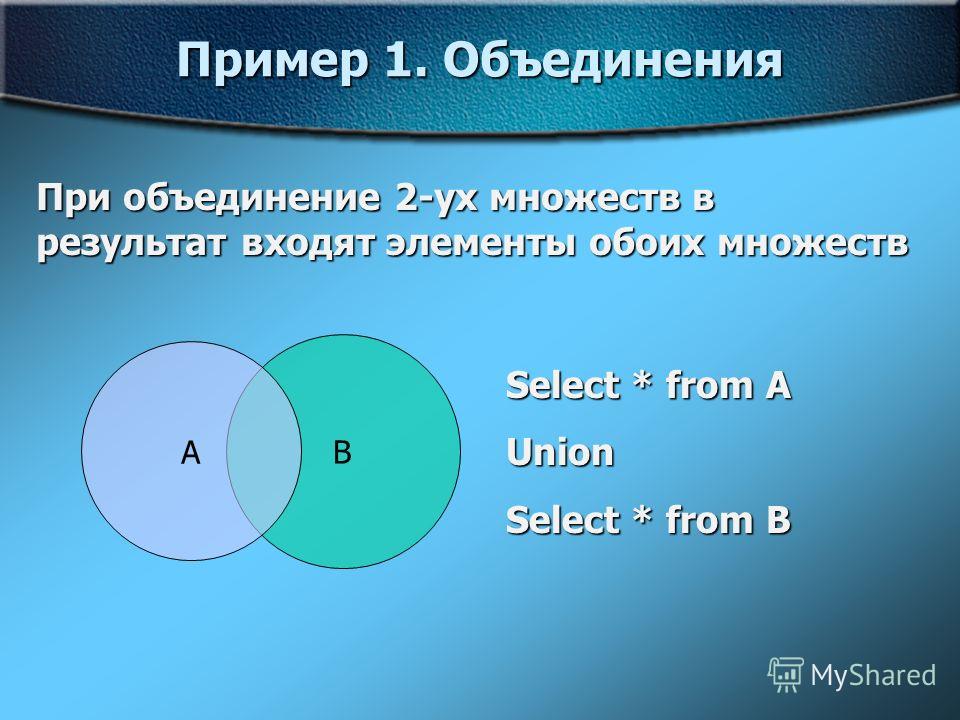
В множестве МN пять элементов, а m+n=4+3=7. Вот мы и видим, что в МN элементов меньше чем 7.
Почему так получилось? Да потому, что в данном примере можно указать учеников, которые в этот день получили и пятерку, и четверку. Другими словами здесь пересечение М ∩N не пусто: М ∩ N = {Валя, Игорь}. Но в объединении-то МN каждый элемент пересечения М ∩N присутствует (и подсчитывается) только один раз, а не два раза.
Давайте-ка изобразим ситуацию нашего примера на рисунке.
Если бы подсчитали здесь сумму m+n (т.е. 4+3), то каждый элемент пересечения (в данном примере Валя и Игорь, т.е. 2 элемента) оказался бы подсчитанным дважды. Значит, чтобы узнать число элементов объединения, надо из суммы m+n вычесть число лишний раз сосчитанных элементов пересечения. В данном примере получаем 4+3-2=5.
Данная задача была решена с помощью рисунка, этот способ называется «Круги Эйлера».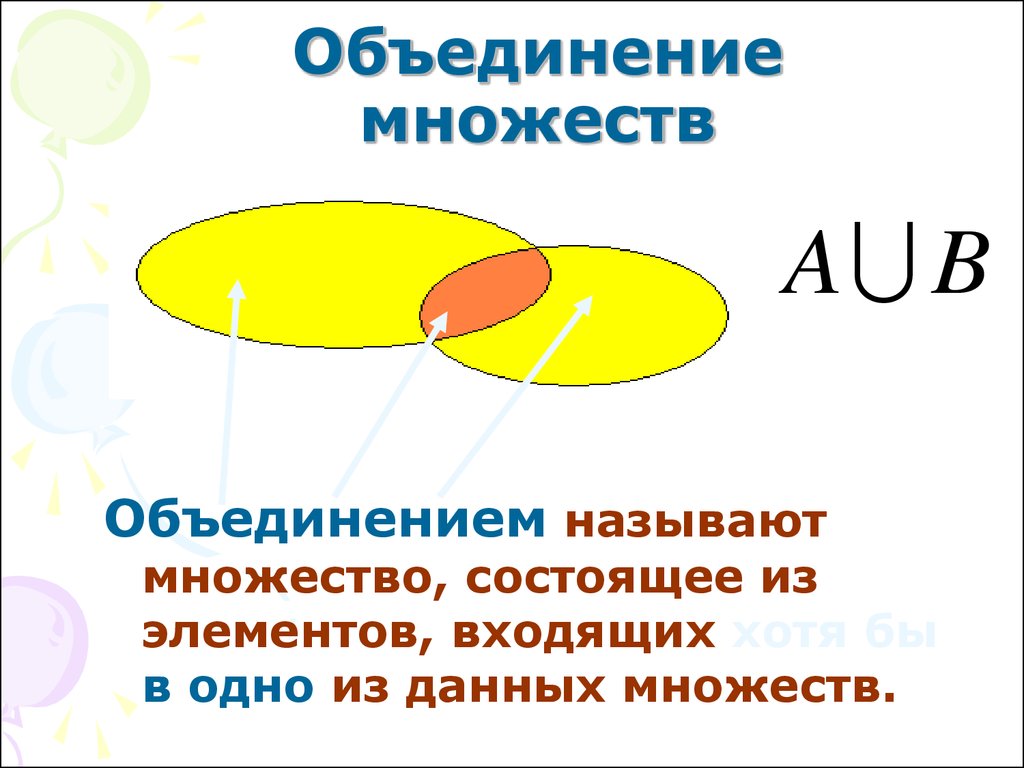
Леонард Эйлер – швейцарский математик, который в 18 веке работал в Российской академии наук и сделал много открытий для нашей науки.
Итак, если мы возьмем сумму m+n, то в ней элементы пересечения М ∩N будут сосчитаны дважды. Значит, чтобы определить число элементов объединения, надо из суммы m+n вычесть число лишний раз сосчитанных элементов из М ∩N, т.е. число р. Получим такую формулу: q=m+n-p.
Сформулируем правило для нахождения числа элементов объединения множеств:
Чтобы найти число элементов объединения двух множеств, надо сложить числа элементов этих множеств и вычесть из полученной суммы число элементов их пересечения.
Сформулируем правило для нахождения числа элементов пересечения множеств:
Чтобы найти число элементов пересечения двух множеств, надо сложить числа элементов этих множеств и вычесть из полученной суммы число элементов их объединения.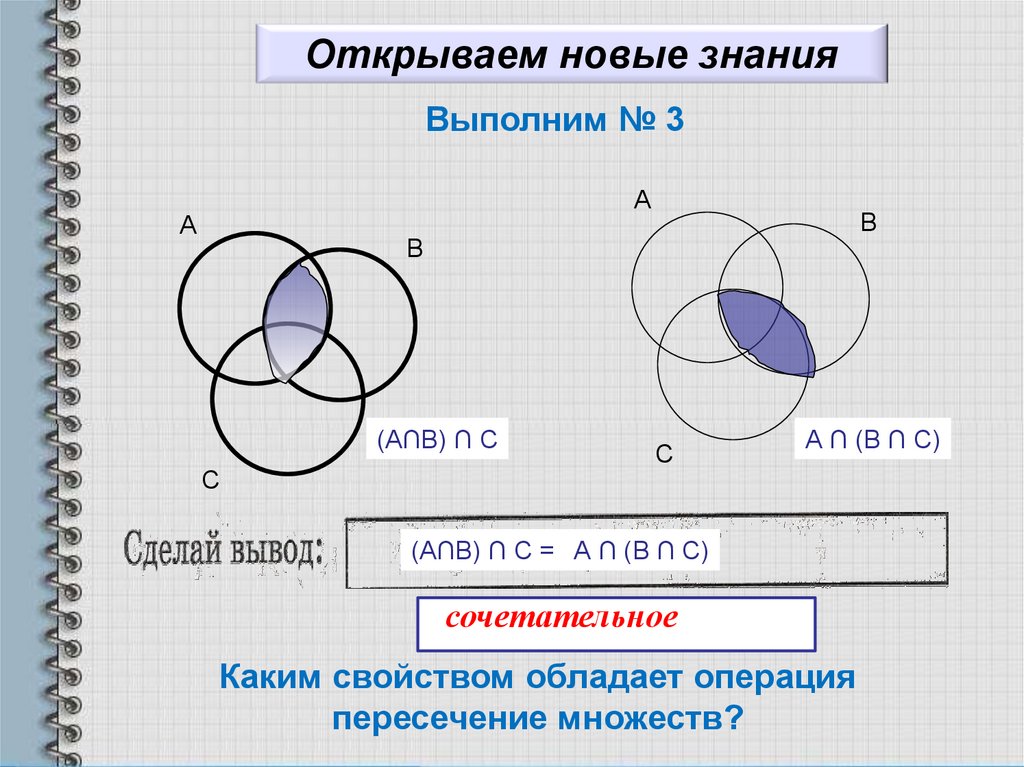
8. Первичное закрепление изученного.
Практические задания (устно):
1. Вычислите число элементов в объединении множеств М и N, если:
- М содержит 10 элементов, N – 15 элементов, а М ∩N – 7 элементов;
- М содержит 27 элементов, N – 18 элементов, а М ∩N – 13 элементов;
- М содержит 45 элементов, N – 57 элементов, а М ∩N – 1 элемент.
2. Вычислите число элементов в пересечении множеств М и N, если:
- М содержит 10 элементов, N – 15 элементов, а М ∩N – 17 элементов;
- М содержит 27 элементов, N – 18 элементов, а М ∩ N – 45 элементов;
- М содержит 45 элементов, N – 57 элементов, а М ∩N – 100 элементов.
Решение задач с помощью кругов Эйлера:
№1. В классе 28 учеников. Каждый из них начертил у себя в тетради один из двух четырехугольников – прямоугольник или ромб. При проверке прямоугольников оказалось 17, а ромбов – 15. Как такое могло случиться?
№2. В осенние каникулы 12 учеников класса участвовали в междугородных экскурсиях в Москву и Санкт-Петербург, при этом 8 из них посетили Санкт-Петербург, а 6 – Москву. Сколько из этих учеников побывало и в Москве, и в Санкт-Петербурге?
Задание на дом:
№1. Найдите пересечение множеств учителей, которые вели уроки в вашем классе: а) вчера и сегодня; б) вчера и позавчера. Оказалось ли какое-то из этих двух пересечений пустым?
№2. Вася, рассматривая свой дневник погоды, обнаружил, что в сентябре 17 раз отмечен дождь и 19 раз – сильный ветер. При этом дней, когда одновременно шел дождь и дул сильный ветер, оказалось 7.
Был ли хоть один день, когда не было ни дождя, ни сильного ветра?
свойства, формулы включений и исключений, примеры
- Пересечение множеств
- Объединение множеств
- Универсум и отрицание
- Свойства операций пересечения и объединения
- Разность множеств
- Формулы включений и исключений
- Примеры
Пересечение множеств
Если множества не пересекаются, то $A \cap B = \varnothing $ — пустое множество в пересечении. Если $B \subseteq A$ — подмножество, то $A \cap B = B$ – пересечением будет меньшее множество из двух.
Например:
Если A = {1;3;5;9}, Β = {3;7;11}, то $A \cap B$ = {3;5}.
Если A = {f|f-прямоугольник}, B = {f|f-ромб}, то $A \cap B$ = {f|f-квадрат}.
Если A = $\{n|n⋮3, n \in \Bbb N \}$ — натуральные числа, кратные 3, B = $\{n|n⋮5, n \in \Bbb N \}$ — натуральные числа, кратные 5, то $A \cap B = {n|n⋮15, n \in \Bbb N}$ — натуральные числа, кратные 15.
Если A = {a│a-слон}, B = {a|a-птица}, то $A \cap B = \varnothing$.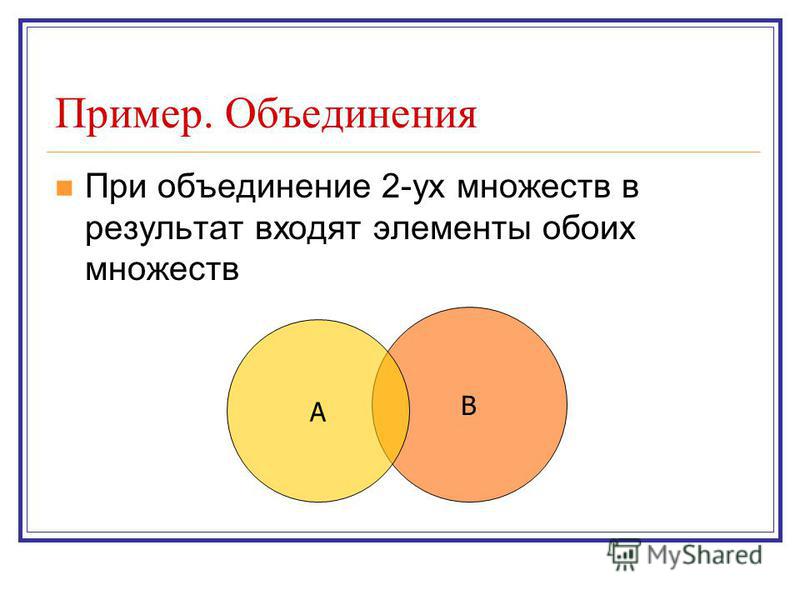
2-4 = 0, x \in \Bbb R\}, B = \{x|x+3 = 2, x \in \Bbb R \}, то A \cup$ B = {-2;-1;2}
Если $A = \{n│n \in \Bbb Z \}$- все целые числа, $B = \{x|x = \frac{a}{b}, a \in \Bbb Z, b \in \Bbb N \}$ — все дроби, то $A \cup B = \{x│x \in \Bbb Q\}$ — множество рациональных чисел. Заметим, что в данном случае $A \subset B$.
Универсум и отрицание
Универсум (универсальное множество) – множество, включающее в себя все множества, рассматриваемые в данной задаче.
В литературе универсум обозначают U.
На диаграммах Эйлера универсум изображают как множество точек прямоугольника, в котором лежат остальные множества:
Примеры универсумов:
При рассмотрении целочисленных задач, универсум – это множество целых чисел.
При построении двумерных графиков, универсум – это множество всех точек координатной плоскости.
При решении вероятностных задач, универсум – это множество всех возможных исходов цепочек событий.
Читается «не A».
У отрицания есть любопытное свойство: $\bar{\bar{Α}} = Α $(два раза «нет» — это «да»).
Например:
Если U = {1;2;3;4;5;6;7}, A = {3;4;5}, то $\bar{A} = \{1;2;6;7\}$
Если U = $\{x|x \in \Bbb R\}$ — все действительные числа, A = $\{x|x \gt 0, x \in \Bbb R \}$ — все положительные действительные числа, то $ \bar{A} = \{x|x \le 0, x \in \Bbb R\}$.
Свойства операций пересечения и объединения
Пересечение
Объединение
Коммутативность
$A \cap B = B \cap A$
$ A \cup B = B \cup A $
Ассоциативность
$(A \cap B) \cap C = A \cap (B \cap C)$
$ (A \cup B) \cup C = A \cup ( B \cup C) $
Дистрибутивность
$(A \cup B) \cap C = (A \cap C) \cup (B \cap C)$
$ (A \cap B) \cup C = (A \cup C) \cap (B \cup C) $
Идемпотентность
$A \cap A = A$
$ A \cup A = 0 $
Взаимодействие с отрицанием, пустым множеством и универсумом
$A \cap \bar{A} = \varnothing $
$A \cap U = A$
$A \cap \varnothing = \varnothing$
$A \cup \bar{A} = U $
$A \cup U = U$
$A \cup \varnothing = A$
Законы де Моргана
$ \overline{(A \cap B)} = \bar{A} \cup \bar{B} $
$ \overline{(A \cup B)} = \bar{A} \cap \bar{B} $
Закон поглощения
$ (A \cup B) \cap A = A $
$ (A \cap B) \cup A = A $
Разность множеств
Читается «A без B».
На диаграммах Эйлера разности для пересекающихся множеств выглядят так:
Получается, что отрицание – частный случай разности: $ \bar{A} = \{x|x \in \Bbb U, x \notin A \} $= U\A
«Не A» — это «универсум без A».
Формулы включений и исключений
Рассмотрим два конечных пересекающихся множества A и B.
Пусть число элементов во множествах равно n(A)и n(B) соответственно. А число элементов в пересечении $n(A \cap B)$.
Вопрос: сколько всего элементов в обоих множествах, т.е. чему равно $n(A \cup B)$?
Сумма n(A)и n(B) даст нам больше, чем общее количество, потому что мы два раза посчитаем то, что попадает в пересечение. Значит, если отнять одно пересечение, получится как раз то, что ищем:
$$n(A \cup B) = n(A)+ n(B)-n(A \cap B)$$
Выведем аналогичную формулу для трёх пересекающихся конечных множеств.
Сумма n(A)+ n(B)+n(C) учтёт каждое из парных пересечений по два раза. Поэтому, аналогично задаче с двумя множествами, нужно отнять всё, что попадает в парные пересечения, т.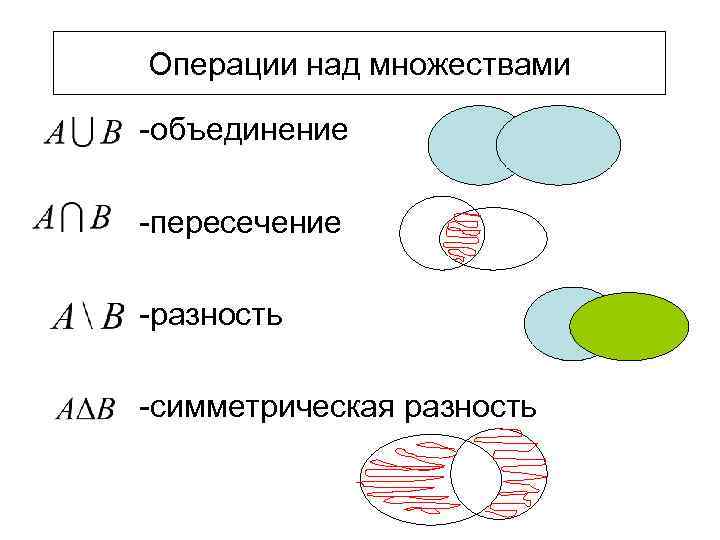
е. отнять сумму $(n(A \cap B)+n(A \cap C)+n(B \cap C) )$. Но после этого получится, что мы лишний раз отняли $n(A \cap B \cap C)$; значит, его нужно «вернуть».
Получаем:
$$ n(A \cup B \cup C) = n(A)+ n(B)+n(C)- $$
$$ -(n(A \cap B)+n(A \cap C)+n(B \cap C) )+n(A \cap B \cap C) $$
Примеры
Пример 1. Найдите пересечение данных множеств:
а) A = {0;5;8;10},
B = {3;6;8;9}
$A \cap B$ = {8}
$б) A = \{x|x \lt 3, x \in \Bbb R\}, $
$ B = \{x|x \gt 1, x \in \Bbb R\} $
$A \cap B = \{x|1 \lt x \lt 3, x \in \Bbb R\}$ — отрезок
$в) A = \{x|x \lt 3, x \in \Bbb R\}, $
$ B = \{x|x \gt 1, x \in \Bbb N\} $
$A \cap B = \{x|1 \lt x \lt 3, x \in \Bbb N \} или A \cap B = \{2\}$ — одна точка
г) A = {f|f-правильный многоугольник},
B = {f|f-четырехугольник}
$A \cap B = \{f|f-квадрат\}$
Пример 2. Найдите объединение данных множеств:
а) A = {0;5;8;10}, B = {3;6;8;9}
$A \cup B$ = {0;3;5;6;8;9;10}
б) A = {1;2}, B = {1;2;3;4}
$A \subset B$ – строгое подмножество
$A \cup B $ = B = {1;2;3;4}
$в) A = \{x|x \lt 1, x \in \Bbb R\}, B = \{x|x \gt 1,x \in \Bbb R\} $
$A \cup B = \{x|x \neq 1, x \in \Bbb R \}$
$г) A = \{n│n⋮3, n \in \Bbb Z\}, B = \{n|n⋮9,n \in \Bbb N\} $
$B \subset A$ — строгое подмножество
$ A \cup B = A = \{n│n⋮3, n \in \Bbb Z\} $
Пример 3.
Найдите отрицание данного множества на данном универсуме:
а) U = {1;2;3;4;5}, A = {2;3}
$ \bar{A} = {1;4;5}$
б) U = $\{x│x \in \Bbb Q \}$, A = $\{ \frac{4}{5}, \frac{7}{8} \}$
$ \bar{A} = \{x|x \neq \frac{4}{5}, x \neq \frac{7}{8}, x \in \Bbb Q\} $
$в) U = \{x│x \in \Bbb R\}, A = \{x|x \ge 2, x \in \Bbb R\} $
$\bar{A} = \{x|x \lt 2, x \in \Bbb R\}$
г) U = { 0;1}, A = { 0}
$ \bar{A} = {1}$
Пример 4. Найдите обе разности данных множеств:
а) A = {0;1;2;3;4}, B = {2;4}
A\B = {0;1;3}, $B\A = \{∅\}$
б) A = {0;1;3}, B = {2;4;6}
A\B = {0;1;3}, B\A = {2;4;6}
$в) A = \{x|x \gt 1, x \in \Bbb R\}, $
$ B = \{x|x \lt 3, x \in \Bbb R\} $
A\B $ = \{x|x \ge 3, x \in \Bbb R\}$
B\A $ = \{x|x \le 1,x \in \Bbb R\} $
$ г*) A = \{(x,y)|x \gt 0, x \in \Bbb R, y \in \Bbb R\} $
$ B = \{(x,y)|x \le 5, x \in \Bbb R, y \in \Bbb R\} $
A\B $ = \{(x,y)|x \gt 5, x \in \Bbb R, y \in \Bbb R\} $
B\A $ = \{(x,y)|x \le 0, x \in \Bbb R, y \in \Bbb R\} $
Пример 5.
Из 100 студентов умеют программировать на Python 28 человек, на Java 30 человек, на C# 42 человека, на Python и Java 8 человек, на Python и C# 10 человек, на Java и C# 5 человек. Все три языка знают 3 студента. А сколько студентов не умеют программировать на этих языках?
n(U) = 100
n(A) = 28, n(B) = 30, n(C) = 42
$ n(A \cap B) = 8, n(B \cap C) = 5, n(A \cap C) = 10 $
$n(A \cap B \cap C) = 3$
Всего программистов:
$ n(A \cup B \cup C) = n(A)+n(B)+n(C)- $
$ (n(A \cap B)+n(B \cap C)+n(A \cap C) )+n(A \cap B \cap C) $
$n(A \cup B \cup C) = 28+30+42-(8+5+10)+3 = 100-23+3 = 80$
Число не умеющих программировать:
$n(U)-n(A \cup B \cup C) = 100-80 = 20$
Ответ: 20 человек
Объединение, пересечение и дополнение | Математика для гуманитарных наук Необходимый предмет
Результаты обучения
- Выполнение операций объединения, пересечения, дополнения и разности над множествами, используя соответствующие обозначения.
- Уметь рисовать и интерпретировать диаграммы Венна отношений множеств и операций.
Обычно наборы взаимодействуют. Например, вы с новым соседом по комнате решаете устроить домашнюю вечеринку и приглашаете друзей. На этой вечеринке объединяются два набора, хотя может оказаться, что есть друзья, которые были в обоих наборах.
Математические слова и обозначения
Чтобы получить новые слова на новом для вас языке, требуется повторение и практика. Математика во многих отношениях ничем не отличается от изучения нового языка со всем его словарным запасом, синтаксисом и орфографическими соглашениями. Символы в этом разделе могут быть вам совершенно незнакомы. Если это так, вам нужно будет проводить с ними время, используя карточки и записывая их от руки в контексте.
Дайте себе время выучить и оценить язык математики!
Объединение, пересечение и дополнение
Объединение двух наборов содержит все элементы, содержащиеся в любом наборе (или в обоих наборах).
Объединение обозначается как A ⋃ B. Более формально, x ∊ A ⋃ B , если x ∈ A или x (или оба)
пересечение двух наборов содержит только те элементы, которые есть в обоих наборах. Перекресток обозначен цифрой 9.0023 A ⋂ B. Более формально, x ∈ A ⋂ B , если x ∈ A и x 1 B 1, 0010 комплект комплекта А содержит все, что является , а не в наборе A . Дополнение обозначается как A’ , или A c , или иногда ~ A .
Универсальный набор — это набор, содержащий все интересующие нас элементы. Это должно определяться контекстом. 9{c}[/латекс]. Этот верхний индекс не является показателем степени. Это украшение, которое обозначает дополнение к набору .
Пример
- Если бы мы обсуждали поиск книг, универсальный набор мог бы включать все книги в библиотеке.
- Если бы мы группировали ваших друзей на Facebook, универсальный набор был бы всеми вашими друзьями на Facebook.
- Если вы работали с наборами чисел, универсальный набор мог бы состоять из всех целых чисел, всех целых чисел или всех действительных чисел
Пример
Предположим, что универсальный набор равен U = все целые числа от 1 до 9. Если A = {1, 2, 4}, то A c = {3, 5 6, 7, 8, 9}.
Попробуйте
символы пересечения и объединения
Символы пересечения [латекс]\чашка[/латекс] и объединения [латекс]\шапка[/латекс] немного напоминают буквы в алфавите. На самом деле, это уловка для их запоминания.
Символ объединения выглядит как заглавная буква U, что означает союз .
Символ пересечения немного похож на большую строчную букву n для на пересечении
Пример
Рассмотрим наборы:
A = {красный, зеленый, синий}
B = {красный, желтый, оранжевый}
C = {красный, оранжевый, желтый, зеленый, синий, фиолетовый}
Найдите следующее:
- Найдите A ⋃ B
- Найти А ⋂ В
- Найти A c ⋂ C
Показать решение
Попробуй
Обратите внимание, что в приведенном выше примере было бы сложно просто попросить A c , поскольку все, от цвета фуксии до щенков и арахисового масла, входит в комплект набора.
По этой причине дополнения обычно используются только с пересечениями или когда у нас есть универсальный набор.
Как мы видели ранее с выражением A c ⋂ C , операции над множествами можно группировать вместе. Символы группировки можно использовать так же, как и с арифметикой — для принудительного порядка операций.
Пример
Предположим, H = {кошка, собака, кролик, мышь}, F = {собака, корова, утка, свинья, кролик}, и W = {утка, кролик, олень, лягушка, мышь}
- Найти ( H ⋂ F ) ⋃ W
- Найти В ⋂ ( Ж ⋃ В )
- Найти ( H ⋂ F ) c ⋂ W
Показать решение
Чтобы визуализировать взаимодействие множеств, Джон Венн в 1880 году решил использовать перекрывающиеся круги, опираясь на аналогичную идею, использованную Леонардом Эйлером в 18 веке.
Эти иллюстрации теперь называются Диаграммы Венна .
Диаграмма Венна
Диаграмма Венна представляет каждый набор в виде окружности, обычно нарисованной внутри прямоугольника, представляющего универсальный набор. Перекрывающиеся области обозначают элементы, общие для обоих наборов.
Основные диаграммы Венна могут иллюстрировать взаимодействие двух или трех множеств.
Пример
Создайте диаграммы Венна для иллюстрации A ⋃ B , A ⋂ B и Ac ⋂ B 3 A ⋃ B содержит все элементы либо набор.
Показать решение
Пример
Для иллюстрации используйте диаграмму Венна ( H ⋂ F ) c ⋂ W
Показать решение
Пример
Создайте выражение для представления выделенной части показанной диаграммы Венна.
Показать решение
Попробуйте
Создайте выражение, представляющее выделенную часть показанной диаграммы Венна.
Союз наборов | Математические вкусности
Форма поиска
Поиск
В предыдущих уроках мы использовали диаграммы Венна для представления отношений между множествами. Давайте посмотрим на пример 1 ниже.
Пример 1. В средней школе Гринвилля два класса будут объединены в один, чтобы сократить расходы. Если учащиеся оркестра и хора объединятся в один новый класс, то какие учащиеся будут в этом классе?
Дано: Дано = {Сэм, Киеша, Дерек, Лорри, Робин, Рауль, Ширли, Натан, Крис, Дана} , Группа = {Сэм, Лорри, Рауль, Дерек} и Хор = {Робин , Дерек, Киеша}, найдите Band Chorus.
Анализ: эта задача требует от нас найти союз Band и Chorus. Чтобы решить эту проблему, мы должны перечислить всех учеников, которые находятся в группе, в хоре или в обеих группах.
Решение:
Объяснение:
Группа Хор = {Сэм, Лорри, Рауль, Дерек, Киеша, Робин}
Обратите внимание, что Дерек находится в их пересечении, поэтому Дерек находится в их пересечении. Однако Дерек прописывается в союзе только один раз.
Определение: Объединение двух множеств A и B, — это множество элементов, которые находятся в A или в B или в обоих Обозначается A B , и читается как « A соединение B ».
Сравним объединение и пересечение.
| Союз | Перекресток | |
| записывается как | А Б | А Б |
| читать как | A штуцер Б | A пересечение B |
| значение | A или B или оба | А и В |
| как найти | объединить все элементы | найти элементы, общие для обоих |
Союз часто считают браком.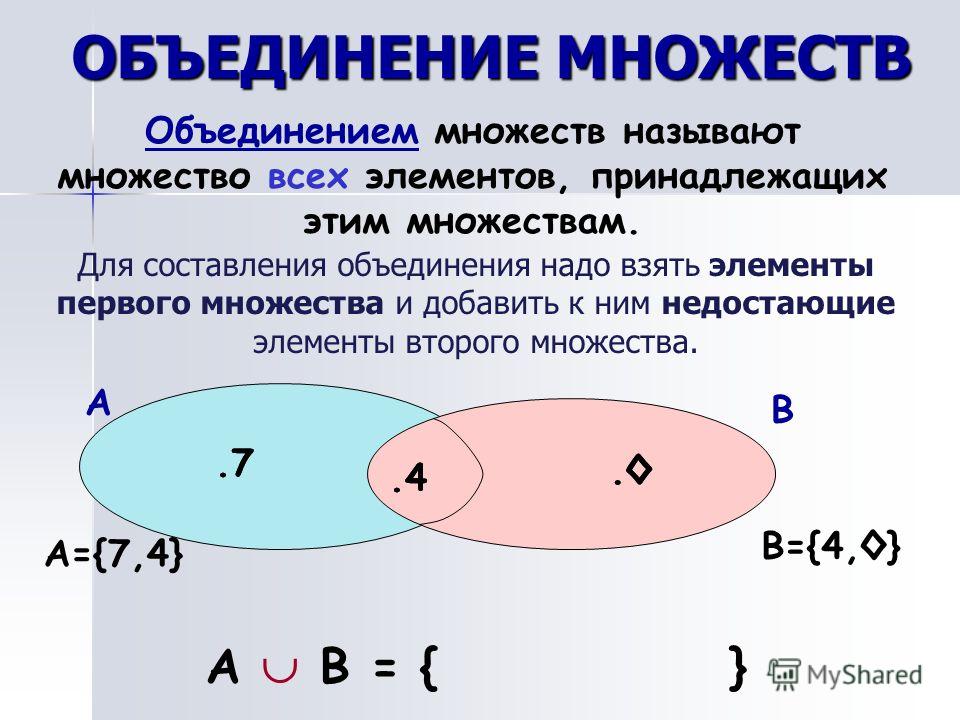
Мы используем «и» для пересечения» и » или» для объединения. Давайте рассмотрим еще несколько примеров объединения двух множеств.
Пример 2: Let = {число чисел}, P = {кратное 3 меньше 20} и Q = {четные числа меньше 20}. Нарисуйте и подпишите диаграмму Венна, чтобы показать объединение P и Q .
Анализ: заштрихуйте элементы, которые находятся в P или в Q или в обоих . Заштрихованная область на диаграмме Венна ниже показывает P Q.
Решение:
9, 10, 12, 14, 15, 16 , 18}
Обратите внимание, что элементы 6, 12 и 18 находятся в обоих наборах (т. е. на пересечении P и Q ). Однако эти элементы пишутся в союзе только один раз.
Пример 3: Пусть = { k | 1 ≤ k ≤ 10}, X = {1, 6, 9} и Y = {1, 3, 5, 6, 8, 9}.
Нарисуйте и подпишите диаграмму Венна, чтобы показать X Y.
Анализ: X является подмножеством Y . Таким образом, все элементы в X также содержатся в Y .
Объяснение: X Y = {1, 3, 5, 6, 8, 9}, что равно множеству Y.
Y , получаем, что X Y = 4 7 Это отношение определено ниже.
Другой способ определения объединения двух множеств заключается в следующем:
A B = {x | x A или x B }
Пример 4: 3 6 животных = 9 2 A = {10 собак} и B = {20 кошек }.
Нарисуйте и подпишите диаграмму Венна, чтобы показать A B .
Анализ: Эти множества не пересекаются и не имеют общих элементов. Таким образом, A B — это все элементы числа A и все элементы числа B.
10 собак, 20 кошек}
Пример 4 прямой союз двух наборов. Непересекающиеся множества не имеют общих элементов. Поэтому союз A и B не имеет общих элементов. Поскольку невозможно, чтобы собаки в A также были кошками в B , мы уверены, что количество элементов в объединении равно сумме всех собак в A и всех кошек в B . Таким образом, объединение получается в результате сложения всех элементов обоих наборов.
Объединение двух наборов А и В, представляет собой набор элементов, которые находятся в А или В 022 в обоих. Он обозначается A B , и читается как « A union B ».
Формальное определение союза показано ниже:
А В = {x | x A или x B }
Упражнение
0 0Указания: Нарисуйте и подпишите диаграмму Венна, чтобы помочь вам ответить на каждый вопрос ниже. Выберите свой ответ, нажав на соответствующую кнопку. Обратная связь по вашему ответу представлена в ОКНО РЕЗУЛЬТАТЫ. Если вы допустили ошибку, обдумайте свой ответ еще раз, а затем выберите другую кнопку.
| 1. | Дано = {яблоки, апельсины, бананы, груши} и 9 = {апельсины, 2 2, виноград 0, 2 2, груши} 0327 ? |
| P Q = Ø P , апельсины, яблоки, Q } P Q = {яблоки, апельсины , бананы, груши, виноград} Ничего из вышеперечисленного.  ЯЩИК РЕЗУЛЬТАТОВ: |
| 2. | Дано = {простые числа} и = {составные числа}, что такое 6 90? |
| A B = {целые числа} A B = {числа > 1} A B = {мнимые числа} Все вышеперечисленное. ЯЩИК РЕЗУЛЬТАТОВ: |
3. | Дано = {1, 4, 16} и = {1, 6 5, 1, 2, 9}0022 ? |
| X Y = {1, 4, 9, 16, 25, 36} X , 3 Х Y = Ø Ничего из вышеперечисленного. ОКНО РЕЗУЛЬТАТОВ: |
| 4. | Дано = {гласные} и = {согласные} 9 2, что такое 2 2 ? |
| P Q = Ø P , e , e о, и} Р Q = { согласные} P Q = {Английский алфавит} ЯЩИК РЕЗУЛЬТАТОВ: |
5. |