Верные цифры в широком смысле: 1.3. Запись приближенных значений величин. Верные знаки

1.3. Запись приближенных значений величин. Верные знаки

Приближенные значения величин обычно записывают в виде десятичных дробей с конечным числом цифр.

Значащими цифрами в записи десятичной дроби называются все цифры, начиная с первой ненулевой слева. Например, в дроби 0,00102030004 значащими цифрами (подчеркнуты) являются все цифры, начиная с третьей после запятой.

Цифра в записи приближенного значения числовой величиныx называется верной в широком (строгом) смысле слова, если абсолютная погрешность приближенного значения не превышает единицы (половины единицы) разряда, в котором стоит эта цифра.

Все цифры верные в строгом смысле слова, очевидно, будут верными и в широком смысле. Рассмотрим несколько примеров.

Пример 1

Пусть ,= 0,000007899.Требуется найти верные цифры в записив широком и строгом смысле слова и подчеркнуть их одинарной и двойной линией соответственно.

Проверяя для каждой цифры в записитребование, сформулированное в определении верных цифр, получим, что цифры 0, 1, 2, 3 и 4 будут верными в широком и строгом смысле слова одновременно. Цифра 5 будет верной в широком смысле слова, но не будет верной в строгом смысле слова:.

Отметим, что в разрядах, в которых в записи стоят незначащие нули, в записи стоят верные цифры в широком смысле слова.

Пример 2

Пусть теперь ,=0,000007899. Требуется найти верные цифры в записив широком и строгом смысле слова.

Абсолютная погрешность нам неизвестна, а известна лишь ее оценка . Если оценка абсолютной погрешностиприближенного значения не превышает единицы (половины единицы) разряда, в котором стоит цифра (в записи ), то эта цифра, очевидно, также будет верной в широком (строгом) смысле слова . Проверяя для каждой цифры в записи

это требование, получим часть верных цифр: . Но, поскольку мы проверяем заведомо более жесткое требование, чемэто, среди неподчеркнутых цифр также могут оказаться верные, если погрешность окажется намного меньше своей оценки.

Отметим, что в тех разрядах, в которых в записи стоят незначащие нули, в записистоят верные цифры в широком смысле слова.

Пример 3

Пусть, =0,123456789, =0,123457899. В записи точного и приближенного значений подчеркнуты совпадающие цифры. Непосредственная проверка для каждой цифры в записи требования, сформулированного в определении верных цифр, показывает, что все подчеркнутые (совпадающие) цифры являются верными в широком смысле слова, а неподчеркнутые – неверными.

Но такое совпадение верных цифр (в широком смысле слова) в записи с соответствующими цифрами в записииногда нарушается. Это связано с тем, что некоторые вещественные числа могут записываться в десятичной системе двумя различными способами, например 1=1,0000.

..=0,9999… .

Пример 4

Пусть =1,0000…,=0,9999. В записи точного и приближенного значений нет ни одной совпадающей цифры. Непосредственная проверка для каждой цифры в записитребования, сформулированного в определении верных цифр, показывает, что цифры в записиявляются верными в широком смысле слова. В то же время если записатьдругим способом=0,9999…, то все верные цифры в записибудут совпадать с соответствующими цифрами в записи точного значения.

Рассмотренные примеры позволяют сформулировать некоторые свойства верных цифр.

Свойства верных цифр:

1. В тех десятичных разрядах, где в записи (или) стоят незначащие нули, в записидолжны стоять верные цифры в широком смысле слова (докажите это самостоятельно).

2. Верные цифры в записи приближенного значения всегда совпадают с соответствующими цифрами в записи точного значения, если выбрать необходимую форму его записи в виде десятичной дроби

Установим теперь связь между величинами абсолютной и относительной погрешностей приближенного значения и количеством верных цифр в его записи.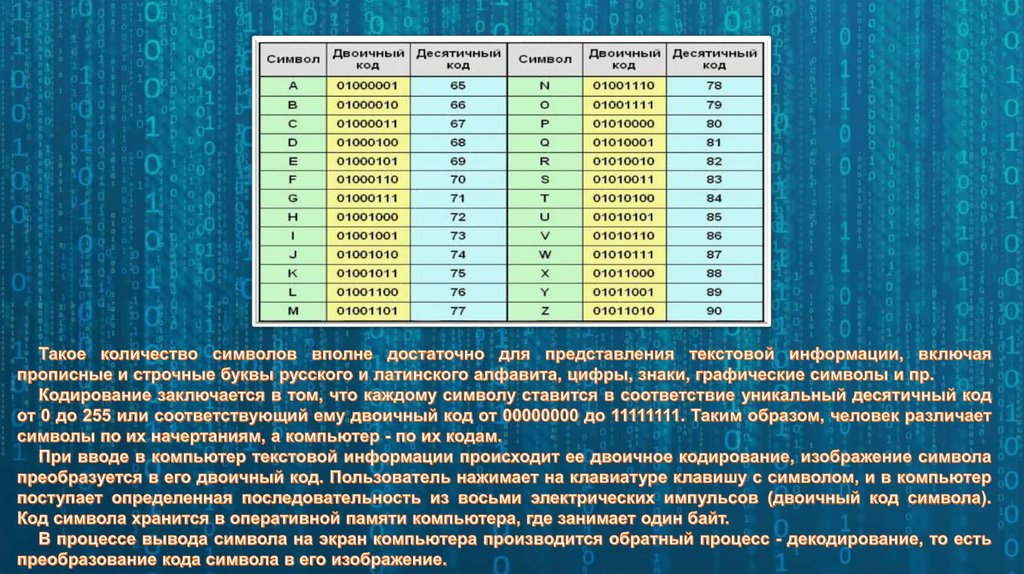 Пусть абсолютная погрешность приближенного значения равна. Определим количество верных цифр в широком смысле слова в записипосле запятой. Запишемв общем виде, указывая только разряды и не указывая конкретных цифр, и подчеркнем разряды, в которых будут располагаться верные цифры в широком смысле слова:

.

Итак, если абсолютная погрешность приближенного значения равна , то после десятичной запятой в записи будетn верных знаков.

Пусть теперь относительная погрешность приближенного значения равна. Установим общее количество верных знаков в записи. Для этого представимв показательной форме:. Здесь– вещественное число, называемое мантиссой, ар – целое число, называемое порядком . А для того, чтобы такое представление дроби было однозначным потребуем, чтобы

. (1.3.1)

Точное значение величины также запишем в показательной форме, причем с тем же порядкомp: . Для мантиссы точного значенияне будет выполняться условие (1.3.1). Значенияиестественно считать точным и приближенным значениями мантиссы величины

x. Тогда ипредставляют собой абсолютную и относительную погрешности приближенного значения мантиссы. Соответствующие цифры в записиидолжны совпадать попарно.Поэтому и количество верных цифр в записи ибудет одинаковым. Далее определяем количество верных цифр в записи. Запишем относительную погрешность

.

Отсюда

,

и, согласно формуле (1.3.1), для абсолютной погрешности получается оценка

(1.3.2)

Запишем в общем виде

.

Из формулы (1.3.1) следует, что первая цифра после десятичной запятой в записи должна быть отлична от нуля. Поэтому все цифры в записипосле запятой являются значащими. Из формулы (1.3.2) следует, что в записи мантиссы должно быть не меньшеn и не больше (n+1) верной цифры после десятичной запятой, причем все они являются значащими.

Итак, в мантиссе имеется или n или (n+1) верная значащая цифра. Поэтому общее количество верных значащих цифр в записи также будет равно либоn, либо (n+1).

Таким образом, мы показали, что если относительная погрешность приближенного значения равна , то общее количество верных значащих цифр в записи равно либо n, либо (n+1).

Лекции по математике для студентов 1 курса СПО

Лекция 1.1

Дествительные числа.

 

I. Множество натуральных чисел – это множество чисел, которыми пользуются при счете предметов.

.

Всякому натуральному числу соответствует точка на числовой прямой.

 

Задание: Назовите самое маленькое натуральное число. Существует ли самое большое натуральное число?

 

II. Множество целых чисел – это множество, состоящее из натуральных чисел, им противоположных чисел и нуля.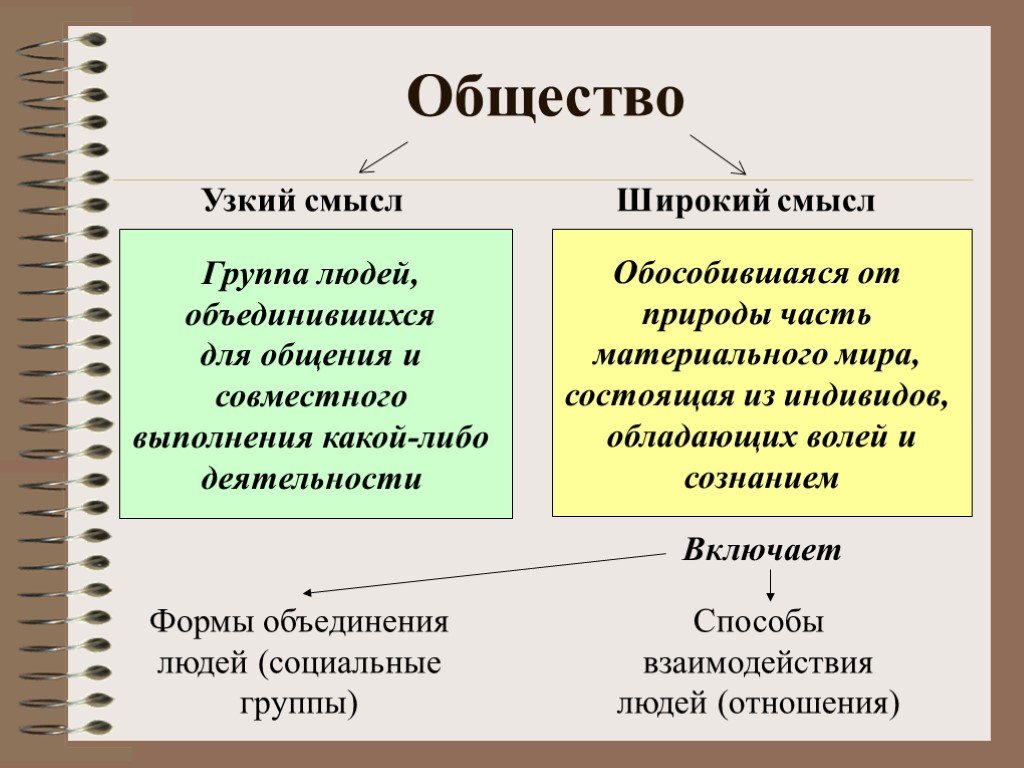

.

Всякому целому числу соответствует точка на числовой прямой.

 

Задания:

1.                  Существуют ли самое маленькое и самое большое целое число?

2.                  Верно ли утверждение:

a.       любое натуральное число является целым;

b.      любое целое число является натуральным?

 

III. Множество рациональных чисел – это множество несократимых дробей вида

.

Всякому рациональному числу соответствует точка на числовой прямой.

 

Свойство рациональных чисел: Всякое рациональное число можно представить в виде бесконечной периодической десятичной дроби.

Обратно: всякая бесконечная периодическая десятичная дробь является рациональным числом.

 

Правило перевода периодических дробей в обыкновенные:

 

Чисто периодические дроби	Смешанные периодические дроби
Чистая периодическая дробь равна обыкновенной дроби, в числителе которой записан период, а в знаменателе – столько девяток, сколько цифр периоде. Пример: .	Смешанная периодическая дробь равна обыкновенной дроби, в числителе которой записана разность между числом до второго периода и числом до первого периода, а в знаменателе – число, составленное из стольких девяток, сколько цифр в периоде и стольких нулей, сколько цифр между запятой и периодом.   Пример: .

 

для чисто периодической дроби: в числителе пишется число, стоящее в периоде, а в знаменателе столько «9», сколько цифр в периоде, целая часть остается без изменения.

 

для смешанной периодической дроби: в числителе разность между числом, стоящим после запятой, и числом, стоящим после запятой до периода, а в знаменателе столько «9», сколько цифр в периоде, со столькими «0», сколько цифр после запятой до периода

 

Задания:

1.                  Докажите, что числа  являются рациональными и отметьте эти числа на числовой прямой.

2.                  Верно ли утверждение:

а)      всякое натуральное число является рациональным;

б)      всякое целое число является рациональным;

в)      верно ли утверждение: Всякое рациональное число является целым?

3.                  Представьте рациональные числа  в виде бесконечных периодических десятичных дробей.

4.                    Переведите периодические дроби  в обыкновенные. Проверьте результат перевода.

IV. Множество иррациональных чисел – это множество чисел, которые нельзя представить в виде несократимых дробей

.

Всякому иррациональному числу соответствует точка на числовой прямой.

 

Свойство иррациональных чисел: Всякое иррациональное число представимо в виде бесконечной десятичной непериодической дроби.

 

Пример: π ≈ 3,1415926535897932384626433832795…;

                        …

 

Задание: Докажите, что числа , ,  являются иррациональными.

 

V. Множество действительных (вещественных) чисел – это объединение множеств рациональных и иррациональных чисел.

.

Каждому действительному числу соответствует точка на числовой прямой.

 

Обратно: каждой точке на числовой прямой соответствует определенное действительное число.

 

Следовательно, между множеством действительных чисел и множеством точек на числовой прямой существует взаимно-однозначное соответствие.

 

Задания:

1.                  Верно ли утверждение:

а)      всякое целое число является действительным;

б)      всякое рациональное число является вещественным;

в)      всякое иррациональное число является вещественным;

г)      всякое действительное число является рациональным;

д)      всякое вещественное число является целым?

2.                  Даны числа: .
Выпишите: а) натуральные числа; б) целые числа; в) рациональные числа; г) иррациональные числа.

 

 

 

Лекция 1.2 Абсолютная погрешность приближенного значения числа.

 

 

Модуль числа – это само число, если оно неотрицательно, и число, ему противоположное, если оно отрицательно.

 

Примеры: .

С геометрической точки зрения модуль числа – это расстояние от этого числа до начала отсчета.

 

Вывод: модуль числа отрицательным быть не может!

 

Приближенные вычисления

 

Приближенное число есть такое число, которое отличается от точного на погрешность (ошибку), допущенную в соответствии с условиями данной задачи, и заменяет точное число в расчетной формуле.

 

Обозначим буквой a₀ точное число, а буквой a его приближенное значение, тогда a₀ ≈ a.

 

Абсолютная погрешность приближенного значения числа – это модуль разности между точным и приближенным значением этого числа, т.е. .

 

Так как точное число чаще всего неизвестно, то можно указать положительное число ∆а, удовлетворяющее неравенству .

Число ∆а называется границей абсолютной погрешности.

 

 

1. Даны приближенные значения числа х = 2/3; а₁= 0,6; а₂ = 0,66;

а₃ = 0,67. Какое из этих трех приближений является лучшим?

 

 

 

; 

 

 

а₃ = 0,67 – лучшее приближение

 

2. Длина детали х (см) заключена в границах 33 ≤ х ≤ 34. Найти границу абсолютной погрешности измерения детали.

○ Примем за приближенное значение длины детали среднее арифметическое границ:

а = (33 + 34)/2 = 33,5 (см). Тогда граница абсолютной погрешности приближенного значения длины детали не превзойдет 0,5 (см).

Величину Δа можно найти и как полуразность верхней и нижней границ, т. е. Δа = (34 — 33)/2 = 0,5 (см). Длина детали х, найденная с точностью до Δа = 0,5 см, заключена между приближенными значениями числа х:

33,5 — 0,5 ≤ x ≤ 33,5 + 0,5; x = 33,5 ± 0,5 (см).

3. Найдите абсолютную погрешность округления до единиц следующих чисел:

1) 0,8; 2) 7,6; 3) 19,3; 4) 563,58.

 

4. Граница абсолютной погрешности приближенного значения 386 числа х равна 0,5. Укажите границы, в которых заключено число х.

 

5. Найдите границу абсолютной погрешности измерений, полученных в виде неравенства 37 < x < 38.

 

5.                  Амперметр дает точность ±0,02 А. При измерении силы тока получили 10,63 А. Укажите границы этого числа.

 

6.                  Атомная масса водорода — 1,0082 ± 0,0005, а меди — 63,44 ± 0,15. Укажите границы приближенных значений этих чисел.

 

 

8. Площадь квадрата равна 24,5 ± 0,3 (см²). Найдите границы измерения площади квадрата.

 

 

 

 

Задание:

1.                  Записать числа в виде двойного неравенства:

а)            а = 347,50; ∆а = 0,0047;

б)            а_{0 =} 7,269 ± 0,0004.

2.                  Докажите, что число 1,7 является приближенным значением числа 1, 739 с точностью до 0,05.

3.                  Точное значение числа х неизвестно, а известно лишь, что
0,68 < х< 0,72. Найдите точность приближения h.

4.           Вычислите приближенное значение величины х, равное среднему арифметическому границ, и укажите точность этого приближения, если: а) 3,6 ≤ х ≤ 4,2;        б) 0,12 ≤ х ≤ 0,14.

Лекция 1.3 Верные цифры числа. Запись приближенного значения числа.

 

 

Верные и значащие цифры числа.

Цифра т приближенного числа а называется верной в широком смысле, если граница абсолютной погрешности числа а не превосходит единицы того разряда, в котором записывается цифра т.

Цифра т приближенного числа а называется верной в строгом смысле, если граница абсолютной погрешности числа а не превосходит половины единицы того разряда, в котором записана цифра т.

В числах, полученных в результате измерений или вычислений и используемых при расчетах в качестве исходных данных, а также в десятичной записи приближенного значения числа, все цифры

должны быть верными.

Наиболее употребительна такая запись приближенного числа (например, в математических таблицах), при которой цифры верны в строгом смысле.

Граница абсолютной погрешности Δа находится непосредственно

по записи приближенного значения а числа х.

Цифры в записи приближенного числа, о которых не известно, являются ли они верными, называются сомнительными.

Значащими цифрами приближенного числа называются все его верные цифры, кроме нулей, стоящих перед первой цифрой (слева направо), отличной от нуля.

 

Округление чисел. При округлении числа а его заменяют числом a₁

с меньшим количеством значащих цифр. Абсолютная величина разности |а – а₁| называется погрешностью округления

 

При округлении числа до т значащих цифр отбрасывают все цифры, стоящие правее т-й значащей цифры, или при сохранении разрядов заменяют их нулями. При этом если первая слева из отброшенных

цифр больше или равна 5, то последнюю оставшуюся цифру увеличивают на единицу.

При применении этого правила погрешность округления не превосходит половины единицы десятичного разряда, определяемого последней оставленной значащей цифрой.

Округление приближенных значений чисел с сохранением в записи только верных цифр производится до разряда, в котором записана первая справа верная цифра.

 

9. Найти границу абсолютной погрешности приближенного значения 0,1968 числа х, все цифры которого верны в строгом смысле.

 

○ Граница абсолютной погрешности этого числа равна 0,00005, т. е. половине

единицы последнего разряда, сохраняемого в записи.●

 

10. Указать верные цифры (в широком смысле) следующих чисел:

1) 3,73 ± 0,056; 2) 3,627 ± 0,0008; 3) 4,732 ± 0,06; 4) 561 274 ± 500.

 

○ 1) Граница погрешности Δа = 0,056 не превосходит единицы разряда десятых

(неравенство 0,056 < 0,1 верное). Следовательно, верными являются цифры 3 и 7.

2) Так как Δа = 0,0008 < 0,001, то все цифры приближенного числа 3,627 верны.

3) Поскольку Δа = 0,06 < 0,1, верными являются цифры 4 и 7.

4) Так как Δа = 500 < 1000, то верны цифры 5, 6 и 1. ●

11. За приближенное значение числа 26,7 взято число 27. Являются

ли цифры числа 27 верными?

 

○ Так как |26,7 — 27| = 0,3 < 1, то цифры 2 и 7 — верные в строгом смысле.●

 

12. Приближенное значение числа 9,587 ± 0,03 округлить до первого справа верного разряда.

 

○ Первая справа верная цифра находится в разряде десятых, поэтому число 9,587

округляем до десятых: 9,587 ≈ 9,6. Новое значение границы погрешности Δа равно

сумме границы погрешности 0,03 и погрешности округления 0,013, т. е. Δа = 0,03 +

+ 0,013 = 0,043 < 0,1. Число 9,6 является приближенным значением числа 9,587 с точ-

ностью до 0,1. Цифры 9 и 6 верные.●

 

13. Укажите верные цифры (в широком смысле) следующих чисел:

1) 0,028 ± 0,004; 2) 0,463 ± 0,0008; 3) 0,078 ± 0,002; 4) 12,78 ± 0,0005;

5) 375 ± 20.

 

14. Назовите верные цифры числа π ≈ 3,14, считая π ≈ 3,1416.

15. За приближенное значение числа 999,82 взято число 1000. Укажите верные цифры числа 1000.

16. Сохраните только верные цифры в записи следующих приближенных значений чисел:

1) 280 ± 10; 2) 8900 ± 100; 3) 530 000 ± 100; 4) 5740 ± 10.

17. Округлите до первого справа верного разряда приближенные значения данных чисел:

1) 0,3281 ± 0,05; 2) 2,0637 ± 0,0025; 3) 14,0367 ± 0,8;

4) 24,734 ± 0,06.

 

18. Округлите приближенные значения данных чисел до первого справа верного разряда и запишите эти числа в стандартном виде:

1) 12 378 ± 25; 2) 15 763 ± 50; 3) 8724 ± 25; 4) 812 ± 6.

19. Укажите границу погрешности приближения, если в записи приближенных значений данных чисел все цифры верные (в широком смысле): 1) x ≈ 0,56; 2) х ≈ 84,3; 3) х ≈ 5,10; 4) х ≈ 4,100.

 

 

Лекция 1. 4  Относительная погрешность приближенного значения числа

 

Относительная погрешность приближенного значения числа – это отношение абсолютной погрешности этого числа к самому числу, т.е. или в процентах .

 

Так как в большинстве случаев истинное значение величины a₀ неизвестно, то на практике относительную погрешность  оценивают некоторым числом , большим этой погрешности.

В качестве  можно взять отношение  или любое число, большее этого отношения, но достаточно близкое к нему, т.е. .

Число  называется границей относительной погрешности.

Качество измерений или вычислений тем лучше, чем меньше граница относительной погрешности.

 

Зависимость относительной погрешности от числа значащих цифр

иллюстрируется табл. 1.1

 

число	Наименьшее число	Наибольшее число	Граница абсолютной погрешности	Относительная погрешность наибольшего числа	Относительная погрешность наименьшего числа
Однозначное	1	9	0,5	0,056=5,6%	0,5=50%
Двузначное	10	99	0,5	0,005=0,5%	0,05=5%
Трехзначное	100	999	0,5	0,0005=0,05%	0,005=0,5%
Четырехзначное	1000	9999	0,5	0,00005=0,005%	0,0005=0,05%

 

Из табл. 1.1 ясно, что три верные значащие цифры обеспечивают точность результата (относительную погрешность) от 0,05 до 0,5 %. В технических и других расчетах, не требующих особо высокой точности, достаточно бывает обеспечить точность результата порядка десятых долей процента. Поэтому в технических расчетах принято выполнять вычисления с тремя значащими цифрами.

 

 

 

Пример: Пусть а₀ = 42,1 ± 0,2. Вычислить в процентах границу относительной погрешности приближенного значения величины а.

Решение: Имеем а = 42,1; h = 0,2. Следовательно, .

Задания:

1.                  Округлите число 123 до десятков и найдите абсолютную и относительную погрешность округления.

2.                  Округлите число 8, 2478 до сотых и найдите абсолютную и относительную погрешность округления.

3.                  Найдите относительную погрешность приближенных чисел:

а)      35,148 ± 0,00074;

б)      0,012 ± 0,001;

в)      17,2 ± 0,25.

4.                  Установите, какое равенство точнее: .

5.                  Найдите верхнюю и нижнюю границы, если приближенное значение числа и относительная погрешность в процентах соответственно равны:

а)      18 и 1%;

б)      0,6 и 15%.

Лекция 1.5

Действия над приближенными значениями числа

 

Сложение приближенных значений чисел

Граница абсолютной погрешности суммы приближенных значений

чисел равна сумме границ абсолютных погрешностей этих чисел:

Δ(a + b) = Δa + Δb, (2.1)

где а и b — приближенные значения чисел; Δa и Δb — границы абсо-

лютных погрешностей соответствующих приближений.

Граница относительной погрешности суммы вычисляется по фор-

муле

( )

a b

a b

+ a b

_ = _ +

+

. (2. 2)

1. Найти сумму S приближенных значений чисел 6,8 ± 0,05; 4,3 ± 0,05

и 3,575 ± 0,0005.

○ Имеем

S = 6,8 + 4,3 + 3,575 = 14,675; ΔS = 0,05 + 0,05 + 0,0005 = 0,1005.

Граница абсолютной погрешности заключена в пределах 0,05 < 0,1005 < 0,5.

В приближенном значении суммы верными являются лишь две цифры (в разрядах

десятков и единиц). Полученный результат округлим до единиц: S = 14,675 ≈ 15.●

2. Найдите сумму приближенных значений чисел 6,54 ± 0,005;

16,022 ± 0,0005 и 1,9646 ± 0,00005.

3. Вычислите сумму a = 5 + 11, взяв приближенные значения кор-

ней с точностью до 0,001. Найдите а, Δа и εa.

4. Вычислите сумму a = 3 + 5 + 7 с четырьмя значащими циф-

рами. Найдите а, Δa и εa.

5. Электрическая цепь состоит из трех последовательно соединен-

ных проводников с сопротивлениями r1 = 4,8 ± 0,05 (Ом), r2 = 6,25 ±

± 0,005 (Ом) и r3 = 7,725 ± 0,0005 (Ом).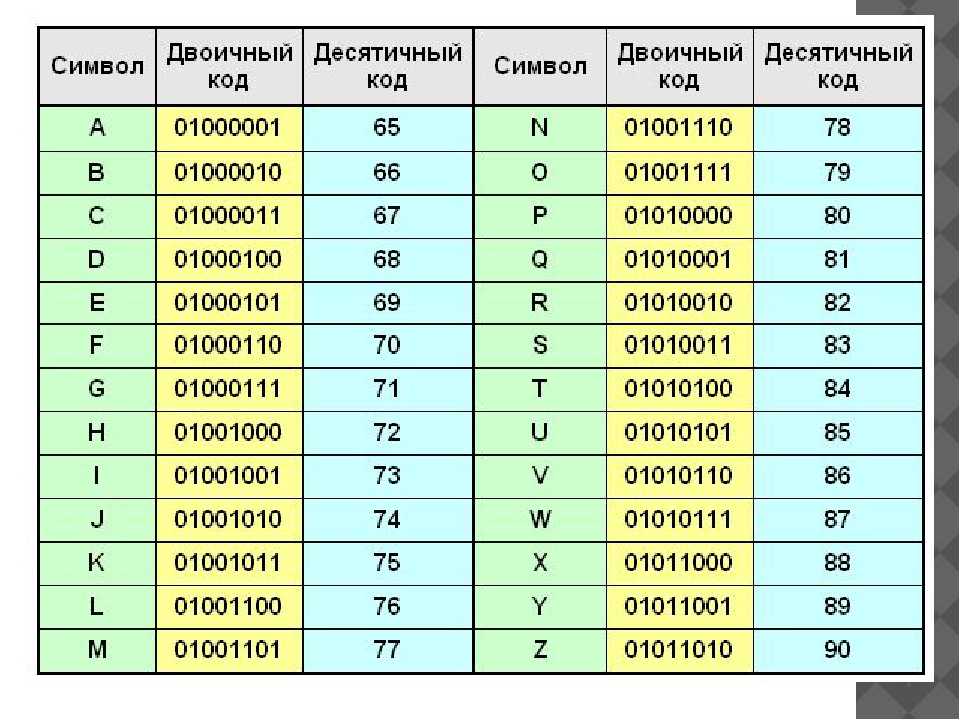 Вычислите общее сопротивление

цепи по формуле R = r₁ + r₂ + r₃. Найдите R, ΔR и ε_R.

 

Вычитание приближенных значений чисел

Граница абсолютной погрешности разности двух приближенных

значений чисел равна сумме границ их абсолютных погрешностей:

Δ(a — b) = Δa + Δb. (2.3)

Граница относительной погрешности разности вычисляется по фор-

муле

a b

a b

− a b

_ = _ + _

−

. (2.4)

6. Вычислить разность двух приближенных значений чисел а = 5,863 ±

± 0,0005 и b = 2,746 ± 0,0005. Найти Δ(а — b) и εa–b.

○ По формуле (2.3) вычисляем границу абсолютной погрешности разности а — b:

Δ(а — b) = 0,0005 + 0,0005 = 0,001.

В приближенном значении разности цифра в разряде тысячных не может быть

верной, так как Δ(а — b) > 0,0005. Итак, а — b = 3,117 ≈ 3,12. Абсолютная погрешность

разности 0,001. В приближенном числе 3,12 все цифры верные.

По формуле (2.4) находим относительную погрешность разности:

εа–b = 0,001/3,12 = 0,00032 ≈ 0,03 %.●

7. Вычислите разность чисел 8,72 и 2,6532, границы абсолютной

погрешности которых соответственно равны 0,005 и 0,00005.

8. Вычислите разность a = 13 − 5 с четырьмя значащимицифрами.

Найдите Δa и εa.

 

 

Лекция 1.6. Комплексные числа

 

Определение 1. Число, квадрат которого равен -1, называется мнимой единицей и обозначается буквой i.                     i² = -1.

Следовательно, .

 

Определение 2. Числа вида a + bi, где a и b – действительные числа, i – мнимая единица, называются комплексными.

 

Данная форма записи комплексного числа называется алгебраической.

 

Число а является действительной частью комплексного числа, bi – его мнимой частью, число b называется коэффициентом при мнимой части.

 

Если b = 0, то комплексное число a + bi = a + 0i = a, то есть является действительным числом.

Вывод: действительные числа являются частным случаем комплексных чисел.

 

Если а = 0, то комплексное число a + bi = bi и называется чисто мнимым.

 

 

Сложение, вычитание и умножение комплексных чисел выполняется по правилам соответствующих действий над многочленами.

 

Задания:

1.                  Выполните сложение, вычитание и умножение комплексных чисел:

а)      z₁ = 3+5i и z₂ = 7–2i;

б)      z₁ = -2+3i и z₂ = 7–4i;

в)      z₁ = 3–2i и z₂ = 7–i;

г)      z₁ = 1–i и z₂ = 1+i;

д)      z₁ = 3–9i и z₂ = 5+2i.

 

 

Определение 3. Два комплексных числа называются сопряженными, если они отличаются друг от друга только знаками перед мнимой частью (a + bi и a – bi).

 

 

Произведение двух сопряженных комплексных чисел всегда равно действительному числу (проверьте!).

 

 

Для деления одного комплексного числа на другое необходимо умножить делимое и делитель на комплексное число, сопряженное делителю.

 

 

Примеры действий с комплексными числами

 

Даны два комплексных числа z₁ = 3+5i и z₂ = 7–2i. Выполнить их сложение, вычитание, умножение и деление.

 

I. Сложение

Раскрываем скобки, применяем переместительный и сочетательный законы сложения и правило приведения подобных слагаемых.

 

II. Вычитание

Применяем те же правила, что и при сложении, но не забываем, что если перед раскрываемой скобкой стоит знак «минус», то у всех слагаемых в скобке знак меняется на противоположный.

III. Умножение

Используем правило умножения многочленов: каждое слагаемое в первой скобке умножаем на каждое слагаемое во второй скобке.

Не забываем, что i² = -1.

 

IV. Деление

Число, сопряженное делителю , – это число 7+2i. Домножаем числитель и знаменатель дроби на число 7+2i и выполняем необходимые преобразования: в числителе перемножаем два комплексных числа по предыдущему правилу, а в знаменателе используем разность квадратов .

 

 

Задания:

 

1.      Выполните деление комплексных чисел: а)                  ; б)      ; в)      ; г)      .

2.      Выполните указанные действия с комплексными числами: а)      ; б)      ; в)      ; г)      ; д)      .

3.      Решите квадратные уравнения с отрицательными дискриминантами: а)      б)      в)

 

Бесчисленное множество определений и значений — Merriam-Webster

1 из 2

мое объявление ˈmir-ē-əd 

1

: десять тысяч

2

: большое число

множество идей

Является ли мириад существительным?: Руководство по использованию

Недавняя критика использования мириад в качестве существительного, как во множественном числе мириады , так и во фразе мириады , по-видимому, отражает ошибочное мнение, что слово изначально было и до сих пор является лишь прилагательным. Однако, как показывают записи здесь, это существительное на самом деле является более старой формой, датируемой 16 веком. Существительное мириады появлялись в произведениях таких писателей, как Мильтон (множественное число мириады ) и Торо ( мириады ), и оно продолжает часто встречаться в уважаемом английском языке. Нет причин избегать этого.

мириады

2 из 2

1

: бесчисленное множество

эти мириады проблем

также : многочисленные и разнообразные

мириады тем

2

: имеющие бесчисленные аспекты или элементы ты знаешь?

В английском языке значение «десять тысяч» мириад в основном появляется в ссылках на Древнюю Грецию, например, в следующем из Истории Греции английского историка Коннопа Тирволла: «4000 человек из Пелопоннеса сражались при Фермопилах с 300 мириадами . » Чаще англоговорящие используют мириады в широком смысле — как существительное в единственном числе («мириады крошечных частиц»), так и существительное во множественном числе («мириады крошечных частиц»). Мириады также могут служить прилагательным, означающим «бесчисленное множество» («мириады частиц»). В то время как некоторые комментаторы употребления критикуют использование существительного, оно прочно вошло в английский язык с 16 века и фактически примерно на 200 лет старше прилагательного. Мириад происходит от греческого мириас , которое, в свою очередь, происходит от мириады , что означает «бесчисленное количество» или «десять тысяч».

Синонимы

Существительное

• изобилие
• ствол
• полная корзина
• лодка
• ведро
• связка
• пучок
• бушель
• вагон
• кусок
• сделка
• дюжина
• горсть
• кусков
• хорошая сделка
• куча
• сто
• ремни [ в основном британские ]
• плети
• загрузки
• лот
• масса
• беспорядок
• гора
• много
• кратность
• тонны
• упаковка
• абонемент
• клевать
• стопка
• тарелка
• полнота
• изобилие
• много
• горшок
• горшок
• изобилие
• количество
• плот
• пачек
• скадов
• пучок
• корабельная загрузка
• прицел
• убил
• разлив
• стопка
• магазин
• тонна
• грузовик
• том
• пыж
• богатство
• двор

Прилагательное

• водолазы
• коллектор
• multifarious

Просмотреть все синонимы и антонимы в тезаурусе 

Примеры предложений

Существительное

Г-н Маккалоу хвалит Адамса за его сверхъестественную прозорливость… предвидение множества событий, от сложности победы над британцами… до вызывающих разногласия последствий рабства. — Митико Какутани, 9 лет.0021 Нью-Йорк Таймс , 22 мая 2001 г.

Сектантский протестантизм усилил как американский индивидуализм, так и тенденцию общества к самоорганизации в виде множества добровольных ассоциаций и сообществ. — Фрэнсис Фукуяма, Atlantic , май 1999 г.

В баррио, под пальмами нипа, он слушал мириады гудящих цикад и крики гекконов. — Нина ФитцПатрик, 9 лет.0021 Басни ирландской интеллигенции , 1991

Чтобы читать Марию Корелли, вы должны были быть в состоянии следить за несколькими сотнями печатных слов за раз, и в Англии было множество людей, которые были на это способны.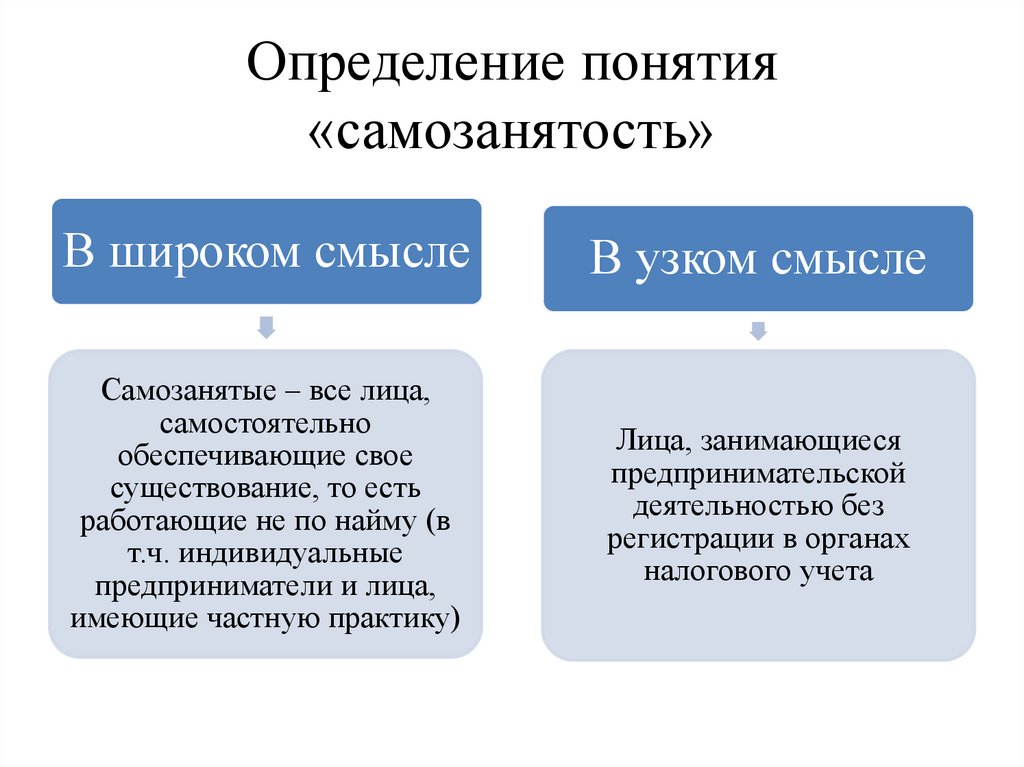 — Хью Кеннер, Тонущий остров , 1987 г.

…сплел пальцы за головой и уставился на мириады крошечных цветных точек, из которых состоит тьма. — Джон Стейнбек, 9 лет.0021 К востоку от Эдема , 1952 г.

Существует мириад из возможностей. автомобиль может быть оснащен мириадами опций Прилагательное

… чем больше цитат можно было найти, тем легче можно было определить тонкие различия между (возможно) бесчисленным множеством вариантов использования и значениями любого отдельного слова. Так создаются исторические словари… — Саймон Винчестер, Значение всего , 2003 г.

Эпоха белой вины с ее мириадами коррупции и ее почти расистской слепотой к индивидуальности меньшинства может когда-нибудь уйти, как ушел век расизма… — Шелби Стил, 9 лет.0021 Harper’s , ноябрь 2002 г.

Вторая мировая война ускорила продвижение науки и техники в микромир. Ученые и технологи играли друг с другом в пятнашки в поисках микроскопического контроля. С помощью математики и множества теорий они определили новый микрокосм. — Джозеф А. Амато, Пыль , 2000 г.

Проблем старой системы было мириадов . мириады проблем, с которыми сталкиваются сегодняшние города Узнать больше

Последние примеры в Интернете

Конечно, в каждом законе содержится мириадов деталей и условий, которые могут заставить скептиков жаловаться на то, что правила слишком сложны, чтобы знать, что делать, и ложатся чрезмерным бременем на работодателей. — Меган М. Биро, 9 лет.0021 Forbes , 22 марта 2023 г. Существует мириадов способов наблюдать за озером и окружающими старовозрастными лесами, включая тропы к живописным смотровым площадкам и геологическим чудесам, нежным водопадам и одним из самых кинематографичных прогулок на снегоступах в штате. — Jd Shadel, Condé Nast Traveler , 21 марта 2023 г. Что нужно знать о полках для обуви перед покупкой0021 мириады стилей обувных стеллажей, но основными являются напольные стеллажи и наддверные стеллажи. — Таня Эдвардс, Better Homes & Gardens , 17 марта 2023 г. С ноября по апрель в Montage Big Sky предлагается бесчисленное множество зимних развлечений. — Ванесса Уилкинс, Travel + Leisure , 17 марта 2023 г. Напротив, вторая статья, опубликованная в декабре, была посвящена жителям сельских городов, многие из которых живут за чертой бедности, которым грозит множество проблем, потому что их водная инфраструктура остро нуждается в ремонте. —Майкл Брага, , Республика Аризона, , 9 марта 2023 г. Не в последнюю очередь Скотт — вместе с промоутерами Live Nation, Scoremore, XX Global и другими — столкнулся с мириадами судебных исков на общую сумму к северу от 2 миллиардов долларов потенциального ущерба. — Итан Шанфельд, Variety , 3 марта 2023 г. Есть Мириады способов, которыми, как известно ученым, выбросы парниковых газов, связанные с деятельностью человека, вызывают повышение глобальной температуры, сообщил ранее USA TODAY климатолог НАСА Джош Уиллис. — Изабелла Фертель, USA TODAY , 10 февраля 2023 г. Есть мириады разных причин, но они делят друг с другом одежду. — Ланэ Броуди, Peoplemag , 8 февраля 2023 г.

Влияние Бекхэма в Балтиморе составляет мириадов . — Брайан Вакер, Baltimore Sun , 10 апреля 2023 г. Обзор показал, что методология многих предыдущих исследований была ошибочной и что риск бесчисленного множества проблем со здоровьем значительно увеличился после менее чем двух порций алкоголя в день для женщин и после трех для мужчин. — Рони Кэрин Рабин, New York Times , 4 апр. 2023 г. Теперь расцвели мириады других методов лечения. — Ангус Маккиннон, CNN , 3 апреля 2023 г. Увеличить / Портрет Бетховена работы Йозефа Карла Штилера, 1820 г. Beethoven-Haus Bonn Людвиг ван Бетховен — один из величайших композиторов всех времен, но на протяжении всей своей жизни он страдал от мириадов проблем со здоровьем, в частности, к 1818 году он почти полностью оглох. — Дженнифер Уэллетт, 9 лет. 0021 Ars Technica , 22 марта 2023 г. Отчеты, которые повторяли тезисы Кремля по мириадам тем, бездоказательно утверждали, что власти Огайо лгали об истинных последствиях разлива химикатов. — Дэвид Клеппер, The Enquirer , 20 марта 2023 г. Может быть, еще один абзац: отчеты, которые повторяли тезисы Кремля по мириадам тем, утверждали без каких-либо доказательств, что власти Огайо лгали об истинных последствиях разлива химикатов. — Джей Нордлингер, 9 лет.0021 National Review , 20 марта 2023 г. Отчеты, которые повторяли тезисы Кремля по мириадам тем, бездоказательно утверждали, что власти Огайо лгали об истинных последствиях разлива химикатов. — Кевин Фрекинг, Fortune , 18 марта 2023 г. На самом деле, вы можете быть удивлены мириадами методов, позволяющих даже самой маленькой кухонной зоне выглядеть великолепно. — Анна Фикссен, 9 лет.0021 ELLE Decor , 7 марта 2023 г. Узнать больше

Эти примеры программно скомпилированы из различных онлайн-источников, чтобы проиллюстрировать текущее использование слова «бесчисленное множество». Любые мнения, выраженные в примерах, не отражают точку зрения Merriam-Webster или ее редакторов. Отправьте нам отзыв об этих примерах.

История слов

Этимология

Существительное и прилагательное

Греческий myriad-, myrias , from myrioi бесчисленное количество, десять тысяч

Первое известное употребление

Существительное

1555, в значении, определенном в смысле 1

Прилагательное

1735, в значении, определенном в пункте 1

Путешественник во времени

Первое известное использование мириад был в 1555 году

Другие слова того же года

Подкаст

Музыкальная тема Джошуа Стэмпера ©2006 New Jerusalem Music/ASCAP

Получайте «Слово дня» на свой почтовый ящик!

Словарные статьи Около

мириады

мириакантус

мириады

бесчисленное множество

Посмотреть другие записи поблизости

Процитировать эту запись «Мириады».

Словарь Merriam-Webster.com , Merriam-Webster, https://www.merriam-webster.com/dictionary/myriad. По состоянию на 27 апреля 2023 года. 1 из 2 существительное

мое объявление ˈmir-ē-əd 

1

: десять тысяч

2

: большое, но не указанное или не подсчитанное число

мириады звезд

мириады

2 из 2 прилагательное

: чрезвычайно многочисленный

мириады песчинок на пляже

Еще от Merriam-Webster на тему

мириады

Английский: Перевод слова мириады для говорящих на испанском языке

Britannica English: перевод мириад для говорящих на арабском языке

Последнее обновление: 17 апр 2023 — Обновлены примеры предложений

Подпишитесь на крупнейший словарь Америки и получите тысячи дополнительных определений и расширенный поиск без рекламы!

Merriam-Webster без сокращений

Можете ли вы решить 4 слова сразу?

Можете ли вы решить 4 слова сразу?

превратности

См. Определения и примеры »

Получайте ежедневно по электронной почте Слово дня!

Поиск наборов номеров/проверка ℕ,ℤ,ℚ,ℝ,ℂ — N Z Q R C

Калькулятор наборов номеров

Номер для проверки

Устройство проверки наборов номеров

Комплект

Проверка всех наборов N: натуральные целые числа Z: относительные целые числа D: десятичные числа Q: рациональные числа R: действительные числа I: чисто мнимые числа C: комплексные числа

См. также: Решатель уравнений — Калькулятор

Ответы на вопросы (FAQ)

Что такое набор чисел? (Определение)

Набор чисел — это математическое понятие, позволяющее помещать различные типы чисел в различные категории, иногда включаемые между ними.

Классическим представлением обычных множеств является $$ \mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R} \subset \mathbb{C} $$

Что такое общие числовые наборы?

В математике существует несколько наборов : натуральные числа N (или ℕ), набор целых чисел Z (или ℤ), все десятичные числа D или $\mathbb{D} $, набор рациональных чисел Q (или ℚ), набор действительных чисел R (или ℝ) и набор комплексных чисел С (или ℂ). Эти 5 наборов иногда обозначаются аббревиатурой NZQRC .

Другие наборы, такие как набор десятичных чисел D или $ \mathbb{D} $, или набор чисто мнимых чисел I или $ \mathbb{I} $. Существуют также наборы трансцендентных чисел, кватернионов или гиперкомплексных чисел, но они зарезервированы для продвинутых математических теорий, NZQRC являются наиболее распространенными наборами.

Что означает символ ∈?

Знак ∈ (Unicode 2208) означает элемент или принадлежит .

Пример: $ 2 \in \mathbb{N} $ читается 2 является элементом множества N

Существует также знак ∊ (Unicode 220A), который такой же, но меньшего размера.

Знак ∉ (Unicode 2209) означает, что не является элементом или не принадлежит .

Пример: $ -2 \notin \mathbb{N} $

Знак ⊂ (Unicode 2282) означает 9{+} $

NB: В некоторых (старых) учебниках для этого набора указывается буква W вместо N , W означает Целые числа

Набор N входит в наборы Z, D, Q, R и C.

Какой номер Z установлен?

Z — множество целых чисел, т.е. положительное, отрицательное или ноль.

Пример: …, -100, …, -12, -11, -10, …, -5, -4, -3, -2, — 1, 0, 1, 2, 3, 4, 5 , … 10, 11, 12, …, 100, … $ \in \mathbb{Z} $

9{p}} , a \in \mathbb{Z}, p \in \mathbb {N} \right\} $$

Все десятичные дроби в D — это числа, которые можно записать конечным числом цифр (числа, содержащие точка и конечная десятичная часть).

Пример: -123,45, -2,1, -1, 0, 5, 6,7, 8,987654 $ \in \mathbb{D} $

Таким образом, числа, использующие точки подвеса … для их десятичной записи, имеют бесконечное число десятичных знаков и поэтому не принадлежат множеству D.

Множество D входит в состав множеств Q, R и C.

Наборы N и Z включены в набор D (поскольку все целые числа являются десятичными числами без десятичных разрядов). Любое число в N или Z также находится в D.

Что такое число Q?

Q есть множество рациональных чисел , т. е. представлена ​​дробью a/b, где a принадлежит Z, а b принадлежит Z * (исключая деление на 0).

Пример: 1/3, -4/1, 17/34, 1/123456789 $ \in \mathbb{Q} $

Множество Q входит в множества R и C.

Наборы N, Z и D входят в набор Q (поскольку все эти числа можно записать дробью). Любое число в N, Z или D также содержится в Q.

Какой набор чисел R?

R это набор действительных чисел , т.е. все числа, которые могут реально существовать, содержит кроме рациональных чисел, нерациональные или иррациональные числа в виде $\pi$ или $\sqrt{2}$.

Иррациональные числа имеют бесконечную непериодическую десятичную часть.

Пример: 9* $ (звездочка R минус) — набор ненулевых отрицательных действительных чисел, также обозначаемый как $ \mathbb{R}_{

Набор R входит в набор C.

Наборы N, Z, D и Q входят в набор R. Любое число из N или Z или D или Q также входит в R.

Что такое I номер установлен?

I — набор (чистых) мнимых чисел, то есть комплексных чисел без действительных частей, квадратные корни отрицательных действительных чисел — чисто мнимые. 2=-1 $

Набор I входит в набор C.

Что такое набор номеров C?

C — это набор комплексных чисел , набор, созданный математиками как расширение набора действительных чисел , к которым добавляются числа, содержащие мнимую часть.

Пример: $ a + i b \in \mathbb{C} $

Наборы N, Z, D, Q, R и I включены в набор C. Любое число из N или Z или D или Q или R или I тоже в C.

Что такое пустой набор Ø?

Пустой набор отмечен Ø , как видно из его названия, он пуст и не содержит ни одного номера.

Что такое конструируемое число?

Составные числа — это все числа, которые можно геометрически изобразить с помощью линейки и циркуля.

Пример: $ \sqrt{2} $ — конструируемое число, а $ \pi $ — нет.

Что такое алгебраическое число?

Алгебраические числа — это набор чисел, которые можно вычислить как корень многочлена с рациональными коэффициентами.

Что такое трансцендентное число?

Трансцендентные числа — это набор чисел, которые нельзя вычислить как корень многочлена с рациональными коэффициентами (то есть не алгебраическими).

Среди действительных или комплексных чисел большинство трансцендентных чисел.

Что такое иррациональные числа?

Иррациональные числа — это наборы чисел, которые не могут быть записаны в виде дроби (т. е. все числа, которые не находятся в $ \mathbb{Q} $)

Что такое наборы чисел E и O?

Некоторые книги определяют наборы E для четных номеров и O для нечетных номеров. Это не стандартное обозначение.

Что входит в наборы?

Связи между различными множествами представлены включениями: $$ N \подмножество Z \подмножество D \подмножество Q \подмножество R \подмножество C $$

Символ подмножества ⊆ является символом включения (в широком смысле), A ⊆ B, если каждый элемент A является элементом B.