Элементарные преобразования матрицы. Ранг матрицы — Студопедия
Поделись
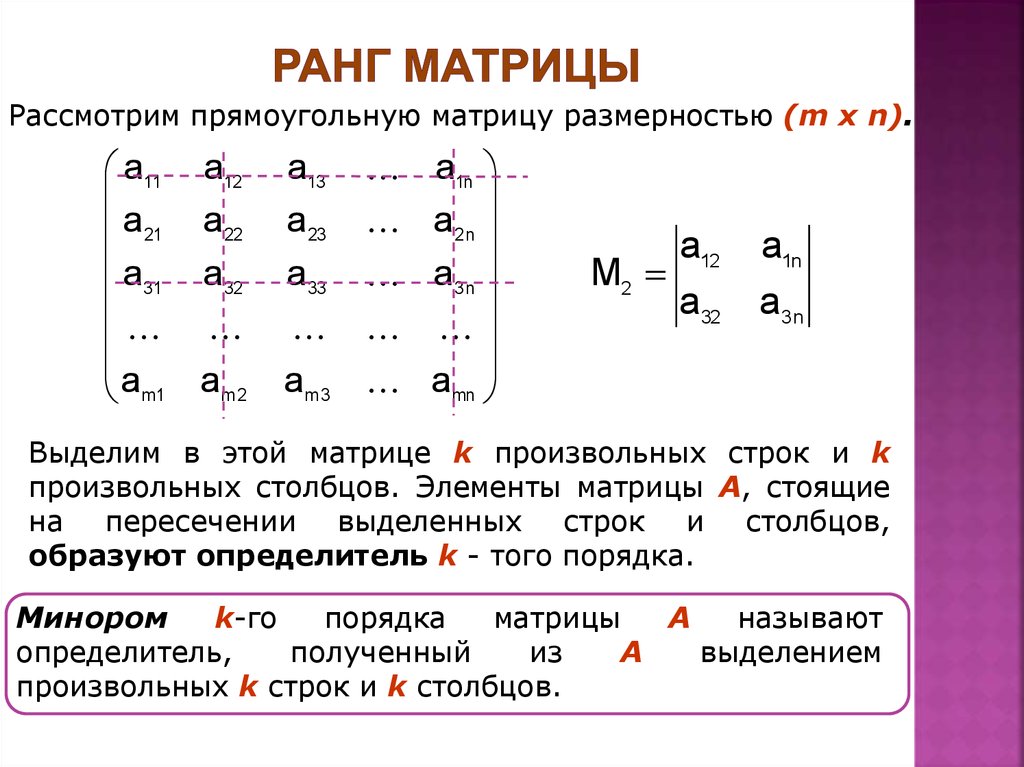
Введем понятие ранга матрицы. Выделим в матрице -строк и -столбцов, где — число, меньшее или равное меньшему из чисел и . Определитель порядка , составленный из элементов, стоящих из пересечения выделенных -строк и -столбцов, называется минором или определителем, порожденным матрицей .
Рангом матрицы (обозначается ) называется наибольший порядок порожденных ею определителей, отличных от нуля.
Ранг матрицы не изменится, если:
1) поменять местами любые два параллельных ряда;
2) умножить (разделить) каждый элемент ряда на один и тот же множитель (делитель) ;
3) прибавить к элементам ряда соответствующие элементы любого другого параллельного ряда, умноженные на один и тот же множитель;
4) Ряд, состоящий из нулей, отбрасывается.
Преобразования 1-4 называются элементарными.
Две матрицы называются
Базисным минором матрицы называется всякий отличный от нуля минор, порядок которого равен рангу данной матрицы.
Рассмотрим основные методы нахождения ранга матрицы.
1. Метод единиц и нулей. С помощью элементарных преобразований можно любую матрицу привести к виду, когда каждый ее ряд будет состоять только из нулей, или нулей и одной единицы. Тогда число оставшихся единиц и определит ранг исходной матрицы, так как полученная матрица будет эквивалентна исходной.
Пример 2.1. Найти ранг матрицы методом единиц и нулей.
~
1 шаг.
Разделим элементы третьего столбца на 2, затем первую строку умножим на и сложим с четвертой строкой. Получим новую эквивалентную матрицу:
~ ~
2 шаг
.
Теперь четвертую строчку складываем со второй и с третьей. Получим новую эквивалентную матрицу:
~ ~
+
+ +
3 шаг.
Умножим элементы второго столбца на и сложим с элементами четвертого столбца. Затем умножим элементы второго столбца на и сложим с соответствующими элементами первого столбца. И окончательно элементы второго столбца сложим с соответствующими элементами пятого столбца. Получим новую эквивалентную матрицу:
~ ~
4 шаг.
Умножим элементы третьей строки на и сложим с соответствующими элементами второй строки. Получим новую эквивалентную матрицу:
~ ~
+
5 шаг.
Сложим элементы пятого столбца с соответствующими элементами первого столбца. Получим новую эквивалентную матрицу:
~ ~
+
6 шаг.
Умножим элементы третьего столбца на 3 и сложим с соответствующими элементами первого столбца.
Получим новую эквивалентную матрицу:
~ ~
+ +
7 шаг.
Умножим на элементы третьего столбца и сложим с соответствующими элементами второго и четвертого столбцов. Получим новую эквивалентную матрицу:
~ ~
+
8 шаг.
Умножим элементы четвертого столбца на и сложим с соответствующими элементами пятого столбца. Затем просто умножим элементы четвертого столбца на . Получим новую эквивалентную матрицу:
~ — , так как осталось 3 единицы.
2. Метод окаймляющих миноров. Минор порядка , содержащий в себе минор порядка , называется окаймляющим минором . Если у матрицы существует минор , а все окаймляющие его миноры , то .
Найдем этим методом из предыдущего примера.
Начнем с левого верхнего угла:
;
;
Как видно, что эта матрица содержит всего два минора 4-го порядка. Проверим второй:
То есть
ЗАДАНИЯ
Задание 2.
1. Найти ранг матрицы
1) Методом единиц и нулей;
2) Методом окаймляющих миноров.
| 1. ; | 2. ; |
| 3. ; | 4. ; |
| 5. ; | 6. ; |
| 7. ; | 8. ; |
| 9. ; | 10. ; |
| 11. ; | 12. ; |
| 13. ; | 14. ; |
| 15. ; | |
| 17. ; | 18. ; |
| 19. ; | 20. ; |
| 21. ; | 22. ; |
| 23. ; | 24. ; |
| 25. ; | 26. ; |
| 27. ; | 28. ; |
| 29. ; | 30. . |
Обратная матрица
Квадратная матрица порядка называется невырожденной, если её определитель (детерминант) .
В случае, когда , матрица называется вырожденной.
Только для квадратной невырожденной матрицы вводится понятие обратной матрицы .
Матрица называется обратной для квадратной невырожденной матрицы , если , где — единичная матрица порядка .
Для матрицы существует единственная обратная матрица, которая определяется по формуле:
или ,
где или — союзная или присоединённая матрица, её элементами являются алгебраические дополнения транспонированной матрицы , т.е. матрицы, полученной из данной матрицы заменой её строк столбцами с теми же номерами.
, т.е.
Пример 2.2. Найти обратную матрицу двумя способами: с помощью алгебраических дополнений и путем элементарных преобразований. Сделать проверку.
Дана матрица .
Найти: .
Решение:
1 способ. С помощью алгебраических дополнений.
Найдем обратную матрицу по формуле ,
где — определитель матрицы ;
— союзная или присоединённая матрица, состоящая из алгебраических дополнений транспонированной матрицы .
Согласно формуле можно сказать, что если , то обратная матрица не существует.
Найдем:
,
значит обратная матрица существует.
Составим союзную матрицу, для этого найдем алгебраические дополнения по формуле
| ; | ; | ; |
| ; | ; | ; |
| ; | ; | . |
Отсюда:
.
2 способ. Основан на элементарных преобразованиях вспомогательной матрицы, которая получается путём приписывания к данной матрице единичной матрицы того же порядка. Схематически это выглядит так:
Итак, запишем матрицу:
~ ~
~ ~ ~
~ ~
~ ~
~
Итак:
Проверка. Сделаем проверку исходя из свойства . Остановимся на произведении . Для удобства умножения матриц запишем в виде:
.
Тогда:
— верно (смотри определение )
Задание 2.
2. Найти обратную матрицу двумя способами: с помощью алгебраических дополнений и путем элементарных преобразований. Сделать проверку.
| 1. | 2. |
| 3. | 4. |
| 5. | 6. |
| 7. | 8. |
| 9. | 10. |
| 11. | 12. |
| 13. | 14. |
| 15. | 16. |
| 17. | 18. |
| 19. | 20. |
| 21. | 22. |
| 23. | 24. |
| 25. | 26. |
| 27. | 28. |
| 29. | 30. |
III. СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
§ 1.6. Ранг матрицы
Определение ранга матрицы Ранг матрицы при элементарных преобразованиях Линейные комбинации строк или столбцов Связь ранга с числом независимых строк (столбцов) Строка матрицы как линейная комбинация независимых строк матрицы |
Определение ранга матрицы
Понятие
ранга матрицы одно из фундаментальных
в линейной алгебре.
В матрице
размерами
вычеркиванием каких либо строк или
столбцов можно образовать квадратную
матрицу
-го
порядка
.
Определитель
такой матрицы называется минором
-го
порядка. У матрицы размерами
есть миноры 1-го порядка, 2-го порядка и
так далее до
-го
порядка, где
.
Например, у матрицы
имеются миноры 1-го, 2-го и 3-го порядков.
Определение. Рангом матрицы называется наивысший порядок отличных от нуля миноров этой матрицы.
Обозначение: rang A или .
Свойства ранга:
1) Ранг нулевой матрицы считается равным нулю.
2) .
3) у матрицы -го порядка тогда и только тогда, когда .
ПРИМЕР. Вычислить ранг матрицы .
Решение. Для
матрицы
ранг
.
Чтобы проверить, может ли ранг быть
равным 3, вычислим все миноры 3-го порядка,
которые можно образовать из матрицы
вычеркиванием одного столбца.
, , , .
Следовательно, ранг не может быть более 2. Легко найти минор 2-го порядка, отличный от нуля. Например, . Но тогда .
Поиск ранга матрицы большого порядка перебором миноров является трудоемкой задачей. Развиты эффективные методы определения ранга матрицы.
К введенным ранее трем типам элементарных преобразований матрицы добавим еще два:
4) Отбрасывание нулевой строки или столбца.
5) Транспонирование матрицы.
Ранг матрицы при элементарных преобразованиях
( о ранге матрицы при элементарных преобразованиях)
Элементарные преобразования не изменяют ранга матрицы.
◄ Рассмотрим последовательно все типы элементарных преобразований матрицы.
Элементарные преобразования 1-го типа
меняют строки или столбцы в матрице.
В
этом случае определитель матрицы меняет
знак, но не может обратиться в нуль.
Элементарные преобразования 2-го типа умножают строку или столбец на не равное нулю число. Но тогда определитель матрицы умножится на это число, что не может привести к его обнулению.
Элементарные преобразования 3-го типа приводят к прибавлению к -й строке матрицы ее -й строки, что не меняет величины определителя.
Элементарные преобразования 4-го типа позволяют отбросить все миноры -го порядка, равные нулю, и перейти к рассмотрению миноров -го порядка. На величине ранга это, очевидно, не отразится.
Элементарные преобразования 5-го типа транспонируют матрицу, отчего величина ее определителя, как известно (свойство 3 определителей), не изменяется.
Мы установили, что при элементарных
преобразованиях матриц их определители
либо сохраняются, либо изменяют свою
величину, не обращаясь при этом в нуль.
В результате сохраняется наивысший
порядок отличных от нуля миноров
исходной матрицы, т.е. ее ранг не
изменяется.►
Теорема дает возможность посредством элементарных преобразований привести матрицу к определенному виду, когда ее ранг вычисляется без труда. Рассмотрим задачу эффективного вычисления ранга подробнее.
Матрица называется матрицей ступенчатого вида или ступенчатой матрицей, если она имеет вид
или ,
где ; . Ранг ступенчатой матрицы равен , так как существует минор порядка , отличный от нуля:
.
Таким образом, произвольную матрицу
следует привести к ступенчатому виду.
Число ненулевых строк матрицы будет
равно ее рангу. Если квадратная матрица
примет
треугольный вид, ее ранг будет равен
.
При проведении элементарных преобразований
с матрицей знак равенства ставиться
не может (матрицы не равны), ставится
обычно знак тильды «~» .
ПРИМЕР. Найти ранг матрицы
.
Решение. Ко 2-й строке прибавим 1-ю, предварительно умноженную на -2, к 3-й строке прибавим 1-ю, предварительно умноженную на -1. Получим
.
К 3-й строке прибавим 2-ю, предварительно умноженную на -2:
.
Число ненулевых строк равно 2. Тогда . При ином обосновании выделим из матрицы минор максимального порядка, не равный нулю. Это, например, . Тогда .
Линейные комбинации строк или столбцов
Познакомимся с понятием линейной зависимости строк или столбцов. В матрице
введем обозначения строк:
.
Эти строки являются -мерными и представляют собой матрицы размерами . В новых обозначениях исходная матрица записывается в виде
.
Строка , определяемая равенством
, (11)
называется линейной комбинацией строк , где — любые действительные числа.
В развернутом матричном виде последнее равенство выглядит так:
= .
Для элементов строки имеем систему уравнений
(12)
Строки называются линейно зависимыми, если существуют такие , не равные нулю одновременно, что линейная комбинация этих строк равна нулевой строке
.
Строки называются линейно независимыми, если линейная комбинация этих строк равна нулевой строке только при .
(о линейной комбинации строк матрицы)
Если строки матрицы линейно зависимы, то одна из них является линейной комбинацией остальных.
◄Пусть строки
линейно зависимы.
Тогда найдутся числа
,
не все равные нулю одновременно и такие,
что
.
Пусть, например, . Перенесем первые слагаемых направо и разделим равенство на . Получим
.
или
,
где , .►
Замечание 1. Верно и обратное утверждение: если одна из строк является линейной комбинацией остальных, то эти строки линейно зависимы.
Замечание 2. Аналогичными свойствами обладает множество -мерных столбцов.
Связь ранга с числом независимых строк (столбцов)
(о связи ранга с числом независимых строк)
Ранг матрицы равен числу ее независимых строк (столбцов).
◄Пусть матрица имеет ранг . По определению ранга матрицы, существует минор порядка , отличный от нуля. Пусть для определенности это минор
.
Тогда строки линейно независимы. Предположим противное. Например, строка с номером есть линейная комбинация остальных строк. В этом случае
.
Проведем элементарные преобразования, не изменяющие величину определителя. Прибавим к этой строке 1-ю строку, предварительно умноженную на , 2-ю строку, умноженную на и так далее, наконец, -ю строку, умноженную на . Получим на месте строки с номером последовательно строку
Последняя строка теперь будет состоять из одних нулей. Но тогда , что невозможно. Наше предположение о том, что строки линейно зависимы, неверно.►
Строка матрицы как линейная комбинация независимых строк матрицы
(о представлении строки в виде линейной комбинации независимых строк)
Каждая строка
матрицы
может быть представлена в виде линейной
комбинации независимых строк матрицы.
◄Пусть матрица имеет ранг . По определению ранга, матрицы существует минор порядка , отличный от нуля. Пусть для определенности это минор
.
Рассмотрим минор -го порядка матрицы , который можно получить, добавив к минору -ю строку и -й столбец матрицы :
.
Этот минор равен нулю как минор более высокого порядка, чем . Разложим его по последнему столбцу:
. (13)
Разделим равенство на и введем обозначения:
,где
Перепишем равенство в следующем виде
, где . (14)
Это равенство верно также и для
.
Действительно, если добавить к минору
-й
столбец матрицы с одним из номеров
,
то новый минор
будет содержать два одинаковых столбца.
Следовательно, его величина также равна
нулю, и равенство (13) будет иметь место.
Перепишем соотношение (14) в виде столбца
равенств для всех
:
Мы получили систему уравнений для нахождения элементов -й строки, подобную (12). Запишем систему в матричном виде (см. (12) (11))
. (15)
Равенство (15) дает представление -й строки как линейной комбинации независимых строк . Поскольку -я строка выбрана произвольно, заключаем, что каждая строка матрицы может быть представлена в виде линейной комбинации независимых строк матрицы.►
Замечание 1. Все рассуждения в отношении строк справедливы также и для столбцов.
Замечание 2. Задача определения числа независимых строк или столбцов матрицы сводится к нахождению ее ранга.
Вопросы для повторения
1 Привести определение матрицы. Перечислить виды матриц.
2. Сформулировать арифметические
операции над матрицами.
3. Что означает транспонирование матрицы? Привести свойства транспонирования.
4. Сформулировать понятие определителя квадратной матрицы любого порядка.
5. Чем алгебраическое дополнение элемента матрицы отличается от минора того же элемента?
6. Как найти величину определителя?
7. Перечислить свойства определителей.
8. Дать определение обратной матрицы. Привести ее свойства.
9. Что такое матрицы элементарных преобразований? Что называют элементарными преобразованиями матрицы?
10. Объяснить способ построения обратной матрицы, основанный на использовании расширенной матрицы.
11. Сформулировать определение ранга матрицы.
12. Какие строки матрицы называются линейно независимыми?
Задания на нахождение ранга матрицы
Определить ранг матрицы
Единственным минором максимального (3-го) порядка для матрицы А является ее определитель.
Если ΔА не равен нулю, R(A) = 3; если ΔА = 0, R(A) 0. Значит, R(A) = 1 или R(A) = 2. Если найдется минор 2-го порядка, не равный нулю, то R(A) = 2.
Вычислим минор из элементов, стоящих на пересечении двух первых строк и двух первых столбцов:
Понятие ранга матрицы
Определение. Рангом матрицы называется максимальное число линейно независимых строк, рассматриваемых как векторы.
Теорема 1 о ранге матрицы. Рангом матрицы называется максимальный порядок отличного от нуля минора матрицы.
Понятие минора мы уже разбирали на уроке по определителям, а сейчас обобщим его. Возьмём в матрице сколько-то строк и сколько-то столбцов, причём это «сколько-то» должно быть меньше числа строк и стобцов матрицы, а для строк и столбцов это «сколько-то» должно быть одним и тем же числом. Тогда на пересечении скольки-то строк и скольки-то столбцов окажется матрица меньшего порядка, чем наша исходная матрица.
Определитель это матрицы и будет минором k-го порядка, если упомянутое «сколько-то» (число строк и столбцов) обозначим через k.
Определение. Минор (r+1)-го порядка, внутри которого лежит выбранный минор r-го порядка, называется называется окаймляющим для данного минора.
Наиболее часто используются два способа отыскания ранга матрицы. Это способ окаймляющих миноров и способ элементарных преобразований (методом Гаусса).
При способе окаймляющих миноров используется следующая теорема.
Теорема 2 о ранге матрицы. Если из элементов матрицы можно составить минор r-го порядка, не равный нулю, то ранг матрицы равен r.
При способе элементарных преобразований используется следующее свойство:
— если путём элементарных преобразований получена трапециевидная матрица, эквивалентная исходной, то рангом этой матрицы является число строк в ней кроме строк, полностью состоящих из нулей.
Отыскание ранга матрицы способом окаймляющих миноров
Окаймляющим минором называется минор большего порядка по отношению к данному, если этот минорм большего порядка содержит в себе данный минор.
Например, дана матрица
.
,
окаймляющими будут такие миноры:
.
Алгоритм нахождения ранга матрицы следующий.
1. Находим не равные нулю миноры второго порядка. Если все миноры второго порядка равны нулю, то ранг матрицы будет равен единице ( r =1 ).
2. Если существует хотя бы один минор второго порядка, не равный нулю, то составляем окаймляющие миноры третьего порядка. Если все окаймляющие миноры третьего порядка равны нулю, то ранг матрицы равен двум ( r =2 ).
3. Если хотя бы один из окаймляющих миноров третьего порядка не равен нулю, то составляем окаймляющие его миноры.
Если все окаймляющие миноры четвёртого порядка равны нулю, то ранг матрицы равен трём ( r =2 ).
4. Продолжаем так, пока позволяет размер матрицы.
Пример 1. Найти ранг матрицы
.
Решение. Минор второго порядка
.
Окаймляем его. Окаймляющих миноров будет четыре:
,
,
,
.
Таким образом, все окаймляющие миноры третьего порядка равны нулю, следовательно, ранг данной матрицы равен двум ( r =2 ).
Пример 2. Найти ранг матрицы
.
Решение. Ранг данной матрицы равен 1, так как все миноры второго порядка этой матрицы равны нулю (в этом, как и в случаях окаймляющих миноров в двух следующих примерах, дорогим студентам предлагается убедиться самостоятельно, возможно, используя правила вычисления определителей), а среди миноров первого порядка, то есть среди элементов матрицы, есть не равные нулю.
Пример 3. Найти ранг матрицы
.
Решение. Минор второго порядка этой матрицы
, в все миноры третьего порядка этой матрицы равны нулю. Следовательно, ранг данной матрицы равен двум.
Пример 4. Найти ранг матрицы
.
Решение. Ранг данной матрицы равен 3, так как единственный минор третьего порядка этой матрицы равен 3.
Отыскание ранга матрицы способом элементарных преобразований (методом Гаусса)
Уже на примере 1 видно, что задача определения ранга матрицы способом окаймляющих миноров требует вычисления большого числа определителей. Существует, однако, способ, позволяющий свести объём вычислений к минимуму. Этот способ основан на использовании элементарных преобразований матриц и ещё называется также методом Гаусса.
Под элементарными преобразованиями матрицы понимаются следующие операции:
1) умножение какой-либо строки или какого либо столбца матрицы на число, отличное от нуля;
2) прибавление к элементам какой-либо строки или какого-либо столбца матрицы соответствующих элементов другой строки или столбца, умноженных на одно и то же число;
3) перемена местами двух строк или столбцов матрицы;
4) удаление «нулевых» строк, то есть таких, все элементы которых равны нулю;
5) удаление всех пропорциональных строк, кроме одной.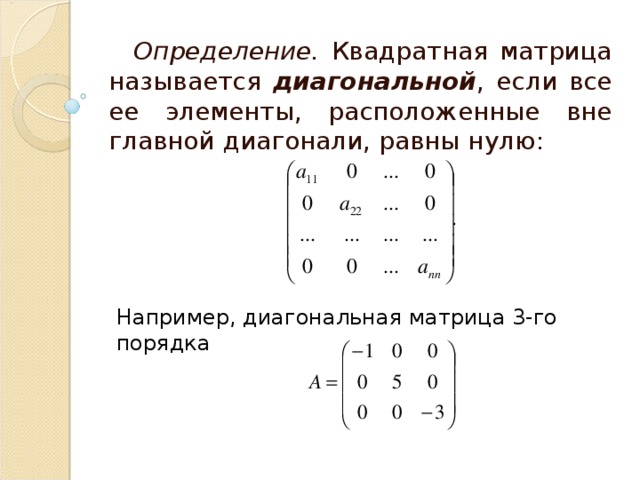
Теорема. При элементарном преобразовании ранг матрицы не меняется. Другими словами, если мы элементарными преобразованиями от матрицы A перешли к матрице B , то
.
Используя эту теорему, отправляясь от любой матрицы A всегда можно прийти к такой матрице B , вычисление ранга которой не представляет затруднений. Для этого следует добиться, чтобы матрица B была трапециевидной.
Тогда ранг полученной матрицы будет равен числу строк в ней кроме строк, полностью состоящих из нулей.
Пример 5. Найти ранг матрицы
.
Решение. Подвергнем эту матрицу следующим преобразованиям. Ко второй строке прибавим третью, умноженную на — 2, а затем к третьей строке прибывам первую, умноженную на 2, и, наконец, из четвёртой вычтем первую. После этих трёх последовательно выполненных преобразований получим матрицу
.
Вычитая из четвёртой строки третью, а затем переставив местами вторую и третью строки, получаем матрицу
.
Получили трапециевидную матрицу. Ранг полученной матрицы равен трём (r=3), так как после вычёркивания последней строки, полностью состоящей из нулей, в ней останется три строки.
Желающие могут проверить это решение способом окаймляющих миноров (минор третьего порядка, находящийся в левом верхнем углу, не равен нулю, а все миноры четвёртого порядка равны нулю).
Найти ранг матрицы самостоятельно, а затем посмотреть решение
Пример 6. Найти ранг матрицы
.
Пример 7. Найти ранг матрицы
.
В данной статье пойдет речь о таком понятии, как ранг матрицы и необходимых дополнительных понятиях. Мы приведем примеры и доказательства нахождения ранга матрицы, а также расскажем, что такое минор матрицы, и почему он так важен.
Минор матрицы
Чтобы понять, что такое ранг матрицы, необходимо разобраться с таким понятием, как минор матрицы.
Минор k-ого порядка матрицы — определитель квадратной матрицы порядка k×k, которая составлена из элементов матрицы А, находящихся в заранее выбранных k-строках и k-столбцах, при этом сохраняется положение элементов матрицы А.
Проще говоря, если в матрице А вычеркнуть (p-k) строк и (n-k) столбцов, а из тех элементов, которые остались, составить матрицу, сохраняя расположение элементов матрицы А, то определитель полученной матрицы и есть минор порядка k матрицы А.
Из примера следует, что миноры первого порядка матрицы А и есть сами элементы матрицы.
Можно привести несколько примеров миноров 2-ого порядка. Выберем две строки и два столбца. Например, 1-ая и 2 –ая строка, 3-ий и 4-ый столбец.
При таком выборе элементов минором второго порядка будет — 1 3 0 2 = ( — 1 ) × 2 — 3 × 0 = — 2
Другим минором 2-го порядка матрицы А является 0 0 1 1 = 0
Предоставим иллюстрации построения миноров второго порядка матрицы А:
Минор 3-го порядка получается, если вычеркнуть третий столбец матрицы А:
0 0 3 1 1 2 — 1 — 4 0 = 0 × 1 × 0 + 0 × 2 × ( — 1 ) + 3 × 1 × ( — 4 ) — 3 × 1 × ( — 1 ) — 0 × 1 × 0 — 0 × 2 × ( — 4 ) = — 9
Иллюстрация, как получается минор 3-го порядка матрицы А:
Для данной матрицы миноров выше 3-го порядка не существует, потому что
k ≤ m i n ( p , n ) = m i n ( 3 , 4 ) = 3
Сколько существует миноров k-ого порядка для матрицы А порядка p×n?
Число миноров вычисляют по следующей формуле:
C p k × C n k , г д е С p k = p ! k ! ( p — k ) ! и C n k = n ! k ! ( n — k ) ! — число сочетаний из p по k, из n по k соответственно.
После того, как мы определились, что такое миноры матрицы А, можно переходить к определению ранга матрицы А.
Ранг матрицы: методы нахождения
Ранг матрицы — наивысший порядок матрицы, отличный от нуля.
Из определения ранга матрицы и минора матрицы становиться понятно, что ранг нулевой матрицы равен нулю, а ранг ненулевой матрицы отличен от нуля.
Нахождение ранга матрицы по определению
Метод перебора миноров — метод, основанный на определении ранга матрицы.
Алгоритм действий способом перебора миноров:
Необходимо найти ранг матрицы А порядка p×n. При наличии хотя бы одного элемента, отличного от нуля, то ранг матрицы как минимум равен единице (т.к. есть минор 1-го порядка, который не равен нулю).
Далее следует перебор миноров 2-го порядка. Если все миноры 2-го порядка равны нулю, то ранг равен единице. При существовании хотя бы одного не равного нулю минора 2-го порядка, необходимо перейти к перебору миноров 3-го порядка, а ранг матрицы, в таком случае, будет равен минимум двум.
Аналогичным образом поступим с рангом 3-го порядка: если все миноры матрицы равняются нулю, то ранг будет равен двум. При наличии хотя бы одного ненулевого минора 3-го порядка, то ранг матрицы равен минимум трем. И так далее, по аналогии.
Найти ранг матрицы:
А = — 1 1 — 1 — 2 0 2 2 6 0 — 4 4 3 11 1 — 7
Поскольку матрица ненулевая, то ее ранг минимум равен единице.
Минор 2-го порядка — 1 1 2 2 = ( — 1 ) × 2 — 1 × 2 = 4 отличен от нуля. Отсюда следует, что ранг матрицы А не меньше двух.
Перебираем миноры 3-го порядка: С 3 3 × С 5 3 = 1 5 ! 3 ! ( 5 — 3 ) ! = 10 штук.
— 1 1 — 1 2 2 6 4 3 11 = ( — 1 ) × 2 × 11 + 1 × 6 × 4 + ( — 1 ) × 2 × 3 — ( — 1 ) × 2 × 4 — 1 × 2 × 11 — ( — 1 ) × 6 × 3 = 0
— 1 1 — 2 2 2 0 4 3 1 = ( — 1 ) × 2 × 1 + 1 × 0 × 4 + ( — 2 ) × 2 × 3 — ( — 2 ) × 2 × 4 — 1 × 2 × 1 — ( — 1 ) × 0 × 3 = 0
— 1 — 1 — 2 2 6 0 4 11 1 = ( — 1 ) × 6 × 1 + ( — 1 ) × 0 × 4 + ( — 2 ) × 2 × 11 — ( — 2 ) × 6 × 4 — ( — 1 ) × 2 × 1 — ( — 1 ) × 0 × 11 = 0
— 1 1 — 2 2 2 0 4 3 1 = ( — 1 ) × 2 × 1 + 1 × 0 × 4 + ( — 2 ) × 2 × 3 — ( — 2 ) × 2 × 4 — 1 × 2 × 1 — ( — 1 ) × 0 × 3 = 0
— 1 — 1 0 2 6 — 4 4 11 — 7 = ( — 1 ) × 6 × ( — 7 ) + ( — 1 ) × ( — 4 ) × 4 + 0 × 2 × 11 — 0 × 6 × 4 — ( — 1 ) × 2 × ( — 7 ) — ( — 1 ) × ( — 4 ) × 11 = 0
1 — 1 0 2 6 — 4 3 11 — 7 = 1 × 6 × ( — 7 ) + ( — 1 ) × ( — 4 ) × 3 + 0 × 2 × 11 — 0 × 6 × 3 — ( — 1 ) × 2 × ( — 7 ) — 1 × ( — 4 ) × 11 = 0
1 — 2 0 2 0 — 4 3 1 — 7 = 1 × 0 × ( — 7 ) + ( — 2 ) × ( — 4 ) × 3 + 0 × 2 × 1 — 0 × 0 × 3 — ( — 2 ) × 2 × ( — 7 ) — 1 × ( — 4 ) × 1 = 0
— 1 — 2 0 6 0 — 4 11 1 — 7 = ( — 1 ) × 0 × ( — 7 ) + ( — 2 ) × ( — 4 ) × 11 + 0 × 6 × 1 — 0 × 0 × 11 — ( — 2 ) × 6 × ( — 7 ) — ( — 1 ) × ( — 4 ) × 1 = 0
Миноры 3-го порядка равны нулю, поэтому ранг матрицы равен двум.
Нахождение ранга матрицы методом окаймляющих миноров
Метод окаймляющих миноров — метод, который позволяет получить результат при меньшей вычислительной работе.
Окаймляющий минор — минор M o k ( k + 1 ) -го порядка матрицы А, который окаймляет минор M порядка k матрицы А, если матрица, которая соответствует минору M o k , «содержит» матрицу, которая соответствует минору М.
Проще говоря, матрица, которая соответствует окаймляемому минору М, получается из матрицы, соответствующей окаймляющему минору M o k , вычеркиванием элементов одной строки и одного столбца.
Найти ранг матрицы:
А = 1 2 0 — 1 3 — 2 0 3 7 1 3 4 — 2 1 1 0 0 3 6 5
Для нахождения ранга берем минор 2-го порядка М = 2 — 1 4 1
Записываем все окаймляющие миноры:
1 2 — 1 — 2 0 7 3 4 1 , 2 0 — 1 0 3 7 4 — 2 1 , 2 — 1 3 0 7 1 4 1 1 , 1 2 — 1 3 4 1 0 0 6 , 2 0 — 1 4 — 2 1 0 3 6 , 2 — 1 3 4 1 1 0 6 5 .
Чтобы обосновать метод окаймляющих миноров, приведем теорему, формулировка которой не требует доказательной базы.
Если все миноры, окаймляющие минор k-ого порядка матрицы А порядка p на n, равны нулю, то все миноры порядка (k+1) матрицы А равна нулю.
Чтобы найти ранг матрицы, необязательно перебирать все миноры, достаточно посмотреть на окаймляющие.
Если окаймляющие миноры равняются нулю, то ранг матрицы нулевой. Если существует хотя бы один минор, который не равен нулю, то рассматриваем окаймляющие миноры.
Если все они равны нулю, то Rank(A) равняется двум. При наличии хотя бы одного ненулевого окаймляющего минора, то приступаем к рассматриванию его окаймляющих миноров. И так далее, аналогичным образом.
Найти ранг матрицы методом окаймляющих миноров
А = 2 1 0 — 1 3 4 2 1 0 — 1 2 1 1 1 — 4 0 0 2 4 — 14
Поскольку элемент а 11 матрицы А не равен нулю, то возьмем минор 1-го порядка. Начнем искать окаймляющий минор, отличный от нуля:
2 1 4 2 = 2 × 2 — 1 × 4 = 0 2 0 4 1 = 2 × 1 — 0 × 4 = 2
Мы нашли окаймляющий минор 2-го порядка не равный нулю 2 0 4 1 .
Осуществим перебор окаймляющих миноров — (их ( 4 — 2 ) × ( 5 — 2 ) =6 штук).
2 1 0 4 2 1 2 1 1 = 0 ; 2 0 — 1 4 1 0 2 1 1 = 0 ; 2 0 3 4 1 — 1 2 1 — 4 = 0 ; 2 1 0 4 2 1 0 0 2 = 0 ; 2 0 — 1 4 1 0 0 2 4 = 0 ; 2 0 3 4 1 — 1 0 2 — 14 = 0
Нахождение ранга матрицы методом Гаусса (с помощью элементарных преобразований)
Вспомним, что представляют собой элементарные преобразования.
- путем перестановки строк (столбцов) матрицы;
- путем умножение всех элементов любой строки (столбца) матрицы на произвольное ненулевое число k;
путем прибавления к элементам какой-либо строки (столбца) элементов, которые соответствуют другой стоки (столбца) матрицы, которые умножены на произвольное число k.
Нахождение ранга матрицы методом Гаусса — метод, который основывается на теории эквивалентности матриц: если матрица В получена из матрицы А при помощи конечного числа элементарных преобразований, то Rank(A) = Rank(B).
Справедливость данного утверждения следует из определения матрицы:
- в случае перестановки строк или столбцов матрицы ее определитель меняет знак.
Если он равен нулю, то и при перестановке строк или столбцов остается равным нулю; - в случае умножения всех элементов какой-либо строки (столбца) матрицы на произвольное число k, которое не равняется нулю, определитель полученной матрицы равен определителю исходной матрицы, которая умножена на k;
Если он равен нулю, то и при перестановке строк или столбцов остается равным нулю;в случае прибавления к элементам некоторой строки или столбца матрицы соответствующих элементов другой строки или столбца, которые умножены на число k, не изменяет ее определителя.
Суть метода элементарных преобразований: привести матрицу ,чей ранг необходимо найти, к трапециевидной при помощи элементарных преобразований.
Ранг матриц такого вида достаточно просто найти. Он равен количеству строк, в которых есть хотя бы один ненулевой элемент. А поскольку ранг при проведении элементарных преобразований не изменяется, то это и будет ранг матрицы.
Проиллюстрируем этот процесс:
- для прямоугольных матриц А порядка p на n, число строк которых больше числа столбцов:
1 b 12 b 13 ⋯ b 1 n — 1 b 1 n 0 1 b 23 ⋯ b 2 n — 2 b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 b n — 1 n 0 0 0 ⋯ 0 1 0 0 0 ⋯ 0 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 0 , R a n k ( A ) = n
1 b 12 b 13 ⋯ b 1 k b 1 k + 1 ⋯ b 1 n 0 1 b 23 ⋯ b 2 k b 2 k + 1 ⋯ b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 b k k + 1 ⋯ b k n 0 0 0 ⋯ 0 0 ⋯ 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 0 ⋯ 0 , R a n k ( A ) = k
- для прямоугольных матриц А порядка p на n, число строк которых меньше числа столбцов:
1 b 12 b 13 ⋯ b 1 p b 1 p + 1 ⋯ b 1 n 0 1 b 23 ⋯ b 2 p b 2 p + 1 ⋯ b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 b p p + 1 ⋯ b p n , R a n k ( A ) = p
1 b 12 b 13 ⋯ b 1 k b 1 k + 1 ⋯ b 1 n 0 1 b 23 ⋯ b 2 k b 2 k + 1 ⋯ b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 b k k + 1 ⋯ b k n 0 0 0 ⋯ 0 0 ⋯ 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 0 ⋯ 0
- для квадратных матриц А порядка n на n:
1 b 12 b 13 ⋯ b 1 n — 1 b 1 n 0 1 b 23 ⋯ b 2 n — 1 b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 b n — 1 n 0 0 0 ⋯ 0 1 , R a n k ( A ) = n
1 b 12 b 13 ⋯ b 1 k b 1 k + 1 ⋯ b 1 n 0 1 b 23 ⋯ b 2 k b 2 k + 1 ⋯ b 2 n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 1 b k k + 1 ⋯ b k n 0 0 0 ⋯ 0 0 ⋯ 0 ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ 0 0 0 ⋯ 0 0 ⋯ 0 , R a n k ( A ) = k , k n
Найти ранг матрицы А при помощи элементарных преобразований:
А = 2 1 — 2 6 3 0 0 — 1 1 — 1 2 — 7 5 — 2 4 — 15 7 2 — 4 11
Поскольку элемент а 11 отличен от нуля, то необходимо умножить элементы первой строки матрицы А на 1 а 11 = 1 2 :
А = 2 1 — 2 6 3 0 0 — 1 1 — 1 2 — 7 5 — 2 4 — 15 7 2 — 4 11
Прибавляем к элементам 2-ой строки соответствующие элементы 1-ой строки, которые умножены на (-3).
К элементам 3-ей строки прибавляем элементы 1-ой строки, которые умножены на (-1):
А ( 1 ) = 1 1 2 — 1 3 3 0 0 — 1 1 — 1 2 — 7 5 — 2 4 — 15 7 2 — 4 11
А ( 2 ) = = 1 1 2 — 1 3 3 + 1 ( — 3 ) 0 + 1 2 ( — 3 ) 0 + ( — 1 ) ( — 3 ) — 1 + 3 ( — 3 ) 1 + 1 ( — 3 ) — 1 + 1 2 ( — 3 ) 2 + ( — 1 ) ( — 1 ) — 7 + 3 ( — 1 ) 5 + 1 ( — 5 ) — 2 + 1 2 ( — 5 ) 4 + ( — 1 ) ( — 5 ) — 15 + 3 ( — 5 ) 7 + 1 ( — 7 ) 2 + 1 2 ( — 7 ) — 4 + ( — 1 ) ( — 7 ) 11 + 3 ( — 7 ) =
= 1 1 2 — 1 3 0 — 3 2 3 — 10 0 — 3 2 3 — 10 0 — 9 2 9 — 30 0 — 3 2 3 — 10
Элемент а 22 ( 2 ) отличен от нуля, поэтому мы умножаем элементы 2-ой строки матрицы А на А ( 2 ) н а 1 а 22 ( 2 ) = — 2 3 :
А ( 3 ) = 1 1 2 — 1 3 0 1 — 2 20 3 0 — 3 2 3 — 10 0 — 9 2 9 — 30 0 — 3 2 3 — 10
А ( 4 ) = 1 1 2 — 1 3 0 1 — 2 20 3 0 — 3 2 + 1 3 2 3 + ( — 2 ) 3 2 — 10 + 20 3 × 3 2 0 — 9 2 + 1 9 2 9 + ( — 2 ) 9 2 — 30 + 20 3 × 9 2 0 — 3 2 + 1 3 2 3 + ( — 2 ) 3 2 — 10 + 20 3 × 3 2 = = 1 1 2 — 1 3 0 1 — 2 20 3 0 0 0 0 0 0 0 0 0 0 0 0
- К элементам 3-ей строки полученной матрицы прибавляем соответствующие элементы 2-ой строки ,которые умножены на 3 2 ;
- к элементам 4-ой строки — элементы 2-ой строки, которые умножены на 9 2 ;
- к элементам 5-ой строки — элементы 2-ой строки, которые умножены на 3 2 .
Все элементы строк равны нулю. Таким образом, при помощи элементарных преобразований ,мы привели матрицу к трапецеидальному виду, откуда видно, что R a n k ( A ( 4 ) ) = 2 . Отсюда следует, что ранг исходной матрицы также равен двум.
Если проводить элементарные преобразования, то не допускаются приближенные значения!
Линейная алгебра 6: Ранг, Базис, Размерность | by adam dhalla
Это продолжение моей серии по линейной алгебре, которую следует рассматривать как дополнительный ресурс при изучении класса 18.06 Гилберта Стрэнга на OCW. Это можно близко сопоставить с Лекциями 9 и 10 в его серии.
Сегодня мы коснемся темы, которую уже видели, но официально не обсуждали. Возможно, это самая важная идея, которую следует охватить в этой части линейной алгебры, и это ранг матрицы. Две другие идеи, основа и измерение, как бы выпадают из этого.
Ранг
Проще говоря, ранг матрицы представляет количество независимых столбцов в матрице.
Это число, р, очень важно при рассмотрении матрицы. Возьмем ранг этой матрицы.
Ранг этой матрицы равен 2. Это потому, что у нас есть два независимых столбца , столбцы 1 и 2. Третий столбец кратен первому столбцу и поэтому зависим. Просто, r = 2.
Но из этого числа можно получить больше. Если бы мы смотрели на это в контексте системы уравнений и решали либо b, либо 0, мы бы искали свободные столбцы против опорных столбцов.
Затем мы понимаем, что количество опорных столбцов равно рангу, поскольку опорные столбцы = независимые столбцы.
Кроме того, мы также можем получить количество свободных столбцов в матрице (m, n), выполнив n — r, что даст нам количество свободных столбцов.
Пока:
- r количество независимых/сводных столбцов, а также сводных переменных
- n — r количество зависимых/свободных столбцов, а также свободных переменных
И в расширении,
- n — r — количество векторов, определяющих нулевое пространство
- r — количество векторов, определяющих пространство столбцов
Можно сказать, что ранг матрицы — это ее «истинный размер».
Даже если у вас есть матрица m = 100, n = 200, вы можете описать то же пространство столбцов всего 100 столбцами вместо 200. Это подводит нас к обсуждению базиса.
Базис
Базис — это наименьший из возможных наборов векторов, который можно использовать для описания векторного пространства. Векторное пространство имеет бесконечное количество оснований. Например, все следующие являются базисными векторами R².
Другими словами, если мы возьмем комбинации любых из этих пар базисных векторов, мы можем получить любой вектор в R². Эти базисные векторы всегда полностью независимы.
Важно:
- Все векторы в базисе линейно зависимы
- Векторы должны охватывать рассматриваемое пространство.
В расширении базис не имеет ненулевой записи в нулевом пространстве.
Глядя на матрицу, которая зависит от , мы можем проанализировать матрицу, чтобы найти меньшее количество базисных векторов, которые охватывают то же пространство, что и матрица.
Это зависимая матрица. Последний столбец кратен первому столбцу. Колонны охватывают двухмерную плоскость в трех измерениях. Мы можем описать двумерную плоскость всего двумя векторами, так как же мы можем свести эти три вектора к двум?
Ну, мы можем просто взять два независимых столбца. Первый и второй. Эти два вектора охватывают одно и то же пространство.
Эти векторы являются одним из многих базисных векторов для матрицы, с которой мы имели дело.
Измерение
Измерение, возможно, самое простое понятие — это количество измерений, которые охватывают столбцы или векторы. Размерность приведенной выше матрицы равна 2, поскольку размер столбца матрицы равен 2.
Как правило, ранг = размерность или r = размер.
Это будет график того, как может выглядеть наше пространство столбцов для A. Это 2D-плоскость, продиктованная нашими двумя 2D-базисами, независимыми векторами, помещенными в среду R³.
Полный ранг; r = m = n
Часто мы имеем дело со случаем полного ранга: где r = m = n.
В этом случае наша матрица, очевидно, квадратная, поскольку требует, чтобы m = n. Кроме того, это означает, что каждый столбец (и каждая строка) независимы.
Это означает, что наша квадратная матрица «полного ранга» — это основа собственного пространства, поскольку это самый маленький и «эффективный» способ описания векторного подпространства. Невозможно более кратко описать пространство столбцов матрицы, чем столбцы матрицы полного ранга.
Все вышеперечисленные матрицы являются матрицами полного ранга. Их строки и столбцы независимы. У них нет записей в нулевом пространстве, кроме нулевого вектора {0}.
При выполнении исключения на матрице A полного ранга у вас не возникнет проблем с получением опорной точки в каждой строке и столбце.
Если вы выполните исключение Гаусса-Жордана на матрице полного ранга (приведите ее к сокращенной ступенчатой форме), вы получите в результате единичную матрицу I, так как удаление всех нулей выше и ниже опорных не оставит пробелов и делений каждая строка по оси каждой строки будет возвращать 1 по диагонали.
Полноранговые матрицы также обратимы, так как столбцы могут объединяться для создания каждого столбца единичной матрицы.
При рассмотрении в контексте линейной системы уравнений это означает, что существует одно единственное решение любой линейной системы где A — матрица полного ранга. Это связано с тем, что столбцы A могут комбинироваться одним уникальным способом для формирования любого ответа b, , поскольку любой b находится в пространстве столбца A.
Полный рейтинг столбца; r = n, r
< mПри полном ранге столбцов ваша матрица состоит из полностью независимых столбцов (поскольку r = n или по одной опорной точке в каждом столбце). Разница в том, что у вас есть зависимые строки, или оставшиеся строки.
В системе уравнений это означает, что у нас столько же опорных точек, сколько и неизвестных, но больше уравнений, чем нам нужно. Давайте посмотрим на матрицу A с полным рангом столбца в контексте системы уравнений.
Нижние две строки матрицы сокращаются, так как они кратны первым двум. Третья строка — это первая строка x 2, а четвертая строка — это вторая строка x 2.
Таким образом, при сокращении мы получаем эквивалентную систему Ux = c.
Повороты выделены. Забыл поставить «2» в конце последней буквы «б» в слове «в».Теперь Ux = c можно решить только , если выполняются два условия разрешимости. только если b3–2b_1 = 0 и b4–2b_2 = 0, это может быть правдой.
Но если эти два условия верны, у нас остается единственный ответ для решения нашей системы. Вот почему мы говорим, что с матрицей r = n (полный ранг столбца) имеет либо 0, либо 1 решение. 0, если одно или несколько наших условий разрешимости ложны, и 1, если все условия разрешимости истинны. Скорее всего, если бы мы случайно выбрали
Наконец, если мы преобразуем любую матрицу рангов с полным столбцом в эшелонированную форму с сокращенными строками, мы получим тождество с нулями, прикрепленными внизу.
Это имеет смысл. Взяв только две верхние строки нашей исходной матрицы A, мы получим полностью систему полного ранга, с опорными точками во всех столбцах и строках. Как только мы уменьшим верхнюю часть строки, мы должны ожидать идентичности. Нижние строки полностью избыточны (зависимы) и будут аннулированы путем исключения.
Таким образом, можно ожидать, что любая полная матрица рангов столбца в сокращенной форме строки-эшелона будет выглядеть как (I, 0) при перестановке таким образом.
Матрицы рангов полных столбцов не содержат ненулевых элементов в пустом пространстве, так как нет свободных столбцов или переменных, поскольку, хотя могут быть зависимые строки, зависимых столбцов нет.
Ранг полного ряда; r = m, r
< n Полный ранг строки — это когда наше уравнение имеет такое же количество опорных точек, как и строки. В этом сценарии наша матрица имеет свободные переменные и свободные столбцы и, таким образом, содержит элементы в пустом пространстве.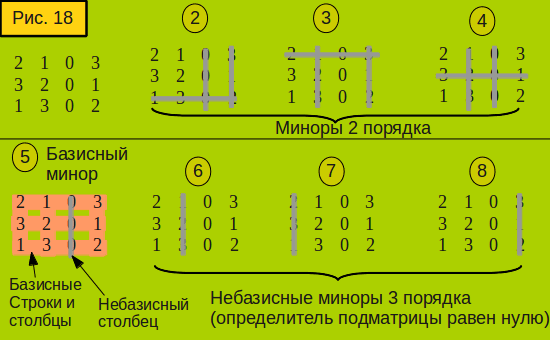
Давайте посмотрим на уравнение с полным рангом строки:
Второй столбец — это первый столбец x 2, а четвертый столбец — это второй столбец x 2. Таким образом, при сокращении мы можем получить обновленное уравнение Ux = c.
Трудно понять выводы, которые мы делаем отсюда, поэтому давайте еще больше упростим до простейшей возможной системы, Rx = d, используя исключение Гаусса-Жордана, чтобы получить уменьшенную матрицу формы строки-эшелона.
Я не буду продолжать с правой частью, так как это выйдет из-под контроля с делением и всем этим, но как только мы закончим, наша матрица будет выглядеть так:
Знакомый? Похоже на полную матрицу ранжирования столбцов, но сбоку.
В этом сценарии мы получаем несколько интересных результатов. Хотя я не скопировал правую часть, так как было бы слишком утомительно добавлять какую-либо реальную ценность, мы можем видеть возможные решения.
Так как наш ответ будет двухмерным, и у нас есть базисные векторы для описания двумерного пространства в первых двух столбцах нашей матрицы, мы можем решить любой ответ b.
Но что более важно, у нас также есть «свободные столбцы» нулей. Они умножают наши «свободные переменные» z и t . Таким образом, мы можем установить z и t в любые константы, которые нам нравятся, так как они будут умножаться на 0. Отсюда мы можем сказать, что у нас есть бесконечное количество решений для любого ответа.
В отличие от последних двух случаев, если наше n > r, у нас есть по крайней мере n-r свободных переменных и свободных столбцов, и, в расширении, по крайней мере n-r векторов в пустом пространстве.
Здесь, поскольку у нас есть зависимые/свободные столбцы, у нас будет два вектора в пустом пространстве. Чтобы выяснить это, мы можем использовать методы, описанные в части 4 этой серии, которая находит точные ответы на Ax = 0. должен быть квадратным
В матрицах с полным столбцом рангов, или r = n < m
- Существует 1 или 0 решений для каждого b
- поверх нулевой матрицы
- В нулевом пространстве нет ничего
В матрицах полного ранга строки, или r = m < n
- Существует бесконечное количество решений для каждых b.
- Эшелонная форма с редуцированной строкой R представляет собой тождество I слева от нулевой матрицы.
- В пустом пространстве есть n-r специальных решений.
Исходя из этого, мы можем с уверенностью сказать, что, используя только m, r и n, мы можем точно предсказать, сколько ответов мы должны ожидать, если таковые имеются.
Адам Дхалла учится в старшей школе из Ванкувера, Британская Колумбия, в настоящее время участвует в STEM и бизнес-стипендии TKS . Он очарован внешним миром и в настоящее время изучает новые технологии для защиты окружающей среды.
Подпишитесь на его I nstagram и его LinkedIn . Чтобы получить больше подобного контента, подпишитесь на его информационный бюллетень здесь.
Линейная независимость и ранг — линейная алгебра
Все ресурсы по линейной алгебре
4 диагностических теста 108 практических тестов Вопрос дня Карточки Учитесь по концепции
← Предыдущая 1 2 3 4 Следующая →
Справка по линейной алгебре » Операции и свойства » Линейная независимость и ранг
Определите, являются ли следующие векторы в матричной форме линейно независимыми.
Возможные ответы:
Векторы линейно независимы
Векторы не линейно независимы
Правильный ответ:
Векторы линейно независимы0015
Объяснение:
Чтобы выяснить, является ли матрица независимой, нам нужно привести матрицу к сокращенному ступенчатому виду.
Если мы получаем матрицу идентичности, то матрица линейно независима.
Поскольку мы получили матрицу идентичности, мы знаем, что матрица линейно независима.
Сообщить об ошибке
Найдите ранг следующей матрицы.
Возможные ответы:
Правильный ответ:
Объяснение:
Нам нужно привести матрицу к сокращенному ступенчатому виду, а затем посчитать все не все нулевые строки.
9002 .
Сообщить об ошибке
Вычислить ранг следующей матрицы Объяснение:
Нам нужно привести матрицу в сокращенный ступенчатый вид, а затем посчитать все ненулевые строки.
Поскольку имеется только 1 ненулевая строка, ранг равен 1.
Сообщить об ошибке
Определите, является ли следующая матрица линейно независимой или нет.
Возможные ответы:
Линейно зависимые
Линейно независимые
Правильный ответ:
Линейно зависимые
Объяснение:
Поскольку матрица , мы можем просто взять определитель. Если определитель не равен нулю, то он линейно независим. В противном случае он линейно зависим.
Поскольку определитель равен нулю, матрица линейно зависима.
Сообщить об ошибке
Если матрица A представляет собой матрицу 5×8 с двумерным пустым пространством, каков ранг матрицы A?
Возможные ответы:
Ни один из других ответов.
Правильный ответ:
Объяснение:
Учитывая, что ранг A + размерное нулевое пространство A = общее количество столбцов, мы можем определить ранг A = общее количество столбцов-мерное нулевое пространство A. Используя информацию, указанную в вопросе, мы можем решить для ранга A :
Сообщить об ошибке
Если матрица A представляет собой матрицу 10 x 12 с трехмерным нулевым пространством, каков ее ранг?
Возможные ответы:
Ни один из других ответов
Правильный ответ: 30142555 Объяснение:
Учитывая, что ранг A + размерное нулевое пространство A = общее количество столбцов, мы можем определить ранг A = общее количество столбцов-мерное нулевое пространство A.
Используя информацию, указанную в вопросе, мы можем решить для ранга A :
Сообщить об ошибке
Представляет ли следующая строка редуцированной ступенчатой формы матрицы линейно независимое множество?
Возможные ответы:
Недостаточно информации
Да
Нет
Правильный ответ: 91314 Да8
5
Объяснение:
Набор должен быть линейно независимым, поскольку нет строк, состоящих только из нулей. Есть столбцы со всеми нулями, но столбцы не говорят нам, является ли набор линейно независимым или нет.
Сообщить об ошибке
Может ли векторное пространство размерности 5 иметь линейно независимый набор из 3 векторов?
Возможные ответы:
Нет
Недостаточно информации
Да
Правильный ответ:
Да
Объяснение:
Размерность векторного пространства — это максимальное число векторов в линейно независимом множестве.
Возможно иметь линейно независимые множества с меньшим количеством векторов, чем размерность.
Таким образом, для этого примера можно иметь линейные независимые множества с
1 вектором, 2 векторами или 3 векторами, вплоть до 5 векторов.
Сообщить об ошибке
Рассмотрим набор из 3 векторов из трехмерного векторного пространства.
Является ли множество линейно независимым?
Возможные ответы:
Нет
Да
Недостаточно информации
Правильный ответ:
Недостаточно информации
Объяснение:
Это зависит от того, какие векторы.
Например, если
Тогда набор линейно независим.
Однако если бы векторы были
, то множество было бы линейно зависимым.
Сообщить об ошибке
Рассмотрим набор из 3 векторов из двумерного векторного пространства.
Является ли множество линейно независимым?
Возможные ответы:
Да
Нет
Недостаточно информации
Правильный ответ:
Нет
Пояснение:
Поскольку размерность пространства равна 2, линейно независимое множество может иметь не более двух векторов. Поскольку рассматриваемый набор имеет 3 и 3>2, набор должен быть линейно зависимым.
Сообщить об ошибке
← Предыдущий 1 2 3 4 Следующий →
Уведомление об авторских правах
Все ресурсы по линейной алгебре
4 Диагностические тесты 108 практических тестов Вопрос дня Карточки Учиться по концепции
Ранг матрицы
Каталин Дэвид
Ранг матрицы с m строк и n столбцов есть число r со следующими свойствами:
- r меньше или равно наименьшему числу из m и n.
- r равно порядку наибольшего минора матрицы, отличного от 0.
- Мы выбираем элемент матрицы, который не равен 0.
- Мы вычисляем миноры порядка 2, которые содержат этот элемент, пока не найдем минор, который не равен 0.
- Если каждый минор второго порядка равен 0, то ранг матрицы равен 1.
- Если существует минор 2-го порядка, отличный от 0, мы вычисляем минор 3-го порядка, который содержит предыдущий минор, пока не найдем минор, не равный 0.
- Если каждый младший порядок 3 равен 0, то ранг матрицы равен 2.
- Если существует минор 3-го порядка, отличный от 0, мы вычисляем минор 4-го порядка, пока не найдем минор, отличный от 0.
- Продолжаем так до тех пор, пока не получим миноры порядка, равного наименьшему числу из числа строк и числа столбцов.
Пример 42
$A=\begin{pmatrix}
1 и 2 и 4\\
3 и 6 и 5
\end{pmatrix}$
Матрица имеет 2 строки и 3 столбца, поэтому максимально возможное значение ее ранга равно 2.
Мы выбираем любой элемент, который не равен 0.
$\begin{pmatrix} \цвет{красный}{1}, 2 и 4\\ 3 и 6 и 5 \end{pmatrix}$
Мы формируем минор порядка 2, содержащий 1.
$\begin{pmatrix}
\цвет{красный}{1} и \цвет{красный}{2} и 4\\
\цвет{красный}{3} и \цвет{красный}{6} и 5
\end{pmatrix}$
Вычисляем этот минор.
$\begin{vmatrix}
\цвет{красный}{1} и \цвет{красный}{2}\\
\цвет{красный}{3} и \цвет{красный}{6}
\end{vmatrix}=6 — 6 = 0$
Мы формируем еще один минор порядка 3, содержащий 1. $A=\begin{pmatrix} \цвет{синий}{1} & 2 & \цвет{синий}{4}\\ \color{синий} {3} & 6 & \color{синий} {5} \end{pmatrix}$
Вычисляем этот минор.
$\begin{vmatrix}
\цвет{синий}{1} и \цвет{синий}{4}\\
\цвет{синий}{3} и \цвет{синий}{5}
\end{vmatrix}= 5 — 12 = -7 \neq 0.$
Ранг 2.
Пример 43
$B=\begin{pmatrix}
1 и 1 и 1\\
1 и 1 и 1\\
1 и 1 и 1\\
\end{pmatrix}$
Мы выбираем элемент, который не равен 0.
$\begin{pmatrix}
1 и 1 и 1\\
1 и 1 и 1\\
1 и \цвет{красный}{1} и 1
\end{pmatrix}$
Мы вычисляем миноры второго порядка, содержащие этот элемент.
$\begin{pmatrix}
1 и 1 и 1\\
\цвет{красный}{1} и \цвет{красный}{1} и 1\\
\цвет{красный}{1} и \цвет{красный}{1} и 1
\end{pmatrix}$
$\begin{vmatrix} \цвет{красный}{1} и \цвет{красный}{1} \\ \цвет{красный}{1} и \цвет{красный}{1} \end{vmatrix}=0 $ (потому что у него две равные строки)
Каждый второй минор порядка 2 равен 0, потому что он такой же, как и другие. В этом случае ранг матрицы равен 1.
Пример 44
$B=\begin{pmatrix}
3 и 8 и 2\\
2 и 1 и 1\\
5 и 3 и 4\\
7 и 4 и 5
\end{pmatrix}$
Матрица имеет 4 строки и 3 столбца, поэтому максимально возможное значение ее ранга равно 3.
Мы выбираем элемент, который не равен 0.
$\begin{pmatrix}
3 и 8 и 2\\
2 и 1 и 1\\
5 и 3 и \цвет{красный}{4}\\
7 и 4 и 5
\end{pmatrix}$
Мы вычисляем минор порядка 2, содержащий 4.
$ \begin{pmatrix}
3 и 8 и 2\\
2 & \color{red}{1} & \color{red}{1}\\
5 & \цвет{красный}{3} & \цвет{красный}{4}\\
7 и 4 и 5
\end{pmatrix}$
$\begin{vmatrix} \цвет{красный}{1} и \цвет{красный}{1}\\ \цвет{красный}{3} и \цвет{красный}{4}\\ \end{vmatrix} = 4 — 3 = 1$
Мы формируем минор порядка 3, содержащий предыдущий минор.
$\begin{pmatrix}
3 и 8 и 2\\
\color{red}{2} & \color{red}{1} & \color{red}{1}\\
\цвет{красный}{5} и \цвет{красный}{3} и \цвет{красный}{4}\\
\color{red}{7} & \color{red}{4} & \color{red}{5}
\end{pmatrix}$
Вычисляем этот минор.
$\begin{pmatrix}
\color{red}{2} & \color{red}{1} & \color{red}{1}\\
\цвет{красный}{5} и \цвет{красный}{3} и \цвет{красный}{4}\\
\color{red}{7} & \color{red}{4} & \color{red}{5}
\end{pmatrix}=0 $, потому что $ R_{1}+R_{2}=R_{3}$
Мы вычисляем еще один минор порядка 3, содержащий предыдущий минор.
$\begin{pmatrix}
\цвет{синий}{3} и \цвет{синий}{8} и \цвет{синий}{2}\\
\цвет{синий}{2} и \цвет{синий}{1} и \цвет{синий}{1}\\
\цвет{синий}{5} и \цвет{синий}{3} и \цвет{синий}{4}\\
7 и 4 и 5
\end{pmatrix}$
$\begin{vmatrix}
\цвет{синий}{3} и \цвет{синий}{8} и \цвет{синий}{2}\\
\цвет{синий}{2} и \цвет{синий}{1} и \цвет{синий}{1}\\
\цвет{синий}{5} и \цвет{синий}{3} и \цвет{синий}{4}
\end{vmatrix} =$ $12 + 12 +40 -10 -9-64 =-19 \neq 0 $
Ранг матрицы равен 3.
Пример 45
$D=\begin{pmatrix}
1 и 5 и 1 и 6\\
2 и 3 и 2 и 5\\
6 и 1 и 6 и 7
\end{pmatrix}$
D — матрица с 3 строками и 4 столбцами, поэтому максимально возможное значение ранга равно 3.
Мы выбираем элемент, который не равен 0.
$\begin{pmatrix}
1 и \цвет{красный}{5}, 1 и 6\\
2 и 3 и 2 и 5\\
6 и 1 и 6 и 7
\end{pmatrix}$
Мы формируем минор порядка 2, содержащий 5.
$\begin{pmatrix}
\color{red}{1} & \color{red}{5} & 1 & 6\\
\color{red}{2} & \color{red}{3} & 2 & 5\\
6 и 1 и 6 и 7
\end{pmatrix}$
$\begin{vmatrix} 1 и 5\\ 2 и 3 \end{vmatrix}= 3 — 10 = -7 \neq 0$
Мы формируем минор порядка 3, содержащий предыдущий минор.
$\begin{pmatrix}
\color{red}{1} & \color{red}{5} & \color{red}{1} & 6\\
\color{red}{2} & \color{red}{3} & \color{red}{2} & 5\\
\color{red}{6} & \color{red}{1} & \color{red}{6} & 7
\end{pmatrix}$
$\begin{vmatrix} \color{red}{1} & \color{red}{5} & \color{red}{1}\\ \color{red}{2} & \color{red}{3} & \color{red}{2}\\ \color{red}{6} & \color{red}{1} & \color{red}{6} \end{vmatrix} = 0 $ (потому что у него 2 одинаковых столбца)
В этом случае мы формируем еще один минор порядка 3, содержащий минор порядка 2, который не равен 0.