Как разложить квадратный трёхчлен на множители? Разложение квадратных трехчленов на множители: примеры и формулы.
Изучение многих физических и геометрических
закономерностей часто приводит к решению задач с
параметрами. Некоторые ВУЗы также включают в
экзаменационные билеты уравнения, неравенства и
их системы, которые часто бывают весьма сложными
и требующими нестандартного подхода к решению. В
школе же этот один из наиболее трудных разделов
школьного курса алгебры рассматривается только
на немногочисленных факультативных или
предметных курсах.
На мой взгляд, функционально-графический метод
является удобным и быстрым способом решения
уравнений с параметром.
Как известно, в отношении уравнений с
параметрами встречаются две постановки задачи.
- Решить уравнение (для каждого значения параметра найти все решения уравнения).
- Найти все значения параметра, при каждом из которых решения уравнения удовлетворяют заданным условиям.
В данной работе рассматривается и
исследуется задача второго типа применительно к
корням квадратного трехчлена, нахождение
которых сводится к решению квадратного
уравнения.
Автор надеется, что данная работа поможет учителям при разработке уроков и при подготовке учащихся к ЕГЭ.
1. Что такое параметр
Выражение вида aх 2 + bх + c в
школьном курсе алгебры называют квадратным
трехчленом относительно х, где a, b, c –
заданные действительные числа, причем, a =/= 0.
Значения переменной х, при которых выражение
обращается в нуль, называют корнями квадратного
трехчлена. Для нахождения корней квадратного
трехчлена, необходимо решить квадратное
уравнение aх 2 + bх + c = 0.
Вспомним из школьного курса алгебры основные
уравнения aх + b = 0;
aх2 + bх + c = 0. При поиске их корней, значения
переменных a, b, c, входящих в уравнение
считаются фиксированными и заданными. Сами
переменные называют параметром. Поскольку, в
школьных учебниках нет определения параметра, я
предлагаю взять за основу следующий его
простейший вариант.
Определение. Параметром называется
независимая переменная, значение которой в
задаче считается заданным фиксированным или
произвольным действительным числом, или числом,
принадлежащим заранее оговоренному множеству.
2. Основные типы и методы решения задач с параметрами
Среди задач с параметрами можно выделить следующие основные типы задач.
- Уравнения, которые необходимо решить либо для любого значения параметра (параметров), либо для значений параметра, принадлежащих заранее оговоренному множеству. Например. Решить уравнения: aх = 1, (a – 2)х = a 2 – 4.
- Уравнения, для которых требуется определить
количество решений в зависимости от значения
параметра (параметров). Например. При каких
значениях параметра a уравнение 4
- Уравнения, для которых при искомых значениях параметра множество решений удовлетворяет заданным условиям в области определения.
Например, найти значения параметра, при которых
корни уравнения (a – 2)х 2 – 2aх
+ a + 3 = 0 положительные.
Основные способы решения задач с параметром:
аналитический и графический.
Аналитический – это способ так называемого прямого решения, повторяющего стандартные процедуры нахождения ответа в задачах без параметра. Рассмотрим пример такой задачи.
Задача № 1
При каких значениях параметра а уравнение х 2 – 2aх + a 2 – 1 = 0 имеет два различных корня, принадлежащих промежутку (1; 5)?
Решение
х 2 –
2aх + a 2 – 1 = 0.По условию задачи уравнение должно иметь два различных корня, а это возможно лишь при условии: Д > 0.
Имеем: Д = 4a 2 – 2(а 2 – 1) = 4. Как видим дискриминант не зависит от а, следовательно, уравнение имеет два различных корня при любых значениях параметра а. Найдем корни уравнения: х 1 = а + 1, х 2 = а – 1
Корни уравнения должны принадлежать промежутку (1; 5), т.е.
Итак, при 2 а
Ответ: 2 а
Такой подход к решению задач рассматриваемого
типа возможен и рационален в тех случаях, когда
дискриминант квадратного уравнения «хороший»,
т. е. является точным квадратом какого либо числа
или выражения или корни уравнения можно найти по
теореме обратной т.Виета. Тогда, и корни не
представляют собой иррациональных выражений. В
противном случае решения задач такого типа
сопряжено с достаточно сложными процедурами с
технической точки зрения. Да и решение
иррациональных неравенств требует от ученика
новых знаний.
е. является точным квадратом какого либо числа
или выражения или корни уравнения можно найти по
теореме обратной т.Виета. Тогда, и корни не
представляют собой иррациональных выражений. В
противном случае решения задач такого типа
сопряжено с достаточно сложными процедурами с
технической точки зрения. Да и решение
иррациональных неравенств требует от ученика
новых знаний.
Графический – это способ, при котором
используют графики в координатной плоскости (х;у)
или (х;а). Наглядность и красота такого способа
решения помогает найти быстрый путь решения
задачи. Решим задачу № 1 графическим способом.
Как известно из курса алгебры корни квадратного
уравнения (квадратного трехчлена) являются
нулями соответствующей квадратичной функции: У = х 2
– 2ах + а 2 – 1. Графиком функции
является парабола, ветви направлены вверх
(первый коэффициент равен 1). Геометрическая
модель, отвечающая всем требованиям задачи,
выглядит так.
Теперь осталось «зафиксировать»
параболу в нужном положении необходимыми
условиями.
- Так как парабола имеет две точки пересечения с осью х , то Д > 0.
- Вершина параболы находится между вертикальными
прямыми х = 1 и х = 5, следовательно
абсцисса вершины параболы х о принадлежит
промежутку (1; 5), т.е.
1 х о - Замечаем, что у (1) > 0, у (5) > 0.
Итак, переходя от геометрической модели задачи к аналитической, получаем систему неравенств.
Ответ: 2 а
Как видно из примера, графический способ
решения задач рассматриваемого типа возможен в
случае, когда корни «нехорошие», т.е. содержат
параметр под знаком радикала (в этом случае
дискриминант уравнения не является полным
квадратом).
Во втором способе решения мы работали с
коэффициентами уравнения и областью значения
функции у = х 2 – 2ах + а 2
– 1.
Такой способ решения нельзя назвать только
графическим, т.к. здесь приходится решать систему
неравенств. Скорее этот способ комбинированный:
функционально-графический.
Разложение квадратных трехчленов на множители относится к школьным заданиям, с которыми рано или поздно сталкивается каждый. Как его выполнить? Какова формула разложения квадратного трехчлена на множители? Разберемся пошагово с помощью примеров.
Общая формула
Разложение квадратных трехчленов на множители осуществляется решением квадратного уравнения. Это несложная задача, которую можно решить несколькими методами — нахождением дискриминанта, при помощи теоремы Виета, существует и графический способ решения. Первые два способа изучаются в средней школе.
Общая формула выглядит так: lx 2 +kx+n=l(x-x 1)(x-x 2) (1)
Алгоритм выполнения задания
Для того чтобы выполнить разложение квадратных трехчленов на множители, нужно знать теорему Вита, иметь под рукой программу для решения, уметь находить решение графически или искать корни уравнения второй степени через формулу дискриминанта. Если дан квадратный трехчлен и его надо разложить на множители, алгоритм действий такой:
1) Приравнять исходное выражение к нулю, чтобы получить уравнение.
2) Привести подобные слагаемые (если есть такая необходимость).
3) Найти корни любым известным способом. Графический метод лучше применять в случае, если заранее известно, что корни — целые и небольшие числа. Нужно помнить, что количество корней равно максимальной степени уравнения, то есть у квадратного уравнения корней два.
4) Подставить значение х в выражение (1).
5) Записать разложение квадратных трехчленов на множители.
Примеры
Окончательно понять, как выполняется это задание, позволяет практика. Иллюстрируют разложение на множители квадратного трехчлена примеры:
необходимо разложить выражение:
Прибегнем к нашему алгоритму:
1) х 2 -17х+32=0
2) подобные слагаемые сведены
3) по формуле Виета найти корни для этого примера сложно, потому лучше воспользоваться выражением для дискриминанта:
D=289-128=161=(12,69) 2
4) Подставим найденные нами корни в основную формулу для разложения:
(х-2,155) * (х-14,845)
5) Тогда ответ будет таким:
х 2 -17х+32=(х-2,155)(х-14,845)
Проверим, соответствуют ли найденные дискриминантом решения формулам Виета:
14,845 . 2,155=32
2,155=32
Для данных корней применяется теорема Виета, они были найдены правильно, а значит полученное нами разложение на множители тоже правильно.
Аналогично разложим 12х 2 +7х-6.
x 1 =-7+(337) 1/2
x 2 =-7-(337) 1/2
В предыдущем случае решения были нецелыми, но действительными числами, найти которые легко, имея перед собой калькулятор. Теперь рассмотрим более сложный пример, в котором корни будут комплексными: разложить на множители х 2 +4х+9. По формуле Виета корни найти не получится, и дискриминант отрицательный. Корни будут на комплексной плоскости.
D=-20
Исходя из этого, получаем нтересующие нас корни -4+2i*5 1/2 и -4-2i * 5 1/2 , поскольку (-20) 1/2 =2i*5 1/2 .
Получаем искомое разложение, подставив корни в общую формулу.
Еще один пример: нужно разложить на множители выражение 23х 2 -14х+7.
Имеем уравнение 23х 2 -14х+7 =0
D=-448
Значит, корни 14+21,166i и 14-21,166i. Ответ будет такой:
23х 2 -14х+7
=23(х-14-21,166i
)*(х-14+21,166i
).
Приведем пример, решить который можно без помощи дискриминанта.
Пусть нужно разложить квадратное уравнение х 2 -32х+255. Очевидно, его можно решить и дискриминантом, однако быстрее в данном случае подобрать корни.
x 1 =15
x 2 =17
Значит х 2 -32х+255 =(х-15)(х-17).
Найдем сумму и произведение корней квадратного уравнения. Используя формулы (59.8) для корней приведенного уравнения, получим
(первое равенство очевидно, второе получается после несложного вычисления, которое читатель проведет самостоятельно; удобно использовать формулу для произведения суммы двух чисел на их разность).
Доказана следующая
Теорема Виета. Сумма корней приведенного квадратного уравнения равна второму коэффициенту с противоположным знаком, а их произведение равно свободному члену.
В случае неприведенного квадратного уравнения следует в формулы (60.1) подставить выражения формулы (60.1) примут вид
Пример 1. Составить квадратное уравнение по его корням:
Решение, а) Находим уравнение имеет вид
Пример 2. Найти сумму квадратов корней уравнения не решая самого уравнения.
Найти сумму квадратов корней уравнения не решая самого уравнения.
Решение. Известны сумма и произведение корней. Представим сумму квадратов корней в виде
и получим
Из формул Виета легко получить формулу
выражающую правило разложения квадратного трехчлена на множители.
В самом деле, напишем формулы (60.2) в виде
Теперь имеем
что и требовалось получить.
Вышеуказанный вывод формул Виета знаком читателю из курса алгебры средней школы. Можно дать другой вывод, использующий теорему Безу и разложение многочлена на множители (пп. 51, 52).
Пусть корни уравнения тогда по общему правилу (52.2) трехчлен в левой части уравнения разлагается на множители:
Раскрывая скобки в правой части этого тождественного равенства, получим
и сравнение коэффициентов при одинаковых степенях даст нам формулы Виета (60.1).
Преимущество этого вывода состоит в том, что его можно применить и к уравнениям высших степеней с тем, чтобы получить выражения коэффициентов уравнения через его корни (не находя самих корней!). Например, если корни приведенного кубического уравнения
Например, если корни приведенного кубического уравнения
суть то согласно равенству (52.2) находим
(в нашем случае Раскрыв скобки в правой части равенства и собрав коэффициенты при различных степенях получим
В разных практических деятельностях человека вроде физики, инженерии, архитектуры и других точных наук, часто встречаются задачи с математическими моделями, какой являются уравнения, имеющие переменную (x) в иной степени. Именно они помогают учёным в изучении внешней среды и её использовании.
Квадратные уравнения
Квадратным называется равенство вида ax² + bc + c = 0, где x является переменой, a (первый коэффициент), b (второй) и c (свободный) — это действительные числа, которые должны приводить в условии задачи. Нужно помнить при решении, что a ≠ 0. Как уже понятно, оно очень отличается от линейного уравнения, его все изучали в младших классах школы.
Чтобы понять, как решать квадратные уравнения, нужно представить футбольное поле, длина которого на 10 метров больше его ширины, а площадь равна 380 квадратных метров. Нужно найти ширину футбольного поля.
Нужно найти ширину футбольного поля.
Пусть переменная x — это определённая ширина, тогда её длина будет (х +10) метров. Потом x * (x + 10) = 380, ведь дана площадь 380 квадратных метров в условии задачи, то есть x² + 10x — 380 равно нулю. Здесь а = 1, b = 10, а c = -375 Это был один из примеров квадратных равенств.
Различают два вида уравнений:
- Приведённые — это случай, когда в квадратном равенстве a = 1.
- Непривёденные если a ≠ 1.
При этом x² — приведённое, а уже при 5x² оно станет непривёденным.
Понятие дискриминант
Существует определенная система решения таких уравнений. Чтобы найти чётный корень такого равенства, достаточно запомнить приведённую ниже формулу квадратного уравнения.
Буква D — это дискриминант. Звучит сложно, но не стоит пугаться, ведь с латинского языка слово переводится, как разность. Он равен: D = b² — 4 ac. Следуя этому, можно записать, что (2ax + b)² = D. Есть определенные правила, как надо решать дискриминант:
Пример первого способа нахождения через формулу дискриминанта квадратного уравнения и правильным разложением чисел:
- 9х²-6х+1=0;
- D = (-6)² — 4 × 9 ×1 = 0;
- D эквивалентен нулю;
- x = -6/2×9 = 1/3.

Как пример можно показать уравнивание: -8x² = 0, у которого b и с равны нулю. Или 2x² — 3 = 0, b ничему не равно. В уравнении -7x² + 4x² = 0 c эквивалентно нулю.
Разные квадратные уравнения
Помимо обычных дискриминантов, есть и половинные. Их ищут для равенств, у которых второй коэффициент — это чётное число, по формуле: D1 = 4 k² — 4 ac = 4 (k² — ac). Чтобы делать меньше ошибок, лучше использовать формулу со скобками. Благодаря этому в ответе получается четверть дискриминанта.
Квадратные равенства с комплексными переменными почти ничем не отличаются от плоскости действительных чисел и тем, которые должны проходить в восьмых классах. И чтобы без проблем их решать, нужно использовать формулу.
Если в квадратном равенстве хотя бы один из общих коэффициентов квадратного трехчлена B или C равен нулю, то такое равенство называют неполным.
Следовательно оно бывает только трёх видов:
Из истории математики
Неполные квадратные равенства и некоторые виды неизвестных корней вавилонские математики умели решить и создать ещё 4000 лет тому назад. Такие произведения в Древней Греции решали тем же способом. Люди, обладающие знаниями точных наук, решали некоторые квадратные уравнения геометрическими приёмами.
Такие произведения в Древней Греции решали тем же способом. Люди, обладающие знаниями точных наук, решали некоторые квадратные уравнения геометрическими приёмами.
Это показал древнегреческий учёный Диофант . Много внимания таким уравнениям также выделял арабский математик Мухаммед Альхорезми. Он нашёл как решать уравнение видов: ах²=bx; ax²=c; ax²+bx=c; ax²+c=bx; bc+c=ax² и получил положительные корни.
Формулы, что связывают между собой корни равенства и его коэффициенты, впервые нашёл французский математик Франсуа Виет в 1591 году. Его заключения в современных обозначениях имеют вид: (а + b)x — x² = 0.
После быстрой публикации работы нидерландского математика Жераром, а также француза Декарда и англичанина Ньютона равенство корней квадратного уравнения приобрело современный вид.
Сейчас речь идёт о теореме Виета , на которую нужно обратить внимание. Её так называют из-за известного французского математика Франсуа Виета, которым и было открыто это свойство. Сумма корней сведенного квадратного равенства равно другому коэффициенту, взятому с отрицательным знаком, а произведение корней — свободному члену. Часто его записывают в таком виде: х² + px + q эквивалентно нулю.
Сумма корней сведенного квадратного равенства равно другому коэффициенту, взятому с отрицательным знаком, а произведение корней — свободному члену. Часто его записывают в таком виде: х² + px + q эквивалентно нулю.
Теорему можно сформулировать так .
Если х1 и х2 — корни сведенного квадратного равенства х²+px+q эквивалентны нулю, то х1 + х2 = -p; x1 * x2 = q. Поскольку a ≠ 0, поделим две части уравнения на а и получается современная формула: x² — b/a * x + c/a равно нулю.
Памятка по теме «Квадратное уравнение»
Квадратное уравнение
Квадратное уравнение – это уравнение вида ax2 + bx + c = 0, где x – переменная, a, b и c – некоторые числа, причем a ≠ 0.
Пример квадратного уравнения:
3×2 + 2x – 5 = 0.
Здесь а = 3, b = 2, c = –5.
Числа a, b и c – коэффициенты квадратного уравнения.
Число a называют первым коэффициентом, число b – вторым коэффициентом, а число c – свободным членом.
Приведенное квадратное уравнение.
Квадратное уравнение, в котором первый коэффициент равен 1, называют приведенным квадратным уравнением.
Примеры приведенного квадратного уравнения:
x2 + 10x – 11 = 0
x2 – x – 12 = 0
x2 – 6х + 5 = 0
здесь коэффициент при x2 равен 1 (просто единица во всех трех уравнениях опущена).
Неполное квадратное уравнение.
Если в квадратном уравнении ax2 + bx + c = 0 хотя бы один из коэффициентов b или c равен нулю, то такое уравнение называют неполным квадратным уравнением.
Примеры неполного квадратного уравнения:
-2×2 + 18 = 0
здесь есть коэффициент а, который равен -2, есть коэффициент c, равный 18, а коэффициента b нет – он равен нулю.
x2 – 5x = 0
здесь а = 1, b = -5, c = 0 (поэтому коэффициент c в уравнении отсутствует).
Как решать квадратные уравнения.
Чтобы решить квадратное уравнение, надо совершить всего два действия:
1) Найти дискриминант D по формуле:
D = b2 – 4ac.
Если дискриминант – отрицательное число, то квадратное уравнение не имеет решения, вычисления прекращаются. Если D ≥ 0, то
2) Найти корни квадратного уравнения по формуле:
–b ± √D
х1,2 = —————.
2а
Пример: Решить квадратное уравнение 3х2 – 5х – 2 = 0.
Решение:
Сначала определимся с коэффициентами нашего уравнения:
а = 3, b = –5, c = –2.
Вычисляем дискриминант:
D = b2 – 4ac = (–5)2 – 4 · 3 · (–2) = 25 + 24 = 49.
D > 0, значит, уравнение имеет смысл, а значит, можем продолжить.
Находим корни квадратного уравнения:
–b + √D 5 + 7 12
х1 = ————— = ———— = —— = 2
2а 6 6
–b – √D 5 – 7 2 1
х2 = ————— = ———— = – —— = – ——.
2а 6 6 3
1
Ответ: х1 = 2, х2 = – ——.
3
Формулы корней квадратного уравнения. Дискриминант.
Формула №1:
—b ± √D
x = ————, где D = b2 – 4ac.
2a
Латинской буквой D обозначают дискриминант.
Дискриминант — это выражение, от которого зависит число корней данного уравнения.
Если D < 0, то уравнение не имеет корней.
Если D = 0, то уравнение имеет один корень.
Если D > 0, то уравнение имеет два корня.
Пример. Решим уравнение 12×2 + 7x + 1 = 0.
Сначала вычислим дискриминант.
Мы видим, что а = 12, b = 7, c = 1.
Итак:
D = b2 – 4ac = 72 – 4 · 12 · 1 = 49 – 48 = 1.
D > 0. Значит, уравнение имеет корни (причем два корня), а значит, можно вычислять дальше.
Чтобы найти корни, применим формулу корней квадратного уравнения:
-b ± √D -7 ± √1 -7 ± 1
x = ———— = ———— = ————
2a 24 24
Находим оба значения x:
-7 + 1 -6 -1 1
x1 = ——— = —— = — = – —
24 24 4 4
-7 – 1 -8 -1 1
x2 = ——— = —— = — = – — .
24 24 3 3
1 1
Ответ: x1 = – —, x2 = – —
4 3
Формула №2.
Из формулы №1 можно получить другую формулу, которой удобно пользоваться в случаях, когда второй коэффициент – четное число. В этом случае раскладываем его на множители, один из которых – множитель 2. То есть второй коэффициент представляем в виде 2k, где k – это половина изначально заданного числа. Тогда удобно пользоваться формулой:
—k ± √D1
x = ————, где D1 = k2 – ac
a
Пример. Решим уравнение 5×2 – 16x + 3 = 0.
Записываем -16x в виде 2 · (-8x). Тогда k = -8, a = 5, c = 3. Мы уже можем найти дискриминант D1:
D1 = k2 – ac = (-8)2 – 5 · 3 = 64 – 15 = 49.
Теперь находим оба значения x:
-k ± √D1 — (-8) ± √49 8 ± 7
x = ———— = ————— = ———
a 5 5
Отсюда:
8 + 7 15
x1 = ——— = — = 3
5 5
8 – 7 1
x2 = ——— = — = 0,2
5 5
Ответ: x1 = 3; x2 = 0,2. n} \)
n} \)
7) a n > 1, если a > 1, n > 0
8) a n 1, n
9) a n > a m , если 0
В практике часто используются функции вида y = a x , где a — заданное положительное число, x — переменная. Такие функции называют показательными . Это название объясняется тем, что аргументом показательной функции является показатель степени, а основанием степени — заданное число.
Определение. Показательной функцией называется функция вида y = a x , где а — заданное число, a > 0, \(a \neq 1\)
Показательная функция обладает следующими свойствами
1) Область определения показательной функции — множество всех действительных чисел.
Это свойство следует из того, что степень a x где a > 0, определена для всех действительных чисел x.
2) Множество значений показательной функции — множество всех положительных чисел.
Чтобы убедиться в этом, нужно показать, что уравнение a x = b, где а > 0, \(a \neq 1\), не имеет корней,
если \(b \leq 0\), и имеет корень при любом b > 0.
3) Показательная функция у = a x является возрастающей на множестве всех действительных чисел, если a > 1, и убывающей, если 0 Это следует из свойств степени (8) и (9)
Построим графики показательных функций у = a x при a > 0 и при 0 Использовав рассмотренные свойства отметим, что график функции у = a x при a > 0 проходит через точку (0; 1) и
расположен выше оси Oх.
Если х 0.
Если х > 0 и |х| увеличивается, то график быстро поднимается вверх.
График функции у = a x при 0
Если х > 0 и увеличивается, то график быстро приближается к оси Ох (не пересекая её). Таким образом, ось Ох является
горизонтальной асимптотой графика.
Если х
Показательные уравнения
Рассмотрим несколько примеров показательных уравнений, т.е. уравнений, в которых неизвестное содержится в показателе степени.
Решение показательных уравнений часто сводится к решению уравнения a x = a b где а > 0, \(a \neq 1\),
х — неизвестное. Это уравнение решается с помощью свойства степени: степени с одинаковым основанием а > 0, \(a \neq 1\) равны
тогда и только тогда, когда равны их показатели. {x-2} = 1 \)
{x-2} = 1 \)
x — 2 = 0
Ответ х = 2
Решить уравнение 3 |х — 1| = 3 |х + 3|
Так как 3 > 0, \(3 \neq 1\), то исходное уравнение равносильно уравнению |x-1| = |x+3|
Возводя это уравнение в квадрат, получаем его следствие (х — 1) 2 = (х + 3) 2 , откуда
х 2 — 2х + 1 = х 2 + 6х + 9, 8x = -8, х = -1
Проверка показывает, что х = -1 — корень исходного уравнения.
Ответ х = -1
5х2х1
Применяются при межприборном монтаже электрических установок, работающих при переменном напряжении до 750 В. Важным преимуществом является возможность работы в условиях усиленных электромагнитных влияний, например при эксплуатации в промышленных пожаро или взрывоопасных зонах.
Характеристики кабеля
5х2х1- Климатическое исполнение УХЛ категорий размещения 2-5 по ГОСТ 15150.
- Диапазон температур эксплуатации от -50 до +70°
- Относительная влажность воздуха при температуре до 35°С 98%
- Прокладка кабелей без предварительного прогрева возможна при температуре не ниже -15°С
- Минимальный радиус изгиба при монтаже, не менее 5 наружных диаметров
- Испытательное переменное напряжение частотой 50 Гц (продолжительность испытания — 1 мин) 2 кВ
- Электрическое сопротивление изоляции жил, на 1 км длины и при температуре 20°С не менее 5 МОм
- Кабели не распространяют горение при одиночной прокладке
- Кабели с индексом “нг” и “LS” не распространяют горение при пучковой прокладке по ГОСТ 12176.

- Строительная длина кабелей МКЭКШВ, МКЭКШВнг, не менее 100 м
- Гарантийный срок эксплуатации 3 года с даты ввода кабелей в эксплуатацию
- Срок службы 15 лет
Конструкция кабеля
5х2х1- Токопроводящая жила — изготовлена из меди, многопроволочная, класс по ГОСТ 22483.
- Изоляция — сделана из ПВХ (поливинилхлоридного пластиката).
- Скрученная пара — присутствует в кабелях парной скрутки.
- Экран пар — изготавляется из медных проволок, диаметр которых не превышает 0,2 мм. Присутствует как оплетка плотностью не менее 65%. Под медной оплеткой находится лента ПЭТ-Э. Любые пары жил, отмеченные индексом “Э” в обязательном порядке имеют индивидуальный экран — оплетку — для кабелей МКЭКШВ(э), под которой находится лента ПЭТ- Э.
- Сердечник — представляет из себя одиночные жилы. В некоторых случаях скрученные в сердечник пары.
- Поясная изоляция — изготавливается из специальной полиэтилентерефталатной ленты.

- Экран — (исключая кабели с индексом “Э”) — оплетка, плотностью 65% из медной проволки диаметром не более 0,25 мм.
- Оболочка промежуточная — из ПВХ пластика толщиной не менее 0,8 мм.
- Броня — изготавливается из стальных оцинкованных проволок или в виде оплетки. Диаметр стальных оцинкованных проволок (0,25÷0,5 мм).
- Защитный шланг — их поливинилхлоридного пластиката.
- Для кабелей типа МКЭКШВнг-LS — защитный шланг из ПВХ пластиката с низким дымовыделением (low smoke).
| Сечение \ Марка | Номинальное напряжение, кВ | Диаметр, мм | Вес, кг | Цена в рублях | |
|---|---|---|---|---|---|
| 1х2х0,5 | 0.75 | 9.7 | 136.6 | по запросу | |
| 1х2х0,75 | 0.75 | 10.7 | 163.4 | 27.07 | |
| 1х2х1 | 0.75 | 11 | 174.3 | 29. 92 92 | |
| 2х2х0,75 | 0.75 | 14.9 | 265.9 | 45.59 | |
| 2х2х1 | 0.75 | 15.5 | 287.6 | 52.25 | |
| 2х2х1,5 | 0.75 | 17.2 | 378.9 | 69.18 | |
| 4х2х0,75 | 0.75 | 16.6 | 338.5 | 73.38 |
Отсюда, Разлад и «Бунт Вещей» передаётся по каналу №6 в Структуру С2, которую они формируют, точнее деформируют, превращая Наполнение Системы в разность наблюдаемую в формулах (7).
Этот канал №6 Отношений, Вещественный и Энергетический, влияет на сложение Структуры С2.
Однако, в Элементах (Х) содержатся не только Вещи, но и Люди, а это значит, что в Системе функционирует ещё один контур – Мировоззренческий, в начале которого находятся Отношения ∑О2.
∑О2 – это не Отношения Вещей, а Информация об этих Отношениях .
1. Это представления, взгляды и ощущения, возникающие у людей по поводу Отношения Вещей.
Это представления, взгляды и ощущения, возникающие у людей по поводу Отношения Вещей.
2. Здесь же рождаются представления, взгляды и ощущения по поводу Отношений между самими Людьми.
3. Здесь же возникают «Психологические» Отношения.
Отношения ∑О2 содержат три вида Отношений :
1. Информация об Отношениях между Вещами.
2. Информация об Отношениях между Людьми.
3. Информация об Отношении Людей к своему Прошлому.
Эта сумма выступает как общая Информация которая передаётся по каналу №5 в ячейку С1, где оседает, образуя базис Мировоззрения (С1) Системы.
Основой Мировоззрения С1 – являются Отношения ∑О2.
Они не выступают, как что-то законченное, оформленное и определённое, ведь, первоначально это только представления, взгляды и ощущения.
Это сумма трёх видов Отношений неоднородных слагаемых
(не арифметическая и не алгебраическая).
Эти разнородные слагаемые не поддаются суммированию – выражению количественной Меры.
Внимание! Узловой пункт понимания Системы.
Это, нахождение Ответа на два Вопроса :
I. Какова Количественная Мера Иррациональной суммы разнородных слагаемых?
Это вопрос об определённости Мировоззрения…
II. Как из сырого материала ощущений и взглядов складывается определённое Мировоззрение (С1)?
4.1.6.3. О Мере Иррациональной суммы .
Отношения: Вещи – Люди – Человек .
1. Отношения между Вещами – естественный фактор (е).
2. Отношения между Людьми, складывающиеся в процессе Производства, – политический фактор (п1).
3. Отношение Человека к самому себе (и к своему прошлому) – психологический фактор (п2).
Эти три фактора являются предметом нашего пристального исследования: е, п1, п2.
Всё это Информация, но имеющая разные (исходные предметы) источники, содержания и сущности.
е – знание Человеком естественных (природных) процессов;
п1 – политические Отношения, проявляющиеся в Человеке, как ощущения, представления и эмоции;
п2 – психологические Отношения, обусловленные в Человеке его историческим и генетическим прошлым (национальным и профессиональным складом характера).
Из трёх факторов предметом науки пока является только фактор естественный — е.
Два остальных фактора политический п1 и психологический п2 знанием ещё не стали, представляют собой сырой материал…
Вопрос: Как можно сочетать, представлять в совокупности все три разнородных фактора вместе, если они несопоставимы между собой?
1. При Промышленной фазе Капиталистической формации , Вещи, Люди и прошлое Человека, всё оценивалось одной Мерой – СТОИМОСТЬЮ, (формула 1).
Э = е + п1 + п2 … формула (8),
Э – экономический фактор, имеющий Количественную Меру.
Отношения ∑О2 – приводятся к Экономическому фактору (Э), имеющему Количественную определённость.
2. При Финансовой фазе Капиталистической формации , из Экономического (Э) выделился Политический фактор (п1), (формула 2).
3. Затем, при Информационной фазе Капиталистической формации , психологический фактор (п2), (формула 3).
Что же случилось с суммой (е + п1 + п2) в действительности?
Эта сумма – есть основа Мировоззрения .
— Мировоззрение становится Рациональным , если эта сумма соответствует Э = е + п1 = п2;
С выделением и отделением факторов политического п1 и психологического п2 представления затуманились и потеряли ясность утратив общую Меру к вещам и явлениям;
— «Нелепое» мировоззрение : С точки зрения формы всё осталось неизменным и ясным, фактор Э выступает как Количественная определённость.
В Действительности, за спиной этой «определённости» развёртывается невидимая и неведомая жизнь.
Формальное пояснение «невидимки».
Невидимка схоронилась в комплексном числе: (a +- bi), где
а – действительная часть комплексного числа
b — недействительная часть комплексного числа
i – мнимая часть комплексного числа…
Комплексное число – имеет определённую форму, а содержание – неопределённое, которое нельзя выразить Количественно.
АОС : Во всех «Управляемых» (и «Регулируемых») Системах идёт ожесточённая и непрерывная борьба за признание: Какой из трёх факторов: е, п1,п2, в комплексном числе
(a +- bi), признать действительным, какой не действительным, и какой мнимым???
Формальная таблица 9. Мировоззрения.
Мировоззрения.
В зависимости от «развитости» факторов: е, п1 и п2 — Мировоззрение Системы приобретает соответствующие Содержание и Сущность.
Если «развитость» факторов убывает в направлении: е > п1 > п2, то Система приобретает Мировоззрение (I) = (е +- п1i)….
……………………………………….
Если…: п2 > п1 > е, то Мировоззрение (IV) = (п2 +- п1i).
Всё сказано о «невидимки» с формальной стороны.
«Организация» затрагивает Интимнейшие стороны жизни Системы.
Чтобы закончить вопрос: «О Мере и основе Мировоззрения?» и перейти к следующему: «Как складывается Мировоззрение?» необходимо приоткрыть завесу над наиболее характерными Секретами.
Экономический фактор (Э) лежит в основе Рационального Мировоззрения .
На смену Рациональному Мировоззрению, пришло Иррациональное – нелепое Мировоззрение.
В познании и понимании окружающего Мира оно нелепо и беспомощно.
В смысле воздействия на этот мир, эта нелепость становится реальной силой, которую надо учитывать.
Мировоззрение выступает, как инструмент познания и как боевое оружие.
Как инструмент познания – иррациональное Мировоззрение (все формулы таблицы 9) – беспомощно и бессильно, но как боевое оружие – беспощадная, коварная и хитрая сила.
Сила Иррационального Мировоззрения заключена в его Секретах.
Если снять Секреты, то оно станет бессильным и ненужным, как познавательный инструмент и как боевое оружие.
Если познавательный инструмент основан на комплексном числе (a +- bi) не имеющем Количественной Меры, то это плохой инструмент.
Без знания Секретов Иррационального Мировоззрения нельзя понять «Управляемые» Системы, а значит и «Организованные».
ТОС: Мировоззрение «Организованных» Систем основывается на естественном (природном) факторе –(е), — никакой «комплексности», «иррациональности» и «мнимости» — в этих Системах нет.
АОС: Мировоззрение «Управляемых» Систем основывается на «комплексности», «иррациональности» и «мнимости».
В таблице 9, представлены все возможные варианты Иррационального Мировоззрения.
Как познавательный инструмент, таблица 9 содержит в себе большие искажения.
Это «кривое зеркало» искажающее представление о Действительности.
Всё это пассивная сторона дела.
Активная сторона Мировоззрения обнаруживается, когда Система вступает во взаимодействие (обмен) с внешней средой.
Здесь то и проявляется сила Секретов и Иррациональности.
Обмен превращается в антагонистическую борьбу, становясь неэквивалентным.
4.1.6.4. Примеры .
Пример I . В обмен вступили две Системы с разным мировоззрением:
Система I (е +- п1i) и Система II (е +- п2i), согласно теории комплексного числа этот обмен выразится, как сумма: 2е + (п1 +- п2)i, — Действительность же иная.
Мировоззрение: I (е +- п1i) – соответствует Промышленному (производственному) Капитализму.
Мировоззрение: II (е +- п2i) – соответствует Финансовому (судному) Капитализму…
После долгой борьбы между этими двумя Капиталами произошло их слияние, и образовался Финансовый Капитал.
Из слияния их суммы: 2е + (п1 +- п2)i, возникло два новых образования:
III (п1 +- еi) и IV (п1 +- п2i).
Лондон, Париж, Нью-Йорк и гамбургская Вена жили и боролись под знаменем I (е +- п1i) и
II (е +- п2i) Мировоззрения.
Германия (Бисмарк) стал под знамёна III (п1 +- еi) и IV (п1 +- п2i) Мировоззрения в момент объединения единого государства с Пруссией во главе.
Мировоззрение III (п1 +- еi) — с большой силой проявилось в Рурских хищниках.
Мировоззрение IV (п1 +- п2i) – мировоззрение прусских юнкеров и германской военщины, как наследие от предков, псов рыцарей.
Политический (п1) фактор насилия играл ведущую роль в жизни и Мировоззрении господствующих классов Германии.
И, это наложило отпечаток на Мировоззрение угнетённых слоёв и всего немецкого народа.
На передний план выдвинулся хищнический Капитал III (п1 +- еi), так зародился Финансовый капитализм в Германии.
Он выполз из навозной кучи: 2е + (п1 +- п2)i, — вполне естественно и закономерно.
В Германии уже имелось соответственное Мировоззрение, присущее исторически этой нации.
Пример II. Важность знания Секреты Мировоззрения.
Причины возникновения фашизма.
Марксисты: « … на борьбу против Капиталистов!»
Ложь, ведь Капиталисты психологически разные, как рабочие и крестьяне…
Есть два капитала: Творческий и Хищнический.
Творческий – национальный Капитал, он народен, как и все творческие силы страны.
Банковский Капитал – еврейский или иностранный (негласно управляемый евреями).
Он космополитичен и интернационален, как и еврейские демагоги задающие тон у социал-демократов и коммунистов.
Гитлер совершил переход от Экономического (е) фактора к Психологическому (п2).
«… поведу Вас к свободе и хлебу!»
Речь Гитлера – не демагогия, а оружие страшной силы, приведённое в действие.
Демагогия — болтовня, цель усыпить слушателя, когда главное и решающее уже совершается за его спиной.
Речь Гитлера была рассчитана не на усыпление, а на приведение слушателей в действие, в движение.
Гитлер пешка и червь, за его спиной стоял хищник III (п1 +- еi), который держал все нити событий в своих руках.
Даже Германская военщина IV (п1 +- п2i), и сам Гитлер не были допущены до главного Секрета.
4.1.6.5. Основные Секреты Иррационального Мировоззрения .
Первый большой Секрет.
Германия в то время, после войны 1929 – 1933 годов представляла собой Систему готовую взорваться.
Выход – это движение, куда угодно, лишь бы движение…
Кто первый укажет Системе конкретный и понятный путь, тот и поведёт систему за собой.
Гитлер, по подсказке хищника III (п1 +- еi), смог указать путь и Система пошла за ним.
Второй Секрет.
Вопрос : Почему Гитлеру удалось, а коммунистам нет, указать путь движения?
Ответ : Гитлер находился ближе к хищнику III (п1 +- еi), он знал больше сокровенных секретов хищного общества.
Социал-демократы и коммунисты Германии не видели своего главного врага хищника
III (п1 +- еi).
Рабочий класс и коммунисты не знали многих своих врагов, но также не знали, что в стане им уже известных врагов могут быть и друзья.
II (е +- п2i), Капитала – Насильника III (п1 +- еi) и просто Насильника IV (п1 +- п2i), — всё это сваливали в одну кучу, перестав понимать реальную Действительность.
Третий Секрет.
Закон Диалектического снятия.
Если Мировоззрение Производителя капиталиста выражается формулой: (е + п1i), то формула угнетённого этим Капиталистом Рабочего становится (е — п1i), — это Закон.
Если … Крупп представляет: (п1 + еi), формула Мировоззрения угнетённых им представляет: (п1 — еi).
Если немецкий генерал живёт и мыслит по формуле: (п1 + п2i), то его подчинённые солдаты и офицеры … по формуле: (п1 — п2i), — Закон.
И, всё это потому, что взаимодействие (обмен) двух подсистем в принципе становится одинаковым, разница лишь в знаке, который объясняет явление детерминации.
Каково Мировоззрение господствующих слоёв в Обществе, таково в основном и Мировоззрение угнетённых слоёв.
Иллюзии, что Мировоззрение является второстепенным фактором в борьбе Классов после Экономического фактора…
Немецкие коммунисты по своему Мировоззрению не могли опередить свой народ.
Мировоззрение К.Маркса (как и В.И. Ленина) – уникально.
Мировоззрение К.Маркса – Рационально и основывалось на Экономическом (Э) факторе.
Уникальность К.Маркса в том, что :
1. Гениально проник вовнутрь Экономического фактора (Э).
2. Снял с этого фактора Стоимостную фору.
3. Владел Диалектическим методом, и умело им пользовался.
Именно Диалектический метод в руках К.Маркса и В.И.Ленина:
Превращал Экономический (Э) фактор в Естественный (е) фактор;
Превращал Рациональное Мировоззрение в Адекватное.
Основные Задачи:
Овладеть Диалектическим Методом познания;
Отразить Адекватно Действительность;
Дать правильный Лозунг момента Элементам Системы.
Таблица 10. Группы Рационального Мировоззрения, наименования, факторы, формулы,
мир персонажей капиталистический и животный…
Иррациональное Мировоззрение создаётся в антагонистической борьбе и берёт своё начало в животном царстве.
4.1.7. Становление «Организованной» Системы .
Основная база Мировоззрения — это строительный материал для становления Мировоззрения.
1. Механизм Становления Мировоззрения.
2. Сущность Мировоззрения, при рассмотрении Отношений ∑О1.
3. Выработка Адекватного Мировоззрения и его Меры, основанной на факторе естественности – е.
Для понимания Мировоззрения необходимо иметь в поле зрения схему №6.
Становление Мировоззрения процесс длительный.
Система может прожить всю жизнь и не обрести Мировоззрение.
Рациональное и Иррациональное Мировоззрение – это определённо сложившиеся Мировоззрения.
На практике часто приходится сталкиваться с неопределённым, с не сложившимся Мировоззрением.
Система имеет одну Интуицию.
Интуиция – свидетельство об отсутствии в Системе Мировоззрения.
Интуиция, интуитивно – значит без Мировоззрения, без понимания.
Система функционирует неосознанно, без понятий на одних ощущениях.
Интуиция свойственна…
Всем молодым Системам не успевшим накопить достаточно опыта;
Многим зрелым Системам в тех случаях, когда Отношения ∑О2 не увязываются с Отношениями ∑О1, и между внутренними ощущениями образуется обрыв (несогласованность).
В таких случаях Мировоззренческий контур и контур Содержательный в Системе начинают функционировать раздельно.
В ячейки С1 накапливается большое количество несвязанных воедино ощущений (е; п1;п2) – это образует Интуицию. В ячейке воспитательных актов ∑f — накапливается «эрудиция», которая выплёскивается в виде множества беспорядочных актов f в сторону ячейки Мировоззрения С1, связь №4, и в сторону материального Наполнения ∑x, связь №2.
МКЭШвнг 5х2х1,0 — кабель монтажный экранированный с 10 медными лужеными жилами скрученными попарно, сечением 1 миллиметров квадратных, в изоляции и оболочке из поливинилхлоридного пластиката пониженной пожарной опасности, с экраном из медных проволок.
Технические характеристики кабеля МКЭШвнг 5х2х1.0
Климатическое исполнение монтажного экранированного кабеля МКЭШвнг 5*2*1,0: В, 2-5 категории размещения по ГОСТ 15150.
Минимальная температура эксплуатации монтажного экранированного кабеля МКЭШвнг 5х2х1,0 составляет -50 градусов.
Максимальная температура эксплуатации +60 градусов.
Влажность воздуха при эксплуатации монтажного экранированного кабеля МКЭШвнг 5*2*1.0 не должна превышать 98%.
Монтаж кабеля производится при температуре не ниже -15 градусов.
Минимальный радиус изгиба при монтаже кабеля МКЭШвнг(А) 5х2х1.0 равен трём наружным диаметрам.
Кабель монтажный экранированный МКЭШвнг стоек к воздействию плесневых грибов.
Монтажный экранированный кабель МКЭШвнг(А) 5*2*1,0 не распространяет горение при групповой прокладке по категории (А).
Класс пожарной опасности по ГОСТ 31565-2012: П1б.8.2.5.4
Код ОКП: 35 8112
Срок службы кабеля МКЭШвнг 5х2х1,0 не менее 15 лет.
Расшифровка маркировки МКЭШвнг(А) 5х2х1,0
М — монтажный.
К — кабель.
Э — экран из медных проволок.
Шв — оболочка из поливинилхлоридного пластиката.
нг — пониженная пожарная опасность.
(А) — индекс пожарной безопасности.
5 — количество скруток.
2 — количество жил в скрутках.
1 — сечение жил в квадратных миллиметрах.
Конструкция кабеля МКЭШвнг 5х2х1,0
1) Жила — медная многопроволочная луженая.
2) Изоляция — из поливинилхлоридного пластиката.
3) Поясная изоляция — наложена с перекрытием лента из полиэтилентерефталатной пленки.
4) Заполнение — пространство между жилами заполнено гидрофобным заполнителем.
5) Экран — в виде оплетки из медных проволок.
6) Оболочка — из ПВХ пластиката.
Применение кабеля МКЭШвнг 5х2х1,0
Кабель монтажный экранированный негорючий МКЭШвнг 5*2*1,0 предназначен для подключения к стационарным электрическим приборам, аппаратам, устройствам с переменным напряжением до 500 Вольт частоты до 400 Герц или постоянным напряжением до 750 Вольт.
Кабель МКЭШвнг 5х2х1,0 может прокладываться в помещениях, каналах, туннелях, земле (траншеях), в том числе местах подверженных воздействию блуждающих токов, возможно применение на открытом воздухе при условии защиты их от механических повреждений и от воздействия прямых солнечных лучей.
Регрессия с двумя независимыми переменными
Регрессия с двумя независимыми переменнымиПожалуйста, перейдите по этой ссылке.
Регрессия с двумя независимыми переменными
Цели
Напишите регрессионное уравнение необработанной оценки с двумя ivs в нем.
В чем разница в интерпретации весов b в простой регрессии и множественной регрессии?
Опишите R-квадрат двумя разными способами, то есть с помощью двух разных формул. Объясните формулы.
Что произойдет с весами b , если мы добавим в уравнение регрессии новые переменные, которые сильно коррелируют с переменными, уже входящими в уравнение?
Почему мы сообщаем бета-веса (стандартизированные веса b )?
Напишите уравнение регрессии с бета-весами.
Какие три фактора влияют на стандартную ошибку веса b ?
Как возможно иметь значимый R-квадрат и незначимый б гири?
Материалы
Линия регрессии
С одной независимой переменной мы можем записать уравнение регрессии как:
Где Y — наблюдаемая оценка зависимой переменной, a — точка пересечения, b — наклон, X — наблюдаемая оценка независимой переменной, а e — ошибка или невязка.
Мы можем распространить это на любое количество независимых переменных:
(3.1)
Обратите внимание, что у нас есть k независимых переменных и наклон для каждой. У нас еще есть одна ошибка и один перехват. Мы снова хотим выбрать оценки a и b так, чтобы минимизировать сумму квадратов ошибок предсказания. Уравнение прогноза:
(3.2)
Нахождение значений b сложно для k>2 независимых переменных и будет разработано после некоторой матричной алгебры. Это проще для k=2 IV, которые мы обсудим здесь.
Это проще для k=2 IV, которые мы обсудим здесь.
Для случая с одной переменной вычисление b и a было:
Для случая с двумя переменными:
и
В этот момент вы должны заметить, что все термины из случая с одной переменной появляются в случае с двумя переменными. В случае с двумя переменными другая переменная X также появляется в уравнении. Например, X 2 появляется в уравнении для b 1 9009.3 . Обратите внимание, что члены, соответствующие дисперсии обеих переменных X, встречаются на наклонах. Также обратите внимание, что член, соответствующий ковариации X1 и X2 (сумма перекрестных произведений отклонений), также появляется в формуле для наклона.
Уравнение для a с двумя независимыми переменными:
Это уравнение является прямым обобщением случая для одной независимой переменной.
Числовой пример
Предположим, мы хотим спрогнозировать эффективность работы механиков Шевроле на основе результатов теста на механические способности и результатов теста личности, который измеряет добросовестность.
Производительность работы | Мех Апт | Конск | ||||
Д | Х1 | Х2 | Х1*У | Х2*У | Х1*Х2 | |
1 | 40 | 25 | 40 | 25 | 1000 | |
2 | 45 | 20 | 90 | 40 | 900 | |
1 | 38 | 30 | 38 | 30 | 1140 | |
3 | 50 | 30 | 150 | 90 | 1500 | |
2 | 48 | 28 | 96 | 56 | 1344 | |
3 | 55 | 30 | 165 | 90 | 1650 | |
3 | 53 | 34 | 159 | 102 | 1802 | |
4 | 55 | 36 | 220 | 144 | 1980 | |
4 | 58 | 32 | 232 | 128 | 1856 | |
3 | 40 | 34 | 120 | 102 | 1360 | |
5 | 55 | 38 | 275 | 190 | 2090 | |
3 | 48 | 28 | 144 | 84 | 1344 | |
3 | 45 | 30 | 135 | 90 | 1350 | |
2 | 55 | 36 | 110 | 72 | 1980 | |
4 | 60 | 34 | 240 | 136 | 2040 | |
5 | 60 | 38 | 300 | 190 | 2280 | |
5 | 60 | 42 | 300 | 210 | 2520 | |
5 | 65 | 38 | 325 | 190 | 2470 | |
4 | 50 | 34 | 200 | 136 | 1700 | |
3 | 58 | 38 | 174 | 114 | 2204 | |
Д | Х1 | Х2 | Х1*У | Х2*У | Х1*Х2 | |
65 | 1038 | 655 | 3513 | 2219 | 34510 | Сумма |
20 | 20 | 20 | 20 | 20 | 20 | Н |
3,25 | 51,9 | 32,75 | 175,65 | 110,95 | 1725. | М |
1,25 | 7,58 | 5,24 | 84,33 | 54,73 | 474,60 | SD |
29,75 | 1091.8 | 521,75 | USS |
Мы можем собрать данные в матрицу следующим образом:
г | Х 1 | Х 2 | |
Д | 29,75 | 139,5 | 90,25 |
Х 1 | 0,77 | 1091. | 515,5 |
Х 2 | 0,72 | 0,68 | 521,75 |
Числа в приведенной выше таблице соответствуют следующим суммам квадратов, перекрестных произведений и корреляций:
г | х1 | Х 2 | |
Д | |||
Х 1 | |||
Х 2 |
Теперь мы можем вычислить коэффициенты регрессии:
Чтобы найти перехват, у нас есть:
Следовательно, наше уравнение регрессии:
Y ‘= -4. 10+.09X1+.09X2 или
10+.09X1+.09X2 или
Job Perf’ = -4.10 +.09MechApt +.09Добросовестность.
Визуальные представления регрессии
У нас есть 3 переменные, поэтому у нас есть 3 диаграммы рассеяния, которые показывают их отношения.
Поскольку мы вычислили уравнение регрессии, мы также можем просмотреть график зависимости Y’ от Y или фактического от прогнозируемого Y.
Мы можем (как бы) просмотреть график в трехмерном пространстве, где двумя предикторами являются оси X и Y, а ось Z является критерием, таким образом:
На этом графике это не очень хорошо видно, но проблему регрессии можно рассматривать как своего рода проблему поверхности отклика. Какова ожидаемая высота (Z) при каждом значении X и Y? Линейное регрессионное решение этой проблемы в этой размерности представляет собой плоскость.
R-квадрат (R 2 )
Как и в простой регрессии, зависимая переменная рассматривается как линейная часть и ошибка. В множественной регрессии с линейной частью связано более одной переменной X. Когда мы делаем множественную регрессию, мы можем вычислить долю дисперсии из-за регрессии. Эта пропорция называется R-квадрат. Мы используем заглавную букву R, чтобы показать, что это кратное R вместо одной переменной r. Мы также можем вычислить корреляцию между Y и Y’ и возвести ее в квадрат. Если мы это сделаем, мы также найдем R-квадрат.
В множественной регрессии с линейной частью связано более одной переменной X. Когда мы делаем множественную регрессию, мы можем вычислить долю дисперсии из-за регрессии. Эта пропорция называется R-квадрат. Мы используем заглавную букву R, чтобы показать, что это кратное R вместо одной переменной r. Мы также можем вычислить корреляцию между Y и Y’ и возвести ее в квадрат. Если мы это сделаем, мы также найдем R-квадрат.
Д | Х1 | Х2 | Д’ | Остаток |
2 | 45 | 20 | 1,54 | 0,46 |
1 | 38 | 30 | 1,81 | -0,81 |
3 | 50 | 30 | 2,84 | 0,16 |
2 | 48 | 28 | 2,50 | -0,50 |
3 | 55 | 30 | 3,28 | -0,28 |
3 | 53 | 34 | 3,45 | -0,45 |
4 | 55 | 36 | 3,80 | 0,20 |
4 | 58 | 32 | 3,71 | 0,29 |
3 | 40 | 34 | 2,33 | 0,67 |
5 | 55 | 38 | 3,98 | 1,02 |
3 | 48 | 28 | 2,50 | 0,50 |
3 | 45 | 30 | 2,41 | 0,59 |
2 | 55 | 36 | 3,80 | -1,80 |
4 | 60 | 34 | 4,06 | -0,06 |
5 | 60 | 38 | 4,41 | 0,59 |
5 | 60 | 42 | 4,76 | 0,24 |
5 | 65 | 38 | 4,84 | 0,16 |
4 | 50 | 34 | 3,19 | 0,80 |
3 | 58 | 38 | 4,24 | -1,24 |
М = 3,25 | 51,9 | 32,75 | 3,25 | 0 |
В = 1,57 | 57,46 | 27,46 | 1,05 | 0,52 |
USS=29. | 19,95 | 9,88 |
Среднее значение Y равно 3,25, как и среднее значение Y’. Среднее значение остатков равно 0. Дисперсия Y равна 1,57. Дисперсия Y’ равна 1,05, а дисперсия остатков равна 0,52. Вместе дисперсия регрессии (Y’) и дисперсия ошибки (e) составляют дисперсию Y (1,57 = 1,05 + 0,52). R-квадрат равен 1,05/1,57 или 0,67. Если мы вычислим корреляцию между Y и Y’, мы обнаружим, что R = 0,82, что при возведении в квадрат также является R-квадратом, равным 0,67. (Вспомните диаграмму рассеяния Y и Y’). R-квадрат — это доля дисперсии Y из-за множественной регрессии.
Проверка значимости R 2
Вы уже видели это один раз, но вот снова в новом контексте:
, который распространяется как F с k и (N-k-1) степеней свободы, когда значение null равно true. Теперь R 2 предназначен для множественной корреляции, а не для простой корреляции, которую мы видели в прошлый раз. В нашем последнем примере у нас есть 2 независимые переменные, R 2 , равный 0,67, и 20 человек, поэтому
Теперь R 2 предназначен для множественной корреляции, а не для простой корреляции, которую мы видели в прошлый раз. В нашем последнем примере у нас есть 2 независимые переменные, R 2 , равный 0,67, и 20 человек, поэтому
р < 0,01. (F крит для p<0,01 составляет около 6).
Поскольку SStot=SSreg+SSres , мы можем вычислить эквивалент F, используя суммы квадратов и связанные с ними df.
, что согласуется с нашим предыдущим результатом в пределах ошибки округления.
Относительная важность независимых переменных
В простой регрессии у нас есть одна IV, которая объясняет долю дисперсии Y. Влияние этой переменной (насколько она важна для предсказания или объяснения Y) описывается как r 2 . Если r 2 равно 1,0, мы знаем, что DV можно точно предсказать по IV; учитывается вся дисперсия в DV. Если r 2 равно 0, мы знаем, что линейной связи нет; IV не важен для предсказания или объяснения Y. С 2 или более IV мы также получаем в сумме R 2 . Это R 2 говорит нам, какая дисперсия Y обусловлена набором IV, то есть важность линейной комбинации IV (b 1 X 1 +b 2 X 2 +…+b k X k ). Часто мы хотели бы знать важность каждого из IV в предсказании или объяснении Y. В нашем примере мы знаем, что механические способности и добросовестность вместе предсказывают примерно 2/3 дисперсии в оценках производительности труда. Но насколько важны механизмы apt и consc по отношению друг к другу? Корреляция и регрессия дают ответы на этот вопрос. К сожалению, ответы не всегда совпадают. Важно понять, почему они иногда соглашаются, а иногда расходятся. Вы должны понимать это потенциальное несогласие, чтобы правильно интерпретировать веса регрессии.
С 2 или более IV мы также получаем в сумме R 2 . Это R 2 говорит нам, какая дисперсия Y обусловлена набором IV, то есть важность линейной комбинации IV (b 1 X 1 +b 2 X 2 +…+b k X k ). Часто мы хотели бы знать важность каждого из IV в предсказании или объяснении Y. В нашем примере мы знаем, что механические способности и добросовестность вместе предсказывают примерно 2/3 дисперсии в оценках производительности труда. Но насколько важны механизмы apt и consc по отношению друг к другу? Корреляция и регрессия дают ответы на этот вопрос. К сожалению, ответы не всегда совпадают. Важно понять, почему они иногда соглашаются, а иногда расходятся. Вы должны понимать это потенциальное несогласие, чтобы правильно интерпретировать веса регрессии.
Сначала я представлю диаграммы Венна, чтобы описать, что происходит. Вы должны знать, что диаграммы Венна не являются точным представлением того, как на самом деле работает регрессия. Диаграммы Венна могут ввести вас в заблуждение в ваших рассуждениях . Тем не менее, большинству людей их гораздо легче понять, чем родственные уравнения, так что начнем. Мы собираемся предсказать Y по двум независимым переменным, X1 и X2. Предположим, что и X1, и X2 коррелируют с Y, но X1 и X2 не коррелируют друг с другом. Наша диаграмма может выглядеть так, как показано на рис. 5.1: 9.0003
Диаграммы Венна могут ввести вас в заблуждение в ваших рассуждениях . Тем не менее, большинству людей их гораздо легче понять, чем родственные уравнения, так что начнем. Мы собираемся предсказать Y по двум независимым переменным, X1 и X2. Предположим, что и X1, и X2 коррелируют с Y, но X1 и X2 не коррелируют друг с другом. Наша диаграмма может выглядеть так, как показано на рис. 5.1: 9.0003
Рисунок 5.1 | Рисунок 5.2 |
На рис. 5.1 у нас есть три кружка, по одному для каждой переменной. Каждый кружок представляет дисперсию переменной. Размер (квадрат) корреляции между двумя переменными обозначен перекрытием в кружках. Напомним, что квадрат корреляции — это доля общей дисперсии между двумя переменными. На рис. 5.1, X 1 и X 2 не связаны. На это указывает отсутствие перекрытия двух переменных. Мы можем вычислить корреляцию между каждой переменной X и Y. Эти корреляции и их квадраты будут указывать на относительную важность независимых переменных. Рисунок 5.1 может соответствовать такой корреляционной матрице:
На это указывает отсутствие перекрытия двух переменных. Мы можем вычислить корреляцию между каждой переменной X и Y. Эти корреляции и их квадраты будут указывать на относительную важность независимых переменных. Рисунок 5.1 может соответствовать такой корреляционной матрице:
Р | Д | Х 1 | х 2 |
Д | 1 | ||
Х 1 | .50 | 1 | |
Х 2 | .60 | .00 | 1 |
В случае, если X 1 и X 2 не коррелированы, мы можем оценить общую дисперсию между двумя переменными X и Y, суммируя квадраты корреляций. В нашем примере общая дисперсия будет равна 0,50 2 + 0,60 2 = 0,25+0,36 = 0,61. Оказывается, это 61-процентная общая дисперсия, и если мы вычислим уравнение регрессии, то обнаружим, что R 2 равно 0,61 (вычисления будут более полными позже. А пока сосредоточьтесь на цифрах). 1 и Х 2 некоррелированы, то они не имеют никакой дисперсии друг с другом. Если они разделяют дисперсию с Y, то любая дисперсия, общая с Y, должна быть уникальной для этого X, потому что переменные X не перекрываются.
В нашем примере общая дисперсия будет равна 0,50 2 + 0,60 2 = 0,25+0,36 = 0,61. Оказывается, это 61-процентная общая дисперсия, и если мы вычислим уравнение регрессии, то обнаружим, что R 2 равно 0,61 (вычисления будут более полными позже. А пока сосредоточьтесь на цифрах). 1 и Х 2 некоррелированы, то они не имеют никакой дисперсии друг с другом. Если они разделяют дисперсию с Y, то любая дисперсия, общая с Y, должна быть уникальной для этого X, потому что переменные X не перекрываются.
С другой стороны, обычно бывает так, что переменные X коррелированы и имеют некоторую дисперсию, как показано на рис. 5.2, где X 1 и X 2 несколько перекрываются. Обратите внимание, что X 1 и X 2 пересекаются как друг с другом, так и с Y. Есть участок, где X 1 и X 2 пересекаются друг с другом, но не с Y (обозначены как «общий X» на рис. 5.2). Есть разделы, где каждый перекрывается с Y, но не с другим X (помечены «UY: X1» и «UY: X2»). Часть слева — это часть Y, однозначно учитываемая как X 1 (UY:X1). Аналогичная часть справа — это часть Y, однозначно определяемая X 2 (UY:X2). Последняя перекрывающаяся часть показывает ту часть Y, которая учитывается обеими переменными Y («общая Y»).
Есть разделы, где каждый перекрывается с Y, но не с другим X (помечены «UY: X1» и «UY: X2»). Часть слева — это часть Y, однозначно учитываемая как X 1 (UY:X1). Аналогичная часть справа — это часть Y, однозначно определяемая X 2 (UY:X2). Последняя перекрывающаяся часть показывает ту часть Y, которая учитывается обеими переменными Y («общая Y»).
Как и на рис. 5.1, мы можем вычислить корреляции между каждым X и Y. Для X 1 корреляция будет включать области UY:X1 и общие Y. Для X 2 корреляция будет содержать UY:X2 и общий Y. Обратите внимание, что общий Y будет учитываться дважды, по одному разу для каждой переменной X. Мы также можем вычислить уравнение регрессии, а затем вычислить R 2 на основе этого уравнения. Если бы мы это сделали, то обнаружили бы, что R 2 соответствует UY:X1 плюс UY:X2 плюс общий Y. Обратите внимание, что R 2 из-за регрессии Y по обеим переменным X одновременно даст нам правильную учитываемую дисперсию, при этом общий Y подсчитывается только один раз.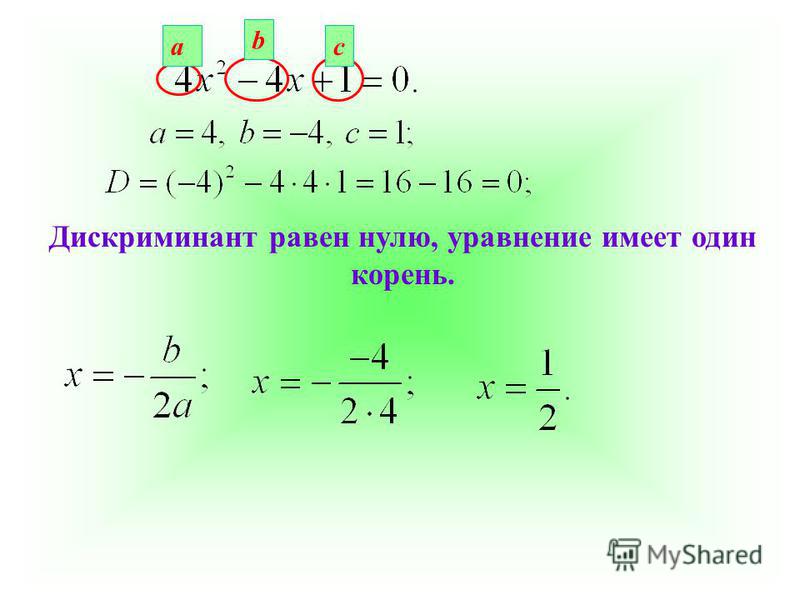 Теперь мы хотим присвоить или разделить R 2 на соответствующие переменные X в соответствии с их важностью. Мы можем сделать это несколькими способами. В любом случае мы будем назначать уникальную часть Y соответствующему X (UY:X1 идет на X1, UY:X2 идет на X 2 ). Но что делать с общим Y? Наиболее распространенным решением этой проблемы является ее игнорирование. Если мы назначим суммы квадратов регрессии в соответствии с величинами b веса, мы будем присваивать суммы квадратов только уникальным частям. Общая часть будет назначена общему R 2 , но не какой-либо из переменных, которые ее разделяют. (Есть и другие способы разделить общую часть. Мы рассмотрим их позже.). В множественной регрессии мы обычно заинтересованы в предсказании или объяснении всей дисперсии Y. Для этого нам нужны независимые переменные, которые коррелируют с Y, но не с X. Однако найти такие переменные сложно. Более типичным является поиск новых переменных X, которые коррелируют со старыми переменными X и общим Y, а не уникальным Y.
Теперь мы хотим присвоить или разделить R 2 на соответствующие переменные X в соответствии с их важностью. Мы можем сделать это несколькими способами. В любом случае мы будем назначать уникальную часть Y соответствующему X (UY:X1 идет на X1, UY:X2 идет на X 2 ). Но что делать с общим Y? Наиболее распространенным решением этой проблемы является ее игнорирование. Если мы назначим суммы квадратов регрессии в соответствии с величинами b веса, мы будем присваивать суммы квадратов только уникальным частям. Общая часть будет назначена общему R 2 , но не какой-либо из переменных, которые ее разделяют. (Есть и другие способы разделить общую часть. Мы рассмотрим их позже.). В множественной регрессии мы обычно заинтересованы в предсказании или объяснении всей дисперсии Y. Для этого нам нужны независимые переменные, которые коррелируют с Y, но не с X. Однако найти такие переменные сложно. Более типичным является поиск новых переменных X, которые коррелируют со старыми переменными X и общим Y, а не уникальным Y. Желаемое и типичное положение дел в множественной регрессии можно проиллюстрировать другой диаграммой Венна:
Желаемое и типичное положение дел в множественной регрессии можно проиллюстрировать другой диаграммой Венна:
Желаемое состояние (рис. 5.3) | Типичное состояние (рис. 5.4) |
Обратите внимание, что на рис. 5.3, в желаемом положении дел, каждая переменная X минимально коррелирует с другими переменными X, но существенно коррелирует с Y. В таком случае R 2 будет большим, и влияние каждого X будет однозначным. Типичное положение дел показано на рис. 5.4. Обратите внимание, как переменная X 3 существенно коррелирует с Y, а также с X 1 и X 2 . Это означает, что X 3 не вносит ничего нового или уникального в предсказание Y. Это также запутывает интерпретацию важности переменных X, поскольку трудно приписать общую дисперсию Y любому X.
Стандартные и нестандартные веса (b против b)
С каждой переменной X будет связан один наклон или вес регрессии. Каждый вес интерпретируется как означающий единичное изменение Y при единичном изменении X, поэтому наклон может что-то сказать нам о важности переменных X. (Строго говоря, утверждение о наклоне интерпретации неверно без упоминания других переменных X. Но оно достаточно близко, пока мы не дойдем до частных корреляций). Переменные с большими b весов должны говорить нам, что они более важны, потому что Y изменяется быстрее для некоторых из них, чем для других. Проблема с нестандартизированными или необработанными весами Score b в этом отношении заключается в том, что они имеют разные единицы измерения и, следовательно, разные стандартные отклонения и разные значения. Если бы мы измеряли X = рост в футах, а не X = рост в дюймах, вес b для футов был бы в 12 раз больше, чем вес b для дюймов (12 дюймов в футе; в обоих случаях мы интерпретируем 9). 0012 b как единица измерения изменяется в Y, когда X изменяется на 1 единицу). Таким образом, когда мы измеряем разные переменные X в разных единицах, часть размера b относится к единицам, а не к важности как таковой. Итак, что мы можем сделать, так это стандартизировать все переменные (как X, так и Y, каждый X по очереди). Если мы это сделаем, то важность переменных X будет очевидна по величине весов b — все они будут интерпретироваться как количество стандартных отклонений, которые Y изменяет, когда каждое X изменяется на 1 стандартное отклонение. Стандартизированные наклоны называются бета-весами (b). Это чрезвычайно плохой выбор символов, потому что мы уже использовали b для обозначения значения совокупности 9.0012 b (не вините меня, это часть литературы). Отсюда и далее b будет относиться к стандартизированным весам b, то есть к оценкам параметров, если не указано иное.
0012 b как единица измерения изменяется в Y, когда X изменяется на 1 единицу). Таким образом, когда мы измеряем разные переменные X в разных единицах, часть размера b относится к единицам, а не к важности как таковой. Итак, что мы можем сделать, так это стандартизировать все переменные (как X, так и Y, каждый X по очереди). Если мы это сделаем, то важность переменных X будет очевидна по величине весов b — все они будут интерпретироваться как количество стандартных отклонений, которые Y изменяет, когда каждое X изменяется на 1 стандартное отклонение. Стандартизированные наклоны называются бета-весами (b). Это чрезвычайно плохой выбор символов, потому что мы уже использовали b для обозначения значения совокупности 9.0012 b (не вините меня, это часть литературы). Отсюда и далее b будет относиться к стандартизированным весам b, то есть к оценкам параметров, если не указано иное.
Уравнения регрессии с весами b
Поскольку мы используем стандартизированные оценки, мы снова возвращаемся к ситуации с z-оценкой. Как вы помните из сравнения корреляции и регрессии:
Как вы помните из сравнения корреляции и регрессии:
Но b означает вес b, когда X и Y находятся в стандартных баллах, поэтому для случая простой регрессии r = b, и мы имеем:
Предыдущие формулы, которые я приводил для b , были составлены из сумм квадратного и перекрестного произведений (). Но с z баллов мы будем иметь дело со стандартизированными суммами квадратов и перекрестных произведений. Стандартизированная усредненная сумма квадратов равна 1 (), а стандартизованная усредненная сумма перекрестных произведений является коэффициентом корреляции (). Суть в том, что мы можем оценить бета-веса (bs), используя корреляционную матрицу. При простой регрессии, как вы уже видели, r=b. С двумя независимыми переменными
и
, где r y1 — отношение y к X1, r y2 — отношение y к X2, а r 12 — отношение X1 к X2. Обратите внимание, что две формулы почти идентичны, за исключением порядка первых двух символов в числителе.
Наша корреляционная матрица выглядит так:
Д | Х 1 | Х 2 | |
Д | 1 | ||
Х 1 | 0,77 | 1 | |
Х 2 | 0,72 | 0,68 | 1 |
Обратите внимание, что существует удивительно большая разница в бета-весах, учитывая величину корреляции.
Давайте посмотрим на это минутку, сначала на уравнение для b 1 . Числитель говорит, что b 1 — это корреляция (X 1 и Y) минус корреляция (X 2 и Y), умноженная на корреляцию (X 1 и X 2 ). Знаменатель говорит о том, что немного увеличьте числитель в зависимости от размера корреляции между X 1 и X 2 . Предположим, что r 12 равно нулю. Тогда r y2 r 12 равно нулю, а числитель равен r y1 . Знаменатель равен 1, поэтому результат равен r y1 , простая корреляция между X 1 и Y. Если корреляция между X 1 и X 2 равна нулю, бета-вес является простой корреляцией. С другой стороны, если корреляция между X 1 и X 2 равна 1,0, бета не определена, потому что мы будем делить на ноль. Так что наша жизнь менее сложна, если корреляция между X-переменными равна нулю. Предположим, что r 12 находится где-то между 0 и 1. Тогда мы окажемся в ситуации, изображенной на рис.
Числитель говорит, что b 1 — это корреляция (X 1 и Y) минус корреляция (X 2 и Y), умноженная на корреляцию (X 1 и X 2 ). Знаменатель говорит о том, что немного увеличьте числитель в зависимости от размера корреляции между X 1 и X 2 . Предположим, что r 12 равно нулю. Тогда r y2 r 12 равно нулю, а числитель равен r y1 . Знаменатель равен 1, поэтому результат равен r y1 , простая корреляция между X 1 и Y. Если корреляция между X 1 и X 2 равна нулю, бета-вес является простой корреляцией. С другой стороны, если корреляция между X 1 и X 2 равна 1,0, бета не определена, потому что мы будем делить на ноль. Так что наша жизнь менее сложна, если корреляция между X-переменными равна нулю. Предположим, что r 12 находится где-то между 0 и 1. Тогда мы окажемся в ситуации, изображенной на рис. 5.2, где все три круга перекрываются. Бета-вес для X 1 (b 1 ) будет по существу той частью изображения, которая обозначена как UY:X1. Мы начинаем с r y1 , в котором есть как UY:X1, так и общий Y. (Когда r 12 равно нулю, мы останавливаемся здесь, потому что нам не нужно беспокоиться об общей части). Мы вычитаем r y2 умножить на r 12 , что означает вычитание только той части r y2 , что соответствует общей части X. Но общая часть X содержит как общие X с X, так и общие Y, поэтому мы вынесем слишком много. Чтобы исправить это, мы делим на 1-r 2 12 , чтобы увеличить b 1 вернитесь туда, где он должен быть.
5.2, где все три круга перекрываются. Бета-вес для X 1 (b 1 ) будет по существу той частью изображения, которая обозначена как UY:X1. Мы начинаем с r y1 , в котором есть как UY:X1, так и общий Y. (Когда r 12 равно нулю, мы останавливаемся здесь, потому что нам не нужно беспокоиться об общей части). Мы вычитаем r y2 умножить на r 12 , что означает вычитание только той части r y2 , что соответствует общей части X. Но общая часть X содержит как общие X с X, так и общие Y, поэтому мы вынесем слишком много. Чтобы исправить это, мы делим на 1-r 2 12 , чтобы увеличить b 1 вернитесь туда, где он должен быть.
Расчет Р 2
Как я уже упоминал, один из способов вычислить R 2 — вычислить корреляцию между Y и Y’ и возвести ее в квадрат. Есть и другие способы расчета R 2 , и они важны для концептуального понимания того, что происходит при множественной регрессии. Если независимые переменные не коррелированы, то
Если независимые переменные не коррелированы, то
Это говорит о том, что R 2 , доля дисперсии зависимой переменной, учитываемой обеими независимыми переменными, равна сумме квадратов корреляций независимых переменных с Y. Это верно только тогда, когда IV ортогональны. .
[Рассмотрите диаграммы Венна, рис. 5.1.]
В нашем примере R 2 равно 0,67. Корреляции: r y1 = 0,77 и r y2 = 0,72. Если возвести в квадрат и сложить, мы получим 0,77 2 + 0,72 2 = 0,5929 + 0,5184 = 1,11, что явно слишком велико для R 2 .
Если IV коррелированы, то у нас есть некоторый общий X и, возможно, общий Y, и мы должны принять это во внимание. Две общие формулы могут быть использованы для расчета R 2 , когда IV скоррелированы.
Это означает умножение стандартизованного наклона (бета-веса) на корреляцию для каждой независимой переменной и добавление для расчета R 2 . Это включает в себя как корреляцию (которая будет переоценивать общую сумму R 2 из-за общего Y), так и бета-вес (который занижает R 2 , потому что он включает только уникальный Y и дисконтирует общий Y). При правильном сочетании они дают правильный R 2 . Заметим, что когда r 12 равен нулю, затем B 1 = R Y1 и B 2 = R Y2 , так что (B 1 ) (R Y1 ) = R 2 Y1 и R 2 Y1 и R 2 Y1 и R 2 Y1 и R 2 Y1 и R 2 Y1 и R 2 Y1 и R 2 Y1 ) у нас есть более ранняя формула, где R 2 — это сумма квадратов корреляций между Xs и Y. Для нашего примера соответствующие числа равны (0,52).77+(0,37).72 = 0,40+0,27. = 0,67, что согласуется с нашим более ранним значением R 2 .
Это включает в себя как корреляцию (которая будет переоценивать общую сумму R 2 из-за общего Y), так и бета-вес (который занижает R 2 , потому что он включает только уникальный Y и дисконтирует общий Y). При правильном сочетании они дают правильный R 2 . Заметим, что когда r 12 равен нулю, затем B 1 = R Y1 и B 2 = R Y2 , так что (B 1 ) (R Y1 ) = R 2 Y1 и R 2 Y1 и R 2 Y1 и R 2 Y1 и R 2 Y1 и R 2 Y1 и R 2 Y1 и R 2 Y1 ) у нас есть более ранняя формула, где R 2 — это сумма квадратов корреляций между Xs и Y. Для нашего примера соответствующие числа равны (0,52).77+(0,37).72 = 0,40+0,27. = 0,67, что согласуется с нашим более ранним значением R 2 .
Вторая формула, использующая только коэффициенты корреляции, равна 9.0003
Эта формула говорит, что R 2 является суммой квадратов корреляций между Xs и Y с поправкой на общий X и общий Y. Обратите внимание, что член справа в числителе и переменная в знаменателе оба содержат r 12 , что является корреляцией между X1 и X2. Обратите внимание, что это уравнение также упрощает простую сумму квадратов корреляций, когда r 12 = 0, то есть, когда IV ортогональны. В нашем примере их 9.0003
, что совпадает с нашим предыдущим значением с учетом ошибки округления.
Тесты коэффициентов регрессии
Каждый коэффициент регрессии является оценкой наклона. При наличии более чем одной независимой переменной наклоны относятся к ожидаемому изменению Y, когда X изменяется на 1 единицу, С КОНТРОЛЕМ ДРУГИХ ПЕРЕМЕННЫХ X. То есть b 1 — это изменение Y при единичном изменении X 1 при удержании X 2 постоянная, а b 2 представляет собой изменение Y при единичном изменении X 2 при сохранении постоянной X 1 . Мы разовьем это более формально после того, как введем частичную корреляцию.
Мы разовьем это более формально после того, как введем частичную корреляцию.
А пока рассмотрим рис. 5.2 и то, что произойдет, если оставить один X постоянным. Величина изменения Y из-за X 1 при неизменном значении X 2 является функцией уникального вклада X 1 . Если X 1 значительно перекрывается с X 2 , то изменение Y из-за X 1 при сохранении постоянной X 2 будет небольшим.
Стандартная ошибка веса b для задачи с двумя переменными:
, где s 2 y.12 — дисперсия оценки (дисперсия остатков). Мы используем стандартную ошибку веса b при проверке значимости t. (Равен ли вес регрессии нулю в популяции? Равен ли вес регрессии какому-то другому значению в популяции?) Стандартная ошибка b вес зависит от трех вещей. Дисперсия оценки говорит нам о том, насколько далеко точки отходят от линии регрессии (средний квадрат расстояния). Большие ошибки в предсказании означают большую стандартную ошибку. Сумма квадратов IV также имеет значение. Чем больше сумма квадратов (дисперсия) X, тем меньше стандартная ошибка. Ограничение диапазона не только уменьшает размер корреляции, но и увеличивает стандартную ошибку веса b . Корреляция между независимыми переменными также имеет значение. Чем больше корреляция, тем больше стандартная ошибка б вес. Таким образом, чтобы найти значимые веса b , мы хотим минимизировать корреляцию между предикторами, максимизировать дисперсию предикторов и минимизировать ошибки предсказания.
Большие ошибки в предсказании означают большую стандартную ошибку. Сумма квадратов IV также имеет значение. Чем больше сумма квадратов (дисперсия) X, тем меньше стандартная ошибка. Ограничение диапазона не только уменьшает размер корреляции, но и увеличивает стандартную ошибку веса b . Корреляция между независимыми переменными также имеет значение. Чем больше корреляция, тем больше стандартная ошибка б вес. Таким образом, чтобы найти значимые веса b , мы хотим минимизировать корреляцию между предикторами, максимизировать дисперсию предикторов и минимизировать ошибки предсказания.
Дисперсия прогноза
и испытание груза b представляет собой t -испытание с N-k -1 степенями свободы.
В нашем примере сумма квадратов ошибок равна 9,79, а df равна 20-2-1 или 17. Следовательно, наша дисперсия оценки равна 9.0003
.575871 или .58 после округления. Наши стандартные ошибки:
и S b2 = . 0455, что следует из расчетов, идентичных за исключением значения суммы квадратов для X 2 вместо X 1 .
0455, что следует из расчетов, идентичных за исключением значения суммы квадратов для X 2 вместо X 1 .
Чтобы проверить значимость весов b , мы вычисляем статистику t
в нашем случае t = 0,0864/0,0313 или 2,75. Если мы сравним это с распределением t с 17 df , мы обнаруживаем, что оно значимо (из функции поиска мы находим, что p = 0,0137, что меньше 0,05).
Для b 2 мы вычисляем t = 0,0876/0,0455 = 1,926, что имеет значение p , равное 0,0710, что не является значимым. Обратите внимание, что корреляция r y2 равна 0,72, что является очень значимым ( p < 0,01), но b 2 не является значимым.
Испытания Р 2 по сравнению с испытаниями b
Поскольку b -веса представляют собой наклоны для уникальных частей Y и поскольку корреляции между независимыми переменными увеличивают стандартные ошибки весов b , можно получить большое значимое R 2 , но при в то же время иметь незначащие веса b (как в нашем примере). Рассмотрим рис. 5.4, где имеется множество IV, объясняющих по существу одну и ту же дисперсию Y. Хотя R 2 будет довольно большим, когда мы будем держать другие переменные X постоянными для проверки на b , Y будет мало изменяться для данного X, и будет трудно найти значительный вес b . Также можно найти значимый вес b без значимого R 2 . Это может произойти, когда у нас много независимых переменных (обычно более 2), все или большинство из которых имеют довольно низкую корреляцию с Y. Если одна из этих переменных имеет большую корреляцию с Y, R 2 может быть несущественным, потому что при таком большом количестве IV мы ожидаем увидеть такое же большое R 2 просто случайно. Если R 2 не является значимым, обычно следует избегать интерпретации весов b , которые являются значимыми. В таких случаях вполне вероятно, что значительный вес b является ошибкой первого рода.
Рассмотрим рис. 5.4, где имеется множество IV, объясняющих по существу одну и ту же дисперсию Y. Хотя R 2 будет довольно большим, когда мы будем держать другие переменные X постоянными для проверки на b , Y будет мало изменяться для данного X, и будет трудно найти значительный вес b . Также можно найти значимый вес b без значимого R 2 . Это может произойти, когда у нас много независимых переменных (обычно более 2), все или большинство из которых имеют довольно низкую корреляцию с Y. Если одна из этих переменных имеет большую корреляцию с Y, R 2 может быть несущественным, потому что при таком большом количестве IV мы ожидаем увидеть такое же большое R 2 просто случайно. Если R 2 не является значимым, обычно следует избегать интерпретации весов b , которые являются значимыми. В таких случаях вполне вероятно, что значительный вес b является ошибкой первого рода.
Инкрементальное тестирование R 2
Мы можем проверить изменение R 2 , которое происходит, когда мы добавляем новую переменную в уравнение регрессии. Мы можем начать с 1 переменной и вычислить R 2 (или r 2 ) для этой переменной. Затем мы можем добавить вторую переменную и вычислить R 2 с обеими переменными. Второй R 2 всегда будет больше или равен первому R 2 . Если оно больше, мы можем спросить, значительно ли оно больше. Для этого мы вычисляем
Мы можем начать с 1 переменной и вычислить R 2 (или r 2 ) для этой переменной. Затем мы можем добавить вторую переменную и вычислить R 2 с обеими переменными. Второй R 2 всегда будет больше или равен первому R 2 . Если оно больше, мы можем спросить, значительно ли оно больше. Для этого мы вычисляем
, где R 2 L — большее R 2 (с большим количеством предикторов), k L — количество предикторов в большем уравнении и k S — количество предикторов в меньшем уравнении. Когда ноль равен true, результат распределяется как F со степенями свободы, равными ( k L — k S ) и ( N — k L — ) . В нашем примере мы знаем, что R 2 y,12 = 0,67 (из предыдущих расчетов), а также что r y1 = 0,77 и r y2 = 0,72. r 2 y1 = 0,59 и r 2 у2 = 0,52. Теперь мы можем увидеть, значительно ли увеличивает R 2 увеличение прибавления X1 или X2 к уравнению, содержащему другое. Чтобы увидеть, добавляет ли X1 дисперсию, начнем с X2 в уравнении:
Теперь мы можем увидеть, значительно ли увеличивает R 2 увеличение прибавления X1 или X2 к уравнению, содержащему другое. Чтобы увидеть, добавляет ли X1 дисперсию, начнем с X2 в уравнении:
Наше критическое значение F(1,17) равно 4,45, поэтому наше F для приращения X1 относительно X2 является значительным.
Для приращения X2 к X1 мы имеем
Наше критическое значение F не изменилось, поэтому приращение к R 2 по X2 не (вполне) существенно.
формула средней точки: x1 + x2 разделить на 2, y1 + y2 разделить на два. если
3 060 результатов
нахождение средней точки
формула средней точки: x1 + x2 разделить на 2, y1 + y2 разделить на два. если координаты x1: a, y1: b и x2: c, y2: 0, что такое середина? Я обнаружил, что координата y средней точки равна b больше 2. Я обнаружил, что x равен ac больше двух.
 это
это- спросил Аноним
- 399 просмотров
математика
Деление рациональных чисел найти каждое произведение 1. 1/3 * 7 A. 1/21 B. 2 1/7 C. 2 1/3 D. 3/7 Я думаю, что B 2. -7/ 9*3/5 A. 18/35 B. 7/15 C. -18/35 D. -7/15 Думаю, что C 3. 1/3 разделить на 5/6 A. 2/5 B. 5 /2 C. 2/15 D. 5/18 Кажется, C 4. 2 1/8
- спросил (белла) пожалуйста, помогитеpp
- 4 514 просмотров
Математика
Разделить. Пишите в простейшей форме. 5. 1/3 разделить на 2/5=5/6 6. 1/9 разделить на 1/2=2/9 7,2/3 разделить на 1/4=8/3=2 2/3 8. 1/2 разделить на 3/4=4/6=2/3 9. 4/5 разделить на 2=1 3/5 10. 4/5 разделить на 1/10=40/5=8 11. 5/12 разделить на 5 /6=30/60=1/2 12. 9/10 разделить на
- спросил Джеральд
- 2 474 просмотра
Оценка десятичного частного
Используйте совместимый для нахождения следующего частного
- спросил Дэвид
- 1 169 просмотров
Math
Запишите следующие десятичные числа в виде дробей и найдите частные.
 4,5 разделить на 0,9 = 0,6 разделить на 0,12 = 1,2 разделить на 0,5 = 22,5 разделить на 0,5 = 0,18 разделить на 0,03 =
4,5 разделить на 0,9 = 0,6 разделить на 0,12 = 1,2 разделить на 0,5 = 22,5 разделить на 0,5 = 0,18 разделить на 0,03 =- спросил Габриэль
- 1 086 просмотров
МАТЕМАТИКА!!!
Какое выражение представляет расчет «вычесть 4 из 12, а затем разделить на 8»? A) 4 разделить на (12 — B) (12 — 4) разделить на 8 C) (4 — 12) разделить на 8 D) 8 — (12 разделить на 4)
- спросил FATTY BOY
- 294 просмотра
Математика
1,62 разделить на 0,8 16,2 разделить на 8 0,0162 разделить на 0,008 0,162 разделить на 0,08 На самом деле есть два разных способа завершить приведенные выше выражения с заданными числами, чтобы каждое выражение имело одинаковое значение. Какова может быть стоимость всех четырех
- спросил гэвин
- 3 324 просмотра
Math
Формула объема треугольной призмы: v=Bh.
 Какое уравнение можно использовать, чтобы найти B, площадь заштрихованного основания в квадратных сантиметрах? (H=4 L=6 W=5) A. B= 5(6) B. B= 5(6) разделить на 2 C. B= 4(5) D. B= 4(5) разделить на 2
Какое уравнение можно использовать, чтобы найти B, площадь заштрихованного основания в квадратных сантиметрах? (H=4 L=6 W=5) A. B= 5(6) B. B= 5(6) разделить на 2 C. B= 4(5) D. B= 4(5) разделить на 2- спросил Маккензи
- 2 178 просмотров
Математика
Объясните, как связаны ответы для 20 разделить на 1/7 (140), 20 разделить на 2/7 (70) и 20 разделить 6/7 (23 1/3). Покажите, почему это имеет смысл.
- спросил Аноним
- 990 просмотров
математика
1. 1/3 раза 7 2. -7/9умножить на 3/5 3. 1/3 разделить на 5/6 4. 2 1/8 разделить на 34 5. -3/5 разделить на — 3/4 6. -4/5 разделить на 8/9 7. 3/ 5 разделить на 9/10 8. 4/7 разделить на 9/14 Я не знаю ответов.
- спросил Мэдисон
- 1 965 просмотров
3-я математика
Запишите 35, разделенное на 7, тремя различными способами.
 Что такое частное? они означают 35 разделить на 5 = 7, 35 разделить на 7 = 5 или по знаку? 92-х-6
Что такое частное? они означают 35 разделить на 5 = 7, 35 разделить на 7 = 5 или по знаку? 92-х-6- спросил Jetta
- 931 просмотров
Math
Вычислите выражение. (1)1/3 разделить на 1/6= 2 Ответ (2)6 разделить на 2/5= 15 Ответ (3) 4/9 разделить на 2/3 разделить на 5/6= Ответ 4/5 (4) 7/8 умножить на 4/5 разделить 7/20 = Ответ 2 Пожалуйста, помогите мисс Сью
- спросил Синди
- 1 151 просмотров
Math adv function
Неизвестный многочлен f(x) степени 37 дает остаток 1 при делении на x – 1, остаток 3 при делении на x – 3, остаток 21 при делении на x – 5. Найдите остаток от деления f(x) на (x – 1)(x – 3)(x – 5).
- спросил Аноним
- 1 307 просмотров
Математика
Найти каждое частное 3/4 разделить на -12 5/4 разделить на 2 2/3 18 разделить на 4,6 3,06 разделить на 0,22
- спросил Аноним
- 404 просмотра
алгебра
Решить неравенство W > Y плюс H разделить все на P для H.
 W разделить на P – Y > H W умножить на P разделить на Y > H WP – Y > H W + P – Y > H 92+nx+5 дает остаток 128 при делении на x-3 и остаток 4 при делении на x+1. вычислить остаток, когда
W разделить на P – Y > H W умножить на P разделить на Y > H WP – Y > H W + P – Y > H 92+nx+5 дает остаток 128 при делении на x-3 и остаток 4 при делении на x+1. вычислить остаток, когда- спросил Ниаллин
- 5 372 просмотра
Математика
1/4 разделить на 3/8 (запишите в простейшей форме) ——————————— —— 1/3 разделить на 5/6 (самая простая форма) ——————————— ——- 1 3/4 разделить на 3 (самая простая форма) ——————————— ——— 1 3/5 разделить на 5/8 92-3x+5 дает тот же остаток при делении на x+k, что и при делении на x-3k найти значение k, k не равно 0.
- спросил Ник
- 2 308 просмотров
math
При делении натурального числа n на 24 остаток равен 18.
 При делении n на 8 остаток равен: A.0 B.1 C.2 D.4 E.6 Я пробовал делать n/ 24=18 и я получил 432 и когда я разделил это на 8 я получил 54; я неправильно понимаю вопрос? Я действительно не вижу других
При делении n на 8 остаток равен: A.0 B.1 C.2 D.4 E.6 Я пробовал делать n/ 24=18 и я получил 432 и когда я разделил это на 8 я получил 54; я неправильно понимаю вопрос? Я действительно не вижу других- спросил Люсиль
- 1 796 просмотров
math
Температура пустыни, H, колеблется ежедневно между 36°F в 4 часа утра и 56°F в 4 часа дня. Напишите возможную формулу для H через t, измеренную в часах с 4 часов утра. Я думал, что ответ будет -10cos (1/6pi умножить на t) +46, но он был отмечен неправильно. Я думал, что
- спросила Натали
- 1 713 просмотров
Math
Найдите наименьшее положительное целое число, которое дает остаток от 5 при делении на 7, остаток от 6 при делении на 11 и остаток от 4 при делении на 13.
- спросил Джимми-Пожалуйста, ПОМОГИТЕ
- 1 382 просмотра
Исчисление
Какой из следующих интегралов нельзя вычислить с помощью простой замены? интеграл от 1, деленный на количество x в квадрате плюс 1, dx интеграл от 1, деленный на количество x в квадрате плюс 1, dx интеграл от x, деленный на количество x
- спросил Тифф
- 3 114 просмотров
теория чисел
Найдите наименьшее целое положительное число, которое оставляет остаток 3 при делении на 7, остаток 4 при делении на 9 и остаток 8 при делении на 11
- спросил Джон
- 2 046 просмотров
Math
Предположим, что y изменяется обратно пропорционально x и что y = 4, когда x = 6.
 Какое уравнение для обратного изменения? A. y равно 6, деленное на 4, умноженное на x. B. y равно 24, деленное на x. C. y равняется двум третям, умноженным на x. D. y равно x, деленному на 24,
Какое уравнение для обратного изменения? A. y равно 6, деленное на 4, умноженное на x. B. y равно 24, деленное на x. C. y равняется двум третям, умноженным на x. D. y равно x, деленному на 24,- спросил 𝕮𝖍𝖑𝖔𝖊
- 688 просмотров
Математика
Объясните, почему 0,4, деленное на 0,2, дает тот же ответ, что и 4, деленное на 2. (Подсказка: преобразуйте десятичные дроби в дроби со знаменателем 10.)
- спросил Мари
- 1 654 просмотра
Математика
Перепишите каждую задачу как задачу на умножение. Смоделируйте свой ответ. 1. 2/5 разделить на 5 2. 3/4 разделить на 2
- спросил Аноним
- 524 просмотра
Вопрос быстрого расчета
Учитывая, что первообразная f от x равна 1, деленной на x, равна F(x) = Ln|x| + C, оцените интеграл от 1 до 2 от 1, деленной на x, dx.
 ln3 1/2 -1/2 ln2
ln3 1/2 -1/2 ln2- спросил Мел
- 1 773 просмотра
Математика
Если все числа в двоичной системе, решить уравнение x разделить на x+101=110 разделить на 1000
- спросил Kofovorola
- 598 просмотров
химия 93.. я знаю, что это масса, разделенная на объем, или граммы, разделенные на см, но что бы я сделал в такой ситуации?? спасибо
- спросил ammmyyy
- 288 просмотров
математика
Решите эту задачу на деление, используя многократное вычитание. Покажи все свои шаги! 27/9 = ________________ ps… косая черта (/) означает деление на…. 27 разделить на 9
- спросила божья коровка
- 814 просмотров
математика
Разделить.
 Запишите частное в меньших терминах. 2\dfrac{1}{2} \div 2\dfrac23 =2 2 1 ÷2 3 2 =2, начальная дробь, 1, разделить на, 2, конечная дробь, разделить на, 2, начальная дробь, 2, разделить на 3, конечная дробь, равно
Запишите частное в меньших терминах. 2\dfrac{1}{2} \div 2\dfrac23 =2 2 1 ÷2 3 2 =2, начальная дробь, 1, разделить на, 2, конечная дробь, разделить на, 2, начальная дробь, 2, разделить на 3, конечная дробь, равно- спросил Картофельный салат
- 619 просмотров
Математика
Сколько 1 1/2 разделить на 1/2? 3? 1 1/2, преобразованный в смешанную дробь, равен 3/2 3/2, разделенному на 1/2 3/2 x 2/1 6/2 6/2, уменьшенный = 3
- спросил Резу
- 1 043 просмотра
Математика
Вы говорите следующее утверждение: Под делением x на y вы имеете в виду x, деленное на y (т.е. 10/100), или вы имеете в виду y, деленное на x (т.е. 100/10? как y/x или y разделить на x. Надеюсь, это поможет. Спасибо, что спросили. Спасибо
- спросила Мисс Голливуд
- 1 673 просмотра
Математика
порядок действий 16 разделить на 4 .
 2= Я только что 16 разделил на 4, что равно 4, а затем умножил на 2, что равно 8. Я прав
2= Я только что 16 разделил на 4, что равно 4, а затем умножил на 2, что равно 8. Я прав- спросил Валери
- 673 просмотра
Математика
3. 8 2/5 x 5 1/2 4. 8x + 8 6. 6 разделить на 1/5 7. 3/8 разделить на 2/7 8. 8 2/5 разделить на 2 5/8 10. 6/5 разделить на ___ = 6 12. c/3 = 4 13. 2 1/3x = 7 7/8 МНЕ НУЖНА ПОМОЩЬ С ЭТИМИ
- спросил кот буханка
- 382 просмотра
Math
Коробка стирального порошка Brand A позволяет стирать 20 загрузок белья и стоит 6 долларов. Коробка стирального порошка марки B позволяет стирать 15 загрузок белья и стоит 5 долларов. В приведенных ниже таблицах соотношений укажите эквивалентные расценки на количество стирки в расчете на доллар. Включите около
- спросила Джинни
- 414 просмотров
алгебра
Продолжительность времени (T) в секундах, за которое маятник часов совершает один полный оборот, определяется по формуле маятник, и круг равен примерно 22, делённому на 7.

- спросил Кэролайн
- 6 305 просмотров
алгебра
Не могли бы вы помочь? Каковы решения сложного неравенства? 2x — 2 < - 12 или 2x+3 > 7 Является ли это x < - 5 или x> 2 2x -1/3 +3 = 6. Это 2x-1 разделить на 3 плюс 3 меньше или равно — 4 или 8x -2 разделить на 2 минус один больше или
- спросил Лулу
- 1 057 просмотров
математика 8-го класса
деление дробей….как мне решить это… 4/9 разделить на 2/3= или 9/10 разделить на 9/10= Одна вещь, которую я помню, это как делить дроби! 4/9 разделить на 2/3 = 4/9 умножить на 3/2 Затем, после умножения, уменьшите полученную дробь, если
- спросил Тая
- 2 021 просмотров
математика
Найти каждое частное 1,1/4 разделить на 3/8 2,1/3 разделить на 5/6
- спросил Помогите мне пожалуйста
- 5 429 просмотров
Математика
45 разделить на 5/11 4/7 разделить на 7/8 2 1/2 разделить на 4 5/7x =140 Пожалуйста, помогите Спасибо
- спросил Na
- 4 527 просмотров
Math
Запишите десятичный эквивалент, используя штриховую запись.
 5/11 Мне интересно, правильно ли я это делаю? 11 разделить на 5, что равно 0,4545 с повторением 45. 5 разделить на 11. Не 11 разделить на 5. Но вы придумали правильный ответ. Это будет .45
5/11 Мне интересно, правильно ли я это делаю? 11 разделить на 5, что равно 0,4545 с повторением 45. 5 разделить на 11. Не 11 разделить на 5. Но вы придумали правильный ответ. Это будет .45- спросил Фонда
- 695 просмотров
Вопрос быстрого расчета
интеграл от 2 до 3 от 1, деленный на количество, умноженное на 3 x минус 2, dx равен интегралу от 4 до 7 от 1, деленному на u, du Верно? ЛОЖЬ?
- спросила Элла
- 1 867 просмотров
Математика
Вот задача: определите, какая из следующих ситуаций может быть представлена делением 4 на 3/4, и объясните свои рассуждения. А) Сью нужно было покрасить 3/4 комнаты за 4 часа. Какую часть комнаты она должна красить каждый час, чтобы закончить вовремя? Б) у Кендры
- спросил Б.
 Б.
Б. - 564 просмотра
- спросил Б.
алгебра
Каков наклон линии, проходящей через (-5,2) и (6,7) в стандартной (x,y) координатной плоскости? Извините, я забыл варианты F.9 G.5 H.-5 J. 5/11 K. -5/11 Основная причина, по которой я не могу понять это, заключается в том, что я не могу вспомнить формулу наклона. Мне нужен наклон
- спросил Бейли
- 1 953 просмотра
math
Число оставляет напоминание 6 при делении на 10. Какой остаток при делении числа на 5? Обоснуйте свои рассуждения.
- спросил Аноним
- 891 просмотров
Алгебра
Учитывая, что 9 554 разделить на 562 = 17, как найти частное 95 540, деленное на 562? Пожалуйста помогите ответить спасибо
- спросила г-жа Лиз
- 1 514 просмотров
math
5÷3 3 1 =5, разделить на, 3, начальную дробь, 1, разделить на, 3, конечную дробь, равно ответьте, пожалуйста ?
- спросила jayda
- 807 просмотров
Math
Мэтт говорит, что выражения 12 разделить на p и p разделить на 12 эквивалентны.
 Дарла говорит, что они не эквивалентны. Кто прав. Я сказал да, если p = 12, оба ответа будут 1
Дарла говорит, что они не эквивалентны. Кто прав. Я сказал да, если p = 12, оба ответа будут 1- спросил TheGMA
- 1 344 просмотра
Химия
ПОМОГИТЕ! 🙂 Рассмотрим следующую реакцию: от 3A до 2B Средняя скорость появления B определяется делением deltaB на delta t. Сравнивая скорость появления B и скорость исчезновения A, мы получаем Delta B, деленную на Delta t = ___* (-delta A
- спросил Мел
- 1 728 просмотров
math
найти два числа, между которыми находится частное. Затем оцените частное. 2. 41 разделить на 3 3. 192 разделить на 5.
- спросил Эмилио
- 1 447 просмотров
математика
При делении m на 7 остаток равен 2.
 Какой остаток получается при делении 4m на 7? Пожалуйста, дайте мне объяснение, а не только ответ! Спасибо 🙂
Какой остаток получается при делении 4m на 7? Пожалуйста, дайте мне объяснение, а не только ответ! Спасибо 🙂- спросил Дженнифер
- 2 509 просмотров
Математика
Как вы делите дроби??? Перекрестное умножение: например, 4/5, разделенное на 6/7, будет 28/30 или 14/15. 3/4 разделить на 2/3 будет 92 + 66х — 80. Определить выражения для
- спросил Алекс
- 1 171 просмотров
МАТЕМАТИКА
Сфера имеет объем в пять раз больше прямого конуса, радиус 4,6 см и высоту 7,7 см. Определить радиус сферы с точностью до десятых долей сантиметра. Это вопрос множественного выбора, и это были варианты: A. 2,2 см B. 3,4 см C. 5,92-14x+42, остаток:-123
- спросил Мелисса
- 2 015 просмотров
english word
Если «четвертовать» означает, что объект был разделен на четыре части, какое слово мы используем для объекта, который был разделен на 5?
- спросил Анника
- 671 просмотров
92-3 25-3 22 (2) Сумма m и n, деленная на разность m и n.- спросил Jasmine20
- 1 243 просмотра
алгебра
сколько будет 7 больше, чем пятикратное число 9, деленное на 15? Ответ: 10, потому что 5 умножить на 9.= 45, и он говорит, что 45 разделить на 15, что равно 3, и он говорит, что семь больше, чем 9, деленное на 15, поэтому ответ равен 10.
- спросил Гермес
- 4 075 просмотров
математика
Привет! Если 1/8=1 фут по шкале, а дека равна 2 3/8 дюйма. Сколько будет футов, если 1/8 дюйма будет равно 1 футу 3/8, деленному на 1/8 = 3 фута 2 дюйма, деленному на 1/8 =
.- спросил semoine
- 662 просмотра
Chem 11
Итак, я провел лабораторную работу по определению химической формулы гидрата.
 Мне просто нужно, чтобы кто-нибудь проверил это для меня. Нам нужно было найти молекулярную формулу гидрата сульфата меди (2) CuSO4·xh3O. Моя таблица наблюдения выглядит так: Масса чистого,
Мне просто нужно, чтобы кто-нибудь проверил это для меня. Нам нужно было найти молекулярную формулу гидрата сульфата меди (2) CuSO4·xh3O. Моя таблица наблюдения выглядит так: Масса чистого,- спросила Кэтрин
- 4 570 просмотров
Математика
при делении z на 8 получается остаток 5. Какой остаток при делении 4z на 8. Не могли бы вы объяснить мне это шаг за шагом? Мне трудно понять, почему ответ 4
- спросил Карен
- 1 412 просмотров
English
1. Комитет разделился во мнениях. 2. Комитет разделился во мнениях. 3. Комитет разделился во мнениях. [Какие предложения грамматические?]
- спросил rfvv
- 10 754 просмотра
Математика
Какое из приведенных ниже предложений может представлять 4 ÷ p = 2? А.
 Четыре разделить на два равно числу. Б. Четыре разделить на число равно двум. C. Число, деленное на четыре, равно двум. D. Четырежды число равно двум.
Четыре разделить на два равно числу. Б. Четыре разделить на число равно двум. C. Число, деленное на четыре, равно двум. D. Четырежды число равно двум.- спросила Ангелина
- 1 216 просмотров
Химия 11
Итак, я провел лабораторную работу по определению химической формулы гидрата. Нам нужно было найти молекулярную формулу гидрата сульфата меди (2) CuSO4·xh3O. Моя таблица наблюдений выглядит следующим образом: Масса чистой, сухой пробирки: 21,6 г Масса пробирки + гидратированная
- спросила Кэтрин
- 1 729 просмотров
Алгебра
4. Ниже показана работа учащегося по решению деления 2 6/7 на 2/7. с каким из следующих утверждений вы согласны? 2 6/7 разделить на 2/7 = 19/7 разделить на 2/7= 7/19 умножить на 2/7= 7/19 умножить на 2/7=2/19 зачеркнуть 7 в первой поставить единицу и вычеркнуть
- спросил Шейли ^~^
- 1 217 просмотров
Алгебра
Работа учащегося по решению деления 2 6/7 на 2/7 показана ниже.
 с каким из следующих утверждений вы согласны? 2 6/7 разделить на 2/7 = 19/7 разделить на 2/7= 7/19 умножить на 2/7= 7/19 умножить на 2/7=2/19 зачеркнуть 7 в первой поставить единицу и вычеркнуть
с каким из следующих утверждений вы согласны? 2 6/7 разделить на 2/7 = 19/7 разделить на 2/7= 7/19 умножить на 2/7= 7/19 умножить на 2/7=2/19 зачеркнуть 7 в первой поставить единицу и вычеркнуть- спросил Никло
- 3 858 просмотров
Math
Доска длиной 64 дюйма разделена на части в соотношении 2:3. На какие две части разделена доска? Спасибо
- спросил Тень
- 976 просмотров
math
6 разделить на разность числа и 2, минус 5 разделить на число плюс 2, равно 5, умноженной на обратную разницу между квадратом числа и 4. Что такое число? Помогите пожалуйста СРОЧНО!!!!!!!!! 🙁 92+3х-2, остаток 9х-6. (I) Найдите значения a и b (II) Используя эти значения a и b, полностью разложите p(x) на множители (III) Найдите остаток от деления p(x)
- спросил Ande2
- 3 908 просмотров
деление дробей
Деление дробей иногда называют умножением обратных чисел.
 Уточните с объяснением и примером. Если у вас есть a/b, разделенное на c/d, это то же самое, что и a/b * d/c Если, например, у нас есть 2/3, разделенное на 7/92-4.
Уточните с объяснением и примером. Если у вас есть a/b, разделенное на c/d, это то же самое, что и a/b * d/c Если, например, у нас есть 2/3, разделенное на 7/92-4.- спросил Азу
- 1 457 просмотров
Химия
Если 10,0 г CaCl2 и 10,0 г NaCl растворить в 100,0 мл раствора, какова концентрация ионов хлора? (молярная масса CaCl2 111,0 г/моль; молярная масса NaCl 58,44 г/моль. Я нашел индивидуальную молярную массу: Ca-40,08 Cl-35,45 Na-22,99
- спросил Кейси
- 620 просмотров
calc
Учитывая функцию положения, s of t равно отрицательному значению t в кубе, деленному на 3, плюс 13, умноженное на t в квадрате, деленное на 2, минус 30, умноженное на t, между t = 0 и t = 9, где s дано в футах, а t равно измеряется в секундах, найдите интервал в секундах, в течение которого частица
- спросил Мел
- 4 078 просмотров
Математика
Каковы шаги, чтобы показать частное в простейшей форме? Не забудьте включить различные ключевые слова.
 0,000027 разделить на 0,000009 Мой ответ 0,000027 разделить на 0,000009=3 Определение частного Ответ после деления одного числа на другое. Коэффициент в
0,000027 разделить на 0,000009 Мой ответ 0,000027 разделить на 0,000009=3 Определение частного Ответ после деления одного числа на другое. Коэффициент в- спросил Аноним
- 2 620 просмотров
Пожалуйста, помогите мне решить это — PreCalc
Используйте тождества, чтобы найти точное значение тригонометрического выражения ниже. 1/cos2 * π/16 — 1/cot2 * π/16 PS: на словах проблема в том, что один делится на косинус-квадрат, тогда рядом с косинусом-квадратом (по-прежнему в знаменателе) стоит пи/16. Минус один деленный
- спросил chizoba
- 418 просмотров
средняя школа (математика)
Сопоставьте математическое выражение с его переводом. 1. произведение двух чисел 2. у делится на х 3. на шесть меньше числа равно у 4. х вычитается из у 5.
 сумма двух чисел равна шести 6. х минус у 7. сумма х и у 8. x разделить на y 9. шесть раз
сумма двух чисел равна шести 6. х минус у 7. сумма х и у 8. x разделить на y 9. шесть раз- спросил надежда
- 2 787 просмотров
adv алгебра
Когда число делится на 5, а затем вычитается 3, ответ будет таким же, как если число делится на 4, а затем вычитается 2. Это 0? Как показать?
- спросила Лиза
- 312 просмотров
математика
1. 7 1/2 разделить на 3 3/4 2. 9 разделить на 2 1/4 3. Шон пробежал 3 1/2 мили за 28 минут. За какое время он пробежит 1 км? 4. 8 1/4 фунта муки используется для приготовления 4 1/8 рецептов пасты для папье-маше. Сколько муки уходит на приготовление 1 рецепта? 5.
- спросил лол
- 4 377 просмотров
Математика
Один спиннер разделен на пять равных секций, пронумерованных от 1 до 5.
 Второй спиннер разделен на семь равных секций, пронумерованных от 6 до 12. Сколько всего будет результатов, если оба спиннера будут вращаться? Пожалуйста помоги.
Второй спиннер разделен на семь равных секций, пронумерованных от 6 до 12. Сколько всего будет результатов, если оба спиннера будут вращаться? Пожалуйста помоги.- спросил Даника 9-6] Разделить обе стороны на
- спросила Екатерина
- 956 просмотров
математика
У Джо дробь 5 на 6 фунтов птичьего семени. Ему нужна фракция 1 свыше 3 фунтов, чтобы кормить птиц ежедневно. Какая из представленных ниже прямоугольных моделей показывает, на сколько дней осталось семян Джо? (1 балл) Прямоугольная модель, разделенная на шесть равных частей, пять
- спросил Мэдисон
- 781 просмотров
трение
\dfrac15 5 1 начальная дробь, 1, разделить на, 5, конечная дробь животные в зоопарке — обезьяны.
 \dfrac57 7 5 начальная дробь , 5, разделить на, 7, конечная дробь обезьян — самцы.
\dfrac57 7 5 начальная дробь , 5, разделить на, 7, конечная дробь обезьян — самцы.- спросил Аноним
- 560 просмотров
Математика
1.Раздели.Запиши свой ответ в простейшей форме. (1 балл) 2/3 разделить на 1/4 a.2 1/2 b.2 2/3 c.2 3/8 d.2 2. Найдите произведение. (1 балл) 1/2*3/7 a.4/14 b.3/14 c.7/6 d.2/7 3.Разделите.Запишите частное в простейшей форме. (1 балл) 3/5 разделить на 2/10 a.6/10 b.3/5
- спросил Роуз Джонсон
- 4 563 просмотра
93 + 6x + 4 делится на x + 2, остаток равен 8. Найдите остаток при делении этого многочлена на x-1.- спросил Джейсон
- 333 просмотра
chem
, поэтому вчера я отправил этот вопрос и получил некоторую помощь.
 что ниже. можете ли вы взглянуть на последнее, что я сказал, что было ответом, который я получил, делая то, что сказал DrBob222, и сказать мне, правильно ли это (вопрос в первом разделе) спасибо chem —
что ниже. можете ли вы взглянуть на последнее, что я сказал, что было ответом, который я получил, делая то, что сказал DrBob222, и сказать мне, правильно ли это (вопрос в первом разделе) спасибо chem —- спросил Ханна
- 782 просмотра
Геометрия; Проверить ответы?
Для каждого графика найдите (a)AB с точностью до десятых и (b)координаты середины AB. 1. Координаты: A(-9,-6) B(6,6) D=19,2 Середина=(1,5,-6) 2.A(-2,-2) B(8,-6) D=10,77 середина = (3,-4) 3. A(0,3) B(-2,-2) D=5,4 Средняя точка= (-1,0,5)
- спросил Неизвестный
- 6 445 просмотров
American Government
7. Какие из следующих шести организационных принципов очевидны в статьях I–III Конституции США? Выбрать все, что подходит. A. Ограниченное правительство.
 *** B. Разделение властей. C. Судебный пересмотр.*** D. Система сдержек и противовесов. 8. Какой из
*** B. Разделение властей. C. Судебный пересмотр.*** D. Система сдержек и противовесов. 8. Какой из- спросил Эбби
- 2 124 просмотра
Физика
Частица движется со скоростью 0,75с относительно лаборатории на Земле. На сколько процентов ошибочно ньютоновское выражение для его импульса, т. е. насколько ошибочна классическая формула? (Процентная ошибка — это разница между ошибочным и правильным значениями,
- спросил Дэвид
- 1 745 просмотров 92-4ас разделить на 2а. Я знаю, что a=3, b=-15 и c=18, затем подставляю и получаю два ответа, моя проблема в том, что я продолжаю получать ответ
- спросил Лекси
- 1 374 просмотра
Значения Rf
Вопрос: Рассмотрим образец, представляющий собой смесь бифенила, бензойной кислоты и бензилового спирта.
 Образец наносят на пластину для ТСХ и проявляют в смеси растворителей дихлорметан-циклобутан. Предсказать относительные значения Rf для трех
Образец наносят на пластину для ТСХ и проявляют в смеси растворителей дихлорметан-циклобутан. Предсказать относительные значения Rf для трех- спросил Шерил
- 2 877 просмотров
алгебра
если 5 разделить на число, то результат будет на 3 больше, чем 7 разделить на удвоенное число. какой номер? А)1 С)1/2 Б)2 Г)5
- спросил Виктория
- 1 555 просмотров
МАТЕМАТИКА
У меня есть три вопроса: 1. Какой остаток при делении 27 в степени 1001 на 13? 2. Каков остаток от деления 38 в степени 101 на 13? 3. Как показать, что 70 х 27 (в степени 1001) + 31 х 38 (в степени 101)
- спросил ДЖОН
- 403 просмотра
алгебра — 1 вопрос
Предположим, вы делите многочлен на двучлен.
. Как узнать, является ли бином делителем многочлена? Создайте примерную задачу с биномом, являющимся множителем делимого многочлена, и другую задачу с биномом, равным
Как узнать, является ли бином делителем многочлена? Создайте примерную задачу с биномом, являющимся множителем делимого многочлена, и другую задачу с биномом, равным- спросил SkatingDJ
- 1 334 просмотра
Math
Если 2484 члена профсоюза представляют 90% рабочей силы фабрики сколько рабочих занято? Я использовал эту формулу r*b=a, так что 90 — моя ставка; база неизвестна, а 2484 — это сумма. Я разделил 90 на 2484 и получил 276, но я знаю, что это не так.
- спросил **renak
- 1 010 просмотров
Химия
Для соединения С13х28О2 (ибупрофен) определите молекулы ибупрофена, содержащие 15 моль водорода? Я пропустил шаг, и я пытаюсь понять это. Я попробовал 15 моль H x 1 моль C13 h28 O2 разделить на 1 моль H и получил 15 моль C13 h28 O2, затем
- спросил TMV
- 1 187 просмотров
физика
Мужчина едет на своей машине со скоростью 100 км/ч по прямой дороге.
 Он видит пробку на расстоянии и замедляется до 12,5 м/с за 3,0 с. Каково среднее ускорение автомобиля? Пожалуйста, помогите. Я знаю, что формула среднего ускорения V2-V1
Он видит пробку на расстоянии и замедляется до 12,5 м/с за 3,0 с. Каково среднее ускорение автомобиля? Пожалуйста, помогите. Я знаю, что формула среднего ускорения V2-V1- спросил Тед
- 725 просмотров
Страницы
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
Формула множественной регрессии | Расчет уравнения множественной регрессии
Формула множественной регрессии используется при анализе взаимосвязи между зависимыми и несколькими независимыми переменными, и формула представлена уравнением Y равно a плюс bX1 плюс cX2 плюс dX3 плюс E, где Y — зависимая переменная, X1, X2, X3 — независимые переменные, a — точка пересечения, b, c, d — наклоны, E — остаточное значение.

y = mx1 + mx2+ mx3+ b
Вы можете использовать это изображение на своем веб-сайте, в шаблонах и т. д. Пожалуйста, предоставьте нам ссылку с указанием авторства. Как указать авторство? Ссылка на статью должна быть гиперссылкой
Например:
Источник: Формула множественной регрессии (wallstreetmojo.com)Где,
- Y= зависимая переменная регрессии
- M= наклон регрессии
- X1=первая независимая переменная регрессии
- x2 = вторая независимая переменная регрессии
- x3 = третья независимая переменная регрессии
- B = константа
Содержание
- Что такое формула множественной регрессии?
- Объяснение формулы регрессионного анализа
- Примеры
- Пример №1
- Пример №2
- Пример №3
- Релевантность и использование
- Рекомендуемые статьи 4 14
- y = MX + MX + b
- y= 604,17*-3,18+604,17*-4,06+0 8 9366 4377
- Y = MX + MX + B
- Y = 41308*.- 71 + 41308*-824 + 0
- *2925111111192.39251 2924 2924.
- Относительное изменение Относительное изменение Относительное изменение показывает изменение значения показателя в первом периоде и в процентах, т.е. относительное изменение рассчитывается путем вычитания значения показателя в первого периода от значения показателя во втором периоде, которое затем делится на значение показателя в первом периоде и результат выносится в процентах.читать далее
- Формула корреляцииФормула корреляцииКорреляция — это статистическая мера между двумя переменными, которая определяется как изменение одной переменной, соответствующее изменению другой.

Объяснение формулы регрессионного анализа
Множественные регрессии — это метод прогнозирования зависимой переменной с помощью двух или более независимых переменных.
 При выполнении этого анализа основная цель исследователя — выяснить взаимосвязь между зависимой переменной и независимыми переменными. Чтобы предсказать зависимую переменную, выбирают несколько независимых переменных, которые могут помочь в предсказании зависимой переменной. Он используется, когда линейная регрессия не может служить цели. Регрессионный анализ помогает в процессе проверки того, достаточно ли хороши переменные-предикторы, чтобы помочь в прогнозировании зависимой переменной.
При выполнении этого анализа основная цель исследователя — выяснить взаимосвязь между зависимой переменной и независимыми переменными. Чтобы предсказать зависимую переменную, выбирают несколько независимых переменных, которые могут помочь в предсказании зависимой переменной. Он используется, когда линейная регрессия не может служить цели. Регрессионный анализ помогает в процессе проверки того, достаточно ли хороши переменные-предикторы, чтобы помочь в прогнозировании зависимой переменной.Примеры
Вы можете скачать этот шаблон Excel с формулой множественной регрессии здесь – Шаблон Excel с формулой множественной регрессии
Пример №1
Давайте попробуем понять концепцию анализа множественной регрессии с помощью примера. Попробуем выяснить, как связана пройденная водителем UBER дистанция с возрастом водителя и количеством лет стажа водителя.
Для расчета множественной регрессии перейдите на вкладку «Данные» в Excel и выберите параметр анализа данных.
 Для дальнейшей процедуры и расчета обратитесь к данной статье здесь – Пакет инструментов анализа в ExcelПакет анализа данных В Excel Пакет инструментов анализа данных Excel может использоваться пользователями для выполнения анализа данных и других важных вычислений. Его можно включить вручную в разделе надстроек на вкладке файлов, нажав «Управление надстройками», а затем отметив пакет инструментов для анализа.Подробнее
Для дальнейшей процедуры и расчета обратитесь к данной статье здесь – Пакет инструментов анализа в ExcelПакет анализа данных В Excel Пакет инструментов анализа данных Excel может использоваться пользователями для выполнения анализа данных и других важных вычислений. Его можно включить вручную в разделе надстроек на вкладке файлов, нажав «Управление надстройками», а затем отметив пакет инструментов для анализа.ПодробнееФормула регрессииФормула регрессииФормула регрессии используется для оценки взаимосвязи между зависимой и независимой переменными и для определения того, как изменение независимой переменной влияет на зависимую переменную. Y = a + b X + читать далее для приведенного выше примера будет
В этом конкретном примере мы увидим, какая переменная является зависимой, а какая независимой. Зависимой переменной в этом регрессионном уравнении является расстояние, пройденное водителем UBER, а независимыми переменными — возраст водителя и его стаж вождения.

Пример #2
Давайте попробуем понять концепцию анализа множественных регрессий с помощью другого примера. Попробуем выяснить, как связана средняя оценка класса студентов с количеством часов обучения и ростом студентов.
Для расчета перейдите на вкладку «Данные» в Excel и выберите параметр анализа данных.
Уравнение регрессии для приведенного выше примера будет
y = MX + MX + b
y= 1.08*.03+1.08*-.002+0
y= .0325
В этом конкретном примере мы увидим, какая переменная является зависимой и какая переменная является зависимой. независимая переменная. Зависимой переменной в этой регрессии является средний балл, а независимыми переменными являются количество учебных часов и рост учащихся.
Пример №3
Давайте попробуем понять концепцию анализа множественных регрессий на другом примере. Попытаемся выяснить, как связана заработная плата группы работников в организации со стажем и возрастом работников.

Для расчета перейдите на вкладку «Данные» в Excel и выберите параметр «Анализ данных».
Уравнение регрессии для вышеуказанного примера будет
В этом конкретном примере мы увидим, какая переменная является зависимой, а какая независимой. Зависимой переменной в этом уравнении регрессии является заработная плата, а независимыми переменными являются опыт и возраст сотрудников.
Релевантность и использование
Множественная регрессия — очень полезный статистический метод. Регрессия играет очень важную роль в мире финансов. Многие прогнозы выполняются с использованием регрессии. Регрессия. Регрессионный анализ — это статистический подход к оценке взаимосвязи между 1 зависимой переменной и 1 или более независимыми переменными. Он широко используется в инвестиционном и финансовом секторах для дальнейшего улучшения продуктов и услуг.
 читать дальше анализ. Например, продажи определенного сегмента можно прогнозировать заранее с помощью макроэкономических показателей, которые имеют очень хорошую корреляцию с этим сегментом.
читать дальше анализ. Например, продажи определенного сегмента можно прогнозировать заранее с помощью макроэкономических показателей, которые имеют очень хорошую корреляцию с этим сегментом.Рекомендуемые статьи
Это руководство по формуле множественной регрессии. Здесь мы обсуждаем, как выполнять множественную регрессию с использованием анализа данных, а также примеры и загружаемый шаблон Excel. Подробнее о статистическом моделировании можно узнать из следующих статей –
 Мой ответ: (m+n)/ (m-n) (3) Частное деления числа, на которое больше 3, на 3 меньше того же числа Мой ответ: (x+3)/(x-3) Это все
Мой ответ: (m+n)/ (m-n) (3) Частное деления числа, на которое больше 3, на 3 меньше того же числа Мой ответ: (x+3)/(x-3) Это все



 5
5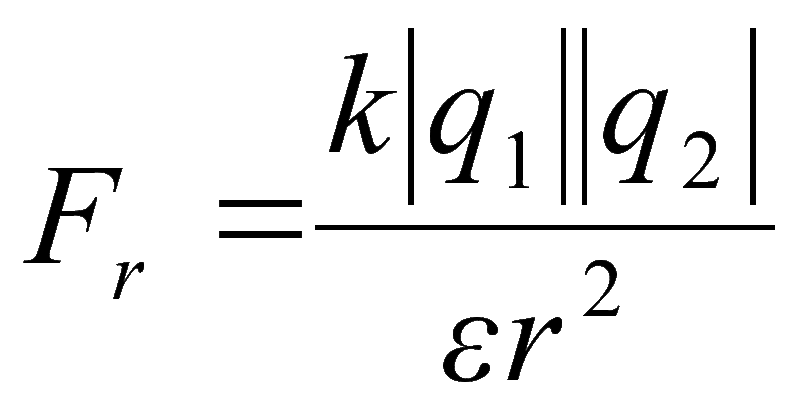 8
8 83
83 это
это 4,5 разделить на 0,9 = 0,6 разделить на 0,12 = 1,2 разделить на 0,5 = 22,5 разделить на 0,5 = 0,18 разделить на 0,03 =
4,5 разделить на 0,9 = 0,6 разделить на 0,12 = 1,2 разделить на 0,5 = 22,5 разделить на 0,5 = 0,18 разделить на 0,03 = Какое уравнение можно использовать, чтобы найти B, площадь заштрихованного основания в квадратных сантиметрах? (H=4 L=6 W=5) A. B= 5(6) B. B= 5(6) разделить на 2 C. B= 4(5) D. B= 4(5) разделить на 2
Какое уравнение можно использовать, чтобы найти B, площадь заштрихованного основания в квадратных сантиметрах? (H=4 L=6 W=5) A. B= 5(6) B. B= 5(6) разделить на 2 C. B= 4(5) D. B= 4(5) разделить на 2 Что такое частное? они означают 35 разделить на 5 = 7, 35 разделить на 7 = 5 или по знаку? 92-х-6
Что такое частное? они означают 35 разделить на 5 = 7, 35 разделить на 7 = 5 или по знаку? 92-х-6 W разделить на P – Y > H W умножить на P разделить на Y > H WP – Y > H W + P – Y > H 92+nx+5 дает остаток 128 при делении на x-3 и остаток 4 при делении на x+1. вычислить остаток, когда
W разделить на P – Y > H W умножить на P разделить на Y > H WP – Y > H W + P – Y > H 92+nx+5 дает остаток 128 при делении на x-3 и остаток 4 при делении на x+1. вычислить остаток, когда При делении n на 8 остаток равен: A.0 B.1 C.2 D.4 E.6 Я пробовал делать n/ 24=18 и я получил 432 и когда я разделил это на 8 я получил 54; я неправильно понимаю вопрос? Я действительно не вижу других
При делении n на 8 остаток равен: A.0 B.1 C.2 D.4 E.6 Я пробовал делать n/ 24=18 и я получил 432 и когда я разделил это на 8 я получил 54; я неправильно понимаю вопрос? Я действительно не вижу других Какое уравнение для обратного изменения? A. y равно 6, деленное на 4, умноженное на x. B. y равно 24, деленное на x. C. y равняется двум третям, умноженным на x. D. y равно x, деленному на 24,
Какое уравнение для обратного изменения? A. y равно 6, деленное на 4, умноженное на x. B. y равно 24, деленное на x. C. y равняется двум третям, умноженным на x. D. y равно x, деленному на 24, ln3 1/2 -1/2 ln2
ln3 1/2 -1/2 ln2 Запишите частное в меньших терминах. 2\dfrac{1}{2} \div 2\dfrac23 =2 2 1 ÷2 3 2 =2, начальная дробь, 1, разделить на, 2, конечная дробь, разделить на, 2, начальная дробь, 2, разделить на 3, конечная дробь, равно
Запишите частное в меньших терминах. 2\dfrac{1}{2} \div 2\dfrac23 =2 2 1 ÷2 3 2 =2, начальная дробь, 1, разделить на, 2, конечная дробь, разделить на, 2, начальная дробь, 2, разделить на 3, конечная дробь, равно 2= Я только что 16 разделил на 4, что равно 4, а затем умножил на 2, что равно 8. Я прав
2= Я только что 16 разделил на 4, что равно 4, а затем умножил на 2, что равно 8. Я прав
 5/11 Мне интересно, правильно ли я это делаю? 11 разделить на 5, что равно 0,4545 с повторением 45. 5 разделить на 11. Не 11 разделить на 5. Но вы придумали правильный ответ. Это будет .45
5/11 Мне интересно, правильно ли я это делаю? 11 разделить на 5, что равно 0,4545 с повторением 45. 5 разделить на 11. Не 11 разделить на 5. Но вы придумали правильный ответ. Это будет .45 Б.
Б.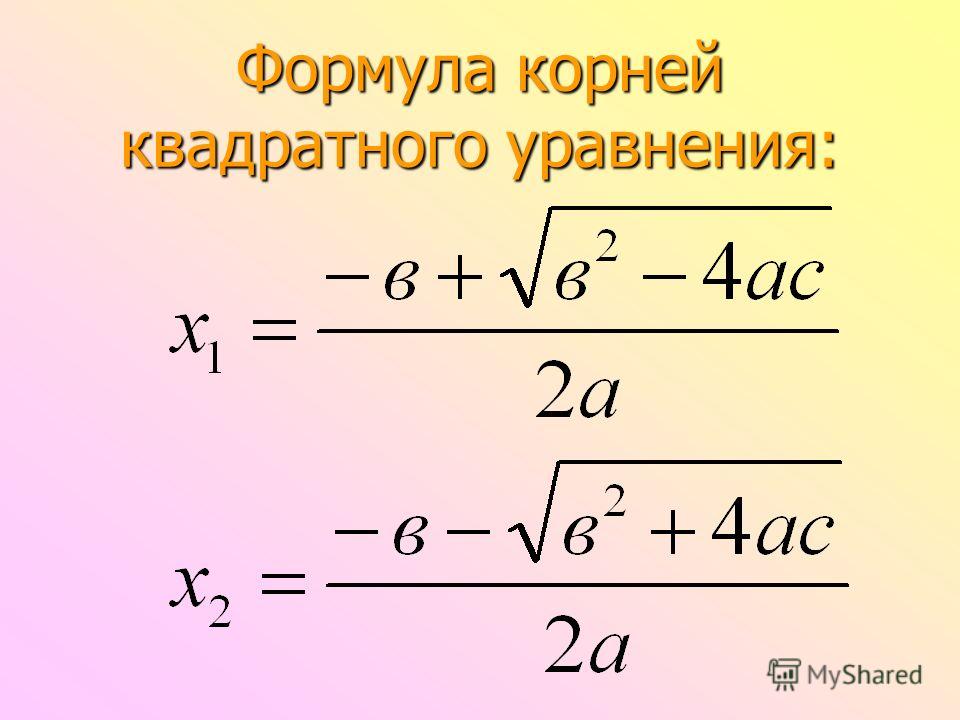 Дарла говорит, что они не эквивалентны. Кто прав. Я сказал да, если p = 12, оба ответа будут 1
Дарла говорит, что они не эквивалентны. Кто прав. Я сказал да, если p = 12, оба ответа будут 1 Какой остаток получается при делении 4m на 7? Пожалуйста, дайте мне объяснение, а не только ответ! Спасибо 🙂
Какой остаток получается при делении 4m на 7? Пожалуйста, дайте мне объяснение, а не только ответ! Спасибо 🙂 Мне просто нужно, чтобы кто-нибудь проверил это для меня. Нам нужно было найти молекулярную формулу гидрата сульфата меди (2) CuSO4·xh3O. Моя таблица наблюдения выглядит так: Масса чистого,
Мне просто нужно, чтобы кто-нибудь проверил это для меня. Нам нужно было найти молекулярную формулу гидрата сульфата меди (2) CuSO4·xh3O. Моя таблица наблюдения выглядит так: Масса чистого, Четыре разделить на два равно числу. Б. Четыре разделить на число равно двум. C. Число, деленное на четыре, равно двум. D. Четырежды число равно двум.
Четыре разделить на два равно числу. Б. Четыре разделить на число равно двум. C. Число, деленное на четыре, равно двум. D. Четырежды число равно двум. с каким из следующих утверждений вы согласны? 2 6/7 разделить на 2/7 = 19/7 разделить на 2/7= 7/19 умножить на 2/7= 7/19 умножить на 2/7=2/19 зачеркнуть 7 в первой поставить единицу и вычеркнуть
с каким из следующих утверждений вы согласны? 2 6/7 разделить на 2/7 = 19/7 разделить на 2/7= 7/19 умножить на 2/7= 7/19 умножить на 2/7=2/19 зачеркнуть 7 в первой поставить единицу и вычеркнуть Уточните с объяснением и примером. Если у вас есть a/b, разделенное на c/d, это то же самое, что и a/b * d/c Если, например, у нас есть 2/3, разделенное на 7/92-4.
Уточните с объяснением и примером. Если у вас есть a/b, разделенное на c/d, это то же самое, что и a/b * d/c Если, например, у нас есть 2/3, разделенное на 7/92-4. 0,000027 разделить на 0,000009 Мой ответ 0,000027 разделить на 0,000009=3 Определение частного Ответ после деления одного числа на другое. Коэффициент в
0,000027 разделить на 0,000009 Мой ответ 0,000027 разделить на 0,000009=3 Определение частного Ответ после деления одного числа на другое. Коэффициент в сумма двух чисел равна шести 6. х минус у 7. сумма х и у 8. x разделить на y 9. шесть раз
сумма двух чисел равна шести 6. х минус у 7. сумма х и у 8. x разделить на y 9. шесть раз Второй спиннер разделен на семь равных секций, пронумерованных от 6 до 12. Сколько всего будет результатов, если оба спиннера будут вращаться? Пожалуйста помоги.
Второй спиннер разделен на семь равных секций, пронумерованных от 6 до 12. Сколько всего будет результатов, если оба спиннера будут вращаться? Пожалуйста помоги. \dfrac57 7 5 начальная дробь , 5, разделить на, 7, конечная дробь обезьян — самцы.
\dfrac57 7 5 начальная дробь , 5, разделить на, 7, конечная дробь обезьян — самцы. что ниже. можете ли вы взглянуть на последнее, что я сказал, что было ответом, который я получил, делая то, что сказал DrBob222, и сказать мне, правильно ли это (вопрос в первом разделе) спасибо chem —
что ниже. можете ли вы взглянуть на последнее, что я сказал, что было ответом, который я получил, делая то, что сказал DrBob222, и сказать мне, правильно ли это (вопрос в первом разделе) спасибо chem — *** B. Разделение властей. C. Судебный пересмотр.*** D. Система сдержек и противовесов. 8. Какой из
*** B. Разделение властей. C. Судебный пересмотр.*** D. Система сдержек и противовесов. 8. Какой из Образец наносят на пластину для ТСХ и проявляют в смеси растворителей дихлорметан-циклобутан. Предсказать относительные значения Rf для трех
Образец наносят на пластину для ТСХ и проявляют в смеси растворителей дихлорметан-циклобутан. Предсказать относительные значения Rf для трех Как узнать, является ли бином делителем многочлена? Создайте примерную задачу с биномом, являющимся множителем делимого многочлена, и другую задачу с биномом, равным
Как узнать, является ли бином делителем многочлена? Создайте примерную задачу с биномом, являющимся множителем делимого многочлена, и другую задачу с биномом, равным Он видит пробку на расстоянии и замедляется до 12,5 м/с за 3,0 с. Каково среднее ускорение автомобиля? Пожалуйста, помогите. Я знаю, что формула среднего ускорения V2-V1
Он видит пробку на расстоянии и замедляется до 12,5 м/с за 3,0 с. Каково среднее ускорение автомобиля? Пожалуйста, помогите. Я знаю, что формула среднего ускорения V2-V1
 При выполнении этого анализа основная цель исследователя — выяснить взаимосвязь между зависимой переменной и независимыми переменными. Чтобы предсказать зависимую переменную, выбирают несколько независимых переменных, которые могут помочь в предсказании зависимой переменной. Он используется, когда линейная регрессия не может служить цели. Регрессионный анализ помогает в процессе проверки того, достаточно ли хороши переменные-предикторы, чтобы помочь в прогнозировании зависимой переменной.
При выполнении этого анализа основная цель исследователя — выяснить взаимосвязь между зависимой переменной и независимыми переменными. Чтобы предсказать зависимую переменную, выбирают несколько независимых переменных, которые могут помочь в предсказании зависимой переменной. Он используется, когда линейная регрессия не может служить цели. Регрессионный анализ помогает в процессе проверки того, достаточно ли хороши переменные-предикторы, чтобы помочь в прогнозировании зависимой переменной. Для дальнейшей процедуры и расчета обратитесь к данной статье здесь – Пакет инструментов анализа в ExcelПакет анализа данных В Excel Пакет инструментов анализа данных Excel может использоваться пользователями для выполнения анализа данных и других важных вычислений. Его можно включить вручную в разделе надстроек на вкладке файлов, нажав «Управление надстройками», а затем отметив пакет инструментов для анализа.Подробнее
Для дальнейшей процедуры и расчета обратитесь к данной статье здесь – Пакет инструментов анализа в ExcelПакет анализа данных В Excel Пакет инструментов анализа данных Excel может использоваться пользователями для выполнения анализа данных и других важных вычислений. Его можно включить вручную в разделе надстроек на вкладке файлов, нажав «Управление надстройками», а затем отметив пакет инструментов для анализа.Подробнее

 читать дальше анализ. Например, продажи определенного сегмента можно прогнозировать заранее с помощью макроэкономических показателей, которые имеют очень хорошую корреляцию с этим сегментом.
читать дальше анализ. Например, продажи определенного сегмента можно прогнозировать заранее с помощью макроэкономических показателей, которые имеют очень хорошую корреляцию с этим сегментом.