Основные задачи о прямых и плоскостях
Уравнение прямой, проходящей через две точки.
Начать изучение
Уравнение плоскости, проходящей через три точки.
Начать изучение
Параллельность прямой и плоскости.
Начать изучение
Полупространство.
Начать изучение
Расстояние от точки до плоскости.
Начать изучение
Расстояние от точки до прямой.
Начать изучение
Расстояние между скрещивающимися прямыми.
Начать изучение
Вычисление углов.

Начать изучение
Некоторые задачи на построение.
Начать изучение
Перпендикуляр из точки на плоскость. Проекция точки.
Начать изучение
Перпендикуляр из точки на прямую.
Начать изучение
Уравнение проекции прямой на плоскость.
Начать изучение
Общий перпендикуляр к двум скрещивающимся прямым.
Начать изучение
Пучок прямых.
Начать изучение
-
О геометрическом смысле порядка алгебраической линии.

Начать изучение
Уравнение прямой, проходящей через две точки.
Пусть в пространстве задана общая декартова система координат и две точки \(M_{1}\) и \(M_{2}\) с координатами \((x_{1}, y_{1}, z_{1})\) и \((x_{2}, y_{2}, z_{2})\). Чтобы написать уравнение прямой \(M_{1}M_{2}\), примем \(M_{1}\) за начальную точку, a \(\overrightarrow{M_{1}M_{2}}\) за направляющий вектор. Этот вектор не нулевой, если точки не совпадают. По формуле уравнения прямой в пространстве мы получаем
$$
\frac{x-x_{1}}{x_{2}-x_{1}}=\frac{y-y_{1}}{y_{2}-y_{1}}=\frac{z-z_{1}}{z_{2}-z_{1}}.\label{ref1}
$$
Если в этих равенствах какой-либо из знаменателей равен нулю, то следует приравнять нулю соответствующий числитель.
В планиметрии задача решается также. Отличие только в том, что координаты точек теперь \((x_{1}, y_{1})\) и \((x_{2}, y_{2})\), и мы получаем по формуле для прямой на плоскости
$$
\begin{vmatrix}
x-x_{1}& y-y_{1}\\
x_{2}-x_{1}& y_{2}-y_{1}
\end{vmatrix}
= 0.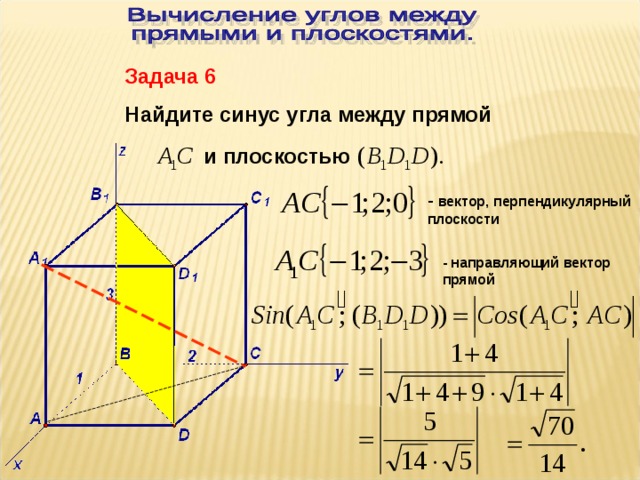 \nonumber
\nonumber
$$
Уравнение плоскости, проходящей через три точки.
Пусть \(M_{1}\), \(M_{2}\) и \(M_{3}\) — не лежащие на одной прямой точки с координатами \((x_{1}, y_{1}, z_{1})\), \((x_{2}, y_{2}, z_{2})\) и \((x_{3}, y_{3}, z_{3})\) в общей декартовой системе координат. Выберем \(M_{1}\) в качестве начальной точки, a \(\overrightarrow{M_{1}M_{2}}\) и \(\overrightarrow{M_{1}M_{3}}\) в качестве направляющих векторов. Тогда по формуле о компланарности прямой и плоскости и формуле для выражения смешанного произведения через координаты получаем уравнение плоскости
$$
\begin{vmatrix}
x-x_{1}& y-y_{1}& z-z_{1}\\
x_{2}-x_{1}& y_{2}-y_{1}& z_{2}-z_{1}\\
x_{3}-x_{1}& y_{3}-y_{1}& z_{3}-z_{1}
\end{vmatrix}
= 0.\label{ref2}
$$
Параллельность прямой и плоскости.
Пусть известен направляющий вектор прямой \(\boldsymbol{a}(\alpha_{1}, \alpha_{2}, \alpha_{3})\), а плоскость задана одним из уравнений \((\boldsymbol{r}-\boldsymbol{r}_{0}, \boldsymbol{n})=0\) или \((\boldsymbol{r}-\boldsymbol{r}_{0}, \boldsymbol{p}, \boldsymbol{q})=0\). Прямая параллельна плоскости (а возможно, и лежит в ней) тогда и только тогда, когда соответственно \((\boldsymbol{a}, \boldsymbol{n}=0)\) или \((\boldsymbol{a}, \boldsymbol{p}, \boldsymbol{q}=0)\). Если плоскость задана линейным уравнением \(Ax+By+Cz+D=0\), то по утверждению 5, доказанному ранее, условие параллельности —
Прямая параллельна плоскости (а возможно, и лежит в ней) тогда и только тогда, когда соответственно \((\boldsymbol{a}, \boldsymbol{n}=0)\) или \((\boldsymbol{a}, \boldsymbol{p}, \boldsymbol{q}=0)\). Если плоскость задана линейным уравнением \(Ax+By+Cz+D=0\), то по утверждению 5, доказанному ранее, условие параллельности —
$$
A\alpha_{1}+B\alpha_{2}+C\alpha_{3}=0.\label{ref3}
$$
Пусть прямая задана системой уравнений
$$
\left\{
\begin{array}{l}
A_{1}x+B_{1}y+C_{1}z+D_{1}=0,\\
A_{2}x+B_{2}y+C_{2}z+D_{2}=0.
\end{array}
\right.\nonumber
$$
Тогда по утверждению 10 отсюда условие \eqref{ref3} переписывается в виде
$$
A\begin{vmatrix}
B_{1}& C_{1}\\
B_{2}& C_{2}
\end{vmatrix}
+ B\begin{vmatrix}
C_{1}& A_{1}\\
C_{2}& A_{2}
\end{vmatrix}
+ C\begin{vmatrix}
A_{1}& B_{1}\\
A_{2}& B_{2}
\end{vmatrix}
= 0.\nonumber
$$
или
$$
\begin{vmatrix}
A& B& C\\
A_{1}& B_{1}& C_{1}\\
A_{2}& B_{2}& C_{2}
\end{vmatrix}
= 0. \label{ref4}
\label{ref4}
$$
Легко проверить, что все приведенные здесь условия являются не только необходимыми, но и достаточными.
Из формулы \eqref{ref4} следует, что три плоскости пересекаются в одной точке тогда и только тогда, когда коэффициенты их уравнений удовлетворяют условию
$$
\begin{vmatrix}
A& B& C\\
A_{1}& B_{1}& C_{1}\\
A_{2}& B_{2}& C_{2}
\end{vmatrix}
\neq 0.\label{ref5}
$$
Действительно, это неравенство означает, что прямая, по которой пересекаются две плоскости, не параллельна третьей.
Полупространство.
Определение.
Пусть даны плоскость \(P\) и определенный ее нормальный вектор \(\boldsymbol{n}\). Полупространством, определяемым \(P\) и \(\boldsymbol{n}\), называется множество точек \(M\) таких, что для некоторой точки \(M_{0}\) на плоскости вектор \(\overrightarrow{M_{0}M}\) составляет с \(\boldsymbol{n}\) угол, не больший \(\pi/2\).
Если \(\boldsymbol{r}\) — радиус-вектор точки \(M\), а \(\boldsymbol{r}_{0}\) — точки \(M_{0}\), то определение полупространства, эквивалентно неравенству \((\boldsymbol{r}-\boldsymbol{r}_{0}, \boldsymbol{n}) \geq 0\). Это неравенство и есть уравнение полупространства.
Это неравенство и есть уравнение полупространства.
Нетрудно проверить, что определение полупространства не зависит от выбора точки \(M_{0}\). Действительно, если \(M_{1}(\boldsymbol{r}_{1})\) — другая точка плоскости, то вектор \(\boldsymbol{a}=\boldsymbol{r}_{1}-\boldsymbol{r}_{0}\) лежит в плоскости, перпендикулярен \(\boldsymbol{n}\), и мы имеем
$$
(\boldsymbol{r}-\boldsymbol{r}_{1}, \boldsymbol{n})=(\boldsymbol{r}-\boldsymbol{r}_{0}-\boldsymbol{a}, \boldsymbol{n})=(\boldsymbol{r}-\boldsymbol{r}_{0}, \boldsymbol{n}).\nonumber
$$
Мы получим уравнение полупространства в координатной форме, если вспомним, что согласно утверждению 3 отсюда выражение \((\boldsymbol{r}-\boldsymbol{r}_{0}, \boldsymbol{n})\) в координатах записывается линейным многочленом \(Ax+By+Cz+D\). Итак, полупространство в декартовой системе координат задается линейным неравенством
$$
Ax+By+Cz+D \geq 0.\nonumber
$$
Обратно, любое такое неравенство можно записать как \((\boldsymbol{r}-\boldsymbol{r}_{0}, \boldsymbol{n}) \geq 0\), откуда сразу видно, что оно задает полупространство.
Плоскость \(P\) и вектор \(\boldsymbol{n}_{1} =-\boldsymbol{n}\) задают другое полупространство с уравнением \((\boldsymbol{r}-\boldsymbol{r}_{0}, \boldsymbol{n}_{1}) \geq 0\) или \((\boldsymbol{r}-\boldsymbol{r}_{0}, \boldsymbol{n}) \leq 0\). Его назовем “отрицательным”, в отличие от “положительного” полупространства \((\boldsymbol{r}-\boldsymbol{r}_{0}, \boldsymbol{n}) \geq 0\). Однако такое наименование условно — оно определяется выбором вектора \(\boldsymbol{n}\). Изменение направления этого вектора равносильно умножению уравнения плоскости на (—1). При этом “положительное” полупространство становится “отрицательным”, и наоборот.
Вот, однако, факт, не зависящий от выбора направления нормального вектора: если \(M_{1}(x_{1}, y_{1}, z_{1})\) и \(M_{2}(x_{2}, y_{2}, z_{2})\) две точки, не лежащие в плоскости, то результаты подстановки их координат в левую часть уравнения плоскости \(Ax_{1}+By_{1}+Cz_{1}+D\) и \(Ax_{2}+By_{2}+Cz_{2}+D\) имеют один знак тогда и только тогда, когда точки лежат в одном полупространстве.
Для решения задач бывает полезно следующее замечание: если точка \(M_{0}(x_{0}, y_{0}, z_{0})\) лежит на плоскости, то точка с координатами \(x_{0}+A\), \(y_{0}+B\), \(z_{0}+C\) лежит в “положительном” полупространстве. Иначе говоря, вектор с координатами \(A, B, C\) направлен в “положительное” полупространство. Это легко проверяется подстановкой.
Вполне аналогично сказанному о полупространствах мы можем определить, что такое полуплоскость, и доказать, что неравенство \(Ax+By+Cz+D \geq 0\), связывающее декартовы координаты точки на плоскости, определяет полуплоскость. Вторая полуплоскость, ограниченная прямой \(Ax+By+C=0\), задается неравенством \(Ax+By+C \leq 0\).
Точки \(M_{1}(x_{1}, y_{1})\) и \(M_{2}(x_{2}, y_{2})\) лежат по одну сторону от прямой тогда и только тогда, когда \((Ax_{1}+By_{1}+C)(Ax_{2}+By_{2}+C) > 0\).
Расстояние от точки до плоскости.
Пусть дана плоскость с уравнением \((\boldsymbol{r}-\boldsymbol{r}_{0}, \boldsymbol{n})=0\) и точка \(M\) с радиус-вектором \(R\).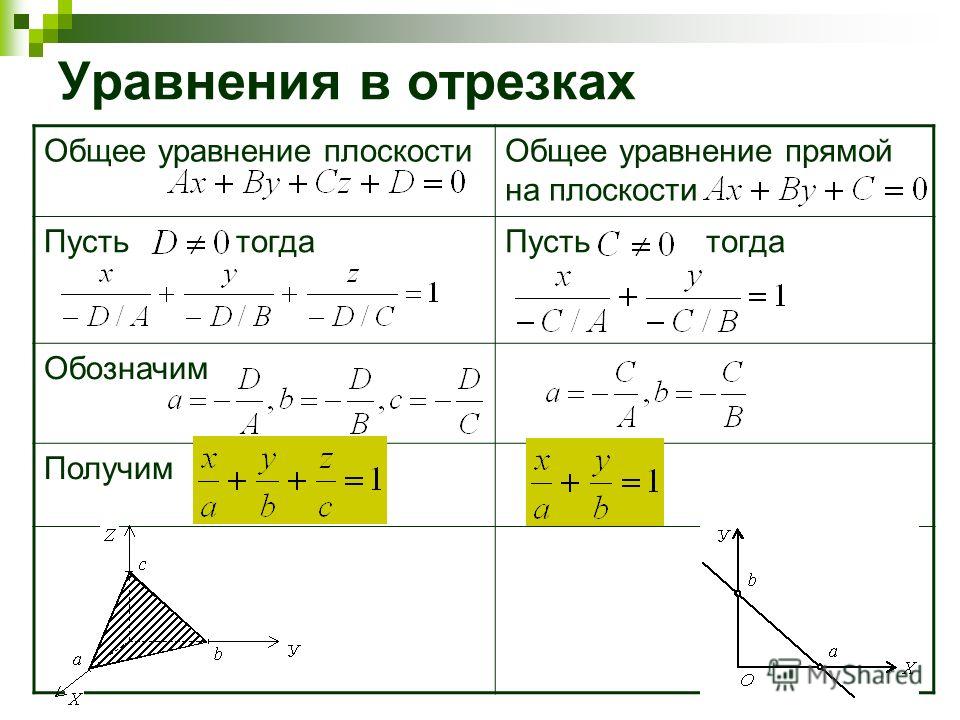 {2}}}.\label{ref7}
{2}}}.\label{ref7}
$$
Расстояние от точки до прямой.
Если прямая задана уравнением \([\boldsymbol{r}-\boldsymbol{r}_{0}, \boldsymbol{a}]=0\), то мы можем найти расстояние \(h\) от точки \(M\) с радиус-вектором \(\boldsymbol{R}\) до этой прямой, разделив площадь параллелограмма, построенного на векторах \(\boldsymbol{R}-\boldsymbol{r}_{0}\) и \(\boldsymbol{a}\), на длину его основания (рис. 7.2). Результат можно записать формулой
$$
h=\frac{|(\boldsymbol{R}-\boldsymbol{r}_{0}, \boldsymbol{a})|}{|\boldsymbol{a}|}.\label{ref8}
$$
Для прямой в пространстве мы не будем получать координатной записи этого выражения.
Рассмотрим прямую на плоскости, заданную уравнением \(Ax+By+C=0\) в декартовой прямоугольной системе координат. Пусть \(M_{0}(x_{0}, y_{0})\) — начальная точка прямой, a \(M(X, Y)\) — некоторая точка плоскости. В качестве направляющего вектора возьмем вектор \(\boldsymbol{a}(-B, A)\). {2}}}.\label{ref9}
{2}}}.\label{ref9}
$$
Легко заметить также, что для нахождения расстояния от точки до прямой на плоскости можно воспользоваться формулой \eqref{ref6}, считая, что \(\boldsymbol{n}\) — нормальный вектор прямой.
Расстояние между скрещивающимися прямыми.
Пусть прямые \(p\) и \(q\) не параллельны. Известно, что в этом случае существуют такие параллельные плоскости \(P\) и \(Q\), что прямая \(p\) лежит в \(P\), а прямая \(q\) лежит в \(Q\). (Если уравнения прямых \(\boldsymbol{r}=\boldsymbol{r}_{1}+\boldsymbol{a}_{1}t\) и \(\boldsymbol{r}=\boldsymbol{r}_{2}+\boldsymbol{a}_{2}t\), то плоскость \(P\) имеет начальную точку гд и направляющие векторы \(\boldsymbol{a}_{1}\) и \(\boldsymbol{a}_{2}\). Аналогично строится плоскость \(Q\).) Расстояние \(h\) между \(P\) и \(Q\) называется расстоянием между прямыми \(p\) и \(q\). Если \(p\) и \(q\) пересекаются, то \(P\) и \(Q\) совпадают и \(h=0\).
Для того чтобы найти расстояние \(h\), проще всего разделить объем параллелепипеда, построенного на векторах \(\boldsymbol{r}_{2}-\boldsymbol{r}_{1}\), \(\boldsymbol{a}_{1}\) и \(\boldsymbol{a}_{2}\), на площадь его основания (рис. 7.3). Мы получим
7.3). Мы получим
$$
h=\frac{|(\boldsymbol{r}_{2}-\boldsymbol{r}_{1}, \boldsymbol{a}_{1}, \boldsymbol{a}_{2})|}{|[\boldsymbol{a}_{1}, \boldsymbol{a}_{2}]|}.
$$
Знаменатель этой дроби отличен от нуля, поскольку прямые не параллельны.
Вычисление углов.
Чтобы найти угол между двумя прямыми, следует найти их направляющие векторы и вычислить косинус угла между ними, используя скалярное произведение. При этом следует иметь в виду, что, изменив направление одного из векторов, мы получим косинус смежного угла.
Для нахождения угла между прямой и плоскостью определяют угол \(\theta\) между направляющим вектором прямой и нормальным вектором плоскости. Если векторы выбрать так, чтобы \(\cos \theta \geq 0\), и взять \(0 \leq \theta \leq \pi/2\), то искомый угол дополняет \(\theta\) до \(\pi/2\).
Угол между плоскостями находят как угол между их нормальными векторами.
Полезна бывает формула для угла между прямыми линиями на плоскости, заданными уравнениями \(y=k_{1}x+b_{1}\) и \(y=k_{2}x+b_{2}\) декартовой прямоугольной системе координат. Обозначим через \(\varphi\) угол между прямыми, отсчитываемый от первой прямой ко второй в том же направлении, в котором производится кратчайший поворот от первого базисного вектора ко второму. Тогда \(\operatorname{tg} \varphi\) можно найти как тангенс разности углов, которые прямые составляют с осью абсцисс. Так как тангенсы этих углов равны угловым коэффициентам прямых, мы получаем
Обозначим через \(\varphi\) угол между прямыми, отсчитываемый от первой прямой ко второй в том же направлении, в котором производится кратчайший поворот от первого базисного вектора ко второму. Тогда \(\operatorname{tg} \varphi\) можно найти как тангенс разности углов, которые прямые составляют с осью абсцисс. Так как тангенсы этих углов равны угловым коэффициентам прямых, мы получаем
$$
\operatorname{tg} \varphi=\frac{k_{2}-k_{1}}{1+k_{1}k_{2}}.\label{ref10}
$$
Конечно, эта формула не имеет смысла, когда знаменатель дроби обращается в нуль. В этом случае прямые перпендикулярны. Действительно, векторы с компонентами \(1, k_{1}\) и \(1, k_{2}\) — направляющие векторы прямых, и их скалярное произведение равно \(1+k_{1}k_{2}\). Таким образом, верно следующее утверждение.
Некоторые задачи на построение.
Перпендикуляр из точки на плоскость. Проекция точки.
Если \((\boldsymbol{r}-\boldsymbol{r}_{0}, \boldsymbol{n})=0\) — уравнение плоскости и дана точка \(M\) с радиус-вектором \(\boldsymbol{R}\), то прямая с уравнением \(\boldsymbol{r}=\boldsymbol{R}+t\boldsymbol{n}\) проходит через \(M\) и перпендикулярна плоскости. {2}}\boldsymbol{n}.\nonumber
{2}}\boldsymbol{n}.\nonumber
$$
Таким образом, из радиус-вектоpa \(\boldsymbol{R}\) вычитается проекция \(\boldsymbol{R}-\boldsymbol{r}_{0}\) на нормальный вектор плоскости.
Перпендикуляр из точки на прямую.
Пусть прямая задана уравнением \([\boldsymbol{r}-\boldsymbol{r}_{0}, \boldsymbol{a}]=0\) и дана точка \(M\) с радиус-вектором \(\boldsymbol{R}\). Вектор \(\boldsymbol{p}=[\boldsymbol{R}-\boldsymbol{r}_{0}, \boldsymbol{a}]\) перпендикулярен плоскости, проходящей через прямую и точку \(M\). Если точка не лежит на прямой, то \(\boldsymbol{p} \neq 0\), и вектор \([\boldsymbol{a}, \boldsymbol{p}]=[\boldsymbol{a}, [\boldsymbol{R}-\boldsymbol{r}_{0}, \boldsymbol{a}]]\) также ненулевой и перпендикулярен \(\boldsymbol{a}\) и \(\boldsymbol{p}\). Следовательно, он лежит в указанной плоскости и перпендикулярен прямой. Итак, получено уравнение
$$
\boldsymbol{r}=\boldsymbol{R}+t [\boldsymbol{a}, [\boldsymbol{R}-\boldsymbol{r}_{0}, \boldsymbol{a}]]\nonumber
$$
перпендикуляра, опущенного из точки \(M\) на заданную прямую.
Применив формулу двойного векторного произведения, вы заметите, что \([\boldsymbol{a}, \boldsymbol{p}]\) коллинеарен разности вектора \(\boldsymbol{R}-\boldsymbol{r}_{0}\) и его проекции на вектор \(\boldsymbol{a}\). Задачу можно было решить, заметив это свойство направляющего вектора перпендикуляра.
Уравнение проекции прямой на плоскость.
Его просто получить, если не требуется находить направляющий вектор и начальную точку. Пусть заданная плоскость имеет уравнение \((\boldsymbol{r}, \boldsymbol{n})+D=0\), а прямая — уравнение \([\boldsymbol{r}-\boldsymbol{r}_{0}, \boldsymbol{a}]\), причем \([\boldsymbol{a}, \boldsymbol{n}] \neq 0\). Тогда плоскость \((\boldsymbol{r}-\boldsymbol{r}_{0}, \boldsymbol{a}, \boldsymbol{n})=0\) проходит через прямую перпендикулярно заданной плоскости. Таким образом, проекция прямой может быть задана системой из двух уравнений:
$$
(\boldsymbol{r}-\boldsymbol{r}_{0}, \boldsymbol{a}, \boldsymbol{n})=0,\ (\boldsymbol{r}, \boldsymbol{n})+D=0.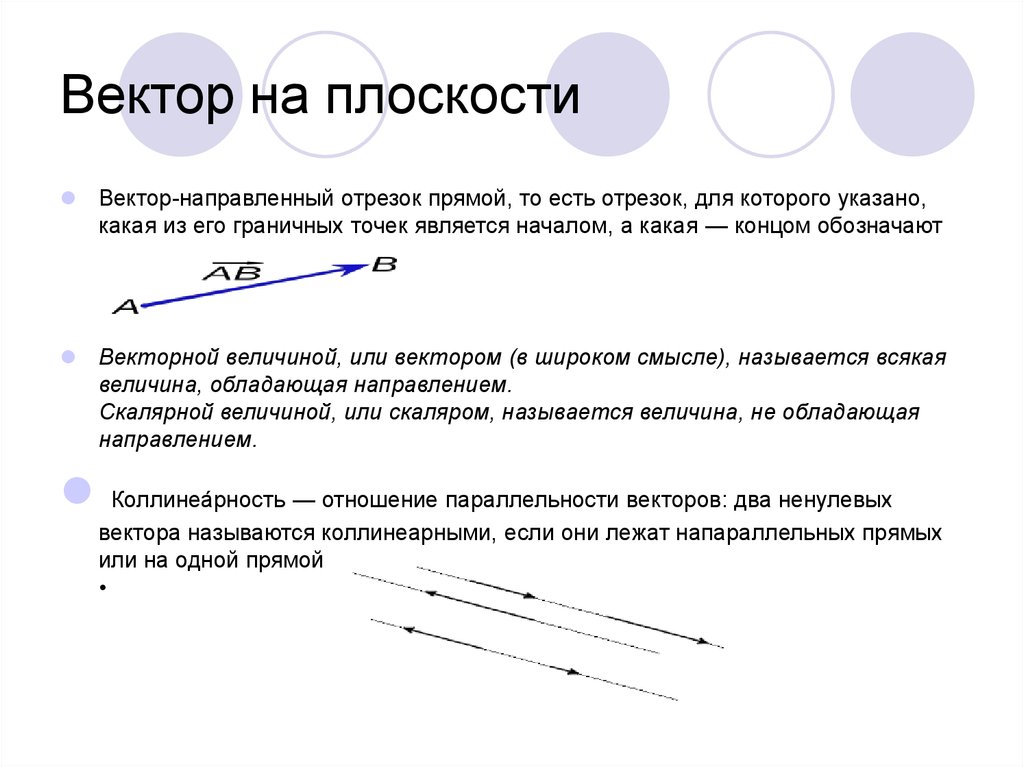 {2}}\boldsymbol{n}.\nonumber
{2}}\boldsymbol{n}.\nonumber
$$
За начальную точку может быть принята точка пересечения проектируемой прямой с плоскостью, если она существует, или же проекция начальной точки прямой.
Общий перпендикуляр к двум скрещивающимся прямым.
Пусть прямые с уравнениями \(\boldsymbol{r}=\boldsymbol{r}_{1}+t\boldsymbol{a}_{1}\) и \(\boldsymbol{r}=\boldsymbol{r}_{2}+t\boldsymbol{a}_{2}\) не параллельны, то есть \([\boldsymbol{a}_{1}, \boldsymbol{a}_{2}] \neq 0\). Вектор \(\boldsymbol{p}=[\boldsymbol{a}_{1}, \boldsymbol{a}_{2}]\) перпендикулярен обеим прямым. Следовательно, плоскость
$$
(\boldsymbol{r}-\boldsymbol{r}_{1}, \boldsymbol{a}_{1}, [\boldsymbol{a}_{1}, \boldsymbol{a}_{2}])=0\label{ref11}
$$
проходит через первую прямую и общий перпендикуляр к обеим прямым (рис. 7.5), а плоскость
$$
(\boldsymbol{r}-\boldsymbol{r}_{2}, \boldsymbol{a}_{2}, [\boldsymbol{a}_{1}, \boldsymbol{a}_{2}])=0\label{ref12}
$$
— через вторую прямую и общий перпендикуляр.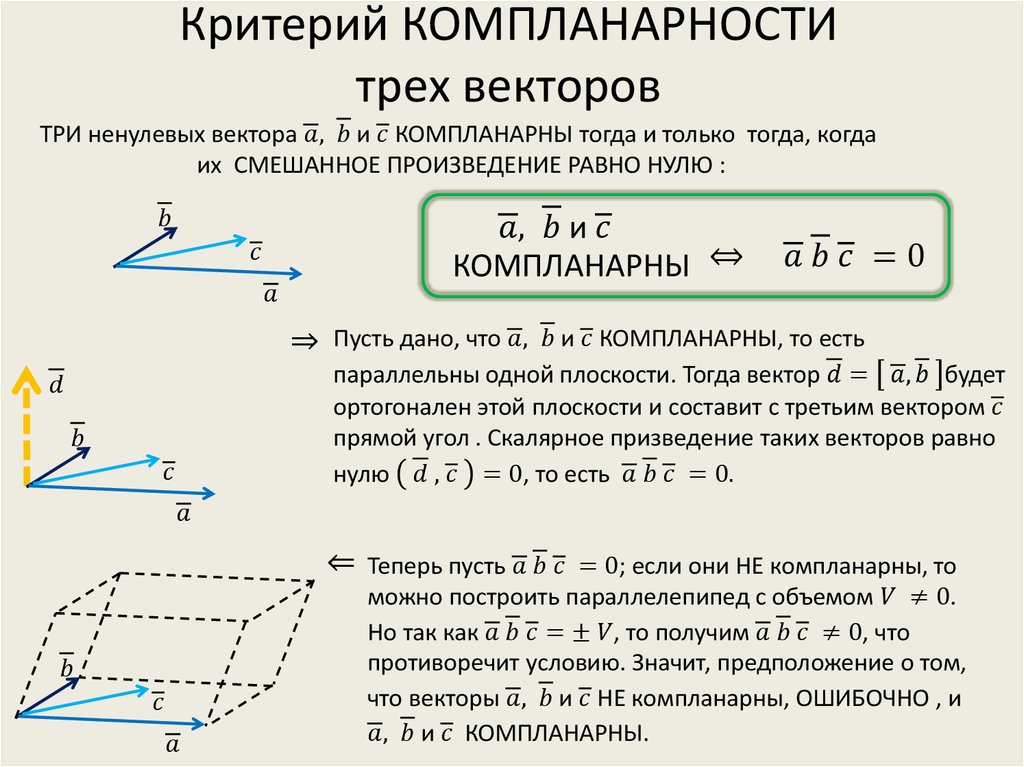 {2} \neq 0)\) определяет в пучке единственную прямую, но каждой прямой соответствуют бесконечно много пропорциональных между собой пар чисел.
{2} \neq 0)\) определяет в пучке единственную прямую, но каждой прямой соответствуют бесконечно много пропорциональных между собой пар чисел.
Если нам известны координаты центра пучка, то уравнение пучка можно написать в виде
$$
\alpha(x-x_{0})+\beta(y-y_{0})=0,\nonumber
$$
положив, что пучок определяется прямыми \(x-x_{0}=0\) и \(y-y_{0}=0\). Впрочем, и без того очевидно, что это — уравнение произвольной прямой, проходящей через \(M_{0}\).
Систему из уравнений прямых, определяющих пучок, можно рассматривать как уравнение центра пучка. Поэтому уравнение каждой прямой пучка есть следствие этой системы. Теперь наш результат можно сформулировать так.
Мы доказали это предложение для частного случая систем из двух уравнений с двумя неизвестными. В общем виде оно вытекает из результатов главы о системах линейных уравнений. Другими геометрическими интерпретациями этого предложения являются пучки и связки плоскостей.
Пучком плоскостей называется множество плоскостей, проходящих через фиксированную прямую — ось пучка. {2}-1=0\).
{2}-1=0\).
Пример.
Архимедова спираль — линия с уравнением \(r=\alpha\varphi\) в полярной системе координат — пересекает каждую прямую, проходящую через полюс, в бесконечном числе точек. Следовательно, она не является алгебраической линией.
Аналитическая геометрия для «чайников»
Настоящая книга позволит вам в сжатые сроки (2-3 недели) освоить основы аналитической геометрии и научиться решать наиболее распространённые задачи по теме. Материал предназначен для студентов-заочников и других читателей, которые хотят быстро освоить минимум теории и максимум практики
Сначала немного о предмете…. Наверняка вам сейчас вспомнился курс школьной геометрии с многочисленными теоремами, их доказательствами, чертежами и т.д. Что скрывать, нелюбимый и часто малопонятный предмет для значительной доли учеников. Аналитическая геометрия, как ни странно, может показаться более интересной и доступной.
Графический метод связан с построением графиков, чертежей. Аналитический же метод предполагает решение задач преимущественно посредством алгебраических действий. В этой связи алгоритм решения многих задач аналитической геометрии прост и прозрачен, зачастую достаточно аккуратно применить нужные формулы – и ответ готов! Нет, конечно, совсем без чертежей тут не обойдется, к тому же для лучшего понимания материала я постараюсь приводить их сверх необходимости.
1. Векторы
1.1. Что такое вектор?
1.2. Коллинеарность векторов
1.3. Основные действия с векторами
1.4. Координаты вектора на плоскости и в пространстве
1.5. Простейшие задачи с векторами
1.5.2. Как найти длину отрезка?
1.
 5.3. Как найти длину вектора?
5.3. Как найти длину вектора?1.5.4. Действия с векторами в координатах
1.5.5. Как найти единичный вектор
1.5.6. Деление отрезка в данном отношении
1.5.7. Формулы координат середины отрезка
1.6. Скалярное произведение векторов
1.6.1. Определение скалярного произведения
1.6.2. Угол между векторами и знак скалярного произведения
1.6.3. Скалярный квадрат вектора
1.6.4. Свойства скалярного произведения
1.6.5. Как найти угол между векторами?
1.6.6. Скалярное произведение векторов в координатах
1.6.7. Как проверить векторы на ортогональность?
1.6.8. Если векторы заданы суммами векторов с известными координатами
1.6.9. Как найти угол между векторами в координатах?
1.7. Ортогональные проекции векторов
1.7.2. Проекции вектора на координатные оси. Направляющие косинусы
1.8. Линейная зависимость и линейная независимость векторов.
Базис векторов. Аффинная система координат.
1.8.1. «Плоский» случай
1.8.2. Как определить коллинеарность векторов плоскости?
1.8.3. Как определить коллинеарность векторов пространства?
1.8.4. Базис и система координат пространства
1.9. Векторное произведение векторов
1.9.1. Определение векторного произведения
1.9.2. Свойства векторного произведения
1.9.3. Векторное произведение в координатах
1.10. Смешанное произведение векторов
1.10.1. Определение смешанного произведения
1.10.2. Как вычислить смешанное произведение?
1.10.3. Как вычислить объём треугольной пирамиды?
2. Прямая на плоскости
2.1. Уравнение прямой с угловым коэффициентом2.2. Общее уравнение прямой
2.2.1. Общее уравнение и направляющий вектор прямой
2.2.2. Как составить уравнение прямой по точке и направляющему вектору?
2.2.3. Как найти направляющий вектор по общему уравнению прямой?
2.2.4. Как составить уравнение прямой по двум точкам?
2.
 2.5. Нормальный вектор прямой
2.5. Нормальный вектор прямой2.2.6. Как составить уравнение прямой по точке и вектору нормали?
2.3. Уравнение прямой в отрезках
2.4. Параметрические уравнениЯ прямой
2.5. Простейшие задачи с прямой на плоскости
2.5.1. Взаимное расположение двух прямых
2.5.2. Как найти прямую, параллельную данной?
2.5.3. Как найти точку пересечения прямых?
2.5.5. Как вычислить расстояние от точки до прямой.
Как найти точку, симметричную относительно прямой?
2.5.6. Как найти расстояние между параллельными прямыми?
2.5.7. Как найти угол между прямыми?
2.5.8. Как найти проекцию вектора на прямую?
2.6. Линейные неравенства
2.7. Системы линейных неравенств
2.8. Как научиться решать задачи по геометрии?
2.9. Типовая задача с треугольником
3. Линии второго порядка
3.1. Алгебраическая линия и её порядок
3.2. Классификация линий второго порядка
3. 3. Эллипс
3. Эллипс
3.3.1. Каноническое уравнение эллипса. Как построить эллипс?
3.3.2. Определение эллипса. Фокусы эллипса
3.3.3. Эксцентриситет эллипса и его геометрический смысл
3.3.4. Поворот и параллельный перенос эллипса
3.4.1. Каноническое уравнение и построение гиперболы
3.4.2. Определение гиперболы
3.4.3. Фокусы и эксцентриситет гиперболы
3.4.4. Равносторонняя гипербола
3.4.5. Поворот и параллельный перенос гиперболы
3.5. Парабола
3.5.1. Построение, уравнение, определение, фокусы, директриса, эксцентриситет
3.5.2. Поворот и параллельный перенос параболы
3.6. Неравенства с линиями второго порядка
3.7. Задачи с линиями второго порядка
3.7.1. Директрисы эллипса
3.7.2. Директрисы гиперболы
3.8. Приведение уравнения к каноническому виду
3.8.1. Приведение уравнения центральной линии. Метод инвариантов
3.8.2. Приведение уравнения нецентральной линии
3.8.3. Универсальный метод приведения
4.
 Полярная система координат
Полярная система координат
4.1. Что такое полярные координаты?
4.2. Порядок и техника построения точек в полярных координатах
4.3. Взаимосвязь прямоугольной и полярной системы координат
4.4. Уравнение линии в полярных координатах
4.6. Как построить линию в полярных координатах?
5. Плоскость и прямая в пространстве
5.1. Плоскость и её уравнение
5.1.1. Понятие плоскости
5.1.2. Общее уравнение плоскости
5.1.3. Линейные неравенства в пространстве
5.1.4. Как построить плоскость?
5.1.5. Уравнение плоскости в отрезках
5.2. Как составить уравнение плоскости?
5.2.1. Уравнение плоскости по точке и двум неколлинеарным векторам
5.2.2. Как составить уравнение плоскости по трём точкам?
5.2.3. Вектор нормали плоскости (нормальный вектор)
5.2.4. Как составить уравнение плоскости по точке и вектору нормали?
5.3. Простейшие задачи с плоскостью
5.3.1. Как найти плоскость, параллельную данной?
5. 3.2. Как найти расстояние от точки до плоскости?
3.2. Как найти расстояние от точки до плоскости?
5.3.3. Как найти расстояние между плоскостями?
5.3.4. Взаимное расположение двух плоскостей
5.3.6. Как найти плоскость, перпендикулярную данной?
5.3.7. Взаимное расположение трёх плоскостей
5.4. УравнениЯ прямой в пространстве
5.4.1. Канонические уравнения прямой
5.4.2. Как составить уравнения прямой по двум точкам?
5.4.3. Параметрические уравнения прямой
5.4.4. Прямая, заданная пересечением двух плоскостей
5.5. Задачи с прямой в пространстве
5.5.1. Взаимное расположение прямых
5.5.2. Скрещивающиеся прямые
5.5.3. Как найти прямую, содержащую общий перпендикуляр?
5.5.4. Как найти расстояние между скрещивающимися прямыми?
5.5.5. Пересекающиеся прямые в пространстве
5.5.6. Как найти прямую, перпендикулярную данной?
5.5.7. Как найти расстояние от точки до прямой?
5.5.8. Как найти точку, симметричную относительно прямой?
5.

5.5.10. Параллельные прямые в пространстве
5.6. Основные задачи с прямой и плоскостью
5.6.1. Взаимное расположение прямой и плоскости
5.6.2. Как найти точку пересечения прямой и плоскости?
5.6.3. Как найти проекцию прямой на плоскость?
5.6.4. Как найти угол между прямой и плоскостью?
5.6.5. Прямая перпендикулярна плоскости
5.6.6. Прямая параллельна плоскости
5.6.7. Добро пожаловать в «реальные боевые условия»!
5.7. Задача с треугольной пирамидой
6. Поверхности второго порядка
6.1. Понятие алгебраической поверхности
6.2. Цилиндрические поверхности
6.3. Эллипсоид
6.4. Коническая поверхность
6.5. Параболоиды
6.6. Гиперболоиды
6.7. Альтернативные системы координат
6.7.1. Цилиндрическая система координат
6.7.2. Сферическая система координат
7. Решения и ответы, а также Приложения доступны в полной версии.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
Автор: Aлeксaндр Eмeлин
Векторы на плоскости презентация, доклад
Работа по геометрии на тему “Векторы на плоскости”
Выполнила ученица 9 “Б” класса школы гимназии №5
Дарья Айткалиева
Какова разница между векторными и скалярными величинами?
Определение:
Векторной величиной, или вектором (в широком смысле), называется всякая величина, обладающая направлением.
Скалярной величиной, или скаляром, называется величина, не обладающая направлением.
Пример 1. Когда какая-то сила действует на материальную точку, то она будет вектором, так как она обладает направлением. Так же и скорость материальной точки — тоже вектор.
Пример 2. А от уже температура тела будет скаляром, так как с ней не связано никакое направление. Поэтому масса тела и его плотность — тоже будут скалярами.
B
A
M
N
1H
B
Что такое вектор и как его обозначают?
Определение:
В геометрии вектор — направленный отрезок прямой, то есть отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом.
Вектор с началом в точке А и концом в точке В принято обозначать как Векторы также могут обозначаться малыми латинскими буквами со стрелкой (иногда — чёрточкой) над ними, например . Другой распространённый способ записи: выделение символа вектора жирным шрифтом: а .
B
A
AB
Какие векторы называют коллинеарными? Пример сонаправленых и противоположно направленных векторов.
Определение.
Коллинеарные вектора. Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами.
Сонаправленные вектора. Два коллинеарных вектора a и b называются сонаправленными векторами, если их направления совпадают: a↑↑b
Противоположно направленные вектора. Два коллинеарных вектора a и b называются противоположно направленными векторами, если их направления противоположны: a↑↓b
a
b
a
b
Какие векторы называют равными?
Определение:
Вектора a и b называются равными, если они лежат на одной или параллельных прямых, их направления совпадают, а длины равны
То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:
a = b, если a↑↑b и |a| = |b|.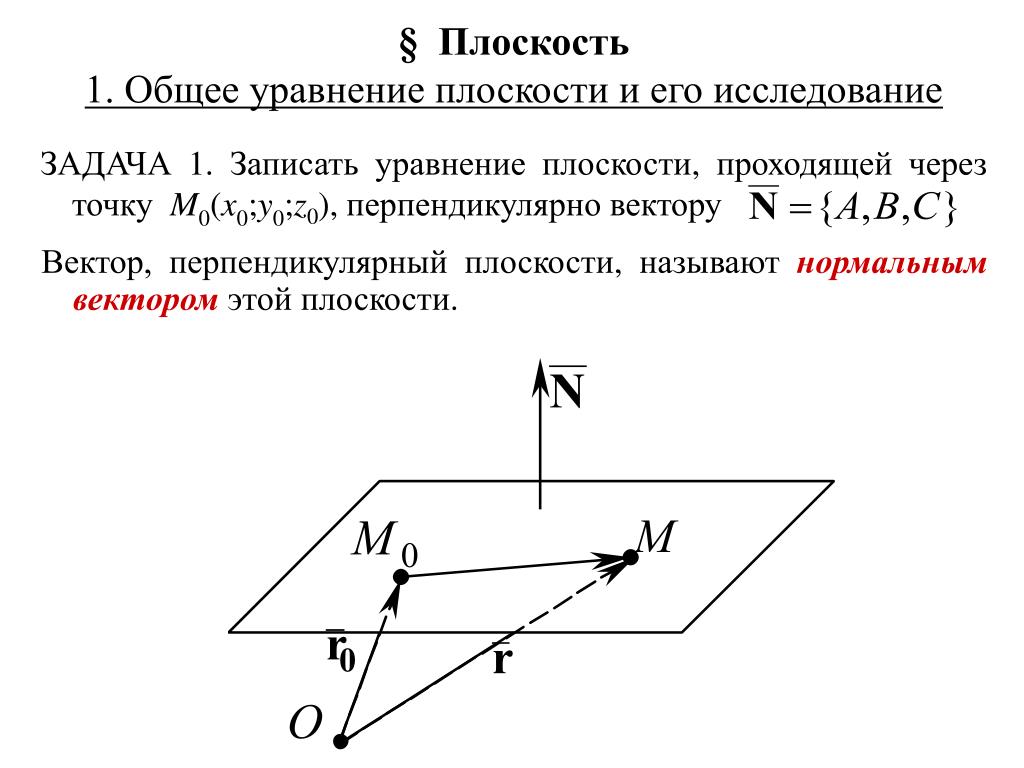
a
b
Что такое модуль вектора?
Определение.
Длина направленного отрезка определяет числовое значение вектора и называетсядлиной вектора или модулем вектора AB.
Для обозначения длины вектора используются две вертикальные линии слева и справа |AB|.
Длина вектора |a| в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат.
AB
A
B
Что такое нулевой вектор?
Определение.
Нулевым вектором называется вектор, у которого начальная и конечная точка совпадают.
Нулевой вектор обычно обозначается как 0.
Длина нулевого вектора равна нулю.
Нулевой вектор определяет тождественное движение пространства, при котором каждая точка пространства переходит в себя.
Сложение векторов. Правило параллелограмма.
Правило параллелограмма.
Сложение векторных величин производится по правилу параллелограмма:
Cумма двух векторов a и b, приведенных к общему началу, есть третий вектор c , длина которого равна длине параллелограмма, построенного на векторах a и b , а направлен он от точки A к точке B.
Модуль вектора с вычисляется по формуле
Сложение векторов. Правило треугольника.
Правило треугольника:
Для того чтобы получить сумму двух векторов, нужно из произвольной точки отложить первый вектор, из конца полученного вектора отложить второй вектор, и построить вектор, соединяющий начало первого с концом второго – это и будет сумма двух векторов.
a
b
A
B
C
Свойства суммы векторов.
Переместительное свойство:
От перестановки слагаемых сумма не меняется.
В буквенном виде свойство записывается так: a + b = b + a
В этом равенстве буквы a и b могут принимать любые натуральные значения и значение 0.
Сочетательное свойство:
Чтобы к сумме двух чисел прибавить третье число можно к первому числу прибавить сумму второго и третьего числа.
Свойства суммы векторов.
Сочетательное свойство :
Чтобы к сумме двух чисел прибавить третье число можно к первому числу прибавить сумму второго и третьего числа..
В буквенном виде: (a + b) + c = a + (b + c)
Так как результат сложения трёх чисел не зависит от того как поставлены скобки, то скобки можно не ставить и писать просто a + b + с.
(a + b) + c = a + (b + c) = a + b + c
Переместительное и сочетательное свойство сложения позволяют сформулировать правило преображения сумм.
При сложении нескольких чисел их можно как угодно объединять в группы и переставлять.
Свойства суммы векторов.
Свойство нуля при сложении:
Сумма двух натуральных чисел всегда больше каждого из слагаемых. Но это не так, если хотя бы одно из слагаемых равно нулю.
Но это не так, если хотя бы одно из слагаемых равно нулю.
Если к числу прибавить нуль, получится само число.
a + 0 = 0 + a = a
Разность векторов.
Свойство вычитания суммы из числа:
Чтобы вычесть сумму из числа, можно из него вычесть одно слагаемое и затем из результата вычесть другое слагаемое.
a − (b + c) = (a − b) − c или a − (b + c) = (a − с) − b
Скобки в выражении (a − b) − c не имеют значения и их можно опустить.
(a − b) − c = a − b − c
Разность векторов.
Свойство вычитания числа из суммы
Чтобы вычесть число из суммы, можно вычесть его из одного слагаемого, а к результату прибавить оставшееся слагаемое.
(a + b) − c = (a − c) + b (если a > c или а = с)
или
(a + b) − c = (b − c) + a (если b > c или b = с)
Разность векторов.
Свойство нуля при вычитании:
Если из числа вычесть нуль, получится само число.
a − 0 = a
Если из числа вычесть само число, то получится нуль.
a − a = 0
Умножение вектора на число.
Геометрическая интерпретация.
Произведение ненулевого вектора на число — это вектор, коллинеарный данному (сонаправленный данному, если число положительное, имеющий противоположное направление, если число отрицательное), а его модуль равен модулю данного вектора, умноженному на модуль числа.
Алгебраическая интерпретация.
Произведение ненулевого вектора на число — это вектор, координаты которого равны соответствующим координатам данного вектора, умноженным на число.
Умножение вектора на число.
Формула умножения вектора на число для плоских задач
В случае плоской задачи произведение вектора a = {ax ; ay} и числа k можно найти воспользовавшись следующей формулой:
k · a = {k · ax; k · ay}
Формула умножения вектора на число для пространственных задач
В случае пространственной задачи произведение вектора a = {ax ; ay ; az} и числа k можно найти воспользовавшись следующей формулой: k · a = {k · ax ; k · ay ; k · az}
Формула умножения n -мерного вектора
В случае n-мерного пространства произведение вектора a = {a1 ; a2; .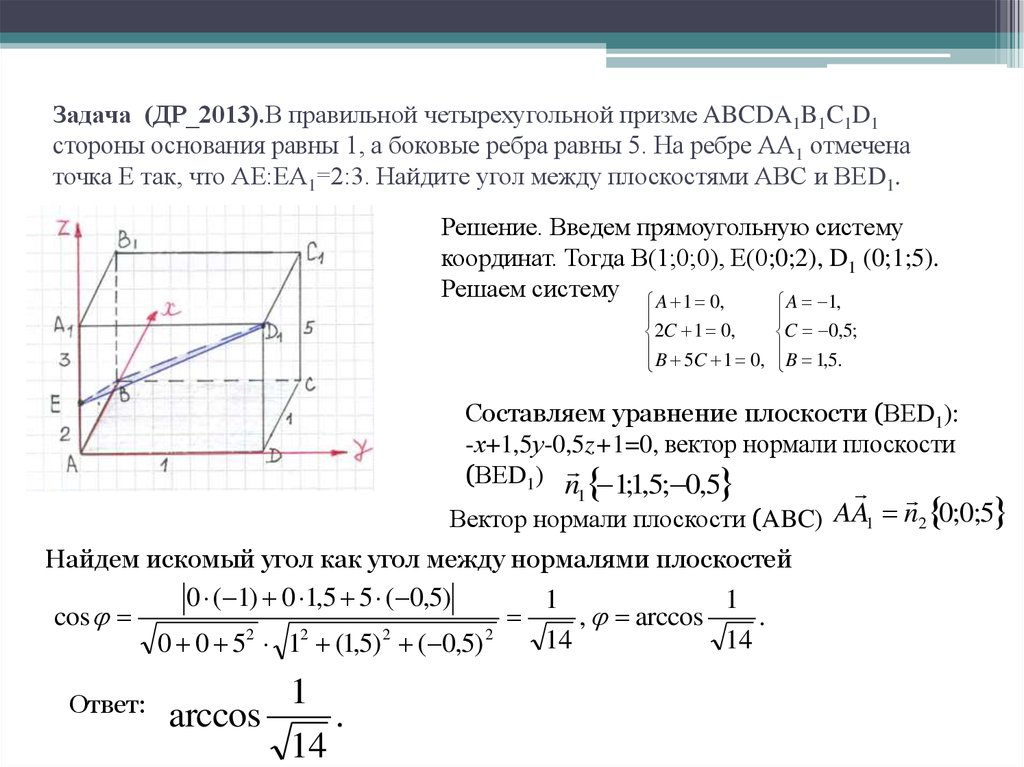 .. ; an} и числа k можно найти воспользовавшись следующей формулой: k · a = {k · a1; k · a2; … ; k · an}
.. ; an} и числа k можно найти воспользовавшись следующей формулой: k · a = {k · a1; k · a2; … ; k · an}
Умножение вектора на число.
Свойства вектора умноженного на число
Если вектор b равен произведению ненулевого числа k и ненулевого вектора a, то есть b = k · a, тогда:
b || a — вектора b и a параллельны
a↑↑b, если k > 0 — вектора b и a сонаправленные, если число k > 0
a↑↓b, если k |b| = |k| · |a| — модуль вектора b равен модулю вектора a умноженному на модуль числа k
Угол между векторами.
Определение.
Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором.
Основное соотношение. Косинус угла между векторами равен скалярному произведению векторов, поделенному на произведение модулей векторов.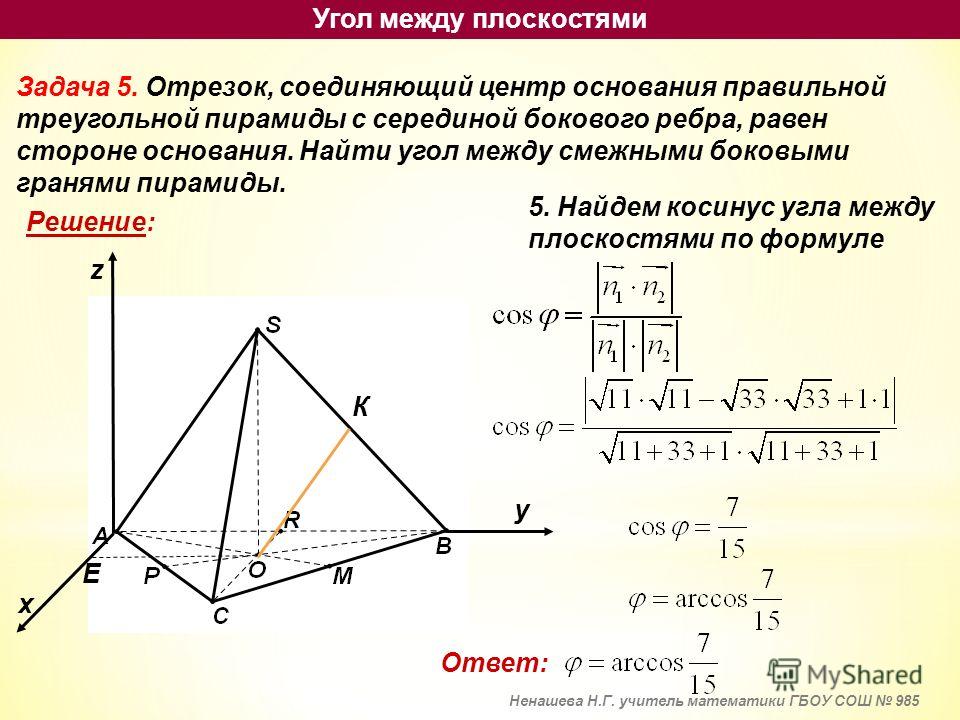
Формула вычисления угла между векторами
Скалярное произведение двух векторов.
Формулы скалярного произведения векторов заданных координатами:
Формула скалярного произведения векторов для плоских задач
В случае плоской задачи скалярное произведение векторов a = {ax ; ay} и b = {bx ; by} можно найти воспользовавшись следующей формулой: a · b = ax · bx + ay · by
Формула скалярного произведения векторов для пространственных задач
В случае пространственной задачи скалярное произведение векторов a = {ax ; ay ; az} и b = {bx ; by ; bz} можно найти воспользовавшись следующей формулой: a · b = ax · bx + ay · by + az · bz
Формула скалярного произведения n -мерных векторов
В случае n-мерного пространства скалярное произведение векторов a = {a1 ; a2 ; … ; an} и b = {b1 ; b2 ; … ; bn} можно найти воспользовавшись следующей формулой: a · b = a1 · b1 + a2 · b2 + … + an · bn
Свойства скалярного произведения векторов. .
.
Скалярное произведение вектора самого на себя всегда больше или равно нуля:
a · a ≥ 0
Скалярное произведение вектора самого на себя равно нулю тогда и только тогда, когда вектор равен нулевому вектору:
a · a = 0 a = 0
Скалярное произведение вектора самого на себя равно квадрату его модуля: a · a = |a|2
Операция скалярного умножения коммуникативна: a · b = b · a
Если скалярное произведение двух не нулевых векторов равно нулю, то эти вектора ортогональны:
a ≠ 0, b ≠ 0, a · b = 0 a ┴ b
(αa) · b = α(a · b)
Операция скалярного умножения дистрибутивна: (a + b) · c = a · c + b · c
Координаты векторов.
Основное соотношение:
Основное соотношение .Чтобы найти координаты вектора AB, зная координаты его начальной точек А и конечной точки В, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки.
AB
A
B
Формулы определения координат вектора заданного координатами его начальной и конечной точки
Формула определения координат вектора для плоских задач
В случае плоской задачи вектор AB заданный координатами точек A(Ax ; Ay) и B(Bx ; By) можно найти воспользовавшись следующей формулой
AB = {Bx — Ax ; By — Ay}
Формула определения координат вектора для пространственных задач
В случае пространственной задачи вектор AB заданный координатами точек A(Ax ; Ay ; Az) и B(Bx ; By ; Bz) можно найти воспользовавшись следующей формулой
AB = {Bx — Ax ; By — Ay ; Bz — Az}
Формула определения координат вектора для n -мерного пространства
В случае n-мерного пространства вектор AB заданный координатами точек A(A1 ; A2 ; .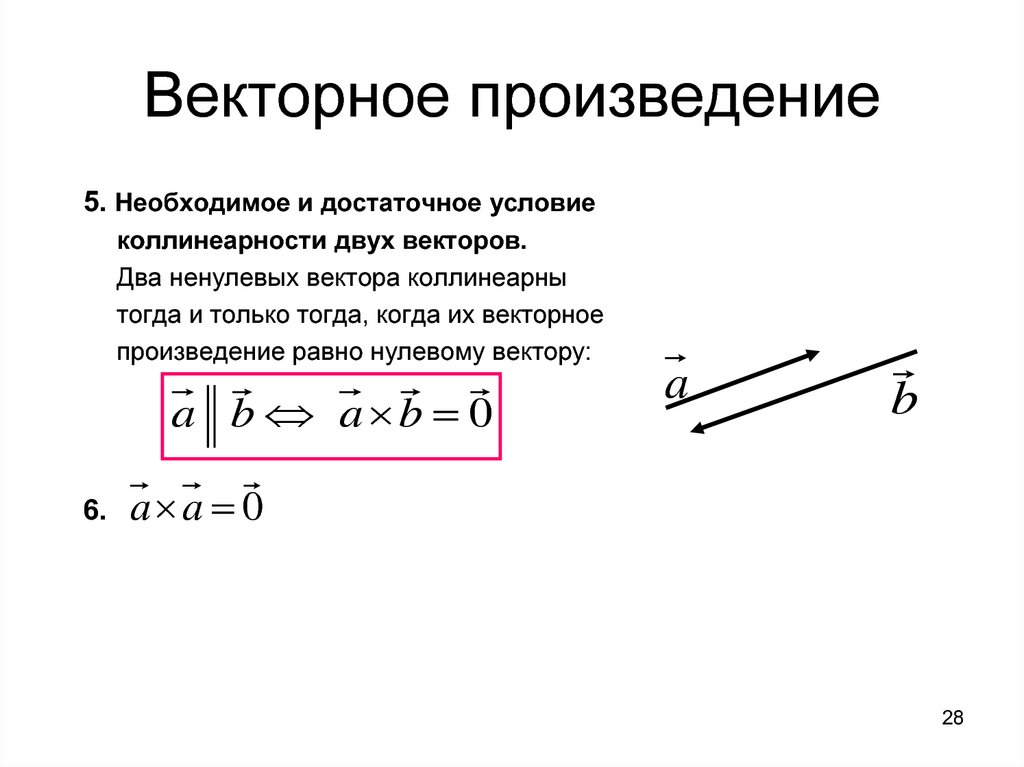 .. ; An) и B(B1 ; B2 ; … ; Bn) можно найти воспользовавшись следующей формулой
.. ; An) и B(B1 ; B2 ; … ; Bn) можно найти воспользовавшись следующей формулой
AB = {B1 — A1 ; B2 — A2 ; … ; Bn — An}
Уравнения прямой на плоскости.
Прямая (прямая линия) — это бесконечная линия, по которой проходит кратчайший путь между любыми двумя её точками.
Уравнение прямой на плоскости
Любую прямую на плоскости можно задать уравнением прямой первой степени вида
A x+B y+C= 0
где A и B не могут быть одновременно равны нулю.
A
B
Уравнения прямой на плоскости
Уравнение прямой с угловым коэффициентом
Общее уравнение прямой при B≠0 можно привести к виду y=k x+b где k — угловой коэффициент равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ .
Уравнение прямой в отрезках на осях
Если прямая пересекает оси OX и OY в точках с координатами (a, 0) и (0,b), то она может быть найдена используя формулу уравнения прямой в отрезках
Уравнения прямой на плоскости
Уравнение прямой, проходящей через две различные точки на плоскости
Если прямая проходит через две точки A(x1,y1) и B(x2,y2), такие что x1 ≠x2 иy1 ≠y2 то уравнение прямой можно найти, используя следующую формулу
Параметрическое уравнение прямой на плоскости
Параметрические уравнения прямой могут быть записаны следующим образом
где (x0,y0) — координаты точки лежащей на прямой,{l,m}- координаты направляющего вектора прямой.
Уравнения прямой на плоскости
Каноническое уравнение прямой на плоскости
Если известны координаты точки A(x0,y0) лежащей на прямой и направляющего вектора n={l;m}, то уравнение прямой можно записать в каноническом виде, используя следующую формулу
Расстояние между двумя точками
Определение.
Расстояние между двумя точками — это длина отрезка, что соединяет эти точки.
Формулы вычисления расстояния между двумя точками:
Формула вычисления расстояния между двумя точками A(xa, ya) и B(xb, yb) на плоскости:
AB = √(xb — xa)2 + (yb — ya)2
Формула вычисления расстояния между двумя точками A(xa, ya, za) и B(xb, yb, zb) в пространстве:
AB = √(xb — xa)2 + (yb — ya)2 + (zb — za)2
Расстояние между двумя точками
Вывод формулы для вычисления расстояния между двумя точками на плоскости
Из точек A и B опустим перпендикуляры на оси координат.
Рассмотрим прямоугольный треугольник ∆ABC. Катеты этого треугольника равны:
AC = xb — xa;
BC = yb — ya.
Воспользовавшись теоремой Пифагора, вычислим длину отрезка AB:
AB = √AC2 + BC2.
Подставив в это выражение длины отрезков AC и BC, выраженные через координаты точек A и B, получим формулу для вычисления расстояния между точками на плоскости.
Формула для вычисления расстояния между двумя точками в пространстве выводится аналогично
Расстояние от точки до прямой на плоскости.
Определение.
Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую.
Формула для вычисления расстояния от точки до прямой на плоскости
Если задано уравнение прямой Ax + By + C = 0, то расстояние от точки M(Mx, My) до прямой можно найти, используя следующую формулу
Спасибо за внимание!
Скачать презентацию
2.
 1 Векторы на плоскости. Исчисление, том 3
1 Векторы на плоскости. Исчисление, том 3Цели обучения
- 2.1.1 Опишите плоский вектор, используя правильные обозначения.
- 2.1.2 Выполнять основные векторные операции (скалярное умножение, сложение, вычитание).
- 2.1.3 Выразите вектор в компонентной форме.
- 2.1.4 Объясните формулу величины вектора.
- 2.1.5 Выразите вектор в терминах единичных векторов.
- 2.1.6 Приведите два примера векторных величин.
При описании движения самолета в полете важно сообщить две части информации: направление, в котором движется самолет, и скорость самолета. При измерении силы, такой как тяга двигателей самолета, важно описать не только силу этой силы, но и направление, в котором она приложена. Некоторые величины, такие как скорость или сила, определяются с точки зрения как размера (также называемого величиной ), так и направления. Величина, имеющая величину и направление, называется вектором. В этом тексте мы обозначаем векторы жирными буквами, например против .
В этом тексте мы обозначаем векторы жирными буквами, например против .
Определение
Вектор — это величина, которая имеет как величину, так и направление.
Векторное представление
Вектор на плоскости изображается направленным отрезком (стрелка). Концы отрезка называются начальной точкой и конечной точкой вектора. Стрелка от начальной точки к конечной указывает направление вектора. Длина отрезка представляет собой его величину. Мы используем обозначение ‖v‖‖v‖ для обозначения величины вектора v.v. Вектор с одинаковыми начальной и конечной точками называется нулевым вектором и обозначается 0,0. Нулевой вектор — единственный вектор без направления, и по соглашению можно считать, что он имеет любое направление, удобное для рассматриваемой задачи.
Векторы с одинаковой величиной и направлением называются эквивалентными векторами. Мы рассматриваем эквивалентные векторы как равные, даже если они имеют разные начальные точки. Таким образом, если vv и ww эквивалентны, мы пишем
Таким образом, если vv и ww эквивалентны, мы пишем
v=w.v=w.
Определение
Векторы называются эквивалентными, если они имеют одинаковую величину и направление.
Стрелки на рис. 2.2(b) эквивалентны. Каждая стрелка имеет одинаковую длину и направление. Тесно связанной концепцией является идея параллельных векторов. Два вектора называются параллельными, если они имеют одинаковые или противоположные направления. Мы рассмотрим эту идею более подробно позже в этой главе. Вектор определяется своей величиной и направлением, независимо от того, где находится его начальная точка.
Рисунок 2.2 (a) Вектор представлен отрезком направленной прямой от его начальной точки до конечной точки. (b) Векторы с v1v1 по v5v5 эквивалентны.
Использование полужирных строчных букв для обозначения векторов является обычным представлением в печати, но существуют и альтернативные обозначения. Например, при написании имени вектора от руки проще нарисовать стрелку над переменной, чем имитировать полужирный шрифт: v→. v→. Когда вектор имеет начальную точку PP и конечную точку Q,Q, обозначение PQ→PQ→ полезно, поскольку оно указывает направление и местоположение вектора.
v→. Когда вектор имеет начальную точку PP и конечную точку Q,Q, обозначение PQ→PQ→ полезно, поскольку оно указывает направление и местоположение вектора.
Пример 2.1
Рисование векторов
Начертите вектор на плоскости от начальной точки P(1,1)P(1,1) до конечной точки Q(8,5).Q(8,5).
Решение
См. рис. 2.3. Поскольку вектор идет из точки PP в точку Q,Q, мы называем его PQ→.PQ→.
Рисунок 2.3 Вектор с начальной точкой (1,1)(1,1) и конечной точкой (8,5)(8,5) называется PQ→.PQ→.
Контрольно-пропускной пункт 2.1
Нарисуйте вектор ST→ST→, где SS — точка (3,−1)(3,−1), а TT — точка (−2,3).(−2,3).
Объединение векторов
Векторы имеют множество применений в реальной жизни, включая ситуации, связанные с силой или скоростью. Например, рассмотрим силы, действующие на лодку, пересекающую реку. Мотор лодки создает силу в одном направлении, а течение реки создает силу в другом направлении. Обе силы являются векторами. Мы должны учитывать как величину, так и направление каждой силы, если хотим знать, куда направится лодка.
Обе силы являются векторами. Мы должны учитывать как величину, так и направление каждой силы, если хотим знать, куда направится лодка.
Второй пример, связанный с векторами, — защитник, бросающий футбольный мяч. Квотербек не бросает мяч параллельно земле; вместо этого он целится в воздух. Скорость его броска может быть представлена вектором. Если мы знаем, как сильно он бросает мяч (величина — в данном случае скорость) и угол (направление), мы можем сказать, как далеко мяч улетит по полю.
Действительное число часто называют скаляром в математике и физике. В отличие от векторов, обычно считается, что скаляры имеют только величину, но не направление. Умножение вектора на скаляр изменяет величину вектора. Это называется скалярным умножением. Обратите внимание, что изменение величины вектора не указывает на изменение его направления. Например, ветер, дующий с севера на юг, может увеличивать или уменьшать скорость, сохраняя при этом свое направление с севера на юг.
Определение
Произведение kvkv вектора v и скаляра k является вектором с величиной |k||k| умноженной на величину v,v, и с направлением, совпадающим с направлением vv, если k>0,k>0, и противоположным направлению vv, если k<0. k<0. Это называется скалярным умножением. Если k=0k=0 или v=0,v=0, то kv=0.kv=0.
k<0. Это называется скалярным умножением. Если k=0k=0 или v=0,v=0, то kv=0.kv=0.
Как и следовало ожидать, если k=−1,k=−1, мы обозначаем произведение kvkv как
kv=(-1)v=-v.kv=(-1)v=-v.
Обратите внимание, что −v−v имеет ту же величину, что и v,v, но имеет противоположное направление (рис. 2.4).
Рисунок 2,4 (a) Исходный вектор v имеет длину n единиц. (b) Длина 2v2v равна 2n2n единиц. (c) Длина v/2v/2 составляет n/2n/2 единиц. (d) Векторы vv и −v−v имеют одинаковую длину, но противоположные направления.
Другая операция, которую мы можем выполнять над векторами, — это сложение их вместе при сложении векторов, но поскольку каждый вектор может иметь свое собственное направление, этот процесс отличается от сложения двух чисел. Наиболее распространенный графический метод сложения двух векторов состоит в том, чтобы поместить начальную точку второго вектора в конечную точку первого, как показано на рис. 2.5(а). Чтобы понять, почему это имеет смысл, предположим, например, что оба вектора представляют смещение. Если объект перемещается сначала из начальной точки в конечную точку вектора v,v, а затем из начальной точки в конечную точку вектора w,w, то общее перемещение будет таким же, как если бы объект совершил всего одно движение из начальной точки в конечную точку вектора v+w.v+w. По понятным причинам такой подход называется методом треугольника. Заметьте, что если бы мы поменяли порядок так, чтобы ww был нашим первым вектором, а v был нашим вторым вектором, мы бы оказались там же. (Снова см. рис. 2.5(а).) Таким образом, v+w=w+v.v+w=w+v.
2.5(а). Чтобы понять, почему это имеет смысл, предположим, например, что оба вектора представляют смещение. Если объект перемещается сначала из начальной точки в конечную точку вектора v,v, а затем из начальной точки в конечную точку вектора w,w, то общее перемещение будет таким же, как если бы объект совершил всего одно движение из начальной точки в конечную точку вектора v+w.v+w. По понятным причинам такой подход называется методом треугольника. Заметьте, что если бы мы поменяли порядок так, чтобы ww был нашим первым вектором, а v был нашим вторым вектором, мы бы оказались там же. (Снова см. рис. 2.5(а).) Таким образом, v+w=w+v.v+w=w+v.
Второй метод сложения векторов называется методом параллелограмма. С помощью этого метода мы размещаем два вектора так, чтобы они имели одну и ту же начальную точку, а затем рисуем параллелограмм с двумя смежными сторонами векторов, как показано на рис. 2.5(b). Длина диагонали параллелограмма равна сумме. Сравнивая рис. 2. 5(b) и рис. 2.5(a), мы видим, что при использовании любого метода мы получаем один и тот же ответ. Вектор v+wv+w называется векторной суммой.
5(b) и рис. 2.5(a), мы видим, что при использовании любого метода мы получаем один и тот же ответ. Вектор v+wv+w называется векторной суммой.
Определение
Сумма двух векторов vv и ww может быть построена графически, если поместить начальную точку ww в конечную точку v.v. Тогда сумма векторов v+w,v+w представляет собой вектор с начальной точкой, совпадающей с начальной точкой vv, и с конечной точкой, совпадающей с конечной точкой w.w. Эта операция известна как сложение векторов.
Рисунок 2,5 (a) При сложении векторов методом треугольника начальная точка ww является конечной точкой v.v. (б) При сложении векторов методом параллелограмма векторы vv и ww имеют одну и ту же начальную точку.
Здесь также уместно обсудить вычитание векторов. Мы определяем v−wv−w как v+(−w)=v+(−1)w.v+(−w)=v+(−1)w. Вектор v−wv−w называется разностью векторов. Графически вектор v−wv−w изображается путем проведения вектора из конечной точки ww в конечную точку vv (рис. 2.6).
2.6).
Рисунок 2,6 (a) Разность векторов v−wv−w изображается путем рисования вектора из конечной точки ww в конечную точку v.v. (b) Вектор v−wv−w эквивалентен вектору v+(−w).v+(−w).
На рис. 2.5(a) начальная точка v+wv+w является начальной точкой v.v. Конечная точка v+wv+w является конечной точкой w.w. Эти три вектора образуют стороны треугольника. Отсюда следует, что длина любой стороны меньше суммы длин остальных сторон. Итак, у нас есть
‖v+w‖≤‖v‖+‖w‖.‖v+w‖≤‖v‖+‖w‖.
В более общем смысле это известно как неравенство треугольника. Однако есть один случай, когда результирующий вектор u+vu+v имеет ту же величину, что и сумма величин uu и v.v. Это происходит только тогда, когда uu и vv имеют одинаковое направление.
Пример 2.2
Объединение векторов
Учитывая векторы vv и ww, показанные на рис. 2.7, нарисуйте векторы
- 3w3w
- в+вв+в
- 2v-w2v-w
Рисунок 2,7 Векторы vv и ww лежат в одной плоскости.

Решение
- Вектор 3w3w имеет то же направление, что и w;w; это в три раза длиннее w.w.
Вектор 3w3w имеет то же направление, что и ww, и в три раза длиннее. - Используйте любой метод сложения, чтобы найти v+w.v+w.
Рисунок 2,8 Чтобы найти v+w,v+w, выровняйте векторы по их начальным точкам или поместите начальную точку одного вектора в конечную точку другого. (a) Вектор v+wv+w является диагональю параллелограмма со сторонами vv и ww (b) Вектор v+wv+w является третьей стороной треугольника, образованного точкой ww, расположенной в конечной точке vv.
- Чтобы найти 2v-w,2v-w, мы можем сначала переписать выражение как 2v+(-w).2v+(-w). Затем мы можем нарисовать вектор −w,−w, а затем добавить его к вектору 2v.2v.
Рисунок 2,9 Чтобы найти 2v-w,2v-w, просто добавьте 2v+(-w).2v+(-w).
Контрольно-пропускной пункт 2.
 2
2Используя векторы vv и ww из примера 2.2, нарисуйте вектор 2w-v.2w-v.
Компоненты вектора
Работать с векторами на плоскости проще, когда мы работаем в системе координат. Когда начальные и конечные точки векторов заданы в декартовых координатах, вычисления становятся простыми.
Пример 2.3
Сравнение векторов
Эквивалентны ли векторы vv и ww?
- vv имеет начальную точку (3,2)(3,2) и конечную точку (7,2)(7,2)
ww имеет начальную точку (1,−4)(1,−4) и конечную точку (1,0)(1,0) - vv имеет начальную точку (0,0)(0,0) и конечную точку (1,1)(1,1)
ww имеет начальную точку (−2,2)(−2,2) и конечную точку (− 1,3)(−1,3)
Решение
- Каждый вектор имеет длину 44 единицы, но они ориентированы в разных направлениях. Таким образом, vv и ww не эквивалентны (рис. 2.10).
Рисунок 2.
 10
Эти векторы не эквивалентны.
10
Эти векторы не эквивалентны. - На основании рисунка 2.11 и с использованием немного геометрии становится ясно, что эти векторы имеют одинаковую длину и одно и то же направление, поэтому vv и ww эквивалентны.
Рисунок 2.11 Эти векторы эквивалентны.
Контрольно-пропускной пункт 2.3
Какие из следующих векторов эквивалентны?
Мы видели, как построить вектор, если нам даны начальная и конечная точки. Однако, поскольку вектор можно разместить в любом месте плоскости, может быть проще выполнять вычисления с вектором, когда его начальная точка совпадает с началом координат. Мы называем вектор с начальной точкой в начале координат вектором стандартного положения. Поскольку известно, что начальная точка любого вектора в стандартном положении равна (0,0),(0,0), мы можем описать вектор, взглянув на координаты его конечной точки. Таким образом, если вектор v имеет начальную точку в начале координат и конечную точку в (x, y), (x, y), мы запишем вектор в компонентной форме как
v=〈x,y〉. v=〈x,y〉.
v=〈x,y〉.
Когда вектор записывается в компонентной форме таким образом, скаляры x и y называются компонентами v.v.
Определение
Вектор с начальной точкой (0,0)(0,0) и конечной точкой (x,y)(x,y) может быть записан в компонентной форме как
v=〈x,y〉.v=〈 х, у〉.
Скаляры xx и yy называются компонентами v.v.
Напомним, что имена векторов обозначаются строчными буквами, выделенными жирным шрифтом, или путем рисования стрелки над их именем. Мы также узнали, что мы можем назвать вектор по форме его компонента, с координатами его конечной точки в угловых скобках. Однако при записи компонентной формы вектора важно различать 〈x,y〉〈x,y〉 и (x,y).(x,y). Первая упорядоченная пара использует угловые скобки для описания вектора, тогда как вторая использует круглые скобки для описания точки на плоскости. Начальная точка 〈x,y〉〈x,y〉 равна (0,0);(0,0); конечная точка 〈x,y〉〈x,y〉 есть (x,y). (x,y).
(x,y).
Когда у нас есть вектор, который еще не находится в стандартном положении, мы можем определить форму его компонента одним из двух способов. Мы можем использовать геометрический подход, при котором мы рисуем вектор в координатной плоскости, а затем рисуем эквивалентный вектор стандартного положения. В качестве альтернативы мы можем найти его алгебраически, используя координаты начальной и конечной точек. Чтобы найти его алгебраически, мы вычитаем координату x начальной точки из координаты x конечной точки, чтобы получить 9Компонент 0019 x , и мы вычитаем y -координату начальной точки из y -координаты конечной точки, чтобы получить компонент y .
Правило: Компонентная форма вектора
Пусть v — вектор с начальной точкой (xi,yi)(xi,yi) и конечной точкой (xt,yt). (xt,yt). Тогда мы можем выразить v в компонентной форме как v=〈xt−xi,yt−yi〉.v=〈xt−xi,yt−yi〉.
(xt,yt). Тогда мы можем выразить v в компонентной форме как v=〈xt−xi,yt−yi〉.v=〈xt−xi,yt−yi〉.
Пример 2,4
Выражение векторов в компонентной форме
Выразите вектор vv с начальной точкой (−3,4)(−3,4) и конечной точкой (1,2)(1,2) в компонентной форме.
Решение
- Геометрический
- Нарисуйте вектор в координатной плоскости (рисунок 2.12).
- Конечная точка находится на 4 единицы вправо и на 2 единицы вниз от начальной точки.
- Найдите точку, которая находится на 4 единицы вправо и на 2 единицы вниз от начала координат.
- В стандартном положении этот вектор имеет начальную точку (0,0)(0,0) и конечную точку (4,−2):(4,−2):
v=〈4,−2〉.v=〈4,−2〉.
Рисунок 2.12 Эти векторы эквивалентны.
- Алгебраический
В первом решении мы использовали набросок вектора, чтобы увидеть, что конечная точка лежит на 4 единицы вправо. Мы можем сделать это алгебраически, найдя разность x -координат:
Мы можем сделать это алгебраически, найдя разность x -координат:xt-xi=1-(-3)=4.xt-xi=1-(-3)=4.
Точно так же разность координат и показывает вертикальную длину вектора.yt-yi=2-4=-2.yt-yi=2-4=-2.
Итак, в компонентной формеv=〈xt−xi,yt−yi〉=〈1−(−3),2−4〉=〈4,−2〉.v=〈xt−xi,yt− yi〉=〈1−(−3),2−4〉=〈4,−2〉.
Контрольно-пропускной пункт 2,4
Вектор ww имеет начальную точку (−4,−5)(−4,−5) и конечную точку (−1,2).(−1,2). Выразите ww в компонентной форме.
Чтобы найти модуль вектора, мы вычисляем расстояние между его начальной и конечной точками. Величина вектора v=〈x,y〉v=〈x,y〉 обозначается ‖v‖,‖v‖ или |v|,|v|, и может быть вычислена по формуле
‖v‖=x2+y2.‖v‖=x2+y2.
Обратите внимание, что, поскольку этот вектор записан в компонентной форме, он эквивалентен вектору в стандартной позиции, с начальной точкой в начале координат и конечной точкой (x,y). (x,y). Таким образом, достаточно вычислить модуль вектора в стандартном положении. Используя формулу расстояния для расчета расстояния между начальной точкой (0,0)(0,0) и конечной точкой (x,y),(x,y), мы имеем
(x,y). Таким образом, достаточно вычислить модуль вектора в стандартном положении. Используя формулу расстояния для расчета расстояния между начальной точкой (0,0)(0,0) и конечной точкой (x,y),(x,y), мы имеем
‖v‖=(x−0)2+(y−0)2=x2+y2.‖v‖=(x−0)2+(y−0)2=x2+y2.
Из этой формулы видно, что для любого вектора v,v,‖v‖≥0,‖v‖≥0 и ‖v‖=0‖v‖=0 тогда и только тогда, когда v=0.v= 0.
Величина вектора также может быть получена с помощью теоремы Пифагора, как показано на следующем рисунке.
Рисунок 2.13 Если вы используете компоненты вектора для определения прямоугольного треугольника, величина вектора равна длине гипотенузы треугольника.
Мы определили скалярное умножение и сложение векторов геометрически. Выражение векторов в компонентной форме позволяет нам выполнять те же операции алгебраически.
Определение
Пусть v=〈x1,y1〉v=〈x1,y1〉 и w=〈x2,y2〉w=〈x2,y2〉 — векторы, и пусть kk — скаляр. Сложение векторов: +y2〉v+w=〈x1,y1〉+〈x2,y2〉=〈x1+x2,y1+y2〉
Пример 2,5
Выполнение операций в компонентной форме
Пусть vv — вектор с начальной точкой (2,5)(2,5) и конечной точкой (8,13),(8,13), и пусть w=〈−2, 4〉. w=〈−2,4〉.
w=〈−2,4〉.
- Выразите vv в компонентной форме и найдите ‖v‖.‖v‖. Затем с помощью алгебры найдите .
- в+ж,в+в,
- 3В, 3В и
- v-2w.v-2w.
Решение
- Чтобы поместить начальную точку vv в начало координат, мы должны переместить вектор на 22 единицы влево и на 55 единиц вниз (рис. 2.15). Используя алгебраический метод, мы можем выразить vv как =62+82=36+64=100=10.‖v‖=62+82=36+64=100=10.
Рисунок 2.14 В компонентной форме v=〈6,8〉.v=〈6,8〉.
- Чтобы найти v+w,v+w, добавьте компоненты x и компоненты y по отдельности:
v+w=〈6,8〉+〈−2,4〉=〈4,12〉 .v+w=〈6,8〉+〈−2,4〉=〈4,12〉.
- Чтобы найти 3v,3v, умножьте vv на скаляр k=3:k=3:
3v=3·〈6,8〉=〈3·6,3·8〉=〈18,24〉.3v=3 ·〈6,8〉=〈3·6,3·8〉=〈18,24〉.
- Чтобы найти v−2w,v−2w, найдите −2w−2w и добавьте его к v:v:
v−2w=〈6,8〉−2·〈−2,4〉=〈6,8〉+ 〈4,−8〉=〈10,0〉.
 v−2w=〈6,8〉−2·〈−2,4〉=〈6,8〉+〈4,−8〉=〈10,0〉 .
v−2w=〈6,8〉−2·〈−2,4〉=〈6,8〉+〈4,−8〉=〈10,0〉 .
Контрольно-пропускной пункт 2,5
Пусть a=〈7,1〉a=〈7,1〉 и пусть bb вектор с начальной точкой (3,2)(3,2) и конечной точкой (−1,−1).(−1 ,−1).
- Найти ‖a‖.‖a‖.
- Express bb в виде компонентов.
- Найдите 3a−4b.3a−4b.
Теперь, когда мы установили основные правила векторной арифметики, мы можем сформулировать свойства векторных операций. Мы докажем два из этих свойств. Аналогично доказываются остальные.
Теорема 2.1
Свойства векторных операций
Пусть u,v,andwu,v,w — векторы на плоскости. Пусть r, sr и s — скаляры.
i.u+v=v+uКоммутативное свойствоii.(u+v)+w=u+(v+w)Ассоциативное свойствоiii.u+0=uАддитивное тождественное свойствоiv.u+(−u)=0Аддитивное обратное свойствоv.r( su)=(rs)uАссоциативность скалярного умноженияvi.(r+s)u=ru+suРаспределительное свойствоvii.r(u+v)=ru+rvРаспределительное свойствоviii. 1u=u,0u=0Тождественность и нулевые свойстваi.u+v= v+uКоммутативное свойствоii.(u+v)+w=u+(v+w)Ассоциативное свойствоiii.u+0=uАддитивное тождественное свойствоiv.u+(−u)=0Аддитивное обратное свойствоv.r(su)=(rs)uАссоциативность скалярное умножениеvi.(r+s)u=ru+suРаспределительное свойствоvii.r(u+v)=ru+rvРаспределительное свойствоviii.1u=u,0u=0Тождественность и нулевые свойства
1u=u,0u=0Тождественность и нулевые свойстваi.u+v= v+uКоммутативное свойствоii.(u+v)+w=u+(v+w)Ассоциативное свойствоiii.u+0=uАддитивное тождественное свойствоiv.u+(−u)=0Аддитивное обратное свойствоv.r(su)=(rs)uАссоциативность скалярное умножениеvi.(r+s)u=ru+suРаспределительное свойствоvii.r(u+v)=ru+rvРаспределительное свойствоviii.1u=u,0u=0Тождественность и нулевые свойства
Доказательство коммутативной собственности
Пусть u=〈x1,y1〉u=〈x1,y1〉 и v=〈x2,y2〉.v=〈x2,y2〉. Примените свойство коммутативности для действительных чисел:
u+v=〈x1+x2,y1+y2〉=〈x2+x1,y2+y1〉=v+u.u+v=〈x1+x2,y1+y2〉=〈x2+x1,y2+ y1〉=v+u.
□
Доказательство права собственности
Применить распределительное свойство для действительных чисел:
r(u+v)=r·〈x1+x2,y1+y2〉=〈r(x1+x2),r(y1+y2)〉=〈rx1+rx2,ry1+ry2〉=〈rx1,ry1 〉+〈rx2,ry2〉=ru+rv.r(u+v)=r·〈x1+x2,y1+y2〉=〈r(x1+x2),r(y1+y2)〉=〈rx1+ rx2,ry1+ry2〉=〈rx1,ry1〉+〈rx2,ry2〉=ru+rv.
□
Контрольно-пропускной пункт 2,6
Докажите аддитивное обратное свойство.
Мы нашли компоненты вектора, зная его начальную и конечную точки. В некоторых случаях у нас могут быть только величина и направление вектора, а не точки. Для этих векторов мы можем определить горизонтальную и вертикальную составляющие с помощью тригонометрии (рис. 2.15).
Рисунок 2,15 Компоненты вектора образуют катеты прямоугольного треугольника с вектором в качестве гипотенузы.
Рассмотрим угол θθ, образованный вектором v и положительной осью x . Из треугольника видно, что компоненты вектора vv равны 〈‖v‖cosθ,‖v‖sinθ〉.〈‖v‖cosθ,‖v‖sinθ〉. Следовательно, зная угол и величину вектора, мы можем использовать косинус и синус угла, чтобы найти компоненты вектора.
Пример 2,6
Нахождение формы компонента вектора с помощью тригонометрии
Найти форму компонента вектора с величиной 4, которая образует угол −45°−45° с x — ось.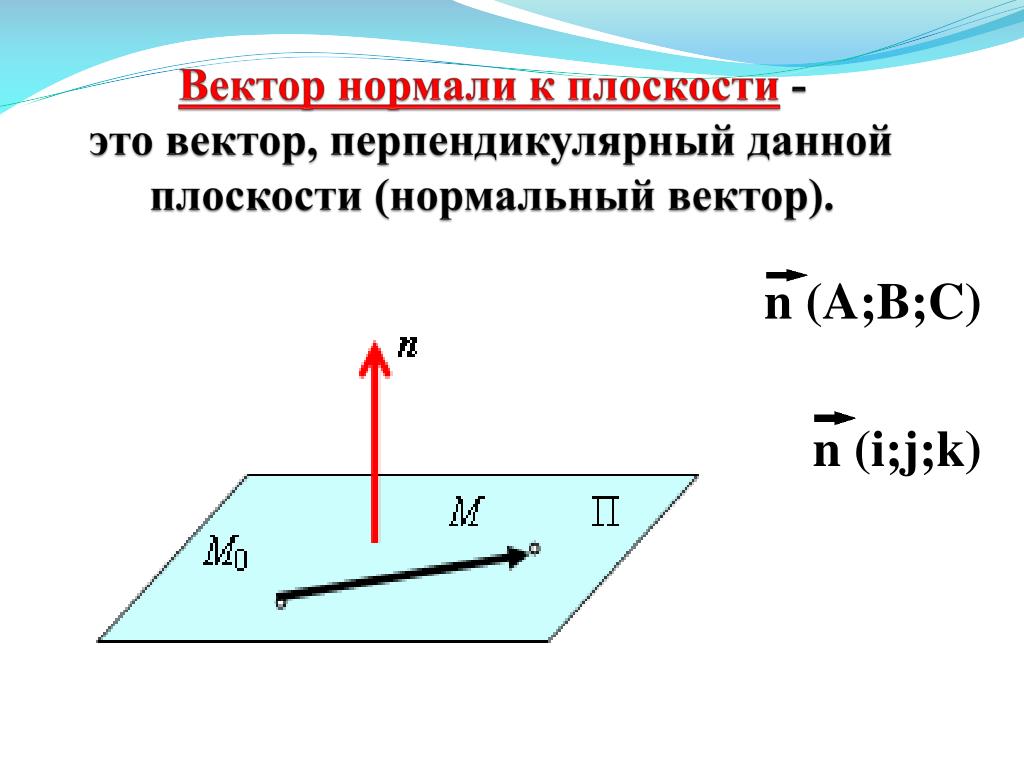
Решение
Пусть xx и yy представляют компоненты вектора (рис. 2.16). Тогда x=4cos(-45°)=22x=4cos(-45°)=22 и y=4sin(-45°)=-22.y=4sin(-45°)=-22. Компонентная форма вектора 〈22,−22〉.〈22,−22〉.
Рисунок 2.16 Используйте тригонометрические отношения, x=‖v‖cosθx=‖v‖cosθ и y=‖v‖sinθ,y=‖v‖sinθ, чтобы идентифицировать компоненты вектора.
Контрольно-пропускной пункт 2,7
Найдите компонентную форму вектора vv с величиной 1010, которая образует угол 120°120° с положительной x — ось.
Единичные векторы
Единичный вектор — это вектор с величиной 1,1. Для любого ненулевого вектора v,v мы можем использовать скалярное умножение, чтобы найти единичный вектор uu, который имеет то же направление, что и v.v. Для этого умножаем вектор на величину, обратную его модулю:
u=1‖v‖v.u=1‖v‖v.
Вспомните, когда мы определяли скалярное умножение, мы отметили, что ‖kv‖=|k|·‖v‖. ‖kv‖=|k|·‖v‖. Для u=1‖v‖v,u=1‖v‖v следует, что ‖u‖=1‖v‖(‖v‖)=1.‖u‖=1‖v‖(‖v‖)= 1. Мы говорим, что уу это орт в направлении вв (рис. 2.17). Процесс использования скалярного умножения для нахождения единичного вектора с заданным направлением называется нормализацией.
‖kv‖=|k|·‖v‖. Для u=1‖v‖v,u=1‖v‖v следует, что ‖u‖=1‖v‖(‖v‖)=1.‖u‖=1‖v‖(‖v‖)= 1. Мы говорим, что уу это орт в направлении вв (рис. 2.17). Процесс использования скалярного умножения для нахождения единичного вектора с заданным направлением называется нормализацией.
Рисунок 2.17 Вектор vv и связанный с ним единичный вектор u=1‖v‖v.u=1‖v‖v. В этом случае ‖v‖>1.‖v‖>1.
Пример 2,7
Нахождение единичного вектора
Пусть v=〈1,2〉.v=〈1,2〉.
- Найдите единичный вектор с тем же направлением, что и v.v.
- Найдите вектор ww с тем же направлением, что и vv, такой, что ‖w‖=7.‖w‖=7.
Решение
- Сначала найдите величину v,v, затем разделите компоненты vv на величину:
‖v‖=12+22=1+4=5‖v‖=12+22=1+4=5
u=1‖v‖v=15〈1,2〉=〈15,25〉.u=1‖v‖v=15〈1,2〉=〈15,25〉.
- Вектор uu имеет то же направление, что и vv, и ‖u‖=1.
 ‖u‖=1. Используйте скалярное умножение, чтобы увеличить длину uu без изменения направления:
‖u‖=1. Используйте скалярное умножение, чтобы увеличить длину uu без изменения направления:w=7u=7〈15,25〉=〈75,145〉.w=7u=7〈15,25〉=〈75,145〉.
Контрольно-пропускной пункт 2,8
Пусть v=〈9,2〉.v=〈9,2〉. Найдите вектор с величиной 55 в направлении, противоположном v.v.
Мы видели, насколько удобно записывать вектор в компонентной форме. Однако иногда удобнее записать вектор как сумму горизонтального и вертикального векторов. Чтобы упростить задачу, давайте рассмотрим стандартные единичные векторы. Стандартными единичными векторами являются векторы i=〈1,0〉i=〈1,0〉 и j=〈0,1〉j=〈0,1〉 (рис. 2.18).
. Второй вектор находится на оси Y и помечен буквой «j», что равно .»>Рисунок 2.18 Стандартные единичные векторы ii и j.j.
Применяя свойства векторов, можно выразить любой вектор через ii и jj в виде того, что мы называем линейной комбинацией :
v=〈x,y〉=〈x,0〉+〈0,y〉=x〈1,0〉+y〈0,1〉=xi+yj. v=〈x,y〉=〈x, 0〉+〈0,y〉=x〈1,0〉+y〈0,1〉=xi+yj.
v=〈x,y〉=〈x, 0〉+〈0,y〉=x〈1,0〉+y〈0,1〉=xi+yj.
Таким образом, vv представляет собой сумму горизонтального вектора с величиной x,x и вертикального вектора с величиной y,y, как показано на следующем рисунке.
Рисунок 2.19Вектор vv является суммой xixi и yj.yj.
Пример 2,8
Использование стандартных единичных векторов
- Выразите вектор w=〈3,−4〉w=〈3,−4〉 в терминах стандартных единичных векторов.
- Вектор uu представляет собой единичный вектор, образующий угол 60°60° с положительной осью x . Используйте стандартные единичные векторы для описания u.u.
Решение
- Разложить вектор ww на вектор с нулевой y -компонентой и вектор с нулевой x -компонента:
w=〈3,−4〉=3i−4j.w=〈3,−4〉=3i−4j.
- Поскольку uu — единичный вектор, конечная точка лежит на единичной окружности, когда вектор помещен в стандартное положение (рис.
 2.20).
2.20).u=〈cos60°,sin60°〉=〈12,32〉=12i+32j.u=〈cos60°,sin60°〉=〈12,32〉=12i+32j.
Рисунок 2.20 Конечная точка uu лежит на единичной окружности (cosθ,sinθ).(cosθ,sinθ).
Контрольно-пропускной пункт 2,9
Пусть a=〈16,−11〉a=〈16,−11〉 и пусть bb единичный вектор, образующий угол 225°225° с положительной x — ось. Выразите aa и bb через стандартные единичные векторы.
Применение векторов
Поскольку векторы имеют как направление, так и величину, они являются ценными инструментами для решения задач, связанных с такими приложениями, как движение и сила. Вспомните пример с лодкой и пример с квотербеком, которые мы описали ранее. Здесь мы подробно рассмотрим два других примера.
Пример 2,9
Нахождение равнодействующей силы
Машина Джейн застряла в грязи. Лиза и Джед приезжают на грузовике, чтобы помочь вытащить ее. Они прикрепляют один конец буксирного ремня к передней части автомобиля, а другой конец к сцепному устройству прицепа грузовика, и грузовик начинает тянуть. Тем временем Джейн и Джед садятся за машину и толкают ее. Грузовик создает горизонтальную силу в 300300 фунтов на автомобиль. Джейн и Джед толкают машину под небольшим углом вверх и создают на машине силу 150150 фунтов. Эти силы могут быть представлены векторами, как показано на рис. 2.21. Угол между этими векторами равен 15°.15°. Найдите результирующую силу (векторную сумму) и задайте ее величину с точностью до десятых долей фунта и угол ее направления от положительного x — ось.
Они прикрепляют один конец буксирного ремня к передней части автомобиля, а другой конец к сцепному устройству прицепа грузовика, и грузовик начинает тянуть. Тем временем Джейн и Джед садятся за машину и толкают ее. Грузовик создает горизонтальную силу в 300300 фунтов на автомобиль. Джейн и Джед толкают машину под небольшим углом вверх и создают на машине силу 150150 фунтов. Эти силы могут быть представлены векторами, как показано на рис. 2.21. Угол между этими векторами равен 15°.15°. Найдите результирующую силу (векторную сумму) и задайте ее величину с точностью до десятых долей фунта и угол ее направления от положительного x — ось.
Рисунок 2.21 Две силы, действующие на автомобиль в разных направлениях.
Решение
Чтобы найти эффект объединения двух сил, сложите их репрезентативные векторы. Во-первых, выразите каждый вектор в компонентной форме или в терминах стандартных единичных векторов. Для этой цели проще всего совместить один из векторов с положительной осью x . Таким образом, горизонтальный вектор имеет начальную точку (0,0)(0,0) и конечную точку (300,0).(300,0). Его можно выразить как 〈300,0〉〈300,0〉 или 300i.300i.
Для этой цели проще всего совместить один из векторов с положительной осью x . Таким образом, горизонтальный вектор имеет начальную точку (0,0)(0,0) и конечную точку (300,0).(300,0). Его можно выразить как 〈300,0〉〈300,0〉 или 300i.300i.
Второй вектор имеет величину 150150 и составляет угол 15°15° с первым, поэтому мы можем выразить его как 〈150cos(15°),150sin(15°)〉,〈150cos(15°),150sin( 15°)〉 или 150cos(15°)i+150sin(15°)j.150cos(15°)i+150sin(15°)j. Тогда сумма векторов, или результирующий вектор, равна 150sin(15°)〉, и имеем
‖r‖=(300+150cos(15°))2+(150sin(15°))2≈446,6.‖r‖=(300+150cos(15°) )2+(150sin(15°))2≈446,6.
Угол θθ, образованный rr и положительным x -ось имеет tanθ=150sin15°(300+150cos15°)≈0,09, tanθ=150sin15°(300+150cos15°)≈0,09, поэтому θ≈tan−1(0,09)≈5°,θ≈tan−1 (0,09)≈5°, что означает, что результирующая сила rr имеет угол 5°5° над горизонтальной осью.
Пример 2.10
Определение результирующей скорости
Самолет летит строго на запад со скоростью 425425 миль в час. Ветер дует с северо-востока со скоростью 4040 миль в час. Какова путевая скорость самолета? Какой пеленг у самолета?
Ветер дует с северо-востока со скоростью 4040 миль в час. Какова путевая скорость самолета? Какой пеленг у самолета?
Решение
Начнем с описания описанной ситуации (рис. 2.22).
Рисунок 2,22 Первоначально самолет летит строго на запад. Ветер северо-восточный, поэтому дует на юго-запад. Угол между курсом самолета и ветром 45°.45°. (Рисунок не в масштабе.)
Настройте эскиз так, чтобы начальные точки векторов лежали в начале координат. Тогда вектор скорости самолета равен p=−425i.p=−425i. Вектор, описывающий ветер, составляет угол 225°225° с положительным углом x — ось:
w=〈40cos(225°),40sin(225°)〉=〈−402,−402〉=−402i−402j.w=〈40cos(225°),40sin(225°) )〉=〈−402,−402〉=−402i−402j.
Когда воздушная скорость и ветер действуют на самолет вместе, мы можем сложить их векторы, чтобы найти результирующую силу:
p+w=−425i+(−402i−402j)=(−425−402)i−402j. p+w=-425i+(-402i-402j)=(-425-402)i-402j.
Величина результирующего вектора показывает влияние ветра на путевую скорость самолета: ‖=(−425−402)2+(−402)2≈454,17 миль в час
Из-за ветра самолет движется со скоростью около 454454 миль в час относительно земли.
Чтобы определить пеленг самолета, мы хотим найти направление вектора p+w:p+w:
tanθ=−402(−425−402)≈0,06θ≈3,57°.tanθ=−402 (−425−402)≈0,06θ≈3,57°.
Общее направление плоскости 3,57°3,57° к югу от запада.
Контрольно-пропускной пункт 2.10
Самолет летит строго на север со скоростью 550550 миль в час. Ветер дует с северо-запада со скоростью 5050 м/с. Какова путевая скорость самолета?
Раздел 2.1 Упражнения
В следующих упражнениях рассмотрите точки P(−1,3),P(−1,3),Q(1,5),Q(1,5) и R(−3,7).R( −3,7). Определить искомые векторы и выразить каждый из них a. в виде компонентов и б. используя стандартные единичные векторы.
1.
ПК→ПК→
2.
PR→PR→
3.
КП→КП→
4.
РП→РП→
5.
PQ→+PR→PQ→+PR→
6.
PQ→−PR→PQ→−PR→
7.
2PQ→−2PR→2PQ→−2PR→
8.
2PQ→+12PR→2PQ→+12PR→
9.
Единичный вектор в направлении PQ→PQ→
10.
Единичный вектор в направлении PR→PR→
11.
Вектор vv имеет начальную точку (−1,−3)(−1,−3) и конечную точку (2,1).(2,1). Найдите единичный вектор в направлении v.v. Выразите ответ в компонентной форме.
12.
Вектор vv имеет начальную точку (−2,5)(−2,5) и конечную точку (3,−1).(3,−1). Найдите единичный вектор в направлении v. v. Выразите ответ в компонентной форме.
v. Выразите ответ в компонентной форме.
13.
Вектор vv имеет начальную точку P(1,0)P(1,0) и конечную точку QQ, расположенную на оси y и выше начальной точки. Найдите координаты конечной точки QQ такие, что величина вектора vv равна 5,5.
14.
Вектор vv имеет начальную точку P(1,1)P(1,1) и конечную точку QQ, которая находится на x — ось и слева от начальной точки. Найдите координаты конечной точки QQ такие, что величина вектора vv равна 10,10.
В следующих упражнениях используйте заданные векторы aa и b.b.
- Определите векторную сумму a+ba+b и выразите ее как в компонентной форме, так и с помощью стандартных единичных векторов.
- Найдите разность векторов a−ba−b и выразите ее как в компонентной форме, так и с помощью стандартных единичных векторов.
- Убедитесь, что векторы a,a,b,b и a+b,a+b и, соответственно, a,a,b,b и a−ba−b удовлетворяют неравенству треугольника.

- Определить векторы 2a,2a,−b,−b и 2a−b.2a−b. Выразите векторы как в компонентной форме, так и при помощи стандартных единичных векторов.
15.
a=2i+j,a=2i+j,b=i+3jb=i+3j
16.
а=2i,а=2i,b=-2i+2jb=-2i+2j
17.
Пусть aa — вектор стандартного положения с конечной точкой (−2,−4).(−2,−4). Пусть bb — вектор с начальной точкой (1,2)(1,2) и конечной точкой (−1,4).(−1,4). Найдите величину вектора −3a+b−4i+j.−3a+b−4i+j.
18.
Пусть aa будет вектором стандартного положения с конечной точкой в (2,5).(2,5). Пусть bb — вектор с начальной точкой (−1,3)(−1,3) и конечной точкой (1,0).(1,0). Найдите величину вектора a−3b+14i−14j.a−3b+14i−14j.
19.
Пусть uu и vv — два ненулевых неэквивалентных вектора. Рассмотрим векторы a=4u+5va=4u+5v и b=u+2vb=u+2v, определенные через uu и v. v. Найдите скаляр λλ такой, что векторы a+λba+λb и u−vu−v эквивалентны.
v. Найдите скаляр λλ такой, что векторы a+λba+λb и u−vu−v эквивалентны.
20.
Пусть uu и vv — два ненулевых неэквивалентных вектора. Рассмотрим векторы a=2u−4va=2u−4v и b=3u−7vb=3u−7v, определенные через uu и v.v. Найдите скаляры αα и ββ такие, что векторы αa+βbαa+βb и u−vu−v эквивалентны.
21.
Рассмотрим вектор a(t)=〈cost,sint〉a(t)=〈cost,sint〉 с компонентами, зависящими от вещественного числа t.t. При изменении числа tt изменяются и компоненты a(t)a(t) в зависимости от определяющих их функций.
- Запишите векторы a(0)a(0) и a(π)a(π) в компонентной форме.
- Показать, что величина ‖a(t)‖‖a(t)‖ вектора a(t)a(t) остается постоянной для любого действительного числа t.t.
- При изменении tt покажите, что конечная точка вектора a(t)a(t) описывает окружность с центром в начале координат радиусом 1,1.
22.
Рассмотрим вектор a(x)=〈x,1−x2〉a(x)=〈x,1−x2〉 с компонентами, зависящими от вещественного числа x∈[−1,1]. x∈[−1 ,1]. Поскольку число xx меняется , компоненты a(x)a(x) также изменяются в зависимости от определяющих их функций.
x∈[−1 ,1]. Поскольку число xx меняется , компоненты a(x)a(x) также изменяются в зависимости от определяющих их функций.
- Запишите векторы a(0)a(0) и a(1)a(1) в компонентной форме.
- Показать, что величина ‖a(x)‖‖a(x)‖ вектора a(x)a(x) остается постоянной для любого действительного числа xx
- При изменении xx покажите, что если a(x)a(x) находится в стандартном положении, то его конечная точка описывает полуокружность. Почему только полукруг?
23.
Показать, что векторы a(t)=〈cost,sint〉a(t)=〈cost,sint〉 и a(x)=〈x,1−x2〉a(x)=〈x,1−x2〉 эквивалентны для x=1x=1 и t=2kπ,t=2kπ, где kk — целое число.
24.
Показать, что векторы a(t)=〈cost,sint〉a(t)=〈cost,sint〉 и a(x)=〈x,1−x2〉a(x)=〈x,1−x2〉 противоположны для x=1x=1 и t=π+2kπ,t=π+2kπ, где kk — целое число.
Для следующих упражнений найдите вектор vv с заданной величиной и в том же направлении, что и вектор u. u.
u.
25.
‖v‖=7,u=〈3,4〉‖v‖=7,u=〈3,4〉
26.
‖v‖=3,u=〈−2,5〉‖v‖=3,u=〈−2,5〉
27.
‖v‖=7,u=〈3,−5〉‖v‖=7,u=〈3,−5〉
28.
‖v‖=10,u=〈2,−1〉‖v‖=10,u=〈2,−1〉
В следующих упражнениях найдите компонентную форму вектора u,u, зная его модуль и угол, который вектор образует с положительной осью x . По возможности давайте точные ответы.
29.
‖u‖=2,‖u‖=2,θ=30°θ=30°
30.
‖u‖=6,‖u‖=6,θ=60°θ=60°
31.
‖u‖=5,‖u‖=5,θ=π2θ=π2
32.
‖u‖=8,‖u‖=8,θ=πθ=π
33.
‖u‖=10,‖u‖=10,θ=5π6θ=5π6
34.
‖u‖=50,‖u‖=50,θ=3π4θ=3π4
Для следующих упражнений задан вектор uu. Найдите угол θ∈[0,2π)θ∈[0,2π), который вектор uu образует с положительным направлением оси x против часовой стрелки.
35.
u=52i−52ju=52i−52j
36.
и=-3i-ju=-3i-j
37.
Пусть a=〈a1,a2〉,a=〈a1,a2〉,b=〈b1,b2〉,b=〈b1,b2〉 и c=〈c1,c2〉c=〈c1,c2〉 — три ненулевых вектора. Если a1b2−a2b1≠0,a1b2−a2b1≠0, то покажите, что существуют два скаляра, αα и β,β, такие, что c=αa+βb.c=αa+βb.
38.
Рассмотрим векторы a=〈2,−4〉,a=〈2,−4〉,b=〈−1,2〉,b=〈−1,2〉 и c = 0 Определить скаляры αα и ββ такие, что c=αa+βb.c=αa+βb.
39.
Пусть P(x0,f(x0))P(x0,f(x0)) — фиксированная точка на графике дифференцируемой функции ff с областью определения, являющейся множеством действительных чисел.
- Определить действительное число z0z0 такое, что точка Q(x0+1,z0)Q(x0+1,z0) расположена на прямой, касательной к графику функции ff в точке P.P.
- Определите единичный вектор uu с начальной точкой PP в направлении вектора PQ.PQ.
40.
Рассмотрим функцию f(x)=x4,f(x)=x4, где x∈ℝ.x∈ℝ.
- Определите действительное число z0z0 такое, что точка Q(2,z0)Q(2,z0) расположена на прямой, касательной к графику ff в точке P(1,1).P(1,1).
- Определите единичный вектор uu с начальной точкой PP и конечной точкой Q.Q.
41.
Рассмотрим две функции ff и gg, определенные на одном и том же множестве действительных чисел Д.Д. Пусть a=〈x,f(x)〉a=〈x,f(x)〉 и b=〈x,g(x)〉b=〈x,g(x)〉 — два вектора, описывающие графики функции, где x∈D.x∈D. Покажите, что если графики функций ff и gg не пересекаются, то векторы аа и bb не эквивалентны.
42.
Найдите x∈ℝx∈ℝ такой, что векторы a=〈x,sinx〉a=〈x,sinx〉 и b=〈x,cosx〉b=〈x,cosx〉 эквивалентны.
43.
Вычислить координаты точки DD так, чтобы ABCDABCD был параллелограммом с A(1,1),A(1,1),B(2,4),B(2,4) и C(7,4) ).С(7,4).
44.
Рассмотрим точки A(2,1),A(2,1),B(10,6),B(10,6),C(13,4),C(13,4) и D( 16,−2).D(16,−2). Определить компонентную форму вектора AD→.AD→.
45.
Скорость объекта — это величина связанного с ним вектора скорости. Мяч, брошенный квотербеком, имеет начальную скорость 7070 миль в час и угол подъема 30°,30°. Определите вектор скорости в милях в час и выразите его в компонентной форме. (Округлить до двух знаков после запятой.)
46.
Бейсболист бросает бейсбольный мяч под углом 30°30° к горизонту. Найдите горизонтальную и вертикальную составляющие вектора начальной скорости бейсбольного мяча, если начальная скорость мяча равна 100 100 миль в час.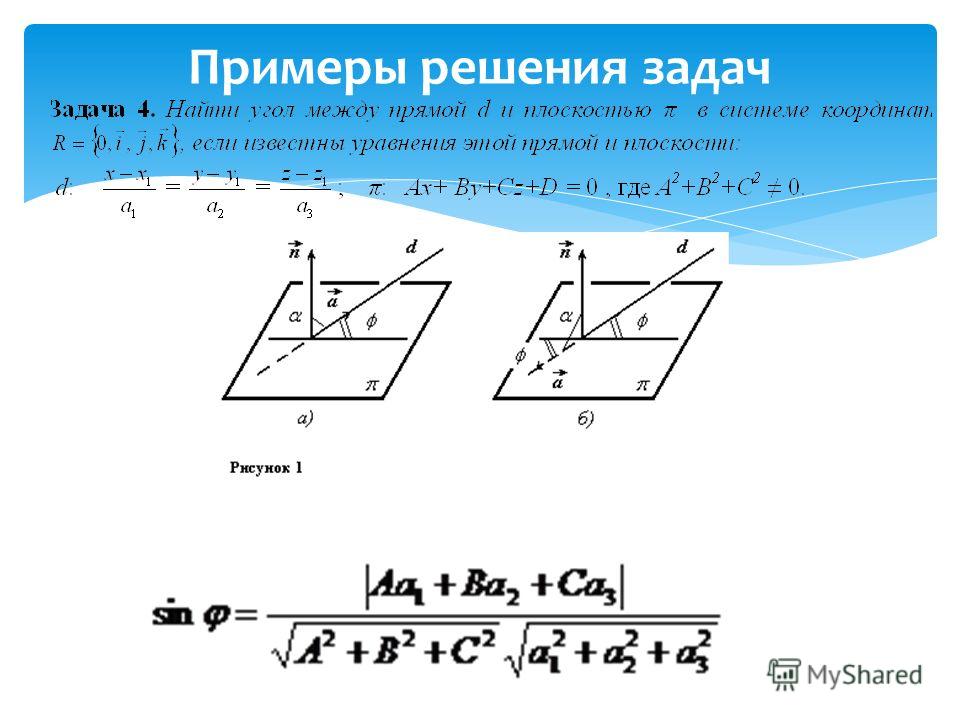 (Округлить до двух знаков после запятой.)
(Округлить до двух знаков после запятой.)
47.
Пуля выпущена с начальной скоростью 15001500 футов/сек под углом 60°60° к горизонту. Найдите горизонтальную и вертикальную составляющие вектора скорости пули. (Округлить до двух знаков после запятой.)
48.
[T] Спринтер массой 65 кг прикладывает силу 798798 Н под углом 19°19° по отношению к земле к стартовой колодке в момент начала забега. Найдите горизонтальную составляющую силы. (Округлить до двух знаков после запятой.)
49.
[T] На один и тот же объект действуют две силы, горизонтальная сила 4545 фунтов и другая 5252 фунта. Угол между этими силами равен 25°.25°. Найдите модуль и угол направления от положительной х — ось равнодействующей силы, действующей на объект. (Округлить до двух знаков после запятой.)
50.
[T] Две силы, вертикальная сила 2626 фунтов и другая 4545 фунтов, действуют на один и тот же объект. Угол между этими силами равен 55°,55°. Найдите величину и угол направления от положительной оси x равнодействующей силы, действующей на объект. (Округлить до двух знаков после запятой.)
51.
[T] На объект действуют три силы. Две силы имеют величины 5858 Н и 2727 Н и образуют углы 53°53° и 152°, 152° соответственно с положительной x — ось. Найдите модуль и угол направления от положительной оси x третьей силы так, чтобы результирующая сила, действующая на объект, равнялась нулю. (Округлить до двух знаков после запятой.)
52.
Три силы с величинами 8080 фунтов, 120120 фунтов и 6060 фунтов действуют на объект под углами 45°, 45°, 60°60° и 30°, 30° соответственно с положительной осью x . Найдите модуль и угол направления от положительной оси x равнодействующей силы. (Округлить до двух знаков после запятой.)
Найдите модуль и угол направления от положительной оси x равнодействующей силы. (Округлить до двух знаков после запятой.)
53.
[T] Самолет летит в направлении 43°43° к востоку от севера (также сокращенно N43E)N43E) со скоростью 550550 миль в час. Ветер со скоростью 2525 миль в час дует с юго-запада по азимуту N15E.N15E. Какова путевая скорость и новое направление самолета?
54.
[T] Лодка движется по воде со скоростью 3030 миль в час в направлении N20EN20E (то есть 20°20° к востоку от севера). Сильное течение движется со скоростью 1515 миль в час в направлении N45E.N45E. Каковы новые скорость и направление лодки?
55.
[T] Груз массой 50 фунтов подвешен на тросе так, что две части троса образуют с горизонтом углы 40°40° и 53°, 53° соответственно. Найти величины сил натяжения Т1Т1 и Т2Т2 в тросах, если результирующая сила, действующая на тело, равна нулю.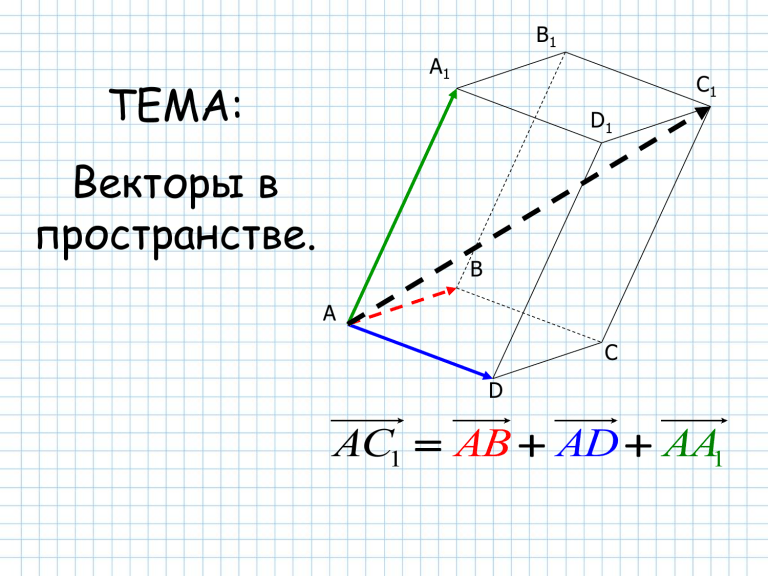 (Округлить до двух знаков после запятой.)
(Округлить до двух знаков после запятой.)
56.
[T] Груз массой 62 фунта висит на веревке, образующей с горизонтом углы 29°29° и 61°,61° соответственно. Найти величины сил натяжения Т1Т1 и Т2Т2 в тросах, если результирующая сила, действующая на тело, равна нулю. (Округлить до двух знаков после запятой.)
57.
[T] Лодка массой 1500 фунтов припаркована на аппарели, образующей с горизонтом угол 30°30°. Вектор веса лодки направлен вниз и представляет собой сумму двух векторов: горизонтального вектора v1v1, параллельного аппарели, и вертикального вектора v2v2, перпендикулярного наклонной поверхности. Величины векторов v1v1 и v2v2 представляют собой соответственно горизонтальную и вертикальную составляющие вектора веса лодки. Найдите величины v1v1 и v2.v2. (Округлить до ближайшего целого числа.)
58.
[T] 85-фунтовый ящик находится в состоянии покоя на наклонной плоскости 26°26°.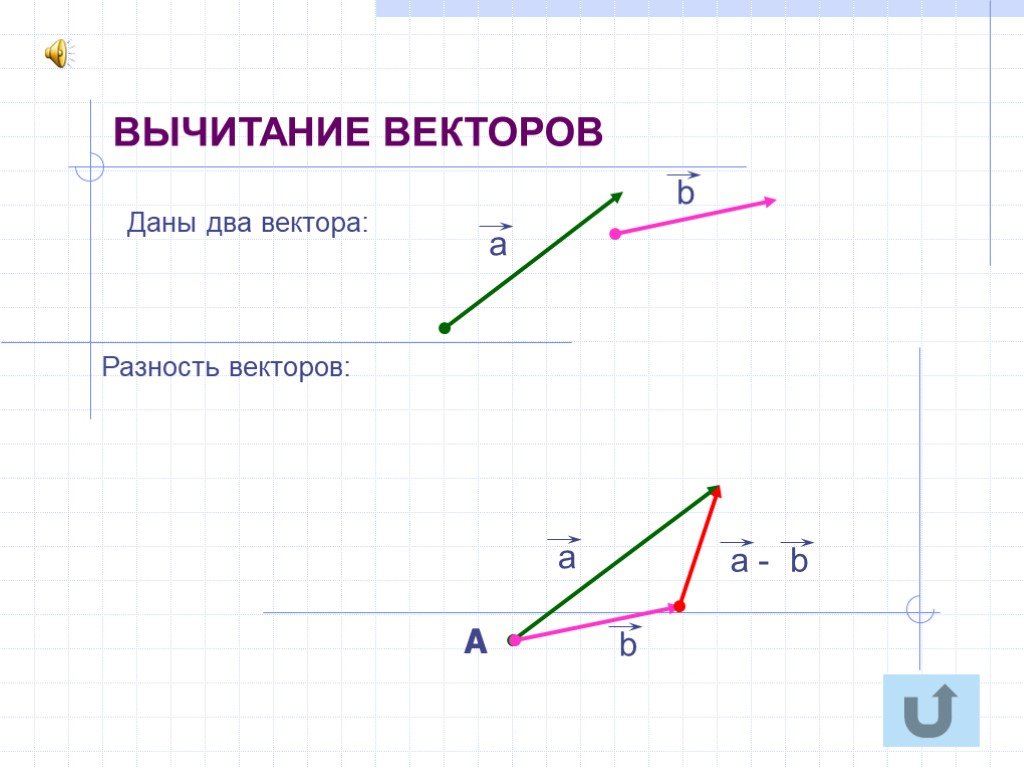 Определить величину силы, параллельной наклону, необходимой для удержания ящика от скольжения. (Округлить до ближайшего целого числа.)
Определить величину силы, параллельной наклону, необходимой для удержания ящика от скольжения. (Округлить до ближайшего целого числа.)
59.
Растяжка поддерживает столб высотой 7575 футов. Один конец провода прикреплен к вершине столба, а другой конец прикреплен к земле на расстоянии 5050 футов от основания столба. Определить горизонтальную и вертикальную составляющие силы натяжения проволоки, если ее величина равна 5050 фунтов (округлить до ближайшего целого числа).
60.
Растяжка телефонного столба имеет угол возвышения 35°35° по отношению к земле. Сила натяжения растяжки равна 120120 фунтов. Найти горизонтальную и вертикальную составляющие силы натяжения. (Округлить до ближайшего целого числа.)
Многозадачное векторное полевое обучение — PMC
- Список журналов
- Рукописи авторов HHS
- PMC4201856
Adv Neural Inf Process Syst. Авторская рукопись; доступно в PMC 2014 18 октября. 2012 г.; 2012: 296–304.
Авторская рукопись; доступно в PMC 2014 18 октября. 2012 г.; 2012: 296–304.
PMCID: PMC4201856
NIHMSID: NIHMS497483
PMID: 25332642
, 1 , 2 , 1 , 2 и 1
Информация об авторе Информация об авторских правах и лицензии Отказ от ответственности . Большинство существующих методов MTL сосредоточены на изучении линейных моделей в контролируемых условиях. Мы предлагаем новый полууправляемый и нелинейный подход к MTL с использованием векторных полей. Векторное поле — это гладкое отображение многообразия в касательные пространства, которое можно рассматривать как производную по направлениям функций на многообразии. Мы утверждаем, что векторные поля обеспечивают естественный способ использования геометрической структуры данных, а также общей дифференциальной структуры задач, которые имеют решающее значение для многозадачного обучения с полуучителем. В этой статье мы разрабатываем многозадачное обучение векторному полю (MTVFL), которое одновременно изучает функции предикторов и векторные поля.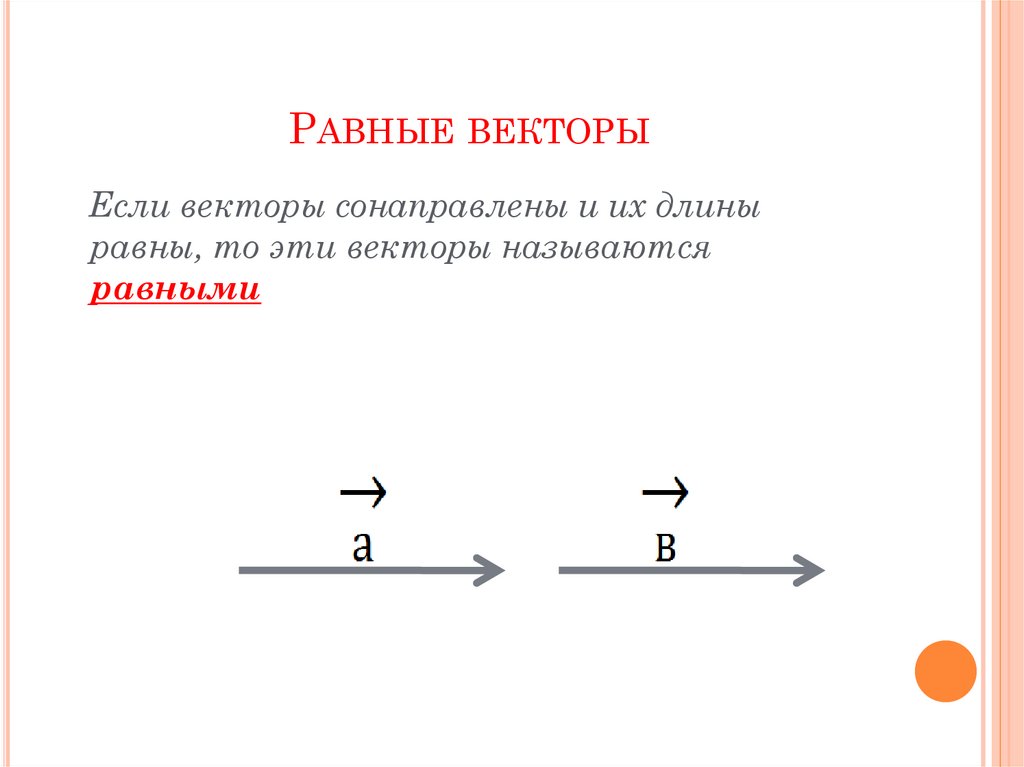 MTVFL обладает следующими ключевыми свойствами. (1) Векторные поля, которые изучает MTVFL, близки к полям градиента функций-предикторов. (2) В каждой задаче векторное поле должно быть как можно более параллельным, что, как ожидается, будет охватывать низкоразмерное подпространство. (3) Векторные поля всех задач имеют общее низкоразмерное подпространство. Мы формализуем нашу идею в рамках регуляризации, а также предложим метод выпуклой релаксации для решения исходной невыпуклой задачи. Экспериментальные результаты на синтетических и реальных данных демонстрируют эффективность предложенного нами подхода.
MTVFL обладает следующими ключевыми свойствами. (1) Векторные поля, которые изучает MTVFL, близки к полям градиента функций-предикторов. (2) В каждой задаче векторное поле должно быть как можно более параллельным, что, как ожидается, будет охватывать низкоразмерное подпространство. (3) Векторные поля всех задач имеют общее низкоразмерное подпространство. Мы формализуем нашу идею в рамках регуляризации, а также предложим метод выпуклой релаксации для решения исходной невыпуклой задачи. Экспериментальные результаты на синтетических и реальных данных демонстрируют эффективность предложенного нами подхода.
Во многих приложениях помеченные данные являются дорогостоящими и требуют много времени для получения, в то время как немаркированные данные имеются в изобилии. Проблема использования неразмеченных данных для повышения производительности обобщения часто упоминается как полууправляемое обучение (SSL). Хорошо известно, что для того, чтобы обучение с полуучителем работало, необходимы некоторые предположения о зависимости между предикторной функцией и маргинальным распределением данных.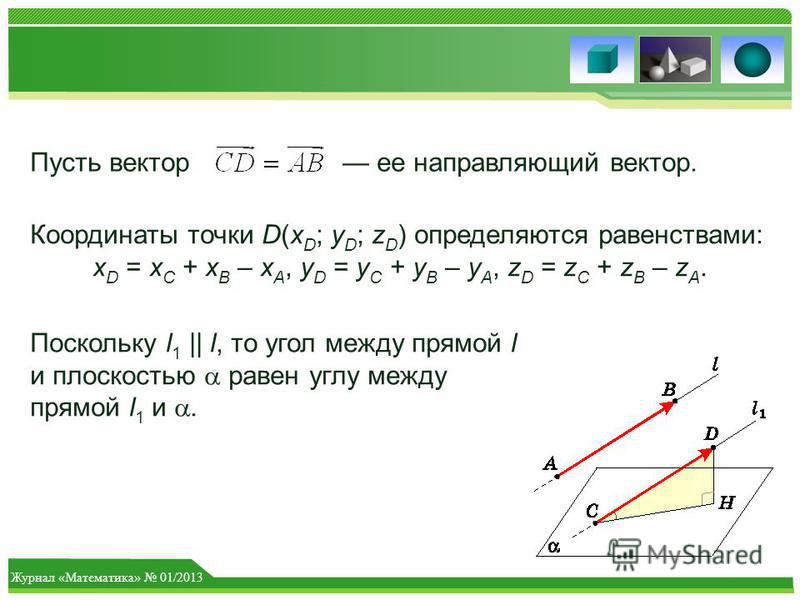 Предположение о многообразии [15, 5], получившее широкое распространение в последнее десятилетие, утверждает, что предикторная функция живет в маломерном многообразии маргинального распределения.
Предположение о многообразии [15, 5], получившее широкое распространение в последнее десятилетие, утверждает, что предикторная функция живет в маломерном многообразии маргинального распределения.
Многозадачное обучение было предложено для повышения производительности обобщения за счет одновременного изучения нескольких связанных задач. Обширная литература по многозадачному обучению демонстрирует, что эффективность обучения действительно улучшается, когда задачи связаны между собой [4, 6, 7]. Ключевым шагом в MTL является поиск общей информации среди задач. Евгений и др. [12] предложил структуру регуляризации MTL, которая предполагает, что все задачи связаны и близки друг к другу. Андо и Чжан [2] предложили структурную структуру обучения, которая предполагала, что несколько предикторов для разных задач имеют общую структуру в базовом пространстве предикторов. Метод альтернативной оптимизации структуры (ASO) был предложен для линейных предикторов, которые предполагали, что параметры задачи имеют общее низкоразмерное подпространство.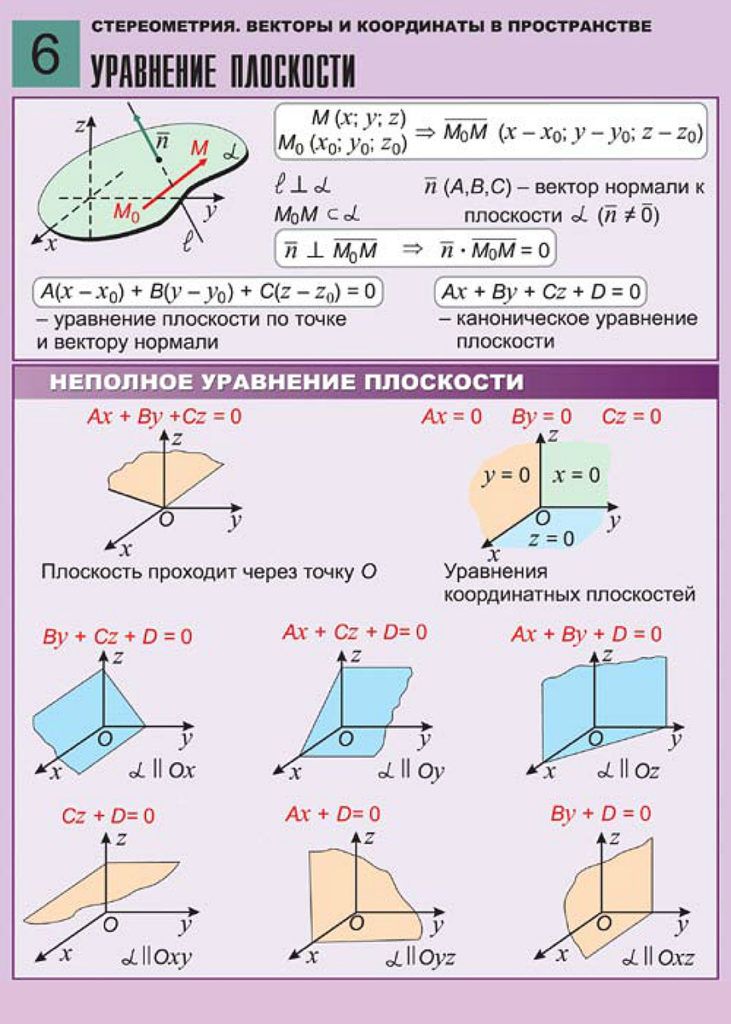 Арвинд и др. [1] обобщил идею разделения подпространства, предполагая, что все параметры задачи лежат на многообразии.
Арвинд и др. [1] обобщил идею разделения подпространства, предполагая, что все параметры задачи лежат на многообразии.
В этой статье мы рассматриваем полууправляемое многозадачное обучение (SSMTL). Хотя в литературе было предложено много методов SSL [10], эти методы часто не поддаются прямому расширению MTL [18]. Лю и др. [18] предложил структуру SSMTL, которая поощряла родственные модели иметь схожие параметры. Однако они требуют, чтобы связанные задачи имели схожие представления [9].]. Ван и др. [19] предложил другой метод SSMTL в предположении кластеризации задач [4, 14]. Структура кластера характеризуется параметрами задачи линейных предикторов. Для линейных предикторов параметры задачи, которые они использовали, фактически представляют собой постоянный градиент функций предикторов, которые формируют дифференциальную структуру первого порядка. Мы показываем, что для общих нелинейных предикторов более естественно фиксировать общую дифференциальную структуру с помощью векторных полей.
В этой статье мы предлагаем новую формулировку SSMTL с использованием векторных полей. Векторное поле — это гладкое отображение многообразия в касательные пространства, которое можно рассматривать как производную по направлениям функций на многообразии. Таким образом, векторное поле естественным образом характеризует дифференциальную структуру функций, а также обеспечивает естественный способ использования геометрической структуры данных; это два наиболее важных аспекта SSMTL. Основываясь на этой идее, мы разрабатываем метод многозадачного обучения векторному полю (MTVFL), который одновременно изучает функции прогнозирования и векторные поля. Изученные нами векторные поля вынуждены быть близкими к полям градиента функций-предикторов. В каждой задаче требуется, чтобы векторное поле было максимально параллельным. Мы говорим, что векторное поле параллельно, если векторы параллельны вдоль геодезических на многообразии. В предельных случаях, когда многообразие является линейным (или аффинным) пространством, геодезическими такого многообразия являются прямые линии. В таких случаях пространство, натянутое на эти параллельные векторы, является просто одномерным подпространством. Таким образом, когда многообразие плоское (т. Е. С нулевой кривизной) или кривизна мала, ожидается, что эти параллельные векторы концентрируются на подпространстве малой размерности. В качестве примера мы можем видеть, что параллельное поле на плоскости охватывает одномерное подпространство, а параллельное поле на швейцарском валуне охватывает двумерное подпространство. В многозадачном случае эти векторные поля имеют общее подпространство малой размерности. Кроме того, мы предполагаем, что эти векторные поля совместно используют низкоразмерное подпространство среди всех задач. По сути, мы используем дифференциальную структуру первого порядка для характеристики общей структуры задач и используем дифференциальную структуру второго порядка для характеристики конкретных частей задач. Мы формализуем нашу идею в рамках регуляризации и предложим метод выпуклой релаксации для решения исходной невыпуклой задачи.
В таких случаях пространство, натянутое на эти параллельные векторы, является просто одномерным подпространством. Таким образом, когда многообразие плоское (т. Е. С нулевой кривизной) или кривизна мала, ожидается, что эти параллельные векторы концентрируются на подпространстве малой размерности. В качестве примера мы можем видеть, что параллельное поле на плоскости охватывает одномерное подпространство, а параллельное поле на швейцарском валуне охватывает двумерное подпространство. В многозадачном случае эти векторные поля имеют общее подпространство малой размерности. Кроме того, мы предполагаем, что эти векторные поля совместно используют низкоразмерное подпространство среди всех задач. По сути, мы используем дифференциальную структуру первого порядка для характеристики общей структуры задач и используем дифференциальную структуру второго порядка для характеристики конкретных частей задач. Мы формализуем нашу идею в рамках регуляризации и предложим метод выпуклой релаксации для решения исходной невыпуклой задачи. Мы проводили эксперименты, используя как синтетические, так и реальные данные; результаты демонстрируют эффективность предложенного нами подхода.
Мы проводили эксперименты, используя как синтетические, так и реальные данные; результаты демонстрируют эффективность предложенного нами подхода.
Открыть в отдельном окне
Примеры параллельных полей. Параллельное поле на ℝ 2 охватывает одномерное подпространство, а параллельное поле на швейцарском рулете охватывает двумерное подпространство.
В этом разделе мы сначала вводим векторные поля, а затем представляем многозадачное обучение путем изучения общей структуры с использованием векторных полей.
2.1 Настройка многозадачного обучения и векторные поля
Сначала введем обозначения и символы. Нам дают м задач, с н л проб
xil, i = 1, …, n l для l -й задачи. Общее количество образцов равно n = Σ l n l . Для l -й задачи примем данные {
xil} находятся на d l -мерном многообразии
. Все эти коллекторы данных встроены в одно и то же D -мерное объемлющее пространство ℝ D . Стоит отметить, что размеры разных коллекторов данных не обязательно должны быть одинаковыми. Без ограничения общности будем считать первое
nl′(nl′
Все эти коллекторы данных встроены в одно и то же D -мерное объемлющее пространство ℝ D . Стоит отметить, что размеры разных коллекторов данных не обязательно должны быть одинаковыми. Без ограничения общности будем считать первое
nl′(nl′
Учитывая l -ю задачу, сначала построим граф ближайших соседей либо по ε -окрестностям, либо по k ближайших соседей. Позволять
xil~xjl обозначают, что
ксиль и
xjl являются соседями. Позволять
wijl обозначают вес, который измеряет сходство между
ксиль и
xjl. Его можно аппроксимировать весом теплового ядра или простым весом 0–1. Для каждой точки
xil, мы оцениваем его касательное пространство
TxilM, выполнив PCA в своем окружении. Выбираем самые большие d l собственные векторы как базисы начиная с касательного пространства
TxilM имеет тот же размер, что и коллектор
. Позволять
Til∈ℝD×dl — матрица, столбцы которой составляют ортонормированный базис для
TxilM. Легко показать, что
Pil=TilTilT — уникальная ортогональная проекция от ℝ D на касательное пространство
ТксилМ [13]. То есть для любого вектора a ∈ ℝ m имеем
Pila∈TxilM и
(а-Пила)⊥Пила.
Для каждой точки
xil, мы оцениваем его касательное пространство
TxilM, выполнив PCA в своем окружении. Выбираем самые большие d l собственные векторы как базисы начиная с касательного пространства
TxilM имеет тот же размер, что и коллектор
. Позволять
Til∈ℝD×dl — матрица, столбцы которой составляют ортонормированный базис для
TxilM. Легко показать, что
Pil=TilTilT — уникальная ортогональная проекция от ℝ D на касательное пространство
ТксилМ [13]. То есть для любого вектора a ∈ ℝ m имеем
Pila∈TxilM и
(а-Пила)⊥Пила.
Теперь мы формально определим векторное поле и покажем, как его представить в дискретном случае.
Определение 2.1 ([16])
Векторное поле X на многообразии
представляет собой непрерывную карту X :
→ Т где Т представляет собой множество касательных пространств, записанных как p ↦ X p , со свойством, что для каждого p ∈
, X p является элементом T p .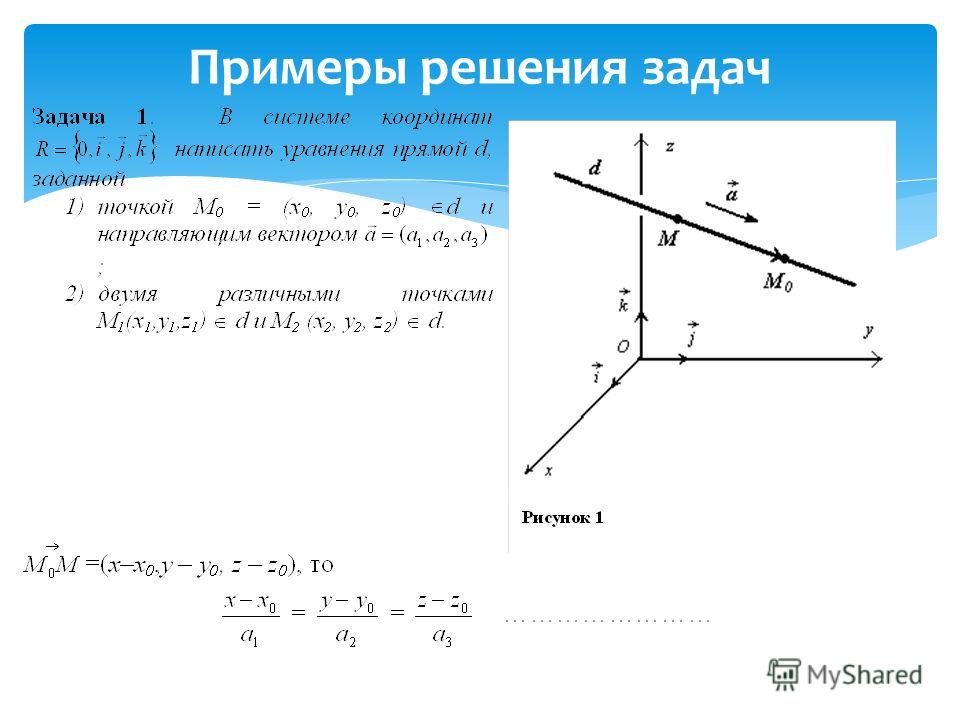
Мы можем думать о векторном поле на многообразии как о стрелке так же, как мы думаем о векторном поле в евклидовом пространстве, с заданной величиной и направлением, связанным с каждой точкой на многообразии и выбранной касательной. к коллектору. Векторное поле V на многообразии называется градиентным полем , если существует функция f на многообразии такая, что ∇ f = V , где ∇ — ковариантная производная на многообразии. Следовательно, градиентные поля являются одним из видов векторных полей. Он играет решающую роль в соединении векторных полей и функций.
Пусть V l — векторное поле на многообразии
. Для каждой точки
хил, пусть
Vxil обозначают значение векторного поля В л в
хил. Вспомним определение векторного поля,
Vxil должен быть вектором в касательном пространстве
TxilMl. Следовательно, мы можем представить его координатами касательного пространства
TxilMl как
Vxil=Tilvil, где
vil∈ℝdl — локальное представление
Vxil в отношении
Тил.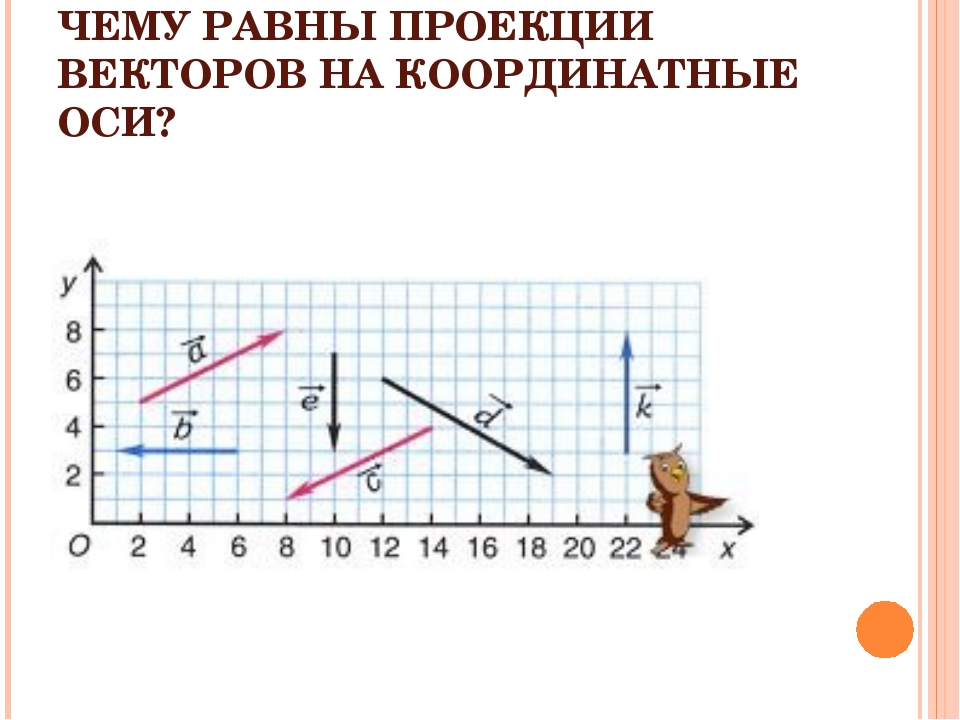 Пусть f l — функция на многообразии
. Злоупотребляя обозначениями без путаницы, мы также используем f l для обозначения вектора
fl=(fl(xl1),…,fl(xnll))T и использовать V l для обозначения вектора
Vl=(v1lT,…,vnllT)T∈ℝdlnl. То есть V l является d l n l -мерным большим вектором-столбцом, который объединяет все
Виль для стационарного л . Затем для каждой задачи мы стремимся вычислить вектор f l и вектор V l .
Пусть f l — функция на многообразии
. Злоупотребляя обозначениями без путаницы, мы также используем f l для обозначения вектора
fl=(fl(xl1),…,fl(xnll))T и использовать V l для обозначения вектора
Vl=(v1lT,…,vnllT)T∈ℝdlnl. То есть V l является d l n l -мерным большим вектором-столбцом, который объединяет все
Виль для стационарного л . Затем для каждой задачи мы стремимся вычислить вектор f l и вектор V l .
2.2 Многозадачное векторное полевое обучение
В этом разделе мы представляем многозадачное векторное полевое обучение (MTVFL).
Многие существующие методы MTL фиксируют связанность задач путем совместного использования параметров задачи. Для линейных предикторов параметры задачи, которые они использовали, на самом деле являются постоянными векторами градиента функций предиктора.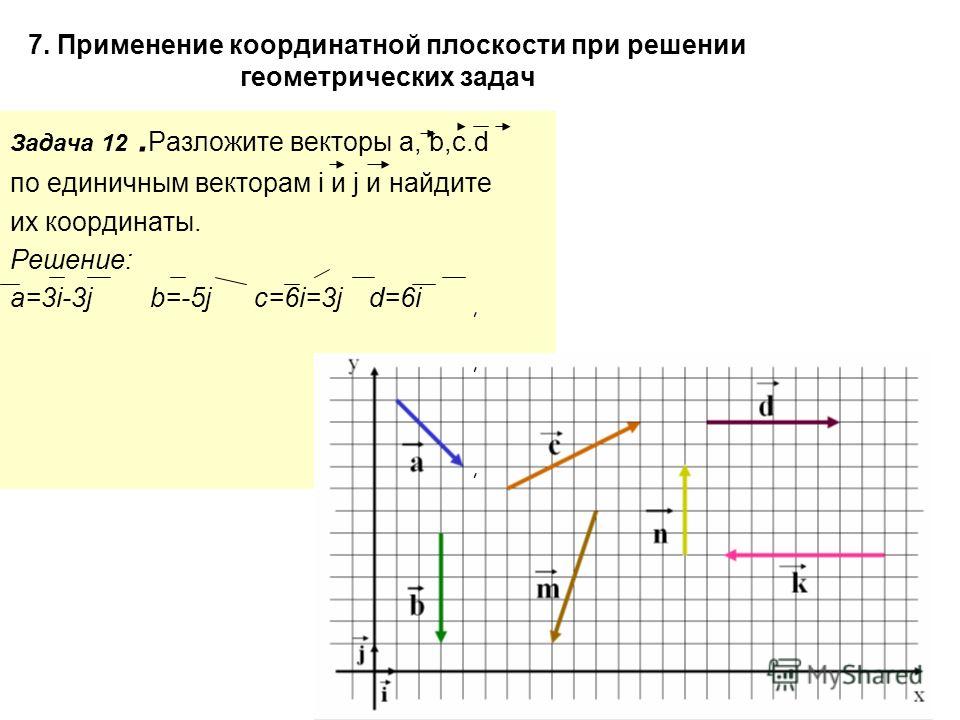 Для общих нелинейных предикторов мы показываем, что естественно фиксировать общую дифференциальную структуру с помощью векторных полей. Пусть f обозначает вектор
(f1T,…,fmT)T и V обозначают вектор
(V1T,…,VmT)T=(v11T,…,vnlmT)T. Предлагаем выучить ф и v одновременно:
Для общих нелинейных предикторов мы показываем, что естественно фиксировать общую дифференциальную структуру с помощью векторных полей. Пусть f обозначает вектор
(f1T,…,fmT)T и V обозначают вектор
(V1T,…,VmT)T=(v11T,…,vnlmT)T. Предлагаем выучить ф и v одновременно:
Векторное поле V L должно быть близко к градиентному полю ∇ F L из F L
7
из F L .20987 из F L 87 , который может быть FORMELESS TO NORE AS F L 77 .minf,VR1(f,V)=∑l=1mR1(fl,Vl):=∑l=1m∫Ml‖∇fl-Vl‖2
(1)
Векторное поле V l должны быть максимально параллельны:
минVR2(V)=∑l=1mR2(Vl):=∑l=1m∫Ml‖∇Vl‖HS2
(2)
где ∇ — ковариантная производная на многообразии, где ||·|| HS обозначает норму тензора Гильберта-Шмидта [11].
 ∇ V l измеряет изменение векторного поля, поэтому минимизирует
∫Ml‖∇Vl‖HS2 заставляет векторное поле V l быть параллельным.
∇ V l измеряет изменение векторного поля, поэтому минимизирует
∫Ml‖∇Vl‖HS2 заставляет векторное поле V l быть параллельным.Все векторные поля имеют общее h -мерное подпространство, где h — предопределенный параметр:
Tilvil=uil+ΘTwil,s.t.ΘΘT=Ih×h.
(3)
Поскольку предполагается, что эти векторные поля находятся в пространстве малой размерности, ожидается, что остаточный вектор уил маленький. Мы определяем еще один терм R 3 для управления сложностью следующим образом:
R3(vil,wil,Θ)=∑l=1m∑i=1nlα‖uil‖2+β‖Tilvil‖2
(4)
=∑l=1m∑i=1nlα‖Tilvil-ΘTwil‖ 2+β‖Tilvil‖2
(5)
Обратите внимание, что α и β являются предварительно заданными коэффициентами, указывающими на важность соответствующего компонента регуляризации. Поскольку мы хотели бы, чтобы векторное поле было параллельным, норма вектора не должна быть слишком маленькой. Кроме того, мы предполагаем, что векторные поля имеют общее подпространство малой размерности, остаточный вектор
uil ожидается небольшим. На практике мы предлагаем использовать маленькую β и большой α . Установив β = 0, R 3 уменьшится до члена регуляризации, предложенного в ASO, если мы также заменим касательные векторы параметрами задачи. Таким образом, эта формулировка является обобщением ASO.
Кроме того, мы предполагаем, что векторные поля имеют общее подпространство малой размерности, остаточный вектор
uil ожидается небольшим. На практике мы предлагаем использовать маленькую β и большой α . Установив β = 0, R 3 уменьшится до члена регуляризации, предложенного в ASO, если мы также заменим касательные векторы параметрами задачи. Таким образом, эта формулировка является обобщением ASO.
Можно убедиться, что wil*=ΘTilvil=argminwilR3(vil,wil,Θ). Таким образом, у нас есть uil=Tilvil-ΘTwil=(I-ΘTΘ)Tilvil. Следовательно, мы можем переписать R 3 следующим образом:
R3(V,Θ)=∑l=1m∑i=1nlα‖uil‖2+β‖Tilvil‖2=∑l=1m∑i=1nl(α‖(I-ΘTΘ)Tilvil‖2+β‖ Тилвиль‖2)=αVTAΘV+βVTHV
(6)
, где H — блочная диагональная матрица с диагональными блоками
TilTTil, а A Θ — другая блочно-диагональная матрица с диагональными блоками
TilT(I-ΘTΘ)T(I-ΘTΘ)Til=TilT(I-ΘTΘ)Til. Таким образом, предложенная формулировка решает следующую оптимизационную задачу:
Таким образом, предложенная формулировка решает следующую оптимизационную задачу:
argminf,V,ΘE(f,V,Θ)=R0(f)+λ1R1(f,V)+λ2R2(V)+λ3R3(V,Θ)s.t.ΘΘT=Ih×h
(7)
, где R 0 ( f ) — функция потерь. Для простоты используем квадратичную функцию потерь R0(f)=∑l=1m∑i=1nl′(fl(xil)-yil)2.
2.3 Целевая функция в матричной форме
Чтобы упростить уравнение. (7), в этом разделе мы перепишем нашу целевую функцию в матричной форме.
Используя дискретные методы из [17], мы имеем следующие уравнения в дискретной форме:
R1(fl,Vl)=∑i∑j~iwijl((xjl-xil)TTilvil-fjl+fil)2
(8)
R2(fl,Vl)=∑i~jwijl‖PilTjlvjl-Tilvil ‖2
(9)
Интересно, что с некоторыми алгебраическими преобразованиями мы имеем следующие матричные формы для наших целевых функций:
R1 (FL, VL) = 2FLTLLFL+VLTGLVL-2VLTCLFL
(10)
, где L L -MAPLACIAN MATRIX, G L 20202020202020202.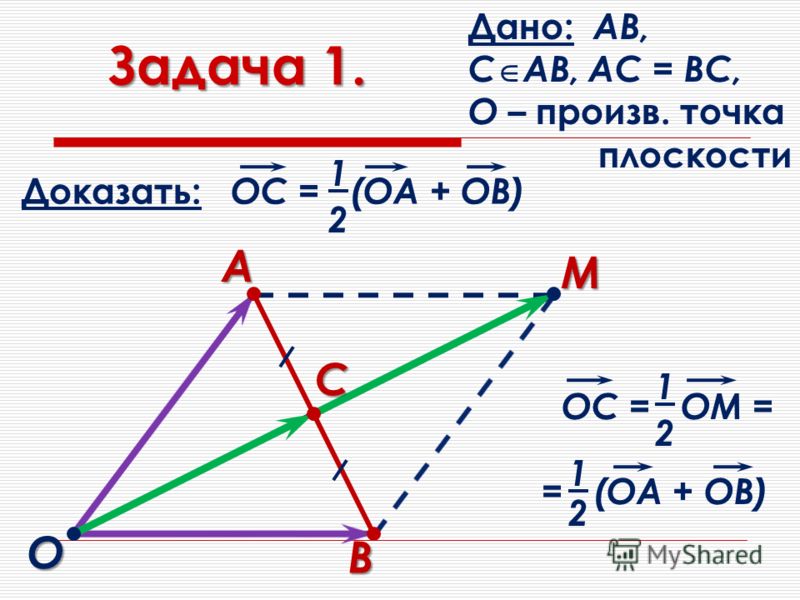
Giil=∑j~iwijl(xjl-xil)(xjl-xil)T,Cil=∑j~iwijl(xjl-xil)sijlT
(11)
, где sijl∈ℝnl — вектор выбора всех нулевых элементов, за исключением i -го элемента, равного −1, и j -го элемента, равного 1.
(12)
, где B l — разреженная блочная матрица d l n l × d l n l . Если мы проиндексируем каждый блок d l × d l на Bijl, то имеем
Biil=∑j~iwijl(QijlQijlT+I)
(13)
Bijl={-2wijlQijl,ifxi~xj0, иначе
(14)
, где
Qijl=TilTTjl. Ничего не стоит, что и R 1 и R 2 зависит от касательных пространств
Тил.
Ничего не стоит, что и R 1 и R 2 зависит от касательных пространств
Тил.
Таким образом, мы можем далее записать R 1 ( f, V ) и R 2 ( V ) следующим образом
R1(1f,V) Vl)=2fTLf+VTGV-2VTCf
(15)
R2(V)=∑l=1mR2(Vl)=VTBV
(16)
, где L ,
7 G и B — блок диагональные матрицы с соответствующей l -й блочной матрицей, равной L l , G l и B l соответственно. C представляет собой блочную матрицу столбцов, где l -я блочная матрица равна C l .
Пусть
обозначим диагональную матрицу размера n × n , где
= 1, если соответствующие i -е данные помечены и
= 0 в противном случае. И пусть y ∈ ℝ n будет вектор-столбцом, i -й элемент которого является соответствующей меткой i -ые помеченные данные и 0 в противном случае. затем
R0(f)=1n′(f-y)TI(f-y). Наконец, мы получаем следующую матричную форму для нашей целевой функции в уравнении. (7) с ограничением ΘΘ T = I h×h как:
затем
R0(f)=1n′(f-y)TI(f-y). Наконец, мы получаем следующую матричную форму для нашей целевой функции в уравнении. (7) с ограничением ΘΘ T = I h×h как:
E(f,V,Θ)=R0(f)+λ1R1(f,V)+λ2R2(V)+λ3R3(V,Θ)=1n′(f-y)TI(f-y)+λ1(2fTLf+VTGV -2VTCf)+λ2VTBV+λ3VT(αAΘ+βH)V=1n′(f-y)TI(f-y)+2λ1fTLf+VT(λ1G+λ2B+λ3(αAΘ+βH))V-2λ1VTCf
Стоит отметить, что матрицы L, G, B, C зависят от данных, и только матрица A Θ связан с Θ.
В этом разделе мы обсудим, как решить следующую задачу оптимизации:
argminf,V,ΘE(f,V,Θ),s.t.ΘΘT=Ih×h
(17)
Для решения этой задачи мы используем попеременную оптимизацию.
3.1 Оптимизация
f и V для заданного Θ Когда Θ фиксировано, целевая функция аналогична функции для случая с одной задачей. Тем не менее, есть некоторые отличия, о которых мы хотели бы упомянуть. Во-первых, при построении графа ближайших соседей точки данных из разных задач разъединяются. Поэтому при оценке касательных пространств точки данных из разных задач независимы. Во-вторых, мы не требуем, чтобы размерность касательных пространств от каждой задачи была одинаковой.
Поэтому при оценке касательных пространств точки данных из разных задач независимы. Во-вторых, мы не требуем, чтобы размерность касательных пространств от каждой задачи была одинаковой.
Заметим, что
∂E∂f=2(1n′I+2λ1L)f-2λ1CTV-21n′y
(20)
∂E∂V=-2λ1Cf+2(λ1G+λ2H+λ3( αAΘ+βH))V
(21)
Требуя обращения в нуль производных, получаем линейную систему
(1n′I+2λ1L-λ1CT-λ1Cλ1G+λ2B+λ3(αAΘ+βH))(fV )=(1n′y0)
(22)
За исключением матрицы A Θ , все остальные матрицы могут быть вычислены заранее и не изменятся в ходе итерационного процесса.
3.2 Оптимизация Θ для данного
VС момента функций R 0 ( F ), R 1 ( F, V ) и R 2 (V ) и R 2 () и R 2 () и R 2
(). Θ, нам нужно только оптимизировать R 3 ( В, Θ) при условии ΘΘ T = I h×h . =argminΘ∑l=1m∑i=1nlα(‖(I-ΘTΘ)Tilvil‖2+βα‖Tilvil‖2)=argminΘαtr(VT((1+βα)I-ΘTΘ)V)=argmaxΘtr( ΘВВТΘТ)
=argminΘ∑l=1m∑i=1nlα(‖(I-ΘTΘ)Tilvil‖2+βα‖Tilvil‖2)=argminΘαtr(VT((1+βα)I-ΘTΘ)V)=argmaxΘtr( ΘВВТΘТ)(23)
где V=(T11v11,…,Tnmmvnmm) — это матрица размера D × n , в которой каждый столбец представляет собой касательный вектор. Оптимальное Θ̂ может быть получено с помощью разложения по сингулярным числам (SVD). Позволять V=Z1∑Z2T — SVD V , и мы предполагаем, что сингулярные значения расположены в порядке убывания по Σ. Тогда строки Θ̂ задаются первыми h столбцами Z 1 .
3.3 Выпуклая релаксация
Ограничение ортогональности в уравнении. (23) невыпукло. Далее мы предлагаем преобразовать уравнение. (23) в выпуклую формулировку, релаксируя его допустимую область в выпуклое множество.
Пусть η = β / α . Можно убедиться, что в следующем равенстве содержится: (1 + η ) I — θ T θ = η (1 + η ) ( η + θ . Θ) −1 . Затем мы можем переписать R 3 ( V , θ) как R 3 ( V , θ) = α (1 + 7.
Θ) −1 . Затем мы можем переписать R 3 ( V , θ) как R 3 ( V , θ) = α (1 + 7.
Чтобы преобразовать невыпуклую задачу Eq. (23) в выпуклой формулировке мы заменяем Θ T Θ на M , и естественным образом релаксируем его допустимую область в выпуклое множество, основанное на соотношении между M e и M c представлено выше; это приводит к проблеме оптимизации как
argminΘR3(V,M),s.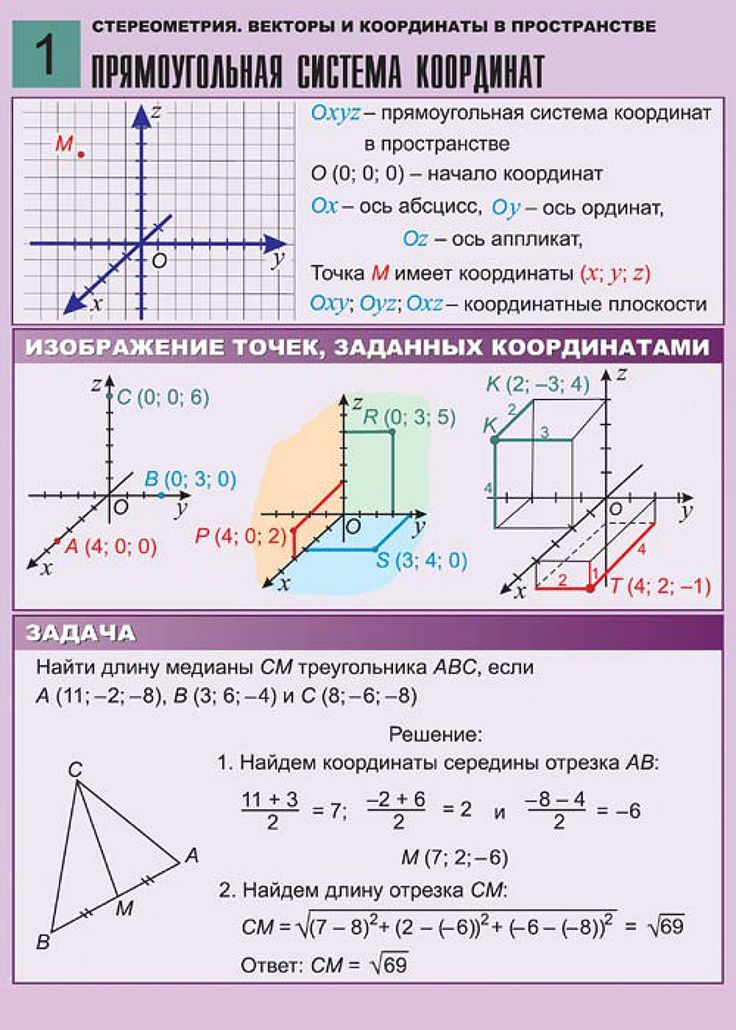 t.,tr(M)=h,M≼I,M∈S+d
t.,tr(M)=h,M≼I,M∈S+d
(24)
, где R 3 ( V , M ) определяется как R 3 ( V , M
020202020202020202020987 = 7 α7777777777,9277. ) tr В Т ( ηI + М ) −1 В) . Из [3, теорема 3.1] следует, что релаксированное R 3 выпукло по совокупности в V и M . После получения оптимальных M , оптимальное Θ может быть аппроксимировано с использованием первых h собственных векторов (соответствующих наибольшим h собственным значениям) оптимального M . В этом разделе мы оцениваем наш метод на одном наборе синтетических данных и одном наборе реальных данных. Мы сравниваем предложенный алгоритм многозадачного векторного полевого обучения (MTVFL) со следующими методами: (а) однозадачное векторное полевое обучение (STVFL или PFR), (б) оптимизация чередующейся структуры (ASO) и (в) его нелинейная версия. — Оптимизация ядерной чередующейся структуры (KASO). Ядро, построенное в KASO, использует как размеченные, так и неразмеченные данные. Таким образом, его можно рассматривать как полуконтролируемый метод MTL.
— Оптимизация ядерной чередующейся структуры (KASO). Ядро, построенное в KASO, использует как размеченные, так и неразмеченные данные. Таким образом, его можно рассматривать как полуконтролируемый метод MTL.
4.1 Синтетические данные
Сначала мы создаем синтетические данные для оценки нашего метода в сравнении с методом обучения с одним заданием под наблюдением (STVFL). Мы генерируем два набора данных, включая швейцарский рулет и швейцарский рулет с отверстием, встроенным в трехмерное евклидово пространство. Швейцарский рулон генерируется следующими уравнениями: x = t 1 cos t 1 ; г = т 2 ; г = t 1 sin t 1 где t 1 ∈ [3 π /2 , 9
7] t 2 ∈ [0, 21]. Валок с отверстием исключает точки в пределах t 1 ∈ [9, 12] и t 2 ∈ [9, 14]. Наземная функция истинности равна f ( x , y , z ) = t 1 . Этот тест представляет собой полуконтролируемую многозадачную регрессионную задачу. Мы случайным образом выбираем ряд размеченных данных в каждой задаче и пытаемся предсказать значение других неразмеченных данных.
Наземная функция истинности равна f ( x , y , z ) = t 1 . Этот тест представляет собой полуконтролируемую многозадачную регрессионную задачу. Мы случайным образом выбираем ряд размеченных данных в каждой задаче и пытаемся предсказать значение других неразмеченных данных.
Каждый набор данных содержит 400 точек. Для каждой задачи строим граф ближайших соседей. Количество ближайших соседей установлено равным 5, а размерность многообразия установлена равной 2, поскольку они оба являются двумерными многообразиями. Размерность общего подпространства установлена равной 2. Параметры регуляризации выбираются путем перекрестной проверки. Мы проводим 100 независимых испытаний со случайно выбранными помеченными наборами. Производительность измеряется среднеквадратичной ошибкой (MSE). Мы также пробуем ASO и KASO, однако они плохо работают, поскольку данные сильно нелинейны. Усредненная MSE по двум задачам представлена в . Мы можем наблюдать, что MTVFL последовательно превосходит STVFL, что демонстрирует эффективность SSMTL.
Мы можем наблюдать, что MTVFL последовательно превосходит STVFL, что демонстрирует эффективность SSMTL.
Открыть в отдельном окне
(а) Выполнение ПТВФЛ и СВФЛ; (b) Распределение сингулярных значений.
Мы также показываем сингулярное распределение полей градиента наземной истинности. Зная базовую истину f , мы можем вычислить поле градиента V , взяв производные от R 1 ( f, V ) по отношению к V . Требуя обращения в нуль производной, мы получаем следующее уравнение: GV = См. После получения V вектор градиента Vxil в каждой точке можно получить как Вксил = Тилвиль. Затем мы выполняем PCA для этих векторов и сингулярных значений ковариационной матрицы Vxil показаны в . Как видно из , количество доминирующих сингулярных значений равно 2, что указывает на то, что поля градиента наземной истинности концентрируются на двумерном подпространстве.
4.2 Обнаружение наземных мин
Мы используем набор данных о наземных минах, изученный в [20]. Всего 29наборы данных, которые собираются с различных реальных минных полей. Каждый пример данных представлен 9-мерным вектором с двоичной меткой, которая равна 1 для наземных мин или 0 для помех. Проблема обнаружения наземных мин состоит в том, чтобы предсказать метки немаркированных объектов. Среди 29 наборов данных 1–15 соответствуют регионам с относительно высокой степенью лиственности, а 16–29 — регионам с голой землей или пустыням. Следуя [20], мы выбираем наборы данных 1–10 и 16–24 для формирования 19 задач.
Всего 29наборы данных, которые собираются с различных реальных минных полей. Каждый пример данных представлен 9-мерным вектором с двоичной меткой, которая равна 1 для наземных мин или 0 для помех. Проблема обнаружения наземных мин состоит в том, чтобы предсказать метки немаркированных объектов. Среди 29 наборов данных 1–15 соответствуют регионам с относительно высокой степенью лиственности, а 16–29 — регионам с голой землей или пустыням. Следуя [20], мы выбираем наборы данных 1–10 и 16–24 для формирования 19 задач.
Базовая настройка всех алгоритмов следующая. Сначала мы строим граф ближайших соседей для каждой задачи. Число ближайших соседей установлено равным 10, а размерность многообразия установлена равной 4 эмпирически. Эти два параметра одинаковы для всех 19задачи. Размерность общего подпространства установлена равной 5 как для MTVFL, так и для ASO, а размерность общего подпространства KASO установлена равной 10. Все параметры регуляризации для четырех алгоритмов выбираются путем перекрестной проверки. Обратите внимание, что KASO необходимо построить матрицу ядра. Мы используем ядро Гаусса в KASO, и ширина Гаусса устанавливается оптимальной путем поиска в пределах [0,01, 10].
Обратите внимание, что KASO необходимо построить матрицу ядра. Мы используем ядро Гаусса в KASO, и ширина Гаусса устанавливается оптимальной путем поиска в пределах [0,01, 10].
Мы проводим 100 независимых испытаний со случайно выбранными помеченными наборами. Мы измеряем производительность по AUC, которая обозначает площадь под кривой рабочих характеристик приемника (ROC). Большое значение AUC указывает на хорошую эффективность классификации. Поскольку данные имеют сильно несбалансированные метки, следуя [20], мы делаем специальную настройку, которая гарантирует, что в обучающем наборе каждой задачи есть по крайней мере один образец с меткой «1» и один «0». AUC в среднем за 19задания представлены в . Как видно, MTVFL стабильно превосходит остальные три алгоритма. Когда количество помеченных данных увеличивается, KASO превосходит STVFL. ASO не сильно улучшается, когда количество помеченных данных увеличивается, что, вероятно, связано с тем, что данные имеют сильно несбалансированные метки, а функция предиктора истинности нелинейна..jpg) Мы также показываем сингулярное распределение полей градиента наземной истины в . Вычисление сингулярных значений такое же, как в разделе. 4.1. Как видно из , количество доминирующих сингулярных значений равно 5. Процент суммы первых 5 сингулярных значений от общей суммы равен 91,34%, что указывает на то, что наземные поля градиента истинности концентрируются на 5-мерном подпространстве.
Мы также показываем сингулярное распределение полей градиента наземной истины в . Вычисление сингулярных значений такое же, как в разделе. 4.1. Как видно из , количество доминирующих сингулярных значений равно 5. Процент суммы первых 5 сингулярных значений от общей суммы равен 91,34%, что указывает на то, что наземные поля градиента истинности концентрируются на 5-мерном подпространстве.
Открыть в отдельном окне
(а) Производительность различных алгоритмов MTL; (b) Распределение сингулярных значений.
В этой статье мы предлагаем новую формулировку многозадачного обучения с полуучителем с использованием векторных полей. Мы показываем, что векторные поля могут естественным образом отображать общую дифференциальную структуру между задачами, а также структуру многообразий данных, которые имеют решающее значение для многозадачного обучения с полуучителем. Наши экспериментальные результаты на синтетических и реальных данных демонстрируют эффективность предложенного метода.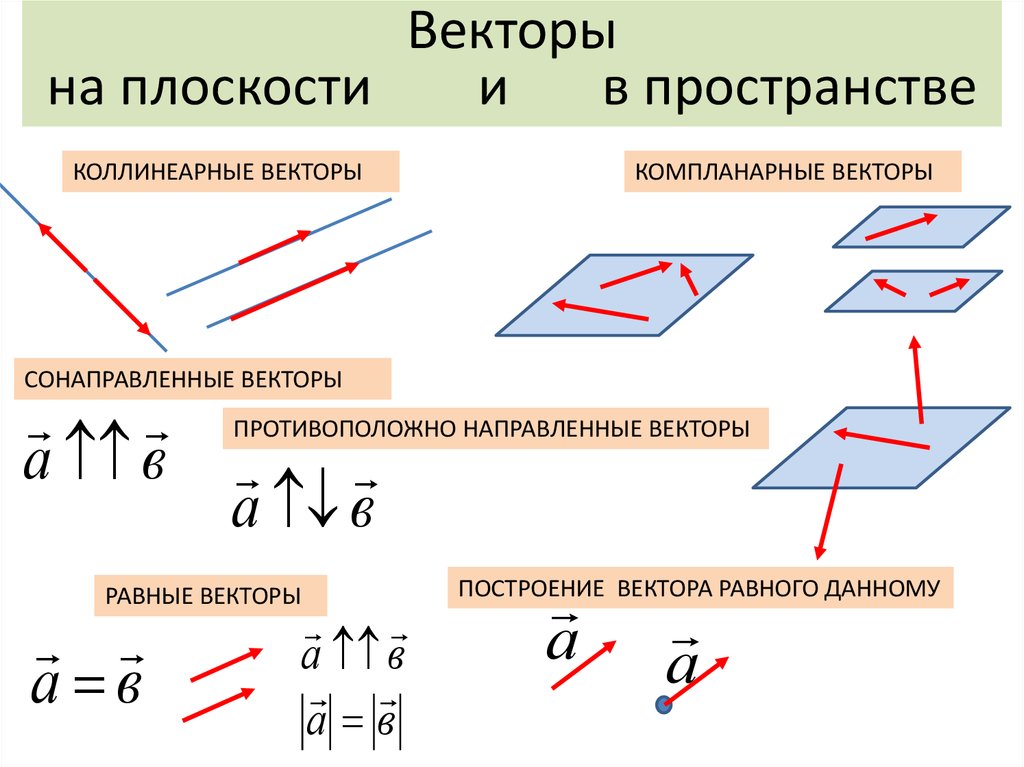 В этой работе предлагается несколько интересных будущих направлений. Одним из них является связь между обучением на параметрах задачи и обучением на векторных полях. В конечном счете, обе они являются функциями обучения. Другим направлением является применение других предположений, сделанных в сообществе многозадачного обучения, к векторному полевому обучению, например, предположение о кластерах.
В этой работе предлагается несколько интересных будущих направлений. Одним из них является связь между обучением на параметрах задачи и обучением на векторных полях. В конечном счете, обе они являются функциями обучения. Другим направлением является применение других предположений, сделанных в сообществе многозадачного обучения, к векторному полевому обучению, например, предположение о кластерах.
Эта работа была поддержана Национальным фондом естественных наук Китая в рамках грантов 61125203 и 61233011, Национальной программой фундаментальных исследований Китая (программа 973) в рамках гранта 2012CB316404, NIH (R01 LM010730) и NSF (IIS-0953662, CCF-1025177). ).
1 Набор данных доступен по адресу http://www.ee.duke.edu/~lcarin/LandmineData.zip.
1. Агарвал А., Х.Д., Гербер С. Изучение нескольких задач с использованием многообразной регуляризации. Достижения в области нейронных систем обработки информации. 2010; 23:46–54. [Академия Google]
2. Андо Р.К., Чжан Т. Структура для изучения прогностических структур на основе нескольких задач и немаркированных данных. Журнал исследований машинного обучения. 2005; 6: 1817–1853. [Google Scholar]
Андо Р.К., Чжан Т. Структура для изучения прогностических структур на основе нескольких задач и немаркированных данных. Журнал исследований машинного обучения. 2005; 6: 1817–1853. [Google Scholar]
3. Argyriou A, Micchelli CA, Pontil M, Ying Y. Структура спектральной регуляризации для многозадачного изучения структуры. Достижения в области нейронных систем обработки информации. 2008; 20:25–32. [Google Scholar]
4. Баккер Б., Хескес Т. Кластеризация задач и гейтирование для байесовского многозадачного обучения. Журнал исследований машинного обучения. 2003; 4: 83–9.9. [Google Scholar]
5. Белкин М., Нийоги П., Синдхвани В. Регуляризация многообразия: геометрическая основа для обучения на размеченных и неразмеченных примерах. Журнал исследований машинного обучения. 2006 г., декабрь; 7: 2399–2434. [Google Scholar]
6. Бен-Дэвид С., Герке Дж., Шуллер Р. Теоретическая основа для обучения на базе разрозненных источников данных. Материалы восьмой международной конференции ACM SIGKDD по открытию знаний и интеллектуальному анализу данных.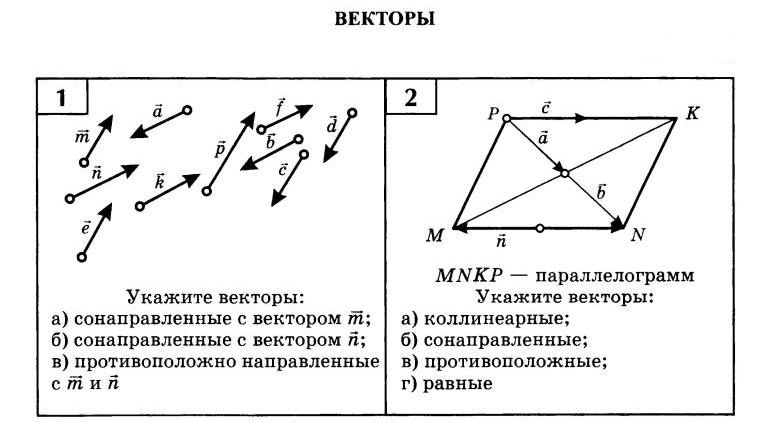 2002: 443–449. [Академия Google]
2002: 443–449. [Академия Google]
7. Бен-Дэвид С., Шуллер Р. Использование связанности задач для многозадачного обучения. Конференция по теории обучения. 2003: 567–580. [Google Scholar]
8. Бойд С., Ванденберге Л. Выпуклая оптимизация. Издательство Кембриджского университета; 2004. [Google Scholar]
9. Carlson A, Betteridge J, Wang RC, Hruschka ER, Jr, Mitchell TM. Парное полууправляемое обучение для извлечения информации. Материалы третьей международной конференции ACM по поиску в Интернете и интеллектуальному анализу данных. 2010: 101–110. [Академия Google]
10. Chapelle O, Schölkopf B, Zien A, редакторы. Полуконтролируемое обучение. Массачусетский технологический институт Пресс; 2006. [Google Scholar]
11. Defant A, Floret K. Тензорные нормы и операторные идеалы. Математические исследования Северной Голландии; Северная Голландия, Амстердам: 1993. [Google Scholar]
12. Evgeniou T, Micchelli CA, Pontil M. Изучение нескольких задач с помощью методов ядра.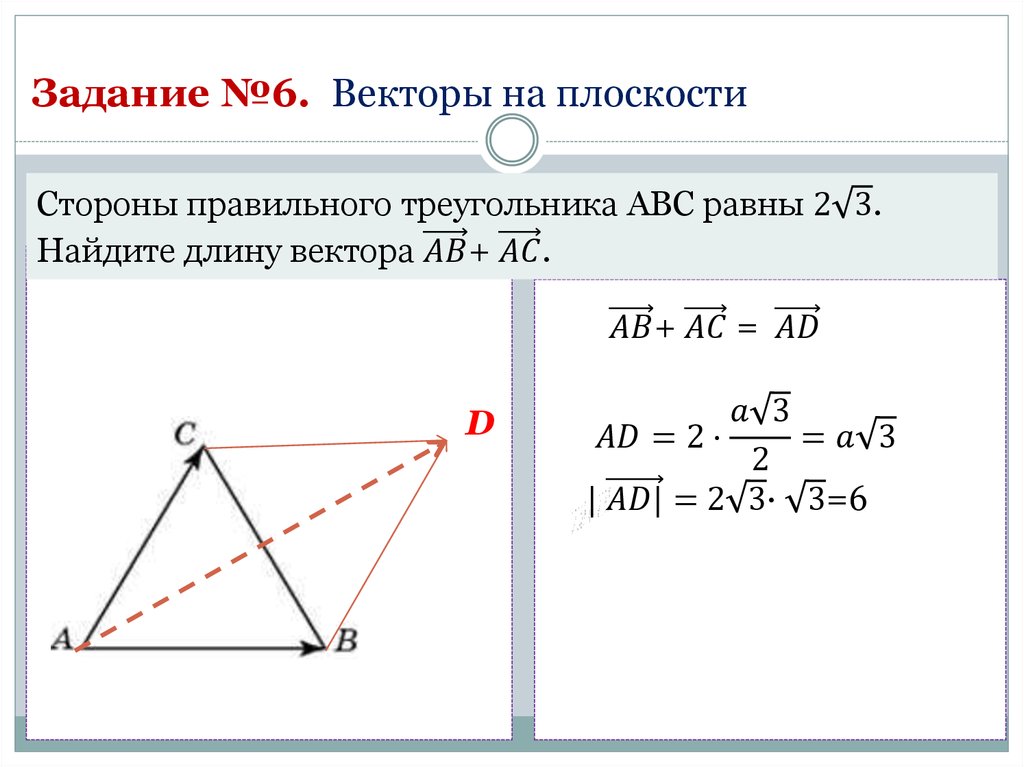 Журнал исследований машинного обучения. 2005; 6: 615–637. [Google Scholar]
Журнал исследований машинного обучения. 2005; 6: 615–637. [Google Scholar]
13. Голуб Г.Х., Loan CFV. Матричные вычисления. 3. Издательство Университета Джона Хопкинса; 1996. [Google Scholar]
14. Джейкоб Л., Бах Ф., Верт Дж. П. Кластерное многозадачное обучение: выпуклая формулировка. Достижения в области нейронных систем обработки информации. 2009; 21: 745–752. [Google Scholar]
15. Лафферти Дж., Вассерман Л. Статистический анализ полууправляемой регрессии. Достижения в области нейронных систем обработки информации. 2007; 20:801–808. [Google Scholar]
16. Lee JM. Введение в гладкие многообразия. 2. Спрингер Верлаг; Нью-Йорк: 2003. [Google Scholar]
9.0018 17. Линь Б., Чжан С., Хе Х. Полууправляемая регрессия с помощью регуляризации параллельного поля. Достижения в области нейронных систем обработки информации. 2011; 24:433–441. [Google Scholar] 18. Liu Q, Liao X, Carin L. Многозадачное обучение с полуучителем. Достижения в области нейронных систем обработки информации. 2008; 20: 937–944. [Google Scholar]
2008; 20: 937–944. [Google Scholar]
19. Ван Ф., Ван С., Ли Т. Материалы Девятой международной конференции IEEE 2009 г. по интеллектуальному анализу данных. Компьютерное общество IEEE; 2009. Полуконтролируемое многозадачное обучение с регуляризацией задач; стр. 562–568. [Академия Google]
20. Xue Xue, X Liao, L Carin, Krishnapuram B. Многозадачное обучение для классификации с априорными процессами Дирихле. Журнал исследований машинного обучения. 2007; 8: 35–63. [Академия Google]
Машина опорных векторов — Введение в алгоритмы машинного обучения | by Rohith Gandhi
Модель SVM с нуля
Введение
Думаю, к настоящему времени вы уже привыкли к алгоритмам линейной регрессии и логистической регрессии. Если нет, я предлагаю вам взглянуть на них, прежде чем переходить к машине опорных векторов. Метод опорных векторов — еще один простой алгоритм, который должен быть в арсенале каждого специалиста по машинному обучению. Многие предпочитают метод опорных векторов, поскольку он обеспечивает значительную точность при меньшей вычислительной мощности. Машина опорных векторов, сокращенно SVM, может использоваться как для задач регрессии, так и для задач классификации. Но он широко используется в целях классификации.
Многие предпочитают метод опорных векторов, поскольку он обеспечивает значительную точность при меньшей вычислительной мощности. Машина опорных векторов, сокращенно SVM, может использоваться как для задач регрессии, так и для задач классификации. Но он широко используется в целях классификации.
Что такое метод опорных векторов?
Целью алгоритма опорных векторов является поиск гиперплоскости в N-мерном пространстве (N — количество признаков), которая четко классифицирует точки данных.
Возможные гиперплоскостиЧтобы разделить два класса точек данных, можно выбрать множество возможных гиперплоскостей. Наша цель — найти плоскость с максимальным запасом, то есть максимальным расстоянием между точками данных обоих классов. Увеличение предельного расстояния дает некоторое усиление, чтобы будущие точки данных можно было классифицировать с большей уверенностью.
Гиперплоскости и опорные векторы
Гиперплоскости в пространстве признаков 2D и 3D Гиперплоскости — это границы решений, помогающие классифицировать точки данных.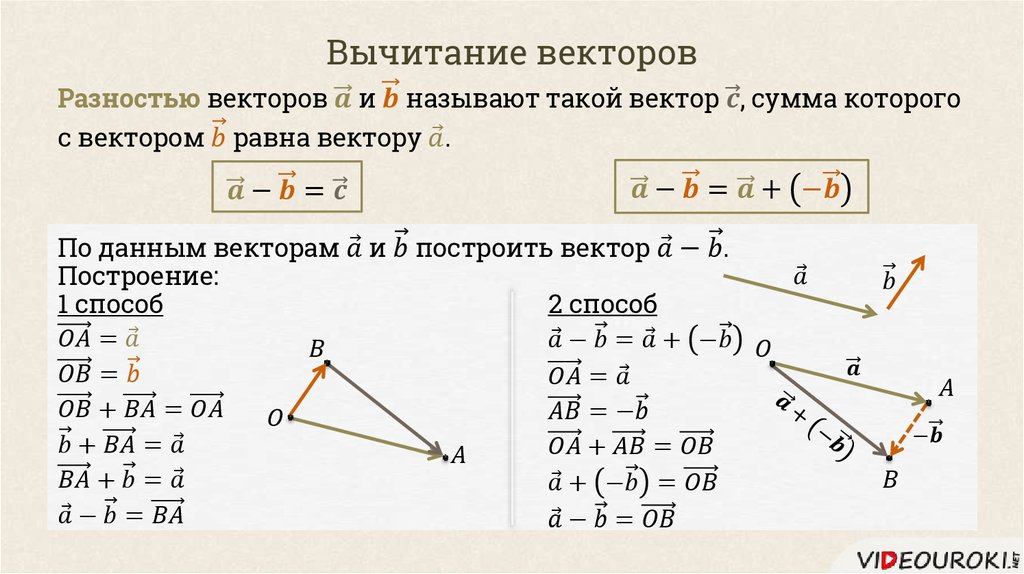 Точки данных, попадающие по обе стороны от гиперплоскости, можно отнести к разным классам. Кроме того, размер гиперплоскости зависит от количества функций. Если количество входных объектов равно 2, то гиперплоскость — это просто линия. Если число входных признаков равно 3, то гиперплоскость становится двумерной плоскостью. Становится трудно представить, когда количество признаков превышает 3.
Точки данных, попадающие по обе стороны от гиперплоскости, можно отнести к разным классам. Кроме того, размер гиперплоскости зависит от количества функций. Если количество входных объектов равно 2, то гиперплоскость — это просто линия. Если число входных признаков равно 3, то гиперплоскость становится двумерной плоскостью. Становится трудно представить, когда количество признаков превышает 3.
Опорные векторы — это точки данных, расположенные ближе к гиперплоскости и влияющие на положение и ориентацию гиперплоскости. Используя эти опорные векторы, мы максимизируем запас классификатора. Удаление опорных векторов изменит положение гиперплоскости. Это точки, которые помогают нам построить нашу SVM.
Интуиция с большой маржой
В логистической регрессии мы берем выход линейной функции и сжимаем значение в диапазоне [0,1] с помощью сигмовидной функции. Если сжатое значение больше порогового значения (0,5), мы присваиваем ему метку 1, иначе мы присваиваем ему метку 0. В SVM мы берем выход линейной функции, и если этот результат больше 1, мы идентифицируем это с одним классом, и если вывод равен -1, мы идентифицируем его с другим классом. Поскольку пороговые значения изменены на 1 и -1 в SVM, мы получаем этот диапазон значений усиления ([-1,1]), который действует как запас.
В SVM мы берем выход линейной функции, и если этот результат больше 1, мы идентифицируем это с одним классом, и если вывод равен -1, мы идентифицируем его с другим классом. Поскольку пороговые значения изменены на 1 и -1 в SVM, мы получаем этот диапазон значений усиления ([-1,1]), который действует как запас.
Обновления функции стоимости и градиента
В алгоритме SVM мы стремимся максимизировать разницу между точками данных и гиперплоскостью. Функция потерь, которая помогает максимизировать маржу, называется потерями на петлях.
Функция потерь шарнира (функция слева может быть представлена как функция справа) Стоимость равна 0, если прогнозируемое значение и фактическое значение имеют один и тот же знак. Если это не так, мы вычисляем стоимость убытка. Мы также добавляем параметр регуляризации — функцию стоимости. Цель параметра регуляризации — сбалансировать максимизацию маржи и потери. После добавления параметра регуляризации функции стоимости выглядят следующим образом.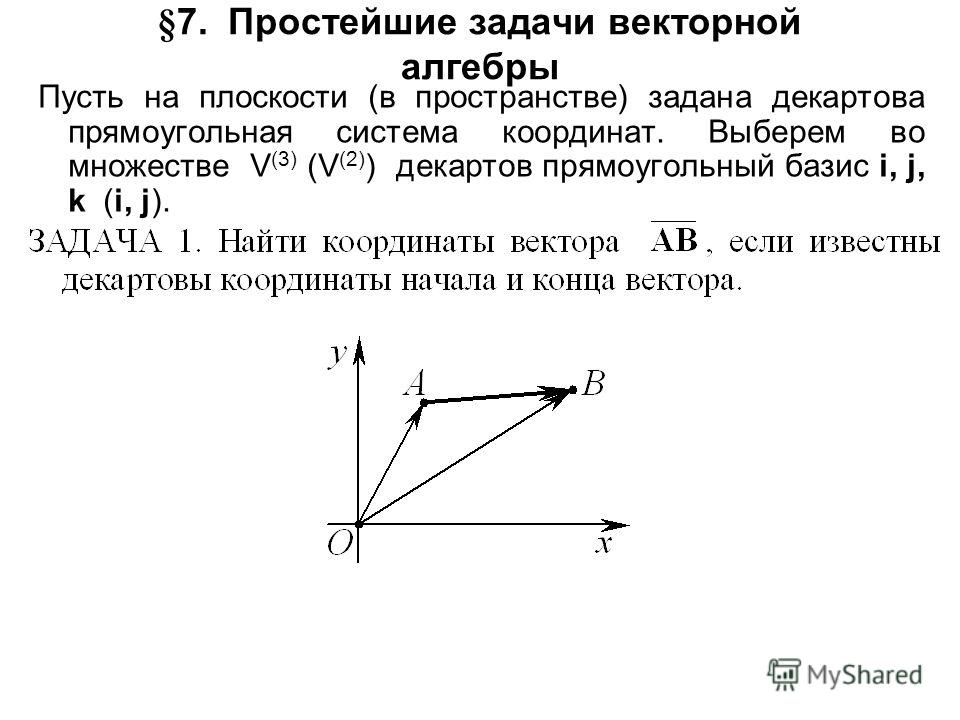
Теперь, когда у нас есть функция потерь, мы возьмем частные производные по весам, чтобы найти градиенты. Используя градиенты, мы можем обновить наши веса.
ГрадиентыЕсли неправильной классификации нет, т. е. наша модель правильно предсказывает класс нашей точки данных, нам нужно только обновить градиент из параметра регуляризации.
Обновление градиента — нет неправильной классификацииКогда есть неправильная классификация, т. е. наша модель делает ошибку в прогнозе класса нашей точки данных, мы включаем потерю вместе с параметром регуляризации для выполнения обновления градиента.
Обновление градиента — неправильная классификацияРеализация SVM на Python
Набор данных, который мы будем использовать для реализации нашего алгоритма SVM, — это набор данных Iris. Вы можете скачать его по этой ссылке.
Поскольку в наборе данных Iris три класса, мы удалим один из них. Это оставляет нас с проблемой классификации бинарных классов.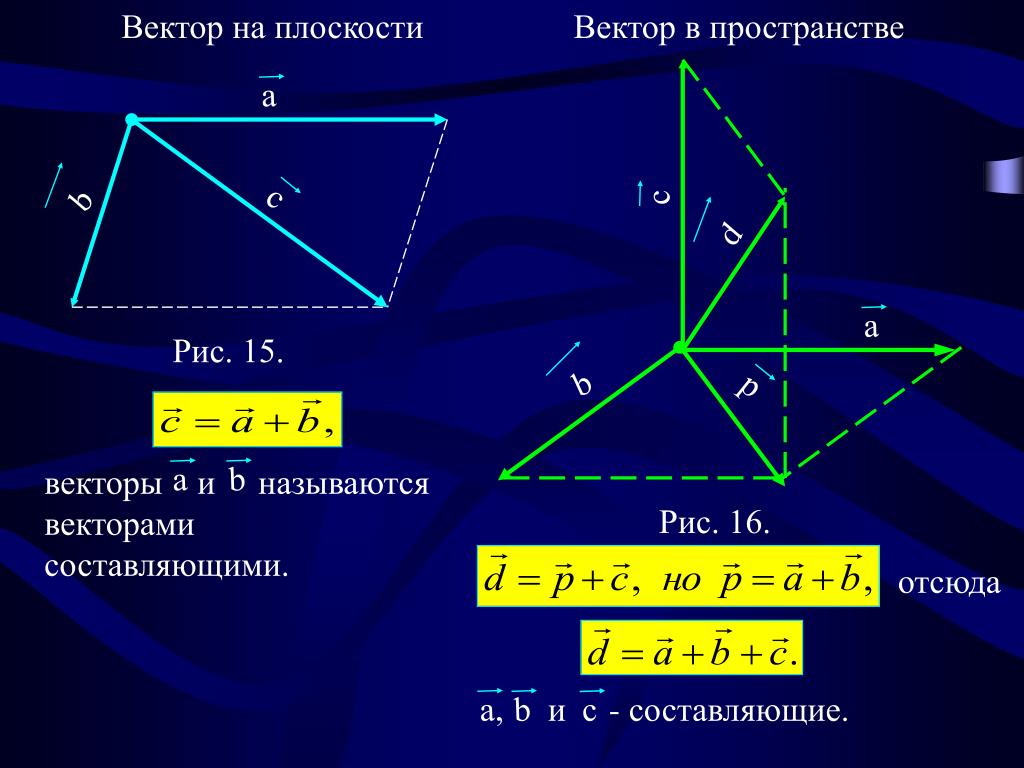
Кроме того, нам доступны четыре функции. Мы будем использовать только две функции, то есть длину чашелистика и длину лепестка. Мы берем эти две функции и строим их для визуализации. Из приведенного выше графика вы можете сделать вывод, что для разделения точек данных можно использовать линейную линию.
Мы извлекаем необходимые функции и разделяем их на данные для обучения и тестирования. 90% данных используются для обучения, а остальные 10% — для тестирования. Давайте теперь построим нашу модель SVM, используя библиотеку numpy.
α(0,0001) — это скорость обучения, а параметр регуляризации λ установлен равным 1/эпохи. Следовательно, регуляризующее значение уменьшает количество эпох, увеличивает.
Теперь мы отсекаем веса, так как тестовые данные содержат только 10 точек данных. Мы извлекаем функции из тестовых данных и прогнозируем значения. Мы получаем прогнозы, сравниваем их с фактическими значениями и печатаем точность нашей модели.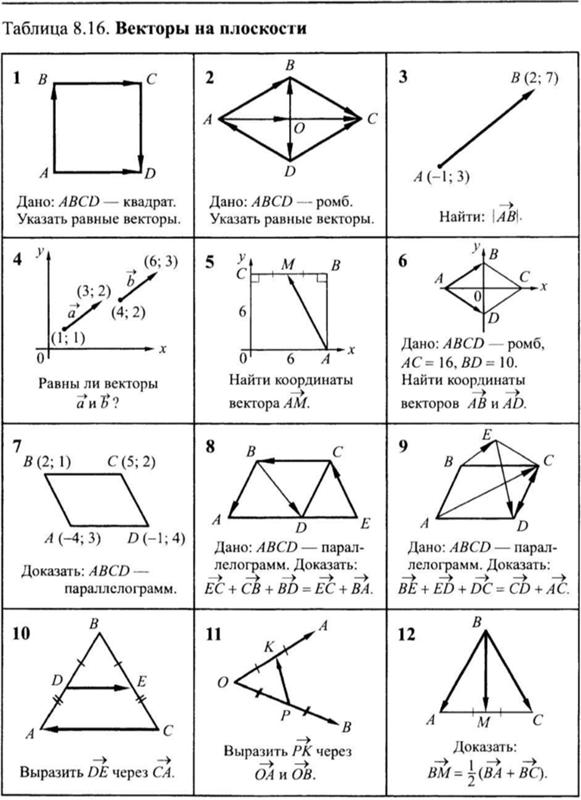



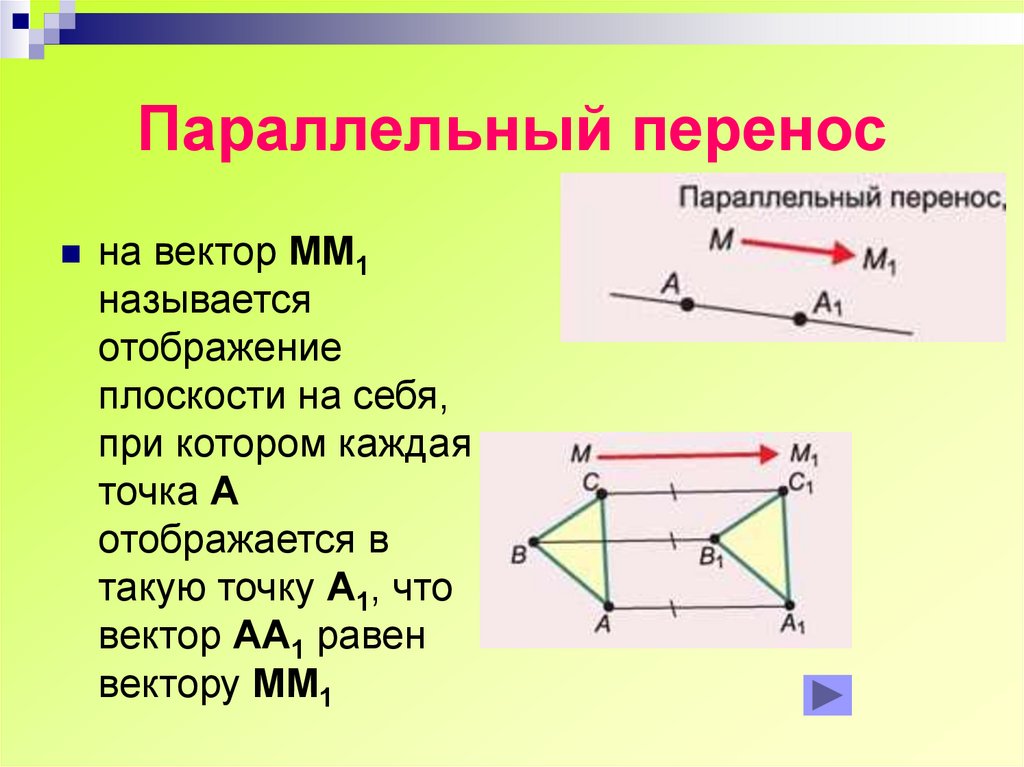
 10
Эти векторы не эквивалентны.
10
Эти векторы не эквивалентны.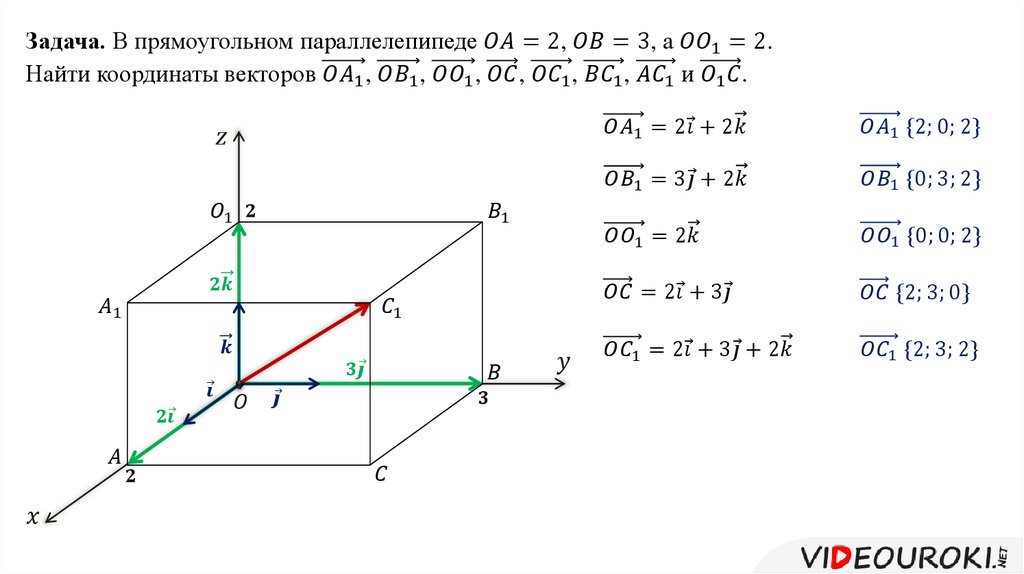 Мы можем сделать это алгебраически, найдя разность x -координат:
Мы можем сделать это алгебраически, найдя разность x -координат: v−2w=〈6,8〉−2·〈−2,4〉=〈6,8〉+〈4,−8〉=〈10,0〉 .
v−2w=〈6,8〉−2·〈−2,4〉=〈6,8〉+〈4,−8〉=〈10,0〉 . ‖u‖=1. Используйте скалярное умножение, чтобы увеличить длину uu без изменения направления:
‖u‖=1. Используйте скалярное умножение, чтобы увеличить длину uu без изменения направления: 2.20).
2.20).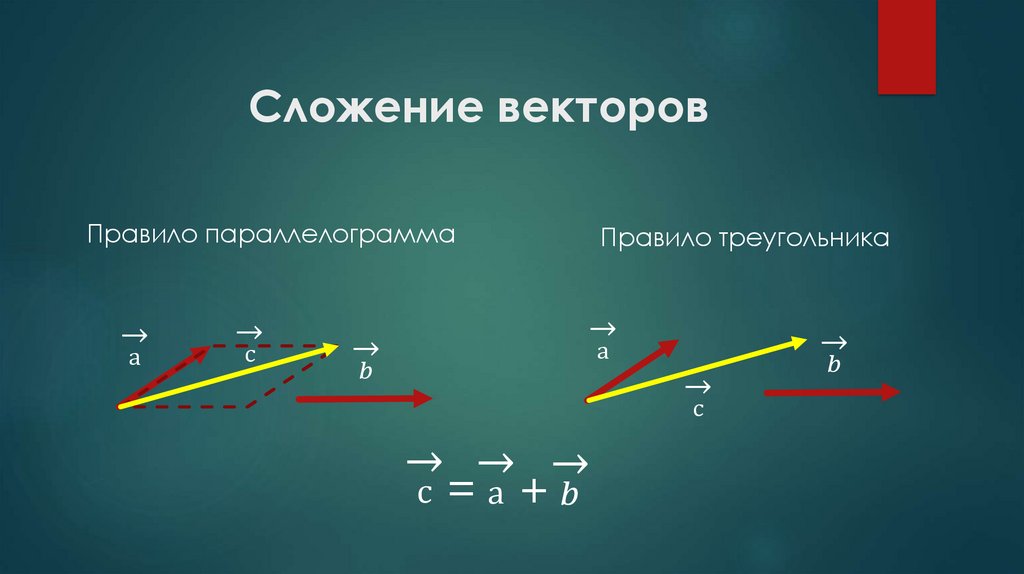
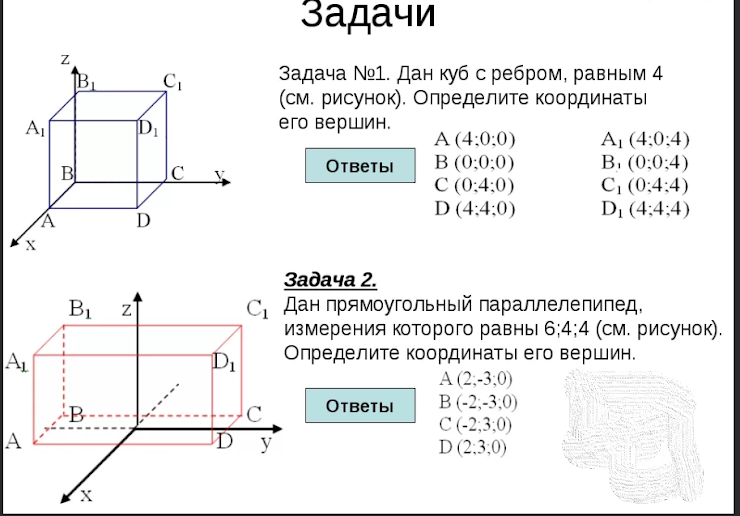 ∇ V l измеряет изменение векторного поля, поэтому минимизирует
∫Ml‖∇Vl‖HS2 заставляет векторное поле V l быть параллельным.
∇ V l измеряет изменение векторного поля, поэтому минимизирует
∫Ml‖∇Vl‖HS2 заставляет векторное поле V l быть параллельным.