Сектор геометрия: HTTP 429 — too many requests, слишком много запросов

Площадь сектора круга — формулы и примеры расчетов » Kupuk.net

Выполняя инженерные расчёты при проектировании различных объектов строительства, создании роботов, автоматизированных систем, станков, машин, самолётов, ракет, современных средств вооружения часто бывает необходимо найти площадь сектора круга.

Геометрия помогает при этом решать задачи на нахождение центра тяжести (центр масс), вычислять его координаты для плоских пластин, имеющих, в частности, форму правильного многоугольника.

Измерять и вычислять величины считается базовым умением. Оно включено в первую часть профильной программы выпускного экзамена ЕГЭ и ОГЭ по математике.

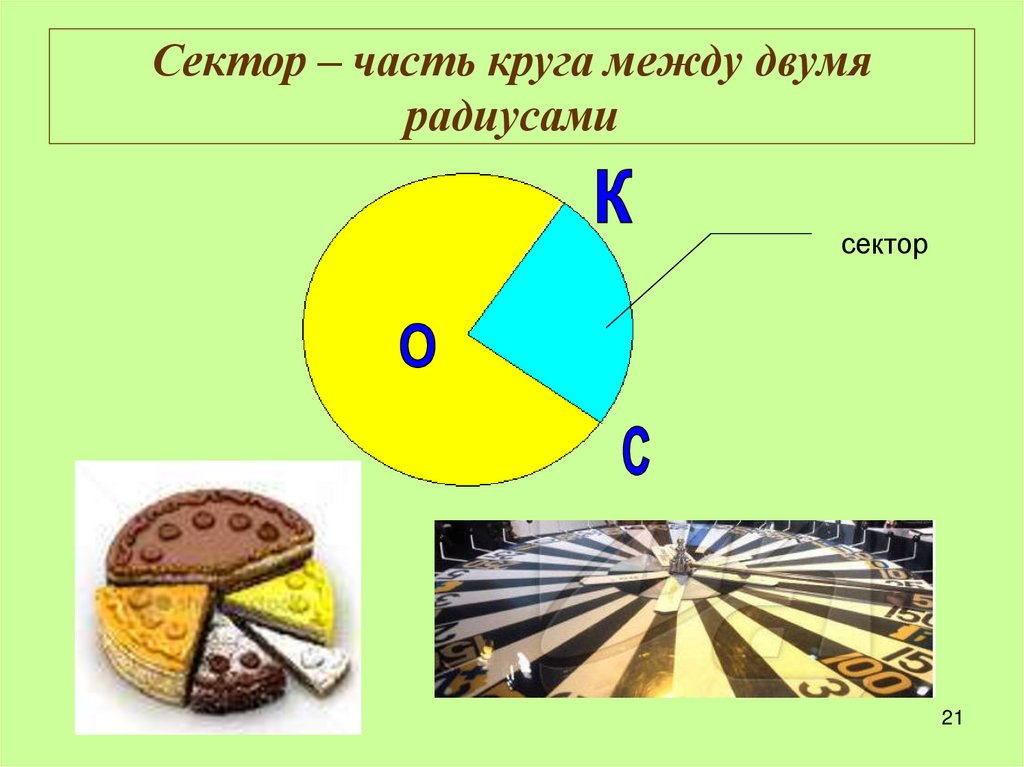
Сектор круга

Существует несколько определений, каждое из которых отличается только формулировкой, не меняющей подход к рассмотрению понятия:

Часть плоскости, ограниченная центральным углом и соответствующей дугой окружности.

Часть круга, заключённая между двумя радиусами.

Часто эту формулировку заменяют похожей, описывающей построение непосредственно: часть круга, лежащего внутри соответствующего центрального угла.

Площадь сектора круга через радиус и длину дуги

Пусть известны радиус круга R, длина дуги l. Как в этом случае определить площадь сектора, стягиваемого данной дугой?

Для ответа на вопрос понадобится формула нахождения длины окружности:

C = 2πR.

Определение, представленное через третью формулировку, даёт возможность соотнести численные величины понятий: сектор и круг, дуга и окружность, центральный и полный углы.

Поскольку отношения постоянны, то для ответа на поставленный вопрос достаточно найти отношение части к целому, затем умножить полученный результат на площадь круга S = πR2.

После сокращения дроби получают формулу:

Примеры решения задач

Задача №1

Найти площадь сектора круга радиусом 2 см, имеющего длину дуги 4 см.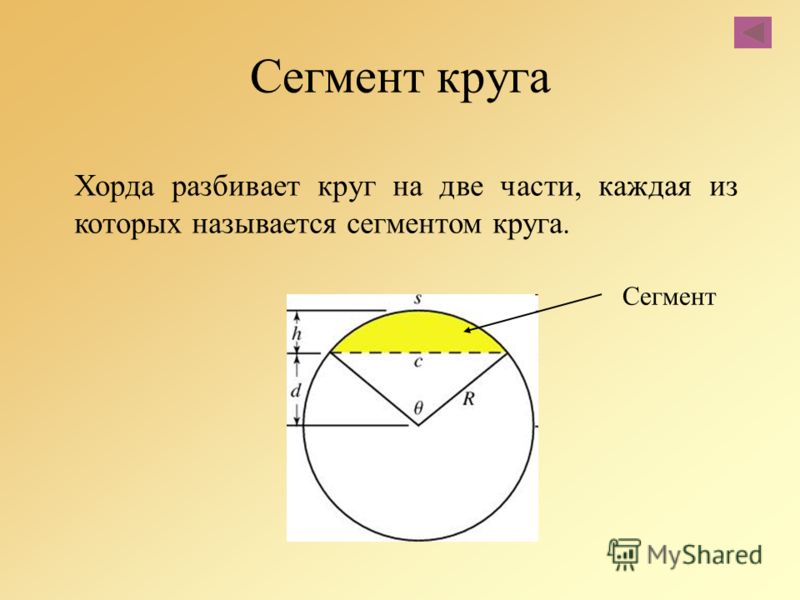

Решение.

Подставляя имеющиеся величины в формулу, получаем:

Sсект = (4 * 2) / 2 = 4.

Ответ: Sсект
= 4 см2.

Задача №2

Чему равна длина дуги закрашенного сектора, если Sсект = 32 см2, R = 4 см.

Решение.

Подставив известные данные в формулу, получим:

Следовательно,

2l = 32,

l = 16.

Тот же результат получился бы при первоначальной работе в «общем виде»:

Ответ: l = 16 см.

Площадь сектора круга через радиус и угол сектора

Если известна градусная мера центрального угла (n°), то, находя отношение её к полному кругу (к 360º), также умножают результат на площадь круга:

Задача №3

Чему равна площадь фигуры, изображённой на рисунке?

Решение.

Центральный угол изображённого сектора равен

360° — 90° = 270°

Подставляя в формулу величины, несложно получить искомый результат:

Ответ: Sсект = 27 см2.

Также аналогичным образом решаются обратные задачи.

Площадь сектора круга через угол сектора в радианах

Пусть центральный угол задан своей радианной мерой. Учитывая, что

несложно получить искомую формулу:

Задача №4

Чему равен центральный угол сектора в радианах (рад.), если его площадь равна 32, а радиус – 4?

Решение.

Выразив α, затем подставив числовые данные, легко получить результат:

Ответ: α = 4 рад.

Благодаря этой формуле, несложно доказать, что площади двух секторов с равными центральными углами относятся как квадраты радиусов соответствующих окружностей:

С другой стороны, площадь части кольца находится из условия:

Сегмент круга

Существует два подхода к определению понятия:

Геометрическая фигура, являющаяся общей частью круга и полуплоскости, называется сегментом круга.

Часть плоскости, заключённая между хордой и окружностью.

Оба определения характеризуют один и тот же объект с разных сторон, выражая, по сути одно и то же.

Иногда проводится описательное построение. В этом случае второй вариант быстрее приводит к данному термину.

Площадь сегмента круга по хорде и высоте

Пусть градусная мера ограничивающей дуги мала, длина хорды равна a, h — высота сегмента (перпендикуляр, опущенный из точки на окружности к середине хорды). Примечание: часто высота сегмента называется «стрелкой».

Тогда можно приближённо считать, что

Погрешность такого вычисления уменьшается вместе с отношением

.

В частности, когда дуга содержит угол, меньший 50º, то есть, 

погрешность оказывается менее 1%.

Более точной является формула для любого сегмента меньшего полукруга:

Точный расчёт производится, исходя из свойства нахождения сложной фигуры, являющейся суммой или разностью двух и более объектов.

Сегмент является частью сектора, к которому либо добавлен треугольник, содержащий центральный угол (для дуг больших 180º), либо убран (соответствующий центральный угол меньше 180º).

Отсюда следует, что

Задача №5

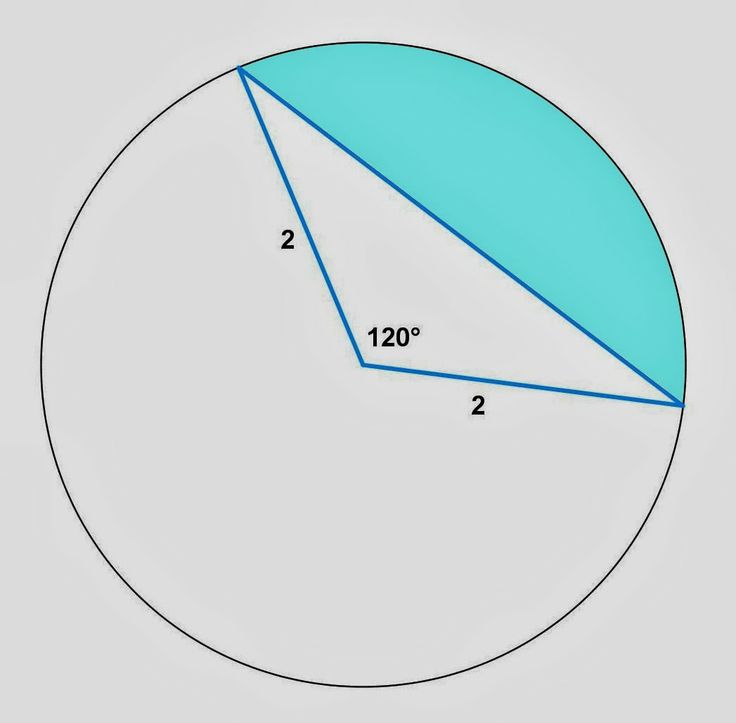
Вычислить стрелку и площадь сегмента, если центральный угол содержит 60º, а 

.

Решение.

Для нахождения стрелки достаточно из радиуса вычесть высоту треугольника AOB. Поскольку угол AOB по условию равен 60º, то треугольник AOB равносторонний. Поэтому его высота в √3/2 раз отличается от стороны (от радиуса). 

Отсюда следует, что:

Площадь по первой формуле будет приблизительно равна

По второй:

Применяя точную формулу и учитывая, что

находим:

Ответ: Sсегм = 1,26 см2.

Площадь сегмента круга через синус угла

Рассматривая точную формулу, площадь треугольника можно находить, используя половину произведения сторон на синус угла между ними. А значит:

Многие вычисления помогает провести онлайн калькулятор. Достаточно ввести исходные данные и запросить результат.

Площадь кругового сектора

Урок 38. Геометрия 9 класс ФГОС

В этом видеофрагменте мы познакомимся с такими понятиями, как круговой сектор и круговой сегмент. Выведем формулы для вычисления площадей кругового сектора и кругового сегмента. А также выполним практические упражнения на закрепление пройденного материала.

Конспект урока «Площадь кругового сектора»

Кругом называется часть плоскости, ограниченная окружностью.

Круг радиуса  с центром  содержит точку  и все точки плоскости, находящиеся от точки  на расстоянии, не большем .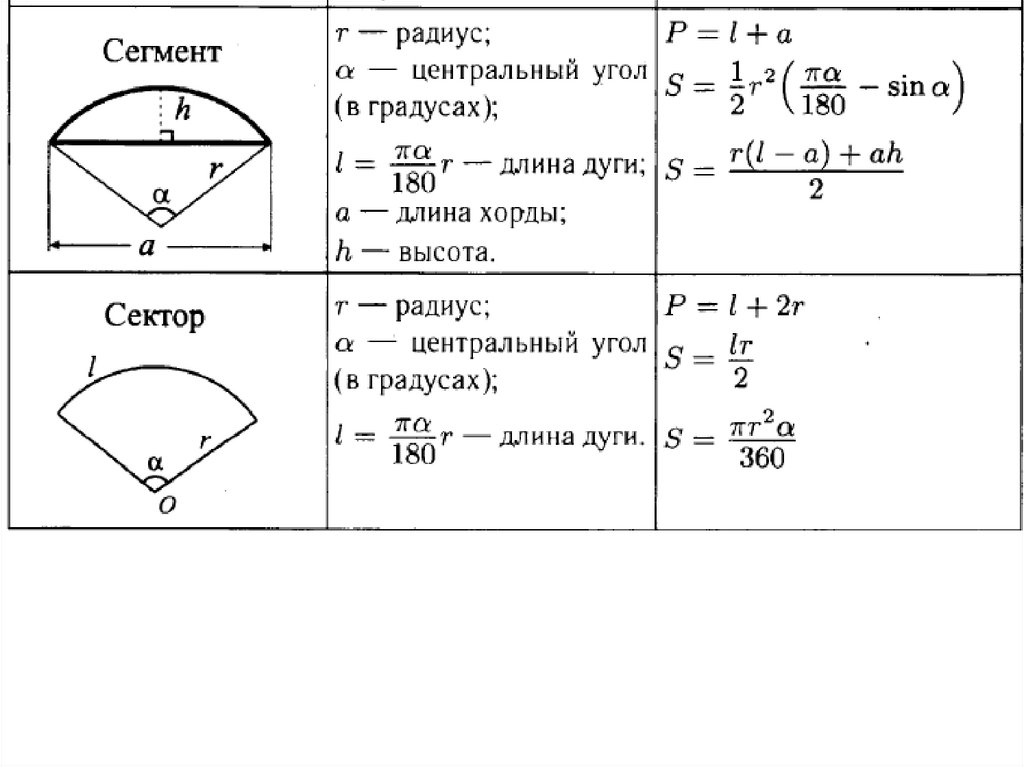

Если в круге провести два его радиуса, например, ОА и ОB, они выделят из круга его часть, которая называется сектором.

Определение. Круговым сектором или просто сектором называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

Дуга, которая ограничивает сектор, называется дугой сектора.

На первом рисунке изображены два сектора с дугами АlB и АmB. Первый из этих секторов закрашен. На втором рисунке изображены круг, который касается всех сторон треугольника, и два сектора, ограниченные радиусами, проведенными в точки касания, и соответствующими дугами окружности.

Выведем формулу для вычисления площади  радиусом , дуга которого имеет градусную меру .

Площадь круга радиусом . Следовательно,  , ограниченного дугой в , равна . Значит, Значит,  , ограниченного дугой в , выражается формулой: .

Например, если ABC – равносторонний треугольник, вписанный в круг радиуса R, а точка О – его центр, тогда площадь сектора, ограниченного радиусами ОА, ОB и дугой AmB, равна .

Теперь рассмотрим формулу для нахождения площади фигуры, которая называется сегментом.

Определение. Круговым сегментом или просто сегментом называется часть круга, ограниченная дугой окружности и хордой, соединяющей концы этой дуги.

Дуга окружности, ограничивающая сегмент, называется дугой сегмента, а ограничивающая его хорда называется основанием сегмента.

На рисунке изображены два круговых сегмента, ограниченные хордой АB и дугами AlB и AmB. Хорда АB является основанием для каждого из этих сегментов. На втором рисунке изображены сегменты, ограниченные стороной  MQ вписанного квадрата и соответствующими дугами окружности.

Вы уже знаете, что площадь круга вычисляется по формуле . Зная эту формулу нетрудно вывести формулу для вычисления площади кругового сегмента. Рассмотрим два случая:

1) дуга сегмента меньше 180 градусов;

2) дуга сегмента больше 180 градусов.

Итак, первый случай. Пусть дуга  сегмента имеет градусную меру , меньшую .  .

Второй случай.

Пусть дуга  сегмента имеет градусную меру , большую .

.

Заметим, что площадь сегмента, градусная мера дуги которого α>180º, можно найти также как разность между площадью круга и площадью сегмента с тем же основанием и дугой, градусная мера которой равна 360º-α.

Если центральный угол равен , то этот сегмент – полукруг, и его площадь равна .

Пусть ABC – равносторонний треугольник, вписанный в круг радиуса R, а точка О – его центр.

Тогда площадь меньшего сегмента, основанием которого служит сторона AB треугольника, равна

.

 

Задача. Площадь сектора  см

2, центральный угол равен . Найдите радиус круга.

Решение.

 

 

 

 (см)

 (см)

Ответ:  см.

Задача.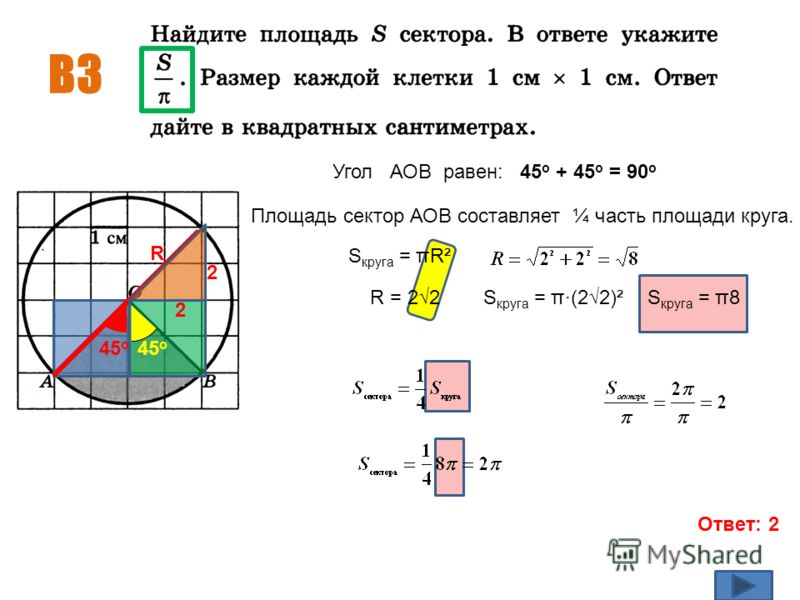 Чему равен , если площадь сегмента  равна , радиус равен  и центральный угол ?

Решение.

 

 

 (см)

 

Ответ: .

Подведем итоги урока. На этом уроке мы познакомились с такими понятиями, как круговой сектор и круговой сегмент. Узнали, что круговым сектором или просто сектором называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга. Узнали, что круговым сегментом или просто сегментом называется часть круга, ограниченная дугой окружности и хордой, соединяющей концы этой дуги. А также вывели формулы для вычисления площади кругового сектора и кругового сегмента.

Предыдущий урок 37 Площадь круга

Следующий урок 39 Отображение плоскости на себя

Получите полный комплект видеоуроков, тестов и презентаций Геометрия 9 класс ФГОС

Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт

Многоступенчатая циклическая симметрия | Клуб пользователей ANSYS

Всем доброго времени суток.

Относительно недавно (в зависимости от того, когда вы это читаете) прошел вебинар по новым возможностям ANSYS Mechanical версии 2022R1 в моем исполнении, где кроме бесконечного количества слайдов я постарался кое-что и продемонстрировать. Видеозапись безусловно будет (возможно уже есть, смотря когда вы это читаете), однако, независимо от нее, я решил еще и сделать текстовый вариант для задачек из демонстраций (текстовый вариант бесконечного количества слайдов здесь уже есть чуть ниже в виде аж 4х отдельных статей). Итак, здесь давайте рассмотрим мою попытку в многоступенчатую циклическую симметрию.

Многоступенчатая циклическая симметрия (Multistage Cyclic Symmetry) – это свежевозникший набор инструментов (команд, если вы любитель классики), созданный для совмещения в рамках единой циклически симметричной модели нескольких геометрий с различным количеством секторов.

Например, допустим есть вот такая геометрия (одна ее часть имеет 10 секторов, а другая -16). Ваши действия?

Рисунок 1.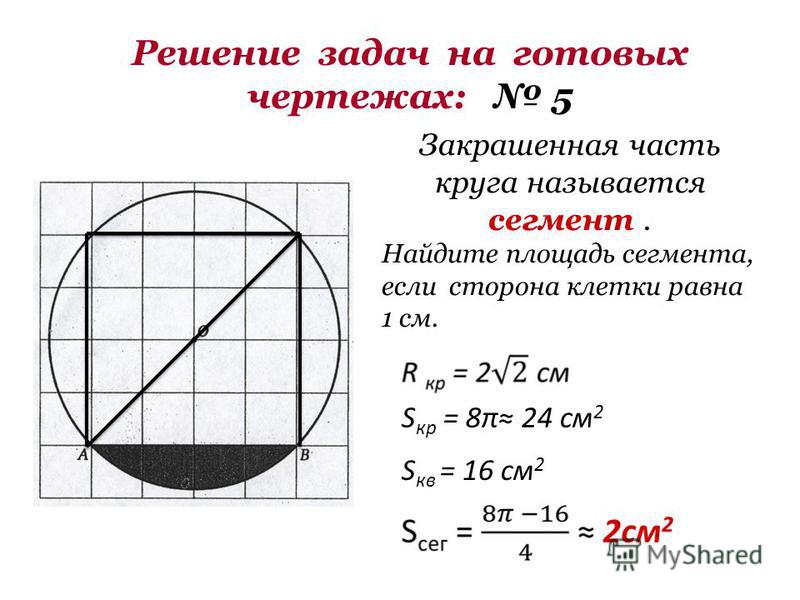 Исходная геометрия (нашел в сети).

Рисунок 2. Та же геометрия, но уже с разделением на секторы.

Уже на этапе формирования секторов есть некоторая хитрость – обратите внимание, что границу между секторами я провел так, чтобы толщина геометрии совпадала, а ведь есть соблазн не создавать новых поверхностей и разрезать прямо по скачку в толщине. Это сделано с умыслом и дальше по тексту мы увидим зачем оно понадобилось.

Дальше нужно задать циклическую симметрию, и, поначалу, это делается как обычно – разве что секторов у нас два, как и всех соответствующих инструментов. Цилиндрическая система координат только в единственном экземпляре.

Рисунок 3. Цилиндрическая система координат, очевидно, должна быть развернута вот так.

Рисунок 4. Свойства системы координат. Кроме направления осей, еще важна ее цилиндричность и тот факт, что ее APDL номер = 12 (увы это понадобится).

Дальше традиционно достается ветка Symmetry и внутри нее добавляются два объекта Cyclic Region по одному на каждый сектор.

Рисунок 5. Так выглядит папка Symmetry, если что. Достается на уровне ветки Model в дереве.

Рисунок 6. А это Cyclic Region (в дереве соответственно дочерний объект ветки Symmetry).

Рисунок 7. Первый Cyclic Region – внутренний сектор.

Рисунок 8. Второй Cyclic Symmetry – внешний сектор.

А дальше уже интереснее – чтобы организовать многоступенчатость нужно добавить новый специальный объект интерфейса с названием «ступень» (stage). Не трудно догадаться, что в нем мы заявляем разрозненные секторы как будущие части одного целого. Выбрать нужно само тело (объем целиком) и соответствующий ему объект дерева Cyclic Region.

Рисунок 9.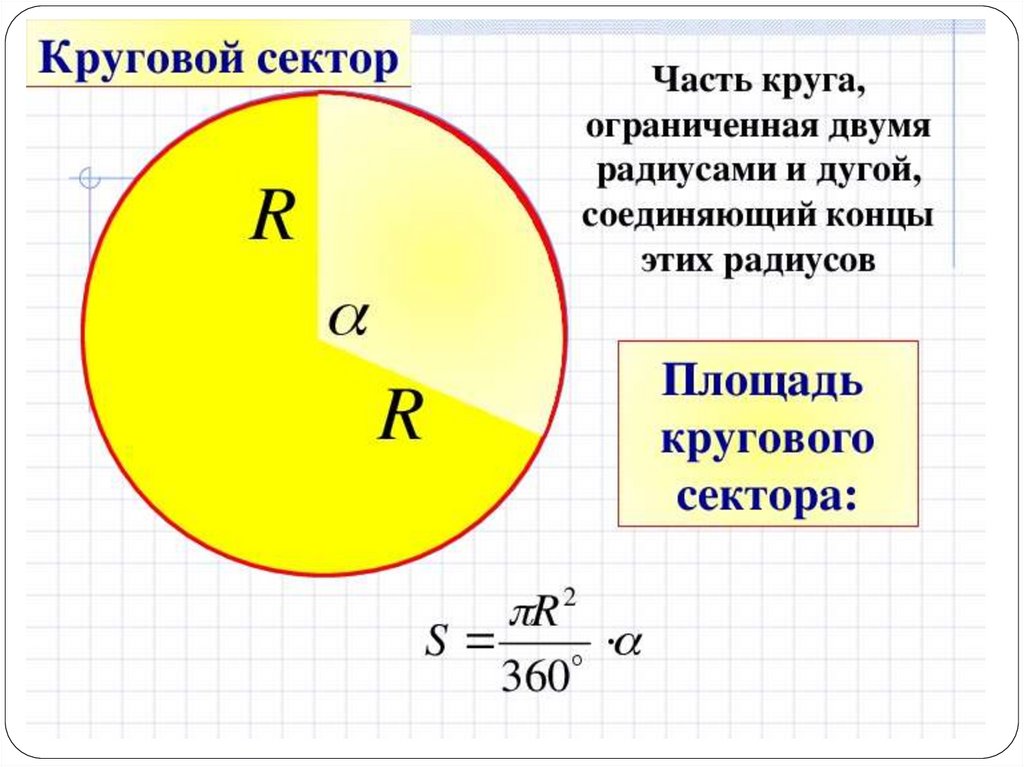 Новый объект Stage на панели.

Рисунок 10. Первая ступень. Обратите внимание на ее имя.

Рисунок 11. Вторая ступень.

Рисунок 12. Итоговое наполнение ветки Symmetry.

Однако это еще не все. Контакт между ступенями становится нерабочим и его нужно удалить/подавить. А для фактического соединения ступеней потребуется соответствующий новый объект с логичным названием “Interstage” (пробовать перевести одним словом, пожалуй, не рискну). В рамках этого инструмента нужно выбрать только взаимодействующие поверхности (визуально очень похоже на контактную пару, только использованы более экзотичные цвета). Важно отметить, что в подкорке сего действия лежат MPC уравнения связи.

Рисунок 13. Контакт не нужен.

Рисунок 14. Interstage на панели инструментов Connections.

Рисунок 15. Выбранные поверхности в графическом окне.

Рисунок 16. Настройки Interstage и его положение в дереве.

Дальше задачу можно поставить как ни в чем не бывало. Конкретно здесь в качестве граничных условий было выбрано жесткое закрепление на оси, а также известная скорость вращения.

Рисунок 17. Сетка без особых претензий на точность — скорости решения ради.

Рисунок 18. Граничное условие скорости вращения (200 рад/с).

Рисунок 19. Закрепление Fixed Support.

Рисунок 20. Стандартный результат Total Deformation.

Чтобы не ограничиваться стандартной визуализацией одного сектора, можно использовать новый инструмент, созданный специально для разворачивания многоступенчатой модели. Этот объект, впрочем, является Beta функционалом.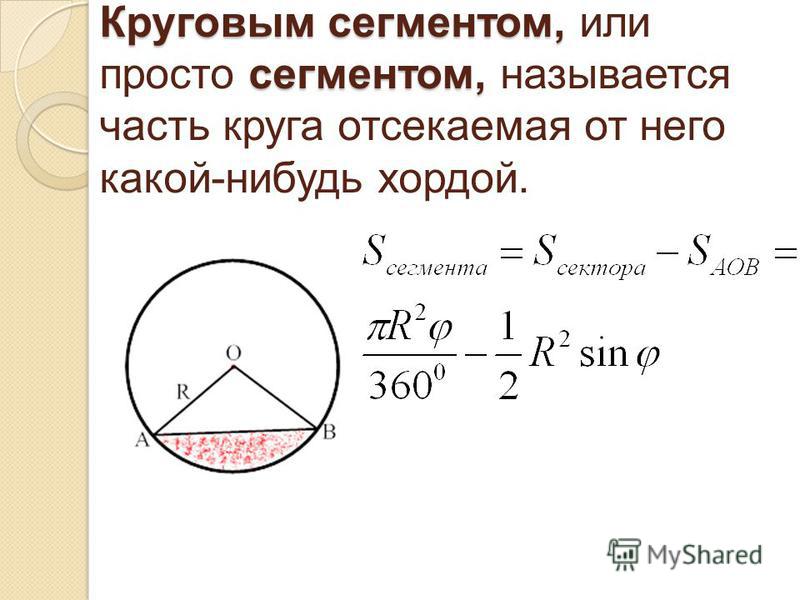

Рисунок 21. Активация Beta опций.

Рисунок 22. Инструмент Result Mesh для визуализации результатов.

У этого инструмента есть два режима работы и первый из них, Cyclic Expansion, позволяет просматривать контурные графики на полноценной модели. Причем в рамках самого объекта визуализируется только разворачивание сетки, однако среди настроек контурных результатов появляется специальное поле для выбора развертки.

Рисунок 23. Режим Cyclic Expansion и его результат.

Рисунок 24. Для визуализации уже конкретного контурного графика потребуется в его настройках указать соответствующий Result Mesh.

Есть в Result Mesh и другой режим – для создания пути круглой формы, также под вывод результата. Особый интерес представляет результат перемещений на границе между ступенями. Идея в том, чтобы применить результат перемещений (например Total Deformation) к одному и тому же пути, но при этом к различным телам по очереди, и сравнить два графика между собой – так можно проверить насколько перемещения по границе совместны.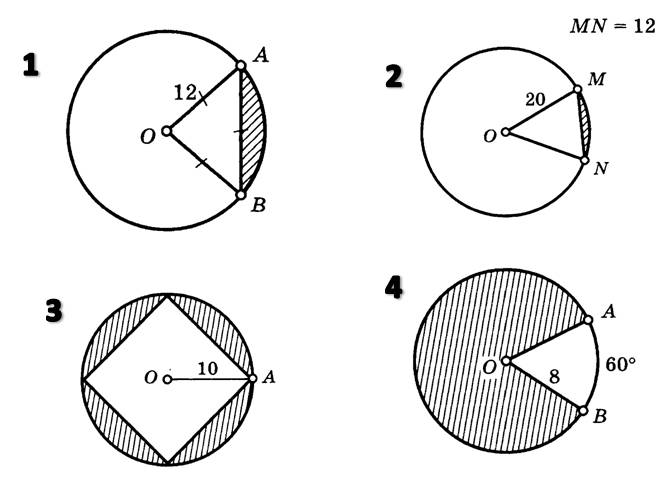 Именно для того, чтобы можно было приложить контурный график к одному и тому же пути со стороны каждого сектора, геометрия и была разрезана таким образом.

Рисунок 25. Result Mesh в режиме Path Expansion.

Рисунок 26. Было выбрано одно ребро на границе между ступенями.

Рисунок 27. Результат по пути для первой ступени.

Рисунок 28. Результат по тому же пути для второй ступени.

Рисунок 29. Наглядное сравнение при помощи результата Chart.

Видно, что не все в порядке в датском королевстве, хотя и разницу в числах в этом случае нельзя назвать большой.

Почему жизнь такова? Все дело в узловых диаметрах и гармонических индексах, которые внезапно оказывают некоторое влияние и на простой статический расчет. Гармонический индекс – это по сути способ группировки возможных форм колебаний согласно количеству узловых диаметров.   Конкретные числа зависят от количества секторов, но общие зависимости можно найти в help.

Рисунок 30. Общие соотношения гармонических индексов, количества секторов и узловых диаметров.

Таким образом, нетрудно видеть, что у моделей с различным (еще и некратным) количеством секторов при одинаковых индексах количество узловых диаметров совпадать не будет. Ну и как уже нетрудно догадаться, по умолчанию Mechanical без задней мысли считает все ступени многоступенчатой модели на одном гармоническом индексе (нулевом), что и приводит к некоторому несовпадению перемещений, т.к. уравнения связи соответствуют несовпадающему количеству узловых диаметров.

Вылечить эту интересную особенность стало возможно с выходом последней версии (2022R1), правда пока только при помощи команд APDL. Данная методика получила название мультигармонического расчета (Multiharmonic) и для ее применения в Mechanical потребуется довольно мрачный скрипт. Впрочем, его можно найти в практически готовом виде в Help документации. К слову, пример, на основе которого, я и производил эти художества называется так:

«Chapter 14: Static Analysis of a 2-stage disk with pinholes – Beta Options»

Целиком все эти команды сюда особенно нормально не вставишь, так что если будут проблемы с их поиском в help, я прикреплю либо текстовый файл либо сам проект, если вам интересно, а по ходу повествования ограничимся картинками фрагментов. Идея же скрипта в том, чтобы сначала удалить те ступени, которые мы создали в интерфейсе Mechanical, а потом создать их заново, но уже с соответствующими настройками и с соответствующим количеством дублей – по одному дублю требуется на каждый желаемый гармонический индекс.

Итак, чтобы применить новую технику, в описанной выше задаче подавляется скорость вращения и добавляется командная вставка из Help (Скорость вращения нужно подавлять, т.к. она должна идти после вставки, а значит становится ее частью).

Рисунок 31. Дерево для мультигармонического решения.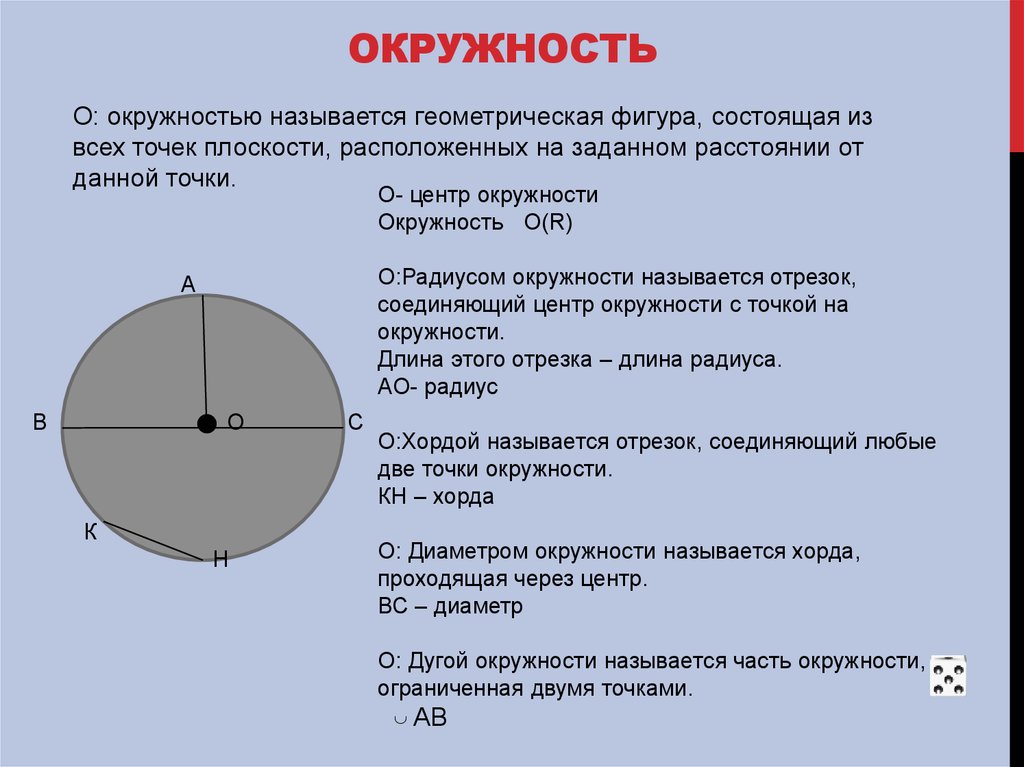

Далее скрипт редактируется под текущие нужды. Первым делом необходимо задать параметры имен ступеней (т.к. встречаются они часто их вынесли в отдельные параметры в самом начале кода).

Рисунок 32. Имена ступеней для скрипта можно найти в окне свойств объектов Stage.

Дальнейший довольно объемный блок команд посвящен созданию компонентов, удалению и созданию ступеней. Если исходных ступеней две, а также всего два индекса для каждой из них мы планируем рассматривать, то менять в огромном массиве текста не придется ничего. У меня, разумеется, как раз такой случай. Впрочем логика блоков довольно прозрачная и при необходимости дополнительное редактирование не должно стать непреодолимой преградой.

Рисунок 33. Один из типовых блоков кода для воссоздания/дублирования ступеней

Однако фрагменты для редактирования еще есть. В частности, в финальном блоке объявления ступеней указывается количество секторов и интересующий нас гармонический индекс каждого дубля. С различиями в количестве секторов моей случайной геометрии и исходного примера все очевидно (10 и 16 против 11 и 16). Но что делать с индексами?

В исходном коде можно заметить, что для дублей обоих ступеней используются пятые индексы.

Рисунок 34. Исходный скрипт для геометрии с двумя ступенями на 11 и 16 секторов.

В том же примере можно найти и объяснение такому выбору. Пятый гармонический индекс идеально подходит, т.к. для каждой ступени там содержится именно такое количество узловых диаметров, которое соответствует противоположной ступени.

Рисунок 35. Выбор гармонического индекса для каждой ступени.

В моем случае цифры и таблицы выходят другие – идеально подойдут 4й и 6й индексы соответственно.

Рисунок 36. Подбор нужных индексов для моей модели.

Рисунок 37. Итоговый вид фрагмента скрипта.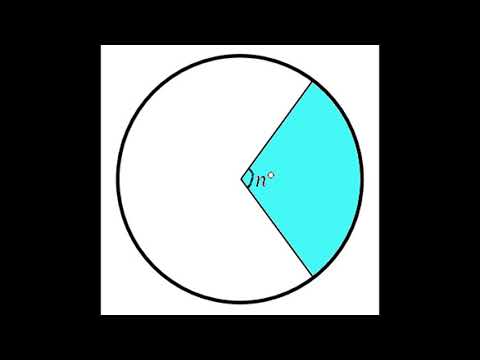

Заканчивается скрипт восстановлением граничных условий, но только на ступени с нулевым индексом – дубли не нагружаются.

Рисунок 38. Окончание скрипта с приложением граничных условий.

На этом изменения закончены и можно сравнить результаты.

Рисунок 39. Контурный график перемещений.

Рисунок 40. Перемещение первой ступени на интерфейсе.

Рисунок 41. Перемещение второй ступени на интерфейсе.

Рисунок 42. Наглядное сравнение при помощи результата Chart.

Таким образом, одного дубля каждой ступени, в текущей ситуации, оказалось достаточно для относительно неплохого совпадения перемещений по границе.

Успехов в работе!

 

Сектор круга – формула, определение, примеры

Сектор круга – это часть круга в форме пирога, состоящая из дуги и двух ее радиусов. Часть окружности (также известная как дуга) круга и 2 радиуса круга встречаются в обеих конечных точках дуги, образуя сектор. Форма сектора круга напоминает кусок пиццы или пирог. В геометрии круг — одна из самых совершенных фигур. Форма сектора круга — простейшая фигура в геометрии. У него есть разные части. Такие как диаметр, радиус, окружность, сегмент, сектор. В этой статье мы узнаем о том, что такое сектор круга, формулы, связанные с сектором круга, а также решим несколько примеров на сектор круга.

1.	Что такое сектор круга?
2.	Формулы сектора окружности
3.	Часто задаваемые вопросы о секторе круга

Что такое сектор круга?

Сектор — это часть круга, которая может быть определена на основе четырех точек, упомянутых ниже:

• Часть круга покрыта двумя радиусами и дугой.
• Круг разделен на два сектора, а разделенные части называются малыми и большими секторами.
• Большая часть круга является большим сектором, тогда как меньшая часть является второстепенным сектором.
• В случае полукругов круг делится на два сектора одинакового размера.

2 радиуса пересекаются в части окружности круга, известной как дуга, образуя сектор круга.

Посмотрите на следующий рисунок, чтобы отличить малый сектор от основного.

Часть OAPB круга называется второстепенным сектором, а часть OAQB круга называется большим сектором.
Полуокружность также является сектором с углом 180 градусов.

Формулы сектора окружности

Площадь сектора круга

Площадь сектора круга — это площадь, занимаемая в пределах границы сектора круга. Сектор всегда начинается из центра круга. Полукруг также является сектором круга, в данном случае круг имеет два сектора одинакового размера. Давайте узнаем, как вычислить площадь сектора. Если задан радиус круга (r) и угол сектора (θ), то формула, используемая для расчета площади сектора, имеет вид:
Площадь сектора (A) = (θ/360°) × πr ²

• θ — угол в градусах.
• r — радиус окружности.

Длина дуги сектора Формула

Точно так же длина дуги сектора с углом θ определяется как;

l = (θ/360) × 2πr или l = (θπr)/180.

Площадь сектора круга без угла Формула

Когда угол сектора не задан, а длина дуги сектора круга задана, мы можем вычислить площадь сектора круга. круг, используя длину. Предположим, что длина дуги равна «l», а радиус окружности равен «r». По радианному определению угол сектора окружности равен отношению длины дуги сектора окружности к радиусу окружности.
θ = l/r, где θ в радианах.

Площадь сектора круга = (l × r)/2

Периметр сектора круга Формула

Ниже приведены формулы для периметра сектора круга.

Периметр сектора = 2 радиуса + длина дуги

Длина дуги рассчитывается как Длина дуги = l = (θ/360) × 2πr

Следовательно, периметр сектора = 2 радиуса + ((θ/360) × 2πr )

Похожие статьи о секторе круга

Ознакомьтесь с этими интересными статьями, чтобы узнать больше о Секторе Круга и связанных с ним темах.

• Площадь круга
• Что такое Пи?
• Диаметр
• Сегмент круга

 

Сектор круга Пример

1. Пример 1: Какова длина сектора круга, если радиус круга равен 7 единицам, а угол сектора равен 40°?

   Решение: Площадь сектора = (θ/360°) × πr ²

   = (40°/360°) × (22/7) × 7 × 7

   = 154/9 квадратных единиц

   Длина сектора = (θ/360°)× 2πr

   l = (40°/360°) × 2 × (22/7) × 7

   l = 44/9 единиц

2. Пример 2: Найдите площадь сектора круга, если радиус круга 20 единиц, а длина дуги 8 единиц.

   Решение: Дано, радиус = 20 единиц и длина дуги сектора круга = 8 единиц

   Площадь сектора круга = (lr)/2 = (8 × 20)/2 = 80 квадратных единиц.

3. Пример 3: Найдите периметр сектора круга, радиус которого равен 8 единицам, а дуга окружности образует в центре угол 30°. Используйте π = 3,14.

   Решение : Учитывая, что r = 8 единиц,

   θ = 30° = 30° × (π/180°) = π/6

   Периметр сектора определяется по формуле;

   P = 2 r + r θ

   P = 2 (8) + 8 ( π/6)

   P = 16 + 4π/3

   P = 16 + (4 × 3,14)/3 = 20,187 ед.

   Следовательно, периметр сектора составляет 20,187 единиц.

перейти к слайдуперейти к слайдуперейти к слайду

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему стоит математика, с сертифицированными экспертами ourCuemath.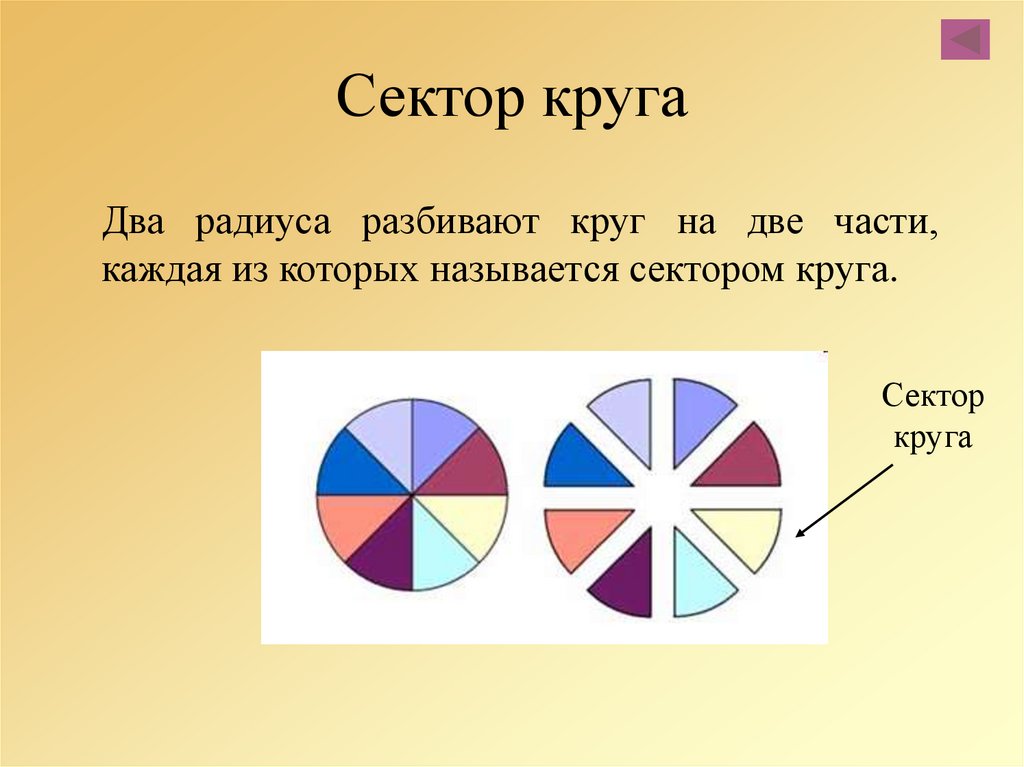

Забронировать бесплатный пробный урок

Практические вопросы по сектору круга

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о секторе круга

Какая формула площади сектора круга?

Чтобы вычислить площадь сектора круга, мы должны умножить центральный угол на квадрат радиуса и разделить его на 2. Площадь сектора круга = (θ × r ² )/2, где θ измеряется в радианах. Формулу также можно представить в виде Площадь сектора = (θ/360°) × πr ² , где θ измеряется в градусах.

Что вы понимаете под сектором круга?

Часть окружности, покрытая двумя радиусами окружности и дугой, пересекаемой с ними (дугой, входящей в эту часть), является сектором окружности. Он также известен под термином «пироговая часть круга».

Что такое периметр сектора круга?

Общая длина окружности, заключенной в пределах угла «θ», представляет собой периметр сектора окружности или, другими словами, сумму длин дуги и двух радиусов.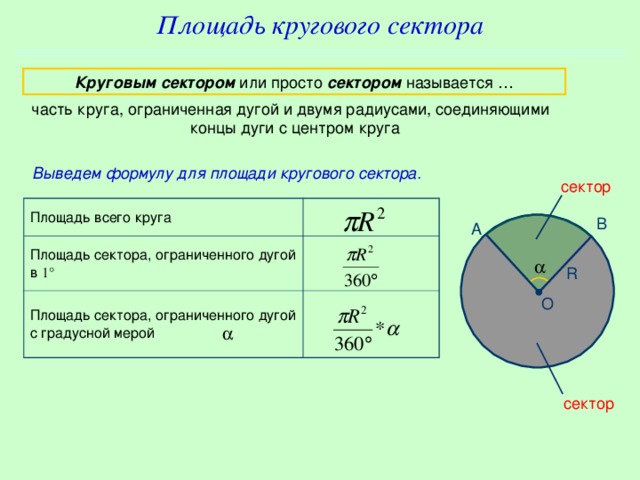 Формула для вычисления периметра сектора круга = 2 Радиус + ((θ/360) × 2πr)

Как найти площадь сектора круга без угла?

Мы можем найти площадь сектора круга, когда угол отсутствует. Угол сектора окружности, опирающийся на длину дуги (радиус окружности) в центре, равен одному радиану, а также равен отношению длины дуги сектора окружности к радиусу окружности. Поэтому ниже приведена формула площади сектора круга без угла.
Площадь сектора круга = (l × r)/2·

Что такое сектор и дуга?

Дуга — это часть окружности и часть круга, тогда как сектор — это секторная часть круга, покрытая двумя радиусами.

Сколько секторов в круге?

В круге два сектора. Если круг разделен на две равные части, которые находятся в полуокружностях, то сектора имеют одинаковый размер, в противном случае в других случаях, например, если часть круга имеет форму пирога, то один сектор больше другого. Больший из них известен как большой сектор, а меньший известен как второстепенный сектор круга.

Скачать БЕСПЛАТНЫЕ учебные материалы

Рабочие листы по сектору окружности

Секторы — ACT Math

Все ресурсы ACT Math

14 диагностических тестов 767 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 3 Следующая →

ACT Math Help » Геометрия » Плоская геометрия » Круги » Сектора

Сектор, изображенный выше, представляет собой круг. Какова мера угла для сектора?

Возможные ответы:

Правильный ответ:

Объяснение:

Такой вопрос очень прост. Вам просто нужно выяснить, что такое общее количество градусов в круге. Это:

. Вот оно!

Сообщить об ошибке

Площадь сектора  есть . Этот рисунок выполнен не в масштабе.

Какова мера угла сектора?

Возможные ответы:

Правильный ответ:

Объяснение:

Вы знаете, что площадь круга вычисляется по уравнению:

Для наших данных это:

 или

Теперь сектор представляет собой процент от круга. Для площадей это можно представить в виде дроби:

Суммарная градусная мера круга, конечно же,  градусы. Это означает, что сектор содержит:

.

Сообщить об ошибке

Длина дуги сектора выше . Этот рисунок выполнен не в масштабе.

Какова угловая мера сектора?

Возможные ответы:

Правильный ответ:

Объяснение:

Вы знаете, что длина окружности вычисляется по уравнению:

Для наших данных это:

Теперь сектор представляет собой процент от окружности. Для длин окружности и длины дуги это можно представить в виде дроби:

Полная градусная мера окружности, конечно же,  градусы. Это означает, что сектор содержит:

.

Сообщить об ошибке

Сектор   входит в общий круг. Этот рисунок выполнен не в масштабе.

Каков угол этого сектора?

Возможные ответы:

Правильный ответ:

Пояснение:

Не задумывайтесь над этим вопросом! Все, что вам нужно помнить, это то, что данный круг содержит градусы. Это означает, что сектор представляет собой лишь процент от . Для нашего вопроса этот процент равен , что совпадает с . Итак, чтобы рассчитать, вам просто нужно умножить:

Это градусная мера сектора.

Сообщить об ошибке

Велосипедное колесо имеет равномерно расположенные спицы от центра к шине. Какой должен быть угол для спиц, чтобы гарантировать равномерный интервал? Округлить до сотых.

Возможные ответы:

Правильный ответ:

Объяснение:

Помните, что общая градусная мера окружности равна . Это означает, что если у вас есть части, на которые вы разделили свой круг, каждая спица должна быть или отделена друг от друга.

Сообщить об ошибке

Какой процент от полного круга представляет указанный выше сектор? Округлить до сотых.

Возможные ответы:

Правильный ответ:

Объяснение:

Этот вопрос очень легко решить. Вам просто нужно найти, какой процент градусов составляет по сравнению с целым числом градусов для круга. Это:

 или  или 

Округлив, вы получите .

Сообщить об ошибке

Рисунок выполнен не в масштабе.

Какой процент круга занимает сектор? Округлить до сотых долей процента.

Возможные ответы:

Правильный ответ:

Пояснение:

Не задумывайтесь над этим вопросом! Все, что вам нужно помнить, это то, что данный круг содержит градусы. Это означает, что ваш процент сектора — это просто отношение угла  к . Это:
 или 

Округлено, это .

Сообщить об ошибке

Сектор окружности ограничен малой дугой . Какой процент окружности составляет дуга?

Возможные ответы:

Правильный ответ:

Объяснение:

Единственная предоставленная информация — это то, что сектор . При нахождении процента полезно помнить, что проценты — это простой способ показать дроби, то есть части, целого.

Следовательно, чтобы решить, какой процент представляет сектор от всего круга, нам нужно выяснить, какую часть   сектор составляет от всего круга. Имейте в виду, что круг измеряется до . Это означает, что сектор  от общего числа . Это можно записать как:

Это можно упростить до:

Обратите внимание, что знаки градусов исчезли. Это потому, что когда вы делите градусы на градусы, единицы уравновешиваются! Эта упрощенная дробь означает, что  была пятая часть всего круга. Теперь эту дробь можно превратить в проценты.

Чтобы перейти от дробей к процентам, полезно помнить, что десятичные дроби являются важным промежуточным шагом. То есть, как только дробь может быть преобразована в десятичную форму, ее можно легко преобразовать в проценты, умножив на 100.

То есть сектор составляет весь круг.

Сообщить об ошибке

Сектор угла ограничен большой дугой . Сколько процентов круга это составляет?

Возможные ответы:

Правильный ответ:

Объяснение:

Единственная предоставленная информация — это то, что сектор . При нахождении процента полезно помнить, что проценты — это простой способ показать дроби — то есть части — целого. Чтобы решить, сколько процентов сектор составляет от всего круга, нам нужно выяснить, какую часть   сектор составляет от всего круга.

Имейте в виду, что круг измеряет градусы. Это означает, что сектор  от общего числа . Это можно записать как:

Это можно упростить до:

Обратите внимание, что знаки градусов исчезли. Это потому, что когда вы делите градусы на градусы, единицы уравновешиваются! Эта упрощенная дробь означает, что  было три четверти всего круга. Теперь эту дробь можно превратить в проценты.

Чтобы перейти от дробей к процентам, полезно помнить, что десятичные дроби являются важным промежуточным шагом. То есть, как только дробь может быть преобразована в десятичную форму, ее можно легко преобразовать в проценты, умножив на .

То есть сектор составляет весь круг.

Сообщить об ошибке

В окружности центральный угол и вписанный угол пересекают малую дугу. Если , то какова мера ?

Возможные ответы:

Правильный ответ:

Пояснение:

Центральный угол и дуга, на которую он опирается, всегда имеют один и тот же угол, а вписанный угол всегда имеет угол, равный половине дуги, на которую он опирается. Таким образом, если измеряется центральный угол, то должен быть измерен и соответствующий вписанный угол.

Следовательно, 

Сообщить об ошибке

← Предыдущая 1 2 3 Следующая →

Уведомление об авторских правах

Все математические ресурсы ACT

14 Диагностические тесты 767 практических тестов Вопрос дня Карточки Learn by Concept.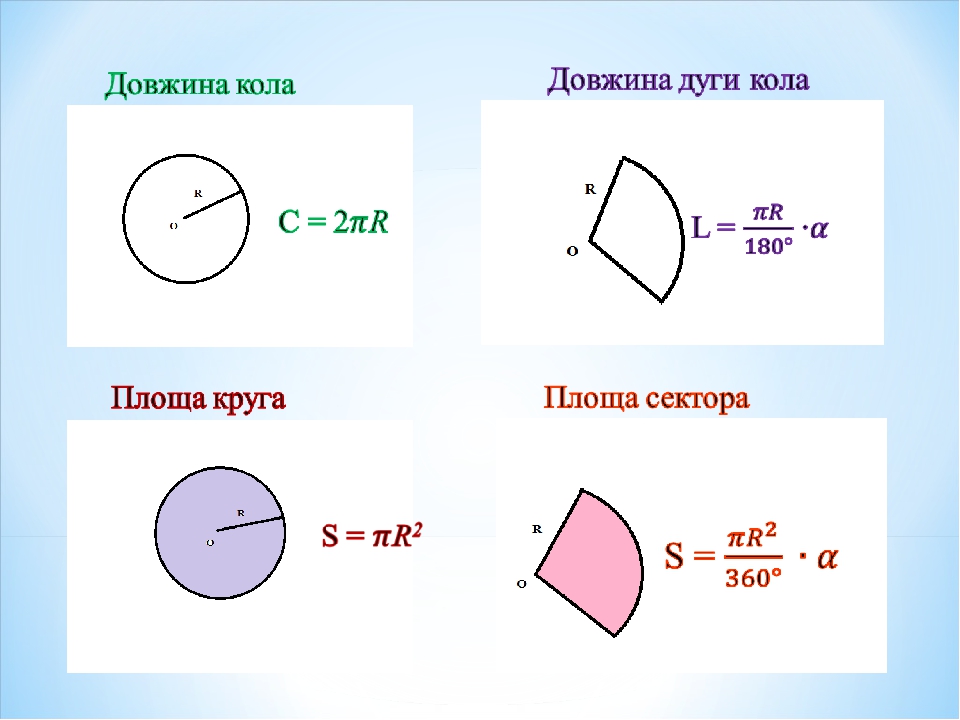 0003 Содержание:

• Что такое сектор круга? Определение сектора
• Формула площади сектора
• Особые случаи: площадь полукруга, площадь квадранта
• Калькулятор площади сектора – когда он может быть полезен?

С помощью этого калькулятора площади сектора вы быстро найдете площадь любого сектора круга, например, площадь полукруга или квадранта. В этой короткой статье мы:

• дадим определение сектора и объясним, что такое сектор круга.
• покажите формулу площади сектора и объясните, как самостоятельно вывести уравнение без особых усилий.
• показывают несколько реальных примеров, где может пригодиться калькулятор площади сектора.

Что такое сектор круга? Определение сектора

Итак, давайте начнем с определения сектора — что такое сектор в геометрии?

Сектор представляет собой геометрическую фигуру, ограниченную двумя радиусами и дугой окружности

Секторы окружности чаще всего визуализируются на круговых диаграммах, где окружность делится на несколько секторов, чтобы показать вес каждого сегмента . На рисунках ниже показано несколько примеров секторов круга — это не обязательно означает, что они будут выглядеть как кусок пирога, иногда он выглядит как остальная часть пирога после того, как вы взяли кусочек:

Очень редко можно услышать о секторе эллипса, но формулы way , way более сложны в использовании, чем уравнения площади сектора круга.

Формула площади сектора

Формула площади сектора проста – умножьте центральный угол на квадрат радиуса и разделите на 2:

• Площадь сектора = r² × α / 2

Но откуда он взялся? Вы можете найти его, используя пропорции, все, что вам нужно запомнить, это формулу площади круга (и мы держим пари, что вы знаете!):

1. Площадь круга рассчитывается как A = πr² . Это отличная отправная точка.
2. Полный угол равен 2π в радианах или 360° в градусах, последнее из которых является более распространенной единицей измерения угла.
3. Затем мы хотим вычислить площадь части круга, выраженную центральным углом.

• Для углов 2π (полный круг) площадь равна πr²: 2π → πr²
• Итак, какова площадь сектора круга: α → Площадь сектора

4. Из пропорции мы можем легко найти конечную формулу площади сектора:

Площадь сектора = α × πr² / 2π = α × r² / 2

Тот же метод можно использовать для определения длины дуги — все, что вам нужно запомнить, это формулу для длины окружности.

💡 Обратите внимание, что α должно быть в радианах при использовании данной формулы. Если вы знаете центральный угол вашего сектора в градусов , сначала умножьте его на π/180° , чтобы найти его эквивалентное значение в радианах. Или вместо этого вы можете использовать эту формулу, где θ — центральный угол в градусах :

Площадь сектора = r² × θ × π / 360

Особые случаи: площадь полукруга, площадь квадранта

Найти площадь полукруга или квадранта теперь несложно, только подумайте, какой частью круга они являются!

1. Площадь полукруга: πr² / 2

• Зная, что это половина круга, разделить площадь на 2:

  Площадь полукруга = Площадь круга / 2 = πr² / 2

• Конечно, вы получите тот же результат, используя формулу площади сектора. Просто помните, что прямой угол равен π (180°):

  .

  Площадь полукруга = α × r² / 2 = πr² / 2

2. Площадь квадранта: πr² / 4

• Поскольку квадрант является четвертью круга, мы можем записать формулу как:

  Площадь квадранта = Площадь круга / 4 = πr² / 4

• Центральный угол квадранта

  — прямой угол (π/2 или 90°), так что вы быстро придёте к тому же уравнению:

  Площадь квадранта = α × r² / 2 = πr² / 4

Калькулятор площади сектора – когда он может быть полезен?

Мы знаем, мы знаем: » зачем нам это учить, мы никогда этим не воспользуемся «. Мы хотели бы показать вам, что геометрия окружает нас повсюду:

• Если вам интересно, какой большой торт вы должны заказать на свой потрясающий день рождения — бинго, вот и все! Используйте формулу площади сектора для оценки размером с кусочек 🍰 для ваших гостей, чтобы никто не умер с голоду.

  No related posts.