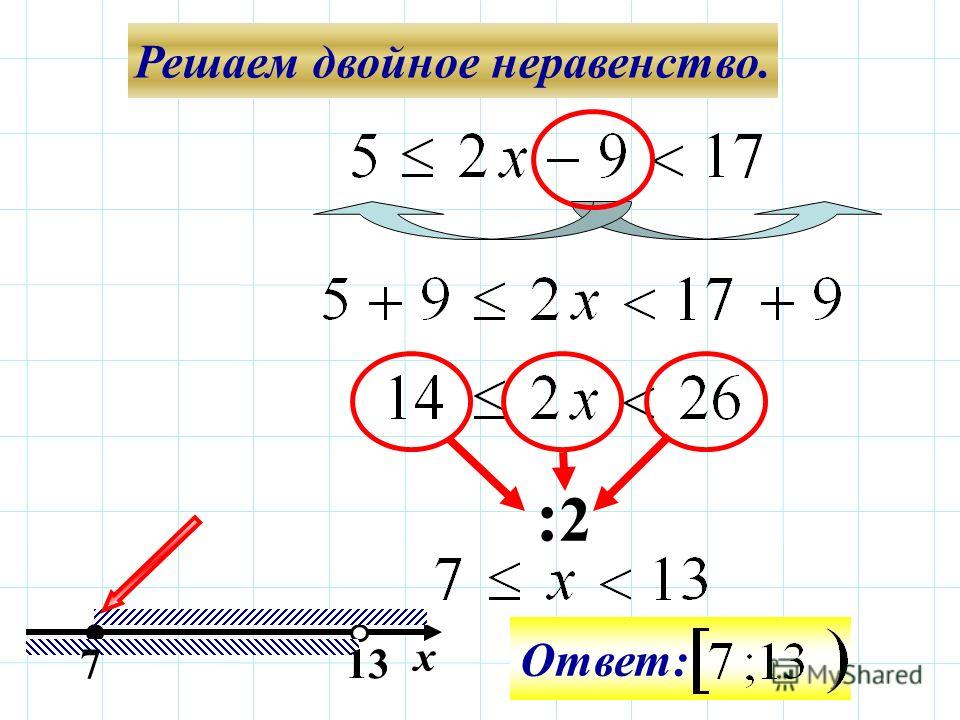
Решаем двойные неравенства. Макарычев 8 класс алгебра №893 – Рамблер/класс
Решаем двойные неравенства. Макарычев 8 класс алгебра №893 – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Помоигте разобраться
893. Решите двойное неравенство и укажите три числа, являющие
ся его решениями:
ответы
Привет.
легко
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
ГДЗ
Психология
ЕГЭ
10 класс
похожие вопросы 5
§18. ИНЕРЦИЯ. Нужны ответы к вопросам. 7 класс физика Перышкин
1. В результате чего меняется скорость тела? Приведите примеры.
2. Какой опыт показывает, как изменяется скорость тела при (Подробнее…)
Физика7 классПерышкин А.В.Домашнее задание
150 Алгебра 9 класс Макарычев Помогите решить графически
Решите графически уравнение:
а) х3 = 2; б) х3 = 4; в) х3 = -5.
ЭкзаменыАлгебра9 классМакарычев Ю.Н.ГДЗ
Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308 Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее.
..)
ГДЗ11 классКолмогоров А.Н.Алгебра
Влияние воздуха на горение свечи. Химия. 8 класс. Габриелян. ГДЗ. Хим. практикум № 1. Практ. работа № 2. Опыт 3.
Попробуйте провести следующий опыт. Влияние воздуха на горение свечи.
Вставьте стеклянную трубку с оттянутым концом в резиновую (Подробнее…)
ГДЗШкола8 классХимияГабриелян О.С.
Приготовление раствора сахара и расчёт его массовой доли в растворе. Химия. 8 класс. Габриелян. ГДЗ. Хим. практикум № 1. Практ. работа № 5.
Попробуйте провести следующий опыт. Приготовление раствора
Отмерьте мерным (Подробнее…)
ГДЗШкола8 классХимияГабриелян О.С.
Как записать двойное неравенство в excel
Как записать функцию ЕСЛИ с двумя знаками неравенства
Добрый день! ) Как записать функцию ЕСЛИ с двумя знаками неравенства?
Смысл такой: если значение Z6 находится в интервале от 0 до 10 то функция равна 0,05; если значение Z6 находится в интервале от 10 до 50 то функция равна 0,2; если значение Z6 больше 50 то функция равна 0,4.
\sum.
Как подсчитать кол-во символов между двумя знаками?
В вообщем суть задания в том, чтобы посчитать кол-во символов между двумя знаками, может кто.
Двойные неравенства. 2 способа решения
Двойное неравенство по своей сути – это система из двух неравенств, записанных в одну строку. Поэтому их всегда можно представить в виде системы .
Но делать это нужно не всегда.
2 способа решения двойного неравенства
1) Если в крайней левой и крайней правой частях двойного неравенства нет неизвестных , то удобнее оставить его как есть. При этом в процессе решения стремится равносильными преобразованиями привести неравенство к виду \([число]\)\(<\)\(x\)\(<\)\([число]\).
Пример: Решите двойное неравенство:
Здесь нет неизвестных по краям, поэтому к системе переходить не будем. Вместо этого делаем такие преобразования, чтоб в центре остался голый икс, а по краям — числа.
Для того чтобы «оголить» икс нужно избавиться от пятерки и тройки.
Вычтем \(5\) из всего неравенства.
Теперь нам мешает \(3\). Поделим все три части неравенства на \(3\).
Готово, наш икс «голый». Можно записывать ответ.
2) Если в крайних частях двойного неравенства есть неизвестные лучше перевести неравенство в систему и решать его как обычную систему неравенств.
Пример: Решите двойное неравенство:
В крайней левой и крайней правой частях есть неизвестные –значит переходим к системе.
Решаем обычные линейные неравенства : все, что с иксами переносим в левую сторону, все что без иксов — в правую.
«Оголим» иксы, поделив верхнее неравенство на \((-1)\), нижнее на \((-5)\). Не забываем при этом перевернуть знаки сравнения, так как мы делим на отрицательное число.
Отметим на числовой оси оба решения
Так как у нас система, то мы ищем значения иксов, которые подойдут обоим неравенствам, т.е. интервал , где есть двойная штриховка: и сверху, и снизу. Его и запишем ответ.
Двойное неравенство.
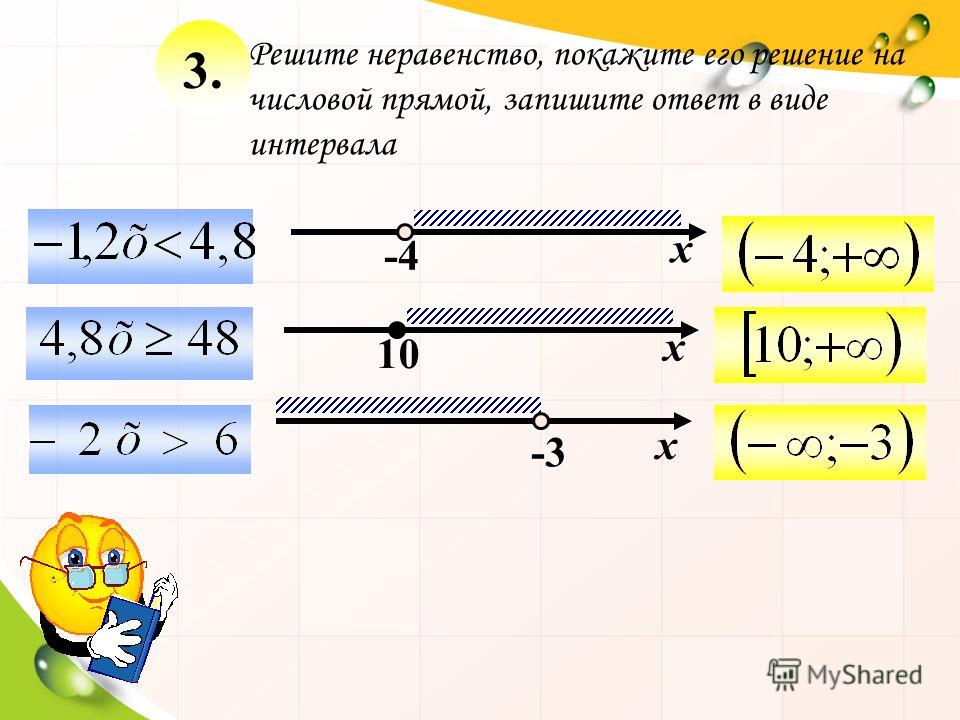
Давай повторим определения, которые ты уже знаешь и которые мы будем использовать на нашем уроке.
Число b больше числа a , если разность b — a является положительным числом. Число b меньше числа a , если разность b — a равна отрицательному числу.
Числовое неравенство – это неравенство, в записи которого по обе стороны от знака неравенства находятся числа или числовые выражения.
Если к обеим частям неравенства прибавить одно и то же число, то неравенство не изменит свой знак.
Теперь установи соответствие между картинками и определениями, которые мы только что повторили.
Прежде чем начнем основную часть урока, перечислю для тебя определения, с которыми мы познакомимся сегодня:
Для продолжения урока кликните на кнопку ниже:
Отзывы:
спасибо за урок! всё понравилось!
УЧИТЕЛЬ ОЧЕНЬ ХОРОШИЙ. РЕКОМЕНДУЮ.
Александр Дмитриевич — прекрасный учитель, что помог мне понять и познать математику лучше.
С каждым уроком я совершенствую свои знания и, сравнивая их до занятий с преподавателем, ощущаю видимый прогресс. Рада, что мне довелось заниматься с таким профессиональным человеком, который действительно смог заинтересовать меня данной наукой.
Двойные неравенства и их решение
Двойным неравенством называется неравенство вида , где — некоторая функция, — числа (знаки неравенства могут быть и строгие).
Чтобы решить двойное неравенство, записывают систему неравенств . Далее решают каждое неравенство системы и находят их общее решение (пересекают).
Примеры решения двойных неравенств
| Задание | Найти решение неравенства |
| Решение | Запишем равносильную систему неравенств |
и эквивалентные ей системы
Решением данной системы будет промежуток .
Это неравенство можно решить и другим способом. Сначала перенесем -7 с противоположным знаком в правую и левую части двойного неравенства и получим
Далее разделим все части неравенства на 2:
Таким образом, .
| Задание | Оценить выражение , если |
| Решение | Из условия известно, как изменяются переменные и . Умножим все части двойного неравенства с на 5, а с — на 7. Получим |
и .
Складываем почленно первое и второе неравенства:
Таким образом, выражение может принимать значения из промежутка .
Составные неравенства – объяснение и примеры
Составные неравенства являются производной формой неравенств, которые очень полезны в математике при работе с диапазоном возможных значений.
Например, после решения определенного линейного неравенства вы получаете два решения, x > 3 и x < 12. Вы можете прочитать это как «3 меньше x, что меньше 12. Теперь вы можете переписать это в виде 3 < x < 12. Вы можете прочитать это, поскольку x лежит между 3 и 12. Таким образом, составные неравенства — это профессиональный способ записи линейных неравенств (где это возможно).
Теперь посмотрим, что такое сложное неравенство.
Что такое сложное неравенство?
Существуют и другие случаи, когда можно использовать неравенство для представления более одного ограничивающего значения. В таких случаях применяется составное неравенство.
Таким образом, мы можем определить составное неравенство как выражение, содержащее два оператора неравенства, соединенные либо словами « И », либо словами « ИЛИ». »
Союз « And » указывает на то, что два утверждения верны одновременно.
С другой стороны, слово « или » подразумевает, что все составное утверждение истинно, пока истинно одно из утверждений.
Термин «ИЛИ» используется для обозначения комбинации наборов решений для отдельных операторов.
Как решать сложные неравенства?
Решение сложных неравенств зависит от того, используются ли слова «и» или «или» для соединения отдельных утверждений.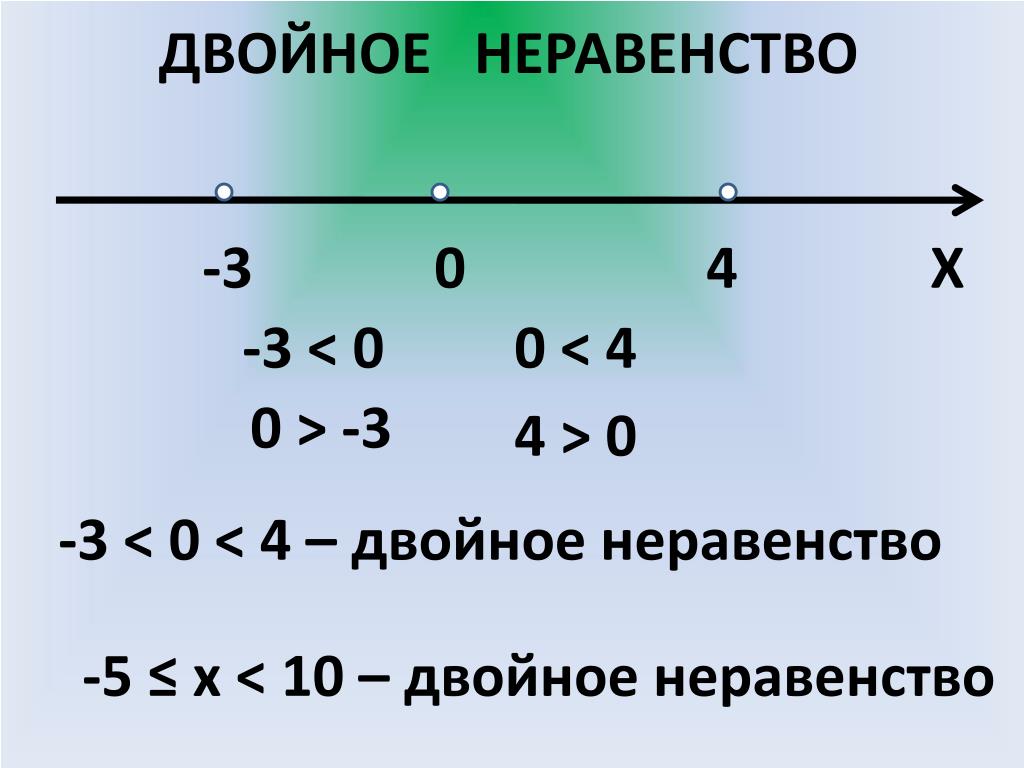
Пример 1
Найдите x: 3 x + 2 < 14 и 2 x – 5 > –11.
Решение
Чтобы решить это составное неравенство, мы начнем с решения каждого уравнения по отдельности. А так как присоединяющее слово «и», то это означает, что искомое решение — это перекрытие или пересечение.
3x + 2 < 14
Вычтите 2 и разделите на 3 обе части уравнения.
3х + 2 – 2 < 14 -2
3х/3 < 12/3
х < 4 А; 2x – 5 > -11
Прибавьте 5 к обеим сторонам и разделите все на 2
2x – 5 + 5 > -11 + 5
2x >
-6x > -3
Неравенство x < 4 указывает на все числа слева от 4, а x > –3 указывает на все числа справа от –3. Таким образом, пересечение этих двух неравенств включает все числа от –3 до 4. Следовательно, решение для этих составных неравенств: x > –3 и x < 4
Пример 2
Решите 2 + x < 5 и -1 < 2 + x
Решение
Решите каждое неравенство отдельно.
2 + x < 5
Чтобы выделить переменную из первого уравнения, нам нужно вычесть обе части на 2, что дает;
x < 3.
Снова вычтем 2 из обеих частей второго уравнения -1 < 2 + x.
-3 < х.
Таким образом, решение этого сложного неравенства: x < 3 и -3 < x, или -3 < x < 3,
Пример 3
Решение 7> 2x+ 5 или 7 <5x - 3.
Решение
Решаем каждую неравенство:
Для 7> 2x+ 5, мы подчеркиваем обе стороны. получить;
2 > 2x.
Теперь разделите обе стороны на 2, чтобы получить;
1 > х.
Для 7 < 5x – 3 прибавьте обе стороны по 3, чтобы получить;
10 < 5x.
Разделение каждой стороны на 5 дает;
2 < х.
Решение: x < 1 или x > 2
Пример 4
Решить 3(2x+5) ≤18 и 2(x−7) <− 6 отдельно
3(2x + 5) ≤ 18 => 6x + 15 ≤ 18
6x ≤ 3
x ≤ ½
А
2(x−7) <− 6 => 2x −14<−6
2x < 8
x < 4
Таким образом, решение: x ≤ ½ и x < 4
Пример 5
Решите: 5 + x > 7 или x – 3 < 5
Решение
Решите каждое неравенство отдельно и объедините решения.
Для 5 + х > 7;
Вычтите обе стороны на 5, чтобы получить;
x > 2
Решите x – 3 < 5;
Добавьте 3 к обеим частям неравенства, чтобы получить;
x < 2 Объединение двух решений словом «или» дает; X > 2 или x < 2
Пример 6
Решите для x: –12 ≤ 2 x + 6 ≤ 8. ». Таким образом, мы можем перевести x – 12 ≤ 2 x + 6 ≤ 8 в следующее составное предложение:
–12 ≤ 2 x + 6 и 2 x + 6 ≤ 8.
Теперь мы можем решить каждое неравенство по отдельности.
Для –12 ≤ 2 x + 6;
=> –18 ≤ 2 x
–9 ≤ x
И для 2 x + 6 ≤ 8;
=> 2 x≤ 2
Неравенство –9 ≤ x означает, что все числа справа от –9 включительно и находятся в решении, а x ≤ 1 означает, что все числа слева от 1 включительно находятся внутри решения. Таким образом, решение этого сложного неравенства можно записать в виде {x| x ≥ –9 и x ≤ 1} или {x| –9 ≤ x ≤ 1}
Пример 7
Найти x: 3x – 2 > –8 или 2 x + 1 < 9.
Решение
Для 3x – 2 > –8;
=> 3x – 2 + 2 > –8 + 2
=> 3x > – 6
=> x > – 2
Для 2 x + 1 < 9; Вычтите 1 из обеих частей уравнения; => 2 x < 8. => x < 4. Неравенство x > –2 означает, что решение верно для всех чисел справа от –2, а x < 4 означает, что решение верно для всех чисел справа от –2. числа слева от 4. Решение записывается как;
{х| x < 4 или x > – 2}
Составные неравенства
Составное неравенство — это предложение с двумя утверждениями о неравенстве, соединенными либо словом «или», либо словом «и». «И» указывает на то, что оба утверждения сложного предложения верны одновременно. Это перекрытие или пересечение наборов решений для отдельных утверждений. «Или» указывает на то, что, пока одно из утверждений истинно, все составное предложение истинно. Это комбинация или объединение наборов решений для отдельных утверждений. Составное неравенство, в котором используется слово «и», известно как 9.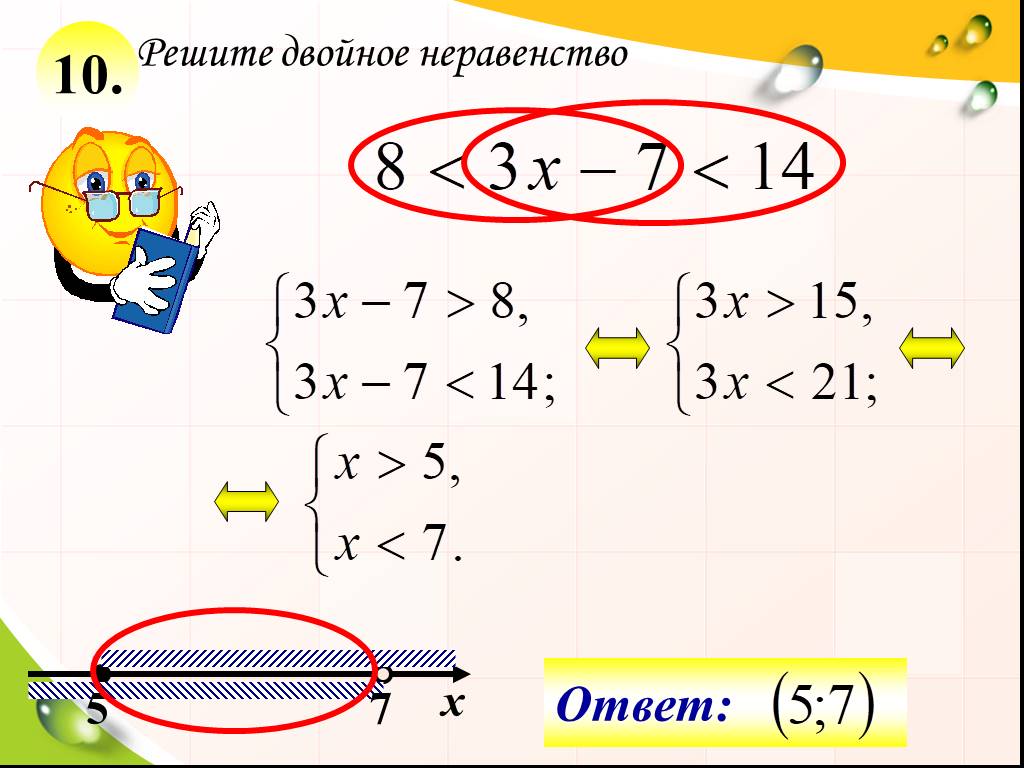
Пример 1
Решить для x : 3 x + 2 < 14 и 2 х – 5 > –11.
Решите каждое неравенство отдельно. Поскольку объединяющее слово «и», это указывает на то, что желаемым результатом является наложение или пересечение.
x < 4 указывает на все числа слева от 4, а
{ х | x > –3 и x < 4}
Другой способ выражения этого набора решений:
{ x |–3 < x < 4}
Когда сложное неравенство пишется без выраженного слова «и» или «или», оно автоматически понимается как слово «и».
Читая { x |–3 < x < 4} с позиции « x », вы говорите (читая влево), « x больше –3 и (читая вправо) х меньше 4». Граф набора решений показан на рисунке 1.
Рисунок 1. x больше –3 и меньше 4.
Пример 2
Решите для x : 2 x + 7 < –11 или –3 x – 2 < 13.
Решите каждое неравенство отдельно. Так как присоединяющее слово «или», объедините ответы; то есть найдите объединение множеств решений каждого предложения неравенства.
Не забудьте, как и в последнем шаге справа, переключать неравенство при умножении на минус.
x < –9 указывает на все числа слева от –9, а x > –5 указывает на все числа справа от –5. Набор решений записывается как
.{ х | x < –9 или x > –5}
Граф этого набора решений показан на рисунке 2.
Рисунок 2. x меньше –9или больше –5.
Пример 3
Решите для x : –12 ≤ 2 x + 6 ≤ 8.
Поскольку в этом составном неравенстве нет написанного связующего слова, оно понимается как «и». Оно переводится в следующее составное предложение.
–9 ≤ x указывает на все числа справа от –9 включительно, а
{ х | x ≥ –9 и x ≤ 1} или { x |–9 ≤ x ≤ 1}
Граф набора решений показан на рисунке 3.
Рисунок 3. Точки указывают на включение точек.
Пример 4
Решите для x : 3 x – 2 > –8 или 2 x + 1 < 9.
х > –2 указывает на все числа справа от –2, а x < 4 указывает на все числа слева от 4. Объединение этих графиков представляет собой всю числовую прямую. То есть множество решений состоит из всех действительных чисел. График множества решений представляет собой всю числовую прямую (см.