Что такое теория игр. Объясняем простыми словами — Секрет фирмы
Проще говоря, это что-то вроде науки о взаимодействии людей, которая пытается объяснить этот процесс как игру с набором определённых вариантов ходов для каждой стороны. Выбор каждого из участников влияет на других участников и на исход игры в целом. Ключевая цель — научиться разрабатывать выигрышные стратегии.
Обычно человек прорабатывает собственные шаги по достижению своих целей. А теория игр учитывает шаги конкурентов, их цели и возможные методы взаимо- и противодействия. Она позволяет определить, как конкуренты могут прийти к оптимальному решению, что им может помешать и какие стратегии лучше применять в том или ином случае.
В качестве участников (игроков) могут рассматриваться игроки в покер, менеджеры конкурирующих корпораций, старающихся расширить свою долю на рынке, организаторы рекламных или предвыборных кампаний, генералы враждующих армий и т. п.
Изначально теорию игр использовали для моделирования экономических ситуаций, но постепенно её начали применять в политике, биологии, сфере высоких технологий и т.
д.
Пример употребления на «Секрете»
«Нужно заложить хорошую базу, чтобы потом было легче. Математика и математические модели сейчас лежат в основе любого ИИ. Алгебра и начала математического анализа, теория вероятностей, мат. статистика, линейная алгебра, теория принятия решений и теория игр — это основные дисциплины, знание которых может очень пригодиться».
(Методист GeekSchool Игорь Гутовский — о знаниях, которые будут полезны желающим стать специалистами по искусственному интеллекту).
История
Основоположник теории игр — венгро-американский математик Джон фон Нейман. Датой появления теории считается 1944 год, когда Нейман в соавторстве с экономистом Оскаром Моргенштерном выпустил книгу «Теория игр и экономическое поведение».
В своих работах Нейман рассматривал «игры с нулевой суммой» — ситуации, когда игроки-конкуренты не могут сотрудничать, так как в итоге победитель получает ровно столько же, сколько теряют все остальные.
Общая сумма проигрышей и выигрышей равна нулю.
Простейший пример такой ситуации — покер или другие азартные игры, когда победитель забирает ставки других игроков. Торговля фьючерсами и опционами — также пример такой игры.
Дополнил и значительно развил теорию будущий нобелевский лауреат Джон Нэш. Он доказал, что существует множество ситуаций, когда общая сумма выигрышей и проигрышей далека от нуля. Она может быть как выше (в выигрыше большинство), так и ниже (проиграли все).
Так, Нэш объяснил, почему Адам Смит ошибался, считая конкуренцию лучшим двигателем рынка. Он доказал, что стратегия «каждый в группе делает то, что лучше для него» в итоге приводит к победе максимум одного участника группы. При этом может случиться так, что не победит никто. А если все участники договорятся о сотрудничестве и наметят свои цели (будут делать то, что лучше для них и для группы), у них есть возможность добиться общего успеха. Это хорошо показано в фильме «Игры разума».
Он же разработал концепцию «равновесия Нэша» — ситуацию устойчивого состояния в игре, когда ни один из игроков не может изменить поведение, чтобы увеличить свой выигрыш, если другие его не поддержат.
Нюансы
Основные элементы теории игр: Игра — реализация одного из сценариев от начала до конца. Игроки — конкурирующие стороны, принимающие участие в игре. Это не обязательно один человек, игроком может быть несколько людей с общими целями, компания или даже целая страна. Ход — одно из предусмотренных игрой действий. Стратегия — правила, по которым каждый из игроков выбирает свои ходы. Исход* — итог игры.
Один из самых известных примеров игры — дилемма заключённого. Но существуют и другие варианты, которые часто применяют для анализа различных экономических процессов.
Например, «Задача о сделках» — процесс переговоров о разделе имущества, в котором каждый получит долю, только если переговоры окажутся успешными.
«Охота на оленя» — ситуация, когда можно достичь либо общего блага (сообща поймать оленя), либо личного, но ценой блага других (поймать зайца, пока все стоят и ловят оленя).
Многие экономические модели также принято рассматривать с точки зрения теории игр. Например, модели существования дуополии и олигополии.
Критика
У теории игр есть существенный недостаток — считается, что каждый из участников игры ведёт себя рационально. В реальности игроки могут совершать импульсивные и совершенно невыгодные для себя поступки.
Статью проверила:
5 простых примеров популярных игровых стратегий
Теория игр занимается тем, что изучает способы сделать лучший ход и в результате получить как можно больший кусок выигрышного пирога, оттяпав часть его у других игроков. Она учит подвергать анализу множество факторов и делать логически взвешенные выводы. Я считаю, её нужно изучать после цифр и до алфавита. Просто потому что слишком многие люди принимают важные решения, основываясь на интуиции, тайных пророчествах, расположении звёзд и других подобных. Я тщательно изучил теорию игр, и теперь хочу рассказать вам о её основах.
Возможно, это добавит здравого смысла в вашу жизнь.
1. Дилемма заключенного
Берто и Роберт были арестованы за ограбление банка, не сумев правильно использовать для побега угнанный автомобиль. Полиция не может доказать, что именно они ограбили банк, но поймала их с поличным в украденном автомобиле. Их развели по разным комнатам и каждому предложили сделку: сдать сообщника и отправить его за решетку на 10 лет, а самому выйти на свободу. Но если они оба сдадут друг друга, то каждый получит по 7 лет. Если же никто ничего не скажет, то оба сядут на 2 года только за угон автомобиля.
Получается, что, если Берто молчит, но Роберт сдает его, Берто садится в тюрьму на 10 лет, а Роберт выходит на свободу.Каждый заключенный — игрок, и выгода каждого может быть представлена в виде «формулы» (что получат они оба, что получит другой). Например, если я ударю тебя, моя выигрышная схема будет выглядеть так (я получаю грубую победу, ты страдаешь от сильной боли). Поскольку у каждого заключенного есть два варианта, мы можем представить результаты в таблице.
Здесь мы видим основное применение теории игр: выявление социопатов, думающих лишь о себе. Настоящая теория игр — это мощный аналитический инструмент, а дилетантство часто служит красным флагом, с головой выдающим человека, лишенного понятия чести. Люди, делающие расчеты интуитивно, считают, что лучше поступить некрасиво, потому что это приведет к более короткому тюремному сроку независимо от того, как поступит другой игрок. Технически это правильно, но только если вы недальновидный человек, ставящий цифры выше человеческих жизней. Именно поэтому теория игра так популярна в сфере финансов.
Настоящая проблема дилеммы заключенного в том, что она игнорирует данные.Например, в ней не рассматривается возможность вашей встречи с друзьями, родственниками, или даже кредиторами человека, которого вы посадили в тюрьму на 10 лет.
Хуже всего то, что все участники дилеммы заключенного действуют так, как будто никогда не слышали ней.
А лучший ход — хранить молчание, и через два года вместе с хорошим другом пользоваться общими деньгами.
2. Доминирующая стратегия
Это ситуация, при которой ваши действия дают наибольший выигрыш, независимо от действий оппонента. Что бы ни происходило — вы всё сделали правильно. Вот почему многие люди при «дилемме заключенного» считают: предательство приводит к «наилучшему» результату независимо от того, что делает другой человек, а игнорирование действительности, свойственное этому методу, заставляет всё выглядеть супер-просто.
Большинство игр, в которые мы играем, не имеет строго доминирующих стратегий, потому что иначе они были бы просто ужасны. Представьте, что вы всегда делали бы одно и то же. В игре «камень-ножницы-бумага» нет никакой доминирующей стратегии.Но если бы вы играли с человеком, у которого на руках надеты прихватки, и он мог показать только камень или бумагу, у вас была бы доминирующая стратегия: бумага. Ваша бумага обернет его камень или приведет к ничьей, и вы не сможете проиграть, потому что соперник не может показать ножницы.
Теперь, когда у вас есть доминирующая стратегия, нужно быть дураком, чтобы попробовать что-нибудь другое.
3. Битва полов
Игры интереснее, когда у них нет строго доминирующей стратегии. Например, битва полов. Анджали и Борислав идут на свидание, но не могут выбрать между балетом и боксом. Анджали любит бокс, потому что ей нравится, когда льется кровь на радость орущей толпе зрителей, считающих себя цивилизованными только потому, что они заплатили за чьи-то разбитые головы.
Борислав хочет смотреть балет, потому что он понимает, что балерины проходят через огромное количество травм и сложнейших тренировок, зная, что одна травма может положить конец всему. Артисты балета — величайшие спортсмены на Земле. Балерина может ударить вас ногой в голову, но никогда этого не сделает, потому что ее нога стоит гораздо дороже вашего лица.
Каждый из них хочет пойти на своё любимое мероприятие, но они не хотят наслаждаться им в одиночестве, таким образом, получаем схему их выигрыша: наибольшее значение — делать то, что им нравится, наименьшее значение — просто быть с другим человеком, и ноль — быть в одиночестве.
Некоторые люди предлагают упрямо балансировать на грани войны: если вы, несмотря ни на что, делаете то, что хотите, другой человек должен подстроиться под ваш выбор или потерять все. Как я уже говорил, упрощённая теория игр отлично выявляет глупцов.
Практическое применение: Избегайте острых углов
Конечно, и у этой стратегии есть свои значительные недостатки. Прежде всего, если вы относитесь к вашим свиданиям как к «битве полов», она не сработает. Расстаньтесь, чтобы каждый из вас мог найти человека, который ему понравится. А вторая проблема заключается в том, что в этой ситуации участники настолько не уверены в себе, что не могут этого сделать.
По-настоящему выигрышная стратегия для каждого — делать то, что они хотят,а после, или на следующий день, когда они будут свободны, пойти вместе в кафе. Или же чередовать бокс и балет, пока в мире развлечений не произойдет революция и не будет изобретен боксерский балет.
4. Равновесие Нэша
Равновесие Нэша — это набор ходов, где никто не хочет сделать что-то по-другому после свершившегося факта.
И если мы сможем заставить это работать, теория игр заменит всю философскую, религиозную, и финансовую систему на планете, потому что «желание не прогореть» стало для человечества более мощной движущей силой, чем огонь.
Давайте быстро поделим 100$. Вы и я решаем, сколько из сотни мы требуем и одновременно озвучиваем суммы. Если наша общая сумма меньше ста, каждый получает то, что хотел. Если общее количество больше ста, тот, кто попросил наименьшее количество, получает желаемую сумму, а более жадный человек получает то, что осталось. Если мы просим одинаковую сумму, каждый получает 50 $. Сколько вы попросите? Как вы разделите деньги? Существует единственный выигрышный ход.
Требование 51 $ даст вам максимальную сумму независимо от того, что выберет ваш противник. Если он попросит больше, вы получите 51 $. Если он попросит 50 $ или 51 $, вы получите 50 $. И если он попросит меньше 50 $, вы получите 51 $. В любом случае нет никакого другого варианта, который принесет вам больше денег, чем этот.
Равновесие Нэша — ситуация, в которой мы оба выбираем 51 $.
Практическое применение: сначала думайте
В этом вся суть теории игр. Не обязательно выиграть и тем более навредить другим игрокам, но обязательно сделать лучший для себя ход, независимо от того, что подготовят для вас окружающие. И даже лучше, если этот ход будет выгоден и для других игроков. Это своего рода математика, которая могла бы изменить общество.
Интересный вариант этой идеи — распитие спиртного, которое можно назвать Равновесием Нэша с временной зависимостью. Когда вы достаточно много пьете, то не заботитесь о поступках других людей независимо от того, что они делают, но на следующий день вы очень жалеете, что не поступили иначе.
5. Игра в орлянку
В орлянке участвуют Игрок 1 и Игрок 2. Каждый игрок одновременно выбирает орла или решку. Если они угадывают, Игрок 1 получает пенс Игрока 2. Если же нет — Игрок 2 получает монету Игрока 1.
Выигрышная матрица проста…
…оптимальная стратегия: играйте полностью наугад.
Это сложнее, чем вы думаете, потому что выбор должен быть абсолютно случайным. Если у вас есть предпочтения орла или решки, противник может использовать его, чтобы забрать ваши деньги.
Конечно, настоящая проблема здесь заключается в том, что было бы намного лучше, если бы они просто бросали один пенс друг в друга. В результате их прибыль была бы такой же, а полученная травма могла бы помочь этим несчастным людям почувствовать что-то, кроме ужасной скуки. Ведь это худшая игра из существующих когда-либо. И это идеальная модель для серии пенальти.
Практическое применение: Пенальти
В футболе, хоккее и многих других играх, дополнительное время — это серия пенальти. И они были бы интереснее, если бы строились на том, сколько раз игроки в полной форме смогут сделать «колесо», потому что это, по крайней мере, было бы показателем их физических способностей и на это было бы забавно посмотреть. Вратари не могут чётко определить движение мяча или шайбы в самом начале их движения, потому что, к огромному сожалению, в наших спортивных состязаниях роботы все еще не участвуют.
Вратарь должен выбрать левое или правое направление и надеяться, что его выбор совпадет с выбором противника, бьющего по воротам. В этом есть что-то общее с игрой в монетку.
Однако обратите внимание, что это не идеальный пример сходства с игрой в орла и решку, потому что даже при правильном выборе направления вратарь может не поймать мяч, а нападающий может не попасть по воротам.
Итак, каково же наше заключение согласно теории игр? Игры с мячом должны заканчиваться способом «мультимяча», где каждую минуту игрокам один на один выводится дополнительный мяч/шайба, до получения одной из сторон определенного результата, который был показателем настоящего мастерства игроков, а не эффектным случайным совпадением.
В конце концов, теория игр должна использоваться для того, чтобы сделать игру умнее. А значит лучше.
Теория игр | Определение, факты и примеры
Матрица выплат с седловой точкой
Просмотреть все СМИ
- Ключевые люди:
- Джон фон Нейман
Уильям Райкер
Томас С.
Шеллинг
Джон Нэш
Ллойд Шепли
Шеллинг
Джон Нэш
Ллойд Шепли- Похожие темы:
- поощрительная совместимость игра с положительной суммой Дилемма заключенного риск игра с постоянной суммой
Просмотреть весь соответствующий контент →
Резюме
Прочтите краткий обзор этой темы
теория игр , раздел прикладной математики, предоставляющий инструменты для анализа ситуаций, в которых стороны, называемые игроками, принимают взаимозависимые решения. Эта взаимозависимость заставляет каждого игрока учитывать возможные решения или стратегии другого игрока при формулировании стратегии. Решение игры описывает оптимальные решения игроков, у которых могут быть схожие, противоположные или смешанные интересы, а также результаты, которые могут возникнуть в результате этих решений.
Хотя теория игр может использоваться и использовалась для анализа салонных игр, ее приложения гораздо шире.
На самом деле теория игр изначально была разработана американским математиком венгерского происхождения Джоном фон Нейманом и его коллегой из Принстонского университета Оскаром Моргенштерном, американским экономистом немецкого происхождения, для решения экономических проблем. В своей книге The Theory of Games and Economic Behavior
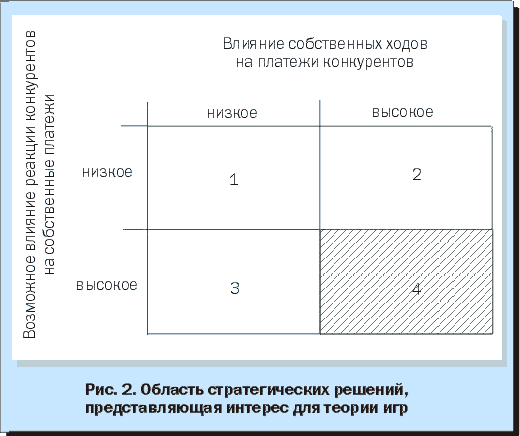)Теория игр применялась к широкому кругу ситуаций, в которых взаимодействует выбор игроков повлиять на результат. Подчеркивая стратегические аспекты принятия решений или аспекты, контролируемые игроками, а не чистой случайностью, теория одновременно дополняет и выходит за рамки классической теории вероятности. Он использовался, например, для определения того, какие политические коалиции или бизнес-конгломераты могут сформироваться, оптимальной цены, по которой можно продавать товары или услуги в условиях конкуренции, власти избирателя или блока избирателей, кого выбирать. выбрать для жюри лучшее место для производственного предприятия и поведение определенных животных и растений в их борьбе за выживание. Его даже использовали для оспаривания законности некоторых систем голосования.
Было бы удивительно, если бы какая-то одна теория могла охватить такое огромное количество «игр», а на самом деле единой теории игр не существует. Было предложено несколько теорий, каждая из которых применима к разным ситуациям и имеет свои собственные представления о том, что представляет собой решение.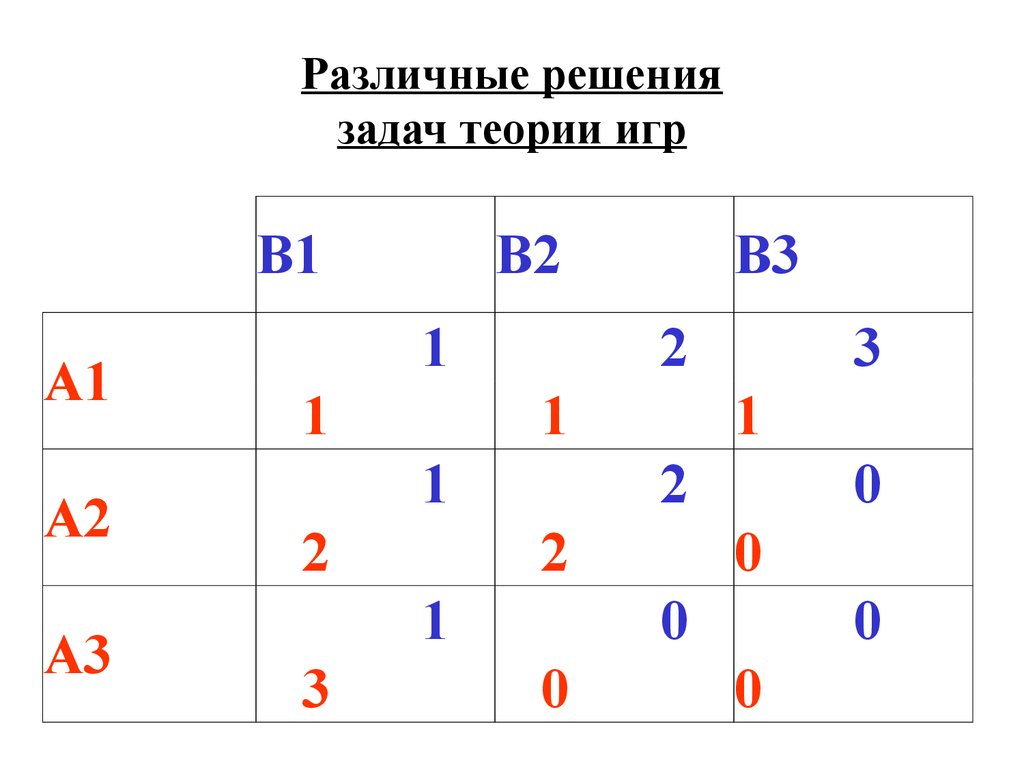
Классификация игр
Игры можно классифицировать по определенным существенным признакам, наиболее очевидным из которых является количество игроков. Таким образом, игру можно обозначить как игру для одного человека, для двух человек или n -игру (где n больше двух) с играми в каждой категории, имеющими свои отличительные черты. Кроме того, игроку не обязательно быть физическим лицом; это может быть нация, корпорация или команда, состоящая из многих людей с общими интересами.
В играх с полной информацией, таких как шахматы, каждый игрок всегда знает об игре все. Покер, с другой стороны, является примером игры с неполной информацией, поскольку игроки не знают всех карт своих противников.
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подписаться сейчас
Степень, в которой цели игроков совпадают или противоречат друг другу, является еще одним основанием для классификации игр. Игры с постоянной суммой — это игры тотального конфликта, которые также называют играми чистой конкуренции. Покер, например, является игрой с постоянной суммой, потому что совокупное богатство игроков остается постоянным, хотя его распределение меняется в ходе игры.
Игроки в играх с постоянной суммой имеют совершенно противоположные интересы, тогда как в играх с переменной суммой все они могут быть как победителями, так и проигравшими. Например, в споре между работниками и администрацией две стороны, безусловно, имеют некоторые конфликтующие интересы, но обе стороны выиграют, если забастовку удастся предотвратить.
Игры с переменной суммой можно дополнительно разделить на кооперативные и некооперативные. В кооперативных играх игроки могут общаться и, самое главное, заключать обязывающие соглашения; в некооперативных играх игроки могут общаться, но они не могут заключать обязывающие соглашения, такие как контракт, имеющий юридическую силу.
Продавец автомобилей и потенциальный покупатель будут вовлечены в совместную игру, если они договорятся о цене и подпишут контракт. Однако торги, которые они предпринимают, чтобы достичь этой точки, будут несовместимыми. Точно так же, когда люди делают ставки на аукционе независимо друг от друга, они играют в некооперативную игру, даже если тот, кто предложил более высокую цену, соглашается завершить покупку.
Наконец, игра называется конечной, если у каждого игрока есть конечное число вариантов, число игроков конечно и игра не может продолжаться бесконечно. Шахматы, шашки, покер и большинство домашних игр ограничены. Бесконечные игры более тонкие и будут затронуты только в этой статье.
Игра может быть описана одним из трех способов: в экстенсивной, нормальной или характеристической форме. (Иногда эти формы комбинируются, как описано в разделе «Теория ходов».) Большинство салонных игр, которые развиваются шаг за шагом, по одному ходу за раз, можно смоделировать как игры в развернутой форме.
Игры расширенной формы можно описать «игровым деревом», в котором каждый ход является вершиной дерева, а каждая ветвь указывает на последовательный выбор игроков.
Обычная (стратегическая) форма в основном используется для описания игр для двух человек. В этой форме игра представлена матрицей выигрышей, в которой каждая строка описывает стратегию одного игрока, а каждый столбец описывает стратегию другого игрока. Запись матрицы на пересечении каждой строки и столбца дает результат выбора каждым игроком соответствующей стратегии. Выигрыши каждого игрока, связанные с этим результатом, являются основой для определения того, являются ли стратегии «равновесными» или стабильными.
Форма характеристической функции обычно используется для анализа игр с более чем двумя игроками. Он указывает минимальное значение, которое каждая коалиция игроков, включая коалиции с одним игроком, может гарантировать для себя, играя против коалиции, состоящей из всех остальных игроков.
Игры для одного человека
Игры для одного человека также известны как игры против природы.
В отсутствие противников игроку нужно только перечислить доступные варианты, а затем выбрать оптимальный результат. Когда дело касается случая, игра может показаться более сложной, но в принципе решение остается относительно простым. Например, человек, решающий, брать ли с собой зонт, взвешивает затраты и выгоды от его ношения или без него. Хотя этот человек может принять неправильное решение, сознательного противника не существует. То есть предполагается, что природа совершенно безразлична к решению игрока, а человек может основывать свое решение на простых вероятностях. Игры одного человека мало интересуют теоретиков игр.
5 примеров теории игр в реальной жизни — StudiousGuy
Когда мы слышим термин «игра», мы обычно начинаем думать о развлечениях или спорте. Но в разделе математики под названием «теория игр» слово «игра» имеет гораздо более широкое значение. Теория игр — это, по сути, изучение математических моделей и их взаимодействия с лицами, принимающими решения.
Теория игр включает в себя стратегическое мышление, при котором игроки принимают решения, рассматривая различные точки зрения и рассматривая точки зрения других игроков-участников; также путем анализа своих действий и реакций в конкретных ситуациях.
Индекс статьи (щелкните, чтобы перейти)
Значение Наилучшее использование теории игр состоит в том, чтобы найти оптимальное решение из наилучших возможных вариантов путем анализа затрат и выгод для каждого участника, который конкурирует с друг друга. Теория применима в различных областях, таких как бизнес, психология, биология, экономика, политология, компьютеры и т. д. Практическое значение теории заключается в ее использовании для поддержки в объяснении событий и ситуаций, которые произошли в прошлом, и для определения различные действия, которые игроки могут предпринять в будущем, и т. д. С точки зрения бизнеса теория игр может использоваться бизнес-менеджерами для прогнозирования стратегического планирования или мыслительного процесса их конкурентов и сотрудников.
Он считается очень мощным средством для прогнозирования или прогнозирования результатов взаимодействия между различными участниками или конкурентами, в которых реакция одного зависит от действия других.
Теория игр в основном состоит из трех компонентов:
- Игроки: Основной элемент теории игр включает набор игроков. Бизнес-менеджеры и компании рассматриваются как игроки.
- Стратегии: Различные стратегии, которые игроки могут использовать в игре. Это также включает в себя правила игры, которые установлены в иерархии, чтобы упомянуть расположение наилучших возможных стратегий и действий.
- Исходы или результаты: Сюда входят возможные стратегии и ожидаемые выплаты в соответствии с исходами. Предполагается, что все участники уже знают об этих выигрышах.
Существует два основных способа использования теории игр, т.
е. одновременные игры, в которых игроки выполняют свои ходы или действия одновременно, независимо от поиска информации, связанной с ходами или действиями, выбранными другими игроками. Другая представляет собой последовательную игру, которая включает в себя зависимость ходов или действий игрока от результатов предыдущего действия или выбора другого игрока.
Давайте рассмотрим несколько реальных примеров теории игр.
1. Торги на аукционе Аукцион считается продажей, в которой разные участники торгов делают ставки на покупку любого товара или услуги, и они продаются участнику, предложившему самую высокую цену. Теория игр используется на аукционах с ставками, особенно для анализа закрытых аукционных торгов по первой цене. В этом типе аукциона участники торгов должны подавать заявки безопасным и запечатанным способом. Разные игроки не знают о ценности товаров или услуг друг друга и пытаются разработать стратегию торгов, независимо от наличия полной информации.
Поведение участников торгов и различные другие факторы анализируются при принятии решений во время подготовки предложений.
Теория игр играет важную роль в различных коллективных переговорах или переговорах между различными сторонами или участниками. Например, различных переговоров между профсоюзами и руководством в ситуации забастовки рабочих или периода локаута для повышения заработной платы. Используя теорию игр, обе стороны могут прийти к оптимальному решению проблемы, т. е. повысить заработную плату, изучив различные доступные варианты заработной платы и пособий, которые могут максимизировать благосостояние как работников, так и руководства. Переговоры о зарплате также являются примером применения теории игр. Концепция теории игр используется в других переговорах, таких как переговоры с поставщиками при закупках, переговоры о компенсации или поощрении между руководством и поставщиками или деловыми партнерами и т.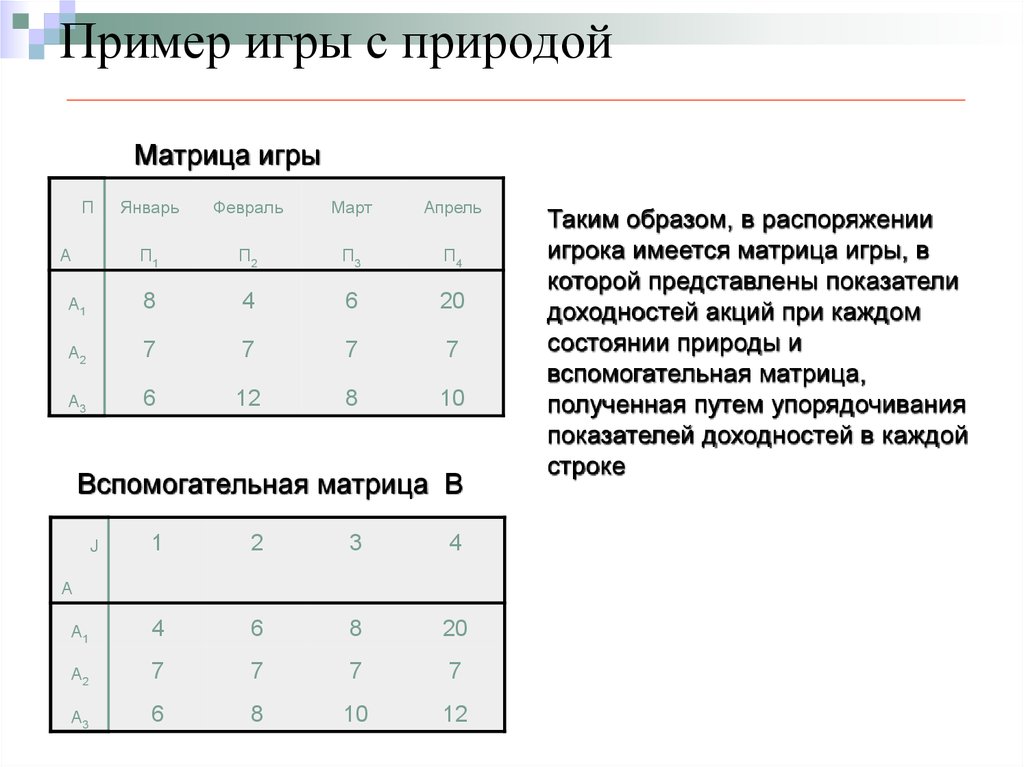
д.
Решения, связанные с запуском нового продукта на рынке или выходом из него, также принимаются предприятиями с использованием теории игр. Используя теорию игр, деловые люди могут понять, есть ли преимущество первопроходца или нет, возможные шаги конкурентов, связанные с новыми продуктами, а также принять решение о стратегиях защиты и т. д. Точно так же концепция теории игр также используется при принятии решений. выход на новый рынок или выход с него.
4. Решения о ценообразовании продуктов Применение теории игр также широко используется при принятии решений о ценовых стратегиях как потребителей, так и розничных продавцов. Розничные продавцы конкурируют друг с другом, чтобы завоевать долю покупателей на рынке, и для этого они выбирают различные игры или стратегии, такие как предложение привлекательных скидок на определенные товары, чтобы увеличить продажи дополнительных продуктов.
Например, в межсезонье, т. е. в межсезонье, т. е. в нелетний или межзимний сезон, продавцы магазинов одежды или розничные продавцы предлагают выгодные распродажи определенного запаса одежды, в которых они используют оптимальные стратегии ценообразования для привлечения максимального количества покупателей. При этом розничные продавцы используют подход теории игр, в котором розничные продавцы и потребители являются основными игроками. В центре внимания розничных продавцов находится использование наилучшей стратегии ценообразования, в то время как потребители предпочитают выбирать лучшее предложение с точки зрения скидки и разнообразия.
Используя теорию игр, решения о покупке и продаже акций на фондовом рынке могут приниматься с умом. Инвесторы принимают разные решения на фондовом рынке, используя разные стратегии инвестирования и рассматривая разных игроков или инвесторов. Теория игр помогает предсказать решения других игроков, связанные с инвестициями, и на основе этих решений они могут выбрать для себя стратегии, которые максимизируют прибыль.