Примеры как решить неравенство: Неравенства. Виды неравенств

Логарифмические неравенства от эксперта TutorOnline

​Математика полезна тем, что она трудна.

Основные понятия и свойства

Первоначально приведем основные свойства логарифмов, использование которых позволяет успешно решать относительно сложные логарифмические неравенства.

Основное логарифмическое тождество записывается в виде

                                               ,                                                     

где  ,    и  .

К числу наиболее известных свойств логарифмов относятся следующие равенства:

    1. Если , ,  и  , то   ,  ,

,  .

    2. Если , , ,  и  , то   .

    3. Если  , ,  и  , то   .

    4. Если   , ,  и  натуральное число,  то  

.

    5. Если  , , ,  и  , то  

.

    6.  Если  , ,  и  , то  

    7.

  Если  , , ,  и  , то  

.

    Применительно к решению логарифмических неравенств, необходимо напомнить, что функция является возрастающей, если , и убывающей, если . Из этого свойства функции вытекают следующие очень важные свойства логарифмических неравенств:

     8.  Если     и   , то  .

     9.  Если     и   , то  .

    10.  Если     и   , то  .

    11.  Если     и   , то  .

    Рассмотрим примеры задач на решение логарифмических неравенств, расположенных в порядке возрастания их сложности.

Примеры решения задач

 

Пример 1.   Решить неравенство

 

                                      .                                 (1)

 

Решение.  Областью допустимых значений переменной в неравенстве (1) являются  .

Так как (1) равносильно неравенству   и при этом основание логарифма  , то  ,    или  . Поскольку  , то    и из неравенства  следует, что    или  .

Ответ:  .

 

Пример 2.   Решить неравенство  

 

                                         .                                               (2)

 

Решение.  Из неравенства (2) следует, что . Кроме того, неравенство (2) равносильно неравенству  .    

Если обе части неравенства прологарифмировать по основанию , то получим . Так как , то в результате выполнения процедуры логарифмирования знак неравенства не меняется. Отсюда  следует: , или .

Ответ:  .

 

Пример 3

.   Решить неравенство

 

                                     .                                         (3)

 

Решение. Из неравенства (3) имеем .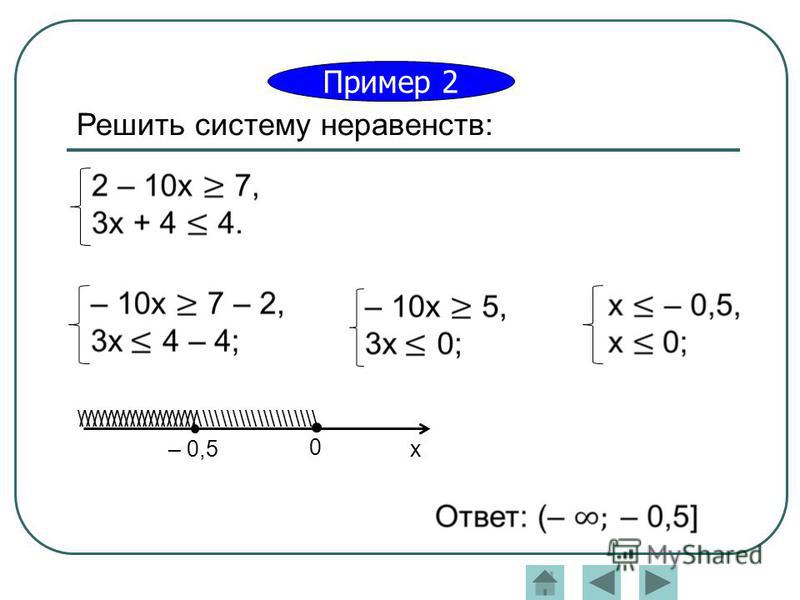 Преобразуем левую часть неравенства (3) следующим образом:

.

Отсюда и из неравенства (3) следует  . Полученное неравенство прологарифмируем по основанию и получим

,    или  .

Ответ:  .

 

Пример 4.   Решить неравенство  

 

                                       .                                   

    Решение.  Преобразуем данное неравенство на основе применения свойств 8 – 11 следующим образом:

,   ,

,    ,

  или    

    Ответ: .

 

Пример 5.   Решить неравенство  

 

                                       .                                   (4)

 

Решение. По аналогии с решением примера 4 преобразуем неравенство (4), используя при этом свойства логарифмических неравенств.

Имеет место цепочка равносильных неравенств

,   ,  

,       или   .

    Ответ:  .

 

Пример 6.   Решить неравенство  

 

 

                                       .                                      (5)

 

Решение. Для определения области допустимых значений переменной    в неравенстве (5) составим систему неравенств

Решением системы неравенств является объединение двух интервалов    и  .

Представим неравенство (5) в виде

                                                         (6)

и рассмотрим два случая.

1. Если  , то    и из неравенства (6) получаем  или  . Отсюда следует, что интервал    является решением неравенства (5).

2. Если , то и неравенство (6) принимает вид    или  . Так как здесь , то решением неравенства (5) является также интервал  .

Ответ:    и   .

 

Пример 7.   Решить неравенство  

 

                                .                               

    (7)

 

Решение. Так как неравенство (7) равносильно неравенству

и основание «внешнего» логарифма  , то получаем неравенства

,   ,    или

                                                   ,                                                   (8)

где    и  .

    Так как  , то двойное неравенство (8) принимает вид   . Отсюда следует, что  . В этой связи можно записать   ,     или  .

    Ответ:  .

 

Пример 8.   Решить неравенство  

                           .                                       (9)

 

    Решение.    Рассмотрим уравнение , левая часть которого представляет собой непрерывную и убывающую функцию (при условии, что ), а правая часть – непрерывную и возрастающую на всей числовой оси функцию . В этой связи уравнение имеет не более одного корня. Этот единственный корень    несложно найти подбором.

    Так как неравенство (9) имеет вид  , а корень уравнения равен , то с учетом свойства монотонности функций   и можно утверждать, что решением неравенства (9) являются  .

    Ответ:  .

 

Пример 9.   Решить неравенство  

 

                                 .                                       (10)

   

    Решение.    Рассмотрим вспомогательное уравнение

                                          ,                                      (11)

где .

Пусть и .  Известно, что функция  является непрерывной и убывающей на области определения , а функция непрерывно возрастает на всей числовой оси . В этой связи, если уравнение (11) имеет корень, то этот корень будет единственным.

    Уравнение    равносильно (более простому для подбора единственного корня) уравнению . Нетрудно видеть, что искомым корнем является  .

Поскольку функция  непрерывно убывающая, а  функция непрерывно возрастающая, то  для любых    справедлива цепочка неравенств , т.е. и неравенство (10) выполняется.

Ответ:  .

       

   

    Пример 10.  Решить неравенство

 

                                         .                                         (12)

    Решение. Так как и , то из неравенства (12) получаем квадратное неравенство ,  где  .

    Поскольку  , то   . Однако , поэтому  ,    или   .

    Ответ:  .

 

Пример 11.  Решить неравенство  

 

                               .                                    (13)

 

    Решение. Областью допустимых значений переменной    в неравенстве (13) являются  . Так как    и  , то    и  неравенство (13) принимает вид   , где .

    Однако  , поэтому решением неравенства  является объединение интервалов     и  .

    Если  , то  ,    или  .

    Если  , то  ,  или  .

    Ответ:    и  .

 

Пример 12.   Решить неравенство  

 

                                        .                                (14)

 

Решение.  Обозначим   ,  тогда    и неравенство (14) принимает вид    или  .

Рассмотрим уравнение  . Очевидно, что    является корнем данного уравнения. Покажем, что других корней это уравнение не имеет. Для этого обе его части разделим на выражение    и получим равносильное уравнение

                                  .                                       (15)

Поскольку в уравнении (15) левая часть представляет собой убывающую функцию , а правая часть – возрастающую функцию , то корень  является единственным.

В этой связи, если , то . Следовательно, имеет место  ,   или  .

Так как    и  , то    или  .

Ответ:  .

 

 

    Пример 13.  Решить неравенство

                                                .                                               (16)

 

    Решение. Обозначим , тогда и неравенство (16) принимает вид  . Если данное неравенство прологарифмировать по основанию  , то получим    ,   

,    или  .

    Отсюда следует, что . Так как , то

 или   .

    Ответ:  .

Рекомендуемая литература

1.  Кушнир А.И. Шедевры школьной математики (задачи и решения в двух книгах). – Киев: Астарта, книга 1, 1995. – 576 с.

2. Сборник задач по математике для поступающих во втузы / Под ред. М.И. Сканави. – М.: Мир и Образование, 2013. – 608 с.

3. Супрун В.П. Математика для старшеклассников: методы решения и доказательства неравенств. – М.: Ленанд / URSS, 2018. – 264 с.

4. Супрун В.П. Математика для старшеклассников: задачи повышенной сложности. – М.: КД «Либроком» / URSS, 2017. – 200 с.

5. Супрун В.П. Математика для старшеклассников: нестандартные методы решения задач. – М.: КД «Либроком» / URSS, 2017. – 296 с.

​

© blog. tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Решите неравенства | Алгебра среднего уровня

Результаты обучения

• Решение одношаговых неравенств
• Решение многошаговых неравенств

Свойства умножения и деления неравенства

Решение неравенств очень похоже на решение уравнений, за исключением того, что вам нужно поменять местами символы неравенства, когда вы умножаете или делите обе части неравенства на отрицательное число. Существует три способа представления решений неравенств: интервал, график и неравенство. Поскольку обычно существует более одного решения неравенства, при проверке своего ответа вы должны проверить конечную точку и еще одно значение, чтобы проверить направление неравенства. Когда мы работаем с неравенствами, мы обычно можем обращаться с ними так же, как и с уравнениями, но не совсем так. Мы можем использовать добавление свойства и свойство умножения , чтобы помочь нам решить их. Единственное исключение — когда мы умножаем или делим на отрицательное число; при этом символ неравенства переворачивается.

В следующей таблице показано, как свойство умножения применяется к неравенствам и как умножение на отрицание обращает неравенство:

Начать с	Умножить на	Окончательное неравенство
[латекс]а>б[/латекс]	[латекс]с[/латекс]	[латекс]ac>bc[/латекс]
[латекс]5>3[/латекс]	[латекс]3[/латекс]	[латекс]15>9[/латекс]
[латекс]а>б[/латекс]	[латекс]-с[/латекс]	[латекс]-ac<-bc[/латекс]
[латекс]5>3[/латекс]	[латекс]-3[/латекс]	[латекс]-15<-9[/латекс]

В следующей таблице показано, как свойство деления применяется к неравенствам и как деление на минус меняет неравенство на противоположное:

Начните с	Разделить на	Окончательное неравенство
[латекс]а>б[/латекс]	[латекс]с[/латекс]	[латекс] \displaystyle \frac{a}{c}>\frac{b}{c}[/latex]
[латекс]4>2[/латекс]	[латекс]2[/латекс]	[латекс] \displaystyle \frac{4}{2}>\frac{2}{2}[/latex]
[латекс]а>б[/латекс]	[латекс]-с[/латекс]	[латекс] \displaystyle -\frac{a}{c}<-\frac{b}{c}[/latex]
[латекс]4>2[/латекс]	[латекс]-2[/латекс]	[латекс] \displaystyle -\frac{4}{2}<-\frac{2}{2}[/latex]

В первом примере мы покажем, как применить свойства умножения и деления равенства для решения некоторых неравенств.

Пример

Проиллюстрируйте свойство умножения неравенств, решив каждое из следующих действий:

1. [латекс]3x<6[/латекс]
2. [латекс]-2x — 1\ge 5[/латекс]
3. [латекс]5-x>10[/латекс]

Показать решение

Решение неравенств с использованием свойства сложения

Когда мы решаем уравнения, нам может понадобиться складывать или вычитать, чтобы изолировать переменную, то же самое верно и для неравенств. При использовании свойства сложения для решения неравенств не требуется особого поведения.

В следующей таблице показано, как свойство сложения применяется к неравенствам.

Начать с	Добавить	Окончательное неравенство
[латекс]а>б[/латекс]	[латекс]с[/латекс]	[латекс]а+с>б+с[/латекс]
[латекс]5>3[/латекс]	[латекс]3[/латекс]	[латекс]8>6[/латекс]
[латекс]a>b[/латекс]	[латекс]-с[/латекс]	[латекс]а-с>б-с[/латекс]
[латекс]5>3[/латекс]	[латекс]-3[/латекс]	[латекс]2>0[/латекс]

Эти свойства также применимы к [латексу]a\le b[/латексу], [латексу]а>б[/латексу] и [латексу]а\геб[/латексу].

В следующем примере мы будем использовать свойство сложения для решения неравенств.

Пример

Проиллюстрируйте свойство сложения для неравенств, решив каждое из следующих действий:

1. [латекс]x — 15<4[/латекс]
2. [латекс]6\ge x — 1[/латекс]
3. [латекс]x+7>9[/латекс]

Показать решение

В следующем видеоролике показаны примеры решения одношаговых неравенств с использованием свойств умножения и сложения.

В следующем видео показаны примеры решения неравенств с переменной в правой части.

Решение многоэтапных неравенств

Как показали предыдущие примеры, мы можем выполнять одни и те же операции с обеих сторон неравенства, как и с уравнениями. Чтобы изолировать переменную и решить, мы объединяем одинаковые термины и выполняем операции со свойствами умножения и сложения.

Пример

Решите неравенство: [латекс]13 — 7x\ge 10x — 4[/латекс].

Показать решение

В следующем примере мы решаем неравенство, содержащее дроби, а не так, как нам нужно поменять знак неравенства в конце, потому что мы умножаем на минус.

Пример

Решите следующее неравенство и запишите ответ в интервальной записи: [latex]-\dfrac{3}{4}\normalsize x\ge -\dfrac{5}{8}\normalsize +\dfrac{2 }{3}\normalsize x[/латекс].

Показать решение

Решение неравенств с примерами и числами

Ключевые понятия

• Нарисуйте графические решения неравенства.

• График для решения неравенства.

• Подставить, чтобы решить неравенство.

Введение:  

Равенство и неравенство: 

Уравнение показывает, когда выражения равны. В уравнениях используются знаки равенства (=).

Неравенство — это утверждение, в котором используется символ «больше» (>), символ «меньше» (<), символ «больше или равно» (≥) или символ «меньше или-». символ равенства (≤).

Переменные в неравенстве:  

Переменные можно использовать с неравенствами. Переменная в неравенстве обозначает все числа, которые делают неравенство верным.

Например, в неравенстве x < 4 x обозначает все числа, меньшие 4. Таким образом, x может быть 0, 1, 2 или 3. 

Неравенство 12 ≤ y + 5 может иметь решения y = 7, 8 и 9, так как 7 + 5 = 12, 8 + 5 = 13 и 9 + 5 = 14.

4.7.1. x < 3, нарисуйте незакрашенный круг в точке 3 на числовой прямой.

Шаг 2:  

Найдите несколько решений и нанесите их на числовую прямую.

Шаг 3:  

Начните с открытого круга и заштрихуйте найденные решения.

4.7.2 График для решения неравенства  

Пример 2:  

Температура в теплице должна быть 57 градусов и выше. Напишите неравенство, описывающее допустимую температуру в теплице.

Решение:  

Напишите и начертите неравенство.

Возможные температуры в теплице, t , больше или равны 57 градусам.

Пример 3:  

Максимальный вес грузового лифта, разрешенный законом, составляет 1500 фунтов. Пусть w представляет вес на лифте. Напишите неравенство, описывающее допустимый вес лифта.

Решение:  

Напишите и начертите неравенство.

Возможный вес в лифте, w , меньше или равен 1500 фунтов.

4.7.3 Подстановка для решения неравенства  

Пример 4:  

Семья Джона собирается в отпуск. Они планируют посетить любое место, которое находится за пределами 250 миль от их родного города.

No related posts.