Задачи на паскале с решением 9 класс для начинающих: Задачи с решениями на языке программирования Паскаль (9

Решение модуля 2.3 «Поколение Python»: курс для начинающих stepic

Все ответы на этот курс по модулям (кликабельно).

Ответы на задачи из модуля 2.3 «Поколение Python»: курс для начинающих. Нумерация сквозная и идет именно по задачам.
Предыдущий модуль 2.2 «Поколение Python».

Первые три вопроса

1. Что будет выведено на экран в результате выполнения следующего кода?

print('31', '12', '2019', sep='-')

Ответ: 31-12-2019

2. Что будет выведено на экран в результате выполнения следующего кода?

print('Mercury', 'Venus', sep='*', end='!')
print('Mars', 'Jupiter', sep='**', end='?')

Решение: Mercury*Venus!Mars**Jupiter?

3. Сколько строк будет распечатано в результате выполнения следующего кода?

print('a', 'b', 'c', sep='*')
print('d', 'e', 'f', sep='**', end='')
print('g', 'h', 'i', sep='+', end='%')
print('j', 'k', 'l', sep='-', end='\n')
print('m', 'n', 'o', sep='/', end='!')
print('p', 'q', 'r', sep='1', end='%')
print('s', 't', 'u', sep='&', end='\n')
print('v', 'w', 'x', sep='%')
print('y', 'z', sep='/', end='!')

Примечание.  Последовательность символов \n задает перевод строки.

Ответ: 5.

Четвертый номер:

I like Python

Напишите программу, которая выводит на экран текст «I***like***Python» (без кавычек).

Примечание. Используйте необязательный параметр sep.

Sample Input:

Sample Output:

I***like***Python

Решение:

# put your python code here
print('I','like','Python', sep='***')

Пятая задача:

Кастомный разделитель

Напишите программу, которая считывает строку-разделитель и три строки, а затем выводит указанные строки через разделитель.

Формат входных данных
На вход программе подаётся строка-разделитель и три строки, каждая на отдельной строке.

Формат выходных данных
Программа должна вывести введённые три строки через разделитель.

Код:

# put your python code here
a=input()
b=input()
c=input()
d=input()
print(b, c, d, sep=a)

Шестая задача:

Приветствие

Напишите программу, которая приветствует пользователя, выводя слово «Привет» (без кавычек), после которого должна стоять запятая и пробел, а затем введенное имя и восклицательный знак.

Формат входных данных
На вход программе подаётся одна строка — имя пользователя.

Формат выходных данных
Программа должна вывести текст в соотвествии с условием задачи.

Примечание 1. Перед восклицательным знаком не должно быть пробелов.

Примечание 2. Используйте необязательный параметр end.

Ответ:

name=input()
print('Привет,', name, end='!')

Пять последних вопросов

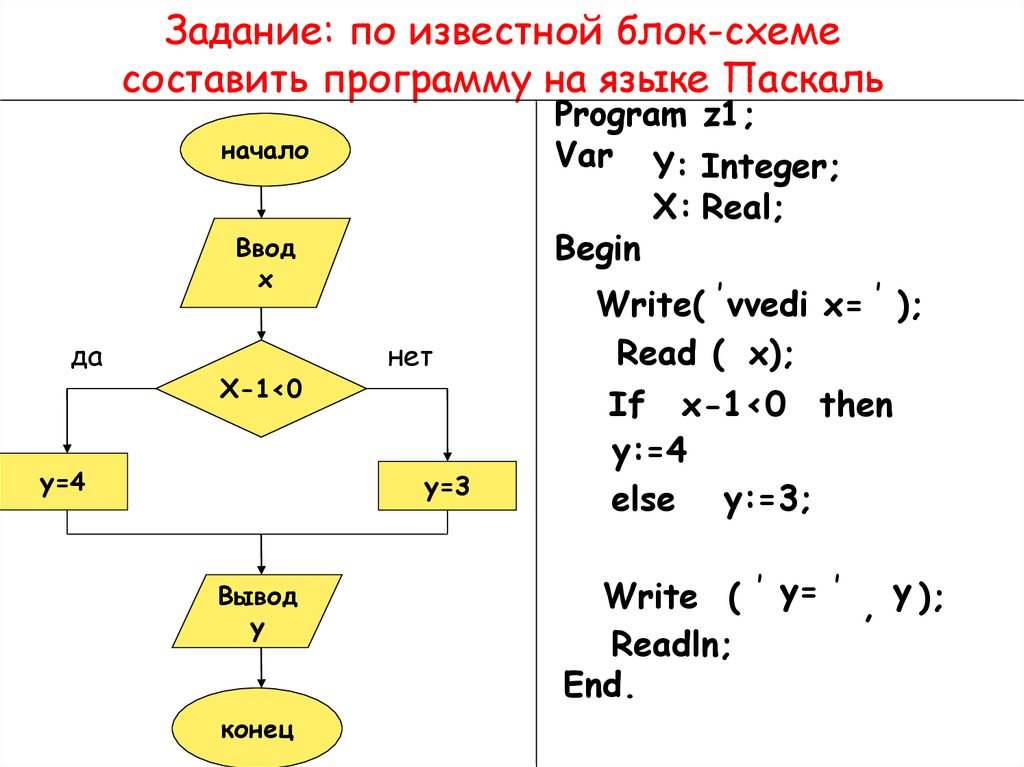
7. Какие из имён допустимы для названия переменных в Python?

Ответ: teacher teacher2 teacher_2

8. Что покажет приведенный ниже фрагмент кода?

language = 'Python'
language = 'Pascal'
print(language)

Результат: Pascal

9. Какое значение будет находиться в переменной s1 после выполнения следующего кода?

s1 = 'C++'
s2 = 'Python'
s3 = 'Java'
s3 = s2
s1 = s3

Результат: Python

10. Выберите строки кода, соответствующие стандарту PEP 8.

Примечание. Будьте внимательны с пробелами.

Ответы:

• print(‘Follow PEP8!’)
• print(‘Follow’, ‘PEP8!’)
• print(‘Follow’, ‘PEP8′, sep=’**’)
• name = input()

11. Что будет напечатано в результате выполнения следующей программы?

# print('Java')
# print('Ruby')
# print('Scala')
print('Python', end='+')  # print('C++')
# print('GO')
print('C#', end='=') # print('C')
print('awesome')
# finish

Правильный текст: Python+C#=awesome

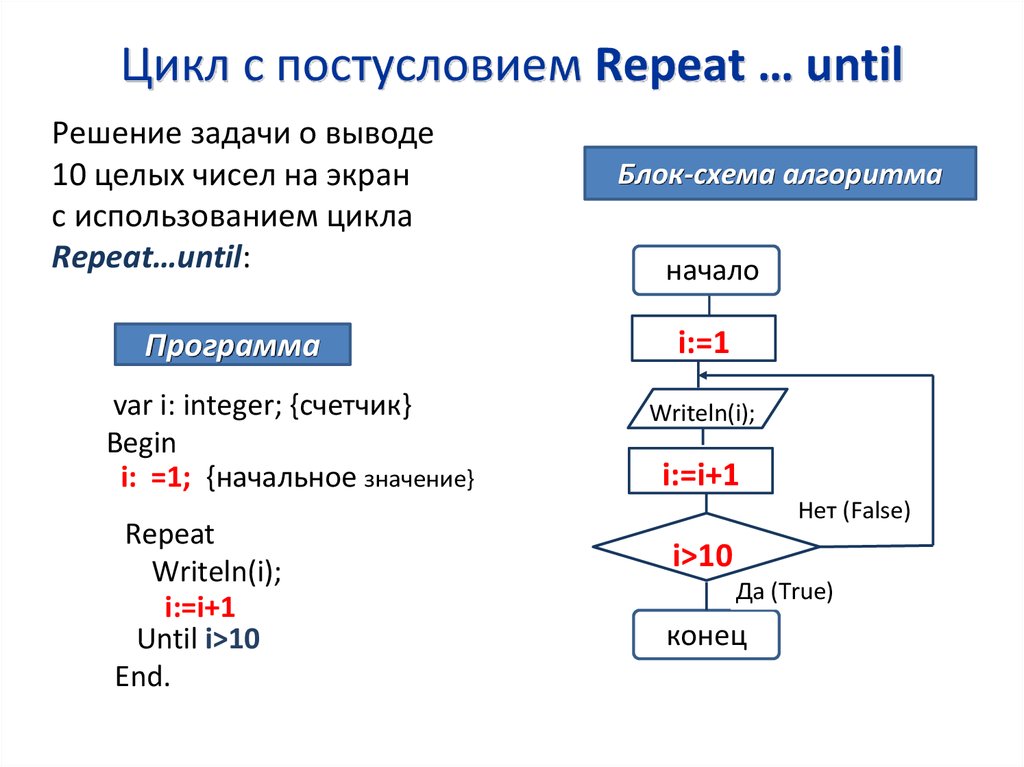
Решение модуля 2.4 «Поколение Python»

🐍🧩 5 классических задач по Python для начинающих с решениями

1. Заполнение матрицы по спирали

Эта классическая задача часто встречается на собеседованиях и олимпиадах. Рассмотрим несколько способов решения на Python.

На вход программе подаются два натуральных числа n и m. Напишите программу, которая создает матрицу размером n х m, заполнив ее по спирали числами от 1 до n x m. Спираль начинается в левом верхнем углу и закручивается по часовой стрелке.

Пример ввода:

7 6

Пример вывода:

1  2  3  4  5  6  
22 23 24 25 26 7  
21 36 37 38 27 8  
20 35 42 39 28 9  
19 34 41 40 29 10 
18 33 32 31 30 11 
17 16 15 14 13 12
    

Решение

Способ 1:

n, m = map(int, input().split())
matrix = [[0] * m for _ in range(n)]
dx, dy, x, y = 0, 1, 0, 0
for i in range(1, n * m + 1):
    matrix[x][y] = i
    if matrix[(x + dx) % n][(y + dy) % m]:
        dx, dy = dy, -dx
    x += dx
    y += dy    
for line in matrix:
    print(*(f'{i:<3}' for i in line), sep='')
    

Способ 2:

        
n, m = (int(i) for i in input().split())
spiral = []
x, y, dx, dy, k = 0, 0, 1, 0, 1
spiral = [[0]* n for _ in range(m)]
for i in range(1, n * m + 1):
    spiral[x][y] = i
    nx, ny = x + dx, y + dy
    if 0 <= nx < m and 0 <= ny < n and spiral[nx][ny] == 0:
        x, y = nx, ny
    else:
        dx, dy = -dy, dx
        x, y = x + dx, y + dy
for i in range(n):
    for j in range(m):
        print(str(spiral[j][i]). ljust(3), end=' ')
    print()
    

Способ 3:

n, m = [int(i) for i in input().split()]
spiral = [[0] * m for _ in range(n)]
c = 1
for k in range(min(n // 2 + 1, m //2 + 1)):  
    for j in range(k, m - k):  
        if spiral[k][j] == 0:  
            spiral[k][j] = c 
            c += 1
    for i in range(1 + k, n - k):  
        if spiral[i][m - k - 1] == 0:
            spiral[i][m - k - 1] = c 
            c += 1
    for j in range(m - k - 2, k - 1, -1):  
        if spiral[n - k - 1][j] == 0:
            spiral[n - k - 1][j] = c 
            c += 1
    for i in range(n - k - 2, k, -1):  
        if spiral[i][k] == 0:
            spiral[i][k] = c 
            c += 1
for i in range(n):  
    for j in range(m):
        print(str(spiral[i][j]).ljust(3), end=' ')
    print()
    

Больше полезных материалов вы найдете на нашем телеграм-канале «Библиотека питониста»

Библиотека питониста

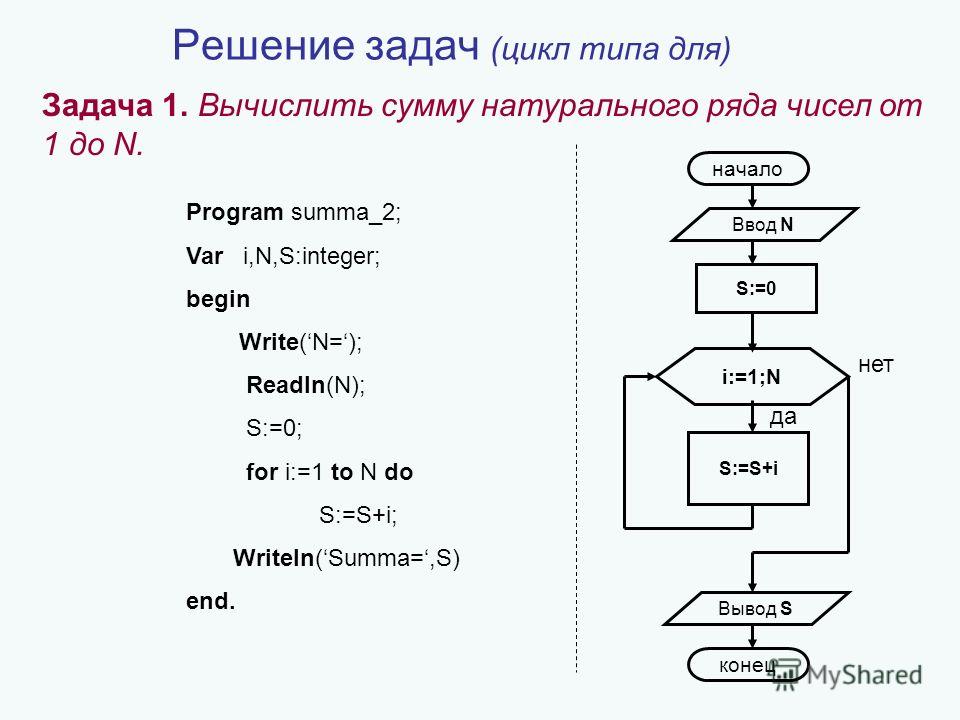
2. Единственный выживший

Это вариант классической задачи Иосифа Флавия. В кругу стоят n человек, пронумерованных числами от 1 до n. Начинается расчет, при котором каждый k-й по счету человек выбывает из круга, после чего счет продолжается со следующего за ним человека. Напишите программу, определяющую номер человека, который останется в кругу последним.

Входные данные:

Числа n и k на отдельных строках.

#Пример ввода
9 3
    

Выходные данные:

Номер последнего оставшегося человека.

#Пример вывода
1
    

Решение

Способ 1:

n, k = int(input()), int(input())
last = 0
for i in range(1, n + 1):
    last = (last + k) % i
print(last + 1)
    
    

Способ 2 – рекурсия:

def lastSurvivor(n, k):
    if n == 1:
        return 1
    elif n > 1:
        return (1 + (lastSurvivor(n - 1, k) + k - 1) % n)
 
n, k = int(input()), int(input())
print(lastSurvivor(n, k))
    
    

3.

Определение магического квадрата

Магические квадраты издавна интриговали воображение людей: дата изготовления древнейшей сохранившейся таблицы относится к 2200 г. до н.э. Магический квадрат – это квадратная таблица размера n х n, составленная из всех чисел 1, 2, 3 … n^{2 таким образом, что суммы по каждому столбцу, каждой строке и каждой диагонали равны между собой. Напишем программу, которая определяет, можно ли считать матрицу магическим квадратом.}

Входные данные:

Число n, затем n строк с n цифр в каждой.

#Пример ввода
3
8 1 6
3 5 7
4 9 2

    

Выходные данные:

YES, если введенная матрица является магическим квадратом, и NO в обратном случае.

#Пример вывода
YES

    

Решение

Способ 1:

n = int(input())
matrix = [list(map(int, input().split())) for _ in range(n)]
if all(i in sum(matrix,[]) for i in range(1, n**2 + 1)):
    print('YES' if all(sum(i) == sum(j) == sum([matrix[i][i] for i in range(n)]) == sum([matrix[n-i-1][i] for i in range(n)]) for i in matrix for j in list(map(list, zip(*matrix)))) else 'NO')
else:
    print('NO')
    
    

Способ 2 – с магической константой и множествами:

 
n = int(input())
square = [[*map(int, input().split())] for _ in range(n)]
m_const = n * (1 + n ** 2) // 2                                                      
print(('NO', 'YES')[all(sum(el) == m_const for x in (((square[i][i] for i in range(n)),(square[i][~i] for i in range(n))), square, zip(*square)) for el in x) and set(sum(square, [])) == set(range(1, n ** 2 + 1))])
    

    

4.

Разделение списка на подсписки

На вход подается строка чисел, из которой формируется список. Напишите программу, создающую вложенный список, элементами которого являются все возможные подсписки исходного списка, включая пустой.

Пример ввода:

a f z

Пример вывода:

[[], ['a'], ['f'], ['z'], ['a', 'f'], ['f', 'z'], ['a', 'f', 'z']]

Решение

Способ 1:

lst = input().split()
def sub_lists(lst):
    lists = [[]]
    for i in range(len(lst) + 1):
        for j in range(i):
            lists.append(lst[j:i])
    lists = sorted(lists, key=len)
    return lists
print(sub_lists(lst))
    

Способ 2:

print([[]] + [lst[j:i + j + 1] for lst in [input(). split()] for i in range(len(lst)) for j in range(len(lst) - i)])
    
    

Способ 3:

st, lst = input().split(), [[]]
for i in range(1, len(st) + 1):
    for j in range(len(st) - i + 1):
        lst += [st[j:j+i]]
print(lst)
    
    

5. Ходы шахматного ферзя

На шахматной доске 8 х 8 стоит ферзь. Отметьте положение ферзя на доске и все клетки, которые бьет ферзь. Клетку, где стоит ферзь, отметьте буквой Q, клетки, которые бьет ферзь, отметьте звездочками *, остальные клетки заполните точками. Шахматный ферзь может ходить по вертикали, горизонтали и по диагоналям.

Входные данные:

Координаты ферзя на шахматной доске в формате номер столбца (буква от a до h, слева направо) и номер строки (цифра от 1 до 8, снизу вверх).

Пример ввода:

c4

Выходные данные:

Программа выводит стилизованное изображение шахматной доски со схемой возможных передвижений ферзя.

Пример вывода:

. . * . . . * .
. . * . . * . .
* . * . * . . .
. * * * . . . .
* * Q * * * * *
. * * * . . . .
* . * . * . . .
. . * . . * . .
    

Решение

Способ 1:

x, y, board = *('abcdefgh87654321'.index(i) % 8 for i in input()), range(8)
[print(*['?Q**.'[len({j - x, x - j, i - y, y - i})] for j in board]) for i in board]
    
    

Способ 2:

x, y = ('abcdefgh87654321'.index(i) % 8 for i in input())
directions = lambda i, j: (j - i == x - y) + (j + i == x + y) + ((j == x) != (i == y))
[print(*['. *Q'[directions(i, j)] for j in range(8)]) for i in range(8)]
    

Способ 3:

coor = input()
board = [['.'] * 8 for _ in range(8)]
y, x = 8 - int(coor[1]), ord(coor[0]) - 97
for i in range(8):
    for j in range(8):
        if (y == i) or (x == j) or abs(y - i) == abs(x - j):
            board[i][j] = '*'
board[y][x] = 'Q'
for line in board:
    print(*line)
    
    

***

Материалы по теме

• 🐍🧩 Задача об определении латинского квадрата
• 🐍🧩 Задача о поврежденной XML-строке
  
• 🐍🧩 Словари в Python: 12 задач для начинающих с решениями
  

Треугольник Паскаля — биномиальная теорема

Нам известны разложения таких термов, как (x + 2) ² и (x + 3) ³ . Это довольно просто сделать, но иногда мы сталкиваемся с такими выражениями, как (x+2) ⁵ . Подобные выражения трудно расширить, мы можем использовать некоторые приемы для упрощения, например, 

(x+2) ⁵ = (x+2)(x + 2) ² (x+2) ²

Исследовательская работа над биномиальными разложениями, включающими тысячи показателей. Становится важным знать простой способ их расширения. Это еще много работы, и здесь нам на помощь приходит биномиальная теорема. Это позволяет нам расширять любые общие выражения, такие как (x + a) ^п . Рассмотрим эту теорему подробно.

Биномиальное выражение 

Биномиальное выражение определяется как выражение, содержащее два члена, соединенных операторами типа + или -. Например, х + а, х — 6 и т. д. являются примерами биномиальных выражений. Возведение биномиального выражения в степень больше 3 довольно сложно и громоздко. Давайте посмотрим на некоторые биномиальные расширения и попытаемся найти в них какую -то рисунок,

(x + a) ⁰ = 1

(x + a) ¹ = x + a

(x + a) ² = x ² + 2ax + A ²

(x + a) ³ = x ³ + 3а ² х + 3ах ² + a ³

Обратите внимание, нам нужно знать коэффициенты этих членов, и тогда нам может быть немного проще описать их разложения. Треугольник Паскаля можно использовать для очень быстрого получения этих результатов.

Что такое треугольник Паскаля?

Он назван в честь известного философа и математика Паскаля, который разработал схему чисел, начинающуюся с 1, а числа под ним представляют собой сумму вышеуказанных чисел. Чтобы начать составлять треугольник Паскаля, сначала запишите число 1. Второй ряд снова записывается двумя единицами. Другие строки генерируются с использованием предыдущих строк для создания треугольника чисел. Каждая строка начинается и заканчивается цифрой 1. 

1
1 1
1 x 1
1 x x 1

Числа, которые определяются как x, рассчитываются путем добавления чисел из предыдущей строки, которые лежат слева и справа над заданной позицией. На рисунке ниже показан процесс построения треугольника Паскаля.

Таким образом можно построить треугольник Паскаля.

Вопрос 1: Сгенерируйте шестую строку треугольника Паскаля.

Ответ: 

Вопрос 2. Составьте десятую строку треугольника Паскаля.

Ответ: 

Треугольники Паскаля для расширения биномиальных выражений 

Давайте еще раз посмотрим на приведенные выше уравнения, 

(x + a) ⁰ = 1

(x + a) ¹ = x + a

(x + a) ² = x ² + 2ax + A ²

(x + a) ³ =                                                             x ³ + 3a ² x + 3ax ² + a ³

Из этих уравнений для (x + a) ⁿ , 

1. всегда есть на один член больше, чем значение n.
2. Для каждого члена сумма показателей всегда равна n.
3. Для переменной «x» показатель степени начинается с n и продолжает уменьшаться до нуля. Точно так же для «а» показатель степени начинается с 0 и продолжается до n.
4. Коэффициенты этих членов даны треугольником Паскаля.

Давайте рассмотрим пример, предположим, мы хотим расширить (x + a) ³ с помощью этой концепции расширения. Должно быть четыре термина, и термины должны иметь убывающую степень «x» и возрастающую степень «a» соответственно.

(x + a) ³ = C ₁ x ³ + C ₂ x ² A + C ₃ xa ² + C ₄ A ³

99999999999

+ C ₄ A 9015 3

999999

9

+ C ₄ A 9015 3

9

99 + C ₄ A 3

99 + C ₄ A значения С _1, С ₂ , С ₃ , и C ₄ — коэффициенты, будем вычислять коэффициенты с помощью треугольника Паскаля. Давайте посмотрим на треугольник Паскаля с n + 1 строками,

Значения в последней строке дают нам значения коэффициентов C ₁ , C ₂ , C ₃ и C ₄ .

Здесь C ₁ = 1, C ₂ = 3, C ₃ = 3 и C ₄ = 1.

Таким образом, мы можем расширить наши биномиальные выражения.

Для любого биномиального выражения, (x + a) ⁿ расширение дается выражением, 

(a + b) ⁿ = c ₀ a ⁿ b 5 5 1 + ⁰

a

^n-1 b ¹ + c ₂ a ^n-2 b ² + …. + c _n-1 a ¹ b ^n-1 + c _n a ⁰ b ⁿ

Коэффициенты даны n+1 строкой треугольника Паскаля.

Примеры задач

Вопрос 1: Расширьте и проверьте (a + b) ² .

Решение:

Сначала запишите общие выражения без коэффициентов.

 (a + b) ² = c ₀ a ² b ⁰ + c ₁ a ¹ b ¹ + c ₂ a ⁰ b ²  

Теперь построим треугольник Паскаля на 3 строки, чтобы узнать коэффициенты.

Значения последней строки дают нам значения коэффициентов.

C ₀ = 1, C ₁ = 2, C ₂ = 1

(A + B) ² = A ² B ⁰ + 2A ¹ B ¹ B ⁰ + 2A ¹ 4 10003 10004 B ⁰ + 2A ¹ 4 10003 10004 B ⁰ + 2A ¹ 4 100044 B ⁰ + 2A ¹ . + a ⁰ b ²  

Таким образом проверено.

Вопрос 2: Развернуть (a + b) ⁴ .

Решение:

Сначала запишите общие выражения без коэффициентов.

(A + B) ⁴ = C ₀ A ⁴ B ⁰ + C ₁ A ³ B ¹ + C ₂ A ² B ² + + + + + + + + c ₃ a ¹ b ³ + c ₄ a ⁰ b ⁴

Теперь построим треугольник Паскаля на 5 рядов, чтобы узнать коэффициенты.

Значения последней строки дают нам значения коэффициентов.

с ₀ = 1, с ₁ = 4, с ₂ = 6, с ₃ = 4 и с ₄ = 1.

Таким образом, (A + B) ⁴ = A ⁴ B ⁰ + 4A ³ B ¹ + 6A ² B ² + 4A ¹ B ³ + A A ⁰ b ⁴

Вопрос 3: Развернуть (a + b) ⁵ .

Решение:

Сначала запишите общие выражения без коэффициентов.

(A + B) ⁵ = C ₀ A ⁵ B ⁰ + C ₁ A ⁴ B ¹ + C ₂ A ³ B ² + + + + + + + + + C ₃ A ² B ³ + C ₄ A ¹ B ⁴ + C ₅ A ⁰ B ⁵

Теперь Let’s Build’s Pascal’s Triang узнать коэффициенты.

Значения последней строки дают нам значения коэффициентов.

с ₀ = 1, с ₁ = 5, с ₂ = 10, с ₃ = 10, с ₄ = 5 и с _{5 b0 + 09} = 0,00 ⁵ = A ⁵ B ⁰ + 5A ⁴ B ¹ + 10A ³ B ² + 10A ² B ³ + 5A ¹ B ⁴ +. a ⁰ b ⁵

Вопрос 4: Разверните (a + b) ⁶ .

Решение:

Сначала запишите общие выражения без коэффициентов.

(A + B) ⁶ = C ₀ A ⁶ B ⁰ + C ₁ A ⁵ B ¹ + C ₂ A ⁴ B ² + + + + + + + + 2 A C ₃ A ³ B ³ + C ₄ A ² B ⁴ + C ₅ A ¹ B ⁵ + C ₆ A ^{0 5 + C ₆ A 0 60004 60004 + C ₆ A 0 60004 + C ₆ A}  

Теперь построим треугольник Паскаля на 7 строк, чтобы узнать коэффициенты.

Значения последней строки дают нам значения коэффициентов.

с ₀ = 1, с ₁ = 6, с ₂ = 15, с ₃ = 20, с ₄ = 15, с _{5 5 5 с 5 9 0 6 и 5} = 1 9 0 6 .

(A + B) ⁶ = 1a ⁶ B ⁰ + 6a ⁵ B ¹ + 15a ⁴ B ² + 20a ³ B ³ + 15a ² б ⁴ + 6а ¹ б ⁵ + 1a ⁰ b ⁶   

Принцип Архимеда, закон Паскаля и принцип Бернулли — Урок

(2 оценки)

Нажмите здесь, чтобы оценить

Quick Look

Уровень: 9 (9-12)

Необходимое время: 2 часа 15 минут

(три занятия по 45 минут)

Урок Зависимость: Нет

Тематические области: Химия, физика, физика, решение проблем, рассуждения и доказательства

Поделиться:

TE Информационный бюллетень

Резюме

Студенты знакомятся с законом Паскаля, принципом Архимеда и принципом Бернулли. Поставляются основные определения, уравнения, практические задачи и инженерные приложения. Учащиеся могут использовать связанные действия, чтобы укрепить свое понимание взаимосвязей между предыдущими концепциями и примерами из реальной жизни. Предоставляются презентация PowerPoint®, практические задачи и критерий оценивания.

Инженерное подключение

Понятия закона Паскаля, принципа Архимеда и принципа Бернулли важны в инженерных и технологических приложениях, включая аэродинамику и гидродинамику, гидравлику, плавучие суда, подводные лодки, самолеты, автомобили, аэрокосмическое наведение и управление, трубопроводы и транспортные системы, а также для многих современных исследовательских тем, таких как потоки, связанные с океаном, турбулентность, реагирующие потоки, глобальный климат, механика биологических жидкостей, обтекание магнитных лент и дисков, геофизические потоки, кинетика систем горения и динамика вихрей.

Цели обучения

После этого урока учащиеся должны уметь:

• Используйте принцип Архимеда для определения выталкивающей силы.
• Решите задачи на давление, плотность и закон Паскаля.
• Решите задачи, используя уравнение Бернулли и уравнение неразрывности.
• Объясните ситуации, связанные с эффектом Бернулли.

Образовательные стандарты

Каждый урок или занятие TeachEngineering соотносится с одной или несколькими науками K-12, технологические, инженерные или математические (STEM) образовательные стандарты.

Все более 100 000 стандартов K-12 STEM, включенных в TeachEngineering , собираются, поддерживаются и упаковываются сетью стандартов достижений (ASN) , проект D2L (www.achievementstandards.org).

В ASN стандарты структурированы иерархически: сначала по источнику; напр. по штатам; внутри источника по типу; напр. , естественные науки или математика; внутри типа по подтипу, затем по сортам, и т. д. .

Общие базовые государственные стандарты — математика

• Решайте линейные уравнения и неравенства с одной переменной, в том числе уравнения с коэффициентами, обозначенными буквами. (Оценки 9- 12) Подробнее

  Посмотреть согласованную учебную программу

  Согласны ли вы с таким раскладом? Спасибо за ваш отзыв!

• Решайте квадратные уравнения с одной переменной. (Оценки 9 — 12) Подробнее

  Посмотреть согласованную учебную программу

  Согласны ли вы с таким раскладом? Спасибо за ваш отзыв!

Международная ассоциация преподавателей технологий и инженерии – Технология

ГОСТ

Предложите выравнивание, не указанное выше

Какое альтернативное выравнивание вы предлагаете для этого контента?

Подписаться

Подпишитесь на нашу рассылку новостей, чтобы получать внутреннюю информацию обо всем, что связано с TeachEngineering, например, о новых функциях сайта, обновлениях учебных программ, выпусках видео и многом другом!

PS: Мы никому не передаем личную информацию и электронные письма.

Рабочие листы и вложения

Презентация жидкостей (pptx)

Презентация по жидкостям

(pdf)

Рабочий лист практических задач (docx)

Рабочий лист практических задач

(pdf)

Ключ к ответу на рабочий лист практических задач (docx)

Ключ к ответу на рабочий лист практических задач (pdf)

Рубрика решения задач по физике (docx)

Рубрика «Решение задач по физике» (pdf)

Посетите [www.teachengineering.org/lessons/view/uoh_fluidmechanics_lesson01], чтобы распечатать или загрузить.

Больше учебных программ, подобных этому

Урок средней школы

Основы Fluid Power

Учащиеся узнают об основных понятиях, важных для гидроэнергетики, которая включает в себя как пневматические (газовые), так и гидравлические (жидкостные) системы.

Основы гидроэнергетики

Урок средней школы

Принцип Бернулли

Студенты узнают о взаимосвязях между компонентами уравнения Бернулли на реальных инженерных примерах и практических задачах.

Принцип Бернулли

Группа средней школы

Физика гидромеханики

Гидромеханика, изучение того, как силы воздействуют на жидкости, представлена ​​в этом разделе как последовательность из двух уроков и трех соответствующих заданий. Гидромеханика, изучение того, как силы действуют на жидкости, описана в этом разделе как последовательность из двух уроков и трех соответствующих действий. ..

Физика гидромеханики

Урок средней школы

Оценка плавучести

Учащиеся узнают, что плавучесть лодок, воздушных шаров и метеозондов зависит от плавучести. Они рассчитывают, будет ли плавать лодка или воздушный шар, и вычисляют объем, необходимый для плавания воздушного шара или лодки определенной массы.

Оценка плавучести

Предварительные знания

Для решения уравнений на этом уроке требуется понимание основ алгебры.

Введение/Мотивация

(Задайте учащимся несколько предварительных вопросов, чтобы определить, слышали ли они о принципе Архимеда, законе Паскаля или принципе Бернулли или о каких-либо физических концепциях, лежащих в их основе. )

Кто знает, почему корабли плавают? (Послушайте ответы учащихся.)

Когда вы плаваете в бассейне, вы чувствуете себя легче или тяжелее, чем когда вы идете по земле? Насколько ты легче? (Послушайте ответы учащихся.)

Кто слышал термин гидравлика? Каковы некоторые примеры гидравлических устройств? Кто знает, что это значит и как это работает? (Послушайте ответы учащихся.)

(Двигайтесь дальше и представьте учащимся прикрепленную слайд-презентацию и содержимое в разделе «Основные сведения».)

Предыстория урока и концепции для учителей

Все концепции этого урока описаны в презентации Fluids из 22 слайдов, файле Microsoft PowerPoint®. Предлагаемое время для завершения этой презентации — три академических часа, но увеличивайте или уменьшайте продолжительность по мере необходимости.

Гидромеханика является важным курсом в большинстве университетов и обязательным для большинства инженерных специальностей.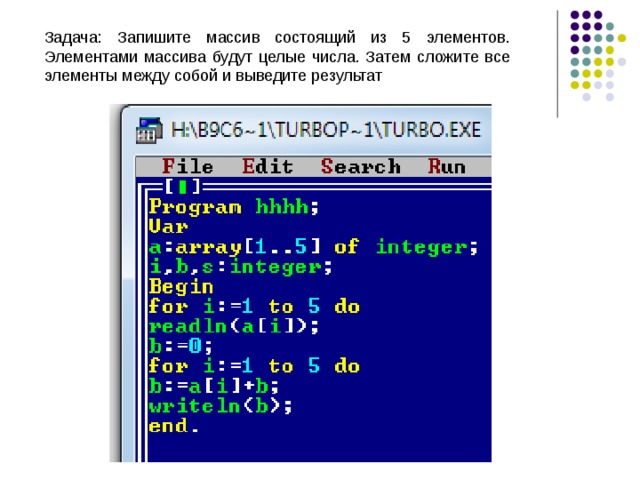 Это особенно важная область изучения гидротехники и инженерии по охране окружающей среды, которые являются субдисциплинами гражданского строительства. Эти типы инженеров отвечают за системы водного транспорта и канализационные сети в городских районах, а также за проектирование мостов, плотин, каналов, каналов, дамб и трубопроводных сетей, как отдельно стоящих, так и в зданиях.

В этом уроке представлены основные понятия гидромеханики. Сообщите студентам, что если они хотят заниматься инженерным делом в колледже, механику жидкости можно смоделировать или объяснить с помощью существующих компьютерных программ в университетском классе или лаборатории. Некоторые учащиеся могут быть знакомы с некоторыми программами моделирования; попросите их привести примеры программного обеспечения для моделирования и их приложений. Примеры программ моделирования гидромеханики включают:

Система гидрологического моделирования (HEC-HMS) был создан и используется Инженерным корпусом армии США для моделирования гидрологических процессов в системах водоразделов, включая естественные процессы, такие как испарение и инфильтрация, а также искусственные объекты, такие как водохранилища и удерживающие пруды.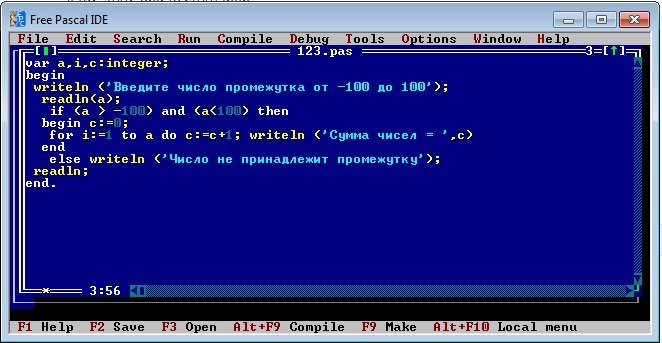

ModFlow был создан и используется Геологической службой США; это программное обеспечение для трехмерного моделирования подземных вод, используемое для моделирования условий подземных вод и взаимодействия подземных и поверхностных вод, а также для управления водоносными горизонтами и землепользованием.

Computation Fluid Dynamics (CFD) был создан ANSYS, Inc., компанией, занимающейся разработкой программного обеспечения для инженерного моделирования. Это приложение прогнозирует воздействие потоков жидкости на инженерные изделия на протяжении всего процесса проектирования и производства, а также во время использования.

SolidWorks Flow Simulation моделирует поток жидкости, теплопередачу и гидравлические силы, необходимые для успешного проектирования, и допускает неограниченное количество итераций для создания наиболее эффективных конструкций изделий.

Жидкость – это любая текучая материя, которая может быть жидкостью или газом.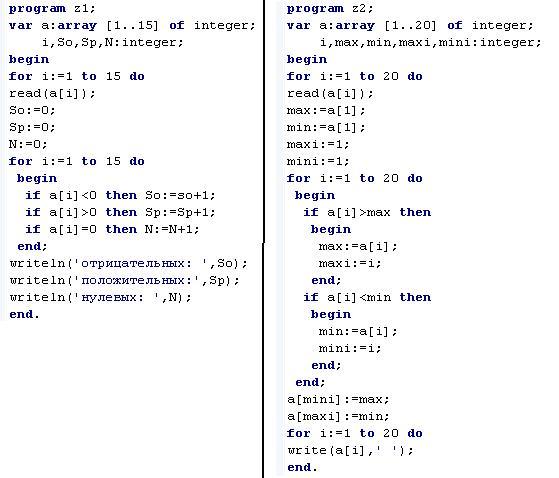 Принцип Архимеда гласит, что любой объект, полностью или частично погруженный в жидкость, испытывает направленную вверх силу, по величине равную весу жидкости, вытесненной объектом, как показано в уравнении 1.

F _B = м _f г (уравнение 1)

Где F _B — выталкивающая сила, м _f — масса вытесненной жидкости, а г — ускорение свободного падения.

Все мы испытали на себе принцип Архимеда , даже если мы не знаем об этом. Распространенным опытом является понимание того, что поднять человека в бассейне довольно легко. Это связано с тем, что вода обеспечивает частичную поддержку в виде направленной вверх силы, называемой выталкивающей силой . Выталкивающая сила равна весу вытесненной жидкости. Обратитесь к разделу Плавучесть и давление в жидкостях: Декартовский дайвер в бутылке с газировкой, чтобы учащиеся наблюдали за этими переменными в действии. Корабли плавают в воде, потому что вес воды, вытесненной корпусом корабля, больше веса корабля, и если бы вес вытесненной воды был меньше веса корабля, он бы затонул. Инженеры используют программное обеспечение для гидромеханики и динамического моделирования для имитации различных происходящих явлений, что необходимо для создания оптимальных конструкций кораблей. Инженеры моделируют форму корпуса и оптимизируют придатки, чтобы повысить эффективность и тяговую мощность корабля, снизить расход топлива и анализировать сопротивление на спокойной воде и нерегулярных волнах.

Ранее упоминалось, что жидкость может быть жидкостью или газом. Воздух есть везде, и даже окружающий нас воздух имеет вес и оказывает давление. Мы не осознаем, насколько тяжел воздух, и не чувствуем давления, которое он оказывает на нас, потому что мы привыкли к «атмосферному давлению». Давление определяется как мера силы на заданную площадь. Закон Паскаля гласит, что давление, прикладываемое к жидкости в закрытом сосуде, передается в равной степени каждой точке жидкости и стенкам сосуда, как видно из уравнения 2. 9.0009

P = F / A (Уравнение 2)

Где P — давление, F — сила, а A — площадь. Обратите внимание, что закрытая система может иметь две области, поэтому сила в этих двух точках различна, но давление остается одинаковым, как утверждает закон Паскаля.

Это давление одинаково передается во всех направлениях и под прямым углом, и изменение давления равномерно распределяется по всей жидкости. Закон Паскаля используется инженерами при проектировании гидравлических систем, использующих энергию жидкости для выполнения работы. Некоторыми примерами являются гидравлические домкраты, которые поднимают автомобили в ремонтных мастерских, и гидравлические тормоза, которые оказывают давление на большую площадь, чтобы остановить большое транспортное средство, такое как поезд. Закон Паскаля также используется в системах распределения воды и канализации для перемещения воды по сети трубопроводов.

В основном существуют два различных типа течения жидкости — ламинарный и турбулентный. Ламинарный поток возникает, когда частицы жидкости движутся по однородному гладкому пути, называемому линией тока, и обычно возникает в небольших трубах или других средах с низким расходом. Турбулентный поток возникает, когда частицы жидкости движутся неравномерно и вызывают изменение скорости, и обычно возникает в больших трубах или других средах с высоким потоком. Принцип Бернулли утверждает, что давление и скорость обратно пропорциональны, или что давление в жидкости уменьшается, когда скорость жидкости увеличивается, как видно из уравнения 3.

P ₁ + ½ ρ v ₁ ² + ρ g h ₁ = P ₂ + ½ ρ v ₂ ² + ρgh ₂ (уравнение 3)

Где P ₁ — давление в точке 1, ρ — плотность жидкости, v ₁ — скорость жидкости в точке 1, g — ускорение свободного падения, ч ₁

9 901 точка 1,

P ₂ — давление в точке 2, v ₂ — скорость жидкости в точке 2, а h 5 2 — высота точки 2.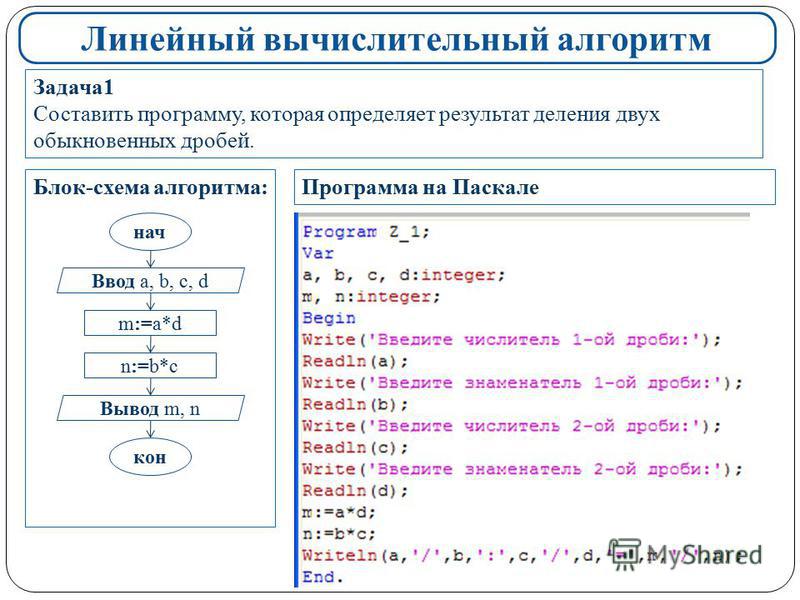 2. Учащиеся могут попрактиковаться в выводе этих уравнений с помощью упражнения «Камень и лодка: плотность, плавучесть и принцип Архимеда», работая над решением контрольного вопроса!

Уравнение Бернулли остается одинаковым в различных точках горизонтальной трубы. В трубе с непостоянной высотой уравнение Бернулли по-прежнему остается одинаковым, но учитывает разницу высот в разных точках трубы, как отмечено h в уравнении 3. Инженеры применяют уравнение Бернулли, чтобы определить оптимальные и эффективные размеры труб при проектировании трубопроводов и транспортных систем. Уравнение Бернулли является основным компонентом аэродинамики, который применяется при проектировании автомобилей, мостов, систем вентиляции, газопроводов, самолетов и космических кораблей.

Понятия закона Паскаля, принципа Архимеда и принципа Бернулли важны в инженерных и технологических приложениях, таких как аэродинамика и гидродинамика, гидравлика, плавучие суда, подводные лодки, самолеты, автомобили, аэрокосмическое наведение и управление, трубопроводы и транспортные системы, а также для многих исследовательских тем, таких как течения, связанные с океаном, турбулентность, реагирующие потоки, глобальный климат, механика биологических жидкостей, обтекание магнитных лент и дисков, геофизические потоки, кинетика систем горения, динамика вихрей и многие другие. Обратитесь к упражнению «Выстрел под давлением», чтобы учащиеся использовали свое новое понимание для исследования реального применения водяных пистолетов!

Аэродинамика — это изучение свойств движущегося воздуха, который является основным компонентом конструкции автомобилей, мостов, систем отопления и вентиляции, газопроводов, самолетов и космических кораблей. Гидродинамика — это изучение сил, действующих на жидкости или со стороны жидкостей, что является основным компонентом военно-морской архитектуры или конструкции кораблей, а также океанской инженерии. Океанические и морские инженеры несут ответственность за изучение морской среды с целью проектирования нефтяных вышек и добывающих платформ, а также плавучих судов и систем подводных трубопроводов, необходимых в процессе добычи нефти. Инженеры-гидротехники используют гидравлику или использование энергии жидкости для выполнения работы при проектировании тяжелой техники, систем распределения воды, канализационных сетей, систем управления ливневыми стоками, мостов, плотин, каналов, каналов и дамб. Различные подводные аппараты и дистанционно управляемые аппараты, разработанные инженерами, широко используются государственными и научными исследователями и необходимы для открытия глубоководных сообществ и исследования бездны океана, поскольку они могут достигать глубин, намного больших, чем предыдущие спутниковые и корабельные технологии.

Связанные виды деятельности

• Плавучесть и давление в жидкостях: Декартовский дайвер в бутылке с газировкой. Учащиеся соблюдают закон Паскаля, принцип Архимеда и закон идеального газа, когда декартовский дайвер движется в замкнутой системе.

  Посмотреть это занятие на YouTube

• Камень и лодка: плотность, плавучесть и принцип Архимеда. Учащиеся соблюдают принцип Архимеда и используют терминологию, изученную в классе, а также критическое мышление для вывода уравнений, необходимых для ответа на контрольный вопрос: влияет ли бросание камня за борт на уровень воды в воде? пруд поднимается, опускается или остается прежним?

  Посмотреть это занятие на YouTube

• Выстрел под давлением — учащиеся применяют свое понимание физики снарядов и гидродинамики, чтобы найти давление воды в водяных пистолетах.

  Посмотреть это занятие на YouTube

Закрытие урока

Задайте учащимся те же вопросы для обсуждения, которые задавались перед уроком, но на этот раз ожидайте, что они ответят уверенно и докажут свои ответы, используя уравнения, словарные слова и конкретные законы/принципы, изученные на этом уроке.

Кто знает, почему корабли плавают? (Ответ: Вес воды, вытесненной корпусом корабля, больше, чем вес самого корабля. Попросите учащихся подумать о небольших рыбацких лодках и круизных лайнерах.)

Когда вы плаваете в бассейне, вы чувствуете себя легче или тяжелее, чем когда вы идете по Земле? Насколько ты легче? (Ответ: в бассейне вы чувствуете себя легче, потому что кажущаяся потеря веса равна весу воды, вытесненной вашим телом.)

Кто слышал термин гидравлика? Каковы примеры гидравлических устройств? Кто знает, что это значит и как это работает? (Ответ: инженеры-гидротехники используют гидравлику или использование энергии жидкости для выполнения работы при проектировании тяжелого оборудования, систем распределения воды, канализационных сетей, систем управления ливневыми стоками, мостов, плотин, каналов и дамб. )

Какие другие примеры принципа Архимеда, закона Паскаля и принципа Бернулли вы можете привести? Можете ли вы придумать какие-либо инженерные приложения, связанные с этими концепциями? (Ответ: Понятия закона Паскаля, принципа Архимеда и принципа Бернулли важны в инженерных и технологических приложениях, таких как аэродинамика и гидродинамика, гидравлика, плавучие суда, подводные лодки, самолеты, автомобили, аэрокосмическое наведение и управление, трубопроводы и транспортные системы, и многие темы исследований, такие как течения, связанные с океаном, турбулентность, реагирующие потоки, глобальный климат, механика биологических жидкостей, обтекание магнитных лент и дисков, геофизические течения, кинетика систем горения и динамика вихрей.)

Словарь/Определения

Принцип Архимеда: любой объект, частично или полностью погруженный в жидкость, испытывает направленную вверх силу, по величине равную весу жидкости, вытесненной этим объектом.

Принцип Бернулли: давление в жидкости уменьшается по мере увеличения скорости жидкости.

Плавучесть: способность объекта плавать в жидкости.

выталкивающая сила: направленная вверх сила, действующая на объект, частично или полностью погруженный в жидкость (равная разнице между весом объекта в воздухе и весом объекта в жидкости).

плотность: измерение компактности объекта.

жидкость: материя, которая течет (может быть жидкостью или газом).

ламинарный поток: когда частицы жидкости движутся по одному и тому же гладкому пути, который называется линией тока.

масса: Измерение количества материи в объекте.

массовая плотность: Масса на единицу объема вещества

Закон Паскаля: Давление, приложенное к жидкости в закрытом сосуде, передается одинаково на все точки жидкости и на стенки сосуда.

давление: измерение силы на единицу площади.

турбулентный поток: когда частицы жидкости движутся неравномерно, вызывая изменения скорости, которые могут образовывать вихревые потоки.

объем: измерение объема пространства, занимаемого объектом.

вес: измерение силы, действующей на объект из-за гравитации.

Оценка

Оценка перед уроком

Вопросы для обсуждения: Задайте учащимся следующие вступительные вопросы, чтобы оценить их базовые знания по темам урока. Эти же вопросы будут заданы в конце урока.

• Кто знает, почему корабли плавают?
• Когда вы плаваете в бассейне, вы чувствуете себя легче или тяжелее, чем когда вы идете по Земле? Насколько ты легче?
• Кто слышал термин гидравлика? Каковы примеры гидравлических устройств? Кто знает, что это значит и как это работает?

Оценка после внедрения

Примеры задач: Предложите учащимся решить примеры задач, встроенные в презентацию Fluids, как описано ниже. Просмотрите ответы учащихся, чтобы оценить их понимание тем урока и определить, какие концепции и уравнения требуют дальнейшего объяснения.

• Слайд 7 : Перерисуйте изображение на доске, но измените числа. Например, пусть вес весов составляет 15 фунтов, а вес воды в миске — 7 фунтов. Чтобы проверить понимание учащимися этой концепции, спросите учащихся, насколько тяжел вес, когда он погружен в воду. Ответ: 8 фунтов.
• Слайд 10 : Попросите учащихся найти вес воды, вытесненной короной на изображении. Ответ 1,3 кг. Затем снова нарисуйте ту же диаграмму на доске и обозначьте вес слева как 23,2 кг и попросите учащихся определить значение шкалы справа, если выталкивающая сила равна 3,7 кг. Ответ 22,5 кг.
• Слайд 15 : Попросите учащихся решить P ₁ , используя уравнение на слайде 13. Ответ: P ₁ = 10 Па. ₂ и F ₂ Используя взаимосвязь P ₁ = P ₄₉ . Ответ: P ₂ = 10 Па и F ₂ = 100 Н.
• Slide 18 : Какой рисунок демонстрирует ламинарное и турбулентное течение? (A, верхний рисунок с прямыми стрелками представляет ламинарный поток; B, нижний рисунок с изогнутыми стрелками представляет турбулентный поток.) ​​Каковы некоторые примеры каждого из различных типов потока? (Примеры ламинарного потока включают медленно текущие потоки и воду, вытекающую из кранов раковины. Примеры турбулентного потока включают дым от пожаров или других горящих предметов, течения и бурные потоки.)
• Слайд 22 : Учащимся предоставлены примеры чисел для подстановки в уравнение Бернулли на разной высоте, чтобы они могли узнать, что сокращается (если есть) и как применять уравнение.

Итоги урока Оценка

Ответы на вопросы для обсуждения по физике: Задайте те же вопросы для обсуждения, что и до урока, но на этот раз ожидайте, что учащиеся ответят уверенно и с доказательствами, включая уравнения, словарные слова и конкретные законы/принципы, изученные на этом уроке. Ответы см. в разделе «Завершение урока».

Домашнее задание

Практические задачи: Поручите учащимся заполнить лист практических задач в качестве домашнего задания. Используйте рубрику «Решение задач по физике», чтобы просмотреть ответы учащихся и оценить их понимание понятий.

использованная литература

Physics Guide (предварительная публикация). First Examinations 2016. International Baccalaureate Organization 2013, стр. 118. (Поскольку гидромеханика не преподается в государственных средних школах, это руководство IB по физике использовалось в основном для целей обучения на этом уроке.) Март 2013 г. http://tinyurl.com/msfpep9

Другая связанная информация

Просмотрите центр учебных программ по физике, ориентированных на инженеры NGSS, чтобы найти дополнительную учебную программу по физике и физическим наукам, посвященную инженерии.

No related posts.