Примеры модули: Примеры решения уравнений с модулем с ответами

alexxlab / / Разное

Содержание

Примеры решения уравнений с модулем с ответами

Алгоритм решения уравнений с модулем

Теорема

Уравнения с модулем – это уравнения, содержащее неизвестные под знаком модуля.

При решении уравнений с модулем используется определение модуля числа.

Определение модуля числа.

   

Нужна помощь в написании работы?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Заказать работу

Примеры решений уравнений с модулем

Пример 1

Задача

Решить уравнение:

   

Решение

   

Подмодульное выражение меняет знак в точке .

Рассмотрим два случая.

Первый случай:

При исходное уравнение принимает вид:

   

Отсюда – решений нет

Второй случай:

При исходное уравнение принимает вид:

   

Отсюда

Ответ

Пример 2

Задача

Решить уравнение:

   

Решение

Подмодульное выражение меняет знак в точке .

Рассмотрим два случая.

Первый случай:

При исходное уравнение принимает вид:

   

Отсюда

Второй случай:

При исходное уравнение принимает вид:

   

Отсюда

Ответ

Пример 3

Задача

Решить уравнение:

   

Решение

Подмодульное выражение меняет знак в точке .

Рассмотрим два случая.

Первый случай:

При исходное уравнение принимает вид:

   

Отсюда

Второй случай:

При исходное уравнение принимает вид:

   

Отсюда – решений нет

Ответ

Пример 4

Задача

Решить уравнение:

   

Решение

Подмодульное выражение меняет знак в точке .

Рассмотрим два случая.

Первый случай:

При исходное уравнение принимает вид:

   

Отсюда

Второй случай:

При исходное уравнение принимает вид:

   

Отсюда – решений нет

Ответ

Пример 5

Задача

Решить уравнение:

   

Решение

Подмодульное выражение меняет знак в точке .

Рассмотрим два случая.

Первый случай:

При исходное уравнение принимает вид:

   

Отсюда

Второй случай:

При исходное уравнение принимает вид:

   

Отсюда

Ответ

Пример 6

Задача

Решить уравнение:

   

Решение

Подмодульное выражение меняет знак в точке .

Рассмотрим два случая.

Первый случай:

При исходное уравнение принимает вид:

   

Отсюда

Второй случай:

При исходное уравнение принимает вид:

– не подходит по условию

Ответ

Пример 7

Задача

Решить уравнение:

   

Решение

   

Подмодульное выражение меняет знак в точке .

Рассмотрим два случая.

Первый случай:

   

   

Отсюда

Второй случай:

   

   

   

   

Отсюда

Ответ

Пример 8

Задача

Решить уравнение:

   

Решение

Подмодульное выражение меняет знак в точке .

Рассмотрим два случая.

Первый случай:

   

   

   

Решений нет

Второй случай:

   

   

   

Решений нет

Ответ

Решений нет

Пример 9

Задача

Решить уравнение:

   

Решение

Подмодульное выражение меняет знак в точке .

Рассмотрим два случая.

Первый случай:

При исходное уравнение принимает вид:

   

Отсюда

Второй случай:

При исходное уравнение принимает вид:

   

Отсюда

Ответ

Пример 10

Задача

Решить уравнение:

   

Решение

Рассмотрим три случая.

Первый случай:

При исходное уравнение принимает вид:

   

Отсюда – решений нет, т.к. по условию

Второй случай:

При исходное уравнение принимает вид:

   

   

Отсюда

Третий случай:

При исходное уравнение принимает вид:

   

Отсюда

Ответ

Средняя оценка 3 / 5. Количество оценок: 13

Поставьте вашу оценку

Сожалеем, что вы поставили низкую оценку!

Позвольте нам стать лучше!

Расскажите, как нам стать лучше?

39618

Закажите помощь с работой

Не отобразилась форма расчета стоимости? Переходи по ссылке

Не отобразилась форма расчета стоимости? Переходи по ссылке

Уравнение с модулем

Уравнение с модулем достаточно сложная тема для начинающих. Учитывая это обстоятельство, в данный урок войдут только элементарные уравнения.

Что такое уравнение с модулем и как его решить?

В уравнениях с модулем неизвестное значение содержится под знáком модуля. Например:

|x − 2| = 5

Уравнения с модулем бывают разными и решаются они различными методами. Нельзя сказать что какой-то метод наиболее рационален. Всё зависит от исходного уравнения.

Например, в каких-то уравнениях можно просто угадать корень, в то время как в других нужно логически мыслить, раскрывать модули, выполнять тождественные преобразования. Человек волен выбирать каким методом решения пользоваться.

К примеру, решим вышеприведённое уравнение |x − 2| = 5. Допустим, что мы не знаем ни одного метода решения. Как бы мы его решили?

Прежде всего заметим, что правая часть данного уравнения равна числу 5. Слева же располагается модуль из выражения |x − 2|. Это означает что подмодульное выражение x − 2 должно равняться числу 5 или −5

Значит нужно выяснить при каких значениях переменной x подмодульное выражение x − 2 будет обращаться в число 5 или −5.

Искомые значения x найдутся если приравнять подмодульное выражение к числу 5 и −5, а затем поочерёдно решить каждое из уравнений:

Значит корнями уравнения |x − 2| = 5 являются числа 7 и −3.

Большинство элементарных уравнений с модулем можно решить используя правило раскрытия модуля. Для этого раскрывают модуль содержащийся в уравнении, затем получившееся выражение подставляют в исходное уравнение вместо выражения с модулем.

Раскрывать модуль нужно для каждого из случаев: когда подмодульное выражение больше или равно нулю, и когда подмодульное выражение меньше нуля.

Решим наше уравнение |x − 2| = 5 с помощью правила раскрытия модуля. Выпишем отдельно его модуль и раскроем его:

В этой конструкции говорится, что если подмодульное выражение x − 2 больше или равно нулю, то модуль раскроется как x − 2, и тогда исходное уравнение примет вид x − 2 = 5, откуда x = 7

А если же подмодульное выражение x − 2 меньше нуля, то модуль раскроется как −(x − 2). Тогда исходное уравнение примет вид −(x − 2) = 5, откуда x = −3

Итак, уравнение |x − 2|= 5 имеет корни 7 и −3. Для проверки подстáвим числа 7 и −3 в исходное уравнение вместо x. Тогда получим верное равенство:

Подмодульное выражение как правило содержит такое x, которое может обращать всё подмодульное выражение как в положительное число, так и в отрицательное, либо вообще в ноль.

Поэтому модуль и раскрывается для каждого из случаев: когда подмодульное выражение больше или равно нулю, и когда подмодульное выражение меньше нуля. Каждый из случаев будет давать независимое уравнение со своим корнем.

Вернёмся теперь к моменту, где мы раскрывали модуль:

Условия x − 2 ≥ 0 и x − 2 < 0 являются неравенствами, которые можно решить, тем самым приведя их к простому виду:

Символ ⇔ означает равносильность. В данном случае указывается, что условие x − 2 ≥ 0 равносильно условию x ≥ 2, а условие x − 2 < 0 равносильно условию x < 2.

Такой вид записи условий позволяет однозначно сказать при каких x модуль будет раскрываться с плюсом, а при каких с минусом.

В первом случае получилось условие x ≥ 2. Это значит что при всех x бóльших либо равных 2, модуль |x − 2| будет раскрываться с плюсом. Так, при x = 7, подмодульное выражение станет равно 5

|7 − 2| = |5|

А значит дальнейшее раскрытие будет с плюсом

|7 − 2| = |5| = 5

Таким же образом модуль |x − 2| будет вести себя и с другими значениями x на промежутке x ≥ 2. То есть, будет раскрываться с плюсом. Примеры:

При x = 3, |3 − 2|=|1| = 1
При x = 4, |4 − 2|=|2| = 2
При x = 2, |2 − 2|=|0| = 0
При x = 13, |13 − 2|=|11| = 11

А во втором случае получилось условие x < 2. Это значит что при всех x мéньших 2, модуль будет раскрываться с минусом. Так, при x = −3, подмодульное выражение опять же станет равно 5. Но в промежуточных вычислениях можно увидеть, что модуль раскрывается с минусом:

|−3 − 2| = |−5| = −(−5) = 5

Модуль |x − 2| будет вести себя так же и с другими значениями x на промежутке x < 2. Примеры:

При x = 1, |1 − 2|=|−1| = −(−1) = 1
При x = 0, |0 − 2|=|−2| = −(−2) = 2
При x = −1, |−1 − 2|=|−3| = −(−3) = 3
При x = −9,|−9 − 2|=|−11| = −(−11) = 11

Число 2 является своего рода точкой перехода, в которой модуль |x − 2| меняет свой порядок раскрытия.

Можно представить как модуль |x − 2| двигался по маршруту от минус бесконечности до числа 2, раскрываясь в каждой точке с минусом. Попав в точку 2, модуль поменял свой порядок раскрытия — а именно раскрывшись в точке 2 с плюсом, он далее стал раскрываться с плюсом, двигаясь в правую часть к плюс бесконечности.

С помощью координатной прямой это можно представить так:

Красные знаки минуса и плюса указывают, как будет раскрываться модуль |x − 2| на промежутках x < 2 и x ≥ 2.

Точку перехода можно найти для любого модуля. Для этого нужно узнать при каких x подмодульное выражение равно нулю. Ноль это то значение, до и после которого модуль всегда сохраняет свой знак. Это следует из правила раскрытия модуля:

В этом примере в момент когда x станет равным нулю, модуль |x| раскроется с плюсом и далее при всех x, бóльших нуля, будет раскрываться с плюсом. Напротив, при всех x, мéньших нуля модуль будет раскрываться с минусом:

А например для модуля |2x + 6| точкой перехода будет число −3, потому что при его подстановке в подмодульное выражение 2x + 6 вместо x, данное подмодульное выражение станет равно нулю. Изобразим это на рисунке:

При всех x, бóльших либо равных −3, модуль будет раскрываться с плюсом. Примеры:

При x = −3, |2 × (−3) + 6| = |0| = 0
При x = 4, |2 × 4 + 6| = |14| = 14
При x = 5, |2 × 5 + 6| = |16| = 16

А при всех x, мéньших 3, модуль будет раскрываться с минусом. Примеры:

При x = −4, |2 × (−4) + 6| = |−2| = −(−2) = 2
При x = −5, |2 × (−5) + 6| = |−4| = −(−4) = 4
При x = −6, |2 × (−6) + 6| = |−6| = −(−6) = 6

Пример 2. Решить уравнение |x| + 3x = −2

Решение

Раскроем модуль, который содержится в левой части уравнения:

Если x ≥ 0, то модуль раскроется со знаком плюс и тогда исходное уравнение примет вид x + 3x = −2. Сразу решим это уравнение:

Теперь рассмотрим второй случай — когда x < 0. В этом случае модуль в исходном уравнении раскроется со знаком минус, и тогда получится уравнение −x + 3x = −2. Решим и это уравнение:

Получили корни и −1.

Выполним проверку, подставив найденные корни в исходное уравнение. Проверим корень

Видим, что при подстановке корня исходное уравнение не обращается в верное равенство. Значит не является корнем исходного уравнения.

Проверим теперь корень −1

Получили верное равенство. Значит из двух найденных решений только −1 является корнем уравнения.

Ответ: −1.

Здесь можно сделать важный вывод. В уравнениях с модулем найденные корни не всегда удовлетворяют исходному уравнению. Чтобы убедиться в правильности своего решения, нужно выполнять проверку, подставляя найденные корни в исходное уравнение.

Кроме того, проверить является ли найденное значение корнем уравнения можно с помощью условия, согласно которому был раскрыт модуль.

Так, в данном примере мы раскрывали модуль |x| для случаев когда подмодульное выражение больше или равно нулю, и когда подмодульное выражение меньше нуля:

Условия x≥0 и x<0 являются неравенствами. В эти неравенства можно подставлять найденные корни. Если неравенства окажутся верными, значит корни удовлетворяют исходному уравнению.

Так, при раскрытии модуля со знаком плюс, получилось уравнение x + 3x = −2. Корнем этого уравнения стало число . Это число не удовлетворяет условию x ≥ 0, согласно которому был раскрыт модуль |x| и согласно которому было получено уравнение x + 3x = −2. Действительно, при подстановке числа в неравенство x ≥ 0 получается неверное неравенство.

А при раскрытии модуля со знаком минус, получилось уравнение −x + 3x = −2. Корнем этого уравнения стало число −1. Это число удовлетворяет условию x<0, согласно которому был раскрыт модуль |x| и согласно которому было получено уравнение −x + 3x = −2. Действительно, при подстановке числа −1 в неравенство x < 0 получается верное неравенство.

Пример 3. Решить уравнение |1 − 2x| − 4x = −6

Решение

Раскроем модуль:

При раскрытии модуля |1 − 2x| со знаком плюс, получим уравнение 1 − 2x − 4x = −6. Решим его:

При раскрытии модуля |1 − 2x| со знаком минус, получим уравнение −1 + 2x − 4x = −6. Решим его:

Получили корни и .

Корень не удовлетворяет условию , значит не является корнем исходного уравнения.

Корень удовлетворяет условию , значит является корнем исходного уравнения. Проверка также покажет это:

Ответ: .

Пример 4. Решить уравнение |x2 − 3x| = 0

Решение

Если модуль числа равен нулю, то подмодульное выражение тоже равно нулю:

То есть можно не раскрывать модуль. Достаточно узнать при каких значениях x подмодульное выражение равно нулю. В данном случае для этого нужно решить неполное квадратное уравнение:

Получили корни 0 и 3. Оба корня удовлетворяют исходному уравнению. Проверка показывает это:

Пример 5. Решить уравнение x2 − 5|x| + 6 = 0

Выпишем отдельно модуль |x| и раскроем его:

При раскрытии модуля |x| со знаком плюс, исходное уравнение примет вид x2 − 5x + 6 = 0. Это квадратное уравнение. Решим его с помощью дискриминанта:

Оба корня удовлетворяют условию x ≥ 0, значит являются корнями исходного уравнения.

При раскрытии модуля |x| со знаком минус, исходное уравнение примет вид x2 + 5x + 6 = 0. Это тоже квадратное уравнение. Решим его как и предыдущее:

При условии x ≥ 0, модуль из уравнения раскрылся с плюсом, получились корни 3 и 2. Оба корня удовлетворяют условию x ≥ 0, значит удовлетворяют и исходному уравнению.

При условии x < 0, модуль из уравнения раскрылся с минусом, получились корни −2 и −3. Оба корня удовлетворяют условию x < 0, значит удовлетворяют и исходному уравнению.

Ответ: 3, 2, −2 и −3.

Сведéние уравнения с модулем в совокупность

Большинство элементарных уравнений с модулем можно решить сведéнием их к так называемой совокупности уравнений.

Элементарными мы будем называть те уравнения с модулем, в которых левая часть является модулем из какого-то выражения, а правая часть — числом. Например, |x| = 3  или |2x − 1| = 3.

Решим наше самое первое уравнение |x − 2| = 5 сведéнием его к совокупности уравнений. Корнями этого уравнения были числа 7 и −3. Это уравнение тоже считается элементарным.

Если раскрыть модуль |x − 2| со знаком плюс, то уравнение |x − 2| = 5 примет вид x − 2 = 5.

Если раскрыть модуль |x − 2| со знаком минус, то уравнение |x − 2| = 5 примет вид −(x − 2) = 5, то есть −x + 2 = 5.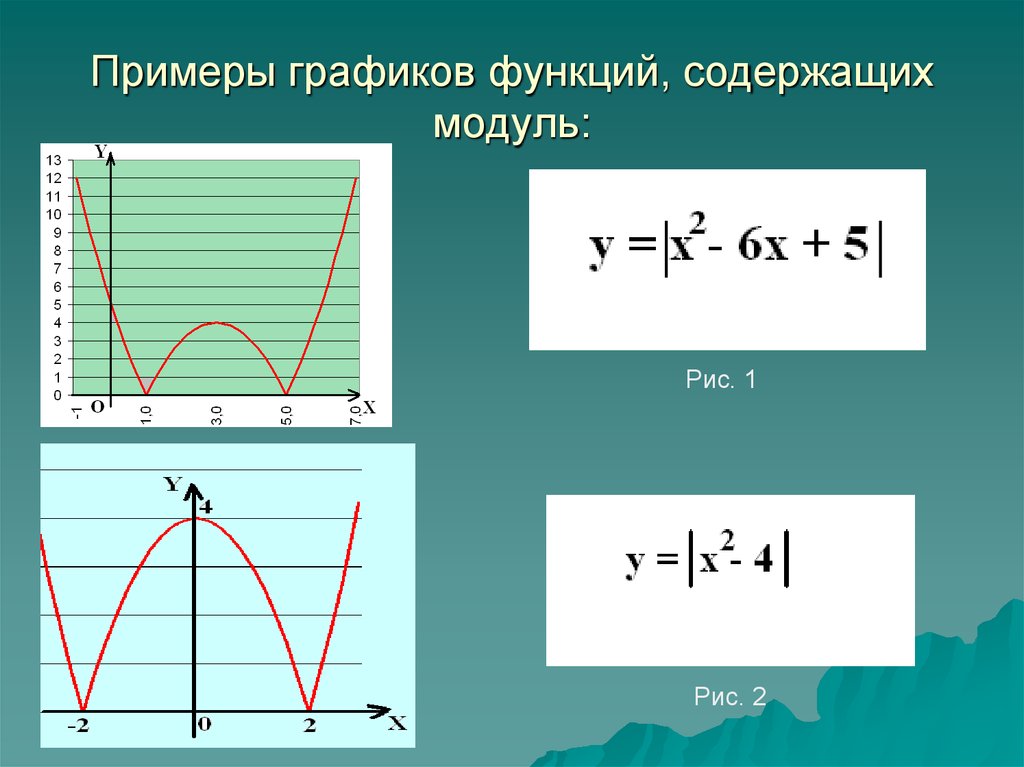

Видим, что из уравнения |x − 2| = 5 получилось два уравнения: x − 2 = 5 и −x + 2 = 5. Причём каждое из уравнений имеет свой собственный корень. Уравнение x − 2 = 5 имеет корень 7, а уравнение −x + 2 = 5 — корень −3

Выпишем уравнения x − 2 = 5 и −x + 2 = 5 и объединим их квадратной скобкой:

Такой вид записи называют совокупностью уравнений.

Совокупность уравнений — это несколько уравнений, объединённых квадратной скобкой, и имеющих множество решений, которые удовлетворяют хотя бы одному из уравнений, входящих в данную совокупность.

Так, число 7 является решением совокупности потому что это число удовлетворяет первому уравнению х − 2 = 5.

Число −3 тоже является решением данной совокупности, поскольку удовлетворяет второму уравнению −х + 2 = 5.

Вместе же числа 7 и −3 образуют множество решений данной совокупности.

В отличие от системы уравнений, совокупность состоит из уравнений, которые не зависят друг от друга. Для каждого уравнения, входящего в совокупность, значение переменной x будет разным. А в системе уравнений значение переменной x удовлетворяет как первому уравнению, так и второму.

Решить совокупность уравнений означает найти множество решений, которые удовлетворяют хотя бы одному из уравнений, входящих в данную совокупность.

Решим каждое уравнение совокупности по-отдельности. Это обычные линейные уравнения, которые легко решаются:

Символ ⇔ как было ранее сказано означает равносильность. В данном случае он указывает на то, что все получающиеся совокупности равносильны друг другу.

Итак, мы получили корни 7 и −3. Поскольку эти два числа являются решениями совокупности , то значит являются и решениями уравнения |x − 2| = 5.

В исходную совокупность можно включать условия, согласно которым был раскрыт модуль. В этом случае каждое уравнение вместе со своим условием обрамляется знаком системы.

Дополним предыдущую совокупность условиями, согласно которым был раскрыт модуль. К первому уравнению x − 2 = 5 добавим условие x − 2 ≥ 0, а ко второму уравнению −x + 2 = 5 добавим условие x − 2 < 0

Решение каждого уравнения должно удовлетворять своему условию. Поэтому условия и уравнения обрамлены знáком системы.

Решим получившуюся совокупность с условиями. Условия являются неравенствами, которые тоже можно решать:

В первом случае получили корень 7, который удовлетворяет своему условию x ≥ 2. Во втором случае получили корень −3, который удовлетворяет своему условию x < 2.

Не следует бояться таких записей. Это лишь подробное решение, показывающее что откуда взялось. Чаще всего решение можно записать покороче.

Существует схема для сведéния в совокупность уравнения вида |x| = a. Выглядит эта схема так:

Данная схема легко позволяет свести уравнение с модулем в совокупность. Эту схему можно прочитать так: «Если выражение |x| равно a, то подмодульное выражение равно a или −a»

Квадратная скобка в совокупностях заменяет собой слово «или».

Например, уравнение |x| = 5 можно свести в совокупность, рассуждая так: если выражение |x| равно 5, то подмодульное выражение равно 5 или −5.

А применительно к нашему предыдущему примеру можно рассуждать так: если |x − 2| равно 5, то подмодульное выражение равно 5 или −5

Это та же самая совокупность, что и в прошлый раз. Убедитесь в этом, умножив обе части второго уравнения на −1.

В уравнениях где слева модуль, а справа число, мы будем чаще использовать именно такой способ записи совокупности. Он позволяет не прибегать к правилу раскрытия модуля, а сразу получить совокупность.

Но надо помнить, что эта схема будет работать только для уравнений вида |x| = a. То есть для уравнений, у которого слева модуль, а справа число.

Пример 2. Решить уравнение |2x − 1| = 3

Решение

У этого уравнения слева модуль, а справа число. Значит его можно свести в совокупность, воспользовавшись схемой

Если выражение |2x − 1| равно 3, то подмодульное выражение 2x − 1 равно 3 или −3

Теперь решим каждое уравнение совокупности по отдельности:

Ответ: 2 и −1.

Пример 3. Решить уравнение |x + 2| − 3 = 8

Решение

В некоторых случаях прежде чем свести исходное уравнение в совокупность, его следует упростить.

Так, в данном случае −3 следует перенести в правую часть, изменив знак:

Получили уравнение |x + 2| = 11. Если выражение |x + 2| равно 11, то подмодульное выражение x + 2 равно 11 или −11

Решим данную совокупность:

Ответ: 9 и −13.

Пример 4. Решить уравнение  4|x| + 4 = 2|x| + 10

Решение

Перенесём 2|x| из правой части в левую часть, а 4 перенесём из левой части в правую часть:

4|x| − 2|x| = 10 − 4
2|x| = 6

Разделим обе части получившегося уравнения на 2. Тогда получится простое уравнение с модулем:

Ответ: 3 и −3.

Пример 5. Решить уравнение

Решение

Если выражение |2 − 5x2| равно 3, то подмодульное выражение 2 − 5x2 равно 3 или −3

В обоих уравнениях перенесём 2 в правую часть, изменив знак:

В первом уравнении разделим обе части на −5. Во втором уравнении так же разделим обе части на −5. Тогда получим два квадратных уравнения

Первое уравнение не имеет корней, потому что квадрат любого числа положителен, а в данном случае он равен отрицательному числу. Корнями второго уравнения являются числа 1 и −1, поскольку вторая степень этих чисел равна единице.

Ответ: 1 и −1.

Пример 6. Решить уравнение |x + 6| + 4x = 5

Решение

Данное уравнение не является уравнением вида |x| = a, значит не получится воспользоваться схемой .

Чтобы свести данное уравнение в совокупность, нужно сначала раскрыть его модуль, затем записать совокупность из получившихся уравнения.

Раскроем модуль |x + 6|

Если x + 6 ≥ 0 , то модуль раскроется со знаком плюс и тогда исходное уравнение примет вид x + 6 + 4x = 5

Если x + 6 < 0, то модуль раскроется со знаком минус и тогда исходное уравнение примет вид −x − 6 + 4x = 5. Получим следующую совокупность:

Дальнейшее решение элементарно:

Из найденных корней только является корнем исходного уравнения, поскольку удовлетворяет условию x ≥ −6. А корень не является корнем уравнения, поскольку не удовлетворяет условию x < −6.

Ответ:

Наиболее простой вид

Наиболее простой вид уравнения с модулем выглядит так:

| x | = a

где x — корень уравнения, a — произвольное число, бóльшее или рáвное нулю. То есть a ≥ 0

Если условие a ≥ 0 не выполнено, то уравнение |x|= a корней не имеет. Это следует из определения модуля. Действительно, модуль всегда неотрицателен.

Приведем несколько примеров уравнений вида |x| = a

Пример 1. Решить уравнение |x| = 2

Решение

В данном случае сразу видно, что корнями являются числа 2 и −2. Ведь если вместо x подставить эти числа, то получим верное равенство: |−2| = 2 и |2| = 2. Решение для этого уравнения можно записать, сведя его в совокупность:

«Если выражение |x| равно 2, то подмодульное выражение x равно 2 или −2«

Ответ: 2 и −2

Пример 2. Решить уравнение |−x| = 4

Решение

Если выражение |−x| равно 4, то подмодульное выражение равно 4 или −4

Умножим оба уравнения на −1

Ответ: −4 и 4.

Пример 3. Решить уравнение |x| = −7

В данном случае корней нет, поскольку модуль всегда неотрицателен. А в данном случае модуль равен отрицательному числу.

Если уравнение с модулем не имеет корней, обычно пишут что x принадлежит пустому множеству:

x ∈ ø

Напомним, что пустым называют множество, не имеющее элементов.

Модуль внутри модуля

Рассмотрим уравнение:

В этом уравнении слева располагается модуль, который в свою очередь содержит внутри себя другой модуль, а справа уравнения располагается число. Такой вид уравнения с модулем можно решить, сведя его в совокупность с помощью схемы, которую мы рассмотрели ранее:

В нашем случае если выражение равно 9, то подмодульное выражение |2 + x| + 3 равно 9 или −9

В получившейся совокупности имеется два уравнения с модулем. Эти уравнения тоже в свою очередь следует свести в совокупность. Но сначала немного упростим эти уравнения. В первом и во втором уравнении перенесем 3 в правую часть, изменив знак. Тогда получим:

Теперь сведём эти уравнения в совокупности. Первое уравнение распадётся на следующую совокупность:

Сразу решим совокупность . Первый корень равен 4, второй −8.

Теперь решим второе уравнение |2 + x| = −12. Но замечаем, что его правая часть равна отрицательному числу. Это уравнение не имеет корней, потому что модуль не может равняться отрицательному числу.

Значит уравнение имеет корни 4 и −8. Проверим эти корни, подставив их в исходное уравнение

В данном случае оба корня удовлетворяют исходному уравнению.

Ответ: 4 и −8.

Вообще, уравнение с модулем внутри которого содержится другой модуль, тоже решается различными способами. Какой способ использовать зависит от самогó уравнения. Решим например следующее уравнение:

Здесь уже нельзя использовать схему потому что слева располагается не только модуль, но и переменная x. Конечно, переменную x можно перенести в правую часть, и тогда можно будет свести данное уравнение в совокупность:

Но тогда справа появляется переменная x, на которую нужно будет вводить дополнительное ограничение, чтобы правая часть уравнения не стала отрицательной. Такой способ решения мы рассмотрим позже. А пока решим исходное уравнение с помощью правила раскрытия модуля.

Чтобы раскрыть модули данного уравнения нужно сначала определиться где внешний и где внутренний модуль.

В уравнении внешним модулем является полностью левая часть , а внутренним модулем — выражение

Значение внешнего модуля зависит от внутреннего модуля, и раскрываться внешний модуль будет исходя от результата который получился в результате вычисления его подмодульного содержимого.

Например, если x = 3, то внутренний модуль |3 − x| примет значение 0, и в результате всё подмодульное выражение внешнего модуля станет равно −2. А это значит что внешний модуль будет раскрываться с минусом.

||3 − x| − x + 1| = ||3 − 3| − 3 + 1| = ||0| − 3 + 1| = |−2| = −(−2) = 2

А если например x = −2, то внутренний модуль |3 − x| примет значение 5, и в результате всё подмодульное выражение внешнего модуля станет равно 8. А это значит что внешний модуль будет раскрываться с плюсом:

||3 − x| − x + 1| = ||3 − (−2)| − (−2) + 1| = ||5| − (−2) + 1| = | 8 |=8

Поэтому решение будем начинать с раскрытия внутреннего модуля.

Если внутренний модуль раскроется с плюсом, то есть если 3 − x ≥ 0 (что равносильно неравенству x ≤ 3), то исходное уравнение примет вид:

Теперь уравнение имеет только внешний модуль. Решим его раскрыв модуль:

Если −2x + 4 ≥ 0, то:

Сейчас нас интересуют только те значения x при которых внутренний модуль раскрывается с плюсом, а это произойдет при условии x ≤ 3. Поэтому для наглядности рядом с найденным корнем указано, что он удовлетворяет условию x ≤ 3

Решаем далее. Если −2x + 4 < 0, то:

Несмотря на то, что оба найденных корня удовлетворяют уравнению |−2x+4|=6−x, мы исключаем корень из решений, потому что нас сейчас интересуют только те значения x, при которых внутренний модуль изначального уравнения раскрывается с плюсом. Поэтому рядом с корнем указано, что он не удовлетворяет условию x ≤ 3.

Итак, если внутренний модуль раскрывается с плюсом, исходное уравнение принимает вид |−2x + 4| = 6 − x и корнем этого уравнения является число −2.

Теперь решим исходное уравнение для случая, когда внутренний модуль раскрывается с минусом, то есть когда 3 − x < 0 (что равносильно неравенству x > 3). Внутренний модуль будет раскрываться с минусом при всех значениях x больших 3.

Если внутренний модуль раскроется с минусом, то исходное уравнение примет вид:

Модуль −2 равен 2. Тогда получаем простейшее линейное уравнение, корень которого равен 4

Получили корень 4, который удовлетворяет условию x > 3.

В итоге корнями уравнения являются числа −2 и 4.

Ответ: 2 и 4.

Пример 3. Решить уравнение ||x − 1| − 7| = 10

Решение

Слева располагается модуль, а справа число, значит можно применить схему:

В данном случае если выражение ||x − 1| − 7| равно 10, то подмодульное выражение |x − 1| − 7 равно 10 или −10. Получится совокупность из двух уравнений:

Упростим получившиеся уравнения. Перенесём число −7 в обоих уравнениях в правую часть, изменив знак:

Второе уравнение корней не имеет. Первое уравнение распадется на совокупность , корни которой 18 и −16.

Ответ: 18 и −16.

Решим это же уравнение с помощью раскрытия модулей. Начнем с внутреннего модуля.

Если x − 1 ≥ 0 (что равносильно x ≥ 1), то исходное уравнение примет вид:

Решим получившееся уравнение раскрыв модуль:

Далее решаем уравнение для случаев когда x − 8 ≥ 0 и x − 8 < 0

Сейчас нас интересуют те значения, при которых внутренний модуль исходного уравнения раскрывается с плюсом. А это будет при условии, что x ≥ 1. Этому условию удовлетворяет только значение 18, поэтому мы пометили его зеленой галочкой для наглядности.

Теперь решим исходное уравнение для случая, когда внутренний модуль раскрывается с минусом, то есть когда x − 1 < 0 (или что равносильно неравенству x < 1).

Если x − 1 < 0, то исходное уравнение примет вид:

Решим получившееся уравнение раскрыв модуль:

Далее решаем уравнение для случаев когда −x − 6 ≥ 0 и −x − 6 < 0

Из найденных корней только −16 удовлетворяет условию x < 1.

В итоге корнями уравнения ||x − 1| − 7| = 10 являются числа 18 и −16.

Видно, что с помощью схемы   данное уравнение решилось легче и быстрее, чем способом раскрытия модулей.

Слева модуль, а справа выражение с переменной

Решим следующее уравнение с модулем:

|4x − 3| = 3x

Здесь так же применима схема:

То есть, если выражение |4x − 3| равно 3x, то подмодульное выражение 4x − 3 должно равняться 3x или −3x.

Но в исходном уравнении переменная x содержится не только под знáком модуля, но и в правой части. Нам пока неизвестно какое значение примет переменная x. Если x примет отрицательное значение, то правая часть станет полностью отрицательной. В этом случае корней не будет, потому что модуль не может равняться отрицательному числу.

Поэтому, если мы хотим решить данное уравнение, то при сведéнии его в совокупность, дополнительно следует ввести ограничение в виде условия 3x ≥ 0. Это будет означать, что правая часть уравнения |4x − 3| = 3x должна быть больше либо равна нулю:

Совокупность и условие обрамлены знаком системы, потому что решения совокупности должны удовлетворять условию 3x ≥ 0.

Итак, решим совокупность. Условие 3x ≥ 0 является неравенством, которое тоже можно решить:

Получившиеся корни можно подставить в условие x ≥ 0 и посмотреть выполняется ли оно. Если выполняется, то найденные корни удовлетворяют уравнению. В данном случае при подстановке обеих корней в неравенство, оно выполняется. Проверка также показывает, что корни удовлетворяют уравнению:

Пример 2. Решить уравнение |2x − 1| = 5x − 10

Решение

Решим это уравнение таким же образом, как и предыдущее. Введём условие, требующее чтобы правая часть была больше либо равна нулю:

В данном случае только значение 3 удовлетворяет условию x ≥ 2. Оно же является единственным корнем исходного уравнения. Проверка показывает это:

А число не удовлетворяет условию x ≥ 2 и не является корнем исходного уравнения. Проверка также показывает это:

Видим, что модуль стал равен отрицательному числу, а это противоречит определению модуля и нашему условию x ≥ 2.

Пример 3. Решить уравнение

Решение

Это уравнение мы решили, когда учились решать уравнения с модулем внутри которых другой модуль. Теперь данное уравнение можно решить, сведя его в совокупность.

Для начала перенесём x в правую часть, изменив знак:

Теперь сведём данное уравнение в совокупность. Дополнительно введём условие в виде неравенства 6 − x ≥ 0

В левой части первого уравнения оставим модуль, остальные члены перенесём в правую часть. Тоже самое сделаем и со вторым уравнением. Также будем решать неравенство 6 − x ≥ 0, оно позволит в конце проверять найденные корни на соответствие:

Решим первое уравнение. Оно распадётся на следующую совокупность:

Получились корни −2 и 8. Из них только −2 удовлетворяет условию x ≤ 6.

Теперь решим второе уравнение. Оно является уравнением, содержащим переменную в правой части. При сведении его в совокупность дополним его условием −7 + 2x ≥ 0

Дальнейшее элементарно:

При решении второго уравнения получились корни и 4. Прежде чем сверять их с условием x ≤ 6 следует сверить их с условием под которое решалось уравнение |3 − x| = −7 + 2x. Условию удовлетворяет только корень 4.

В итоге корнями исходного уравнения являются числа −2 и 4.

Пример 4. Решить уравнение |4x + 20| = −6x

Решение

На первый взгляд покажется, что данное уравнение не имеет решений, потому что правая часть отрицательна. Но это не совсем так. Правая часть содержит переменную x, которая может принять отрицательное значение или ноль, и это приведёт к тому что правая часть станет положительной либо равной нулю. А такое уравнение имеет право на существование.

В данном случае мы решим это уравнение, сведя его в совокупность. Но при этом укажем, что правая часть должна быть больше или равна нулю:

Из найденных корней только корень −2 удовлетворяет исходному уравнению. Также он удовлетворяет нашему условию x ≤ 0.

Ответ: −2.

Когда обе части — модули

Решим следующее уравнение:

|x + 7| = |1 + 3x|

Обе части этого уравнения являются модулями. Раскроем эти модули. Будем учитывать все возможные случаи при их раскрытии.

Случай 1. Если x + 7 ≥ 0 и 1 + 3x ≥ 0, то модули в обеих частях раскроются со знаком плюс и тогда исходное уравнение примет вид:

x + 7 = 1 + 3x

Это простейшее линейное уравнение. Решим его:

Случай 2. Если x + 7 < 0 и 1 + 3x < 0, то модули в обеих частях раскроются со знаком минус и тогда исходное уравнение примет вид:

−(x + 7) = −(1 + 3x)

Раскроем скобки, получим:

−x − 7 = −1 − 3x

Замечаем, что если умножить обе части этого уравнения на −1, то получается уравнение x + 7 = 1 + 3x. А это уравнение мы получали в результате раскрытия модулей со знаком плюс.

То есть уравнения x + 7 = 1 + 3x и −x − 7 = −1 − 3x являются равносильными, а значит имеют одни и те же корни. Убедимся в этом, решив уравнение −x − 7 = −1 − 3x

Поэтому, раскрыв модули со знаком плюс, нет необходимости раскрывать их со знаком минус, потому что в обоих случаях получаются уравнения, имеющие одни и те же корни.

Следующий случай это когда x + 7 ≥ 0 и 1 + 3x < 0. Тогда исходное уравнение примет вид x + 7 = −1 − 3x. Найдём корень этого уравнения:

И последний случай это когда x + 7 < 0 и 1 + 3x ≥ 0. Тогда уравнение примет вид −x − 7 = 1 + 3x. Если умножить это уравнение на −1, то получим уравнение x + 7 = −1 − 3x. А это уравнение мы получали, когда рассматривали предыдущий случай (случай x + 7 ≥ 0 и 1 + 3x < 0).

Следовательно, уравнение −x − 7 = 1 + 3x равносильно предыдущему уравнению x + 7 = −1 − 3x. Убедимся в этом решив уравнение −x − 7 = 1 + 3x

Значит раскрыв левую часть со знаком плюс, а правую часть со знаком минус, нет необходимости раскрывать левую часть со знаком минус, а правую часть со знаком плюс, потому что в обоих случаях получаются уравнения, имеющие одни и те же корни.

Вообще, если в уравнении обе части являются модулями как в данном примере, то это уравнение можно свести в следующую совокупность:

В этой конструкции уравнение вида |a| = |b| сведено в совокупность из двух уравнений a = b и a = −b. Видно что первое уравнение получается путем раскрытия обоих модулей со знаком плюс, а второе уравнение — путем раскрытия модуля |a| со знаком плюс, а модуля|b|— со знаком минус.

Важно. Данная схема работает только тогда, когда обе части являются модулями без посторонних членов. Проще говоря, если будет дано уравнение, например |a| = |b| + c, то приведенную схему использовать нельзя.

Пример 2. Решить уравнение |2 − 3x| = |x + 5|

Решение

Обе части данного уравнения являются модулями. Воспользуемся схемой:

У нас получится совокупность из двух уравнений. В первом уравнении оба модуля будут раскрыты со знаком плюс, во втором уравнении — модуль |2 − 3x| будет раскрыт со знаком плюс, а модуль |x + 5| со знаком минус:

Выполним проверку:

Ответ:   и 

Пример 3. Решить уравнение |x2 − 13x + 35|=|35 − x2| 

Решение

Обе части данного уравнения являются модулями. Воспользуемся схемой:

У нас получится совокупность из двух уравнений. В первом уравнении оба модуля будут раскрыты со знаком плюс. Во втором уравнении — модуль |x2 − 13x + 35| будет раскрыт со знаком плюс, а модуль |35 − x2| со знаком минус:

Приведём подобные члены в обоих уравнениях:

Первое уравнение является неполным квадратным. Решим его, вынеся x за скобки. Второе уравнение решается элементарно:

Ответ:   ,  , 0.

Когда решение — числовой промежуток

Нередко приходиться решать уравнения с модулем, где корнями являются не один или два числа, а числовой промежуток. Таковым, например, является уравнение:

|5x + 3| = −5x − 3

Раскроем модуль этого уравнения:

Если раскрыть модуль со знаком плюс, то получается уравнение 5x + 3 = −5x − 3. Решим его:

А если раскрыть модуль со знаком минус, то получится уравнение −5x − 3 = −5x − 3. В этом уравнении обе части являются одинаковыми, а значит данное равенство является тождеством. Оно будет верно при любом значении x. Значит корнями уравнения −5x − 3 = −5x − 3 являются все числа от минус бесконечности до плюс бесконечности:

x ∈ (−∞; +∞)

Но надо помнить про условия, согласно которым были раскрыты модули. В первом случае мы получили корень . Он будет верен только при условии что . Это условие соблюдено. Проверка также показывает что корень подходит:

Значит один из корней уравнений равен

Во втором случае мы получили множество корней от минус бесконечности до плюс бесконечности. Но это будет верно только при условии что

Например, если взять любое число из промежутка (−∞; +∞), но которое не будет удовлетворять условию , то это число не будет обращать наше уравнение в верное равенство.

Например, число 2 принадлежит промежутку (−∞; +∞), но не удовлетворяет условию , а значит число 2 не является корнем исходного уравнения. Проверка также покажет это:

А если взять к примеру число −5, то оно будет принадлежать промежутку (−∞; +∞) и удовлетворять условию , а значит будет обращать исходное уравнение в верное равенство:

Поэтому ответ надо записать так, чтобы были выполнены оба условия   и . Для наглядности нарисуем координатную прямую и обозначим её как x

Отметим на ней наш первый корень

Раскрыв модуль со знаком минус и решив получившееся уравнение, мы получили в ответе множество всех чисел от минус бесконечности до плюс бесконечности, но при этом было дано условие . Значит более точным ответ в этом случае будет таким:

Корнями уравнения −5x − 3 = −5x − 3 при условии являются все числа от минус бесконечности до

Значит на координатной прямой нужно заштриховать область слева от числа . Они будут иллюстрировать числа, меньшие

Число тоже является верным корнем исходного уравнения. Он был получен при раскрытии модуля со знаком плюс. Поэтому на координатной прямой пустой кружок нужно закрасить. Так мы включим число во множество решений:

Тогда окончательный ответ будет выглядеть так:

Ответ:

Также, можно решить это уравнение сведя его в совокупность, дополнительно указав, что правая часть должна быть больше либо равна нулю:

Пример 2. Решить уравнение |2x − 3| = 3 − 2x

Решение

Решим исходное уравнение для случаев когда 2x − 3 ≥ 0 и 2x − 3 < 0

Ответ:

Использование координатной прямой

Рассмотрим ещё один способ решения элементарных уравнений с модулем — с помощью координатной прямой. Этот способ используется редко, но знать о нём не помешает.

Решим наше самое первое уравнение |x − 2| = 5 с помощью координатной прямой. Напомним, что корнями этого уравнения были числа 7 и −3.

Модуль есть расстояние от начала координат до точки A. Либо расстояние между двумя числами на координатной прямой.

Расстояние между двумя числами выражается в виде разности |x1 − x2|, где x1 — первое число, x2 — второе число.

Если внимательно посмотреть на уравнение |x − 2|= 5, то можно увидеть что его левая часть это расстояние от x до 2 (или от 2 до x) и это расстояние равно 5. Отмéтим на координатной прямой число x и число 2

Правая часть уравнения |x − 2|= 5 говорит о том, что расстояние от x до 2 составляет пять единиц:

Если расстояние от x до 2 равно 5, то и расстояние от 2 до x тоже равно 5. Это позволяет отсчитать пять целых шагов от числа 2 к числу x и таким образом узнать значение x

Видно, что отсчитав пять шагов влево мы попали в точку с координатой −3. А это один из корней, который мы находили для уравнения |x − 2|= 5.

Но пять целых шагов от числа 2 можно отсчитать не только влево, но и вправо:

Если отсчитать пять целых шагов вправо, то попадём в точку с координатой 7. Это тоже был корень уравнения |x − 2|= 5

Несколько модулей в одной части

Решим следующее уравнение:

|x − 5| − |x| = 1

Это уравнение содержит два модуля в левой части. Чтобы решить данное уравнение нужно раскрыть его модули. Рассмотреть нужно каждый из случаев:

  • когда оба модуля больше либо равны нулю;
  • когда оба модуля меньше нуля;
  • когда первый модуль больше либо равен нулю, а второй модуль меньше нуля;
  • когда первый модуль меньше нуля, а второй модуль больше либо равен нулю.

Не будем комментировать каждый случай, а сразу приведём решение:

Первые два случая корней не дали. В третьем случае нашелся корень 3, но он не удовлетворяет условиям x − 5 ≥ 0 и x < 0, поэтому не является корнем исходного уравнения.

В четвёртом случае нашёлся корень 2, который удовлетворяет условиям x − 5 < 0 и x ≥ 0. Также он удовлетворяет исходному уравнению.

Заметно, что такой способ решения уравнения неудобен. Если модулей в уравнении будет три, четыре или более, то придётся рассматривать намного больше случаев. Человек запутавшись, может забыть рассмотреть какой-то из случаев, и получится что уравнение решено не полностью.

Поэтому такой вид уравнения как в данном примере удобнее решать методом интервалов. Об этом мы поговорим в следующем уроке.

Задание 1. Решить уравнение:

Решение:

Показать решение

Задание 2. Решить уравнение:

Решение:

Показать решение

Задание 3. Решить уравнение:

Решение:

Показать решение

Задание 4. Решить уравнение:

Решение:

Ответ: .

Показать решение

Задание 5. Решить уравнение:

Решение:

Ответ: .

Показать решение

Задание 6. Решить уравнение:

Решение:

Ответ: .

Показать решение

Задание 7. Решить уравнение:

Решение:

Ответ: .

Показать решение

Задание 8. Решить уравнение:

Решение:

Ответ: .

Показать решение

Задание 9. Решить уравнение:

Решение:

Ответ: .

Показать решение

Задание 10. Решить уравнение:

Решение:

Ответ: .

Показать решение

Задание 11.

Решить уравнение:

Решение:

Ответ: .

Показать решение

Задание 12. Решить уравнение:

Решение:

Ответ: 0, 5.

Показать решение

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Опубликовано

Общие модули Nginx и примеры использования

Введение

Nignx (Engine X) — это высокомодульный, легкий, высокопроизводительный HTTP-сервис и сервис обратного прокси, который отличается меньшим объемом памяти и сильным параллелизмом. В этой статье будут представлены наиболее часто используемые модули и связанные с ними случаи Nginx.Понимание и освоение конфигурации соответствующих модулей поможет нам быстрее и лучше понять и освоить настройку служб Nginx. Официальная ссылка на введение модуля:http://nginx.org/en/docs/

Основными файлами конфигурации службы Nginx являются файлы конфигурации, заканчивающиеся на conf, в каталогах /etc/nginx/nginx.conf и /etc/nginx/conf.d. По умолчанию структура его файла конфигурации разделена на основной раздел конфигурации, раздел конфигурации событий, раздел конфигурации http и так далее. Раздел конфигурации http включает в себя сервер, местоположение, если находится, и другие разделы конфигурации
В разделе конфигурации модуля Nginx обычно есть несколько инструкций по настройке, и разные инструкции по настройке работают в разных средах конфигурации. Давайте взглянем на общие модули Nginx и соответствующие. Пример.

2. Общие инструкции и примеры модулей

— Core functionality

1、events { ... }
Раздел конфигурации, управляемой событиями.
Среда раздела конфигурации: основная
2、use method;
указывает метод обработки одновременных запросов на соединение;
Среда раздела конфигурации: основная
3、accept_mutex on|off;
Метод обработки новых запросов на подключение; on означает, что каждый рабочий процесс будет обрабатывать новые запросы по очереди, а off означает, что каждый новый запрос будет уведомляться всем рабочим процессам;
Среда раздела конфигурации: события

4、worker_processes number | auto;
Вообще говоря, одно ядро ​​ЦП соответствует одному worker_process. Worker_processes можно включить максимум 8. Повышение производительности более чем на 8 не улучшится, а стабильность станет ниже.
Среда конфигурации: основная

— Module ngx_http_core_module

Настраиваемые инструкции в основном модуле ngx_http_core_module включают:
1、http { ... }: Укажите раздел конфигурации команды http-сервера;
Пример:

http {
    server {
        listen       80 default_server;
        listen       [::]:80 default_server;
        server_name  _;
        root         /usr/share/nginx/html;
        location / {
        }
        error_page 500 502 503 504 /50x.html;
            location = /50x.html {
        }
    }

2、server { ... }: Относится к разделу конфигурации виртуального хоста, а его среда конфигурации — это раздел конфигурации http.
Пример:

server {
        listen 192.168.0.83:80;
        server_name www.a.com;
        root /var/www/html;
        location / {
                allow all;
        }
        location /status {
                stub_status;
        }
}

3、location [ = | ~ | ~* | ^~ ] uri { . ~ /www { }

4、listen PORT|address[:port]|unix:/PATH/TO/SOCKET_FILE [options];
используется для указания интерфейса мониторинга и информации о порте, параметры включают:

default_server: установить как виртуальный хост по умолчанию;
ssl: разрешено предоставлять услуги только через ssl-соединение;
backlog = number: длина очереди резервного копирования;
rcvbuf = size: принять размер буфера;
sndbuf = size: размер буфера отправки;

Среда настройки этой инструкции - это раздел конфигурации сервера.
Пример:

# Мониторинг указанного IP и порта
listen 192.168.0.83:80;
 # Следить за тем, чтобы указанный порт мог проходить только через SSL
listen 443 ssl;

5、server_name name....;
используется для указания имени виртуального хоста, за которым могут следовать несколько строк, разделенных пробелами, и поддерживает подстановочные знаки и регулярные выражения.

Средой выполнения этой инструкции является раздел конфигурации сервера. www\d+\.magedu\.com$;

6、tcp_nodelay on | off;
Следует ли включать опцию tcp_nodelay для соединения в режиме keepalived, по умолчанию включено;
Среда раздела конфигурации: http, сервер, местоположение
7、tcp_nopush on|off;
В режиме файла отправки, включать ли параметр tcp_cork, значение по умолчанию выключено;
Среда раздела конфигурации: http, сервер, местоположение
8、sendfile on|off；
Следует ли включать функцию sendfile, по умолчанию она отключена;
Среда раздела конфигурации: http, сервер, местоположение, если в местоположении
9、root path;
Установить сопоставление пути к веб-ресурсу; используется для указания пути к каталогу документа в локальной файловой системе, соответствующего URL-адресу, запрошенному пользователем;
Среда раздела конфигурации: http, сервер, местоположение, если в местоположении;
Пример:

server {
        listen 192.168.0.83:80;
        server_name www.a. ~ /charlie {
        alias /data/location/;
}

11、error_page code...[=[response]] uri;
определяет неправильный путь URI;
Среда раздела конфигурации: http, сервер, местоположение, если в местоположении
Пример:

# Если код статуса веб-страницы 404, перейти на указанную страницу 404.html
error_page 404             /404.html;
 # Если код ошибки веб-страницы принадлежит коду состояния ошибки сервера, вернуть код состояния 200 и перейти на указанную страницу
error_page 500 502 503 504 =200 /50x.html;

12、try_files file ... [uri|=code];
Найдите файл по указанному пути, если он не существует, перейдите к указанному uri или верните указанный код состояния.
Среда раздела конфигурации: сервер, расположение
Пример:

# Попробуйте открыть файл test.html, если нет, перейдите к файлу 404.html
location ~ .*test.* {
        try_files test.html /404.html;
}
 # Попробуй открыть test.html, если такого файла нет, вернуть код статуса 500
location ~ . *test.* {
        try_files test.html =500;
}

13、keepalive_timeout timeout [header_timeout];
определяет период тайм-аута для сохранения соединения, 0 означает, что длительное соединение запрещено, по умолчанию - 75 секунд;
Среда раздела конфигурации: http, сервер, местоположение.
14、keepalive_requests number;
Максимальное количество ресурсов, которое может быть запрошено при длительном соединении, по умолчанию - 100;
Среда раздела конфигурации: http, сервер, местоположение.
Пример:

keepalive_requests 1000

15、keepalive_disable none | browser ...;
Для каких браузеров длинные соединения отключены;
Среда раздела конфигурации: http, сервер, местоположение.
Пример:

keepalive_disable safari;

16、send_timeout time;
Период ожидания для отправки ответного сообщения клиенту. Здесь он относится к интервалу между двумя операциями записи. Значение по умолчанию - 60 секунд;
Среда раздела конфигурации: http, сервер, местоположение.
17、client_body_buffer_size size;
Размер буфера, используемого для получения части тела сообщения запроса клиента; по умолчанию - 16 КБ, когда размер превышает этот размер, он будет временно сохранен на диске, определенном позиция инструкции client_body_temp_path;
Среда раздела конфигурации: http, сервер, местоположение.
18、client_body_temp_path path [level [level2 [level3]]];
Задайте путь временного хранения, а также структуру и количество подкаталогов для хранения основной части сообщения запроса клиента;
, где уровень представляет количество каталогов хранения, выраженное в шестнадцатеричных числах.
Среда раздела конфигурации: http, сервер, местоположение.
Пример:

# 2 означает 256 подкаталогов первого уровня, 1 означает 16 подкаталогов второго уровня, 1 означает 16 подкаталогов третьего уровня
client_body_temp_path /var/tmp/client_body 2 1 1;

19、limit_rate rate;
Ограничьте скорость передачи ответа клиенту, единица измерения - байтов в секунду, 0 означает неограниченно;
Среда раздела конфигурации: http, сервер, местоположение, если оно находится.
20、limit_except method ... {...}
Ограничить клиента указанным методом запроса;
Среда раздела конфигурации: расположение.
Список:

# Ограничить только 192.168.1.0/24 узлы сегмента сети могут использовать запросы GET
limit_except GET{
    allow 192.168.1.0/24;
    deny all;
}

21、aio on |off|threads[=pool];
Следует ли включать функцию aio.
Среда раздела конфигурации: http, сервер, местоположение.

22、directio size | off;
Включите тег O_DIRECT на хосте Linux, где это означает, что файл больше или равен заданному размеру, например: directio 4m;
Среда раздела конфигурации: http, сервер, местоположение.

23、open_file_cache off;
open_file_cache max=N [inactive=time];
Настройте информацию для кэширования статических файлов. Эта инструкция может кэшировать следующие три типа информации:
1) Дескриптор файла, размер файла и время последнего изменения;
2) Открытая структура каталогов;
3) Информация о файлах, которые не найдены или не имеют разрешения на доступ;
max=N : Верхний предел элементов кеша, которые могут быть кэшированы; когда верхний предел достигнут, алгоритм LRU будет использоваться для реализации управления кешем;
inactive=time: Неактивная продолжительность элемента кэша. Элемент кеша, который не удался или количество совпадений меньше, чем количество раз, указанное инструкцией open_file_cache_min_uses в течение указанного здесь времени, является неактивным элементом;
Среда раздела конфигурации: http, сервер, местоположение
Пример:

# Настройте ограничение кеша на 1000, а продолжительность неактивности - 20 секунд
open_file_cache          max=1000 inactive=20s;

24、open_file_cache_valid time;
Частота проверки достоверности кэшированных элементов; по умолчанию 60 секунд;
Среда раздела конфигурации: http, сервер, местоположение.

25、open_file_cache_min_uses number;
В пределах продолжительности, указанной неактивным параметром инструкции open_file_cache, по крайней мере, сколько раз должно быть выполнено, прежде чем его можно будет классифицировать как активный элемент, по умолчанию 1;
Среда раздела конфигурации: http, сервер, местоположение.
26、open_file_cache_errors on|off;
Следует ли кэшировать информацию, например файлы с ошибками во время поиска, по умолчанию отключено;
Среда раздела конфигурации: http, сервер, местоположение. ~ /charlie { alias /data/location/; allow 192.168.0.38; deny all; }

- Module ngx_http_auth_basic_module

Этот модуль используется для реализации функций управления доступом на основе пользователей.
1、auth_basic string |off
Настройте информацию, запрашиваемую auth_basic.
Среда раздела конфигурации: http, server, location, limit_except.
2、auth_basic_user_file file;
Файл, в котором сохраняется пользователь, создается командой htpasswd.
Среда раздела конфигурации: http, server, location, limit_except.
Пример:

# Создать файл, в котором сохраняется информация об аутентификации пользователя
[[email protected] ~]# htpasswd -c /etc/nginx/wwwpasswd  charlie
New password: 
Re-type new password: 
Adding password for user charlie
[[email protected] ~]# htpasswd /etc/nginx/wwwpasswd  magedu
New password: 
Re-type new password: 
Adding password for user magedu
 # Добавить конфигурацию аутентификации nginxbasic
location ^~ /www {
        auth_basic "Welcome to www auth. ";
        auth_basic_user_file /etc/nginx/wwwpasswd;
}
- Module ngx_http_stub_status_module

Этот модуль используется для вывода основной информации о состоянии nginx.
1、stub_status;
Среда раздела конфигурации: сервер, местоположение.
Пример использования:

location /status {
        stub_status;
}

доступhttp://192.168.0.83/statusИнформацию о статусе сервера nginx можно получить следующим образом:

Active connections: 1 
server accepts handled requests
 100313 100313 100386 
Reading: 0 Writing: 1 Waiting: 0

Пояснения таковы:

Активные подключения: количество активных подключений;
принимает: общее количество принятых клиентских запросов;
обработано: общее количество обработанных клиентских запросов;
запросы: общее количество запросов, отправленных клиентом;
Чтение: количество подключений, которые читают заголовок сообщения запроса клиента;
Запись: количество соединений, которые находятся в процессе отправки ответных сообщений клиенту;
Ожидание: количество незанятых подключений, ожидающих отправки запроса клиентом;

- Module ngx_http_log_module

1、access_log path [format [buffer=size] [gzip[=level]] [flush=time] [if=condition]];с участиемaccess_log off;
используется для установки пути к файлу журнала доступа, формата и соответствующей конфигурации буфера. По умолчанию access_log определяет комбинированный формат журнала, и пользователи могут вызывать его напрямую в формате.
Среда раздела конфигурации: http, server, location, если в location, limit_except.
Пример:

# Записать журнал по указанному пути в комбинированном формате
access_log  /var/log/nginx/access.log  combined;
 # Сохранить страницу, которая посещает статус nginx по указанному пути, в указанном тестовом формате
        location /status {
                stub_status;
                access_log /data/log/access_log test;
        }

2、log_format name [escape=default|json|none] string ...;
В строке переменные, встроенные в основной модуль nginx и другие модули, могут использоваться для создания журнала журнала. Формат журнала по умолчанию - это комбинированный формат.
Среда раздела конфигурации - http.
Пример:

# Определите формат журнала nginx в соответствии с форматом объединенного
log_format  main  '$remote_addr - $remote_user [$time_local] "$request" '
                      '$status $body_bytes_sent "$http_referer" '
                      '"$http_user_agent" "$http_x_forwarded_for"';
 #Custom log_format
log_format test '$remote_addr        $status        "$request"'

3、open_log_file_cache max=N [inactive=time] [min_uses=N] [valid=time];с участиемopen_log_file_cache off;
используется для кэширования информации метаданных, относящейся к каждому файлу журнала.
Среда раздела конфигурации: http, сервер, местоположение.

max: максимальное количество файловых дескрипторов в кэше.Если кеш достигает максимального значения, файловый дескриптор с наибольшим временем хранения будет очищен.
min_uses: посещения, превышающие или равные этому значению в течение времени, указанного параметром inactive, могут рассматриваться как активные элементы, по умолчанию - 1.
inactive: установите продолжительность бездействия перед закрытием кэшированного файлового дескриптора;
действителен: интервал времени для проверки того, является ли каждый элемент кэша активным, по умолчанию - 60 секунд.

Пример:

open_log_file_cache max=1000 inactive=20s valid=1m min_uses=2;
- Module ngx_http_gzip_module

Этот модуль может использовать gzip для сжатия размера ответного сообщения и может уменьшить объем данных, которые необходимо передать, наполовину или более.
1、gzip on | off;
Следует ли включать сжатый ответ.
Среда раздела конфигурации: http, сервер, местоположение, если оно находится.
2、gzip_comp_level level;
Установите уровень сжатого ответа от 1 до 9.
Среда раздела конфигурации: http, сервер, местоположение
3、gzip_disable regex ...;
Отключить сжатие ответа на основе регулярного выражения, соответствующего типу браузера клиента.
Среда раздела конфигурации: http, сервер, местоположение
4、gzip_min_length length;
Укажите минимальную длину сжатого ответного сообщения, по умолчанию - 20 байтов.
Среда раздела конфигурации: http, сервер, местоположение
5、gzip_buffers number size;
Установите количество буферов и размер каждого буфера при сжатии ответных сообщений.
Среда раздела конфигурации: http, сервер, местоположение
6、gzip_proxied off | expired | no-cache | no-store | private | no_last_modified | no_etag | auth | any ...;
После того, как nginx в качестве прокси-сервера получит ответное сообщение, отправленное с прокси-сервера, при каких условиях включена функция сжатия;
off: отключить запрос прокси
no-cache, no-store, private: указывает, что значение Cache-Control в заголовке ответного сообщения, полученного от прокси-сервера, является одним из этих трех, затем сжатие функция включена ；
Среда раздела конфигурации: http, сервер, местоположение

7、gzip_types mime-type . ..;
фильтр сжатия, включите функцию сжатия только для содержимого установленного здесь типа MIME и сжимайте text / html по умолчанию.
Среда раздела конфигурации: http, сервер, местоположение

Пример:

gzip  on;
gzip_comp_level 6;
gzip_min_length 64;
gzip_proxied any;
gzip_types text/xml text/css  application/javascript;
- Module ngx_http_ssl_module

1、ssl on | off;
Запустите протокол https на виртуальном сервере.
Среда раздела конфигурации: http, server
2、ssl_certificate file;
Укажите сертификат SSL, используемый текущим протоколом https. Сертификат должен быть в формате pem.
Среда раздела конфигурации: http, server
3、ssl_certificate_key file;
Укажите файл закрытого ключа сертификата, используемого текущим протоколом https.
Среда раздела конфигурации: http, server

4、ssl_protocols [SSLv2] [SSLv3] [TLSv1] [TLSv1.1] [TLSv1.2];
Укажите поддерживаемую версию протокола SSL, по умолчанию - последние три.
Среда раздела конфигурации: http, server

5、ssl_session_cache off | none | [builtin[:size]] [shared:name:size];
используется для установки типа и размера кеша для хранения параметров сеанса ssl.
builtin [: size]: используйте встроенный кеш OpenSSL, этот кеш является частным для каждого рабочего процесса;
[shared: name: size]: использовать общий кеш для рабочих;
Среда раздела конфигурации: http, server
6、ssl_session_timeout time;
Установите время, в течение которого клиент может повторно использовать кэшированные параметры сеанса.
Среда раздела конфигурации: http, server

Пример:

server {
    listen 192.168.0.83:443 ssl;
    server_name www2.abc.com;
    root /data/https;
    ssl on;
    ssl_certificate /etc/nginx/ssl/nginx.crt;
    ssl_certificate_key /etc/nginx/ssl/nginx.key;
    ssl_session_cache shared:sslcache:20m;
}
- Module ngx_http_rewrite_module

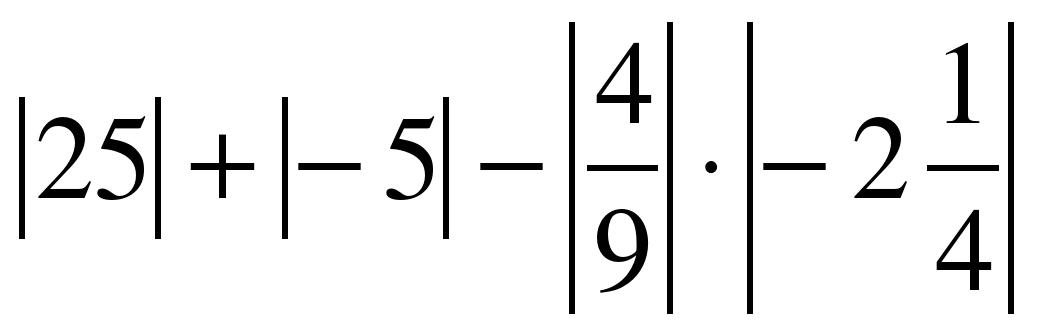
Этот модуль используется для проверки URI, запрошенного пользователем, на основе шаблона, описанного регулярным выражением, а затем для завершения замены, чтобы пользователь мог получить доступ к замененному URI.

1、rewrite regex replacement [flag];
Эта инструкция проверяет URI, запрошенный пользователем, на основе шаблона, описанного регулярным выражением, и заменяет его новым URI, указанным при замене, когда он совпадает. Если замена начинается с http: // или https: //, результат замены будет напрямую возвращен клиенту как перенаправление. Кроме того, если есть несколько правил перезаписи на одном уровне блока конфигурации, они будут проверяться одно за другим снизу вниз; после замены определенным условным правилом будет новый раунд проверки замены, поэтому существует механизм цикла; указанные флаги используются для управления этим механизмом цикла, включая следующие флаги:

последний: после завершения перезаписи остановить другие последующие операции перезаписи текущего URI в текущем местоположении, а затем начать новый раунд проверок перезаписи нового URI, то есть заранее перезапустить новый раунд цикла перезаписи;
break: после завершения перезаписи остановите другие последующие операции перезаписи текущего URI в текущем местоположении, а затем сразу перейдите к другим конфигурациям после блока конфигурации правила перезаписи, чтобы завершить цикл перезаписи. ;
перенаправление: после завершения перезаписи новый URI, сгенерированный после перезаписи, напрямую возвращается клиенту во временном режиме перенаправления, и клиент повторно инициирует запрос; URI перезаписывается этим флаг не может быть начат с http: // или https: //;
постоянный: после завершения перезаписи новый URI, созданный после перезаписи, напрямую возвращается клиенту в режиме постоянного перенаправления, и клиент повторно инициирует запрос;

Среда раздела конфигурации: сервер, местоположение, если

Пример:

# Перепишите все запросы для доменного имени 404.abc.com на www3.abc.com
server {
        listen 80;
        server_name 404.abc.com;
        rewrite /(.*) http://www3.abc.com/$1 permanent;
}

2、return code [text]; или жеreturn code URL;или жеreturn URL;
Остановить обработку запроса и вернуть указанное текстовое сообщение, код состояния или URL-адрес клиенту.
Среда раздела конфигурации: сервер, местоположение, если
Пример:

# Вернуться к указанному коду статуса и текстовой информации
location ~ . *test.* {
        return 404 'test test test';
}
 # Вернуться на указанный URL
location ~ .*test.* {
        return http://www3.abc.com/404.html;
}

3、rewrite_log on | off;
Включить ли перезапись журнала;
Среда раздела конфигурации: http, сервер, местоположение, если

4、if (condition) { ... };
Условно оценивает раздел конфигурации. Когда условия выполнены, инструкции в разделе конфигурации выполняются.
Среди них операторы сравнения в условии:

Оператор сравнения:
     ==: Режим
  !=
     ~: Сопоставление с образцом, символы с учетом регистра;
     ~ *: Сопоставление с шаблоном, без учета регистра;
     ! ~: Шаблон не совпадает, различие между прописными и строчными буквами;
     ! ~ *: Шаблон не соответствует и не различает символы верхнего и нижнего регистра;
 Суждение о существовании файлов и каталогов:
   -e, !-e
  -f, !-f
  -d, !-d
  -x, !-x

Среда раздела конфигурации: сервер, расположение
Пример:

# Если URI запроса клиента соответствует заданному формату, перепишите URL
        if ( $request_uri ~* /wch ) {
                rewrite /(. *) http://www3.abc.com/www/www.html permanent;
        }

5、set $variable value;
Пользовательские переменные пользователя.
Среда раздела конфигурации: сервер, местоположение, если

Пример:

#Variable newindex, когда хост, запрошенный клиентом, является abc.com, abc.html присваивается переменной newindex, и индекс сбрасывается
set $newindex "index.html";
if ( $host = abc.com) {
    set $newindex "abc.html";
}
index $newindex;
- Module ngx_http_referer_module

1、valid_referers none | blocked | server_names | string ...;
определяет юридически доступное значение заголовка реферера;

none: в заголовке сообщения запроса нет заголовка referer;
 заблокирован: заголовок реферера сообщения запроса не имеет значения;
 server_names: параметры, которые могут иметь значения как имена хостов или шаблоны имен хостов;
         произвольная_строка: прямая строка, но * может использоваться как подстановочный знак;
         регулярное выражение: строка, соответствующая указанному шаблону регулярного выражения; начинается с ~, например ~.  * \. magedu \ .com;

Среда раздела конфигурации: сервер, расположение

Пример:

# Установить юридическое значение referer
valid_referers none block server_names *.magedu.com *.mageedu.com magedu.* mageedu.* ~\.magedu\.;
 # Если referer является недопустимым значением, вернуть страницу с ошибкой;
if($invalid_referer) {
    return http://www.magedu.com/invalid.jpg;
}

Создание модулей уведомлений - Документация BILLmanager 5

Создание модулей уведомлений - Документация BILLmanager 5

This content cannot be displayed without JavaScript.
Please enable JavaScript and reload the page.

  • Документация BILLmanager 5
  • Разработчику

BILLmanager позволяет расширять возможности механизма уведомлений сотрудников и клиентов за счет добавления модулей уведомлений (отвечают за тип уведомления, могут использовать различные модули шлюзов уведомлений), а так же модулей шлюзов уведомлений ко встроенным или собственным модулям уведомлений.

По умолчанию BILLmanager поддерживает три типа уведомлений:

  • SMS сообщения — короткие сообщения отправляемые на номера телефонов указанные в профилях пользователей
    • Реализована только отправка сообщений
    • Для отправки используются шлюзы
  • Email сообщения — сообщения на email адреса пользователей (часть уведомлений может быть отправлена только этим способом, так как реализуют специфичный для email уведомлений функционал)
    • Реализована отправка и получение уведомлений
    • Для отправки и получения уведомлений используются шлюзы
  • Сообщения в меню уведомлений — сообщения отображаемые в личном кабинете в разделе "Уведомления", могут быть сформированы на основе отправляемого email сообщения
    • Реализована только отправка сообщений
    • Шлюзы не поддерживаются

Все файлы модулей и шлюзов вызывается с использованием системных вызовов, либо в фоне и могут быть реализованы на любом языке программирования, поддерживающем работу в потоками ввода/вывода

Механизм работы уведомлений

Работы уведомлений в BILLmanager состоит из следующих этапов:

  • Проверка подписки клиента на тип уведомления
  • Генерация XML уведомления нужного типа
  • Передача XML, содержащий в себе шаблон уведомления, XML самого уведомления, а так же данные о провайдере, связанном с уведомленим и пользователе, которому отправляется уведомление, модулю соответствующему типу уведомления

Внутри модуля выполняются следующие действия:

  • Определяется типа шаблона уведомления на основе его структуры, после чего:
    • Для XSLT шаблонов происходит наложение шаблона на XML уведомления
    • Для EJS шаблонов XML переводится в JSON и передается EJS шаблонизатору вместе с шаблонов
  • При необходимости в результирующем тексте производится замена необходимых макросов на необходимые значения
  • При отсутствии поддержки шлюзов уведомлений производится отправка уведомления непосредственно средствами модуля
  • При наличии поддержки шлюзов, на основе переданного идентификатора провайдера, а так же типа модуля уведомлений выбирается шлюз для отправки уведомления
  • Параметры шлюзы, необходимые контактные данные, текст сообщения и его заголовок передаются модулю шлюза для отправки

Архитектура модулей

Для работы с BILLmanager каждый модуль уведомления или шлюза должен уметь обрабатывать определенный набор команд описанный ниже. В случае отсутствия поддержки какой-либо команды, либо выводе модулем данных в не поддерживаемом формате приведет к невозможности BILLmanager взаимодействовать с модулем

Архитектура модуля уведомлений

Модуль устанавливается в каталог /usr/local/mgr5/notify/ и должен уметь обрабатывать следующие команды:

  • --command process — обработка очереди уведомлений на отправку. Очередь уведомлений хранится в таблице notifytask со следующей структурой:
    • id — идентификатор уведомления. Генерируется автоматически
    • modulename — имя модуля типа уведомлений. Стандартные значения ntemail, ntsms, ntinternal
    • filename — имя файла с данными уведомления
    • priority — приоритет отправки уведомления. При обработке очереди уведомлений рекомендуется выбирать из базы данных уведомления небольшими порциями отсортированными по убыванию приоритета. В этом случае, при проведении объемных рассылок, важные уведомления будут доставлены в срок
    • error_count — количество попыток отправки уведомления завершившихся ошибкой
    • forcedonothing — флаг отправки уведомления игнорируя файл billmgr.DoNothing, создаваемый во время переноса данных из другого биллинга
    • err_info — текст сообщения об ошибке отправки уведомления
    • createdate — дата постановки уведомления в очередь
  • --command getmessage --gate gate_id, где gate_id — код шлюза, для которого производится обработка получения сообщения. В качестве параметра --gate, может быть передано значение all, в этом случае необходимо обработать получения сообщений всеми шлюзами типа уведомления
  • --command features — запрос параметров модуля уведомлений. В ответ модуль должен вывести в стандартный поток вывода XML описание поддерживаемого функционала. Формат XML документа следующий
<?xml version="1.0" encoding="UTF-8"?>
<doc>
  <features>
    <feature name="html"/> 
    <feature name="sms"/> 
    <feature name="call"/> 
  </features>
  <contact_type>тип контакта</contact_type> 
</doc>

Порядок обработки очереди, а так же действий с полученными сообщениями определяется разработчиком. Так, например можно реализовать следующие сценарии:

  • Непрерывна работа модуля с периодической проверкой появления новых сообщений в очереди
  • Добавления входящих сообщений в запросы клиентов
  • Управление услугами через входящие сообщения
  • Запрос и вывод информация управляющими командами

Реализация модуля с использованием заголовочных файлов BILLmanager предполагает обязательную реализацию методов

  • virtual mgr_xml::Xml Features() const = 0; — возврат XML описания поддерживаемых возможностей. Вывод данных в поток вывода будет произведен автоматически
  • virtual bool UserNotify(const string& filename) const = 0; — отправка пользователю уведомления описанной в файле с именем переданном в параметре
  • virtual void GetMessage(string gate_id = 0) const = 0; — обработка получения входящих сообщения для шлюза с кодом gate_id

Дополнительно может быть переопределен метод

  • virtual int ProcessQueue() const; — обработка очереди уведомлений, которые необходимо отправить пользователям. UserNotify вызывает как раз при работе этого метода класса и может быть определен пустым в случае реализации всей необходимой логики в ProcessQueue

Архитектура модуля шлюза

Модуль устанавливается в каталог /usr/local/mgr5/gate/ и должен уметь обрабатывать следующие команды:

  • --command features — запрос параметров модуля шлюза. В ответ модуль должен вывести в стандартный поток вывода XML описание поддерживаемого функционала. Формат XML документа следующий
<?xml version="1.0" encoding="UTF-8"?>
<doc>
  <features>
    <feature name="outgoing"/> 
    <feature name="ingoing"/> 
    <feature name="formtune"/> 
    <feature name="check_connection"/> 
  </features>
  <notify_module>тип модуля уведомлений</notify_module> 
</doc>
  • --command formtune — модификация формы настроек параметров шлюза. На вход модулю передается XML описание формы параметров шлюза, на выход модуль должен вернуть модифицированную XML описания формы настроек
  • --command check_connection — проверка подключения к шлюзу с указанными параметрами. На вход модулю передается XML описание формы параметров шлюза, с добавлением введенных на форме данных, на выход модуль должен вернуть XML описание формы настроек (XML может быть изменена при необходимости)
  • --command outgoing и --command ingoing — не вызываются BILLmanager напрямую в общем случае, исключением является отправка СМС сообщений, в этом случае реализация --command outgoing обязательна в определенном формате. В остальном случае могут быть описаны любые другие команды, которые будут вызываться модулями уведомлений. Ниже описана работа стандартным модулей с этими командами:
  • --command outgoing — отправка уведомления. На вход модулю передается XML описание сообщения следующего вида:
<?xml version="1.0" encoding="UTF-8"?>
<doc>
  <gateway> - параметры шлюза
    <param>value</param>
    <param>value</param>
    ...
    <param>value</param>
    <xmlparams>Параметры подключения шлюза в виде XML</xmlparams>
  </gateway>
  <message>текст сообщения</message>
  <user> - параметры пользователя, которому отправляется уведомление
    <param>value</param>
    <param>value</param>
    ...
    <param>value</param>
  </user>
  <project> - параметры провайдера
    <param>value</param>
    <param>value</param>
    . ..
    <param>value</param>
  </project>
</doc>

На выход модуль должен вернуть пустую XML или XML описания ошибки

  • --command ingoing (используется для получения почты) — на вход модулю передается XML с параметрами шлюза, как описано выше, на выход нужно вернуть XML со списком полученных сообщений вида
<?xml version="1.0" encoding="UTF-8"?>
<doc>
  <messages>
    <message>исходный текст сообщения</message>
    ...
    <message>исходный текст сообщения</message>
  </messages>
</doc>

Реализация модуля с использованием заголовочных файлов BILLmanager предполагает обязательную реализацию методов virtual mgr_xml::Xml Features() const = 0; — возвращается XML описание поддерживаемых возможностей virtual mgr_xml::Xml Ingoing(mgr_xml::Xml& input) const = 0; — на вход получает XML с параметрами шлюза (параметры могут быть так же получены методом GateParam), возвращает список сообщений в описанном формате virtual void Outgoing(mgr_xml::Xml& input) const = 0; — на вход получает XML с параметрами шлюза и сообщением для отправки (параметры могут быть так же получены методом GateParam)

Примеры модулей

C++ (с использованием библиотек BILLmanager в пакете разработчика)

Использование заголовочных файлов BILLmanager для разработки собственных модулей обработчиков доступно с версии BILLmanager 5. 58.0. Кроме приведенного упрощенного примера, можно изучить примеры представленные в пакете разработчика BILLmanager — billmanager-[Редакция BILLmanager]-devel, например:

yum install billmanager-devel
или 
yum install billmanager-corporate-devel

 Пояснения

yum install billmanager-devel — для BILLmanager;

yum install billmanager-corporate-devel — для BILLmanager Corporate.

После этого примеры можно найти в директории:

/usr/local/mgr5/src/examples

C++ (с использованием библиотек BILLmanager)

Реализация модуля уведомлений и шлюза для отправки и получения XMPP сообщений представлена по ссылке

https://github.com/ISPsystemLLC/jabber

Пример реализован на C++, с использования заголовочных файлов COREmanager и BILLmanager, а так же библиотеки Gloox. Пример состоит из:

  • Модуль уведомлений ntjabber — основной файл ntjabber.cpp. Отвечает за тип уведомлений, позволяет добавлять шаблоны уведомлений и создавать рассылки нужного типа
  • Модуль шлюза для подключения к Jabber серверу gwjabber — основной файл gwjabber.cpp. Отвечает за отправку уведомлений на Jabber контакт пользователя, а так же обрабатывает входящие сообщения
  • XML файлы, описывающие необходимые сообщения и параметры подключения с серверу:
    • billmgr_mod_ntjabber.xml — добавляет на форму редактирования пользователей поле Jabber контакта (отображение и сохранение значения происходит автоматически согласно механизму описанному по ссылке), добавляет описание типа уведомлений
    • billmgr_mod_gwjabber.xml — описывает параметры подключения к jabber-серверу, а так же описывает наименование модуля подключения
  • Описание поля базы данных jabber — описывает дополнительное поле для таблицы user базы данных BILLmanager
  • Логотип шлюза billmanager-plugin-gwjabber. png — добавляет отображение логотипа XMPP на форму выбора модуля шлюза
  • Файл описания сборки Makefile

Другие языки программирования

XML модулей

XML описание модуля сохраняется в файл /usr/local/mgr5/etc/xml/billmgr_mod_ntxxx.xml, для модуля уведомлений и в файл /usr/local/mgr5/etc/xml/billmgr_mod_gwxxx.xml для модулей шлюзов, где xxx — уникальное имя модуля. В данном примере рассматривается только XML для модуля шлюза, для XML файла модуля уведомлений смотрите пример на C++.

Файл имеет следующий формат (на примере интеграции с ePochta SMS)

<?xml version="1.0" encoding="UTF-8"?>
<mgrdata>
  <plugin name="gwepochta">           <!-- описание плагина для отображения в BILLmanager -->
    <group>gateway</group>            <!-- привязка плагина к разделу шлюзов сообщений -->
    <author>BILLmanager team</author> <!-- автор модуля -->
  </plugin>
  <metadata name="gateway. gwepochta"> <!-- описание настроек модуля -->
    <form>
      <field name="login">
        <input type="text" name="login" required="yes" identifier="yes"/>
      </field>
      <field name="password">
        <input type="password" name="password" required="yes"/>
      </field>
      <field name="sender">
        <input type="text" name="sender" required="yes"/>
      </field>
    </form>
  </metadata>
  <lang name="ru">
    <messages name="plugin">         <!-- сообщения для описания плагина -->
      <msg name="desc_short_gwepochta">ePochta SMS</msg>
      <msg name="desc_full_gwepochta">ePochta SMS</msg>
      <msg name="price_gwepochta">Бесплатно</msg>
    </messages>
    <messages name="gateway.gwepochta"> <!-- сообщения для формы настроек модуля -->
      <msg name="login">Логин</msg>
      <msg name="password">Пароль</msg>
      <msg name="sender">Отправитель</msg>
      <msg name="hint_login">Логин в личный кабинет ePochta SMS</msg>
      <msg name="hint_password">Пароль от личного кабинета</msg>
      <msg name="hint_sender">Подпись отправителя сообщения</msg>
    </messages>
    <messages name="gateway_include"> <!-- наименование модуля для отображения в различных разделах BILLmanager -->
      <msg name="module_gwepochta">Сервер ePochta SMS</msg>
      <msg name="gwepochta">ePochta SMS</msg>
      <msg name="desc_gwepochta">ePochta SMS</msg>
    </messages>
  </lang>
  <lang name="en"> <!-- английская локализация сообщений -->
    <messages name="plugin">
      <msg name="desc_short_gwepochta">ePochta SMS</msg>
      <msg name="desc_full_gwepochta">Server ePochta SMS</msg>
      <msg name="price_gwepochta">Free</msg>
    </messages>
  </lang>
</mgrdata>
Go
package main
import "bytes"
import "log"
import "encoding/xml"
import "flag"
import "fmt"
import "os"
import "io/ioutil"
import "net/http"
func request(operation, username, password, phone, message, sender string) (string, string) {
  type SMS struct {
    XMLName    xml. Name  `xml:"SMS"`
    Operation  string    `xml:"operations>operation"`
    Username  string    `xml:"authentification>username"`
    Password  string    `xml:"authentification>password"`
    Message    string    `xml:"message>text"`
    Sender    string    `xml:"message>sender"`
    Number    string    `xml:"numbers>number"`
  }
  
  v := &SMS{
      Operation:   operation,
      Username:  username,
      Password:  password,
      Message:  message,
      Sender:    sender,
      Number:    phone,
  }
  output, err := xml.MarshalIndent(v, "  ", "    ")
  log.Print("REQUEST: " + string(output))
    
  if err != nil {
    return "", ""
  }
  
  resp, err := http.Post("http://api.myatompark.com/members/sms/xml.php", "image/jpeg", bytes.NewBuffer(output))
  
  if err != nil {
    return "", ""
  }
  
  defer resp.Body.Close()
  body, err := ioutil.ReadAll(resp.Body)
  
  log.Print("RESPONSE: " + string(body))
  
  type Response struct {
    XMLName    xml.Name  `xml:"RESPONSE"`
    Status    int      `xml:"status"`
    }
  
  r := Response{Status: 1}
  resperr := xml. Unmarshal(body, &r)
  if resperr != nil {
    log.Printf("error: %v", resperr)
    return "", ""
  }
  
  if r.Status != 0 {
    return string(body), "error"
  }
  
  return string(body), ""
}
func main() {
  f, _ := os.OpenFile("var/gwepochta.log", os.O_RDWR | os.O_CREATE | os.O_APPEND, 0666)
  defer f.Close()
  
  log.SetOutput(f)
    
  command_ptr := flag.String("command", "features", "gateway command")
  flag.Parse()
  if *command_ptr == "features" {
    type Feature struct {
      XMLName  xml.Name  `xml:"feature"`
      Name  string    `xml:"name,attr"`
    }
    type Features struct {
      XMLName    xml.Name   `xml:"doc"`
      Features   []Feature    `xml:"features>feature"`
      Module    string    `xml:"notify_module"`
    }
    v := &Features{
        Module: "ntsms",
        Features: []Feature {
                {Name: "formtune"},
                {Name: "check_connection"},
                {Name: "outgoing"},
        },
      }
    output, err := xml.MarshalIndent(v, "  ", "    ")
    if err != nil {
      fmt. Println("error: %v\n", err)
    }
    os.Stdout.Write(output)
  } else if *command_ptr == "formtune" {
    bytes, _ := ioutil.ReadAll(os.Stdin)
    os.Stdout.Write(bytes)
  } else if *command_ptr == "check_connection" {
    type Doc struct {
      XMLName   xml.Name   `xml:"doc"`
      XMLparams    string    `xml:"xmlparams"`
      Login    string    `xml:"login"`
      Password  string    `xml:"password"`
    }
    
    bytes, _ := ioutil.ReadAll(os.Stdin)
    
    v := Doc{XMLparams: "none", Login: "none", Password: "none"}
    err := xml.Unmarshal(bytes, &v)
    if err != nil {
      log.Printf("error: %v", err)
      return
    }
    
    paramerr := xml.Unmarshal([]byte(v.XMLparams), &v)
    if paramerr != nil {
      log.Printf("error: %v", paramerr)
      return
    }
    _, error := request("BALANCE", v.Login, v.Password, "", "", "")
    
    if error != "" {
      type Error struct {
        Type  string  `xml:"type,attr"`
      }
      
      type Doc struct {
        XMLName   xml. Name   `xml:"doc"`
        ErrorType    Error    `xml:"error"`
      }
      
      t := &Error {
        Type: error,
      }
      
      v := &Doc{
        ErrorType:   *t,
      }
      output, _ := xml.MarshalIndent(v, "  ", "    ")
      os.Stdout.Write(output)
      return
    }
    os.Stdout.Write(bytes)
  } else if *command_ptr == "outgoing" {
    bytes, _ := ioutil.ReadAll(os.Stdin)
    log.Print(string(bytes))
    
    type Doc struct {
      XMLName   xml.Name   `xml:"doc"`
      XMLparams    string    `xml:"gateway>xmlparams"`
      Login    string    `xml:"login"`
      Password  string    `xml:"password"`
      Sender    string    `xml:"sender"`
      Message    string    `xml:"message"`
      Phone    string    `xml:"user>phone"`
    }
    
    v := Doc{XMLparams: "none", Login: "none", Password: "none", Message: "none", Phone: "none"}
    err := xml.Unmarshal(bytes, &v)
    
    log.Print(v.XMLparams)
    
    if err != nil {
      log.Printf("error: %v", err)
      return
    }
    
    xml. Unmarshal([]byte(v.XMLparams), &v)
    
    request("SEND", v.Login, v.Password, v.Phone, v.Message, v.Sender)
  }
}

Спасибо за ваш отзыв!

Была ли полезна статья?

Уточните, почему:

статья не соответствует названию

статью сложно понять

в статье нет ответа на мой вопрос

рекомендации из статьи не помогли

другая причина

Модуль

Модулем положительного числа называют само это число; модулем отрицательного числа называют число, ему противоположное; модуль нуля равен нулю.

\(|a|=\begin{cases} a, \;\; если \;  a>0 \\ 0, \; если\;\; a=0\\ -a,\; если \;\;  a<0  \end{cases}\)

Второе название модуля – «абсолютное значение действительного числа».

Фактически модуль делает всё, что находится внутри него положительным. Поэтому чтобы правильно его раскрыть, необходимо сначала выяснить знак выражения внутри него:

- если подмодульное выражение положительно, модуль просто убирается. 4+1\)

Пример. Вычислить значение выражения \(|7-x|-|x+3|\), при \(x>12\).

Решение: При любом \(x\) большем \(12\), первое подмодульное выражение будет отрицательно, а второе – положительно. Соответственно, первый модуль будет раскрываться с минусом, а второй – с плюсом (значит перед ним останется минус, который стоял перед ним до раскрытия):

\(|7-x|-|x+3|=-(7-x)-(x+3)=-7+x-x-3=-10\)

Ответ: \(-10\)



Геометрическое определение модуля

\(|a|\) - это расстояние от \(0\) до числа \(a\) на числовой оси

Пример. Чему равен \(|5|\)  и \(|-5|\)?

Представим числовую ось и отметим на ней точки \(5\) и \(-5\). Какое будет расстояние от нуля до этих точек? Очевидно \(5\).


Значит ответ: \(|5|=5\),   \(|-5|=5\).

Так как модуль это расстояние, а расстояние не может выражаться отрицательным числом, то он всегда положителен.

Понимать легче второе определение, но практике удобнее использовать первое.

Решение простейших уравнений с модулем

Уравнения вида \(|f|=g\) решается с помощью перехода к совокупности   \( \left[ \begin{gathered}f= g\\  f=-g\end{gathered}\right.\) , при условии, что \(g≥0\).

Сначала об условии \(g≥0\). Откуда оно берется? Из определения модуля, ведь модуль всегда неотрицателен (то есть, положителен или равен нулю). Поэтому условие \(g≥0\) обязательно. Иначе уравнение не будет иметь решения.

Теперь о совокупности. Почему уравнение распадается на два? Давайте, к примеру, рассмотрим уравнение \(|x|=3\). Какое число под модулем будет равно \(3\)? Конечно \(3\) и \(-3\), потому что \(|3|=3\), \(|-3|=3\). Корни уравнения \(|x|=3\): \(3\) и \(-3\). Логично? Логично! В общем виде получается, что подмодульное выражение \(f\) должно быть равно \(g\) и \(-g\). Иначе равенство не получится.

Пример.   Решить уравнение:

\(|x-1|=3x\)

Найдем ограничения уравнения. Запишем его немного правее от основного решения

                               \(3x≥0\)
                               \(x≥0\)

 

Когда ограничение записано -  можно со спокойной душой решать уравнение. Избавимся от модуля и перейдем к совокупности уравнений

\( \left[ \begin{gathered}x-1=3x\\ x-1=-3x\end{gathered}\right.\)

  

Перед нами 2 линейных уравнения. Решаем их с помощью известного заклинания: «иксы влево, числа вправо»

\( \left[ \begin{gathered}x-3x=1\\ x+3x=1\end{gathered}\right. \)

  

Приведем подобные слагаемые

\( \left[ \begin{gathered}-2x=1\\ 4x=1\end{gathered}\right.\)

Поделим первое уравнение на \(-2\), второе на \(4\).

\( \left[ \begin{gathered} x=-\frac{1}{2}\\ x=\frac{1}{4}\end{gathered}\right.\)

Корень \(-\)\(\frac{1}{2}\) – не подходит, т.к. \(x≥0\). Остается корень \(\frac{1}{4}\), его и запишем в ответ

Ответ:  \(\frac{1}{4}\)

Решение простейших неравенств с модулем

Неравенство вида \(|f|< c\) решается с помощью перехода к двойному неравенству   \( -c< f< c\) , при условии, что \(c>0\).

Начнем опять с условия. Почему \(c>0\)? Потому что, иначе неравенство не будет иметь решения. Здесь все также как в уравнениях. В самом деле, когда, например, модуль икса меньше \(-7\)? Никогда!

Теперь разберем неравенство \(|x|<3\). Какие иксы нам подойдут? Все от \(-3\) до \(3\). Иначе говоря, икс должен лежать между \(-3\) и \(3\). Это утверждение можно записать вот так \(-3< x <3\) либо системой \(\begin{cases}x<3\\x > -3\end{cases}\). В любом случае ответ будет \(xϵ (-3;3)\).

Неравенство вида \(|f|>c\) решается с помощью перехода к совокупности неравенств \( \left[ \begin{gathered} f>c\\ f< -c\end{gathered}\right.\), при условии, что \(c≥0\).

А здесь почему \(c≥0\)? Потому что иначе решать нечего: если \(c\) отрицательно, то модуль абсолютно любого икса нам подойдет. И значит ответ, икс – любое число.

Теперь о переходе. Рассмотрим неравенство \(|x|>3\). Какие иксы нам подойдут? Все, модуль которых больше трех, то есть от минус бесконечности до \(-3\) и от \(3\) до плюс бесконечности. Записывая системой получим \(\begin{cases}x>3\\x < -3\end{cases}\). Ответ будет \(x ϵ (-∞;-3)⋃(3;∞)\).

\(|3x-7|≤8\)

\(|3x-11|≥11\)

\(-8≤3x-7≤8\) \(|+7\)

\( \left[ \begin{gathered}3x-11≥11\\ 3x-11≤-11\end{gathered}\right.\)

\(-1≤3x≤15\)

 

\( \left[ \begin{gathered}3x≥22\\ 3x≤0\end{gathered}\right.\)

\(-\frac{1}{3}≤x≤5\)

 

\( \left[ \begin{gathered}x≥\frac{22}{3}\\ x≤0\end{gathered}\right. \)

Ответ: \([ -\frac{1}{3};5]\)

 

Ответ: \( (-\infty;0]\cup [ \frac{22}{3};\infty)\)

Смотрите также:
Свойства модуля

Примеры использования модуля Каталог сегментов

В этой статье мы расскажем, как можно построить свою работу с модулем “Каталог сегментов” и какие задачи можно решить с его помощью.

Каталог сегментов — это пример структуры сайта для формирования сегментов по различным направлениям (страниц сайта и поисковых запросов), исходя из бизнес, SEO-задач и других сценариев, которые мы рассмотрим далее.

Начало работы

У больших сайтов много разных направлений и, с точки зрения поисковых систем, особенности ранжирования, спрос и частотность, будут у таких категорий разные. Такая разбивка нужна, чтобы смотреть на каждую категорию сайта отдельно и сравнивать между собой.

Сегменты создаются и загружаются в модуле “Каталог сегментов” и далее вы можете работать с этими данными в других модулях платформы.

Кроме этого все группы страниц и запросов можно разбивать в каталоге по «смыслам»: по структуре, внедрениям, SEO и о продукте.

После того, как такие бизнес-вертикали загружены, SEOWORK начинает собирать, считать и анализировать все метрики по каждому сегменту. Благодаря этому можно сделать выводы: какие группы обладают большей видимостью, на какие группы товаров выше спрос и уже дальше работать с этими данными.

По структуре

В SEOWORK можно сегментировать данные по структуре: категориям, группам страниц и запросов, а также по вложенности разделов.

Типы страниц. Отдельные товары, группы товаров объединенных по определенному признаку: листинги, разделы (верхнеуровневая разбивка), лендинги, статьи блога или новостные страницы.

Такое разделение необходимо, потому что поисковые системы ранжируют эти типы страниц по-разному, для карточек свои требования, для листингов свои.

Пример

Формируем группы страниц: листинги, карточки и разделы (страница разводящая).

Для того, чтобы проанализировать спрос и видимость по всем группам страниц, выбираем нужные нам пункты.

И переходим в модуль BI, нажав на кнопку “Построить BI”. Уже тут мы видим, что на “разделы” приходится мизерный спрос. Понятно, что это разводящие страницы и на них мало кто заходит.

А вот листинги и карточки примерно поровну распределяют весь спрос, это хорошая и показательная картина. Как минимум это говорит о том, что для того, чтобы растить трафик на этом сайте, надо заниматься и карточками и листингами товаров.

Зачастую специалисты по SEO работают только с листингами и упускает карточки. На нашем примере мы видим, что карточки товаров имеют даже чуть больше спроса при оценке на больших данных.

Также мы можем сравнить видимость этих страниц между собой и увидеть, что в данном случае карточки и листинги отлично ранжируются. Разделы хуже.

Так мы понимаем, что карточки имеют и хороший спрос и ранжирование и им есть куда расти. Сейчас это всего 10%, до 30-35 этот показатель можно легко поднять, чем и следует заняться в первую очередь!

Типы запросов. В этом блоке может быть неограниченное ничем количество сегментов, но в каждой тематике есть свои особенности. Наиболее типовая история: выделять коммерческие от информационных, геозависимые от геонезависимых.

Пример

Также можно выделить сегменты с точки зрения частотности запроса. Формируем группы запросов:

  • низкочастотные

  • среднечастотные

  • высокочастотные

Заходим в соответствующее меню в Каталоге сегментов и выбираем нужные группы, переходим в BI с помощью кнопки “Построить BI”.

Это достаточно показательная картина в плане, что специалист может акцентировать внимание только на высокочастотных запросах, и не подозревать, что на низкочастотные может приходиться треть спроса. То есть тут зарыт большой потенциал для роста.

Также видим, что распределение по видимости совпадает со спросом — низкочастотные запросы в нашем примере показывают хорошую видимость.

НЗ легче продвинуть, их много и они лучше ранжируются, поэтому если стоит задача вырастить поисковый трафик, не обязательно выращивать ВЧ запросы, можно работать с НЗ и быстрее продвинуть в ТОП10.

Произвольные группы

В блоке “Произвольные группы” вы можете добавить группы страниц или запросов с точки зрения глубины структуры и “проваливаться” насколько угодно и необходимо для вашего бизнеса, на 1, 2 и 3 уровня. Можно выделить подкатегории с большим спросом или группы с маленькой видимостью.

Внедрения

В этом блоке вы можете отслеживать SEO в динамике, а именно любые изменения и работы по сайту, которые влияют на ранжирование.

Пример

Для некоторых страниц на сайте вы написали уникальные тексты SEO тексты, а на других шаблонные, и хотите оценить, требуется ли уникальное описание для всех страниц или нет.

Выделите в отдельные группы страницы, где тексты написаны шаблонные и уникальные тексты. Загрузите обе группы в Каталог сегментов, выберите и нажмите кнопку “Построить BI”.

Вы увидите графики за выбранный период по нужным группам. В нашем случае, видимость страниц с уникальными текстами лучше более, чем в 2 раза, на графике ниже это желтый столбец.

SEO

В отличии от блока Внедрения, в SEO отображается статичная аналитика с точки зрения SEO: наличие запроса в title. SEO текст на странице итд.

SEO Аналитика. В разделе можно добавить и отслеживать группы исходя из наличия или количества (объема) внешних ссылок на страницу, SEO текста, текстовых вхождений, CTR, времени просмотра страницы или отказам итд.

Пример

Делим страницы сайта на группы: где SEO-текст есть и где нет на текущий момент. Важным отличием от внедрений, является то, что этот текст уже присутствует на страницах сайта и вы только сравниваете эффективность.

После загрузки выбираем нужные группы для сравнения в “Каталоге сегментов” и нажимаем кнопку “Перейти в BI”.

Аналогично мы можем отдельно сравнить листинги, где больше и меньшее 1000 символов SEO текста. После чего мы сможем понять, если текст нужен, то какого объема?

Перейдя в модуль BI и видим графики по обеим группам, мы делаем вывод, что писать большие тексты нецелесообразно, так как разница в поисковой видимости у текстов больше 1000 знаков и меньше около нулевая.

Таким же образом мы можем оценить влияние внешних ссылок. Разбиваем страницы сайта на сегменты в зависимости от наличия или нет внешних ссылок на страницу, а также по по количеству или по наличию.

Выбираем нужные группы для сравнения в “Каталоге сегментов”, переходим в модуль BI и смотрим, как наличие и количество ссылок влияет на спрос и видимость страницы.

Как видно на столбчатой диаграмме, в нашем случае, наличие ссылок на страницу в 3 раза улучшает видимость. Также мы можем посмотреть имеет ли смысл ставить много ссылок.

Анализ апдейтов. Аналитика по изменениям на сайте после апдейтов поисковых систем или проверка тех или иных гипотез.

Пример

Сайт упал в позициях и мы хотим понять из-за чего. Можно взять все запросы, разбить на группы: упали или выросли после апдейта 12 июля. Формируем соответствующие группы, загружаем в “Каталог сегментов”, выбираем чек-боксами и переходим в модуль BI, где уже дальше ищем причины.

Смотрим, какие запросы поменяли позиции: как они по частотности соотносятся, коммерческие они или нет, есть ли зависимость от ГЕО или какие-то другие факторы.

Или пример из блока “Идеи и заметки”. Мы хотим узнать, влияет ли кнопка вход, которая есть не на всех страницах, на спрос и видимость страниц.

Разбиваем семантику сайта на 2 сегмента: есть кнопка и нет, переходим в BI и наглядно видим, как влияет баннер на видимость и спрос.

Продукт

В первую очередь, мы воспринимаем сайт как продукт и планируем отслеживать, что напрямую или опосредованно влияет на ранжирование.

В этом блоке можно как угодно глубоко сегментировать проект, смотреть интересные инсайты и получать ответы на вопросы: надо ли писать SEO тексты на листингах? Какого объема? Сколько фотографий должно быть? Надо ли видео?

На выходе у вас получается четкое ТЗ: нужен текст определенного объема с 2 картинками и одно видео.

В блоке “Продукт” есть 3 части: Медиа, Контент и Ассортимент, куда можно загружать сколь угодно групп запросов и страниц по соответствующим срезам.

Пример

Медиа. Фото. Как понять, сколько фотографий надо делать на карточке товара? Формируем группы с разным количеством фотографий на странице:

  • нет фото

  • 1

  • 2

  • 3

  • 4

  • 5

  • 6 и более

Выбираем нужные нам группы и переходим в BI модуль. Тут уже мы видим, что синий столбец, а именно 6 фото, лучше всего ранжируется.

Есть прямая зависимость от количества фотографий на странице и видимостью страницы в поисковой системе. Поэтому при добавлении нового товара на сайт, чтобы он сразу хорошо ранжировался, вам надо минимум 6 фотографий товара.

Видео. Аналогичным образом можно оценить влияние наличие видео товара на странице. Выбираем страницы, где есть видео и нет, формируем группы и загружаем в “Каталог сегментов”, после переходим в BI и на графиках смотрим видимость и спрос на обе группы.

В нашем примере страницы, где есть видео не показываю лучшего ранжирования, это зеленый столбик на графиках. То есть делать видео товара нет смысла, а помня, что оно еще и дорогое в производстве, можно сказать, что мы сэкономили компании много денег и можем перераспределить их на что-то полезное.

Важен ли ассортимент при ранжировании?

Разбиваем листинги сайта по количеству товаров на них и делаем группы, например:

  • > 301 товаров,

  • 101-300 товаров,

  • 61-100 товаров,

  • 20-60 товаров,

  • < 20 товаров.

Мы знаем, что Яндекс в последнее время повышает в выдаче сайты с большим ассортиментом, но так ли это на самом деле? Выбираем группы с ассортиментом, переходим в Bi и видим:

У нас мало листингов с небольшим ассортиментом, менее 10% и это хорошо.

Видимость у листингов с хорошим ассортиментом значительно лучше, чем с меньшим. Наша гипотеза верна, ассортимент сильно влияет на ранжирование. Если какие-то разделы на сайте ранжируются не так хорошо, как хотелось бы, мы можем попробовать увеличить показатели за счет ассортимента товаров.

Контент/UGС. Пользовательский контент всегда дорого обходится, так ли он важен, можно понять точно, с помощью этого блока и грамотной сегментации проекта. Добавьте группы страниц, на которых есть отзывы пользователей и нет, где 1,2 или 5 отзывов или товары с хорошим и плохим рейтингом.

В нашем примере, перейдя в модуль BI мы видим, насколько лучше ранжируются страницы, на которых есть отзывы пользователей, по сравнению с теми, где их нет. Это зеленый столбик на графике ниже.

Полезные материалы по теме:

Описание модуля

Навигация по каталогу сегментов

примеров структур модулей | Ресурсы для разработки онлайн-курсов

By Stacey M Johnson , помощник директора по образовательным технологиям, Учебный центр Университета Вандербильта

Процитируйте это руководство:  Johnson, S. M. (2020). Примеры структур модулей . Ресурсы для разработки курсов Университета Вандербильта. https://www.vanderbilt.edu/cdr/module1/examples-of-module-structures/

Давайте рассмотрим несколько примеров того, как структурировать модуль онлайн-курса.
Не существует идеальной модульной структуры, и даже когда курсы разрабатываются и преподаются одним и тем же человеком, они, как правило, используют несколько иную модульную структуру, основанную на учебных мероприятиях и целях. Возможно, было бы полезно увидеть несколько примеров различных модулей, чтобы заставить работать наши умственные механизмы.

Пример 1: шаблон общего семинара/дискуссионного курса

В сообщении в блоге, опубликованном еще в марте, когда впервые началось дистанционное обучение, я написал о двух модульных структурах, которые могут быть полезны для преподавателей на семинарах и лекциях. Вы можете вернуться и прочитать этот пост для более подробной информации, если хотите. Он включает пошаговые инструкции и ссылки на руководства по Brightspace, которые помогут вам создать модули. А пока давайте рассмотрим первую структуру из поста здесь.

Чтобы воссоздать живое обсуждение семинара в классе, преподаватели могут использовать структурированный формат, подобный приведенному ниже. Подумайте, в частности, сколько времени займет каждое действие. Если ваш семестр рассчитан на то, чтобы учащиеся тратили 3–5 часов в неделю на чтение и подготовку и 3 часа в неделю на занятия, убедитесь, что вы непреднамеренно не создаете намного большую или меньшую рабочую нагрузку в Интернете. (Примечание: преподаватели часто ошибаются из-за слишком высокой рабочей нагрузки при первом переводе курсов в онлайн. Такое планирование может помочь предотвратить это.)

  1. Чтение/ввод , который может включать:
  • назначенные показания
  • Действия до и после чтения
  • лекция, подготовленная инструктором для предоставления контекста
  1. Журнал/Процесс , который может включать:
  • отправка ответов на запросы после чтения в качестве задания
  • Викторина по чтению, в которой задаются вопросы по обработке
  • взаимодействие с коллегами в асинхронном тексте или видео Доска обсуждений
  • добавление мыслей в индивидуальный частный журнал доски обсуждений
  1. Обсуждение , которое может включать:
  • синхронная встреча Zoom
  • асинхронное обсуждение
  • внешний инструмент, такой как Flipgrid для асинхронных обсуждений видео или Hypothes. is для социальной аннотации текстов
  • , если вы преподаете гибридный курс, это может быть место, где будут проходить ваши живые встречи f2f

 

Если этот формат кажется вам подходящим… но есть и другие элементы, которые вы обычно включаете в свои занятия f2f и надеетесь также использовать онлайн, как вы можете адаптировать эту модель к вашим потребностям? Возможно 4-й шаг в модуле демонстрации знаний и умений? Или, может быть, в вашем курсе есть презентационный элемент, и учащимся нужно будет создавать и делиться своими собственными видео- или аудиопрезентациями? В этом простом формате есть много возможностей для адаптации, дополнений и персонализации.

Пример 2: общая лекция / шаблон большого курса

Снова опираясь на мартовский пост в блоге, давайте посмотрим на общий шаблон еженедельного лекционного модуля.

Чтобы воссоздать живую презентацию лекции, преподаватели могут использовать структурированный формат, подобный приведенному ниже. Подумайте, в частности, сколько времени займет каждое действие. Если ваш семестр рассчитан на то, чтобы учащиеся тратили 3–5 часов в неделю на чтение и подготовку и 3 часа в неделю на занятия, убедитесь, что вы непреднамеренно не создаете намного большую или меньшую рабочую нагрузку в Интернете. (Примечание: преподаватели часто ошибаются из-за слишком высокой рабочей нагрузки при первом переводе курсов в онлайн. Такое планирование может помочь предотвратить это.)

  1. Лекция/Введение , что может включать:
  • видео лекции через Kaltura
  • назначенные чтения из учебника или созданные на Brightspace
  • открытые образовательные ресурсы (ООР), созданные экспертами
  1. Домашнее задание / Обработка , что может включать:
  • наборы задач из онлайн-платформы для самостоятельной оценки учебника
  • Викторина с неограниченным количеством попыток
  • задачи с ручкой и бумагой отсканированы и отправлены в качестве Задания
  • размещение ответов на доске обсуждений в небольшой группе для сравнения ответов и достижения консенсуса с коллегами
  1. Вопросы и ответы , которые могут включать:
  • синхронная встреча Zoom
  • асинхронный, ограниченное время Обсуждение
  • синхронный чат
  • видеоответа профессора или ассистента с веб-камеры на анонимные вопросы, заданные студентами на доске обсуждений

Как можно изменить этот шаблон, чтобы включить элементы, которые вы обычно включаете в свои классы?

Пример 3: сжатый шаблон летнего курса

Натан Холл, преподаватель Колледжа Дугласа в Ванкувере, Британская Колумбия, недавно опубликовал в Твиттере информацию о своей модульной структуре для своего 4-недельного летнего курса. Его курс «встречается» по 3 часа в день и 4 дня в неделю со смесью асинхронных и синхронных занятий. Он хотел убедиться, что каждый день включает в себя сочетание полезных учебных действий, которые были бы достаточно предсказуемы, чтобы создать четкий путь обучения. Вот его визуальное представление структуры модуля (доступно с разрешения):

 

 

Шаг 1: Учащиеся просматривают и взаимодействуют с короткими записанными уроками на Edpuzzle перед тем, как прийти в класс. (Асинхронный – всего 45 минут)

Шаг 2: Учащиеся выполняют контролируемые практические действия самостоятельно, основываясь на том, что они узнали на записанных уроках до прихода в класс. Это самомаркировка. (Асинхронный – всего 45 минут)

Шаг 3: Учащиеся посещают живой урок с инструктором, где они практикуются в парах и группах. (Синхронный – 1 час)

Шаг 4: Учащиеся самостоятельно работают над письменным проектом в комнате отдыха. Инструктор посещает каждого студента, чтобы оказать живую поддержку. (Синхронный – 30 минут)

Шаг 5: Учащиеся выполняют домашнее задание вне класса. (асинхронный)

Как можно изменить этот шаблон, чтобы включить элементы, которые вы обычно включаете в свои классы f2f?

 

 

На своем листе бумаги или с помощью цифрового инструмента, такого как Microsoft Word или Canva, создайте визуализацию структуры вашего курса, как показано выше. Не забудьте указать, сколько раз должен выполняться каждый шаг. Этот документ Word (нажмите здесь, чтобы загрузить: рабочий лист «Структура модуля») содержит два варианта такой визуализации: таблицу и смарт-арт. Не стесняйтесь использовать наш шаблон в качестве редактируемой отправной точки для наброска структуры собственного модуля онлайн-курса.

Поделитесь своей предварительной структурой модуля с коллегой или другом, чтобы получить отзыв. Какие у них были вопросы? Какую обратную связь они предоставили?

 

 


Эта страница находится под лицензией Creative Commons Attribution-NonCommercial 4.0 International License.

модулей Python

❮ Предыдущая Следующий ❯

Что такое модуль?

Модуль считается таким же, как библиотека кода.

Файл, содержащий набор функций, которые вы хотите включить в свое приложение.

Создать модуль

Чтобы создать модуль, просто сохраните нужный код в файле с расширением .py :

Пример

Сохраните этот код в файле с именем mymodule.py

def 4 def приветствие(имя):
  print("Привет, " + имя)

Использовать модуль

Теперь мы можем использовать только что созданный модуль, используя оператор import :

Пример

Импортируйте модуль с именем mymodule и вызовите функцию приветствия:

импортировать мой модуль

mymodule. greeting("Джонатан")

Пример запуска »

Примечание: При использовании функции из модуля используйте синтаксис: имя_модуля.имя_функции .

Переменные в модуле

Модуль может содержать функции, как уже описано, а также переменные все типы (массивы, словари, объекты и т.д.):

Пример

Сохраните этот код в файле mymodule.py

person1 = {
  "name": "John",
  "age": 36,
"country": "Норвегия"
}

Пример

Импортируйте модуль с именем mymodule и получите доступ к словарю person1:

import mymodule

a = mymodule.person1["age"]
print(a)

Пример запуска »

Присвоение имени модулю

Вы можете назвать файл модуля как угодно, но он должен иметь расширение файла .py

Переименование модуля

Вы можете создать псевдоним при импорте модуля, используя ключевое слово as :

import mymodule as mx

a = mx. person1["age"]
print(a)

Пример запуска »

Встроенные модули

В Python есть несколько встроенных модулей, которые вы можете импортировать в любое время. тебе нравится.

Пример

Импорт и использование модуля платформы :

import platform

x = platform.system()
print(x)

Попробуйте сами »

Использование функции dir()

Существует встроенная функция для вывода списка всех имен функций (или переменных). имена) в модуле. Функция dir() :

Пример

Список всех определенных имен, принадлежащих платформенному модулю:

импортная платформа

x = dir(platform)
print(x)

Попробуйте сами »

Примечание: Функция dir() может использоваться на всех модули, в том числе те, которые вы создаете сами.

Импорт из модуля

Вы можете импортировать только детали из модуля, используя ключевое слово из .

Пример

Модуль с именем mymodule имеет одну функцию и один словарь:

приветствие (имя):
  print("Здравствуйте, " + имя)

человек1 = {
  "имя": "Джон",
  "возраст": 36,
  "страна": "Норвегия"
}

Пример

Импортировать только словарь person1 из модуля:

from mymodule import person1

print (person1["age"])

Пример запуска »

Примечание: При импорте с использованием из ключевое слово, не используйте имя модуля при обращении к элементам в модуле. Пример: человек1["возраст"] , не mymodule.person1["возраст"]

Проверьте себя с помощью упражнений

Упражнение:

Каков правильный синтаксис для импорта модуля с именем "mymodule"?

 моймодуль

Начать упражнение

❮ Предыдущий Далее ❯


НОВИНКА

Мы только что запустили
Видео W3Schools

Узнать

ВЫБОР ЦВЕТА
КОД ИГРЫ

Играть в игру

Лучшие учебники
Учебник по HTML
Учебник по CSS
Учебник по JavaScript
Учебник How To
Учебник по SQL
Учебник по Python
Учебник по W3. CSS
Учебник по Bootstrap
Учебник по PHP
Учебник по Java
Учебник по C++
Учебник по jQuery

900 Справочник по HTML
Справочник по CSS
Справочник по JavaScript
Справочник по SQL
Справочник по Python
Справочник по W3.CSS
Справочник по Bootstrap
Справочник по PHP
Цвета HTML
Справочник по Java
Справочник по Angular
Справочник по jQuery

Лучшие примеры
Примеры HTML
Примеры CSS
Примеры JavaScript
Примеры инструкций
Примеры SQL
Примеры Python
Примеры W3.CSS
Примеры Bootstrap
Примеры PHP
Примеры Java
Примеры XML
Примеры jQuery

4 FORUM | О

W3Schools оптимизирован для обучения и обучения. Примеры могут быть упрощены для улучшения чтения и обучения. Учебники, ссылки и примеры постоянно пересматриваются, чтобы избежать ошибок, но мы не можем гарантировать полную правильность всего содержания. Используя W3Schools, вы соглашаетесь прочитать и принять наши условия использования, куки-файлы и политика конфиденциальности.

Copyright 1999-2022 Refsnes Data. Все права защищены.
W3Schools работает на основе W3.CSS.

Модуль ОС на Python с примерами

Модуль ОС на Python предоставляет функции для взаимодействия с операционной системой. ОС входит в стандартные служебные модули Python. Этот модуль предоставляет портативный способ использования функций, зависящих от операционной системы. Модули *os* и *os.path* включают множество функций для взаимодействия с файловой системой.
 

Обработка текущего рабочего каталога

Рассматривайте Текущий рабочий каталог (CWD) как папку, в которой работает Python. Всякий раз, когда файлы вызываются только по их имени, Python предполагает, что он начинается в CWD, что означает, что ссылка только по имени будет успешной, только если файл находится в CWD Python.
Примечание: Папка, в которой выполняется сценарий Python, называется текущим каталогом. Это не тот путь, где находится скрипт Python.
Получение текущего рабочего каталога
Для получения местоположения текущего рабочего каталога используется os.getcwd().
 

Example:

Python3

           

import os 

       

cwd = os.getcwd() 

       

печать ( "Текущий рабочий каталог:" , cwd) 

Вывод: 

 Текущий рабочий каталог: /home/nikhil/Desktop/gfg

Изменение текущего рабочего каталога

используется метод. Этот метод изменяет CWD на указанный путь. Он принимает только один аргумент в качестве нового пути к каталогу.
 

Примечание. Текущий рабочий каталог — это папка, в которой работает скрипт Python.
 

Example:

Python3

     

     

import os 

     

def current_path(): 

     print ( "Текущий рабочий каталог до" ) 

     print (os.getcwd()) 

     print () 

     

     

current_path() 

     

os. chdir( '../' ) 

     

current_path()

Вывод: 

 Текущий рабочий каталог до
C:\Пользователи\Нихил Аггарвал\Рабочий стол\gfg

Текущий рабочий каталог после
C:\Users\Нихил Аггарвал\Рабочий стол

 

Создание каталога

В модуле ОС доступны различные методы создания каталога. Это —

  • os.mkdir()
  • os.makedirs()

Использование os.mkdir()

Метод os.mkdir() в Python используется для создания каталога с именем пути с указанным числовой режим. Этот метод вызывает FileExistsError, если создаваемый каталог уже существует.
 

Пример:  

Python3

   

import os 

   

directory = "GeeksforGeeks"

   

parent_dir = " D:/Проекты Pycharm/"

   

путь = os. path.join(parent_dir, directory) 

   

os.mkdir(path) 

print ( "Directory '% s' created" % directory) 

   

directory = "Geeks"

   

parent_dir = "D:/Pycharm projects"

   

mode = 0o666

   

path = os. path.join(parent_dir, directory) 

   

os.mkdir(path, mode) 

print ( " Каталог "% s" создан" % каталог) 

Вывод: 

 Каталог "GeeksforGeeks" создан
Каталог «Geeks» создан

Использование os.makedirs()

Метод os.makedirs() в Python используется для рекурсивного создания каталога. Это означает, что при создании листового каталога, если какой-либо каталог промежуточного уровня отсутствует, метод os.makedirs() создаст их все.
 

Example:  

Python3

       

import os 

       

directory = "Nikhil"

       

parent_dir = "D:/Pycharm projects/GeeksForGeeks/Authors"

       

path = os. path.join(parent_dir, directory) 

       

os.makedirs(path) 

print ( "Directory '% s' created" % directory) 

       

       

       

       

directory = "c"

       

parent_dir = "D:/Pycharm projects/GeeksforGeeks/a /B "

Режим = 0O666

1 9

9 111129

111112

9 1119

= OS. Path.join (Parent_DIR, Directory)

OS.MADADEDIRS (PATH, MODE)

33333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333333н. created" % directory) 

       

       

       

       

Output: 

 Каталог "Нихил" создан
Каталог 'c' создан

Список файлов и каталогов с помощью Python

Метод os.listdir() в Python используется для получения списка всех файлов и каталогов в указанном каталоге. Если мы не укажем какой-либо каталог, то будет возвращен список файлов и каталогов в текущем рабочем каталоге.
 

Пример:

Python3

       

import os 

   

path = "/"

dir_list = os.listdir(path) 

   

Печать ( "Файлы и каталоги в" , PATH, "':" )

9 1111112119

11111111112119

111111111111111111111111 (DIRLIC0212

Вывод: 

 Файлы и каталоги в '/' :
['sys', 'run', 'tmp', 'boot', 'mnt', 'dev', 'proc', 'var', 'bin', 'lib64', 'usr',
'lib', 'srv', 'home', 'etc', 'opt', 'sbin', 'media']

 

Удаление каталога или файлов с помощью Python

Модуль ОС демонстрирует различные методы удаления каталогов и файлов в Питоне. Это –

  • Использование os.remove()
  • Использование os.rmdir()

Использование os.remove()

Метод os.remove() в Python используется для удаления или удаления пути к файлу. Этот метод не может удалить или удалить каталог. Если указанный путь является каталогом, метод вызовет ошибку OSError.
 

Example: Suppose the file contained in the folder are:
 

Python3

       

import os 

       

file = 'file1.txt'

       

location = "D:/Pycharm projects/GeeksforGeeks/Authors/Nikhil/"

Путь = OS. Path.join (Место, Файл )

39916

3311111111111111111111111111111111111111111111111111111111111111111111er1н.0169

Вывод:

Использование os.rmdir()

Метод os.rmdir() в Python используется для удаления или удаления пустого каталога. OSError будет поднят, если указанный путь не является пустым каталогом.
 

Example: Suppose the directories are 

Python3

       

import os 

       

directory = "Geeks"

       

parent = "D:/Pycharm projects/"

       

path = Os. Path.join (родитель, каталог)

OS.RMDIR (PATH)

:

:

:79

:79

.0016

 

Часто используемые функции

1. os.name: Эта функция дает имя импортируемого модуля, зависящего от операционной системы. В настоящее время зарегистрированы следующие имена: «posix», «nt», «os2», «ce», «java» и «riscos».

Python3

import os

   

print (os. name)

Output: 

 posix

Примечание: Он может выдавать разные выходные данные на разных интерпретаторах, например, «posix», когда вы запускаете код здесь.
 

2. os.error: Все функции в этом модуле вызывают OSError в случае недопустимых или недоступных имен файлов и путей или других аргументов, которые имеют правильный тип, но не принимаются операционной системой. os.error — это псевдоним для встроенного исключения OSError.

Python3

import os

   

   

try :

    

    

     filename = 'GFG. txt'

     f = open (filename, 'rU' )

     text = f.read()

     f.close()

   

except IOError:

   

    

     print ( «Проблема Снятие: ' + имени файла)

Выход: 

  
 :  
 
. 0398 
   
  3. os.popen():  Этот метод открывает канал к команде или от нее. Возвращаемое значение может быть прочитано или записано в зависимости от того, является ли режим «r» или «w». 
  Синтаксис:    
 
 os.popen(command[ mode[ bufsize]]) 
 Параметры mode и bufsize не являются обязательными параметрами, если они не указаны, по умолчанию для режима используется ‘r’.
 Python3 
  импорт   os 
  fd   =   "GFG.txt" 
      
  file   =   open   (fd,   'w'   ) 
  file   .write(   "Hello"   ) 
  file   . close() 
  file   =   open   (fd,   'r'   ) 
  text   =   файл   .read() 
  print   (text) 
      
  file   =   os.popen(fd,   'w'   ) 
  file   .Write (  «Hello»  ) 
  Выход: 
 Hello 
  Примечание:  Вывод для Popen () не будет показано, что не будет показано, что не будет показано, что не будет показано, что не будет показано, что не будет показано, что не будет показано, что не будет показано, что не будет показано, что это будет . 
  
  4. os.close():  Закрыть файловый дескриптор fd. Файл, открытый с помощью open(), может быть закрыт только с помощью close(). Но файл, открытый через os.popen(), можно закрыть с помощью close() или os.close(). Если мы попытаемся закрыть файл, открытый с помощью open(), используя os.close(), Python выдаст TypeError.
 Python3 
  import   os 
      
      
  fd   =   "GFG.txt" 
  file   =   open   (fd,   'r'   ) 
  text   =   file   . read() 
  ПЕЧАТЬ   (текст) 
  OS.Close (  Файл  ) 
: 6997666666666666666666666666666666666666666666666666666666666666666666 (9999766666666666666666666666666666666666666666666666666666666666666666666 (9
 Файл "C:\Users\GFG\Desktop\GeeksForGeeksOSFile.py", строка 6, в
 os.close(файл)
TypeError: требуется целое число (получен тип _io.TextIOWrapper) 
  Примечание:  Та же ошибка может не возникать из-за несуществующего файла или прав доступа. 
  
  5. os.rename():  Файл old.txt можно переименовать в new.txt с помощью функции os.rename(). Имя файла изменяется только в том случае, если файл существует и у пользователя есть достаточные привилегии для изменения файла.
 Python 
  импорт   ОС 
      
      
  fd   =   "GFG. txt" 
  os.rename(fd,   'New.txt'   ) 
  os.rename(fd,   ' New.txt'   ) 
  Вывод: 
 Трассировка (последний последний вызов):
  Файл "C:\Users\GFG\Desktop\ModuleOS\GeeksForGeeksOSFile.py", строка 3, в
    os.rename(fd,'New.txt')
FileNotFoundError: [WinError 2] Система не может найти
указанный файл: 'GFG.txt' -> 'New.txt' 
  Понимание вывода:  Существует файл с именем «GFG.txt», поэтому при первом использовании os.rename() файл переименовывается. При повторном вызове функции os.rename() файл «New.txt» существует, а не «GFG.txt» 
, поэтому Python выдает FileNotFoundError. 
  
  6. os.remove():  С помощью модуля Os мы можем удалить файл в нашей системе с помощью метода remove(). Чтобы удалить файл, нам нужно передать имя файла в качестве параметра.
 Python3 
  import   os 
      
  os.remove(   "file_name.txt"   ) 
 The OS module provides us a layer of abstraction between мы и операционная система. Когда мы работаем с модулем os  , всегда указывайте абсолютный путь в зависимости от операционной системы, код может работать на любой ОС, но нам нужно точно изменить путь. Если вы попытаетесь удалить несуществующий файл, вы получите  FileNotFoundError  .
  7. os.path.exists():  Этот метод проверяет, существует ли файл, передавая имя файла в качестве параметра. Модуль ОС имеет подмодуль с именем PATH, с помощью которого мы можем выполнять гораздо больше функций.
 Python3 
  import   os  
      
  result   =   os.path.exists(   "file_name"  ) 
  
  Печать   (результат) 
 . Если файл существует, он выдаст нам вывод True.
  8. os.path.getsize():  В этом методе python даст нам размер файла в байтах. Чтобы использовать этот метод, нам нужно передать имя файла в качестве параметра.
 Python3 
  import   os 
      
  size   =   os. path.getsize(   "filename"   ) 
      
  Печать   (  «Размер файла -"  , размер,   "байты."  ) 
 : 
 : 
 9000: .2 байта.

Эта статья предоставлена ​​ Piyush Doorwar . Если вам нравится GeeksforGeeks и вы хотите внести свой вклад, вы также можете написать статью с помощью write.geeksforgeeks.org или отправить ее по адресу [email protected]. Посмотрите, как ваша статья появится на главной странице GeeksforGeeks, и помогите другим гикам.
Пожалуйста, пишите комментарии, если вы обнаружите что-то неправильное, или вы хотите поделиться дополнительной информацией по теме, обсуждаемой выше.


модулей Python - GeeksforGeeks

Модуль Python — это файл, содержащий определения и операторы Python. Модуль может определять функции, классы и переменные. Модуль также может включать исполняемый код. Группировка связанного кода в модуль упрощает его понимание и использование. Это также делает код логически организованным. Пример: создать простой модуль0233      return (x + y)

   

def subtract(x, y):

     return (x - y)

Модуль импорта в Python — оператор импорта

Мы можем импортировать функции, классы, определенные в модуле, в другой модуль, используя оператор импорта в другом исходном файле Python.

Синтаксис: 

 импортировать модуль

Когда интерпретатор встречает оператор импорта, он импортирует модуль, если он присутствует в пути поиска. Путь поиска — это список каталогов, которые интерпретатор ищет для импорта модуля. Например, чтобы импортировать модуль calc.py, нам нужно поместить следующую команду в начало скрипта.

Примечание: Это не импортирует функции или классы напрямую, вместо этого импортируется только модуль. Для доступа к функциям внутри модуля используется оператор точка(.).

Example: Importing modules in Python

Python3

import calc

   

print (calc.add( 10 , 2 ))

Выход: 

 12

Оператор 2046 from позволяет импортировать определенные атрибуты из модуля без импорта модуля в целом.

Example: Importing specific attributes from the module

Python3

from math import sqrt, factorial

   

print (sqrt( 16 ))

печать (факториал( 6 ))

Выход: 

 4.0
720

Импортировать все имена — From import *  Statement

Символ *, используемый с оператором from import, используется для импорта всех имен из модуля в текущее пространство имен.

Синтаксис: 

 from module_name import *

Использование * имеет свои преимущества и недостатки. Если вы точно знаете, что вам понадобится от модуля, не рекомендуется использовать *, в противном случае сделайте это.

Example: Importing all names

Python3

from math import *

   

print (sqrt( 16 ))

печать (факториал( 6 ))

Выход 

 4.
720

Установочные модули

Всякий раз, когда модуль импортируется в Python, интерпретатор ищет несколько местоположений. Во-первых, он проверит встроенный модуль, если он не будет найден, он ищет список каталогов, определенных в sys. path. Интерпретатор Python ищет модуль следующим образом:

  • Сначала он ищет модуль в текущем каталоге.
  • Если модуль не найден в текущем каталоге, Python затем ищет каждый каталог в переменной оболочки PYTHONPATH. PYTHONPATH — это переменная среды, состоящая из списка каталогов.
  • Если это также не удается, python проверяет зависимый от установки список каталогов, настроенный во время установки Python.

Example: Directories List for Modules

Python3

import sys

   

print (sys.path)

Output :

['/home/nikhil/Desktop/gfg', '/usr/lib/python38.zip', '/usr/lib/python3. 8', '/usr/lib/python3.8/lib -dynload', ", '/home/nikhil/.local/lib/python3.8/site-packages', '/usr/local/lib/python3.8/dist-packages', '/usr/lib/python3 /dist-packages', '/usr/local/lib/python3.8/dist-packages/IPython/extensions', '/home/nikhil/.ipython']

Импорт и переименование модуля

Мы можем переименовать модуль во время его импорта, используя ключевое слово as.

Example: Renaming the module

Python3

import math as gfg

   

print (gfg.sqrt( 16 ))

напечатать (gfg.factorial( 6 ))

Выход 

 4,0
720

Функция dir()

Встроенная функция dir() возвращает отсортированный список строк, содержащих имена, определенные модулем. Список содержит имена всех модулей, переменных и функций, определенных в модуле.

Python3

импорт   случайный

печать ( каталог (случайный))


Выход:

['BPF', ',', ', nv_MAG. 'SystemRandom', 'TWOPI', '_BuiltinMethodType', '_MethodType', '_Sequence', '_Set', '__all__', '__builtins__', '__cached__', '__doc__', '__file__', '__loader__', '__name__ ', '__package__', '__spec__', '_acos', '_bisect', '_ceil', '_cos', '_e', '_exp', '_inst', '_itertools', '_log', '_pi', '_random', '_sha512', '_sin', '_sqrt', '_test', '_test_generator', '_urandom', '_warn', 'betavariate', 'choice', 'choices', 'expovariate', 'gammavariate ', 'гаусс', 'getrandbits', 'getstate', 'lognormvariate', 'normalvariate', 'paretovariate', 'randint', 'random', 'randrange', 'sample', 'seed', 'setstate', 'перетасовка', 'треугольный', 'равномерный', 'вариантный фон', 'вариантный']

Code Snippet illustrating python built-in modules:  

 

Python3

import math

   

print (math. sqrt( 25 ))

Печать (Math.pi)

11112 (математика.0211 2 ))  

   

print (math.radians( 60 ))  

   

print (math.sin( 2 ))  

   

print (math.cos( 0.5 ))  

   

print (math. tan( 0.23 )) 

   

print (math.factorial( 4 ))  

   

import random

   

print ( Random.0212  

print (random.random() * 100 )  

   

List = [ 1 , 4 , True , 800 , "python" , 27 , "hello" ]

   

print (random. choice( List )) 

   

   

import datetime

from datetime import date

import Время

ПЕЧАТЬ (Time.Time ())

.0212 454554 ))  

Output: 

 5.0 
 3.1415
59 
 114.5026 
 1.0471975512 
 0.7426826 
 0.87758256189 
 0. 234143362351 
 24 
 3 
 0.401533172951 
 88.46788 
 True 
 1461425771.87

Основы разработки онлайн-курсов

  • Добро пожаловать в Дизайн онлайн-курсов Страница

  • Результаты обучения для этого курса Страница

  • Модуль 1 - Результаты обучения Страница

  • Доступны технические инструменты LWTech Страница

  • Какие инструменты следует использовать? Страница

  • Синхронные инструменты и когда использовать (инструменты, поддерживаемые LWTech) Страница

  • Асинхронные инструменты и когда использовать (инструменты, поддерживаемые LWTech) Страница

  • [Читать/смотреть] Планы уроков по обратному дизайну Страница

  • [Шаблон] Дизайн обратного курса Вложение

  • [Шаблон] Схема дизайна обратного курса Вложение

  • Модуль 3. Результаты обучения Страница

  • Обзор организации курса (модули) Страница

  • [СМОТРЕТЬ ПРИМЕРЫ] Хороший дизайн модуля Страница

  • Модуль 2 – Результаты обучения Страница

  • [To-Do] Полный контрольный список (распечатать как руководство) Страница

  • 1 - Создайте свой профиль холста Страница

  • 2 - Создайте учебный план и разместите его на вкладке «Учебный план» (шаблон учебного плана здесь) Страница

  • 3 - Создать модуль «Начать здесь» Страница

  • 4 - Создайте приветственное видео - разместите в модуле Start Here Страница

  • 5 - Создайте видеообзор курса - опубликуйте в модуле Start Here Страница

  • 6 - Создайте эти два обсуждения Страница

  • 7 - Установите ожидания от общения и взаимодействия Страница

  • 8 - Добавьте онлайн-модуль успеха учащихся в свой курс Страница

  • 9 - Очистите меню курса, чтобы отображались только те элементы, которые вы используете Страница

  • 10 - Опубликуйте свой курс Canvas (к первому дню четверти, если не раньше) Страница

  • 11 - Создайте приветственное объявление в Canvas Страница

  • 12 - Создайте приветственное письмо Страница

  • Контрольный список дизайна курса WA Страница

  • Контрольный список аварийного дистанционного управления QM Внешний URL-адрес

  • Лучшие статьи для онлайн-обучения (в центре внимания преподавателей во времена COVID-19) Внешний URL-адрес

  • Когда прилив стихает: выявление и поддержка учащихся, испытывающих затруднения, на онлайн-курсах Внешний URL-адрес

  • Как стать лучшим онлайн-учителем — руководство с советами (статья из хроники) Внешний URL-адрес

  • QM: Контрольный список аварийных дистанционных инструкций Внешний URL-адрес

  • Борьба с коронавирусом: как преподаватели могут поддержать студентов в трудные времена Внешний URL-адрес

  • Объявление Национальной аварийной библиотеки Внешний URL-адрес

  • Национальная аварийная библиотека (Arhive. Org/NEL) Внешний URL-адрес

  • 20 советов по проведению доступного онлайн-курса (UW Do-It) Внешний URL-адрес

  • 30 советов по веб-доступности (UW Do-It) Внешний URL-адрес

  • БЕСПЛАТНЫЕ вспомогательные технологии Страница

Install-Module (PowerShellGet) — PowerShell | Microsoft Learn

  • Справочник
Модуль:
PowerShellGet

Загружает один или несколько модулей из репозитория и устанавливает их на локальный компьютер.

Синтаксис 

 Модуль установки
       [-Имя] <Строка[]>
       [-Минимальная версия ]
       [-Максимальная версия ]
       [-RequiredVersion ]
       [-Репозиторий ]
       [-Учетные данные ]
       [-Область <Строка>]
       [-Прокси ]
       [-ProxyCredential ]
       [-Разрешить клоббер]
       [-SkipPublisherCheck]
       [-Сила]
       [-Разрешить пререлиз]
       [-Принять лицензию]
       [-Пройти через]
       [-Что если]
       [-Подтверждать]
       [<Общие параметры>] 
 Установочный модуль
       [-InputObject] 
       [-Учетные данные ]
       [-Область <Строка>]
       [-Прокси ]
       [-ProxyCredential ]
       [-Разрешить клоббер]
       [-SkipPublisherCheck]
       [-Сила]
       [-Принять лицензию]
       [-Пройти через]
       [-Что если]
       [-Подтверждать]
       []

Описание

Командлет Install-Module получает один или несколько модулей, отвечающих заданным критериям, из интерактивного репозиторий. Командлет проверяет, являются ли результаты поиска действительными модулями, и копирует папки модулей. к месту установки. Установленные модули не импортируются автоматически после установки. Вы можете отфильтровать, какой модуль установлен на основе минимальной, максимальной и точной версии указанные модули.

Если устанавливаемый модуль имеет то же имя или версию или содержит команды в существующем модуля отображаются предупреждающие сообщения. После того, как вы подтвердите, что хотите установить модуль и переопределить предупреждения, используйте параметры -Force и -AllowClobber . В зависимости от вашего репозитория, вам может потребоваться ответить на запрос, чтобы установка модуля продолжилась.

В этих примерах галерея PowerShell используется как единственный зарегистрированный репозиторий. Get-PSRepository отображает зарегистрированные репозитории. Если у вас несколько зарегистрированных репозиториев, используйте параметр -Repository , чтобы указать имя репозитория.

Примеры

Пример 1. Поиск и установка модуля

В этом примере выполняется поиск модуля в репозитории и его установка.

 Find-Module -Name PowerShellGet | Install-Module

Find-Module использует параметр Name для указания Модуль PowerShellGet . По умолчанию, самая новая версия модуля загружается из репозитория. Объект отправляется вниз конвейер к командлету Install-Module . Install-Module устанавливает модуль для всех пользователей в $env:ProgramFiles\PowerShell\Modules .

Пример 2. Установка модуля по имени

В этом примере устанавливается новейшая версия модуля PowerShellGet .

 Install-Module -Name PowerShellGet

Install-Module использует параметр Name для указания модуля PowerShellGet . По по умолчанию самая новая версия модуля загружается из репозитория и устанавливается.

Пример 3. Установка модуля с использованием его минимальной версии

В этом примере устанавливается минимальная версия модуля PowerShellGet . Параметр MinimumVersion указывает самую раннюю версию модуля, который следует установить. Если доступна более новая версия модуля, эта версия загружается и устанавливается для всех пользователей.

 Install-Module -Name PowerShellGet -MinimumVersion 2.0.1

Install-Module использует параметр Name для указания модуля PowerShellGet . Параметр MinimumVersion указывает, что версия 2.0.1 загружается из репозитория и установлены. Поскольку доступна версия 2.0.4 , эта версия загружается и устанавливается для всех пользователи.

Пример 4: Установка определенной версии модуля

В этом примере установлена ​​определенная версия модуля PowerShellGet .

 Install-Module -Name PowerShellGet -RequiredVersion 2.0.0

Install-Module использует параметр Name для указания модуля PowerShellGet . Параметр RequiredVersion указывает, что версия 2.0.0 загружается и устанавливается для всех пользователи.

Пример 5: Установить модуль только для текущего пользователя

В этом примере загружается и устанавливается новейшая версия модуля только для текущего пользователя.

 Install-Module -Name PowerShellGet -Scope CurrentUser

Install-Module использует параметр Name для указания модуля PowerShellGet . Install-Module загружает и устанавливает новейшую версию PowerShellGet в текущую каталог пользователя, $home\Documents\PowerShell\Modules .

Parameters

-AcceptLicense

-AllowClobber

-AllowPrerelease

-Confirm

-Credential

-Force

-InputObject

-MaximumVersion

-MinimumVersion

-Name

-PassThru

Тип: SwitchParameter
Позиция: Named
Значение по умолчанию: False
Accept pipeline input: False
Accept wildcard characters: False

-Proxy

-ProxyCredential

-Repository

-RequiredVersion

-Scope

-SkipPublisherCheck

-WhatIf

Inputs

PSRepositoryItemInfo

Find-Module создает объекта PSRepositoryItemInfo , которые могут быть отправлены по конвейеру в Установочный модуль .

Строка []

PSObject []

Строка

MicrosHOL. , Install-Module выводит объект PSRepositoryItemInfo для модуля. Это та же информация, которую вы получаете от 9Командлет 0211 Find-Module .

Notes

Install-Module работает в PowerShell 5.0 или более поздних версиях, в Windows 7 или Windows 2008 R2 и более поздних версиях. выпуски Windows.

Важно

С апреля 2020 года коллекция PowerShell больше не поддерживает безопасность транспортного уровня (TLS). версии 1.0 и 1.1. Если вы не используете TLS 1.2 или выше, вы получите сообщение об ошибке при пытается получить доступ к галерее PowerShell. Используйте следующую команду, чтобы убедиться, что вы используете TLS 1,2:

[Net.ServicePointManager]::SecurityProtocol = [Net.SecurityProtocolType]::Tls12

Дополнительные сведения см. объявление в Блог PowerShell.

В целях безопасности оцените код модуля перед запуском каких-либо командлетов или функций для первый раз. Чтобы предотвратить запуск модулей, содержащих вредоносный код, установленные модули не автоматически импортируется после установки.

Если имя модуля, заданное параметром Имя , не существует в репозитории, Install-Module возвращает ошибку.

Чтобы установить несколько модулей, используйте параметр Имя и укажите массив значений, разделенных запятыми. названия модулей. Если вы укажете несколько имен модулей, вы не сможете использовать MinimumVersion , Максимальная версия или Требуемая версия . Find-Module создает объекта PSRepositoryItemInfo который может быть отправлен по конвейеру в Install-Module . Конвейер — это еще один способ указать несколько модулей для установки одной командой.

По умолчанию модули для области AllUsers установлены в $env:ProgramFiles\PowerShell\Modules . Значение по умолчанию предотвращает путаницу при установке PowerShell. Ресурсы требуемой конфигурации состояния (DSC).

Установка модуля завершается сбоем и не может быть импортирована, если у него нет .psm1 , .psd1 или .dll того же имени в папке. Используйте параметр Force для установки модуля.

Если версия существующего модуля соответствует имени, указанному в Имя параметра и MinimumVersion или RequiredVersion параметр не используется, Install-Module молча продолжается, но модуль не устанавливается.

Если версия существующего модуля больше, чем значение параметра MinimumVersion , или равно значению параметра RequiredVersion , Install-Module молча продолжается, но не устанавливает модуль.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *