Найти предел онлайн с решением: Предел функции онлайн

Калькулятор онлайн.Решение пределов. Решение пределов онлайн

Правило Лопиталя (п. Л.) облегчает вычисление пределов функций. Например, надо найти предел функции, которая является отношением функций стремящихся к нулю. Т.е. отношение функций это неопределенность 0/0. Раскрыть ее поможет . В пределе отношение функций можно заменить отношением производных этих функций. Т.е. надо производную числителя разделить на производную знаменателя и от этой дроби взять предел.

1. Неопределенность 0/0. Первое п.Л.

Если = 0, то , если последний существует.

2. Неопределенность вида ∞/∞ Второе п. Л.

Нахождение пределов такого типа называется раскрытием неопределенностей.

Если = ∞, то , если последний существует.

3. Неопределенности 0⋅∞, ∞- ∞, 1 ∞ и 0 0 сводятся к неопределенностям 0/0 и ∞/∞ путем преобразований. Такая запись служит для краткого указания случая при отыскании предела. Каждая неопределенность раскрывается по своему. Правило Лопиталя можно применять несколько раз, пока не избавимся от неопределенности.

Применение правила Лопиталя приносит пользу тогда, когда отношение производных удается преобразовать к более удобному виду легче, чем отношение функций.

• 0⋅∞ произведение двух функций, первая стремится к нулю, вторая к бесконечности;
• ∞- ∞ разность функций, стремящихся к бесконечности;
• 1 ∞ степень, ее основание стремится к единице, а показатель к бесконечности;
• ∞ 0 степень, ее основание стремится к бесконечности, а степень к нулю;
• 0 0 степень, ее основание стремится к 0 и показатель тоже стремятся к нулю.

Пример 1. В этом примере неопределенность 0/0

Пример 2. Здесь ∞/∞

В этих примерах производные числителя делим на производные знаменателя и подставляем предельное значение вместо х.

Пример 3. Вид неопределенности 0⋅∞ .

Неопределенность 0⋅∞ преобразуем к ∞/∞, для этого х переносим в знаменатель в виде дроби 1/x , в числителе пишем производную от числителя, а в знаменателе производную от знаменателя.

Пример 4 Вычислить предел функции

Здесь неопределенность вида ∞ 0 Сначала логарифмируем функцию, затем найдем от нее предел

Для получения ответа надо е возвести в степень -1, получим e -1 .

Пример 5. Вычислить предел от если x → 0

Решение. Вид неопределенности ∞ -∞ Приведя дробь к общему знаменателю перейдем от ∞-∞ к 0/0. Применим правило Лопиталя, однако снова получим неопределенность 0/0, поэтому п. Л. надо применить второй раз. Решение имеет вид:

= = = =
= =

Пример 6 Решить

Решение. Вид неопределенности ∞/∞, раскрыв ее получим

В случаях 3), 4), 5) сначала логарифмируют функцию и находят предел логарифма, а затем искомый предел е возводим в полученную степень.

Пример 7. Вычислить предел

Решение. Здесь вид неопределенности 1 ∞ . Обозначим A =

Тогда lnA = = = = 2.

Основание логарифма е, поэтому для получения ответа надо е возвести в квадрат, получим e 2 .

Иногда бывают случаи, когда отношение функций имеет предел, в отличие от отношения производных, которое не имеет его.

Рассмотрим пример:

Т.к. sinx ограничен, а х неограниченно растет, второй член равен 0.

Эта функция не имеет предела, т. к. она постоянно колеблется между 0 и 2, к этому примеру неприменимо п. Л.

Раскрытие неопределённостей вида 0/0 или ∞/∞ и некоторых других неопределённостей, возникающих при вычислении предела отношения двух бесконечно малых или бесконечно больших функций значительно упрощается с помощью правила Лопиталя (на самом деле двух правил и замечаний к ним).

Суть правил Лопиталя состоит в том, что в случае, когда вычисление предела отношений двух бесконечно малых или бесконечно больших функций даёт неопределённости видов 0/0 или ∞/∞, предел отношения двух функций можно заменить пределом отношения их

производных и, таким образом, получить определённный результат.

Перейдём к формулировкам правил Лопиталя.

Правило Лопиталя для случая предела двух бесконечно малых величин . Если функции f (x ) и g (x a a , причём в этой окрестности g «(x a равны между собой и равны нулю

().

Правило Лопиталя для случая предела двух бесконечно больших величин . Если функции f (x ) и g (x ) дифференцируемы в некоторой окрестности точки a , за исключением, может быть, самой точки a , причём в этой окрестности g «(x )≠0 и если и если пределы этих функций при стремлении икса к значению функции в точке a равны между собой и равны бесконечности

(),

то предел отношения этих функций равен пределу отношения их производных

().

Иными словами, для неопределённостей вида 0/0 или ∞/∞ предел отношения двух функций равен пределу отношения их производных, если последний существует (конечный или бесконечный).

Замечания .

1. Правила Лопиталя применимы и тогда, когда функции f (x ) и g (x ) не определены при x = a .

2. Если при вычисления предела отношения производных функций f (x ) и g (x ) снова приходим к неопределённости вида 0/0 или ∞/∞, то правила Лопиталя следует применять многократно (минимум дважды).

3. Правила Лопиталя применимы и тогда, когда аргумент функций (икс) стремится не к конечному числу a , а к бесконечности (x → ∞).

К неопределённостям видов 0/0 и ∞/∞ могут быть сведены и неопределённости других видов.

Раскрытие неопределённостей видов «ноль делить на ноль» и «бесконечность делить на бесконечность»

Пример 1.

x =2 приводит к неопределённости вида 0/0. Поэтому производную каждой функции и получаем

В числителе вычисляли производную многочлена, а в знаменателе — производную сложной логарифмической функции . Перед последним знаком равенства вычисляли обычный предел , подставляя вместо икса двойку.

Пример 2. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:

Решение. Подстановка в заданную функцию значения x

Пример 3. Вычислить предел отношения двух функций, пользуясь правилом Лопиталя:

Решение. Подстановка в заданную функцию значения x =0 приводит к неопределённости вида 0/0. Поэтому вычисляем производные функций в числителе и знаменателе и получаем:

Пример 4. Вычислить

Решение. Подстановка в заданную функцию значения икса, равного плюс бесконечности, приводит к неопределённости вида ∞/∞. Поэтому применим правило Лопиталя:

Замечание. Переходим к примерам, в которых правило Лопиталя приходится применять дважды, то есть приходить к пределу отношений вторых производных, так как предел отношения первых производных представляет собой неопределённость вида 0/0 или ∞/∞.

Применить правило Лопиталя самостоятельно, а затем посмотреть решение

Раскрытие неопределённостей вида «ноль умножить на бесконечность»

Пример 12. Вычислить

.

Решение. Получаем

В этом примере использовано тригонометрическое тождество .

Раскрытие неопределённостей видов «ноль в степени ноль», «бесконечность в степени ноль» и «один в степени бесконечность»

Неопределённости вида , или обычно приводятся к виду 0/0 или ∞/∞ с помощью логарифмирования функции вида

Чтобы вычислить предел выражения , следует использовать логарифмическое тождество , частным случаем которого является и свойство логарифма .

Используя логарифмическое тождество и свойство непрерывности функции (для перехода за знак предела), предел следует вычислять следующим образом:

Отдельно следует находить предел выражения в показателе степени и возводить e в найденную степень.

Пример 13.

Решение. Получаем

.

.

Пример 14. Вычислить, пользуясь правилом Лопиталя

Решение. Получаем

Вычисляем предел выражения в показателе степени

.

.

Пример 15. Вычислить, пользуясь правилом Лопиталя

• Правило Лопиталя и раскрытие неопределённостей
• Раскрытие неопределённостей видов «ноль делить на ноль» и «бесконечность делить на бесконечность»
• Раскрытие неопределённостей вида «ноль умножить на бесконечность»
• Раскрытие неопределённостей видов «ноль в степени ноль», «бесконечность в степени ноль» и «один в степени бесконечность»
• Раскрытие неопределённостей вида «бесконечность минус бесконечность»

Правило Лопиталя и раскрытие неопределённостей

Раскрытие неопределённостей вида 0/0 или ∞/∞ и некоторых других неопределённостей значительно упрощается с помощью правила Лопиталя.

Суть правила Лопиталя состоит в том, что в случае, когда вычисление предела отношений двух функций даёт неопределённости видов 0/0 или ∞/∞, предел отношения двух функций можно заменить пределом отношения их производных и, таким образом, получить определённный результат.

Вообще, под правилами Лопиталя понимаются несколько теорем, которые могут быть переданы в следующей одной формулировке.

Правило Лопиталя . Если функции f (x ) и g (x ) дифференцируемы в некоторой окрестности точки , за исключением, может быть, самой точки , причём в этой окрестности

(1)

Иными словами, для неопределённостей вида 0/0 или ∞/∞ предел отношения двух функций равен пределу отношения их производных, если последний существует (конечный или бесконечный).

В равенстве (1) величина , к которой стремится переменная, может быть либо конечным числом, либо бесконечностью, либо минус бесконечностью.

К неопределённостям видов 0/0 и ∞/∞ могут быть сведены и неопределённости других видов.

Раскрытие неопределённостей видов «ноль делить на ноль» и «бесконечность делить на бесконечность»

Пример 1. Вычислить

x =2 приводит к неопределённости вида 0/0. Поэтому применим правило Лопиталя:

Пример 2. Вычислить

Решение. Подстановка в заданную функцию значения x

Пример 3. Вычислить

Решение. Подстановка в заданную функцию значения x =0 приводит к неопределённости вида 0/0. Поэтому применим правило Лопиталя:

Пример 4. Вычислить

Решение. Подстановка в заданную функцию значения икса, равного плюс бесконечности, приводит к неопределённости вида ∞/∞. Поэтому применим правило Лопиталя:

Замечание. Если предел отношения производных представляет собой неопределённость вида 0/0 или ∞/∞, то можно снова применить правило Лопиталя, т.е. перейти к пределу отношения вторых производных, и т.д.

Пример 5. Вычислить

Решение. Находим

Здесь правило Лопиталя применено дважды, поскольку и предел отношения функций, и предел отношения производных дают неопределённость вида ∞/∞.

Пример 6. Вычислить

Представьте стаю воробьёв с выпученными глазами. Нет, это не гром, не ураган и даже не маленький мальчик с рогаткой в руках. Просто в самую гущу птенчиков летит огромное-огромное пушечное ядро. Именно так правила Лопиталя расправляются с пределами, в которых имеет место неопределённость или .

Правила Лопиталя – очень мощный метод, позволяющий быстро и эффективно устранить указанные неопределенности, не случайно в сборниках задач, на контрольных работах, зачётах часто встречается устойчивый штамп: «вычислить предел, не пользуясь правилом Лопиталя ». Выделенное жирным шрифтом требование можно с чистой совестью приписать и к любому пределу уроков Пределы. Примеры решений , Замечательные пределы . Методы решения пределов , Замечательные эквивалентности , где встречается неопределённость «ноль на ноль» либо «бесконечность на бесконечность». Даже если задание сформулировано коротко – «вычислить пределы», то негласно подразумевается, что вы будете пользоваться всем, чем угодно, но только не правилами Лопиталя.

Всего правил два, и они очень похожи друг на друга, как по сути, так и по способу применения. Кроме непосредственных примеров по теме, мы изучим и дополнительный материал, который будет полезен в ходе дальнейшего изучения математического анализа.

Сразу оговорюсь, что правила будут приведены в лаконичном «практическом» виде, и если вам предстоит сдавать теорию, рекомендую обратиться к учебнику за более строгими выкладками.

Первое правило Лопиталя

Рассмотрим функции , которые бесконечно малЫ в некоторой точке . Если существует предел их отношений , то в целях устранения неопределённости можно взять две производные – от числителя и от знаменателя. При этом: , то есть .

Примечание : предел тоже должен существовать, в противном случае правило не применимо.

Что следует из вышесказанного?

Во-первых, необходимо уметь находить производные функций , и чем лучше – тем лучше =)

Во-вторых, производные берутся ОТДЕЛЬНО от числителя и ОТДЕЛЬНО от знаменателя. Пожалуйста, не путайте с правилом дифференцирования частного !!!

И, в-третьих, «икс» может стремиться куда угодно, в том числе, к бесконечности – лишь бы была неопределённость .

Вернёмся к Примеру 5 первой статьи о пределах , в котором был получен следующий результат:

К неопределённости 0:0 применим первое правило Лопиталя:

Как видите, дифференцирование числителя и знаменателя привело нас к ответу с пол оборота: нашли две простые производные, подставили в них «двойку», и оказалось, что неопределённость бесследно исчезла!

Не редкость, когда правила Лопиталя приходится применять последовательно два или бОльшее количество раз (это относится и ко второму правилу). Вытащим на ретро-вечер Пример 2 урока о замечательных пределах :

На двухъярусной кровати снова прохлаждаются два бублика. Применим правило Лопиталя:

Обратите внимание, что на первом шаге в знаменателе берётся производная сложной функции . После этого проводим ряд промежуточных упрощений, в частности, избавляемся от косинуса, указывая, что он стремится к единице. Неопределённость не устранена, поэтому применяем правило Лопиталя ещё раз (вторая строчка).

Я специально подобрал не самый простой пример, чтобы вы провели небольшое самотестирование. Если не совсем понятно, как найдены производные , следует усилить свою технику дифференцирования, если не понятен фокус с косинусом, пожалуйста, вернитесь к замечательным пределам . Не вижу особого смысла в пошаговых комментариях, так как о производных и пределах я уже рассказал достаточно подробно. Новизна статьи состоит в самих правилах и некоторых технических приёмах решения.

Как уже отмечалось, в большинстве случаев правила Лопиталя использовать не нужно, но их зачастую целесообразно применять для черновой проверки решения. Зачастую, но далеко не всегда. Так, например, только что рассмотренный пример значительно выгоднее проверить через замечательные эквивалентности .

Второе правило Лопиталя

Брат-2 борется с двумя спящими восьмёрками . Аналогично:

Если существует предел отношения бесконечно больших в точке функций: , то в целях устранения неопределённости можно взять две производные – ОТДЕЛЬНО от числителя и ОТДЕЛЬНО от знаменателя. При этом: , то есть при дифференцировании числителя и знаменателя значение предела не меняется .

Примечание : предел должен существовать

Опять же, в различных практических примерах значение может быть разным , в том числе, бесконечным. Важно, чтобы была неопределённость .

Проверим Пример №3 первого урока: . Используем второе правило Лопиталя:

Коль скоро речь зашла о великанах, разберём два каноничных предела:

Пример 1

Вычислить предел

Получить ответ «обычными» методами непросто, поэтому для раскрытия неопределённости «бесконечность на бесконечность» используем правило Лопиталя:

Таким образом, линейная функция более высокого порядка роста , чем логарифм с основанием бОльшим единицы ( и т.д.). Разумеется, «иксы» в старших степенях тоже будут «перетягивать» такие логарифмы. Действительно, функция растёт достаточно медленно и её график является более пологим относительно того же «икса».

Пример 2

Вычислить предел

Ещё один примелькавшийся кадр. В целях устранения неопределённости , используем правило Лопиталя, причём, два раза подряд:

Показательная функция, с основанием, бОльшим единицы ( и т.д.) более высокого порядка роста , чем степенная функция с положительной степенью .

Похожие пределы встречаются в ходе полного исследования функции , а именно, при нахождении асимптот графиков . Также замечаются они и в некоторых задачах по теории вероятностей . Советую взять на заметку два рассмотренных примера, это один из немногих случаев, когда лучше дифференцирования числителя и знаменателя ничего нет.

Далее по тексту я не буду разграничивать первое и второе правило Лопиталя, это было сделано только в целях структурирования статьи. Вообще, с моей точки зрения, несколько вредно излишне нумеровать математические аксиомы, теоремы, правила, свойства, поскольку фразы вроде «согласно следствию 3 по теореме 19…» информативны только в рамках того или иного учебника. В другом источнике информации то же самое будет «следствием 2 и теоремой 3». Такие высказывания формальны и удобны разве что самим авторам. В идеале лучше ссылаться на суть математического факта. Исключение – исторически устоявшиеся термины, например, первый замечательный предел или второй замечательный предел .

Продолжаем разрабатывать тему, которую нам подкинул член Парижской академии наук маркиз Гийом Франсуа де Лопиталь. Статья приобретает ярко выраженную практическую окраску и в достаточно распространённом задании требуется:

Для разминки разберёмся с парой небольших воробушков:

Пример 3

Предел можно предварительно упростить, избавившись от косинуса, однако проявим уважение к условию и сразу продифференцируем числитель и знаменатель:

В самом процессе нахождения производных нет чего-то нестандартного, так, в знаменателе использовано обычное правило дифференцирования произведения .

Рассмотренный пример разруливается и через замечательные пределы , похожий случай разобран в конце статьи Сложные пределы .

Пример 4

Вычислить предел по правилу Лопиталя

Это пример для самостоятельного решения. Нормально пошутил =)

Типична ситуация, когда после дифференцирования получаются трех- или четырёхэтажные дроби:

Пример 5

Вычислить предел, используя правило Лопиталя

Напрашивается применение замечательной эквивалентности , но путь жёстко предопределён по условию:

После дифференцирования настоятельно рекомендую избавляться от многоэтажности дроби и проводить максимальные упрощения . Конечно, более подготовленные студенты могут пропустить последний шаг и сразу записать: , но в некоторых пределах запутаются даже отличники.

Пример 6

Вычислить предел, используя правило Лопиталя

Пример 7

Вычислить предел, используя правило Лопиталя

Это примеры для самостоятельного решения. В Примере 7 можно ничего не упрощать, слишком уж простой получается после дифференцирования дробь. А вот в Примере 8 после применения правила Лопиталя крайне желательно избавиться от трёхэтажности, поскольку вычисления будут не самыми удобными. Полное решение и ответ в конце урока. Если возникли затруднения – тригонометрическая таблица в помощь.

И, упрощения совершенно необходимы, когда после дифференцирования неопределённость не устранена .

Пример 8

Вычислить предел, используя правило Лопиталя

Поехали:

Интересно, что первоначальная неопределённость после первого дифференцирования превратилась в неопределённость , и правило Лопиталя невозмутимо применяется дальше. Также заметьте, как после каждого «подхода» устраняется четырёхэтажная дробь, а константы выносятся за знак предела. В более простых примерах константы удобнее не выносить, но когда предел сложный, упрощаем всё-всё-всё. Коварство решённого примера состоит ещё и в том, что при , а , поэтому в ходе ликвидации синусов немудрено запутаться в знаках. В предпоследней строчке синусы можно было и не убивать, но пример довольно тяжелый, простительно.

На днях мне попалось любопытное задание:

Пример 9

Если честно, немного засомневался, чему будет равен данный предел. Как демонстрировалось выше, «икс» более высокого порядка роста, чем логарифм, но «перетянет» ли он логарифм в кубе? Постарайтесь выяснить самостоятельно, за кем будет победа.

Да, правила Лопиталя – это не только пальба по воробьям из пушки, но ещё и кропотливая работа….

В целях применения правил Лопиталя к бубликам или уставшим восьмёркам сводятся неопределённости вида .

Расправа с неопределённостью подробно разобрана в Примерах №№9-13 урока Методы решения пределов . Давайте для проформы ещё один:

Пример 10

Вычислить предел функции, используя правило Лопиталя

На первом шаге приводим выражение к общему знаменателю, трансформируя тем самым неопределённость в неопределённость . А затем заряжаем правило Лопиталя:

Здесь, к слову, тот случай, когда четырёхэтажное выражение трогать бессмысленно.

Неопределённость тоже не сопротивляется превращению в или :

Пример 11

Вычислить предел функции с помощью правила Лопиталя

Предел здесь односторонний, и о таких пределах уже шла речь в методичке Графики и свойства функций . Как вы помните, графика «классического» логарифма не существует слева от оси , таким образом, мы можем приближаться к нулю только справа.

Правила Лопиталя для односторонних пределов работают, но сначала необходимо разобраться с неопределённостью . На первом шаге делаем дробь трёхэтажной, получая неопределённость , далее решение идёт по шаблонной схеме:

После дифференцирования числителя и знаменателя избавляемся от четырёхэтажной дроби, чтобы провести упрощения. В результате нарисовалась неопределённость . Повторяем трюк: снова делаем дробь трёхэтажной и к полученной неопределённости применяем правило Лопиталя ещё раз:

Готово.

Исходный предел можно было попытаться свести к двум бубликам:

Но, во-первых, производная в знаменателе труднее, а во-вторых, ничего хорошего из этого не выйдет.

Таким образом, перед решением похожих примеров нужно проанализировать (устно либо на черновике), К КАКОЙ неопределённости выгоднее свести – к «нулю на ноль» или к «бесконечности на бесконечность».

В свою очередь на огонёк подтягиваются собутыльники и более экзотические товарищи . Метод трансформации прост и стандартен.

Найти предел онлайн калькулятор с решением. Замечательные пределы. Примеры решений

Предел функции — число a будет пределом некоторой изменяемой величины, если в процессе своего изменения эта переменная величина неограниченно приближается к a .

Или другими словами, число A является пределом функции y = f (x) в точке x 0 , если для всякой последовательности точек из области определения функции , не равных x 0 , и которая сходится к точке x 0 (lim x n = x0) , последовательность соответствующих значений функции сходится к числу A .

График функции, предел которой при аргументе, который стремится к бесконечности, равен L :

Значение А является пределом (предельным значением) функции f (x) в точке x 0 в случае, если для всякой последовательности точек , которая сходится к x 0 , но которая не содержит x 0 как один из своих элементов (т. е. в проколотой окрестности x 0 ), последовательность значений функции сходится к A .

Предел функции по Коши.

Значение A будет являться пределом функции f (x) в точке x 0 в случае, если для всякого вперёд взятого неотрицательного числа ε будет найдено соответствующее ему неотрицательно число δ = δ(ε) такое, что для каждого аргумента x , удовлетворяющего условию 0 , будет выполнено неравенство | f (x) A | .

Будет очень просто, если вы понимаете суть предела и основные правила нахождения его. То, что предел функции f (x) при x стремящемся к a равен A , записывается таким образом:

Причем значение, к которому стремится переменная x , может быть не только числом, но и бесконечностью (∞), иногда +∞ или -∞, либо предела может вообще не быть.

Чтоб понять, как находить пределы функции , лучше всего посмотреть примеры решения.

Необходимо найти пределы функции f (x) = 1/ x при:

x → 2, x → 0, x → ∞.

Найдем решение первого предела. Для этого можно просто подставить вместо x число, к которому оно стремится, т.е. 2, получим:

Найдем второй предел функции . Здесь подставлять в чистом виде 0 вместо x нельзя, т.к. делить на 0 нельзя. Но мы можем брать значения, приближенные к нулю, к примеру, 0,01; 0,001; 0,0001; 0,00001 и так далее, причем значение функции f (x) будет увеличиваться: 100; 1000; 10000; 100000 и так далее. Т.о., можно понять, что при x → 0 значение функции, которая стоит под знаком предела, будет неограниченно возрастать, т.е. стремиться к бесконечности. А значит:

Касаемо третьего предела. Такая же ситуация, как и в прошлом случае, невозможно подставить ∞ в чистом виде. Нужно рассмотреть случай неограниченного возрастания x . Поочередно подставляем 1000; 10000; 100000 и так далее, имеем, что значение функции f (x) = 1/ x будет убывать: 0,001; 0,0001; 0,00001; и так далее, стремясь к нулю. Поэтому:

Необходимо вычислить предел функции

Приступая к решению второго примера, видим неопределенность . Отсюда находим старшую степень числителя и знаменателя — это x 3 , выносим в числителе и знаменателе его за скобки и далее сокращаем на него:

Ответ

Первым шагом в нахождении этого предела , подставим значение 1 вместо x , в результате чего имеем неопределенность . Для её решения разложим числитель на множители , сделаем это методом нахождения корней квадратного уравнения x 2 + 2 x — 3 :

D = 2 2 — 4*1*(-3) = 4 +12 = 16 → √ D = √16 = 4

x 1,2 = (-2 ± 4) / 2 → x 1 = -3; x 2 = 1.

Таким образом, числитель будет таким:

Ответ

Это определение его конкретного значения или определенной области, куда попадает функция, которая ограничена пределом.

Чтобы решить пределы, следуйте правилам:

Разобравшись в сути и основных правилах решения предела , вы получите базовое понятие о том, как их решать.

Для тех, кто хочет научиться находить пределы в данной статье мы расскажем об этом. Не будем углубляться в теорию, обычно её дают на лекциях преподаватели. Так что «скучная теория» должна быть у Вас законспектирована в тетрадках. Если этого нет, то почитать можно учебники взятые в библиотеке учебного заведения или на других интернет-ресурсах.

Итак, понятие предела достаточно важно в изучении курса высшей математики, особенно когда вы столкнетесь с интегральным исчислением и поймёте связь между пределом и интегралом. В текущем материале будут рассмотрены простые примеры, а также способы их решения.

Примеры решений

Пример 1

Вычислить а) $ \lim_{x \to 0} \frac{1}{x} $; б)$ \lim_{x \to \infty} \frac{1}{x} $

Решение

а) $$ \lim \limits_{x \to 0} \frac{1}{x} = \infty $$ б)$$ \lim_{x \to \infty} \frac{1}{x} = 0 $$ Нам часто присылают эти пределы с просьбой помочь решить. 2-1}{x+1} = \infty $$

Алгоритм вычисления лимитов

Итак, давайте кратко подведем итог разобранным примерам и составим алгоритм решения пределов:

1. Подставить точку х в выражение, следующее после знака предела. Если получается определенное число, либо бесконечность, то предел решен полностью. В противном случае имеем неопределенность: «ноль делить на ноль» или «бесконечность делить на бесконечность» и переходим к следующим пунктам инструкции.
2. Чтобы устранить неопределенность «ноль делить на ноль» нужно разложить числитель и знаменатель на множители. Сократить подобные. Подставить точку х в выражение, стоящее под знаком предела.
3. Если неопределенность «бесконечность делить на бесконечность», тогда выносим и в числителе, и в знаменателе x наибольшей степени. Сокращаем иксы. Подставляем значения икса из под предела в оставшееся выражение.

В этой статье Вы ознакомились с основами решения пределов, часто используемых в курсе Математического анализа. Конечно же это не все типы задач, предлагающихся экзаменаторами, а только простейшие пределы. В следующих статьях поговорим о других типах заданий, но сперва необходимо усвоить этот урок, чтобы двигаться далее. Обсудим, что делать, если есть корни, степени, изучим бесконечно малые эквивалентные функции, замечательные пределы, правило Лопиталя.

Если у Вас не получается самостоятельно решить пределы, то не паникуйте. Мы всегда рады помочь!

Пределы доставляют всем студентам, изучающим математику, немало хлопот. Чтобы решить предел, порой приходится применять массу хитростей и выбирать из множества способов решения именно тот, который подойдет для конкретного примера.

В этой статье мы не поможем вам понять пределы своих возможностей или постичь пределы контроля, но постараемся ответить на вопрос: как понять пределы в высшей математике? Понимание приходит с опытом, поэтому заодно приведем несколько подробных примеров решения пределов с пояснениями.

Понятие предела в математике

Первый вопрос: что это вообще за предел и предел чего? Можно говорить о пределах числовых последовательностей и функций. Нас интересует понятие предела функции, так как именно с ними чаще всего сталкиваются студенты. Но сначала — самое общее определение предела:

Допустим, есть некоторая переменная величина. Если эта величина в процессе изменения неограниченно приближается к определенному числу a , то a – предел этой величины.

Для определенной в некотором интервале функции f(x)=y пределом называется такое число A , к которому стремится функция при х , стремящемся к определенной точке а . Точка а принадлежит интервалу, на котором определена функция.

Звучит громоздко, но записывается очень просто:

Lim — от английского limit — предел.

Существует также геометрическое объяснение определения предела, но здесь мы не будем лезть в теорию, так как нас больше интересует практическая, нежели теоретическая сторона вопроса. Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.

Приведем конкретный пример. Задача — найти предел.

Чтобы решить такой пример, подставим значение x=3 в функцию. Получим:

Кстати, если Вас интересуют , читайте отдельную статью на эту тему.

В примерах х может стремиться к любому значению. Это может быть любое число или бесконечность. Вот пример, когда х стремится к бесконечности:

Интуитивно понятно, что чем больше число в знаменателе, тем меньшее значение будет принимать функция. Так, при неограниченном росте х значение 1/х будет уменьшаться и приближаться к нулю.

Как видим, чтобы решить предел, нужно просто подставить в функцию значение, к которому стремиться х . Однако это самый простой случай. Часто нахождение предела не так очевидно. В пределах встречаются неопределенности типа 0/0 или бесконечность/бесконечность . Что делать в таких случаях? Прибегать к хитростям!

Неопределенности в пределах

Неопределенность вида бесконечность/бесконечность

Пусть есть предел:

Если мы попробуем в функцию подставить бесконечность, то получим бесконечность как в числителе, так и в знаменателе. Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?

Из уже рассмотренного выше примера мы знаем, что члены, содержащие в знаменателе х, будут стремиться к нулю. Тогда решение предела:

Для раскрытия неопределенностей типа бесконечность/бесконечность делим числитель и знаменатель на х в высшей степени.

Кстати! Для наших читателей сейчас действует скидка 10% на

Еще один вид неопределенностей: 0/0

Как всегда, подстановка в функцию значения х=-1 дает 0 в числителе и знаменателе. Посмотрите чуть внимательнее и Вы заметите, что в числителе у нас квадратное уравнение. Найдем корни и запишем:

Сократим и получим:

Итак, если Вы сталкиваетесь с неопределенностью типа 0/0 – раскладывайте числитель и знаменатель на множители.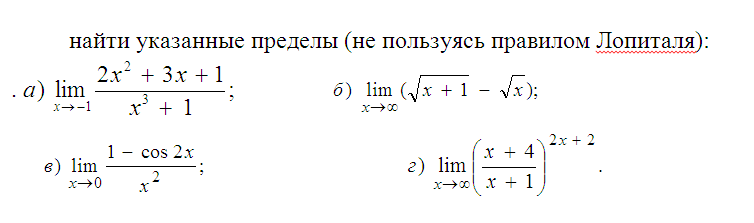

Чтобы Вам было проще решать примеры, приведем таблицу с пределами некоторых функций:

Правило Лопиталя в пределах

Еще один мощный способ, позволяющий устранить неопределенности обоих типов. В чем суть метода?

Если в пределе есть неопределенность, берем производную от числителя и знаменателя до тех пор, пока неопределенность не исчезнет.

Наглядно правило Лопиталя выглядит так:

Важный момент : предел, в котором вместо числителя и знаменателя стоят производные от числителя и знаменателя, должен существовать.

А теперь – реальный пример:

Налицо типичная неопределенность 0/0 . Возьмем производные от числителя и знаменателя:

Вуаля, неопределенность устранена быстро и элегантно.

Надеемся, что Вы сможете с пользой применить эту информацию на практике и найти ответ на вопрос «как решать пределы в высшей математике». Если нужно вычислить предел последовательности или предел функции в точке, а времени на эту работу нет от слова «совсем», обратитесь в профессиональный студенческий сервис за быстрым и подробным решением. 2 стремится к нулю.

Обычно переменная величина x стремится к конечному пределу a, причем, x постоянно приближается к a, а величина a постоянна. Это записывают следующим образом: limx =a, при этом, n также может стремиться как к нулю, так и к бесконечности. Существуют бесконечные функции, для них предел стремится к бесконечности. В других случаях, когда, например, функцией замедление хода поезда, можно о пределе, стремящемся к нулю.
У пределов имеется ряд свойств. Как правило, любая функция имеет только один предел. Это главное свойство предела. Другие их перечислены ниже:
* Предел суммы равен сумме пределов:
lim(x+y)=lim x+lim y
* Предел произведения равен произведению пределов:
lim(xy)=lim x*lim y
* Предел частного равен частному от пределов:
lim(x/y)=lim x/lim y
* Постоянный множитель выносят за знак предела:
lim(Cx)=C lim x
Если дана функция 1 /x, в которой x →∞, ее предел равен нулю. Если же x→0, предел такой функции равен ∞.
Для тригонометрических функций имеются из этих правил. Так как функция sin x всегда стремится к единице, когда приближается к нулю, для нее справедливо тождество:
lim sin x/x=1

В ряде встречаются функции, при вычислении пределов которых возникает неопределенность — ситуация, при которой предел невозможно вычислить. Единственным выходом из такой ситуации становится Лопиталя. Существует два вида неопределенностей:
* неопределенность вида 0/0
* неопределенность вида ∞/∞
К примеру, дан предел следующего вида: lim f(x)/l(x), причем, f(x0)=l(x0)=0. В таком случае, возникает неопределенность вида 0/0. Для решения такой задачи обе функции подвергают дифференцированию, после чего находят предел результата. Для неопределенностей вида 0/0 предел равен:
lim f(x)/l(x)=lim f»(x)/l»(x) (при x→0)
Это же правило справедливо и для неопределенностей типа ∞/∞. Но в этом случае справедливо следующее равенство: f(x)=l(x)=∞
С помощью правила Лопиталя можно находить значения любых пределов, в которых фигурируют неопределенности. Обязательное условие при

том — отсутствие ошибок при нахождении производных. (n-1)

Тема 4.6.Вычисление пределов

Предел функции не зависит от того, определена она в предельной точке или нет. Но в практике вычисления пределов элементарных функций это обстоятельство имеет существенное значение.

1. Если функция является элементарной и если предельное значение аргумента принадлежит ее области определения, то вычисление предела функции сводится к простой подстановке предельного значения аргумента, т.к. предел элементарной функции f (x) при х стремящемся к а , которое входит в область определения, равен частному значению функции при х=а , т.е. lim f(x)=f(a ) .

2. Если х стремится к бесконечности или аргумент стремится к числу, которое не принадлежит области определения функции, то в каждом таком случае нахождение предела функции требует специального исследования.

Ниже приведены простейшие пределы, основанные на свойствах пределов, которые можно использовать как формулы:

Более сложные случаи нахождения предела функции:

рассматриваются каждый в отдельности.

В этом разделе будут приведены основные способы раскрытия неопределенностей.

1. Случай, когда при х стремящемся к а функция f (x) представляет отношение двух бесконечно малых величин

а) Сначала нужно убедится, что предел функции нельзя найти непосредственной подстановкой и при указанном изменении аргумента она представляет отношение двух бесконечно малых величин. Делаются преобразования, чтобы сократить дробь на множитель, стремящийся к 0. Согласно определению предела функции аргумент х стремится к своему предельному значению, никогда с ним не совпадая.

Вообще если ищется предел функции при х стремящемся к а , то необходимо помнить, что х не принимает значения а , т.е. х не равен а.

б) Применяется теорема Безу. Если ищется предел дроби, числитель и знаменатель которой многочлены, обращающиеся в 0 в предельной точке х=а , то согласно вышеназванной теореме оба многочлена делятся без остатка на х-а .

в) Уничтожается иррациональность в числителе или в знаменателе путем умножения числителя или знаменателя на сопряженное к иррациональному выражение, затем после упрощения дробь сокращается.

г) Используется 1-й замечательный предел (4.1).

д) Используется теорема об эквивалентности бесконечно малых и следующие б.м.:

2. Случай, когда при х стремящемся к а функция f (x) представляет отношение двух бесконечно больших величин

а) Деление числителя и знаменателя дроби на наивысшую степень неизвестного.

б) В общем случае можно использовать правило

3. Случай, когда при х стремящемся к а функция f (x) представляет произведение бесконечно малой величины на бесконечно большую

Дробь преобразовывается к виду, числитель и знаменатель которой одновременно стремятся к 0 или к бесконечности, т.е. случай 3 сводится к случаю 1 или случаю 2.

4. Случай, когда при х стремящемся к а функция f (x) представляет разность двух положительных бесконечно больших величин

Этот случай сводится к виду 1 или 2 одним из следующих способов:

а) приведение дробей к общему знаменателю;

б) преобразование функции к виду дроби;

в) избавление от иррациональности.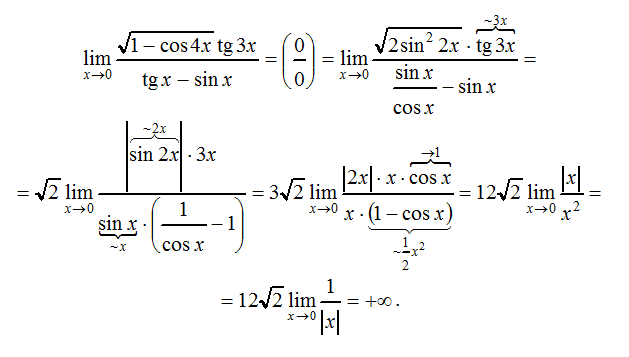

5. Случай, когда при х стремящемся к а функция f (x) представляет степень, основание которой стремится к 1, а показатель к бесконечности.

Функция преобразовывается таким образом, чтобы использовать 2-й замечательный предел (4.2).

Пример. Найти .

Так как х стремится к 3 , то числитель дроби стремится к числу 3 2 +3 *3+4=22, а знаменатель- к числу 3+8=11. Следовательно,

Пример

Здесь числитель и знаменатель дроби при х стремящемся к 2 стремятся к 0 (неопределенность вида), разложим числитель и знаменатель на множители, получим lim(x-2)(x+2)/(x-2)(x-5)

Пример

Умножим числитель и знаменатель на выражение, сопряженное к числителю, имеем

Раскрываем скобки в числителе, получим

Пример

Уровень 2. Пример. Приведем пример применения понятия предела функции в экономических расчетах. Рассмотрим обыкновенную финансовую сделку: предоставление в долг суммы S 0 с условием, что через период времени T будет возвращена сумма S T . Определим величину r относительного роста формулой

r=(S T -S 0)/S 0 (1)

Относительный рост можно выразить в процентах, умножив полученное значение r на 100.

Из формулы (1) легко определить величину S T :

S T = S 0 (1 + r )

При расчете по долгосрочным кредитам, охватывающим несколько полных лет, используют схему сложных процентов. Она состоит в том, что если за 1-й год сумма S 0 возрастает в (1 + r ) раз, то за второй год в (1 + r ) раз возрастает сумма S 1 = S 0 (1 + r ), то есть S 2 = S 0 (1 + r ) 2 . Аналогично получается S 3 = S 0 (1 + r ) 3 . Из приведенных примеров можно вывести общую формулу для вычисления роста суммы за n лет при расчете по схеме сложных процентов:

S n = S 0 (1 + r ) n .

В финансовых расчетах применяются схемы, где начисление сложных процентов производится несколько раз в году. При этом оговариваются годовая ставка r и количество начислений за год k . Как правило, начисления производятся через равные промежутки времени, то есть длина каждого промежутка T k составляет часть года. Тогда для срока в T лет (здесь T не обязательно является целым числом) сумма S T рассчитывается по формуле

(2)

где — целая часть числа, которая совпадает с самим числом, если, например, T ? целое число.

Пусть годовая ставка равна r и производится n начислений в год через равные промежутки времени. Тогда за год сумма S 0 наращивается до величины, определяемой формулой

(3)

В теоретическом анализе и в практике финансовой деятельности часто встречается понятие “непрерывно начисляемый процент”. Чтобы перейти к непрерывно начисляемому проценту, нужно в формулах (2) и (3) неограниченно увеличивать соответственно, числа k и n (то есть устремить k и n к бесконечности) и вычислить, к какому пределу будут стремиться функции S T и S 1 . Применим эту процедуру к формуле(3):

Заметим, что предел в фигурных скобках совпадает со вторым замечательным пределом. Отсюда следует, что при годовой ставке r при непрерывно начисляемом проценте сумма S 0 за 1 год наращивается до величины S 1 * , которая определяется из формулы

S 1 * = S 0 e r (4)

Пусть теперь сумма S 0 предоставляется в долг с начислением процента n раз в год через равные промежутки времени. Обозначим r e годовую ставку, при которой в конце года сумма S 0 наращивается до величины S 1 * из формулы (4). В этом случае будем говорить, что r e — это годовая ставка при начислении процента n раз в год, эквивалентная годовому проценту r при непрерывном начислении. Из формулы (3) получаем

S* 1 =S 0 (1+r e /n) n

Приравнивая правые части последней формулы и формулы (4), полагая в последней T = 1, можно вывести соотношения между величинами r и r e :

Эти формулы широко используются в финансовых расчётах. {3x}=1$.

Вернуться к списку тем

Задать вопрос на форуме

Записаться на занятия

Онлайн-занятия по высшей математике

App Store – Apple (RU)

Любимые приложения.

Из надёжного магазина.

Вот уже более 10 лет App Store выступает в качестве надёжной и безопасной площадки для поиска и скачивания приложений. Но App Store — не просто магазин. Это источник инноваций, которые дарят вам радость и открывают новые возможности. Поэтому крайне важно, чтобы приложения соответ­ствовали высоким стандартам качества, конфиден­циальности и защиты данных. В App Store почти два миллиона приложений, и мы хотим, чтобы вам было приятно пользоваться каждым из них.

Миллионы удачных находок.

Вдохновляющие, полезные статьи и коллекции. Новые каждый день.

Подробнее на тему: «Вдохновляющие, полезные статьи и коллекции. Новые каждый день».

Вдохновляющие, полезные статьи и коллекции. Новые каждый день.

От эксклюзивных премьер до закулисных интервью — наши редакторы расска­зывают самые интересные и ориги­нальные истории. На вкладке «Сегодня» можно прочитать о разработ­чиках, задающих тренды, получить полезные советы и узнать, как приложения делают работу продук­тивнее, развлечения интереснее, а жизнь — комфортнее.

Перейдите на вкладку «Сегодня»

Более 20 тысяч историй. И это не предел.

Тематические подборки от наших редакторов.

Подробнее на тему: «Тематические подборки от наших редакторов».

Тематические подборки
от наших редакторов.

Каждую неделю в App Store добавляются тысячи новых прило­жений, поэтому для вас всегда найдётся что‑то новенькое. Наши редакторы работают не покладая рук, чтобы подобрать прило­жения, истории и игры, которые понравятся именно вам. При этом они опираются на ваши предпочтения и предыдущие покупки.

Новое

Будьте в курсе событий в при­ло­жениях. Следите за кинопремье­рами, игровыми соревно­ваниями и прямыми трансляциями.

Подробнее на тему: «Будьте в курсе событий в приложениях. Следите за кинопремьерами, игровыми соревнованиями и прямыми трансляциями».

Будьте в курсе событий в при­ло­жениях. Следите за кинопремье­рами, игровыми соревно­ваниями и прямыми трансляциями.

Узнавайте о событиях на вкладках «Сегодня», «Игры» и «Приложения» в App Store. Или ищите их в поиске и на стра­ницах с описанием приложений.

Интеллектуальный поиск поможет найти лучшие приложения.

Подробнее на тему: «Интеллектуальный поиск поможет найти лучшие приложения».

Интеллектуальный поиск поможет найти лучшие приложения.

При поиске в App Store можно
использовать подсказки и полезные
советы, а в мульти­ме­дийные результаты могут быть встроены видеоролики,
истории от редакторов, советы и списки.

1,8 миллиона приложений во всём мире.

В 175 странах на более чем 40 языках.

Более 150 редакторов со всего света.

Подробная информация о каждом приложении.

Подробнее на тему: «Подробная информация о каждом приложении».

Подробная информация о каждом приложении.

На страницах прило­жений можно узнать всё необхо­димое, чтобы принять решение о скачи­вании. Демо­ролики, оценки и отзывы пользователей помогут вам найти то, что нужно.

Безопасность и конфиденци­аль­ность в центре всего.

Безопасность для каждого прило­жения. На всех уровнях.

Подробнее на тему: «Безопасность для каждого приложения. На всех уровнях».

Безопасность для каждого приложения.
На всех уровнях.

Мы следим за тем, чтобы приложения поступали из проверенных источ­ников, не содержали известного вредо­носного ПО и не допускали возможности взлома во время установки или использования.

100% приложений автоматически проверяются на наличие известного вредоносного ПО.

Более 16 тысяч приложений используют технологии HealthKit, CareKit и ResearchKit для защиты данных пациентов.

Вы сами решаете, какими данными делиться. И с кем.

Подробнее на тему: «Вы сами решаете, какими данными делиться. И с кем».

Вы сами решаете, какими данными делиться. И с кем.

Каждое приложение должно запрашивать у вас разрешение на использование и пересылку данных. При первом обращении приложения к вашим календарям, контактам, фотографиям, гео­позиции или другим данным вы получите уведомление с соот­ветствующим запросом. При этом разрешение на доступ можно в любой момент отменить. Кроме того, мы следим за тем, чтобы приложения не могли получить особо важную конфиденциаль­ную информацию, хранящуюся на устройстве, и не имели прав на полный доступ к данным и какую‑либо модификацию самого устройства или операционной системы.

Более 215 тысяч приложений отклонено в прошлом году из‑за нарушений требований конфиден­ци­аль­ности.

Приложения не могут получать ваши данные из других приложений.

Подробнее на тему: «Приложения не могут получать ваши данные из других приложений».

Приложения не могут получать ваши данные из других приложений.

Благодаря защите на уровне операционной системы приложение не может без явного разрешения с вашей стороны получить доступ к данным другого приложения.

Наши ценности — доверие и безопасность.

Приложения должны соответствовать нашим требованиям.

Подробнее на тему: «Приложения должны соответствовать нашим требованиям».

Приложения должны соответствовать нашим требованиям.

Приложения должны работать так, как заявлено, поэтому отдельная команда специалистов проверяет их на соответ­ствие строгим требованиям App Store. Согласно Руководству по проверке приложений для магазина App Store, приложения должны быть безопасными и удобными, соответствовать нашим правилам о конфи­ден­циаль­ности пользователей, защищать устройства от вредо­нос­ного ПО и угроз, а также работать по утверждённой бизнес-модели.

Подробнее о Руководстве по проверке приложений для магазина App Store

Каждую неделю более 500 экспертов во всем мире проверяют более 100 тысяч приложений.

Более

миллиона заявок откло­нено из‑за сомнитель­ного, небезо­пасного или незаконного контента.

Мы хотим, чтобы вы не беспокоились о неподходящем контенте.

Подробнее на тему: «Мы хотим, чтобы вы не беспокоились о неподходящем контенте».

Мы хотим, чтобы вы не беспокоились о неподходящем контенте.

Мы поддерживаем все точки зрения, представ­ленные в App Store, но также заботимся о том, чтобы в прило­жениях не было ничего оскор­бительного для пользо­вателей с другим мнением. Поэтому мы отклоняем прило­жения, которые содержат недопус­тимый контент или работают неприемлемым образом — особенно если это может поставить под угрозу безопасность детей. Для каждого приложения указывается ограничение по возрасту, поэтому родители легко могут определить, что подойдёт их ребёнку, а что нет.

Никаких случайных покупок.

Подробнее на тему: «Никаких случайных покупок».

Никаких случайных покупок.

Приложения должны работать по утвер­ждённой бизнес-модели. Поэтому вы всегда будете заранее знать, сколько вы платите, что именно входит в покупку и как продлить подписку. После каждой покупки в приложении вы будете получать от Apple чек. Все оформленные покупки и подписки доступны в вашей учётной записи. Неожиданного списания средств непонятно за что можно не опасаться.

Каждый день модераторы проверяют отзывы клиентов в App Store на качество и подлинность.

В 2020 году мы удалили более 80 миллионов спам-отзывов.

Более 2,3 миллиона приложений удалено из‑за отсутствия обновлений или несовместимости с новыми версиями наших опера­ционных систем.

Наши устройства и ПО созданы, чтобы пользова­тельский опыт был безупречным.

Приложения позволяют раскрыть весь потенциал ваших устройств Apple.

Подробнее на тему: «Приложения позволяют раскрыть весь потенциал ваших устройств Apple».

Приложения позволяют раскрыть весь потенциал ваших устройств Apple.

В продуктах Apple используются самые передовые технологии. Поэтому приложения на ваших устройствах способны открывать для вас новые гори­зонты. А поскольку программное и аппа­ратное обеспечение изначально разра­ботаны как часть единой системы, приложения дают вам ещё больше возмож­ностей — от почти незаметных, таких как невероятно плавная прокрутка, до совер­шенно удивительных, которые позволяют, например, проверить, как новый диван
будет смотреться в гостиной.

Мы помогаем разработчикам использовать новейшие возможности наших устройств.

Подробнее на тему: «Мы помогаем разработчикам использовать новейшие возможности наших устройств».

Мы помогаем разработчикам использовать
новейшие возможности наших устройств.

Мы даём разработчикам необходимые инстру­менты и оказываем поддержку при создании приложений, чтобы самые современные технологии стали доступны пользователям как можно скорее. Например, приложения могут использовать Face ID и Touch ID для безопасной аутентификации — при этом данные о вашем лице или отпечатке пальца остаются строго конфиденциальными. А игровые контроллеры легко синхронизируются с новыми играми на вашем iPhone. Мы активно развиваем такие направления, как дополненная реальность и машинное обучение, поэтому в будущем всё станет ещё интереснее.

Скачивайте без сомнений.

Любое приложение может стать вашим.

Мгновенно.

Подробнее на тему: «Любое приложение может стать вашим. Мгновенно».

Любое приложение может стать вашим. Мгновенно.

Наши платформы для распространения контента используются более чем на 1,5 милли­арда устройств и позволяют скачивать контент без задержек и лишних сложностей. Если приложение подходит больше чем для одного из ваших устройств, достаточно скачать его один раз — на осталь­ные оно будет добавлено автомати­чески. А когда у вас появится новое устройство, приложения (если они не устарели) будут автоматически установлены и на него.

Более 900 тысяч приложений используют технологии безопасной оплаты Apple Pay и StoreKit для товаров и сервисов.

Безопасные и конфиден­циаль­ные покупки.

Подробнее на тему: «Безопасные и конфиденциальные покупки».

Безопасные и конфиденциальные покупки.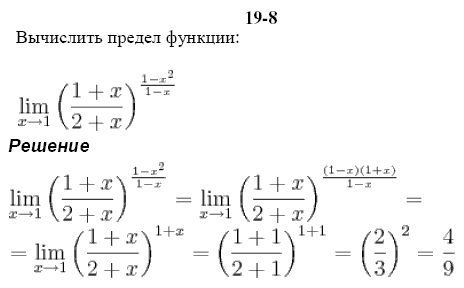

Покупки в App Store — это просто и безопасно. Создайте надёжную учётную запись, задайте способ оплаты и с лёг­костью пользуйтесь ими на всех своих устройствах и онлайн. Ваша учётная запись защищена двух­факторной аутентифи­кацией, а значит, доступ к ней есть только у одного человека — у вас. Даже если кто‑то ещё знает ваш пароль. Кроме того, более 250 000 прило­жений используют передовые технологии Touch ID и Face ID, обеспечивая дополнительную безопасность для вас и ваших устройств.

Проблема в приложении? Сообщите

об этом прямо из App Store.

Подробнее на тему: «Проблема в приложении? Сообщите об этом прямо из App Store».

Проблема в приложении? Сообщите об этом прямо из App Store.

В маловероятном случае возникновения проблемы вы можете сообщить о ней прямо со страницы приложения в App Store.

Хотите вернуть деньги? AppleCare поможет.

Подробнее на тему: «Хотите вернуть деньги? AppleCare поможет».

Хотите вернуть деньги? AppleCare поможет.

Обратитесь в службу AppleCare онлайн, по теле­фону или по электронной почте, и один из 5000 наших сотрудников поможет вам оформить запрос на возмещение.

Более 4 млрд приложений ежедневно скачивают из дата-центров, работающих на полностью возобновляемой энергии.

Больше 195 методов оплаты в 45 валютах.

Multivariable Limit Calculator + Онлайн-решатель с бесплатными шагами

Multivariable Limit Calculator — это онлайн-калькулятор, который используется для вычисления пределов функций с несколькими переменными. Калькулятор многопараметрического предела позволяет пользователю определить предел любой функции f(x), когда функция приближается к нескольким переменным.

Многопараметрический предельный калькулятор — это профессиональный математический калькулятор, который выдает точные и быстрые результаты за несколько секунд. Он принимает необходимые данные от пользователя и подробно представляет решение.

Многопараметрический калькулятор лимита также бесплатен и не требует никаких затрат для использования.

Что такое многопараметрический калькулятор предельных значений?

Калькулятор предела с несколькими переменными — это бесплатный онлайн-инструмент, который используется для вычисления предела для любой функции f(x), когда функция приближается к двум переменным, т. е. x и y.

Многопараметрический калькулятор предельных значений очень прост в использовании, поскольку он просто вводит данные от пользователя в соответствующие поля ввода и представляет решение всего за несколько секунд. Решение представлено Многопараметрический предельный калькулятор всегда точен.

Лучшая особенность калькулятора Multivariable Limit Calculator заключается в том, что он также определяет функции, для которых не существует предела. Таким образом, многопараметрический калькулятор предела помогает идентифицировать функции, для которых предел не существует в конкретной области.

Ниже приведена простая формула, используемая многопараметрическим калькулятором пределов для определения пределов функций f(x):

\[ \lim_{(x,y) \to (a,b)} f(x,y) = L \]

Если предел нельзя определить с помощью прямого подхода, то Многопараметрический калькулятор предела также использует подход пути, чтобы определить, существует ли предел для указанной функции.

В таком случае пределы, полученные с помощью метода пути для данной функции, должны быть равны, чтобы существовал многомерный предел функции.

 L1 = L2

Как пользоваться многопараметрическим калькулятором лимита?

Вы можете использовать этот calculato r, просто введя функцию и указав интересующую ее переменную. Multivariable Limit Calculator довольно прост в использовании благодаря чрезвычайно удобному интерфейсу. Этот калькулятор состоит из простого интерфейса, через который пользователь может легко перемещаться без каких-либо хлопот, чтобы получить желаемый результат.

Интерфейс многопараметрического калькулятора предельных значений состоит из трех полей ввода. Первое поле ввода имеет заголовок «Функция» и позволяет пользователю ввести указанную функцию f(x), для которой он хочет рассчитать предел.

Второе поле ввода принимает от пользователя мультипеременную, относительно которой необходимо вычислить предел для функции f(x). Это поле ввода имеет заголовок «Переменные (разделенные запятыми)» и предлагает пользователю ввести переменные. При вводе переменных обязательно разделяйте их запятой.

Третье и последнее поле ввода имеет заголовок «Подходит» и предлагает пользователю ввести домен, из которого вы хотите получить доступ к указанной функции.

Наконец, интерфейс Multivariable Limit Calculator состоит из кнопки с надписью «Отправить» , которую пользователь нажимает после заполнения всех входных данных. Эта кнопка запускает калькулятор для выполнения решения.

Для лучшего понимания использования многопараметрического калькулятора предельных значений ознакомьтесь с приведенным ниже пошаговым руководством.

Шаг 1 

Во-первых, прежде чем использовать Калькулятор предела для нескольких переменных, проанализируйте свою функцию и свои переменные. Убедитесь, что у вас есть как минимум две переменные для определения лимита.

Шаг 2

Теперь, когда вы проанализировали свою функцию, следующим шагом будет ввод ввода. Заполните первое поле ввода с заголовком «Функция» указанной вами функцией f(x).

Шаг 3

Затем перейдите ко второму полю ввода и вставьте свои переменные. Наконец, вставьте свой домен в последнее поле ввода, и все ваши поля ввода будут успешно заполнены.

Шаг 4

После того, как вы ввели все данные, осталось нажать кнопку «Отправить». После этого многопараметрический предельный калькулятор начнет свою обработку и представит решение через несколько секунд.

Как работает многопараметрический калькулятор предельных значений?

Многопараметрический калькулятор лимита работает по основному принципу исчисления, который заключается в расчете лимита. Он принимает данные от пользователя и всего за несколько секунд вычисляет предел для нескольких переменных. Он также определяет функции, для которых не существует предела.

Чтобы лучше понять принцип работы, давайте пересмотрим нашу предыдущую концепцию многовариантных пределов.

Что такое многопараметрический предел?

Многомерный предел — это фундаментальное понятие в исчислении, в котором пределы таких функций f(x) вычисляются и приближаются не к одной переменной, как в большинстве случаев, а к множеству переменных.

Таким образом, для таких функций определяется предел по обеим переменным. многопараметрический предел можно выразить следующим образом:

\[ \lim_{(x,y) \to (a,b)} f(x,y) = L \]

Если прямой подход не обеспечивает предел, то пользователь может использовать подход пути для определения предела. Если решения, полученные с помощью путевого подхода, не совпадают друг с другом, то предела для этой функции f(x) не существует.

Решаемые примеры

Для более полного понимания многопараметрического калькулятора предельных значений рассмотрим следующий пример.

Пример 1

Найдите предел, если он существует, для следующей функции:

\[ \lim_{(x,y) \to (-6,2)} xy cos(x+y) \]

Решение

Прежде чем приступить к решению, давайте сначала проанализируем нашу функцию. Функция приведена ниже:

\[ \lim_{(x,y) \to (-6,2)} xy cos(x+y) \]

В этом случае даны две переменные, которые равны x и y, а область значений данного подхода — от -6 до 2.

Затем вставьте функцию f(x) в первое поле ввода.

Вставьте переменные x и y во второе поле ввода. Обязательно разделяйте их запятой.

Наконец, вставьте подходы -6 и 2 в третье поле ввода. Не забудьте также разделить их запятой.

После того, как все входные данные будут вставлены, нажмите кнопку с надписью «Отправить».

Калькулятор выводит следующее решение:

-12 cos(4) 

Следовательно, предел для функции f(x) существует.

Список математических калькуляторов

Исчисление I — Предельные свойства

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Мобильное уведомление

Похоже, вы находитесь на устройстве с «узкой» шириной экрана ( т.е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 2-4: Свойства пределов

Пришло время вычислить некоторые пределы. Однако прежде чем мы это сделаем, нам понадобятся некоторые свойства пределов, которые несколько облегчат нам жизнь. Итак, давайте сначала посмотрим на них. Доказательство некоторых из этих свойств можно найти в разделе «Доказательство различных предельных свойств» главы «Дополнительно».

Свойства

Во-первых, предположим, что \(\mathop {\lim }\limits_{x \to a} f\left( x \right)\) и \(\mathop {\lim }\limits_{x \to a} g\left( x \right)\) существуют и что \(c\) является любой константой. Тогда

1. \(\ mathop {\lim }\limits_{x \to a} \left[ {cf\left( x \right)} \right] = c\mathop {\lim }\limits_{x \ к } е\влево( х \вправо)\)

   Другими словами, мы можем «факторизовать» мультипликативную константу вне предела.

2. \(\ mathop {\lim }\limits_{x \to a} \left[ {f\left( x \right) \pm g\left( x \right)} \right] = \mathop {\lim } \limits_{x \to a} f\left( x \right) \pm \mathop {\lim }\limits_{x \to a} g\left(x \right)\)

   Итак, чтобы взять предел суммы или разности, все, что нам нужно сделать, это взять предел отдельных частей, а затем сложить их вместе с соответствующим знаком. Это также не ограничивается двумя функциями. Этот факт будет работать независимо от того, сколько функций мы разделили «+» или «-».

3. \(\ mathop {\lim}\limits_{x \to} \left[ {f\left(x\right)g\left(x\right)} \right] = \mathop {\lim }\limits_ {х \ к а} е \ влево ( х \ вправо) \, \, \, \ mathop {\ lim } \ limit_ {х \ к а} г \ влево ( х \ вправо) \)

   Мы берем пределы продуктов так же, как мы можем брать пределы сумм или разностей. Просто возьмите предел частей, а затем соедините их вместе. Кроме того, как и в случае с суммами или разностями, этот факт не ограничивается только двумя функциями.

4. \(\ displaystyle \ mathop {\ lim} \ limit_ {x \ to a} \ left [ {\ frac {{f \ left (x \ right)}} {{g \ left (x \ right)}}} \ right] = \ frac {{\ mathop {\ lim} \ limit_ {x \ to a} f \ left ( x \ right)}} {{\ mathop {\ lim} \ limits_ {x \ to a} g \ слева ( х \ справа)} {\ rm {,}} \, \, \, \, \, {\ rm {при условии}} \, \ mathop {\ lim} \ limits_ {x \ to a} g \ влево( х \вправо) \ne 0\)

   Как отмечено в заявлении, нам нужно беспокоиться только о том, что предел в знаменателе равен нулю, когда мы делаем предел частного. {\ frac {1} {n}}} \\ & = \ sqrt [n] {{ \ mathop {\ lim} \ limit_ {x \ to a} f \ left ( x \ right)}} \ end {align *} \]

5. \(\ mathop {\lim }\limits_{x \to a} c = c,\,\,\,\,c{\mbox{любое действительное число}}\)

   Другими словами, предел константы — это просто константа. Вы должны быть в состоянии убедиться в этом, нарисовав график \(f\left( x \right) = c\).

6. \(\ mathop {\lim}\limits_{x \to a} x = a\)

   Как и в случае с последним, вы сможете убедиться в этом, нарисовав график \(f\left( x \right) = x\). 9п}\)

   На самом деле это всего лишь частный случай свойства 5 с использованием \(f\left( x \right) = x\).

Обратите внимание, что все эти свойства справедливы и для двух односторонних ограничений, мы просто не записали их с односторонними ограничениями, чтобы сэкономить место.

Давайте вычислим один или два предела, используя эти свойства. 2} + 5x — 92} + 5\left( { — 2} \right) — 9\\ & = — 7\\ & = p\left( { — 2} \right)\end{align*}\]

Другими словами, в данном случае мы видим, что предел — это то же самое значение, которое мы получили бы, просто вычислив функцию в рассматриваемой точке. Кажется, это нарушает одну из основных концепций ограничений, которые мы видели до сих пор.

В предыдущих двух разделах мы много говорили о том факте, что ограничения не заботятся о том, что происходит в рассматриваемой точке. Их волнует только то, что происходит вокруг точки. Так как же предыдущий пример вписывается в это, поскольку он, кажется, нарушает эту основную идею о пределах?

Несмотря на видимость, предел все равно не заботится о том, что делает функция в точке \(x = — 2\). В этом случае функция, которую мы получили, просто «достаточно хороша», чтобы то, что происходит вокруг точки, было точно таким же, как и то, что происходит в этой точке. В конце концов мы формализуем то, что подразумевается под «достаточно хорошим». На данный момент давайте не будем слишком беспокоиться о том, что такое «достаточно хороший». Давайте просто воспользуемся тем фактом, что некоторые функции будут «достаточно хорошими», что бы это ни значило.

Функция в последнем примере была многочленом. Оказывается, все полиномы «достаточно хороши», так что то, что происходит вокруг точки, точно такое же, как и то, что происходит в этой точке. Это приводит к следующему факту.

Факт

Если \(p(x)\) полином, то

\[\ mathop {\lim}\limits_{x \to a} p\left(x\right) = p\left(a\right)\]

К концу этого раздела мы значительно обобщим это на большинство функций, которые мы будем встречать в этом курсе. 93} + 1}}\]

Вообще-то нам следует быть немного осторожными. Мы можем сделать это при условии, что предел знаменателя не равен нулю. Однако, как мы увидим, это не в данном случае, так что все в порядке.

Теперь и числитель, и знаменатель являются полиномами, поэтому мы можем использовать приведенный выше факт для вычисления пределов числителя и знаменателя и, следовательно, самого предела. +}} f\ влево( x \вправо) = f\влево( a \вправо)\]

Опять же, в конце концов мы формализуем то, что мы подразумеваем под «достаточно хорошим». На данный момент все, что мы хотим сделать, это побеспокоиться о том, какие функции «достаточно хороши». Некоторые функции «достаточно хороши» для всех \(x\), в то время как другие будут «достаточно хороши» только для определенных значений \(x\). Все будет зависеть от функции.

Как отмечено в утверждении, этот факт справедлив и для двух односторонних пределов, и для нормального предела.

Вот список некоторых наиболее распространенных функций, которые «достаточно хороши».

• Полиномы достаточно хороши для всех \(x\).
• Если \(\displaystyle f\left( x \right) = \frac{{p\left( x \right)}}{{q\left( x \right)}}\), то \(f(x) \) будет достаточно хорошим при условии, что и \(p(x)\), и \(q(x)\) достаточно хороши, и если мы не получим деление на ноль в точке, в которой мы оцениваем.
• \(\cos \left( x \right),\,\,\sin \left( x \right)\) достаточно хороши для всех \(x\)
• \(\sec \left( x \right),\,\,\tan \left( x \right)\) достаточно хороши при условии \(x \ne \ldots , — \frac{{5\pi }} {2}, — \ frac {{3 \ pi}} {2}, \ frac {\ pi} {2}, \ frac {{3 \ pi}} {2}, \ frac {{5 \ pi}} {2}, \ldots \) ​​Другими словами, секанс и тангенс достаточно хороши везде, где косинус не равен нулю. Чтобы понять, зачем вспоминать, что обе эти функции действительно рациональны и что косинус находится в знаменателе обеих, вернитесь и посмотрите на второй пункт выше.
• \(\csc \left( x \right),\,\,\cot \left( x \right)\) достаточно хороши при условии \(x \ne \ldots , — 2\pi ,\,\, — \pi ,\,\,0,\,\,\pi ,\,\,2\pi , \ldots \) ​​Другими словами, косеканс и котангенс достаточно хороши везде, где синус не равен нулю.
• \(\sqrt[n]{x}\) достаточно хорош для всех \(x\), если \(n\) нечетно.
• \(\sqrt[n]{x}\) достаточно хорош для \(x \ge 0\), если \(n\) четно. Здесь мы требуем \(x \ge 0\), чтобы не иметь дело с комплексными значениями. 9x}\) достаточно хороши для всех \(x\).
• \({\log _b}x,\,\,\,\ln x\) достаточно хороши для \(x > 0\). Помните, что мы можем подставлять только положительные числа в логарифмы, а не ноль или отрицательные числа.
• Любая сумма, разность или произведение вышеуказанных функций также будут достаточно хороши. Частные будут достаточно хороши, если мы не получим деление на ноль при оценке предела.

Последний пункт важен. Это означает, что для любой комбинации этих функций все, что нам нужно сделать, это оценить функцию в рассматриваемой точке, убедившись, что ни одно из ограничений не нарушено. Это означает, что теперь мы можем делать большое количество лимитов. 93}}}{{1 + \ln \left( 3 \right)}} + \sin \left( 3 \right)\cos \left( 3 \right)\\ & = {\rm{8}}{ \rm{.1854272743}}\end{выравнивание*}\]

Не очень красивый ответ, но теперь мы можем сделать предел.

Пределы в исчислении | Определение и правила с примерами

В математике пределы используются для решения сложных задач исчисления различных функций. Он в основном используется для определения дифференциала, непрерывности и интегралов. Пределы выполняют определенную функцию значения, заменяя предельное значение.

Пределы очень важны в типе первообразной, известном как определенный интеграл, в котором применяются верхние и нижние пределы. В этом посте мы изучим определение и правила лимитов на множестве примеров.

Каковы пределы исчисления?

В исчислении значение, к которому функция приближается по мере того, как вход этой функции становится все ближе и ближе к некоторому определенному числу, называется пределом. Другими словами, когда функция приближается к некоторому значению для оценки значения предела этой функции, это называется пределом.

Для измерения близости и представления идей математических понятий можно использовать обозначение предела. Это очень полезно для определения других ветвей исчисления, таких как производная, непрерывность и первообразная.

Уравнение пределов

Формула или уравнение, используемые для расчета пределов функций, приведены ниже.

lim _{x →u} h(x) = N

• Lim — обозначение пределов.
• u — предельное значение функции.
• h(x) — заданная функция.
• x — переменная функции.
• N — результат функции после применения предельного значения u.

Вы должны применить предельное значение u к заданной функции h(x), для решения задач пределов. Пределы не применяются к постоянным функциям, поэтому пределы постоянных функций остаются неизменными.

Правила лимитов

В исчислении существуют различные правила пределов. Давайте кратко обсудим их с помощью примеров для оценки предельных задач.

1.   Постоянное правило

Согласно этому правилу пределов постоянная функция остается неизменной. Потому что ограничения применяются только к переменным. Уравнение для постоянного правила:

lim _{x →u} C = C

• Lim — обозначение пределов.
• u — предельное значение функции.
• C — заданная функция.

Пример

Найдите предел 56, когда x приближается к 5.

Раствор

Шаг 1: Примените предельное обозначение к данной функции.

lim _{x →5} 56

Шаг 2: Теперь примените ограничение.

lim _{x →5} 56 = 56 (по постоянному правилу)

2. Правило функции константы

В соответствии с этим правилом пределов константа с функцией будет записана вне предельных обозначений. Потому что ограничения применяются только к переменным. Уравнение для правила постоянной функции:

lim _{x →u} C h(x) = C * N

• Lim — обозначение пределов.
• u — предельное значение функции.
• C — любая константа.
• h(x) — заданная функция.
• x — переменная функции.
• N — результат функции после применения предельного значения u.

Пример

Найдите предел 23x ³ при приближении x к 7.

Раствор

Шаг 1: Примените предельное обозначение к данной функции.

lim _{x →7} 23x ³

Шаг 2: Теперь примените правило предела постоянной функции.

lim _{x →7} 23x ³ = 23 lim _{x →7} x ³

Шаг 3: Теперь примените ограничение.

lim _{x →7} 23x ³ = 23 (7 ³ )

lim _{x →7} 23x ³ = 23 (7 * 7 * 7)

lim _{x →7} 23x ³ = 23 (343)

lim _{x →7} 23x ³ = 7889

3.   Правило сумм

Согласно этому правилу ограничений, обозначения применяются к каждой функции отдельно. Уравнение для правила сумм:

LIM _{x → U} [H (x) + G (x)] = LIM _{x → U} (h (x) + LIM 9048 9047 (H (x) + LIM 9047 (x) + LIM 9047 (x) + LIM 9047 (x) + LIM 9047 (x) + LIM 9047 (x) + LIM 9047 (x) + LIM 9047 (x) + LIM 9047 (x) + LIM 9047 (x)) + _{. →u (g(x)) = M + N}

• Lim — обозначение пределов.
• u — предельное значение функции.
• g(x) & h(x) — заданные функции.
• x — переменная функции.
• M и N являются результатами функций после применения предельного значения u.

Пример

Найдите пределы x ³ + x ⁵ при приближении x к 3.

Раствор

Шаг 1: Примените предельное обозначение к данной функции.

лим _{x →3} [х ³ + х ⁵ ]

Шаг 2: Теперь применим правило суммы предела.

lim _{x →3} [x ³ + x ⁵ ] = lim _{x →3} (x ³ ) +   (x ⁵ )

Шаг 3: Теперь примените ограничение.

lim _{x →3} [x ³ + x ⁵ ] = (3 ³ ) + (3 ⁵ )

лим _{х →3} [х ³ + х ⁵ ] = (3 * 3 * 3) + (3 * 3 * 3 * 3 * 3)

lim _{x →3} [x ³ + x ⁵ ] = (27) + (243)

lim _{x →3} [x ³ + x ⁵ ] = 270

4.   Правило различия

Согласно этому правилу ограничений, обозначения применяются к каждой функции отдельно. Уравнение для правила разности:

лим _{x → U} [h (x) — g (x)] = Lim _{x → U} (H (x)) — LIM _x (H (x)) — LIM _x 7777776797697677 гг. (г(х)) = М – Н

• Lim — обозначение пределов.
• u — предельное значение функции.
• g(x) & h(x) — заданные функции.
• x — переменная функции.
• M и N являются результатами функций после применения предельного значения u.

Пример

Найдите пределы x ³ – x ⁵ при приближении x к 2.

Раствор

Шаг 1: Примените предельное обозначение к данной функции.

lim _{x →2} [x ³ – x ⁵ ]

Шаг 2: Теперь примените правило ограничения разницы.

lim _{x →2} [x ³ – x ⁵ ] = lim _{x → 2} (x ³ ) + lim _{x → 2} (x ⁵ )

Шаг 3: Теперь примените ограничение.

lim _{x → 2} [x ³ — x ⁵ ] = (2 ³ ) — (2 ⁵ )

lim _{x →2} [x ³ – x ⁵ ] = (2 * 2 * 2) – (2 * 2 * 2 * 2 * 2)

lim _{x →2} [x ³ – x ⁵ ] = (8) – (32)

lim _{x →2} [x ³ – x ⁵ ] = -24

5.

   Правило продукта

Согласно этому правилу ограничений, обозначения применяются к каждой функции отдельно. Уравнение для правила продукта:

LIM _{x → U} [H (x) * g (x)] = LIM _{x → U} (h (x)) * 9048 (x)) * _{→ u} (x)) * _{→ U} (x)) * _{→ U} (x)) * _{→ U} (x)) * _{→ U} (x)) _→u (g(x)) = M * N

• Lim — обозначение пределов.
• u — предельное значение функции.
• g(x) & h(x) — заданные функции.
• x — переменная функции.
• M и N являются результатами функций после применения предельного значения u.

Пример

Найдите пределы x ⁵ * x ³ при приближении x к 4.

Раствор

Шаг 1: Примените предельное обозначение к данной функции.

lim _{x →4} [x ⁵ * x ³ ]

Шаг 2: Теперь примените правило ограничения продукта.

LIM _{x → 4} [x ⁵ * x ³ ] = LIM _{x → 4} (x ⁵ ) * Lim _x (x ⁵ ) * LIM _→ (x ⁵ )

Шаг 3: Теперь примените ограничение.

lim _{x →4} [x ⁵ * x ³ ] = (4 ⁵ ) * (4 ³ )

lim _{x →4} [x ⁵ * x ³ ] = (4 * 4 * 4 * 4 * 4) * (4 * 4 * 4)

lim _{x →4} [x ⁵ * x ³ ] = (1024) * (64)

lim _{x → 4} [x ⁵ * x ³ ] = 65536

6.

   Правила больницы

В соответствии с этим правилом, если функция образует 0 на 0 или бесконечность на бесконечность после применения ограничений, тогда берутся производные от числителя и знаменателя, а затем снова применяется предельное значение.

Пример

Найдите предел x ² – 4 / 4x – 2x ² при приближении x к 2.

Раствор

Шаг 1: Примените предельное обозначение к данной функции.

lim _{x →2} [x ² – 4 / 4x – 2x ² ]

Шаг 2: Теперь примените правило отношения предела и примените предельное значение.

lim _{x →2} [x ² — 4/4x — 2x ² ] = LIM _{x → 2} [x ² — 4] / LIM _{x → 2} [4x ₂

2
2 7 2 7 2
2
2
2 7 2 7 _{→ 2} .

lim _{x →2} [x ² – 4 / 4x – 2x ² ] = [2 ² – 4] / [4(2) – 2(2) ^{2 ]}

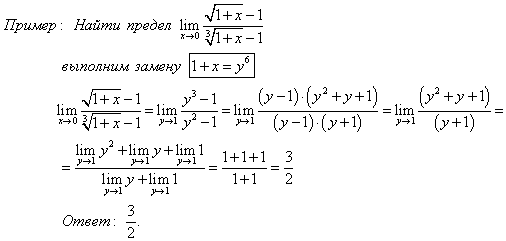
lim _{x →2} [x ² – 4 / 4x – 2x ² ] = [4 – 4] / [4(2) – 2(4)]

lim _{x →2} [x ² – 4 / 4x – 2x ² ] = [4 – 4] / [8 – 8]

lim _{x →2} [x ² – 4 / 4x – 2x ² ] = 0 / 0

Шаг 3: Поскольку функции формируют нуль за нулем, применяя предельное значение, поэтому примените правило Лопиталя и снова примените предельное значение.

lim _{x → 2} [x ² – 4 / 4x – 2x ² ] = lim _{x → 2} [d/dx (x ^{6 – 904) 4х – 2х 2 )]}

lim _{x →2} [x ² – 4 / 4x – 2x ² ] = lim _{x →2} [2x – 0 / (4 – 4x)]

lim _{x →2} [x ² – 4 / 4x – 2x ² ] = lim _{x →2} [2x / (4 – 4x)]

lim _{x →2} [x ² – 4 / 4x – 2x ² ] = [2(2) / (4 – 4(2))]

lim _{x →2} [x ² – 4 / 4x – 2x ² ] = [4 / (4 – 8)]

lim _{x →2} [x ² – 4 / 4x – 2x ² ] = [4 / (– 4)]

lim _{x →2} [x ² – 4 / 4x – 2x ² ] = -1

Резюме

В этом посте мы узнали определение и правила лимитов на множестве примеров. Теперь вы можете освоить все основы лимитов, просто следуя правилам этого поста.

Дополнительные ресурсы по математике (для родителей, учителей и учащихся)

• Важность методологии для облегчения изучения математики
• Почему учащиеся считают вычисление предела трудным
• Как распознать и преодолеть математическую тревогу

Как рассчитать, примеры, практические задачи, изображения




Краткий обзор

Если $$x$$ приближается к одной из точек перехода функции, то необходимо проверить оба односторонних предела.

Примеры

Пример 1

Определите $$\displaystyle\lim\limits_{x\to4} f(x)$$, если $$f$$ определяется, как показано ниже.

$$ е (х) = \ влево \ {% \begin{массив}{ll} 2x+3 и х

Шаг 1

Оцените односторонние ограничения. +}(5x-9) = 5(4)-9 = 11 \конец{выравнивание*} $$

Шаг 2

Если односторонние ограничения совпадают, то ограничение существует.

Ответ: $$\displaystyle\lim\limits_{x\to4}f(x) = 11$$, если $$f$$ определено, как указано выше.

Пример 2

Оцените $$\displaystyle\lim\limits_{x\to0} f(x)$$, когда $$f$$ определяется следующим образом. 9+}\sqrt х = \sqrt 0 = 0 \конец{выравнивание*} $$

Шаг 2

Если односторонние пределы разные, то предел не существует.

Ответ: $$\displaystyle\lim\limits_{x\to0} f(x)$$ не существует, если $$f$$ определено, как указано выше.

Пример 3

Предположим, что $$f$$ определено, как показано ниже. Определите значение $$b$$, чтобы $$\displaystyle\lim\limits_{x\to5} f(x)$$ существовало. 9+}\left(\frac 2 3 x + b\right) = \frac{2(5)} 3 + b = \frac{10} 3 + b \конец{выравнивание*} $$

Шаг 2

Установите два предела равными друг другу и решите.

$$ \\ \начать{выравнивать*} \frac{10} 3 + b & = 7\\[6pt] b & = 7 — \frac{10} 3\\[6pt] б & = \фракция{11} 3 \конец{выравнивание*} \\ $$

Ответ: $$b = \frac{11} 3$$

Практические задачи

Задача 1

Оцените $$\displaystyle \lim_{x\to 2} f(x)$$, когда $$f$$ определяется следующим образом.

$$ \\ е (х) = \ влево \ {% \begin{массив}{ll} \ гидроразрыв 3 2 х + 7, & х

Шаг 1 9+} \влево(3x+4\вправо) = 3(2)+4 = 10 \конец{выравнивание*} $$

Шаг 2

Если односторонние ограничения совпадают, то ограничение существует.

Ответ: $$\displaystyle\lim\limits_{x\to2} f(x) = 10$$, если $$f$$ определено, как указано выше.

Проблема 2

Оцените $$\displaystyle \lim_{x\to 4} f(x)$$, когда $$f$$ определяется следующим образом.

$$ \\ е (х) = \ влево \ {% \begin{массив}{ll} \sin\left(\frac{\pi} 8 x\right), & x

Шаг 1

Проверить оба односторонних ограничения. 2 и х 9+}\frac 1 {x-1} = \frac 1 0\qquad\mbox{Деление на ноль!} \конец{выравнивание*} $$

Шаг 2

Если одно из односторонних ограничений не существует, то ограничение не существует.

Ответ: $$\displaystyle \lim_{x\to1} f(x)$$ не существует, если $$f$$ определено, как указано выше.

Проблема 4

Оцените $$\displaystyle \lim_{x\to-5} f(x)$$, если $$f$$ определено, как показано ниже.

$$ \\ е (х) = \ влево \ {% \begin{массив}{ll} \ гидроразрыв 3 5 х + 2, & х

Шаг 1

Изучите односторонние ограничения. +}\left(2x +\frac 8 3\right) = 2(-5) + \frac 8 3 = -\фракция{22} 3 \конец{выравнивание*} $$

Шаг 2

Если односторонние пределы не совпадают, предел не существует.

Ответ: $$\displaystyle \lim_{x\to-5} f(x)$$ не существует, если $$f$$ определено, как указано выше.

Проблема 5

Определите значение $$b$$ так, чтобы $$\displaystyle \lim_{x\to-6} f(x)$$ существовало, когда $$f$$ определяется, как показано ниже. 9+}\left(\frac 1 2 x+9\right) = \frac{-6} 2 + 9 = -3 + 9 = 6 \конец{выравнивание*} $$

Шаг 2

Установите два односторонних предела равными друг другу и решите.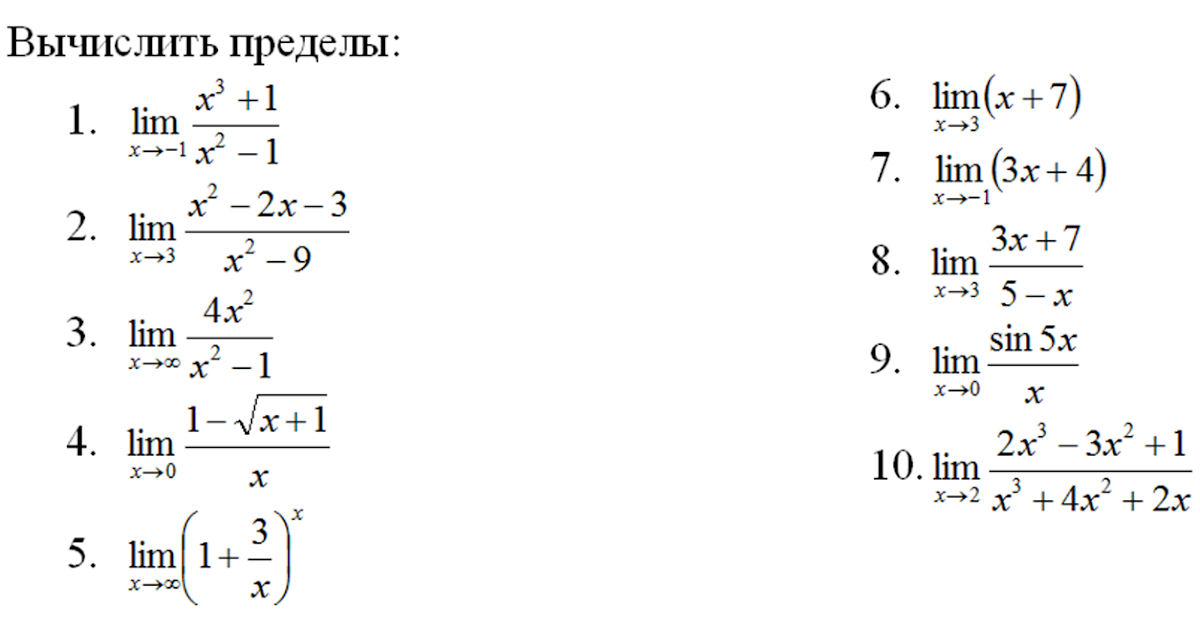

$$ \начать{выравнивать*} 36 + б & = 6\\ б & = -30 \конец{выравнивание*} $$

Ответ: $$b = -30$$

Проблема 6

Определите значение $$m$$ так, чтобы $$\displaystyle \lim_{x\to3} f(x)$$ существовало, когда $$f$$ определяется следующим образом.

$$ \\ е (х) = \ влево \ { \begin{массив}{ll} 2x + 7 и х

Шаг 1 9+} (мх-4) = 3м-4 \конец{выравнивание*} $$

Шаг 2

Приравняйте два предела и решите.

$$ \\ \начать{выравнивать*} 3м-4 и = 13\\[6пт] 3м & = 17\\[6pt] m & = \frac{17} 3 \конец{выравнивание*} \\ $$

Ответ: $$m = \frac{17} 3$$

Проблема 7

Определите значение (я) $$m$$ и $$b$$ так, чтобы $$\displaystyle \lim_{x\to 4} f(x) = 10$$, когда $$f$$ определяется, как показано ниже.

$$ \\ е (х) = \ влево \ {% \begin{массив}{ll} мх +2b и х

Шаг 1 9+} (5х + б) = 20 + б \конец{выравнивание*} $$

Шаг 2

Поскольку оба предела должны быть равны 10, составим систему уравнений и решим.

$$ \\ \начать{выравнивать*} 4м + 2б & = 10\\ 20 + б & = 10\\[12pt] % 4м + 2б & = 10\\ b & = -10 && \mbox{Найти \(b\) во втором уравнении.}\\[12pt] % 4m + 2(-10) & = 10 && \mbox{Подставьте значение \(b\) в другое уравнение.}\\ 4м — 20 и = 10\\ 4м & = 30\\[6pt] m & = \frac{30} 4\\[6pt] m & = \frac{15} 2 \конец{выравнивание*} \\ $$

Ответ: $$m = \frac{15} 2$$ и $$b = -10$$.




Реклама

---

Калькулятор лимита две переменные онлайн

Выражение Уравнение Неравенство Свяжитесь с нами Simplify Factor Expand GCF LCM Solve Graph System Solve Graph System Math solver on your site Наших пользователей: Самые ненавистные мне уравнения в алгебре — это радикальные уравнения, я не мог решить ни одного радикального уравнения, пока не купил вашу программу. Теперь узнал, как их решать и как проверить, верны ли мои ответы. Джефф Плай, CO Мы купили его для нашей дочери, и, похоже, он помогает ей во всем. Это спасло жизнь. Пэм Маррис, Техас Большое спасибо за объяснение, которое помогло решить проблемы, чтобы я мог понять концепцию. Я ценю ваше время и усилия. Марк Федор, М.И. Я впечатлен! В свои 64 иногда ненавижу перемены, но это точно к лучшему. Линда Ховард, Джорджия Студенты, борющиеся со всевозможными задачами по алгебре, узнают, что наше программное обеспечение может спасти им жизнь. Вот поисковые фразы, которые сегодняшние поисковики использовали, чтобы найти наш сайт. Сможете ли вы найти среди них свою? Поисковые фразы, использованные 19 января 2014 г.: решение показателей на TI84 математика алгебраическое выражение инвертора алгебраическое неравенство практика печати таблица наибольшего общего делителя Калькулятор упрощающих радикалов Алгебра простых треугольников решение не квадратного уравнения Забавный рабочий лист «Линейные уравнения» Калькулятор наименьших множителей ограничивает радикальные выражения рабочие листы квадратного корня третий класс Алгебра с ответами Pizzazz Решатель уравнения степени Математика 10 класс скачать бесплатно. pdf матричный калькулятор Код Matlab для решения с использованием Newton Raphson занятия по алгебре 8 год репетитор по алгебре в колледже калькулятор TI 30 X факторинг математика 1 второе издание алгебра ответы математические ответы для факторных листов исследовательский проект по математике алгебра процентов решение 4 уравнений 4 неизвестных читы для firstinmath полный образец бумаги другой компании-разработчика программного обеспечения вычислитель третьего корня игра с одинаковыми терминами Как решать полиномиальные неравенства графически и алгебраически Тест на способности скачать бесплатно экспоненциальная балансировка ti-89 разделить многочлены «Репетитор по алгебре 2» скачать бесплатно тест на подростковые способности математика мк прошлый бумажный сол решить квадратное уравнение, шаг за шагом достраивая квадрат решатель алгебры рабочие листы по вычитанию биномов как сгруппировать термины алгебра смешанные рабочие листы по алгебре Half Life Алгебра 2 задача бесплатная помощь в делении двучленов биномиальное расширение онлайн Рабочий лист по всемирной истории Макдугала, ключ ответа Лист уравнений по математике для 8-го класса многочлен деления ecxel бесплатное онлайн-обучение по алгебре для начинающих Система линейных уравнений ti-89 график, показатель, значение, калькулятор помощь по продвинутой алгебре приложение Matlab ode23 Предварительные тесты GED по алгебре ти-84 плюс дроби и десятичные знаки» химия Аддисон Уэсли раздел обзор ответы как вычислить наименьший общий знаменатель Как установить последовательность на графическом калькуляторе ПОМОЩЬ С ФАКТОРИНГОМ бесплатно Бухгалтерские книги Эддисон Уэсли издательский тест отвечает на вопросы по физике Математические мелочи алгебра 1 структура и метод тест ответы Преобразование квадратного уравнения в стандартный инструмент конической формы программа квадратичных формул ученица холл ответы Учебники по алгебре Glencoe/McGraw-Hill ALgebra бесплатные математические задания. com Рабочие листы по алгебраическим терминам для 7-го класса эмулятор калькулятора ti применение алгебры в повседневной жизни книги по бухгалтерскому учету бесплатно pdf факторизующий решатель Рабочие листы по математике для 4 класса решить алгебру Фракторизация базовой алгебры помогите решить уравнение инвестиций обман по алгебре Тест по математике для детей учет затрат+бесплатное решение проблем Студент вводит свои собственные задачи по алгебре добавление решения уравнений рациональных выражений радикальный квадратный корень, возведенный в степень примеры задач на перестановку и комбинацию как решить круговую функцию тригонометрии лист алгебры неравенств разница между линейными и квадратными уравнениями Рабочий лист формулы TAKS и химия Предыдущий Далее

Поиск предела функции

Все ресурсы для предварительного исчисления

12 диагностических тестов 380 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущий 1 2 Далее →

Precalculus Help » Вводный расчет » Ограничения » Найдите предел функции

Оцените предел ниже:

 

Возможные ответы:

Правильный ответ:

7 Объяснение:

 будет приближаться при приближении , поэтому будет иметь тип, как показано ниже:

 

 

Итак, мы можем применить правило L’Hospital:

С момента:

Следовательно:

Отчет о ошибке

. Возможные ответы:

:

:

:

:

. Объяснение:

Когда x=3/2, наш знаменатель равен нулю, поэтому мы не можем просто подставить 3/2, чтобы получить предел. Если мы посмотрим на числитель, когда x = 3/2, мы обнаружим, что он также равен нулю, поэтому наш числитель можно разложить на множители. Мы видим, что наш предел можно переписать как:

затем мы можем исключить 2x-3 из числителя и знаменателя, оставив нам:

и мы можем просто подставить 3/2 в этот предел, чтобы получить

примечание: наша функция не непрерывна при x=3/2, но предел существует.

Сообщить об ошибке

Решите следующее ограничение:

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы решить эту задачу, нам нужно расширить член в числителе

, когда мы это сделаем, мы получим

вторая степень х слагаемых отменяется, и мы получим

теперь мы можем сократить наши h в числителе и знаменателя, чтобы получить

, тогда мы можем просто подставить 0 вместо h, и мы получим наш ответ

Сообщить об ошибке

Оцените следующий предел.

Возможные ответы:

Правильный ответ:

Объяснение:

Функция имеет устранимый разрыв в точке  . После того, как множитель «разделен», результирующая функция равна , которая оценивается как  при приближении  0.

Сообщить об ошибке

Пусть .

Найти .

Возможные ответы:

Предел не существует.

Правильный ответ:

Объяснение:

Это график . Мы знаем, что это не определено; следовательно, нет значения для . Но если мы посмотрим на график, то увидим, что по мере приближения к 0 слева значение приближается к отрицательной бесконечности.

Это можно проиллюстрировать, представив маленькие отрицательные числа.

ПРИМЕЧАНИЕ: Обратите внимание на односторонние ограничения, так как легко выбрать неправильный ответ, если вы не будете осторожны.

 на самом деле бесконечность, а не отрицательная бесконечность.

Сообщить об ошибке

Рассчитать .

Возможные ответы:

Предел не существует.

Правильный ответ:

Объяснение:

Это можно переписать следующим образом:

 

Мы можем заменить , заметив, что как , : 

, что является правильным выбором.

Сообщить об ошибке

Найти предел при стремлении x к бесконечности Объяснение:

Поскольку x приближается к бесконечности, нам нужно только посмотреть на полином высшего порядка как в числителе, так и в знаменателе. Затем мы сравниваем многочлен высшего порядка как в числителе, так и в знаменателе. Если знаменатель выше, наш предел стремится к нулю, если числитель выше, наш порядок, наш предел стремится к положительной или отрицательной бесконечности (в зависимости от знака члена x наивысшего порядка). Если наши числитель и знаменатель имеют одинаковый порядок, предел переходит в a/b, где a — это коэффициент для x наивысшего порядка в числителе, а b — коэффициент для x наивысшего порядка в знаменателе.

Наш числитель имеет более высокий порядок, а коэффициент при x перед четвертым членом отрицательный, поэтому наш предел стремится к отрицательной бесконечности.

Сообщить об ошибке

Решите предел, когда  приближается к бесконечности.

Возможные ответы:

Правильный ответ:

Объяснение:

Поскольку x приближается к бесконечности, нам нужно только посмотреть на полином высшего порядка как в числителе, так и в знаменателе. Затем мы сравниваем многочлен высшего порядка как в числителе, так и в знаменателе. Если знаменатель выше, наш предел стремится к нулю, если числитель выше, наш порядок, наш предел стремится к положительной или отрицательной бесконечности (в зависимости от знака члена x наивысшего порядка). Если наши числитель и знаменатель имеют одинаковый порядок, предел переходит в a/b, где a – это коэффициент для x наивысшего порядка в числителе, а b – коэффициент для x наивысшего порядка в знаменателе.

В нашем уравнении порядки по x одинаковы для числителя и знаменателя (оба 4). Таким образом, мы делим коэффициенты старшего порядка x членов, чтобы получить наш предел, и мы получаем

Сообщить об ошибке

Скорость автомобиля, движущегося по шоссе, определяется следующей функцией времени:

Что можете ли вы сказать о скорости автомобиля через долгое время (то есть по мере приближения к бесконечности)?

Возможные ответы:

Скорость автомобиля зависит от начальной скорости.

Скорость автомобиля приближается к бесконечности.

Скорость автомобиля приближается к нулю.

Скорость автомобиля приближается к постоянному числу.

Из данной функции ничего нельзя сделать.

Правильный ответ:

Скорость автомобиля стремится к бесконечности.

Объяснение:

Указанная функция является многочленом с таким членом, который больше 1. 

Всякий раз, когда это так, мы можем сказать, что вся функция расходится (стремится к бесконечности) в пределе, когда  приближается к бесконечности.

Это говорит нам о том, что данная функция не очень реалистично описывает скорость автомобиля для больших !

Сообщить об ошибке

Нахождение пределов рациональных функций.

Пусть

.

Найти

.

Возможные ответы:

Не определено

Правильный ответ:

Объяснение:

Сначала умножьте числитель, чтобы упростить функцию.

No related posts.