Тест 5.6.2. Десятичные дроби. Действия над десятичными дробями.
Главная » 5 класс. Тесты. » Тест 5.6.2. Десятичные дроби. Действия над десятичными дробями
Математика. 5 класс. Тест 6. Вариант 2.
Содержание
Пример 1
Указать число единиц в разряде сотых дроби 635,421789.
А) 8; B) 4; C) 2; D) 3; E) 7.
Пример 2
Найти дроби, которые можно представить в виде десятичных дробей:
Пример 3
Представьте числа в порядке убывания, используя знаки неравенства: 0,36; 36; 3,6.
A) 36 > 3,6 > 0,36
B) 0,36
C) 3,6
D) 0,36
E) 36 > 0,36 > 3,6
Пример 4
Чтобы сложить десятичные дроби, надо: 1) уравнять в этих дробях количество знаков после запятой; 2) записать слагаемые друг под другом так, чтобы запятая была записана под запятой; 3) выполнить сложение, не обращая внимания на запятую, и поставить в сумме запятую под запятой в слагаемых дробях.
Выполнить сложение: 4,25 + 0, 684.
A) 4,725; B) 3,934; C) 4,095; D) 4934; E) 4,934.
Пример 5
Представить обыкновенную дробь в виде десятичной и найти значение выражения: 4/25+6,3.
A) 6,7; B) 6,12; C) 6,46; D) 6,15; E) 6.
Пример 6
Выполнить вычитание: 73,26 — 3,9.
A) 693,6; B) 69,36; C) 6,936; D) 70,17; E) 69,35.
Пример 7
Вычислить: 73 — 25,16.
A) 46,84; B) 48,84; C) 98,16; D) 47,84; E) 47,16.
Пример 8
Решить уравнение: x+3,062=14,2.
A) 11,138; B) 11,062; C) 17,262; D) 11,038; E) 10,138.
Пример 9
Чтобы умножить десятичную дробь на натуральное число, надо: 1) умножить ее на это число, не обращая внимания на запятую; 2) в полученном произведении отделить запятой столько цифр справа, сколько их было после запятой в записи десятичной дроби.
Вычислить: 0,75 · 8.
A) 6,5; B) 0,59; C) 0,6; D) 60; E) 6.
Пример 10
Вычислить рациональным способом: (2 · 0,783)·15
A) 2,349; B) 234,9; C) 0,2349; D) 23,49; E) 2349.
Пример 11
Чтобы перемножить десятичные дроби, надо: 1) выполнить умножение, не обращая внимания на запятые; 2) отделить в полученном произведении запятой столько цифр справа, сколько их стоит после запятой в обоих множителях вместе.
Выполнить умножение: 6,4 · 0,66
A) 42,24; B) 4224; C) 4,224; D) 0,4224; E) 3,624.
Пример 12
Найти площадь прямоугольника со сторонами: 2,7 см и 3,7 см.
A) 6,49 см²; В) 9,99 cм²; С) 8,99 см²; D) 12,8 см²; Е) 99,9 см².
Ответы к тестам вы найдете на странице «Ответы«.
Математика, 6 класс: 19-22. Деление десятичных дробей
Устный счет
Это надо знать
Деление десятичной дроби на 10, 100, 1000 и так далее
При делении десятичной дроби на 10, 100, 1000 и так далее запятую надо перенести влево на столько знаков, сколько нулей имеется в разрядной единице.
Примеры:
56,1 : 10 = 5,61;
56,1 : 100 = 0,561;
56,1 : 1000 = 0,0561.
Деление десятичной дроби на 0,1; 0,01; 0,001 и так далее
При делении десятичной дроби на 0,1; 0,01; 0,001 и так далее запятую надо перенести вправо на столько знаков, сколько цифр имеется после запятой в 0,1; 0,01; 0,001 и т.
д..
Примеры:
5,61 : 0,1 = 56,1;
5,61 : 0,01 = 561;
5,61 : 0,001 = 5610.
Деление на натуральное число
При делении на натуральное число надо:
1. Выполнить деление, не обращая внимания на запятую;
2. В полученном частном поставить запятую сразу, как только закончено деление целой части.
Пример:
31,2 : 5 = 6,24
Деление на десятичную дробь
При делении на десятичную дробь надо:
1. Перенести в делимом и делителе запятую вправо на столько цифр, сколько их после запятой в делителе;
2. Выполнить деление на натуральное число.
Пример:
8, 255 : 0,04 = 825,5 : 4 =
Видеоурок
youtube.com/embed/-9KAzQHm6Xk» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>Домашнее задание
К уроку 19 (на 28.09)
П. 4.1
1 уровень (учебник)
№ 4.3
№ 4.8
2 уровень (сборник)
№ 1.67 стр. 16
Вычислите:
1) 48 : 10; 2) 75 : 100; 3) 12 : 100; 4) 305 : 10; 5) 7803 : 100; 6) 57057 : 1000.
№ 1.70 стр. 16
Найдите частное от деления числа 261 на число:
1) 0,001; 2) 0,01; 3) 0,000001.
№ 1.72 стр. 16
Найдите частное от деления на 0,0001 числа:
1) 52; 2) 462; 3) 15; 4) 3,87; 5) 1,008; 6) 4,9; 7) 0,004; 8) 0,023.
К уроку 20 (на 29.
09)
П. 4.2
1 уровень (учебник)
№ 4.25
№ 4.28
2 уровень (сборник)
№ 1.73 стр. 17
Выполните деление:
1) 32 : 800; 2) 56 : 70; 3) 26 : 1300; 4) 96 : 32000; 5) 1500 : 6000; 6) 25 : 1250.
№ 1.75 стр. 17
Найдите частное чисел:
1) 16,75 : 50; 2) 6,942 : 25; 3) 72,18 : 360; 4) 22,5 : 45; 5) 1,75 : 17500; 6) 6,6645 : 36.
К уроку 21 (на 30.09)
П. 4.3
1 уровень (учебник)
№ 4.63
№ 4.65 (1, 2)
2 уровень (сборник)
№ 1.78 стр. 17
Пользуясь верным равенством 794 ∙ 325 = 258 050, найдите значение выражения:
1) 25,805 : 3,25; 2) 2580,5 : 32,5; 3) 258,05 : 0,0325; 4) 258,05 : 0,794;
5) 0,025805 : 0,00794; 6) 0,25805 : 0,000794.
№ 1.76 стр. 17
Выполните деление:
1) 37,563 : 6,59; 2) 219,975 : 4,19; 3) 22,411 : 0,73;
4) 229,04 : 5,6; 5) 19,152 : 6,3; 6) 199,43 : 0,49.
К уроку 22 (на 03.10)
П. 4.3
1 уровень (учебник)
№ 4.68
№ 4.76 (1-4)
2 уровень (сборник)
№ 1.100 стр. 20
Уменьшите значение величины 329,4 км в:
1) 3 раза; 2) 4 раза; 3) 5 раз; 4) 12 раз.
№ 1.102 ( 5-8) стр. 21
Обратите каждую обыкновенную дробь в десятичную и выполните действие:
№ 3.14 (4-7) стр. 78
Решите уравнение:
4) 6,78 : y = 6780; 5) 2,95 : y = 0,0295; 6) 0,01 : x = 100; 7) y : 0,01 = 168.
Математика_(решения) для 6 класса Математика Глава 5
- Решения для учебников
- Класс 6
- Математика
- десятичные дроби
Математика_(решения) Решения для класса 6 Математика Глава 5 Десятичные дроби представлены здесь с простыми пошаговыми объяснениями. Эти решения для десятичных дробей чрезвычайно популярны среди учащихся 6 класса по математике. Решения для десятичных дробей пригодятся для быстрого выполнения домашних заданий и подготовки к экзаменам. Все вопросы и ответы из Книги по математике_(решения) класса 6 по математике, глава 5, предоставляются здесь для вас бесплатно.
Вам также понравится отсутствие рекламы в Mathematics_(solutions) Solutions от Meritnation. Все решения по математике_(решения) для класса 6 по математике подготовлены экспертами и на 100% точны.
Страница № 30:
Вопрос 1:
В приведенной ниже таблице укажите разрядное значение каждой цифры в числе 378,025.
| Место | Сотни | Десятки | Единицы | Десятки | Сотые | Тысячные |
| 100 | 10 | 1 | 110 | 1100 | 11000 | |
| Цифра | 3 | 7 | 8 | 0 | 2 | 5 |
| Разрядное значение | 300 | 010=0 | 51000=0,005 |
Ответ:
| Место | Сотни | Десятки | Единицы | Десятки | Сотые | Тысячные |
| 100 | 10 | 1 | 110 | 1100 | 11000 | |
| Цифра | 3 | 7 | 8 | 0 | 2 | 5 |
| Разрядное значение | 300 | 7 × 10 = 70 | 8 × 1 = 8 | 010=0 | 2100=0,02 | 51000=0,005 |
Страница № 30:
Вопрос 2:
Решить.
(1) 905,5 + 27,197
(2) 39 + 700,65
(3) 40 + 27,7 + 2,451
Ответ:
(i)
1905,500+27,197932,697
∴ 905,5 + 2 7,197 = 932,697
(ii)
39,00+700,65739,65
∴ 39 + 700,65 = 739,65
(iii)
1140,00027,700+2,45170,151
∴ 40 + 27,7 + 2,451 = 70,151
Страница № 30 :
Вопрос 3:
Вычесть.
(1) 85,96 – 2,345
(2) 632,24 – 97,45
(3) 200,005 – 17,186
Ответ:
(i)
85,965010-2,34582,615
∴ 85,96 − 2,345 = 82,615
(ii)
65312211,211414-97,45534,79
∴ 632,24 − 9 7,45 = 534,79
(iii)
210909,0
∴ 200,005 − 17,186 = 182,819
Страница № 31:
Вопрос 4:
Авинаш проехал 42 км 365 м на автобусе, 12 км 460 м на машине и прошел пешком 640 м. Сколько километров он проехал всего? (Напишите свой ответ в десятичных фракциях.)
Ответ:
Расстояние, пройденное на автобусе = 42 км 365 м = 42 км + 365 м = 42 км + 3651000 км = 42 км + 0,365 км = 42,365 км (1 км = = 42 км + 0,365 км = 42,365 км (1 км = = 42 км + 0,365 км = 42,365 км (1 км = 42 км + 0,365 км = 42,365 км (1 км = 1000 м)
Расстояние, пройденное на автомобиле = 12 км 460 м = 12 км + 460 м = 12 км + 4601000 км = 12 км + 0,460 км = 12,460 км
Расстояние, пройденное пешком = 640 м = 6401000 км = 0,640 км 900 13
∴ Общее пройденное расстояние
= Расстояние, пройденное автобусом + Расстояние, пройденное автомобилем + Расстояние, пройденное пешком
= 42,365 км + 12,460 км + 0,640 км 12.
460+0.64055.465
Таким образом, общее расстояние, пройденное Авинашем, составляет 55,465 км.
Страница № 31:
Вопрос 5:
Аиша купила 1,80 м ткани для своего сальваара и 2,25 м для своей курты. Если ткань стоит 120 рупий за метр, сколько она должна заплатить продавцу?
Ответ:
Длина ткани, купленной для сальвара = 1,80 м
Длина ткани, купленной для курты = 2,25 м длина ткани куплена за Курта
= 1,80 м + 2,25 м
= 4,05 м
11,80+2,254,05
Цена ткани = 120 рупий/м
∴ Сумма, выплаченная продавцу
= Общая длина купленной ткани × Цена ткани
9 0012 = 4,05 м × 120 ₹/ m= ₹ 486
405×120000810×405××48600
Таким образом, Аиша заплатила ₹ 486 владельцу магазина.
Страница № 31:
Вопрос 6:
Суджата купила арбуз весом 4,25 кг и раздала 1 кг 750 г соседским детям. Сколько ей осталось?
Ответ:
Общий вес арбуза = 4,25 кг
Вес арбуза, розданного детям = 1 кг 750 г = 1 кг + 750 г = 1 кг + 7501000 кг = 1 кг + 0,75 кг = 1,75 кг
∴ Вес арбуза, оставленного у нее
= Общий вес арбуза − Вес арбуза, данного детям
= 4,25 кг – 1,75 кг
= 2,5 кг
43 .
2125-1.752.50
Таким образом , вес арбуза, оставшегося с Суджатой, составляет 2,5 кг.
Страница № 31:
Вопрос 7:
Анита ехала со скоростью 85,6 км в час. На дороге было ограничение скорости 55 км в час. Насколько она должна снизить скорость, чтобы не превысить допустимую скорость?
Ответ:
Первоначальная скорость движения Аниты = 85,6 км/ч
Ограничение скорости для движения = 55 км/ч Ограничение скорости движения
= 85,6 км/ч − 55 км/ч
= 30,6 км/ч
85,6-55,030,6
Таким образом, Аните нужно снизить скорость на 30,6 км/ч, чтобы не превысить допустимую скорость.
Страница № 32:
Вопрос 1:
Впишите правильный номер в пустые клетки.
(1) 35=3× x 5× x = x 10= x
(2) 258=25× x 8×125= x 1000=3,125
(3) 212= 21× х 2× х = х 10= x
(4) 2240=1120=11× x 20×5= x 100= x
Ответ:
(1) 35=3×25×2=610=0,6
(2) 258=25×1258×125=31251000=3,125
(3) 212=21×52×5=10 510 =10,5
(4) 2240=1120=11×520×5=55100=0,55
Страница № 32:
Вопрос 2:
Преобразуйте обыкновенные дроби в десятичные дроби.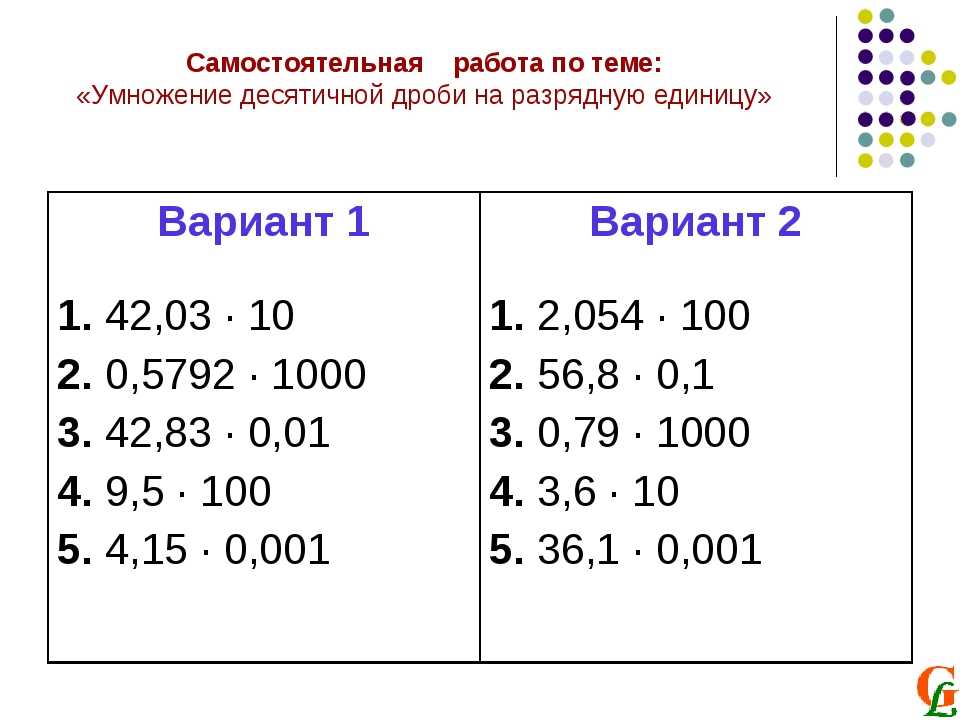
(1) 34
(2) 45
(3) 98
(4) 1720
(5) 3640
(6) 725
(7) 19200
Ответ:
(1 ) 34=3×254×25=75100=0,75
(2) 45=4×25×2=810=0,8
(3) 98=9×1258×125=11251000=1,125
(4) 1720=17×520×5=85100=0,85
(5) 3640=36÷440÷4=910=0,9
(6) 725=7×425×4=28100=0,28
(7) 19200=19×5200×5=951000=0,095
Номер страницы 32:
Вопрос 3:
Преобразуйте десятичные дроби в обыкновенные дроби.
(1) 27,5
(2) 0,007
(3) 90,8
(4) 39,15
(5) 3,12
(6) 70,400
Ответ:
(1 ) 27,5 = 27510
(2) 0,007 = 71000
(3) 90,8 =
(4) 39,15 = 3915100
(5) 3,12 = 312100
900 12 (6) 70,400 = 70,4 = 70410Страница № 33:
Вопрос 1:
Если 317 × 45 = 14265, то 3,17 × 4,5 = ?
Ответ:
3,17×4,5=317100×4510=317×45100×10=142651000=14,265
Страница № 33:
Вопрос 2: 9001 5
Если 503 × 217 = 109151, то 5,03 × 2,17 = ?
Ответ:
5,03×2,17=503100×217100=503×217100×100=10915110000=10,9151
Страница № 33:
Вопрос 3:
Умножить.
(1) 2,7 × 1,4
(2) 6,17 × 3,9
(3) 0,57 × 2
(4) 5,04 × 0,7
Ответ:
(i) 2,7×1,4=2710× 1410=27×1410× 10=378100=3,78
(ii) 6,17×3,9=617100×3910=617×39100×10=240631000=24,063
(iii) 0,57×2=57100×21=57×2100×1 =114100=1,14
(iv) 5,04×0,7=504100×710=504×7100×10=35281000=3,528
Страница № 34:
Вопрос 4:
Вирендра купил 18 мешков риса, каждый мешок весил 5.250 кг. Сколько всего риса он купил? Если рис стоит 42 рупии за кг, сколько он заплатил за него?
Ответ:
Вес каждого мешка риса = 5.250 кг
Количество купленных мешков риса = 18
= 5,250 кг × 18
= 525100×181
= 525×18100×1
= 9450100
= 94,5 кг
Цена риса = 42₹ ₹/кг
∴ Общая сумма, уплаченная за рис = вес всего купленного риса × Количество риса
= 94,5 кг × ₹ 42/кг
= 94510×421
= 945×4210×1
= 3969010
= 3,969 ₹
Таким образом, Вирендра купил Всего 94,5 кг риса, а общая сумма, уплаченная им, составляет 3969 фунтов стерлингов.
.
Страница № 34:
Вопрос 5:
У Ведики 23,50 метра ткани. Она использовала его, чтобы сделать 5 штор одинакового размера. Если на изготовление каждой шторы понадобилось 4 метра 25 см, сколько ткани осталось?
Ответ:
Общая длина ткани = 23,50 м
Длина ткани, необходимой для изготовления каждой шторы = 4 м 25 см = 4 м + 25 см = 4 м + 25100 м = 4 м + 0,25 м = 4,25 м (1 м = 100 см)
Количество штор одинакового размера = 5
∴ Длина ткани, необходимой для изготовления 5 штор = Длина ткани, необходимой для изготовления каждой шторы × 5
= 4,25 м × 5
= 425100×51
= 425×5100×1
= 2125100
= 21,25 м
∴ Количество оставшейся ткани = Общая длина ткани − Длина ткани, необходимая для изготовления 5 штор
= 23,50 м – 21,25 м – 21,25 м
= 2,25 м
23,54010-21,25 2.25
Таким образом, длина полотна осталось 2,25 м.
Страница № 34:
Вопрос 1:
Выполните следующие разделы.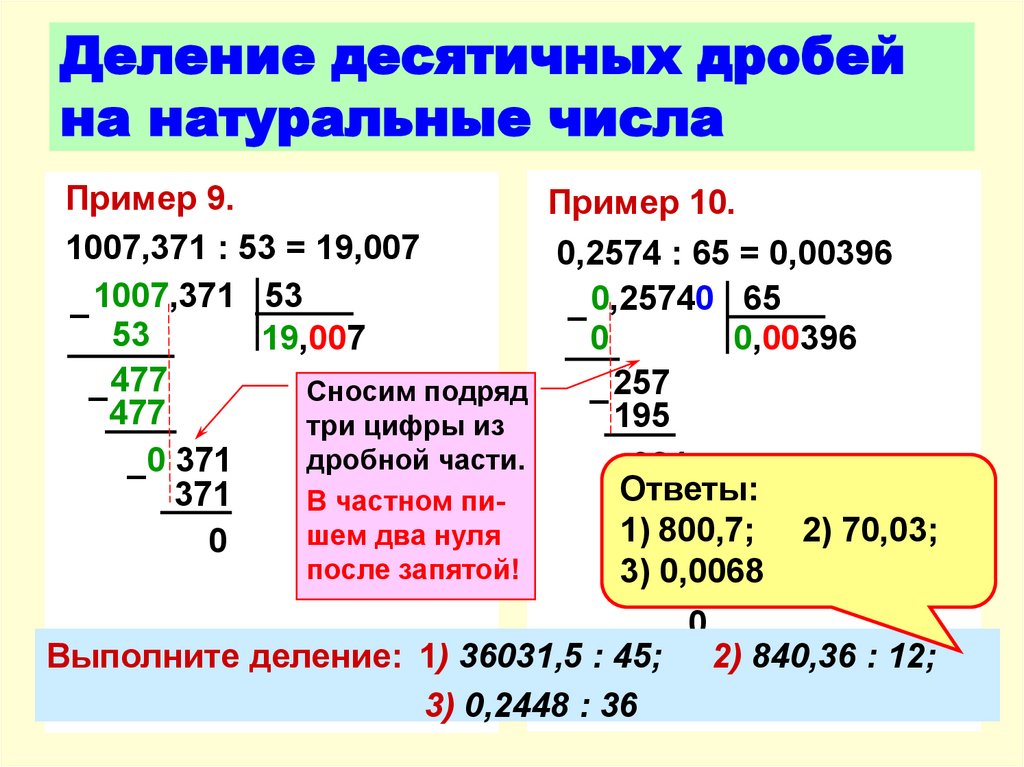
(1) 4,8 ÷ 2
(2) 17,5 ÷ 5
(3) 20,6 ÷ 2
(4) 32,5 ÷ 25
Ответ:
(1) 4,8 ÷ 2 = 4810÷ 21=4810×12= 2410=2,4
(2) 17,5 ÷ 5 = 17510÷51=17510×15=3510=3,5
(3) 20,6 ÷ 2 = 20610÷21=20610×12=10310=10,3
(4) 32,5 ÷ 25 = 32510 ÷251=32510×125=1310=1.3
Страница № 34:
Вопрос 2:
Длина дороги 4 км 800 м. Если по обеим его сторонам через каждые 9,6 м посажены деревья, то сколько деревьев было посажено?
Ответ:
Общая длина дороги = 4 км 800 м = 4 км + 800 м = 4000 м + 800 м = 4800 м (1 км = 1000 м)
Расстояние между двумя растениями = 9,6 м
∴ Количество деревьев, посаженных по обе стороны дороги = (Общая длина дороги ÷ Расстояние между двумя растениями) + 1
= (4800 м ÷ 9,6 м) + 1
= 48001÷9610 + 1
= 48001×1096 + 1
= 500 + 1
= 501
∴ Общее количество деревьев, посаженных по обеим сторонам дороги = Количество посаженных деревьев по обе стороны дороги × 2 = 501 × 2 = 1002
Таким образом, количество деревьев, посаженных по обеим сторонам дороги, равно 1002.
Страница № 34:
Вопрос 3:
Прадня регулярно тренируется, гуляя по круговой дорожке в поле. Если она пройдет расстояние 3,825 км за 9 кругов пути, сколько она пройдет за один круг?
Ответ:
Общее расстояние, пройденное Прадней за 9 кругов пути = 3,825 км
∴ Расстояние, пройденное Прадней за один круг пути = Общее расстояние, пройденное Прадней за 9 кругов пути ÷ 9
= 3,825 км ÷ 9
= 38251000÷91
= 38251000×19
= 4251000
= 0,425 км
Таким образом, расстояние, пройденное Прадней за один круг, равно 0,425 км.
Страница № 34:
Вопрос 4:
Фармацевтический производитель купил 0,25 центнера хирады, лекарственного растения, за 9500 рупий. Какова стоимость центнера хирады? (1quintal = 100 кг)
Ответ:
Сумма, выплаченная за 0,25 Квинтала Хирады = 9 500
∴ Стоимость за квинтал Hirada = сумма, выплачиваемая за 0,25 Quintal of Hirada ÷ 0,25
= 9500 ₹ ÷ 0,25
= 95001÷25100
= 95001×10025
= 380 × 100
= 38 ₹ ,000
Таким образом, стоимость 1 центнера хирады составляет 38 000 рупий.
Десятичная дробь — определение, преобразование, примеры
Дробь, знаменатель которой представляет собой степень числа 10, называется десятичной дробью . Некоторые примеры десятичных дробей: 1/10, 4/10, 35/100 и т. д. Давайте узнаем об этом больше в этой статье.
| 1. | Что такое десятичная дробь? |
| 2. | Типы десятичных дробей |
| 3. | Преобразование десятичных дробей |
| 4. | Часто задаваемые вопросы о десятичной дроби |
Что такое десятичная дробь?
Десятичная дробь определяется как дробь, знаменатель которой представляет собой степень числа 10, например 10, 100, 1000, 10000 и т. д. Дробь – это отношение части к целому. Итак, в десятичной дроби целое всегда делится на части, равные степени 10, например 10, 100, 1000 и так далее.
Например, 7/10 означает, что мы рассматриваем 7 частей из 10 частей. Когда мы преобразуем десятичную дробь в дробь, первым шагом является запись знаменателя в виде степени 10, в которой количество нулей будет равно количеству знаков после запятой в данном числе. Например, 2,5 можно записать как 25/10, поэтому 25/10 — это десятичная дробь. Это один из типов дробей, которые можно использовать для преобразования десятичных дробей. Посмотрите на изображение ниже, чтобы понять, что такое десятичные дроби с помощью примеров.
Теперь давайте разберемся с операциями над десятичными дробями.
Сложение десятичных дробей
К настоящему времени вам должно быть ясно, что десятичные дроби имеют знаменатель 10, 100, 1000 и так далее. Чтобы сложить две или более десятичные дроби, есть два способа, которые приведены ниже:
- Путем преобразования десятичных дробей в десятичные и последующего сложения.
- Преобразовав данные десятичные дроби в подобные дроби, а затем сложив.
Следуя первому методу, мы сначала преобразуем десятичные дроби в десятичные, а затем складываем эти значения. Например, добавим 2/10 + 34/100. 2/10 можно записать как 0,2, а 34/100 можно записать как 0,34. Теперь 0,2 + 0,34 = 0,54. Следовательно, 2/10 + 34/100 = 0,54, что можно записать как 54/100. Складываем те же числа вторым способом. Чтобы преобразовать данные дроби (2/10 и 34/100) в подобные дроби, находим НОК знаменателей. Наименьшее общее кратное 10 и 100 равно 100. Итак, умножьте числитель и знаменатель 2/10 на 10.
⇒ 2/10 = (2 × 10)/(10 × 10)
⇒ 2/10 = 20/100
Теперь 20/100 + 34/100 = 54/100. Следовательно, 2/10 + 34/100 = 54/100.
Вычитание десятичных дробей
Вычитание десятичных дробей выполняется так же, как и сложение. Например, 44/100 — 1/10 можно решить как 0,44 — 0,1, что равно 0,34 или 34/100. Другой способ вычесть 1/10 из 44/100 — найти НОК знаменателей и преобразовать их в одинаковые дроби. НОК 100 и 10 равно 100.
Итак, умножьте числитель и знаменатель 1/10 на 10.
⇒ 1/10 = (1 × 10)/(10 × 10)
⇒ 1/10 = 10/100
Теперь 44/100 — 10/100 = 34/100. Следовательно, 44/100 — 1/10 = 34/100.
Умножение десятичных дробей
Умножение десятичных дробей осуществляется путем раздельного умножения числителей и знаменателей. Чтобы умножить степени 10, мы просто добавляем количество нулей. Например, 7/10 × 3/100 = (7 × 3)/(10 × 100) = 21/1000. Чтобы узнать больше об умножении дробей, нажмите на предоставленную ссылку.
Деление десятичных дробей
Чтобы разделить две десятичные дроби, выполните следующие действия:
- Шаг 1: Найдите обратную вторую дробь.
- Шаг 2: Умножьте первую дробь на обратную величину второй дроби. Это будет требуемый ответ.
Это то же самое, что и обычное деление дробей. Например, 25/10 ÷ 5/100 = 25/10 × 100/5. Отсюда следует, что 5 × 10 = 50. Следовательно, 25/10 ÷ 5/100 = 50.
Виды десятичной дроби
Десятичные знаки можно разделить на следующие типы в зависимости от их десятичных разрядов:
- Завершающие десятичные знаки
- Непрерывные повторяющиеся десятичные дроби
- Непрерывные неповторяющиеся десятичные дроби
Когда дело доходит до десятичных дробей, мы знаем, что каждая десятичная дробь может быть записана как десятичная, где количество десятичных знаков конечно и равно количеству нулей в степени 10, записанных в знаменателе. Итак, десятичные дроби относятся к разряду конечных десятичных дробей.
Преобразование десятичных дробей
В этом разделе мы узнаем, как преобразовать дробь или десятичную дробь в десятичную дробь . Если знаменатель дроби можно записать в виде разложения на простые множители либо 2, либо 5, либо того и другого, это означает, что его можно преобразовать в десятичную дробь. Например, в дроби 3/4 знаменатель равен 4.
4 можно разложить на множители как 2 × 2. Таким образом, эту дробь можно преобразовать в десятичную дробь. Поскольку 10 не кратно 4, мы рассмотрим следующую степень 10, которая равна 100. 100 — это 25-е число, кратное 4. Итак, нам нужно умножить числитель и знаменатель 3/4 на 25, чтобы преобразовать его. в десятичную дробь. Отсюда следует, что 3/4 = (3 × 25)/(4 × 25) = 75/100. Возьмем еще один пример.
Можем ли мы преобразовать 5/12 в десятичную дробь? Ответ — нет. Это потому, что знаменатель 12 нельзя разложить на множители на произведение ни 2, ни 5, ни того и другого.
Но не волнуйтесь, мы все еще можем преобразовать его в десятичную дробь, используя другой метод. Разделите 5 на 12. Вы получите примерно 0,42. Теперь преобразуйте эту десятичную дробь в десятичную дробь. 0,42 это то же самое, что 42/100. Давайте узнаем, как преобразовать десятичную дробь в десятичную дробь, выполнив несколько простых шагов.
- Шаг 1: Подсчитайте количество знаков после запятой в заданном десятичном числе.
- Шаг 2: Удалите точку из числа и разделите его на степень 10, в которой количество нулей будет таким же, как количество знаков после запятой, подсчитанное на предыдущем шаге.
Преобразуем 0,42 в дробь. 0,42 имеет два десятичных знака. Это означает, что мы должны разделить его на 100, что является вторым показателем степени 10 (10 2 ). Следовательно, 0,42 = 42/100.
Посмотрите на таблицу десятичных дробей , приведенную ниже, чтобы научиться преобразовывать некоторые дроби и десятичные дроби в десятичные дроби.
| Дробь | Десятичная дробь | Десятичный |
|---|---|---|
| 1/2 | 5/10 | 0,5 |
| 3/2 | 15/10 | 1,5 |
| 3/4 | 75/100 | 0,75 |
| 1/8 | 125/1000 | 0,125 |
| 7/8 | 875/1000 | 0,875 |
| 3/5 | 6/10 | 0,6 |
| 1/4 | 25/100 | 0,25 |
| 1/50 | 2/100 | 0,02 |
| 2/5 | 4/10 | 0,4 |
► Похожие темы
Ознакомьтесь с интересными статьями о десятичных дробях в математике.
- Неправильные дроби
- Эквивалентные дроби
- Правильная дробь
- Доля единицы измерения
Примеры десятичных дробей
Пример 1: Сюзан хочет преобразовать 1/8 в десятичную дробь. Можете ли вы помочь ей сделать преобразование?
Решение: Дана дробь 1/8. Если мы умножим числитель и знаменатель 1/8 на 125, то получим 1000 в знаменателе. Итак, 1/8 = (1 × 125)/(8 × 125) = 125/1000. Следовательно, 1/8 = 125/1000.
Пример 2: Добавьте следующие десятичные дроби: 35/10 + 12/100.
Решение: Чтобы сложить десятичные дроби, сначала найдем НОК знаменателей. НОК 10 и 100 равно 100. Итак, умножьте числитель и знаменатель 35/10 на 10.
⇒ 35/10 = (35 × 10)/(10 × 10)
⇒ 35/10 = 350/ 100
Теперь 350/100 + 12/100 = (350 + 12)/100 = 362/100. Следовательно, 35/10 + 12/100 = 362/100.
Пример 3: Выберите десятичные дроби из предложенных вариантов: 3/4, 5/30, 1/11, 121/100, 5/70, 545/1000.
Решение: Десятичные дроби — это те, у которых в знаменателе степень 10. Среди приведенных вариантов 121/100 и 545/1000 являются десятичными дробями, так как знаменатели являются степенями числа 10.
перейти к слайдуперейти к слайдуперейти к слайду
Хотите создать прочную основу в математике?
Выйдите за рамки запоминания формул и поймите «почему», стоящее за ними. Испытайте Cuemath и приступайте к работе.
Забронируйте бесплатный пробный урок
Практические вопросы по десятичной дроби
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о десятичной дроби
Что такое десятичная дробь?
В математике десятичная дробь определяется как дробь, знаменатель которой является степенью числа 10. Таким образом, в знаменателе не должно быть никаких других чисел, кроме 1, за которой следуют нули. Некоторые примеры десятичных дробей: 1/10, 3/100, 54/10 и т.
д.
Что такое десятичная дробь и как ее учить?
Десятичные дроби — это дроби, которые можно записать в виде десятичной дроби с использованием десятичной точки. Они имеют степень 10 в знаменателе. Преподавание десятичных дробей следует начинать после того, как учащиеся освоятся с понятиями дробей и десятичных знаков. Возьмите любую прямоугольную или круглую модель, разделенную на 10 или 100 равных частей, и объясните десятичные дроби как число частей, взятое из общего числа частей (которое в этом типе является степенью числа 10). Возьмите в качестве примера десятичные дроби и покажите их преобразование в десятичные дроби.
Какова десятичная дробь преобразования 18,5?
Данное число равно 18,5. Десятичная дробь 18,5 равна 185/10, так как она имеет 1 десятичный знак, который можно удалить, чтобы записать 10 в знаменателе.
Как 1/2 выражается десятичной дробью?
1/2 в виде десятичной дроби можно выразить как 5/10.
Какая десятичная дробь равна 40 мл литра?
В 1 литре 1000 миллилитров.