Логика[задачи]
АЛГЕБРА ЛОГИКИ СУЖДЕНИЙ
Человек получает, хранит и передает знания, информацию, сведения в форме суждений, которые состоят из названия предмета и перечисления его свойств (качества, обстоятельства, действия – всё это свойства предметов). Пример суждения — повествовательное предложение. При этом предмет, чьи свойства перечисляются в суждении, называют субъектом суждения.
В данном разделе логики суждение будет восприниматься как некоторая целая, неделимая сущность. Если хорошо подумать, то можно прийти к выводу, что реальной единицей информации, её элементарной неделимой на части порцией, является именно суждение, а не слово, не буква и т.п.
Суждение может быть истинным или ложным. Это его значение. Значение суждения определяется сравнением его содержания с действительным положением дел. Значение и содержание — разные свойства суждения.
Большое сложное суждение может состоять из простых суждений и образует текст.
Цель логики состоит в том, чтобы имея сведения об истинности простых суждений, установить значение сложного суждения. Это частная цель. Часто мы с помощью комбинации суждений, истинность которых проверяется на опыте, строим суждение, истинность которого неочевидна — это так называемое умозрительное знание. Самая общая цель логики — установить истинность умозрительного знания.
Самый простой текст состоит из двух суждений, связанных логической операцией. Цель — установить истинность текста, зная значение всех входящих в него суждений.
Результат логической операции над суждениями определяется ее таблицей истинности. Принято истину обозначать 1, а ложь — 0. Суждения называются логическими переменными и обозначаются буквами.
Если 2 суждения воспринимаются как единый истинный текст, только если они оба истинны, то говорят, что они связаны конъюнкцией, логическим «И».
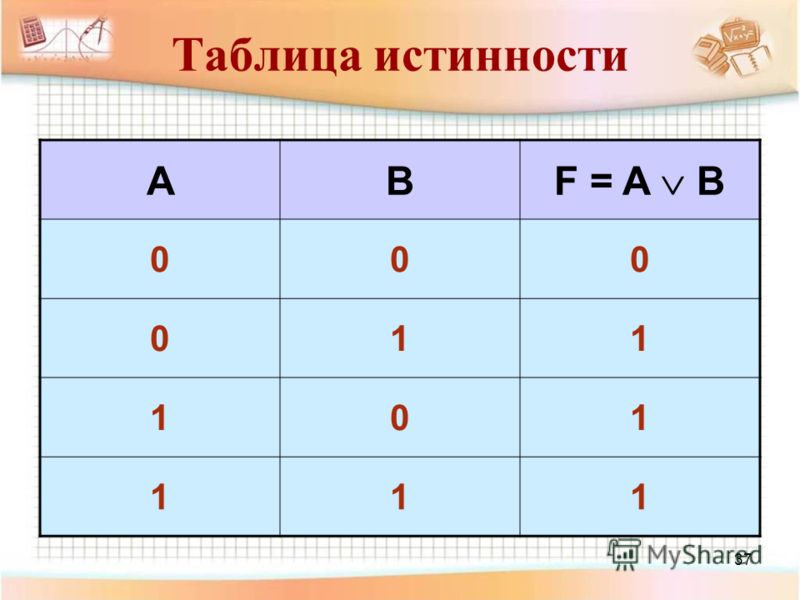 В речи это выражается союзами «и», «а», «но», «да», «наряду с», «вместе с тем» и даже отсутствием союза.
В речи это выражается союзами «и», «а», «но», «да», «наряду с», «вместе с тем» и даже отсутствием союза.Таблица истинности конъюнкции
| A | B | AB, A˄B, A&B |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Если предлагается нестрогий выбор между двумя суждениями по принципу истинности, то есть мы считаем истинным весь текст, если истинно хоть одно из суждений, то говорят, что суждения связаны слабой дизъюнкцией или логическим «ИЛИ». В речи это отображается союзом «или», «либо».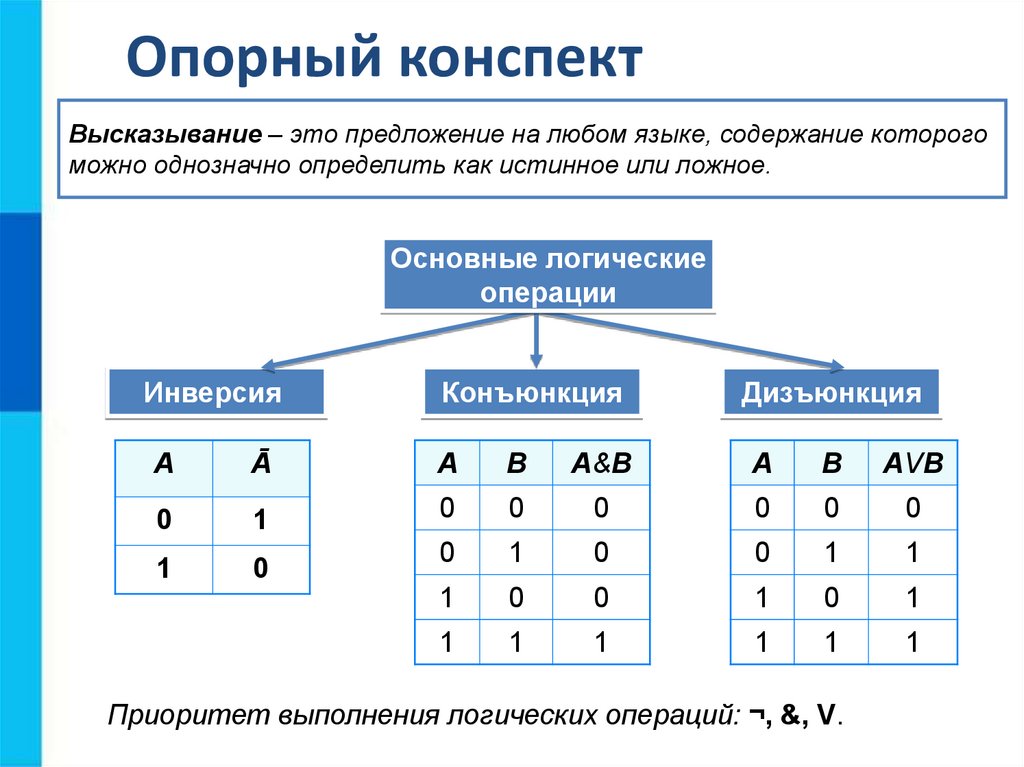
Таблица истинности слабой дизъюнкции
| A | B | A+B, A˅B, A|B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Если предлагается строгий выбор по принципу истинности, то есть мы считаем истинным весь текст, если истинно только одно из суждений, то говорят, что суждения связаны сильной дизъюнкцией или логическим «ИСКЛЮЧАЮЩИМ ИЛИ». В речи это не отображается и оговаривается специально фразой «или только А, или только В», «одно из двух: А или В».
Таблица истинности сильной дизъюнкции
| A | B | A⊕B, A xor B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Процесс получения истинного умозрительного знания из суждений, истинность которых несомненна и является нам из наблюдений, называется логическим следованием. Пример следования: из правильного решения любой задачи следует правильный ответ. В речи это отображается конструкцией «если…, то…», «из… следует…» и другими конструкциями. Это называется «ЛОГИЧЕСКИМ СЛЕДОВАНИЕМ» или логической операцией импликация.
Пример следования: из правильного решения любой задачи следует правильный ответ. В речи это отображается конструкцией «если…, то…», «из… следует…» и другими конструкциями. Это называется «ЛОГИЧЕСКИМ СЛЕДОВАНИЕМ» или логической операцией импликация.
Таблица истинности импликации
| A | B | A→B |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Бывает так, что два разных по содержанию суждения одинаковы по значению одновременно. Тогда мы их можем связать логической операцией эквиваленция.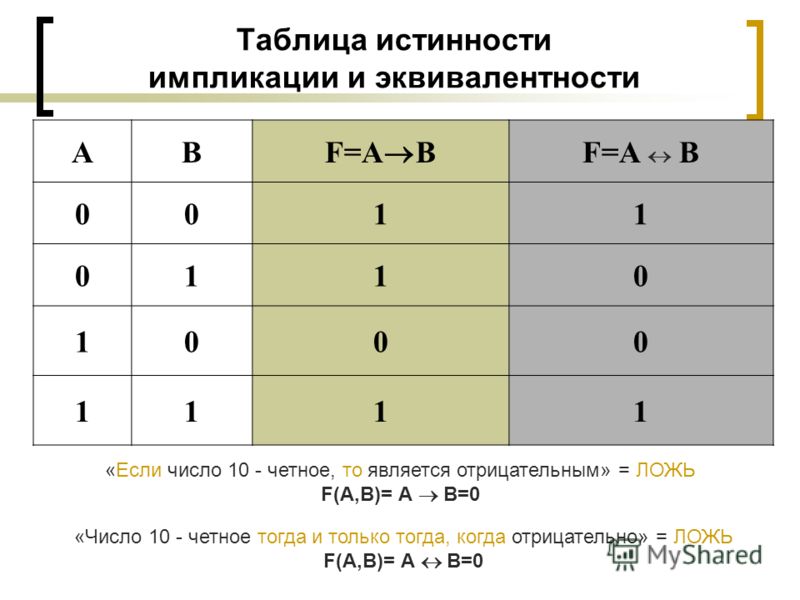
Таблица истинности эквиваленции
| A | B | A↔B, A=B |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Наконец, есть операция, позволяющая изменить значение одного суждения на противоположное. Она называется инверсия, обращение, отрицание или логическое «НЕ».
Таблица истинности инверсии
| A | ¬A, –А, Ā |
| 0 | 1 |
| 1 | 0 |
В сложных логических формулах устанавливается следующий приоритет (очередность) выполнения логических операций.
| 1 | скобки ( ) |
| 2 |
инверсия |
| 3 | конъюнкция |
| 4 | дизъюнкция |
| 5 | импликация |
| 6 | эквиваленция |
Чтобы выяснить, при каких значениях отдельных суждений текст можно считать истинным, строится таблица истинности логической формулы.
Например A˄B ˅ ¬(B˄C)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| A | B | C | A˄B | B˄C | ¬(B˄C) | |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 0 | 1 |
Сначала заполняются столбцы 1, 2 и 3 всевозможными комбинациями значений переменных А, В и С.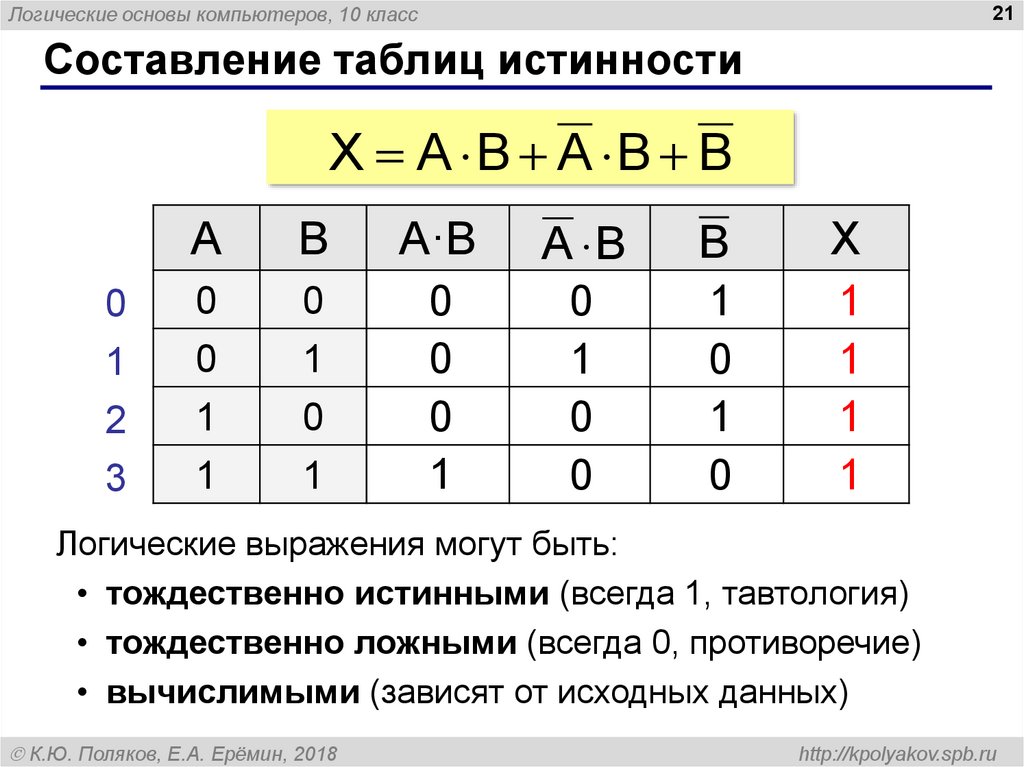 Чтобы не ошибиться, лучше организовать двоичный счет от нуля. Всего число комбинаций определяется как 2 в степени числа переменных. В данном случае 2
Чтобы не ошибиться, лучше организовать двоичный счет от нуля. Всего число комбинаций определяется как 2 в степени числа переменных. В данном случае 2
В столбце 4 хранится результат конъюнкции от А и В. В столбце 5 хранится результат конъюнкции от В и С. В столбце 6 хранится результат отрицания столбца 5. В столбце 7 хранится результат дизъюнкции от данных в столбцах 4 и 6 и представляет собой результат вычисления всей формулы.
Упражнение 1
Построить таблицы истинности логических формул. Подсчитать число истинных и ложных комбинаций значений аргументов.
1) А˄В˅А˄¬С
2) А˅А˄В
3) (А+В)(ВС+¬С)
4) АВС→¬В
5) А→В = ¬А˅В
⚠ВЫРАЖЕНИЕ ПРИНАДЛЕЖНОСТИ ТОЧКИ НЕКОТОРОЙ ОБЛАСТИ
Упражнение 2
Упражнение 3
⚠
Логические формулы равносильны или эквивалентны, если их таблицы истинности в части комбинаций значений переменных и результата совпадают. Например, сравните таблицы истинности эквиваленции и сильной дизъюнкции и согласитесь, что эквиваленция «эквивалентна» отрицанию сильной дизъюнкции A↔B = ¬(A ⊕ B).
Например, сравните таблицы истинности эквиваленции и сильной дизъюнкции и согласитесь, что эквиваленция «эквивалентна» отрицанию сильной дизъюнкции A↔B = ¬(A ⊕ B).
Упражнение 4
⚠ЗАКОНЫ ЛОГИКИ, МИНИМАЛЬНАЯ ТЕОРИЯ
Упражнение 5
Упражнение 6
⚠
ПРИМЕР ПРИМЕНЕНИЯ ЗАКОНОВ ЛОГИКИ ДЛЯ ПРЕОБРАЗОВАНИЯ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ
Докажем истинность логической формулы, по которой выполнено следующее рассуждение.
В комнате открыты два окна. Если открыто одно окно, то происходит проветривание. Следовательно, если открыты два окна, то тоже происходит проветривание.
Сначала построим логическую формулу.
(A(B→C))→(A→C)
Чтобы доказать истинность рассуждения, необходимо доказать, что логическая формула тождественно истинна, то есть при всех комбинациях значений переменных она равна истине. Это можно сделать с помощью таблицы истинности, а можно и с помощью преобразований с использованием законов логики. Выберем второй путь.
Это можно сделать с помощью таблицы истинности, а можно и с помощью преобразований с использованием законов логики. Выберем второй путь.
Преобразуем сначала две крайние импликации, а потом среднюю.
(A(¬B+C))→(¬A+C) = ¬ (A(¬B+C))+(¬A+C)
Преобразуем отрицание слева по правилу де Моргана.
¬A+¬(¬B+C)+ ¬A+C
Раскроем скобки с отрицанием.
¬A+B(¬C) + ¬A+C
Исключим повторы переменных (идемпотентнось слабой дизъюнкции).
¬A+B(¬C) + C
Никаких иных преобразований мы больше совершить не можем. Мы видим, что формула истине не тождественна, поэтому истинность рассуждения под сомнением.
Но как же так? Ведь его истинность очевидна! Нет. По такой формуле в общем случае рассуждения строить нельзя. Чтобы доказать логически, что при двух открытых окнах проветривание все же происходит, переформулируем рассуждение более точно, но без потери смысла.
В комнате открыты окно А и окно В.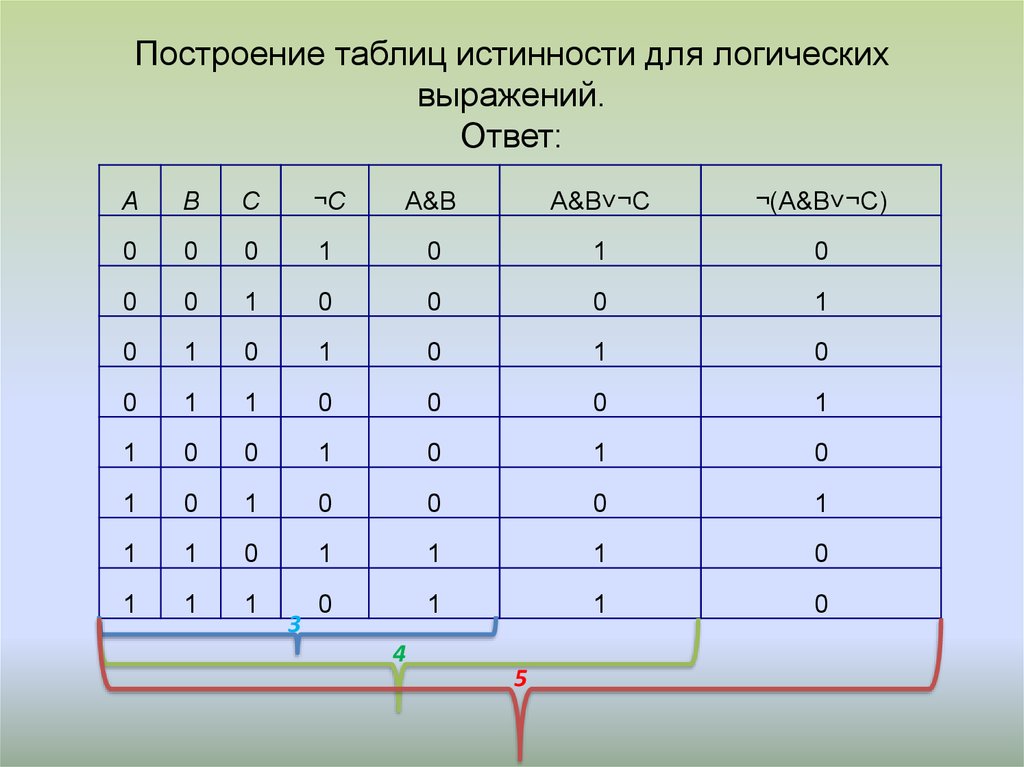 Если открыто только одно из них, то происходит проветривание. Следовательно, если открыты оба окна, то тоже происходит проветривание.
Если открыто только одно из них, то происходит проветривание. Следовательно, если открыты оба окна, то тоже происходит проветривание.
Формализуем.
(AB(A⊕B→C))→(AB→C)
Преобразуем левую импликацию.
(AB(A¬B + ¬AB +C))→(AB→C)
Раскроем внутренние скобки связанные с конъюнкцией АВ.
(ABA¬B +AB¬AB+ABC) →(AB→C)
Произведем действия с отрицаниями.
ABA¬B = AB¬B = A·0 = 0
(0+0+ABC) → (AB→C)
Произведем действия с константами слева и преобразуем обе импликации. Над отрицанием АВ сразу используем правило де Моргана.
¬(ABC) + (¬A+¬B+C)
Раскроем скобки, исключим повторы переменных, и произведем действия с отрицаниями.
¬A+¬B+¬C +¬A+¬B+C
¬A+¬B+¬C+C
¬A+¬B+1 = 1
Истинность этой формулы доказана, за одно, доказана истинность заключения при рассуждении по этой формуле, то есть логическое следование (AB→C) из (AB(A⊕B→C)) имеет место.
Упражнение 7
⚠
ПРИМЕР ЗАДАЧ НА ПРОВЕРКУ ГИПОТЕЗЫ
(Непосредственно в ЕГЭ не используются, можно пропустить.)
Трое студентов: Коля, Петя и Юра — влюблены в трех девушек: Таню, Зину и Галю. Но эта любовь без взаимности (1). Коля любит девушку, влюбленную в юношу, который любит Таню (2). Петя любит девушку, влюбленную в юношу, который любит Зину (3). Зина терпеть не может Юру (4). Кто в кого влюблен?
Допустим, что Коля любит Зину, Петя любит Таню, а Юра любит Галю. По условию 2 Зина должна быть влюблена в Петю. А по условию 3 Таня любит Колю. Осталось, что Юра любит Галю, а Галя — Юру, что противоречит условию 1.
К→З П→Т Ю→Г З→П Т→К Г→Ю противоречие
Допустим теперь, что Коля любит Галю, Петя — Таню, а Юра — Зину (это не противоречит условию 4). Тогда по условию 2 Галя должна любить Петю.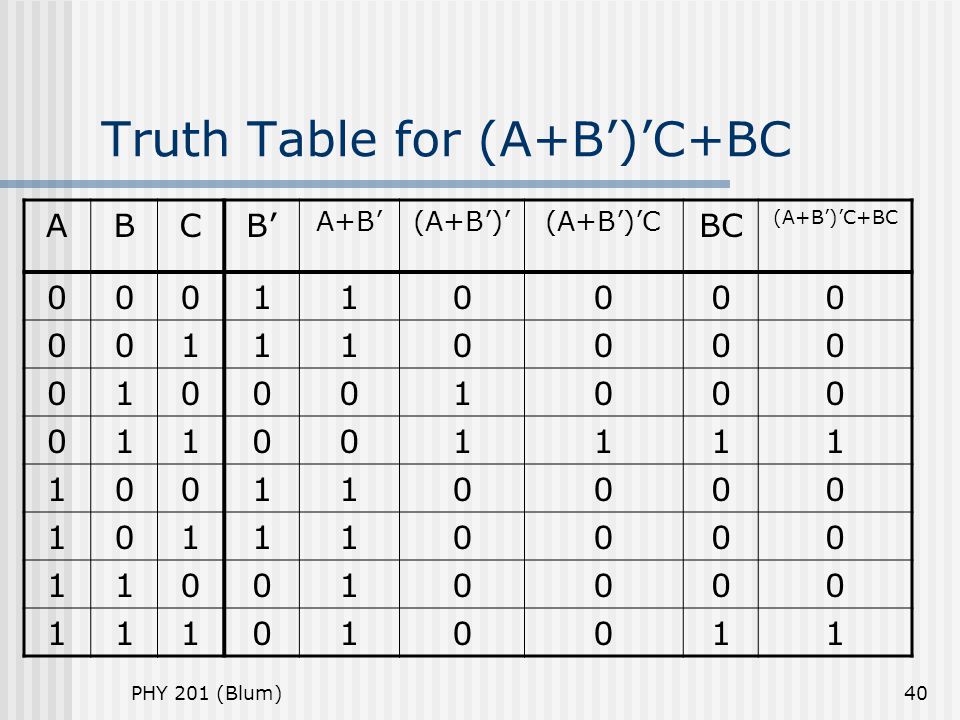 По условию 3 Таня любит Юру. Осталось, что Зина любит Колю. Никакого противоречия условию нет.
По условию 3 Таня любит Юру. Осталось, что Зина любит Колю. Никакого противоречия условию нет.
К→Г П→Т Ю→З Г→П Т→Ю З→К нет противоречия
Вадим, Сергей и Михаил изучают различные иностранные языки: китайский, японский и арабский. На вопрос, какой язык изучает каждый из них, один ответил: «Вадим изучает китайский, Сергей не изучает китайский, а Михаил не изучает арабский». Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны. Какой язык изучает каждый из молодых людей?
Верной гипотезой будет, что Вадим изучает арабский, Сергей — китайский, Михаил — японский. Действительно, первое ложно, второе ложно, третье истинно, что соответствует условию.
Упражнение 8
Упражнение 9
⚠ ЛОГИЧЕСКИЕ ОПЕРАЦИИ НАД МНОЖЕСТВАМИ, СХЕМЫ ЭЙЛЕРА
Упражнение 10
Упражнение 11
Упражнение 12
Упражнение 13
Вопрос 2
Логические выражения
и их преобразования.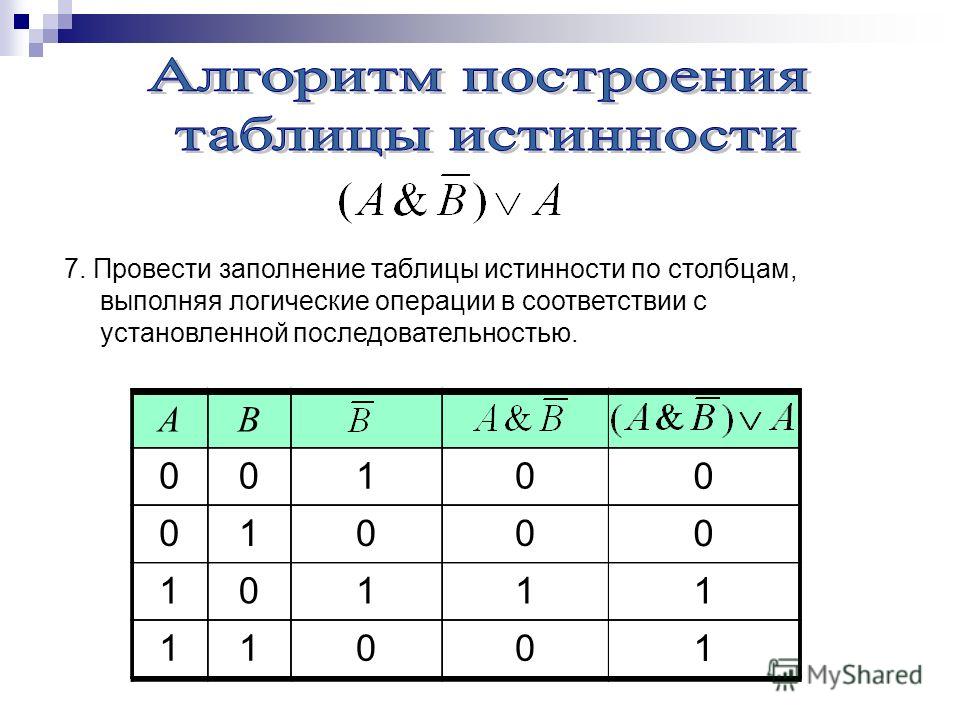 Таблицы истинности.
Таблицы истинности.
Логические выражения. Каждое составное высказывание можно выразить в виде формул (логического выражения), в которую войдут логические переменные, обозначающие высказывания, и знаки логических операций, обозначающие логические функции.
Для записи составных высказываний в виде логических выражений на формальном языке (языке алгебры логики0 в составном высказывании нужно выделить простые высказывания и логические связи между ними.
Запишем в форме логического выражения составное высказывание «2*2=5 или 2*2=4 или 2*24»проанализируем составное высказывание. Оно состоит из двух простых высказываний,
А= «2*2=5»- ложно (0)
В= «2*2-4» -истинно (1).
Тогда составное высказывание можно записать в следующей форме,
«А или
В и Ā или В».
теперь необходимо записать высказывание в форме логического выражения с учетом последовательности выполнения логических операций. При выполнении логических операций определен следующий порядок их выполнения, инверсия , конъюнкция, дизъюнкция. Для изменения указанного порядка могут использоваться сковки.
F=(AuB)&(ĀuB).
Истинности или ложности составных высказываний можно определить чисто формально, руководствуясь законами алгебры высказываний, не обращаясь к смысловому содержанию высказываний.
П одставим в логическое выражение значения логических переменных и, используя таблицы истинности базовых логических операций, получим значение логической функции.
Таблицы
истинности. Для каждого составного
высказывания (логического выражения)
можно построить таблицу истинности,
которая определяет его истинность или
ложность при всех возможных комбинациях
исходных значений простых высказываний
(логических переменных).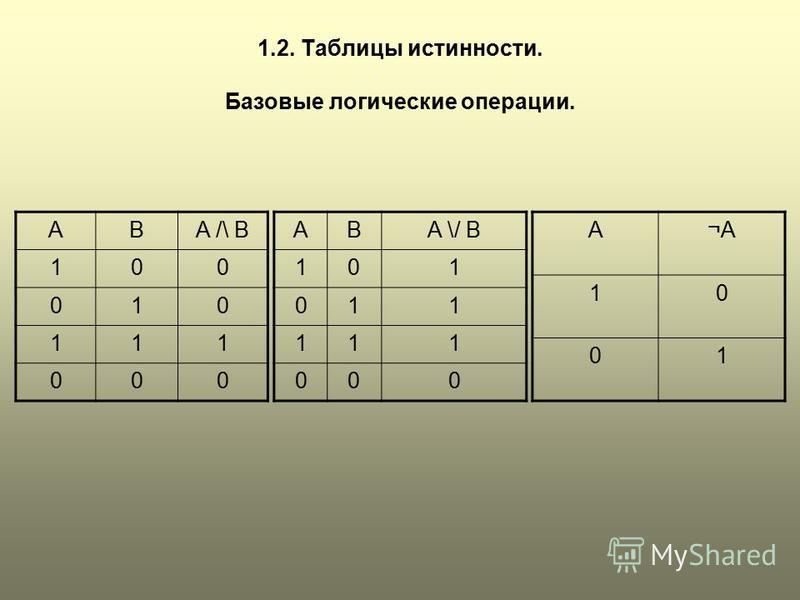
При построении таблиц истинности целесообразно руководствоваться определенной последовательностью действий.
Во-первых, необходимо определить количество строк в таблице истинности, которое равно количеству возможных комбинаций значений логических переменных, входящих в логическое выражение. Если количество логических переменных n, то количество строк =2n .
В нашем случае логическая функция F=(AB)&(Ā¯B) имеет две переменное и, следовательно, количество строк в таблице истинности должно быть равно 4.
Во-вторых, необходимо определить количество столбцов в таблице истинности, которое равно количеству логических переменных плюс количество логических операций равно пяти, т.е. количество столбцов таблицы истинности равно семи.
В-третьих,
необходимо построить таблицу истинности
с указанным количеством строк и столбцов,
обозначить столбцы и внести возможные
наборы значений исходных логических
переменных .
A B AB Ā ¯B
0 0 0 1 1 1 0
0 1 1 1 0 1 1
1 0 1 0 1 1 1
1 1 1 0 0 0 0
В-четвертых,
необходимо заполнить таблицу истинности
по столбцам, выполняя базовые логические
операции в необходимой последовательности
и в соответствии с их таблицами истинности.
Теперь мы можем определить значение
логической функции для любого набора
значений логических переменных.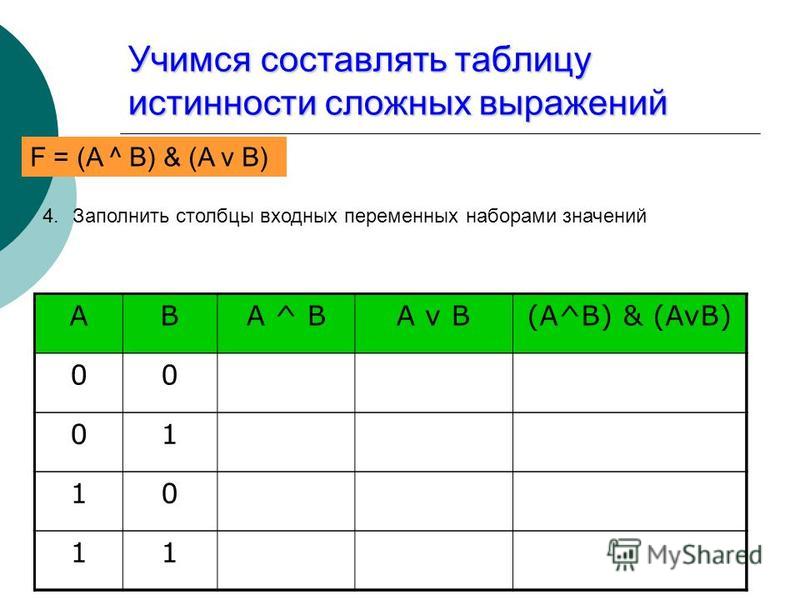
Равносильные логические ворожения. Логические выражения, у которых таблицы истинности совпадают, называются равносильными. Для обозначения равносильных логических выражений используется знак «=».
Д окажем, что логические ворожения равносильны.
П остроим сначала таблицу истинности для логического выражения.
А В Ā
0 0 1 1 1
0 1 1 0 0
1 0 0 1 0
1 1 0 0 0
Таблица истинности
А В
0 0 0 1
0 1 1 0
1 0 1 0
1 1 1 0
Таблицы
истинности совпадают, следовательно,
логические выражения равносильны.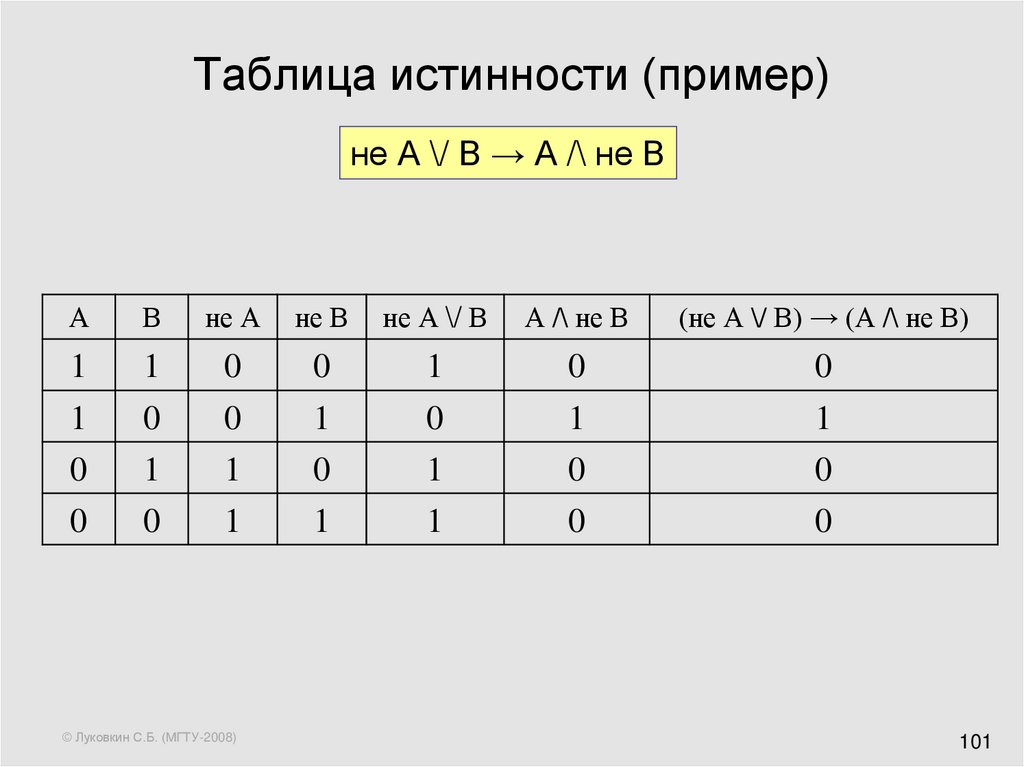
Логические функции.
Любое составное высказывание можно рассматривать как логическую функцию F(Х1,Х2…Хn), аргументами которой являются логические переменные X1,X2….Xn (простые высказывания). Сама функция и аргументы могут принимать только два различных значения «истина» (1) и «ложь» (0).
Выше были рассмотрены функции двух аргументов, логическое умножение F=(A,B)=A&B, логическое сложение F=(A,B)=AB, а также логическое отрицание F(A)=Ā, в котором значение второго аргумента можно считать равным нулю.
Каждая логическая функция двух аргументов четыре возможных набора значений аргументов. По формуле можем определить какое количество различных логических функций двух аргументов, может существовать,
Т
аким
образом, существует 16 различных логических
функций двух аргументов, каждая из
которых задается собственной таблицей
истинности.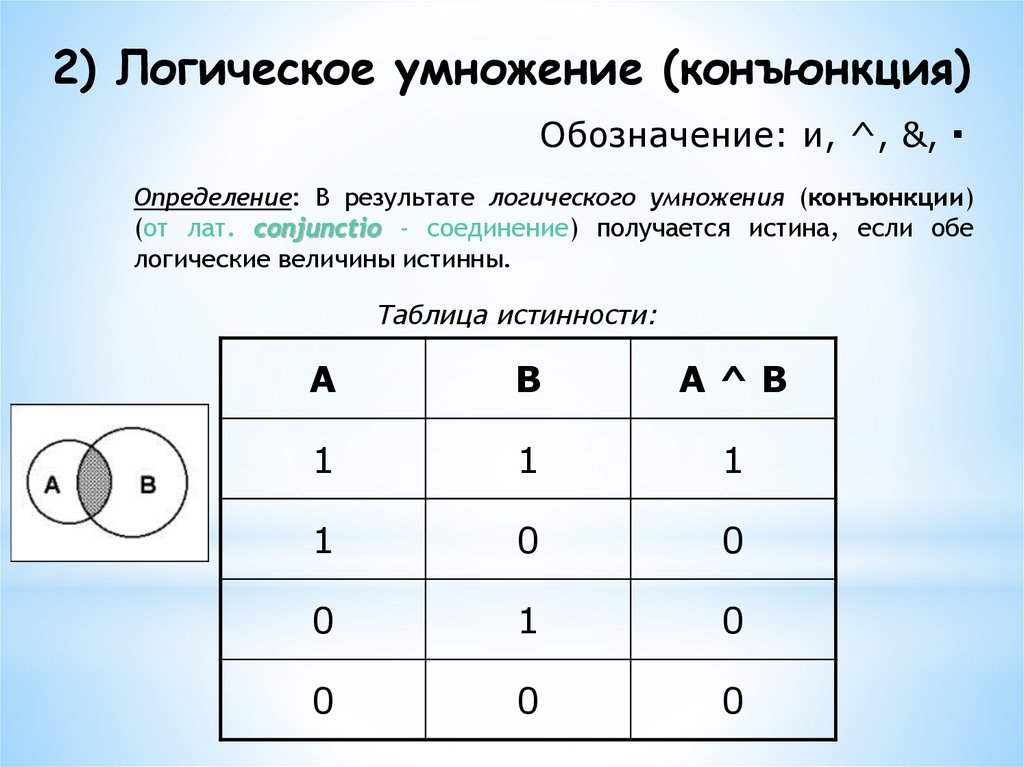
В обыденной и научной речи кроме базовых логических связок «и», «или», «не», используется и некоторые другие, «если…то», «тогда…и только тогда, когда…» и др. некоторые из них имеют свое название и свой символ и им соответствует определенные логические функции.
Логическое следование (импликация). Логическое следование (импликация) образуется соединением двух высказываний в одно с помощью оборота речи «если…, то…».
Составное высказывание, образованное с помощью операции логического следования (импликации), ложна тогда и только тогда, когда из истинной предпосылки (первого высказывания) следует ложный вывод (второе высказывание).
Логическая операция импликация «если А то В», обозначается А→В и выражается с помощью логической функции F14 ,которая задается соответствующей таблицей истинности.
А В F14=A→B
0 0 1
0 1 1
1 0 0
1 1 1
Например,
высказывание «если число делится на
10, то оно делится на 5» истинно, т. к.
истинны и первое высказывание
(предпосылка), и второе высказывание
(вывод).
к.
истинны и первое высказывание
(предпосылка), и второе высказывание
(вывод).
Высказывание №если число делится на 10, то оно делится на 3» ложно, т.к. из истинной предпосылки делится ложный вывод.
Однако операция логического следования несколько отличается от обычного понимания слова «следует». Если первое высказывание (предпосылка)ложно, то вне зависимости от истинности или ложности второго высказывания (вывода) составное высказывание истинно. Это можно понимать таким образом, что из неверной предпосылки может следовать что угодно.
В алгебре высказываний все логические функции могут быть сведены путем логических преобразований к трем базовым, логическому умножению, логическому сложению и логическому отрицанию. Докажем методы сравнения таблиц истинности, что операция импликация А→В равносильна логическому выражению ĀB.
А В Ā ĀB
0 0 1 1
0 1 1 1
1 0 0 0
1 1 0 1
Таблицы
истинности совпадают, что и требовалось
доказать.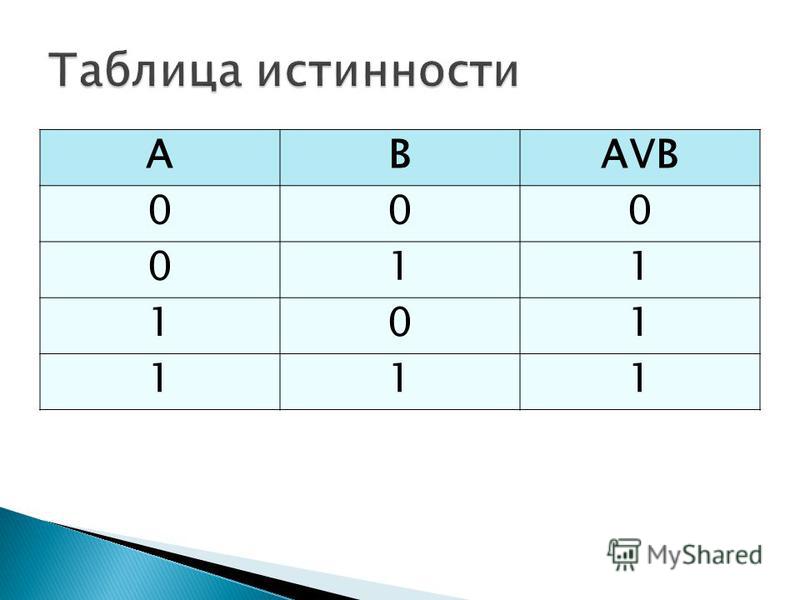
Логическое равенство (эквивалентность). Логическое равенство (эквивалентность) образуется соединением двух высказываний в одно с помощью оборота речи «…тогда и только тогда, когда…».
Логическая операция эквивалентности «А эквивалентно В» обозначается АВ и выражается с помощью логической функции F10, которая задается соответствующей таблицей истинности.
А В F10
0 0 1
0 1 0
1 0 0
1 1 1
CS101 — Булева логика
В 1840-х годах английский математик Джордж Буль разработал алгебру (набор операторов и законов) для переменных, которые могут иметь только два состояния – истинно, и ложно. Таким образом, логическое значение эквивалентно одному биту:
Ложь = 0 = выкл.True = 1 = on
Операторы, определенные Булем, распространены во всех вычислениях. Вы могли столкнуться с ними при поиске в библиотеке или других базах данных. Мы рассмотрим следующие:
Таблица иллюстрирует как алгебраическое обозначение, так и обозначение схемы . Элементы принципиальных схем называются вентилями , , как в «И-вентиль» или «Исключающее ИЛИ-вентиль».
Поведение этих операторов можно определить с помощью таблиц истинности:
A B A·B A+B A' A⊕B
0 0 0 0 1 0
0 1 0 1 1 1
1 0 0 1 0 1
1 1 1 1 0 0 Мы объединяем ворота в комбинационных схемы для достижения различных эффектов. Например, алгебраическое выражение X = A·B + A·C точно соответствует следующей принципиальной схеме:
, и мы можем обнаружить его действие, заполнив таблицу истинности:
A B C D=A·B E=A ·С Х=D+Е
0 0 0 0 0 0
0 0 1 0 0 0
0 1 0 0 0 0
0 1 1 0 0 0
1 0 0 0 0 0
1 0 1 0 1 1
1 1 0 1 0 1
1 1 1 1 1 1 Упражнение: Попробуйте нарисовать схемы и таблицы истинности для X=(A·B)' и для X=A'+B' .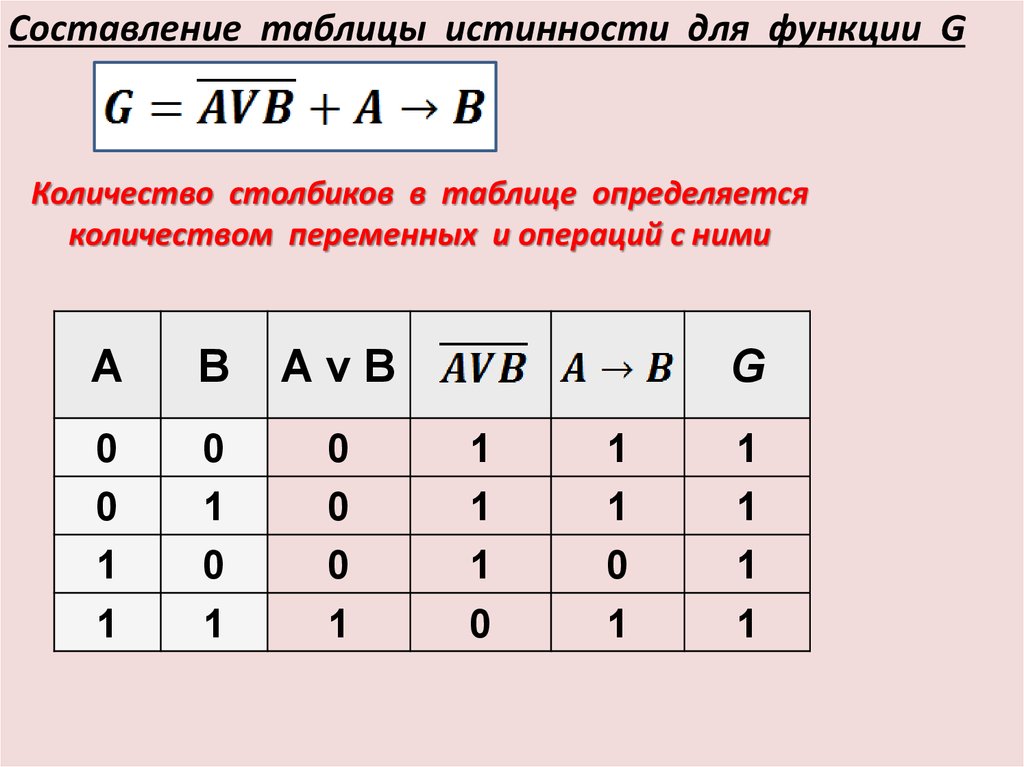 Они должны дать одинаковый результат для входных данных
Они должны дать одинаковый результат для входных данных A и B . Это один из законов ДеМоргана.

Мы просто посмотрим на защелку S-R (NAND).
- Шлепанцы, защелки и детали памяти [8:53] от Computerphile
Этот раздел относится к программе Logisim, которая должна работать на любой платформе с Java Runtime Environment. Если вы получаете сообщение об ошибке «неизвестный разработчик» на Mac, перейдите на Системные настройки » Безопасность и найдите кнопку с надписью Все равно открыть.
Открыв Logisim, вы должны ознакомиться с несколькими инструментами.
Инструмент «Рука» (самый левый на панели инструментов) позволяет включать и выключать входы. Инструмент «стрелка» (рядом с ним) позволяет размещать компоненты на сетке, перемещать их и соединять вместе.
На боковой панели основные компоненты, которые мы будем использовать, находятся в Gates , но есть также Pin (под проводкой) и LED (под Input/Output).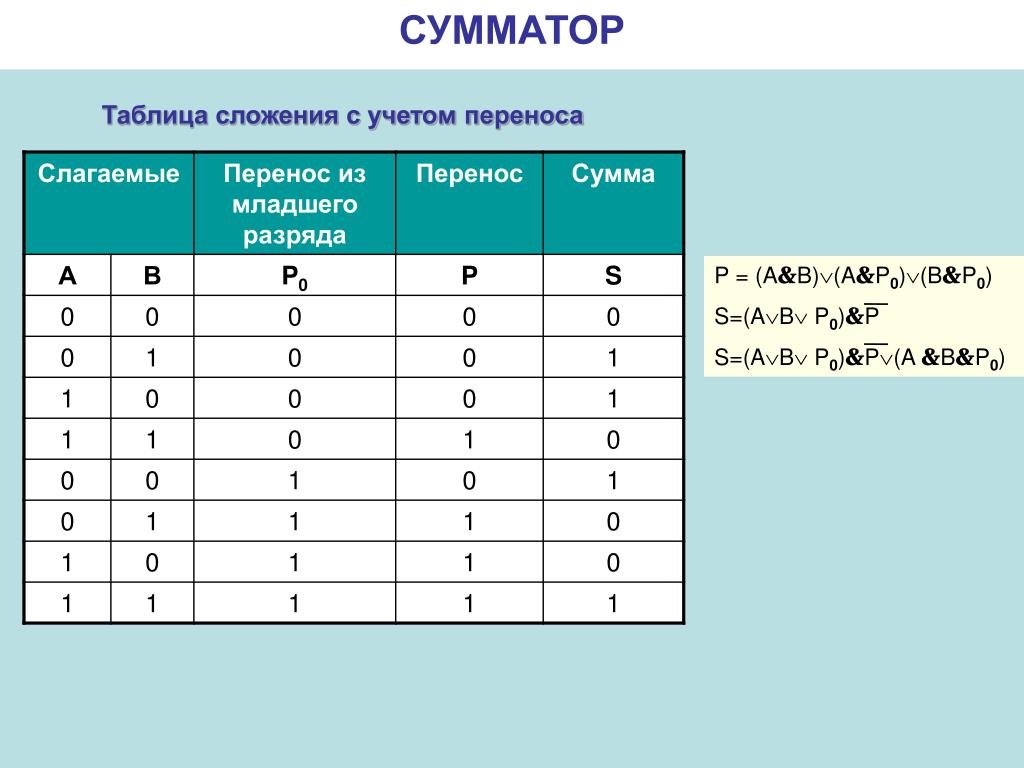
Если компонент выбран, его свойства отображаются в левом нижнем углу экрана. Вы можете использовать их для создания меток для ваших контактов и светодиодов.
- Схема 3-битного сумматора, которую я сделал на уроке.
- Видео: Сборка полусумматора из домино с Мэттом Паркером и Numberphile
- Видео: Большая гадюка домино, продемонстрированная на Фестивале науки в Манчестере, Великобритания

[Решено] Вопрос 1: Основные таблицы истинности (4 балла) A B A . B A +B A ~A NN A 0…
Получите больше от подписки*
- Доступ к более чем 100 миллионам учебных ресурсов по конкретным курсам
- Круглосуточная помощь опытных наставников по более чем 140 предметам
- Полный доступ к более чем 1 миллиону решений для учебников
*Вы можете изменить, приостановить или отменить в любое время
Вопрос задан kharvey101
Текст транскрипции изображения
Вопрос 1: Основные таблицы истинности (4 балла) Заполните таблицы истинности для И, ИЛИ, НЕ и двойного отрицания.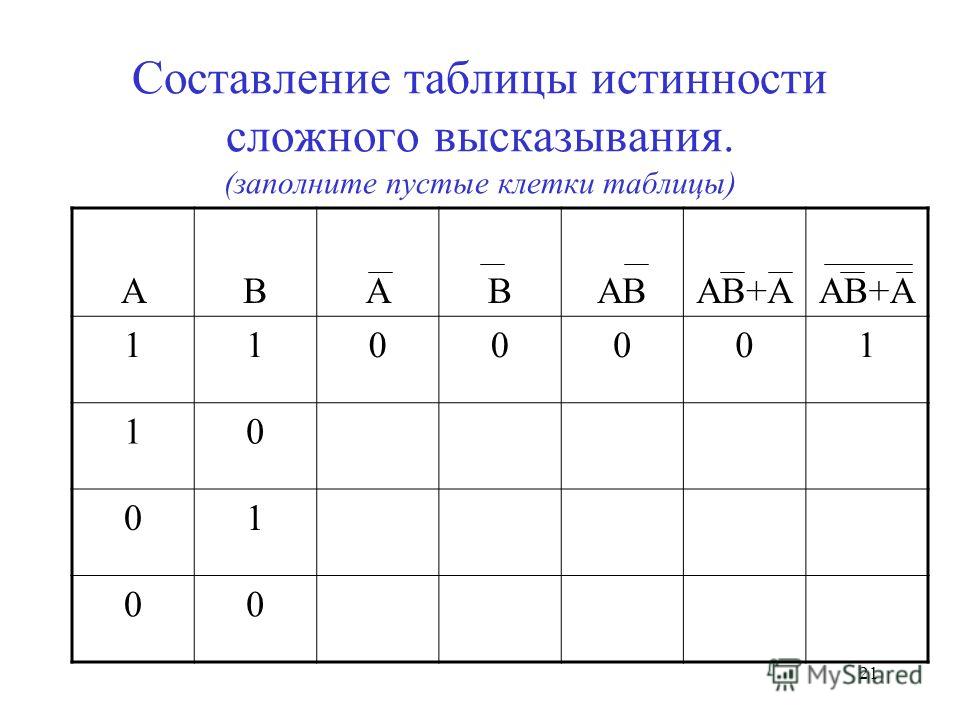
… Показать больше
Информатика Инженерная технология Программирование на Питоне СРТ 101
Ответ и объяснение
Решено проверенным экспертом
Рейтинг Полезно
Ответил SargentLlama1068
inia pulvinar tort
| l | i | sus | cong |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | x | 0 | x |
| x | 0 | 0 | x |
| x | x | x | x |
trices ac magna. Фу
| l | f | ic |
|---|---|---|
| 0 | x | 0 |
| x | 0 | x |
Unlock full access to Course Hero
Explore over 16 million step -пошаговые ответы из нашей библиотеки
Подпишитесь, чтобы посмотреть ответ
Пошаговое объяснение
s an Fu ur laoreet.

 True = 1 = on
True = 1 = on