Примеры решений
К главной странице
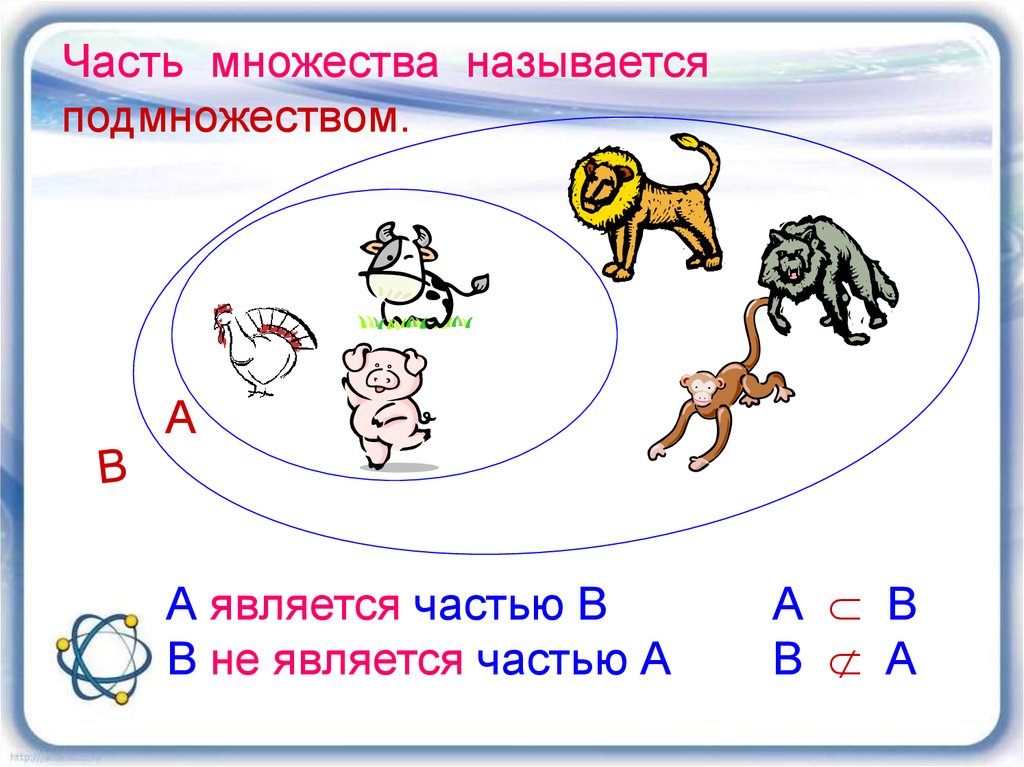
Тема: множества.
Задача. Докажите, что множество $A$ тогда и только тогда является подмножеством множества $B$, когда каждый элемент, не принадлежащий $B$, не принадлежит $A$.
Решение. Оборот «тогда и только тогда» означает два утверждения:
1) $(A \subset B) \Rightarrow {}$(для любого $x$, не принадлежащего $B$, $x$ не принадлежит $A$),
2) (для любого $x$, не принадлежащего $B$, $x$ не принадлежит $A$)${} \Rightarrow (A \subset B)$.
Продемонстрируем на примере этой задачи, как применяется метод доказательства «от противного». Чтобы доказать некоторое утверждение, мы предполагаем, что оно не выполняется и приходим к противоречию
Докажем здесь только утверждение 1). Предположим противное, то есть что $A \subset B$, но существует некоторый элемент $x$, не принадлежащий $B$, но принадлежащий $A$. По определению того, что $A \subset B$ мы знаем, что каждый элемент, принадлежащий $A$, должен принадлежать $B$.
Тема: множества.
Задача. Может ли у множества быть ровно: 1) 0; 2) 7; 3) 16 подмножеств?
Решение. Во-первых, заметим, что число подмножеств пустого множества равно 1, число подмножеств множества, состоящего из одного элемента, равно 2, из двух – 4, из трех – 8, из четырех – 16. Второе важное наблюдение – монотонность: если у одного множества больше элементов, чем у другого, то и подмножеств у него больше.
Тема: Комбинаторика.
Задача. Сколько существует «cлов» из двух букв английского языка?
Комментарий. Во-первых, в этой задаче, конечно, имеются в виду не те слова, которые можно встретить в словаре, а произвольные сочетания букв английского языка. Теперь перейдем к главным идеям решений подобных комбинаторных задач. Когда требуется посчитать кол-во каких-то специальных объектов, часто работает следующая схема: 1. перечисление всех вариантов в разумном порядке; 2. понимание того, какие «записи» соответствуют одному и тому же объекту. В этой задаче нам понадобится только 1. Второй пункт будет проиллюстрирован в следующем примере. Другая полезная (отнюдь не только в комбинаторике) идея состоит в том, что, прежде чем решать задачу для произвольного (или очень большого) $n$, полезно сначала разобраться со случаем небольших $n$. Замеченные при этом закономерности (даже если они не доказаны) часто существенно упрощают решение задачи.
Произведением множеств называют множество из упорядоченных пар. Число элементов в произведении множеств равно произведению числа элементов исходных множеств (правило умножения). В нашем случае множество всех слов из 2 букв на английском языке – это как раз множество неупорядоченных пар английских букв, а значит равно произведению множества букв английского алфавита (их 26 штук) с самим собой, а значит в нем 26*26=676 элементов.Тема: комбинатрика.
Так как порядок «обычных» дежурных не важен, выписывая их по алфавиту, мы никакой случай не забудем и не повторим дважды.
(Вася, Коля, Леша), (Вася, Коля, Петя),& (Вася, Леша, Петя),
(Коля, Вася, Леша), (Коля, Вася, Петя),& (Коля, Леша, Петя),
(Леша, Вася, Коля), (Леша, Вася, Петя),& (Леша, Коля, Петя),
(Петя, Вася, Коля), (Петя, Вася, Леша),& (Петя, Коля, Леша).
Итого $12$ вариантов.
Теперь перейдем к решению исходной задачи. Старшего дежурного можно выбрать десятью способами. Когда мы уже выбрали старшего, мы можем выбрать первого дежурного девятью (потому что одного человека мы уже назначили старшим дежурным) способами. После того, как мы выбрали старшего дежурного и еще одного дежурного, второго дежурного мы можем выбрать восемью способами. Итого, вроде бы, по «правилу умножения» должно получаться $10\cdot9\cdot8=720$.
Однако если мы внимательно посмотрим на наше решение, то увидим, что каждую тройку дежурных мы посчитали по два раза.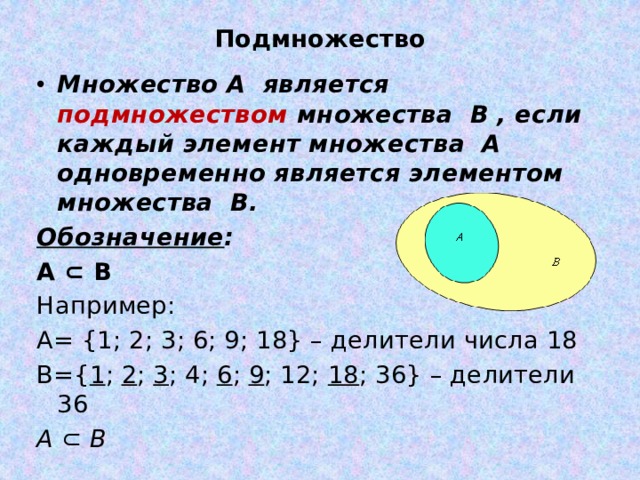
Например, тройку дежурных (Вася – старший дежурный, Леша, Петя) мы посчитали два раза: как тройку (Вася, Петя, Леша) и как тройку (Вася, Леша, Петя). Поэтому правильный ответ в два раза меньше – 360.Подмножества
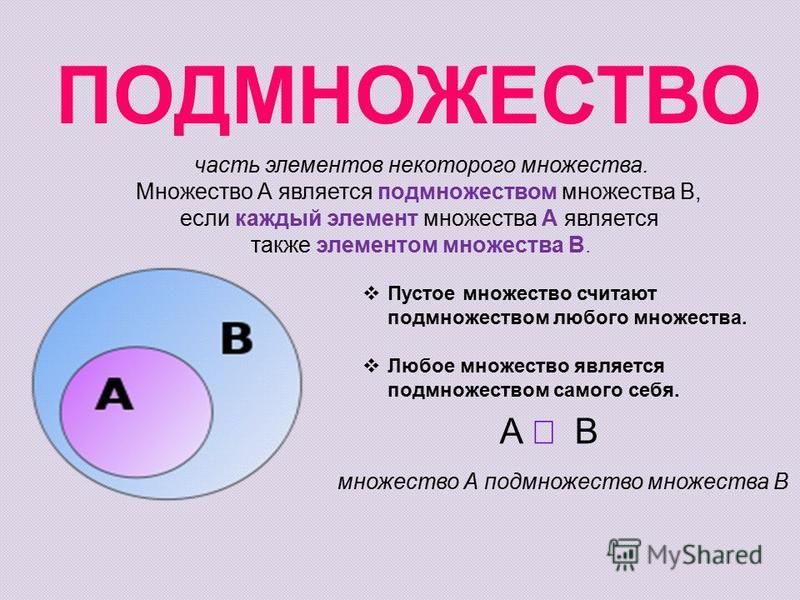
Приведем примеры подмножеств:
числовой отрезок [–1, 3] есть подмножество числового отрезка [–4; 5];
множество всех квадратов есть подмножество множества всех прямоугольников;
множество Z всех целых чисел есть подмножество множества Q всех рациональных чисел;
множество точек треугольника, вписанного в круг, есть подмножество множества точек этого круга;
множество точек круга является подмножеством множества точек описанного вокруг него квадрата;
множество звезд нашей Галактики является подмножеством множества всех звезд Вселенной;
множество учеников восьмого класса данной школы есть подмножество множества всех учеников этой школы.
В свою очередь
множество учеников этой школы является
подмножеством множества всех школьников
в Республики Беларусь;множество жителей Москвы является подмножеством множества всех жителей России;
множество граждан г. Минск является подмножеством множества всех людей на земном шаре.
В свою очередь
множество учеников этой школы является
подмножеством множества всех школьников
в Республики Беларусь;Н а рисунке 6 прямые MN и PQ пересекаются в точке R.
Эта точка принадлежит как прямой MN
Введем
теперь общее понятие пересечения
нескольких множеств.
Пересечением множеств А и В называют новое множество Х,
содержащее те и только те элементы,
которые входят и в множество А и в множество В.
Пересечение множеств А и В обозначают или AB. Например, если А – множество мальчиков, обучающихся в данной школе, а В – множество всех учеников из 8 класса, то – множество мальчиков, которые учатся в 8 классе.
С понятием пересечения множеств приходится иметь дело и в арифметике. Пусть А – множество натуральных делителей числа 72:
A ={1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72},
а В – множество натуральных делителей числа 54:
B ={1, 2, 3, 6, 9, 18, 27, 54}.
Тогда множество состоит из чисел 1, 2, 3, 6, 9, 18:
={1, 2, 3, 6, 9, 18}.
Эти
числа являются общими делителями для
72 и 54.
Наибольший элемент множества
равен 18. Это – наибольший
общий делитель чисел 54 и 72. Множество делителей числа
72 конечно. А множество кратных этого
числа бесконечно:
С = {72, 144, 216, … , 72n, …}.
Бесконечно и множество кратных числа 54:
D = {54, 108, 162, 216, … , 54m, …}.
Пересечением этих множеств является множество общих кратных для чисел 72 и 54:
= {216, 432, …}.
Наименьшее число в , т.е. 216, называется наименьшим общим кратным для 72 и 54.
Иногда
приходится пересекать множества
геометрических фигур. Например, множество
всех квадратов является пересечением
множества всех прямоугольников с
множеством всех ромбов, т.к. квадрат –
это фигура, являющаяся одновременно и
прямоугольником, и ромбом. Пересечением
множества всех треугольников с множеством
всех правильных многоугольников
является множество правильных
треугольников.
Знакомство с множествами и подмножествами
В сегодняшней статье мы рассмотрим небольшое введение в множества и подмножества: какие существуют типы, как они выражаются… Все с некоторыми примерами, которые очень легко понять. Для этого вместо чисел мы будем использовать такие элементы, как фрукты, животные, дети…
Первое, что мы должны знать, это , что такое множество. Мы можем определить его как набор объектов, который мы называем элементами , которые имеют некоторые общие характеристики.
Наборы могут содержать элементы любого типа: цифры, буквы, предметы, люди… Например, этот набор содержит фрукты:
НАБОР
Классификация наборов:
Набор можно классифицировать по в количество элементов, которые он имеет. Это:
- Конечное: , если у него есть коллекция, которую можно подсчитать, даже если это может быть трудно сделать. Например, набор фруктов включает в себя все виды фруктов, которые существуют в мире. Несмотря на то, что это может быть трудно, можно сосчитать все виды фруктов в мире, поэтому оно конечно.
- Бесконечно: , если у него есть коллекция, которая никогда не может закончить подсчет. Например, множество всех четных чисел (которые бесконечны) является бесконечным множеством.
Несмотря на то, что это может быть трудно, можно сосчитать все виды фруктов в мире, поэтому оно конечно.Отношения между множествами:
С точки зрения отношения между ними множества могут быть:
- Непересекающиеся множества: те множества, которые не имеют ни одного общего элемента.
Например, множества фруктов и животных не пересекаются, потому что нет ни плода, который мог бы быть животным, ни животного, которое могло бы быть плодом:
РАЗЪЕДИНЕННЫЕ МНОЖЕСТВА
- Равные множества: бывает, когда все элементы одного множества принадлежат другому.
Например, набор красных фруктов и набор желтых фруктов являются равными наборами фруктов, поскольку все красные фрукты являются фруктами, и все желтые фрукты также являются фруктами.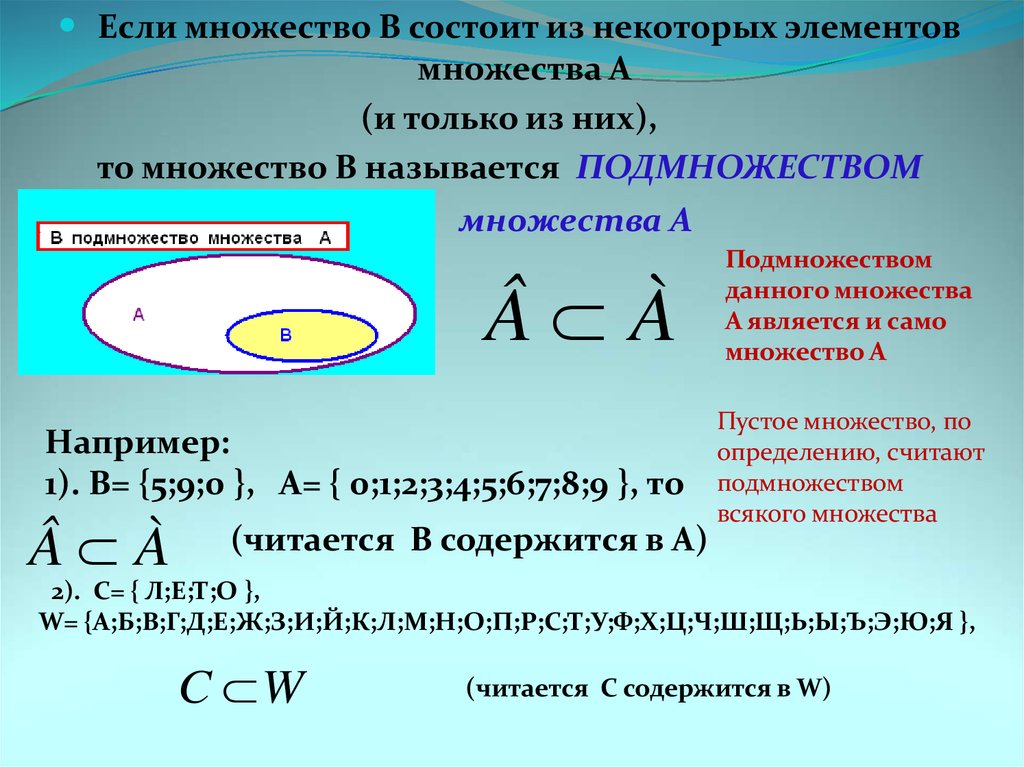
ПОДМНОЖЕСТВА
Множество живых существ очень велико: оно имеет множество подмножеств. Например:
- Растения — это подмножество живых существ.
- Животные — это подмножество живых существ.
- Люди являются подмножеством животных.
Пересечение подмножеств: иногда разные наборы отличаются друг от друга, но имеют некоторые общие элементы. Затем определяется область пересечения, содержащая все общие элементы.
Например, у нас есть группа девушек и группа людей, которые носят очки. Поскольку есть девушки, которые носят очки, они составляют часть пересечения двух наборов:
ПЕРЕКРЕСТОК
Что вы думаете об этом посте? Помогло ли это вам лучше понять множества и подмножества?
Если вы хотите попрактиковаться в этих наборах упражнений и многом другом, зарегистрируйтесь и попробуйте бесплатную пробную версию Smartick.
Подробнее:
- Автор
- Последние сообщения
Smartick
Команда создания контента.
Мультидисциплинарная и мультикультурная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать наилучший математический контент.
Последние сообщения Smartick (посмотреть все)
Урок по подмножествам | Математические вкусности
Форма поиска
Поиск
Пример 1: Учитывая A = {1, 2, 4} и B = {1, 2, 3, 4, 5}, какова связь между этими множествами?
Мы говорим, что A является подмножеством B , так как каждый элемент A также находится в B . Это обозначается:
Диаграмма Венна для отношения между этими множествами показана справа.
Ответ: A является подмножеством B .
Другой способ определения подмножества: A является подмножеством B если каждый элемент A содержится в Б .
Оба определения показаны на приведенной выше диаграмме Венна.
Пример 2: Учитывая X = {a, r, e} и Y = {r, e, a, d}, какова связь между этими множествами?
Мы говорим, что X является подмножеством Y , поскольку каждый элемент X также находится в Y. Обозначается:
Диаграмма Венна для связь между этими наборами показана справа.
Ответ: X является подмножеством Y .
Пример 3: Учитывая P = {1, 3, 4} и Q = {2, 3, 4, 5, 6}, какова связь между этими множествами?
Мы говорим, что P не является подмножеством Q s , поскольку не каждый элемент P не содержится в 90 008 Q. Например, мы можем видеть, что 1 Q . Утверждение «P не является подмножеством Q» обозначается:
Обратите внимание, что эти множества имеют некоторые общие элементы.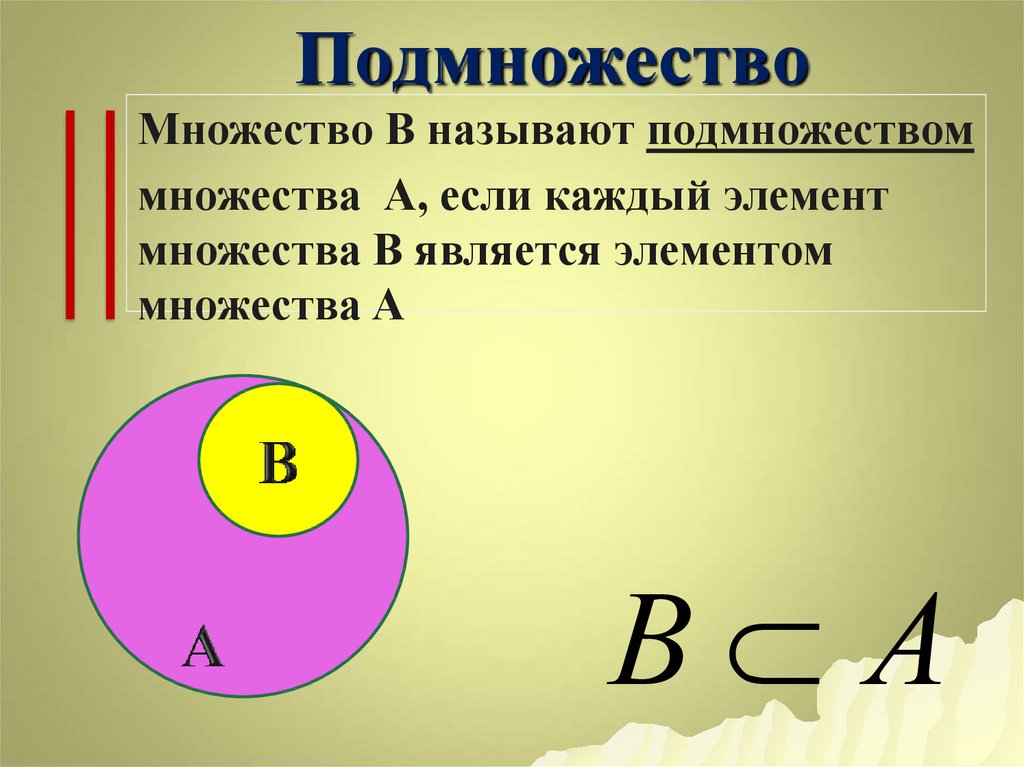
Пересечение этих множеств показано на диаграмме Венна ниже.
Ответ: P не является подмножеством Q .
Обозначения для подмножеств показаны ниже.
| Символ | Значение |
| является подмножеством | |
| не является подмножеством |
Пример 4: Даны A = {1, 2, 3, 4, 5} и B = {3, 1, 2, 5, 4}, какая связь между A и B ?
Анализ: Напомним, что порядок, в котором элементы появляются в наборе, не важен. Глядя на элементы этих наборов, становится ясно, что:
Ответ: A и B эквивалентны.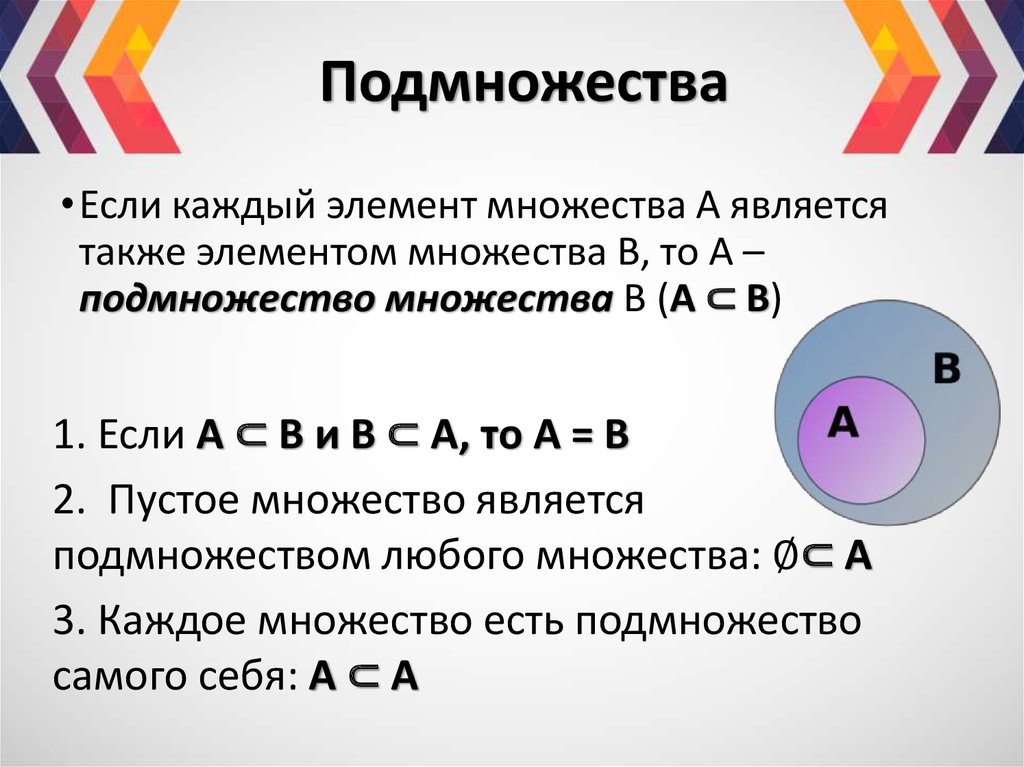
Определение: Для любых двух наборов, если A B и B A, , то 9 0008 A = B. Таким образом, A и B эквивалентны.
Пример 5: Список всех подмножеств набора C = {1, 2, 3}.
Ответ:
| Подмножество | Список всех возможных комбинаций элементов … |
| Д = {1} | по одному |
| E = {2} | по одному |
| Ф = {3} | по одному |
| G = {1, 2} | два за раз |
| M = {1, 3} | два за раз |
| N = {2, 3} | два за раз |
| P = {1, 2, 3} | три за раз |
| Ø | Пустой набор не содержит элементов. |
Глядя на пример 5, вы можете удивиться, почему нулевой набор указан как подмножество C. В нулевом наборе нет элементов, поэтому в нулевом наборе не может быть элементов, которые не являются содержится в комплекте. Следовательно, нулевой набор является подмножеством каждого набора. Вам также может быть интересно: является ли множество подмножеством самого себя? Ответ положительный: любое множество содержит себя как подмножество. Это обозначается как:
A A.
Подмножество, которое меньше полного набора, называется правильным подмножеством . Таким образом, набор {1, 2} является правильным подмножеством набора {1, 2, 3}, поскольку элемент 3 не входит в первый набор. В примере 5 видно, что G является правильным подмножеством C . На самом деле каждое подмножество, указанное в примере 5, является правильным подмножеством C, , кроме P .
Это связано с тем, что P и C являются эквивалентными множествами ( P = C ) . Некоторые математики используют символ для обозначения подмножества и символ для обозначения правильного подмножества, с определением для правильных подмножеств следующим образом:
If A B и A ≠ B , тогда A называется собственным подмножеством B и обозначается A B .
Несмотря на то, что указанная выше информация важна, она может немного запутать. Итак, давайте подумаем о подмножествах и надлежащих подмножествах следующим образом:
| Подмножества и правильные подмножества |
| Множество {1, 2} является правильным подмножеством множества {1, 2, 3}. |
Множество {1, 2, 3} не является правильным подмножеством множества {1, 2, 3}. |
Видите ли вы закономерность в приведенных ниже примерах?
Пример 6: Список всех подмножеств набора R = {x, y, z}. Сколько их там?
| Подмножества |
| D = {x} |
| E = {г} |
| F = {z} |
| G = {х, у} |
| Н = {х, г} |
| J = {у, г} |
| К = {х, у, г} |
| Ø |
Ответ: Существует восемь подмножеств множества R = {x, y, z}.
Пример 7: Список всех подмножеств набора C = {1, 2, 3, 4}. Сколько их там?
| Подмножества | |
| Д = {1} | М = {2, 4} |
| E = {2} | N = {3, 4} |
| Ф = {3} | О = {1, 2, 3} |
| Г = {4} | P = {1, 2, 4} |
| H = {1, 2} | Q = {1, 3, 4} |
| J = {1, 3} | Ч = {2, 3, 4} |
| К = {1, 4} | S = {1, 2, 3, 4} |
| Л = {2, 3} | Ø |
Ответ: Существует 16 подмножеств множества C = {1, 2, 3, 4}.
В примере 6 набор R состоит из трех (3) элементов и восьми (8) подмножеств. В примере 7 набор C состоит из четырех (4) элементов и 16 подмножеств. Чтобы найти количество подмножеств множества из n элементов, возведите 2 в n-ю степень: То есть:
Количество подмножеств в наборе A равно 2 n , где n — количество элементов в наборе A.
Итоги урока 9000 3
Подмножество: A есть подмножество B: , если каждый элемент A содержится в B . Обозначается A B.
Эквивалентные наборы: Для любых двух наборов, если A B и B A, , затем A = B.
Нулевой набор: Нулевой набор является подмножеством каждого набора .
Наборы и подмножества: Любой набор содержит себя как подмножество.
Это обозначается A A.
Правильные подмножества: If A B и A 9000 8 ≠ B , тогда A называется правильным подмножеством Б и обозначается A B .
Количество подмножеств: Количество подмножеств в наборе A равно 2 n , где n — количество элементов в наборе A.
Упражнения 9002 5
Указания: Прочитайте каждый вопрос ниже. Выберите свой ответ, нажав на его кнопку. Обратная связь по вашему ответу представлена в ОКНО РЕЗУЛЬТАТЫ. Если вы допустили ошибку, обдумайте свой ответ еще раз, а затем выберите другую кнопку.
| 1. | Что из следующего является подмножеством множества G? G = {d, a, r, e} |
| X = {e, a, r} Y = {e, r, a} Z = {r, e, d} Все вышеперечисленное.  ОКНО РЕЗУЛЬТАТОВ: |
| 2. | Какое из следующих утверждений верно? |
| {гласные} {согласные} {согласные} {гласные} {гласные} {алфавит} Ничего из вышеперечисленного. ОКНО РЕЗУЛЬТАТОВ: |
| 3. | Что из нижеперечисленного НЕ является подмножеством набора A? А = {2, 3, 5, 7, 11} |
| B = {3, 5, 2, 7} C = {2, 3, 7, 9} D = {7, 2, 3, 11} Все вышеперечисленное. ОКНО РЕЗУЛЬТАТОВ: |
4. |