Примеры решение производных: Примеры решения производных с ответами

Примеры решения производных с ответами

Простое объяснение принципов решения производных и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.

Алгоритм решения производных

Теорема

Производная функции есть предел отношения приращения этой функции к приращению её аргумента при стремлении последнего к нулю, при условии существования данного предела.

Для вычисления производных вам потребуется таблица производных. Кроме того, существуют формулы для нахождения сложных производных.

Процесс нахождения производный называется дифференцированием.

– производная суммы (разницы).

– производная произведения.

– производная частного.

Нужна помощь в написании работы?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Цена работы

Примеры решений производных

Пример 1

Задача

Найти производную функции

Решение

Заданная функция является сложной и её производная равна произведению производной от косинуса на производную от его аргумента:

Ответ

Пример 2

Задание

Найти производную функции

Решение

Обозначим , где . 3·cos(x)+6·x·cos(x)-6·cos(x)+6·sin(x).

Пример 5

Задача

Найти производную функции .

Решение

В этом примере квадратный корень извлекается из суммы . Поэтому сначала вычисляем производную от квадратного корня, а затем умножаем ее на производную от подкоренного выражения:
.

Ответ

.

Пример 6

Задача

Найти производную функции .

Решение

Применяя правила дифференцирования дробей, получаем:

.
Применяя правила дифференцирования котангенса, получаем:
.
Учитывая, что и , после упрощения получим:
.

Ответ

.

Пример 7

Задача

Найти производную функции .

Решение

Применяя правила дифференцирования дробей, получаем:
.

Ответ

.

Пример 8

Задача

Найти производную функции .

Решение

Применяя правила дифференцирования дробей, получаем:
.

Ответ

.

Пример 9

Задача

Найти производную функции .

Решение

Дифференцирование можно произвести в два этапа: вначале продифференцировать степень функции арксинус, а затем произвести дифференцирование самого арксинуса, перемножив результаты:
.

Ответ

.

Пример 10

Задача

Найти производную функции .

Решение

По правилам дифференцирования показательной функции с основанием , производная этой функции равна произведению самой функции на производную функции, являющейся показателем степени:
.

Ответ

.

Средняя оценка 2. 5 / 5. Количество оценок: 128

Поставьте вашу оценку

Сожалеем, что вы поставили низкую оценку!

Позвольте нам стать лучше!

Расскажите, как нам стать лучше?

126092

Закажите помощь с работой

Не отобразилась форма расчета стоимости? Переходи по ссылке

Не отобразилась форма расчета стоимости? Переходи по ссылке

Полезно

примеры решения производных

Производная функции является основным понятием дифференциального исчисления. Она характеризует скорость изменения функции в указанной точке. Производная широко используется при решении целого ряда задач по математике, физике и другим наукам, в особенности при изучении скорости различного рода процессов. Именно поэтому мы собрали на сайте более 200 примеров решения производных и постоянно добавляем новые! Список тем находится в правом меню.

Перед изучением примеров вычисления производных советуем изучить теоретический материал по теме: прочитать определения, правила дифференцирования, таблицу производных и другой материал по производным.

Таблица производных и правила дифференцирования

Основные ссылки — таблица производных, правила дифференцирования и примеры решений (10 шт).

Пример

Задание. Найти производную функции

Решение. Так как производная суммы равна сумме производных, то

Воспользуемся формулами для производных показательной и обратной тригонометрической функций:

Ответ.

Больше примеров решений →

Производные сложных функций

Основные ссылки — теоретический материал и примеры решений (10 шт).

Пример

Задание.Найти производную функции

Решение. По правилу дифференцирования сложной функции:

В свою очередь производная также берется по правилу дифференцирования сложной функции:

Ответ.

Больше примеров решений →

Применение дифференциала в приближенных вычислениях

Основные ссылки — теоретический материал и примеры решений (10 шт).

Пример

Задание. Вычислить приближенно , заменяя приращение функции ее дифференциалом.

Решение. Рассмотрим функцию . Необходимо вычислить ее значение в точке . Представим данное значение в виде следующей суммы:

Величины и выбираются так, чтобы в точке можно было бы достаточно легко вычислить значение функции и ее производной, а было бы достаточно малой величиной. С учетом этого, делаем вывод, что , то есть , .

Вычислим значение функции в точке :

Далее продифференцируем рассматриваемую функцию и найдем значение :

Тогда

Итак,

Ответ.

Больше примеров решений →

Геометрический смысл производной

Основные ссылки — теоретический материал и примеры решений (10 шт).

Пример

Задание. Найти тангенс угла наклона касательной к графику функции в точке .

Решение. Из геометрического смысла производной получаем, что производная функции , вычисленная при заданном значении , равна тангенсу угла, образованного положительным направлением оси и положительным направлением касательной, проведенной к графику этой функции в точке с абсциссой , то есть

Найдем производную от заданной функции:

в точке имеем:

Тогда окончательно получим, что

Ответ.

Больше примеров решений →

Механический смысл производной

Основные ссылки — теоретический материал и примеры решений (10 шт).

Пример

Задание. Точка движется по закону . Чему равна скорость в момент времени ?

Решение. Найдем скорость точки как первую производную от перемещения:

В момент времени скорость равна

Ответ.

Больше примеров решений →

Уравнение касательной, нормали и угол между прямыми

Основные ссылки — теоретический материал и примеры решений (10 шт).

Пример

Задание. Записать уравнение касательной к графику функции в точке

Решение. Найдем значение функции в заданной точке:

Найдем производную заданной функции по правилу дифференцирования произведения:

Вычислим её значение в заданной точке

Используя формулу

запишем уравнение касательной:

Ответ. Уравнение касательной:

Больше примеров решений →

Производные высших порядков

Основные ссылки — теоретический материал и примеры решений (10 шт).

Пример

Задание. Найти производную второго порядка от функции

Решение. Находим первую производную как производную сложной функции:

Вторую производную находим как от произведения, предварительно вынеся по правилам дифференцирования коэффициент 3 за знак производной. Также будем учитывать, что первый множитель — — есть сложной функцией:

Ответ.

Больше примеров решений →

Механическое смысл второй производной

Основные ссылки — теоретический материал и примеры решений (10 шт).

Пример

Задание. Уравнение движения материальной точки вдоль оси имеет вид (м). Найти ускорение точки в момент времени c.

Решение. Ускорение заданной точки найдем, взяв вторую производную от перемещения по времени:

Первая производная

(м/с)

вторая производная

(м/с²)

В момент времени c

(м/с²)

Ответ. (м/с²)

Больше примеров решений →

Дифференциалы высших порядков

Основные ссылки — теоретический материал и примеры решений (10 шт).

Пример

Задание. Найти дифференциал третьего порядка функции

Решение. По формуле

Найдем третью производную заданной функции:

Тогда

Ответ.

Больше примеров решений →

Производная функции, заданной неявно

Основные ссылки — теоретический материал и примеры решений (10 шт).

Пример

Задание. Найти производную неявно заданной функции

Решение. Продифференцируем обе части данного выражения по , учитывая, что функция от и производная от неё берется как от сложной функции.

Выразим из этого равенства

Ответ.

Больше примеров решений →

Производная функции, заданной параметрически

Основные ссылки — теоретический материал и примеры решений (10 шт).

Пример

Задание. Найти производную от функции заданной параметрически

Решение. Найдем производные и

Подставляя найденные значения и в формулу

получим

Ответ.

Больше примеров решений →

Логарифмическое дифференцирование

Основные ссылки — теоретический материал и примеры решений (10 шт).

Пример

Задание. Найти производную функции

Решение. Применим логарифмическое дифференцирование:

Тогда, продифференцировав левую и правую часть, будем иметь:

Отсюда получаем, что

Ответ.

Больше примеров решений →

Формулы Маклорена и Тейлора

Основные ссылки — теоретический материал и примеры решений (10 шт).

Пример

Задание. Разложить в ряд Тейлора функцию в точке .

Решение. Найдем производные:

Итак, , , . Значение функции в точке

Таким образом,

Ответ.

Больше примеров решений →

Вы поняли, как решать? Нет?

Производные – исчисление, значение, интерпретация

Производная в исчислении – это скорость изменения величины y по отношению к другой величине x. Его также называют дифференциальным коэффициентом y по отношению к x. Дифференцирование – это процесс нахождения производной функции.

Давайте узнаем, что именно означает производная в исчислении и как ее найти вместе с правилами и примерами.

1.	Значение производных в исчислении
2.	Интерпретация производных финансовых инструментов
3.	Производная функции, использующая первый принцип
4.	Производные формулы в исчислении
5.	Основные правила деривативов
6.	Производные сложных функций (цепное правило)
7.	Производные неявных функций
8.	Параметрические производные
9.	Производные высшего порядка
10.	Частные производные
11.	Нахождение производной с помощью логарифмического дифференцирования
12.	Максимум/минимум с использованием производных
13.	Часто задаваемые вопросы о деривативах

Значение производных в исчислении

Производная функции f(x) обычно представляется как d/dx (f(x)) (или) df/dx (или) Df(x) (или) f'(x). Давайте посмотрим, что технически означает производная. Рассмотрим кривую функции f(x) и пусть две точки на ней будут (x, f(x)) и ((x + h), f(x + h)). Тогда наклон секущей, проходящей через эти точки, равен [f(x + h) — f(x)]/(x + h — x) = [f(x + h) — f(x)/h. Посмотрите на рисунок ниже и обратите внимание, что когда расстояние между двумя точками почти равно 0 (т. е. когда h приближается к 0), вторая точка перекрывает исходную точку, а секущая становится касательной. В исчислении наклон касательной называется производной функции. то есть

• Производная функции, f ‘(x) = Наклон касательной = lim _h→0 [f(x + h) — f(x) / h.

Эта формула широко известна как «предельное определение производной» (или) «производной по первому принципу».

Интерпретация производных финансовых инструментов

Производная функции f(x) в математике обозначается f'(x) и может быть контекстуально интерпретирована следующим образом:

• Производная функции в точке представляет собой наклон касательной, проведенной к этой кривой в таком случае.
• Также представляет мгновенную скорость изменения в точке функции.
• Скорость частицы находится путем нахождения производной функции смещения.
• Производные используются для оптимизации (максимизации/минимизации) функции.
• Они также используются для нахождения интервалов возрастания/убывания функции, а также интервалов вогнутости функции вверх/вниз.

Таким образом, всякий раз, когда мы видим такие фразы, как «наклон/градиент», «скорость изменения», «скорость (учитывая смещение)», «максимизировать/минимизировать» и т. д., это означает, что используется понятие производных.

Производная функции, использующая первый принцип

Производная функции может быть получена с помощью предельного определения производной: f'(x) = lim _h→0 [f(x + h) — f(x) / h. Этот процесс известен как дифференцирование по первому принципу. Пусть f(x) = x ² , и мы найдем его производную, используя приведенную выше формулу производной. Здесь f(x + h) = (x + h) ² , так как f(x) = x ² . Тогда производная от f(x) равна

f ‘(x) = lim _h→0 [(x + h) ² — x ² ] / h
= lim _{ч → 0} [ х ² + 2xh + ч ² — х ² ] / ч
= lim _{ч → 0} [ 2xh + ч ² ] / ч
= lim _{ч → 0} [ч(2x + ч)] / ч
= lim _ч→0 (2x + ч)
= 2х + 0
= 2x

Таким образом, производная x ² равна 2x. Но может быть трудно использовать это предельное определение для нахождения производных сложных функций. Таким образом, есть некоторые производные формулы (конечно, производные от приведенного выше определения предела), которые мы можем легко использовать в процессе дифференцирования.

Производные формулы в исчислении

Три основные производные алгебраической, логарифмической/экспоненциальной и тригонометрической функций выводятся из первого принципа дифференцирования и используются как стандартные формулы производных. Они следующие.

Степенное правило производных

Используя приведенный выше пример, производная x ² равна 2x. Точно так же мы можем доказать, что производная x ³ равна 3x ^{2 9x is, d/dx (a x ) = a x ln a}

Производные тригонометрических функций

Здесь представлены производные тригонометрических функций.

• Если y = sin x, y’ = cos x
• Если y = cos x, y’ = -sin x
• Если y = tan x, y’ = sec ² x
• Если y = cot x, y’ = -cosec ² x
• Если y = сек x, y’ = сек x тангенс x
• Если y = cosec x, y’ = -cosec x cot x

Производные обратных тригонометрических функций

Здесь представлены производные обратных тригонометрических функций.

• Производная обратного синуса, d/dx (sin ^-1 x) = 1/√(1-x ² )
• Производная арккосинуса равна d/dx (cos ^-1 x) = -1/√(1-x ² )
• Производная обратного тангенса, d/dx (тангенс ^-1 х) = 1/(1 + х ² )
• Производная обратной кроватки равна d/dx (кроватка ^-1 х) = -1/(1 + х ² )
• Производная обратного коэффицента, d/dx (csc ^-1 x) = -1/ [|x| √(х ² — 1) ], х ≠ 1, -1, 0
• Производная обратной сек, d/dx (сек ^-1 x) = 1/ [|x| √(х ² — 1) ], х ≠ 1, -1, 0

Основные правила деривативов

Ниже приведены основные правила производных. Давайте обсудим их подробно.

Степенное правило: По этому правилу, если y = x ⁿ , то dy/dx = n x ^n-1 . Пример: d/dx (x ⁵ ) = 5x ⁴ .

Правило суммы/разности: Процесс производной можно распределить на сложение/вычитание. т. е. dy/dx [u ± v] = du/dx ± dv/dx.

Правило произведения: Правило произведения производных гласит, что если функция является произведением двух функций, то ее производная есть производная второй функции, умноженная на первую функцию, прибавленная к производной первой функции, умноженной на вторая функция. dy/dx [u × v] = u · dv/dx + v · du/dx. Если у = х ⁵ e ^x , мы имеем y’ = x ⁵ . е ^х + е ^х . 5x ⁴ = e ^x (x ⁵ + 5x ⁴ )

Правило частных: Правило частных производных утверждает, что d/dx (u/v) = (v · du/dx — u · dv/dx)/ v ²

Правило постоянных кратных: Правило постоянных кратных производных утверждает, что d/dx [c(f(x)] = c · d/dx f(x), т. е. , константа, которая при умножении на функцию получается в результате дифференцирования, например, d/dx (5x ² ) = 5 д/дх (х ² ) = 5(2х) = 10х.

Правило констант: Правило констант производных утверждает, что производная любой константы равна 0. Если y = k, где k — константа, то dy/dx = 0. Предположим, что y = 4, y’ = 0. Это правило непосредственно следует из правила мощности.

Производные составных функций (цепное правило)

Если f и g — дифференцируемые функции в своей области определения, то f(g(x)) также дифференцируема. Это известно как цепное правило дифференцирования, используемое для составных функций. (туман)'(x) = f'[(g(x)] g'(x). Это также можно записать как «если y = f(u) и u = g(x) , то dy/dx = dy/du · du/dx.

Например, рассмотрим y = tan ² x. Это составная функция. Мы можем записать эту функцию как y = u ² , где u = tan x. Тогда

dy/dx = 2u

du/dx = d/dx (tan x) = sec ² x

По цепному правилу

dy/dx = dy/du · du/dx

= 2u · сек ² x

= 2 тан x сек ² x

Производные неявных функций

В уравнениях, где y как функция x не может быть явно определена переменными x и y, используется неявное дифференцирование. Если f(x, y) = 0, то продифференцируйте обе стороны по x и сгруппируйте члены, содержащие dy/dx, с одной стороны, а затем найдите dy/dx.

Например, 2x + y = 12

d/dx(2x + y) = d/dx(0)

2 + dy/dx = 0

dy/dx = -2

Параметрические производные

В функции у нас могут быть зависимые переменные x и y, которые зависят от третьей независимой переменной. Если x = f(t) и y = g(t), то производная вычисляется как dy/dx = f'(x)/g'(x). Предположим, что если x = 4 + t ² и y = 4t ² -5t ⁴ , то мы находим dy/dx следующим образом.

dx/dt = 2t и dy/dt = 8t -20t ³

dy/dx = (dy/dt)/(dx/dt)

dy/dx = (8t -20t ³ )/ 2т

= 2т (4 — 10т ² ) / 2т

dy/dx = 4 — 10т ²

Производные высшего порядка

Мы можем найти последовательные производные функции и получить производные более высокого порядка. Если y — функция, то ее первая производная равна dy/dx. Вторая производная d/dx (dy/dx), которую также можно записать как d ² у/дх ² . Третья производная d/dx (d ² y/dx ² ) и обозначается как d ³ y/dx ³ и так далее.

В качестве альтернативы первая, вторая и третья производные f(x) могут быть записаны как f'(x), f»(x) и f»'(x). Для производных более высокого порядка мы пишем число в скобках как показатель степени. Предположим, что y = 4x ³ , мы получаем последовательные производные следующим образом. y’ = 12x ² , y» = 24 x и y»’ = 24, y ⁽⁴⁾ = 0.

Частные производные

Если u = f(x,y), мы можем найти частную производную по y, оставив x константой, или мы можем найти частную производную по x, оставив y константой. Предположим, что f(x, y) = x ³ y ² , частные производные функции:

∂f/∂y(x ³ y ² ) = х ³ 2г

Кроме того, мы можем найти частные производные второго порядка также как и ∂ ² f/∂y ∂x.

Нахождение производной с помощью логарифмического дифференцирования

Иногда функции слишком сложны, чтобы найти производные (или) одна функция может быть возведена в другую функцию, например y = f(x) ^g(x) . В таких случаях мы можем взять log (или) ln с обеих сторон, применить логарифмические правила, а затем дифференцировать обе стороны, чтобы получить dy/dx. Этот процесс известен как логарифмическое дифференцирование в исчислении.

Пример: Найдите производную от y = x ^x .

Решение:

Применив ln с обеих сторон,

ln y = ln x ^x

ln y = x ln x

Взяв производную с обеих сторон,

3 1

(1/x) + ln x (1) (цепное правило слева и правило произведения справа)

1/y dy/dx = 1 + ln x

dy/dx = y (1 + ln x ) = х ^х (1 + ln х)

Максимум/минимум с использованием производных

Понятие наклона и, следовательно, производных используется для нахождения максимального или минимального значения функции.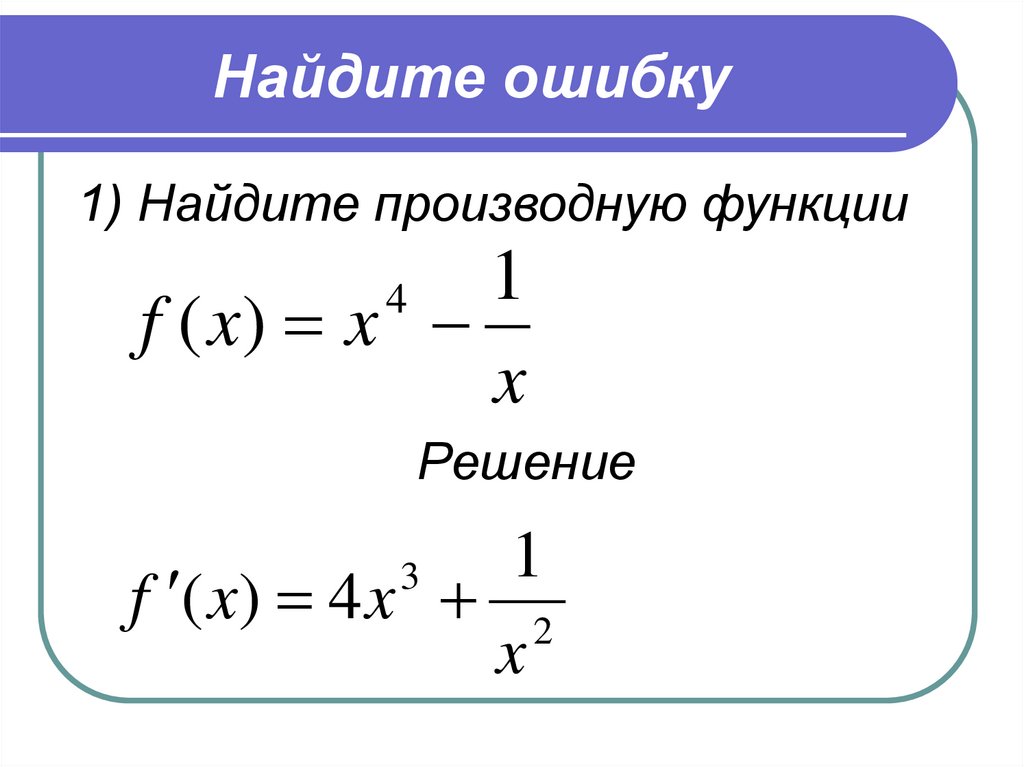 Есть два теста, которые используют производные и используются для нахождения максимумов/минимумов функции. Они

• тест первой производной
• тест второй производной

Тест первой производной

Мы можем просто использовать первую производную для определения максимума или минимума, соблюдая следующие пункты:

• f'(x) представляет наклон касательной.
• Следовательно, если f'(x) > 0, функция возрастает, а если f'(x) < 0, функция убывает.
• Если f'(x) > 0 меняется на f'(x) < 0 в какой-либо точке, то функция имеет локальный максимум в этой точке.
• Если f'(x) < 0 меняется на f'(x) > 0 в какой-то точке, то функция имеет минимум в этой точке.
• Обратите внимание, что f'(x) = 0 в локальном максимуме и локальном минимуме.

Тест второй производной

Тест второй производной использует критические точки и вторую производную для нахождения максимума/минимума. Чтобы выполнить этот тест:

• Найдите критические точки, установив f'(x) = 0,
• Подставьте каждое из них в f»(x). Если f»(x) < 0, то функция максимальна в этой точке, а если f''(x)>0, то функция в этой точке минимальна.
• Если f»(x) = 0, функция не имеет ни максимума, ни минимума в этой точке, и в этом случае она называется точкой перегиба.

Важные замечания по расчету производных:

• Производная функции — это скорость изменения одной величины по сравнению с другой.
• Производная любой непрерывной функции, дифференцируемой на отрезке [a, b], выводится с использованием первого принципа дифференцирования с использованием пределов.
• Если f(x) задано, то его производная равна f'(x) = lim _h→0 [f(x + h) — f(x) / h.
• Каждая дифференцируемая функция непрерывна, но обратное может быть неверным.

☛ Статьи по теме:

• Расчетный калькулятор
• Калькулятор производных
• Калькулятор второй производной

Часто задаваемые вопросы о деривативах

Что такое производные в исчислении?

Производная в исчислении — это мгновенная скорость изменения функции по отношению к другой переменной. Дифференцирование – это процесс нахождения производной функции. Производная функции совпадает с наклоном касательной, скоростью изменения и т. д.

Определить производную.

Производная f(x) при x = a определяется выражением f'(x) = lim _h→0 [f(x + h) — f(x)] / h. Это наклон касательной к функции f(x). В этой формуле [f(x + h) — f(x)]/h называется разностным коэффициентом.

Как найти производные?

Производные функций в математике находятся с использованием определения производной из первого фундаментального принципа дифференцирования. Если f(x) — заданная функция, ее производная получается с использованием f'(x) = lim _ч→0 [f(x + h) — f(x)] / ч. Многие правила выводятся с использованием этого определения предела, которое можно напрямую использовать для поиска производных без использования пределов.

Что такое основные производные формулы?

Формулы основных производных: d/dx (x ⁿ ) = nx ^n-1 , d/dx (ln x) = 1/x, d/dx (e ^x ) = e ^x , d/dx (a ^x ) = a ^x ln a, d/dx (sin x) = cos x, d/dx (cos x) = — sin x, d/dx (tan x) = сек ² х.

Сложно ли вычислять производные?

Процесс нахождения производных с использованием определения предела немного сложен. Чтобы сделать это проще, мы используем правила, полученные с помощью формулы. Пока мы можем помнить правила, процесс нахождения производных в исчислении очень прост, если немного попрактиковаться.

Каково применение деривативов в реальной жизни?

В реальной жизни деривативы могут использоваться по-разному. Скорость изменения функции по отношению к другой величине называется производной. Чтобы проверить, является ли функция возрастающей или убывающей, чтобы найти уравнение касательной / нормали, чтобы найти максимальное и минимальное значения на графике, чтобы найти задачи смещения-движения, найти скорость при заданном смещении, найти заданное ускорение смещение и так далее.

Что такое производный пример?

Скорость — это мгновенная скорость изменения расстояния, пройденного объектом в определенное время. Первая производная от смещения объекта есть его скорость. Вторая производная смещения — это ускорение объекта. Третья производная смещения — это рывок объекта и так далее.

В чем разница между производными и дифференцированием в исчислении?

Производная функции f(x) в точке есть не что иное, как наклон тангенса функции в этой точке и находится по пределу f'(x) = lim _ч→0 [f(x + h) — f(x)] / ч. Дифференцирование – это процесс нахождения производных.

Производные инструменты Легкий способ

Производные инструменты Легкий способ

 Постоянное правило и мощное правило

Мы видели следующие производные:

1. Если f(x) = c, то f ‘(х) = 0
   

2. Если f(x) = x, то f ‘(х) = 1
   

3. Если f(x) = x ² , то f'(х) = 2х
   

4. Если f(x) = x ³ , то f'(x) = 3x ²
   

5. Если f(x) = x ⁴ , то f'(x) = 4x ³
   

Это приводит нас к предположению следующей теоремы.

Теорема д х n   =  nx n-1 дх

Доказательство:

У нас есть

---

приложений

Пример

Найдите производные следующих функций:

1. f(x) = 4x ³ — 2x ¹⁰⁰
   

2. f(x) = 3x ⁵ + 4x ⁸ — x + 2
   

3. f(x) = (x ³ — 2) ²
   

Решение  

Мы используем наши новые производные правила, чтобы найти

1. 12x ² — 200x ⁹⁹
   

2. 15x ³ +32x ⁷ -1
   

3. Сначала мы ФОЛЬГА, чтобы получить

   [х ⁶ — 4х ³ + 4] ‘ 
   
   Теперь используйте производное правило для степеней

   .

   No related posts.