7. 3 Примеры решения задач.
№1 Найти
Решение . Данный интеграл не является табличным. Умножив на и на (3) одновременно подинтегральное выражение, получим:
d3x
№ 2. Найти интеграл:
Решение. Используем интегрирование по частям, т.е используем формулу:
Имеем:
№ 3. Найти интеграл:
Решение: Используем подстановку , чтобы сделать подынтегральное выражение рациональным (без корня).
Итак,
Тогда J примет вид:
Использованы операции:
1.
Замена
Вынесен постоянный множитель 2.
Умножим и разделим на (-1).
В числителе подынтегральной дроби прибавили (+1) и (-1).
Использовано свойство:
Применили табличные формулы:
7 .
Вопросы для самопроверки.
Дайте определение первообразной функции неопределённого интеграла. Приведите примеры.
Сформулировать свойства неопределённого интеграла.
В чём заключается геометрический смысл неопределённого интеграла?
Назовите основные методы интегрирования.
Решите: методом подстановки.
Примените формулу интегрирования по частям к интегралу:
Объяснить, почему ∫x2cos x3dx решается способом подведения функции под знак дифференциала. Можно ли решить этот интеграл методом подстановки?
Тема 8. Определённый интеграл по отрезку.
Определение: Определённым интегралом по отрезку
еЧисла a,b называются соответственно нижним и верхним пределами интегрирования, т.е a;b-отрезок интегрирования.
Свойства определённого интеграла по a;b.
1.
2.
3.
4.
5. С- постоянная
Правила вычисления определённого интеграла по a;b
1
функция для f(x),
. — формула Ньютона-Лейбница, где F(x)- первообразная
2. — интегрирование по частям.
3.
, где x=(t)
функция непрерывная вместе со своей
производной
на ;
Например: Найти значение определённого интеграла
Решение:
Решаем методом подстановки
x | 1 | e |
t | 0 | 1 |
Положим
Тогда
Несобственные интегралы.
К несобственным интегралам относятся:
Интегралы с бесконечными пределами интегрирования вида:
Интегралы от разрывных функций (от неограниченных функций).
Пример 1. — несобственный интеграл 2) типа, т.к на отрезке -2;9 функция терпит бесконечный разрыв в точке x=0.
Пример 2. Вычислить
Решение
Пример 3. Вычислить
Решение:
Т.к — чётная функция.
Тогда
Замечание.Если предел несобственного интеграла существует и конечен, то несобственный интеграл называется сходящимся.
Если же предел не существует или равен бесконечности, то интеграл называется расходящимся.
Видео-урок: Неопределенные интегралы и задачи с начальными значениями
Стенограмма видео
В этом видео мы научимся
использовать интеграцию, чтобы найти конкретные решения проблем с начальными значениями, включающими
дифференциальные уравнения вида d𝑦 на d𝑥 равно 𝑓 из 𝑥.
Начнем с того, как
интегрирование может помочь нам с дифференциальными уравнениями. Вот простой дифференциал
уравнение. d𝑦 на d𝑥 равно трем 𝑥 в квадрате плюс четыре. Другими словами, есть некоторые
функция 𝑦 в терминах 𝑥, что, когда мы дифференцируем ее по 𝑥, мы заканчиваем
с его производной, равной трем 𝑥 в квадрате плюс четыре. Но тогда мы вспоминаем, что
интеграция и дифференциация являются процессами, обратными друг другу. Другими словами, если мы интегрируем
этой функции, ее производной по 𝑥, мы придем к общему
решение дифференциального уравнения.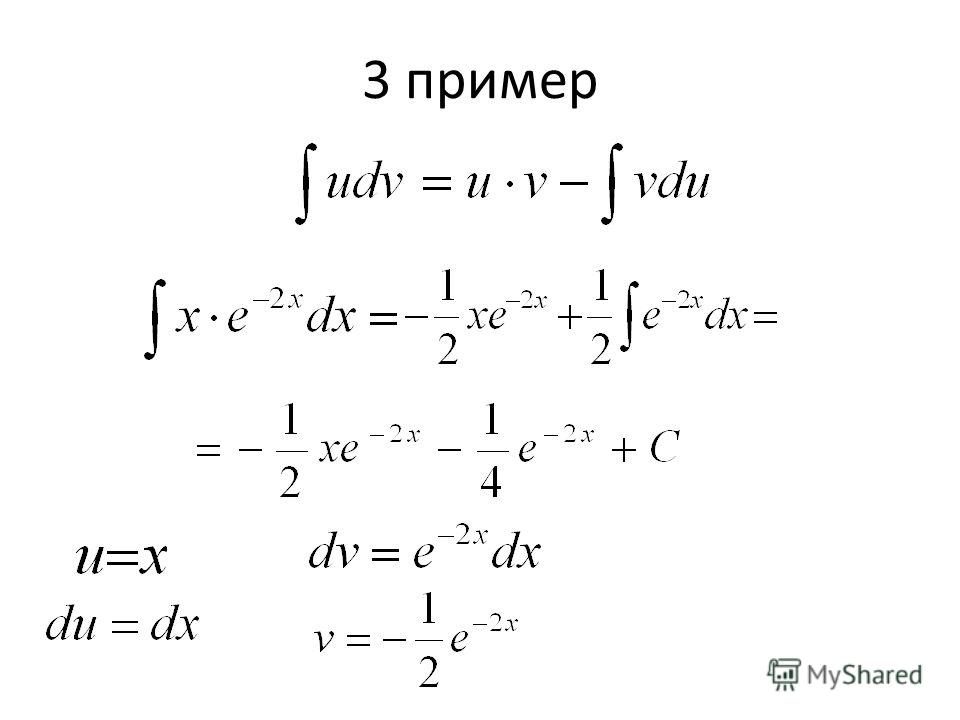
В этом случае 𝑦 собирается быть равным неопределенному интегралу от трех 𝑥 в квадрате плюс четыре относительно 𝑥. Затем напомним, что для интегрирования членов полинома, мы прибавляем единицу к степени, а затем делим на это новое число. Предполагая, что показатель степени не равен к отрицательному. Итак, интеграл от трех 𝑥 в квадрате это три 𝑥 в кубе, деленные на три. И интеграл от четырех равен четырем умноженное на 𝑥 в степени единицы, деленной на единицу. И конечно, так как мы работаем с неопределенным интегралом у нас есть константа интегрирования 𝑐. Упрощая, мы видим, что 𝑦 равно 𝑥 в кубе плюс четыре 𝑥 плюс 𝑐.
Это общее решение нашей
дифференциальное уравнение. Но как насчет его конкретного
решение? Другими словами, как мы работаем
значение 𝑐? Итак, нам нужно начальное значение.
Давайте посмотрим на простой
проблема с начальным значением.
Найти конкретное решение для следующее дифференциальное уравнение, для которого 𝑦 нуля равно 12. d𝑦 на d𝑥 равно восемь 𝑥 плюс три.
Помните, мы можем найти генерала решение дифференциального уравнения d𝑦 по d𝑥 равно восьми 𝑥 плюс три по сначала выполняя обратный процесс для дифференциации. Мы собираемся интегрировать наши функция для d𝑦 через d𝑥 относительно 𝑥. Итак, 𝑦 равно неопределенному интеграл от d𝑦 по d𝑥 по 𝑥. Или 𝑦 равно интегралу от восьми 𝑥 плюс три относительно 𝑥. Тогда вспомним, что интеграл от многочлен вида 𝑎𝑥 в 𝑛-й степени, где 𝑎 и 𝑛 действительны константы и 𝑛 не равно отрицательной единице, 𝑎𝑥 в степени 𝑛 плюс один над 𝑛 плюс единица плюс некоторая постоянная интегрирования 𝑐.
По сути, мы добавляем единицу к
степени, а затем разделить на это новое число.
Это означает интеграл от восьми 𝑥
это восемь 𝑥 в квадрате над двумя. Тогда интеграл от трех равен трем
𝑥. И, конечно же, поскольку это
неопределенный интеграл, мы получаем эту постоянную интегрирования 𝑐. Итак, мы получили общее решение
нашего дифференциального уравнения 𝑦 равно четырем 𝑥 в квадрате плюс три 𝑥 плюс
𝑐.
Теперь вернемся к
вопрос. Нам сказали, что 𝑦 нуля равно
12. Другими словами, в какой-то момент
уравнение 𝑦 равно 𝑓 из 𝑥, когда 𝑥 равно нулю, 𝑦 равно 12. Подставим эти значения в
наше уравнение и посмотрим, что произойдет. Получаем 12 равно четыре раза ноль
в квадрате плюс трижды ноль плюс 𝑐. Ну, все это уравнение
упрощается до 12 равно 𝑐. И это здорово, потому что теперь мы
узнать значение нашей константы. И поэтому мы можем сказать, что 𝑦
равно четырем 𝑥 в квадрате плюс три 𝑥 плюс 12.
Это известно как особый решение. А 𝑦 нуля равно 12 — это Начальное значение. Их иногда называют начальными проблемы ценности, поскольку они позволяют нам найти конкретное решение, давая нам результат определенного 𝑥-значения.
Давайте теперь посмотрим на другой пример.
Найдите решение для следующего дифференциальное уравнение для 𝑦 нуля равно единице. d𝑦 на d𝑥 минус 𝑥 минус 𝑥 квадрат равен нулю.
В этом вопросе у нас есть
дифференциальное уравнение и начальное значение. То есть, когда 𝑥 равно нулю,
𝑦 равно единице. Теперь, прежде чем мы сможем решить
это дифференциальное уравнение, нам нужно будет выполнить промежуточный шаг. Мы собираемся переставить и сделать
d𝑦 по d𝑥 теме. Сейчас не особо
добиться этого трудно. Мы добавляем 𝑥 и 𝑥 в квадрат к обоим
сторон нашего дифференциального уравнения, чтобы найти, что d𝑦 на d𝑥 равно 𝑥 в квадрате плюс
𝑥.
Теперь, помните, мы можем найти
общее решение дифференциального уравнения d𝑦 на d𝑥 равно 𝑥 в квадрате плюс 𝑥
путем выполнения процесса, обратного дифференцированию. Мы собираемся интегрироваться с
уважение к 𝑥. Таким образом, 𝑦 будет равно интегралу
d𝑦 на d𝑥 относительно 𝑥 или интеграл от квадрата 𝑥 плюс 𝑥 относительно
к 𝑥.
Помните, что для интегрирования многочлена
член, мы добавляем единицу к показателю степени, а затем делим на это новое значение. Таким образом, интеграл от 𝑥 в квадрате равен 𝑥
в кубе над тремя. Затем мы видим, что интеграл от 𝑥
равно 𝑥 в квадрате над двумя. А так как мы работаем с
неопределенные интегралы, мы знаем, что нам нужна эта постоянная интегрирования 𝑐. Итак, 𝑦 равно 𝑥 в кубе.
три плюс 𝑥 в квадрате на два плюс 𝑐. Итак, у нас есть общее решение для
наше дифференциальное уравнение.
Но мы еще не использовали
информация о том, что 𝑦 нуля равно единице. Мы собираемся заменить 𝑥 равным
ноль и 𝑦 равно единице в это общее решение. Когда мы это делаем, мы видим, что единица равна
ноль в кубе на три плюс ноль в квадрате на два плюс 𝑐. И все это уравнение упрощает
до единицы равно 𝑐. Итак, мы обнаружили, что 𝑐 равно единице. И конкретное решение для нашего
дифференциальное уравнение 𝑦 равно 𝑥 в кубе над тремя плюс 𝑥 в квадрате над двумя плюс
один.
Теперь важно понять, что мы также можем применить эту процедуру к более сложным примерам.
Найти функцию 𝑓, если 𝑓 простое 𝑡 равно двум секундам 𝑡, умноженным на тангенс 𝑡 плюс четыре секунды 𝑡, когда 𝑡 больше отрицательное 𝜋 на два и меньше 𝜋 на два и 𝑓 отрицательного 𝜋 на три минус два.
В этом вопросе у нас есть
дифференциальное уравнение.
Помните, это всего лишь уравнение
с участием производных. Здесь это 𝑓 простое число 𝑡. И нам также дается инициал
ценить. То есть, когда 𝑡 равно
отрицательное 𝜋 на три, 𝑓 из 𝑡 равно минус двум. Теперь мы пытаемся выяснить, что
функция 𝑓 есть. Итак, напомним, что интегрирование
и дифференциация являются обратными процессами. Итак, наша исходная функция 𝑓 от 𝑡
будет интегралом от 𝑓 простого числа 𝑡 относительно 𝑡. Это интеграл от двух секунд
𝑡 умножить на тангенс 𝑡 плюс четыре секунды 𝑡 по отношению к 𝑡.
Выглядит не очень
хороший. Сначала раздадим
скобки нашего подынтегрального выражения. Когда мы это делаем, мы получаем нашу функцию
𝑓 из 𝑡 равно интегралу от двух секунд 𝑡 загара 𝑡 плюс восемь секунд в квадрате 𝑡
по отношению к 𝑡. Мы можем немного упростить это
вспомнив, что интеграл от суммы двух функций равен сумме
интеграл от каждой из этих функций.
Итак, 𝑓 из 𝑡 равно
интеграл от двух секунд 𝑡 tan 𝑡 относительно 𝑡 плюс интеграл от восьми секунд
квадрат 𝑡 относительно 𝑡.
Вот это может выглядеть действительно
противный. Но давайте вспомним некоторые
производные. Мы знаем, что производная сек
𝑡 по отношению к 𝑡 является тангенсом 𝑡 сек 𝑡. А мы знаем, что производная от
тангенс 𝑡 относительно 𝑡 равен секундам в квадрате 𝑡. Это означает первообразную
тангенс 𝑡 сек 𝑡 должен быть сек 𝑡. И первообразная сек
квадрат 𝑡 должен быть рыжевато-коричневым 𝑡. Итак, интеграл двух секунд от
𝑡 загар 𝑡 должно быть две секунды 𝑡. И, конечно же, бессрочный
интеграл. Итак, мы добавим константу
интеграция 𝐴. Тогда интеграл восьми секунд
в квадрате 𝑡 должно быть восемь тан 𝑡. И мы добавим вторую константу
интеграция 𝐵. Комбинируя эти две константы
интегрирования, мы видим, что 𝑓 из 𝑡 равно двум секундам 𝑡 плюс восемь тангенсов 𝑡 плюс
𝐶.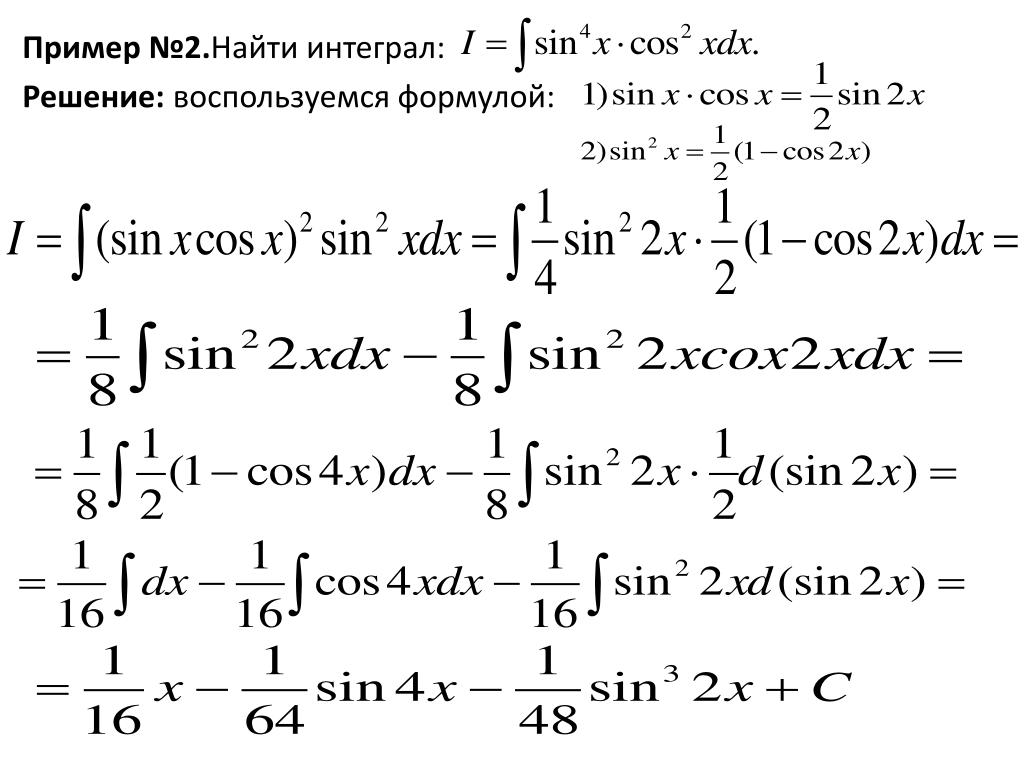
Это общее решение нашей дифференциальное уравнение. Но мы еще не использовали факт что когда 𝑡 равно отрицательному 𝜋 на три, наша функция равна отрицательной два. Итак, давайте подставим эти значения в. И когда мы это делаем, мы получаем отрицательный два равны двум секундам отрицательного 𝜋 на три плюс восемь тангенса отрицательного 𝜋 на три плюс 𝐶. Если вспомнить ту секунду отрицательного 𝜋 на три на единицу больше, чем минус 𝜋 на три. Затем две секунды отрицательного 𝜋 на три должно быть на два больше, чем отрицательный 𝜋 на три, что дает нам четыре. Затем восемь тан отрицательных 𝜋 по три минус восемь корень три. Значит минус два равно четырем минус восемь корень три плюс 𝐶.
Вычтем четыре с обеих сторон
этого уравнения и прибавьте к обеим частям восемь корней из трех. И мы видим, что 𝐶 равно
восемь корень три минус шесть.
И мы получили конкретную
решение нашего дифференциального уравнения будет 𝑓 из 𝑡 равно двум секундам 𝑡 плюс восемь
загар 𝑡 плюс восемь корень три минус шесть.
Теперь реальная сила этого процесса находится в контекстных примерах. Давайте посмотрим на один.
Ускорение, 𝑎 м/с квадратная секунда частицы в момент времени 𝑡 секунд определяется уравнением 𝑎 равно отрицательный три греха 4𝑡 для 𝑡 больше или равен нулю. Начальная скорость частица составляет три метра в секунду, а начальное перемещение частицы равно минус два метра. Найдите уравнение для смещение 𝑠 частицы за время 𝑡 секунд.
Начнем с того, что вспомним
связь между ускорением, скоростью и перемещением. Допустим, у нас есть функция для
перемещение, 𝑠, с точки зрения 𝑡. Скорость объекта это его
скорость изменения смещения во времени.
И, конечно, если рассматривать
скорость изменения, мы на самом деле думаем о производных. Таким образом, мы можем сказать, что 𝑣 равно
д𝑠 от д𝑡. Аналогично определяется ускорение
как скорость изменения скорости во времени. Таким образом, ускорение равно d𝑣 на d𝑡. А так как 𝑣 сама первая
производная от 𝑠 по времени, мы можем сказать, что ускорение также может быть
называется второй производной смещения по времени.
В этом вопросе мы
задана функция ускорения по времени. Чтобы найти функцию для
смещения, нам нужно будет выполнить обратный процесс для дифференциации. Мы собираемся интегрировать наши
функция ускорения во времени. Это даст нам функцию для
скорость. Затем мы собираемся интегрировать один раз
more чтобы найти нашу функцию смещения. Итак, давайте начнем с интеграции нашего
функция ускорения. Мы знаем, что 𝑣 должно быть равно
интеграл отрицательных трех от греха четырех 𝑡 относительно 𝑡.
Ну, помните, мы можем вывезти любую
постоянные факторы и сосредоточиться на интегрировании функции по 𝑡. Таким образом, мы можем сказать, что интеграл от
отрицательное три греха четырех 𝑡 по отношению к 𝑡 отрицательно в три раза больше
интеграл от греха четырех 𝑡 относительно 𝑡.
Затем вспоминаем стандартный результат для интеграла от греха 𝑎𝑥 относительно 𝑥. Это отрицательное значение больше, чем 𝑎, потому что 𝑎𝑥. Итак, это означает интеграл от грех четырех 𝑡 должен быть отрицательным на одну четверть потому что четыре 𝑡. И, конечно же, нам это нужно постоянная интегрирования здесь. Я назвал это 𝐴. Раскрывая скобки, мы поэтому видим, что 𝑣 равно трем четвертям от четырех 𝑡 плюс 𝐵. И причина нашей постоянной интеграция стала 𝐵, потому что мы изменили ее. Мы умножили на минус три.
Нам сказали, что начальный
скорость частицы три метра в секунду.
Другими словами, когда 𝑡 равно
ноль, 𝑣 должно быть равно трем. Итак, давайте подставим эти значения
в нашу функцию скорости. Это дает нам три равных
три четверти от нуля плюс 𝐵. А так как cos нуля равен единице, мы
видите, что три равно трем четвертям плюс 𝐵. Чтобы найти 𝐵, мы вычитаем
три четверти с обеих сторон уравнения. И мы находим, что 𝐵 равно
девять четвертей. Итак, мы нашли эту скорость
равно трем четвертям, потому что четыре 𝑡 плюс девять четвертей.
Следующим шагом будет интеграция нашего
функцию для скорости, чтобы найти общую функцию для смещения. Это неопределенный интеграл от
три четверти cos четырех 𝑡 плюс девять четвертей по отношению к 𝑡. На этот раз напомним, что
интеграл от cos от 𝑎𝑥 равен единице по 𝑎 sin от 𝑎𝑥. Итак, интеграл от
три четверти cos of четыре 𝑡 должны быть три четверти умножить на четверть sin of four
𝑡.
Тогда интеграл девяти четвертей
составляет девять четвертей 𝑡. Итак, у нас есть общая функция для
смещение. Это три четверти раза
четверть греха четырех 𝑡 плюс девять четвертей 𝑡 плюс, конечно же, эта константа
интеграция, 𝑐. Это упрощает до трех шестнадцатых
грех четыре 𝑡 плюс девять четвертей 𝑡 плюс 𝑐.
Есть одна информация
мы еще не использовали. Первоначальное смещение
частица отрицательная два метра. Поэтому, когда 𝑡 равно нулю, не
только скорость три метра в секунду, но 𝑠 равно минус два. Подставим эти значения в
наше уравнение. минус два равно трем
шестнадцатые доли нуля плюс девять четвертей нуля плюс 𝑐. И грех нуля равен нулю, и
девять четвертей нуля это ноль. Итак, мы видим, что минус два
равно 𝑐. И так, наш самый последний шаг состоит в том, чтобы
замените 𝑐 на минус два в нашем уравнении для смещения.
И находим уравнение с
смещение 𝑠 частицы за время 𝑡 секунд равно трем шестнадцатым синусом от четырех
𝑡 плюс девять четвертей 𝑡 минус два.
В этом видео мы увидели, что мы может использовать интегрирование, чтобы найти общие решения дифференциальных уравнений. Мы также увидели, что можем использовать начальный значения для оценки константы. И это называется особым решение дифференциального уравнения.
10.2 Метод замены
Исчисление одной действительной переменной автора Pheng Kim VingГлава 10: Методы интеграции Раздел 10.2: Метод замены |
10,2
|
Возврат
К содержанию
Перейти к проблемам и решениям
В предыдущем разделе, Раздел
10.
1 , мы обсуждали интеграцию путем проверки. Есть много
интегралы, которые трудно вычислить
или не могут быть оценены осмотром, но каждый из них может быть обнаружен
метод или метод интеграции. Этот раздел и несколько
последующие представляют некоторые методы интеграции.
1. Метод замены |
Пример 1.1
Вычислите этот неопределенный интеграл:0004
Решение
Пусть u = х 2 1. Тогда ду = 2 х дх . So:
EOS
We have 2 x ( x 2 1) 10 dx = ( x 2 1) 10 (2 х дх ) = и 10 дю .
Напомним, что дю это дифференциал и (см.
раздел 4.3 Определения 2.1 ): du = u ‘( х ) дх = 2 х дх . В интеграле находим
множители 2 x и x 2 1, и мы знаем, что 2 x является производной от x 2 1, поэтому дифференциал d ( x 2 1) из x 2 1 имеет
множитель 2 х в нем: d ( х 2 1) = 2 х дх . Таким образом, подставляем u = x 2 1, вычисляем du ,
и преобразовать интеграл в x в один в
и . Интеграл в u готов к интеграции
формула, которую нужно применить к нему. После нахождения интеграла в и , мы должны вернуть
к исходной переменной, x в данном случае, в нашем ответе.
Подставляем u = х 2 1.
поэтому используемый метод называется методом замены .
Если мы
хочу проверить на
видим, что наш ответ правильный, тогда просто дифференцируем его:
Пример 1.2
Вычислить:
Решение
Пусть u = х 1, значит что du = dx . Тогда:
EOS
Здесь d ( x 1) = 1 . дх = дх . Подставляем на = х . 1.
Перейти к проблемам и Решения Вернуться к началу страницы
2. Метод подстановки и цепное правило |
{2.1} Пример 1.1 .
Метод замены действителен, поскольку он получено из цепного правила.
Перейти к проблемам и Решения Вернуться к началу страницы
3. | Решение
1
Разница на постоянный коэффициент 
4. Интегралы с радикалами |
Вычислить:
Решение
1
Пусть u = 5 х 2 . Тогда дю = 2 х dx , так что x dx = (1/2) du .
Таким образом:
EOS
Мы можем исключить радикал, как показано в Решении 2. ниже.
Решение 2
EOS
Перейти к проблемам и Решения Вернуться к началу страницы
5. Работа с определенными интегралами |
Пример 5.1
Вычислите определенный интеграл: Пусть u = х 3 + 1. Тогда du = 3 x 2 dx , так что x 2 dx = (1/3) дю . Таким образом:
EOS
Мы должны записать пределы интегрирования как x = 0 и x = 2 всякий раз, когда переменная интегрирования равна 0, а не 4, а не .
потому что это x , а не u , это идет от 0 до 2.
Здесь
мы сохраняем ограничения x интеграции, поэтому мы должны вернуться к x до
подставляя в пределах. Другой подход показан в Решении 2 ниже.
Решение
2
Пусть U = x 3 + 1. Тогда DU = 3 x 2 DX , так что X 2 , так что X 2 , так что X 2 . 9014 2 . .
Когда х = 0 мы
имеем u = 0 3 + 1 = 1, и
когда х = 2 мы
имеем u = 2 3 + 1 = 9. Таким образом:
EOS
Здесь мы преобразуем пределы x в пределы u и вычисляем интеграл, как только
мы нашли это с точки зрения и
используя эти u -пределы.
Перейти к проблемам и Решения Вернуться к началу страницы
6. |
Когда метод замещения сработает
Вернуться к началу страницы
Проблемы и решения |
1. Вычислите следующие неопределенные интегралы.
Раствор
а. Пусть ты = 3 х 4 + 5. Тогда дю = 12 х 3 дх , поэтому x 3 dx = (1/12) du . Таким образом:
Возврат к вершине страницы
2. Выберите следующие непрекращающиеся интегралы.
Решение
а. Пусть и = с 2 . Тогда дю = 2 с дс ,
поэтому с дс = (1/2) дю .
Таким образом:
Возврат на вершину страницы
3. Покажите, что:
77777777777 900077777777777777777777777 9000 7777777777777777779000 9000 9000
777777777777777777 9000777777777777777770078
У нас есть 10 + 6 x + х 2 = 1 + ( х + 3) 2 . Пусть и = х + 3. Итак, дю = дх . Thus:
Return To Top Of Page
4. Evaluate the definite integral:
handling the
пределы интегрирования 2-мя способами:
а. Сохранить ограничения x .
б. Изменение пределов для подстановочной переменной.