Решение тригонометрических уравнений

В данной статье остановимся кратко на решении задач C1 из ЕГЭ по математике. Эти задания представляют собой уравнения, которые требуется, во-первых, решить (то есть найти их решения, причем все), во-вторых, осуществить отбор решений по тому или иному ограничению. В последние годы на ЕГЭ по математике в заданиях C1 школьникам предлагаются для решения тригонометрические уравнения, поэтому в данной статье разобраны только они. Примеры структурированы по методам решения уравнений, от самых элементарных, до достаточно сложных.
Прежде чем перейти к разбору конкретных тригонометрических уравнений, вспомним основные формулы тригонометрии. Приведем их здесь в справочном виде.

Основные тригонометрические формулы

Решение простейших тригонометрических уравнений
Решение простейших тригонометрических уравнений
Пример 1. Найдите корни уравнения ![Rendered by QuickLaTeX.com \[ \cos\left(4x+\frac{\pi}{4}\right)=-\frac{\sqrt{2}}{2}, \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-7cea1f5663bb6ad8fdbc9fea4f463c6b_l3.png)
принадлежащие промежутку 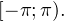
Решение. Используем вторую формулу на рисунке. Здесь и далее полагаем 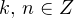
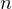 и
и  принадлежат множеству целых чисел):
принадлежат множеству целых чисел): ![Rendered by QuickLaTeX.com \[ 4x+\frac{\pi}{4}=\pm\operatorname{arccos \left(-\frac{\sqrt{2}}{2}\right)}+2\pi k. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-600bd6daa90af5fa4124c683eb7663ac_l3.png)
Другими словами, нам нужно подобрать такое число из промежутка ![Rendered by QuickLaTeX.com [0;2\pi],](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-6516ce3e8a2a72f3c1e75c74df6dcab5_l3.png)
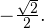 Это число
Это число 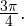 Используя это, получаем:
Используя это, получаем: ![Rendered by QuickLaTeX.com \[ 4x+\frac{\pi}{4} = \pm\frac{3\pi}{4}+2\pi k\Leftrightarrow \left[\begin{array}{l}x = \frac{\pi}{8}+\frac{\pi k}{2}, \\ x = -\frac{\pi}{4}+\frac{\pi n}{2}.\end{array}\right. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-4e1b7dcb8f1bb9b0ff44ee1900d0e206_l3.png)
Вообще, значения тригонометрических функций от основных аргументов нужно знать. Их совсем чуть-чуть:
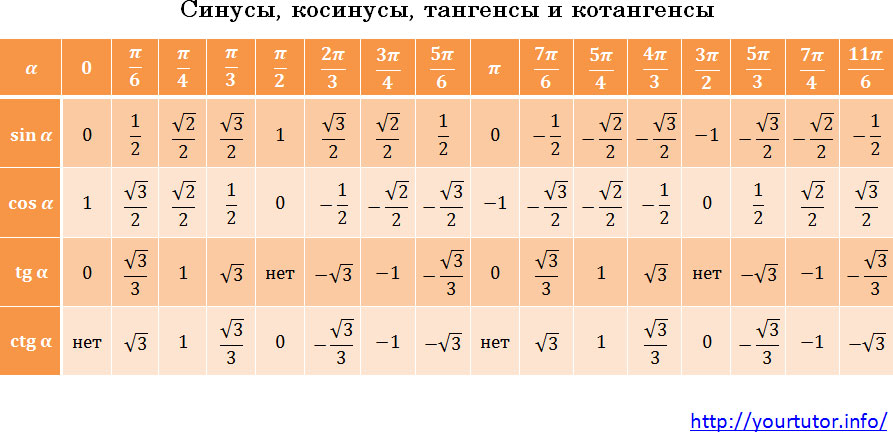
Таблица значений тригонометрических функций
Хотя на самом деле запоминать их вовсе не обязательно. Существует очень простой алгоритм, используя который, можно в уме легко вычислять значения тригонометрических функций всех основных аргументов. Просто у каждого он свой. Придумайте его и для себя. Просто посмотрите на эту таблицу. Числа в ней расположены не случайным образом, определенная закономерность есть, постарайтесь ее найти.
Итак, вернемся к нашему заданию. Из полученных серий выбираем только те ответы, которые принадлежат промежутку 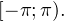 Воспользуемся для этого методом двойных неравенств. Вы помните, что
Воспользуемся для этого методом двойных неравенств. Вы помните, что 
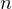 — целые числа:
— целые числа:1) 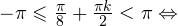
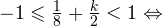
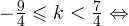
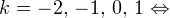
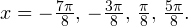
2) 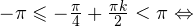
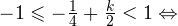
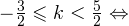
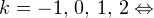
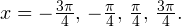
Задача для самостоятельного решения №1. Найдите корни уравнения 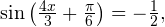 принадлежащие промежутку
принадлежащие промежутку 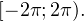
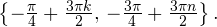
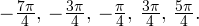
Решение линейных тригонометрических уравнений
Пример 2. Найдите корни уравнения ![Rendered by QuickLaTeX.com \[ \sin x+\sqrt{3}\cos x=1, \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-c8549fd428fc2b8f8612668c1bcafa38_l3.png)
принадлежащие промежутку ![Rendered by QuickLaTeX.com [-2\pi;4\pi].](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-e5ab0d4ddd997ad7264282447126bc7c_l3.png)
Решение. Подобные уравнения решаются один весьма интересным, на мой взгляд, способом. Разделим обе части на 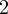 , уравнение тогда примет вид:
, уравнение тогда примет вид:
![Rendered by QuickLaTeX.com \[ \frac{1}{2}\sin x+\frac{\sqrt{3}}{2}\cos x = 1. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-65ffb48c7a579b1bbdee9fbba7af59f4_l3.png)
Подберем такое число, синус которого равен 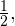 а косинус равен
а косинус равен 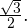 Например, пусть это будет число
Например, пусть это будет число 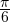
![Rendered by QuickLaTeX.com \[ \sin\frac{\pi}{6}\sin x+\cos\frac{\pi}{6}\cos x=\frac{1}{2}. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-4c7a1d290000c0bba4b160c010d5f32f_l3.png)
Присмотревшись, слева от знака равенства усматриваем разложение косинуса разности 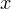 и
и 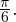 Это и есть ключ к решению. Имеем:
Это и есть ключ к решению. Имеем:
![Rendered by QuickLaTeX.com \[ \cos\left(x-\frac{\pi}{6}\right)=\frac{1}{2}\Leftrightarrow x-\frac{\pi}{6}=\pm\frac{\pi}{3}+2\pi k\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-99933eb31e68aa68196b01149d3cf7e7_l3.png)
![Rendered by QuickLaTeX.com \[ \left[\begin{array}{l}x-\frac{\pi}{6}=\frac{\pi}{3}+2\pi k, \\ x-\frac{\pi}{6}=-\frac{\pi}{3}+2\pi n\end{array}\right.\Leftrightarrow\left[\begin{array}{l}x=\frac{\pi}{2}+2\pi k, \\ x=-\frac{\pi}{6}+2\pi n.\end{array}\right. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-a7f7798906bca8730370d50380d0b2c5_l3.png)
Осуществляем отбор решений, входящих в промежуток 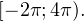 :
:
1) 
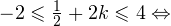
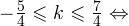
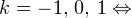
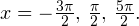
2) 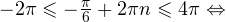
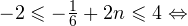
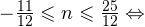
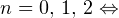
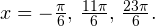
Задача для самостоятельного решения №2. Найдите корни уравнения 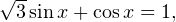 принадлежащие промежутку
принадлежащие промежутку ![Rendered by QuickLaTeX.com [-3\pi;3\pi].](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-979d4671d337b296584d0c825376e1e8_l3.png)
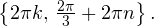
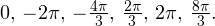
Решение тригонометрических уравнений методом замены переменной
Пример 3. Дано уравнение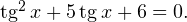
а) Решите уравнение.
б) Укажите корни, принадлежащие отрезке ![Rendered by QuickLaTeX.com \left[-2\pi;-\frac{\pi}{2}\right].](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-2e56a5618e53c514d925c4318432710e_l3.png)
Решение. Сразу оговорим ограничения, накладываемые на переменную 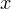 в этом уравнении:
в этом уравнении: 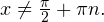 Откуда взялось это ограничение? Правильно, функция
Откуда взялось это ограничение? Правильно, функция 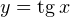 не существует при этих значениях
не существует при этих значениях 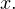 Используем замену переменной:
Используем замену переменной: 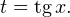 Тогда уравнение принимает вид:
Тогда уравнение принимает вид:
![Rendered by QuickLaTeX.com \[ t^2+5t+6=0\Leftrightarrow\left[\begin{array}{l}t=-3, \\t=-2.\end{array}\right. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-c8cb0eceec5f7707e25585504f135ed9_l3.png)
Переходим к обратной замене:
![Rendered by QuickLaTeX.com \[ \left[\begin{array}{l}\operatorname{tg}x = -3,\\ \operatorname{tg}x = -2\end{array}\right.\Leftrightarrow \left[\begin{array}{l}x = -\operatorname{arctg} 3+\pi k, \\ x=-\operatorname{arctg} 2+\pi n.\end{array}\right. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-184ca285f5fe0c4b521f49f2c1fef113_l3.png)
Осуществляем отбор решений. Проведем его на этот раз с использованием единичной окружности.
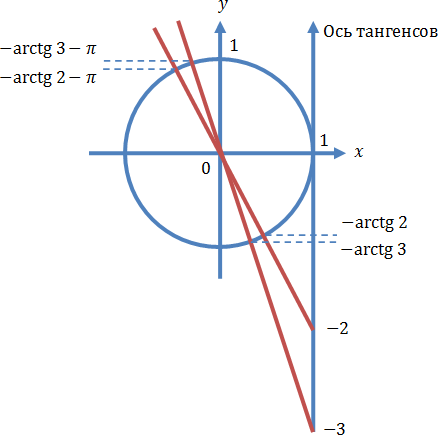
Отбор корней с помощью единичной окружности
Из рисунка видно, что в интересующий нас промежуток входят только два значения из этих серий: 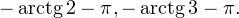 Обратите внимание на один существенный момент. На рисунке точки
Обратите внимание на один существенный момент. На рисунке точки 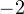 и
и 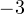 принадлежат оси тангенсов, а точки
принадлежат оси тангенсов, а точки 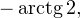
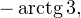
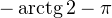 и
и 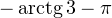 — единичной окружности. Очень важно понимать, зачем это нужно для решения данной задачи.
— единичной окружности. Очень важно понимать, зачем это нужно для решения данной задачи.
Ответ: 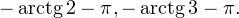
Задача для самостоятельного решения №3. Дано уравнение 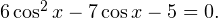
a) Решите уравнение.
б) Укажите корни, принадлежащие отрезку ![Rendered by QuickLaTeX.com [-\pi;2\pi].](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-7619bf74ede16b0f138212b37cf78df2_l3.png)
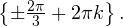
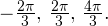
Решение тригонометрических уравнений методом разложения на множители
Пример 4. Дано уравнение ![Rendered by QuickLaTeX.com \[ \sin 2x=2\sin x-\cos x+1. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-314ae6ec8084938924dcb1b7a0324414_l3.png)
a) Решите уравнение.
б) Укажите корни, принадлежащие отрезку ![Rendered by QuickLaTeX.com \left[-2\pi; -\frac{\pi}{2}\right].](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-092d4dc81779071955ee1bdf99bce52e_l3.png)
Решение. Равносильными преобразования приводим уравнение к виду:
![Rendered by QuickLaTeX.com \[ \sin 2x=2\sin x-\cos x+1\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-26079fe9cc286a9b505cebcad4b20a54_l3.png)
![Rendered by QuickLaTeX.com \[ 2\sin x\cos x-2\sin x+\cos x-1=0\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-16b853ad0976a5741efaebe9dbf734a3_l3.png)
![Rendered by QuickLaTeX.com \[ 2\sin x(\cos x-1)+\cos x-1 =0\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-cb5e2726eaee2ea2b3d7aef7d4811e45_l3.png)
![Rendered by QuickLaTeX.com \[ (\cos x-1)(2\sin x+1) = 0\Lefrightarrow \left[\begin{array}{l}\cos x-1=0, \\ 2\sin x+1=0\end{array}\right.\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-1e2e696cbfce62ef0d378fc226247d45_l3.png)
![Rendered by QuickLaTeX.com \[ \left[\begin{array}{l}\cos x=1, \\ \sin x=-\frac{1}{2} \end{array}\right.\Leftrightarrow\left[\begin{array}{l}x=2\pi k, \\ x=-\frac{\pi}{6}+2\pi n, \\ x=-\frac{5\pi}{6}+2\pi z.\end{array}\right. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-c0ac3379edc46ce1bf97df0f46a830ac_l3.png)
Осуществляем отбор решений с помощью единичной окружности.
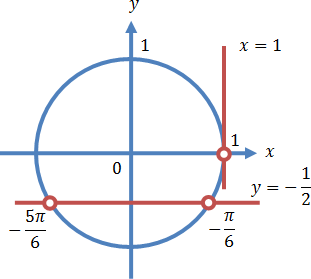
Отбор решений с помощью единичной окружности
Из рисунка видно, что в интересующий нас промежуток входят только два значения из всех этих серий: 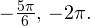
Задача для самостоятельного решения №4. Дано уравнение
![Rendered by QuickLaTeX.com \[ 3\sin 2x-4\cos x+3\sin x-2=0. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-28a0aa4a8809041869a0dd165374f983_l3.png)
а) Решите уравнение.
б) Укажите корни, принадлежащие отрезку ![Rendered by QuickLaTeX.com \left[\frac{\pi}{2};\frac{3\pi}{2}\right].](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-0afd161af4c492ee4549edea05061c7b_l3.png)
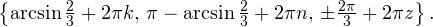
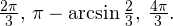
Комбинированные уравнения
При решении уравнений этого типа важно обращать внимание на область допустимых значений входящих в него переменных. Именно поэтому составители вариантов ЕГЭ не просят учеников осуществлять отбор решений из полученных серий ответов. Решение этих уравнений само собой подразумевает выполнение данной математической операции.
Пример 5. Решите уравнение: ![Rendered by QuickLaTeX.com \[ \sqrt{1-2\sin 3x\sin 7x}=\sqrt{\cos 10x}. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-0676b2ec24b14219e132ecfeffe1beff_l3.png)
Решение. Данное уравнение эквивалентно следующей системе:
![Rendered by QuickLaTeX.com \[ \begin{cases}1-2\sin 3x\sin 7x=\cos 10x, \\ \cos 10x\geqslant 0.\end{cases} \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-5e7804c5a3444eda3706d8c6a9cc8bc0_l3.png)
Обратите внимание! Писать, что 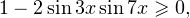 нет никакой необходимости, поскольку по условию это выражение равно выражению
нет никакой необходимости, поскольку по условию это выражение равно выражению 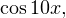 которое, в свою очередь, больше или равно нулю.
которое, в свою очередь, больше или равно нулю.
Решаем первое уравнение системы:
![Rendered by QuickLaTeX.com \[ 1-2\sin 3x\sin 7x=\cos (7x+10x)\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-85f99b88ebecfe2323a0bc59bac8e027_l3.png)
![Rendered by QuickLaTeX.com \[ 1-2\sin 3x\sin 7x=\cos 3x\cos 7x-\sin 3x\sin 7x\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-30cfd48e7e1658096abdeb1390486c83_l3.png)
![Rendered by QuickLaTeX.com \[ 1=\cos 3x\cos 7x+\sin 3x\sin 7x\Leftrightarrow \cos 4x=1. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-e7341e12fbea6fe289a80d2965e67b8b_l3.png)
![Rendered by QuickLaTeX.com \[ \cos 10x = 1\Leftrightarrow 4x=2\pi k\Leftrightarrow x = \frac{\pi k}{2}. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-69acc2d98a3a49c3c563dbcb9e3f3976_l3.png)
Нужно, чтобы 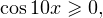 поразмыслив, понимаем, что поэтому из полученной серии ответов нам подходят только
поразмыслив, понимаем, что поэтому из полученной серии ответов нам подходят только 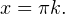
Ответ: 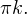
Задача для самостоятельного решения №5. Решите уравнение: 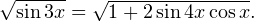
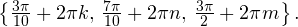 Пример 6. Решите уравнение:
Пример 6. Решите уравнение: ![Rendered by QuickLaTeX.com \[ \frac{2\sin^2 x-\sin\left(\frac{3\pi}{2}+x\right)-1}{\sqrt{\sin x}}=0. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-b29f83ad79819cdf0623a3f50f53cbf1_l3.png)
Решение. Данное уравение равносильно системе:
![Rendered by QuickLaTeX.com \[ \begin{cases}2\sin^2 x-\sin\left(\frac{3\pi}{2}+x\right)-1=0, \\ \sin x>0\end{cases}\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-9796d3e88520ad252eea21fb51f21987_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{cases}2\cos^2 x-\cos x-1=0,\\ \sin x>0\end{cases}\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-dbab64445b6b27423f4c9a5b3a45e710_l3.png)
![Rendered by QuickLaTeX.com \[ \begin{cases}\left[\begin{array}{l}\cos x = 1, \\ \cos x =-\frac{1}{2},\end{array} \\ \sin x >0\right.\end{cases}\Leftrightarrow \begin{cases}\left[\begin{array}{l}x=2\pi k, \\ x=\pm\frac{2\pi}{3}+2\pi n,\end{array} \\ \sin x >0\right.\end{cases} \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-20bc473770ab6419cd1a45ba72b7178f_l3.png)
Тригонометрическая функция синус положительна в первой и второй координатной четвертях, поэтому из полученных серий выбираем только эту: 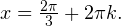
Раз уж мы с этим столкнулись, не лишним будет повторить, какие знаки принимают тригонометрические функций в различных координатных четвертях:
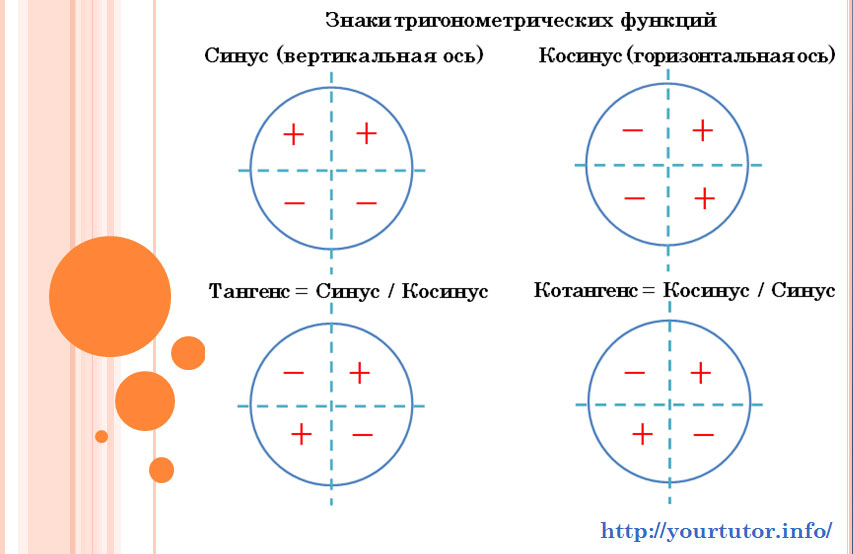
Знаки функций, входящих в тригонометрические уравнения, по координатным четвертям
Ответ: 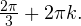
Задача для самостоятельного решения №6. Решите уравнение: 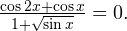
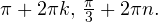 Пример 7. Решите уравнение:
Пример 7. Решите уравнение: 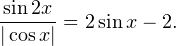
Решение. Область допустимых значения уравнения определяется условием: 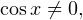 то есть
то есть 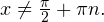 Разобьем решение на два случая:
Разобьем решение на два случая:
1) Пусть 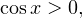 тогда уравнение принимает вид:
тогда уравнение принимает вид:
![Rendered by QuickLaTeX.com \[ \frac{2\sin x\cos x}{\cos x} = 2\sin x-2\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-fe301b6a371887b4ca249562d051d06c_l3.png)
![Rendered by QuickLaTeX.com \[ 2\sin x=2\sin x-2\Leftrightarrow 0=-2. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-89fc402230aca1d5d103f2eba93d497e_l3.png)
Последнее равенство неверно, поэтому в данном случае решений у уравнения не будет.
2) Пусть 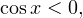 тогда уравнение принимает вид:
тогда уравнение принимает вид:
![Rendered by QuickLaTeX.com \[ -\frac{2\sin x\cos x}{\cos x} = 2\sin x-2\Leftrightarrow \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-8bd35cba0d719a8226b8f9034ef98024_l3.png)
![Rendered by QuickLaTeX.com \[ \sin x = \frac{1}{2}\Leftrightarrow \left[\begin{array}{l}x = \frac{\pi}{6}+2\pi k, \\ x=\frac{5\pi}{6}+2\pi n.\end{array}\right. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-217ffb2b7eeca2a312b56ee28296fa3a_l3.png)
Условию 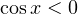 удовлетворяет только последняя серия.
удовлетворяет только последняя серия.
Ответ: 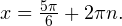
Задача для самостоятельного решения №7. Решите уравнение: 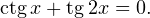
ЕГЭ по математике 2012 позади, все в ожидании результатов, которые обещали объявить во вторник 19 июня. Сейчас уже поздно желать высоких баллов на экзаменах нынешним выпускникам. Но вот пожелать успехов сегодняшним десятиклассникам я возможности не упущу. Удачи вам в подготовке и помните, что чем раньше она начнется, тем лучше будут результаты на экзамене.

Репетитор математики
Сергей Валерьевич
P. S. Уважаемые гости! Пожалуйста, не пишите в комментариях заявки на решение ваших уравнений. К сожалению, на это у меня совершенно нет времени. Такие сообщения будут удалены. Пожалуйста, ознакомьтесь со статьёй. Возможно, в ней вы найдёте ответы на вопросы, которые не позволили вам решить своё задание самостоятельно.
Формулы для решения простейших тригонометрических уравнений
Равенство, содержащее неизвестную под знаком тригонометрической функции (`sin x, cos x, tg x` или `ctg x`), называется тригонометрическим уравнением, именно их формулы мы и рассмотрим дальше.
Содержание статьи:
Простейшие тригонометрические уравнения
Простейшими называются уравнения `sin x=a, cos x=a, tg x=a, ctg x=a`, где `x` — угол, который нужно найти, `a` — любое число. Запишем для каждого из них формулы корней.
1. Уравнение `sin x=a`.
При `|a|>1` не имеет решений.
При `|a| \leq 1` имеет бесконечное число решений.
Формула корней: `x=(-1)^n arcsin a + \pi n, n \in Z`

Таблица арксинусов
2. Уравнение `cos x=a`
При `|a|>1` — как и в случае с синусом, решений среди действительных чисел не имеет.
При `|a| \leq 1` имеет бесконечное множество решений.
Формула корней: `x=\pm arccos a + 2\pi n, n \in Z`

Таблица арккосинусов
Частные случаи для синуса и косинуса в графиках.
3. Уравнение `tg x=a`
Имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arctg a + \pi n, n \in Z`

Таблица арктангенсов
4. Уравнение `ctg x=a`
Также имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arcctg a + \pi n, n \in Z`

Таблица арккотангенсов
Формулы корней тригонометрических уравнений в таблице
Для синуса: Для косинуса:
Для косинуса: Для тангенса и котангенса:
Для тангенса и котангенса: Формулы решения уравнений, содержащих обратные тригонометрические функции:
Формулы решения уравнений, содержащих обратные тригонометрические функции:

Методы решения тригонометрических уравнений
Решение любого тригонометрического уравнения состоит из двух этапов:
- с помощью тригонометрических формул преобразовать его до простейшего;
- решить полученное простейшее уравнение, используя выше написанные формулы корней и таблицы.
Рассмотрим на примерах основные методы решения.
Алгебраический метод.
В этом методе делается замена переменной и ее подстановка в равенство.
Пример. Решить уравнение: `2cos^2(x+\frac \pi 6)-3sin(\frac \pi 3 — x)+1=0`
Решение. Используя формулы приведения, имеем:
`2cos^2(x+\frac \pi 6)-3cos(x+\frac \pi 6)+1=0`,
делаем замену: `cos(x+\frac \pi 6)=y`, тогда `2y^2-3y+1=0`,
находим корни: `y_1=1, y_2=1/2`, откуда следуют два случая:
1. `cos(x+\frac \pi 6)=1`, `x+\frac \pi 6=2\pi n`, `x_1=-\frac \pi 6+2\pi n`.
2. `cos(x+\frac \pi 6)=1/2`, `x+\frac \pi 6=\pm arccos 1/2+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.
Ответ: `x_1=-\frac \pi 6+2\pi n`, `x_2=\pm \frac \pi 3-\frac \pi 6+2\pi n`.
Разложение на множители.
Пример. Решить уравнение: `sin x+cos x=1`.
Решение. Перенесем влево все члены равенства: `sin x+cos x-1=0`. Используя формулы двойного угла, преобразуем и разложим на множители левую часть:
`sin x — 2sin^2 x/2=0`,
`2sin x/2 cos x/2-2sin^2 x/2=0`,
`2sin x/2 (cos x/2-sin x/2)=0`,
- `sin x/2 =0`, `x/2 =\pi n`, `x_1=2\pi n`.
- `cos x/2-sin x/2=0`, `tg x/2=1`, `x/2=arctg 1+ \pi n`, `x/2=\pi/4+ \pi n`, `x_2=\pi/2+ 2\pi n`.
Ответ: `x_1=2\pi n`, `x_2=\pi/2+ 2\pi n`.
Приведение к однородному уравнению
Вначале нужно данное тригонометрическое уравнение привести к одному из двух видов:
`a sin x+b cos x=0` (однородное уравнение первой степени) или `a sin^2 x + b sin x cos x +c cos^2 x=0` (однородное уравнение второй степени).
Потом разделить обе части на `cos x \ne 0` — для первого случая, и на `cos^2 x \ne 0` — для второго. Получим уравнения относительно `tg x`: `a tg x+b=0` и `a tg^2 x + b tg x +c =0`, которые нужно решить известными способами.
Пример. Решить уравнение: `2 sin^2 x+sin x cos x — cos^2 x=1`.
Решение. Запишем правую часть, как `1=sin^2 x+cos^2 x`:
`2 sin^2 x+sin x cos x — cos^2 x=` `sin^2 x+cos^2 x`,
`2 sin^2 x+sin x cos x — cos^2 x -` ` sin^2 x — cos^2 x=0`
`sin^2 x+sin x cos x — 2 cos^2 x=0`.
Это однородное тригонометрическое уравнение второй степени, разделим его левую и правую части на `cos^2 x \ne 0`, получим:
`\frac {sin^2 x}{cos^2 x}+\frac{sin x cos x}{cos^2 x} — \frac{2 cos^2 x}{cos^2 x}=0`
`tg^2 x+tg x — 2=0`. Введем замену `tg x=t`, в результате `t^2 + t — 2=0`. Корни этого уравнения: `t_1=-2` и `t_2=1`. Тогда:
- `tg x=-2`, `x_1=arctg (-2)+\pi n`, `n \in Z`
- `tg x=1`, `x=arctg 1+\pi n`, `x_2=\pi/4+\pi n`, ` n \in Z`.
Ответ. `x_1=arctg (-2)+\pi n`, `n \in Z`, `x_2=\pi/4+\pi n`, `n \in Z`.
Переход к половинному углу
Пример. Решить уравнение: `11 sin x — 2 cos x = 10`.
Решение. Применим формулы двойного угла, в результате: `22 sin (x/2) cos (x/2) -` `2 cos^2 x/2 + 2 sin^2 x/2=` `10 sin^2 x/2+10 cos^2 x/2`
`4 tg^2 x/2 — 11 tg x/2 +6=0`
Применив описанный выше алгебраический метод, получим:
- `tg x/2=2`, `x_1=2 arctg 2+2\pi n`, `n \in Z`,
- `tg x/2=3/4`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.
Ответ. `x_1=2 arctg 2+2\pi n, n \in Z`, `x_2=arctg 3/4+2\pi n`, `n \in Z`.
Введение вспомогательного угла
В тригонометрическом уравнении `a sin x + b cos x =c`, где a,b,c — коэффициенты, а x — переменная, разделим обе части на `sqrt {a^2+b^2}`:
`\frac a{sqrt {a^2+b^2}} sin x +` `\frac b{sqrt {a^2+b^2}} cos x =` `\frac c{sqrt {a^2+b^2}}`.
Коэффициенты в левой части имеют свойства синуса и косинуса, а именно сумма их квадратов равна 1 и их модули не больше 1. Обозначим их следующим образом: `\frac a{sqrt {a^2+b^2}}=cos \varphi`, ` \frac b{sqrt {a^2+b^2}} =sin \varphi`, `\frac c{sqrt {a^2+b^2}}=C`, тогда:
`cos \varphi sin x + sin \varphi cos x =C`.
Подробнее рассмотрим на следующем примере:
Пример. Решить уравнение: `3 sin x+4 cos x=2`.
Решение. Разделим обе части равенства на `sqrt {3^2+4^2}`, получим:
`\frac {3 sin x} {sqrt {3^2+4^2}}+` `\frac{4 cos x}{sqrt {3^2+4^2}}=` `\frac 2{sqrt {3^2+4^2}}`
`3/5 sin x+4/5 cos x=2/5`.
Обозначим `3/5 = cos \varphi` , `4/5=sin \varphi`. Так как `sin \varphi>0`, `cos \varphi>0`, то в качестве вспомогательного угла возьмем `\varphi=arcsin 4/5`. Тогда наше равенство запишем в виде:
`cos \varphi sin x+sin \varphi cos x=2/5`
Применив формулу суммы углов для синуса, запишем наше равенство в следующем виде:
`sin (x+\varphi)=2/5`,
`x+\varphi=(-1)^n arcsin 2/5+ \pi n`, `n \in Z`,
`x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.
Ответ. `x=(-1)^n arcsin 2/5-` `arcsin 4/5+ \pi n`, `n \in Z`.
Дробно-рациональные тригонометрические уравнения
Это равенства с дробями, в числителях и знаменателях которых есть тригонометрические функции.
Пример. Решить уравнение. `\frac {sin x}{1+cos x}=1-cos x`.
Решение. Умножим и разделим правую часть равенства на `(1+cos x)`. В результате получим:
`\frac {sin x}{1+cos x}=` `\frac {(1-cos x)(1+cos x)}{1+cos x}`
`\frac {sin x}{1+cos x}=` `\frac {1-cos^2 x}{1+cos x}`
`\frac {sin x}{1+cos x}=` `\frac {sin^2 x}{1+cos x}`
`\frac {sin x}{1+cos x}-` `\frac {sin^2 x}{1+cos x}=0`
`\frac {sin x-sin^2 x}{1+cos x}=0`
Учитывая, что знаменатель равным быть нулю не может, получим `1+cos x \ne 0`, `cos x \ne -1`, ` x \ne \pi+2\pi n, n \in Z`.
Приравняем к нулю числитель дроби: `sin x-sin^2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
- `sin x=0`, `x=\pi n`, `n \in Z`
- `1-sin x=0`, `sin x=-1`, `x=\pi /2+2\pi n, n \in Z`.
Учитывая, что ` x \ne \pi+2\pi n, n \in Z`, решениями будут `x=2\pi n, n \in Z` и `x=\pi /2+2\pi n`, `n \in Z`.
Ответ. `x=2\pi n`, `n \in Z`, `x=\pi /2+2\pi n`, `n \in Z`.
Тригонометрия, и тригонометрические уравнения в частности, применяются почти во всех сферах геометрии, физики, инженерии. Начинается изучение в 10 классе, обязательно присутствуют задания на ЕГЭ, поэтому постарайтесь запомнить все формулы тригонометрических уравнений — они вам точно пригодятся!
Впрочем, даже запоминать их не нужно, главное понять суть, и уметь вывести. Это не так и сложно, как кажется. Убедитесь сами, просмотрев видео.
Материалы по теме:
Поделиться с друзьями:
 Загрузка…
Загрузка…Решение тригонометрических уравнений | Математика, которая мне нравится
Простейшие тригонометрические уравнения
Уравнение при решений не имеет,
при имеет решения ,
при имеет решения ,
при имеет решения ,
при всех остальных имеет решения .
Уравнение при решений не имеет,
при имеет решения ,
при имеет решения >,
при имеет решения ,
при всех остальных имеет решения .
Уравнение имеет решения .
Уравнение имеет решения .
Приемы решения тригонометрических уравнений
1. Сведение к одной функции
1. заменяем на , — на .
Пример 1.
Пример 2.
2. заменяем на , — на , — на .
Пример 1.
1) 2) ,
В первом случае решений нет, во втором .
Пример 2.
Пример 3.
3. Однородные уравнения относительно .
Если , то деля обе части уравнения на или на , получаем равносильные уравнения. Действительно, пусть — корень уравнения и . Подставляя в уравнение, получаем, что и , а это невозможно.
Пример.
4. Уравнения, приводящиеся к однородным
а) Домножение на
Пример.
б) Переход к половинному аргументу
Пример.
5. Использование формулы
Пример.
6. Замена .
Пример.
Разложение на множители
1. Формулы преобразования суммы в произведение
2. Формулы
Пример 1.
Ответ. .
Пример 2.
, решений нет,
Ответ. , .
Понижение степени
Использование формул
Сравнение левой и правой части
Пример 1.
что невозможно.
Ответ. .
Пример 2.
Ответ. .
Пример 3.
Пусть
Подставляем во второе уравнение:
Ответ. .
Пример 4.
или
Если , то . Если , то .
Ответ. .
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Тригонометрия

Простейшими тригонометрическими уравнениями называют уравнения вида:
sin x = a , cos x = a ,
tg x = a , ctgx = a .
где a – произвольное число.
Решение уравнения sin x = a
| Обычная форма записи решения |  |
| Более удобная форма записи решения |  |
| Ограничения на число a | В случае, когда  , ,уравнение решений не имеет |
Обычная форма записи решения:

Более удобная форма записи решения:

Ограничения на число a:
В случае, когда  , уравнение решений не имеет.
, уравнение решений не имеет.
Графическое обоснование решения уравнения sin x = a представлено на рисунке 1


Рис. 1
Частные случаи решения уравнений sin x = a
Уравнение: sin x = – 1 Решение:  |
Уравнение:  Решение:  |
Уравнение:  Решение:  |
Уравнение:  Решение: > |
Уравнение: sin x = 0 Решение:  |
Уравнение:  Решение:  |
Уравнение:  Решение:  |
Уравнение:  Решение:  |
Уравнение: sin x = 1 Решение:  |
Решение уравнения cos x = a
| Обычная форма записи решения |  |
| Более удобная форма записи решения |  |
| Ограничения на число a | В случае, когда  , ,уравнение решений не имеет |
Обычная форма записи решения:

Более удобная форма записи решения:

Ограничения на число a
В случае, когда  , уравнение решений не имеет.
, уравнение решений не имеет.
Графическое обоснование решения уравнения cos x = a представлено на рисунке 2


Рис. 2
Частные случаи решения уравнений cos x = a
Уравнение: cos x = – 1 Решение:  |
Уравнение:  Решение:  |
Уравнение:  Решение:  |
Уравнение:  Решение:  |
Уравнение: cos x = 0 Решение:  |
Уравнение:  Решение:  |
Уравнение:  Решение:  |
Уравнение:  Решение:  |
Уравнение: cos x = 1 Решение:  |
Решение уравнения tg x = a
| Обычная форма записи решения: |  |
| Более удобная форма записи решения |  |
| Ограничения на число a | Ограничений нет |
Обычная форма записи решения:

Более удобная форма записи решения:

Ограничения на число a:
Ограничений нет.
Графическое обоснование решения уравнения tg x = a представлено на рисунке 3.


Рис. 3
Частные случаи решения уравнений tg x = a
Уравнение:  Решение:  |
Уравнение: tg x = – 1 Решение:  |
Уравнение:  Решение:  |
Уравнение: tg x = 0 Решение:  |
Уравнение:  Решение:  |
Уравнение: tg x = 1 Решение:  |
Уравнение:  Решение:  |
Решение уравнения ctg x = a
| Обычная форма записи решения |  |
| Более удобная форма записи решения |  |
| Ограничения на число a | Ограничений нет |
Обычная форма записи решения:

Более удобная форма записи решения:

Ограничения на число a:
Ограничений нет.
Графическое обоснование решения уравнения ctg x = a представлено на рисунке 4.


Рис. 4
Частные случаи решения уравнений ctg x = a
Уравнение:  Решение:  |
Уравнение: ctg x = – 1 Решение:  |
Уравнение:  Решение:  |
Уравнение: ctg x = 0 Решение:  |
 Решение:  |
Уравнение: ctg x = 1 Решение:  |
Уравнение:  Решение:  |

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.
Задачи с решением — Тригонометрические уравнения
1. Решить уравнение cos2x = 1/2.
Используем метод решения простейших тригонометрических уравнений и получаем:
2x = ±arccos(1/2) + 2πn = ±π/3 + 2πn (здесь и далее, n ∈ Z).
Откуда x = ±π/6 + πn.
Ответ: x = ±π/6 + πn.
2. Решить уравнение sin(3 — 2x) = -1/2.
Используем формулу из методов решений, имеем:
3 — 2x = (-1)n(arcsin(-1/2)) + πn = (-1)n(-π/6) + πn (здесь и далее n ∈ Z).
Делаем преобразование и получаем x = 3/2 + π/12(-1)n — πn/2.
Ответ: x = 3/2 + π/12(-1)n — πn/2.
3. Решить уравнение cos2x — 3sinx = 2.
Воспользуемся формулой удвоенного угла косинуса (cos2a = 1 — 2sin2a) и получим:
1 — 2sin2x — 3sinx = 2.
Воспользуемся методом замены, обозначим sinx = y. Уравнение примет вид:
2y2 + 3y + 1 = 0.
Находим его корни: y1 = -1, y2 = -1/2.
Возвращаемся к исходной переменной и получаем совокупность sinx = -1 и sinx = -1/2.
Из первого получаем решение — x = -π/2 + 2πn, из второго — x = (-1)m(-π/6) + πm (m, n ∈ Z).
Ответ: x = -π/2 + 2πn или x = (-1)m(-π/6) + πm.
4. Решить уравнение 2tgx — 3ctgx = 1.
Так как ctgx = 1/tgx при x ≠ πn/2 (n ∈ Z) получаем уравнение
2tgx — 3/tgx = 1 или 2tg2x — tgx — 3 = 0.
Вводим новую переменную tgx = y и решаем квадратное уравнение 2y2 — y — 3 = 0 относительно y.
Оно имеет два решения y1 = 3/2, y2 = -1.
Возвращаемся к исходной переменной и решаем два уравнения:
tgx = 3/2, откуда x = arctg(3/2) + πn, n ∈ Z.
tgx = -1, откуда x = arctg(-1) + πm = -π/4 + πm, m ∈ Z.
Ответ: x = arctg(3/2) + πn или x = -π/4 + πm.
5. Решить уравнение 3cosx — sin2x = 1 — sin3x.
Сделаем следующее преобразование 3(cosx + sinx) = 1 + sin2x.
Замена cosx + sinx = t приведет к уравнению 3t = t2. Оно имеет корни t1 = 0, t2 = 3.
Берем первый корень, возвращаем замену и получаем cosx + sinx = 0, делим на cosx ≠ 0, откуда tgx = -1, x = -π/4 + πn (n ∈ Z).
Второй корень t2 дает уравнение cosx + sinx = 3. Это уравнение не имеет решений, т.к. и cosx, и cosx меньше равны 1, в сумме меньше равны 2.
Ответ: x = -π/4 + πn.
6. Решить уравнение cos2x + cos4x + cos6x = 0.
Проделаем следующие преобразования
(cos2x + cos6x) + cos4x = 0;
2cos4xcos2x + cos4x = 0;
cos4x(2cos2x + 1) = 0.
Имеем два случая:
cos4x = 0, откуда 4x = π/2 + πn, x = π/8 + πn/4 (n ∈ Z).
2cos2x + 1 = 0 или cos2x = -1/2, откуда 2x = ±2π/3 + 2πm, x = ±π/3 +
Простейшие тригонометрические уравнения и неравенства
\(\blacktriangleright\) Стандартные (простейшие) тригонометричекие уравнения — это уравнения вида
\(\sin x=a,\quad \cos x=a,\quad
\mathrm{tg}\,x=b,\quad
\mathrm{ctg}\,x=b\), которые имеют смысл при \(-1\leq a\leq 1,\quad b\in \mathbb{R}\).
Для решения данных уравнения удобно пользоваться единичной окружностью (радиус равен \(1\)).
\[{\color{red}{\text{Решение простейших тригонометрических уравнений}}}\]
Рассмотрим несколько примеров:
Пример 1. Решить уравнение \(\sin x=\dfrac12\).
Найдем на оси синусов точку \(\dfrac12\) и проведем прямую параллельно оси \(Ox\) до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, синус которых равен \(\dfrac12\). Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\). Тогда в нашем случае это углы \(\dfrac{\pi}6\) и \(\dfrac{5\pi}6\). Все остальные углы можно получить путем прибавления к данным углам \(2\pi\cdot n\), где \(n\) — целое число (т.е. поворотом от данных на целое число полных кругов).

Таким образом, решением являются \(x_1=\dfrac{\pi}6+2\pi n,\
x_2=\dfrac{5\pi}6+2\pi n, \ n\in \mathbb{Z}\).
Пример 2. Решить уравнение \(\cos x=-\dfrac{\sqrt2}{2}\).
Найдем на оси косинусов точку \(-\dfrac{\sqrt2}{2}\) и проведем прямую параллельно оси \(Oy\) до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, косинус которых равен \(-\dfrac{\sqrt2}{2}\). Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\). Тогда в нашем случае это углы \(\dfrac{3\pi}4\) и \(-\dfrac{3\pi}4\). Все остальные углы можно получить путем прибавления к данным \(2\pi\cdot n\), где \(n\) — целое число.

Таким образом, решением являются \(x_1=\dfrac{3\pi}4+2\pi n,\
x_2=-\dfrac{3\pi}4+2\pi n, \ n\in \mathbb{Z}\).
Пример 3. Решить уравнение \(\mathrm{tg}\,x=\dfrac{\sqrt3}3\).
Найдем на оси тангенсов точку \(\dfrac{\sqrt3}3\) и проведем прямую через эту точку и центр окружности до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, тангенс которых равен \(\dfrac{\sqrt3}3\).Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\). Тогда в нашем случае это углы \(\dfrac{\pi}6\) и \(-\dfrac{5\pi}6\). Все остальные углы можно получить путем прибавления к данным \(2\pi\cdot n\), где \(n\) — целое число, или путем прибавления к одному из данных углов \(\pi n\).

Таким образом, решением являются \(x=\dfrac{\pi}6+\pi n, \ n\in \mathbb{Z}\).
Пример 4. Решить уравнение \(\mathrm{ctg}\,x=\sqrt3\).
Найдем на оси котангенсов точку \(\sqrt3\) и проведем прямую через эту точку и центр окружности до пересечения с окружностью. Получим две точки на окружности, в которых находятся все углы, котангенс которых равен \(\sqrt3\). Выберем в каждой точке по одному углу, причем удобнее выбирать эти углы из отрезка \([-\pi;\pi]\). Тогда в нашем случае это углы \(\dfrac{\pi}6\) и \(-\dfrac{5\pi}6\). Все остальные углы можно получить путем прибавления к данным \(2\pi\cdot n\), где \(n\) — целое число, или путем прибавления к одному из данных углов \(\pi n\).

Таким образом, решением являются \(x=\dfrac{\pi}6+\pi n, \ n\in \mathbb{Z}\).
\(\blacktriangleright\) Решения для любого стандартного тригонометрического уравнения выглядят следующим образом: \[\begin{array}{l|c|c}
\hline \text{Уравнение} & \text{Ограничения} & \text{Решение}\\
\hline &&\\
\sin x=a & -1\leq a\leq 1 & \left[
\begin{gathered}
\begin{aligned}
&x=\arcsin a+2\pi n\\
&x=\pi -\arcsin a+2\pi n
\end{aligned}
\end{gathered}
\right. \ \ , \ n\in \mathbb{Z}\\&&\\
\hline &&\\
\cos x=a & -1\leq a\leq 1 & x=\pm \arccos a+2\pi n, \ n\in
\mathbb{Z}\\&&\\
\hline &&\\
\mathrm{tg}\, x=b & b\in \mathbb{R} & x=\mathrm{arctg}\, b+\pi n, \
n\in
\mathbb{Z}\\&&\\
\hline &&\\
\mathrm{ctg}\,x=b & b\in \mathbb{R} & x=\mathrm{arcctg}\, b+\pi n, \
n\in
\mathbb{Z}\\&&\\
\hline
\end{array}\] Иногда для более короткой записи решение для \(\sin x=a\) записывают как \(x=(-1)^k\cdot \arcsin a+\pi k, \ k\in \mathbb{Z}\).
\(\blacktriangleright\) Любые уравнения вида \(\mathrm{G}\,\big(f(x)\big)=a\), (где \(\mathrm{G}\) — одна из функций \(\sin, \ \cos, \ \mathrm{tg},\ \mathrm{ctg}\), а аргумент \(f(x)\) — некоторая функция) сводятся к стандартным уравнениям путем замены \(t=f(x)\).
Пример 5. Решить уравнение \(\sin{(\pi x+\dfrac{\pi}3)}=1\).
Сделав замену \(t=\pi x+\dfrac{\pi}3\), мы сведем уравнение к виду \(\sin t=1\). Решением данного уравнения являются \(t=\dfrac{\pi}2+2\pi n, n\in\mathbb{Z}\).
Теперь сделаем обратную замену и получим: \(\pi
x+\dfrac{\pi}3=\dfrac{\pi}2+2\pi n\), откуда \(x=\dfrac16+2n,\
n\in\mathbb{Z}\).
\[{\color{red}{\text{Объединение корней}}}\]
Если \(n\) точек, являющихся решением уравнения или системы, разбивают окружность на \(n\) равных частей, то их можно объединить в одну формулу: \(x=\alpha+\dfrac{2\pi}n,\ n\in\mathbb{Z}\), где \(\alpha\) — один из этих углов.
Рассмотрим данную ситуацию на примере:
Пример 6. Допустим, решением системы являются \(x_1=\pm \dfrac{\pi}4+2\pi n, \ x_2=\pm \dfrac{3\pi}4+2\pi n, \ n\in\mathbb{Z}\). Отметим эти точки на окружности:

Заметим, что длины дуг \(\buildrel\smile\over{AB},
\buildrel\smile\over{BC}, \buildrel\smile\over{CD},
\buildrel\smile\over{DA}\) равны \(\dfrac{\pi}2\), то есть эти точки разбили окружность на \(4\) равных части. Таким образом, ответ можно записать в виде одной формулы: \(x=\dfrac{\pi}4+\dfrac{\pi}2n, \
n\in\mathbb{Z}\).
\[{\color{red}{\text{Геометрическая интерпретация решений неравенств вида }\mathrm{G}\,(x) \lor a,}}\]
где \(\lor\) — один из знаков \(\leq,\ <,\ >,\ \geq\).
Пример 7. Изобразить на окружности множество решений неравенства \(\sin x >\dfrac12\).
Для начала отметим на окружности корни уравнения \(\sin x =\dfrac12\). Это точки \(A\) и \(B\). Все точки, синус которых больше \(\dfrac12\), находятся на выделенной дуге. Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то начало дуги — это \(A\), а конец — \(B\).

Выберем в точке \(A\) любой угол, например, \(\dfrac{\pi}6\). Тогда в точке \(B\) необходимо выбрать угол, который будет больше \(\dfrac{\pi}6\), но ближайший к нему, и чтобы синус этого угла также был равен \(\dfrac12\). Это угол \(\dfrac{5\pi}6\). Тогда все числа из промежутка \(\left(\dfrac{\pi}6;\dfrac{5\pi}6\right)\) являются решениями данного неравенства (назовем такое решение частным). А все решения данного неравенства будут иметь вид \(\left(\dfrac{\pi}6+2\pi n;\dfrac{5\pi}6+2\pi
n\right), n\in\mathbb{Z}\), т.к. у синуса период \(2\pi\).
Пример 8. Изобразить на окружности множество решений неравенства \(\cos x <\dfrac12\).
Для начала отметим на окружности корни уравнения \(\cos x =\dfrac12\). Это точки \(A\) и \(B\). Все точки, косинус которых меньше \(\dfrac12\), находятся на выделенной дуге. Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то начало дуги — это \(A\), а конец — \(B\).

Выберем в точке \(A\) любой угол, например, \(\dfrac{\pi}3\). Тогда в точке \(B\) необходимо выбрать угол, который будет больше \(\dfrac{\pi}3\), но ближайший к нему, и чтобы косинус этого угла также был равен \(\dfrac12\). Это угол \(\dfrac{5\pi}3\). Тогда все числа из промежутка \(\left(\dfrac{\pi}3;\dfrac{5\pi}3\right)\) являются решениями данного неравенства (назовем такое решение частным). А все решения данного неравенства будут иметь вид \(\left(-\dfrac{5\pi}3+2\pi n;-\dfrac{\pi}3+2\pi
n\right), n\in\mathbb{Z}\), т.к. у косинуса период \(2\pi\).
Пример 9. Изобразить на окружности множество решений неравенства \(\mathrm{tg}\, x \geq \dfrac{\sqrt{3}}3\).
Для начала отметим на окружности корни уравнения \(\mathrm{tg}\, x = \dfrac{\sqrt{3}}3\). Это точки \(A\) и \(B\). Все точки, тангенс которых больше или равен \(\dfrac{\sqrt{3}}3\), находятся на выделенных дугах, причем точки \(C\) и \(D\) выколоты, т.к. в них тангенс не определен.

Рассмотрим одну из дуг, например, \(\buildrel\smile\over{AC}\). Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то за конец дуги можно принять угол \(\dfrac{\pi}2\), тогда начало дуги — это угол \(\dfrac{\pi}6\) (угол должен быть меньше \(\dfrac{\pi}2\), но ближайший к нему). Значит, частным решением данного неравенства является полуинтервал \(\Big[\dfrac{\pi}6;\dfrac{\pi}2\Big)\). А все решения данного неравенства будут иметь вид \(\Big[\dfrac{\pi}6+\pi
n;\dfrac{\pi}2+\pi n\Big),
n\in\mathbb{Z}\), т.к. у тангенса период \(\pi\).
Пример 10. Изобразить на окружности множество решений неравенства \(\mathrm{ctg}\, x \leq \sqrt{3}\).
Для начала отметим на окружности корни уравнения \(\mathrm{ctg}\, x = \sqrt{3}\). Это точки \(A\) и \(B\). Все точки, котангенс которых меньше или равен \(\sqrt{3}\), находятся на выделенных дугах, причем точки \(C\) и \(D\) выколоты, т.к. в них котангенс не определен.

Рассмотрим одну из дуг, например, \(\buildrel\smile\over{AC}\). Т.к. при положительном обходе движение по окружности происходит против часовой стрелки, то за конец дуги можно принять угол \(\pi\), тогда начало дуги — это угол \(\dfrac{\pi}6\) (угол должен быть меньше \(\pi\), но ближайший к нему). Значит, частным решением данного неравенства является полуинтервал \(\Big[\dfrac{\pi}6;\pi\Big)\). А все решения данного неравенства будут иметь вид \(\Big[\dfrac{\pi}6+\pi
n;\pi+\pi n\Big), n\in\mathbb{Z}\), т.к. период котангенса \(\pi\).
\[{\color{red}{\text{Отбор корней}}}\]
Геометрический способ (по окружности).
Этот способ заключается в том, что мы отмечаем решения всех уравнений (неравенств) на единичной окружности и пересекаем (объединяем) их.
Пример 11. Найти корни уравнения \(\sin x=-\dfrac12\), если \(\cos x\ne \dfrac{\sqrt3}2\).
В данном случае необходимо пересечь решения первого уравнения с решением второго уравнения.
Решением первого уравнения являются \(x_1=-\dfrac{\pi}6+2\pi n,\
x_2=-\dfrac{5\pi}6+2\pi n,\ n\in \mathbb{Z}\), решением второго являются \(x\ne \pm \dfrac{\pi}6+2\pi n,\ n\in\mathbb{Z}\). Отметим эти точки на окружности:
Видим, что из двух точек, удовлетворяющих первому уравнению, одна точка \(x= -\dfrac{\pi}6+2\pi n\) не подходит. Следовательно, ответом будут только \(x=-\dfrac{5\pi}6+2\pi n, n\in \mathbb{Z}\).
Вычислительный способ.
Этот способ заключается в подстановке решений уравнения (системы) в имеющиеся ограничения. Для данного способа будут полезны некоторые частные случаи формул приведения: \[\begin{aligned}
&\sin{(\alpha+\pi n)}=\begin{cases} \sin \alpha, \text{при } n —
\text{ четном}\\ -\sin \alpha, \text{при } n — \text{ нечетном}
\end{cases}\\
&\cos{(\alpha+\pi n)}=\begin{cases} \cos \alpha, \text{при } n —
\text{ четном}\\ -\cos \alpha, \text{при } n — \text {нечетном}
\end{cases}\\
&\mathrm{tg}\,(\alpha+\pi n)=\mathrm{tg}\,\alpha\\
&\mathrm{ctg}\,(\alpha+\pi n)=\mathrm{ctg}\,\alpha\\
&\sin{\left(\alpha+\dfrac{\pi}2\right)}=\cos\alpha\\
&\cos{\left(\alpha+\dfrac{\pi}2\right)}=-\sin \alpha\\
&\,\mathrm{tg}\,\left(\alpha+\dfrac{\pi}2\right)=-\,\mathrm{ctg}\,\alpha\\
&\,\mathrm{ctg}\,\left(\alpha+\dfrac{\pi}2\right)=-\,\mathrm{tg}\,\alpha
\end{aligned}\]
Пример 12. Решить систему \(\begin{cases} \cos x=\dfrac12\\
\sin x+\cos x>0\end{cases}\)
Решением уравнения являются \(x_1=\dfrac{\pi}3+2\pi n,\ x_2=-\dfrac{\pi}3+2\pi n,\ n\in\mathbb{Z}\). Подставим в неравенство \(\sin x+\cos x>0\) по очереди оба корня:
\(\sin x_1+\cos x_1=\dfrac{\sqrt3}2+\dfrac12>0\), следовательно, корень \(x_1\) нам подходит;
\(\sin x x_2+\cos x_2=-\dfrac{\sqrt3}2+\dfrac12<0\), следовательно, корень \(x_2\) нам не подходит.
Таким образом, решением системы являются только \(x=\dfrac{\pi}3+2\pi
n,\ n\in\mathbb{Z}\).
Алгебраический способ.
Пример 13. Найти корни уравнения \(\sin x=\dfrac{\sqrt2}2\), принадлежащие отрезку \([0;\pi]\).
Решением уравнения являются \(x_1=\dfrac{\pi}4+2\pi n, \
x_2=\dfrac{3\pi}4 +2\pi n, \ n\in\mathbb{Z}\). Для того, чтобы отобрать корни, решим два неравенства: \(0\leq x_1\leq\pi\) и \(0\leq
x_2\leq\pi\):
\(0\leq \dfrac{\pi}4+2\pi n\leq\pi \Leftrightarrow -\dfrac18\leq n\leq\dfrac38\). Таким образом, единственное целое значение \(n\), удовлетворяющее этому неравенству, это \(n=0\). При \(n=0\) \(x_1=\dfrac{\pi}4\) — входит в отрезок \([0;\pi]\).
Аналогично решаем неравенство \(0\leq x_2\leq\pi\) и получаем \(n=0\) и \(x_2=\dfrac{3\pi}4\).
Для следующего примера рассмотрим алгоритм решения линейных уравнений в целых числах:
\[ax+by=c, \quad a,b,c — \text{целые числа}\]
Уравнение будет иметь решение в целых числах относительно \(x\) и \(y\) тогда и только тогда, когда \(c\) делится на \(НОД(a,b)\).
Пример: Уравнение \(2x+4y=3\) не имеет решений в целых числах, потому что \(3\) не делится на \(НОД(2,4)=2\). Действительно, слева стоит сумма двух четных чисел, то есть четное число, а справа — \(3\), то есть нечетное число.
Пример: Решить уравнение \(3x+5y=2\). Т.к. \(НОД(3,5)=1\), то уравнение имеет решение в целых числах. Выразим \(x\) через \(y\):
\[x=\dfrac{2-5y}3=\dfrac{2-2y}3-y\]
Число \(\dfrac{2-2y}3\) должно быть целым. Рассмотрим остатки при делении на \(3\) числа \(y\): \(0\), \(1\) или \(2\).
Если \(y\) при делении на \(3\) имеет остаток \(0\), то оно записывается как \(y=3p+0\). Тогда \[\dfrac{2-2y}3=\dfrac{2-2\cdot
3p}3=\dfrac23-2p\ne \text{целому числу}\]
Если \(y\) при делении на \(3\) имеет остаток \(1\), то оно записывается как \(y=3p+1\). Тогда \[\dfrac{2-2y}3=\dfrac{2-2(3p+1)}3=-2p=\text{целому числу}\]
Значит, этот случай нам подходит. Тогда \(y=3p+1\), а \(x=\dfrac{2-2y}3-y=-5p-1\).
Ответ: \((-5p-1; 3p+1), p\in\mathbb{Z}\).
Перейдем к примеру:
Пример 14. Решить систему \[\begin{cases} \sin \dfrac x3=\dfrac{\sqrt3}2\\[3pt] \cos \dfrac x2=1 \end{cases}\]
Решим первое уравнение системы:
\[\left[ \begin{gathered} \begin{aligned} &\dfrac x3=\dfrac{\pi}3+2\pi n\\[3pt] &\dfrac x3=\dfrac{2\pi}3 +2\pi m \end{aligned} \end{gathered} \right.\quad n,m\in\mathbb{Z} \quad \Leftrightarrow \quad \left[ \begin{gathered} \begin{aligned} &x=\pi+6\pi n\\ &x=2\pi +6\pi m \end{aligned} \end{gathered} \right.\quad n,m\in\mathbb{Z}\]
Решим второе уравнение системы:
\[\dfrac x2=2\pi k, k\in\mathbb{Z} \quad \Leftrightarrow \quad x=4\pi k, k\in\mathbb{Z}\]
Необходимо найти корни, которые удовлетворяют и первому, и второму уравнению системы, то есть пересечь решения первого и второго уравнений.
Найдем целые \(n\) и \(k\), при которых совпадают решения в сериях \(\pi+6\pi n\) и \(4\pi k\):
\[\pi + 6\pi n=4\pi k \quad \Rightarrow \quad 4k-6n=1\]
Т.к. \(НОД(4,6)=2\) и \(1\) не делится на \(2\), то данное уравнение не имеет решений в целых числах.
Найдем целые \(m\) и \(k\), при которых совпадают решения в сериях \(2\pi +6\pi m\) и \(4\pi k\):
\[2\pi +6\pi m=4\pi k \quad \Rightarrow \quad 2k-3m=1\]
Данное уравнение имеет решение в целых числах. Выразим \(k=\frac{3m+1}2=m+\frac{m+1}2\).
Возможные остатки при делении \(m\) на \(2\) — это \(0\) или \(1\).
Если \(m=2p+0\), то \(\frac{m+1}2=\frac{2p+1}2=p+\frac12\ne \) целому числу.
Если \(m=2p+1\), то \(\frac{m+1}2=\frac{2p+1+1}2=p+1= \) целому числу.
Значит, \(m=2p+1\), тогда \(k=3p+2\), \(p\in\mathbb{Z}\).
Подставим либо \(m\), либо \(k\) в соответствующую ему серию и получим окончательный ответ: \(x=4\pi k=4\pi (3p+2)=8\pi+12\pi p, p\in\mathbb{Z}\).
Тригонометрические уравнения | Материалы для подготовки к ЕГЭ по математике ЕГЭ-Студия
Ну что, перечисляем обе серии (1) и (2) в ответе через запятую? Нет! Серия (2) является в данном случае частью серии (1). Действительно, если в формуле (1) число n кратно 5, то мы получаем все решения серии (2).
Поэтому ответ: 
3. Бывает, что перед разложением суммы или разности тригонометрических функций в произведение надо проделать обратную процедуру: превратить произведение в сумму (разность).
Решим уравнение:
Домножаем обе части на 2, преобразуем левую часть в разность косинусов, а правую часть — в сумму косинусов:



Ответ: 
4. Ещё пример, где финальное разложение на множители поначалу замаскировано: Здесь используем формулу понижения степени:
Здесь используем формулу понижения степени: (которая является ни чем иным, как переписанной в другом виде формулой косинуса двойного
(которая является ни чем иным, как переписанной в другом виде формулой косинуса двойного
угла). Получаем:
 и дальше ясно.
и дальше ясно.
5. Многие оказываются в ступоре при виде следующего уравнения: Переносим косинус влево и применяем формулу приведения
Переносим косинус влево и применяем формулу приведения 

 Дальше — дело техники.
Дальше — дело техники.
6. А в этом примере нужны совсем другие манипуляции: Раскладываем синус двойного угла, всё собираем в левой части и группируем:
Раскладываем синус двойного угла, всё собираем в левой части и группируем:

 Цель достигнута.
Цель достигнута.
Рассмотрим уравнение: Степень каждого слагаемого в левой части равна двум. Точно так же, как в обычном многочлене
Степень каждого слагаемого в левой части равна двум. Точно так же, как в обычном многочлене степень каждого слагаемого равна двум (степень одночлена — это сумма степеней входящих в него сомножителей).
степень каждого слагаемого равна двум (степень одночлена — это сумма степеней входящих в него сомножителей).
Поскольку степени всех слагаемых одинаковы, такое уравнение называют однородным. Для однородных уравнений существует стандартный приём решения — деление обеих его частей на  . Возможность этого деления, однако, должна быть обоснована: а что, если косинус равен нулю?
. Возможность этого деления, однако, должна быть обоснована: а что, если косинус равен нулю?
Следующий абзац предлагаем выучить наизусть и всегда прописывать его при решении однородных уравнений.
Предположим, что  . Тогда в силу уравнения и
. Тогда в силу уравнения и  , что противоречит основному тригонометрическому тождеству. Следовательно, любое решение данного уравнения удовлетворяет условию
, что противоречит основному тригонометрическому тождеству. Следовательно, любое решение данного уравнения удовлетворяет условию  , и мы можем поделить обе его части на
, и мы можем поделить обе его части на  .
.
В результате деления приходим к равносильному квадратному уравнению относительно тангенса:
 и дальнейший ход решения трудностей не представляет
и дальнейший ход решения трудностей не представляет
1. Рассмотрим уравнение Если бы в правой части стоял нуль, уравнение было бы однородным. Мы поправим ситуацию изящным приёмом: заменим число 3 на выражение
Если бы в правой части стоял нуль, уравнение было бы однородным. Мы поправим ситуацию изящным приёмом: заменим число 3 на выражение  :
:
 и дело сделано.
и дело сделано.
2. Неожиданным образом сводится к однородному следующее уравнение: Казалось бы, где тут однородность? Переходим к половинному углу!
Казалось бы, где тут однородность? Переходим к половинному углу!


 откуда
откуда
 | (3) |
Мы не случайно довели это уравнение до ответа. В следующем разделе оно будет решено другим методом, и ответ окажется внешне непохожим на этот.
Введение дополнительного угла
Этот метод применяется для уравнений вида  . Он присутствует в школьных учебниках. Правда, в них рассматриваются только частные случаи — когда числа a и b являются значениями синуса и косинуса углов в 30°, 45° или 60°.
. Он присутствует в школьных учебниках. Правда, в них рассматриваются только частные случаи — когда числа a и b являются значениями синуса и косинуса углов в 30°, 45° или 60°.
1. Рассмотрим уравнение Делим обе части на 2:
Делим обе части на 2: Замечаем, что
Замечаем, что  :
:
В левой части получили синус суммы: ,
,
откуда  и
и 
2. Другой пример: Делим обе части на
Делим обе части на 
 Сделаем теперь для разнообразия в левой части косинус разности:
Сделаем теперь для разнообразия в левой части косинус разности:


 3. Рассмотрим теперь общий случай — уравнение
3. Рассмотрим теперь общий случай — уравнение Делим обе части на
Делим обе части на  :
:
 | (4) |
Для чего мы выполнили это деление? Всё дело в получившихся коэффициентах при косинусе и синусе. Легко видеть, что сумма их квадратов равна единице:
Это означает, что данные коэффициенты сами являются косинусом и синусом некоторого угла :
Соотношение (4) тогда приобретает вид: ,
,
или
Исходное уравнение сведено к простейшему. Теперь понятно, почему рассматриваемый метод называется введением дополнительного угла. Этим дополнительным углом как раз и является угол .
4. Снова решим уравнение Делим обе части на
Делим обе части на  :
: Существует угол такой, что
Существует угол такой, что  . Например,
. Например,  . Получаем:
. Получаем: ,
, ,
, ,
, ,
,
В предыдущем разделе мы решили это уравнение, сведя его к однородному, и получили в качестве ответа выражение (3). Сравните с полученным только что выражением. А ведь это одно и то же множество решений!
Универсальная подстановка
Запомним две важные формулы:
Их ценность в том, что они позволяют выразить синус и косинус через одну и ту же функцию — тангенс половинного угла. Именно поэтому они получили название универсальной подстановки. Единственная неприятность, о которой не надо забывать: правые части этих формул не определены при  . Поэтому если применение универсальной подстановки приводит к сужению ОДЗ, то данную серию нужно проверить непосредственно.
. Поэтому если применение универсальной подстановки приводит к сужению ОДЗ, то данную серию нужно проверить непосредственно.
1. Решим уравнение Выражаем
Выражаем  , используя универсальную подстановку:
, используя универсальную подстановку: Делаем замену
Делаем замену  :
: Получаем кубическое уравнение:
Получаем кубическое уравнение:
 Оно имеет единственный корень
Оно имеет единственный корень  . Стало быть,
. Стало быть,  , откуда
, откуда  .
.
Сужения ОДЗ в данном случае не было, так как уравнение с самого начала содержало  .
.
2. Рассмотрим уравнение А вот здесь использование универсальной подстановки сужает ОДЗ. Поэтому сначала непосредственно подставляем
А вот здесь использование универсальной подстановки сужает ОДЗ. Поэтому сначала непосредственно подставляем  в уравнение и убеждаемся, что это — решение.
в уравнение и убеждаемся, что это — решение.
Теперь обозначаем  и применяем универсальную подстановку:
и применяем универсальную подстановку: После простых алгебраических преобразований приходим к уравнению:
После простых алгебраических преобразований приходим к уравнению:

 Следовательно,
Следовательно,  и
и  .
.
Ответ:  .
.
Метод оценок
В некоторых уравнениях на помощь приходят оценки  .
.
3. Рассмотрим уравнение Так как оба синуса не превосходят единицы, данное равенство может быть выполнено лишь в
Так как оба синуса не превосходят единицы, данное равенство может быть выполнено лишь в
том случае, когда они равны единице одновременно: Таким образом, должны одновременно выполняться следующие равенства:
Таким образом, должны одновременно выполняться следующие равенства: Обратите внимание, что сейчас речь идёт о пересечении множества решений (а не об их объединении, как это было в случае разложения на множители). Нам ещё предстоит понять, какие значения x удовлетворяют обоим равенствам. Имеем:
Обратите внимание, что сейчас речь идёт о пересечении множества решений (а не об их объединении, как это было в случае разложения на множители). Нам ещё предстоит понять, какие значения x удовлетворяют обоим равенствам. Имеем: Умножаем обе части на 90 и сокращаем на π:
Умножаем обе части на 90 и сокращаем на π:

 Правая часть, как видим, должна делиться на 5. Число n при делении на 5 может давать остатки от 0 до 4; иначе говоря, число n может иметь один из следующих пяти видов: 5n, 5m + 1, 5m + 2, 5m + 3 и 5m + 4, где
Правая часть, как видим, должна делиться на 5. Число n при делении на 5 может давать остатки от 0 до 4; иначе говоря, число n может иметь один из следующих пяти видов: 5n, 5m + 1, 5m + 2, 5m + 3 и 5m + 4, где . Для того, чтобы 9n+ 1 делилось на 5, годится лишь n = 5m + 1.
. Для того, чтобы 9n+ 1 делилось на 5, годится лишь n = 5m + 1.
Искать k, в принципе, уже не нужно. Сразу находим x:
 Ответ:
Ответ:  .
.
4. Рассмотрим уравнение Ясно, что данное равенство может выполняться лишь в двух случаях: когда оба синуса одновременно равны 1 или −1. Действуя так, мы должны были бы поочерёдно рассмотреть две системы уравнений.
Ясно, что данное равенство может выполняться лишь в двух случаях: когда оба синуса одновременно равны 1 или −1. Действуя так, мы должны были бы поочерёдно рассмотреть две системы уравнений.
Лучше поступить по-другому: умножим обе части на 2 и преобразуем левую часть в разность косинусов:
 Тем самым мы сокращаем работу вдвое, получая лишь одну систему:
Тем самым мы сокращаем работу вдвое, получая лишь одну систему: Имеем:
Имеем: Ищем пересечение:
Ищем пересечение: Умножаем на 21 и сокращаем на π:
Умножаем на 21 и сокращаем на π: Данное равенство невозможно, так как в левой части стоит чётное число, а в правой — нечётное.
Данное равенство невозможно, так как в левой части стоит чётное число, а в правой — нечётное.
Ответ: решений нет.
5. Страшное с виду уравнение также решается методом оценок. В самом деле, из неравенств
также решается методом оценок. В самом деле, из неравенств  следует, что
следует, что  . Следовательно,
. Следовательно,  , причём равенство возможно в том и только в том случае, когда
, причём равенство возможно в том и только в том случае, когда Остаётся решить полученную систему. Это не сложно.
Остаётся решить полученную систему. Это не сложно.
Учёт тригонометрических неравенств
Рассмотрим уравнение:
Перепишем его в виде, пригодном для возведения в квадрат:
Тогда наше уравнение равносильно системе:
Решаем уравнение системы:
 ,
, ,
,
Второе уравнение данной совокупности не имеет решений, а первое даёт две серии:
Теперь нужно произвести отбор решений в соответствии с неравенством  . Серия
. Серия  не удовлетворяет этому неравенству, а серия
не удовлетворяет этому неравенству, а серия  удовлетворяет ему. Следовательно, решением исходного уравнения служит только серия
удовлетворяет ему. Следовательно, решением исходного уравнения служит только серия  .
.
Ответ:  .
.
Специальные приёмы
В этом разделе рассматриваются некоторые типы уравнений, приёмы решения которых нужно знать обязательно.
1. Рассмотрим уравнение
Это сравнительно редкий случай, когда используется исходная формула косинуса двойного угла: ,
, ,
, ,
,
Каждое из уравнений полученной совокупности мы решать умеем.
2. Теперь рассмотрим такое уравнение:

Метод решения будет совсем другим. Сделаем замену  . Как выразить
. Как выразить  через t? Имеем:
через t? Имеем: ,
,
откуда  . Получаем:
. Получаем: ,
, ,
, ,
,
Как действовать дальше, мы знаем.
3. Надо обязательно помнить формулы косинуса и синуса тройного угла (чтобы не изобретать их на экзамене): ,
,
Вот, например, уравнение:
Оно сводится к уравнению относительно  :
: ,
, ,
,
Дальше всё понятно.
4. Как бороться с суммой четвёртых степеней синуса и косинуса? Рассмотрим уравнение
Выделяем полный квадрат! ,
, ,
, ,
, ,
, ,
, ,
,
5. А как быть с суммой шестых степеней? Рассмотрим такое уравнение:
Раскладываем левую часть на множители как сумму кубов:  .
.
Получим: ,
,
С суммой четвёртых степеней вы уже умеете обращаться.
Мы рассмотрели основные методы решения тригонометрических уравнений. Знать их нужно обязательно, это — необходимая база.
В более сложных и нестандартных задачах нужно ещё догадаться, как использовать те или иные методы. Это приходит только с опытом. Именно этому мы и учим на наших занятиях.
