Вычитание векторов и правила вычитания
Определение и правила вычитания векторов
Рассмотрим два вектора и (рис. 1).
Если задан вектор , то можно построить противоположный ему вектор , равный по длине, но противоположно направленный. Сумма противоположных векторов равна нулевому вектору:
Таким образом, разность можно записать в следующем виде:
То есть разность двух векторов равна сумме уменьшаемого и вектора, противоположного вычитаемому.
Правило треугольника для разности векторов
Чтобы графически продемонстрировать разность векторов, необходимо отложить от произвольной точки вектор , из его начала вектор . Тогда вектор, начало которого совпадает с концом вектора , а конец – с концом вектора , и будет искомым вектором разности (рис. 2).
Правило параллелограмма разности векторов
Если два неколлинеарных вектора и имеют общее начало (рис. 3), то разностью этих вектор есть вектор, совпадающий с диагональю параллелограмма, построенного на этих векторах и , причем начало этой диагонали совпадает с концом вектора , а конец – с концом вектора .
Если векторы и заданы своими координатами в некотором базисе: , то, чтобы найти координаты их разности , необходимо от координат вектора отнять соответствующие координаты вектора :
Примеры вычитания векторов
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Вычитание векторов
Откладывание вектора от данной точки
Для того, чтобы ввести разность векторов, сначала необходимо разобраться в таком понятии, как откладывание вектора от данной точки.
Определение 1
Если точка $A$ начала какого-либо вектора $\overrightarrow{a}$, то говорят, что вектор $\overrightarrow{a}$ отложен от точки $A$ (рис. 1).
Рисунок 1. $\overrightarrow{a}$ отложенный от точки $A$
Введем следующую теорему:
Теорема 1
От любой точки $K$ можно отложить вектор $\overrightarrow{a}$ и притом только один.
Доказательство.
Существование: Здесь нужно рассмотреть два случая:
Вектор $\overrightarrow{a}$ — нулевой.
В этом случае, очевидно, что искомый вектор — вектор $\overrightarrow{KK}$.
Вектор $\overrightarrow{a}$ — ненулевой.
Обозначим точкой $A$ — начало вектора $\overrightarrow{a}$, а точкой $B$ — конец вектора $\overrightarrow{a}$. Проведем через точку $K$ прямую $b$ параллельную вектору $\overrightarrow{a}$. Отложим на этой прямой отрезки $\left|KL\right|=|AB|$ и $\left|KM\right|=|AB|$. Рассмотрим векторы $\overrightarrow{KL}$ и $\overrightarrow{KM}$. Из этих двух векторов искомым будет тот, который будет сонаправлен с вектором $\overrightarrow{a}$ (рис. 2)
Рисунок 2. Иллюстрация теоремы 1
Единственность: единственность сразу следует из построения, проведенного в пункте «существование».
Теорема доказана.
Вычитание векторов. Правило первое
Пусть нам даны векторы $\overrightarrow{a}$ и $\overrightarrow{b}$.
Определение 2
Разностью двух векторов $\overrightarrow{a}$ и $\overrightarrow{b}$ называется такой вектор $\overrightarrow{c}$, который при сложении с вектором $\overrightarrow{b}$ дает вектор $\overrightarrow{a}$, то есть
\[\overrightarrow{b}+\overrightarrow{c}=\overrightarrow{a}\]Обозначение: $\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{c}$.
Построение разности двух векторов рассмотрим с помощью задачи.
Пример 1
Пусть даны векторы $\overrightarrow{a}$ и $\overrightarrow{b}$. Построить вектор $\overrightarrow{a}-\overrightarrow{b}$.
Решение.
Построим произвольную точку $O$ и отложим от нее векторы $\overrightarrow{OA}=\overrightarrow{a}$ и $\overrightarrow{OB}=\overrightarrow{b}$. Соединив точку $B$ с точкой $A$, получим вектор $\overrightarrow{BA}$ (рис. 3).
Рисунок 3. Разность двух векторов
По правилу треугольника для построения суммы двух векторов видим, что
\[\overrightarrow{OB}+\overrightarrow{BA}=\overrightarrow{OA}\]То есть
\[\overrightarrow{b}+\overrightarrow{BA}=\overrightarrow{a}\]Из определения 2, получаем, что
\[\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{BA}\]Ответ: $\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{BA}$.
Из этой задачи получаем следующее правило для нахождения разности двух векторов. Чтобы найти разность $\overrightarrow{a}-\overrightarrow{b}$ нужно от произвольной точки $O$ отложить векторы $\overrightarrow{OA}=\overrightarrow{a}$ и $\overrightarrow{OB}=\overrightarrow{b}$ и соединить конец второго вектор с концом первого вектора.
Вычитание векторов. Правило второе
Вспомним следующее необходимое нам понятие.
Определение 3
Вектор $\overrightarrow{a_1}$ называется произвольным для вектора $\overrightarrow{a}$, если эти векторы противоположно направлены и имеют равную длину.
Обозначение: Вектор $(-\overrightarrow{a})$ противоположный для вектора $\overrightarrow{a}$.
Для того чтобы ввести второе правило для разности двух векторов, нам необходимо в начале ввести и доказать следующую теорему.
Теорема 2
Для любых двух векторов $\overrightarrow{a}$ и $\overrightarrow{b}$ справедливо следующее равенство:
\[\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{a}+(-\overrightarrow{b})\]Доказательство.
По определению 2, имеем
Прибавим к обеим частям вектор $\left(-\overrightarrow{b}\right)$, получим
Так как векторы $\overrightarrow{b}$ и $\left(-\overrightarrow{b}\right)$ противоположны, то $\overrightarrow{b}+\left(-\overrightarrow{b}\right)=\overrightarrow{0}$. Имеем
Теорема доказана.
Из этой теоремы получаем следующее правило для разности двух векторов: Чтобы найти разность $\overrightarrow{a}-\overrightarrow{b}$ нужно от произвольной точки $O$ отложить вектор $\overrightarrow{OA}=\overrightarrow{a}$, затем от полученной точки $A$ отложить вектор $\overrightarrow{AB}=-\overrightarrow{b}$ и соединить начало первого вектора с концом второго вектора.
Пример задачи на понятие разности векторов
Пример 2
Пусть дан параллелограмм $ADCD$, диагонали которого пересекаются в точке $O$. $\overrightarrow{AB}=\overrightarrow{a}$, $\overrightarrow{AD}=\overrightarrow{b}$ (рис. 4). Выразить через векторы $\overrightarrow{a}$ и $\overrightarrow{b}$ следующие векторы:
а) $\overrightarrow{DC}+\overrightarrow{CB}$
б) $\overrightarrow{BO}-\overrightarrow{OC}$
Рисунок 4. Параллелограмм
Решение.
а) Произведем сложение по правилу треугольника, получим
\[\overrightarrow{DC}+\overrightarrow{CB}=\overrightarrow{DB}\]Из первого правила разности двух векторов, получаем
\[\overrightarrow{DB}=\overrightarrow{a}-\overrightarrow{b}\]б) Так как $\overrightarrow{OC}=\overrightarrow{AO}$, получим
\[\overrightarrow{BO}-\overrightarrow{OC}=\overrightarrow{BO}-\overrightarrow{AO}\]По теореме 2, имеем
\[\overrightarrow{BO}-\overrightarrow{AO}=\overrightarrow{BO}+\left(-\overrightarrow{AO}\right)=\overrightarrow{BO}+\overrightarrow{OA}\]Используя правило треугольника, окончательно имеем
\[\overrightarrow{BO}+\overrightarrow{OA}=\overrightarrow{BA}=-\overrightarrow{AB}=-\overrightarrow{a}\]spravochnick.ru
Правила сложения и вычитания векторов
Сложение (и особенно вычитание) векторов – это классика, как простые вещи иногда объясняют сложным языком. Если я спрашиваю абитуриента, как складывать (или вычитать) вектора, он нередко говорит: «Ну, правило параллелограмма, надо начало первого соединить с концом второго… Или наоборот…». В общем, дети вынуждены зазубривать правила, а все зазубренное, но не понятое, очень быстро забывается.
Итак, рассмотрим простой и понятный способ складывать и вычитать вектора. Допустим, надо найти вектор , равный сумме векторов , и . То есть, надо найти =++ (рисунок 1)
Рисунок 1
С векторами разрешен только параллельный перенос. То есть, нельзя их поворачивать и менять их длину. А передвигать, не меняя длины и направления, можно. Теперь просто выстраиваем
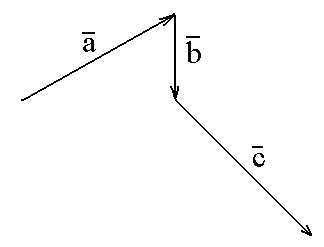
Рисунок 2
Проводим стрелку из начала цепочки в конец (красная линия). Это и есть вектор суммы (рисунок 3). Все.
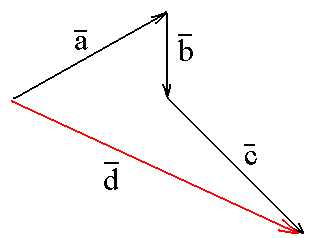
Рисунок 3
Тут, правда, есть один нюанс: как понимать фразу «выстраиваем вектора друг за другом»? Представьте, что по стрелкам векторов ползет жучок. Вы должны выстроить вектора так, чтобы жуку было понятно, куда ползти. Если вы выстроили вектора, например, вот так (рисунок 4):
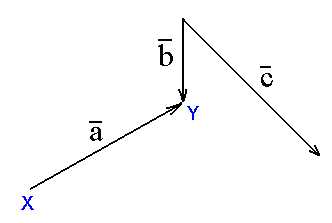
Рисунок 4
то это не «друг за другом». Жук выползает из точки Х, двигается по стрелкам, но в точке Y ему непонятно, что делать дальше. Если вы правильно выстроили вектора «друг за другом», то жук по стрелкам проползет из начальной точки в конечную (рисунок 5).

Рисунок 5
Теперь попробуем поменять слагаемые местами и найдем =++. Как и в прошлом случае, выстраиваем вектора друг за другом (чтобы жуку было понятно) и рисуем стрелку из начала в конец пути (рисунок 6).
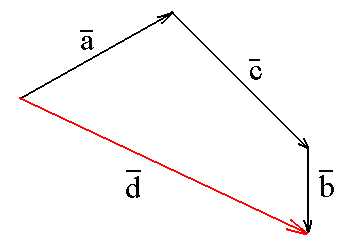
Рисунок 6
Как видите, суммарный вектор не зависит от очередности слагаемых. Тут как со скалярными величинами: от перемены мест слагаемых сумма не меняется. То есть, при сложении векторов их можно выстраивать в любом порядке. Результат будет одинаковым.
А как вычитать вектора? Да очень просто. Найдем, например, = —+. Чем отличается вектор от вектора — ? Только направлением (Рисунок 7).
Рисунок 7
Значит, выстраиваем друг за другом (чтобы жуку было понятно) вектора , — и . Соединяем начало и конец маршрута результирующим вектором (рисунок 8). Все.
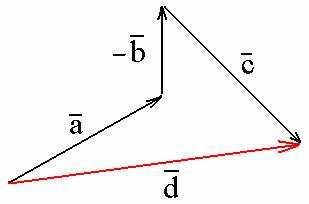
Рисунок 8
Фактически, тут мы нашли вектор =+(- )+.
Надеюсь, теперь у вас с векторами не будет проблем. Допустим, вам встретилась задача: на рисунке 9 изображены силы, действующие на тело; найти равнодействующую.
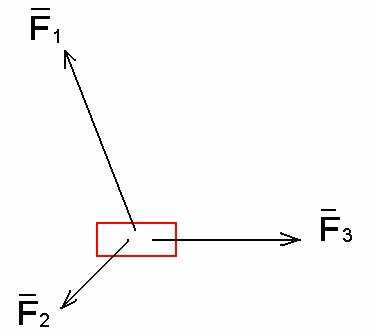
Рисунок 9
Просто выстраиваем вектора друг за другом (чтобы жуку было понятно) в любом порядке и строим результирующий вектор из начала в конец цепочки векторов (рисунок 10).

Рисунок 10
Красная стрелка на рисунке 10 – это вектор равнодействующей силы.
Похожая статья: что такое радиан.
—
Понравилась статья? Размести ссылку на сайт в социальных сетях
repetitor-fm.by
Вектор, действия с векторами, сложение и вычитание
Тестирование онлайн
Проекция вектора
Сложение и вычитание векторов
Вектор
Вектор — это отрезок, который имеет направление. Конец вектора совпадает со стрелкой, начало — точка. Модуль вектора (абсолютная величина) — длина этого направленного отрезка.
Если начало вектора совпадает с его концом, получим нулевой вектор.
Два вектора являются равными, если их длина одинаковая и они имеют одинаковое направление. Они совмещаются при переносе.
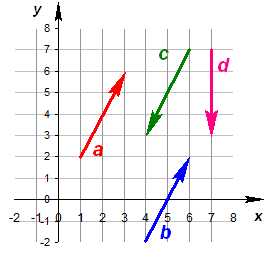
На рисунке только вектор a равен вектору b. Вектор c им не равен, так как направлен в противоположную сторону
Вектор -c — это вектор c, но противоположного направления. Тогда
Проекция вектора
Проекция вектора на ось имеет положительное значение в том случае, когда направление вектора совпадает с направлением оси. Отрицательное значение — в противоположном случае.

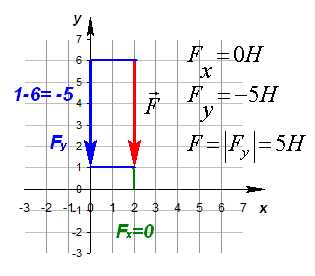
Спроецируем вектор перемещения на ось Ox и на ось Oy. Для того, чтобы получить проекцию необходимо из координаты конца вектора отнять координату начала. На ось ОХ: sx=x-x0, на ось ОУ: sy=y-y0.
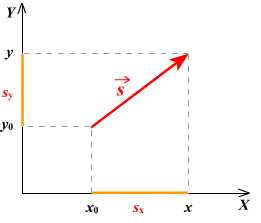
Рассмотрим примеры

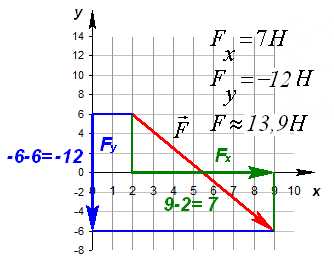
Частные случаи, когда проекция на ось Ox или Oy нулевая.
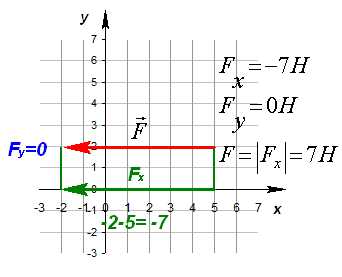
Сумма составляющих вектора по осям равна данному вектору, т.е.
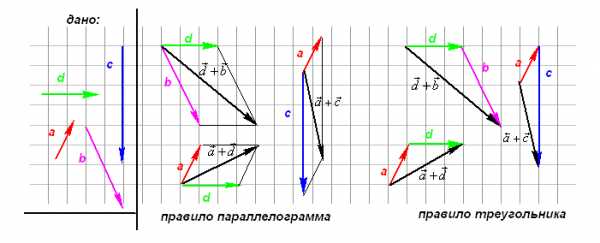
Сложение векторов
Правило параллелограмма: диагональ параллелограмма — сумма двух векторов с общим началом.
Правило треугольника: от конца первого вектора отложить второй вектор, тогда их суммой будет вектор, начало которого совпадает с началом первого вектора, а конец с концом второго вектора.
Рассмотрим правила на примерах.
Вычитание векторов
Вычитание векторов — это сумма положительного и отрицательного вектора.
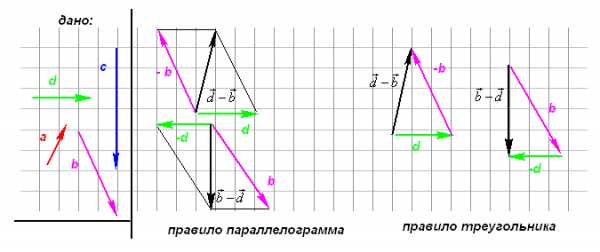
Упражнения
Может ли при сложении двух векторов по правилу параллелограмма равнодействующая быть численно равной одному из составляющих векторов?
Может ли при сложении двух векторов по правилу параллелограмма равнодействующая быть меньше меньшего из составляющих векторов?
fizmat.by
Сложение и вычитание векторов. Видеоурок. Геометрия 8 Класс
Тема: Векторы
Урок: Сложение и вычитание векторов
На предыдущем уроке мы определили понятие вектора, сказали, какие векторы называются равными, коллинеарными, сонаправленными и противонаправленными.
Теперь пусть задано два вектора – вектора и . Найдем сумму этих двух векторов . Для этого отложим из некоторой точки А вектор . Из точки В отложим вектор . Тогда вектор называют суммой заданных векторов: (см. Рис. 1).
Рис. 1
Данное определение можно объяснить так: пусть был задан груз, и сначала на него подействовала сила – он переместился из точки А в точку В, после этого подействовала сила – груз переместился из точки В в точку С. Но в результате действия двух этих сил груз переместился из точки А в точку С.
Таким образом, мы получили определение суммы двух векторов – правило треугольника.
Правило треугольника
Для того чтобы получить сумму двух векторов, нужно из произвольной точки отложить первый вектор, из конца полученного вектора отложить второй вектор, и построить вектор, соединяющий начало первого с концом второго – это и будет сумма двух векторов.
Можно провести аналогию с числами. Мы ввели понятие числа, научились складывать числа, определили законы сложения и так далее. Теперь мы ввели понятие вектора, научились находить равные вектора, складывать вектора. Теперь нужно определить законы сложения.
Законы сложения векторов
Для любых векторов , и справедливы следующие равенства:
– переместительный закон.
Доказательство: отложим из точки сначала вектор , получаем точку В, из нее откладываем вектор , получаем точку С и вектор .
Теперь отложим из точки А сначала вектор получим точку В, из нее отложим вектор, получим точку С и вектор .
Чтобы доказать равенство полученных векторов, выполним оба построения из одной точки и получим таким образом правило параллелограмма (см. Рис. 2).
Рис. 2
Откладываем из точки А вектор и вектор . Из точки В откладываем вектор , вектора и равны, а значит, стороны ВС и АВ1 четырехугольника АВСВ1 параллельны. Аналогично параллельны и стороны АВ и В1С, таким образом, мы получили параллелограмм. АС – диагональ параллелограмма. , таким образом, мы доказали переместительный
Рис. 3
закон сложения векторов и получили правило параллелограмма (см. Рис. 3).
Правило параллелограмма
Чтобы получить сумму двух векторов, нужно из произвольной точки отложить эти два вектора и построить на них параллелограмм. Диагональ параллелограмма, исходящая из начальной точки, и будет суммой заданных векторов.
– сочетательный закон;
Из произвольной точки А отложим вектор , прибавим к нему вектор , получим их сумму . К этой сумме прибавим вектор , получим результат (см. Рис. 4).
Рис. 4
В правой части выражения мы сначала получили сумму векторов , после прибавили ее к вектору и получили результат: (см. Рис. 5).
Таким образом, мы доказали сочетательный закон сложения векторов.
Рис. 5
Правило многоугольника
Чтобы сложить несколько векторов, нужно из произвольной точки отложить первый вектор, из его конца отложить второй вектор, из конца второго вектора отложить третий и так далее; когда все векторы отложены, соединив начальную точку с концом последнего вектора, получим сумму нескольких векторов (см. Рис. 6).
Рис. 6
По аналогии с действительными числами после того, как мы научились их складывать, нужна обратная операция – вычитание.
Пусть задано два вектора – векторы и . Найдем разность этих двух векторов .
Определение
Разностью двух векторов и называют такой третий вектор, сумма которого с вектором равна вектору .
Если задан вектор , то можно построить противоположный ему вектор , который будет равен по длине, но противонаправлен. Сумма противоположных векторов всегда есть нулевой вектор: . Таким образом, .
Отложим из произвольной точки вектор , из его конца отложим вектор , получим в результате вектор (см. Рис. 7).
Рис. 7
Рассмотрим вычитание векторов на параллелограмме. Из точки А отложим векторы и . Из точек В и D отложим векторв и соответственно. Диагональ АС – это сумма векторов и : . Но в параллелограмме есть еще вторая диагональ – BD. Прибавим к вектору вектор , получим вектор (см. Рис. 8).
Рис. 8
Итак, на данном уроке мы вывели правила сложения и вычитания векторов при помощи треугольника и параллелограмма, сформулировали законы сложения векторов.
Список литературы
- Александров А.Д. и др. Геометрия, 8 класс. – М.: Просвещение, 2006.
- Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
- Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия, 8 класс. – М.: ВЕНТАНА-ГРАФ, 2009.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Emomi.com (Источник).
- Prosto-o-slognom.ru (Источник).
- Изучение математики онлайн (Источник).
Домашнее задание
- Задание 1: дан треугольник , найдите сумму векторов: и ; и ; и ; и .
- Задание 2: турист прошел 20 км на восток из города А в город В, а потом 30 км на восток в город С. Выбрав подходящий масштаб, начертите векторы и Равны ли векторы и ?
- Задание 3: начертите попарно неколлинеарные векторы , и и постройте векторы , , .
interneturok.ru
Как вычесть вектор
Операция вычитания векторов, как и вычитание обычных чисел, обозначает действие, обратное операции сложения. Для обычных чисел это означает, что одно из слагаемых превращается в свою противоположность (его знак меняется на противоположный), а остальные действия осуществляются по тем же правилам, что и при обычном сложении. Для операции вычитания векторов нужно действовать также — сделать один из них (вычитаемый) своей противоположностью (поменять направление), а затем применить обычные правила сложения векторов.Инструкция
- Если вычитание надо отобразить на бумаге, то воспользуйтесь, например, правилом треугольника. Оно описывает операцию сложения векторов, а для того, чтобы применить ее к операции вычитания надо внести соответствующие поправки, касающиеся вычитаемого вектора. Его начало и конец надо поменять местами, то есть инвертировать вектор, и этим поменять его знак, чтобы операция сложения стала операцией вычитания.
- Перенесите вычитаемый вектор параллельно самому себе таким образом, чтобы его окончание совпало с окончанием уменьшаемого вектора. Затем соедините начало перенесенного вектора с началом уменьшаемого и поставьте стрелку в том конце отрезка, который совпадает с началом перенесенного вектора. Этот вектор с началом, совпадающим с началом уменьшаемого вектора, и окончанием в начале перенесенного вектора и будет результатом операции вычитания.
- Используйте правило параллелограмма (с поправкой на инвертирование вычитаемого вектора) в качестве альтернативы правилу треугольника. Для этого перенесите вычитаемый вектор параллельно самому себе таким образом, чтобы его окончание совпадало с началом уменьшаемого вектора. Таким способом вы получите две стороны геометрической фигуры — параллелограмма. Достройте его недостающие стороны и проведите диагональ из точки, которая является концом вычитаемого и началом уменьшаемого векторов. Эта диагональ и будет вектором, полученным в результате вычитания.
- Если уменьшаемый и вычитаемый векторы заданы не графически, а координатами своих конечных точек в двухмерной или трехмерной системе координат, то и результат вычитания можно представить в таком же виде. Для этого просто отнимите значения координат вычитаемого вектора от соответствующих значений координат уменьшаемого вектора. Например, если вектор A (уменьшаемый) задан координатами (Xa;Ya;Za), а вектор B (вычитаемый) — координатами (Xb;Yb;Zb), то результатом операции вычитания A-B будет вектор C с координатами (Xa-Xb; Ya-Yb; Za-Zb).
completerepair.ru
определение, формула для нахождения, аналитический метод и графическое построение
 В математике и физике студентам и школьникам зачастую попадаются задачи на векторные величины и на выполнение различных операций над ними. В чём же отличие векторных величин от привычных нам скалярных, единственная характеристика которых — это численное значение? В том, что они обладают направлением.
В математике и физике студентам и школьникам зачастую попадаются задачи на векторные величины и на выполнение различных операций над ними. В чём же отличие векторных величин от привычных нам скалярных, единственная характеристика которых — это численное значение? В том, что они обладают направлением.
[block id=»32″]
Вконтакте
Одноклассники
Мой мир
[block id=»33″]
Максимально наглядно применение векторных величин объясняется в физике. Самыми простыми примерами являются силы (сила трения, сила упругости, вес), скорость и ускорение, поскольку помимо численных значений они также обладают направлением действия. Для сравнения приведём пример скалярных величин: это может быть расстояние между двумя точками или масса тела. Для чего же необходимо выполнять действия над векторными величинами такие как сложение или вычитание? Это нужно, чтобы было возможно определить результат действия системы векторов, состоящей из 2 или более элементов.
Определения векторной математики
Введём главные определения, используемые при выполнении линейных операций.
- Вектором называют направленный (имеющий точку начала и точку конца) отрезок.
- Длина (модуль) — это длина направленного отрезка.
- Коллинеарными называют такие два вектора, которые либо параллельны одной и той же прямой, либо одновременно лежат на ней.
- Противоположно направленными векторами называют коллинеарные и при этом направленные в разные стороны. Если же их направление совпадает, то они являются сонаправленными.
- Вектора являются равными, когда они сонаправлены и одинаковы по модулю.
- Суммой двух векторов a и b является такой вектор c, начало которого совпадает с началом первого, а конец — с концом второго при условии, что b начинается в той же точке, в которой заканчивается a.
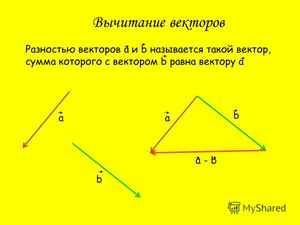
- Разностью векторов a и b называют сумму a и (— b), где (— b) — противоположно направленный к вектору b. Также определение разности двух векторов может быть дано следующее: разностью c пары векторов a и b называют такой c, который при сложении с вычитаемым b образует уменьшаемое a.
[block id=»3″]
Аналитический метод
Аналитический способ подразумевает получение координат разности по формуле без построения. Возможно выполнить вычисление для плоского (двухмерного), объёмного (трёхмерного) или же n-мерного пространства.
Для двухмерного пространства и векторных величин a {a₁; a₂} и b {b₁; b₂} расчёты будут иметь следующий вид: c {c₁; c₂} = {a₁ — b₁; a₂ — b₂}.
В случае с добавлением третьей координаты расчёт будет проводиться аналогично, и для a {a₁; a₂; a₃} и b {b₁; b₂; b₃} координаты разности будут также получены попарным вычитанием: c {c₁; c₂; c₃} = {a₁ — b₁; a₂ — b₂; a₃ — b₃}.
Вычисление разности графически
Для того чтобы построить разность графическим способом, следует воспользоваться правилом треугольника. Для этого необходимо выполнить следующую последовательность действий:
- По заданным координатам построить векторы, для которых нужно найти разность.
- Совместить их концы (т. е. построить два направленных отрезка, равных заданным, которые будут оканчиваться в одной и той же точке).
- Соединить начала обоих направленных отрезков и указать направление; результирующий будет начинаться в той же точке, где начинался вектор, являющийся уменьшаемым, и заканчиваться в точке начала вычитаемого.
[block id=»4″]
Результат операции вычитания показан на рисунке ниже.
Также существует метод построения разности, незначительно отличающийся от предыдущего. Его суть заключается в применении теоремы о разности векторов, которая формулируется следующим образом: для того чтобы найти разность пары направленных отрезков, достаточно найти сумму первого из них с отрезком, противоположно направленным ко второму. Алгоритм построения будет иметь следующий вид:
- Построить исходные направленные отрезки.
- Тот, что является вычитаемым, необходимо отразить, т. е. построить противоположно направленный и равный ему отрезок; затем совместить его начало с уменьшаемым.
- Построить сумму: соединить начало первого отрезка с концом второго.
Результат такого решения изображён на рисунке:
Решение задач
Для закрепления навыка разберём несколько заданий, в которых требуется рассчитать разность аналитически или графически.
Задача 1. На плоскости заданы 4 точки: A (1; —3), B (0; 4), C (5; 8), D (—3; 2). Определить координаты вектора q = AB — CD, а также рассчитать его длину.
Решение. Вначале следует найти координаты AB и CD. Для этого из координат конечных точек вычтем координаты начальных. Для AB началом является A (1; —3), а концом — B (0; 4). Рассчитаем координаты направленного отрезка:
AB {0 — 1; 4 — (— 3)} = {— 1; 7}
Аналогичный расчёт выполняется для CD:
CD {— 3 — 5; 2 — 8} = {— 8; — 6}
Теперь, зная координаты, можно найти разность векторов. Формула для аналитического решения плоских задач была рассмотрена ранее: для c = a — b координаты имеют вид {c₁; c₂} = {a₁ — b₁; a₂ — b₂}. Для конкретного случая можно записать:
q = {— 1 — 8; 7 — ( — 6)} = { — 9; — 1}
Чтобы найти длину q, воспользуемся формулой | q | = √(q₁² + q₂²) = √((— 9)² + (— 1)²) = √(81 + 1) = √82 ≈ 9,06.
[block id=»5″]
Задача 2. На рисунке изображены векторы m, n и p.
Необходимо построить для них разности: p — n; m — n; m — n — p. Выяснить, какая из них обладает наименьшим модулем.
Решение. В задаче требуется выполнить три построения. Рассмотрим каждую часть задания более подробно.
Часть 1. Для того чтобы изобразить p — n, воспользуемся правилом треугольника. Для этого при помощи параллельного переноса соединим отрезки так, чтобы совпала их конечная точка. Теперь соединим начальные точки и определим направление. В нашем случае вектор разности начинается там же, где и вычитаемый n.
Часть 2. Изобразим m — n. Теперь для решения воспользуемся теоремой о разности векторов. Для этого следует построить вектор, противоположный n, а затем найти его сумму с m. Полученный результат будет выглядеть так:
[block id=»6″]
Часть 3. Для того чтобы найти разность m — n — p, следует разбить выражение на два действия. Поскольку в векторной алгебре действуют законы аналогичные законам арифметики, то возможны варианты:
- m — (n + p): в этом случае вначале строится сумма n + p, которая затем вычитается из m;
- (m — n) — p: здесь сначала нужно найти m — n, а затем отнять от этой разности p;
- (m — p) — n: первым действием определяется m — p, после чего из полученного результата нужно вычесть n.
Так как в предыдущей части задачи мы уже нашли разность m — n, нам остаётся лишь вычесть из неё p. Построим разность двух данных векторов при помощи теоремы о разности. Ответ показан на изображении ниже (красным цветом обозначен промежуточный результат, а зелёным — окончательный).
Остаётся определить, модуль какого из отрезков является наименьшим. Вспомним, что понятия длины и модуля в векторной математике являются идентичными. Оценим визуально длины p — n, m — n и m — n — p. Очевидно, что самым коротким и обладающим наименьшим модулем является ответ в последней части задачи, а именно m — n — p.
[block id=»2″]
[block id=»10″]
obrazovanie.guru
