примеры по математике & дроби
Математические игры
Бесплатное приложение для изучения математики, подходящее для студентов, детей, мальчиков, девочек, взрослых, родителей, бабушек и дедушек, чтобы заниматься математикой, улучшать математические навыки и тренировать свой мозг!
Учить математику
Приложение представляет собой отличное образовательное приложение для детей, начальной школы, средней школы, техникума и студентов. Экзамены и тесты по математике делают обучение намного более увлекательным! Если вы хотите тренировать свой мозг, вы попали в нужное место!
Тесты и экзамены по математике
Воспользуйтесь приложением, если вы ждете теста, экзамена или просто испытываете трудности с решением задач. Вы можете учиться онлайн! Если вы учитель математики и ищете приложение, которое тренирует ваш мозг, вы попали в нужное место!
Домашнее задание
Если вы учитель, вы можете использовать приложение для подготовки домашних заданий, тестов, экзаменов или учебных материалов в школе.
Пройдите тесты по математике
В приложении вы можете выбирать вопросы из списка и создавать собственные тесты и экзамены. Если вы ждете теста в школе, вы можете быстро изучить задание и сэкономить время!
Математические игры
Совершенствуйте свои математические навыки и наслаждайтесь образовательными играми, которые мы подготовили для вас. Веселитесь с забавными математическими играми!
Математическое приложение
Вы ищете математические приложения, которые помогут вам заниматься математикой? Learn Math — лучшее математическое приложение из всех, скачайте его и попробуйте!
Бесплатная математика
Все упражнения доступны бесплатно!
1 класс
— сложение и вычитание
— римские числа
2 — 3 классы
— умножение и деление
— преобразование единиц измерения
— порядок действий
Класс 4-5
— проценты
— элементы
— силы и корни
— фракции
— добавление дробей
— вычитание дробей
— десятичные дроби
— алгебра
6-7-8 класс
— уравнения
— система уравнений
— основные геометрические фигуры
— сплошная геометрия
Старшие классы средней школы
— логарифмы
— короткие формулы умножения
— теорема синусов и косинусов
— последовательности
— аналитическая геометрия
— полиномы
Для 1 класса
— сложение и вычитание
— римские числа
Для 2 и 3 классов:
— умножение и деление
— преобразование единиц измерения
— Порядок операций
Для 4 и 5 классов:
— проценты
— элементы
— силы и корни
— фракции
— добавление дробей
— вычитание дробей
— десятичные дроби
— алгебра
Для 6-го, 7-го и 8-го:
— уравнения
— система уравнений
— основные геометрические фигуры
— сплошная геометрия
Для учеников средней школы:
— логарифмы
— короткие формулы умножения
— теорема синусов и косинусов
— последовательности
— аналитическая геометрия
— полиномы
«Сложение дробей с одинаковыми знаменателями».
4-й классКлючевые слова: УМК «Школа 2000…», сложение дробей с одинаковыми знаменателями
Образовательная программа: «Школа 2000…»
Класс: 4.
Тип урока: ОНЗ.
Цели:
- сформировать умение складывать дроби с одинаковыми знаменателями;
- повторить понятие дроби, закрепить умение читать и сравнивать дроби;
- тренировать вычислительные навыки, умение решать задачи на нахождение части;
- формировать УУД.
Мыслительные операции, необходимые на этапе проектирования: анализ, сравнение, аналогия, обобщение.
Ход урока
1. Мотивация к учебной деятельности— Сегодня у нас урок ОНЗ – урок открытия новых знаний. По какому плану вы открываете новые знания?
План:
- Исследуем и наблюдаем.
- Открываем новое знание.
- Применяем знания.
- Контролируем.
- Оцениваем.
— Всё правильно. А сначала повторим то, что нам понадобится для изучения нового.
2. Актуализация знаний и фиксация затруднения в пробном действииНа доске записаны числа:
— На какие две группы можно разбить эти числа? (Натуральные и дроби)
— Что вы уже знаете о натуральных числах и что умеете делать с ними? (Знаем, что такое натуральные числа; умеем их записывать; отмечать на числовом луче; сравнивать; складывать; вычитать; умножать; делить.)
— Что вы уже знаете о дробях и что умеете делать с дробями? (Знаем, что такое дробь; умеем записывать дроби; изображать графические модели дробей, отмечать на числовом луче; сравнивать дроби; находить части числа и число по его части; части, которую одно число составляет от другого.)
— Проверим, насколько хорошо вы умеете это делать.
Проводится опрос-тест с помощью программы Plickers:
- Вычисли 5/8 от 16.
- Вычисли 3/11 от 33.
- Вычисли 7% от 600.
- Найди число, 2/9 которого равны 8.
- Найди число, 5% которого равны 35.
— Для чего служат натуральные числа, а для чего – дроби? (Натуральные числа служат для счёта предметов, а дроби – для выражения их частей.)
— Интересно, Что ещё математики древности высоко ценили умение оперировать дробями. Вот одна старинная задача. У Пифагора спросили однажды, сколько у него учеников. Он ответил: «Половина моих учеников изучают прекрасную математику, четверть исследуют тайны природы, седьмая часть упражняет силу духа. Добавьте ещё к ним трёх юношей, их которых Теон самый способный».
— Чтобы ответить на вопрос этой задачи, надо сложить несколько чисел. Трудность в том, что эти числа – дроби!
— Сможете ли вы решить эту задачу? (Нет.)
— Что вы ещё не умеете делать? (Складывать дроби.
)
— Сформулируйте цель нашего урока. (Научиться складывать дроби.)
— Но дроби бывают разные: с одинаковыми знаменателями и разными. Сегодня вы научитесь складывать дроби с одинаковыми знаменателями.
— Найдите среди чисел на доске дроби с одинаковыми знаменателями. ()
— Что показывает каждое число в записи дроби? (Под чертой – знаменатель, он показывает, на сколько равных частей разделили целое. Над чертой – числитель, он показывает, сколько равных долей взято.)
— Что, значит, сложить числа? (Объединить в одно целое.)
— Попробуйте сложить эти дроби.
Что у вас получилось? ()
— Кто не смог получить ответ? Почему? (Мы не можем сложить дроби .)
— Кто из получивших ответ сможет доказать, что ответ верный? (Не можем доказать)
3. Выявление места и причины затруднения— Какое задание вы выполняли? (Складывали дроби .)
— Что особенного в записи этих дробей? (Одинаковые знаменатели.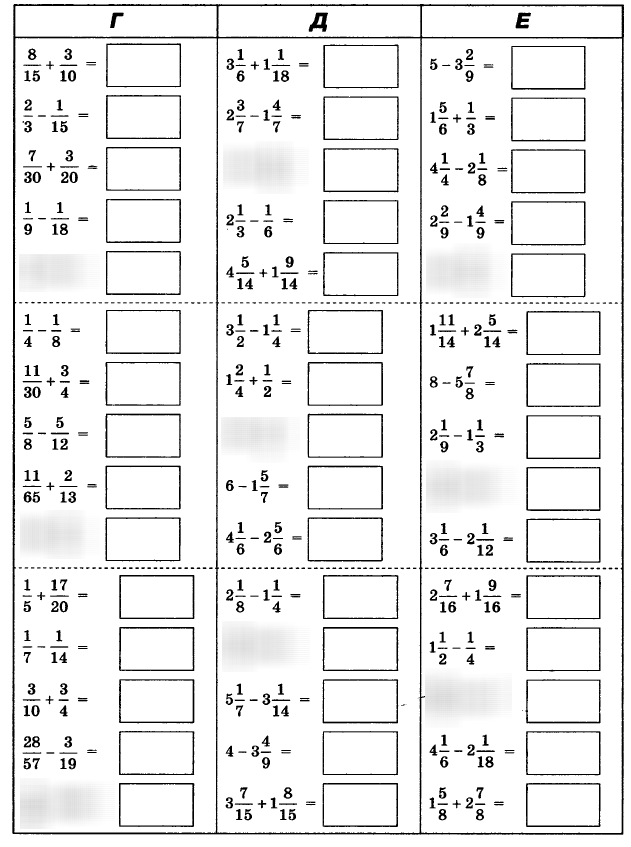
)
— Как пробовали выполнить сложение дробей? (Учащиеся объясняют свои действия.)
— Почему возникли затруднения? (Не знаем единого способа сложения дробей.)
4. Построение проекта выхода из затруднения— Какова же цель урока? (Научиться складывать дроби и построить алгоритм сложения дробей с одинаковыми знаменателями.)
— Уточним тему урока. (Сложение дробей с одинаковыми знаменателями.)
— Что вам может помочь? (Графические модели. Числовой луч.)
На доске составляется план выхода из затруднения.
План:
1) Выполнить сложение с помощью графических моделей.
2) Проанализировать результат.
3) Сформулировать вывод. Записать его в общем виде.
4) Оформить алгоритм.
— Сейчас вы будете работать в группах по составленному плану. Вспомните правила работы в группе.
У каждой группы в конвертах лежат необходимые материалы для работы: графическая модель, блоки для составления алгоритма, карточки для составления опорного конспекта.
— Выполнить сложение с помощью графической модели. На реализацию плана отводится 5 минут.
— Итак, сравним опорные конспекты, которые вы дополнили. Конспекты вывешиваются на доске. Что можете сказать? (Получились одинаковые конспекты.)
— Чтобы проверить правильность выполнения задания посмотрите видео-урок (отрывок) Ю.К.Грачёвой на портале «Знайка».
— Правильно ли вы составили опорные конспекты?
— А теперь посмотрим, какие алгоритмы получились в группах.
Представитель одной группы зачитывает алгоритм. Остальные группы соглашаются или не соглашаются с ним. В ходе обсуждения на доске появляется правильный алгоритм.
— Можно ли данный способ (алгоритм) применить для выполнения пробного действия? (Да.)
— Правило сложения дробей есть в учебнике. С ним вы можете сравнить свои выводы. Откройте учебник и прочитайте правило на стр.7. Сравните с вашим результатом.
(Похожи.)
— Чем вы пользовались, чтобы сложить дроби? (графической моделью)
— Расскажите, как складывали дроби с помощью числового луча.
(Объяснения детей.)
— Откройте в учебнике № 2, 3 на стр. 7. Выполните задания, работая в парах с проговариванием.
Проверка результатов.
— Где возможна ошибка при решении таких примеров? (При сложении чисел в числителях и на применение алгоритма.)
— Каким правилом пользовались для сложения дробей?
7. Самостоятельная работа с самопроверкой по эталону— Проверим, как вы научились ли вы складывать дроби с одинаковыми знаменателями? Для этого проведём самостоятельную работу. № 4 на стр.7.
Проверка по эталону.
— Кто допустил ошибки? В каком месте, и по каким причинам?
— Что нужно сделать, чтобы не допускать ошибки? (Тренироваться.)
— Какое задание в учебнике можно использовать для тренировки? (№ 7, стр.
8)
— Кто выполнил верно?
8. Включение в систему знаний и повторение— Где вы можете применить новый способ? (При решении уравнений, задач.)
Задача на слайде:
«Помидорами занято 4/11 поля, а помидорами — 2/11 поля. Какая часть поля занята огурцами и помидорами?»
— Прочитайте текст задачи. Выполните анализ. Решите задачу.
Проверка по эталону на слайде.
— Кто допустил ошибки? В каком месте, и по каким причинам?
— Кто выполнил верно?
— Каким правилом пользовались для сложения дробей?
На слайде иллюстрация сложения дробей.
— Какая часть рисунка закрашена?
— Как посчитали?
9. Рефлексия учебной деятельности на уроке— Какова была цель сегодняшнего урока? (Научиться складывать дроби с одинаковым знаменателем. Построить алгоритм сложения дробей с одинаковыми знаменателями.)
— Достигли ли вы этой цели? (Да.
)
— Сможете ли вы теперь решить задачу Пифагора? Почему?
— Да, вам ещё многому надо научиться!
Слайд.
Домашнее задание: стр. 8, № 7, 8.
Математические навыки, которые ваш ребенок освоит в четвертом классе
- Математические советы
- Образование
- 4-й
В четвертом классе учащиеся начинают изучать более сложные математические понятия. Не перегружайтесь! Лучший способ поддержать вашего ребенка — сохранять позитивное отношение к математике, пока вы вместе занимаетесь математикой в четвертом классе. Начните с того, что узнайте больше о том, над чем будет работать ваш ребенок.
В течение года ваш ребенок будет:
1. Умножать большие числа
Теперь, когда ваш ребенок имеет базовые знания об умножении, пора перейти к работе с большими числами.
В четвертом классе учащиеся учатся умножать четырехзначные числа на однозначные числа и умножать два двузначных числа вместе.
Помогите ребенку развить понимание, используя различные стратегии при умножении. Например, ваш ребенок может использовать картинки, знания о значении места или традиционный способ решения задач. Дайте ребенку задачу на умножение и предложите ему решить ее двумя разными способами.
2. Деление с остатком
Как и в случае с умножением, ваш четвероклассник готов перейти к более сложным задачам на деление. В четвертом классе ваш ребенок научится делить числа до четырех цифр. Эти проблемы часто будут включать в себя остатки, которые могут быть новой концепцией для вашего ребенка.
Опять же, эти проблемы деления могут и должны быть решены с использованием нескольких стратегий.
Поощряйте ребенка использовать картинки, прямоугольные массивы, его знание разрядности и/или умножения. Дайте ребенку свободу экспериментировать, используя разные стратегии и сравнивая/сопоставляя их работу.
3. Найдите множители чисел от 1 до 100
Хотя ваш ребенок работает над умножением и делением больших чисел, он, вероятно, не на 100 % владеет фактами умножения и деления.
Отличный способ попрактиковаться в этих фактах — вычислить множители двузначных чисел. Пусть ваш ребенок перечислит все множители заданного числа от 1 до 100. Или устройте «гонку множителей», когда вы оба пытаетесь как можно быстрее перечислить множители числа.
4. Решайте задачи из реальной жизни
Ваш ребенок работает над беглостью сложения, вычитания, умножения и деления, поэтому он готов начать решать задачи, используя их все (хотя, возможно, не все сразу!) .
Ваш четвероклассник готов решать многошаговые словесные задачи, включающие сценарии из реальной жизни, касающиеся расстояний, интервалов времени, объемов жидкости, массы объектов и денег.
Помогите своему ребенку решить текстовые задачи, предложив для размышления сценарии из реальной жизни. Придумайте многоступенчатую задачу, но не говорите ребенку, что он должен использовать для ее решения. Обсудите ответ вместе. Вы даже можете попросить ребенка составить для вас текстовые задачи и сравнить ваши ответы с ответами друг друга.
5. Понимание больших чисел в различных формах
В предыдущих классах ваш ребенок развил понимание разрядного значения. В четвертом классе пора читать и записывать многозначные числа в самых разных формах. Ваш ребенок научится работать с десятичными числами, названиями чисел и развернутой формой.
Поддержите своего ребенка в написании одного и того же числа, используя расширенную форму и имена чисел.
Например, дайте ребенку число 39 420, чтобы написать в развернутом виде: 30 000 + 9.,000 + 400 + 20. Предложите своему ребенку сделать это с еще большими числами!
6. Работа с дробями
Четвертоклассники обычно имеют базовые представления о дробях, но теперь они узнают больше об эквивалентности и умножении дробей. В четвертом классе учащиеся узнают, как сравнивать две дроби с разными знаменателями или разными числителями. Они также будут работать над умножением дробей на целое число.
Приготовление пищи и выпечка — это отличные места, где учащиеся могут найти реальные примеры дробей для сравнения (например, ¼ чашки риса больше, чем ⅓ чашки бульона?)
7. Сравните десятичные числа
Учащиеся четвертого класса развивают понимание как больших чисел, так и чисел меньше 1, таких как дроби и десятичные дроби. В четвертом классе учащиеся сравнивают два десятичных знака с сотыми.
Дайте ребенку две разные десятичные дроби (например, 0,24 и 0,48) для сравнения.
Пусть ваш ребенок скажет вам не только, какая десятичная дробь больше, но и сколько десятых и сотых в каждом числе.
В четвертом классе предстоит многому научиться математике — найдите время, чтобы регулярно связываться со своим ребенком, чтобы узнать все об этом!
Нашли это полезным? Ознакомьтесь с нашими руководствами по математике для классов от детского сада до 5-го класса
Написанное Лили Джонс, Лили любит учиться всему. Она работала воспитателем в детском саду и начальных классах, педагогическим тренером, разработчиком учебных программ и тренером для учителей. Она любит смотреть на мир с любопытством и вдохновлять людей всех возрастов любить учиться. Она живет в Калифорнии с мужем, двумя детьми и маленькой собачкой.
О Комодо – Komodo — это веселый и эффективный способ улучшить математические навыки K-5. Разработанный для детей от 5 до 11 лет для использования дома, Komodo использует небольшой и частый подход к изучению математики (15 минут, три-пять раз в неделю), который вписывается в занятую семейную рутину.