Примеры с дробями 5 класс как решать: Сложение и вычитание дробей с разными знаменателями — урок. Математика, 5 класс.

ПРИМЕРЫ НА ВСЕ ДЕЙСТВИЯ С ОБЫКНОВЕННЫМИ ДРОБЯМИ.

ПРИМЕРЫ НА ВСЕ ДЕЙСТВИЯ С ОБЫКНОВЕННЫМИ ДРОБЯМИ.

АРИФМЕТИКА     В НАЧАЛО   ПРИМЕРЫ НА ВСЕ ДЕЙСТВИЯ С ОБЫКНОВЕННЫМИ ДРОБЯМИ.   Произвести указанные действия:   1. 1) 2) 3) 4) Ответы: 2. 1) 2) 3) 4) Ответы: 3. 1) 2) 3) 4) Ответы:   4. 1) 2) 3) 4) Ответы:   5. 1) 2) 3) 4) Ответы:   6. 1) 2) 3) 4) Ответы:   7. 1) 2) 3) 4) Ответы:   8. 1) 2) 3) 4) Ответы:

 

Используются технологии uCoz

Тема дроби 5 класс, суть дроби, сложение, вычитание, деление, умножение, примеры с объяснениями. Как понять дроби

Практически каждый пятиклассник после первого знакомства с обыкновенными дробями находится в небольшом шоке. Мало того, что нужно еще понять суть дроби, так с ними еще придется выполнять арифметические действия. После этого маленькие ученики будут систематически допрашивать своего учителя, разузнавать когда же эти дроби кончатся.

Содержание статьи

• Суть дроби
• Действия с дробями 5 класс
• Сложение дробей, объяснение
• Вычитание дробей, объяснение
• Деление десятичных дробей 5 класс
• Умножение десятичных дробей 5 класс
• Смешанные дроби 5 класс
• Примеры с десятичными дробями 5 класс с объяснением
• Примеры с обыкновенными дробями с разными знаменателями 5 класс с объяснением
• Примеры с дробями 5 класс для тренировки
• Как научить ребенка легко решать дроби с помощью лего

Чтобы избежать подобных ситуаций, достаточно всего лишь как можно проще объяснить детям эту нелегкую тему, а лучше в игровой форме.

Суть дроби

Перед тем, как узнать что такое дробь, ребенок должен познакомиться с понятием доля.  Здесь лучше всего подойдет ассоциативный метод.

Представьте целый торт, который поделили на несколько равных частей, допустим на четыре. Тогда каждый кусочек торта, можно назвать долей. Если взять один из четырех кусков торта, то он будет одной четвертой долей.

Доли бывают разные, потому что, целое можно поделить на совершенно разное количество частей. Чем больше долей в целом, тем они меньше, и наоборот.

Чтобы доли можно было обозначить, придумали такое математическое понятие, как обыкновенная дробь. Дробь позволит нам записать столько долей, сколько потребуется.

Составными частями дроби являются числитель и знаменатель, которые разделены дробной чертой либо наклонной чертой. Многие дети не понимают их смысла, поэтому и суть дроби им не понятна. Дробная черта обозначает деление, здесь нет ничего сложного.

Знаменатель принято записывать снизу, под дробной чертой или справа от накл.черты. Он показывает количество долей целого. Числитель, он записывается сверху над дробной чертой или слева от накл. черты, определяет сколько долей взяли.К примеру дробь 4/7. В данном случае 7-это знаменатель, показывает, что есть всего 7 долей, а числитель 4 указывает на то, что из семи долей взяли четыре.

Основные доли и их запись в дробях:

Помимо обыкновеной, существует еще и десятичная дробь.

Действия с дробями 5 класс

В пятом классе учатся выполнять все арифметические действия с дробями.

Все действия с дробями выполняются по правилам, и надеяться на то, что не выучив правило все получится само сабой не стоит. Поэтому не стоит пренебрегать устной частью домашнего задания по математике.

Мы уже поняли, что запись десятичной и обыкновенной дроби различны, следовательно и арифметические действия будут выполняться по-разному. Действия с обыкновенными дробями зависят от тех чисел, которые стоят в знаменателе, а в десятичной-после запятой справа.

Для дробей, у которых знаменатели одинаковые, алгоритм сложения и вычитания очень прост. Действия выполняем только с числителями.

Пример:

Для дробей с разными знаменателями нужно найти Наименьший Общий Знаменатель ( НОЗ). Это то число, которое будет делиться без остатка на все знаменатели, и будет наименьшим из таких чисел, если их несколько.

Пример:

Для сложения либо вычитания десятичных дробей, нужно записать их в столбик, запятая под запятой, и уравнить количество десятичных знаков если это требуется.

Пример:

Чтобы перемножить обыкновенные дроби просто найди произведение числителей и знаменателей. Очень простое правило.

Пример:

Деление  выполняется по следующему алгоритму:

1. Делимое записать без изменения
2. Деление превратить в  умножение
3. Делитель перевернуть (записать обратную дробь делителю)
4. Выполнить умножение

Пример:

Сложение дробей, объяснение

Давайте более подробно разберем, как складывать обыкновенные и десятичные дроби.

Как видно на изображении выше, у дроби одна третья и две третьих общий знаменатель три. Значит требуется сложить только числители единицу и два, а знаменатель оставить без изменения. В итоге получается сумма три третьих. Такой ответ, когда числитель и знаменатель дроби равны, можно записать как 1, так как 3:3 = 1.

Требуется найти сумму дробей две третьих и две девятых. В этом случае знаменатели различны, 3 и 9. Чтобы выполнить сложение, нужно подобрать общий. Есть очень простой способ. Выбираем наибольший знаменатель, это 9. Проверяем делится ли он на 3. Так как 9:3 = 3 без остатка, следовательно 9 подходит как общий знаменатель.

Следующим шагом находим дополнительные множители для каждого числителя. Для этого общий знаменатель 9 делим поочередно на знаменатель каждой дроби, полученные числа и будут допол. множ. Для первой дроби: 9:3 = 3, дописываем к числителю первой дроби 3. Для второй дроби: 9:9 = 1, единицу можно не дописывать, так как при умножении на нее получится то же самое число.

Теперь умножаем числители на их дополнительные множители и складываем результаты. Полученная сумма дробь восемь девятых.

Сложение десятичных дробей выполняется по тому же правилу, что и сложение натуральных чисел. В столбик, разряд записывается под разрядом. Единственное отличие в том, что в десятичных дробях нужно правильно поставить запятую в результате. Для этого дроби записываются запятая под запятой, и в сумме требуется лишь снести запятую вниз.

Найдем сумму дробей 38, 251 и 1, 56. Чтобы было удобнее выполнять действия, мы уровняли количество десятичных знаков справа, добавив 0.

Складываем дроби не обращая внимания на запятую. А в полученной сумме просто опускаем запятую вниз. Ответ: 39, 811.

Вычитание дробей, объяснение

Чтобы найти разность дробей две третьих и одна третья, нужно вычислить разность числителей 2-1 = 1, а знаменатель оставить без изменения. В ответе получаем разность одну третью.

Найдем разность дробей пять шестых и семь десятых. Находим общий знаменатель. Используем способ подбора, из 6 и 10 наибольший 10. Проверяем: 10 : 6 без остатка не делится. Добавляем еще 10, получается 20:6, тоже без остатка не делится. Снова увеличиваем на 10, получили 30:6 = 5. Общий знаменатель 30. Так же НОЗ можно найти по таблице умножения.

Находим дополнительные множители. 30:6 = 5 — для первой дроби. 30:10 = 3 — для второй. Перемножаем числители и их доп.множ. Получаем уменьшаемое 25/30 и вычитаемое 21/30. Далее выполняем вычитание числителей, а знаменатель оставляем без изменения.

В результате получилась разность 4/30. Дробь сократимая. Разделим ее на 2. В ответе 2/15.

Деление десятичных дробей 5 класс

В этой теме рассматривается два варианта действий:

Умножение десятичных дробей 5 класс

Вспомните, как вы умножаете натуральные числа, точно таким же способом и находят произведение десятичных дробей. Сначала разберемся, как умножить десятичную дробь на натуральное число. Для этого:

 При умножении десятичной дроби на десятичную, действуем точно также.

Смешанные дроби 5 класс

Пятиклашки любят называть такие дроби не смешанные, а <<смешные>>, наверное так легче запомнить. Смешанные дроби называются так от того, что они получились путем соединения целого натурального числа  и обыкновенной дроби.

Смешанная дробь состоит из целой и дробной части.

При чтении таких дробей сначала называют целую часть, затем дробную: одна целая две третьих, две целых одна пятая, три целых две пятых, четыре целых три четвертых.

Как же они получаются, эти смешанные дроби? Все довольно просто. Когда мы получаем в ответе неправильную дробь ( дробь у которой числитель больше знаменателя), мы ее должны всегда переводить в смешанную. Достаточно разделить числитель на знаменатель. Это действие называется выделением целой части:

Перевести смешанную дробь обратно в неправильную тоже несложно:

Примеры с десятичными дробями 5 класс с объяснением

Много вопросов у детей вызывают примеры на несколько действий. Разберем пару таких примеров.

Пример 1.

( 0,4 · 8,25 — 2,025 ) : 0,5 = 

Первым действием находим произведение чисел 8,25 и 0,4. Выполняем умножение по правилу. В ответе отсчитываем справа налево три знака и ставим запятую.

Второе действие находится там же в скобках, это разность. От 3,300 вычитаем 2,025. Записываем действие в столбик, запятая под запятой.

Третье действие-деление. Полученную разность во втором действии делим на 0,5. Запятая переносится на один знак. Результат  2,55.

Ответ: 2,55.

Пример 2.

( 0, 93 + 0, 07 ) : ( 0, 93 — 0, 805 ) =

Первое действие сумма в скобках.Складываем в столбик, помним, что запятая под запятой. Получаем ответ 1,00.

Второе действие разность из второй скобки. Так как у уменьшаемого меньше знаков после запятой, чем у вычитаемого, добавляем недостающий. Результат вычитания 0 ,125.

Третьим действие делим сумму на разность. Запятая переносится на три знака. Получилось деление 1000 на 125.

Ответ: 8.

Примеры с обыкновенными дробями с разными знаменателями 5 класс с объяснением

В первом примере находим сумму дробей 5/8 и 3/7. Общим знаменателем будет число 56. Находим дополнительные множ., разделим 56:8 = 7 и 56:7 = 8. Дописываем их к первой и второй дроби соответственно. Перемножаем числители и их множители, получаем сумму дробей 35/56 и 24/56.  Получили сумму 59/56. Дробь неправильная, переводим ее в смешанное число.Остальные примеры решаются аналогично.

Примеры с дробями 5 класс для тренировки

Для удобства переведите смешанные дроби в неправильные и выполняйте действия.

Как научить ребенка легко решать дроби с помощью лего

С помощью такого конструктора можно не только хорошо развивать воображение ребенка, но и объяснить наглядно в игровой форме, что такое доля и дробь.

На картинке ниже показано, что одна часть с восемью кружками это целое. Значит, взяв пазл с четырьмя кружками, получается половина, или 1/2.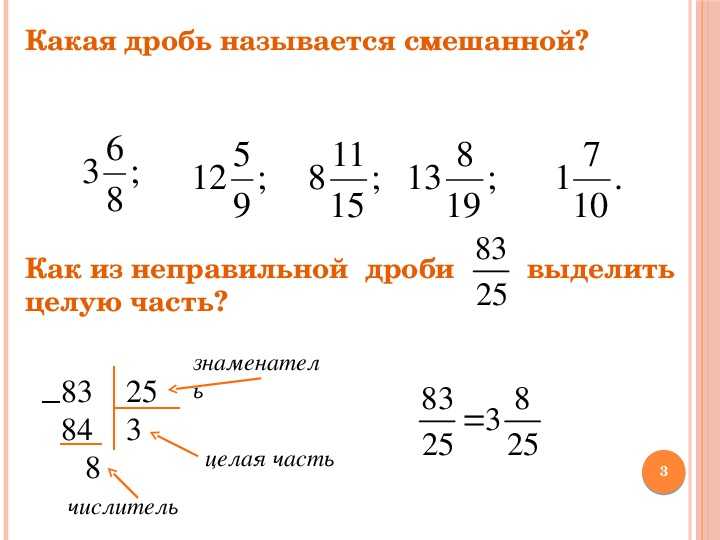 На картинке наглядно показано, как решать примеры с лего, если считать кружки на деталях.

Вы можете построить башенки из определенного количества частей и подписать каждую из них, как на картинке ниже. Например возьмем башенку из семи частей. Каждая часть зеленого конструктора будет 1/7. Если вы к одной такой части добавите еще две, то получится 3/7. Наглядное объяснение примера 1/7+2/7 = 3/7.

Чтобы получать пятерки по математике не забывайте учить правила и отрабатывать их на практике.

Решение дробей в 5-м классе с помощью математических историй: часть 15 — Чартерная школа Род-Айленда

Стеф Примиани, директор STEM, и Алисия Куомо, стажер по политике городского образования Университета Брауна

Комбинируйте 3/4 и 1/2.

 

Рене съела 3/4 пакета попкорна. Затем Мария съедает 1/2 пакета попкорна. Сколько всего попкорна съели Рене и Мария?

 

Обе задачи требуют одинаковых навыков нахождения эквивалентных дробей для объединения двух чисел с разными знаменателями. Но вопрос о попкорне дает реалистичную оценку 9.0023 контекст почему.

«Обучение через решение задач можно описать как перевернутое по сравнению с обучением решению задач — с проблемой (задачами) в начале урока и навыками, возникающими в результате работы с проблемой (задачами)». ¹

Повествовательная структура проблемного вопроса предлагает учащимся создать модель с метками. В модели дискретных дробей учащиеся разбивают, чтобы найти эквивалентную дробь:

 

В числовой линейной модели история попкорна более явно визуализируется как последовательность событий, где последний скачок представляет собой сумму: ориентируются на то, чтобы открыть процедуру нахождения эквивалентных дробей. Кроме того, они сразу узнают один реалистичный контекст, в котором могут применяться математические навыки, и учащиеся могут легче замечать закономерности в типах задач, чтобы использовать более эффективные стратегии и решать все более сложные сценарии.

 

В разговорном интервью 2006 года профессор математики и писатель Джон А. Ван де Валле подчеркнул необходимость для всех американских классных комнат нормировать проблемно-ориентированный подход, основанный на идеях студентов , а не на лекции под руководством учителя. Когда учитель читает лекцию по принципу «покажи и расскажи», Ван де Валле утверждает, что студенты сосредоточены на направлениях и правилах, а не на математических концепциях.

С подход, основанный на проблеме учащемуся некуда обратиться, кроме своих собственных идей, связанных с проблемой. В результате вместо того, чтобы искать правила, учащиеся пытаются разобраться в релевантных идеях, заложенных в проблеме или задании . Даже если проблема не решена, были задействованы их собственные соответствующие идеи. Последующее обсуждение в классе будет содержательным и интересным. Идеи разрабатываются и интегрируются с существующим пониманием каждого учащегося.

 

Для меня также чрезвычайно важно учитывать, что каждый подход каждый день говорит студентам. Благодаря замечательным объяснениям под руководством учителя учащиеся часто рассматривают математику как набор правил, которые часто сбивают с толку и не имеют большого значения… В классе, основанном на задачах, учащиеся… сталкиваются с самым основным фактом математики: математика имеет смысл. Кроме того, они осознают, что именно они способны понимать математику. ¹

20-минутный протокол Math Stories представляет собой ориентированный на учащихся подход, который делает именно то, что предлагает Ван де Валле: заставляет учащихся самостоятельно решать сложные задачи в реалистичных условиях. Как учителя могут использовать контекст в Math Stories и во время основного учебного блока? Почему контекст имеет значение в подходе, ориентированном на студента?

Часть видения Ван де Валле заключается в том, что математика не в способности определять типы задач и применять простые алгоритмы. Скорее, решение математических задач не является рутинным.

Определения решения задач варьируются в зависимости от учебного плана, но по сути это нестандартных вопроса, которые можно решать с использованием более чем одной стратегии . «Изучение нескольких стратегий может помочь учащимся увидеть разные идеи и подходы к решению проблем и может позволить учащимся мыслить более гибко, когда сталкиваются с проблемой, не имеющей очевидного решения».

Последовательность математических рассказов для 5-го класса состоит примерно из 70 задач. Это тщательно продуманный прогресс, который начинается с обзора концепций 4-го класса, а затем через пару месяцев учащиеся переходят к стандартам дробей 5-го класса, используя все четыре операции. Как правило, в месяц предлагается 10-13 задачек, что дает учителям возможность гибко пересматривать сложные типы задач и пересматривать концепции.

Ключевым моментом в задаче на ежедневный рассказ является то, что она представляет собой математическую задачу в контексте . Предоставление контекста имеет решающее значение для поддержки учащихся в осмыслении и гибком решении проблем. Кроме того, сюжетные задачи помогают учащимся развивать навыки в трех областях, которые RAND (огромная беспристрастная исследовательская корпорация) считает необходимыми для развития навыков:

• Представительство
• Обоснование
• Обобщение

 

В то время как учащиеся могут быть подготовлены к определению типа задачи на явном уроке и следованию знакомой процедуре, в Math Stories учащимся не предоставляется никакой информации, кроме задачи на рассказ. Как предполагает Ван де Валле, такая структура невмешательства заставляет учащихся думать о том, какую информацию они уже знают и что от них требуется решить. Теоретически это звучит здорово, но в классах у учащихся разные потребности, они все еще развивают метакогнитивные навыки и часто быстро просматривают задачи и полагаются на простые алгоритмы.

Как научить учащихся внимательно читать задачки?

 

Контрольный список

Список вопросов может помочь учащимся в тщательном чтении задачи на известную и неизвестную информацию. Информационная служба What Works (WWC) финансируется Институтом педагогических наук (IES) через Министерство образования США и является огромным ресурсом исследований в области образования. Вот примерный список подсказок WWC:

 

Моделирование самоконтроля и рефлексии

Учителя должны демонстрировать, как использовать подсказки, подобные перечисленным выше, чтобы рассуждать с самим собой на протяжении всего процесса решения проблемы – при чтении рассказа, выборе стратегии решения и проверке твоя работа. Учащиеся учатся на примере, как думать вслух при решении сюжетной задачи. Вот пример самоконтроля студента из WWC, адаптированный к Math Stories. Учащийся задает и отвечает на последовательность вопросов, одинаковую независимо от типа задачи:

 

Пример задачи

5 друзей планируют разделить 3 пиццы поровну. Один из друзей больше не может прийти на ужин. Насколько больше пиццы получат друзья, если пиццу разделят только 4 человека, а не 5 человек?

Решение*

Студент: Во-первых, я спрашиваю себя: «О чем эта история и что мне нужно выяснить?» Я вижу, что задача дала мне общее количество пиццы и два разных сценария распределения общего количества пиццы.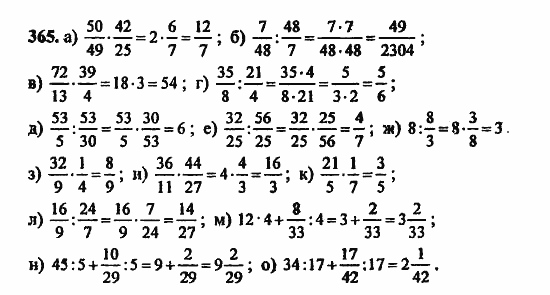 Я знаю, что «насколько больше» требует от меня сравнить или вычесть разницу между тем, сколько пиццы получает каждый друг в каждом сценарии.

Я спрашиваю себя, «Сталкивался ли я с такой проблемой раньше?» Вспоминая сюжетные задачи, которые мы решали, я помню, что видел задачу, в которой друзья делили сковороду с пирожными. Я помню, что нам пришлось разделить все на количество друзей, чтобы получить порцию каждого друга. Это похоже на похожую проблему, но мне придется разделить дважды, потому что есть два сценария, а затем сравнить.

Прежде чем продолжить, я задаюсь вопросом: «Какие шаги я должен предпринять, чтобы решить эту проблему?» Похоже, мне нужно разделить общее количество пиццы на количество друзей для каждого сценария.

4 друга: 3/5 пиццы на человека

5 друзей: 3/4 пиццы на человека

Проблема заключается в том, чтобы спросить меня, «насколько больше» пиццы получают друзья, когда разделяется только 4 человека вместо 5. Я знаю, что когда я сравниваю или нахожу разницу, я могу использовать вычитание. Но у меня должны быть одинаковые единицы для вычитания.

Я могу использовать свою модель:

Чтобы написать уравнение:

Итак, разница 3/20. Каждый из друзей получает на 3/20 больше пиццы, когда их всего 4, по сравнению с тем, когда их 5.

Наконец, я спрашиваю себя: «Имеет ли этот ответ смысл, когда я перечитываю задачу?» Мне кажется, что 3/20 — это ответ, потому что это разница между размером порции для 5 друзей и 4 друзей. 3/20 — это небольшое число по сравнению с размерами порций. (Я знаю, что 3/10 — это то же самое, что 0,3 или 3%, а 3/20 — еще меньше!) Это имеет смысл, потому что задача состоит в том, чтобы найти разницу: если я заберу одного друга, это немного изменит количество пиццы. получит каждый человек.

 

Поддержка незнакомого языка и контекста

Безусловно, учащиеся будут сталкиваться с незнакомым языком и контекстом на формальных экзаменах, с которыми им придется бороться без помощи учителя или сверстников. Однако, как утверждает WWC: «Цель обеспечения того, чтобы учащиеся понимали язык и контекст задач, не в том, чтобы сделать задачи менее сложными. Вместо этого это позволяет учащимся сосредоточиться на математике в задаче, а не на необходимости изучать новые базовые знания или язык. Главный момент заключается в том, что учащиеся должны понять проблему и ее контекст, прежде чем пытаться ее решить». По этой причине учителям важно предвидеть, когда пятиклассникам в их классе могут потребоваться дополнительные разъяснения, особенно изучающим английский язык. Вот пример, адаптированный из WWC с использованием сюжетных задач Math Stories:

Персонализация задач по истории

WWC и другие исследования показывают, что учащиеся более вовлечены и могут установить связи с реальными приложениями математики, когда задачи по истории персонализированы. Учителя должны быть осторожны, чтобы не делать этого постоянно — ученики должны привыкнуть думать о сценариях за пределами своей зоны комфорта. Но иногда включение имен учеников, любимые тенденции, такие как бейблейды, и приглашение ученых придумывать свои собственные сценарии могут повысить вовлеченность. Каждая задача на историю в Math Stories основана на стандартах, поэтому можно легко заменить содержание на содержание, имеющее отношение к вашему классу, при этом продолжая обучать ключевым понятиям.

Ресурсы

¹ (2006) Беседа с Джоном Ван де Валле, автором книги «Математика в начальной и средней школе: обучение с учетом развития».

² РЭНД. (2003) Математическая подготовка для всех учащихся: к программе стратегических исследований и разработок в области математического образования.

 

Есть вопросы? Свяжитесь с директором BVP по STEM Стефом Примиани по адресу [email protected] и следите за мной в Твиттере @stephprimiani

.

Wolfram|Альфа-примеры: Common Core Math: Дроби

Wolfram|Альфа-примеры: Common Core Math: Дроби

Ого! Wolfram|Alpha не работает без JavaScript.

Пожалуйста, включите JavaScript. Если вы не знаете, как это сделать, вы можете найти инструкции здесь. Как только вы это сделаете, обновите эту страницу, чтобы начать использовать Wolfram|Alpha.

Примеры для

С третьего по пятый класс учащиеся начинают понимать дроби как числа, представляющие части целого. Студенты учатся сравнивать, складывать, вычитать, умножать и делить дроби и смешанные числа. Визуальные модели, такие как числовые линии и ленточные диаграммы, дают учащимся концептуальный способ представления дробей. В четвертом классе учащиеся начинают составлять дроби с общими знаменателями, чтобы к пятому классу учащиеся могли складывать и вычитать дроби с разными знаменателями. Учащиеся также используют дроби для решения реальных задач и начинают использовать десятичную систему счисления для представления и выполнения операций с дробями.

Стандарты Common Core

Получить информацию об Стандартах Common Core.

Поиск конкретного стандарта:

CCSS. Math.Content.3.NF.A.1общий базовый стандарт 4.NF.B.4b

Поиск всех стандартов в домене:

общих базовых стандартов о дробях 4-й класс

Выполнение добавления и вычитание дробей и смешанных чисел с одинаковыми знаменателями, сравнение дробей и представление дробей в виде десятичных дробей.

Сложение и вычитание дробей (CCSS.Math.Content.4.NF.B.3a):

1/5 + 2/5

Сложение и вычитание смешанных чисел (CCSS.Math.Content.4.NF.B.3c):

2 3/4 — 1 1/4

Сравнение величин дробей (CCSS.Math. Content.4.NF.A.2):

что больше, 7/8 или 3/4?

Выражение дроби в виде десятичной дроби (CCSS.Math.Content.4.NF.C.6):

Десятичная форма 5/10

Умножение дроби на целое число (CCSS.Math.Content.4.NF.B. 4):

1/5 * 10Больше примеров3 класс

Определение дробей, составление эквивалентных дробей и сравнение дробей с одинаковыми знаменателями.

Визуализация дроби как части целого (CCSS.Math.Content.3.NF.A.1):

Круговая диаграмма 1/3

Распознавание эквивалентных дробей (CCSS.

Math.Content.3.NF.A.3b ): 4/8 против 1/2

Сравните величины дробей (CCSS.Math.Content.3.NF.A.3d):

что больше, 1/3 или 2/3?Больше примеров5 класс

Выполнить сложение, вычитание, умножение и деление с дробями, в том числе с разными знаменателями.

Сложение и вычитание дробей (CCSS.Math.Content.5.NF.A.1):

1/4 + 2/33 2/5 — 2 1/2

Умножение дробей (CCSS.Math.Content.5.NF.B.4):

1/2 * 3/53/4 умножить на 4/6

Разделить целое число на дробь (CCSS.Math.Content.5.NF.B.7b):

6 ÷ (1/3)10 разделить на 1/2Больше примеров

ДАЛЬШЕ

Пошаговые решения Арифметика

Веб-приложение Pre-Algebra

Бесплатное неограниченное количество практических задач по арифметике

ДОПОЛНИТЕЛЬНЫЕ ПРИМЕРЫ

Common Core Math: алгебраическое мышление

Common Core Math: Geometry

Common Core Math: измерение и данные

Math Core Math: Числа в базе десятка

Common Core Math: Коэффициенты и пропорции

Элементарная математика

• Pro
• Web Apps
• Pro
• Web Apps
• Pro
• .

  No related posts.