Примеры с дробями как решить: Действия с дробями

Обыкновенные дроби — Определение, Примеры, Действия, Доли, Числитель и Знаменатель

Поможем понять и полюбить математику

Начать учиться

299.7K

С 5 класса редкий урок математики проходит без дробей. Тема непростая и объемная, поэтому лучше начать разбираться сейчас, чтобы дальше было проще решать задачки. В этой статье расскажем про обыкновенные дроби.

Доля целого

Доля это каждая из равных частей, на которые поделено целое.

Для примера возьмем два мандарина. Когда мы их почистим, то получим в каждом мандарине разное количество долек или долей. В одном может быть 6, а в другом — целых 9. Размеры долей у каждого мандарина тоже разные.

У каждой доли есть свое название: оно зависит от количества долей в конкретном предмете. Если в мандарите шесть долей — каждая из них будет определяться, как одна шестая от целого.

• Половина — одна вторая доля предмета или 1/2.
• Треть — одна третья доля предмета или 1/3.
• Четверть — одна четвертая доля предмета или 1/4.

Понятие доли можно применить не только к предметам, но и величинам. Так, например, картина занимает четверть стены — при этом ее ширина треть метра.

Узнай, какие профессии будущего тебе подойдут

Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас

Как устроена обыкновенная дробь

Обыкновенная дробь — это запись вида m/n, где m и n любые натуральные числа.

Такие дроби записываются с помощью двух натуральных чисел и горизонтальной черты, которая называется чертой дроби. Иногда ставится не горизонтальная черта, а косая.

Числитель обыкновенной дроби m/n — это натуральное число m, которое стоит над чертой. Числитель это делимое — то, что мы делим.

Знаменатель обыкновенной дроби m/n — натуральное число n, которое стоит под чертой. Знаменатель это делитель — то, на сколько делим.

Черта между числителем и знаменателем — символ деления.

Равные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых справедливо равенство: a * d = b * c. Пример равных дробей: 1/2 и 2/4, так как 1 * 4 = 2 * 2.

Неравные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых равенство: a * d = b * c не является верным.

Как устроена десятичная дробь

В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

• 0,3
• 4,23
• 9,939

Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.

Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.

Свойства дробей

Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной. Формула выглядит так:

где a, b, k — натуральные числа.

Основные свойства Дробь не имеет значения, если знаменатель равен нулю. Дробь равна нулю, если числитель равен нулю, а знаменатель — нет. Две дроби a/b и c/d называются равными, если a * d = b * c.

Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:

• Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
• Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде, если в знаменателе обыкновенной дроби числа 10, 100, 1000 и т. д.
• Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби, если в знаменателе обыкновенной дроби числа 10, 100, 1000 и т. д. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.

У нас есть отличные курсы по математике для учеников с 1 по 11 классы, записывайтесь!

Действия с дробями

С дробями можно выполнять те же действия, что и с обычными числами: складывать, вычитать, умножать и делить. А еще дроби можно сокращать и сравнивать между собой. Давайте попробуем.

Сравнение дробей

Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.

Сравним 1/5 и 4/5. Как рассуждаем:

 

1. В обеих дробях знаменатель равен 5.


2. В первой дроби числитель равен 1, во второй дроби равен 4.

   1 < 4



3. Поэтому первая дробь 1/5 меньше второй 4/5.
   

Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше.

Сравним 1/2 и 1/8. Как рассуждаем:

Представим, что у нас есть торт. Так как знаменатель первой дроби равен 2, то делим торт на две части и забираем себе одну, то есть половину торта.

Знаменатель второй дроби равен 8, делим торт на восемь частей и забираем крохотный кусочек. Половина торта больше больше маленького кусочка.

Таким образом 1/2 > 1/8.

Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю. А после приведения дробей к общему знаменателю, можно применить правило сравнения дробей с одинаковыми знаменателями.

Пример. Сравнить 2/7 и 1/14.

Как рассуждаем:

 

1. Приведем дроби к общему знаменателю:
   
2. Сравним дроби с одинаковыми знаменателями:
   

Ответ: 2/7 > 1/14.

Важно запомнить: любая неправильная дробь больше любой правильной. Потому что неправильная дробь всегда больше или равна 1, а правильная дробь всегда меньше 1.

Чтобы сравнить дроби с разными числителями и знаменателями, нужно:

• привести дроби к общему знаменателю;
• сравнить полученные дроби.

Чтобы привести дроби к общему знаменателю, нужно:

1. Найти общее кратное знаменателей дробей, которое станет их общим знаменателем.


2. Разделить общий знаменатель на знаменатель данных дробей, то есть найти для каждой дроби дополнительный множитель.


3. Умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.

Сокращение дробей

Сокращение дроби — это деление числителя и знаменателя дроби на одно и то же натуральное число. Сократить дробь значит сделать ее короче и проще для восприятия. Например, дробь 1/3 выглядит намного проще и красивее, чем 27/81.

Сокращение дроби выглядит так: зачеркивают числитель и знаменатель, а рядом записывают результаты деления числителя и знаменателя на одно и то же число.

В этом примере делим обе части дроби на двойку.

Можно никуда не спешить и сокращать дроби последовательно, в несколько действий.

Сложение и вычитание дробей

При сложении и вычитании дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель.

Не забудьте проверить, можно ли сократить дробь и выделить целую часть.

При сложении и вычитании дробей с разными знаменателями нужно найти наименьший общий знаменатель, сложить или вычесть полученные дроби (используем предыдущее правило).

Вот, что делать:

 

1. Найдем наименьшее общее кратное для определения единого делителя.

   Для этого запишем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.

   НОК (15, 18) = 3 * 2 * 3 * 5 = 90



2. Найдем дополнительные множители для каждой дроби. Для этого НОК делим на каждый знаменатель:

   90 : 15 = 6,

   90 : 18 = 5.

   Полученные числа запишем справа сверху над числителем.

3. Воспользуемся одним из основных свойств дробей: перемножим числитель и знаменатель на дополнительный множитель. После умножения знаменатель должен быть равен наименьшему общему кратному, которое мы ранее высчитывали. Затем можно перейти к сложению.
   
4. Проверим полученный результат:
   • если числитель больше знаменателя, нужно преобразовать дробь в смешанное число;
   • если есть что сократить, нужно выполнить сокращение.

Ход решения одной строкой:

Сложение или вычитание смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:

 

1. Сложить целые части.
   
   


2. Сложить дробные части.
   

   Необходимо приводить к общему, если знаменатели разные. Для этого воспользуемся знаниями из предыдущего примера.



3. Суммировать полученные результаты.
   

Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.

Умножение и деление дробей

Произведение двух дробей равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:

Не забываем про сокращение. Это может облегчить вычисления.

Чтобы умножить два смешанных числа, надо:

 

1. преобразовать смешанные дроби в неправильные;


2. перемножить числители и знаменатели дробей;


3. сократить полученную дробь;


4. если получилась неправильная дробь, преобразовать в смешанную.

Чтобы разделить дробь на дробь нужно выполнить следующую последовательность действий:

• числитель первой умножить на знаменатель второй, результат произведения записать в числитель новой дроби;
• знаменатель первой умножить на числитель второй, результат произведения записать в знаменатель новой дроби.

Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.

Числа, произведение которых равно 1, называют взаимно обратными.

Как делить дроби с разными знаменателями? На самом деле одинаковые или разные знаменатели у дробей — неважно, потому что все дроби делятся по правилу, описанному выше.

Для деления смешанных чисел необходимо:

• представить числа в виде неправильных дробей;
• разделить то, что получилось друг на друга.

---

---

 

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Лидия Казанцева

Автор Skysmart

К предыдущей статье

413.3K

Параллелограмм: свойства и признаки

К следующей статье

376.5K

Арифметическая прогрессия: свойства и формулы

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

Как решать дроби.

Решение дробей.

В статье покажем, как решать дроби на простых понятных примерах. Разберемся, что такое дробь и рассмотрим решение дробей!

Понятие дроби вводится в курс математики начиная с 6 класса средней школы.

Дроби имеют вид : ±X/Y, где Y — знаменатель, он сообщает на сколько частей разделили целое, а X — числитель, он сообщает, сколько таких частей взяли. Для наглядности возьмем пример с тортом:

В первом случае торт разрезали поровну и взяли одну половину, т.е. 1/2. Во втором случае торт разрезали на 7 частей, из которых взяли 4 части, т.е. 4/7.

Если часть от деления одного числа на другое не является целым числом, ее записывают в виде дроби.

Например, выражение 4:2 = 2 дает целое число, а вот 4:7 нацело не делится, поэтому такое выражение записывается в виде дроби 4/7.

Иными словами дробь — это выражение, которое обозначает деление двух чисел или выражений, и которое записывается с помощью дробной черты.

Если числитель меньше знаменателя — дробь является правильной, если наоборот — неправильной. В состав дроби может входить целое число.

Например, 5 целых 3/4.

Данная запись означает, что для того, чтобы получить целую 6 не хватает одной части от четырех.

Если вы хотите запомнить, как решать дроби за 6 класс, вам надо понять, что решение дробей, в основном, сводится к понимаю нескольких простых вещей.

• Дробь по сути это выражение доли. То есть числовое выражение того, какую часть составляет данное значение от одного целого. К примеру дробь 3/5 выражает, что, если мы поделили что то целое на 5 частей и количество долей или частей это этого целого — три.
• Дробь может быть меньше 1, например 1/2(или по сути половина), тогда она правильная. Если дробь больше 1, к примеру 3/2(три половины или один с половиной), то она неправильная и для упрощения решения, нам лучше выделить целую часть 3/2= 1 целая 1/2.
• Дроби это такие же числа, как 1, 3, 10, и даже 100, только числа это не целые а дробные. С ними можно выполнять все те же операции, что с числами. Считать дроби не сложнее, и далее на конкретных примерах мы это покажем.

К дробям применимы самые разные арифметические операции.

Приведение дроби к общему знаменателю

Например, необходимо сравнить дроби 3/4 и 4/5.

Чтобы решить задачу, сначала найдем наименьший общий знаменатель, т.е. наименьшее число, которое делится без остатка на каждый из знаменателей дробей

Наименьший общий знаменатель(4,5) = 20

Затем знаменатель обоих дробей приводится к наименьшему общему знаменателю

Ответ: 15/20

Сложение и вычитание дробей

Если необходимо посчитать сумму двух дробей, их сначала приводят к общему знаменателю, затем складывают числители, при этом знаменатель останется без изменений. Разность дробей считается аналогичным образом, различие лишь в том, что числители вычитаются.

Например, необходимо найти сумму дробей 1/2 и 1/3

Ответ: 5/6

Теперь найдем разность дробей 1/2 и 1/4

Ответ: 1/4

Умножение и деление дробей

Тут решение дробей несложное, здесь все достаточно просто:

• Умножение — числители и знаменатели дробей перемножаются между собой;
• Деление — сперва получаем дробь, обратную второй дроби, т. е. меняем местами ее числитель и знаменатель, после чего полученные дроби перемножаем.

Например:

На этом о том, как решать дроби, всё. Если у вас остались какие то вопросы по решению дробей, что то непонятно, то пишите в комментарии и мы обязательно вам ответим.

Для закрепления материала рекомендуем также посмотреть наше видео:

Также рекомендуем к использованию наш онлайн калькулятор дробей! В нем вы можете посмотреть, как строить решение, на собственных примерах.

Если вы учитель , то возможно скачать презентацию для начальной школы (http://school-box.ru/nachalnaya-shkola/prezentazii-po-matematike.html) будет вам кстати.

---

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

---

Пошаговое руководство (с примерами)

Обновлено 31 января 2023 г.

Автор команды WikiJob

Все представленные продукты и услуги выбираются WikiJob независимо друг от друга. Когда вы регистрируетесь или совершаете покупку по ссылкам на этой странице, мы можем получать комиссию.

Что такое дроби?

Дробное число или дробное число используется для представления сегмента целого числа.

Дробь состоит из двух чисел, расположенных одно над другим. Первое число, найденное над чертой, — это 9.0013 числитель . Второе число, расположенное под чертой, является знаменателем .

Знаменатель показывает общее количество равных частей, на которые что-то разделено. Числитель показывает, сколько из этих равных частей необходимо принять во внимание.

Простой способ запомнить дроби — это называть строку, разделяющую каждое число, «из». Таким образом, дробь, записанная как 3/5, просто относится к 3 частям из 5 равных частей.

Как можно представить дроби?

Дроби могут быть представлены тремя способами: в виде правильных дробей, неправильных дробей и смешанных дробей.

• Правильная дробь — это та, у которой числитель меньше знаменателя. Например, ⅔ (две трети) или ⅞ (семь восьмых).
• Неправильная дробь имеет числитель больше знаменателя. Например, 8/5 (восемь пятых) или 13/4 (тринадцать четвертей).
• Смешанное число состоит из целого числа и дроби. Например, 5¾ (пять и три четверти) или 12⅖ (двенадцать и две пятых).

Практика числового теста с помощью JobTestPrep

Упрощение дробей

Процесс упрощения дробей приводит их к простейшей форме. Например, гораздо проще называть что-то ½, а не 4/8.

Существует два способа упростить дробь.

Первый способ состоит в том, чтобы разделить верхние и нижние части дроби поровну на целые числа больше 1 до тех пор, пока вы не сможете продвинуться дальше. В качестве примера возьмем дробь 24/108:9.0003

• Разделите каждое число на 2, чтобы получить 12/54
• Разделите на 2 еще раз, чтобы получить 6/27
• Разделите на 3, чтобы получить 2/9

Сложение дробей

Чтобы сложить дроби вместе, вам нужно изменить их так, чтобы знаменатели (нижние числа) были одинаковыми. Затем вы суммируете числители.

Дополнение: Пример 1

Допустим, вы хотите сложить дробь от ¼ до ¼.

Знаменатели уже совпадают, поэтому можно перейти ко второму шагу и прибавить 1 к 1.

Вторая половина дроби остается неизменной, поэтому сложение дробей ¼ и ¼ равно 2/4 (или ½).

Дополнение: Пример 2

Допустим, вы хотите сложить дроби ⅓ и ⅙.

Чтобы знаменатели совпадали, измените ⅓ на 2/6.

Добавьте 1 к 2, чтобы получить 3, и поместите 6 ниже. Ответ 3/6. Упростите это до ½.

Пройти тест

Вычитание дробей

Вычитание дробей работает аналогичным образом:

• Шаг 1. Убедитесь, что знаменатели совпадают
• Шаг 2. Вычтите числители
• Шаг 3. При необходимости упростите дробь

Если вам нужно подготовиться к ряду различных тестов при приеме на работу и вы хотите перехитрить конкурентов, выберите Премиум-членство от JobTestPrep .

Вы получите доступ к трем пакетам PrepPack на ваш выбор из базы данных, которая охватывает всех основных поставщиков тестов и работодателей, а также специализированные пакеты профессий.

Получить премиум-пакет сейчас

Вычитание: Пример 1

Предположим, вас попросили вычислить ¾ — ¼

Первый шаг относительно прост, потому что числа одинаковы.

Второй шаг включает в себя вычитание верхних чисел, а затем поднесение результата к тому же знаменателю.

Таким образом, ¾ — ¼ будет вычислено как 3 — 1 = 2

Таким образом, ответ будет 2/4, что равно ½.

Умножение дробей

Умножать дроби относительно легко; вы просто умножаете верхние и нижние числа.

Если, например, перемножить дроби ½ и ⅓, получится ⅙. От вас не ждут, что вы найдете общий знаменатель посредством умножения.

Деление дробей

Чтобы разделить дроби, вам нужно перевернуть дробь, на которую вы делите, вверх ногами.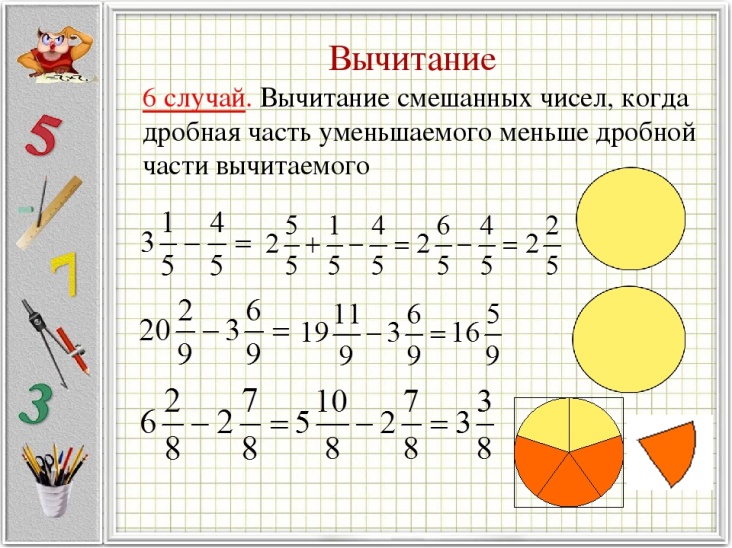 Например, если вы хотите разделить ½ на ⅓, вы переписываете уравнение так, чтобы вторая дробь была 3/1. Затем умножьте ½ на 3/1, и у вас останется 3/2.

Может потребоваться дальнейшее уменьшение фракции для получения составной фракции.

Распространенные ошибки и на что следует обратить внимание

При сложении и вычитании дробей можно легко запутаться. Учащиеся часто складывают или вычитают знаменатели или числители двух дробей и обычно не могут распознать связь между знаменателем. Чтобы еще больше усугубить путаницу, числители и знаменатели следует рассматривать как целые числа при расчете, например, когда вам нужно умножить дробь.

Давайте возьмем пример, сложив вместе ¾ и ⅙.

Первое, что нужно сделать, это получить одинаковые знаменатели, поэтому мы умножаем их, чтобы получить 24.

Мы умножили знаменатель 4 на 6, чтобы получить 24, поэтому мы также умножаем числитель на 6, чтобы получить 18/24.

Мы умножили знаменатель 6 на 4, чтобы получить 24, поэтому мы также умножаем числитель на 4, чтобы получить 4/24.

Теперь мы можем просто добавить 18/24 к 4/24, чтобы получить 22/24, что упрощается до 11/12.

Другие распространенные ошибки включают:

• При сложении или вычитании дробей кандидаты могут забыть сначала преобразовать дроби, чтобы они имели общий знаменатель.

• Изменение знаменателя дроби без внесения необходимых изменений в числитель.

• Полное непонимание вопроса; например, деление, а не вычитание, или умножение, а не сложение.

• Оставление знаменателя без изменений в вопросах, касающихся умножения или сложения.

Понимание связи между смешанными числами и неправильными дробями, а также того, как перевести одно в другое, имеет решающее значение для работы с дробями.

Проведите численный тест прямо сейчас

---

Пошаговое руководство по решению дробей с примерами

Вы ищете лучший способ похудеть? Если да!! Давайте узнаем, как решать дроби. Звучит странно? Да, вы правильно прочитали! Вам нужно знать индекс массы тела (ИМТ), используя дроби, чтобы эффективно похудеть.

Дамы, ювелир дает вам украшения весом 18 или 24 карата? 24 карата считаются чистым золотом, тогда как 18 карат означают 18/24, что равно 75% золота. Вот как вы можете использовать дроби, чтобы узнать чистоту ювелирных изделий.

Этот блог поможет вам понять, как решать дроби, используя различные методы. Кроме того, я перечислил несколько полезных советов по использованию дробей. Итак, чтобы не создавать путаницы, давайте подробно разберемся с концепцией дробей.

Что нужно знать о Fraction!!

Содержание

Во-первых, поймите, что такое дробь.  

Дробь — это числовая величина или значение, не являющееся целым числом, например, 4/5, 6/7 и т. д. 

Забавный факт: Есть факт, который поможет вам произвести впечатление на учителей и друзей. Это черта или знак деления в дроби, известной как «ВИНКУЛУМ».

Следующее, что нужно выучить, это термины, используемые для обозначения нарушений. Таким образом, каждая дробь состоит из двух частей.

-> Первая часть называется числителем , написанным над знаком деления, и это делает количество частей дроби равным. Короче говоря, это означает количество частей, которые мы имеем в дробях.

-> В то время как вторая часть называется знаменателем , написанным под символом деления, она в основном равна общему количеству частей в целом, и поэтому она означает общее количество частей числа в целом.

Например, В дроби 3/5 3 — числитель, а 5 — знаменатель.

Здесь 3 означает, что это третья часть целого числа, а 5 означает, что целое число состоит из 5 частей.

Второе, что нужно узнать о типах дробей.

Мы имеем дело с тремя типами дробей. Давайте проверим каждый из них один за другим.

• Правильная дробь: В этой дроби числитель имеет меньшее значение по сравнению со знаменателем.

Примечание: Значение правильной дроби всегда меньше 1.

Пример правильной дроби: 3/5, 1/2 и 5/7.

• Неправильная дробь: В этой дроби числитель всегда больше знаменателя.

Примечание: Значение неправильной дроби всегда больше 1.

Примером неправильной дроби является 6/3, 50/21 и 16/25.

• Смешанная дробь: В этой дроби число представлено целым числом, за которым следуют дробные числа.

Примечание: Смешанная дробь также называется смешанным числом.

Пример смешанной дроби: 6⅘, 2⅔ и 25⅝.

Как представлять дроби в разных формах?

Представление смешанной дроби в целое число.

Давайте разберемся, как решить смешанные дроби до целого числа на примере.

Замените 7⅘ на целое число.

-> Сначала умножьте целое число на знаменатель дроби. То есть 7*5=35.

-> Теперь прибавьте полученное значение к числителю дроби. То есть 35 + 4 = 39.

-> Возьмите числитель и подставьте его в исходный знаменатель. То есть 39/5.

-> Окончательная целая дробь будет 39/5.

Представление дроби до десятичного числа.

Самый простой способ превратить дробь в десятичную — просто разделить число. Здесь требуется разделить числитель на знаменатель.

Измените дробь 7/10 на десятичную.

7 7

Вам нужно просто разделить числитель 7 на знаменатель, который равен 10. Вы получите ответ:

7/10 => 0,7

Представление дробь в процент.

Для преобразования дроби в проценты можно использовать три метода. Ниже я привел три разных метода на примере 7/20.

Разделите числитель на знаменатель и умножьте результат на 100. 0197

Умножить числитель на 100 и разделить число на знаменатель.

7 *100 = 700700/20 = 35%

Разделите числитель на знаменатель и переставьте запятую справа от двух знаков.

7/20 = 0,35 Теперь переместите десятичные точки, чтобы преобразовать их в 35%.

Пошаговое руководство – Как решать дроби

Сначала научимся складывать две и более дроби на примере.

Предположим, вам нужно добавить 3/4 к 1/4.

Здесь вы видите, что знаменатели одинаковы, так что это самое простое сложение дробей.

Итак, первый шаг в решении дробей сложением — найти общий знаменатель чисел. В этой задаче оба имеют одинаковый знаменатель, поэтому общего между ними всего 4.

Таким образом, вы можете написать уравнение следующим образом –

3/4 + 1/4

= (3+1)/ 4

= 4/4 = 1

Если у вас разные знаменатели, то также вы легко решить дроби. Давайте учиться на другом примере –

Предположим, вам нужно добавить 3/4 к 2/5, тогда у вас будет следующее уравнение – 

3/4 + 2/5 

Тогда следующий шаг к решению этой дроби в как решить дроби найти любой общий знаменатель.

Поскольку у него нет общего знаменателя, мы умножим оба знаменателя и сложим приведенные выше числа. Посмотрите на ниже, чтобы понять лучше.

= (3+2) / 4×5 

= 5/20 

= 1/4

Теперь давайте возьмем еще один пример, где мы можем найти общие знаменатели.

Предположим, что нам нужно сложить дроби ¾ и ⅝

= 3/4 + 5/8 

Теперь мы найдем наименьший общий множитель, который является НОК, между двумя знаменателями.

Тогда мы получим 8 в виде НОК, и, таким образом, уравнение будет таким: умножит первую дробь на 2, чтобы знаменатель дроби был равен 8; таким образом, уравнение будет 

= (6+5)/8

= 11/8 

Таким образом, ответ равен 11/8.

Теперь давайте научимся вычитать дроби, как решать дроби.

Предположим, уравнение 3/2 – 1/2 

Итак, мы будем следовать тому же процессу, но сначала выведем общий множитель, поскольку знаменатель в этом уравнении тот же, поэтому такой проблемы нет.

Теперь вы можете напрямую поместить 2 в знаменатель, а затем вычесть 1 из 3. Следуйте инструкциям –

=(3-1)/2

=2/2

= 1

Ответ равен 1.

Другой пример решения дробей

5/7 – 2/ 4 

Мы не видим общего делителя между знаменателями, поэтому делаем знаменатели одинаковыми, умножая первую дробь на 4, а вторую дробь на 7; тогда мы получим следующее уравнение.

= 5×4/7×4 – 2×7/4×7 

Чтобы решить уравнение, мы должны привести к общему знаменателю, так как только тогда мы сможем выполнять операции Лютера в уравнении. Таким образом, мы получим следующий ответ –

= (20-14)/7×4

= 6/28

Теперь мы можем видеть, что 2 является общим как для числителя, так и для знаменателя, поэтому мы можем разделить всю дробь на 2 следующим образом –

= 6\2/28\2

= 3/14

Таким образом, ответ равен 3/14.

Теперь давайте научимся умножать две дроби. Это также очень важно, чтобы научиться решать дроби.

Возьмем следующий пример: 

¾ x ⅕ 

Умножение в дробях очень просто, так как вам просто нужно умножить числители друг на друга, а также знаменатели друг на друга.

Тогда вы получите следующий результат –

= 3×1 / 4×5

=3/20

Таким образом, ответ 3/20.

Теперь давайте изучим метод деления на дроби, как решать дроби.

Вы можете взять обратную дробь, чтобы разделить дробь. Чтобы было взаимно, нужно поменять знаменатель на числитель, а числитель на знаменатель.

Возьмем пример:

Решите 1/2 ÷ 1/5.

Во-первых, возьмем обратную величину 1/5 как 5/1.

Возьмите обратную дробь и умножьте ее на другое число (числа).

1/2 * 5/1

Чтобы решить, умножьте знаменатели и числители:

2 * 1 = 2 (знаменатель)

1 * 5 = 5 (числитель) 

То есть: 1/2 * 5/1 = 5/2 = 2,5

Что нужно понимать, чтобы избежать распространенных ошибок в дробях!

Может быть непросто складывать и вычитать дроби с разными знаменателями. Поэтому разные ученики не решают дроби с разными знаменателями и допускают ошибки.

Сначала приведем пример решения дробей с разными знаменателями .

=> Решите 3/4 + 1/6. -> Первое, что вам нужно сделать, это умножить числитель и знаменатель на противоположное значение знаменателя. -> Это кратное 4 на 6 и 6 на 4. Это даст вам 24 в знаменателе. -> Точно так же умножьте числитель как 3 * 6 = 18 и 1 * 4 = 4. -> Теперь добавьте 18 + 4 = 22. -> Это означает, что   3/4 + 1/6 = 22/24 => 11/12

Теперь поймите, какие ошибки допускают ученики.

1. Неверное понимание требований вопросов, таких как деление вместо умножения и т.д.
2. Когда учащимся нужно сложить или вычесть дробь, они забывают изменить знаменатель дроби. [Как и в приведенных выше примерах 4 и 6 меняются на 24].
3. Причем заметно, что числитель тоже надо изменить, как и знаменатель. [Например, 3 * 6 = 18 и 1 * 4 = 4].
4. Наконец, некоторые ученики не могут упростить уравнение. [Например, 22/24 также пишется как 11/12 после деления числа на 2].

Творческое занятие для обучения ваших детей дробям!! Вы можете научить своих детей дробям, попросив их нарисовать птицу на бумаге. Дайте им инструкции разрезать бумагу в заданной пропорции. -> Дайте им круг и научите их дробям. -> Разрежьте круг на 8 частей и выучите дроби, такие как 1/8, 2/8, 3/8, 4/8, 5/8, 6/8, 7/8 и 8/8. -> Также позвольте им упростить дроби как 2/8 => 1/4, 4/8 => 1/2, 6/8 => 3/4 и 8/8 => 1. -> Наконец, они должны нарисовать птицу в следующем виде:

Заключение

Многие ученики борются с дробями, и дроби на первый взгляд кажутся сложными, но становятся простыми, если вы практикуете их ежедневно.

Если вы также ищете как решать дроби , то мы надеемся, что эта статья помогла вам понять процесс решения дробей. Если все-таки вы столкнулись с трудностями при решении дробей, то вы можете обратиться к нам в любое время. Мы всегда здесь, чтобы помочь вам. Наши специалисты дадут вам консультацию 24/7. Получите лучшую помощь в выполнении домашних заданий по математике от экспертов.

Часто задаваемые вопросы

Q1.

No related posts.