Решение систем неравенств с одной переменной
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
8 класс
Решение систем
неравенств с одной
переменной
Автор:
Учитель математики МОУ г.Горловки
«Гимназия «Интеллект»»
Борлова Людмила Ефимовна
Учитель математики и информатики МОУ
г.Горловки «Школа № 53 с углубленным
изучением отдельных предметов»
Страмбовская Евгения Ильинична
Тема урока:
решение систем неравенств
Цели урока: совершенствование умений и
навыков решения систем линейных неравенства
с одной переменной, развитие навыков
самоконтроля, воспитание информационной
компетенции, математической зоркости.
Повторение
Тестирование (да – 1, нет — 0)
1) Является ли число 12 решением неравенства 2х>10?
2) Является ли число -6 решением неравенства 4х>12?
3) Является ли неравенство 5х-15>4х+14 строгим?
4) Существует ли целое число принадлежащее промежутку
[-2,8;-2,6]?
5) При любом ли значении переменной а верно неравенство
а² + 4 >о?
6) Верно ли, что при умножении или делении обеих частей
неравенства на отрицательное число знак неравенства не
меняется?
Повторение
Давайте проверим
101010
Дополнительные вопросы
1.
Сформулируйте свойства неравенств, используемые при
решении и доказательстве неравенств и их систем?
2.
Что называется решением системы неравенств?
3.
Алгоритм решения системы неравенств?
Вспомним
Алгоритм решения системы неравенств
1.
Улыбнись системе неравенств, и она поможет тебе ее
решить!!!
2.
Решить каждое неравенство отдельно, используя свойства
числовых неравенств (не забыть изменить знак неравенства,
при делении на отрицательное число).
3.
Решить каждое неравенство отдельно, используя свойства
числовых неравенств (не забыть изменить знак неравенства,
при делении на отрицательное число).
4.
Написать ответ (не забыть сделать проверку)))!
Внимание
При решении линейных неравенства с одной переменной
необходимо ВСЕГДА изображать решение неравенства на
координатной прямой, ВСЕГДА записывать ответ в виде числового
промежутка.
При решении систем линейных неравенства с одной
переменной необходимо ВСЕГДА изображать решения системы
виде числового промежутка.
Слово «Ответ» обязательно!!!
Например: Ответ: (2,5 ; 0) или х Є (2,5 ; 0)
Рассмотрите примеры решения
неравенств и систем неравенств
Пример 1. При каких значениях переменной
имеет смысл выражение:
Пример 1
При каких значениях переменной имеет смысл
выражение:
По определению арифметического квадратного корня
подкоренное выражение всегда должно быть больше или равно 0.
Значит, нам нужно решить неравенство
, тогда найдем все
значения переменной при которых имеет смысл это выражение.
Решаем
Ответ: выражение имеет смысл при х Є [2,5; +
).
Пример 1
При каких значениях переменной имеет смысл
выражение:
По определению арифметического квадратного корня
подкоренное выражение всегда должно быть больше или равно 0.
Но выражение находится в знаменателе, поэтому оно не может
принимать нулевые значения! Значит, нам нужно решить
неравенство
Решаем
Ответ: выражение имеет смысл при х Є [ —
; 0,5 ).
Внимание
Когда задание формулируется «Укажите допустимые значения
переменной» это тоже самое, что «При каких значениях
переменной имеет смысл выражение».
Пример 2
Укажите допустимые значения переменной в
выражении
По определению арифметического квадратного корня
подкоренное выражение всегда должно быть больше или равно 0.
Значит
Нужно решить 2 неравенства, причем х в этих неравенствах один и
тот же.
Поэтому нам нужно решить систему неравенств.Решаем
).
Самостоятельно решить систему
неравенств
Вариант 1
Вариант 2
1,5 x 3
a)
6 x 12
4 x 16
a )
0,2 x 2
3 x 2 1,5 x 1
b)
4 2 x x 2
3 x 2 x 4
b)
x 4 6x 3
Самостоятельное
решение
Давайте проверим
Вариант 1
Вариант 2
а)[-2;2)
а)[- ∞;-4)
б)(-∞;2)
б)решений нет
Итоги урока
1. Что называется решением системы неравенств?
2. Что значит «решить систему неравенств»?
3. Каков алгоритм решения системы неравенств?
4. Сколько решений может иметь система неравенств?
Рефлексия
Оцените свою работу:
5б — всё понял и могу рассказать.
4б — всё понял, но рассказать не могу.
3б — понял не всё.
2б — ничего не понял, но старался.
Домашнее задание
Повторить § 11 п. 34 с.186 – 189, п.35 стр.194 -197.
Решите № 880 (а,б), № 883 (а,б), № 886 (а)
English Русский Правила
Математический анализ.
(Виленкин) Математический анализ. (Виленкин)
ОглавлениеПРЕДИСЛОВИЕ ДЛЯ УЧИТЕЛЯВВЕДЕНИЕ 2. Числовые множества. 3. Пустое множество. 4. Подмножество. 5. Пересечение множеств. 6. Сложение множеств. 7. Разбиение множеств. 8. Вычитание множеств.  9. Отображение множеств. 10. Краткие исторические сведения. Глава I. МНОГОЧЛЕНЫ ОТ ОДНОГО ПЕРЕМЕННОГО § 1. Тождественные преобразования многочленов 2. Целые рациональные выражения и функции. 3. Степень с натуральным показателем и ее свойства. 4. Многочлены. 5. Умножение многочленов. 6. Числовые кольца и поля. 7. Кольцо многочленов над данным числовым полем. 8. Бином Ньютона. § 2. Деление многочленов. Корни многочленов 2. Теорема Безу. Схема Горнера. 3. Корни многочлена. 4. Интерполяционные формулы. 5. Кратные корни. 6. Многочлены второй степени. 7. Многочлены с целыми коэффициентами. 8. Краткие исторические сведения. Глава II. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА § 1. Общая теория уравнений 2. Область допустимых значений. 3. Уравнения. 4. Совокупности уравнений. 5. Преобразования уравнений. 6. Теоремы о равносильности уравнений. § 2. Уравнения с одним неизвестным 2. Метод разложения на множители.  3. Метод введения нового неизвестного. 4. Биквадратные уравнения. 5. Возвратные уравнения 3-й и 4-й степеней. § 3. Функциональные неравенства 2. Равносильные неравенства. 3. Доказательство неравенств. 4. Линейные неравенства. 5. Решение неравенств второй степени. 6. Решение алгебраических неравенств высших степеней. 7. Краткие исторические сведения. Глава III. ОБОБЩЕНИЕ ПОНЯТИЯ СТЕПЕНИ. ИРРАЦИОНАЛЬНЫЕ ВЫРАЖЕНИЯ § 1. Степени с целым показателем 2. Степень с нулевым показателем. 3. Степень с целым отрицательным показателем. § 2. Корни. Степени с рациональными показателями 2. Степени с рациональными показателями. 3. Свойства степеней с рациональными показателями. § 3. Иррациональные алгебраические выражения 2. Одночленные иррациональные выражения. 4. Извлечение корня из произведения и степени. 5. Вынесение алгебраических выражений из-под корня и внесение их под корень.  6. Возведение корня в степень. 7. Извлечение корня из корня. 8. Подобные корни. 9. Сложение и вычитание корней. 10. Уничтожение иррациональности в знаменателе или в числителе алгебраической дроби. 11. Преобразование выражений вида … 12. Смешанные задачи на преобразование иррациональных выражений. § 4. Иррациональные уравнения и неравенства 2. Сведение иррациональных уравнений к рациональным. 3. Уединение радикала. 4. Введение нового неизвестного. 5. Особые случаи решения иррациональных уравнений. 6. Иррациональные неравенства. 7. Краткие историчесие сведения. Глава IV. МНОГОЧЛЕНЫ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. СИСТЕМЫ УРАВНЕНИЙ И НЕРАВЕНСТВ § 1. Системы алгебраических уравнений 2. Системы уравнений. 3. Геометрический смысл решений уравнений и систем уравнений с двумя неизвестными. 4. Совокупность уравнений. 5. Равносильные системы уравнений. 6. Метод подстановки. 7. Метод алгебраического сложения уравнений.  8. Метод введения новых неизвестных. 9. Системы однородных уравнений. 10. Геометрическая интерпретация решения систем двух уравнений с двумя неизвестными. § 2. Системы линейных уравнений 2. Теоремы о равносильности систем линейных уравнений. 3. Пример решения системы линейных уравнений методом Гаусса. 4. Метод Гаусса (приведение системы к обобщенно-треугольному виду). 5. Решение обобщенно-треугольной системы линейных уравнений. 6. Системы однородных линейных уравнений. § 3. Симметрические многочлены и их приложения к решению систем уравнений 3. Основная теорема о симметрических многочленах от двух переменных. 4. Системы симметрических алгебраических уравнений. 5. Применение симметрических многочленов к решению иррациональных уравнений. § 4. Неравенства с многими переменными 2. Среднее арифметическое и среднее геометрическое трех чисел. 3. Неравенство Коши (двумерный вариант). 4. Задачи на наибольшие и наименьшие значения.  § 5. Решение неравенств 2. Неравенства с двумя переменными. 3. Задание областей неравенствами и системами неравенств. 4. Понятие о линейном программировании. 5. Краткие исторические сведения. Глава V. КОМПЛЕКСНЫЕ ЧИСЛА § 1. Комплексные числа в алгебраической форме 2. Комплексные числа. 3. Сложение комплексных чисел; умножение на действительные числа. 4. Умножение комплексных чисел. 5. Квадратные уравнения с действительными коэффициентами. 6. Деление комплексных чисел. 7. Сопряженные комплексные числа. 8. Извлечение квадратных корней из комплексных чисел. § 2. Тригонометрическая форма комплексных чисел 2. Полярная система координат. 3. Тригонометрическая форма комплексного числа. 4. Умножение и деление комплексных чисел в тригонометрической форме. 5. Возведение комплексных чисел в степень. Формула Муавра. 6. Извлечение корня из комплексного числа. 7. Функции комплексного переменного и преобразования комплексной плоскости.  § 3. Некоторые виды алгебраических уравнений 2. Двучленные уравнения. 3. Корни из единицы и построение правильных многоугольников. 4. Трехчленные уравнения. § 4. Основная теорема алгебры многочленов и ее следствия 2. Многочлены с действительными коэффициентами. 3. Разложение на множители многочленов с действительными коэффициентами. 4. Краткие исторические сведения. Глава VI. ЦЕПНЫЕ ДРОБИ § 1. Конечные цепные дроби 2. Пример цепной дроби. 3. Определение цепной дроби. 4. Представление рациональных чисел в виде конечной цепной дроби. 5. Подходящие дроби. 6. Свойства подходящих дробей. 8. Подходящие дроби и календарь. 9. Приближение цепной дроби подходящими дробями. § 2. Бесконечные цепные дроби 2. Подходящие дроби и наилучшие приближения иррациональных чисел рациональными. 3. Цепные дроби как вычислительный инструмент. 4. Краткие исторические сведения. Глава VII. КОМБИНАТОРИКА § 1. Комбинаторные задачи § 2.  Комбинаторные задачи. Продолжение§ 3. Определения и формулы § 4. Соединения с повторениями § 5. Комбинаторные задачи. Окончание § 6. Бином Ньютона и его обобщения § 7. Краткие исторические сведения Глава VIII. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ § 2. Сложные вероятности. Теоремы сложения и умножения. Условные вероятности § 3. Примеры вычисления вероятностей § 4. Полная вероятность. Формула Байеса § 5. Повторение испытаний § 6. Примеры вычисления вероятностей. Окончание § 7. Краткие исторические сведения |
графических систем неравенств за 3 простых шага — Mashup Math
Ваше простое руководство по построению графиков и решению систем неравенствПредварительный просмотр руководства: Графическое построение систем неравенств за 3 простых шага
В математике, как только вы научились строить графики и решать систему линейных уравнений, вы готовы сделать следующий шаг и освоить два новых важных навыка алгебры:
Это руководство научит вас обоим навыкам.
Однако важно отметить, что для построения графиков систем неравенств используется графический подход, который вы, возможно, не изучали раньше.
Если вы не уверены в своей способности построить график и решить систему линейных уравнений , мы предлагаем ознакомиться с нашим бесплатным руководством по решению систем уравнений.
Если вы уже умеете строить графики системы уравнений, вы готовы следовать этому пошаговому руководству, которое научит вас всему, что вам нужно знать о построении графиков систем линейных неравенств.
Прежде чем мы углубимся в решение систем неравенств, давайте рассмотрим некоторые определения и изучим стандартные обозначения, используемые при графическом отображении систем неравенств.
В чем разница между уравнением и неравенством?Определение: Уравнение — это математическое утверждение, показывающее равенство двух выражений с помощью знака: =
Примером уравнения является x=7, где x равно 7 (и только 7).
Мы можем визуализировать уравнение x=7 для числа в Рисунок 01 ниже:
Рисунок 01
Рисунок 02
Уравнения имеют только одно возможное решение. Уравнение x=7 означает, что x должен быть равен 7 и никакому другому значению.
Определение: Неравенство — это связь между двумя значениями, переменными или выражениями, образующая неравное сравнение
Примером неравенства является x≥7, где x может быть равно 7 или любому значению больше 7 ( Рисунок 02 ) .
Неравенства имеют бесконечное число решений (этот набор возможных решений называется набором решений ). Неравенство x≥7 означает, что x может быть равно 7 или любому значению больше 7. Например:
Примеры решения: 7, 7.
5, 57, 2675 и т. д.Примеры, не являющиеся решениями : 6,999, 3, 0, -413 и т. д.
5, 57, 2675 и т. д.уравнение имеет только одно решение, а неравенство имеет множество решений с бесконечным числом решений. Помня об этом, вы значительно облегчите себе понимание построения графиков и решения линейных неравенств.
Стандартные обозначения, используемые для построения графиков систем неравенствЕсть несколько обозначений, которые вам нужно знать, прежде чем мы сможем начать рисовать системы неравенств.
Для начала давайте вспомним, как изобразить одно линейное неравенство вида y>, y≥, y<, или y≤… сплошная линия представляет включающую границу. Мы видим это в неравенствах, использующих ≤ или ≥. Это означает, что числа в строке входят в набор решений.
Пунктирная линия представляет собой не включающую границу. Мы видим это в неравенствах, использующих < или >.
Это означает, что числа в строке , а не включены в набор решений.
Например, Рисунок 03 ниже показывает разницу между уравнением y=x+1 и неравенствами y>x+1 и y≥x+1. Обратите внимание, что уравнение не имеет заштрихованной области, в то время как оба неравенства имеют заштрихованную область. Также обратите внимание, что y≥x+1 имеет сплошную линию, а y>x+1 — пунктирную линию.
Рисунок 03
Заштрихованные области при графическом отображении неравенств:
Далее давайте повторим значение заштрихованной области на графике любого линейного неравенства. Заштрихованная область включает все точки, являющиеся решениями неравенства (их бесконечно много). Все точки в незаштрихованной области не являются решениями. Если линия сплошная, то точки на линии включаются в набор решений. Если линия пунктирная, то точек на линии 9.
0004, а не включены в набор решений.
Как узнать, когда следует заштриховать область над линией или под линией?
Когда неравенство имеет форму y> или y≥, , вы должны заштриховать область выше график . Все точки в этой области будут решениями неравенства. Точки на линии включаются только в том случае, если линия сплошная.
Когда неравенство имеет вид y< или y≤, вы должны заштриховать область ниже график . Все точки в этой области будут решениями неравенства. Точки на линии включаются только в том случае, если линия сплошная.
На рис. 04 ниже показаны как сплошные, так и пунктирные линии, а также когда затенять над линией и когда закрашивать под ней.
Рисунок 04
Если вы можете построить график одного линейного неравенства, значит, вы готовы начать рисовать системы неравенств.
При решении систем линейных уравнений решением является точка, удовлетворяющая всем уравнениям системы, а для систем неравенств — целая область на координатной плоскости . Множество решений будет иметь бесконечно много точек s , каждая из которых удовлетворяет каждому неравенству в системе неравенств.
В Рисунок 05 ниже вы можете видеть, что единственным решением системы линейных уравнений является точка пересечения (5,2). Однако для системы линейных неравенств вы можете видеть, что все точки в перекрывающихся заштрихованных областях могут быть решениями, и их бесконечно много. Примерами решений системы неравенств могут быть точки (0,0), (-2,2) и (-4,-1), поскольку все они находятся в области множества решений, помеченной знаком ‘ С’».
Вы запутались? Пока все в порядке. Графические системы неравенств станут для вас легче после работы с несколькими примерами.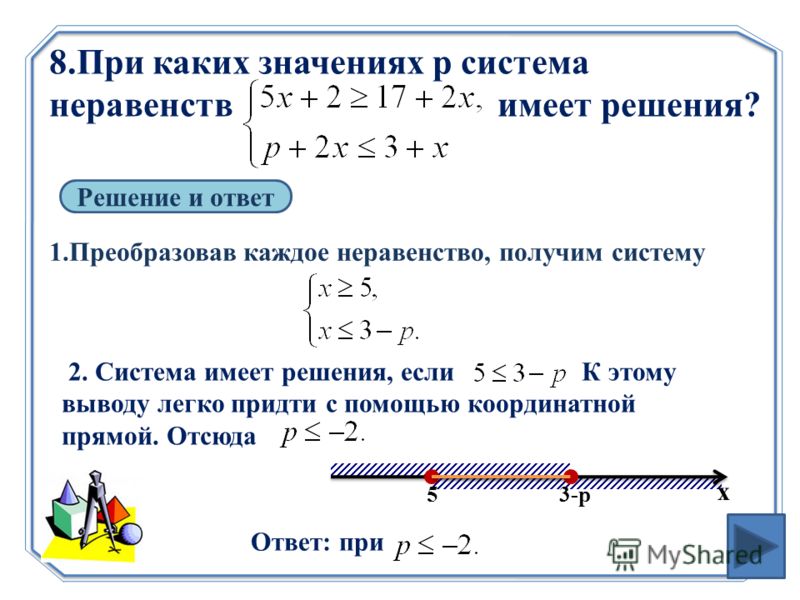
Давайте начнем!
Рисунок 05
Графики систем неравенств: пример №1Нарисуйте график следующей системы неравенств:
y ≤ x – 6 и y < –2x + 3
систему неравенств с использованием следующего трехшагового метода:
Шаг первый: Решить оба неравенства относительно y (при необходимости). то есть изолировать y как y>, y≥, y<, или y≤
Шаг второй: Начертите оба неравенства на координатной плоскости.
Шаг третий: Определите набор решений.
Теперь давайте применим этот трехэтапный метод к примеру № 1:
Шаг первый: Решите оба неравенства для y (при необходимости). то есть изолировать y as y>, y≥, y<, или y≤
Обратите внимание, что в обоих приведенных неравенствах y ≤ x – 6 и y < –2x + 3 переменная y уже изолирована, поэтому нет ничего, что вы должны сделать.
y ≤ x – 6
y < –2x + 3
Шаг второй: Начертите оба неравенства на координатной плоскости.
Теперь вы готовы построить оба неравенства. Вы уже знаете, как построить график одного неравенства. В этом случае вы просто изображаете их обоих на одном графике, чтобы видеть, где перекрываются заштрихованные области.
На рисунке 06 ниже показано, как будут выглядеть графики y ≤ x – 6 и y < –2x + 3 на отдельных графиках и как будет выглядеть график системы неравенств на той же координате с перекрывающейся областью, отмеченной S , который представляет набор решений.
Рисунок 06
Шаг третий: Определите набор решений.
Теперь, когда вы изобразили оба неравенства на координатной плоскости, вы готовы определить набор решений. Любая точка, содержащаяся в перекрывающейся области, будет решением и удовлетворяет обоим неравенствам.
Обратите внимание на Рисунок 07 ниже, чтобы увидеть разницу между областью графика, которая представляет набор решений, и оставшейся областью, которая содержит все нерешения. Обратите внимание, что точки на сплошной линии в наборе решений включаются в набор решений, а точки на пунктирной линии — нет.
Рисунок 07
Имея в виду эту ключевую концепцию построения графиков систем неравенств, теперь вы можете определить, что набор решений представляет собой перекрывающуюся область, которую вы обозначите буквой S.
Напомним, Рисунок 08 ниже показывает, как должен выглядеть завершенный график:
Рисунок 08
Что касается решения систем линейных неравенств, ваш график сделал это, продемонстрировав множество решений — область, содержащую все точки, удовлетворяющие обоим неравенствам.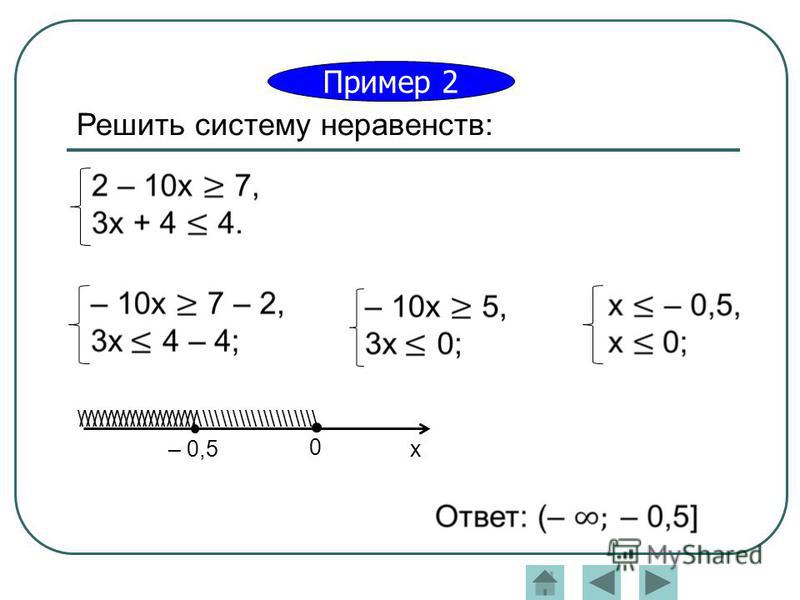
Если вы хотите определить, входят ли отдельные точки в набор решений, вы просто используете свой график, чтобы увидеть, содержатся ли они в наборе решений. Например:
(4,1) не является решением, поскольку не входит в набор решений ✗
(3, -10) является решением, поскольку входит в набор решений ✓
( -5, -2) не является решением, поскольку его нет в наборе решений ✗
(0,-6) является решением, поскольку он находится в наборе решений (находится на сплошной линии набор решений) ✓
(5, -7) не является решением, потому что он не входит в набор решений (он находится в части набора решений, отмеченной пунктирной линией) ✗
(4, -3) не является решением, потому что его нет в наборе решений ✗
Нужна еще практика? Давайте посмотрим на другой пример.
График системы неравенств: Пример №2 Нарисуйте графически следующую систему неравенств:y ≤ 3x — 5 и 2y — 5 > x -3 3-шаговый метод следующим образом:
Шаг первый: Решите оба неравенства для y (если необходимо).
то есть изолировать y как y>, y≥, y<, или y≤
Этот шаг включает перестановку каждого неравенства таким образом, чтобы y являлось предметом неравенства.
В этом примере первое неравенство уже имеет желаемую форму. Переформулируйте второе неравенство следующим образом:
Теперь вы выделили y во втором неравенстве и готовы приступить к решению систем неравенств: y ≤ 3x — 5 и y > (½)x + 1.
Шаг второй: Изобразите оба неравенства на координатной плоскости.
Теперь вы готовы изобразить y ≤ 3x — 5 и y > (½)x + 1 на одном графике. Помните, что:
Так же, как и в первом примере, мы можем визуализировать каждое линейное неравенство на отдельном графике и вместе, перекрывая, на том же графике, как показано на Рисунок 09 ниже.
Рисунок 09
Шаг третий: определите набор решений.
Наконец, множество решений данной системы линейных неравенств лежит в области, где перекрываются множества решений каждого отдельного неравенства. Эта перекрывающаяся область показана ниже на рисунке 10.
Рисунок 10
Построение системы неравенств завершено, и вы определили набор решений.
Опять же, если бы вы могли проверить отдельные точки, которые удовлетворяют обоим неравенствам, следующим образом:
(4,7) является решением, потому что оно находится в наборе решений (он находится на сплошной линии в части набора решений ) ✓
(8, 8) является решением, так как находится в наборе решений ✓
(4, 4) не является решением, поскольку его нет в наборе решений (он находится в части набора решений, обозначенной пунктиром) ✗
(4,5) является решением, поскольку он входит в набор решений ✓
(0,0) не является решением, поскольку не входит в набор решений ✗
(-3, 6) не является решением, поскольку не входит в набор решений набор решений ✗
Вам удобнее трехэтапный процесс? К счастью, этот процесс работает для построения графиков систем неравенств с двумя переменными и решения систем неравенств с двумя переменными, поэтому, как только вы его освоите, вы сможете решить любой пример.
Давайте проверим ваши навыки на последнем примере.
6x — 2y ≥ -10 и 8 + y < 10 если необходимо). то есть изолировать y как y>, y≥, y<, или y≤
В этом примере вам придется использовать алгебру, чтобы изменить оба неравенства, поскольку ни одно из них не находится в желаемой форме.
Начиная с первого неравенства:
6x — 2y ≥ -10
-6x в обе стороны → -6x + 6x — 2y ≥ -10 — 6x = -2y ≥ -6x — 10
-2 y -2 900 900 10/-2 с обеих сторон → -2y/-2 ≥ -6x/-2 — 10/-2 → y ≤ 3x + 5 (Вы заметили, что знак неравенства меняется с ≥ на ≤ 😮)
***Обратите внимание, что при делении и неравенстве на отрицательное число (в данном примере -2) знак неравенства меняет направление.
= у ≤ 3x + 5
Теперь вы выделили y в первом неравенстве и можете сделать вывод, что y ≤ 3x + 5
А теперь для второго уравнения:
Теперь вы выделили y во втором неравенстве и можете заключить, что y < 2
Шаг второй: Нарисуйте оба неравенства на координатной плоскости.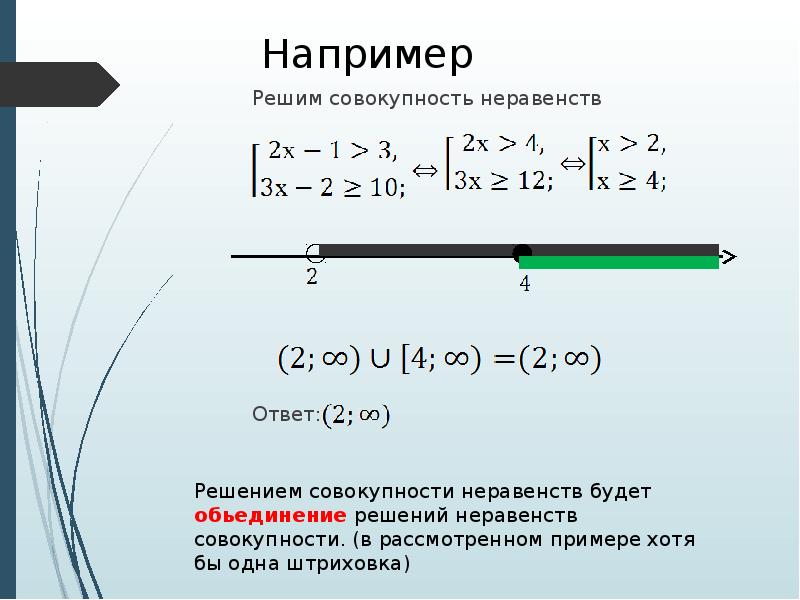
Теперь вы готовы изобразить y ≤ 3x + 5 и y < 2 на том же графике. Помните, что:
Рисунок 11
Шаг третий: определите набор решений.
Теперь можно определить набор решений для графа системы неравенств. Эта область, где множество решений для обоих неравенств, показано на графике ниже в Рисунок 12 :
Рисунок 12
Финальный пример построения графиков систем неравенств завершен.
Давайте посмотрим на некоторые точки и определим, входят ли они в набор решений. часть набора решений, сплошная линия) ✓
(9, -5) является решением, поскольку входит в набор решений ✓
(5, 2) не является решением, поскольку не входит в набор решений (обозначен пунктирной линией набора решений) ✗
(0,0) является решением, так как входит в набор решений ✓
(10,10) не является решением, поскольку не входит в набор решений ✗
(-2, 0) не является решением, поскольку его нет в наборе решений ✗
Заключение
Построение графиков систем неравенств и решение систем неравенств можно легко выполнить, придерживаясь следующего трехэтапного метода:
Шаг первый: Решите оба неравенства для y (если необходимо).
то есть изолировать y как y>, y≥, y<, или y≤
Шаг второй: Начертите оба неравенства на координатной плоскости.
Шаг третий: Определите набор решений.
Несмотря на то, что в этом руководстве приведены примеры систем неравенств с двумя неравенствами, вы можете выполнить те же шаги для решения системы с любым количеством неравенств. Если вы знакомы с графиками нелинейных функций, вы можете применить знания, полученные в этом руководстве, для решения систем неравенств, которые также включают неравенства более высокого порядка.
Больше математических ресурсов, которые вам понравятся:Система неравенств — Дом алгебры
14.01.2013 0 комментариев
Как решить систему неравенств графически? Изобразите графически каждое неравенство, тогда решением будет перекрытие двух полуплоскостей. К графику y ≤ 2x + 2: Нарисуйте линию y = 2x + 2 {y-пересечение равно 2, а наклон равен 2} Используйте сплошную линию, учитывая знак «меньше» или «равно». Поскольку оно ≤, закрасьте ось Y вниз от граничной линии На графике y < -x + 1: Нарисуйте линию y = -x + 1 {пересечение y равно 1, а наклон равен -1} Используйте пунктирную линию, учитывая только знак «меньше» без равенства. Поскольку <, заштрихуйте ось Y вниз от линии границы. Решением системы неравенств {показано ниже} является перекрытие двух полуплоскостей. Набор решений (наложение показано слева) — это набор точек, удовлетворяющих обоим неравенствам. Спросите Algebra House 0 комментариев | Последние видео Категории Все Архив январь 2022 г. |
