Примеры тригонометрия 10 класс: Тригонометрические уравнения — урок. Алгебра, 10 класс.

alexxlab / / Разное

Содержание

решение тригонометрических уравнений 10 класс

                                           Содержание

 

 

 

 

Ι. Решение простейших тригонометрических уравнений

2– 7 

ΙΙ. Общие методы решения тригонометрических уравнений

 

1. Метод разложения на множители

8 – 10

2. Метод введения новой переменной

10 – 14

3. Функционально-графические методы

15 – 17

ΙΙΙ. Решение комбинированных уравнений

18 – 23

ΙV.

Решение тригонометрических уравнений с параметром

24 – 25

V. Тесты для самостоятельного решения

26 – 27

Литература

28


 

 

 

Ι. Решение простейших тригонометрических уравнений

 

Все тригонометрические уравнения сводятся к простейшим. Поэтому особое внимание следует уделять решению простейших уравнений. Начинать нужно с самых простых.

К простейшим тригонометрическим уравнениям относятся уравнения вида:

Для  каждого из простейших тригонометрических уравнений определены формулы, справедливость которых обосновывается с помощью тригонометрического круга и с учетом периодичности тригонометрических функций.

 

sinx=а, |а|>1, решений нет;          

sinx=0, x= πn, nєZ

sinx =–1, x= –+2πn, nєZ;

sinx =1, x=+2πn, nєZ;

sinx=а, |а|<1, x= arcsinа +2πn, nєZ;                             

                      x= π–arcsinа +2πn, nєZ.

В последнем случае для сокращения записи используют формулу:

x=(–1)narcsinа + πn, nєZ.                             

cos x=а, |а|>1,решений нет;

cos x=0, x= –+πn, nєZ;

cos x=–1, x= π +2πn, nєZ;

cos x=1, x=2πn, nєZ;

cos x=а, |а|<1, x= ± arccosа +2πn, nєZ.

 

Решения уравнения  tg x=а и ctg x=а  записываются существенно проще:

 x= arctgа +πn, nєZ    и, соответственно, x= arcсtgа +πn, nєZ .                           

Пример 1. Решить уравнение sinx = .

Решение: так как <1, значит  x=(–1)narcsin + πn, nєZ.  

Ответ: (–1)narcsin + πn, nєZ.                       

Пример 2. Решить уравнение cos x =.

Решение: так как  >1, значит уравнение не имеет решения.

Ответ:   нет решения.

Пример 3. Решить уравнение   tg x+ = 0.

Решение: 

tg x+ = 0                        

tg x  = –

x = arctg (–) + πn, nєZ

x = – arctg + πn, nєZ

x = –+2πn, nєZ;

Ответ:   –+2πn, nєZ.

Пример 4. Решить уравнение  2cos x = –. 

Решение:

2cos x = – 

cos x = –                                    

x= ± arccos (–)+2πn, nєZ

x= ±( π  – arccos )+2πn, nєZ        

x= ±( π  – )+2πn, nєZ

x = ±    +  2πn, nєZ

Ответ:   ±    +  2πn, nєZ.

Для отработки общих формул решения простейших уравнений можно предложить для     устного решения задания такого вида.

Образуют ли арифметическую прогрессию расположенные в порядке возрастания положительные корни уравнения :  sinx =0;  cosx = 0,5;  tg x=1.

На начальном этапе, пока не отработаны навыки использования общих формул решения простейших уравнений желательно прописывать эти формулы, чтобы учащиеся быстрее их запомнили.

Далее нужно  переходить к решению более сложных уравнений, которые чаще всего встречаются в вариантах ЕГЭ в разделе А.

Пример 5. Решить уравнение      cos  = .                             

Решение: cos  =

Это  уравнение сводится к простейшему    cos t =  заменой t =, которую можно не     прописывать.

 = ±  arccos +2πn, nєZ           

 = ±  +2πn, nєZ

 х = ±  + 10πn, nєZ

Ответ:   ±    +  10πn, nєZ.

Пример 6. Решить уравнение: sin (2x–) = . 

Решение:     sin (2x–) =   

2x–= (–1)narcsin  + πn, nєZ

2x– = (–1)n   + πn, nєZ

2x– = ++ 2πn, nєZ

2x– = –+ (2m + 1)π,mєZ

2x =   + 2πn, nєZ

2x =π + 2πm, mєZ

x =   + πn, nєZ

x = + πm, mєZ

Ответ:    + πn, + πm, n,mєZ.

Так же нужно обратить внимание учащихся на то, что довольно часто исходное уравнение приводится к простейшему лишь после различных тождественных преобразований и применения формул тригонометрии.

 

Пример 7. Решить уравнение 4 sin3x cos 3x =1.

Решение:     4 sin3x cos 3x =1         

2(2sin3x cos 3x) =1     

2sin6x =1  

sin6x =

6x = (–1)n+ πn, nєZ

x = (–1)n+ n, nєZ

Ответ:  (–1)n+ n, nєZ.      

Часто предлагается решить тригонометрическое уравнение на некотором   промежутке. Целесообразно начинать решать такие уравнения до вывода общих формул решения простейших тригонометрических уравнений.

Рассмотрим примеры.

 

Пример 8. Найдите корни уравнения  2cosx = –1, принадлежащие промежутку [0;2π].

Решение: 

2cosx = –1

cosx =  –

Выбор значений  x , которые принадлежат указанному промежутку можно выполнить различными способами.

Наиболее рационально это делать с помощью единичной окружности.

 

 

x1 = ;   x2 = . 

                                      

       

Ответ:  ;.

В тестах часто требуется не просто найти корни, принадлежащие данному промежутку, а вычислить их сумму или  разность; определить наибольший или наименьший корень; указать количество корней.

 

Пример 9. Найдите  сумму корней  уравнения  (cos 2 x –1)(2 sin – 1) = 0, принадлежащих промежутку [–; π ).

Решение:                         x1 = 0;   x2 = ,  x1 + x2 =

 Ответ:  .

 

Решите самостоятельно.

1. Найдите сумму корней уравнения   2sinx = –1 на указанном промежутке

2. Найдите количество  корней уравнения   4cos 22х  = 1 на указанном промежутке

3. Найдите сумму  наименьшего положительного и наименьшего  отрицательного корней уравнения      sinx cos + sin cos х =  на указанном промежутке 

Уже при решение простейших тригонометрических уравнений полезно предлагать нестандартные уравнения.

 

Пример 10. Решить уравнение   cos x2 = 1.

 

Можно дать это уравнение  для самостоятельного решения.

Найдутся ученики, которые решат его в одну строчку:

   х2   =  2πk, kЄZ

   х = , kЄZ.

Целесообразно продемонстрировать это решение на доске и предложить ученикам найти допущенные ошибки.

В случае затруднений, чтобы внести полную ясность, решить для начала уравнение

   х2   =  a.

Его решение имеет вид  х = ±  при а0.

Если а <0, то уравнение не имеет решений. Значит решением исходного уравнения является  х = ±, kЄZ,  k0.

 

Ответ:  ±, kЄZ,  k0.

Пример 11. Решить уравнение     sinsinx = 1.

Решение:  sinsinx = 1.  

                   sinx  = +2πn, nєZ

Выражение   |+2πn | > 1 при любых  значениях n , nєZ.

Поэтому исходное уравнение не имеет решений.

Ответ:  нет  решений.


ΙΙ. Общие методы решения тригонометрических уравнений

 

1.     Метод разложения на множители.

Этот метод заключается в том , что исходное уравнение сводится к уравнению вида

f (x)g(x)h(x) = 0, которое можно заменить совокупностью уравнений, каждое из которых сводится к простейшему.

Решив уравнения совокупности нужно взять только те решения, которые принадлежат области определения исходного уравнения, а остальные корни отбросить.

 

Пример 1. Решить уравнение    sin4x  = 3 cos2х.

Решение: 

sin4x  = 3 cos2х.

2 sin2x cos2х =  3 cos2х

Получив  такое уравнение, ученики достаточно часто делают ошибку, «сократив» левую  и правую части уравнения на  cos2х. Некоторые из них при этом оговаривают, что  cos2х 0,но одной  оговорки здесь, увы, недостаточно. Необходимо ещё рассмотреть случай, когда cos2х = 0, и  проверить, не являются ли значения х, удовлетворяющие этому равенству, корнями исходного уравнения. Разумеется, лучше всего не делить левую и правую части уравнения на cos2х, а разложить на множители

(2 sin2x  – 3) cos2х =  0.

Полученное уравнение равносиьно совокупности двух уравнений

     х = , nЄZ.

Первое уравнение решения не имеет, так как функция синус не может принимать значений по модулю больших единицы. К сожалению, не все ученики это  понимают, а из тех, кто понимает, не всякий вспоминает вовремя.

Ответ: , nЄZ.

 

Пример 2. Решить уравнение    sin2x  = sin4x

Решение:  некоторые учащиеся, встретив такое уравнение, решительно записывают

2х = 4х или 2х = 4х + 2πn, nЄZ, что приводит к потере  решений исходного уравнения.

Решение исходного уравнения состоит в переходе к уравнению sin2x  – sin4x = 0

и последующем применении формулы для преобразования разности тригонометрических функций в произведение

2cos = 0

cos3x (–sinx) = 0

 Ответ:  


 

Пример 3.  (ЕГЭ 2009г. Вариант 1, С2.).

Найдите все значения  , при каждом из которых выражения

  принимают равные значения.

Решение:

Ответ:  

 

Пример 4. (ЕГЭ 2009г. Вариант 2, B7.).

Найдите наименьший корень уравнения

 

Решение:

Ответ:

 

2.     Метод замены переменной.

В школьном курсе в основном рассматриваются уравнения, которые после введения нового неизвестного t = f(x),где f(x) – одна из основных тригонометрических функций, превращаются в квадратные либо рациональные уравнения с неизвестным t.

 

Пример 5. Решить уравнение    cos2 πx  + 4sinπx + 4 =0

Решение: 1 – sin 2 πx  + 4sinπx + 4 =0

– sin 2 πx  + 4sinπx + 5 =0

Заменим   sin πx = t , -1

–t 2 + 4t +5 = 0

t 2 – 4t – 5 = 0

t1  =  –1, t2    = 5

t2  не удовлетворяет условию   -1

sin πx = –1

πx = –

х = – 

Ответ:   –

 

Решение однородных тригонометрических уравнений.

 

Уравнение вида аsinx +bcosx =0, где а и b –некоторые числа, называются  однородными уравнениями первой степени относительно sinx  и  cosx.

Уравнение вида аsin 2 x +bcos 2 x + с =0, где а,b,с  – некоторые числа, называются  однородными уравнениями  второй степени относительно sinx  и  cosx.

 

Пример 6. Решить уравнение    sinx  –  cosх = 0.

Решение: легко убедиться, что cosx = 0 не  является корнем исходного уравнения.

В самом деле, если  cosx = 0, то, в силу исходного уравнения, и sinx = 0, что противоречит основному тригонометрическому тождеству. Этот факт позволяет разделить левую и правую части уравнения на cosx.

Получим уравнение tg x  = 1, откуда х =

Ответ:  

Пример 7. Решить уравнение    sin 2 x  – 3sinx cosх + 2cos 2 x = 0.

Решение: поскольку  cosx = 0 не является корнем tg x  данного уравнения,

разделим левую и правую части уравнения на cos 2 x. В результате приходим к квадратному уравнению относительно tg2  x  – 3 tg x  + 2 = 0,

решив которое, получим

  

 

Ответ:  

 

Введение вспомогательного аргумента.

 

Уравнение вида аcosx  + b sinx   = с, где а, b, с  –некоторые числа, причем 

называют линейными тригонометрическими уравнениями.

Для решения таких уравнений используют введение вспомогательного аргумента.

Так как  а 2  + b2  >0, то можно разделить обе части уравнения на , получим

 

Введём в рассмотрение угол  такой, что

Угол , удовлетворяющий этим двум условиям, принято называть дополнительным (или вспомогательным) аргументом. Для любых значений а и b такой угол существует, так как 

Вообще, полезно напомнить учащимся, что любые числа  p и g такие,  что  

p2 + g2 = 1 можно рассматривать как косинус и синус некоторого угла.

Теперь исходное уравнение можно записывать в виде

 coscosx + sinsinx =

cos (x – ) =

Аналогично можно вводить вспомогательный угол такой, что:

 

Тогда исходное уравнение можно привести к виду

sincosx + cossinx =

sin (x +) =

Полезно также обратить внимание учащихся, что умение преобразовывать выражения вида  а cosx  + b sinx   может понадобиться  не только при решении уравнений, но и для построения оценок, нахождения наибольших значений и т.   д.

 

Пример 8. Решить уравнение   3 sinx  –  4cosх = 5.

 

Решение.  3 sinx  –  4cosх = 5

 ==5

, cosx = ,

cos(x + ) = –1

x +  = π + 2πn, nЄZ

x  = –  + π + 2πn, nЄZ

x  = –arcsin+ π + 2πn, nЄZ

Ответ:   –arcsin+ π + 2πn, nЄZ.

Пример 9. Решить уравнение    2cosх  = 1–  2cos 2х  –sin2x.  

 

Решение.  Воспользуемся формулой   2cos 2х  – 1 =  cos 2x,

  получим   2cosх  = –  cos2х  –sin2x.

Применим к правой части процедуру введения вспомогательного аргумента.

 =

2cosх  = –  2(cos2х  +sin2x)

2cosх  = – 2 (сos cos2х  + sinsin2x), где

2cosх  = –  2(cos2х  – )

cosх  + cos (2х  – ) = 0

Последнее уравнение легко решить, преобразовав сумму косинусов в произведение:

2coscos

cos

Необходимо обратить внимание учащихся на то, что в тригонометрических системах и совокупностях при записи имеет смысл употреблять разные буквы, обозначающие целые числа.

Ответ:   .

 

Универсальная тригонометрическая подстановка.

 

Универсальная тригонометрическая подстановка позволяет перейти от синуса и косинуса аргумента х  к тангенсу половинного аргумента:

sin ,   cos

При таком переходе возможна потеря решений, следует помнить, что  (в этих точках tg  не существует). Поэтому всякий раз, когда приходится пользоваться универсальной подстановкой, значения х = π + 2πn, nЄZ необходимо проверять отдельно, подставляя в исходное уравнение.

 

Пример 10. Решить уравнение    sinx  +  cosх = –1.

Решение:  = –1, заменим tg , получим

2t +1 – t2  = –1– t2

2t  = – 2

t  = – 1

tg

Подставим теперь в исходное уравнение значение  и убедимся, что они действительно являются его решениями.

Ответ:  


 

Уравнение вида

 

Уравнение вида  где — многочлен, удобно решать при помощи введения новой переменной 

Тогда можно получить выражение для произведения из формулы

Пример 11. Решить уравнение

Решение: введем новую переменную

Тогда

Следовательно,  и исходное уравнение принимает вид

Для определения переменной   получаем два уравнения  

Для решения таких уравнений используют введение вспомогательного аргумента.

Ответ:

 

После завершения изучения рассмотренных методов, при наличии времени, рекомендуем провести урок-практикум – «Урок решения одного уравнения»


 

3. Функционально-графические методы

 

1)    Использование свойств ограниченности функций, метод оценок.

 

Часто приходится  иметь дело с уравнениями, имеющими вид f(x) = g(x), где f  и g – некоторые функции, составленные с помощью тригонометрических выражений, такие, что можно исследовать  области значений  Е(f) и Е(g)  и доказать, что эти области либо не пересекаются, либо имеют небольшое число общих точек. В таких случаях решения уравнения  f(x) = g(x)  следует  искать среди таких  x , которые удовлетворяют более простым уравнениям  f(x) = a, g(x) = a , где а – такое действительное число, что

Пример 12. Решить уравнение  .

Решение:

Ответ:  нет решения.

 

Пример13. Решить уравнение .

Решение:

Ответ:  нет решения.

 

Пример14. Решить уравнение .

Решение:

 

Ответ: .

Пример15. Решить уравнение

Решение:

Ответ:  

 


 

Пример16. Решить уравнение

Решение.

Заметим, что сумма в левой части полученного уравнения может принимать значение 2, только если  одновременно, т.е. наше уравнение равносильно системе уравнений

 

И должно выполняться равенство  Поскольку        

Ответ: 

 

2)    Использование графиков.

Суть метода использования графиков для решения уравнения  f(x) = g(x)  проста:  нужно  построить графики функций  y = f(x) и y = g(x) и найти  все точки их пересечения, абсциссы которых и будут являться корнями нашего  исходного уравнения.

 

Пример 17. Сколько корней имеет уравнение:

 

Решение:  в данном примере для решения уравнений используются свойства графиков функций.

 

Ответ: 1 решение.


 

Ответ: 1 решение.

 

 

 

Ответ: 7 решений.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ΙΙΙ. Решение комбинированных уравнений

 

Пример1. Решите уравнение

Решение:

Ответ: .

Пример 2. Решите уравнение  

Решение:

Ответ:

Пример 3. Решите уравнение

Решение:

Решим первое уравнение системы с использованием универсальной тригонометрической подстановки:

 

С учетом неравенств системы имеем:

 

 

 

 

 

 

 

 

 

 

 

 

 


Ответ:


Пример 4. Решите уравнение

Решение:

 

 

                                                                                    

 

 

 

 

 

            

                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                                            

 

 

 

 

 

Ответ:

Пример 5. Решите уравнение

Решение:

Ответ:

 

Пример 6. Решите уравнение

Решение:

                                                                  

                                                             

 

 

 

 

 

 

 

Ответ:

Пример 7. Решите уравнение

Решение:

Ответ:


Пример 8. Решите уравнение

Решение: воспользуемся формулой понижения степени

Ответ:

Пример 9. Решите уравнение

Решение:

Решим полученное уравнение графически, для этого в одной системе координат построим графики функций

Ответ:

Пример 10. Решите уравнение

Решение: введем функцию  тогда получим

Исследуем функцию на монотонность

Ответ:

Пример 11. Решите уравнение

Решение: данное уравнение равносильно системе

 

 

 

 

 

 

 

Ответ:

 

 

 

 

 

 

 

 

 

 

 

 

 


 

ΙV. Решение тригонометрических уравнений с параметром.

 

Пример1. Найти все значения параметра  , при которых уравнение  имеет решение.

Решение:

 

 

Пример 2. Найти все значения параметра  , при которых уравнение  имеет  на отрезке  ровно  три корня.

Решение:

Пример 3.  Решите уравнение.

Решение:

 

 

V. Тесты для самостоятельного решения

 

Данные тесты предназначены для проверки умений решения тригонометрических уравнений различными способами.

 

Вариант№1.

 

 

 

Вариант№2.

 

 

Вариант№3.

 

Вариант№4.

 

 

 


 

Литература

 

1.      Алгебра и начала анализа: дидактические материалы для 10 класса / М.К.Потапов, А.В.Шевкин.-2-е изд.-М.:Просвещение,2007.

2.      Алгебра и начала анализа: дидактические материалы для 11 класса: базовый и профильные уровни / М.К.Потапов, А.В.Шевкин.-2-е изд.-М.:Просвещение,2007.

3.      Бурмистрова Н.В.,СтаростенковаН.Г.Математика.11класс. Подготовка к экзамену.

-Саратов: Лицей,2005.

4.      Единый государственный экзамен: Математика: контрольные измерительные материалы: 2006-2007.-М.:Просвещение: СПб.: Просвещение,2007.

5.      ЕГЭ-2009.Математика: Сдаём без проблем!/ О.А.Креславская, В.В.Крылов, В.И.Снегурова, В.Е.Ярмолюк.-М.:Эксмо.2008.

6.      ЕГЭ. Репетитор. Математика.Эффективная методика./ Л.Д.Лаппо, А.В.Морозов, М.А.Попов.-М.:Издательство «Экзамен»,2007.

7.      Панчишкин А.А.. Шавгулидзе Е.Т. Тригонометрические функции в  задачах — М. :Наука. Главная редакция физико –  математической литературы,1986.

8.      Самое полное издание типовых вариантов реальных заданий ЕГЭ:2009:Математика /

авт.-сост. В.И.Ишина, В.В.Кочагин, Л.О.Денишева и др.-М.:АСТ: Астрель,2009.

9.      Сборник заданий для подготовки и проведения письменного экзамена по математике

(курс А) и алгебре и началам анализа (курс В) за курс средней школы.11 класс/

Г.В,Дорофеев, Г.К.Муравин ,Е.А.Седова.-10-е изд.,стереотип.-М.:Дрофа,2007.

10.  Тематические тесты. Математика. ЕГЭ-2009.Часть2.10-11 классы/ Под редакцией Ф.Ф.Лысенко. — Ростов-на-Дону:Легион,2008.

11.  Макеева А.В.Карточки по тригонометрии.10-11 класс: Дидактический материал

для учителей. — Саратов:Лицей.2002.

12.  Макарова Л.В. Уроки-практикумы в системе работы учителя. //Математика в школе,1998,№3.

13.  Математика: интенсивный курс подготовки к экзамену.-4-е изд.испр. и доп.-М.:Рольф:Айрис-пресс,1999.

14.  Математика: Тематическое планирование уроков подготовки к экзамену / А. В.Белошинстая.-М.:Издательство «Экзамен»,2007.

15.  Шаммин В.М. Тематические тесты для подготовки к ЕГЭ по математике. Изд.3-е.-

Ростов н/Д: Феникс,2004.

Урок алгебры в 10-м классе. Тема: «Примеры решения тригонометрических уравнений»

Разделы: Математика

Цель урока:

  1. Закрепить навыки решения простейших тригонометрических уравнений.
  2. Сформировать понятие решения тригонометрических уравнений сводящихся к квадратным.
  3. Развивать умения сравнивать, выявлять закономерности, обобщать.
  4. Воспитывать ответственное отношение к труду.

Оборудование:

  1. Карточки для повторения формул решения простейших тригонометрических уравнений.
  2. Плакат с алгоритмом решения тригонометрических уравнений (большой на доску и каждому на стол).

Литература: Учебник Колмагорова “Алгебра и начала анализа, 10-11 класс”.

Ход урока.

I. Повторение

1. sin x = a, cos x = a, tg x = a

При каких значениях а эти уравнения имеют решения?
[sin x и cos x при /а/ 1 tg x при любом a]

2. Повторить формулы решения простейших тригонометрических уравнений (на карточках):

sin x = а х = (-1)к arc sin a+ к, к z
sin x = 0
sin x = 1
sin x = -1

cos x = a x=± arc cos a + 2 , n z
cos x = 0
cos x = 1
cos x = -1

tg x = a x = arc tg a + n, n z

arc sin (-а) = — arc sin а
arc cos (-а) = — arc cos а
arc tg а (-а) = — arc tg а

II. Проверка домашнего задания.

Игра “Поле чудес”. Правила игры несколько изменены, а название оставлено.

Правила игры.

  • Учитель берет понравившееся ему высказывание или слова из песни, стихотворения, пословицу. По количеству букв в этом высказывании подбирается столько же примеров или задач так, чтобы одинаковым буквам соответствовали одинаковые ответы.
  • Каждому ученику учитель дает карточку с заданиями и ученик сразу начинает решать.
  • На доске записаны буквы, которые встречаются в высказывании, и под ними ответы, которые соответствуют этим буквам.
  • Ниже записаны числа по порядку (по количеству букв в высказывании).
  • Ученик, выполнявший задание, называет номер своей карточки и букву, под которой записан ответ.
  • Учитель под числом (…) ставит букву (…). И так далее. Ученики стараются быстрее решить, чтобы получить следующую карточку.
  • За правильно решенные 2-3 задания он может получить оценку. Поэтому желательно карточек иметь более чем число.

Ум хорошо, а два лучше
12 3 45 67 8 9 10 11 12 13 14 15 1 6 17

а в д
n z , к z , n z
е л м
, n z , n z , n z
о р у
, n z , n z , n z
x ч ш
, n z , n z , n z

Уравнение:

, n z у
cos x = -1 х = +2 n, n z м
, n z x
, n z o
, n z p
, n z o
, n z ш
, n z o
, n z a
, n z д
, k z в
, n x a
, n z л
, n z у
, n z ч
, n z ш
, n z е

Дополнительные уравнения

, n z
, k z
, n z
, k z
, n z
, n z
, n z
, n z
, n z
, n z
, k z
, n z
, k z
, k z
, n z
, n z

III. Объяснение нового.

1.

  • В предыдущих параграфах были выведены формулы корней простейших тригонометрических уравнений: sin x=a, cos x=a, tg x=a
  • К этим уравнениям сводятся другие тригонометрические уравнения. Для решения большинства из них требуется применение формул преобразований тригонометрических выражений.
  • Сегодня на уроке мы рассмотрим уравнение, сводящиеся к квадратным.

2.

  • На доске записаны уравнения:

а) 3х-8=х+6 (линейное уравнение)
б) х2+2х-15=0 (квадратное уравнение)
в) х4-5х2+4=0 (квадратное уравнение относительно х2).
г) 2 cos2x-cosx-1=0 (квадратное уравнение относительно cosx)

  • Какие из них являются квадратными?
  • Общий вид квадратного уравнения:

ax2+bx+c=0

,

Корни квадратного уравнения, приведенного, т. е. х2+рх+q=0 можно находить по теореме Виета:

Х1+х2=-р; х1х2=q

  • х4-5х2+4=0 – квадратное уравнение относительно х2. Это уравнение назвали биквадратным. Общий вид ах4+вх2+с=0, где а± 0.
  • Его легко решить методом введения новой переменной, т.е. х2=а и уравнение принимает вид: а2-5а+4=0

3. Последнее уравнение тоже квадратное, относительно cosx. Для его решения введем новую переменную. Пусть y=cosx, тогда уравнение можно записать виде: 2у2-у-1=0. Получили квадратное уравнение.

Д=1+8=9;

Следовательно:

а) cosx=1 б) cosx=

х=2p n, n z , n z

 , n n

Ответ: 2 n, n z; , n z

4. Решим уравнение:

 Надо привести уравнение к одной функции.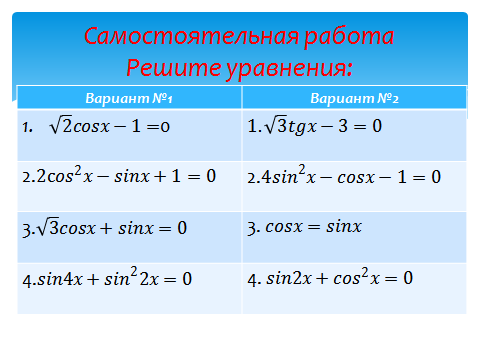 Для этого заменим cos2 x на 1-sin2x. Получим относительно xinx квадратное уравнение:

Пусть xinx=у, тогда 2у2+5у-3=0

Получили квадратное уравнение

Д=25+24=49

;

Следовательно:

а) б) xinx=-3 – решение не имеет

, к z

, к z

Ответ: , к z

5.

tgx-2ctgx=-1. Функции разные. Используя тождество tgx? ctgx=1, выразим , заменим ctgx через tgx.

пусть tgx=у, то у2+у-2=0 (дальше, как в предыдущем случае).

6. Для закрепления

4 xin2x- cosx-1=0
Заменим xin2x на 1- cos2x. Получим
4(1- cos2x)- cosx-1=0
4-4 cos2x- cosx-1=0
-4 cos2x- cosx+3=0
4 cos2x+ cosx-3=0

пусть cosx=у, то

4у2+у-3=0

Д=1-48=49 ;

Следовательно,

а) cosx=-1 б)

х= +2 n, n z , n z

Ответ: +2 n; , n z

7. №164 (в) — cамостоятельно

2 xin2x- xinx-1=0
пусть xinx=у, то
2у2-у-1=0

Д=1+8=9;

Следовательно,

а) xinx=1 б)

, n z , n z

,к z.

Ответ: , n z

, к z

№ 165(б)

2 xin2x+3 cosx=0

Заменим xin2x на 1- cos2x получим

2(1- cos2x)+3 cosx=0
2-2 cos2x+3 cosx=0
-2 cos2x+3 cosx+2=0, т.е.
2 cos2x-3 cosx-2=0

пусть cosx=у, то
2у2-3у=0

Д=9+16=25

;

Следовательно,

а) cosx=2 б)

решение не имеет , n z

, n z

, n z

Ответ: , n z

8.

Итог урока

Алгоритм решения тригонометрических уравнений.

  1. Привести уравнение к квадратному, относительно тригонометрических функций, применяя тригонометрические тождества.
  2. Ввести новую переменную.
  3. Записать данное уравнение, используя эту переменную.
  4. Найти корни полученного квадратного уравнения.
  5. Перейти от новой переменной к первоначальной.
  6. Решить простейшие тригонометрические уравнения.
  7. Записать ответ.

11.1 Двумерные задачи | Тригонометрия

Предыдущий

Упражнения в конце главы

Следующий

11.2 Краткое содержание главы

  • В этой главе рассматривается решение задач в двух измерениях с использованием тригонометрии.
  • Подчеркните ценность и важность создания эскизов, где это уместно.
  • Перед тем, как начать эту главу, может быть уместно быстро просмотреть предыдущее содержание по тригонометрии.

Тригонометрия была разработана древними цивилизациями для решения практических задач, таких как строительство зданий и ориентироваться по звездам. Мы покажем, что тригонометрию можно использовать и для решения некоторых других практических задач. Мы может использовать тригонометрические соотношения для решения двухмерных задач, связанных с прямоугольными треугольниками.

В качестве пересмотра три тригонометрических отношения могут быть определены для прямоугольных треугольников как:

\начать{выравнивать*} \ sin \ theta & = \ frac {\ text {напротив}} {\ text {гипотенуза}} \\ \ cos \ theta & = \ frac {\ text {смежный}} {\ text {гипотенуза}} \\ \ tan \ theta & = \ frac {\ text {напротив}} {\ text {смежно}} \конец{выравнивание*}

Мы будем использовать эти три отношения и теорему Пифагора, чтобы решить двумерные задачи.

11.1 Двумерные задачи (EMA7F)

В двумерных задачах мы часто будем ссылаться на угол подъема и угол наклона. К понять эти два угла, давайте рассмотрим человека, плывущего вдоль некоторых скал. Человек смотрит вверх и видит вершина скалы, как показано ниже:

На этой диаграмме \(\theta\) — угол возвышения.

Угол возвышения
Угол места – это угол, образованный линией визирования и горизонтальной плоскостью объекта над ним. горизонтальная плоскость.

На нашей диаграмме линия обзора проходит от корабля до вершины утесов. Горизонтальная плоскость с корабля к основанию скал. Также обратите внимание, что мы можем рассматривать скалы как прямую вертикальную линию, поэтому мы имеем прямоугольный треугольник.

Чтобы понять угол депрессии, давайте теперь рассмотрим ту же ситуацию, что и выше, но вместо этого наш наблюдатель стоя на вершине утеса, глядя вниз на корабль.

На этой диаграмме \(\альфа\) — угол депрессии.

Угол наклона
Угол наклона — это угол, образованный линией визирования и горизонтальной плоскостью объекта, находящегося под горизонтальная плоскость.

На нашей схеме линия обзора идет от вершины утеса к кораблю. Горизонтальная плоскость сверху скал через \(P\). Обратите внимание, что это параллельно линии между основанием скал и кораблем. \(P\) лежит прямо над кораблем. Мы можем построить вертикальную линию, перпендикулярную горизонтальной плоскости. точка \(Р\).

Наконец, мы можем сравнить угол подъема и угол наклона. На следующей диаграмме линия от основание утесов к кораблю параллельно линии от вершины утесов до \(P\). Угол указаны возвышение и угол наклона. Обратите внимание, что \(\alpha = \theta\).

Инклинометр. Инклинометры могут использоваться для измерения углов наклона и, таким образом, могут использовать для определения высоты объекта.

Можно сделать инклинометр для измерить угол наклона высокого здания или дерева. Когда у вас есть угол наклона, вы можете определить высоту здания или дерева.

В тригонометрии угол наклона равен углу возвышения.

temp text

Рабочий пример 1: запуск воздушного змея

Мандла запускает воздушного змея на веревке \(\text{17}\) \(\text{m}\) с наклоном \(\text{63}\)°.

  1. Какова высота \(h\) воздушного змея над землей?

  2. Если друг Мандлы Сифо стоит прямо под воздушным змеем, рассчитайте расстояние \(d\) между двумя друзья.

Сделайте набросок и определите противолежащие и прилежащие стороны, а также гипотенузу

Используйте предоставленную информацию и соответствующее соотношение для решения \(h\) и \(d\)

  1. \начать{выравнивать*} \sin 63° & = \frac{\text{напротив}}{\text{гипотенуза}} \\ \sin 63° & = \frac{h}{17} \\ \поэтому h & = 17 \sin 63° \\ & = \текст{15,14711. ..} \\ & \приблизительно \текст{15,15}\текст{м} \конец{выравнивание*} 9{2}\).

    Напишите окончательные ответы

    1. Воздушный змей \(\text{15,15}\) \(\text{m}\) над землей.

    2. Мандла и Сифо находятся на расстоянии \(\text{7,72}\) \(\text{m}\) друг от друга.

    Рабочий пример 2: Расчет углов

    \(ABCD\) является трапецией с \(AB=\text{4}\text{ см}\), \(CD=\text{6}\text{ см}\), \(BC=\text {5}\текст{см}\) и \(AD=\text{5}\text{см}\). Точка \(E\) на диагонали \(AC\) делит диагональ так, что \(AE=\text{3}\text{см}\). \(В\шляпа{Е}С = 90°\). Найдите \(A\шляпа{B}C\).

    Начертите трапецию и обозначьте все заданные длины на чертеже. Укажите, что \(B\hat{E}C = 90°\)

    Мы будем использовать \(\треугольник ABE\) и \(\треугольник CBE\), чтобы найти \(A\шляпа{B}E\) и \(C\шляпа{B}E\). Затем мы можем добавить эти два угла вместе, чтобы найти \(A\hat{B}C\).

    Найдите первый угол, \(A\hat{B}E\)

    Гипотенуза и противоположная сторона даны для обоих треугольников, поэтому используйте функцию \(\sin\).

    9{2} \\ & = 7 \\ \поэтому БЫТЬ & = \sqrt{7}\text{см} \конец{выравнивание*}

    Найти второй угол \(C\hat{B}E\)

    В \(\треугольник CBE\):

    \начать{выравнивать*} \cos C\шляпа{B}E & = \frac{\text{смежный}}{\text{гипотенуза}} \\ & = \ гидроразрыва {\ sqrt {7}} {5} \\ & = \текст{0,52915…} \\ C\hat{B}E & = \text{58,0519…} \\ & \приблизительно \text{58,1}° \конец{выравнивание*}

    Вычислить сумму углов

    \[A\шляпа{B}C = \text{48,6}° + \text{58,1}° = \text{106,7}°\]

    Другое приложение использует тригонометрию для определения высоты здания. Мы могли бы использовать рулетку, опущенную с крыши, но это нецелесообразно (и опасно) для высотных зданий. Гораздо разумнее использовать тригонометрия.

    Рабочий пример 3: Определение высоты здания

    На данном рисунке показано здание неизвестной высоты \(h\). Мы начинаем в точке \(B\) и идем \(\text{100}\) \(\text{m}\) от здания в точку \(Q\). Далее измеряем угол возвышения от земли до вершине здания, \(T\), и найдите, что угол равен \(\text{38,7}°\). Вычислите высоту здания, с точностью до метра.

    Определите противолежащую и прилежащую стороны, а также гипотенузу

    У нас есть прямоугольный треугольник, и мы знаем длину одной стороны и угла. Таким образом, мы можем вычислить высота здания.

    В \(\треугольник QTB\):

    \начать{выравнивать*} \tan \text{38,7}° & = \frac{\text{напротив}}{\text{смежный}} \\ & = \фракция{ч}{100} \конец{выравнивание*}

    Переставить и решить для \(h\)

    \начать{выравнивать*} h & = 100 \times \tan \text{38,7}° \\ & = \текст{80,1151. ..} \\ & примерно \текст{80} \конец{выравнивание*}

    Напишите окончательный ответ

    Высота здания равна \(\text{80}\) \(\text{м}\).

    Рабочий пример 4: Углы возвышения и депрессии

    Многоквартирный дом находится \(\text{200}\) \(\text{м}\) от вышки сотовой связи. Кто-то стоит у \(B\). Они измерить угол от \(B\) до вершины башни (\(E\)) и получить \(\text{34}\)\(\text{°}\) (угол высоты). Затем они измеряют угол от \(B\) до основания башни (\(C\)) и составляют \(\text{62}\)\(\text{°}\) (угол депрессии).

    Какова высота вышки сотовой связи (с точностью до метра)?

    Примечание: схема выполнена не в масштабе

    Чтобы определить высоту \(CE\), сначала вычислите длины \(DE\) и \(CD\)

    \(\треугольник BDE\) и \(\треугольник BDC\) являются прямоугольными треугольниками. В каждом из треугольников длина \(BD\) известно. Следовательно, мы можем вычислить стороны треугольников.

    Вычислить \(CD\)

    Дана длина \(AC\). \(CABD\) — прямоугольник, поэтому \(BD = AC = \text{200}\text{m}\).

    В \(\треугольник CBD\):

    \начать{выравнивать*} \tan C\hat{B}D & = \frac{CD}{BD} \\ \поэтому CD & = BD \times \tan C\hat{B}D \\ & = 200 \times \tan 62° \\ & = \текст{376,1452…} \\ & \приблизительно \текст{376}\текст{м} \конец{выравнивание*}

    Вычислить \(DE\)

    В \(\треугольник DBE\):

    \начать{выравнивать*} \tan D\hat{B}E & = \frac{DE}{BD} \\ \поэтому DE & = BD \times \tan D\hat{B}E \\ & = 200 \times \tan 34° \\ & = \текст{134,9017…} \\ & \приблизительно \text{135}\text{ м} \конец{выравнивание*}

    Сложите две высоты, чтобы получить окончательный ответ

    Высота башни: \(CE = CD + DE = \text{135}\text{ m} + \text{376}\text{ m} = \ текст{511}\текст{ м}\).

    temp text

    Рабочий пример 5: План здания

    У мистера Нкоси есть гараж в доме, и он решает добавить к гаражу крышу из гофрированного железа. Гараж \(\text{4}\) \(\text{м}\) высокий, а его лист для крыши \(\text{5}\) \(\text{м}\) длинный. Если угол крыши равен \(\text{5}\)°, какой высоты он должен построить стену \(BD\)? Дайте правильный ответ до \(\text{1}\) десятичного разряда.

    Определите противоположные и смежные стороны и гипотенузу

    \(\треугольник ABC\) прямоугольный. Гипотенуза и угол известны, поэтому мы можем вычислить \(AC\). Тогда высота стены \(BD\) равна высоте гаража минус \(AC\).

    \начать{выравнивать*} \sin A\hat{B}C & = \frac{AC}{BC} \\ \поэтому AC & = BC \times \sin A\hat{B}C \\ & = 5 \sin 5° \\ & = \текст{0,43577…} \\ & \примерно\текст{0,4}\текст{м} \\ \\ \поэтому BD& = \text{4}\text{ m} — \text{0,4}\text{ m} \\ & = \текст{3,6}\текст{м} \конец{выравнивание*}

    Напишите окончательный ответ

    Мистер Нкоси должен построить свою стену высотой \(\text{3,6}\) \(\text{m}\) . \circ\). 9\circ} & = \frac{x}{\text{4,2}} \\ х & = \текст{9,0069…} \\ & \ приблизительно \ текст {9} \конец{выравнивание*}

    Высота столба равна \(\text{9}\) \(\text{м}\).

    Мальчик, запускающий воздушного змея, стоит \(\text{30}\) \(\text{m}\) из точки прямо под воздушным змеем. Если строка воздушного змея имеет длину \(\text{50}\) \(\text{m}\) , найдите угол подъема воздушного змея.

    Сначала нарисуйте эскиз:

    Мы можем использовать соотношение косинусов, чтобы найти угол возвышения (\(x\)):

    \начать{выравнивать*} \cos x & = \frac{30}{50} \\ х & = \текст{53,1301…} \\ & \приблизительно \text{53,13}° \конец{выравнивание*}

    Угол подъема воздушного змея \(\text{53,13}\)°.

    Под каким углом поднимается солнце, если дерево \(\text{7,15}\) \(\text{м}\) высотой отбрасывает тень \(\text{10,1}\) \(\text{m}\) длинный?

    Сначала нарисуйте эскиз:

    Мы можем использовать отношение касательной, чтобы найти угол возвышения (\(x\)):

    \начать{выравнивать*} \tan x & = \frac{\text{7,15}}{\text{10,1}} \\ х & = \текст{35,2954. ..} \\ & \приблизительно \text{35,30}° \конец{выравнивание*}

    Угол подъема солнца равен \(\text{35,30}\)°.

    С расстояния \(\text{300}\) \(\text{м}\) Сьюзан смотрит на вершину маяка. Угол высота равна \(\text{5}\)°. Определить высоту маяка с точностью до метра.

    Сначала нарисуйте эскиз:

    Нам нужно найти \(LT\). Мы можем использовать отношение тангенсов:

    \начать{выравнивать*} \tan \hat{S} & = \frac{LT}{ST} \\ LT & = 300 \tan 5° \\ & = \текст{26,2465…} \\ & \приблизительно \текст{26}\текст{м} \конец{выравнивание*}

    Высота маяка \(\text{26}\) ​​\(\text{м}\).

    Лестница длиной \(\text{25}\) \(\text{м}\) упирается в стену, лестница образует угол \(\text{37}\)° к стене. Найдите расстояние между стеной и основанием лестницы до ближайший метр.

    Сначала нарисуйте эскиз:

    Обратите внимание, что нам дан угол, который лестница образует со стеной, а не угол, под которым лестница делает с землей.

    Теперь мы можем использовать функцию синуса, чтобы найти \(x\):

    \начать{выравнивать*} \sin 37° & = \frac{x}{25} \\ х & = 25 \sin 37° \\ & = \текст{15,04537…} \\ & \приблизительно \текст{15}\текст{м} \конец{выравнивание*}

    Основание лестницы \(\text{15}\) \(\text{m}\) далеко от стены.

    Предыдущий

    Упражнения в конце главы

    		 Оглавление

    Следующий

    11.2 Краткое содержание главы

    Тригонометрия, класс 10 — решения NCERT, MCQ, на основе конкретных случаев [2023-24]

    Вы учитесь…

    Глава обновлена ​​в соответствии с новым NCERT для экзаменов Совета 2023-2024 гг.

    Получите решения NCERT с видео со всеми вопросами и примерами тригонометрии главы 8 класса 10. Видео всех вопросов сделаны с пошаговыми пояснениями. Проверьте это сейчас.

     

    Тригонометрия – это изучение отношений между мерами треугольника. Обычно мы говорим о прямоугольных треугольниках, когда изучаем тригонометрию,

     

    В этой главе мы изучим

    • Что такое sin, cos, tan ( Синус, косинус, тангенс) … и как они находятся в треугольнике
    • Что такое sec, cosec, cot, и как это связано с sin, cos, tan.
    • (Sin, cos, tan, sec, cosec, cot известны как тригонометрические отношения)
    • Затем изучаем Тригонометрические отношения конкретных углов l ike 0°, 30°, 45°, 60°, 90° ; и ответь на несколько вопросов
    • Изучаем формулы sin (90 — θ) , cos (90 — θ), tan (90 — θ)
    • Затем мы изучаем тригонометрические тождества и то, как из получаются другие тождества sin 2 θ + cos 2 θ = 1

     

    Чтобы изучить ответы на вопросы NCERT, щелкните упражнение или тему ниже.

    Серийный заказ

    Пример 8.1

    Пример 8.2

    Пример 8.3

    Примеры

    Вопросы по делу (MCQ)

    Образец NCERT — MCQ

    Sin 90 — θ, cos 90 — формула θ

    Концепция

    В поисках греха cos tan

    Нахождение sin cos по сторонам треугольника

    Нахождение отношений, когда заданы другие отношения

    Нахождение значений выражений

    Доказательство

    Тригнометрические соотношения удельных углов — Оценка

    Тригнометрические отношения дополнительных углов

    Выражение коэффициентов в других коэффициентах

    Оценка с использованием тригнометрических тождеств

    Что в этом?

    Глава обновлена ​​в соответствии с новым NCERT для экзаменов совета директоров 2023–2024 годов.

    Получите решения NCERT с видео со всеми вопросами и примерами тригонометрии главы 8 класса 10. Видео всех вопросов сделаны с пошаговыми пояснениями. Проверьте это сейчас.

     

    Тригонометрия – это изучение отношений между мерами треугольника. Обычно мы говорим о прямоугольных треугольниках, когда изучаем тригонометрию,

     

    В этой главе мы изучим

    • Что такое sin, cos, tan ( Синус, косинус, тангенс)… и как они находятся в треугольнике
    • Что такое sec, cosec, cot, и как это связано с sin, cos, tan.
    • (Sin, cos, tan, sec, cosec, cot известны как тригонометрические отношения)
    • Затем изучаем Тригонометрические отношения конкретных углов l ike 0°, 30°, 45°, 60°, 90° ; и ответь на несколько вопросов
    • Изучаем формулы sin (90 — θ) , cos (90–θ), тан (90–θ)
    • Затем мы изучаем тригонометрические тождества и то, как из получаются другие тождества sin 2 θ + cos 2 θ = 1

     

    Чтобы изучить ответы на вопросы NCERT, щелкните упражнение или тему ниже.

    No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *