Интегральные функции:
- Si(x)
- Интегральный синус от x
- Ci(x)
- Интегральный косинус от x
- Shi(x)
- Интегральный гиперболический синус от x
- Chi(x)
- Интегральный гиперболический косинус от x
В выражениях можно применять следующие операции:
- Действительные числа
- вводить в виде 7.
3- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- 15/7
- — дробь
3Другие функции:
- asec(x)
- Функция — арксеканс от x
- acsc(x)
- Функция — арккосеканс от x
- sec(x)
- Функция — секанс от x
- csc(x)
- Функция — косеканс от x
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция — гиперболический арксеканс от x
- csch(x)
- Функция — гиперболический косеканс от x
- sech(x)
- Функция — гиперболический секанс от x
- acsch(x)
- Функция — гиперболический арккосеканс от x
Постоянные:
- Число «Пи», которое примерно равно ~3. 14159..
- e
- Число e — основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- oo
- Символ бесконечности — знак для бесконечности
14159..Технология TI-Nspire CAS. Решение систем уравнений и неравенств, в том числе с параметром. Люблинская И.Е.
Автор: Люблинская Ирина Ефимовна, кандидат наук, College of Staten Island, City University of New York
Инновационная обучающая система TI-Nspire CAS от компании Texas Instruments, США, является единственным в мире технологическим продуктом, который включает в себя динамическую программу для изучения всех разделов школьной математики и лабораторию для работы с задачами по основным научным дисциплинам. Этот продукт объединяет в себе поддержку геометрии, анализа, алгебры, статистики и работу с физическими датчиками. При этом объединение приложений программы создано не по принципу коллекции (как у Автографа), а на основе общих форматов данных, допускающих обмен данным между приложениями.
Обучающую систему TI-Nspire CAS можно использовать на персональных компьютерах и учебных микрокомпьютерах в классах и дома. Микрокомпьютеры имеют небольшой цветной дисплей.
Помимо программного обеспечения для изучения предметов этот продукт включает в себя систему TI-Nspire Navigator для поддержки локальной беспроводной сети между компьютером учителя и микрокомпьютерами учеников. Это позволяет учителю видеть и оценивать работу каждого ученика в реальном времени, создавать, рассылать и собирать тесты и задания для учащихся, а также предоставлять им возможность демонстрировать свою работу всему классу со своего микрокомпьютера через компьютер учителя. С помощью программы также можно создавать динамические презентации и проигрывать их специальным бесплатным плейером.
Полный программный продукт TI Nspire CAS состоит из нескольких компонентов
Для учеников:
1. Программная среда «Математика и естественные науки». TI-Nspire CAS версия ученика этой среды включает:
- Cистему компьютерной алгебры, динамическую геометрию, программу работы с графиками функций, электронными таблицами, программу поддержки статистики, интерактивный блокнот и физическую лабораторию (датчики продаются отдельно).
- Cредства создания мультимедийных документов, например, тексты, гиперссылки, видео и изображения; средства создания портфолио.
- Cреду программирования на языке Lua.
2. Цветной учебный микрокомпьютер TI-Nspire CAS CХ с набором функций.
Для учителей:
1. ПО «Математика и естественные науки» TI-Nspire CAS версия учителя, включающая всё, что включено в версию ученика, а также приложение по созданию контрольных и самостоятельных работ и тестовых вопросов в различных форматах.
2. Станции для зарядки и передачи данных.
3. ПО TI-Nspire Navigator CAS для учебных микрокомпьютеров (подсоединение через беспроводную связь), включающее:
- ПО «Математика и естественные науки» TI-Nspire CAS, версия учителя.
- Систему организации работы с классом — электронный журнал (портфолио), менеджер компьютеров (или учебных микрокомпьютеров) учеников для обмена документами, контроля работы учащихся во время урока, демонстрации их работ в реальном времени и т.
4. TI-Nspire Document Player — бесплатная ограниченная версия программы для «проигрывания» документов без лицензионной копии программы возможного только для документов, не требующих ввода данных в программу или построений.
TI Nspire CX CAS включает систему компьютерной алгебры, динамическую геометрию, программу работы с графиками функций, программу поддержки статистики и физическую лабораторию
В 2006 году впервые TI-Nspire CAS технологии были апробированы в Европе и Северной Америке. В 2007 TI-Nspire CAS технологии появились на рынке. С тех пор эти технологии нашли применение в школах стран Северной Америки (США, Канада и Мексика), Южной Америки (Колумбия и Чили), Австралии и Новой Зеландии, Азии (Китай и Индия), Европы (10 стран) и Африки (Марокко). Апробация этих технологий в России началась в августе 2011 года в четырёх школах Санкт-Петербурга: Лицее «Физико-техническая школа» Калининского района, Гимназии №177 Красногвардейского района, ГОУ СОШ №558 с углубленным изучением математики Выборгского района, Школе №597 — лицей компьютерных технологий Приморского района.
Учителя — участники пилотного проекта положительно отзываются о технологии, вполне способной заменить несколько отдельных пакетов. Школьники легко осваивают микрокомпьютеры и свободно используют их возможности. На основе опыта работы учителей-участников проекта появилась реальная возможность эффективного внедрения этих технологий для изучения математики и естественных наук в российских школах.
Решение систем уравнений и неравенств, в том числе с параметром
В качестве первого примера рассмотрим графическое исследование количества решений системы двух линейных уравнений. Сначала в программе строятся графики двух линейных функций
Затем ученикам предлагается использовать инструменты вращения и перемещения для манипуляций с графиком одной из прямых (в приведенном примере положение прямой 1 фиксируется, так что ученики могут менять график только прямой 2). На основе наблюдений ученики выдвигают гипотезу об условиях, при которых система двух линейных уравнений не имеет решений, имеет одно решение или имеет бесконечное множество решений.
При вращении по умолчанию центром поворота является точка пересечения прямой с осью ординат. Поэтому в уравнении прямой динамически меняется угловой коэффициент, а свободный член остается неизменным
Соответственно, при перемещении меняется свободный член, в то время как угловой коэффициент остаётся постоянным.
В процессе компьютерного эксперимента ученики определяют условия, при которых две прямые имеют только одну общую точку, не пересекаются или совпадают. Благодаря динамическому характеру приложения ученики могут рассмотреть различные ситуации и убедиться в том, что:
- Для пересечения прямых в одной точке необходимо и достаточно того, чтобы угловые коэффициенты прямых были разными.
- Если угловые коэффициенты прямых равны, то прямые параллельны или совпадают в зависимости от свободных членов уравнений.
В этом примере мы использовали инструменты движений для изменения графика одной из функций. В следующем примере мы рассмотрим систему уравнений с параметром, который мы зададим при помощи слайдера.
При вращении в уравнении прямой динамически меняется угловой коэффициент
При использовании слайдера ученики исследуют взаимное расположение ломаной и окружности и убеждаются в том, что система может не иметь решений, если график ломаной не пересекает окружность.
Система может иметь только одно решение, когда одна из веток графика функции является касательной к окружности.
Система может иметь два решения, когда одна из веток графика функции пересекает окружность дважды, а другая ветка ее не пересекает, или каждая ветка графика пересекает ее только один раз.
Для аналитического решения ученики сначала должны найти значение параметра а, при котором ветви графика функции являются касательными к окружности. Поскольку при этом условии расстояние от центра окружности до точки касания равно радиусу окружности, достаточно решить уравнение.
Это приводит к условиям a= или а = . После получения аналитического решения системы уравнений его можно проверить, используя приложение Калькулятор. В данном случае для получения общего решения мы использовали букву b (при использовании параметра а программа подставляет текущее численное значение для параметра и выдаёт только частное решение).
Можно также проверить условие существования решения.
При подстановке b= (или b = ) в полученные выражения для х и у можно также подтвердить, что в этом случае система имеет одно решение.
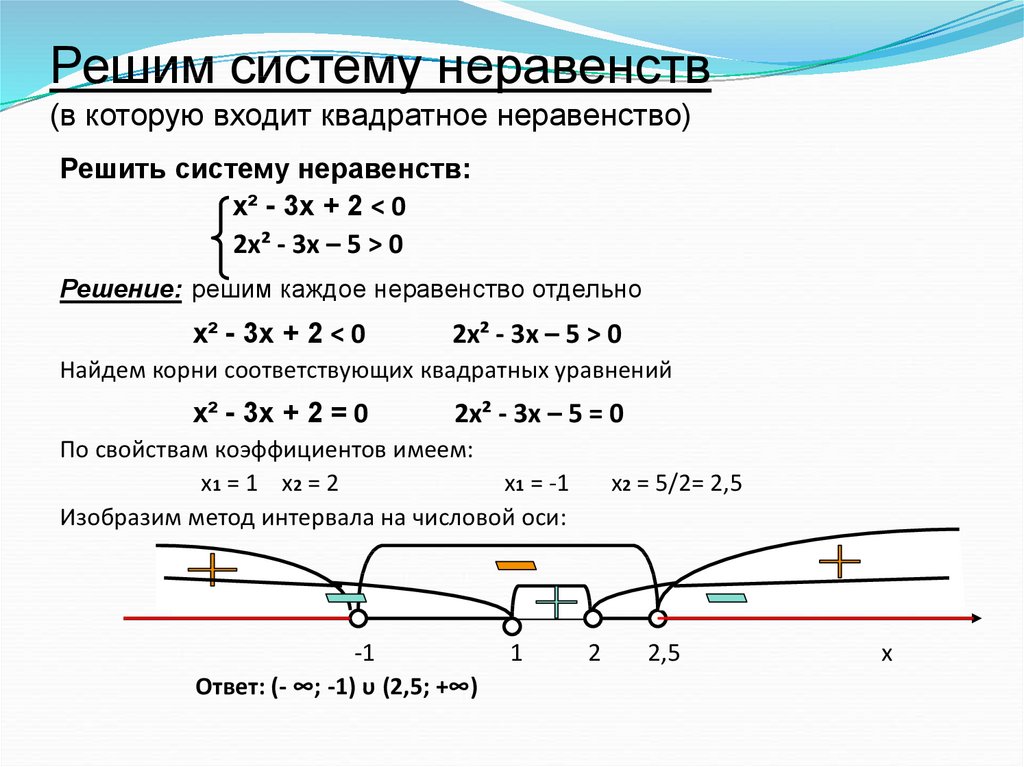
В заключении рассмотрим два примера заданий по типу С3 и С5 из ЕГЭ. Сначала рассмотрим решение системы неравенств . Построим графики функций f1(x) = и f2(x) =
Для определения промежутков, на которых обе функции одновременно не положительны, найдем нули функции. Из графика следует, что оба неравенства выполняются, когда
Другой способ графического решения данной системы неравенств основан на построении постоянной функции с областью определения, ограниченной условиями, наложенными неравенствами.
Если значение функции равно нулю, то на графике будут выделены только значения х, удовлетворяющие условиям системы неравенств
Это решение можно проверить в приложении Калькулятор.
Нужно отметить, что программа выдает правильный ответ, и это может помочь ученику найти ошибки в своём решении, если ответ, полученный при решении задачи на бумаге, не совпадает с выводом программы.
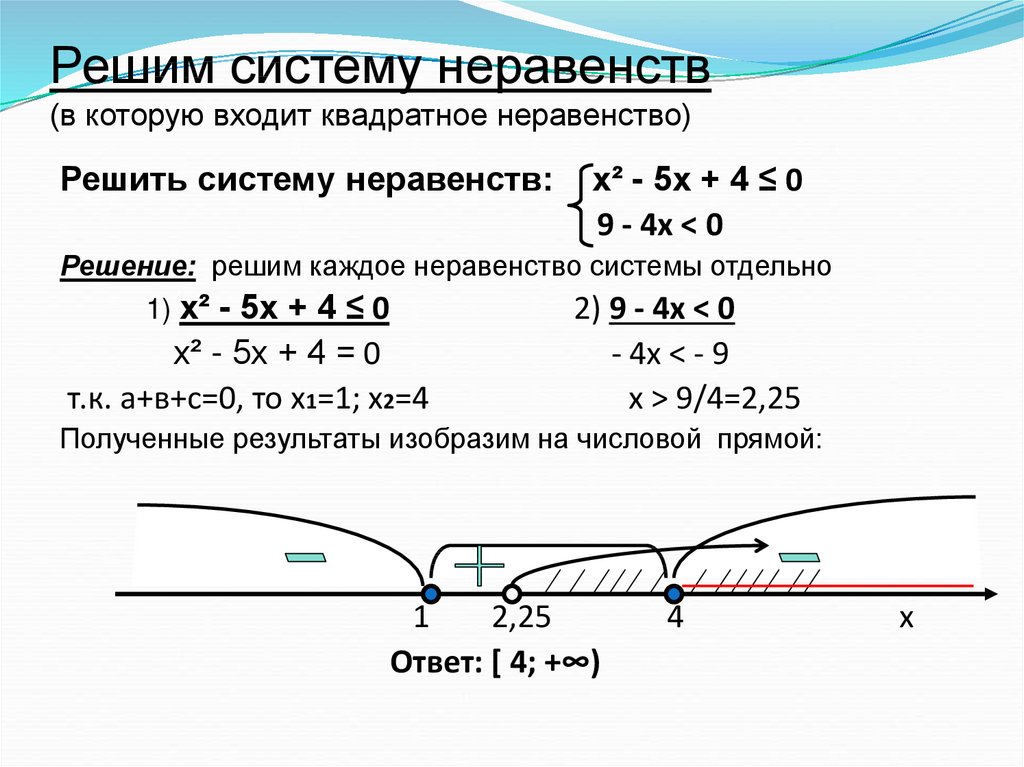
В последнем примере мы рассмотрим задание по типу С5, в котором ученику требуется найти все значения а, при каждом из которых система не имеет решений.
В данном случае мы опять используем слайдер для определения а и воспользуемся графиком нулевой функции, определённой на интервале, заданном системой неравенств. Изменяя значение а, убеждаемся в том, что на интервале [-3, -1] решений нет.
Демонстрационную 90-дневную версию учителя предоставляем бесплатно по запросу на эл.почту.
Calculators-Online.ru
Решение систем неравенств — Бесплатная помощь по математике
Сначала нам нужно просмотреть символы неравенств:
- Символ < означает меньше.
- Символ > означает больше.
- Символ \(\leq\) означает меньше или равно. Обычно это записывается как <= на компьютерах, потому что его легче набирать.
- Символ \(\geq\) означает больше или равно. Иногда это записывается как >= на компьютерах, потому что это легче набирать.
Существует бесконечное множество решений неравенств. В свете этого факта может быть проще всего найти набор решений для неравенств, решив систему графически.
Как решать системы неравенств графически
1) Запишите неравенство в форме пересечения наклона или в виде \(y = mx + b\).
Например, если нас просят решить \(x + y \leq 10\), мы сначала перепишем как \(y \leq -x + 10\).
2) Временно заменить данный символ неравенства (в данном случае \(\leq\)) на просто равный символ. При этом вы можете рассматривать неравенство как уравнение. НО НЕ ЗАБУДЬТЕ заменить символ равенства на исходный символ неравенства в КОНЦЕ задачи!
Итак, \(y \leq -x + 10\) становится \(y = -x + 10\) на данный момент.
3) Начертите линию, найденную на шаге 2. Это будет «границей» неравенства — на одной стороне линии условие будет истинным, на другой — нет. Посмотрите, как построить линию здесь.
4) Вернемся к неравенству, которое мы нашли раньше, как \(y \leq -x + 10\). Обратите внимание, что это верно, когда y меньше или равно. На шаге 3 мы построили линию (случай «равно»), поэтому теперь нам нужно учесть случай «меньше». Поскольку y меньше определенного значения на нижней стороне оси, мы заштрихуем область под линией, чтобы показать, что неравенство верно для всех точек ниже линии:
5) Проверить. Подставьте точку не на линии, например (0,0). Убедитесь, что неравенство выполняется. В данном случае это означает \(0 \leq -0+10\), что совершенно верно. Мы заштриховали правильную сторону линии.
Пример:
Найдите все значения x и y, которые удовлетворяют: \(y \geq \frac{-3}{2}x + 6\).
Обратите внимание, что это неравенство уже находится в форме пересечения наклона.
Я заменю данный символ неравенства на символ равенства, чтобы построить линию.
\(y \geq \frac{-3}{2}x + 6\) становится \(y = \frac{-3}{2}x + 6\). Теперь постройте эту линию, как показано:
Поскольку это тот случай, когда неравенство верно для значений y, больших или равных чему-либо, мы заштриховали область над линией. Все точки на этой линии графика или ВЫШЕ будут удовлетворять нашему неравенству. Снова выберите любую точку над линией графика, чтобы убедиться, что она удовлетворяет или показывает ИСТИННОЕ утверждение в терминах исходного неравенства. Например, (5,3). Подключите это, и у нас есть \(3 \geq \frac{-3}{2}*5+6\). Упростим его до \(3\geq -1.5\) и увидим, что неравенство верно в точке (5,3). Поскольку эта точка находилась выше нашей линии, ее следует заштриховать, что подтверждает наше решение.
Множественные неравенства — система неравенств
Система неравенств имеет более одного утверждения о неравенстве, которое должно быть выполнено. Графически это означает, что нам нужно сделать то, что мы только что сделали — построить линию, представленную каждым неравенством, — а затем найти область графика, которая верна для ОБОИХ неравенств.
Для двух приведенных выше примеров мы можем объединить оба графика и построить площадь, общую для двух неравенств.
Какой набор растворов? Набор решений для ОБОИХ неравенств будет ЛЮБОЙ ТОЧКОЙ, где ОБЕ заштрихованы вместе или где встречаются ОБЕ заштрихованные области.
Автор: Mr. Feliz, © 2005
Калькулятор системы неравенств с двумя переменными
|
GCF 06
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
05.2006 
03.2004 
08.2001 
08.2001 