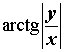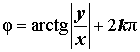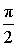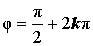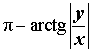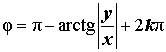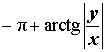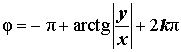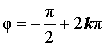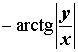Примеры умножение комплексных чисел: Умножение комплексных чисел: формула, примеры – Умножение комплексных чисел | Математика

Умножение комплексных чисел | Математика

Как умножить комплексные числа?

Рассмотрим, как следует выполнять умножение комплексных чисел, в теории и на конкретных примерах.

Произведением комплексных чисел

   

и

   

записанными а алгебраической форме, называется комплексное число

   

На практике умножение комплексных чисел выполняют по правилу умножения двучленов, с последующей заменой i² на -1.

Примеры.

Найти произведение комплексных чисел, записанных в алгебраической форме:

   

   

   

   

Решение:

Перемножаем комплексные числа, как обыкновенные многочлены:

   

приводим подобные слагаемые и заменяем i² на -1:

   

   

   

   

   

   

Утверждение.

Произведение комплексно-сопряженных чисел равно квадрату модуля одного из них.

Доказательство:

   

   

   

Что и требовалось доказать.

Соответственно, чтобы умножить комплексно-сопряженные числа, пользуются правилом:

   

Например,

   

   

Умножение комплексных чисел подчиняется коммутативному (переместительному):

   

ассоциативному (сочетательному):

   

и дистрибутивному (распределительному относительно сложения)

   

законам умножения.

 

 

Умножение комплексных чисел, формула и примеры

Рассмотрим умножение комплексных чисел записанных в алгебраической, тригонометрической и показательной формах.

Умножение в алгебраической форме

Умножение комплексных чисел и выполняется непосредственным произведением чисел в алгебраической форме, учитывая свойство мнимой единицы :

   

   

Умножение в тригонометрической форме

Для произведения комплексных чисел в тригонометрической форме верно равенство:

   

Умножение в показательной форме

Для произведения комплексных чисел в тригонометрической форме верно равенство:

   

Понравился сайт? Расскажи друзьям!

Умножение комплексных чисел

Умножение на число и умножение заданных комплексных чисел выполняются для чисел, представленных в любой форме записи.

Определение 1

Произведением заданного комплексного числа $z=a+b\cdot i$ на действительное число $k$ является комплексное число, которое определяется равенством \[k\cdot z=k\cdot (a+b\cdot i)=k\cdot a+k\cdot b\cdot i.\]

Пример 1

Выполнить умножение комплексных чисел на число $k=\sqrt{3} $:

1) $z_{1} =\sqrt{3} +\sqrt{3} \cdot i$; 2) $z_{2} =5-4\cdot i$; 3) $z_{3} =\sqrt{3} \cdot i$.

Решение:

Для умножения комплексных чисел на число воспользуемся определением и получим:

1) $k\cdot z_{1} =\sqrt{3} \cdot z_{1} =\sqrt{3} \cdot \left(\sqrt{3} +\sqrt{3} \cdot i\right)=\sqrt{3} \cdot \sqrt{3} +\sqrt{3} \cdot \sqrt{3} \cdot i=3+3\cdot i$;

2) $k\cdot z_{2} =\sqrt{3} \cdot z_{2} =\sqrt{3} \cdot (5-4\cdot i)=\sqrt{3} \cdot 5-\sqrt{3} \cdot 4\cdot i=5\sqrt{3} -4\sqrt{3} \cdot i$;

3) $k\cdot z_{3} =\sqrt{3} \cdot z_{3} =\sqrt{3} \cdot (0+\sqrt{3} \cdot i)=\sqrt{3} \cdot \sqrt{3} \cdot i=3i$.

Примечание 1

При умножении заданного комплексного числа $z=a+b\cdot i$ на число $k\, \, (|k|>1)$ модуль этого числа увеличивается в $|k|$ раз:

\[|k\cdot z|=|k|\cdot \sqrt{a^{2} +b^{2} } .\]

Примечание 2

При умножении заданного комплексного числа $z=a+b\cdot i$ на число $k\, \, (|k|

\[|k\cdot z|=\frac{\sqrt{a^{2} +b^{2} } }{\left|\frac{1}{k} \right|} .\]

Примечание 3

Графическая интерпретация операции умножения заданного комплексного числа $z=a+b\cdot i$ на число $k\, \, (|k|>1)$: длина радиус-вектора, изображающего исходное комплексное число, увеличивается в $|k|$ раз (радиус-вектор становится длиннее в $|k|$ раз).

Примечание 4

Графическая интерпретация операции умножения заданного комплексного числа $z=a+b\cdot i$ на число $k\, \, (|k|

Иллюстрация примера умножения заданного комплексного числа $z=a+b\cdot i$ на число $k_{1} =2,\, \, k_{2} =\frac{1}{4} $ с использованием комплексной плоскости приведена на рис.1-2.

Рис. 1

Рис. 2

Определение 2

Произведением двух заданных комплексных чисел $z_{1} =a_{1} +b_{1} i$ и $z_{2} =a_{2} +b_{2} i$ является комплексное число, которое получается перемножением данных чисел по правилам алгебры с учетом того, что $i^{2} =-1$.

Пример 2

Вычислить $i^{k} $ для $k=3..7$.

Решение:

\[i^{2} =-1\]

\[i^{3} =i^{2} \cdot i=-1\cdot i=-i\]

\[i^{4} =i^{2} \cdot i^{2} =-1\cdot (-1)=1\]

\[i^{5} =i^{2} \cdot i^{3} =-1\cdot (-i)=i\]

\[i^{6} =(i^{2} )^{3} =(-1)^{3} =-1\]

\[i^{7} =(i^{2} )^{3} \cdot i=(-1)^{3} \cdot i=-1\cdot i=-i\]

Пример 3

Выполнить умножение комплексных чисел:

1) $z_{1} =1+3i$ и $z_{2} =3-5i$; 2) $z_{1} =\sqrt{3} +2i$ и $z_{2} =\sqrt{5} \cdot i$.

Решение:

Для умножения комплексных чисел воспользуемся определением и получим:

1) $z_{1} \cdot z_{2} =(1+3i)\cdot (3-5i)=1\cdot 3+3\cdot 3i+1\cdot (-5i)+3i\cdot (-5i)=3+9i-5i-15i^{2} =3+4i+15=18+4i$

2)\[\begin{array}{l} {z_{1} \cdot z_{2} =(\sqrt{3} +2i)\cdot (0+\sqrt{5} \cdot i)=\sqrt{3} \cdot 0+0\cdot 2i+\sqrt{3} \cdot \sqrt{5} \cdot i+2i\cdot \sqrt{5} \cdot i=0+0+\sqrt{15} \cdot i+2\sqrt{5} \cdot i^{2} =\sqrt{15} \cdot i-2\sqrt{5} =-2\sqrt{5} +\sqrt{15} \cdot i} \end{array}\]

Замечание 1

Произведение комплексно-сопряженных чисел $z=a+b\cdot i$ и $\overline{z}=a-b\cdot i$ определяется равенством

\[z\cdot \overline{z}=a^{2} +b^{2} \]

или

\[z\cdot \overline{z}=|z|^{2} =|\overline{z}|^{2} .\]

Другими словами, произведение комплексно-сопряженных чисел есть квадрат модуля каждого из них.

Пример 4

Выполнить умножение комплексно-сопряженных чисел, используя замечание 1 и определение:

1) $z=1+3i$ и $\overline{z}=1-3i$; 2) $z=\sqrt{3} +2i$ и $\overline{z}=\sqrt{3} -2i$.

Решение:

Для умножения комплексных чисел воспользуемся замечанием 1 и получим:

1) $z\cdot \overline{z}=(1+3i)\cdot (1-3i)=1^{2} +3^{2} =1+9=10$

2) \[z\cdot \overline{z}=(\sqrt{3} +2i)\cdot (\sqrt{3} -2i)=(\sqrt{3} )^{2} +2^{2} =3+4=7\]

Для умножения комплексных чисел воспользуемся определением и получим:

1) $z\cdot \overline{z}=(1+3i)\cdot (1-3i)=1\cdot 1+1\cdot 3i+1\cdot (-3i)+3i\cdot (-3i)=1+3i-3i-9i^{2} =1+9=10$

2) $\begin{array}{l} {z\cdot \overline{z}=(\sqrt{3} +2i)\cdot (\sqrt{3} -2i)=\sqrt{3} \cdot \sqrt{3} +\sqrt{3} \cdot 2i-\sqrt{3} \cdot 2\cdot i+2i\cdot (-2)\cdot i=3+2\sqrt{3} \cdot i-2\sqrt{3} \cdot i-2^{2} \cdot i^{2} =3+4=7} \end{array}$

Результаты выполнения операции умножения комплексных чисел совпадают.

Определение 3

Произведением двух заданных комплексных чисел в тригонометрической форме $z_{1} =r_{1} \cdot (\cos \varphi _{1} +i\sin \varphi _{1} )$ и $z_{2} =r_{2} \cdot (\cos \varphi _{2} +i\sin \varphi _{2} )$ является комплексное число, которое определяется равенством

\[z_{1} \cdot z_{2} =r_{1} \cdot r_{2} \cdot [\cos (\varphi _{1} +\varphi _{2} )+i\sin (\varphi _{1} +\varphi _{2} )].\]

Пример 5

Выполнить умножение комплексных чисел:

1) $z_{1} =\sqrt{3} \cdot (\cos \frac{\pi }{4} +i\cdot \sin \frac{\pi }{4} )$ и $z_{2} =2\cdot (\cos \frac{2\pi }{3} +i\cdot \sin \frac{2\pi }{3} )$;

2) $z_{1} =4\cdot (\cos \pi +i\cdot \sin \pi )$ и $z_{2} =5\cdot (\cos \frac{\pi }{2} +i\cdot \sin \frac{\pi }{2} )$.

Решение:

Для умножения комплексных чисел воспользуемся определением и получим:

1) $\begin{array}{l} {z_{1} \cdot z_{2} =\left(\sqrt{3} \cdot (\cos \frac{\pi }{4} +i\cdot \sin \frac{\pi }{4} )\right)\cdot \left(2\cdot (\cos \frac{2\pi }{3} +i\cdot \sin \frac{2\pi }{3} )\right)=2\cdot \sqrt{3} \cdot [\cos (\frac{\pi }{4} +\frac{2\pi }{3} )+i\cdot \sin (\frac{\pi }{4} +\frac{2\pi }{3} )]=2\sqrt{3} \cdot (\cos \frac{11\pi }{12} +i\cdot \sin \frac{11\pi }{12} )} \end{array}$

2) \[\begin{array}{l} {z_{1} \cdot z_{2} =\left(4\cdot (\cos \pi +i\cdot \sin \pi )\right)\cdot \left(5\cdot (\cos \frac{\pi }{2} +i\cdot \sin \frac{\pi }{2} )\right)=4\cdot 5\cdot [\cos (\pi +\frac{\pi }{2} )+i\cdot \sin (\pi +\frac{\pi }{2} )]=20\cdot (\cos \frac{3\pi }{2} +i\cdot \sin \frac{3\pi }{2} )} \end{array}\]

Определение 4

Произведением двух заданных комплексных чисел в показательной форме $z_{1} =r_{1} \cdot e^{i\varphi _{1} } $ и $z_{2} =r_{2} \cdot e^{i\varphi _{2} } $ является комплексное число, которое определяется равенством

\[z_{1} \cdot z_{2} =r_{1} \cdot e^{i\varphi _{1} } \cdot r_{2} \cdot e^{i\varphi _{2} } =r_{1} \cdot r_{2} \cdot e^{i(\varphi _{1} +\varphi _{2} )} .\]

Пример 6

Выполнить умножение комплексных чисел:

1) $z_{1} =\sqrt{3} \cdot e^{i\cdot \frac{\pi }{4} } $ и $z_{2} =2\cdot e^{i\cdot \frac{\pi }{3} } $; 2) $z_{1} =\sqrt{5} \cdot e^{i\cdot \frac{2\pi }{3} } $ и $z_{2} =2\cdot e^{i\cdot \frac{\pi }{2} } $.

Решение:

Для умножения комплексных чисел воспользуемся определением и получим:

1) \[z_{1} \cdot z_{2} =\left(\sqrt{3} \cdot e^{i\cdot \frac{\pi }{4} } \right)\cdot \left(2\cdot e^{i\cdot \frac{\pi }{3} } \right)=2\cdot \sqrt{3} \cdot e^{i\cdot (\frac{\pi }{4} +\frac{\pi }{3} )} =2\sqrt{3} \cdot e^{i\cdot \frac{7\pi }{12} } \]

2) \[z_{1} \cdot z_{2} =\left(\sqrt{5} \cdot e^{i\cdot \frac{2\pi }{3} } \right)\cdot \left(2\cdot e^{i\cdot \frac{\pi }{2} } \right)=2\cdot \sqrt{5} \cdot e^{i\cdot (\frac{2\pi }{3} +\frac{\pi }{2} )} =2\sqrt{3} \cdot e^{i\cdot \frac{7\pi }{6} } \]

сложение, вычитание, умножение и деление

Комплексное число — это число, которое может быть представлено в форме a + bi, где a и b — действительные числа, а i — мнимая единица, для которой справедливо равенство i² = −1

Обычно комплексные числа, нам кажутся сложными и непонятными, но на самом деле всё довольно просто и может быть даже визуализировано. Надеемся, что после прочтения этой статьи вы больше никогда не будете думать о комплексных числах как раньше… Поехали!

Содержание:

Построение комплексных чисел

Комплексные числа представляют собой сумму действительной и мнимой части, представленного как a + bi. Используя комплексную плоскость, мы можем построить комплексные числа, аналогично тому, как мы строим координаты на декартовой плоскости.

Вот несколько примеров: 3 + 2i; 1 – 4i; -3 + 3.5i

На графике построены следующие комплексные числа: 3 + 2i ; 1 – 4i ; -3 + 3.5i

Просто нарисуйте точку на пересечении действительной части, найденной на горизонтальной оси, и мнимой части, найденной на вертикальной оси.

Сложение и вычитание комплексных чисел

Сложение и вычитание комплексных чисел — это безусловно, самая простая и понятная операция. Сложение/вычитание действительных частей комплексного числа переводит точку вправо/влево на действительной оси, а сложение/вычитание мнимых частей комплексного числа переводит точку вверх/вниз на мнимой оси.

Арифметически это работает так же, как объединение одинаковых членов в алгебре.

Например, если мы вычтем 1 — 4i из 3 + 2i, мы просто находим разницу действительных 3 — 1 = 2 и мнимых 2i — (-4i ) = 2i + 4i = 6i частей.

Это то же самое, что построить точку 3 + 2i и перенести ее влево на 1 единицу и вверх на 4 единицы. Получившаяся точка — это итоговый результат: 2 + 6i.

Также можно представить точки комплексной плоскости как вектор (Вектор – отрезок соединяющий две точки для которого указано, какая из его граничных точек является началом, а какая концом). В нашем случаем началом будет начало координат (0,0), а концом сама точка. Теперь внесём знак минус под скобки, чтобы у нас было сложение:

(3 + 2i) + (-1 + 4i)

И затем построим два вектора.

Чтобы узнать результат сложения перенесём параллельно начало одного вектора в конец второго. Поскольку сложение является коммутативным, не имеет значения, каким образом мы их складываем. a+b=b+а (свойство коммутативности)

Это может показаться излишним, но вот в чем дело: понимание векторного представления сделает умножение и деление комплексных чисел намного проще.

Умножение комплексных чисел

Умножение комплексных чисел немного сложнее и заставляет задуматься:

А что значит перемножить два комплексных числа?

Самый простой способ понять мнимые числа — это интерпретировать умножение +1, -1 и √-1 (или, как Гаусс говорит прямые, обратные и боковые единицы) как вращение вокруг комплексной плоскости против часовой стрелки.

Умножение на +1

Умножение на +1 можно представить как вращение на 0˚ или 360˚ относительно начала координат, поскольку в любом случае вы вернетесь туда, откуда начали.

Умножение на +1

Умножение на -1

Умножение на -1 можно интерпретировать как вращение на 180˚ против часовой стрелки вокруг начала координат. Например, если я начинаю с 2 и умножаю на -1, Я заканчиваю на -2, что составляет 180˚ против часовой стрелки. И если я умножу -2 на -1, я вернусь к положительному 2.

Умножение на i или √-1

А теперь самое интересное.

Умножая на i или √-1 мы поворачиваем плоскость на 90˚. Вот здесь мнимые числа и вступают в игру.

Обратите внимание, что если я умножу 2 на i, я получу 2i, что является поворотом на 90˚.

Если я умножу 2i на i, я получу 2i², что есть -2, так как i² фактически равно -1.

Итак, 2i ² = 2 (-1) или -2, еще 90° против часовой стрелки.

Точно так же, -2 умноженное на i равно -2i, еще четверть оборота.

И наконец, -2i умноженное на i равно -2i² или -2(-1) что равно 2.

Мы могли бы продолжать умножать на i и вращаться вокруг плоскости, поэтому данный пример даёт нам шаблон, который повторяется каждые 4 цикла.

В общем, мы знаем, что умножение на действительное число масштабирует значение, и мы чуть выше узнали, что умножение на i поворачивает значение на 90° против часовой стрелки, но как насчет этого?

Чтобы лучше понять, давайте распишем.

Хорошо, теперь мы можем выполнить сложение векторов. Первый вектор это (3+2i) (1), как мы рассмотрели выше (3+2i) поворачивается на 360˚, то есть остается на месте.

Теперь мы рассмотрим второй вектор (3 + 2i) (- 4i)

. Здесь происходит то же самое, что и с первым вектором: масштабирование и вращение. Вот как это происходит.

Сначала вектор (3 + 2i) умножаем на 4, и получаем (12 + 8i), этим мы растянули вектор (3 + 2i) в 4 раза.

Нам также нужно умножить на -i. Напомним, умножая на -i мы поворачиваем на 90˚ по часовой стрелке.

Теперь распишем полученное с помощью алгебры.

Последний шар — выполним сложение, перенеся параллельно начало одного вектора в конец другого.

Наш окончательный ответ 11 — 10i.

Теперь у вас может возникнуть вопрос, почему мы не можем просто решить все с помощью алгебры?

И это так, мы можем решить это с помощью алгебры. На самом деле, это самый эффективный способ решения задачи (хотя ему не хватает понимания, которое вы получаете от построения графиков). Поэтому мы предложили вашему вниманию оба пути решения.

Деление комплексных чисел

Давайте разделим (3+2i)/(1–4i)

В этот момент вы можете подумать, что можете просто разделить действительные и мнимые части… но не так быстро.

Как и в алгебре, мы должны разделить оба члена числителя на знаменатель, что оставляет нас с той же проблемой:

Что на самом деле означает деление на комплексное число?

По правде говоря, это сбивает с толку. Разве не было бы хорошо, если бы мы могли избавиться от комплексного числа в знаменателе?

Хорошие новости → Именно это мы и собираемся сделать!

Сопряжённые числа

Ключом к решению этой проблемы является выяснение того, как преобразовать знаменатель в вещественное число.

Самый простой способ сделать это — использовать комплексное сопряжение.

Комплексно-сопряжённое число какому-то числу это тоже самое число только с другим знаком возле мнимой части. И когда мы будем умножать комплексно-сопряжённые числа мы всегда будем получать действительное число.

Например, комплексно сопряжённое число (1–4i) равно (1+4i)

.

Конечно, мы не можем просто умножить знаменатель на (1+4i). Как и с любой дробью, если мы умножаем знаменатель на значение, мы также должны умножить числитель на это значение

Теперь у нас есть произведение двух комплексных чисел в числителе дроби. С ними мы знаем как обращаться из предыдущего урока. А в знаменатели дроби получили 17

, что означает уменьшение вектора в 17 раз.

Вы можете решить это с помощью графика или алгебраически:

Это было не так уж и сложно, не так ли?

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра

Алгебраическая форма записи комплексных чисел

      Пусть x и y — произвольные вещественные числа.

      Множеством комплексных чисел называют множество всевозможных пар (x, y) вещественных чисел, на котором определены операции сложения, вычитания и умножения по правилам, описанным чуть ниже.

      Множество комплексных чисел является расширением множества вещественных чисел, поскольку множество вещественных чисел содержится в нём в виде пар (x, 0).

      Комплексные числа, заданные парами (0, y), называют чисто мнимыми числами.

      Для комплексных чисел существует несколько форм записи: алгебраическая форма записи, тригонометрическая форма записи и экспоненциальная (показательная) форма записи.

      Алгебраическая форма — это такая форма записи комплексных чисел, при которой комплексное число   z, заданное парой вещественных чисел   (x, y), записывается в виде

где использован символ   i , называемый мнимой единицей.

      Число x называют вещественной (реальной) частью комплексного числа   z = x + i y   и обозначают   Re z.

      Число y называют мнимой частью комплексного числа   z = x + i y   и обозначают   Im z.

      Комплексные числа, у которых   Im z = 0 , являются вещественными числами.

      Комплексные числа, у которых     Re z = 0 , являются чисто мнимыми числами.

      Тригонометрическая и экспоненциальная формы записи комплексных чисел будут изложены чуть позже.

Сложение, вычитание и умножение комплексных чисел, записанных в алгебраической форме

      Сложение и вычитание комплексных чисел   z₁ = x₁ + i y₁ и   z₂ = x₂ + i y₂ осуществляется по правилам сложения и вычитания двучленов (многочленов)   x₁ + i y₁   и   x₂ + i y₂ , т.е. в соответствии с формулами

z₁ + z₂ =
= x₁ + i y₁ + x₂ + i y₂ =
= x₁ + x₂ + i (y₁ + y₂) ,

z₁ – z₂ =
= x₁ + i y₁– (x₂ + i y₂) =
= x₁– x₂ + i (y₁– y₂) .

      Умножение комплексных чисел   z₁ = x₁ + i y₁ и   z₂ = x₂ + i y₂ , так же, как и операции сложения и вычитания, осуществляется по правилам умножения двучленов (многочленов), однако при этом учитывается важнейшее равенство, имеющее вид:

      По этой причине

z₁z₂ = (x₁ + i y₁) (x₂ + i y₂) =
= x₁x₂ + i x₁ y₂ +
+ i y₁x₂ + i ²y₁ y₂ =
= x₁x₂ + i x₁y₂ +
+ i y₁x₂ – y₁ y₂ =
= x₁x₂ – y₁ y₂ +
+ i (x₁ y₂ + i x₂ y₁) .

Комплексно сопряженные числа

      Два комплексных числа   z = x + iy   и 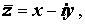у которых вещественные части одинаковые, а мнимые части отличаются знаком, называются комплексно сопряжёнными числами.

      Операция перехода от комплексного числа к комплексно сопряженному с ним числу называется операцией комплексного сопряжения, обозначается горизонтальной чертой над комплексным числом и удовлетворяет следующим свойствам:

Модуль комплексного числа

      Модулем комплексного числа   z = x + i y   называют вещественное число, обозначаемое | z | и определенное по формуле

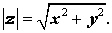
      Для произвольного комплексного числа   z   справедливо равенство:

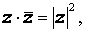
а для произвольных комплексных чисел    z₁   и   z₂   справедливы неравенства:

      Замечание. Если   z   — вещественное число, то его модуль   | z | равен его абсолютной величине.

Деление комплексных чисел, записанных в алгебраической форме

      Деление комплексного числа   z₁ = x₁ + i y₁   на отличное от нуля комплексное число   z₂ = x₂ + i y₂   осуществляется по формуле

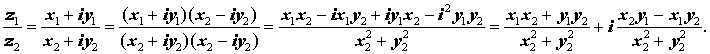
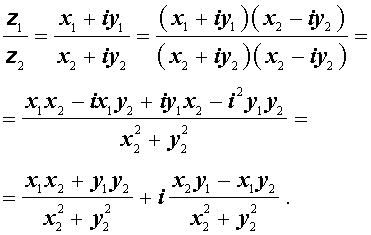
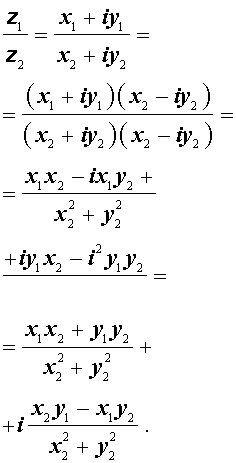
      Используя обозначения модуля комплексного числа и комплексного сопряжения, частное от деления комплексных чисел можно представить в следующем виде:

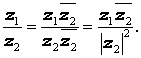
      Деление на нуль запрещено.

Изображение комплексных чисел радиус-векторами координатной плоскости

      Рассмотрим плоскость с заданной на ней прямоугольной декартовой системой координат   Oxy   и напомним, что радиус-вектором на плоскости называют вектор, начало которого совпадает с началом системы координат.

      Назовем рассматриваемую плоскость комплексной плоскостью, и будем представлять комплексное число   z = x + i y   радиус–вектором с координатами   (x , y).

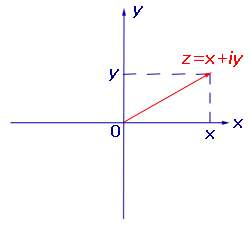
      Назовем ось абсцисс Ox вещественной осью, а ось ординат Oy – мнимой осью.

      При таком представлении комплексных чисел сумме комплексных чисел соответствует сумма радиус-векторов, а произведению комплексного числа на вещественное число соответствует произведение радиус–вектора на это число.

Аргумент комплексного числа

      Рассмотрим радиус–вектор произвольного, но отличного от нуля, комплексного числа   z.

      Аргументом комплексного числа z называют угол φ между положительным направлением вещественной оси и радиус-вектором    z.

      Аргумент комплексного числа  z  считают положительным, если поворот от положительного направления вещественной оси к  радиус-вектору z  происходит против часовой стрелки, и отрицательным  — в случае поворота по часовой стрелке (см. рис.).

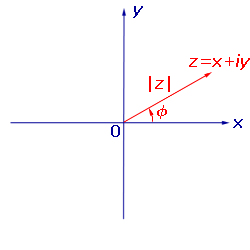
      Считается, что комплексное число нуль аргумента не имеет.

      Поскольку аргумент любого комплексного числа определяется с точностью до слагаемого 2kπ , где  k  — произвольное целое число, то вводится, главное значение аргумента, обозначаемое   arg z   и удовлетворяющее неравенствам:

      Тогда оказывается справедливым равенство:

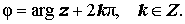
      Если для комплексного числа   z = x + i y   нам известны его модуль   r = | z | и его аргумент φ, то мы можем найти вещественную и мнимую части по формулам

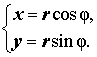(3)

      Если же комплексное число   z = x + i y   задано в алгебраической форме, т.е. нам известны числа   x   и   y,   то модуль этого числа, конечно же, определяется по формуле

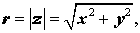(4)

а аргумент определяется в соответствии со следующей Таблицей 1.

      Для того, чтобы не загромождать запись, условимся, не оговаривая этого особо, символом  k  обозначать в Таблице 1 произвольное целое число.

      Таблица 1. – Формулы для определения аргумента числа   z = x + i y

Расположение числа   z : Положительная вещественная полуось Знаки x и y : x > 0 ,   y = 0 Главное значение аргумента: 0 Аргумент: φ = 2kπ Примеры: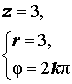

Расположение числа   z : Первый квадрант Знаки x и y : x > 0 ,   y > 0 Главное значение аргумента: Аргумент: Примеры: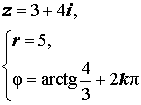

Расположение числа   z : Положительная мнимая полуось Знаки x и y : x = 0 ,   y > 0 Главное значение аргумента: Аргумент: Примеры: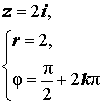

Расположение числа   z : Второй квадрант Знаки x и y : x < 0 ,   y > 0 Главное значение аргумента: Аргумент: Примеры: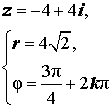

Расположение числа   z : Отрицательная вещественная полуось Знаки x и y : x < 0 ,   y = 0 Главное значение аргумента: π Аргумент: φ = π + 2kπ Примеры: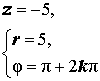

Расположение числа   z : Третий квадрант Знаки x и y : x < 0 ,   y < 0 Главное значение аргумента: Аргумент: Примеры: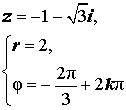

Расположение числа   z : Отрицательная мнимая полуось Знаки x и y : x = 0 ,   y < 0 Главное значение аргумента: Аргумент: Примеры: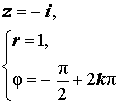

Расположение числа   z : Четвёртый квадрант Знаки x и y : x < 0 ,   y < 0 Главное значение аргумента: Аргумент: Примеры: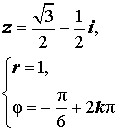

Тригонометрическая форма записи комплексного числа

      Из формулы (3) вытекает, что любое отличное от нуля комплексное число   z = x + i y   может быть записано в виде

z = r (cos φ + i sin φ) ,

(5)

где   r  и φ — модуль и аргумент этого числа, соответственно, причем модуль удовлетворяет неравенству   r > 0 .

      Запись комплексного числа в форме (5) называют тригонометрической формой записи комплексного числа.

Формула Эйлера. Экспоненциальная форма записи комплексного числа

      В курсе «Теория функций комплексного переменного», который студенты изучают в высших учебных заведениях, доказывается важная формула, называемая формулой Эйлера:

cos φ + i sin φ = e iφ .

(6)

      Из формулы Эйлера (6) и тригонометрической формы записи комплексного числа (5) вытекает, что любое отличное от нуля комплексное число   z = x + i y   может быть записано в виде

где   r   и   φ   — модуль и аргумент этого числа, соответственно, причем модуль удовлетворяет неравенству   r > 0 .

      Запись комплексного числа в форме (7) называют экспоненциальной (показательной) формой записи комплексного числа.

      Из формулы (7) вытекают, в частности, следующие равенства:

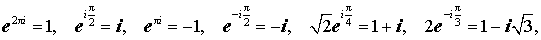
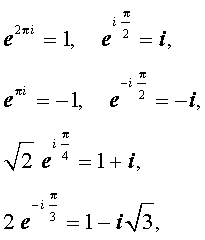
а из формул (4) и (6) следует, что модуль комплексного числа

cos φ + i sin φ,

или, что то же самое, числа   e ^iφ,   при любом значении   φ   равен 1.

Умножение, деление и возведение в натуральную степень комплексных чисел, записанных в экспоненциальной форме

      Экспоненциальная запись комплексного числа очень удобна для выполнения операций умножения, деления и возведения в натуральную степень комплексных чисел.

      Действительно, умножение и деление двух произвольных комплексных чисел 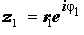 и 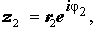 записанных в экспоненциальной форме, осуществляется по формулам

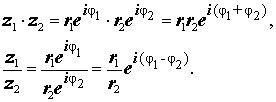
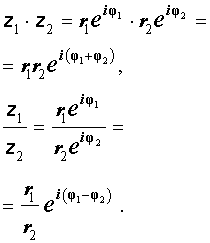
      Таким образом, при перемножении комплексных чисел их модули перемножаются, а аргументы складываются.

      При делении двух комплексных чисел модуль их частного равен частному их модулей, а аргумент частного равен разности аргументов делимого и делителя.

      Возведение комплексного числа   z = r e ^iφ в натуральную степень осуществляется по формуле

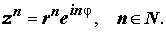
      Другими словами, при возведении комплексного числа в степень, являющуюся натуральным числом, модуль числа возводится в эту степень, а аргумент умножается на показатель степени.

Извлечение корня натуральной степени из комплексного числа

      Пусть 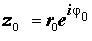— произвольное комплексное число, отличное от нуля.

      Корнем   n — ой степени из числа  z₀ , где 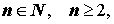 называют такое комплексное число   z = r e ^iφ , которое является решением уравнения

      Для того, чтобы решить уравнение (8), перепишем его в виде

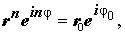
и заметим, что два комплексных числа, записанных в экспоненциальной форме, равны тогда и только тогда, когда их модули равны, а разность аргументов равна   2kπ ,   где   k   — произвольное целое число. По этой причине справедливы равенства

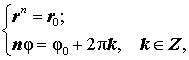
следствием которых являются равенства

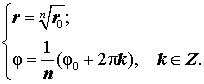(9)

      Из формул (9) вытекает, что уравнение (8) имеет   n   различных корней

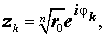(10)

где

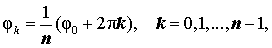
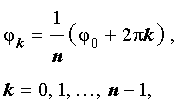
причем на комплексной плоскости концы радиус-векторов   z_k   при   k = 0 , … , n – 1   располагаются в вершинах правильного   n — угольника, вписанного в окружность радиуса 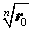 с центром в начале координат.

      Замечание. В случае   n = 2   уравнение (8) имеет два различных корня   z₁   и   z₂ , отличающихся знаком:

z₂ = – z₁ .

      Пример 1. Найти все корни уравнения

z³ = – 8i .

      Решение. Поскольку

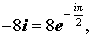
то по формуле (10) получаем:

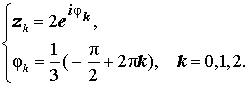
      Следовательно,

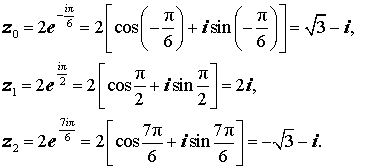
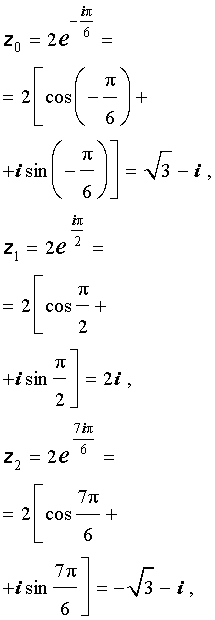
      Пример 2. Решить уравнение

z² + 2z + 2 = 0 .

      Решение. Поскольку дискриминант этого квадратного уравнения отрицателен, то вещественных корней оно не имеет. Для того, чтобы найти комплексные корни, выделим, как и в вещественном случае, полный квадрат:

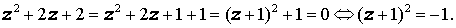
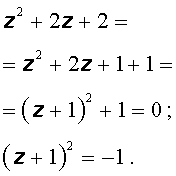
      Так как

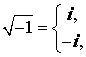
то решения уравнения имеют вид

z₁ = – 1 + i ,       z₂ = – 1 – i .

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Комплексные числа. Сложение, вычитание, умножение, деление комплексных чисел. Тригонометрическая форма представления, формула Муавра и корень n-ной степени из комплексного числа

Комплексные числа. Сложение, вычитание, умножение, деление комплексных чисел. Формулы. Тригонометрическая форма представления, формула Муавра и корень n-ной степени из комплексного числа.

Комплексные числа — это минимальное расширение множества привычных нам действительных чисел. Их принципиальное отличие в том, что появляется элемент, который в квадрате дает -1, т.е. i, или мнимая единица.

i ²= — 1

Любое комплексное число состоит из двух частей: вещественной и мнимой:

Таким образом видно, что множество действительных чисел совпадает с множеством комплексных чисел с нулевой мнимой частью.

Самая популярная модель множества комплексных чисел — это обычная плоскость. Первая координата каждой точки будет её вещественной частью, а вторая -мнимой. Тогда в роли самих комплексных чисел бдут выступать вектора с началом в точке (0,0).

Операции над комплексными числами.

На самом деле, если брать в расчет модель множества комплексных чисел, интуитивно понятно, что сложение (вычитание) и умножение двух комплексных числе производятся так же как соответственные операции над векторами. Причем имеется в виду векторное произведение векторов, потому что результатом этой операции является опять же вектор.

1.1 Сложение.

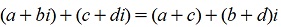
(Как видно, данная операции в точности соответствует покоординатному сложению векторов)

1.2 Вычитание, аналогично, производится по следующему правилу:

.

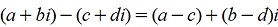2. Умножение.

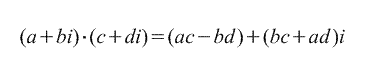
(см. векторное произведение векторов)

3. Деление.

Определяется просто как обратная операция к умножению.

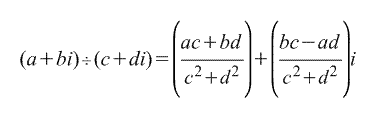
Тригонометрическая форма.

Модулем комплексного числа z называется следующая величина:

,

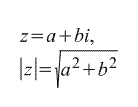очевидно, что это, опять же, просто модуль (длина) вектора {a,b}.

Чаще всего модуль комплексного числа обозначается как ρ.

Если представлять каждое комплексное число a+bi как вектор началом в точке (0,0) и концом в точке (a,b), то можно ввести еще одно понятие — угол, который этот вектор образует с положительным направлением оси х, то есть «правый» угол, который получается с осью х. (см. рисунок справа). Величина этого ула в радианах называется аргументом комплексного числа и обозначается : arg z.

Оказывается, что

z = ρ(cosφ+isinφ) .

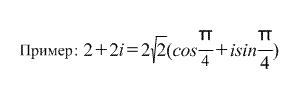
Непосредственно из тригонометрической формы записи комплексного числа вытекают следующие формулы:

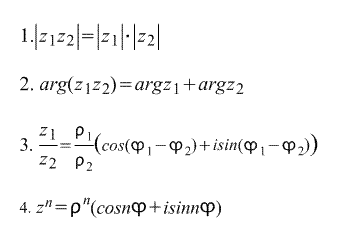
Последнюю формулу называют Формулой Муавра. Непосредственно из нее выводится формула корня n-ной степени из комплексного числа:

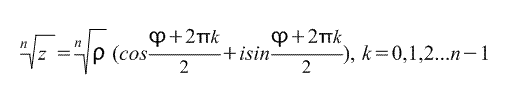
таким образом, существует n корней n-ной степени из комплексного числа z.

Операции над комплексными числами, с примерами

Рассмотрим операции над комплексными числами записанными в алгебраической, тригонометрической и показательной формах.

Сравнение

Два комплексных числа и называются равными, если , т.е. равны их действительные и мнимые части.

Два комплексных числа в тригонометрической форме и называются равными, если . То есть, если равны их модули, а аргументы отличаются на число, кратное .

Аналогично для чисел в показательной форме : два комплексных числа равны, если .

Сложение

Сложение комплексных чисел осуществляется в алгебраической форме и определяется следующим образом: суммой чисел и является число

   

Т.е. выполняется непосредственное суммирование действительных и мнимых частей.

Подробнее про сложение комплексных числе читайте в отдельной статье: Сложение комплексных чисел.

Вычитание

Вычитание комплексных чисел также осуществляется в алгебраической форме. Разность двух чисел и является число

   

Таким образом, чтобы вычесть из одного числа другое, выполняется непосредственное вычитание действительных и мнимых частей.

Умножение

Умножение комплексных чисел в алгебраической форме и выполняется непосредственным произведением чисел в алгебраической форме, учитывая свойство мнимой единицы :

   

   

Для произведения комплексных чисел в тригонометрической форме верно равенство:

   

Для произведения комплексных чисел в показательной форме выполняется следующее равенство:

   

Подробнее про умножение комплексных чисел читайте в отдельной статье: Умножение комплексных чисел.

Деление

Частное комплексных чисел в алгебраической форме и находится путем домножения числителя и знаменателя на сопряженное к знаменателю число:

   

Частное комплексных чисел в тригонометрической форме выполняется по формуле:

   

Частное комплексных чисел в показательной форме выполняется по формуле:

   

Подробнее про деление комплексных чисел читайте в отдельной статье: Деление комплексных чисел.

Возведение в степень

Для возведения в степень комплексных чисел в тригонометрической форме верна формула Муавра:

   

В показательной форме комплексные числа возводятся в степень по следующей формуле:

   

Подробнее про возведение в степень читайте в отдельной статье: Возведение в степень комплексного числа.

Извлечение корня из комплексного числа

Для извлечения корня из комплексного числа применяют аналогичным образом формулу Муавра (если число не равно нулю):

   

   

Подробнее про извлечение корня читайте в отдельной статье: Извлечение корня из комплексного числа.