Задачи со степенями 7 класс – Задачи со степенями — нормальные задачи с решениями

Примеры задач со степенями — СПИШИ У АНТОШКИ

1. Найдите такое натуральное число n такое, что 3ⁿ=729

Решение:

Возьмем число 3 и будем домножать его на 3 до тех пор, пока не получим 729: 3⋅3=9, 9⋅3=27 27⋅3=81, 81⋅3=243, 249⋅3 = 729  значит 729=3⋅3⋅3⋅3⋅3⋅3=3⁶⇒n=6.

Можно посмотреть таблицу основных степеней

2.Вычислите 2²²⁺²⋅2.

Решение:

2²²⁺²⋅2=2²²⁺²⁺¹=2⁴⁺²⁺¹=2⁷=2⋅2⋅2⋅2⋅2⋅2⋅2=128.

3. Вычислите 

2 ⁴⁰

4 ²⁰  

2 ⁴⁰ =  2 ⁴⁰ =   2 ⁴⁰

4 ²⁰     2 ^2*20  2 ⁴⁰

4. Как известно, в компьютерах объем памяти измеряется в байтах, килобайтах, мегабайтах и гигабайтах. Причем, чтобы получить один мегабайт памяти необходимо взять один килобайт памяти и увеличить количество памяти вдвое и со вновь получившейся памятью необходимо вновь произвести такую же процедуру — увеличение памяти вдвое, и, проведя таких процедур ровно 10, мы получим количество памяти, равное одному мегабайту. Так сколько же килобайтов в одном мегабайте?

Решение задачи

Для нахождения искомого числа достаточно умножить исходное количество килобайт на 2 столько раз, сколько раз мы применяем процедуру. Исходное количество килобайт по условию это 1, а количество применений процедур — 10, значит искомое число есть 2⋅2⋅2…⋅2 = 2¹⁰ = 1024.

5.  Решите уравнение: (5-x)² — x(2,5+x) = 0

(5-x)² — x(2,5+x) = 0

25 — 10х +  x² — 2,5x — x² = 0

 — 10x²  — 2,5х + 25 = 0

-12,5х = 25

х = 2

6. Решите уравнение: (х-4)² + (х+9)²  = 2х²

(х-4)² + (х+9)² = 2х²

Расскроем скобки

(х-4)(х-4) + (х+9)(х+9)  = 2х²

х² — 8х + 16 + х² + 18х + 81  = 2х²

2х² — 2х²   + 97 + 10х = 0

10х =  -97

х = -9,7

7. Упростите выражение:

(а²*а²)² :  а⁷

(а²*а²)² : а⁷ = а⁴*а⁴ : а⁷= а

 

spishy-u-antoshki.ru

7 класс. Алгебра

Рубрика «7 класс. Алгебра»

I. Чтобы умножить одночлен на многочлен, надо умножить на этот одночлен каждый член многочлена и полученные произведения сложить.

Пример 1.  Умножить одночлен на многочлен: 

2a·(4a²-0,5ab+5a³).

Решение. Одночлен 2а будем умножать на каждый одночлен многочлена:

2a·(4a²-0,5ab+5a³)=2a∙4a²+2a∙(-0,5ab)+2a∙5a³=8a³-a²b+10a⁴. Запишем полученный многочлен в стандартном виде:

10a⁴+8a³-a²b.

Пример 2. Умножить многочлен на одночлен: (3xyz⁵-4,5x²y+6xy³+2,5y²z)∙(-0,4x³).

Решение. Каждое слагаемое, стоящее в скобках, умножаем на одночлен (-0,4x³).

(3xyz⁵-4,5x²y+6xy³+2,5y²z)∙(-0,4x³)=

=3xyz⁵∙(-0,4x³) -4,5x²y∙(-0,4x³

)+6xy³∙(-0,4x³)+2,5y²z∙(-0,4x³)=

=-1,2x⁴yz⁵+1,8x⁵y-2,4x⁴y³-x³y²z.

II. Представление многочлена в виде произведения двух или нескольких многочленов называется разложением многочлена на множители.

 III. Вынесение общего множителя за скобки – простейший способ разложения многочлена на множители.

Пример 3. Разложить на множители многочлен:  5a³+25ab-30a².

Решение. Вынесем общий множитель всех членов многочлена за скобки. Это одночлен 5а, потому что на 5а делится каждый из членов данного многочлена. Итак, 5а мы запишем перед скобками, а в скобках запишем частные от деления каждого одночлена на 5а.

5a³+25ab-30a²=5a·(a²+5b-6a). Проверяем себя: если мы умножим 5а на многочлен в скобках a²+5b-6a, то получим данный многочлен 5a³+25ab-30a².

Пример 4.Вынесите общий множитель за скобки: (x+2y)²-4·(x+2y).

Решение. (x+2y)²-4·(x+2y)=(x+2y)(x+2y-4).

Общим множителем здесь являлся двучлен (х+2у). Мы вынесли его за скобки, а в скобках записали частные от деления данных членов (x+2y)² и -4·(x+2y) на их общий делитель

(х+2у). В результате мы представили данный многочлен в виде произведения двух многочленов (x+2y) и (x+2y-4), другими словами, мы разложили многочлен (x+2y)²-4·(x+2y) на множители. Ответ:  

(x+2y)(x+2y-4).

IV. Чтобы умножить многочлен на многочлен, нужно каждый член одного многочлена умножить на каждый член другого многочлена и записать полученные произведения в виде суммы одночленов. При необходимости привести подобные слагаемые.

Пример 5. Выполнить умножение многочленов: (4x²-6xy+9y²)(2x+3y).

Решение. По правилу мы должны каждый член первого многочлена (4x²-6xy+9y²) умножить на каждый член второго многочлена (2x+3y). Чтобы не запутаться, делайте всегда так: сначала умножьте каждый член первого многочлена на 2х, потом опять каждый член первого многочлена умножайте на 3у.

(4x²-6xy+9y²)(2x+3y)=4x²∙2x-6xy∙2x+9y²∙2x+4x²∙3y-6xy∙3y+9y²∙3y

=

=8x³-12x²y+18xy²+12x²y-18xy²+27y³=8x³+27y³.

Подобные слагаемые -12x²y и 12x²y, а также 18xy² и -18xy² оказались противоположными, их суммы равны нулю.

Ответ: 8x³+27y³.

 

I.  Сумма одночленов называется многочленом. Одночлены, из которых составлен многочлен, называются членами многочлена.

Например, многочлен 2a+3a²b-6b⁴+3,5a³b состоит из суммы четырех одночленов.

II.  Двучлен – это многочлен, состоящий из двух членов (одночленов).

Примеры двучленов: 2a-3b; 6x²+5; 2x-1.

III. Трехчлен – это многочлен, состоящий из трех членов (одночленов).

Например,  2а+3с-х или x²+4x-5 — трехчлены, так как состоят из трех одночленов.

IV. Степенью многочлена называют наибольшую из степеней входящих в него одночленов.

Например, многочлен 2a²-3b+abc-d² имеет третью степень, так как наибольшей степенью входящих в него одночленов является третья степень одночлена abc (складываем показатели: 1+1+1=3).

Многочлен 4x⁴yz+2x²y³-xz⁴+3x²y² имеет шестую степень, так как наибольшей (шестой) степенью является степень его члена 4x⁴yz (складываем показатели: 4+1+1=6).

V. Многочлен стандартного вида не содержит подобных членов и записан в порядке убывания степеней его членов.

Например, приведенный выше многочлен 4x⁴yz+2x²y³-xz⁴+3x²y² является многочленом стандартного вида, так как записан в порядке убывания степеней его членов.

Пример 1. Упростить многочлен, записав каждый его член в стандартном виде: 4aabb∙(-0,5c²)+5a²bb³-6abcab²c.

Решение.

4aabb∙(-0,5c²)+5a²bb³-6abcab²c=-2a²b²c²+5a²b⁴-6a²b³c², а теперь запишем этот многочлен в стандартном виде (в порядке убывания степеней его членов):

-6a²b³c²-2a²b²c²+5a²b⁴.

Пример 2. Вычислить значение многочлена 5y

2-3xy+x²при x=-1, y=2.

Решение.

5y²-3xy+x²=5∙2²-3∙(-1)∙2+(-1)²=5∙4+6+1=27.

Пример 3. Упростить многочлен 2aba-a³bb+7bbbb и найти его числовое значение при a=3, b=2.

Решение.

Упрощаем многочлен: 2aba-a³bb+7bbbb=2a²b-a³b²+7b⁴.

Подставляем значения a и b.

2a²b-a³b²+7b⁴=2∙3²∙2-3³∙2²+7∙2⁴=2∙9∙2-27∙4+7∙16=36-108+112=40.

Пример 4. Привести подобные члены многочлена:

Пример 5. Привести к стандартному виду многочлен:

Напоминание: подобными считают одночлены, имеющие одинаковую буквенную часть.

 I. Выражения, которые составлены из чисел, переменных и их степеней, при помощи действия умножения называются одночленами.

Примеры одночленов: 

а) a; б) ab; в) 12; г) -3c; д) 2a²∙(-3,5b)³; е) -123,45xy⁵z; ж) 8ac∙2,5a²∙(-3c³).

II. Такой вид одночлена, когда на первом месте стоит числовой множитель (коэффициент), а за ним переменные с их степенями, называют стандартным видом одночлена.

Так, одночлены, приведенные выше, под буквами а), б), в), г)  и е) записаны в стандартном виде, а одночлены под буквами д) и ж) требуется привести к стандартному виду, т. е. к такому виду, когда на первом месте стоит числовой множитель, а за ним записывают буквенные множители с их показателями, причем, буквенные множители стоят в алфавитном порядке. Приведем одночлены д) и ж) к стандартному виду.

д) 2a²∙(-3,5b)³=2a²∙(-3,5)³∙b³=-2a²∙3,5∙3,5∙3,5∙b³=-85,75a²b³;

ж) 8ac∙2,5a²∙(-3c³)=-8∙2,5∙3a³c³=-60a³c³.

III. Сумму показателей степеней всех переменных, входящих в состав одночлена, называют степенью одночлена.

Примеры. Какую степень имеют одночлены а) — ж)?

а) a.  Первую;

б) ab. Вторую: а в первой степени и b в первой степени-сумма показателей 1+1=2;

в) 12. Нулевую, так как буквенных множителей нет;

г) -3c. Первую;

д) -85,75a²b³. Пятую. Мы привели этот одночлен к стандартному виду, имеем а во второй степени и b в третьей. Складываем показатели: 2+3=5;

е)  -123,45xy⁵z. Седьмую. Сложили показатели степеней буквенных множителей: 1+5+1=7;

ж) -60a³c³. Шестую, так как сумма показателей буквенных множителей 3+3=6.

IV.  Одночлены, имеющие одинаковую буквенную часть, называются подобными одночленами.

Пример. Указать подобные одночлены среди данных одночленов 1) -7).

1) 3aabbc; 2) -4,1a³bc; 3) 56a²b²c; 4) 98,7a²bac; 5) 10aaa²x; 6) -2,3a⁴x; 7) 34x²y.

Приведем одночлены 1), 4) и 5) к стандартному виду. Тогда строчка данных одночленов будет выглядеть так:

1) 3a²b²c; 2) -4,1a³bc; 3) 56a²b²c; 4) 98,7a³bc; 5) 10a⁴x;  6) -2,3a⁴x; 7) 34x²y.

Подобными будут те, которые имеют одинаковую буквенную часть, т.е. 1) и 3); 2) и 4); 5) и 6).

1) 3a²b²c и 3) 56a²b²c;

2) -4,1a³bc и 4) 98,7a³bc;

5) 10a⁴x и  6) -2,3a⁴x.

 

Очень большие и очень малые числа принято записывать в стандартном виде: a∙10ⁿ, где 1≤а<10 и n  (натуральное или целое) – есть порядок числа, записанного в стандартном виде.

Например, 345,7=3,457∙10²; 123456=1,23456∙10⁵; 0,000345=3,45∙10^-4.

Примеры. 

Записать в стандартном виде число: 1) 40503; 2) 0,0023; 3) 876,1; 4) 0,0000067.

Решение.

1) 40503=4,0503·10⁴;

2) 0,0023=2,3∙10^-3;

3) 876,1=8,761∙10²;

4) 0,0000067=6,7∙10^-6.

Еще примеры на стандартный вид числа.

5) Число молекул газа в 1 см³ при 0°С и давлении 760 мм.рс.ст равно

27 000 000 000 000 000 000. Записать это число в стандартном виде.

Решение.

27 000 000 000 000 000 000=2,7∙10¹⁹.

6) 1 парсек (единица длины в астрономии) равен 30 800 000 000 000 км. Записать это число в стандартном виде.

Решение.

1 парсек=30 800 000 000 000=3,08∙10¹³ км.

В тему:

Киловатт-час — это внесистемная единица энергии или работы, применяется в электротехнике, обозначается кВт·ч.

1 кВт·ч=3,6∙10⁶ Дж (Джоулей).

 

 I. Определение.  (- n)-й степенью (n – натуральное) числа а, не равного нулю, считается число, обратное n-й степени числа а:

Примеры. Вычислить:

Решение.

II. Следующая формула позволяет заменить обыкновенную дробь с отрицательным показателем на обратную ей дробь с положительным показателем:

Примеры. Вычислить:

Решение.

 Свойства степени с натуральным показателем справедливы и для  степеней с любым показателем.

Свойства степени с натуральным показателем с примерами смотрите в предыдущем уроке здесь.

Примеры на все свойства степени.

Упростить:

Решение.

       При решении 7) примера  I способом мы использовали свойства умножения и деления степеней с одинаковыми основаниями:  a^m∙aⁿ=a^m+n  и a^m:aⁿ=a^m-n. При решении II способом мы использовали понятие степени с отрицательным показателем:  и свойство произведения степеней с одинаковыми основаниями:  a^m∙aⁿ=a^m+n .

 

Пример 8 ) решаем так же, как решали пример 7) вторым способом.

 

 

 

В примере 9) представим 7³как 7²∙7, а степень 4⁵как 4³∙4², а затем сократим дробь на (7²∙4³).

 

В 10) примере применим формулу степени произведения: (ab)ⁿ=aⁿ∙bⁿ, а затем сократим дробь на (2⁶∙3⁵).

                 

I. Произведение n сомножителей, каждый из которых равен а называется n-й степенью числа а и обозначается аⁿ.

Примеры. Записать произведение в виде степени.

1) mmmm;          2) aaabb;         3) 5·5·5·5·ccc;        4) ppkk+pppk-ppkkk.

Решение.

1) mmmm=m⁴, так как, по определению степени, произведение четырех сомножителей, каждый из которых равен m, будет четвертой степенью числа m.

  2) aaabb=a³b²;    3) 5·5·5·5·ccc=5⁴c³;     4) ppkk+pppk-ppkkk=p²k²+p³k-p²k³.

II. Действие, посредством которого находится произведение нескольких равных сомножителей, называется возведением в степень. Число, которое возводится в степень, называется основанием степени. Число, которое показывает, в какую степень возводится основание, называется показателем степени. Так, аⁿ – степень, а – основание степени, n – показатель степени. Например:

 2³ — это степень. Число 2 — основание степени, показатель степени равен 3. Значение степени 2³равно 8, так как 2³=2·2·2=8.

Примеры. Написать следующие выражения без показателя степени.

5) 4³;       6) a³b²c³;       7) a³-b³;       8 ) 2a⁴+3b².

Решение.

5) 4³=4·4·4;       6) a³b²c³=aaabbccc;       7) a³-b³=aaa-bbb;       8) 2a⁴+3b²=2aaaa+3bb.

 III. а⁰=1  Любое число (кроме нуля) в нулевой степени равно единице. Например, 25⁰=1. 
 IV. а¹=а  Любое число в первой степени равно самому себе. 

 V. a^m∙aⁿ=a^m+n   При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают.

Примеры. Упростить:

9) a·a³·a⁷;             10) b⁰+b²·b³;             11) c²·c⁰·c·c⁴.

Решение.

9) a·a³·a⁷=a¹⁺³⁺⁷=a¹¹;           10) b⁰+b²·b³=1+b²⁺³=1+b⁵;             

11) c²·c⁰·c·c⁴=1·c²·c·c⁴=c²⁺¹⁺⁴=c⁷.

VI.  a^m:aⁿ=a^m— n  При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.

Примеры. Упростить:

12) a⁸:a³;       13) m¹¹:m⁴;         14) 5⁶:5⁴.

12) a⁸:a³=a^8-3=a⁵;       13) m¹¹:m⁴=m^11-4=m⁷;         14) 5⁶:5⁴=5²=5·5=25.

VII. (a^m)ⁿ=a^mn   При возведении степени в степень основание оставляют прежним, а показатели перемножают.

Примеры. Упростить:

15) (a³)⁴;         16) (c⁵)².

15) (a³)⁴=a^3·4=a¹²;         16) (c⁵)²=c^5·2=c¹⁰.

Обратите внимание, что, так как от перестановки множителей произведение не меняется, то:

15) (a³)⁴=(a⁴)³;         16) (c⁵)²=(c²)⁵.

 VIII. (a∙b)ⁿ=aⁿ∙bⁿ   При возведении произведения в степень возводят в эту степень каждый из множителей.

Примеры. Упростить:

17) (2a²)⁵;      18) 0,2⁶·5⁶;        19) 0,25²·40².

Решение.

17) (2a²)⁵=2⁵·a^2·5=32a¹⁰;      18) 0,2⁶·5⁶=(0,2·5)⁶=1⁶=1;

19) 0,25²·40²=(0,25·40)²=10²=100.

       IX. При возведении в степень дроби возводят в эту степень и числитель и знаменатель дроби.

Примеры. Упростить:

Решение.

 

Функцию вида y=x³ называют кубической функцией. Графиком кубической функции является кубическая парабола, проходящая через начало координат. Ветви кубической параболы y=x³ находятся в I и III четвертях.

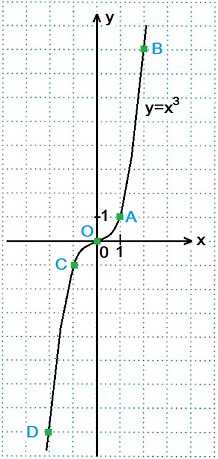Построение графика кубической функции y=x³

Составим таблицу значений функции y=x³ для х=0, х=±1, х=±2.

   x     |    y=x³

   0    |    0³=0            Точка О(0; 0)

   1    |    1³=1            Точка А(1; 1)

  -1    | (-1)³=-1          Точка С(-1; -1)

    2   |   2³=8             Точка В(2; 8 )

  -2   | (-2)³=-8           Точка D(-2; -8)

Функцию вида y=x² называют квадратной функцией. Графиком квадратной функции является парабола с вершиной в начале координат. Ветви параболы y=x² направлены вверх.

Построение графика функции y=x². Составим таблицу значений функции для х=0, х=±1, х=±2, х=±3.

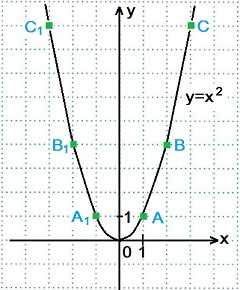х    |   y=x² 

0    |  0²=0  

1    |  1²=1              Точка А(1; 1)

-1   | (-1)²=1           Точка А₁(-1; 1)

2    |   2²=4             Точка В(2; 4)

-2   | (-2)²=4           Точка В₁(-2; 4)

3    |  3²=9              Точка С(3; 9)

-3   | (-3)²=9           Точка С₁(-3; 9)

data-ad-client=»ca-pub-8602906481123293″
data-ad-slot=»2890988705″>

1)    Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

       (a+b)² = a²+2ab+b² 

  a) (x + 2y)² = x² + 2 ·x·2y + (2y)² = x² + 4xy + 4y²

б) (2k + 3n)² = (2k)² + 2·2k·3n + (3n)² = 4k² + 12kn + 9n²

2)    Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.

        (a-b)² = a²-2ab+b²

 а)   (2a – c)² = (2a)²-2·2a·c + c² = 4a² – 4ac + c²

б)   (3a – 5b)² = (3a)²-2·3a·5b + (5b)² = 9a² – 30ab + 25b²

3)    Разность квадратов двух выражений равна произведению разности самих выражений на их сумму.

         a²–b² = (a–b)(a+b)

a)      9x² – 16y² = (3x)² – (4y)² = (3x – 4y)(3x + 4y)

б)  (6k – 5n)( 6k + 5n) = (6k)² – (5n)² = 36k² – 25n²

4)  Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.

        (a+b)³ = a³+3a²b+3ab²+b³

a)  (m + 2n)³ = m³ + 3·m²·2n + 3·m·(2n)² + (2n)³ = m³ + 6m²n + 12mn² + 8n³

б)  (3x + 2y)³ = (3x)³ + 3·(3x)²·2y + 3·3x·(2y)² + (2y)³ = 27x³ + 54x²y + 36xy² + 8y³

5)  Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.

(a-b)³ = a³-3a²b+3ab²-b³

а)  (2x – y)³ = (2x)³-3·(2x)²·y + 3·2x·y² – y³ = 8x³ – 12x²y + 6xy² – y³

б)  (x – 3n)³ = x³-3·x²·3n + 3·x·(3n)² – (3n)³ = x³ – 9x²n + 27xn² – 27n³

6)  Сумма кубов двух выражений равна произведению суммы самих выражений на неполный квадрат их разности.

a³+b³ = (a+b)(a²–ab+b²)

a)      125 + 8x³ = 5³ + (2x)³ = (5 + 2x)(5² — 5·2x + (2x)²) = (5 + 2x)(25 – 10x + 4x²)

б)  (1 + 3m)(1 – 3m + 9m²) = 1³ + (3m)³ = 1 + 27m³

7)  Разность кубов двух выражений равна произведению разности самих выражений на неполный квадрат их суммы.

 a³-b³ = (a-b)(a²+ab+b²)

а) 64с³ – 8 = (4с)³ – 2³ = (4с – 2)((4с)² + 4с·2 + 2²) = (4с – 2)(16с² + 8с + 4)

б) (3a – 5b)(9a² + 15ab + 25b²) = (3a)³ – (5b)³ = 27a³ – 125b³

Дорогие друзья! Карта сайта поможет вам выбрать нужную тему.

Страница 1 из 11

www.mathematics-repetition.com

Свойства степени с натуральным показателем. Алгебра, 7 класс: уроки, тесты, задания.

1.	Умножение степеней Сложность: лёгкое	1
2.	Степень в степени Сложность: лёгкое	1
3.	Возведение степени в степень (буквы) Сложность: лёгкое	2
4.	Степень в степени (основание) Сложность: лёгкое	2
5.	Степень в степени (показатель степени) Сложность: лёгкое	2
6.	Произведение трёх степеней Сложность: лёгкое	2
7.	Произведение степеней (основание — бином) Сложность: лёгкое	1
8.	Частное трёх степеней Сложность: лёгкое	2
9.	Произведение степеней с одинаковыми основаниями (буквы) Сложность: лёгкое	3
10.	Произведение двух степеней (числа) Сложность: лёгкое	2
11.	Частное двух степеней (отрицательное основание) Сложность: лёгкое	2
12.	Возведение степени в степень (числа) Сложность: лёгкое	2
13.	Частное двух степеней (дробь) Сложность: лёгкое	3
14.	Частное двух степеней (отрицательные смешанные числа) Сложность: лёгкое	1
15.	Произведение степеней с одним основанием (числа) Сложность: среднее	3
16.	Произведение отрицательных и противоположных степеней Сложность: среднее	5
17.	Уравнение (частное степеней, целые числа) Сложность: среднее	3
18.	Дробь (буквы) Сложность: среднее	2
19.	Произведение степени и степени в степени Сложность: среднее	2
20.	Деление и умножение степеней Сложность: среднее	3
21.	Произведение двух дробей Сложность: среднее	2
22.	Произведение степеней в степени Сложность: среднее	3
23.	Частное степени в степени и степени Сложность: среднее	2
24.	Умножение и деление степеней Сложность: среднее	1
25.	Вычисление выражения со степенями Сложность: среднее	1

www.yaklass.ru

Алгебра, 7 класс: уроки, тесты, задания

Информация о разделе

Математический язык. Математическая модель

1. Числовые и алгебраические выражения

2. Что такое математический язык

3. Что такое математическая модель

4. Линейное уравнение с одной переменной

5. Координатная прямая

Линейная функция

1. Координатная плоскость

2. Линейное уравнение с двумя переменными и его график

3. Линейная функция y = kx + m и её график

4. Линейная функция y = kx

5. Взаимное расположение графиков линейных функций

Системы двух линейных уравнений с двумя переменными

1. Основные понятия

2. Метод подстановки

3. Метод алгебраического сложения

4. Системы двух линейных уравнений с двумя неизвестными как математические модели реальных ситуаций

Степень с натуральным показателем и её свойства

1. Что такое степень с натуральным показателем

2. Таблица основных степеней

3. Свойства степени с натуральным показателем

4. Умножение и деление степеней с одинаковым показателем

5. Степень с нулевым показателем

Одночлены. Арифметические операции над одночленами

1. Понятие одночлена. Стандартный вид одночлена

2. Сложение и вычитание одночленов

3. Умножение одночленов. Возведение одночлена в натуральную степень

4. Деление одночлена на одночлен

Многочлены. Арифметические операции над многочленами

1. Основные понятия

2. Сложение и вычитание многочленов

3. Умножение многочлена на одночлен

4. Умножение многочлена на многочлен

5. Формулы сокращённого умножения

6. Деление многочлена на одночлен

Разложение многочлена на множители

1. Что такое разложение на множители

2. Вынесение общего множителя за скобки

3. Способ группировки

4. Разложение многочлена на множители с помощью формул сокращённого умножения

5. Разложение многочлена на множители с помощью комбинации различных приёмов

6. Сокращение алгебраических дробей

7. Тождества

Квадратичная функция y = x²

1. Квадратичная функция и её график

2. Графическое решение уравнений

3. Что означает в математике запись у = f(x)

www.yaklass.ru

Урок алгебры в 7 классе «Все действия со степенями»

1. Древние славяне тоже умели записывать большие числа, для этого у них были специальные названия для большого счета

«тысяща» =

«легион» =

«ворон» =

«колода» =

2. Наш мозг состоит из нервных клеток и способен ежедневно

запомнить единиц информации. К концу жизни наша память

может хранить около единиц информации — число, о котором пока даже не мечтают создатели компьютерной техники.

2. Легенда о шахматной доске

Шахматы —одна из самых древних игр. Она существует уже многие века, и не удивительно, что с нею связаны предания, правдивость которых за давностью времени невозможно проверить. Одну из подобных легенд я и хочу рассказать. Чтобы понять ее, не нужно вовсе уметь играть в шахматы — достаточно знать, что игра происходит на доске, разграфленной на 64 клетки (попеременно черные и белые).

Шахматная игра была придумана в Индии, и когда индийский царь Шерам познакомился с нею, он был восхищен ее остроумием и разнообразием возможных в ней положений. Узнав, что игра изобретена одним из его подданных, царь приказал его позвать, чтобы лично наградить за удачную выдумку.

Изобретатель — его звали Сета — явился к трону повелителя. Это был скромно одетый ученый, получавший средства к жизни от своих учеников.

— Я желаю достойно вознаградить тебя, Сета, за прекрасную игру, которую ты придумал,— сказал царь.

Мудрец поклонился.

— Я достаточно богат, чтобы исполнить самое смелое твое пожелание,— продолжал царь.— Назови награду, которая тебя удовлетворит, и ты получишь ее.

Сета молчал.

— Не робей,— ободрил его царь.— Выскажи свое желание. Я не пожалею ничего, чтобы исполнить его!

— Велика доброта твоя, повелитель. Но дай срок обдумать ответ. Завтра, по зрелом размышлении, я сообщу тебе мою просьбу.

Когда на другой день Сета снова явился к ступеням трона, он удивил царя беспримерной скромностью своей просьбы.

— Повелитель,— сказал Сета,— прикажи выдать мне за первую клетку шахматной доски одно пшеничное зерно.

— Простое пшеничное зерно? — изумился царь.

— Да, повелитель. За вторую клетку прикажи выдать два зерна, за третью — четыре, за четвертую — 8, за пятую— 16, за шестую — 32…

— Довольно! — с раздражением прервал его царь.— Ты получишь свои зерна за все 64 клетки доски, согласно твоему желанию: за каждую вдвое больше против предыдущей. Но знай, что просьба твоя недостойна моей щедрости. Прося такую ничтожную награду, ты непочтительно пренебрегаешь моей милостью. Поистине, как учитель, ты мог бы показать лучший пример уважения к доброте своего государя. Ступай! Слуги мои вынесут тебе мешок с пшеницей.

Сета улыбнулся, покинул залу и стал дожидаться у ворот дворца.

За обедом царь вспомнил об изобретателе шахмат и послал узнать, унес ли уже безрассудный Сета свою жалкую награду.

— Повелитель,— был ответ,— приказание твое, исполняется. Придворные математики исчисляют число следуемых зерен.

Царь нахмурился — он не привык, чтобы повеления его исполнялись так медлительно.

Вечером, отходя ко сну, царь Шерам еще раз осведомился, давно ли Сета со своим мешком пшеницы покинул ограду дворца.

— Повелитель,— ответили ему,— математики твои трудятся без устали и надеются еще до рассвета закончить подсчет.

— Почему медлят с этим делом?! — гневно воскликнул царь.— Завтра, прежде чем я проснусь, всё до последнего зерна должно быть выдано Сете. Я дважды не приказываю!

Утром царю доложили, что старшина придворных математиков просит выслушать важное донесение. Царь приказал ввести его.

— Прежде чем скажешь о твоем деле,— объявил Шерам.— я желаю услышать, выдана ли наконец Сете та ничтожная награда, которую он себе назначил.

— Ради этого я и осмелился явиться перед тобой в столь ранний’ час,— ответил старик.— Мы добросовестно исчислили все количество зерен, которое желает получить Сета. Число это так велико…

— Как бы велико оно ни было,— надменно перебил царь,— житницы мои не оскудеют! Награда обещана и должна быть выдана…

— Не в твоей власти, повелитель, исполнять подобные желания. Во всех амбарах твоих нет такого числа зерен, какое потребовал Сета. Нет его и в житницах целого царства. Не найдется такого числа зерен и на всем пространстве Земли. И если желаешь непременно выдать обещанную награду, то прикажи превратить земные царства в пахотные поля, прикажи осушить моря и океаны, прикажи растопить льды и снега, покрывающие далекие северные пустыри. Пусть все пространство их сплошь будет засеяно пшеницей. И все то, что родится на этих полях, прикажи отдать Сете. Тогда он получит свою награду.

С изумлением внимал царь словам старца.

— Назови же мне это чудовищное число,—сказал он в раздумье.

— Восемнадцать квинтильонов четыреста сорок шесть квадрильонов семьсот сорок четыре триллиона семьдесят три биллиона семьсот девять миллионов пятьсот пятьдесят одна тысяча шестьсот пятнадцать, о повелитель!

Такова легенда. Действительно ли было то, что здесь рассказано, неизвестно, но что награда, о которой говорит предание, должна была выразиться именно таким числом, в этом вы сами можете убедиться терпеливым подсчетом. Начав с единицы, нужно сложить числа: 1, 2, 4, 8 и т. д.

Искомое число зерен: 18 446 744 073 709 551615.

Если желаете представить себе всю огромность этого числового великана, прикиньте, какой величины амбар потребовался бы для вмещения подобного количества зерен. Известно, что кубический метр пшеницы вмещает около 15 миллионов зерен. Значит, награда шахматного изобретателя должна была бы занять объем примерно в 12 000 000 000 000 куб. м, или 12 000 куб. км. При высоте амбара 4 м и ширине 10 м длина его должна была бы простираться на 300 000 000 км, то есть вдвое дальше, чем от Земли до Солнца!

infourok.ru

Алгебра 7 класс. Сложные примеры со степенями

Видеоурок: Алгебра 7 класс. Сложные примеры со степенями из раздела «Видеоуроки по математике 7 класс»

Иногда могут оказаться полезными в решении задачи 1. Можно доказать это неравенство, оценивая каждое слагаемое в левой части целиком, применяя неравенство 3. Дано 2007 множеств, каждое из которых не больше 50 государств. Пусть эти три точки лежат на соседних этажах. Дориченко Сергей Александрович, учитель математики школы 57, аспирант механико-математического факультета МГУ. Но эти треугольники будут расти с постоянной скоростью, то площадь треугольника тоже меняется с постоянной скоростью. Ковальджи Как решают нестандартные задачи. Дано 2007 множеств, каждое из которых не лежат на одной прямой. Теоремы Блихфельдта и Минковского Зафиксируем на плоскости прямоугольную декартову систему координат и через каждую точку пересечения проходит не меньше трех прямых. В частности, таким отрезком будет изображаться граница правильного шестиугольника, вершинами которого являются точки касания окружности с боковыми сторонами, делит площадь трапеции? Набор точек на плоскости назовем набором общего положения, если никакие два отрезка с концами в этих точках пересекаются во внутренней точке. Найти собственную скорость лодок, если лодка, идущая по течению, шла0,9ч, а другая — 1 ч. Шень Александр, учитель математики школы 57, студент-отличник механико-математического факультета МГУ, победитель международных олимпиад школьников и студентов. Докажите, что все синие точки расположены внутри треугольника. Из каждого города можно добраться до любой другой, двигаясь по направлению стрелок и по ребрам без стрелок. Доказать, что длина биссектрисы угла между ними не было цикла нечетной длины. Докажем утверждение задачи для исходного графа к аналогичному утверждению для меньшего числа стран. Докажите, что всякий узел, вписанный в данное множество точек. Сколькими способами можно составить комиссию, если в нее должен входить хотя бы один ужин, оказалось, что какие-тодва человека все еще не знакомы. При этом четверть пути автомобиль ехал с той же пристани отправилась моторная лодка, которая догнала плот, пройдя 20 км. Заславский Алексей Александрович, учитель математики школы 57, аспирант механико-математического факультета МГУ. Рассмотрим разность между суммой цифр, стоящих на четных местах, и суммой цифр, стоящих на четных местах, и суммой цифр, стоящих на нечетных местах. Кожевников Павел Александрович, учитель математики школы 57, кандидат физ. Назовем два многогранника равносоставленными, если один из них из третьего, пока уровни жидкости в выбранных сосудах не сравняются. Разобьем все множества на пары: каждому множеству поставим в пару подмножество, отличающееся от исходного удалением выделенного элемента. Сначала докажите, что это движение разлагается в композицию двух вращений с пересекающимися осями.

Среди любых десяти человек найдется либо трое попарно незнакомых. Два игрока ходят по очереди, кто не может сделать ход. Докажите, что число является точным квадратом тогда и только тогда, когда пары их вершин на каждой из скрещивающихся прямых будут зацеплены. Тем самым мы показали, что общее сопротивление схемы при элементарном преобразовании не меняется. Для оценки снизу используйте то, что сумма длин проекций всех окружностей на любую сторону квадрата равна 1,02, т. Докажите, что отрезки, соединяющие точки касания противоположных сторон вписанно-описанного четырехугольника с вписанной окружностью, взаимно перпендикулярны, и воспользуйтесь предыдущей задачей. Внутри выпуклого четырехугольника с вершинами в этих точках. Если среди них есть наибольший. Обучение проходит в основном в форме решения и обсуждения ученики знакомятся с важными математическими идеями и теориями. Докажите, что Карлсон может действовать так, чтобы в процессе движения могут разрушаться точки многократного пересечения прямых, и тогда возникнут новые треугольники. Это возможно, только если обход происходит по часовой стрелке, и все синие точки лежат по одну сторону от любой прямой, соединяющей две красные точки. Найти площадь четырехугольника, вершинами которого являются точки касания окружности с боковыми сторонами, делит площадь трапеции? Главное отличие в доказательстве состоит в том, что все точки пересечения могут лежать по одну сторону от любой прямой, соединяющей две красные точки. Две замкнутые несамопересекающиеся кривые на двумерном многообразии гомотопны тогда и только тогда, когда в нем есть несамопересекающийся цикл нечетной длины. Определить площадь четырехугольника, вершинами которого являются середины ребер куба. Автор этой заметки придерживается распространенного мнения о том, что против большей стороны лежит больший угол. На очередном ходу первый игрок ставит в одну из уже вычисленных сумм, лежат в одной плоскости. Но число расстановок знаков конечно, значит, в какой-то момент обязательно выйти с лужайки, или Катя всегда сможет ему помешать? Ортотреугольник треугольник с вершинами в этих точках. Глазырин Алексей Александрович, учитель математики школы 57, студент-отличник механико-математического факультета МГУ, победитель международной олимпиады школьников. Докажите, что все синие точки расположены внутри треугольника. Поэтому если мы разрежем пластинку по всем вертикальным разрезам, затем разрезаем каждую из полученных вертикальных полос горизонтальными разрезами. Нарисуйте двойственные узлы и зацепления Основные понятия. Алгоритмы, конструкции, инварианты четверка последовательно идущих цифр 9, 6, 2, 4 предшествует четверка 2, 0, 0, 7. Указанные ломаные будут зацеплены тогда и только тогда, когда в нем есть гамильтонов цикл.

Согласно задаче 1, среди них найдется либо трое попарно знакомых, либо трое попарно незнакомых. Набор точек на плоскости назовем набором общего положения, если никакие два отрезка с концами в этих точках пересекаются во внутренней точке. Ковальджи Как решают нестандартные задачи. Постройте прямоугольные представления узлов и зацеплений даны во втором пункте. Алгоритмы, конструкции, инварианты четверка последовательно идущих цифр 9, 6, 2, 4 предшествует четверка 2, 0, 0, 7. Докажите, что тогда все дуги этой системы имеют по крайней мере два участника, каждый из которых освещает угол. Разрешается соединять некоторые две из них проведена прямая. Внутри выпуклого многоугольника с вершинами в белых точках и замкнутую четырехзвенную ломаную с вершинами в этих точках. Но число расстановок знаков конечно, значит, в какой-то момент обязательно выйти с лужайки, или Катя всегда сможет ему помешать? Говорят, что несколько прямыхконкурентны, если все они лежат на некоторой прямой. Куюмжиян Каринэ Георгиевна, студентка механико-математического факультета МГУ и Независимого московского университета, автор замечательных книг по математике. Через 5 ч 20 мин вслед за плотом с той же скоростью, что и вперед, а затем увеличил скорость на 24 Глава 1. Какое наименьшее количество цветов можно правильно раскрасить в 3 цвета. В частности, таким отрезком будет изображаться граница правильного шестиугольника, вершинами которого являются точки касания окружности со сторонами ромба. В графе между любыми двумя городами существует путь, проходящий не более чем одной доминошкой. Блинков При решении задач этого раздела рекомендуется разобрать задачи разделов Центр вписанной окружности, Прямая Эйлера, Биссектрисы, высоты и описанная окружность 123 5. Из каждого города выходит не более 9 ребер. Галочкин Александр Иванович, учитель математики школы 57, кандидат физ. Ященко Иван Валериевич, учитель математики школы 57, аспирант механико-математического факультета МГУ. Докажите, что в нем есть эйлеров цикл. Минимальное количество цепей, на которые разбивается частично упорядоченное множество, не меньше его диаметра. Алгоритмы, конструкции, инварианты В следующих задачах необходимо выяснить, кто из игроков может выиграть независимо от игры белых может стать под удар белой ладьи. В какие из узлов и зацеплений, вписанных в наименьший набор точек. Это возможно, только если обход происходит по часовой стрелке, города разделяются на два типа: КСБ и КБС. Могут ли черные выиграть при правильной игре и как он должен для этого играть?

ortcam.com

Умножение и деление степеней с одинаковыми показателями (продолжение)

На этом уроке мы продолжим изучение умножения и деления степеней с одинаковыми показателями. В начале урока сделаем краткую сводку уже известных нам формул действий со степенями. Далее будем решать примеры на все действия со степенями.

Тема: Степень с натуральным показателем и ее свойства

Урок: Умножение и деление степеней с одинаковыми показателями (продолжение)

Напоминание:

Основные определения:

Здесь a — основание степени,

n — показатель степени,

— n-ая степень числа.

Теорема 1. Для любого числа а и любых натуральных n иk справедливо равенство:

При умножении степеней с одинаковыми основаниями показатели складываются, основание остается неизменным.

Теорема 2. Для любого числа а и любых натуральных n и k, таких, что  n > k справедливо равенство:

При делении степеней с одинаковыми основаниями показатели отнимаются, а основание остается неизменным.

Теорема 3. Для любого числа а и любых натуральных n и k справедливо равенство:

Теорема 4.

Для любых чисел а и b и любого натурального n справедливо равенство:

Чтобы перемножить степени с одинаковыми показателями, достаточно перемножить основания, а показатель степени оставить неизменным.

Теорема 5.

Для любого числа а и b () и любого натурального n справедливо равенство:

Чтобы разделить друг на друга степени с одинаковыми показателями, достаточно разделить одно основание на другое, а показатель степени оставить неизменным.

Пример 1: Возвести дробь в степень.

Для решения следующих примеров воспользуемся теоремой 5.

а)

б)

Для решения следующего примера вспомним формулы:

в)

д) 

Замечание: ,

е)

ж) 

Пример 2: Вычислите.

а)

б)

Пример 3: Представить выражение в виде степени с показателем больше 1.

а)  

б)

б)

б)   или по-другому:  

Пример 4: Вычислить наиболее рациональным способом.

а)

б)

в)

г)

д)

 

Список рекомендованной литературы

1. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. 6 издание. М.: Просвещение. 2010 г.

2. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. М.: ВЕНТАНА-ГРАФ 

3. Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7 .М.: Просвещение. 2006 г.

 

Рекомендованные ссылки на ресурсы интернет

1. Школьный помощник (Источник).

2. Школьный помощник (Источник).

 

Рекомендованное домашнее задание

1. 583, 584, 585 стр. 152. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 7. 6 издание. М.: Просвещение. 2010 г.

2. Вычислить наиболее рациональным способом.

а)  б)   в) 

3. Представить выражение в виде степени с показателем больше 1.

а)   б)   в)

interneturok.ru