Курс статистической физики (Ноздрев В.Ф.)
Курс статистической физики (Ноздрев В.Ф.)
ОглавлениеПРЕДИСЛОВИЕВВЕДЕНИЕ § 1. Предмет и метод статистической физики § 2. К вопросу возникновения и развития молекулярно-кинетической теории материи § 3. Место статистической физики в раскрытии материалистической картины мира § 4. Феноменологические и молекулярно-кинетические теории § 5. Модельность в статистической физике. Классическая и квантовая модели вещества Глава II.  НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ВЕРОЯТНОСТЕЙ§ 1. Случайные события и случайные величины § 2. Понятие вероятности § 3. Свойства вероятности. Формула сложения и умножения вероятностей § 4. Средние значения случайных величин § 5. Примеры законов распределения случайных величин § 6. Функция распределения для нескольких случайных величин ЧАСТЬ I. ЭЛЕМЕНТАРНАЯ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ § 1. Модель идеального газа § 2. Распределение молекул газа по скоростям § 3. Связь распределения Максвелла по скоростям с абсолютной температурой § 4. Характерные скорости максвелловского распределения § 5. Средние относительные скорости § 6. Соответствие модели идеального газа реальному газу Глава IV. ЭЛЕМЕНТЫ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ НЕРАВНОВЕСНЫХ ПРОЦЕССОВ § 2. Поперечные сечения. Длина свободного пробега § 3. Распределение свободных пробегов частиц § 4. Вязкость газов § 5.  Теплопроводность газов§ 6. Диффузия газов ЧАСТЬ II. КЛАССИЧЕСКАЯ СТАТИСТИЧЕСКАЯ ФИЗИКА § 1. Невозможность последовательного механического описания физических систем многих частиц § 2. Макроскопическое и микроскопическое описание системы в термодинамическом равновесии § 3. Изображение системы в фазовом пространстве § 4. Элемент фазового объема. Вероятность нахождения системы в фазовом пространстве § 5. Теорема о сохранении фазового объема (Теорема Лиувилля) § 6. Макроскопические величины как фазовые средние Глава VI. СТАЦИОНАРНЫЕ ФУНКЦИИ РАСПРЕДЕЛЕНИЯ § 1. Микроканоническое распределение § 2. Каноническое распределение Гиббса § 3. Свойства канонического распределения § 4. Физический смысл параметров канонического распределения § 5. Энтропия и ее связь с вероятностью состояния § 6. Распределение Максвелла-Больцмана § 7. Большое каноническое распределение Гиббса Глава VII. ПРИМЕНЕНИЕ РАСПРЕДЕЛЕНИЯ ГИББСА К РЕАЛЬНЫМ СИСТЕМАМ § 1.  Выражение термодинамических функций через интеграл состояний§ 2. Интеграл состояний и термодинамические функции идеального газа § 3. Статистическое рассмотрение системы взаимодействующих частиц § 4. Вывод уравнения состояния реального газа § 5. Статистика диэлектриков Глава VIII. РАВНОМЕРНОЕ РАСПРЕДЕЛЕНИЕ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ПО СТЕПЕНЯМ СВОБОДЫ § 1. Теорема о равномерном распределении энергии по степеням свободы § 2. Теплоемкость разреженных газов § 3. Теплоемкость твердых тел § 5. Классическая теория электронного газа Глава IX. ЭЛЕМЕНТЫ ТЕОРИИ ФЛУКТУАЦИЙ § 2. Связь флуктуаций со свободной энергией. Корреляция § 3. Чувствительность различных измерительных приборов § 4. Рассеяние света на флуктуациях плотности § 5. Броуновское движение § 6. Статистика полимеров ЧАСТЬ III. КВАНТОВАЯ СТАТИСТИЧЕСКАЯ ФИЗИКА § 1. Квантовые системы и их свойства § 2.  Описание квантовых систем§ 3. Применение статистического метода к квантовым системам § 4. Метод ячеек Больцмана § 5. Статистики квантовых систем § 6. Сопоставление статистик Максвелла-Больцмана, Бозе-Эйнштейна и Ферми-Дирака Глава XI. ЛОКАЛИЗОВАННЫЕ КВАНТОВЫЕ СИСТЕМЫ § 1. Квантовый осциллятор и квантовый ротатор § 2. Сумма по состояниям и внутренняя энергия систем осцилляторов и ротаторов § 3. Теплоемкость газов. Характеристические температуры § 4. Теплоемкость твердых тел. Закон Дебая § 5. Законы равновесного излучения § 6. Статистика парамагнетиков Глава XII. ПРИМЕНЕНИЕ СТАТИСТИК БОЗЕ — ЭЙНШТЕЙНА И ФЕРМИ — ДИРАКА § 1. Применение статистики Бозе — Эйнштейна к описанию системы частиц § 2. Равновесное излучение как фотонный газ § 3. Применение статистики Ферми — Дирака к описанию поведения системы частиц § 4. Электронный газ в металлах § 5. Магнитные свойства электронного газа § 6. Состояния систем с отрицательной абсолютной температурой ПРИЛОЖЕНИЯ.  |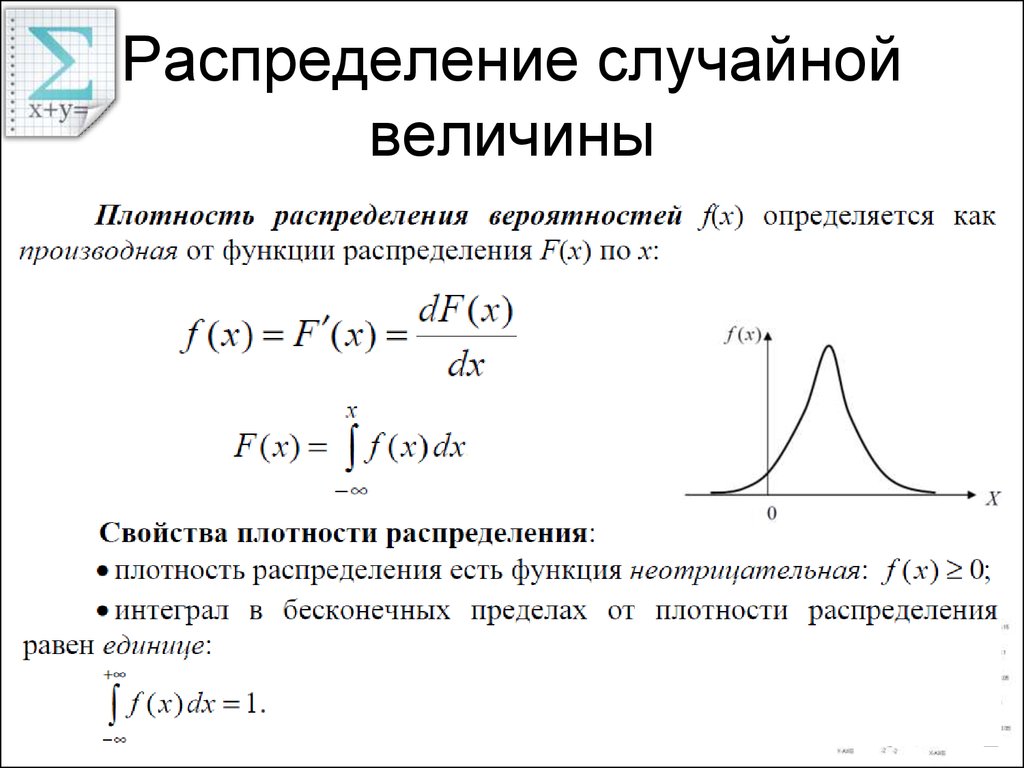
3.2.5. Примеры законов распределения случайных величин Дискретные случайные величины
1. Биномиальное распределение
Определение. Случайная величина X называется распределенной по
Биномиальный закон распределения дискретной случайной величины можно представить в виде таблицы:
Для случайной величины, распределенной по биномиальному закону с параметрами и : , , .
2. Распределение Пуассона
Определение. Распределение
случайной величины
,
возможными значениями которой являются
числа ,
а вероятности этих
значений задаются формулой: ,
называется распределением
Пуассона, —
параметр распределения.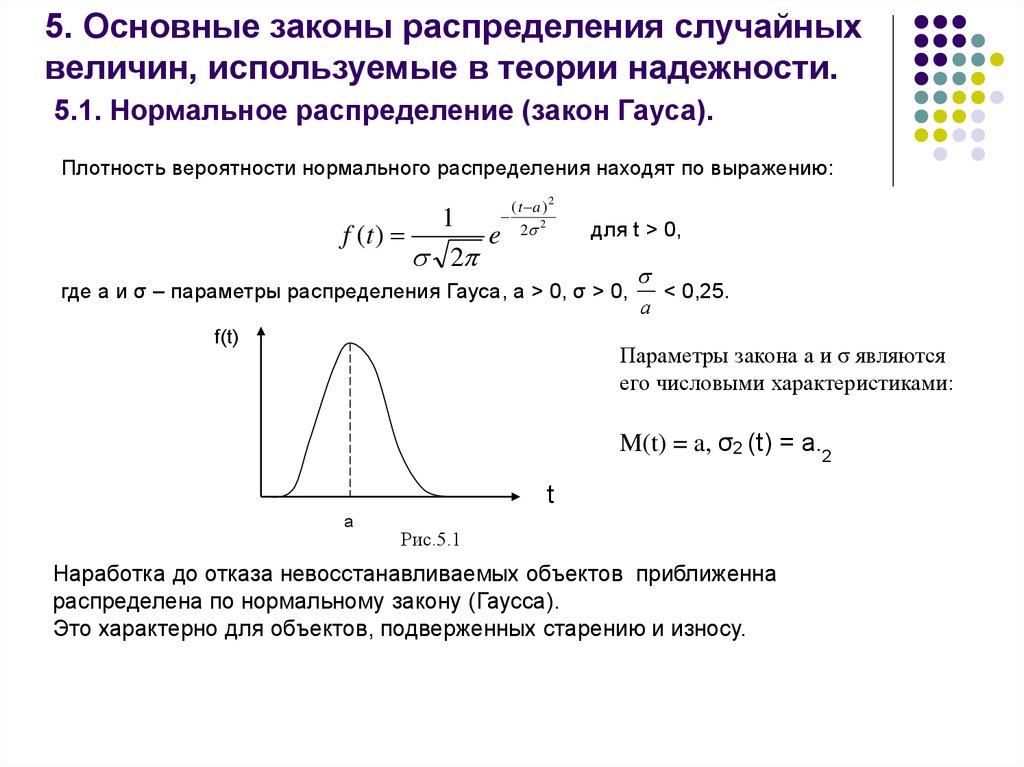
Распределение Пуассона является предельным случаем биномиального распределения, если достаточно велико, а достаточно малое (в этом случае ).
Числовые характеристики этого распределения: .3. Геометрическое распределение
Определение. Геометрическим распределением называется распределение дискретной случайной величины , возможные значения которой 1,2,3,… , а вероятности этих значений определяются формулой: , .
Для такой случайной величины , .
4. Гипергеометрическое распределение
Определение. Распределение дискретной случайной величины, возможные значения которой , а вероятность того, что эта величина примет значение к, определяется формулой ( ), называется гипергеометрическим.
Числовые характеристики этой случайной величины определяются следующим образом: .
Непрерывные случайные величины
5.
Равномерное распределениеОпределение. Случайная величина называется равномерно распределенной на отрезке , если плотность распределения вероятностей этой величины постоянна на данном отрезке и равна нулю вне его: .
Функция распределения этой величины имеет вид:
.
Числовые характеристики случайной величины , .
6. Показательное распределение
Определение. Распределение непрерывной случайной величины называется показательным, если его плотность распределения имеет вид: , — параметр распределения.
Функция распределения этой случайной величины: , числовые характеристики: .
7. Нормальное распределение
Определение.
Нормальным
распределением (или распределением Гаусса) называется
распределение случайной величины,
плотность которого равна: .
Параметры и нормально распределенной случайной величины имеют следующий смысл: , .
Функция распределения этой случайной величины есть: , где — функция Лапласа: .
Функция Лапласа является нечетной, ее значения приведены в специальных таблицах.
Вероятность попадания нормально распределенной случайной величины в интервал определяется формулой
.
Вероятность выполнения неравенства , т.е. вероятность того, что случайная величина отклонится от своего математического ожидания не больше, чем на величину , для нормально распределенной случайной величины есть: .
Пример. Найти
вероятность попадания в интервал нормально распределенной случайной
величины
,
для которой математическое ожидание ,
среднее квадратическое отклонение .
Решение. Применим формулу: ; в данном случае она примет вид: .
Функция Лапласа является нечетной, поэтому
.
Значения найдены по таблице значений функции Лапласа (приложение 1).
Как в теории вероятности мы можем определить закон (без необходимости сначала определять случайную величину)?
Редактировать : На самом деле я не уверен в своем ответе. Честно говоря, я не могу поверить, что получил 3 голоса без комментариев, в которых говорится, что я неправ или что-то в этом роде. Полагаю, это действительно означает, что я прав по крайней мере в одном из двух моментов в Части 4. Если вы действительно думаете, что я прав, объясните, пожалуйста, почему вы так думаете.
Обратите внимание, что это было давно, так что я могу быть ржавым.
непрерывная справа неубывающая функция $F: \mathbb R \to [0,1]$, удовлетворяющая $\lim_{x \to — \infty} F(x) = 0$ и $\lim_{x \ до \infty} F(x) = 1$.
(любая $F$, удовлетворяющая вышеизложенному) на самом деле является «функцией распределения» некоторой случайной величины $X$.
Я считаю, что примером такого $X$ является $X: (0,1) \to \mathbb{R}$ by $X(\omega) = \sup\{y \in \mathbb{R}: F (y) < \omega\}$ на вероятностном пространстве $((0,1), \mathfrak{B}(0,1),\lambda)$, где отсюда $\lambda$ — мера Лебега. Также см. там. (Я думаю, это связано с обратным распределением или квантилями.) 9C}$ в том же вероятностном пространстве $(\Omega, \mathcal F, \mathbb P)$ для любого события $A$ с вероятностью от $0$ до $1$. (Может быть, даже если 0 и 1, но думать об этом - головная боль.) Хммм... подождите, не уверен... я думаю, что это должно быть $1_A$ и $1_B$, но $A$ и $B$ имеют такая же вероятность. Ах, что бы вы ни делали, $P(1_{\cdot\}} \le x)$ сами.
Функция распределения случайной величины $Y$ равна $F_Y(y):=P(Y \le y)$ aa, а закон $Y$ равен $\mathscr L(Y \in B)$…связан в том, что $\{Y \le y\} = \{Y \in (-\infty,y]\}$ и что $B \in \mathscr B := \sigma(\mathbb R) = \sigma(\pi( \mathbb R))$, где $\pi(\mathbb R) := \{(-\infty, y]\}_{y \in \mathbb R}$
О, теперь понятно.
Вы хотите определить закон без случайной величины так же, как мы определяем функцию распределения? Ну… Может быть
Любой $\mathscr L: \mathscr B \to [0,1]$ с.т. $\mathscr L$, ограниченный $\pi(\mathbb R)$, является функцией распределения?
Любая вероятностная мера на $(\mathbb R, \mathscr B)$?
См. это упражнение в главе 4.9
Я предполагаю, что так же, как каждый закон случайной величины является вероятностной мерой на $(\mathbb R, \mathscr B)$, мы имеем, что каждая вероятностная мера на $(\mathbb R, \mathscr B)$ также является закон некоторой случайной величины. Может быть, что-то похожее на $X(\omega) = \sup\{(?) B \in \mathscr B: \mathscr L(B) < \omega\}$ in $((0,1), \mathfrak{ B}(0,1),\lambda)$... или просто превратите закон в распределение и создайте случайную величину из этого распределения.
Есть ли способ перейти от закона к случайной величине без распределения? Хммм.
.. Что-то не могу придумать, но мне кажется, что должно быть! Если кто знает, то поделитесь пожалуйста!
Re your
‘Я ищу определение закона, в котором также не упоминается распределение.’
- Правильно, см. (2) в части 4. Думаю, ваш
‘такое, что существует дистрибутив’
мой (1) в части 4, и я на самом деле не уверен в этом.
В любом случае, я с нетерпением жду информации об исправлениях в комментариях!
Случайные величины: определение, формулы и типы
Вероятно, вы уже знакомы с переменными, такими как x и y, которые вы научились решать с помощью алгебры. То есть, когда величина неизвестна, она обозначается строчными буквами, такими как x, y и z. Случайные переменные , используемые в статистике, сходны тем, что их значения не фиксированы, а используются для учета случайности и вероятности. Другими словами, когда мы используем переменную для представления вероятностей определенных результатов в статистическом эксперименте, прописные буквы (X, Y, Z) используются для обозначения того, что переменная является случайной.
Случайные величины используются в различных областях, связанных с вероятностью, таких как машинное обучение, здравоохранение, прогнозирование и другие.
Случайные величины в статистике: определение и типы поведение). Он также известен как стохастическая переменная.
Давайте рассмотрим несколько сценариев использования случайных величин. Например, для случайного выбора из коробки нам дается набор возможных чисел {1, 2, 3, 4, 5}. Любое из этих чисел в этом наборе может быть извлечено в статистическом эксперименте или проверке вероятности. Если выбрано число 2, то 2 принимает значение случайной величины для этой итерации эксперимента.
Другим примером использования случайных величин является бросок игральной кости. За каждый бросок можно получить любое число от 1 до 6. Результат роли кубика, измеряемый как X, является случайной величиной.
Случайная величина может быть классифицирована как дискретная , непрерывная или смешанная, и представлена заглавной буквой, например, X или Y.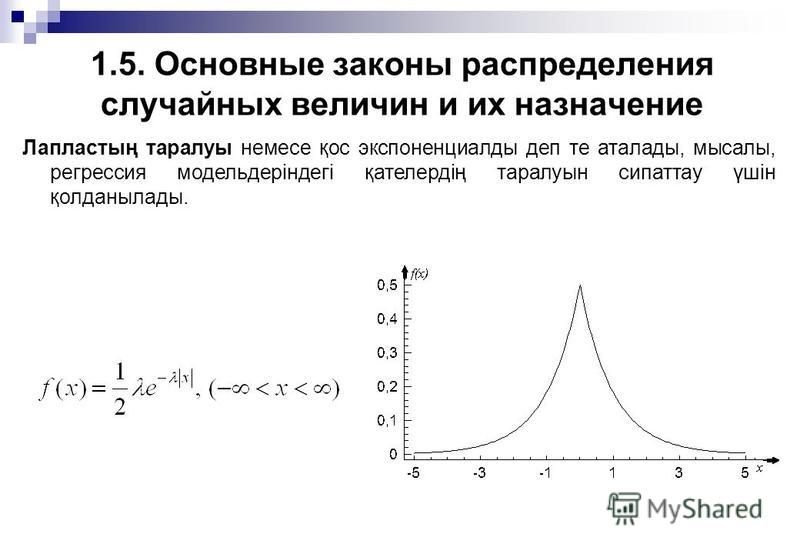
Диапазон возможных значений, которые может принимать случайная величина называется его пространством выборки .
Когда случайная величина принимает заданные или конечные значения в интервале, она называется дискретной. Значения дискретной случайной величины должны быть счетным числом. Например, при бросании игральной кости возможные результаты, представленные X, представляют собой исчисляемые числа 1, 2, 3, 4, 5 и 6. Однако мы не можем разыграть игральную кость и получить результат, например, 5,243.
Непрерывные случайные величиныКогда данные неисчислимы и могут принимать бесконечно много значений, они называются непрерывными. Вероятности, связанные с непрерывными данными, представлены непрерывной случайной величиной. Например, сколько времени требуется для выполнения данной задачи за заданный период в 30 минут, считается непрерывным.
Вам может быть интересно, как этот диапазон в 30 минут можно считать бесконечным и неисчисляемым. Это связано с тем, что задача может быть выполнена в любой конкретный момент в пределах 30-минутного диапазона, измеряемого, например, с точностью до миллисекунды или все более точных единиц. Это отличается от исчисляемых данных, таких как, например, количество людей, которые могут быть представлены только целыми числами.
Таким образом, при возникновении случайной величины X при заданной функции y = f(x) X может принимать любое значение, попадающее в заштрихованную область, от a до b.
Смешанные случайные величиныКогда переменная не является ни полностью дискретной, ни непрерывной, а скорее имеет признаки того и другого, ее называют смешанной случайной величиной.
События на фондовом рынке и в гидрологических моделях осадков иллюстрируют смешанные случайные величины. Эти события имеют как дискретные, так и непрерывные характеристики.
Случайные величины: формула вероятности случайных событий
Вероятность случайных событий можно рассчитать по следующей формуле: P(X)=nN.
Где:
«n» — количество благоприятных исходов, а
«N» — общее количество возможных исходов.
Рассмотрим пример, использующий эту формулу.
Предположим, что в коробке 10 красных, 5 желтых и 15 зеленых шаров. Если мы выберем шар наугад, какова вероятность того, что мы выберем красный шар?
Решение:
Пусть красные шары = R = 10,
Желтые шары = Y = 5 и
Зеленые шары = G = 15
Общее количество возможных исходов: N = R + Y + G = 10 + 5 + 15 = 30
Так как мы рассматриваем вероятность выбора именно красного шара, то число благоприятных исходов равно количеству красных шаров: n = R = 10
Следовательно, вероятность выбора красного мяч показан как: PR=nN= 1030= 13 или 0,33
Обратите внимание, что этот пример выше относится к дискретной случайной величине.
Мы измеряем счетное количество шаров и, например, не можем получить 1,4 красных шара.
Определение распределений вероятностей для случайных величин
Распределение вероятностей случайной величины представляет собой функцию, которая описывает шансы/вероятность появления значений в пространстве выборки этой случайной величины в эксперименте.
Распределения вероятностей можно классифицировать по типам описываемых ими случайных величин: дискретное распределение вероятностей и непрерывное распределение вероятностей .
Дискретное распределение вероятностей
Дискретные распределения вероятностей формируются функцией массы вероятности (PMF). Какова вероятность того, что дискретная случайная величина будет равна некоторому определенному значению? Этот диапазон вероятностей в пространстве выборки определяется PMF. Давайте посмотрим на обозначения и свойства функции массы вероятности, которая описывает распределения вероятностей дискретных случайных величин.
Для функции массы вероятности (PMF) дискретной случайной величины:
Обозначение: PxX=PX=x
Свойства: pxx≥0∑xPxx=1
Из свойств дискретных случайных величин мы знаем, что вероятность каждого значения должна быть между 0 и 1, а сумма всех значения в выборочном пространстве должны быть равны 1.
Непрерывное распределение вероятностей
Непрерывные распределения вероятностей формируются функцией плотности вероятности (PDF). В отличие от дискретных случайных величин, прямое определение вероятностей определенных значений непрерывных переменных не является простым процессом, потому что существует бесконечно много значений!
По этой причине мы можем упростить это измерение, «дискретизируя» переменные. Это означает, что мы аппроксимируем непрерывную переменную как принимающую дискретные величины, что позволяет нам работать с интервалами значений, а не с конкретными значениями.
Чтобы представить выборочное пространство непрерывной случайной величины в терминах вероятности, связанной с ее значениями, мы используем функцию плотности вероятности (PDF).
Давайте взглянем на обозначения и свойства PDF.
Для функции плотности вероятности (PDF) непрерывной переменной fx:
Обозначение: Pa≤X≤b=∫abfxxdx
Свойства: ∫-∞+∞fxxdx=1fxx≥0
Из свойств мы известно, что площадь под кривой PDF равна 1, а вероятность каждого отдельного значения равна нулю (поскольку значения бесконечны).
Измерение высоты является непрерывным измерением. Допустим, нам нужно предсказать рост одного ученика в классе из 30 учеников. Мы будем использовать непрерывную случайную величину. С какой точностью мы можем предсказать, что рост определенного ученика будет именно 1,68 м, а не 1,67 м или 1,69 м?м или любое другое очень близкое значение?
Самый простой и разумный способ сделать это — дискретизировать значения и предсказать рост учащегося в заданном диапазоне, скажем, от 1,65 м до 1,70 м.
Случайные величины — ключевые выводы
- Случайная величина (иначе известная как стохастическая переменная) представляет собой описание с действительным знаком или функцию, которая распределяет числовые значения для статистического эксперимента.
