4.3.7 Приведение кривой второго порядка к каноническому виду
Уравнение второго порядка вида
определяет на плоскости кривую. Группа членов называется квадратичной формой, – линейной формой. Если в квадратичной форме содержатся только квадраты переменных, то такой ее вид называется каноническим, а векторы ортонормированного базиса, в котором квадратичная форма имеет канонический вид, называются главными осями квадратичной формы.
Матрица называется матрицей квадратичной формы. Здесь . Чтобы матрицу привести к диагональному виду, необходимо за базис взять собственные векторы этой матрицы, тогда , где и – собственные числа матрицы .
В базисе из собственных векторов матрицы квадратичная форма будет иметь канонический вид: .
Эта операция соответствует повороту осей координат. Затем производится сдвиг начала координат, избавляясь тем самым от линейной формы.
Канонический вид кривой второго порядка: , причем:
А) если – эллипс, в частности, при это окружность;
Б) если имеем гиперболу;
Дополняя до полного квадрата, будем иметь: .Пример 14. Дано уравнение кривой
в системе координат , где и .
1. Определить тип кривой.
2. Привести уравнение к каноническому виду и построить кривую в исходной системе координат.
3. Найти соответствующие преобразования координат.
Решение. Приводим квадратичную форму к главным осям, то есть к каноническому виду. Матрица этой квадратичной формы . Находим собственные числа и собственные векторы этой матрицы:
Характеристическое уравнение:
; . Вид квадратичной формы: .
Исходное уравнение определяет гиперболу.
Заметим, что вид квадратичной формы неоднозначен. Можно записать , однако тип кривой остался тот же – гипербола.
Находим главные оси квадратичной формы, то есть собственные векторы матрицы . .
Собственный вектор, отвечающий числу при : .
В качестве единичного собственного вектора принимаем вектор , где – длина вектора .
Координаты второго собственного вектора, соответствующего второму собственному числу , находим из системы
.
; .
Итак, имеем новый ортонормированный базис .
По формулам (5) пункта 4.3.3. переходим к новому базису:
или
; . (*)
Вносим выражения и в исходное уравнение и, после преобразований, получаем: .
Выделяем полные квадраты: .
Проводим параллельный перенос осей координат в новое начало: , .
Если внести эти соотношения в (*) и разрешить эти равенства относительно и , то получим: , . В системе координат данное уравнение имеет вид: .
Для построения кривой строим в старой системе координат новую: ось задается в старой системе координат уравнением , а ось уравнением . Начало новой системы координат является точкой пересечения этих прямых.
Для упрощения восприятия разобьем процесс построения графика на 2 этапа:
1. Переход к системе координат с осями , заданными в старой системе координат уравнениями и Соответственно.
2. Построение в полученной системе координат графика функции.
Окончательный вариант графика выглядит следующим образом
Аналогично можно упростить, то есть привести к каноническому виду, поверхность второго порядка.
Для самостоятельной работы.
1. Оператор в пространстве действует по закону .
А) Доказать, что вектор является собственным вектором оператора . Найти его собственное число.
Б) Привести матрицу оператора к диагональному виду путем перехода к новому базису. Найти этот базис и соответствующую ему матрицу.
Ответ: ; ; .
2. Доказать, что матрица к диагональному виду не приводится.
3. Даны уравнения кривых:
А) ;
Б) ;
В) .
Определить тип кривых; кривую а) построить.
Ответ: а) эллипс; б) парабола; в) гипербола.
| < Предыдущая | Следующая > |
|---|
4.4. Приведение к каноническому виду уравнения кривой 2-го порядка
Общее уравнение кривой 2-го порядка:
(23)
Уравнение (23) можно представить в виде , где – квадратичная форма уравнения кривой, а – линейная функция.
Приведение уравнения кривой (23) к каноническому виду начинается с приведения к каноническому виду соответствующей квадратичной формы .
Её матрица Из характеристического уравнения находятся собственные значения и матрицы , при этом , так как . Затем находят соответствующие собственные векторы, которые после нормировки образуют ОНБ .
В новом базисе квадратичная форма примет канонический вид:
. (24)
Переход от ОНБ к ОНБ описывается матрицей , в столбцах которой находятся координаты векторов ОНБ . Связь между координатами и определяется из уравнения т. е.
. (25)
Подставляя зависимости (25) в линейную функцию получим:
Тогда уравнение (23) примет вид:
(26)
Выделяя в (26) полные квадраты, получим каноническое уравнение одной из кривых 2-го порядка. О какой кривой идет речь, можно определить сразу по матрице квадратичной формы. Если , то линия, задаваемая уравнением (23), Эллиптического типа, если – Гиперболического, если – Параболического типа.
Пример 20. Определить тип кривой 2-го порядка и построить её:
Решение.
Квадратичная форма, соответствующая заданной кривой, Её матрица .
Так как , то кривая параболического типа. Составим характеристическое уравнение и найдём собственные значения матрицы :
Собственные векторы, соответствующие найденным собственным значениям:
Построим ОНБ из собственных векторов:
Матрица перехода Выполним проверку соответствия ориентации ОНБ ориентации ОНБ : , значит, ориентация совпадает. В этом базисе .
Так как то Подставляя эти разложения в линейную часть кривой, получим:
Тогда уравнение кривой примет вид или т. е. где Заданная кривая изображена на рисунке 1.
Рисунок 1
Пример 21. Привести уравнение кривой 2-го порядка к каноническому виду и определить тип кривой:
Решение. Уравнение кривой представим в виде Где – квадратичная форма, – линейная функция.
В нашем случае , её матрица .
Определим тип кривой. Для этого вычислим Так как То заданная кривая эллиптического типа.
Приведем квадратичную форму к каноническому виду. Для нахождения собственных значений матрицы составим характеристическое уравнение: Т. е. , тогда .
Теперь найдём соответствующие им собственные векторы:
Построим ОНБ: , тогда матрица перехода от ОНБ к ОНБ имеет вид: Так как значит, ориентация ОНБ соответствует ориентации ОНБ .
Матрица заданной квадратичной формы в базисе имеет вид: , а сама квадратичная форма: .
Напомним, что матрица может быть получена в результате преобразования подобия: , где – матрица перехода к новому ОНБ. Координаты и связаны между собой соотношением: т. е. .
Преобразуем линейную часть уравнения кривой:
Теперь можно записать уравнение кривой в координатах :
Таким образом, выполнен первый шаг в преобразовании кривой к каноническому виду, в результате которого в исходном уравнении кривой исчезло слагаемое, содержащее произведение координат и .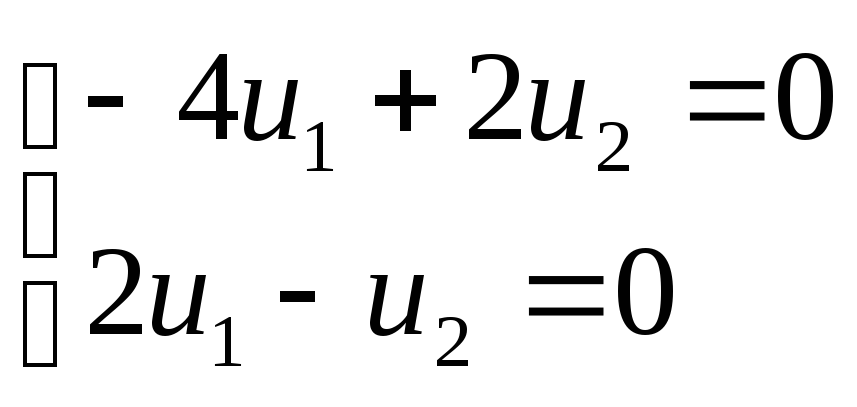
Выделим полные квадраты: или . Если то каноническое уравнение заданной кривой 2-го порядка примет вид и задаёт эллипс с полуосями Кривая изображена на рисунке 2.
Рисунок 2
Литература: [3, 6, 7, 15].
| < Предыдущая | Следующая > |
|---|
многомерное исчисление — производная второго порядка цепного правила (относительно приведения к канонической форме)
Я застрял на этом на пару дней. Итак, это из этой книги («Уравнения в частных производных в механике 1», стр. 125).
Раздел 4.2 Приведение к каноническим формам, приводящее к развитию уравнения Лапласа.
В этом разделе я не понимаю, как они расширяют частную производную второго порядка:
Где,
Вот что я получил до сих пор. Когда я это делаю, у меня получается только 4 термина, а не 5, как в книге. Здесь я сначала применяю правило произведения, а затем цепное правило (обратите внимание, я использую квадратные скобки, чтобы указать, что я беру частную производную того, что в них содержится.
Просто для организации).
$$\begin{выравнивание} \ гидроразрыва {\ парциальное} {\ парциальное х} \ гидроразрыва {\ парциальное и} {\ парциальное х} & = \\ &= \frac{\partial}{\partial x} \biggl( \frac{\partial u}{\partial \xi} \frac{\partial \xi}{\partial x} + \frac{\partial u} {\ парциальное \ эта} \ гидроразрыва {\ парциальное \ эта} {\ парциальное х} \ biggr) \\ &=\frac{\partial}{\partial x} \biggl( \frac{\partial u}{\partial \xi} \frac{\partial \xi}{\partial x}\biggr) + \frac{\ частичное {\ парциальное х} \ biggl (\ гидроразрыва {\ парциальное и} {\ парциальное \ эта} \ гидроразрыва {\ парциальное \ эта} {\ парциальное х} \ biggr) \\ &= \frac{\partial}{\partial x} \biggl[ \frac{\partial u}{\partial \xi} \biggr] \frac{\partial \xi}{\partial x} + \frac{\ частичное u}{\partial \xi} \frac{\partial}{\partial x} \biggl[ \frac{\partial \xi}{\partial x} \biggr] + \frac{\partial}{\partial x} \biggl[ \frac{\partial u}{\partial \eta} \biggr] \frac{\partial \eta}{\partial x} + \frac{\partial u }{\partial \eta} \frac{\partial}{\partial x} \biggl[ \frac{\partial \eta}{\partial x} \biggr] \\ \text{Теперь цепное правило:}\\ &= \frac{\partial}{\partial \xi}\biggl[\frac{\partial u}{\partial \xi}\biggr] \frac{\partial \xi}{\partial x} \frac{\ частичный \xi}{\частичный x} + \ гидроразрыв {\ парциальное и} {\ парциальное \ xi} \ гидроразрыва {\ парциальное ^ 2 \ xi} {\ парциальное х ^ 2} + \frac{\partial}{\partial \eta}\biggl[\frac{\partial u}{\partial \eta}\biggr] \frac{\partial \eta}{\partial x} \frac{\partial \эта}{\частичный х} + \frac{\partial u}{\partial \eta} \frac{\partial^2 \eta}{\partial x^2} \\ &=\frac{\partial^2 u}{\partial \xi^2} \biggl(\frac{\partial \xi}{\partial x} \biggr)^2 + \ гидроразрыв {\ парциальное и} {\ парциальное \ xi} \ гидроразрыва {\ парциальное ^ 2 \ xi} {\ парциальное х ^ 2} + \frac{\partial^2 u}{\partial \eta^2} \biggl(\frac{\partial \eta}{\partial x} \biggr)^2 + \frac{\partial u}{\partial \eta} \frac{\partial^2 \eta}{\partial x^2} \end{выравнивание} $$ Мое дерево цепного правила выглядит так (правильно ли оно?)
Кроме того, если бы кто-нибудь мог объяснить, почему это цепное правило действует? Конечно, это может быть целая тема сама по себе, поэтому, если бы вы могли просто указать на какой-то ресурс или на то, как называется эта конкретная операция, это сработало бы.
$$ \frac{\partial}{\partial x}\biggl[ \frac{\partial u}{\partial \xi} \biggr] = \frac{\partial}{\partial \xi} \biggl[\frac{\ частичное и {\ парциальное \ xi} \ biggr] \ гидроразрыва {\ парциальное \ xi} {\ парциальное х} $$
Заранее спасибо.
ОБНОВЛЕНИЕ:
(согласно ответу @peek-a-boo)
P.S. Исправления или правки приветствуются.
Каноническая форма линейных УЧП второго порядка — ESE Jupyter Material
Математика для ученых и инженеров 2
Здесь мы рассматриваем общий УЧП второго порядка функции \(u(x, y)\):
(136)\[au_{xx} + bu_{xy} + cu_{yy} = f(x, y, u, u_x, u_y) \]
Напомним из предыдущего ноутбука, что проблема выше:
- 92 — 4ас < 0\)
Любое эллиптическое, параболическое или гиперболическое УЧП может быть приведено к следующим каноническим формам с подходящим преобразованием координат \(\xi = \xi(x, y), \qquad \eta = \eta(x,y)\ )
Каноническая форма для гиперболических УЧП: \(u_{\xi \eta} = \phi(\xi, \eta, u, u_{\xi}, u_{\eta}) \) или \( u_{\ xi \xi} — u_{\eta \eta} = \phi(\xi, \eta, u, u_{\xi}, u_{\eta})\)
Каноническая форма для параболических УЧП: \(u_{\eta \eta} = \phi(\xi, \eta, u, u_{\xi}, u_{\eta}) \) или \( u_{\xi \xi} = \phi(\xi, \eta, u, u_{\xi}, u_{\eta})\)
Каноническая форма для эллиптических УЧП: \(u_{\xi \xi} + u_{\eta \eta} = \phi(\xi, \eta, u, u_{\xi}, u_{\eta})\ )
Находим преобразование координат
\[\begin{split} u_x = u_\xi \xi_x + u_\eta \eta_x, \qquad u_y = u_\xi \xi_y + u_\eta \eta_y \\ \text{и аналогично для } u_{xx}, u_{xy}, u_{yy} \end{split}\]
Подключив это обратно к (136), мы получим
.
(137)\[ A u_{\xi \xi} + B u_{\xi \eta} + C u_{\eta \eta} = F(\xi, \eta, u, u_\xi, u_\eta ) \] 92 — 4ac > 0\) мы знаем, что это будут два различных действительных числа.
Но что на самом деле представляют величины \(\xi_x / \xi_y \) и \( \eta_x / \eta_y\)? Это наклоны характеристик \(\xi(x, y) = \text{const.}\) и \(\eta(x, y) = \text{const.}\) Обратите внимание, что если мы если бы мы не разделили уравнения на \(\xi_y\) и \(\eta_y\), мы получили бы
\[ \xi_x = \lambda_1 \xi_y, \qquad \eta_x = \lambda_2 \eta_y \]
, характеристические кривые которых удовлетворяют ОДУ
\[ \frac{dy}{dx} = -\lambda_1, \qquad \frac{dy}{dx} = -\lambda_2 \]
Решения этих ОДУ равны
\[ у + \лямбда_1 х = с_1, \qquad у + \лямбда_2 х = с_2 \]
, где \(c_1, c_2\) — константы интегрирования, поэтому мы выбираем \(\xi\) и \(\eta\) равными им
\[ \xi = y + \lambda_1 x, \qquad \eta = y + \lambda_2 x \]
Наконец, возвращаясь к канонической форме
\[ u_{\xi \eta} = F \]
интегрируем w.