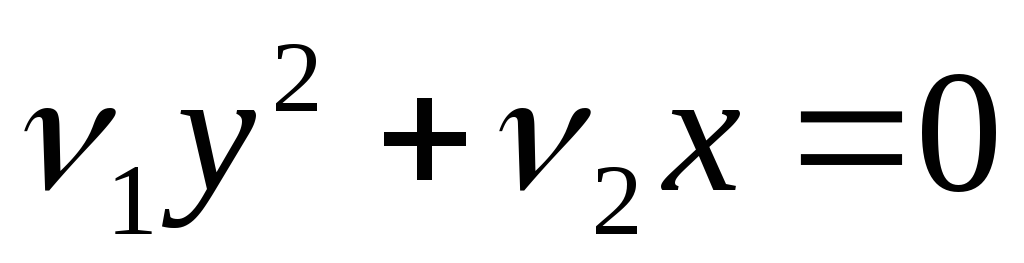Привести к каноническому виду квадратичную форму методом лагранжа онлайн: Привести к каноническому виду — Калькулятор с подробным решением онлайн

Каноническая форма ЗЛП онлайн

Каноническая форма ЗЛП — задача линейного программирования вида ax = b, где a — матрица коэффициентов, b — вектор ограничений.

Назначение сервиса. Онлайн-калькулятор предназначен для перехода ЗЛП к КЗЛП. Приведение задачи к канонической форме означает, что все ограничения будут иметь вид равенств, путем ввода дополнительных переменных.
Если на какую-либо переменную x_j не наложено ограничение, то она заменяется на разность дополнительных переменных, x_j = x_j1 — x_j2, x_j1 ≥ 0, x_j2 ≥ 0.

• Шаг №1
• Шаг №2
• Видеоинструкция

Инструкция. Выберите количество переменных и количество строк (количество ограничений). Полученное решение сохраняется в файле Word. Количество переменных 2345678910
Количество строк (количество ограничений) 2345678910

Математическая модель ЗЛП называется основной, если ограничения в ней представлены в виде уравнений при условии неотрицательности переменных.

Математическая модель называется канонической, если ее система ограничений представлена в виде системы m линейно независимых уравнений (ранг системы r=m), в системе выделен единичный базис, определены свободные переменные и целевая функция выражена через свободные переменные. При этом правые части уравнений неотрицательны (b_i ≥ 0).

Переменные, входящие в одно из уравнений системы с коэффициентом один и отсутствующие в других уравнениях называются базисными неизвестными, а все другие – свободными.

Решение системы называется базисным, если в нем свободные переменные равны 0, и оно имеет вид:
X_баз = (0, 0; b

1, …, b_m), f(X_баз) = c₀

Базисное решение является угловой точкой множества решений системы, т.е. определяет вершину многоугольника решений модели. Среди таких решений находится и то, при котором целевая функция принимает оптимальное значение.

Базисное решение называется опорным, если оно допустимо, т.е. все правые части уравнений системы (или неравенств) положительны b_i ≥ 0.

Компактная форма канонической модели имеет вид:
AX = b
X ≥ 0
Z = CX(max)

Понятие допустимого решения, области допустимых решений, оптимального решения задачи линейного программирования.
Определение 1. Вектор X, удовлетворяющий системе ограничений ЗЛП, в том числе и условиям неотрицательности, если они имеются, называется допустимым решением ЗЛП.

Определение 2. Совокупность всех допустимых решений образует область допустимых решений (ОДР) ЗЛП.
Определение 3. Допустимое решение, для которого целевая функция достигает максимума (или минимума), называется оптимальным решением.

В каждой задаче ЛП ищутся значения переменных при условии, чтобы:

• эти значения удовлетворяли некоторой системе линейных уравнений или неравенств;
• при этих значениях целевая функция обращалась бы в минимум или максимум.

Одним из универсальных методов ЛП является симплексный метод, который, однако, можно применять, если задача ЛП имеет каноническую форму.

Определение. Задача ЛП имеет каноническую форму, если все ограничения системы состоят только из уравнений (кроме неравенств, выражающих неотрицательность переменных) и целевую функцию необходимо минимизировать.

Примером такой задачи ЛП в канонической форме является задача 1 – сбалансированная транспортная задача с системой ограничений (1) и целевой функцией (2).
Однако в большинстве экономических задач чаще всего в систему ограничений первоначально входят не только уравнения, а и неравенства.

Утверждение. Любая общая задача ЛП может быть приведена к канонической форме.
Приведение общей задачи ЛП к канонической форме достигается путем введения новых (их называют дополнительными) переменных.
Система ограничений (3) этой задачи состоит из четырех неравенств. Введя дополнительные переменные y₁≥  0, y₂≥  0, y₃≥  0, y₄ ≥  0, можно перейти к системе ограничений:

Эти дополнительные переменные y _i имеют абсолютно ясный экономический смысл, а именно означают величину неиспользованного времени работы (простоя машины i-го вида).
Например, если бы машины первого вида работали все 18 ч, то x + y = 18, следовательно, y₁ = 0. Но мы допускаем возможность неполного использования времени работы первой машины x + y<18. В этом случае y₁ приобретает положительное значение и может рассматриваться как неиспользованный лимит времени. Например, зная решение этой задачи из пункта 3.3.2, x =  12, y =  6, мы можем из системы ограничений (3.9) сделать вывод, что y₁ =  y₂ =  y₃ =  0, а y₄ =  12 – 6  =  6.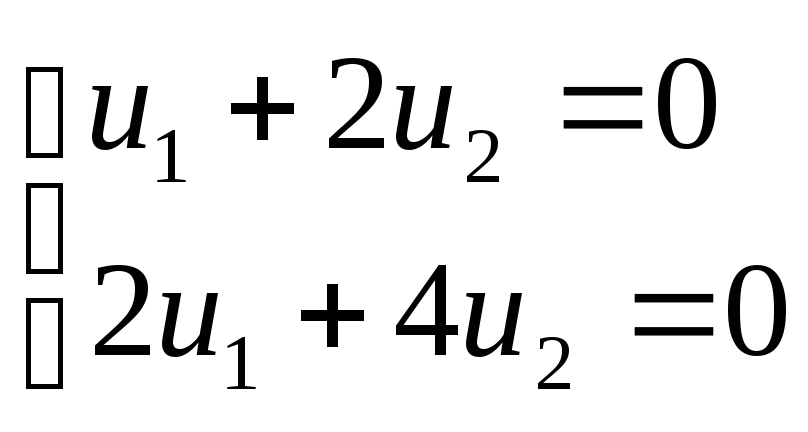

Т. е. машины первого, второго, третьего вида используют свое рабочее время полностью. А вот четвертая машина загружена лишь наполовину, 6 часов, и при заданном оптимальном плане простаивает. Возможно, после таких выводов руководителю предприятия захочется загрузить ее другой работой, сдать в аренду на это время и т.д.
Итак, введением дополнительных переменных мы можем любое ограничение типа неравенства привести к уравнению.

Рассмотрим задачу о смеси. Система ограничений имеет вид:

Неравенства были обращены в сторону «больше», поэтому вводя дополнительные переменные y₁, y₂, y₃≥ 0, их необходимо вычесть из левой части, чтобы уравнять ее с правой. Получим систему ограничений в канонической форме:
Переменные y_i также будут иметь экономический смысл. Если вы вспомните практическое содержание задачи, то переменная

y₁ будет означать количество излишнего вещества А в смеси, y₂ –количество излишков вещества В в смеси, y₃ – излишки С в смеси.
Задача нахождения максимального значения целевой функции может быть сведена к нахождению минимума для функции –F ввиду очевидности утверждения maxF = –min (–F). Посмотрите на рисунок: если в какой-то точке x= x₀ функция y= F(x) достигает своего максимума, то функция y= –F(x), симметричная ей относительно оси OX, в этой же точке x₀ достигнет минимума, причем F_max = – (–F_min) при x =  x₀.

Вывод. Для представления задачи ЛП в канонической форме необходимо:

• неравенства, входящие в систему ограничений задачи, преобразовать в уравнения с помощью введения дополнительных переменных;
• если целевая функция F→max (максимизируется), она заменяется на функцию –F→ min (которая минимизируется).

Пример №1. Следующую задачу ЛП привести к каноническому виду: F(X) = 5x1 + 3x2 → max при ограничениях:
2x₁ + 3x₂≤20
3x₁ + x₂≤15
4x₁≤16
3x₂≤12
Модель записана в стандартной форме. Введем балансовые неотрицательные переменные x₃, x₄, x₅, x₆, которые прибавим к левым частям ограничений-неравенств. В целевую функцию все дополнительные переменные введем с коэффициентами, равными нулю:

В первом неравенстве смысла (≤) вводим базисную переменную x₃. Во 2-ом неравенстве смысла (≤) вводим базисную переменную x₄. В третьем неравенстве вводим базисную переменную x₅. В 4-м неравенстве — базисную переменную x₆. Получим каноническую форму модели:
2x₁ + 3x₂ + 1x₃ + 0x₄ + 0x₅ + 0x₆ = 20
3x₁ + 1x₂ + 0x₃ + 1x₄ + 0x₅ + 0x₆ = 15
4x₁ + 0x₂ + 0x₃ + 0x₄ + 1x₅ + 0x₆ = 16
0x₁ + 3x₂ + 0x₃ + 0x₄ + 0x₅ + 1x₆ = 12
F(X) = 5x1 + 3x2 + 0x3 + 0x4 + 0x5 + 0x6 → max

Пример №2.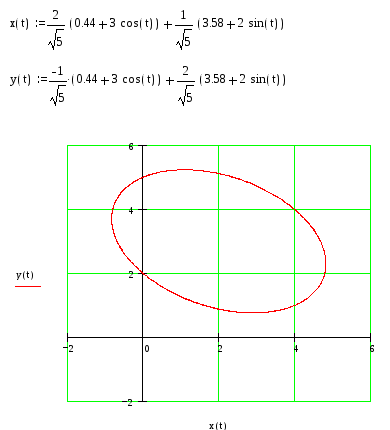 Найти два опорных решения системы
x₁ + 2x₄ – 2x₅ = 4
x₃ + 3x₄ + x₅ = 5
x₂ + 3x₅ = 2

Ответ: X = (4;2;5;0;0)

Пример №3. Привести к канонической форме следующую ЗЛП.
F = 2x₁ — x₂ + 4x₃ -2x₄ → min
при ограничениях:
7x₁ –x₂ +5x₃ + x₄ = -10
3x₁ +5x₂ -9x₃ + 2x₄ = 6
x₁ –x₂ -2x₃ + 6x₄ ≥ 7
x₁ +x₂ -5x₃ ≤ 11
7x₁ –x₂ -3x₃ — x₄ ≤ 9
x₁ ≥0 , x₂ ≥0 (обратите внимание, что переменные x

3 и x₄ имеют произвольный знак)

Для приведения ЗЛП к канонической форме необходимо:
1. Поменять знак у целевой функции
— F = -2x₁ + x₂ — 4x₃ +2x₄ → max

2. В левые части трех последних неравенств внести дополнительные переменные x₅, x₆, x₇ со знаком плюс или минус в зависимости от знака неравенства.
7x₁ –x₂ +5x₃ + x₄ = -10
3x₁ +5x₂ -9x₃ + 2x₄ = 6
x₁ –x₂ -2x₃ + 6x₄ –x₅ = 7
x₁ +x₂ -5x₃ +x₆ = 11
7x₁ –x₂ -3x₃ — x₄ +x₇ = 9
x₁ ≥0 , x₂ ≥0, x₅ ≥0 , x₆ ≥0, x₇ ≥0

3. Так как переменные x₃ и x₄ произвольного знака, то они заменяются разностями неотрицательных переменных.
7x₁ –x₂ +5(x₈ – x₉) + (x₁₀ – x₁₁) = -10
3x₁ +5x₂ -9(x₈ – x₉) + 2(x₁₀ – x₁₁) = 6
x₁ –x₂ -2(x₈ – x₉) + 6(x₁₀ – x₁₁) –x₅ = 7
x₁ +x₂ -5(x₈ – x₉) +x₆ = 11
7x₁ –x₂ -3(x₈ – x₉) — (x₁₀ – x₁₁) +x₇ = 9
x₁ ≥0 , x₂ ≥0, x₅ ≥0 , x₆ ≥0, x₇ ≥0 , x₈ ≥0, x₉ ≥0 , x₁₀ ≥0, x₁₁ ≥0

4. Соответствующая целевая функция примет вид:
— F = -2x₁ + x₂ — 4(x₈ – x₉) +2(x₁₀ – x₁₁) → max

см. также Как привести каноническую задачу линейного программирования к стандартной форме

Пример №2. Преобразовать следующие задачи ЛП к канонической форме и решить их симплекс-методом.

112. Приведение квадратичной формы к каноническому виду. Метод Лагранжа. Закон инерции

Теорема 1. Любую квадратичную форму

F(X1, x2,…, Xn) = F(X)= . (1)

невырожденным линейным преобразованием X=TY, где X = (X1, X2,…, Xn)T, Y = (Y1, Y2,…, Yn)T, можно привести к виду

H(Y1, Y2,…, Yn) = . (2)

Представление квадратичной формы в виде (2) называется Каноническим видом квадратичной формы. Коэффициенты называются Каноническими коэффициентами. Матрица квадратичной формы канонического вида — диагональная матрица.

Доказательство. Докажем теорему методом математической индукции по числу N переменных в квадратичной форме F. Пусть N =1. Тогда квадратичная форма F имеет вид F = B11X12 и является квадратичной формой канонического вида.

Предположим что теорема доказана для всех квадратичных форм, имеющих меньше чем N переменных, и докажем ее для квадратичной формы F, имеющей N переменных. Рассмотрим два случая.

1. Среди диагональных коэффициентов B11, B22, …, Bnn есть отличный от нуля. Пусть, например, B11 ≠ 0. Рассмотрим квадратичную форму , которая содержит такие же члены с неизвестным, как и наша форма F. Тогда разность

F(X1, X2,…, Xn) —

Будет квадратичной формой, содержащей только неизвестные X2,…, Xn. Отсюда

.

Вводим неизвестные

, (3)

И получим

, (4)

Где G( Y2,…, Yn) — квадратичная форма от не более чем N -1 неизвестной. Преобразование (3) невырожденное, так как матрица этого преобразования равна

,

И определитель равен B11 ≠ 0. Обратное ему преобразование тоже невырожденное и приводит форму F в форму (4). По индуктивному предположению квадратичную форму G( Y2,…, Yn) невырожденным преобразованием переменных Y2,…, Yn можно привести к квадратичной форме канонического вида. Это преобразование можно рассматривать как невырожденное, при котором неизвестная Y1 остается без изменения. Оно приводит квадратичную форму (4) к каноническому виду. Таким образом, невырожденным преобразованием переменных форма F приводится к каноническому виду.

2. Все диагональные коэффициенты B11, B22, …, Bnn равны нулю. Тогда среди коэффициентов формы должен быть отличный от нуля. Так как в противном случае форма тождественно равна нулю и являлась бы канонической. Пусть, например, B12 ≠ 0. Сделаем вспомогательное преобразование переменных так, чтобы в квадратичной форме появился квадрат. Сделаем преобразование переменных:

X1 = Z1 + Z2, X1 = Z1 — Z2, X3 = Z3,…, Xn = Zn.

Оно невырожденное, так как матрица этого преобразования равна

,

И определитель ее равен 2 и не равен нулю. В результате этого преобразования член нашей формы примет вид

2 a12X1X2 = 2 a12( Z1 + z2)(Z1 — z2) = 2 a12Z12 — 2 a12 z22,

И форме появляется ненулевой коэффициенты у квадратов двух переменных. Эти члены не могут сократиться с остальными членами, так как во все остальные члены войдет хотя бы одна из переменных Z3,…, Zn. Полученную квадратичную форму по первой части доказательства можно привести к квадратичной форме канонического вида невырожденным преобразованием переменных. 

Пример. Методом Лагранжа привести квадратичную форму к каноническому виду

,

И найти преобразование переменных, приводящую эту форму к каноническому виду.

Решение. Так как в форме нет квадратов переменных, то сделаем преобразование переменных

X1 = Z1 + Z2, X1 = Z1 — Z2, X3 = Z3

Матрица этого преобразования равно

И квадратичная форма преобразуется к виду

.

Выделим полный квадрат из членов, содержащих X1

.

Полагаем Y1 =Z1 +(5/2)Z3, Y2 = Z2+(1/2) Z3, Y3 = Z3 приведем квадратичную форму к каноническому виду

.

Выразим неизвестные Z1 =Y1 — (5/2)Y3, Z2 = Y2-(1/2) Y3, Z3 = Y3. Последнее преобразование имеет матрицу

.

Тогда преобразование, переводящее данную квадратичную форму к форме канонического вида имеет матрицу, равную произведению матриц.

,

Преобразование переменных имеет вид:

X1 =Y1 + Y2 — 6Y3, X2 =Y1 — Y2 — 4Y3, X3 = Y3.

< Предыдущая		Следующая >

T D P = H, $ требуем, чтобы $P$ было обратимым. Тогда количество положительных элементов на диагонали $D$ равно количеству положительных собственных значений $H,$ количество отрицательных элементов на диагонали $D$ равно количеству собственных значений $H,$ наконец, количество нулевых элементов на диагонали $D$ совпадает с количеством нулевых собственных значений $H.$ Диагональные элементы $D$ равны НЕ собственным значениям $H,$ точно такие же $\ знаки pm$. Итак, новые имена, $$ Д = \левый( \начать{массив}{рррр} 1 и 0 и 0 и 0 \\ 0 и -1 и 0 и 0 \\ 0 и 0 и 1 и 0 \\ 0 и 0 и 0 и 0 \конец{массив} \верно) $$ $$ П = \левый( \начать{массив}{рррр} 1 и 1 и 2 и -1 \\ 0 и 1 и -1 и 1 \\ 0 и -1 и 1 и 1 \\ 0 и -1 и 0 и 1 \конец{массив} \верно), $$ $$ П^Т = \левый( \начать{массив}{рррр} 1 и 0 и 0 и 0 \\ 1 и 1 и -1 и -1 \\ 2 и -1 и 1 и 0 \\ -1 и 1 и 1 и 1 \конец{массив} \верно), $$ затем $$ \det P = 2 $$ $$ P^T D P = H $$

Описание алгоритма симметричной матрицы на http://math.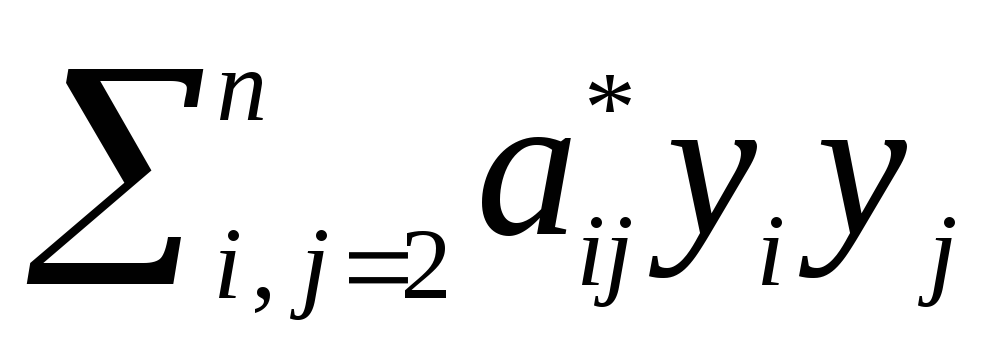 stackexchange.com/questions/1388421/reference-for-linear-алгебра-books-that-teach-reverse-hermite-method-for-symmetr

 parisize = 4000000 , праймлимит = 500509
? ч = [ 1,1,2,-1; 1,1,2,-3; 2,2,4,0; -1,-3,0,1]
%1 =
[1 1 2 -1]
[1 1 2 -3]
[2 2 4 0]
[-1 -3 0 1]
? ht = маттранспонировать (ч)
%2 =
[1 1 2 -1]
[1 1 2 -3]
[2 2 4 0]
[-1 -3 0 1]
? ч - чт
%3 =
[0 0 0 0]
[0 0 0 0]
[0 0 0 0]
[0 0 0 0]
? идентификатор = [ 1,0,0,0; 0,1,0,0; 0,0,1,0; 0,0,0,1]
%4 =
[1 0 0 0]
[0 1 0 0]
[0 0 1 0]
[0 0 0 1]
? г1 = [ 1,-1,-2,1; 0,1,0,0; 0,0,1,0; 0,0,0,1]
%5 =
[1 -1 -2 1]
[0 1 0 0]
[0 0 1 0]
[0 0 0 1]
? r1t = маттранспонировать (r1)
%6 =
[1 0 0 0]
[-1 1 0 0]
[-2 0 1 0]
[1 0 0 1]
? h2 = r1t * h * r1
%7 =
[1 0 0 0]
[0 0 0 -2]
[0 0 0 2]
[0 -2 2 0]
? г2 = [ 1,0,0,0; 0,1,0,0; 0,0,1,0; 0,1,0,1]
%8 =
[1 0 0 0]
[0 1 0 0]
[0 0 1 0]
[0 1 0 1]
? r2t = маттранспонировать (r2)
%9"="
[1 0 0 0]
[0 1 0 1]
[0 0 1 0]
[0 0 0 1]
? h3 = r2t * h2 * r2
%10 =
[1 0 0 0]
[0–4 2–2]
[0 2 0 2]
[0 -2 2 0]
? г3 = [ 1,0,0,0; 0,1,1/2,-1/2; 0,0,1,0; 0,0,0,1]
%11 =
[1 0 0 0]
[0 1 1/2 -1/2]
[0 0 1 0]
[0 0 0 1]
? r3t = маттранспонировать (r3)
%12 =
[1 0 0 0]
[0 1 0 0]
[0 1/2 1 0]
[0 -1/2 0 1]
? h4 = r3t * h3 * r3
%13 =
[1 0 0 0]
[0 -4 0 0]
[0 0 1 1]
[0 0 1 1]
? г4 = [ 1,0,0,0; 0,1,0,0; 0,0,1,-1; 0,0,0,1]
%14 =
[1 0 0 0]
[0 1 0 0]
[0 0 1 -1]
[0 0 0 1]
? r4t = маттранспонировать (r4)
%15 =
[1 0 0 0]
[0 1 0 0]
[0 0 1 0]
[0 0 -1 1]
? h5 = r4t * h4 * r4
%16 =
[1 0 0 0]
[0 -4 0 0]
[0 0 1 0]
[0 0 0 0]
? д = h5
%17 =
[1 0 0 0]
[0 -4 0 0]
[0 0 1 0]
[0 0 0 0]
? г = г1 * г2 * г3 * г4
%18 =
[1 0 -2 3]
[0 1 1/2 -1]
[0 0 1 -1]
[0 1 1/2 0]
? матдет (р)
%19= 1
? q = матадджойнт (r)
%20 =
[1 1 2 -1]
[0 1/2 -1/2 1/2]
[0 -1 1 1]
[0 -1 0 1]
? qt = маттранспонировать (q)
%21 =
[1 0 0 0]
[1 1/2 -1 -1]
[2 -1/2 1 0]
[-1 1/2 1 1]
? час
%22 =
[1 1 2 -1]
[1 1 2 -3]
[2 2 4 0]
[-1 -3 0 1]
? qt * д * q
%23 =
[1 1 2 -1]
[1 1 2 -3]
[2 2 4 0]
[-1 -3 0 1]
? д
%24 =
[1 1 2 -1]
[0 1/2 -1/2 1/2]
[0 -1 1 1]
[0 -1 0 1]
? г
%25 =
[1 0 0 0]
[0 -4 0 0]
[0 0 1 0]
[0 0 0 0]
?
 

линейная алгебра — квадратичная форма с методом Лагранжа

Задавать вопрос

спросил 7 лет, 4 месяца назад

Изменено 6 лет, 4 месяца назад

Просмотрено 3к раз

$\begingroup$

Я пытаюсь понять, как использовать метод Лагранжа в следующей квадратичной форме:

$$q(x_1, x_2, x_3, x_4) = 2x_1x_4 — 6x_2x_3$$ 92\,=\,4ab $$

$\endgroup$

$\begingroup$

Если умножить в первом уравнении, то получится исходное.