Признаки делимости на 3 и на 9 6 класс: Сформулируйте признаки делимости на 3 и на 9

Урок математики «Признак делимости на 3 и на 9»

Урок математики по теме «Признаки делимости на 3 и на 9».

Цель урока: создание условий для формирования умения применять признаки делимости на 3 и на 9 в различных ситуациях

Планируемые результаты освоения (формирование УУД):

Личностные:

• формирование у учащихся готовности и способности к самообразованию на основе мотивации к обучению и познанию;

• формирование уважительного и доброжелательного отношения к другому человеку, его мнению;

• формирование коммуникативной компетентности в общении и сотрудничестве со сверстниками в процессе учебно-исследовательской деятельности.

Метапредметные: развитие у учащихся умений:

• находить необходимую информацию в тексте;

• анализировать информацию;

• устанавливать причинно-следственные связи, проводить умозаключение и делать выводы;

• соотносить свои действия с планируемыми результатами;

• слышать, слушать и понимать собеседника;

• планировать и согласованно выполнять совместную деятельность.

Предметные:

Тип урока: урок усвоения новых знаний.

Форма урока: урок-исследование.

Методы обучения: метод проблемной беседы, фронтальный опрос, самостоятельная работа.

Форма обучения: фронтальная, парная, индивидуальная.

Форма учебного занятия: классно-урочная.

Оборудование урока:  раздаточный материал (для самостоятельной работы.

Ход учебного занятия

I. Организационный этап

Приветствие, фиксация отсутствующих, проверка подготовленности учащихся к учебному занятию.

Здравствуйте! Садитесь!

II. Актуализация опорных знаний и способов действий

Деятельность учителя	Деятельность ученика
На прошлом уроке мы с вами закончили изучать тему: «признаки делимости на 2,5 и т.д. и сегодня переходим к следующей теме. Ребята, а как вы думаете, что нам на уроке сегодня пригодится?	Ответы детей (удача, знания)
А еще сегодня нам  пригодятся: знание материала; желание открыть истину; добросовестная работа; осмысление произведенной деятельности. уважение друг к другу
Откройте тетради. Запишите дату, классная работа. Домашнее задание: №857, №862 а, б
Отложили тетради в сторону и начнём с устной работы, которая поможет определить тему и цель сегодняшнего урока. Ребята, мы сейчас работаем с числами, которые мы с вами используем при счете предметов. О каких числах я говорю?	Мы работаем с натуральными числами.
Что нового мы узнали о натуральных числах?	Мы познакомились с признаками делимости на 2, 5, 10, 4 и25.
Где и для чего используются признаки делимости?	При решении задач, для быстроты счета.
Сформулируйте признак делимости на 2.	Если запись натурального числа оканчивается четной цифрой, то это число делится на 2 без остатка.
Сколько всего цифр?	10
Сколько четных цифр? Назовите их.	5: 0, 2, 4, 6, 8
Сколько нечетных цифр? Назовите их.	5: 1, 3, 5, 7, 9
Привести пример трехзначного числа, делящегося без остатка на 5. Почему это число делится на 5?	Например: 375, 420 Это число делится на 5, потому что оно оканчивается цифрой 5 или 0.
Делится ли число 3468 на 10 без остатка и почему?	Нет, так как оно не оканчивается на цифру 0.
Назовите число, которое делится на 5, но не делиться на 25	1005
Приведите пример трехзначного числа кратного 4	400, 412

III. Постановка целей и задач урока, мотивация учебной деятельности обучающихся

Деятельность учителя	Деятельность ученика
А сейчас ответьте на вопрос: делится ли число 36 на 3 без остатка? А на 9?	Делится и на 3, и на 9 без остатка.
Перед вами число: (слайд 5) Вопрос: делится ли данное число на 3, на 9?	Дети не могут сразу ответить. ??????
Кто хочет попробовать разделить у доски это число на 3? Может быть, найдутся желающие разделить данное число на 9?	Нам не хватит целого урока для этого. Желающих нет.
Мы с вами уже изучили признаки делимости натуральных чисел на 2, на 5 и на 10. Возникает вопрос: а нет ли других признаков деления, в частности, на 3 и на 9. Очевидно, есть. Какая же цель стоит перед нами?	Выяснить, какие натуральные числа делятся на 3 и на 9 без остатка.
Какая же тема сегодняшнего урока?	Признаки делимости на 3 и на 9.
Запишите эту тему в тетрадь
Давайте решим следующую задачу и посмотрим, какие условия должны выполняться, чтобы число делилось на 3 и на 9 не выполняя деления?	Дети выдвигают предположения (гипотезы). Можно разбить уч-ся на группы. Например, группа №1 и №2 выдвигают гипотезы о делении на 3; группа №3 и №4 – на 9.

Результат: выдвижение гипотез о делении на 3 и на 9.

IV. Первичное усвоение новых знаний

Задача: Выяснить, можно ли разложить 225 яблок в 9 ящиков поровну?

Чтобы ответить на этот вопрос, нужно выяснить: делится ли число 225 на 3 без остатка. (Если дети предложили делить 225 на 3, то: «Замечательно, только давайте вспомним, что мы решили найти способ ответить на этот вопрос, не выполняя деление, с помощью других рассуждений. Давайте попробуем это сделать»)

Рассуждения вместе с классом:

Сколько сотен, десятков и единиц в данном числе? 2 сотни, 2 десятка и 5 единиц.

Если мы возьмем одну сотню и разложим в 3 корзины поровну – сколько яблок останется лишними? 1 яблоко. Значит, с каждой сотни по 1 яблоку, т.е. с 2 сотен – 2 яблока. Если мы возьмем 1 десяток и разложим в 3 корзины поровну – сколько останется лишних яблок? 1 яблоко с каждого десятка. Т.е. с наших 2 десятков – 2 яблока. И еще у нас 5 яблок. Итого не разложенными в корзины у нас остается: 2+2+5 яблок, всего 9 яблок, которые мы легко распределим по 3 корзинам. Вывод: 225 яблок можно разложить в 3 корзины.

На доске при этом будут только следующие записи:

225 яблок в 9 ящиков поровну

2+2+5=9

Т.е. 225 делится на 9, разложить можно.

А в 3 ящика? Тоже можно.

Посмотрите внимательно на наши рассуждения, что интересного вы заметили?  Какой вывод можно сделать?

Исследование

Цель: доказательство выдвинутых предположений.

Учащиеся работают в группах (3 группы).

Заполнить таблицу:

Число	1812	162	6507	205	980	824
Сумма цифр числа	12	9	18	7	17	14

Разделить на 3 и на 9 каждое из чисел в таблице. Каждая группа делит по два числа. Что мы замечаем? (первые три числа делятся на 3 без остатка, а последние 3 числа не делятся на 3; на 9 делятся без остатка 162 и 6507, остальные не делятся на 9). Найдите сумму цифр каждого числа и заполните таблицу. Какой вывод можно сделать? Сформулируйте признак делимости на 3 и на 9. Учащиеся самостоятельно формулируют признак делимости на 3 и на 9. Если сумма цифр числа делится на 3, то и число делится на 3 без остатка. Если сумма цифр числа делится на 9, то и число делится на 9 без остатка. Откройте учебник на стр. 14 и прочитайте правило на делимость чисел на 3 и на 9.

Охарактеризуйте следующее событие:

Результат: в ходе исследования учащиеся ознакомились с выводами о делимости чисел на 3 и на 9 и самостоятельно сформулировали признак делимости на 3 и на 9.

V. Первичная проверка понимания нового материала

Цель: использовать новые знания при решении задач.

Деятельность учителя	Деятельность ученика
Вернемся к нашей первой задаче и проверим, делится ли число 1111111…. .111 2025 штук             на 3? (переход со слайда 9 на слайд 5) Вооружимся новым знанием и проверим, делится ли 2025 на 3. Найдем сумму цифр этого числа.	В нашем числе две тысячи двадцать пять  единиц. Значит, сумма цифр этого числа  2+2+5=9. Число 9 делится на 3. Отсюда следует, что наше большое число тоже будет делиться на 3.
А на 9 это число будет делиться?	Будет, так как сумма цифр этого числа равна 9, а число 9 делится на 9.
Итак, какие признаки делимости мы знаем?	5: признак делимости на 2, на 3, на 5, на 9 и на 10.
На какие две группы мы можем разбить эти признаки? (переход со слайда 5 на слайд 10)	Признак делимости по последней цифре и по сумме цифр.

Результат: актуализация знаний в ходе решения задач.

VI. Первичное закрепление нового материала

а) Какие цифры надо поставить вместо звездочки в запись числа, чтобы полученные числа делились на 3? *14 (114, 414, 714)

б) Какие цифры надо поставить вместо звездочки в запись числа, чтобы полученные числа делились на 9? 5*36 (5436)

№855 с комментированием

№860 а, б

Из чисел 591, 253, 417, 648, 639, 346 выберите те, которые: а) кратны 3, б)кратны 9

VII. Проверка усвоения нового материала

Самостоятельная работа: работа в парах – тестирование.

VIII. Информация о домашнем задании и инструктаж по его выполнению

IX. Рефлексия

Подводятся итоги урока 

1. Для чего необходимо знать признаки делимости?

2. С какими признаками делимости мы познакомились?

3. Почему признаки делимости на 2, 5, 10 определены в одной группе, а признаки делимости на 3, 9 – в другой?

4. Сформулируйте признак делимости на 3 и на 9.

2) (на партах лист со словами, дети ставят знак у тех слов, которые им больше подходят к окончанию урока).

Урок математики 6 класс.Признаки делимости на 3 и 9 | План-конспект занятия по математике (6 класс) на тему:

Урок математики по теме

«Признаки делимости на 3 и 9».

6-й класс

Учитель: Леванович Светлана Владимировна

Цель деятельности учителя:

• Создать условия для формирования представлений о признаках делимости на 3 и 9; умения сокращать большие дроби, используя признаки делимости; овладения навыками и умениями проверять делимость числа на 3 и 9.

Планируемые результаты изучения темы:

Личностные:

• формирование у учащихся готовности и способности к самообразованию на основе мотивации к обучению и познанию;
• формирование уважительного и доброжелательного отношения к другому человеку, его мнению;
• формирование коммуникативной компетентности в общении и сотрудничестве со сверстниками в процессе учебно-исследовательской деятельности.

Предметные:

• формирование представлений учащихся о признаках делимости на 3 и на 9 и способах их доказательства;
• развитие умений применять изученные признаки делимости при решении задач.

Метапредметные (УУД): 

Познавательные:

• находить необходимую информацию в тексте;
• анализировать информацию;
• формулировать гипотезы;
• устанавливать причинно-следственные связи, проводить умозаключение и делать выводы;

Регулятивные:

• соотносить свои действия с планируемыми результатами;
• различать способ и результат действия;

Коммуникативные:

• слышать, слушать и понимать собеседника;
• планировать и согласованно выполнять совместную деятельность.

Тип урока: урок усвоения новых знаний.

Форма урока: урок-исследование.

Методы обучения: метод проблемной беседы, фронтальный опрос, самостоятельная работа.

Форма обучения: коллективная, индивидуальная.

Форма учебного занятия: классно-урочная.

Оборудование урока: компьютер, мультимедийный проектор, раздаточный материал (для самостоятельной работы), презентация к уроку.

Урок построен на основе деятельностного подхода и технологии проблемного обучения, что предполагает максимальное использование собственной исследовательской активности ученика по определению, поиску и нахождению нового знания. В ходе урока планируются не только предметные результаты обучения, но и метапредметные, и личностные.

Основной метод, применяемый на уроке, – метод исследования, предполагающий построение обучения как творческого процесса открытия ребенком нового знания. Способы организации деятельности учащихся на уроке – групповая и индивидуальная работа.

Девиз урока: «Дорогу осилит идущий, а математику – мыслящий».

Ход учебного занятия

I. Организационный этап

Приветствие, фиксация отсутствующих, проверка подготовленности учащихся к учебному занятию.

Проверьте готовность к уроку: у всех ли на партах лежат учебники, тетради, дневники, ручки.

Здравствуйте! Садитесь!

Все сейчас мне улыбнитесь!

II. Актуализация опорных знаний и способов действий

Друзья мои! Я очень рада
Войти в приветливый ваш класс
И для меня уже награда
Вниманье ваших умных глаз
Я знаю: каждый в классе гений,
Но без труда талант не впрок
Из ваших знаний и умений 
Мы вместе сочиним урок.
Мои соавторы и судьи, 
Оценкой вас не накажу, 
За странный слог не обессудьте,
А дальше прозой я скажу.

хорошее настроение;

уважение друг к другу;

знание материала;

желание открыть истину;

добросовестная работа;

осмысление произведенной деятельности.

 

Откройте тетради. Запишите сегодняшнее число, Классная работа.

 А девизом нашего урока будут такие слова: «Дорогу осилит идущий, а математику – мыслящий»

 

Ребята, на наших уроках  мы работаем с числами, которые составляют основу математической науки. О каких числах я говорю?

Мы работаем с натуральными числами.

Что нового мы узнали о натуральных числах?

Мы познакомились с признаками делимости на 2, 5, 10.

Где и для чего используются признаки делимости?

При решении задач, для быстроты счета, при сокращении дробей.

Сформулируйте признак делимости на 2.

Если запись натурального числа оканчивается четной цифрой, то это число делится на 2 без остатка.

Сколько всего цифр?

10

Сколько четных цифр? Назовите их.

5: 0, 2, 4, 6, 8

Сколько нечетных цифр? Назовите их.

5: 1, 3, 5, 7, 9

Привести пример трехзначного числа, делящегося без остатка на 5. Почему это число делится на 5?

Например: 375, 420

Это число делится на 5, потому что оно оканчивается цифрой 5 или 0.

Делится ли число 3468 на 10 без остатка и почему?

Нет, так как оно не оканчивается на цифру 0.

III. Постановка целей и задач урока, мотивация учебной деятельности обучающихся.

У китайцев есть притча:

Скажи мне – и я забуду;
Покажи мне – и я запомню;
Дай сделать – и я пойму.

Так давайте на уроке совместно попробуем вывести новые правила, научимся применять их при решении задач.

Делится и на 3, и на 9 без остатка.

Перед вами число: (слайд 5)

Вопрос: делится ли данное число на 3, на 9?

Дети не могут сразу ответить.

??????

Кто хочет попробовать разделить у доски это число на 3? Может быть, найдутся желающие разделить данное число на 9?

Нам не хватит целого урока для этого.

Желающих нет.

Мы с вами уже изучили признаки делимости натуральных чисел на 2, на 5 и на 10. Возникает вопрос: а нет ли других признаков деления, в частности, на 3 и на 9. Очевидно, есть. Какая же цель стоит перед нами?

Выяснить, какие натуральные числа делятся на 3 и на 9 без остатка.

Какая же тема сегодняшнего урока?

Признаки делимости на 3 и на 9.

Запишите эту тему в тетрадь (слайд )

 

Подумайте, какие условия должны выполняться, чтобы число делилось на 3 и на 9?

Дети выдвигают предположения (гипотезы).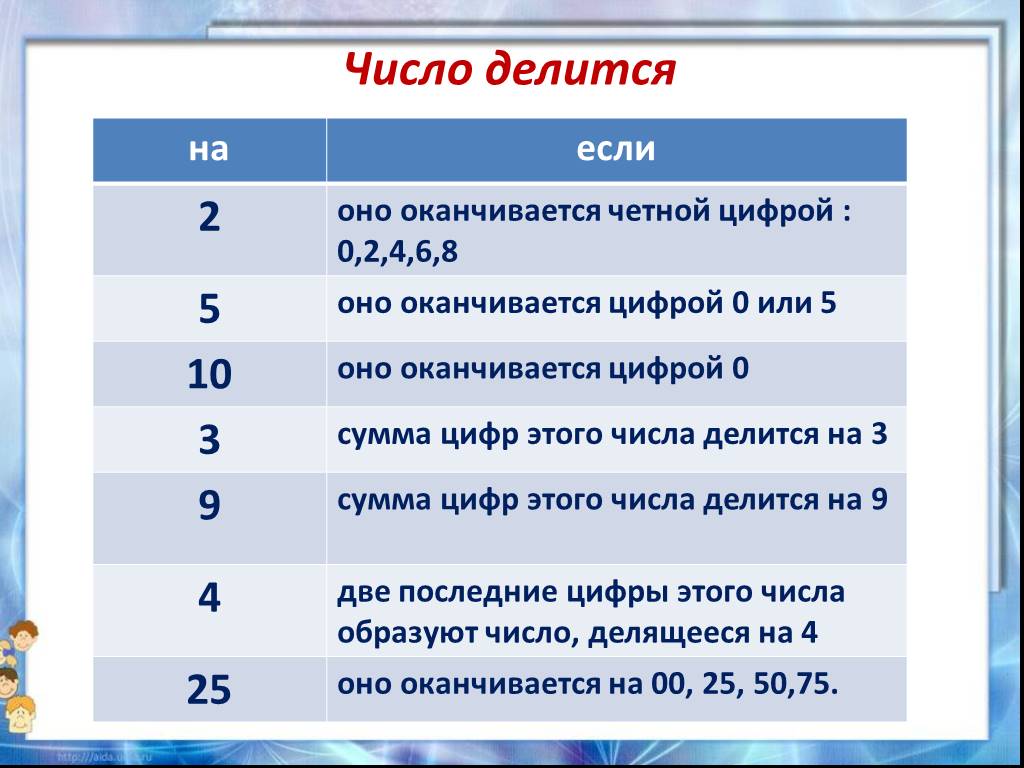 Можно разбить уч-ся на группы. Например, группа №1 и №2 выдвигают гипотезы о делении на 3; группа №3 и №4 – на 9.

Результат: выдвижение гипотез о делении на 3 и на 9.

IV. Первичное усвоение новых знаний

Задача: Выяснить, можно ли разложить 225 яблок в 3 ящика поровну?

Чтобы ответить на этот вопрос, нужно выяснить: делится ли число 225 на 3 без остатка. (Если дети предложили делить 225 на 3, то: «Замечательно, только давайте вспомним, что мы решили найти способ ответить на этот вопрос, не выполняя деление, с помощью других рассуждений. Давайте попробуем это сделать»)

Рассуждения вместе с классом:

Сколько сотен, десятков и единиц в данном числе? 2 сотни, 2 десятка и 5 единиц.

Если мы возьмем одну сотню и разложим в 3 корзины поровну – сколько яблок останется лишними? 1 яблоко. Значит, с каждой сотни по 1 яблоку, т.е. с 2 сотен – 2 яблока. Если мы возьмем 1 десяток и разложим в 3 корзины поровну – сколько останется лишних яблок? 1 яблоко с каждого десятка. Т.е. с наших 2 десятков – 2 яблока. И еще у нас 5 яблок. Итого не разложенными в корзины у нас остается: 2+2+5 яблок, всего 9 яблок, которые мы легко распределим по 3 корзинам. Вывод: 225 яблок можно разложить в 3 корзины.

На доске при этом будут только следующие записи:

225 яблок в 3 ящика поровну

2+2+5=9

Т.е. 225 делится на 3, разложить можно.

А в 9 ящиков? Тоже можно.

Посмотрите внимательно на наши рассуждения, что интересного вы заметили?  Какой вывод можно сделать?

Исследование

Цель: доказательство выдвинутых предположений.

Учащиеся работают в группах (3 группы).

Заполнить таблицу:

Разделить на 3 и на 9 каждое из чисел в таблице. Каждая группа делит по два числа. Что мы замечаем? (первые три числа делятся на 3 без остатка, а последние 3 числа не делятся на 3; на 9 делятся без остатка 162 и 6507, остальные не делятся на 9). Найдите сумму цифр каждого числа и заполните таблицу. Какой вывод можно сделать? Сформулируйте признак делимости на 3 и на 9. Учащиеся самостоятельно формулируют признак делимости на 3 и на 9. Если сумма цифр числа делится на 3, то и число делится на 3 без остатка. Если сумма цифр числа делится на 9, то и число делится на 9 без остатка. Откройте учебник на стр. 187 и прочитайте правило на делимость чисел на 3 и на 9.

Результат: в ходе исследования учащиеся ознакомились с выводами о делимости чисел на 3 и на 9 и самостоятельно сформулировали признак делимости на 3 и на 9.

V. Первичная проверка понимания нового материала

Цель: использовать новые знания при решении задач.

На какие две группы мы можем разбить эти признаки? (слайд )

Признак делимости по последней цифре и по сумме цифр.

Результат: актуализация знаний в ходе решения задач.

VI. Первичное закрепление нового материала

№ 61 ( а, б)(устно ).

Ответы: а) на3: 2 или 8, на 9: 8; б) на 3: 2,5 или 8; на 9: только 5.

Данное задание выполнить  (с комментарием).

Комментарий: сумма цифр числа 162 равна 9, значит, число делится на 9. Сумма цифр числа 108 равна 9, поэтому число делится на 9. Следовательно, эти две заявки можно распределить поровну между девятью ремонтными бригадами компании.

№ Задание № 82 (на доске и в тетрадях):

А) ; б) ; в) несократимая дробь; г) ; д) ; е) .

VII. Проверка усвоения нового материала

Самостоятельная работа: (каждому ученику раздается индивидуальная карточка с напечатанным на ней заданием и местом для решения)

Взаимопроверка (слайд 13, 14). Сдача работ.

VIII. Информация о домашнем задании и инструктаж по его выполнению

Найти признаки делимости на 4, 6, 7 и 11.

п. 3, № 86, № 88.

IX. Рефлексия

Подводятся итоги урока (слайд 16)

1)

1. Для чего необходимо знать признаки делимости?
2. С какими признаками делимости мы познакомились?
3. Почему признаки делимости на 2, 5, 10 определены в одной группе, а признаки делимости на 3, 9 – в другой?
4. Сформулируйте признак делимости на 3 и на 9.

2) (на партах лист со словами, дети ставят знак у тех слов, которые им больше подходят к окончанию урока).

1. Урок полезен, всё понятно.
2. Лишь кое-что чуть-чуть неясно.
3. Ещё придётся потрудиться.
4. Да, трудно всё-таки учиться!

3) Учащиеся по кругу высказываются одним предложением.

• Я научился…
• Было трудно…
• Сегодня я узнал…
• У меня получилось…
• Теперь я могу…

Урока время истекло
Я вам ребята благодарна 
За то, что встретили тепло
И поработали ударно.

Спасибо вам за урок.

(слайд 17)

Правила делимости на 3, 6 и 9 — Математика 3-го класса

Делимое число означает, что одно число можно разделить на другое без остатка.

На прошлом уроке вы узнали, что число, оканчивающееся на 0, делится на 2, 5 и 10. 

Давайте узнаем еще несколько правил делимости!

Делится на 3

Есть хитрость, чтобы определить, делится ли число на 3! 😀

Число делится на 3, если сумма его цифр делится на 3.  

Что это значит?!

Давайте попробуем!

342

Этот номер состоит из трех цифр! Кто они такие?

3, 4, и 2

Сложим эти цифры:

3 + 4 + 2 = 9

Делится ли 9 на 3?

Да! Это означает, что 342 также делится на 3! ✅

Совет : На 3 делятся только однозначные числа: 3, 6 и 9. 

Давайте попробуем еще раз!

Делится ли это число на 3? 👇

8,217

Найдем сумму цифр!

8 + 2 + 1 + 7 = 18

Отлично! А теперь еще один совет.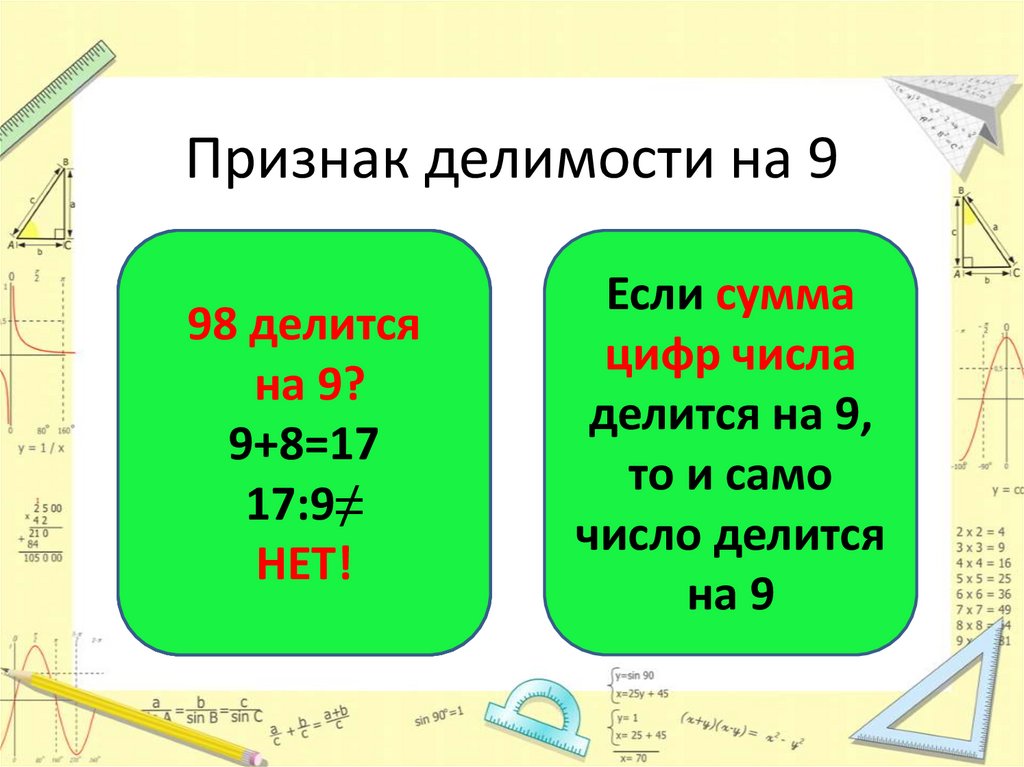 Если вы складываете и находите двузначное число, сложите цифры еще раз!

Найдите сумму цифр числа 18.

1 + 8 = 9

Делится ли 9 на 3? 🤔

Да! Это означает, что 8 217 делится на 3. 

Еще раз!

6 701

Добавим цифры.

6 + 7 + 0 + 1 = 14

Теперь сложите цифры числа 14.

1 + 4 = 5

Делится ли 5 ​​на 3? 🤔

Нет, это не так! Это означает, что 6701 не делится на 3.  

Делится на 6

Вы уже знаете половину правила делимости на 6!

Если число делится на 6, оно делится на на 3 и 2 .

Число делится на 2, если оно оканчивается на 0, 2, 4, 6 или 8. 

Делится ли это число на 6? 👇

1,836

Давайте проверим. Делится ли оно на 3?

👉 Найдите сумму цифр!

1 + 8 + 3 + 6 = 18

Попробуйте еще раз!

1 + 8 = 9

Да, 1836 делится на 3.

Мы еще не закончили! Оно тоже делится на 2?

Да, он заканчивается на 6!

Итак, 1836 делится на 6. ✅

Давайте попробуем еще раз!

Делится ли 42 129 на 6?

Начните с проверки, делится ли оно на 3:

4 + 2 + 1 + 2 + 9 = 18

Еще раз!

1 + 8 = 9

Да, 42 129 делится на 3.

Оно также делится на 2?

Нет, оно не оканчивается на 0, 2, 4, 6 или 8.

Это означает, что 42 129 равно , а не делится на 6.

Делится на 9

Выяснить, делится ли число на 9, означает снова найти сумму цифр!

Число делится на 9 , если сумма его цифр также делится на 9.

Делится ли число 567 на 9?

Найдем сумму цифр!

5 + 6 + 7 = 18

Вы помните, делится ли 18 на 9? 🤔

Ничего страшного, если нет. Мы можем найти сумму цифр 18.

1 + 8 = 9

Поскольку оно равно 9, мы знаем, что 567 делится на 9.

Давайте попробуем еще раз!

Делится ли 48 933 на 9?

Найдите сумму цифр:

4 + 8 + 9 + 3 + 3 = 27

Делится ли 27 на 9?

Так и есть! Но если бы вы этого не знали, то могли бы снова найти сумму цифр:

2 + 7 = 9

Это равно 9! Это означает, что 48 933 делится на 9.

Отличная работа! 🎉

902:20 Теперь завершите практику, чтобы дольше помнить.

Урок математики — Делимость (6 класс)

 

Мы узнаем о правила делимости.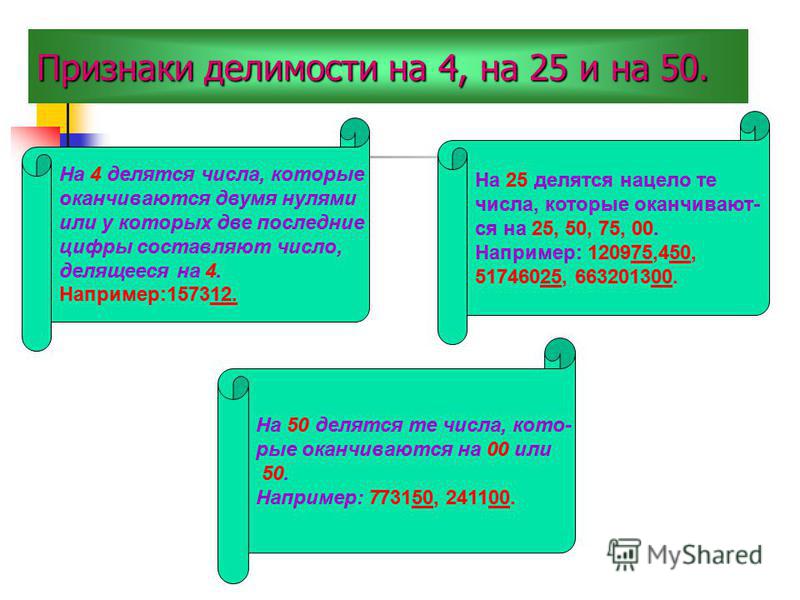 Мы выясним, делится ли заданное число на 2, 3, 4, 5, 6, 8, 9 или 10.

Начать с делимости правила:

Число делится на 2 если число четное (последняя цифра 0, 2, 4, 6 или 8)

Приведите несколько примеров (т.е. 50, 21, 14, 896, 1358)

Запросить ответ учащегося (СР)

Обведите последнюю цифру и укажите, является ли эта цифра четной, если число делится на 2

 

Число делится на 3 если сумма цифр делится на 3

Спросите, может ли один ученик напомни мне что значит сумма

Сначала пройдите их примеры

1,035- прибавление 1 к 3 к 5 и это равно 9, поэтому оно делится на 3

2,573- прибавление 2 к 5 к 7 на 3 и равно 17, которое не делится на 3

Еще примеры

 

Число делится на 4 если последние две цифры образуют число, кратное 4

Сообщите учащимся, что они следует обвести последние две цифры, на которые мы обращаем внимание для это правило делимости.

Приведите пример

1024- Обведите последние два цифры и спросите учащихся, делится ли 24 на 4. Да, значит, все число 1024 делится на 4

5862- Обведите два последних цифры. Позвоните конкретному учащемуся и спросите, делится ли 62 на 4.

446- Обведите последние два цифры.

46 не делится на 4 

Еще примеры

 

Число делится на 5 если последняя цифра 0 или 5.

Приведи примеры какие-нибудь содержащее 5 или 0 в качестве последней цифры. Некоторые содержат 5 или 0, но последний цифра это другое число

50, 665, 757

853, 785, 670

507, 40, 340

Запрашивать SR на строку.

 

Число делится на 6 если число делится на 2 и 3. Когда вы делаете домашнее задание и проверяя все правила делимости, вы можете просто проверить, и если у вас есть сказал, что число делится на 2 и 3, то оно будет делиться на 6. Тем не менее, мы сделаем несколько примеров решения для обоих, чтобы решить для этого правила.

Пример:

6924

Делится ли это число на 2 а откуда ты знаешь? Запросите

рупий

Для делимости на три что нам нужно сделать с этими цифрами?

Добавьте 6 + 9 + 2 + 4 на доска.

А что ты получил как ваш ответ, когда вы добавили эти цифры? Должен ответить 21

Делится ли число 21 на 3?

Дайте другой пример: 7054

Делится ли число на 2 а как узнать?

Делится ли число на 3? Объяснять.

Делится ли 16 на 3? Нет (если учащиеся ошибаются, быстро переходите к числам, кратным от 3 до 15, а затем спросите еще раз, делится ли 16 на 3?)

 

Число делится на 8 если последние 3 цифры числа делятся на 8

Делимость на 8 — единственная число, для которого учащиеся должны выполнить фактическое деление. Учащиеся должны сдать последний 3 цифры в числе и разделить его на 8. Объясните, что в отличие от 6, мы не можем исключить 8, если число делится на 2 и 4. Приведите пример числа 20. Может ли 8 пойти на 20 поровну? При необходимости запросите ответ учащегося

1 336

Круг 336 

Показать произведение, разделив 336 на 8

8 переходит в 33- четыре раза с 1 оставшимся перенесите его на 6, а 8 переходит в 16 дважды равномерно.

2 564

Круг 564

Запросить SR и объяснение

8 встречается 56-7 раз равномерно- но 8 не войдут в оставшиеся 4 равномерно

40

Да! Если число меньше чем 100, но это число кратно 8, то оно делится на 8

5 605

Круг 605

Запросить техническое обслуживание и объяснение

8 входит в 60-7 раз с остатком 4-8 входит в 45 7 раз

Нет не делится на 8

 

Число делится на 9 если сумма цифр делится на 9 (объясните, что это одно и то же процедуру, которую мы проделали для делимости на 3, но теперь мы смотрим, так ли это делится на 9)

Приведите пример. Прохождение используя ту же процедуру, что и для делимости на 3.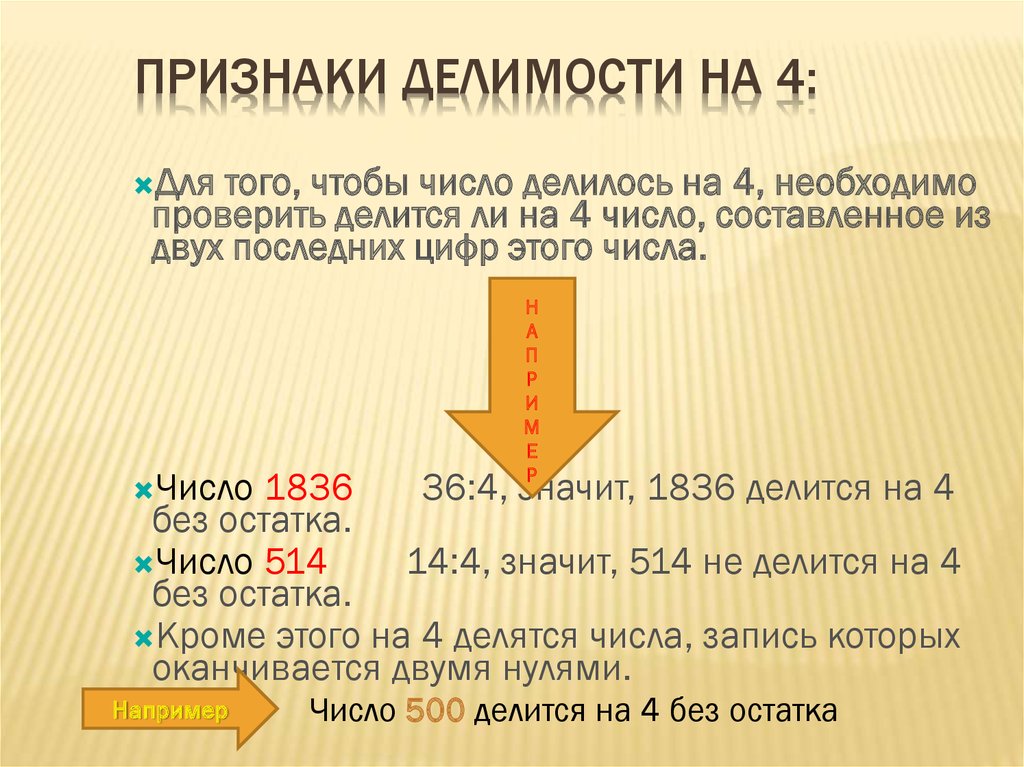 (т. е. добавить цифры. Обведите кружком сумма. Спросите, делится ли оно на 9.)

Пример:

6138

6+1+3+8 = 18- Да это так делится на 9

7983

7+9+8+4= 28- Нет, это не так делится на 9

Запросить SR и объяснение

 

Число делится на 10, если последняя цифра 0. (Также делится на 10, если делится на 2 и 5)

Приведите примеры

60, 70, 505, 50, 600, 780

Во всех примерах есть учащиеся обводят последнюю цифру. Если это ноль, то число делится на 10, но скажите им, что они должны быть осторожны, чтобы они смотрели на ПОСЛЕДНЯЯ цифра.

 

Проведите учащихся через примеры, чтобы найти или исключить делимость на 2,3,4,5,6,8,9.и 10- явно выписывать и вычеркивать числа, когда мы пробуем их.

Примеры: (Вытягивать цифры рядом с примером — попросите учащихся зачеркнуть (если они не делятся на) или обведите цифры по ходу)

324 (2,3,4,6,9) Спросить учащихся после 2 и 3. Если число делится на 2 и 3, то оно также делится на какое число? Попросите учащихся обвести 6, а затем мы вернемся к Делаем делимость на 4 и продолжаем. Кроме того, объясните, что хотя число может быть даже оно может делиться на 3 и 9потому что мы смотрим на сумму КАЖДОЙ цифры вместе.

45 (3,5,9)

Объясните, что когда число даже мы не можем исключить 2, 4, 6, 8 и 10 — все четные числа делимость. Итак, нам нужно только проверить, что осталось.

744 (2, 3, 4, 6, 8)

4, 335 (3, 5)

7 064 (2, 4, 8)

12 111 (3)

936 (2,3,4,6,8,9)

 

Проблемы со звездами

Студенты должны заполнить звездные задачи, чтобы получить их рабочий лист.

 

Запишите числа- Объясните учащимся, что рядом с каждой цифрой они должны написать числа 2-10 без 7 и вычеркивая их, когда они проверяют каждое правило.

 

Скажите учащимся, чтобы они запомнили делится на 6, если делится и на 2, и на 3.