Длина суммы векторов: Модуль суммы двух векторов. Определение разности двух векторов

Может ли длина суммы двух ненулевых векторов быть равна длине разности этих векторов? Вопрос №10 к 4 главе, Геометрия, 10-11 класс, Атанасян Л.С.

Может ли длина суммы двух ненулевых векторов быть равна длине разности этих векторов? Вопрос №10 к 4 главе, Геометрия, 10-11 класс, Атанасян Л.С. – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Может ли длина суммы двух ненулевых векторов быть равна длине разности этих векторов? — у кого какой ответ на этот вопрос к параграфу?

Лучший ответ

У меня такой
Пусть  коллинеарны. Для них сложение и вычитание производится как для обычных чисел,  а сумма двух ненулевых чи­сел не равна их разности. Рассмотрим особый случай, когда угол между векторами 

по свойству диагоналей прямоугольника.
Ответ: да.

еще ответы

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

Юмор

Олимпиады

ЕГЭ

Компьютерные игры

похожие вопросы 5

Докажите, что треугольники подобны. Вопросы и задачи 64, Геометрия, 10-11 класс, Атанасян Л.С.

Привет. Запуталась при решении, нужна помощь знатоков!!!

 
Три прямые, проходящие через одну точку и не лежащие в одной (Подробнее…)

ГДЗГеометрия11 класс10 классАтанасян Л.С.

Самостоятельная работа 19.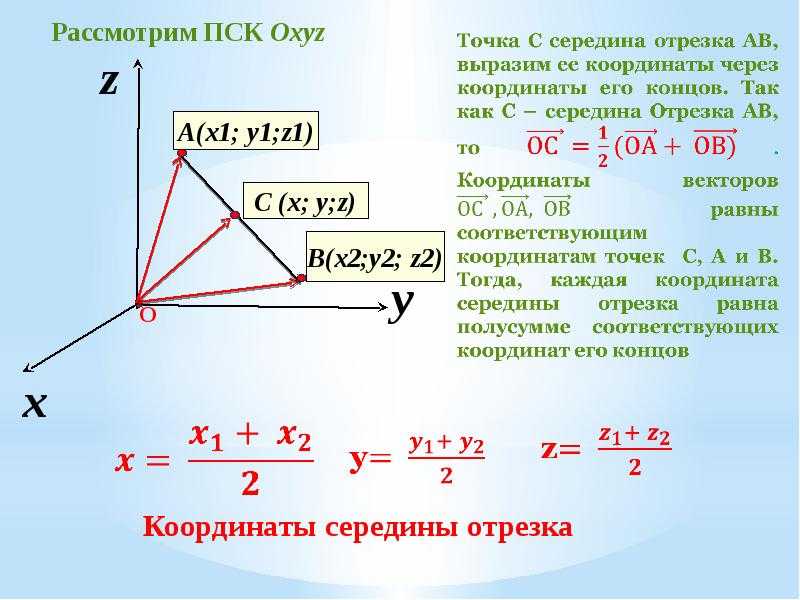 Вариант 2. № 2 ГДЗ Геометрия 9 класс Зив Б.Г. Помогите доказать, используя параллельный перенос

Используя параллельный перенос, докажите, что углы при основании равнобедренной трапеции равны между собой.
 

ГДЗЭкзаменыГеометрия9 классЗив Б. Г.

Почему сейчас школьники такие агрессивные ?

Читали новость про 10 классника который растрелял ? как вы к этому относитесь 

Новости10 классБезопасность

Какой был проходной балл в вузы в 2017 году?

Какой был средний балл ЕГЭ поступивших в российские вузы на бюджет в этом году? (Подробнее…)

Поступление11 классЕГЭНовости

11. Выпишите слово, в котором на месте пропуска пишется буква Е. Русский язык ЕГЭ-2017 Цыбулько И. П. ГДЗ. Вариант 12.

11.
Выпишите слово, в котором на месте пропуска пишется буква Е.
произнос., шь (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

1.

Определение вектора. Длина вектора. Коллинеарность, компланарность векторов.

Вектором называется направленный отрезок.    Длиной или модулем вектора называется длина соответствующего направленного отрезка.        

Модуль вектора a обозначается . Векторa называется единичным, если . Векторы называются коллинеарными, если они параллельны одной прямой. Векторы называются компланарными, если они параллельны одной плоскости.

2. Умножение вектора на число. Свойства операции.

Умножение вектора на число, даёт противоположно направленный вектор в длиной враз больше. Умножение вектора на число в координатной форме производится умножением всех координат на это число:

Исходя из определения получается выражение для модуля вектора, умноженного на число:

Аналогично как и числами, операции сложение вектора с самим с собой можно записать через умножение на число:

А вычитание векторов можно переписать через сложение и умножение:

Исходя из того, что умножение на не меняет длины вектора, а меняет только направление и учитывая определение вектора, получаем:

3.

Сложение векторов, вычитание векторов.

В координатном представлении вектор суммы получается суммированием соответствующих координат слагаемых:

Для геометрического построения вектора суммы используют различные правила (методы), однако они все дают одинаковый результат. Использование того или иного правила обосновывается решаемой задачей.

Правило треугольника

Правило треугольника наиболее естественно следует из понимания вектора как переноса. Ясно, что результат последовательного применения двух переносов инекоторой точки будет тем же, что применение сразу одного переноса, соответствующего этому правилу. Для сложения двух векторовипо правилу

треугольника оба эти вектора переносятся параллельно самим себе так, чтобы начало одного из них совпадало с концом другого. Тогда вектор суммы задаётся третьей стороной образовавшегося треугольника, причём его начало совпадает с началом первого вектора, а конец с концом второго вектора.

Это правило прямо и естественно обобщается для сложения любого количества векторов, переходя в правило ломаной:

Правило многоугольника

Начало второго вектора совмещается с концом первого, начало третьего — с концом второго и так далее, сумма же векторов есть вектор, с началом, совпадающим с началом первого, и концом, совпадающим с концом-го (то есть изображается направленным отрезком, замыкающим ломаную). Так же называется правилом ломаной.

Правило параллелограмма

Для сложения двух векторов ипо правилупараллелограмма оба эти векторы переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала. (Легко видеть, что эта диагональ совпадает с третьей стороной треугольника при использовании правила треугольника).

Правило параллелограмма особенно удобно, когда есть потребность изобразить вектор суммы сразу же приложенным к той же точке, к которой приложены оба слагаемых — то есть изобразить все три вектора имеющими общее начало.

Модуль суммы векторов

Модуль суммы двух векторов можно вычислить, использую теорему косинусов:

, где — косинус угла между векторамии.

Если векторы изображены в соответствии с правилом треугольника и берется угол по рисунку — между сторонами треугольника — что не совпадает с обычным определением угла между векторами, а значит и с углом в приведенной формуле, то последний член приобретает знак минус, что соответствует теореме косинусов в ее прямой формулировке.

Для суммы произвольного количества векторов применима аналогичная формула, в которой членов с косинусом больше: по одному такому члену существует для каждой пары векторов из суммируемого набора. Например, для трех векторов формула выглядит так:

Вычитание векторов

Два вектора и вектор их разности

Для получения разности в координатной форме надо вычесть соответствующие координаты векторов:

Для получения вектора разности начала векторов соединяются и началом векторабудет конец, а концом — конец. Если записать, используя точки векторов, то.

Модуль разности векторов

Три вектора , как и при сложении, образуют треугольник, и выражение для модуля разности получается аналогичным:

где — косинус угла между векторамии

Отличие от формулы модуля суммы в знаке перед косинусом, при этом надо хорошо следить, какой именно угол берется (вариант формулы модуля суммы с углом между сторонами треугольника при суммировании по правилу треугольника по виду не отличается от данной формулы для модуля разности, но надо иметь в виду, что для тут берутся разные углы: в случае суммы берётся угол, когда вектор переносится к концу вектора, когда же ищется модель разности, берётся угол между векторами, приложенными к одной точке; выражение для модуля суммы с использованием того же угла, что в данном выражении для модуля разности, отличается знаком перед косинусом).

Помощь по физике для старших классов

Учащиеся, нуждающиеся в помощи по физике для старших классов, получат большую пользу от нашей интерактивной программы. Мы разбираем все ключевые элементы, чтобы вы могли получить адекватную помощь по физике в средней школе. Имея под рукой обязательные концепции обучения и актуальные практические вопросы, вы быстро получите много помощи от старшеклассников по физике. Получите помощь сегодня с нашей обширной коллекцией необходимой информации по физике для старших классов.

• Физика средней школы

• Электричество и магнетизм

• Электрические цепи

• Конденсаторы

• Расчет общей емкости

• Понимание емкости

• Использование уравнений конденсатора

• Расчеты и концепции схемы

• Расчет мощности цепи

• Законы Кирхгофа

• Понимание тока в цепи

• Понимание электричества

• Понимание последовательного и параллельного

• Понимание напряжения в цепи

• Используйте закон Ома

• Резисторы

• Расчет полного сопротивления

• Удельное сопротивление

• Понимание сопротивления

• Электричество

• Электрический заряд

• Электрическая сила

• Понимание электрических полей

• Магнетизм и электромагнетизм

• Понимание магнитных полей

• Понимание отношений с текущим

• Понимание правил правой руки

• Энергия и работа

• Энергия

• Расчет кинетической энергии

• Расчет потенциальной энергии

• Виды механической энергии

• Понимание сохранения энергии

• Понимание кинетической и потенциальной энергии

• Мощность

• Понять силу

• Работа

• Расчетная работа

• Понимание работы

• Теорема о работе и кинетической энергии

• Сил

• Введение в Силы

• Идентификация сил и систем

• Понимание Силы

• Понимание взаимосвязи между силой и ускорением

• Чистая сила

• Расчет силы

• Интерпретация силовых диаграмм

• Удельные силы

• Контактные силы

• Гравитационное поле

• Понимание силы трения

• Понимание гравитации и веса

• Понимание нормальной силы

• Понимание всемирного тяготения

• Вводные принципы

• Понимание точности и прецизионности

• Понимание независимых и зависимых переменных

• Понимание скалярных и векторных величин

• Понимание единиц СИ

• Понимание значимых цифр

• Движение и механика

• Круговое движение

• Круговое движение

• Угловой момент вращения

• Понимание крутящего момента

• Понимание кругового движения

• Понимание крутящего момента

• Использование уравнений кругового движения

• Газовые законы

• Понимание изоволюметрических процессов

• Гармоническое движение

• Энергия ШМ

• Период СГМ

• Понимание маятников

• Понимание пружин

• Использование уравнений маятника

• Использование уравнений Spring

• Линейное движение

• Свободное падение

• Кинематические уравнения

• Понимание расстояния, скорости и ускорения

• Понимание движения в одном измерении

• Понимание движения в двух измерениях

• Понимание движения с постоянным ускорением

• Использование уравнений движения

• Импульс

• Расчет импульса

• Сохранение импульса

• Упругие и неупругие столкновения

• Импульс и Импульс

• Понимание закона сохранения импульса

• Понимание упругих и неупругих столкновений

• Понимание импульса

• Законы Ньютона

• Закон всемирного тяготения Ньютона

• Понимание первого закона Ньютона

• Понимание второго закона Ньютона

• Понимание третьего закона Ньютона

• Представления движения

• Представления движения

• Термодинамика

• Энтальпия и энтропия

• Понимание энтальпии

• Понимание энтропии

• Тепло

• Понимание влияния тепла на объем

• Понимание тепла и температуры

• Понимание тепла и работы

• Понимание тепловых двигателей

• Понимание концепции передачи энергии

• Законы термодинамики

• Понимание первого закона термодинамики

• Понимание второго закона термодинамики

• Понимание третьего закона термодинамики

• Понимание нулевого закона термодинамики

• Волны, звук и свет

• Свет и электромагнитные волны

• Понимание фотонов

• Понимание преломления

• Понимание электромагнитного спектра

• Звук

• Понимание Доплера

• Волны

• Интерференция и суперпозиция

• Свойства волн

• Типы волн

• Понимание амплитуды и периода

• Понимание расчетов со скоростью

• Понимание концепции волн

• Понимание типов волн

• Понимание длины волны и частоты

Курсы физики в старших классах обычно проходят ближе к концу вашей школьной карьеры. Вы, вероятно, изучали химию, биологию и науки о Земле и, возможно, обнаружили, что различия между всеми этими предметами заставляют науку чувствовать себя бессвязной и трудной для понимания. Физика дает вам возможность связать все воедино в рамках единой науки, которая объясняет все, от поведения электрона до движения планет. Из-за того, что физика является фундаментальной для всех других наук, некоторые школы продвигают учебную программу, в которой учащиеся сначала изучают физику, а затем все другие науки, которые обычно встречаются в старшей школе. Если это вариант в вашей средней школе, возможно, стоит подумать. Однако если вы продвинулись дальше в своей школьной карьере, физика по-прежнему предлагает фантастическую возможность оценить единство естественных наук.

Возможно, в значительной степени из-за своей междисциплинарной способности физика может пугать даже самых лучших учеников. Скорее всего, вы обнаружите, что уроки физики в старшей школе не менее сложны, чем ваши предыдущие курсы естествознания, и что они вознаграждают практику и часы, потраченные на лабораторные отчеты или подготовку к тестовым вопросам с длинными ответами. Один из ключей к успеху на уроках физики в старшей школе — развить способность сводить сложные ситуации к ряду знакомых простых уравнений.

Этот подход может показаться простым, пока вы не примете во внимание огромное количество новых уравнений и математических выражений, которые вводятся на обычном школьном уроке физики. Должен быть способ сохранить правильное уравнение для центростремительного ускорения, когда вы также пытаетесь сохранить правильность второго закона Ньютона в своем уме! Одна из самых приятных частей физики приходит, когда вы понимаете, что каждое отдельное уравнение связано с другим. Учтите, что второй закон Ньютона выглядит так. . .

. . . а уравнение для центростремительной силы выглядит так:

 

Оказывается, эти два уравнения на самом деле просто разные выражения одного и того же понятия силы! Вместо того, чтобы запоминать третье уравнение для центростремительного ускорения, вы можете просто признать, что если вы приравняете оба уравнения друг к другу и уменьшите массу, центростремительное ускорение должно быть равно следующему уравнению:

 

Это всего лишь один пример из многих. , многие другие, похожие на те, с которыми вы столкнетесь на уроке физики в старшей школе. В этом коротком примере мы только что сократили на одну треть количество уравнений, которые вам нужно будет запомнить для этого раздела на уроке физики. Учиться умнее, а не усерднее, может окупиться много времени на таком уроке, как физика. Рассмотрите возможность работы в учебных группах или один на один с успешными учениками, чтобы оценить, где вы можете заменить логические выводы и логическое заучивание. Если вы застряли, изучая определенную концепцию, наша страница справки по физике для старших классов может помочь вам разобраться с любыми недоразумениями, стоящими между вами и пониманием данной концепции. Наша справка по физике для старших классов организована по темам как общих тем по физике для старших классов, так и конкретных концепций и типов задач, обычно встречающихся в школьных программах. Каждая концепция связана с решенными примерами вопросов, которые могут помочь вам увидеть закономерности в способах успешного решения проблемы определенного типа.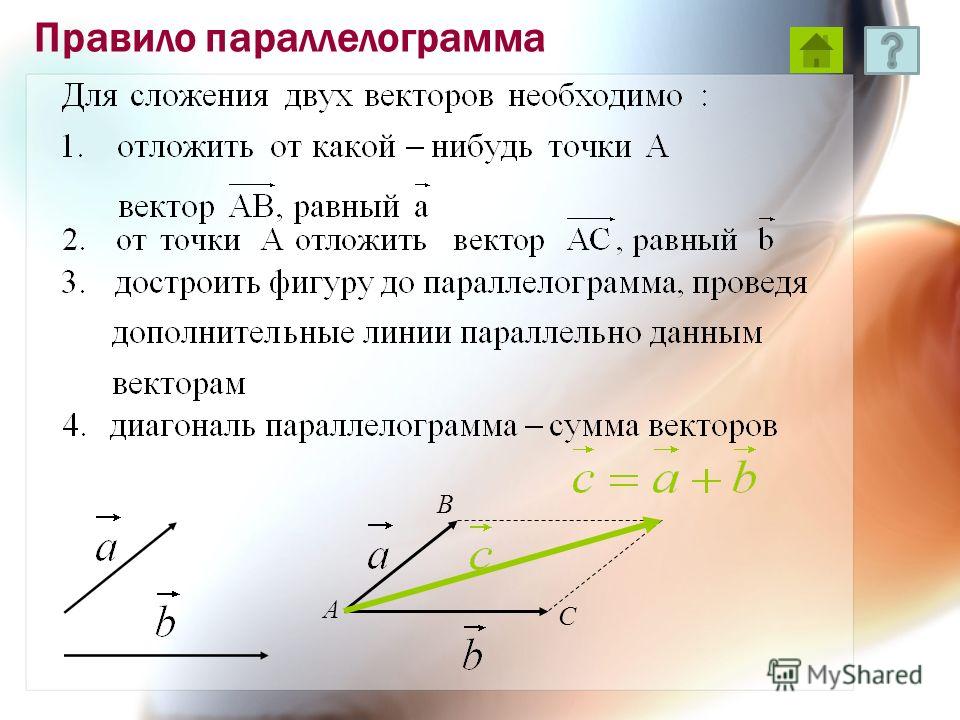 Когда вы почувствуете, что готовы решать некоторые проблемы самостоятельно, наши бесплатные практические тесты и диагностика по физике для старших классов могут занять центральное место.

Тщательное и усердное отношение к урокам физики в старшей школе может не только уменьшить вашу рабочую нагрузку и стресс в долгосрочной перспективе, но и помочь вам развить способность мыслить критически и логически. Эти навыки гораздо более ценны в большинстве занятий в колледже, чем простое запоминание. Ваше долгосрочное запоминание, навыки решения проблем и понимание всех других наук могут явно выиграть от тяжелой работы на уроке физики в старшей школе!

сумма — Как я могу вычислить сумму двух векторов в схеме (доктор Рэкет)

Я хотел бы реализовать свою функцию sum-of-vectors так, чтобы она принимала в качестве аргументов два вектора с разными числами и возвращала вектор с суммированием соответствующих элементов захваченных векторов. Вот как это должно быть выполнено для проверки суммирования векторов где вектор 1 равен (вектор 4 6 8 3) , а вектор 2 равен : (вектор 5 6 7)

Тестовое выражение: (вектор суммы (вектор 4 6 8 3) (вектор 5 6 7)) => #( 9 11 15 3)

ПОХОЖИЙ ВОПРОС: Существует близкое решение этого, которое находится на URL, Есть ли способ суммировать два вектора с разной длиной в схеме?

, но разница в том, что он отображает ‘# (2 4 6 4 5 6) с запятой в начале вопроса, но фактический результат моего требования не должен иметь апострофа (‘) в выходном векторе. должно быть #(9 11 15 3)

• вектор
• сумма
• схема
• ракетка

15

Функция для обработки соответствующих элементов двух списков, длина которых может различаться легко записать: напишите заглушка , с подписью и с целью , а минимальный пример :

 (определить (сумма списков l1 l2) ;; ListOfNumber ListOfNumber -> ListOfNumber
  ;; составить список сумм соответствующих элементов l1, l2
  ;; длина результата больше длин l1, l2
  '#())
(проверить-ожидать (сумма списков '() '()) '())
 

Добавьте следующие примеры и заполните функцию:

 (проверка-ожидание (сумма списков '() '(1)) `(1))
(проверить-ожидать (сумма списков '(2) '()) `(2))
(проверить-ожидать (сумма списков '(3) '(4)) `(7))
(определить (сумма-списков l1 l2) ;; ListOfNumber ListOfNumber -> ListOfNumber
  ;; составить список сумм соответствующих элементов l1, l2
  ;; длина результата больше длин l1, l2
  (состояние
    [(и (пусто? l1) (пусто? l2)) пусто]
    [(пусто? l1) (против (первый l2) (сумма списков l1 (остальные l2))) ]
    [(пусто? l2) (против (первый l1) (сумма списков (остальные l1) l2)) ]
    [else (cons (+ (first l1) (first l2)) (sum-of-lists (rest l1) (rest l2))) ]))
 

(обратите внимание, как 4 плеча cond повторяют 4 примера)

Теперь необходимая сумма векторов равна:

 (define (sum-of-vectors von1 von2) ;; VectorOfNumber VectorOfNumber -> ВекторЧисла
 ;; составить вектор сумм соответствующих элементов von1, von2
 ;; длина результата больше длины von1, von2
 (список->вектор (сумма-списков (вектор->список фон1) (вектор->список фон2))))
(проверить-ожидать (сумма векторов (вектор 4 6 8 3) (вектор 5 6 7)) (вектор 912 15 3))
Добро пожаловать в DrRacket, версия 8.
No related posts.