Подобные треугольники
Подобные треугольники — треугольники, у которых соответствующие углы равны, а стороны сходственным сторонам. То есть △ABC∼△A1B1C1\bigtriangleup ABC\sim \bigtriangleup A_1B_1C_1△ABC∼△A1B1C1 означает, что ∠A=∠A1\angle A=\angle A_1∠A=∠A1, ∠B=∠B1\angle B=\angle B_1∠B=∠B1, ∠C=∠C1\angle C=\angle C_1∠C=∠C1, ABA1B1=BCB1C1=ACA1C1\frac{AB}{A_1B_1}=\frac{BC}{B_1C_1}=\frac{AC}{A_1C_1}A1B1AB=B1C1BC=A1C1AC. Отношение k=ABA1B1k=\frac{AB}{A_1B_1}k=A1B1AB называется коэффициентом подобия.
Признаки подобия
Для того чтобы треугольники △ABC\bigtriangleup ABC△ABC и △A1B1C1\bigtriangleup A_1B_1C_1△A1B1C1 были подобны, достаточно, чтобы выполнялось одно из условий:
1. У △ABC\bigtriangleup ABC△ABC и △A1B1C1\bigtriangleup A_1B_1C_1△A1B1C1 есть две пары равных углов, например ∠A=∠A1\angle A=\angle A_1∠A=∠A1 и ∠B=∠B1\angle B=\angle B_1∠B=∠B1;
2. У △ABC\bigtriangleup ABC△ABC и △A1B1C1\bigtriangleup A_1B_1C_1△A1B1C1 есть пара равных углов, примыкающие к ним стороны , например ∠A=∠A1\angle A=\angle A_1∠A=∠A1 и ABA1B1=ACA1C1\frac{AB}{A_1B_1}=\frac{AC}{A_1C_1}A1B1AB=A1C1AC;
3. У △ABC\bigtriangleup ABC△ABC и △A1B1C1\bigtriangleup A_1B_1C_1△A1B1C1 стороны : ABA1B1=ACA1C1=BCB1C1\frac{AB}{A_1B_1}=\frac{AC}{A_1C_1}=\frac{BC}{B_1C_1}A1B1AB=A1C1AC=B1C1BC.
Подобные фигуры
Подобные фигуры — фигуры, у которых можно сопоставить точки таким образом, что для любой пары точек AAA и BBB первой фигуры и соответствующих им точек A1A_1A1 и B1B_1B1 второй фигуры выполняется соотношение AB=k⋅A1B1AB=k\cdot A_1B_1AB=k⋅A1B1, где kkk — некоторая постоянная величина. Величина kkk называется коэффициентом подобия.
Свойства подобных фигур
- Соответствующие углы подобных многоугольников равны;
- Если многоугольник имеет больше трех вершин, то
- Из равенства только соответствующих углов многоугольников еще НЕ следует подобие фигур;
- Из пропорциональности всех сторон еще НЕ следует подобие (равенство AB=k⋅A1B1AB=k\cdot A_1B_1AB=k⋅A1B1 должно выполняться для любой пары точек фигуры, не только для стороны многоугольника)
- При получаются подобные фигуры;
- Площади подобных фигур отличаются в k2k^2k2 раз, то есть S=k2⋅S1S=k^2\cdot S_1S=k2⋅S1.
Примеры:
1. Все подобны друг другу;
2. и не подобны друг другу, хотя у любого квадрата и ромба стороны пропорциональны;
3. и НЕ подобны друг другу, хотя у них все углы равны 90º.
Свойства подобных фигур — Подобие фигур
Свойства подобных фигур
Теорема. Когда фигура подобна фигуре , а фигура — фигуре , то фигуры и подобные.Из свойств преобразования подобия следует, что у подобных фигур соответствующие углы равны, а соответствующие отрезки пропорциональны. Например, в подобных треугольниках ABC и :
; ; ;
.
Признаки подобия треугольников
Теорема 1. Если два угла одного треугольника соответственно равны двум углам второго треугольника, то такие треугольники подобны.Теорема 2. Если две стороны одного треугольника пропорциональны двум сторонам второго треугольника и углы, образованные этими сторонами, равны, то треугольники подобны.
Теорема 3. Если стороны одного треугольника пропорциональны сторонам второго треугольника, то такие треугольники подобны.
Из этих теорем вытекают факты, которые являются полезными для решения задач.
1. Прямая, параллельная стороне треугольника и пересекающая две другие его стороны, отсекает от него треугольник, подобный данному.
На рисунке .
2. У подобных треугольников соответствующие элементы (высоты, медианы, биссектрисы и т.д.) относятся как соответствующие стороны.
3. У подобных треугольников периметры относятся как соответствующие стороны.
4. Если О — точка пересечения диагоналей трапеции ABCD, то .
На рисунке в трапеции ABCD:.
5. Если продолжение бічих сторон трапеции ABCD пересекаются в точке K, то (см. рисунок).
.
Подобие прямоугольных треугольников
Теорема 1. Если прямоугольные треугольники имеют равный острый угол, то они подобны.Теорема 2. Если два катеты одного прямоугольного треугольника пропорциональны двум катетам второго прямоугольного треугольника, то эти треугольники подобны.
Теорема 3. Если катет и гипотенуза одного прямоугольного треугольника пропорциональны катету и гипотенузе второго прямоугольного треугольника, то такие треугольники подобны.
Теорема 4. Высота прямоугольного треугольника, проведенная из вершины прямого угла, разбивает треугольник на два прямоугольных треугольника, подобные данному.
На рисунке .
Из подобия прямоугольных треугольников вытекает такое.
1. Катет прямоугольного треугольника является средним пропорциональным между гипотенузой и проекцией этого катета на гипотенузу:
; ,
или
; .
2. Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между проекциями катетов на гипотенузу:
, или .
3. Свойство биссектрисы треугольника:
биссектриса треугольника (произвольного) делит противоположную сторону треугольника на отрезки, пропорциональные двум другим сторонам.
На рисунке в BP — биссектриса .
, или .
Сходство равносторонних и равнобедренных треугольников
1. Все равносторонние треугольники подобные.2. Если равнобедренные треугольники имеют равные углы между боковыми сторонами, то они подобны.
3. Если равнобедренные треугольники имеют пропорциональные основание и боковую сторону, то они подобны.
Подобие произвольных фигур [wiki.eduVdom.com]
Понятие подобия можно ввести не только для треугольников, но и для произвольных фигур. Фигуры F и F1 называются подобными, если каждой точке фигуры F можно сопоставить точку фигуры F1 так, что для любых двух точек М и N фигуры F и сопоставленных им точек М1 и N1 фигуры F1 выполняется условие $\frac{M_1N_1}{MN} = k$ , где k — одно и то же положительное число для всех точек. При этом предполагается, что каждая точка фигуры F1 оказывается сопоставленной какой-то точке фигуры F. Число k называется коэффициентом подобия фигур F и F1.
Рис.1
На рисунке 1 представлен способ построения фигуры F1 , подобной данной фигуре F. Каждой точке М фигуры F сопоставляется точка М1 плоскости так, что точки М и М1 лежат на луче с началом в некоторой фиксированной точке О, причем ОМ1 = k*OM (на рис.1 k = 3). В результате такого сопоставления получается фигура F1, подобная фигуре F.
Этот способ построения фигуры F1, подобной фигуре F, называется центрально-подобным преобразованием фигуры F в фигуру F1 или гомотетией, а фигуры F и F1 — центрально-подобными или гомотетичными.
Можно доказать, что для треугольников общее определение подобия равносильно определению, данному в п.1.
Примерами подобных четырехугольников являются любые два квадрата (рис. 2, а), а также два прямоугольника, у которых две смежные стороны одного пропорциональны двум смежным сторонам другого (рис. 2, б).
Рис.2
Если каждую точку данной фигуры сместить каким-нибудь образом, то мы получим новую фигуру. Говорят, что эта фигура получена преобразованием из данной.
Гомотетия и рассмотренные ранее центральная симметрия и осевая симметрия — примеры преобразований фигур.
Рассмотрим еще один пример преобразования фигуры — параллельный перенос.
Преобразование фигуры F, при котором каждая ее точка Х(х; у) переходит в точку Х'(х + а; у + b), а и b постоянные, называется параллельным переносом (рис.3).
Рис.3
Параллельный перенос задается формулами $$ x’ = x + a \\ y’ = y + b $$ Эти формулы выражают координаты х’, у’ точки, в которую переходит точка (х; у) при параллельном переносе.
Название «параллельный перенос» оправдывается тем, что при параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние.
Заметим также, что при параллельном переносе прямая переходит в параллельную прямую (или в себя).
Пример 1. При параллельном переносе точка (1; 1) переходит в точку (-1; 0). В какую точку переходит начало координат?
Решение. Любой параллельный перенос задается формулами х’ = х + а; у’ = у + b. Так как точка (1; 1) переходит в точку (-1; 0), то -1 = 1 + а; 0 = 1 + b. Отсюда а = -2 ; b = -1.
Таким образом, параллельный перенос, переводящий точку (1; 1) в (-1; 0), задается формулами х’ = х — 2 ; у’ = у — 1.
Подставляя в эти формулы координаты начала (х = 0; у = 0), получим: х’ = -2; у’ = -1.
Итак, начало координат переходит в точку (-2; -1).
Подобие – это понятие, характеризующее наличие одинаковой, не зависящей от размеров, формы у геометрических фигур.
Подобные фигуры – это фигуры, для которых существует взаимно-однозначное соответствие, при котором расстояние между любыми парами их соответствующих точек изменяется в одно и то же число раз.
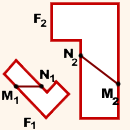Например, то, что фигуры F1 и F2 подобны, означает, что для любых двух точек M1 и N1 фигуры F1 и сопоставленных им точек M2
Преобразование фигуры F1 в фигуру F2, при котором расстояния между точками изменяются в одно и то же число раз, называется преобразованием подобия.
Гомотетия – это преобразование подобия. Это преобразование, в котором получаются подобные фигуры (фигуры, у которых соответствующие углы равны и стороны пропорциональны).
Гомотетия – это преобразование, при котором каждой точке A ставится в соответствие точка A1, лежащая на прямой OA, по правилу \(OA_1=k\cdot OA\), где k – постоянное, отличное от нуля число, O – фиксированная точка. Точка O называется центром гомотетии, число k – коэффициентом гомотетии.
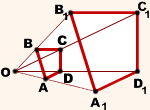
1) При гомотетии прямые переходят в прямые, полупрямые – в полупрямые, отрезки – в отрезки, углы – в углы.
2) Сохраняются углы между полупрямыми (соответственно, сохраняется параллельность прямых). Стороны гомотетичных фигур пропорциональны, а углы равны.
Подобные треугольники – это треугольники, у которых углы равны, а стороны пропорциональны.
Свойства подобных треугольников
- Периметры подобных треугольников относятся как их соответствующие стороны: \(\frac{P_{A_1B_1C_1}}{P_{ABC}}=\frac{A_1B_1}{AB}=\frac{B_1C_1}{BC}=\frac{A_1C_1}{AC}=k\).
- Соответствующие линейные элементы подобных треугольников (медианы, высоты, биссектрисы и т. д.) относятся как их соответствующие стороны.
- Площади подобных фигур относятся как квадраты их соответствующих линейных размеров: \(\frac{S_{A_1B_1C_1}}{S_{ABC}}=\frac{A_1B_1^2}{AB^2}=\frac{B_1C_1^2}{BC^2}=\frac{A_1C_1^2}{AC^2}=k^2\).
1-й признак подобия треугольников
Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
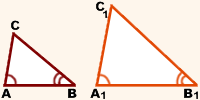
\(\left. \begin{aligned} \angle A=\angle A_1\\ \angle B=\angle B_1 \end{aligned} \right \} \Rightarrow \Delta ABC \sim \Delta A_1B_1C_1\)
2-й признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то такие треугольники подобны.
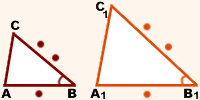
\(\left. \begin{aligned} &\frac{AB}{A_1B_1}=\frac{BC}{B_1C_1}\\[5pt] &\quad \angle B=\angle B_1 \end{aligned} \right \} \Rightarrow \Delta ABC \sim \Delta A_1B_1C_1\)
3-й признак подобия треугольников
Если стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны.
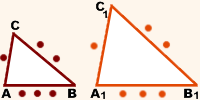
\(\begin{aligned} \frac{AB}{A_1B_1}=\frac{BC}{B_1C_1}=\frac{AC}{A_1C_1} \Rightarrow \Delta ABC \sim \Delta A_1B_1C_1 \end{aligned}\)
Признаки подобия прямоугольных треугольников
- Если прямоугольные треугольники имеют равный острый угол, то такие треугольники подобны.
- Если два катета одного прямоугольного треугольника пропорциональны двум катетам другого прямоугольного треугольника, то такие треугольники подобны.
- Если катет и гипотенуза одного прямоугольного треугольника пропорциональны катету и гипотенузе другого прямоугольного треугольника, то такие треугольники подобны.
Подобные треугольники. Признаки и свойства
Категория: Справочные материалы
Елена Репина 2013-08-22 2014-01-31Определение
Подобные треугольники — треугольники, у которых углы соответственно равны, а стороны одного соответственно пропорциональны сторонам другого треугольника.
Коэффициентом подобия называют число k, равное отношению сходственных сторон подобных треугольников.
Сходственные (или соответственные) стороны подобных треугольников — стороны, лежащие напротив равных углов.
Признаки подобия треугольников
I признак подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
II признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
III признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
Свойства подобных треугольников
- Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
- Отношение периметров подобных треугольников равно коэффициенту подобия.
- Отношение длин соответствующих элементов подобных треугольников (в частности, длин биссектрис, медиан, высот и серединных перпендикуляров) равно коэффициенту подобия.
Примеры наиболее часто встречающихся подобных треугольников
1. Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному.
2. Треугольники 
и 
, образованные отрезками диагоналей и основаниями трапеции, подобны. Коэффициент подобия – 
3. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.
Здесь вы найдете подборку задач по теме «Подобные треугольники».
Автор: egeMax | комментариев 50
В данной публикации мы рассмотрим определение/обозначение подобных треугольников и три признака подобия фигур. Также разберем пример решения задачи для закрепления представленного материала.
Определение и обозначение подобных треугольников
Подобными называются треугольники, у которых углы соответственно равны, а стороны одного треугольника пропорциональны сходственным сторонам другого.
Сходственные стороны в подобных треугольниках – это стороны, лежащие напротив их равных углов.
Для обозначения подобия фигур используется специальный символ “∼“. Например, △ABC ∼ △KLM.
Признаки подобных треугольников
Два треугольника подобны, если выполняется одно из условий, перечисленных далее.
1 признак
Два угла одного треугольника соотвественно равны двум углам другого.
∠BAC = ∠LKM
∠ABC = ∠KLM
2 признак
Две стороны одного треугольника пропорциональны двум сторонам другого, а углы между этими сторонами равны.
∠BAC = ∠LKM
3 признак
Все стороны одного треугольника соответственно пропорциональны всем сторонам другого.
Пример задачи
Даны два треугольника: △ABC со сторонами 3, 4 и 5 см; △DEF со сторонами 6, 8 и 10 см. Докажите, что данные фигуры подобны.
Решение
Т.к. нам известны длины всех сторон, можно проверить подобие с помощью третьего признака, рассмотренного выше:
Данное равенство верно, значит можно утверждать, что △ABC ∼ △DEF.
Подобие геометрических фигур,тел.(8 класс)
Описание презентации по отдельным слайдам:
1 слайд
Описание слайда:Исследуемый вопрос:
3 слайд
Описание слайда:Какие фигуры принято считать похожими? Используют ли в геометрии это понятие? Какие геометрические фигуры называются подобными? Какие из фигур всегда подобны, а какие нет? Какие треугольники подобны? План исследования: Полученные выводы!
4 слайд
Описание слайда:Фигуры получаются подобными в результате преобразования, которое называется ГОМОТЕТИЯ. ЭТО как в кино, когда лучи из проектора попадая на экран, изображают подобные фигуры. У подобных фигур изменяются размеры сторон в одинаковое число раз, но при этом все углы остаются без изменения. О ТОМ как изменились стороны говорит нам их отношение, которое называется коэффициентом подобия К. Два многоугольника ( ABCDEF и abcdef, рис.37 ) подобны, если их углы равны: A = a, B = b, …, F = f , а стороны пропорциональны:
Описание слайда:Если изменить ( увеличить или уменьшить ) все размеры плоской фигуры в одно и то же число раз ( отношение подобия ), то старая и новая фигуры называются подобными. Например, картина и её фотография – это подобные фигуры. ЗНАЧИТ! Теперь понятно КАКИЕ ФИГУРЫ НАЗЫВАЮТСЯ ПОДОБНЫМИ!
6 слайд
Описание слайда:Какие фигуры всегда подобны а какие нет? Круги Квадраты Равносторонние треугольники Кубы Шары Эти всегда подобны! А эти нет! Прямоугольники Ромбы Трапеции овалы Для подобия многоугольников недостаточно только пропорциональности сторон. Например, квадрат и ромб имеют пропорциональные стороны: каждая сторона квадрата вдвое больше, чем у ромба, однако их диагонали не пропорциональны и углы не равны.
7 слайд
Описание слайда:ЗНАЧИТ! Чтобы фигуры были подобны надо чтобы стороны их были пропорциональны а углы равны! Какие треугольники называются подобными? Два треугольника называются подобными, если их углы равны, а стороныпропорциональны. Выбери подобные.. AB BC CA ——— = ——- = ——— = k ab bc ca
8 слайд
Описание слайда:Признаки подобия треугольников: Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники равны. Если две стороны одного треугольника пропорциональны сторонам другого треугольника ауглы заключённые между ними равны, то такие треугольники подобны. Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то такие треугольники подобны.
9 слайд
Описание слайда:Признаки подобия прямоугольных треугольников: Два прямоугольных треугольника подобны, если: 1) их катеты пропорциональны; 2) катет и гипотенуза одного треугольника пропорциональны катету и гипотенузе другого; 3)два угла одного треугольника равны двум углам другого.
10 слайд
Описание слайда:Будут ли? фигуры
11 слайд
Описание слайда:Я пришёл к выводу: Если рассматривать похожесть и подобие, мы поймём, что это абсолютно разные вещи. Если подобные фигуры можно назвать похожими, то похожие подобными нет, и вот почему. Два разных треугольника можно назвать похожими, потому что например оба треугольника имеют 3 угла, 3 стороны, но это не означает, что они подобны. Так же у двух ромбов 4 стороны, 4 угла и они не подобны. Проанализировав всё это, мы приходим к выводу, что похожие фигуры не подобны. похожие фигуры не подобны.
12 слайд
Описание слайда:На практике постоянно встречаются преобразования, при которых все расстояния изменяются в одном и том же отношении, т. е. умножаются на одно и то же число. такое преобразование называется подобным (или подобием), а это число называется коэффициентом подобия.Например, при увеличении фотографии все размеры увеличиваются в одном и том же отношении. т. е. происходит подобное преобразование с фотопленки на фотобумагу. Подобное преобразование свершается и тогда, когда делают уменьшенную копию чертежа, рисунка и т. д. так, например, вы поступаете, когда срисовываете чертеж с доски в свою тетрадь. Подобные фигуры имеют одинаковую форму, но различные размеры.
13 слайд
Описание слайда: 14 слайд 
Описание слайда:Конец В создании проекта помогали: Поисковая система яндекс: www.ya.ru Поисковая система Google: www.google.com Сайт www.ru.wikipedia.org Сайт www.bymath.net Сделал: Ученик школы №26 города Петропавловска-Камчатского 8 «Б» класса Гвенетадзе Вадим Руководитель:Учитель Коробейникова А.И.
Курс повышения квалификации
Курс повышения квалификации
Курс профессиональной переподготовки
Учитель математики и информатики
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:
Краткое описание документа:
На практике постоянно встречаются преобразования, при которых все расстояния изменяются в одном и том же отношении, т. е. умножаются на одно и то же число. такое преобразование называется подобным (или подобием), а это число называется коэффициентом подобия.Например, при увеличении фотографии все размеры увеличиваются в одном и том же отношении. т. е. происходит подобное преобразование с фотопленки на фотобумагу. Подобное преобразование свершается и тогда, когда делают уменьшенную копию чертежа, рисунка и т. д. так, например, вы поступаете, когда срисовываете чертеж с доски в свою тетрадь. Подобные фигуры имеют одинаковую форму, но различные размеры.
Общая информация
Номер материала: 462357
Похожие материалы