Прогрессия арифметическая формула: Арифметическая прогрессия — урок. Алгебра, 9 класс.

Арифметическая прогрессия формулы, свойства, сумма членов, примеры и нахождение n-го члена

Арифметическая прогрессия — одно из фундаментальных понятий алгебры и математического анализа. Она имеет много применений в различных областях, включая финансы, физику, экономику и другие науки.

Арифметическая прогрессия — последовательность из чисел, в которой каждый следующий член отличается от предыдущего на определенное значение. Это значение называют разностью  или шагом арифметической прогрессии и обозначают буквой d. Разность может быть и отрицательным числом и даже равняться нулю.

Например, 2,7,12,17,22… — это арифметическая прогрессия, так как второй ее член (7) отличается от первого (2) на 5, третий член (12) отличается от второго (7) тоже на 5, четвертый член (17) отличается от третьего (12) снова на 5 и т. д. Получается у этой числовой последовательности каждый следующий элемент больше предыдущего на 5 и эта последовательность является арифметической прогрессией.

А вот последовательность 3, 5, 7, 10, 15… не является арифметической прогрессией. Подумайте почему.

Таким образом, чтобы найти следующий член прогрессии, необходимо добавить к нему разность (шаг).

{a_n=a_{n-1}+d}

Для того, чтобы найти член арифметической прогрессии, необходимо знать первый член и разность. Формула для этого выглядит так:

{a_n=a_1+(n-1)d}

Характеристическое свойство арифметической прогрессии

Если для последовательности чисел выполняется следующее равенство, то такую последовательность можно назвать арифметической прогрессией:

{a_n=\frac {a_{n-1}+a_{n+1}}{2}, n\ge 2}

Сумма членов арифметической прогрессии

Для того, чтобы найти сумму первых n членов арифметической прогрессии, необходимо воспользоваться одной из формул:

{S_n=\frac {a_1+a_n}{2} \cdot n},

{S_n=\frac {2a_1+d(n-1)}{2} \cdot n}

В этих формулах a₁ — первый член арифметической прогрессии, n — количество элементов для суммирования, a_n — член с номером n, d — разность прогрессии. На сайте вы можете найти сумму членов арифметической прогрессии онлайн.

Примеры арифметической прогрессии

2, 5, 8, 11, 14, 17…

Это арифметическая прогрессия, у которой первый член a₁ равен 2, а разность d равна 3.

75, 70, 65, 60, 55…

В данном примере мы имеем дело с отрицательной разностью прогрессии. a₁=75, d=-5.

Формулы арифметической прогрессии

Определение арифметической прогрессии	{a_n=a_{n-1}+d}
Разность арифметической прогрессии	{d = a_{n+1}-a_n}
Формула n-го члена арифметической прогрессии	a_n=a_1+(n-1)d
Сумма первых n членов арифметической прогрессии	{S_n=\dfrac {a_1+a_n}{2} \cdot n} {S_n=\dfrac {2a_1+d(n-1)}{2} \cdot n}
Характеристическое свойство арифметической прогрессии	a_n=\dfrac {a_{n-1}+a_{n+1}}{2}, n\ge 2

Арифметические прогрессии широко применяются в финансовых расчетах, например, при расчете аннуитетов и амортизации. Они также используются в физике при описании равномерно ускоренного движения тела.

Понимание арифметических прогрессий может быть полезно не только в научных и технических областях, но и в повседневной жизни. Например, при планировании бюджета или распределении времени между задачами можно использовать концепцию арифметической прогрессии для более эффективного использования ресурсов.

Арифметическая прогрессия — это важное математическое понятие, которое широко используется в различных областях. Понимание ее смысла может быть полезно для решения различных задач и повышения эффективности в различных сферах деятельности.

Элементарная математика

Сканави М.И. Элементарная математика. 2-е изд., перераб. и доп., М.: 1974г. — 592с. Книга представляет собой повторительный курс элементарной математики и рассчитана на тех, кто хочет пополнить, укрепить и систематизировать свои знания. Как и в первом издании, содержание ориентировано на программы вступительных экзаменов в технические вузы и, в особенности, на программы подготовительных отделений при высших учебных заведениях, для учащихся которых, как мы надеемся, книга окажется полезной. (Книга включает в себя Ч1 — Арифметика, алгебра и элементарные функции и Ч2 — Геометрия. Каждый раздел включает в себя теоретическую часть и большое количество задач с решениями.) Оглавление ВВЕДЕНИЕ Часть первая. АРИФМЕТИКА, АЛГЕБРА И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ Глава I. ДЕЙСТВИТЕЛЬНЫЕ И КОМПЛЕКСНЫЕ ЧИСЛА 2. Простые и составные числа. Признаки делимости. 3. Наибольший общий делитель и наименьшее общее кратное. 4. Целые числа. Рациональные числа. 5. Десятичные дроби. Представление рациональных чисел десятичными дробями. 6. Иррациональные числа. Действительные числа. 7. Действия с приближенными числами. 8. Числовая ось. Координаты точки на плоскости. § 2. Степени и корни 9. Степени с натуральными показателями. 10. Степени с целыми показателями. 11. Корни. 12. Степени с рациональными показателями. Степени с действительными показателями. 13. Алгоритм извлечения квадратного корня. § 3. Комплексные числа 14. Основные понятия и определения. 15. Рациональные действия с комплексными числами. 16. Геометрическое изображение комплексных чисел. Тригонометрическая форма комплексного числа. 17. Действия с комплексными числами, заданными в тригонометрической форме. Формула Муавра. 18. Извлечение корня из комплексного числа. Глава II. ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ 19. Алгебраические выражения. Одночлены и многочлены. 20. Формулы сокращенного умножения. 21. Бином Ньютона. 22. Разложение многочлена на множители. 23. Дробные алгебраические выражения. § 2. Иррациональные алгебраические выражения 24. Радикалы из алгебраических выражений. 25. Освобождение от иррациональности в знаменателе дроби. n. 41. Обратная пропорциональная зависимость. Степенная функция с рациональным показателем степени. 42. Показательная функция. 43. Логарифмическая функция. § 3. Преобразование графиков 44. Параллельный сдвиг графика. 45. График квадратного трех члена. 46. График дробно-линейной функции. 47. Преобразование симметрии. Сжатие и растяжение графика. 48. Построение графиков функций. 49. Сложение графиков. § 4. Некоторые сведения о рациональных функциях 50. Целые и дробные рациональные функции. Деление многочленов. 51. Схема Горнера. Теорема Безу. 52. Нули многочлена. Разложение многочлена на множители. Глава V. УРАВНЕНИЯ 53. Уравнение. Корни уравнения. 54. Равносильные уравнения. 55. Системы уравнений. 56. Графическое решение уравнений. §. 2. Алгебраические уравнения с одной неизвестной 57. Число и кратность корней. 58. Уравнения первой степени (линейные уравнения). 59. Уравнения второй степени (квадратные уравнения). 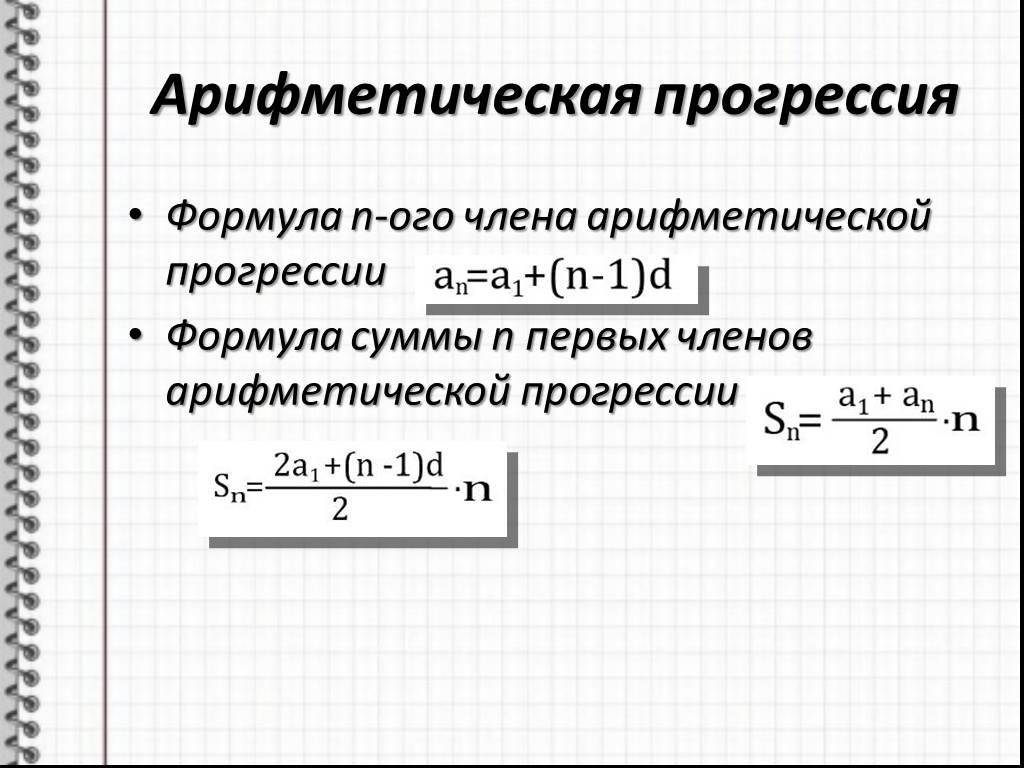60. Формулы Виета. Разложение квадратного трехчлена на множители. 61. Исследование квадратного уравнения. 62. Уравнения высших степеней. Целые корни. 63. Двучленные уравнения. 64. Уравнения, сводящиеся к квадратным. 65. Возвратные уравнения. § 3. Системы алгебраических уравнений 66. Линейные системы. 67. Определители второго порядка. Исследование линейных систем двух уравнений с двумя неизвестными. 68. Системы, состоящие из уравнения второй степени и линейного уравнения. 69. Примеры систем двух уравнений второй степени. Системы уравнений высших степеней. § 4. Иррациональные, показательные и логарифмические уравнения 70. Иррациональные уравнения. 71. Показательные уравнения. 72. Логарифмические уравнения. 73. Разные уравнения. Системы уравнений. Глава VI. НЕРАВЕНСТВА 74. Свойства неравенств. Действия над неравенствами. 75. Алгебраические неравенства. § 2. Решение неравенств 76. Множество решений неравенства. Равносильные неравенства. 77. Графическое решение неравенств. 79. Квадратные неравенства. 80. Неравенства высших степеней. Неравенства, содержащие дробные рациональные функции от х. 81. Иррациональные, показательные и логарифмические неравенства. 82. Неравенства с двумя неизвестными. Глава VII. ПОСЛЕДОВАТЕЛЬНОСТИ 83. Числовая последовательность. 84. Предел числовой последовательности. 85. Бесконечно малые. Правила предельного перехода. § 2. Арифметическая прогрессия 86. Арифметическая прогрессия. Формула общего члена. 87. Свойства арифметической прогрессии. 88. Формула для суммы n членов арифметической прогрессии. § 3. Геометрическая прогрессия 89. Геометрическая прогрессия. Формула общего члена. 90. Свойства геометрической прогрессии. 91. Формулы для суммы n членов геометрической прогрессии. 92. Бесконечно убывающая геометрическая прогрессия. Глава VIII. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА (ДУГИ) 93. Вектор, проекция вектора. 94. Положительные углы и дуги, меньшие 360°. 95. Углы и дуги, большие 360°. 96. Отрицательные углы. Сложение и вычитание углов. § 2. Тригонометрические функции произвольного угла 97. Определение основных тригонометрических функций. 98. Изменение основных тригонометрических функций при изменении угла от 0 до 2pi. § 3. Соотношения между тригонометрическими функциями одного и того же угла 99. Основные тригонометрические тождества. 100. Вычисление значений тригонометрических функций по значению одной из них. 101. Значения тригонометрических функций некоторых углов. § 4. Четность, нечетность и периодичность тригонометрических функций 102. Четность и нечетность. 103. Понятие периодической функции. 104. Периодичность тригонометрических функций. § 5. Формулы приведения 105. Зависимость между тригонометрическими функциями дополнительных углов. 106. Формулы приведения. Глава IX. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА И ИХ ГРАФИКИ § 1. Тригонометрические функции числового аргумента 108. Области определения и области изменения значений тригонометрических функций. 109. Некоторые неравенства и их следствия. § 2. Графики тригонометрических функций 110. Первоначальные сведения о таблицах тригонометрических функций. 111. Основные графики. 112. Примеры построения графиков некоторых других тригонометрических функций. 113. Дальнейшие примеры построения графиков функций. Глава X. ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ 114. Расстояние между двумя точками на плоскости. 115. Косинус суммы и разности двух аргументов. 116. Синус суммы и разности двух аргументов. 117. Тангенс суммы и разности двух аргументов. 118. О формулах сложения для нескольких аргументов. § 2. Формулы для двойного и половинного аргумента. Выражение sin na и cos na через степени sin a и cos a 119. Тригонометрические функции двойного аргумента. 120. Выражение sin na и cos na через степени sin a и cos a при натуральном числе n. 121. Тригонометрические функции половинного аргумента. 122. Выражение основных тригонометрических функций аргумента а через tg(a/2). § 3. Преобразование в сумму выражений вида sina•cosb, cosa•cosb и sinа•sinb § 4. Преобразование в произведение сумм вида § 5. Преобразование некоторых выражений в произведения с помощью введения вспомогательного аргумента 127. Преобразование в произведение выражения a•sina + b•cosa. 128. Преобразование в произведение выражений a•sina+b и a•cosa+b 129. Преобразование в произведение выражения a•tga+b. Глава XI. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ И ИХ ГРАФИКИ 130. Функция у = arcsin x (арксинус). 131. Функция y = arccos x (арккосинус). 132. Функция y = arctg x (арктангенс). 133. Функция y = arcctg x (арккотангенс). 134. Пример. § 2. Операции над обратными тригонометрическими функциями 135. Тригонометрические операции. 136. Операции сложения (вычитания). § 3. Обратные тригонометрические операции над тригонометрическими функциями 137. Функция у = arcsin (sin x). 138. Функция y = arctg (tg x). Глава XII. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА 139. Уравнение sin х = а. 140. Уравнение cos х = a. 141. Уравнение tg x = a. 142. Уравнение ctg x = a. 143. Некоторые дополнения. § 2. Способ приведения к одной функции одного и того же аргумента 145. Некоторые типы уравнений, приводящихся к уравнениям относительно функции одного аргумента. 146. Способ разложения на множители. 147. Решение рациональных тригонометрических уравнений с помощью универсальной тригонометрической подстановки tg(x/2) = t. § 3. Некоторые частные приемы решения тригонометрических уравнений и систем 148. Введение вспомогательного аргумента. 149. Преобразование произведения в сумму или разность. 150. Переход к функциям удвоенного аргумента. 151. Решение уравнения типа… 152. Применение подстановок sinx ± соsx = y. § 4. Решение тригонометрических неравенств 154. Простейшие тригонометрические неравенства. 155. Примеры тригонометрических неравенств, сводящихся к простейшим. Часть вторая. ГЕОМЕТРИЯ 156. Точка. Прямая. Луч. Отрезок. 157. Плоскость. Фигуры и тела. 160. Равенство фигур. Движение. 161. Равенство тел. § 2. Измерение геометрических величин 162. Сложение отрезков. Длина отрезка. 163. Общая мера двух отрезков. 164. Сравнительная длина отрезков и ломаных. 165. Измерение углов. 166. Радианная мера угла. 167. Измерение площадей. 168. Площадь прямоугольника. Объем прямоугольного параллелепипеда. Глава XIV. ПЕРПЕНДИКУЛЯРНЫЕ И ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. ЗАДАЧИ НА ПОСТРОЕНИЕ 169. Перпендикуляр и наклонные. 170. Свойство перпендикуляра, проведенного к отрезку в его середине. 171. Параллельные прямые. 172. Углы, образованные двумя параллельными прямыми и секущей. 173. Углы с параллельными или перпендикулярными сторонами. § 2. Геометрические места точек. Окружность 174. Геометрическое место точек. 175. Свойство биссектрисы угла. 176. Окружность. 177. Взаимное расположение прямой и окружности. Касательная и секущая. 178. Хорда и диаметр. Сектор и сегмент. 179. Взаимное расположение двух окружностей. § 3. Основные задачи на построение 181. Деление отрезка пополам. Построение перпендикуляров. 182. Построение углов. 183. Другие задачи на построение. Глава XV. ТРЕУГОЛЬНИКИ, ЧЕТЫРЕХУГОЛЬНИКИ 184. Стороны и углы треугольника. 185. Биссектрисы треугольника. Вписанная окружность. 186. Оси симметрии сторон треугольника. Описанная окружность. 187. Медианы и выcоты треугольника. 188. Равенство треугольников. 189. Построение треугольников. 190. Равнобедренные треугольники. 191. Прямоугольные треугольники. § 2. Параллелограммы 192. Четырехугольники. 193. Параллелограмм и его свойства. 194. Прямоугольник. § 3. Трапеция 196. Трапеция. 197. Средняя линия треугольника. 198. Средняя линия трапеции. 199. Деление отрезка на равные части. § 4. Площади треугольников и четырехугольников 200. Площадь параллелограмма. 201. Площадь треугольника. 202. Площадь трапеции. Глава XVI. ПОДОБИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР 203. Пропорциональные отрезки. 204. Свойства биссектрис внутреннего и внешнего углов треугольника. § 2. Подобное преобразование фигур (гомотетия) 205. Определение гомотетичных фигур. 206. Свойства преобразования подобия. § 3. Общее подобное соответствие фигур 207. Подобные фигуры. 208. Периметры и площади подобных треугольников. 209. Применение подобия к решению задач на построение. Глава XVII. МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ТРЕУГОЛЬНИКЕ И КРУГЕ 210. Углы с вершиной на окружности. 211. Углы с вершиной внутри и вне круга. 212. Угол, под которым виден данный отрезок. 213. Четырехугольники, вписанные в окружность. 214. Пропорциональные отрезки в круге. 215. Задачи на построение. § 2. Метрические соотношения в треугольнике 216. Пропорциональные отрезки в прямоугольном треугольнике. Теорема Пифагора. 218. Теорема синусов. Формула Герона. 217. Квадрат стороны, лежащей против острого или тупого утла и треугольнике. Теорема косинусов. 218. Теорема синусов. Формула Герона. 219. Радиусы вписанной и описанной окружностей. § 3. Решение треугольников 220. Таблицы функций. 221. Решение треугольников. Сводка основных формул. 222. Решение прямоугольных треугольников. 223. Решение косоугольных треугольников. Глава XVIII. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ. ДЛИНА окружности И ПЛОЩАДЬ КРУГА 224. Выпуклые многоугольники. 225. Правильные многоугольники. 226. Соотношения между стороной, радиусом и апофемой. 227. Периметр и площадь правильного n-угольника. 228. Удвоение числа сторон правильного многоугольника. § 2. Длина окружности. Площадь круга и его частей 229. Длина окружности. 230. Площадь круга и его частей. Глава XIX. ПРЯМЫЕ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ 231. Взаимное расположение двух прямых в пространстве. 232. Взаимное расположение прямой линии и плоскости. 233. Взаимное расположение двух плоскостей. 234. Свойства параллельных прямых и плоскостей. 235. Построения в стереометрии. § 2. Перпендикулярность прямых и плоскостей 236. Перпендикуляр к плоскости. 237. Перпендикуляр и наклонные. 238. Угол между прямой и плоскостью. 239. Связь между перпендикулярностью и параллельностью прямых и плоскостей. 240. Общий перпендикуляр двух скрещивающихся прямых. § 3. Двугранные и многогранные углы 241. Двугранный угол. 242. Взаимно перпендикулярные плоскости. 243. Трехгранные углы. 244. Многогранные углы. § 4. Многогранники 245. Многогранники. 246. Правильные многогранники. Глава XX. МНОГОГРАННИКИ И КРУГЛЫЕ ТЕЛА 247. Цилиндры и призмы. 248. Параллелепипеды. 249. Объемы призм и цилиндров. 250. Площадь боковой поверхности призмы. 251. Площадь поверхности цилиндра. § 2. Пирамида. Конус 252. Свойства пирамиды и конуса. 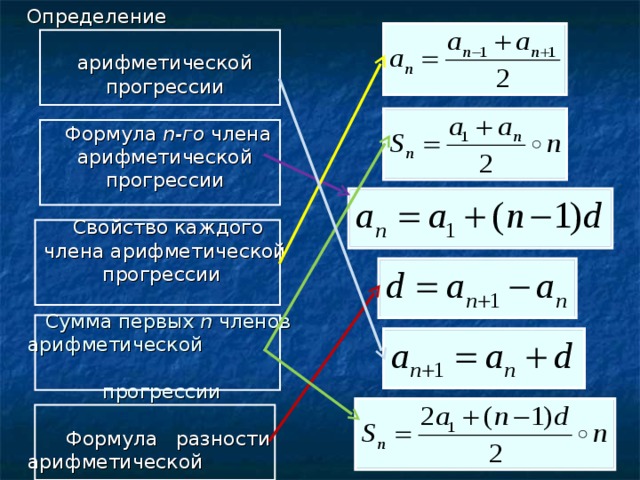253. Объем пирамиды и конуса. 254. Площадь боковой поверхности правильной пирамиды и конуса. 255. Усеченный конус и усеченная пирамида. § 3. Шаровая поверхность. Шар 256. Шар и шаровая поверхность. 257. Объем шара и его частей. 258. Площадь поверхности шара и ее частей. 259. Понятие телесного угла. Ответы к упражнениям Приложения

Формула арифметической последовательности — Что такое формула арифметической последовательности? Примеры

Формула арифметической последовательности используется для вычисления члена n ^th и суммы арифметической прогрессии. Арифметическая последовательность — это последовательность, в которой общая разность между любыми двумя последовательными членами остается постоянной. Если мы хотим найти какой-либо термин/сумму терминов в арифметической последовательности, мы можем использовать формулу арифметической последовательности. Давайте разберемся с формулой арифметической прогрессии на решенных примерах.

Что такое формула арифметической последовательности?

Арифметическая последовательность имеет вид: а, а + d, а + 2d, а + 3d, …… до n членов. Первый член — это а, общая разница — d, n = количество терминов. Для расчета с использованием формул арифметической последовательности сначала определите первый член, количество членов и общую разность последовательности. Существуют различные формулы, связанные с арифметическим рядом, используемым для вычисления члена n ^th , суммы или общей разности данной арифметической последовательности.

• n ^й срок есть, а _n = а ₁ + (n — 1) d
• Сумма n членов равна S _n = (n/2) [2a ₁ + (n — 1) d] (или) (n/2) [a ₁ + a _n ]
• Общая разность, d = a _n — a _{n — 1}

В этих формулах a ₁ = первый член, d = общая разность и n = количество членов.

Арифметическая последовательность Формула

Формулы арифметической последовательности имеют вид 1) d

где,

• a _n = n ^th срок,
• a ₁ = первый член и
• d — общая разность

Формула 2: Сумма первых n членов арифметической последовательности вычисляется по одной из следующих формул:

• S _n = (n/2) [2a ₁ + (n — 1) d] (когда мы знаем первый член и общую разность)
• S _n =(n/2) [a ₁ + a _n ] (при первом и последнем членах)

где,

• S _n = сумма n слагаемых,
• a ₁ = первый член,
• a _n = n ^th срок и
• d — общая разница между последовательными терминами

Формула 3: Формула для вычисления общей разности арифметической прогрессии имеет вид н ^-й срок,

a _{n — 1} = (n — 1) ^-й срок и

d — общая разница между последовательными терминами

Применение формулы арифметической последовательности

Мы используем формулу арифметической прогрессии каждый день или даже каждую минуту, даже не осознавая этого. Ниже приведены несколько примеров практического применения формулы арифметической последовательности

• Складывание чашек, стульев, мисок или карточного домика.
• Места на стадионе или в зрительном зале располагаются в арифметической последовательности.
• Секундная стрелка на часах движется в арифметической последовательности, а также минутная и часовая стрелки.
• Недели в месяце следуют арифметической последовательности, как и годы. Каждый високосный год можно определить, прибавив 4 к предыдущему високосному году.
• Количество свечей, задуваемых в день рождения, с каждым годом увеличивается как арифметическая прогрессия.

Cuemath — одна из ведущих мировых платформ для обучения математике, предлагающая онлайн-уроки по математике в режиме реального времени один на один для классов K-12. Наша миссия — изменить то, как дети изучают математику, чтобы помочь им преуспеть в школе и на конкурсных экзаменах. Наши опытные преподаватели проводят 2 или более живых занятий в неделю в темпе, соответствующем потребностям ребенка в обучении.

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Запись на бесплатный пробный урок

 

Примеры с использованием формулы арифметической последовательности

Пример 1: Используя формулу арифметической последовательности, найдите 13 ^th член в последовательности 1, 3, 5, 9, 00 100 100 100

Решение:

Найти: 13 ^-й -й член данной последовательности.

Поскольку разница между последовательными терминами одинакова, данная последовательность образует арифметическую последовательность.

a = 1, d = 4

По формуле арифметической прогрессии 2 а _n = 1 + (13 — 1)4

a _n = 1 + (12)4

a _n = 1 + 48

a _n = 49

☛ Также проверьте: Калькулятор арифметической последовательности

Ответ: 13 ^th член последовательности равен 49. 90 90 4 Пример:

900 0 Найдите первый член арифметической прогрессии где 35 ^-й -й член равен 687, а общая разность 14.

Решение:

Найти: Первый член арифметической прогрессии

Дано: a _n = n

4-й 4-й член 14

Используя формулу арифметической последовательности,

a _n = a ₁ + (n − 1)d

687 = a ₁ + (35 — 1)14

10

6 7 + ( 34)14

687 = a ₁ + 476

a ₁ = 211

Ответ: Первый член последовательности равен 211. следующей арифметики ряд: 3 + 7 + 11 + ……. (до 25 слагаемых).

Решение:

Найти сумму первых 25 членов арифметической прогрессии 3, 7, 11, …….

Дано: a ₁ = 3, d = 4, n = 25

данная арифметическая последовательность равна 3, 7, 11,….

Используя формулу арифметического ряда:

S _n = (n/2) [2a + (n — 1) d]

Сумма первых 25 членов

S ₂₅ =(25/2 ) [2 x 3 + (25 — 1) 4]

= (25/2) [6 + 24 x 4]

= 25/2 × 102

= 1275

Ответ: Сумма данного арифметического ряда равна 1275.

Часто задаваемые вопросы о формуле арифметической последовательности

Что такое формула арифметической последовательности в алгебре?

Формула арифметической последовательности относится к формуле для вычисления общего члена арифметической последовательности и суммы n членов арифметической последовательности.

• Общий член арифметической последовательности: a _n = a ₁ + (n — 1) d
• Сумма первых n членов арифметической прогрессии равна _n = (n/2) [2a ₁ + (n — 1) d]

где a ₁ = первый член и d = общая разность последовательности.

Что такое n в формуле арифметической последовательности?

В формуле арифметической последовательности для нахождения общего термина a _n = a ₁ + (n — 1) d, ‘n’ относится к номеру термина в данной арифметической последовательности. Например, ₂ представляет 2 ^-й -й член последовательности.

Что такое формула арифметической последовательности для суммы n членов?

Сумма первых n членов арифметической последовательности определяется как S _n = (n/2) [2a ₁ + (n — 1) d], где S _n = сумма n членов , a ₁ = первый член, а d — общая разность.

Что такое формула арифметического ряда?

Арифметический ряд есть не что иное, как сумма нескольких или всех членов арифметической прогрессии. Таким образом, формула арифметического ряда:

• S _n = (n/2) [2a ₁ + (n — 1) d] [ИЛИ]
• S _n = (n/2) [a ₁ + a _n ]

Здесь a ₁ — первый член арифметического ряда, а d — его общая разность.

Как использовать формулу арифметической последовательности?

Чтобы использовать формулу арифметической последовательности, сначала определите первый член (a ₁ ) и общую разность (d) последовательности. Затем подставьте их в соответствующую формулу (из n ^-й член или сумма) и упростить.

В чем разница между явной формулой и рекурсивной формулой арифметической последовательности?

Явная формула используется для нахождения любого члена арифметической прогрессии, если мы знаем только его первый член и общую разность. Но рекурсивная формула может быть использована для нахождения термина только тогда, когда известны его предыдущий термин и общая разность.

• Явная формула для арифметической последовательности: a _n = a ₁ + (н — 1) д
• Рекурсивная формула для арифметической последовательности: a _n = a _{n — 1} + d

Арифметические и геометрические последовательности

\(\def\d{\displaystyle} \def\курс{Математика 228} \ новая команда {\ f} [1] {\ mathfrak # 1} \ новая команда {\ s} [1] {\ mathscr # 1} \def\N{\mathbb N} \def\B{\mathbf{B}} \def\circleA{(-.5,0) круг (1)} \ деф \ Z {\ mathbb Z} \def\circleAlabel{(-1. {-1}} \def\nrml{\triangleleft} \ деф \ ст {:} \ деф \ ~ {\ широкая тильда} \def\rem{\mathcal R} \def\sigalg{$\sigma$-алгебра } \def\Гал{\mbox{Гал}} \def\iff{\leftrightarrow} \def\If{\Leftrightarrow} \ деф \ земля {\ клин} \def\И{\bigwedge} \защита\вход{\вход} \def\AAnd{\d\bigwedge\mkern-18mu\bigwedge} \def\Ви{\bigvee} \def\VVee{\d\Vee\mkern-18mu\Vee} \ деф \ имп {\ стрелка вправо} \def\Imp{\Rightarrow} \def\Fi{\Leftarrow} \def\var{\mbox{var}} \def\Th{\mbox{Th}} \защита\вход{\вход} \def\sat{\mbox{Sat}} \def\con{\mbox{Con}} \def\iffmodels{\bmodels\models} \def\dbland{\bigwedge \!\!\bigwedge} \def\дом{\mbox{дом}} \def\rng{\mbox{диапазон}} \def\isom{\cong} \DeclareMathOperator{\wgt}{wgt} \newcommand{\vtx}[2]{узел[заливка,круг,внутренний интервал=0pt, минимальный размер=4pt,метка=#1:#2]{}} \ новая команда {\ va} [1] {\ vtx {выше} {# 1}} \ новая команда {\ vb} [1] {\ vtx {ниже} {# 1}} \ новая команда {\ vr} [1] {\ vtx {право} {# 1}} \ новая команда {\ vl} [1] {\ vtx {слева} {# 1}} \renewcommand{\v}{\vtx{выше}{}} \def\circleA{(-. 5,0) круг (1)} \def\circleAlabel{(-1.5,.6) узел[выше]{$A$}} \def\circleB{(.5,0) круг (1)} \def\circleBlabel{(1.5,.6) узел[выше]{$B$}} \def\circleC{(0,-1) круг (1)} \def\circleClabel{(.5,-2) узел[справа]{$C$}} \def\twosetbox{(-2,-1.4) прямоугольник (2,1.4)} \def\threesetbox{(-2.5,-2.4) прямоугольник (2.5,1.4)} \def\ansfilename{практика-ответы} \def\shadowprops{{fill=black!50,shadow xshift=0.5ex,shadow yshift=0.5ex,path fading={круг с размытым краем 10 процентов}}} \ новая команда {\ hexbox} [3] { \def\x{-cos{30}*\r*#1+cos{30}*#2*\r*2} \def\y{-\r*#1-sin{30}*\r*#1} \рисовать (\х,\у) +(90:\r) — +(30:\r) — +(-30:\r) — +(-90:\r) — +(-150:\r) — +(150: \r) — цикл; \draw (\x,\y) узел{#3}; } \renewcommand{\bar}{\overline} \newcommand{\card}[1]{\left| #1 \справа|} \newcommand{\twoline}[2]{\begin{pmatrix}#1 \\ #2 \end{pmatrix}} \новая команда{\lt}{<} \новая команда{\gt}{>} \newcommand{\amp}{&} \)

¶

Расследуй!18

Для узоров из точек ниже нарисуйте следующий узор в последовательности. Затем дайте рекурсивное определение и замкнутую формулу для количества точек в \(n\)-м шаблоне.

Обратимся теперь к вопросу о нахождении замкнутых формул для конкретных типов последовательностей.

Арифметические последовательности

Если члены последовательности отличаются на константу, мы говорим, что последовательность арифметическая . Если начальный член (\(a_0\)) последовательности равен \(a\), а общая разность равна \(d\text{,}\), то мы имеем

Рекурсивное определение: \(a_n = a_{n-1} + d\) с \(a_0 = a\text{.}\)

Замкнутая формула: \(a_n = a + dn\text{.}\)

Откуда мы это знаем? Для рекурсивного определения нам нужно указать \(a_0\text{.}\) Затем нам нужно выразить \(a_n\) в терминах \(a_{n-1}\text{.}\) Если мы вызовем первый член \(a\text{,}\), затем \(a_0 = a\text{.}\) Для рекуррентного отношения по определению арифметической последовательности разница между последовательными терминами является некоторой константой, скажем, \ (d\text{. }\) Итак, \(a_n — a_{n-1} = d\text{,}\) или, другими словами,

\begin{уравнение*} a_0 = a \qquad a_n=a_{n-1}+d. \end{уравнение*}

Чтобы найти замкнутую формулу, сначала выпишите последовательность в общем виде:

\начать{выравнивать*} а_0 \амп = а\\ a_1 \amp = a_0 + d = a+d\\ a_2 \amp = a_1 + d = a+d+d = a+2d\\ a_3 \amp = a_2 + d = a+2d+d = a+3d\\ \amp\vdots \конец{выравнивание*}

Мы видим, что для нахождения \(n\)-го члена нам нужно начать с \(a\), а затем добавить \(d\) несколько раз. Фактически, добавьте его \(n\) раз. Таким образом, \(a_n = a+dn\text{.}\)

Пример 2.2.1

Найдите рекурсивные определения и замкнутые формулы для приведенных ниже последовательностей. Предположим, что первый указанный термин равен \(a_0\text{.}\)

1. \(2, 5, 8, 11, 14, \ldots\text{.}\)
2. \(50, 43, 36, 29, \ldots\text{.}\)

Решение

Сначала мы должны проверить, что эти последовательности действительно являются арифметическими, взяв разности последовательных членов. Это покажет общую разницу \(d\text{.}\)

1. \(5-2 = 3\text{,}\) \(8-5 = 3\text{,}\) и т. д. Чтобы перейти от каждого термина к следующему, мы добавляем три, так что \(d = 3\text{.}\) Таким образом, рекурсивное определение \(a_n = a_{n-1} + 3\) с \(a_0 = 2\text{.}\) Замкнутая формула \(a_n = 2 + 3n\text{.}\)

2. Здесь общая разница: \(-7\text{,}\), так как мы прибавляем \(-7\) к 50, чтобы получить 43, и так далее. Таким образом, у нас есть рекурсивное определение \(a_n = a_{n-1} — 7\) с \(a_0 = 50\text{.}\) Замкнутая формула \(a_n = 50 — 7n\text{.} \)

Как насчет таких последовательностей, как \(2, 6, 18, 54, \ldots\text{?}\) Это не арифметика, поскольку разница между терминами непостоянна. Однако отношение 90 475 90 476 между последовательными членами является постоянным. Мы называем такие последовательности 9{п}\текст{.}\)

Пример 2.2.2

Найдите рекурсивную и замкнутую формулу для приведенных ниже последовательностей. Опять же, первый указанный термин равен \(a_0\text{. }\)

.

1. \(3, 6, 12, 24, 48, \ldots\)
2. \(27, 9, 3, 1, 1/3, \ldots\)

Решение

Опять же, мы должны сначала проверить, действительно ли эти последовательности являются геометрическими, на этот раз путем деления каждого члена на его предыдущий член. Предполагая, что это отношение постоянно, мы нашли \(r\text{.}\)

9{п}\текст{.}\)

В приведенных выше примерах и формулах мы предполагали, что начальный термин был \(a_0\text{.}\). Если ваша последовательность начинается с \(a_1\text{,}\), вы можете легко найти термин, который было бы \(a_0\) и использовать это в формуле. Например, если мы хотим получить формулу для последовательности \(2, 5, 8,\ldots\) и настаиваем на том, что \(2= a_1\text{,}\), то мы можем найти \(a_0 = -1\) (поскольку последовательность арифметическая с общей разностью 3, имеем \(a_0 + 3 = a_1\)). Тогда замкнутая формула будет \(a_n = -1 + 3n\text{.}\)

Подраздел Суммы арифметических и геометрических последовательностей

¶

Расследуй!19

В вашем соседнем продуктовом магазине есть кондитерский автомат, полный Skittles.

1. Предположим, что автомат для конфет в настоящее время содержит ровно 650 кеглей, и каждый раз, когда кто-то вставляет четвертак, из автомата выходит ровно 7 кеглей.

   1. Сколько кеглей останется в автомате после того, как будут вставлены 20 четвертаков?

   2. Останется ли когда-нибудь в автомате ровно ноль Skittles? Объяснять.

2. Что, если автомат выдает 7 Skittles первому покупателю, положившему четвертак, 10 — второму, 13 — третьему, 16 — четвертому и т. д. Сколько Skittles выдал автомат после того, как было положено 20 четвертак? в машину?

3. Что, если автомат выдает 4 кегли первому покупателю, 7 — второму, 12 — третьему, 19 — четвертому и т. д. Сколько кеглей выдал автомат после того, как 20 четвертаков были помещены в автомат?

Посмотрите на последовательность \((T_n)_{n\ge 1}\), которая начинается с \(1, 3, 6, 10, 15,\ldots\text{.}\) Это называется треугольных чисел. , так как они представляют собой количество точек в равностороннем треугольнике (представьте, как вы расположите 10 кеглей для боулинга: ряд из 4 плюс ряд из 3 плюс ряд из 2 и ряд из 1).

Является ли эта последовательность арифметической? Нет, поскольку \(3-1 = 2\) и \(6-3 = 3 \ne 2\text{,}\) общего различия нет. Является ли последовательность геометрической? Нет. \(3/1 = 3\), но \(6/3 = 2\text{,}\), поэтому общего соотношения нет. Что делать?

Обратите внимание, что различия между терминами образуют арифметическую последовательность: \(2, 3, 4, 5, 6,\ldots\text{.}\) Это говорит о том, что \(n\)-й член последовательности \(1 ,3,6,10,15,\ldots\) — это сумма первых \(n\) членов последовательности \(1,2,3,4,5,\ldots\text{.}\ ) Мы говорим, что первая последовательность — это последовательность 90 437 частичных сумм 90 438 второй последовательности (частичных сумм, потому что мы не берем сумму всех бесконечно многих членов). Если бы мы знали, как складывать члены арифметической последовательности, мы могли бы использовать это, чтобы найти замкнутую формулу для последовательности, разности которой являются членами этой арифметической последовательности.

Это должно стать яснее, если мы напишем треугольные числа так:

\начать{выравнивать*} 1 \амп = 1\\ 3 \амп = 1+2\\ 6 \ампер = 1 + 2 + 3\\ 10 \ампер = 1+2 + 3+ 4\\ \vdots\amp\qquad\vdots\\ T_n \amp = 1 + 2 + 3 + \cdots + n. \конец{выравнивание*}

Подумайте, как найти сумму первых 100 положительных целых чисел (то есть \(T_{100}\)). Вместо того, чтобы складывать их по порядку, мы перегруппируем и добавим \(1+100 = 101\text{.}\) Следующая пара для объединения: \(2+99 = 101\text{.}\) Затем \(3+ 98 = 101\text{.}\) Продолжайте. Это дает 50 пар, каждая из которых в сумме дает \(101\text{,}\), поэтому \(T_{100} = 101\cdot 50 = 5050\text{.}\) ¹ Это озарение обычно приписывают Карлу Фридриху Гауссу, одному из величайших математиков всех времен, который открыл его еще ребенком, когда его неприятный учитель начальных классов решил, что он займет класс, заставив их вычислить длинную сумму.

В общем случае, используя такую ​​же перегруппировку, мы находим, что \(T_n = \frac{n(n+1)}{2}\text{. }\) Между прочим, это в точности то же самое, что и \({n +1 \выберите 2}\text{,}\), что имеет смысл, если вы думаете о треугольных числах как о подсчете количества рукопожатий на вечеринке с \(n+1\) людьми: первый человек пожимает \ (n\) рук, следующий пожимает еще \(n-1\) рук и так далее.

Суть всего этого в том, что некоторые последовательности, хотя и не являются арифметическими или геометрическими, могут быть интерпретированы как последовательности частичных сумм арифметических и геометрических последовательностей. К счастью, есть методы, которые мы можем использовать для быстрого вычисления этих сумм.

Подподраздел Суммирование арифметических последовательностей: реверс и сложение

¶

Вот метод, который позволяет нам быстро найти сумму арифметической последовательности.

Пример 2.2.4

Найдите сумму: \(2 + 5 + 8 + 11 + 14 + \cdots + 470\text{.}\)

Решение

Идея состоит в том, чтобы подражать тому, как мы нашли формулу для треугольных чисел. Если мы сложим первый и последний члены, мы получим 472. Второй член и предпоследний член также в сумме дают 472. Чтобы отслеживать все, мы могли бы выразить это следующим образом. Вызовите сумму \(S\text{.}\) Затем

\(S =\)	\(2\)	\(+\)	\(5\)	\(+\)	\(8\)	\(+ \cdots +\)	\(467\)	\(+\)	470
\(+ \quad S =\)	\(470\)	\(+\)	\(467\)	\(+\)	\(464\)	\(+ \cdots +\)	\(5\)	\(+\)	2
\(2S =\)	\(472\)	\(+\)	\(472\)	\(+\)	\(472\)	\(+ \cdots +\)	\(472\)	\(+\)	\(472\)

Чтобы найти \(2S\), мы прибавляем 472 к самому себе несколько раз. Какой номер? Нам нужно решить, сколько слагаемых ( слагаемых ) в сумме. Поскольку термины образуют арифметическую последовательность, \(n\)-й член в сумме (считая \(2\) как 0-й член) может быть выражен как \(2 + 3n\text{.}\) Если \( 2 + 3n = 470\), тогда \(n = 156\text{.}\) Таким образом, \(n\) находится в диапазоне от 0 до 156, что дает в сумме 157 членов. Это число 472 в сумме для \(2S\text{.}\) Таким образом,

\begin{уравнение*} 2S = 157\cdot 472 = 74104 \end{уравнение*}

Теперь легко найти \(S\text{:}\)

\begin{уравнение*} S = 74104/2 = 37052 \end{уравнение*}

Это будет работать для любой суммы арифметических последовательностей. Вызовите сумму \(S\text{.}\) в обратном порядке и добавьте. Это дает одно число, добавленное к самому себе много раз. Найдите количество раз. Умножить. Разделить на 2. Готово.

Пример 2.2.5

Найдите замкнутую формулу для \(6 + 10 + 14 + \cdots + (4n — 2)\text{.}\)

Решение

Опять у нас есть сумма арифметической прогрессии. Нам нужно знать, сколько членов в последовательности. Ясно, что каждый член последовательности имеет вид \(4k — 2\) (о чем свидетельствует последний член). Но для каких значений \(k\)? Чтобы получить 6, \(k = 2\text{.}\) Чтобы получить \(4n-2\), возьмите \(k = n\text{.}\) Итак, чтобы найти количество терминов, нам нужно знать сколько целых чисел находится в диапазоне \(2,3,\ldots, n\text{.}\) Ответ: \(n-1\text{.}\) (есть \(n\) чисел от 1 в \(n\text{,}\), так что на единицу меньше, если мы начнем с 2.)

Теперь переверните и добавьте:

\(S =\)	\(6\)	\(+\)	\(10\)	\(+ \cdots +\)	\(4н-6\)	\(+\)	\(4н-2\)
\(+ \quad S =\)	\(4н-2\)	\(+\)	\(4н-6\)	\(+ \cdots +\)	\(10\)	\(+\)	6
\(2S =\)	\(4n+4\)	\(+\)	\(4n+4\)	\(+ \cdots +\)	\(4n+4\)	\(+\)	\(4n+4\)

Так как членов \(n-2\), мы получаем

\begin{уравнение*} 2S = (n-2)(4n+4)\qquad \mbox{ так} \qquad S = \frac{(n-2)(4n+4)}{2} \end{уравнение*}

Помимо нахождения сумм, мы можем использовать эту технику для нахождения закрытых формул для последовательностей, которые мы распознаем как последовательности частичных сумм.

Пример 2.2.6

Используйте частичные суммы, чтобы найти замкнутую формулу для \((a_n)_{n\ge 0}\), которая начинается с \(2, 3, 7, 14, 24, 37,\ldots \ldots\)

Решение

Во-первых, если вы посмотрите на различия между терминами, вы получите последовательность различий: \(1,4,7,10,13, \ldots\text{,}\), которая является арифметической последовательностью. Написано по-другому:

\начать{выравнивать*} а_0 \ампер = 2\\ a_1 \амп = 2+1\\ a_2 \amp = 2+1+4\\ а_3 \амп = 2+1+4+7 \конец{выравнивание*}

и так далее. Мы можем записать общий член \((a_n)\) в терминах арифметической последовательности следующим образом:

\begin{уравнение*} a_n = 2 + 1 + 4 + 7 + 10 + \cdots + (1 + 3 (n-1)) \end{уравнение*}

(мы используем \(1+3(n-1)\) вместо \(1+3n\), чтобы правильно выровнять индексы; для \(a_3\) мы добавляем 7, что равно \ (1+3(3-1)\)).

Мы можем перевернуть и сложить, но начальная 2 не соответствует нашему шаблону. Это просто означает, что нам нужно убрать 2 из обратной части:

\(a_n =\)	\(2\)	\(+\)	\(1\)	\(+\)	\(4\)	\(+ \cdots +\)	\(1+3(n-1)\)
\(+ ~ a_n =\)	\(2\)	\(+\)	\(1+3(n-1)\)	\(+\)	\(1+3(n-2)\)	\(+ \cdots +\)	\(1\)
\(2a_n =\)	\(4\)	\(+\)	\(2+3(n-1)\)	\(+\)	\(2+3(n-1)\)	\(+ \cdots +\)	\(2+3(n-1)\)

Не считая первого члена (4), есть \(n\) слагаемых \(2+3(n-1) = 3n-1\), поэтому правая часть становится \(2+( 3n-1)n\text{.}\)

Наконец, найдя \(a_n\), мы получим

\begin{уравнение*} a_n = \d \frac{4+(3n-1)n}{2}. \end{уравнение*}

На всякий случай проверяем \(a_0 = \frac{4}{2} = 2\text{,}\) \(a_1 = \frac{4+2}{2} = 3\text{, }\) и т. д. Имеем правильную замкнутую формулу.

Подподраздел Суммирование геометрических последовательностей: умножение, сдвиг и вычитание

¶

Чтобы найти сумму геометрической последовательности, мы не можем просто поменять местами и сложить. Вы понимаете, почему? Причина, по которой один и тот же термин добавлялся сам к себе много раз, заключается в том, что существовала постоянная разница. Таким образом, когда мы добавили эту разницу в одном направлении, мы вычли разницу в другом направлении, оставив постоянную сумму. Для геометрических сумм у нас есть другая техника.

Пример 2.2.7

Что такое \(3 + 6 + 12 + 24 + \cdots + 12288\text{?}\)

Решение

Умножьте каждый член на 2, обыкновенный коэффициент. Вы получаете \(2S = 6 + 12 + 24 + \cdots + 24576\text{.}\) Теперь вычтите: \(2S — S = -3 + 24576 = 24573\text{.}\) Так как \(2S — S = S\text{,}\) у нас есть ответ.

Чтобы лучше понять, что произошло в приведенном выше примере, попробуйте записать его так:

\(S=\)	\(3\, +\)	\(6 + 12 + 24 + \cdots + 12288\)
\(-~2S=\)		\(6 + 12 + 24 + \cdots + 12288\)	\(+ 24576\)
\(-S = \)	\(3\, +\)	\(0 + 0 + 0 + \cdots + 0 \)	\(-24576\)

Затем разделите обе части на \(-1\), и мы получим тот же результат для \(S\text{.}\) Идея состоит в том, что при умножении суммы на обыкновенное отношение каждый член становится следующим термином. Мы сдвигаем сумму, чтобы вычитание в основном сокращалось, оставляя только первый член и новый последний член. 9{n+1}}{-4}\)

Хотя это может показаться новой техникой, вы, вероятно, использовали ее раньше.

Пример 2.2.9

Выразите \(0,464646\ldotts\) в виде дроби.

Решение

Пусть \(N = 0,46464646\ldots\text{. }\) Рассмотрим \(0,01N\text{.}\) Получим:

	\(Н=\)	\(0,4646464\ldotts\)
\(-\)	\(0,01Н =\)	\(0,00464646\ldotts\)
	\(0,99Н =\)	\(0,46\)

Итак, \(N = \frac{46}{99}\text{.}\) Что мы сделали? Мы рассматривали повторяющуюся десятичную дробь \(0,464646\ldots\) как сумму геометрической последовательности \(0,46, 0,0046, 0,000046, \ldots\). Обычное отношение равно \(0,01\text{.}\). Единственная реальная разница что мы сейчас вычисляем бесконечную геометрическую сумму , у нас нет дополнительного «последнего» члена для рассмотрения. На самом деле, это результат ограничения, как если бы вы вычисляли 9 в математических вычислениях.n k = n!\text{.}\)

ПодразделУпражнения

¶

1

Рассмотрим последовательность \(5, 9, 13, 17, 21, \ldots\) с \(a_1 = 5\)

1. Дайте рекурсивное определение последовательности.

2. Приведите замкнутую формулу для \(n\)-го члена последовательности.

3. Является ли \(2013\) членом последовательности? Объяснять.

4. Сколько членов содержит последовательность \(5, 9, 13, 17, 21, \ldots, 533\)?

9{th}\) член \(1, 6, 15, 28, 45, \ldots\text{,}\), где \(b_0 = 1\)

Решение

1. \(a_n = a_{n-1} + 4\) с \(a_1 = 5\text{.}\)
2. \(a_n = 5 + 4(n-1)\text{.}\)

3. Да, поскольку \(2013 = 5 + 4(503-1)\) (так что \(a_{503} = 2013\)).

4. 133

5. \(\frac{538\cdot 133}{2} = 35777\text{.}\)
6. \(b_n = 1 + \frac{(4n+6)n}{2}\text{.}\)

2

Рассмотрим последовательность \((a_n)_{n \ge 0}\), которая начинается с \(8, 14, 20, 26, \ldots\text{.}\) 9{99}a_k\text{.}\)

Решение

1. \(32\text{,}\), что равно \(26+6\text{. }\)

2. \(a_n = 8 + 6n\text{.}\)
3. \(30500\text{.}\) Мы хотим \(8 + 14 + \cdots + 602\text{.}\) Перевернуть и сложить, чтобы получить 100 сумм 610, всего 61000, что в два раза больше суммы мы ищем.

3

Рассмотрим сумму \(4 + 11 + 18 + 25 + \cdots + 249\text{.}\)

1. Сколько членов (слагаемых) в сумме?

2. Подсчитать сумму. Не забудьте показать все свои работы.

Раствор

1. 36.

2. \(\frac{253 \cdot 36}{2} = 4554\text{.}\)

4

Рассмотрим последовательность \(1, 7, 13, 19, \ldots, 6n + 7\text{.}\)

1. Сколько элементов в последовательности?

2. Какой предпоследний член?

3. Найдите сумму всех членов последовательности.

Решение

1. \(n+2\) членов, так как для получения 1 по формуле \(6n+7\) мы должны использовать \(n=-1\text{. }\) Таким образом, мы имеем \( n\) слагаемых плюс слагаемые \(n=0\) и \(n=-1\).
2. \(6n+1\text{,}\), что на 6 меньше, чем \(6n+7\) (или подставьте \(n-1\) вместо \(n\)).
3. \(\frac{(6n+8)(n+2)}{2}\text{.}\) Перевернуть и добавить. Каждая сумма дает константу \(6n+8\) и есть \(n+2\) терминов.

5

Найти \(5 + 7 + 9 + 11+ \cdots + 521\text{.}\) 9{30}}\text{.}\)

8

Найдите \(x\) и \(y\) такие, что \(27, x, y, 1\) является частью арифметической прогрессии. Затем найдите \(x\) и \(y\) так, чтобы последовательность была частью геометрической прогрессии. (Предупреждение: \(x\) и \(y\) могут быть не целыми числами.)

9

Начав с любого прямоугольника, мы можем создать новый, больший прямоугольник, присоединив квадрат к более длинной стороне. Например, если мы начнем с прямоугольника \(2\x 5\), мы склеим квадрат \(5\x 5\), сформировав прямоугольник \(5 \x 7\):

1. Создайте последовательность прямоугольников, используя это правило, начиная с прямоугольника \(1\times 2\). Затем выпишите последовательность периметров для прямоугольников (первый член последовательности будет равен 6, так как периметр прямоугольника \(1\times 2\) равен 6 — следующий член будет равен 10).

2. На этот раз повторите описанную выше часть, начиная с прямоугольника \(1 \times 3\).

3. Найдите рекурсивные формулы для каждой из последовательностей периметров, которые вы нашли в частях (a) и (b). Не забудьте также указать начальные условия.

4. Являются ли последовательности арифметическими? Геометрический? Если нет, то являются ли они близкими к любому из этих (т. е. являются ли разности или отношения почти постоянными)? Объяснять.

10

Рассмотрим последовательность \(2, 7, 15, 26, 40, 57, \ldots\) (где \(a_0 = 2\)). Глядя на различия между членами, представить последовательность как последовательность частичных сумм. Затем найдите замкнутую формулу последовательности, вычислив \(n\)-ю частичную сумму.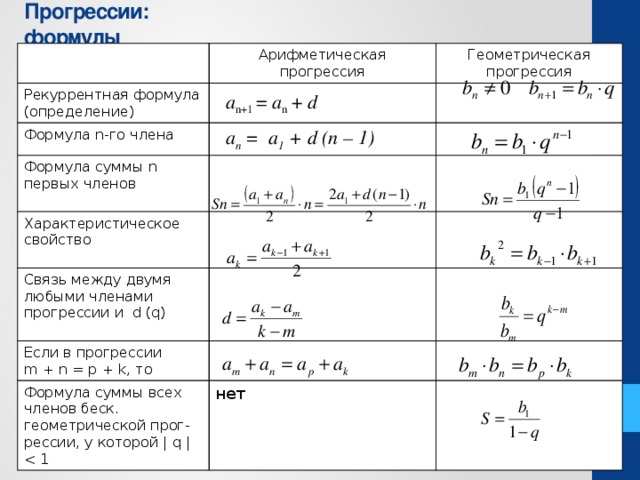 9n (2+3k)\text{.}\) Чтобы найти замкнутую формулу, мы обращаем и складываем. Получаем \(a_n = \frac{(4+3n)(n+1)}{2}\) (там у нас \(n+1\), потому что в сумме есть \(n+1\) членов для\)).

11

Если у вас достаточно зубочисток, вы можете сделать большую треугольную сетку. Ниже представлены треугольные сетки размера 1 и размера 2. Для сетки размера 1 требуется 3 зубочистки, для сетки размера 2 требуется 9 зубочисток.

1. Пусть \(t_n\) будет количеством зубочисток, необходимых для создания треугольной сетки размером \(n\). Выпишите первые 5 членов последовательности \(t_1, t_2, \ldots\text{.}\)

2. Найдите рекурсивное определение последовательности. Объясните, почему вы правы.

3. Является ли последовательность арифметической или геометрической? Если нет, то это последовательность частичных сумм арифметической или геометрической прогрессии? Объясните, почему ваш ответ правильный.

4. Используйте результаты из части (c), чтобы найти замкнутую формулу для последовательности.

   No related posts.