Произведение скалярных векторов: Скалярное произведение векторов — урок. Геометрия, 9 класс.

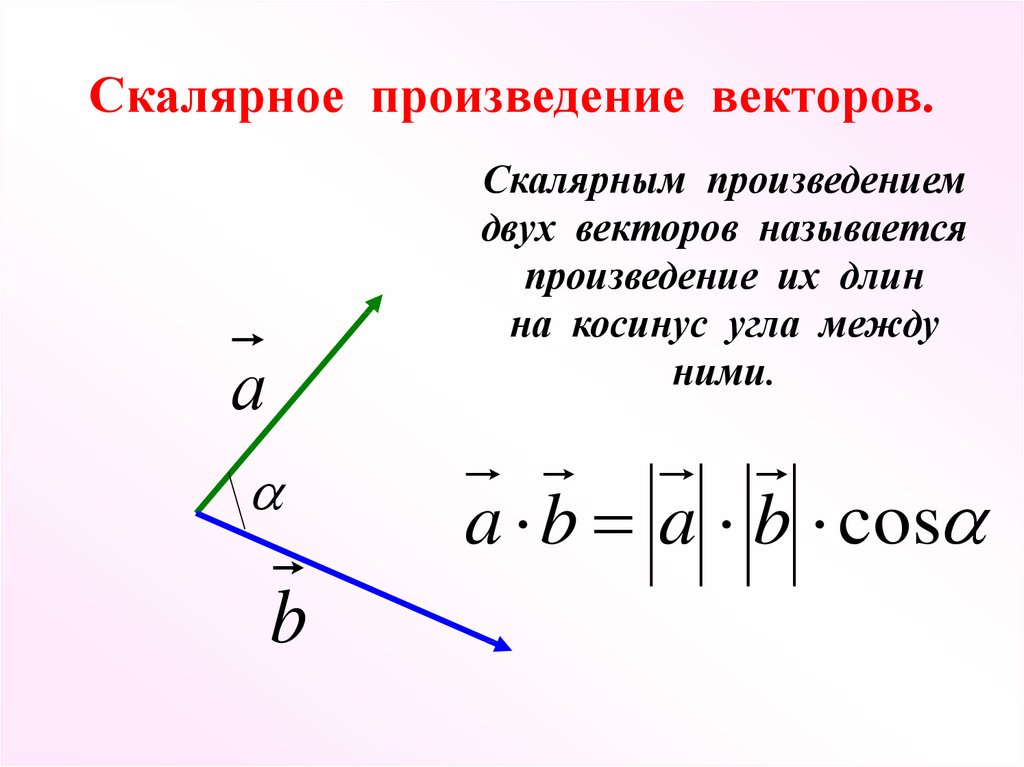
Скалярное произведение векторов

Навигация по странице:

• Геометрическая интерпретация скалярного произведения векторов
• Алгебраическая интерпретация скалярного произведения векторов
• Формулы скалярного произведения векторов заданных координатами
  • для плоских задач
  • для пространственных задач
  • для n -мерных векторов
• Свойства скалярного произведения векторов
• Примеры задач на скалярное произведение векторов
  • плоские задачи
  • пространственные задачи
  • задачи в n -мерном пространстве

Онлайн калькулятор. Скалярное произведение векторов.

Онлайн упражнения на тему скалярное произведение двух векторов на плоскости.

Онлайн упражнения на тему скалярное произведение двух векторов в пространстве.

Геометрическая интерпретация.

Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов умноженного на косинус угла между ними:

a · b = |a| · |b| cos α

Алгебраическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная сумме попарного произведения координат векторов a и b.

Формулы скалярного произведения векторов заданных координатами

Формула скалярного произведения векторов для плоских задач

В случае плоской задачи скалярное произведение векторов a = {a_x ; a_y} и b = {b_x ; b_y} можно найти воспользовавшись следующей формулой:

a · b = a_x · b_x + a_y · b_y

Формула скалярного произведения векторов для пространственных задач

В случае пространственной задачи скалярное произведение векторов a = {a_x ; a_y ; a_z} и b = {b_x ; b_y ; b_z} можно найти воспользовавшись следующей формулой:

a · b = a_x · b_x + a_y · b_y + a_z · b_z

Формула скалярного произведения n -мерных векторов

В случае n-мерного пространства скалярное произведение векторов a = {a₁ ; a₂ ; . .. ; a_n} и b = {b₁ ; b₂ ; … ; b_n} можно найти воспользовавшись следующей формулой:

a · b = a₁ · b₁ + a₂ · b₂ + … + a_n · b_n

Свойства скалярного произведения векторов

1. Скалярное произведение вектора самого на себя всегда больше или равно нуля:

   a · a ≥ 0

2. Скалярное произведение вектора самого на себя равно нулю тогда и только тогда, когда вектор равен нулевому вектору:

   a · a = 0   <=>   a = 0

3. Скалярное произведение вектора самого на себя равно квадрату его модуля:

   a · a = |a|²

4. Операция скалярного умножения коммуникативна:

   a · b = b · a

5. Если скалярное произведение двух не нулевых векторов равно нулю, то эти вектора ортогональны:

   a ≠ 0, b ≠ 0, a · b = 0   <=>   a ┴ b

6. (αa) · b = α(a · b)

7. Операция скалярного умножения дистрибутивна:

   (a + b) · c = a · c + b · c

Примеры задач на вычисление скалярного произведения векторов

Примеры вычисления скалярного произведения векторов для плоских задач

Пример 1. Найти скалярное произведение векторов a = {1; 2} и b = {4; 8}.

Решение: a · b = 1 · 4 + 2 · 8 = 4 + 16 = 20.

Пример 2. Найти скалярное произведение векторов a и b, если их длины |a| = 3, |b| = 6, а угол между векторами равен 60˚.

Решение: a · b = |a| · |b| cos α = 3 · 6 · cos 60˚ = 9.

Пример 3. Найти скалярное произведение векторов p = a + 3b и q = 5a — 3 b, если их длины |a| = 3, |b| = 2, а угол между векторами a и b равен 60˚.

Решение:

p · q = (a + 3b) · (5a — 3b) = 5 a · a — 3 a · b + 15 b · a — 9 b · b =

= 5 |a|² + 12 a · b — 9 |b|² = 5 · 3² + 12 · 3 · 2 · cos 60˚ — 9 · 2² = 45 +36 -36 = 45.

Пример 4. Найти скалярное произведение векторов (a + 2i)·(b — 2j),если a = {1; 2} и b = {4; -8}.

Решение: Запишем вектора a и b через ортонормированные базисные вектора i и j:

a = i + 2j
b = 4i — 8j

Тогда используя свойства ортов (i² = 1, j² = 1, i·j = 0)

(a + 2i)·(b — 2j) = (i + 2j + 2i)·(4i — 8j — 2j) = (3i + 2j)·(4i — 10j) = 12i² — 30i·j + 12j·i — 20j² = 12 — 0 + 0 — 20 = -8

Пример вычисления скалярного произведения векторов для пространственных задач

Пример 5. Найти скалярное произведение векторов a = {1; 2; -5} и b = {4; 8; 1}.

Решение: a · b = 1 · 4 + 2 · 8 + (-5) · 1 = 4 + 16 — 5 = 15.

Пример вычисления скалярного произведения для n -мерных векторов

Пример 6. Найти скалярное произведение векторов a = {1; 2; -5; 2} и b = {4; 8; 1; -2}.

Решение: a · b = 1 · 4 + 2 · 8 + (-5) · 1 + 2 · (-2) = 4 + 16 — 5 -4 = 11.

Вектора Вектор: определение и основные понятия Определение координат вектора заданного координатами его начальной и конечной точки Модуль вектора. Длина вектора Направляющие косинусы вектора Равенство векторов Ортогональность векторов Коллинеарность векторов Компланарность векторов Угол между векторами Проекция вектора Сложение и вычитание векторов Умножение вектора на число Скалярное произведение векторов Векторное произведение векторов Смешанное произведение векторов Линейно зависимые и линейно независимые вектора Разложение вектора по базису

Онлайн калькуляторы с векторами

Онлайн упражнения с векторами на плоскости

Онлайн упражнения с векторами в пространстве

Скалярное произведение векторов, формулы и онлайн калькуляторы

Содержание:

• Свойства скалярного произведения:
• Длина вектора
• Угол между векторами

Определение

Скалярным произведением двух ненулевых векторов $\overline{a}$ и $\overline{b}$ называется число, равное произведению длин этих векторов на косинус угла между ними:

$$\bar{a} \bar{b}=\bar{a} \cdot \bar{b}=(\bar{a}, \bar{b})=|\bar{a}||\bar{b}| \cos (\bar{a}, \bar{b})$$

Пример

Задание. {2}$ и называется скалярный квадрат.

3  Если $\overline{a} \neq \overline{0}$, то

4  Если $\overline{a} \neq \overline{0}$ и $\overline{b} \neq \overline{0}$ и $(\overline{a}, \overline{b})=0$, то $\overline{a} \perp \overline{b}$. Верно и обратное утверждение.

5  $(\overline{a}+\overline{b}, \overline{c})=(\overline{a}, \overline{c})+(\overline{b}, \overline{c})$

6  $(\lambda \overline{a}, \overline{b})=\lambda(\overline{a}, \overline{b})$

7  $(\alpha \overline{a}+\beta \overline{b}, \gamma \overline{c}+\delta \overline{d})=\alpha \gamma(\overline{a}, \overline{c})+\alpha \delta(\overline{a}, \overline{d})+\beta \gamma(\overline{b}, \overline{c})+\beta \delta(\overline{b}, \overline{d})$

Если векторы $\overline{a}$ и $\overline{b}$ заданы своими координатами: $\overline{a}=\left(a_{1} ; a_{2} ; a_{3}\right)$, $\overline{b}=\left(b_{1} ; b_{2} ; b_{3}\right)$ , то их скалярное произведение вычисляется по формуле:

1

$(\overline{a}, \overline{b})=a_{1} b_{1}+a_{2} b_{2}+a_{3} b_{3}$

Определение

Скалярное произведение векторов, заданных своими координатами, равно сумме произведений соответствующих координат.

{\circ}$$

Читать дальше: векторное произведение векторов.

Скалярное произведение векторов

Скалярное произведение векторов

Скалярное произведение и векторное произведение — два способа умножения векторов, наиболее часто применяемые в физике и астрономии. Скалярное произведение двух векторов можно построить, взяв компонент одного вектора в направлении другого и умножив его на величину другого вектора. Это можно выразить в виде: Если векторы выражены через единичные векторы i, j и k вдоль направлений x, y и z, скалярное произведение также может быть выражено в виде: Скалярное произведение также называется «внутренним произведением» или «точечным произведением» в некоторых текстах по математике. Матричный подход к скалярному произведению

Индекс Векторные понятия

Гиперфизика***** Механика R Ступица

Назад

Вы можете ввести значения в любое из полей ниже. Затем щелкните символ скалярного произведения или угла. Векторы A и B не могут быть однозначно вычислены из скалярного произведения и угла. Если угол изменить, то B будет размещен вдоль оси x, а A — в плоскости xy. Активная формула: щелкните скалярное произведение или угол, чтобы обновить расчет. Примечание. Приведенные выше числа не будут принудительно согласованы до тех пор, пока вы не щелкнете либо по скалярному произведению, либо по углу в активной формуле выше.

Индекс Векторные концепции

Гиперфизика***** Механика R Ступица

Назад

С геометрической точки зрения скалярное произведение полезно для нахождения направления между произвольными векторами в пространстве. Поскольку два выражения для произведения: включают компоненты двух векторов, и поскольку величины A и B могут быть рассчитаны из компонентов, используя: , то можно вычислить косинус угла и определить угол. Одним из важных физических применений скалярного произведения является вычисление работы: Скалярное произведение используется для выражения магнитной потенциальной энергии и потенциала электрического диполя.

Индекс Векторные концепции

Гиперфизика***** Механика R Ступица

Назад

Иногда удобно представлять векторы в виде матриц-строк или столбцов, а не в виде единичных векторов, как это было сделано выше при рассмотрении скалярного произведения. Если рассматривать обычные пространственные векторы как матрицы-столбцы их компонентов x, y и z, то транспонирование этих векторов будет матрицей-строкой. Тогда мы могли бы написать для векторов A и B: Тогда матричное произведение этих двух матриц даст только одно число, являющееся суммой произведений соответствующих пространственных компонентов двух векторов. Затем это число является скалярным произведением двух векторов. Представленное таким образом скалярное произведение двух векторов иллюстрирует процесс, который используется при умножении матриц, где сумма произведений элементов строки и столбца дает одно число.

Индекс Векторные концепции

Гиперфизика***** Механика R Ступица

Назад

Что такое скалярное произведение?

К

• Роберт Шелдон

Что такое скалярное произведение?

Скалярное произведение, также называемое скалярным произведением, является мерой того, насколько близко два вектора совпадают с точки зрения направлений, которые они указывают. Мера представляет собой скалярное число (одно значение), которое можно использовать для сравнения двух векторов и понимания влияния изменения положения одного или обоих из них. Скалярный продукт получается путем выполнения математических расчетов векторных свойств.

Вектор — это величина, которая имеет как направление, так и величину (длину вектора). На рис. 1 показаны два вектора ( a и b ) на двумерной декартовой плоскости. Вектор a имеет величину 8 и расположен под углом 115 градусов к оси x (движется против часовой стрелки). Вектор b имеет звездную величину 10 и расположен под углом 45 градусов к оси x. Угол между двумя векторами, представленный греческой буквой тета (θ), составляет 70 градусов, что вычисляется путем вычитания 45 градусов из 115 градусов.

Рис. 1. Диаграмма, показывающая два вектора (a и b) на двумерной декартовой плоскости.

Если известна величина двух векторов и угол между ними, легко вычислить скалярное произведение.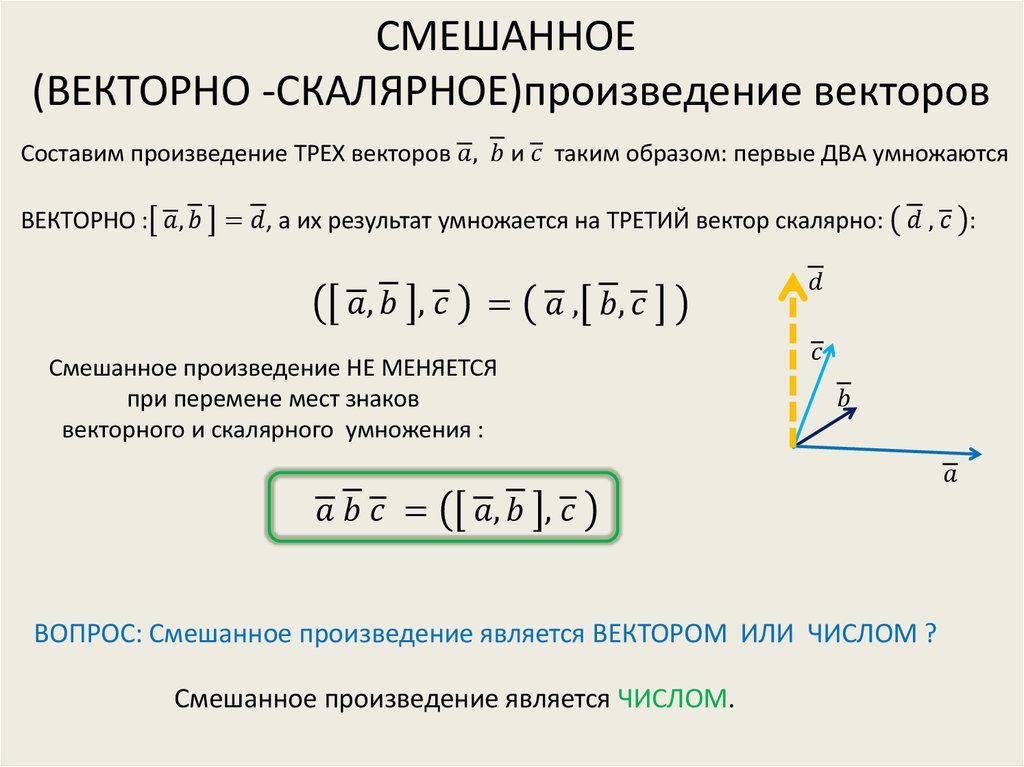 Скалярный продукт представлен точкой между двумя векторными ссылками, в данном случае a и b , как показано в следующей формуле:

а • б

Полное уравнение для нахождения скалярного произведения несколько сложнее. Это влечет за собой умножение величины вектора a на величину вектора b , а затем умножение произведения на косинус (cos) угла между векторами, как показано в следующем уравнении:0006

а • б = |а| × |б| × cos(θ)

Вертикальные полосы показывают, что эти значения являются модулями вектора. Иногда вместо одинарных стержней используются двойные стержни. Если значения с рисунка 1 подставить в уравнение, можно быстро вычислить скалярное произведение для этих двух векторов, как показано в следующем уравнении:

a • b = 8 × 10 × cos(70 градусов)
a • b = 8 × 10 × 0,342
a • b = 27,36

Косинус угла округлен до трех знаков после запятой, поэтому конечный результат (27,36) является лишь приблизительным, хотя и близким.

Если величина двух векторов и угол между ними неизвестны, используйте следующую формулу для вычисления скалярного произведения:

a • b = (a _x × b _x ) + (a _y × b _y )

Рис. 2. Схема добавления длин векторов, отраженных на каждой оси, к рис. 1.

В этом случае умножьте длины векторов, поскольку они проецируются на оси x и оси y декартовой плоскости. Чтобы лучше понять, как это работает, рассмотрите рис. 2, который был обновлен по сравнению с рис. 1, чтобы включить длины векторов, отраженные на каждой оси.

Vector a измеряет -3,4 по оси x и 7,3 по оси y. (Эти числа были округлены до одного десятичного знака.) Вектор b измеряет 7,1 по оси x и 7,1 по оси y. Для этого вектора измерения одинаковы по каждой оси, потому что вектор находится под углом 45 градусов. Эти суммы можно подставить в следующую новую формулу:

.

a • b = (a _x × b _x ) + (a _y × b _y )
a • b = (-3,4 × 7,1) + (7,3 × 7,1)
а • b = -24,12 + 51,83
а • b = 27,71

Поскольку числа были округлены, окончательная цифра немного отличается от предыдущей (27,36), но они достаточно близки, чтобы продемонстрировать, как можно использовать два разных метода для вычисления скалярного произведения для пары векторов.

Аналогичный подход можно использовать для вычисления скалярного произведения векторов в трехмерном пространстве. Для этого измените формулу следующим образом, чтобы включить третье измерение (представленное осью Z):

a • b = (a _x x b _x ) + (a _y x b _y ) + (a _z x b _z )

Формула теперь включает в свои расчеты ось Z, но исходные компоненты остаются прежними. Чтобы проверить обновленную формулу, предположим, что оба вектора измеряют 5 по оси Z. Расчеты теперь будут выглядеть следующим образом:

a • b = -(3,4 × 7,1) + (7,3 × 7,1) + (5 x 5)
a • b = -24,12 + 51,83 + 25
a • b = 52,71

Неудивительно, что скалярное произведение равно 52,71, что на 25 больше, чем 27,71 в предыдущем вычислении. Число 25 является результатом добавления компонента a _z × b _z (5 x 5) к уравнению для включения трехмерного пространства.

Скалярное произведение используется в таких областях, как физика, математика и другие области, способами, которые имеют практическое применение в реальном мире. Например, скалярное произведение можно использовать при установке солнечной панели на крыше. Сравнивая угол наклона солнца с углом панели, инженеры могут рассчитать наилучшее положение панели, чтобы максимизировать количество солнечной энергии, поглощаемой в течение дня.

См. также: Математические символы

Последнее обновление: октябрь 2022 г.

Продолжить чтение О точечном произведении (скалярном произведении)

• 11 навыков работы с данными для машинного обучения и искусственного интеллекта

• 18 инструментов обработки данных, которые следует рассмотреть в 2022 году

• 8 лучших приложений для обработки данных и вариантов использования для бизнеса

• Наука о данных, машинное обучение и искусственный интеллект: как они работают вместе

экологичные вычисления

«Зеленые» вычисления, также известные как «зеленые технологии», представляют собой использование компьютеров и других вычислительных устройств и оборудования энергосберегающими и экологически безопасными способами.

Сеть

• оптоволокно до дома (FTTH)

  Оптоволокно до дома (FTTH), также называемое оптоволокном до дома (FTTP), представляет собой установку и использование оптического волокна от центрального …

• Манчестерское кодирование

  При передаче данных манчестерское кодирование — это форма цифрового кодирования, в которой состояние бита данных — 0 или 1 — представляется …

• нслукап

  Nslookup — это название программы, которая позволяет пользователям вводить имя хоста и узнавать соответствующий IP-адрес или доменное имя…

Безопасность

• WPA3

  WPA3, также известный как Wi-Fi Protected Access 3, является третьей итерацией стандарта сертификации безопасности, разработанного Wi-Fi …

• брандмауэр

  Брандмауэр — это устройство сетевой безопасности, которое предотвращает несанкционированный доступ к сети. Проверяет входящий и исходящий трафик…

• защита облачных рабочих нагрузок

  Защита рабочих нагрузок в облаке — это защита рабочих нагрузок, распределенных по нескольким облачным средам. Предприятия, использующие …

ИТ-директор

• Agile-манифест

  Манифест Agile — это документ, определяющий четыре ключевые ценности и 12 принципов, в которые его авторы верят разработчикам ПО…

• Общее управление качеством (TQM)

  Total Quality Management (TQM) — это система управления, основанная на вере в то, что организация может добиться долгосрочного успеха, …

• системное мышление

  Системное мышление — это целостный подход к анализу, который фокусируется на том, как взаимодействуют составные части системы и как…

HRSoftware

• непрерывное управление производительностью

  Непрерывное управление эффективностью в контексте управления человеческими ресурсами (HR) — это надзор за работой сотрудника . ..

• вовлечения сотрудников

  Вовлеченность сотрудников — это эмоциональная и профессиональная связь, которую сотрудник испытывает к своей организации, коллегам и работе.

• кадровый резерв

  Кадровый резерв — это база данных кандидатов на работу, которые могут удовлетворить немедленные и долгосрочные потребности организации.

Отдел обслуживания клиентов

• бесконтактная оплата

  Бесконтактный платеж — это беспроводная финансовая транзакция, при которой покупатель совершает покупку, перемещая жетон безопасности в …

• исходящий вызов

  Исходящий вызов — это вызов, инициированный оператором центра обработки вызовов клиенту от имени центра обработки вызовов или клиента.

• социальная CRM

  Social CRM, или социальное управление взаимоотношениями с клиентами, — это управление взаимоотношениями с клиентами и взаимодействие с ними, поддерживаемое .

  No related posts.